Critical soil moisture thresholds of plant water stress in terrestrial ecosystems

Abstract

Plant water stress occurs at the point when soil moisture (SM) limits transpiration, defining a critical SM threshold (θ_crit). Knowledge of the spatial distribution of θ_crit is crucial for future projections of climate and water resources. Here, we use global eddy covariance observations to quantify θ_crit and evaporative fraction (EF) regimes. Three canonical variables describe how EF is controlled by SM: the maximum EF (EF_max), θ_crit, and slope (S) between EF and SM. We find systematic differences of these three variables across biomes. Variation in θ_crit, S, and EF_max is mostly explained by soil texture, vapor pressure deficit, and precipitation, respectively, as well as vegetation structure. Dryland ecosystems tend to operate at low θ_crit and show adaptation to water deficits. The negative relationship between θ_crit and S indicates that dryland ecosystems minimize θ_crit through mechanisms of sustained SM extraction and transport by xylem. Our results further suggest an optimal adaptation of local EF-SM response that maximizes growing-season evapotranspiration and photosynthesis.

The critical soil moisture thresholds of plant water stress depend on soil texture and vegetation structure.

INTRODUCTION

The critical soil moisture (SM) threshold (θ_crit) of plant water stress occurs near the point when evapotranspiration becomes SM-limited (1). Below this threshold, a marginal reduction of SM leads to reduced evapotranspiration and increased sensible heat flux (2). Crossing this threshold results into decreased evaporative fraction (EF), the ratio of latent heat to the sum of latent and sensible heat fluxes, making the air above the canopy warmer and drier, which, in turn, further reduces transpiration and plant carbon dioxide uptake (3–5). The existence of critical SM thresholds plays a crucial role in the surface energy partitioning (6–8). SM-controlled energy partitioning determines local climate and land-atmosphere coupling and can amplify warming in transition regions (9, 10). A better knowledge of critical SM thresholds is also important to assess crop yield risks and ecosystem vulnerability from drought exposure (7).

The land surface hydrology community has historically observed that the θ_crit level at which water limitation of evapotranspiration begins is above the SM wilting point of extreme stress (7). However, it is not clear whether plant photosynthetic processes become water-stressed at the same θ_crit as evapotranspiration. For evapotranspiration, the θ_crit can be quantified by evaluating the EF-SM relationship (2, 5, 8, 11, 12). For photosynthesis, the onset of water stress at ecosystem level was found to correspond to the SM critical value at which the sign of the covariance between daily gross primary production (GPP) and vapor pressure deficit (VPD) switches from a positive to negative sign when SM decreases during a soil drying period (13). GPP and evapotranspiration are tightly coupled on short time scales (4), and VPD combines the effects of both water stress and energy demand (via temperature) on GPP (14–16). Comparing θ_crit values diagnosed from the covariance of GPP and VPD (the “VPD-GPP-SM method”) with those calculated from EF-SM relationships (the “EF-SM method”) can help us understand whether evapotranspiration and photosynthetic processes become water-limited under similar SM conditions.

The relationship between EF and SM shows two regimes: energy-limited and water-limited evapotranspiration (2, 5, 11, 12). When SM is higher than θ_crit, the system is energy-limited, as less SM does not necessarily lead to lower evapotranspiration (17, 18). Evapotranspiration is at or near its potential value when net radiation is limiting, and EF stays near a maximum value (EF_max). In contrast, when SM is lower than θ_crit, the capacity of plants to extract soil water by roots and xylem transport becomes progressively reduced. Under this SM-limited regime, evapotranspiration decreases with decreasing SM until the wilting point, where transpiration is blocked because of full stomatal closure, with little or no further change in EF with SM decrease (8). In the SM-limited regime, EF decreases with decreasing SM, and this decrease is approximately linear (8, 12, 19). The SM regime can self-amplify itself because a lower evapotranspiration increases surface temperature and VPD and prevents the formation of boundary layer clouds (3, 20). These feedbacks further increase net radiation and atmospheric dryness at larger scales, which accelerates the depletion of SM, causing a positive “dry gets dryer” land-atmosphere climate feedback (4, 5, 21).

The relationship between EF and SM can thus be summarized by three parameters: a constant EF_max in the energy-limited regime, the θ_crit breaking point at which EF decreases with SM, and the linear slope (S) between EF and SM below this breaking point. This EF-SM framework is conceptually well established, but quantifying θ_crit to delineate the transition from energy to water-limited regimes across biomes and climate zones has been mainly limited to model-based studies due to a lack of observations (11, 18, 22, 23). At the global scale, so far, there is no observation-based assessment of θ_crit, S, and EF_max, although few studies reported some of them at sites or regional scales (13, 18, 22). Even less is known about the mechanisms that control the three parameters of the EF-SM relationship. Earth system models include parametric functional SM–evaporation relationships, with parameters set to ad hoc values and kept constant in space and time (24). Differences in parameter values and functional relationships across models is a key source of divergence and uncertainty in their water and carbon cycle projections (6, 18, 25). Dirmeyer et al. (25) reported that an ensemble of models had no consistent representation of the connection between EF and SM. Quantifying the parameters of θ_crit, S, and EF_max and their drivers across biomes and climates is therefore critical to identify the mechanisms of water stress tipping points and improve models to predict future climate accurately.

To quantify θ_crit directly, we used accurate and high-frequency measurements of EF from eddy covariance flux towers during extensive periods without rainfall, when a transition from energy to water limitation is likely to happen. These periods during when SM decreases are known as dry-downs (18, 26, 27). From a systematic analysis of multiple dry-downs, we derive the EF-SM relationship and θ_crit using daily latent and sensible heat flux observations from each site of the global network of flux tower measurements (see Materials and Methods). The objectives of this study are (i) to quantify the three parameters θ_crit, S, and EF_max of the EF-SM relationship across diverse plant functional groups and climate types; (ii) to examine the climatic, biotic, and edaphic predictors that control the spatial variability of θ_crit, S, and EF_max; and (iii) to investigate the consistency of θ_crit derived from the EF-SM and VPD-GPP-SM methods globally to determine whether evapotranspiration and photosynthetic processes become water-limited under similar SM conditions. On the basis of these results, we then evaluate possible relationships between the parameters and test whether the observed varying responses of EF-SM can be explained by an optimality principle.

RESULTS

Consistency of θ_crit derived from the EF-SM and VPD-GPP-SM methods

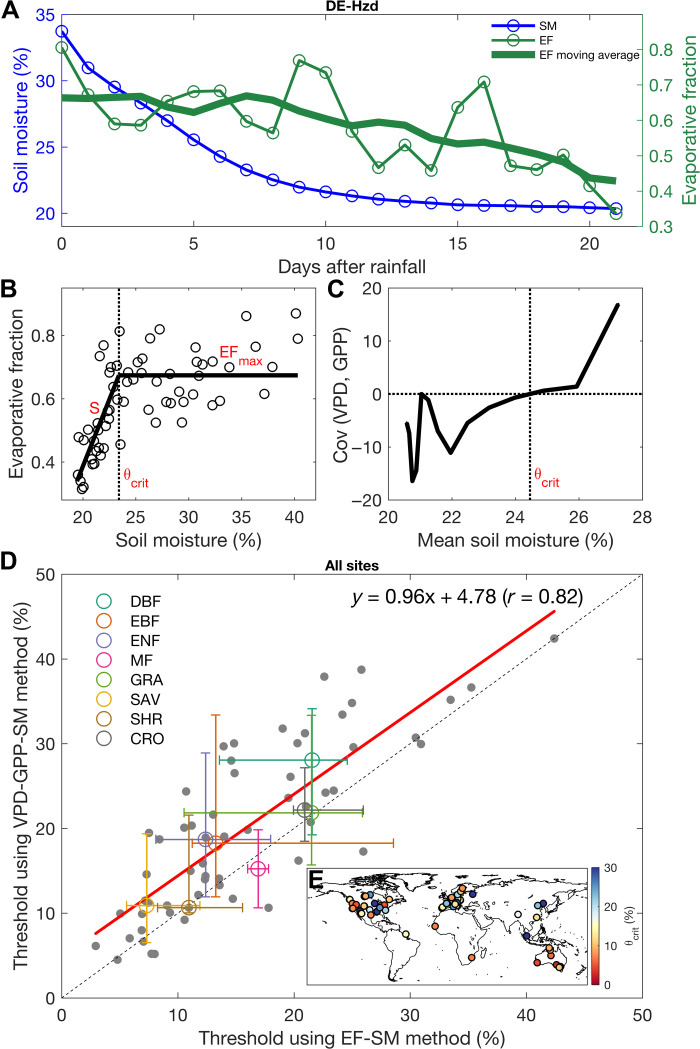
During a dry-down, EF remains relatively steady at first (energy-limited evapotranspiration stage) but then decreases when surface SM (volumetric soil water content; see Materials and Methods) becomes lower than a given threshold. Figure 1A shows this behavior at a forest site in Germany, DE-Hzd (table S1). The EF-SM relationship is characterized by the θ_crit transition point in SM, separating the water and energy-limited regimes. Using eight dry-downs recorded during two peak growing seasons, we find that surface θ_crit for EF is equal to 23.4 ± 0.5% at this site (Fig. 1B). From the change in sign of the covariance between daily VPD and GPP (Fig. 1C), we find that surface θ_crit for GPP has a value of 24.5%, which is very close to the EF-based estimate. Thus, θ_crit values estimated for EF and GPP at this site are very similar.

Fig. 1. Quantifying the critical SM threshold during SM dry-downs using the EF-SM method and the VPD-GPP-SM method.

SM and EF changes during a dry-down at a forest site, DE-Hzd (A). Estimating SM threshold from the EF-SM method (B) and the VPD-GPP-SM method (C) using all dry-downs at DE-Hzd. Comparison between the SM thresholds estimated from the VPD-GPP-SM method and the EF-SM method across all sites (D). Median and the 25th and 75th percentiles are shown for each biome. The dashed line is the 1:1 line. Covariance and mean SM were calculated using a 9-day moving window (e.g., 1 to 9 days, 2 to 10 days, and 3 to 11 days) following Fu et al. (13). The units of covariance between VPD and GPP are micromoles of CO₂ per square meter per second hectopascal. Map of the flux tower sites used in this analysis (E). Colors indicate the θ_crit values using EF-SM method. EBF, evergreen broadleaf forests; ENF, evergreen needleleaf forests; MF, mixed forests; GRA, grasslands; SAV, savannas; SHR, shrublands; CRO, croplands.

Next, we systematically compared the two θ_crit values estimated from EF and GPP. Across all sites, the two methods give consistent results [correlation coefficient (r) = 0.82; Fig. 1D], suggesting that EF and GPP both become water-limited under similar SM conditions. Thus, the EF-SM relationship during dry-downs is an effective method to quantify the SM threshold of plant water stress, despite the fact that EF is also affected by changes in bare soil evaporation, which is partly decoupled from the water stress on transpiration and GPP. A second point is that the VPD-GPP-SM method originally proposed for European ecosystems works globally, extending previous results from Fu et al. (13). Because the VPD-GPP-SM method requires longer dry-down periods to calculate the covariance between daily VPD and GPP, the EF-SM method was retained for this study involving a large numbers of sites on a global scale (Fig. 1E). We systematically calculated the three parameters that fully explain the EF-SM relationship at each site, as shown in Fig. 1B, namely, EF_max during the first part of the dry-downs in the absence of water stress, θ_crit for the inception of the EF decrease with SM, and the S of the linear relationship between EF and SM below θ_crit, when water stress intensifies.

θ_crit, S, and EF_max among biomes and climate zones

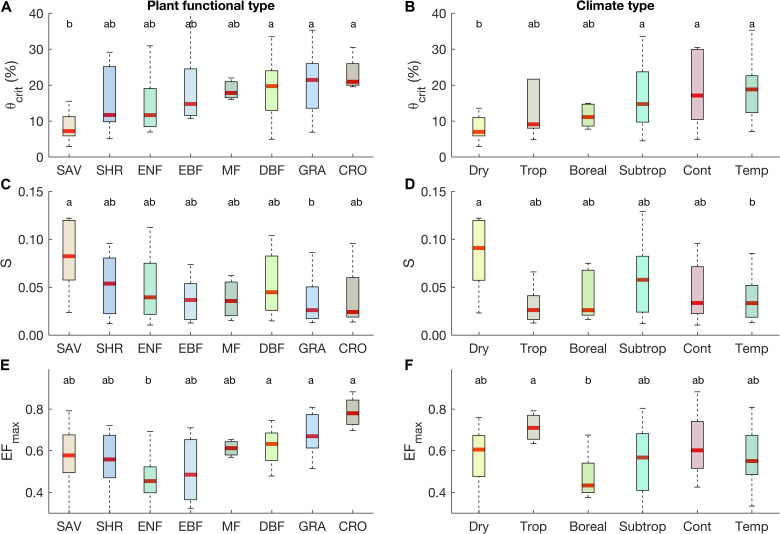
We find that the θ_crit diagnosed from recurrent dry-downs of surface SM is highly correlated with the θ_crit estimated from deeper SM (fig. S3). As surface SM measurements are available at all sites, we focus on surface SM. Across all sites globally, we find that the median θ_crit, S, and EF_max are 14.0 ± 0.9% (±SE), 0.045 ± 0.005, and 0.57 ± 0.02, respectively (fig. S4). These three canonical parameters have notably large spatial variations, suggesting differences in behavior across biomes and climate zones (Fig. 2). The value of θ_crit in savannas (7.2 ± 1.1%) is much lower than in deciduous broadleaf forests (DBFs; 19.7 ± 2.4%), grasslands (21.4 ± 2.4%), and croplands (20.9 ± 2.5%; Fig. 2A). Ecosystems in temperate (18.8 ± 1.3%), continental (17.1 ± 3.3%), and subtropical climates (14.7 ± 1.7%) have higher θ_crit values than in dry climates (7.0 ± 1.1%; Fig. 2B). The S value in savannas (0.082 ± 0.019) is three times higher than in grasslands (0.026 ± 0.009; Fig. 2C). Sites in temperate climates (0.033 ± 0.005) have lower S values than dry climates (0.090 ± 0.025; Fig. 2D). Regarding EF_max, the high values are mainly in croplands (0.78 ± 0.04), grasslands (0.67 ± 0.02), and DBFs (0.63 ± 0.02), and they are significantly larger than in evergreen needleleaf forests (0.45 ± 0.02; Fig. 2E). Boreal climates (0.43 ± 0.04) have smaller EF_max values than tropical climates (0.71 ± 0.03; Fig. 2F). Combining biomes and climate types, the values of θ_crit, S, and EF_max also vary among different ecosystems (fig. S5), although statistical testing of these differences is impractical because of the limited sample size in each bin. We also find that variations of the three parameters θ_crit, S, and EF_max are substantial within any one biome or climate zone (Fig. 2), implying the existence of other local controlling factors.

Fig. 2. θ_crit, S, and EF_max among different plant functional types and climate types.

θ_crit (A and B), S (C and D), and EF_max (E and F) among different plant functional types (A, C, and E) and climate types (B, D, and F). Letters represent statistically significant differences in the median values (Kruskal-Wallis test, P < 0.05), such that groups not containing the same letter are different. For each box plot, the middle line indicates the median; the box indicates the upper and lower quartiles and the whiskers indicate the 5th and 95th percentiles of the data. Plant functional types were defined according to the International Geosphere–Biosphere Programme classification, including SAV, SHR, ENF, EBF, DBF, MF, GRA, and CRO. Climate types were defined according to the Köppen-Geiger classification as in Migliavacca et al. (65): tropical (Aw, Af, and Am), dry (BSh, BSk, and BWh), subtropical (Cfa, Csa, Csb, and Cwa), temperate (Cfb), continental (Dfa, Dfb, Dwa, Dwb, and Dwc), and boreal (Dfc and Dsc).

Drivers of the spatial variability of θ_crit, S, and EF_max

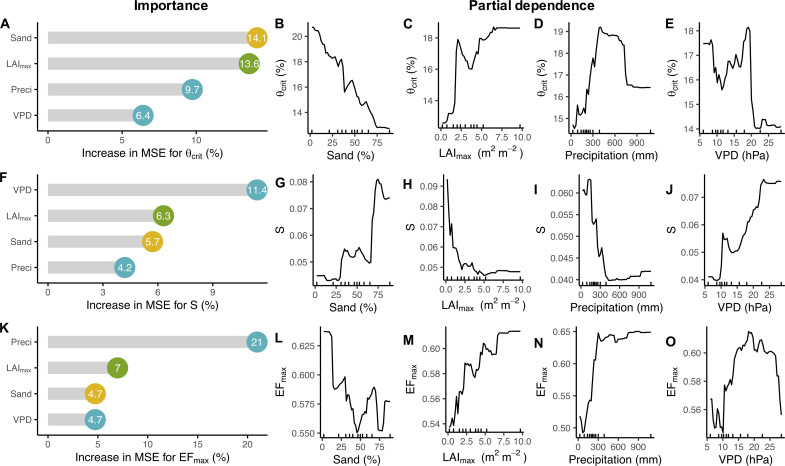
We analyze the relative importance of soil texture (sand fraction), vegetation structural characteristics [approximated by maximum leaf area index (LAI_max)], and mean climatic variables (mean VPD and total precipitation during peak growing season) on the spatial variability of θ_crit, S, and EF_max using random forests (see Materials and Methods). The cross-validation shows that these predictors explain 43, 46, and 38% of the spatial variability of θ_crit, S, and EF_max, respectively. The dominant predictors of the spatial variability of θ_crit, S, and EF_max were, however, different. We find that the spatial variability of θ_crit is mostly explained by the sand fraction and LAI_max (Fig. 3A), while the spatial variability of S is mainly explained by VPD and LAI_max (Fig. 3F). The spatial variability of EF_max is mostly explained by precipitation amount, followed by LAI_max (Fig. 3K). Partial dependence analysis confirms that θ_crit across sites is reduced considerably with a higher sand fraction (Fig. 3B) but increased with LAI_max (Fig. 3C). In addition, θ_crit shows a positive dependence on precipitation (Fig. 3D) and a negative dependence on VPD (Fig. 3E). In contrast, S increases greatly with higher VPD (Fig. 3J) but decreases with increasing LAI_max (Fig. 3H). S is also less steep at higher precipitation (Fig. 3I) and for soils with a lower sand fraction (Fig. 3G). The opposite responses of θ_crit and S to all these four environmental factors (Fig. 3, B to E and G to J) indicate that there is a negative relationship between θ_crit and S (see later). For EF_max, we find that increasing precipitation and LAI_max mainly enhances EF_max (Fig. 3, M and N), while EF_max decreases with increasing sand fraction (Fig. 3L).

Fig. 3. Importance of soil, vegetation structure, and climate properties and partial dependence.

Predictive relative importance for θ_crit (A), S (F), and EF_max (K). Numbers in the circles represent the percentage increase in mean squared error (MSE). Yellow circles represent soil variable; green circles represent vegetation structure variable; light blue circles represent climate variables. Partial dependence plots of the predictors for θ_crit (B to E), S (G to J), and EF_max (L to O). The slopes of the partial dependence plot indicate the sensitivity of the response variable to the specific predictor. Sand, sand fraction (%); LAI_max, maximum leaf area index (in square meters per square meter); VPD, mean VPD during the peak growing season (in hectopascals); Preci, total precipitation amount during the peak growing season (in millimeters). Tick marks in the x axis represent the minimum, maximum, and deciles of the variable distribution.

Relationships between θ_crit, S, and EF_max and the optimal adaptation of local EF-SM responses

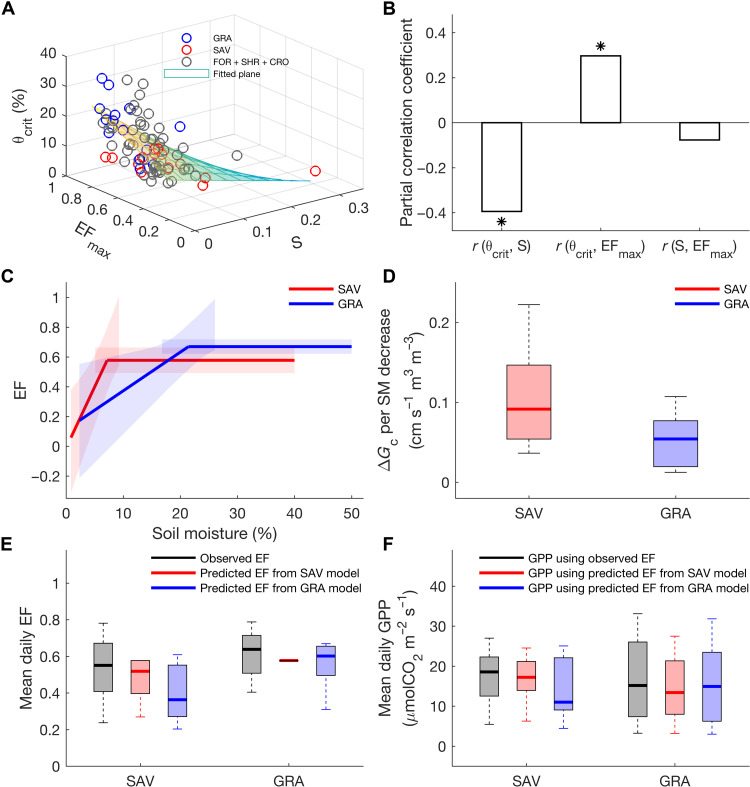
Across all sites, we find that θ_crit exhibits a significant negative correlation with S and a positive correlation with EF_max (Fig. 4A). This is further confirmed by partial correlation analysis (Fig. 4B). Thus, there is a trade-off between θ_crit and S: Sites with low θ_crit often have high S values, while sites with high θ_crit often have low S values (Fig. 4, A and B). To understand the negative relationship between θ_crit and S, we define the intersection of the fitted segmented curve with the x axis at each site as θ₀ (see Materials and Methods). Across sites, the value of θ₀ does not significantly differ from zero (fig. S7). The S values in different biomes can therefore be predicted using the ratio of EF_max and θ_crit (fig. S8). The relationships between θ_crit, S, and EF_max can be related to the dryness of the climate. We thus calculated the aridity index (AI), defined as the ratio of annual potential evapotranspiration (PET) to annual precipitation, from the eddy covariance measurements at each site (see Materials and Methods). We find that low θ_crit and high S values are more common in dry sites (AI > 4), while high θ_crit and low S values are more common in wet sites (AI < 3; fig. S9).

Fig. 4. Relationships between θ_crit, S, and EF_max and the optimal adaptation of local EF-SM response function.

The distribution of θ_crit, S, and EF_max across all sites in different biomes (A). Partial correlation between θ_crit, S, and EF_max across all sites (B). *P < 0.05 The mean response functions of EF-SM in savannas and grasslands (C), while the shading bounds the 95% confidence interval. The canopy conductance (G_c) change rates per SM decrease during water-limited stage in savannas and grasslands (D). Observed and predicted mean daily EF during the peak growing season in savannas and grasslands by swapping two response functions of EF-SM: one from savannas and one from grasslands (E). Calculated mean daily GPP during the peak growing season in savannas and grasslands using observed and predicted EF from two response functions of EF-SM (F). For each box plot, the middle line indicates the median; the box indicates the upper and lower quartiles, and the whiskers indicate the 5th and 95th percentiles of the data.

The distribution of θ_crit and S across different biomes leads us to hypothesize two strategies for how ecosystem has adapted to prevailing recurrent water stress: (i) low θ_crit with high S (e.g., savannas) and (ii) high θ_crit with low S [e.g., grasslands (mainly in temperate and continental climates)] (Figs. 2, A and C, and 4A). The first strategy reflects a resistance to soil dryness and is more successful for ecosystems experiencing frequent dry-downs. However, below the infrequently reached θ_crit value, transpiration and ecosystem function may collapse rapidly. The second strategy, which consists in having a high EF_max and a high θ_crit, is better adapted to humid and subhumid environments where dry-downs are shorter, less severe, and less frequent, so that the number of days with SM below θ_crit is low, and ecosystems can maximize EF_max to sustain water use for photosynthesis.

As both θ_crit and S values are significantly different between savannas and grasslands (Fig. 2, A and C), the response functions of EF-SM in these two biomes are further compared (see Materials and Methods). We find that the response curve of mean EF-SM in savannas and grasslands is in line with the general results observed across sites; namely, θ_crit is negatively related to S but positively related to EF_max (Fig. 4, A to C). The higher S value found in savannas implies that canopy conductance (G_c) may be reduced more strongly when SM passes below θ_crit, while the lower S value in grasslands indicates that G_c may decrease more progressively when SM unfrequently gets below θ_crit. To test this hypothesis, we calculated the reduction rate of G_c with decreasing SM under the water-limited stage in these two biomes, respectively (see Materials and Methods). We find that the reduction rate of G_c with SM in savannas (9 ± 2 cm s⁻¹ m³ m⁻³) is significantly larger than in grasslands (5 ± 1 cm s⁻¹ m³ m⁻³; Fig. 4D). Thus, the higher S values in savannas correspond to a stronger stomatal closure in response to an SM decrease under water-limited conditions to prevent hydraulic failure. In contrast, the lower S values in grasslands imply a more gradual stomatal closure in response to SM decrease, favoring photosynthesis in periods of low to moderate water stress.

We formulated a second hypothesis that the contrasted response functions of EF-SM between savannas (low θ_crit and high S) and grasslands (high θ_crit and low S) locally maximize growing-season evapotranspiration and EF. To test this, we predicted the mean daily EF during the peak growing season for each site in savannas and grasslands by exchanging the two responses of EF-SM (from savannas to grasslands and vice versa) (see Materials and Methods). Comparing with observed and predicted mean daily EF using the true EF-SM response, we find that the predicted mean daily EF using the EF-SM response curve from the other biome is underestimated (Fig. 4E). This finding suggests that EF-SM response curves are adapted so as to maximize growing-season EF. To further test whether maximizing EF also implies maximization of photosynthesis during the peak growing season, we performed the same analysis for GPP (see Materials and Methods). We find that, in both savannas and grasslands, the predicted mean growing-season GPP using the EF-SM model of the other biome is always lower than the predicted GPP using the true EF-SM model (Fig. 4F). Thus, our results show that the trade-off between θ_crit and S helps to maximize the growing-season EF and the optimal adaptation of the local EF-SM response function of the ecosystem can maximize growing-season evapotranspiration and photosynthesis. Except for savannas and grasslands, we could not compare the response functions of EF-SM among other biomes (forests, shrublands, and croplands) because they do not have significant differences in either θ_crit or S (Fig. 2, A and C).

DISCUSSION

Vegetation regulates the terrestrial water and carbon cycles, as it controls and adapts to changing SM availability. However, our ability to characterize the θ_crit at the global scale is limited. By examining the consistency of θ_crit estimated from the VPD-GPP-SM and EF-SM methods, this study showed that plant photosynthetic processes become water-stressed at an SM threshold similar to that of EF, suggesting that the EF-SM relationship is able to quantify the SM threshold of plant water stress. We noted that the absolute magnitudes of θ_crit values estimated from the VPD-GPP-SM method are slightly higher than those from the EF-SM method (Fig. 1D). This higher value is likely due to the fact that the VPD-GPP covariance is calculated using a 9-day moving window that, therefore, can overestimate the threshold during dry-downs (13). Meanwhile, this bias may be also related to the bias in GPP for different flux tower sites due to the inhibition of leaf respiration in the light (28) and uncertainty in the gap-filling routine. The uncertainty in tower-estimated GPP depends, in part, on radiation, which would affect the SM thresholds estimated from VPD-GPP-SM method for different sites. Nevertheless, the relatively small mean difference but strong spatial correlation between the two thresholds across all sites and all biomes shows that SM limitation occurs at a similar SM level for GPP and evapotranspiration. This EF-SM approach used here also provided a practical application of the original conceptual Budyko curve (11) yet based on a temporal approach rather than spatial approach. The Budyko framework is commonly used to estimate the long-term mean actual evaporation as a function of the mean AI at the catchment scale and applied as a spatial analysis for mean evapotranspiration/precipitation (29). We focused here on the transient shift between energy and water limitations at the site scale (and at short time scales) and used SM to quantify ecosystem water limitation.

Land-surface models typically represent SM stress effects on evapotranspiration and GPP as a segmented function (30), consistent with our empirical analysis. Some models set θ_crit at field capacity; then, at lower SM, evapotranspiration and GPP are multiplied by a moisture scalar, which declines either linearly or nonlinearly from 1 at field capacity to 0 at wilting point (30). Our results suggest that a linear formula with θ_crit set to field capacity will overestimate water stress. Other models more realistically define a θ_crit that is less than field capacity and greater than the wilting point (31). In addition, a moisture scalar is also used in some satellite GPP and evapotranspiration algorithms. For example, satellite-driven light use efficiency (LUE) GPP models used environmental scalars to represent biophysical constraints on maximum LUE (32, 33), but many of the existing and widely used LUE models do not currently incorporate SM constraints directly (34). Our study provides an SM stress framework and parameterization that could be incorporated in the future to improve these models. The formulation introduced in this study is also compatible with formulations already used in light-use efficiency and process-based land surface models, but the three parameter values here are based on analysis of measured data, providing observations of key parameters of the SM control on evapotranspiration. The θ_crit value that we found is in line with the value found in the Netherlands (16%) (35) and Africa (14%) (18) using satellite observations, while our estimates of S and EF_max across sites are slightly higher than the values reported in Europe (S = 0.03 and EF_max = 0.54) (13). We also found that there are large and systematic differences in these three parameters across biomes and climate zones. Even within a given plant functional type or climate type, the spatial variations in θ_crit, S, and EF_max are also large. Thus, it is unrealistic to parameterize these variables as universal constants, similar to those in many models. Although models simulate SM in different layers, whereas our analysis was based on surface observations, our results demonstrate that the surface θ_crit is highly correlated with the θ_crit in deep soil layers (fig. S3), which is consistent with the recent findings that surface and rootzone SM are equivalently skillful for identifying evapotranspiration regime changes (36). We also found that, when surface θ_crit is larger than 20%, θ_crit based on SM dry-downs of the deep soil layers is higher than surface θ_crit (fig. S3). This may be because the deep SM is relatively stable and acts as a low-pass filter so that it will not be depleted as efficiently by plant roots compared with surface SM.

In addition to helping improve the representation of water stress in models, eddy covariance observations from globally distributed and automated sensor networks analyzed here with a machine learning approach also unravel previously unidentified relationships between parameter values and environmental variables. Our results showed that the spatial variability of θ_crit, S, and EF_max is mostly explained by soil texture, mean growing-season VPD, and precipitation, respectively, while LAI_max also affects their values. The variability of θ_crit is dominantly explained by the sand fraction, consistent with lower wilting points observed in sandy soils (37). Plant water stress is related to water potential, which largely is affected by the soil capacity to hold water (38, 39). Sandy soils have greater hydraulic conductivity and lower porosity than other soil types (e.g., clay) (40, 41); thus, there is a lower soil water holding capacity in sandy soils. The spatial variability of S is mainly explained by VPD, while the spatial variability of EF_max is mostly explained by the precipitation amount. Increasing VPD triggers stomatal closure (14) and reduces transpiration and EF, thus increasing S. LAI_max has important contributions to the spatial variability of all these three parameters, highlighting the critical role of vegetation structure in controlling evapotranspiration processes. This result is in keeping with a previous study from Williams and Torn (42), showing that LAI controls surface heat flux partitioning and land-atmosphere coupling. As they have a lower LAI_max and grow on more sandy soils (fig. S10), savannas have lower θ_crit and higher S than that of grasslands. Grasslands also tend to have greater soil organic carbon, helping to increase the water holding capacity (43). Our results also showed that the θ_crit and S have opposite responses to all these environmental factors (soil texture, LAI_max, VPD, and precipitation; Fig. 3, B to E and G to J). We noted that these environmental factors only explained about 40% of the variance in θ_crit, S, and EF_max. The portion of unexplained variance might be related to plant hydraulic or functional traits, such as rooting depth or ability of roots to switch from surface to deep water uptake (44–47) and hydraulic traits diversity (48). Diverse communities are more likely to contain species with different traits that regulate how they respond to drought; higher hydraulic diversity, for example, buffers variation in ecosystem fluxes during dry periods across temperate and boreal forests (48). Given the large variations of these parameters over diverse ecosystems and the limited observational data that we could use, we provide here a comprehensive analysis across global sites.

Our study sheds a new light on varying EF-SM relationships in different ecosystems. Dryland ecosystems, such as savannas, operate at low θ_crit. Across sites, there is a negative relationship between θ_crit and S, indicating that dryland ecosystems, which minimize θ_crit through mechanisms of sustained soil water extraction and plant hydraulic transport, are also more vulnerable once extreme stress below θ_crit is reached. There is therefore a trade-off between θ_crit and S: Sites with low θ_crit values often have high S values, while sites with high θ_crit values often have low S values, indicating two different adaptation strategies. The first strategy reflects a resistance to soil dryness and is more successful for ecosystems experiencing frequent dry-downs. However, below the infrequently reached θ_crit value, ecosystem function may collapse rapidly. The second strategy with a high θ_crit is more adapted to humid and subhumid environments where dry-downs are shorter and less severe. For the first strategy, the higher S values correspond to a more rapid stomatal closure in response to an SM decrease under water-limited conditions to prevent hydraulic failure (49, 50). In contrast, for the second strategy, the lower S values which are related to a more gradual stomatal closure in response to an SM decrease, benefit photosynthesis in periods of limited water stress, and reduce the risk of carbon starvation, but this can lead to hydraulic failure if drought is sufficiently intense: Plants will run out of water before they run out of carbon (51).

The θ_crit values quantified in this study reflect a background ecosystem resistance to aridity. Berdugo et al. (52) recently reported that aridification is associated to systemic and abrupt changes, which occurred sequentially in three phases characterized by abrupt decays in plant productivity, soil fertility, and plant cover and richness at aridity values of 0.54, 0.7, and 0.8, respectively. Our results imply that ecosystems with lower θ_crit should have higher aridity thresholds. We do not have a map of θ_crit, but with advances in remote sensing, this may be possible [e.g., Feldman et al. (18)], and we could then test whether systems with a higher θ_crit have a lower threshold response to increased aridity compared to more resistant systems with a lower θ_crit. Consistent with the ecosystem optimality concepts, our results showed that the trade-off between θ_crit and S helps to increase the growing-season EF and that optimal adaptation of the EF-SM response also maximizes growing-season carbon uptake. Note that different rooting depths across different sites may affect the θ_crit, although recent studies showed that surface and rootzone SM are equivalently skillful for identifying evapotranspiration regime changes (36). We also noted that some species could use adaptation strategies to reduce LAI (e.g., drought deciduous functional types) in addition to stomatal regulation during dry periods (53, 54), but our analysis focused on peak growing season and soil dry-downs at short time scales; thus, the impacts of drought deciduousness should be muted. Moreover, our analysis of the temporal dynamics of θ_crit showed that the interannual variability of θ_crit is not significant (fig. S6), indicating the relative stability of θ_crit through time in this study.

In summary, this study quantified the θ_crit, S, and EF_max in terrestrial ecosystems using globally distributed eddy covariance measurement sites. Our formulation is similar to one commonly used in land surface models, although models consider deeper SM than observations. We found systematic differences of the three parameters across biomes and climates and uncovered the relationships between parameter values and environmental factors, including climatic, biotic, and edaphic variables. These results help in identifying tipping points of water stress impairing ecosystem functioning and should help toward a better representation of water stress in land surface models. Future research will aim to use our new understanding of θ_crit, S, and EF_max to improve model representation of SM constraints on water and carbon fluxes. As soil matric potential and VPD interact with vegetation function to control water flow, future research deriving relationships between SM during dry-downs, VPD, and soil water potentials will be a central challenge.

MATERIALS AND METHODS

Eddy covariance observations

We used half-hourly SM, latent heat flux, sensible heat flux, VPD, GPP, and precipitation from the recently released ICOS (Integrated Carbon Observation System) (55), AmeriFlux (56, 57), and the FLUXNET2015 dataset of energy, water, and carbon fluxes and meteorological data, all of which have undergone a standardized set of quality control and gap filling (58, 59). Data were processed following a consistent and uniform processing pipeline (58). There are 279 flux tower sites in total by combing ICOS, AmeriFlux, and FLUXNET2015 datasets. We first removed 62 sites without SM measurements and then dropped all wetland sites because they have a perched water table and infrequently show SM limitations such that 212 sites remained. Because, for some sites, there was no dry-down detected during the peak growing season across all available years, these sites were also excluded (195 sites remaining). The EF-SM relationships in these 195 sites were evaluated to detect the θ_crit for each site.

SM was measured as volumetric soil water content (percentage) at different depths. Surface SM (SM_1: 0 to 10 cm, varying across sites) was measured at all sites, and some sites also provided deeper SM measurements (e.g., SM_2: 10 to 30 cm; SM_3: 20 to 60 cm). We mainly explored the surface SM observations, but deeper SM measurements were also used when available. The GPP estimates from the nighttime partitioning method were used for the analysis (60). Data were quality controlled so that only measured and good-quality gap-filled data (quality control = 0 or 1) were used. Daytime half-hourly data (9 a.m. to 16 p.m. local standard time) were averaged to daily values, while SM values were averaged over the full day.

SM dry-down identification

Dry-downs following rainfall are episodes with no rain for several consecutive days during which SM shows a short-term “pulse” rise after rain and then decays until the next rain event. A dry-down is retained for our analysis when SM decreases consecutively for at least 10 days after rainfall following previous studies (13, 26, 27, 61, 62). Days with intermittent rainfall are excluded to remove the rainfall impacts on latent heat flux measurements. To minimize the irrigation effects on EF in croplands, we checked whether there were peaks of SM without rain at each cropland site, which would indicate irrigation events. Then, we removed the dry-downs with intense irrigation episodes at cropland sites. We focused on the soil dry-downs during the peak growing season for all available site years, defined as 3-month period with the maximum mean GPP across the available years. This resulted in 2035 dry-down events that form the basis of our study.

θ_crit, S, and EF_max estimation using EF-SM method

We calculated the daily EF as the ratio of the observed latent heat flux to the sum of latent and sensible heat fluxes. Then, we characterized the EF-SM relationship at each site using all available soil dry-downs, from a regression between these two variables with a linear-plus-plateau model

$$\text{EF}=\{\begin{array}{c}{\text{EF}}_{\text{max}}+\mathrm{S}(\text{SM}-{\mathrm{\theta }}_{\text{crit}}) \text{if} \text{SM}<{\mathrm{\theta }}_{\text{crit}}\\ {\text{EF}}_{\text{max}} \text{if} \text{SM}\ge {\mathrm{\theta }}_{\text{crit}}\end{array}$$ (1)

where EF_max is the maximum value of EF in absence of SM stress (energy-limited stage), S represents the slope of the linear increase phase (water-limited stage), and θ_crit is the critical SM threshold. These three parameters and their SEs were simultaneously estimated by least-squares fit with the R software package “segmented” (63) for each site, leading to site-specific estimated values of EF_max, S, and θ_crit. θ_crit is the break point until which EF increases linearly as a function of SM. The S represents the EF sensitivity to SM in the water-limited regime, indicating the magnitude of EF increase for each additional 1% soil water content (or 0.01 m³ m⁻³) change in SM when SM is below its break point. The plateau is the maximum EF value reached when SM exceeds its threshold. An example to estimate the EF_max, S, and θ_crit is shown in Fig. 1B.

On the basis of the EF-SM relationships, there were 85, 29, and 19 sites with the θ_crit estimates using the first (SM_1), second (SM_2), and third (SM_3) soil water content measurement depth, respectively. For the rest of sites, it was not possible to estimate a θ_crit because samples were too infrequent, or there were no thresholds. These 85 sites included 11 DBFs, 5 evergreen broadleaf forests, 26 evergreen needleleaf forests, 3 mixed forests, 8 shrublands, 4 croplands, 14 grasslands, and 14 savannas (table S1).

Differences in θ_crit, S, and EF_max between groups (different plant functional types or climate types) were analyzed using the Kruskal-Wallis test, a nonparametric test of difference (64). A P < 0.05 was used to identify significant differences between groups. Plant functional types were defined according to the International Geosphere–Biosphere Programme classification (58). Climate types were defined according to the Köppen-Geiger classification as in Migliavacca et al. (65): tropical (Aw, Af, and Am), dry (BSh, BSk, and BWh), subtropical (Cfa, Csa, Csb, and Cwa), temperate (Cfb), continental (Dfa, Dfb, Dwa, Dwb, and Dwc), and boreal (Dfc and Dsc).

θ_crit estimation using VPD-GPP-SM method

For the threshold in plant photosynthetic processes, Fu et al. (13) recently reported that the initiation of water stress could be detected as the SM value when the sign of the covariance between daily GPP and VPD changes from positive to negative during a dry-down. GPP and evapotranspiration are tightly coupled on short time scales (4), and the sign of the covariance between daily VPD and GPP reflects the relative strength of water versus energy limitation on ecosystem function, because VPD combines the effects of both water stress and energy demand (via temperature) on GPP (14–16). Following Fu et al. (13), we also calculated the covariance between daily VPD and GPP across 9-day moving windows during the dry-down (e.g., 1 to 9 days, 2 to 10 days, and 3 to 11 days). A positive covariance indicates that higher VPD is associated with increases in GPP (which we term “radiation effects”), while a negative covariance indicates that water stress limits GPP, i.e., with a higher VPD caused by dryer soils results in a lower GPP. We excluded some short dry-downs because their covariances during the dry-down are all positive or negative, suggesting that the entire dry-down period is under energy-limited or water-limited stage. We only chose the long soil dry-downs with at least 15 days (with at least seven covariance values), and their covariances must include both positive and negative values. Similar to the VPD-GPP covariance, the average of SM during the moving window (e.g., 1 to 9 days, 2 to 10 days, and 3 to 11 days) was also calculated to detect the θ_crit when the sign of VPD-GPP covariance changes from positive to negative. An example to quantify the θ_crit using VPD-GPP-SM method is shown in Fig. 1C.

To compare the θ_crit values from the VPD-GPP-SM method with that from the EF-SM method, we fitted the θ_crit values from these two methods using linear [f(x) = p1 × x + p2] and nonlinear [f(x) = p1 × x² + p2 × x + p3] function, respectively (fig. S1). We found that the coefficients of p1 and p2 in the linear fitting are significantly different from 0 at the significance level of 0.05, while both the p1 and p3 in the nonlinear fitting do not significantly differ from 0 (fig. S1), suggesting that the linear assumption is reasonable. To test whether the closure of the energy balance from eddy covariance measurements affects the bias of θ_crit values (66), we repeated the analysis using the “LE.CORR” and “H.CORR” variables from FLUXNET database to calculate the EF and quantify θ_crit, instead of “LE” and “H.” LE.CORR and H.CORR are the “energy balance–corrected” version of latent and sensible heat flux, based on the assumption that the Bowen ratio is correct (67). Our results were robust to either variable (fig. S2). The differences in SM threshold values based on the two energy fluxes were negligible (fig. S2).

Drivers of the spatial variability of θ_crit, S, and EF_max

A random forests analysis was used to identify the soil property, vegetation structure, and climate variables that contribute the most to the spatial variability of θ_crit, S, and EF_max. For climatic variables, we calculated the AI, mean VPD, incoming shortwave radiation, wind speed, and total precipitation during the peak growing season from flux tower observations at each site. As vegetation structure variable, LAI_max was collected for 53 sites, from the literature (65, 68, 69). Using the Application for Extracting and Exploring Analysis Ready Samples (AppEEARS) (70), LAI_max values in the rest of 32 sites were extracted from MODIS LAI product (MCD15A2) at 500-m spatial resolution (71). Soil property variables were extracted from SoilGrids, a collections of soil property maps for the world at 250-m resolution (72), including sand fraction, soil organic carbon content, total nitrogen, pH, bulk density, volumetric fraction of coarse fragments, and cation exchange capacity.

The performances of random forests model were assessed by fivefold cross-validation using two criteria: the mean absolute error (MAE) and the R-squared value (R²). MAE quantifies the overall error, while R² estimates the proportion of variance in response variable that is captured by the predictive variables. We favored the model with the smallest MAE and the highest R² (73, 74). Following Huang et al. (73), we first run the random forests model with all predictor variables included and then sequentially excluded predictors that did not improve model performance one after another. The best model with the minimum number of predictors and same predictors for all three response variables (θ_crit, S, and EF_max) was selected. The final set of predictors included the following predictor variables: as soil property variable, sand fraction (%); as vegetation structure variable, LAI_max (in square meters per square meter); as climatic variables, mean daily VPD (in hectopascals) and total precipitation amount (in millimeters) during the peak growing season.

We used partial dependencies of variables to assess the relationship between individual predictors and the response variables (that is, θ_crit, S, or EF_max). The results from the partial dependency analysis can be used to determine the effects of individual variables on the response, without the influence of the other variables (74). The partial dependencies were calculated restricted to the values falling within the convex hull of their training values to reduce the risk of interpreting the partial dependence plot outside the range of the data (extrapolation risk) (65). The partial dependence function was computed using the pdp R package (75). Partial dependence plots derived for θ_crit, S, and EF_max are shown in Fig. 3 (B to E, G to J, and L to O) for various inputs.

Temporal variability of θ_crit, S, and EF_max

Besides their spatial variability across sites, θ_crit, S, and EF_max may also change with time. Although the temporal variability in θ_crit, S, and EF_max is difficult to evaluate given the relatively short observation record at most sites, we analyzed the temporal dynamics of these three parameters at a forest site with long observational periods (2000–2019), DE-Hai (table S1). We quantified θ_crit, S, and EF_max using dry-downs every 3 years, respectively (table S2; note that we could not estimate a θ_crit during 2009–2017 because samples were too infrequent, or SM was always above or below the threshold in these years). We found that θ_crit values changed slightly over time (table S2). The mean θ_crit, S, and EF_max across results from every 3 years were similar to that of during 2000–2019; thus, our results reflect the average of θ_crit, S, and EF_max during the available observational periods. To further test whether there was a trend change through time in θ_crit, S, and EF_max, we performed the same analysis at five sites with at least 15 years of measurements. We found that there was no significant trend change with time in the three parameters over all site years (fig. S6). This initial exploration should be treated with caution given the relatively few sites and short observation record.

Relationships between θ_crit, S, and EF_max

To understand the relationships between θ_crit, S, and EF_max, we plotted these three variables in three dimensions across all sites, distributed in different biomes or AI. AI was defined as the ratio of annual PET to annual precipitation. We calculated the PET using the Priestley-Taylor equation following Novick et al. (16) for each site. The AI calculated using PET from Priestley-Taylor equation matched well with that of the Penman-Monteith equation. We also performed the partial correlation analysis to test the significance of the relationships between θ_crit, S, and EF_max (P < 0.05).

To further explore the negative relationship between θ_crit and S, we define the intersection of the fitted segmented curve with the x axis as θ₀ (the value of SM at which EF is equal to zero); thus, θ₀ can be calcualted using the Eq. 2

$$\mathrm{S}=\frac{{\text{EF}}_{\text{max}}}{({\mathrm{\theta }}_{\text{crit}}-{\mathrm{\theta }}_0)}$$ (2)

We then compared the θ₀ with zero using t test across sites and found that the θ₀ does not significantly differ from zero (fig. S7). The S values in different biomes can therefore be predicted using the ratio of EF_max and θ_crit (fig. S8).

Mean response function of EF-SM in savannas and grasslands

On the basis of the distribution of θ_crit and S in different plant functional types, we proposed two schema: (i) low θ_crit with high S (e.g., savannas) and (ii) high θ_crit with low S (e.g., grasslands). As both θ_crit and S were significantly different between savannas and grasslands (Fig. 2, A and C) and the number of sites in savannas (n = 14) and grasslands (n = 14) were same, the response functions of EF-SM in these two biomes were further compared. We were not able to compare the response functions of EF-SM among other biomes because they did not show any significant difference in either θ_crit or S (Fig. 2, A and C). The mean response functions of EF-SM in savannas and grasslands were obtained by calculating the median values of the θ_crit, S, and EF_max across all sites for savannas and grasslands, respectively. The uncertainty of mean EF-SM response function for each biome was quantified by calculating the 95% confidence interval across all sites.

Derivation of G_c from eddy covariance measurements

At each site in savannas and grasslands, G_c under water-limited stage (SM < θ_crit) was calculated using half-hourly eddy covariance measurements by inverting the Penman-Monteith equation (76)

$$G_{\mathrm{c}}=r_{\mathrm{a}}\mathrm{\gamma }/(\frac{∆(R_{\mathrm{n}}-G)+\mathrm{\rho }{c}_{\mathrm{p}}{r}_a(e_{\mathrm{s}}(T_a)-e_{\mathrm{a}})}{\mathrm{\lambda }E}-(\mathrm{\Delta }+\mathrm{\lambda }))$$ (3)

where G_c and r_a are canopy stomatal conductance and aerodynamic resistance, respectively; γ is the psychrometric constant; Δ is the S of the water vapor deficit with respect to temperature; R_n and G are observed net radiation and soil heat flux, respectively; ρ is air density, C_p is the specific heat capacity of dry air; e_s and e_a are saturated and actual vapor pressure, respectively; and λE is observed evapotranspiration. r_a is calculated following Novick et al. (16) (Eq. 4), using the von Kármán constant (k = 0.4), available wind speed data (w_s), measurement height (𝑧_m), momentum roughness length (𝑧₀ = 0.1h), and zero plane displacement (𝑧_d = 0.67h), both based on calculated canopy height (h) under near-neutral conditions (Eq. 5) (77)

$$r_{\mathrm{a}}=\frac{\text{ln}{\left(\frac{z_{\mathrm{m}-}{z}_{\mathrm{d}}}{z_0}\right)}^2}{w_{\mathrm{s}}{k}^2}$$ (4)

$$h=\frac{z_{\mathrm{m}}}{0.6+0.1\times \text{exp}\left(\frac{k{w}_{\mathrm{s}}}{u^{*}}\right)}$$ (5)

To evaluate the reduction rate of G_c per SM decrease under water-limited stage, we further calculated the change rate of G_c under water-limited stage for each site in savannas and grasslands by the ratio between the change of G_c and the change of SM as follows (Eq. 6)

$$∆G_{\mathrm{c}}=\frac{\text{Median}(G_{\text{SM} \text{in} 80-100\text{th}})-\text{Median}(G_{\text{SM} \text{in} 0-20\text{th}})}{\text{Median}({\text{SM}}_{80-100\text{th}})-\text{Median}({\text{SM}}_{0-20\text{th}})}$$ (6)

where ∆G_c is the reduction rate of G_c per SM decrease, Median(G_{SM in 80−100th}) is the median G_c during the 80th to 100th percentiles of SM under water-limited stage, Median(G_{SM in 0−20th}) is the median G_c during the 0th to 20th percentiles of SM under water-limited stage, Median(SM_80−100th) is the median SM during the 80th to 100th percentiles of SM under water-limited stage, and Median(SM_0−20th) is the median SM during the 0th to 20th percentiles of SM under water-limited stage.

Predicting EF and GPP during the peak growing season

We formulated the hypothesis that the distinct response functions of EF-SM between savannas (low θ_crit with high S) and grasslands (high θ_crit with low S) locally maximize growing-season EF. To test this, we predicted the mean daily EF during the peak growing season in savannas by swapping two response functions of EF-SM: one from savannas and one from grasslands. Similarly, we predicted mean daily EF during the peak growing season in grasslands for each site using daily SM in grasslands and running two response functions of EF-SM, respectively.

To further test whether the maximizing EF also reflect a production maximization during the peak growing season, we performed the same analysis for savannas and grasslands GPP using daily observed EF and predicted EF from two response functions of EF-SM, respectively. Mean daily GPP during the peak growing season for each site was calculated using daily EF, net radiation (R_n), and water use efficiency (WUE) as Eq. 7. WUE was calculated as the ratio of the observed GPP to the observed latent heat flux (78). Except for savannas and grasslands, we cannot compare the response functions of EF-SM among other biomes because they have no significant difference in either θ_crit or S (Fig. 2, A and C)

$$\text{GPP}=\text{EF}\times R_{\mathrm{n}}\times \text{WUE}$$ (7)

Supplementary Materials

This PDF file includes:

Figs. S1 to S10

Tables S1 to S2