In silico investigation and surmounting of Lipopolysaccharide barrier in Gram-Negative Bacteria: How far has molecular dynamics Come?

Graphical abstract

Abstract

Lipopolysaccharide (LPS), a main component of the outer membrane of Gram-negative bacteria, has crucial implications on both antibiotic resistance and the overstimulation of the host innate immune system. Fighting against these global concerns calls for the molecular understanding of the barrier function and immunostimulatory ability of LPS. Molecular dynamics (MD) simulations have become an invaluable tool for uncovering important findings in LPS research. While the reach of MD simulations for investigating the immunostimulatory ability of LPS has been already outlined, little attention has been paid to the role of MD simulations for exploring its barrier function and synthesis. Herein, we give an overview about the impact of MD simulations on gaining insight into the shield role and synthesis pathway of LPS, which have attracted considerable attention to discover molecules able to surmount antibiotic resistance, either circumventing LPS defenses or disrupting its synthesis. We specifically focus on the enhanced sampling and free energy calculation methods that have been combined with MD simulations to address such research. We also highlight the use of special-purpose MD supercomputers, the importance of appropriate LPS and ions parameterization to obtain reliable results, and the complementary views that MD and wet-lab experiments provide. Thereby, this work, which covers the last five years of research, apart from outlining the phenomena and strategies that are being explored, evidences the valuable insights that are gained by MD, which may be useful to advance antibiotic design, and what the prospects of this in silico method could be in LPS research.

Nomenclature

List of abbreviations and acronyms

A. baumannii

Acinetobacter baumannii

A. ferrooxidans

Acidithiobacillus ferrooxidans

AA

All-atom

ABF

Adaptive biasing force

ADP

Adenosine diphosphate

AMP

Antimicrobial peptide

C. crescentus

Caulobacter crescentus

CDL

Cardiolipin

CL

1,1′-palmitoyl-2,2′-vacenoyl

GAFF

General AMBER force field

CG

Coarse-grained

CGenFF

CHARMM general force field

DDM

n-Dodecyl-β-d-Maltopyranoside

DMPC

1,2-dimyristoyl-sn-glycero-3-phosphocholine

DOPE

1,2-dioleoyl-sn-glycero-3-phosphoethanolamine

DOPG

1,2-dioleoyl-sn-glycero-3-phospho-rac-(1-glycerol)

DPPC

Dipalmitoyl-phosphocholine

DPPE

Dipalmitoylphosphatidylethanolamine

E. coli

Escherichia coli

ECA

Enterobacterial common antigen

ECA_DPPG

Dipalmitoylphosphatidylglycerol (DPPG)-linked ECA

ECA_LPS

LPS-associated ECA

ECA_PG

Phosphatidylglycerol (PG)-linked ECA

ECA_PSPG

Palmitoylstearoylphosphatidylglycerol (PSPG)-linked ECA

ECA_PVPG

Palmitoylvacenoylphosphatidylglycerol (PVPG)-linked ECA

EN

Elastic network

FL

Full length

GPU

Graphics processing unit

HD5

Human α-defensin 5

HepI

Heptosyltransferase I

HEP-III

Heptosyltransferase-III

IL

Inner leaflet

IM

Inner membrane

K. pneumoniae

Klebsiella pneumoniae

KDO

3-deoxy-d-manno-oct-2-ulosonic acid

KDO8P

3-deoxy-d-manno-octulosonate 8-phosphate

KdsC

3-deoxy-d-manno-octulosonate 8-phosphate phosphatase

Lipid A_Ara4N

Lipid A containing 4-amino-4-deoxy-l-arabinose

LPS

Lipopolysaccharide

Lpt

LPS transport

MD

Molecular dynamics

MM

Molecular mechanics

MM-GBSA

Molecular mechanics generalized Born surface area

MM-PBSA

Molecular mechanics Poisson − Boltzmann surface area

N. meningitidis

Neisseria meningitidis

n.s.

Not specified

NTD

N-terminal domain

OAH

Oligo(allylamine hydrochloride)

OL

Outer leaflet

OM

Outer membrane

Omps

Outer membrane proteins

P. aeruginosa

Pseudomonas aeruginosa

PAMP

Pathogen associated molecular pattern

PMB

Polymixyn B

PMF

Potential of mean force

POPC

1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine

POPE

Palmitoyl-oleoyl-phosphatidylethanolamine; phosphoethanolamine

POPG

1-palmitoyl-2-oleoyl-phosphatidylglycerol; phosphatidylglycerol

PPPE

1-palmitoyl(16:0)-2-palmitoleoyl(16:1 cis-9)-phosphatidylethanolamine

PVCL2

1,1′-palmitoyl-2,2′-vacenoyl-cardiolipin with a net charge of − 2e

PVPG

1-palmitoyl(16:0)-2-vacenoyl(18:1 cis-11)-phosphatidylglycerol

REUS

Replica exchange umbrella sampling

R-LPS

Rough lipopolysaccharide

S. dysenteriae

Shigella dysenteriae

S. enterica

Salmonella enterica

S. flexneri

Shigella flexneri

SA

Simulated annealing

SIE

Solvated interaction energy

S-LPS

Smooth lipopolysaccharide

SMD

Steered molecular dynamics

TempL

Temporin L

TOCL1

Tetraoleoyl cardiolipin

UDP-GlcNAc

UDP-N-acetylglucosamine

US

Umbrella sampling

V. cholerae

Vibrio cholerae

WHAM

Weighted histogram analysis method

WT

Wild type

1. Introduction

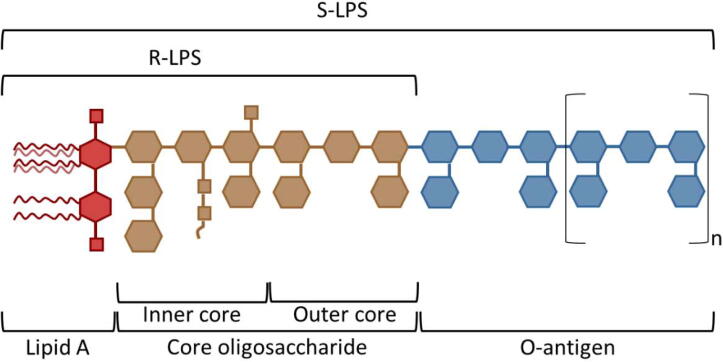
Gram-negative bacteria are characterized by the complex structure of their cell envelope, which comprises two membranes. The inner membrane (IM) is a symmetric bilayer that consists of phospholipids, whereas the outer membrane (OM) is an asymmetric bilayer, comprising of phospholipids in the inner leaflet (IL) and predominantly lipopolysaccharides (LPSs) in the outer leaflet (OL); these membranes are separated by the periplasm, which is an aqueous compartment that accommodates a thin layer of peptidoglycan [1], [2], [3], [4], [5]. LPS, also referred to as endotoxin, is an amphiphilic molecule that consists of three domains, namely, lipid A, core oligosaccharide and O-antigen (see Fig. 1) [6], [7], [8], [9], [10]. LPS molecules that comprise these three constituents are referred to as smooth LPS (S-LPS), whereas rough LPS (R-LPS) lacks the O-antigen and/or parts of the core oligosaccharide [8], [11]. Lipid A, the most conserved component of LPS, consists of a β-(1 → 6)-linked glucosamine disaccharide that generally bears several saturated fatty acid moieties (from four to eight acyl tails), and is typically phosphorylated. Lipid A acts as a hydrophobic anchor for LPS to the bacterial OM, and is considered the most toxic constituent of LPS [2], [4], [8], [9], [11], [12], [13]. The core oligosaccharide is covalently attached to the glucosamines of lipid A and comprises two regions, namely, the inner and outer core, which are proximal and distal to lipid A, respectively. The inner core oligosaccharide is generally conserved and incorporates at least one residue of 3-deoxy-d-manno-oct-2-ulosonic acid (KDO) and several heptoses. Conversely, the components of the outer core oligosaccharide are less conserved; in general the outer core is composed of a series of hexoses [2], [8], [9]. The O-antigen, which is linked to the core oligosaccharide, is the most variable component of LPS. It is constituted of repeating oligosaccharide units (up to 40), being each of them made of three to eight sugar residues [2], [8], [9], [10], [14]. In contrast to lipid A, both the core oligosaccharide and the O-antigen are hydrophilic and extend outwards from the OM [5], [8].

Fig. 1.

Schematic representation of the general structure of Gram-negative bacterial LPS.

Bacterial LPS is involved in several processes of pathophysiological relevance [9], [11], [15]. Specifically, LPS provides Gram-negative bacteria with an effective protective barrier against noxious substances, such as small molecules, antimicrobial peptides or antibiotics. Hence, LPS is a main contributor to the resistance to antibiotics that Gram-negative bacteria display, which has become a major health threat globally [1], [9], [11], [16], [17], [18], [19], [20]. On the other hand, LPS is a pathogen associated molecular pattern (PAMP), and thus it can be recognized by the host immune system, which can initiate the eradication of the bacterial infection. The immune system activation is beneficial in order to fight against the invading bacteria; however, uncontrolled activation can lead to life-threatening sepsis, which remains the primary cause of mortality from infection [9], [11], [21], [22], [23]. The expected increase of sepsis frequency and occurrence due to the worldwide expanding antibiotic resistance calls for the rational design and development of effective strategies, such as novel antibiotics or extracorporeal LPS sequestration systems, for treating LPS-caused infections [22], [23], [24], [25]. In this regard, understanding at the atomic level the structure, dynamics and interplay between molecules that underlie the synthesis, barrier function and immunostimulatory ability of LPS is of paramount importance in order to rationally design and optimize therapeutics.

Molecular dynamics (MD) is recognized as a valuable computer simulation method for investigating biomolecular systems at atomic detail, thus, providing important insights that cannot be often experimentally reached [26], [27], [28], [29]. As such, MD procedures have been widely employed for investigating LPS-phenomena, including its barrier and immunostimulatory functions, as well as strategies to overcome them [6], [13], [22], [24], [30], [31], [32], [33], [34], [35], [36]. With the pace of advances in the development of algorithms and in the computing power, the investigation of more complex LPS systems as well as the access to biologically meaningful time scales have been made possible [37], [38], [39]. Therefore, important progress on the elucidation of both the mechanisms underlaying the bacterial resistance to different agents and key steps of the immune system activation has been achieved by combining MD and different computational methods [12], [15], [30], [40], [41], [42]. Recognizing such methods is crucial for moving a step forward on the elucidation of different events related to LPS, and thus on the development of strategies to fight against bacterial infections. In our previous work [30], we outlined how MD simulations can help to elucidate phenomena related to the immunostimulatory ability of LPS and to design molecules for modulating the exaggerated LPS-induced immune response or capturing LPS, as well as, to the development of O-antigen based vaccines. We specifically emphasized the enhanced sampling and free energy calculation methods that are combined with MD simulations in order to address the above-mentioned investigations. The knowledge derived from this work could be valuable for designing therapeutics (immunomodulatory molecules, LPS sequestration agents and vaccines) to treat bacterial infections. However, it does not address the exploration of both the mechanisms underlaying the antibiotic resistance and the strategies to overcome such resistance, which are key in order to deal with the worldwide challenge of Gram-negative bacterial resistance by developing molecules that evade LPS defenses or disrupt its synthesis.

Hence, this work aims at providing an overview of the impact of MD simulations for shedding light into different phenomena related to the barrier function of LPS or its synthesis. Thereby, the knowledge derived from these MD simulations can pave the way for discovering molecules able to surmount antibiotic resistance, either circumventing LPS defenses or disrupting its synthesis. Therefore, the information gathered in the present review, both the LPS-phenomena that are being explored and the computational strategies that are used to address such investigation, may be valuable to progress on the design of novel antibiotics for treating bacterial infections. Herein, articles that have been published in the last five years and made use of MD simulations in order to investigate the above-mentioned phenomena are reviewed. With a special focus on the coupling of MD simulations with several computational methods (namely, enhanced sampling and free energy calculation approaches), we also emphasize the possibility of using special-purpose MD supercomputers for performing the simulations. The importance of employing appropriate LPS and ions parameterizations to obtain meaningful results from MD simulations is also underlined. Additionally, caveats of several works are discussed and guidelines for tackling this research are briefly presented to provide the reader with useful insights for investigating different LPS-phenomena through MD simulations. We close this work with the importance of combining MD simulations and wet-lab experiments for gaining in-depth knowledge about LPS phenomena. Finally, challenges and perspectives in the field are also discussed. Thereby, this work not only surveys the MD methods applied in LPS research, but also results notably valuable for unveiling the phenomena and strategies that are currently being explored for circumventing antibiotic resistance. Collectively, this review provides an overall picture of the importance of MD simulations to move a step forward in the fight against LPS-caused infections and bacterial resistance.

2. MD methods in LPS research

MD has been used for calculating the motions as a function of time (trajectories) of biological molecules involved in different LPS phenomena, namely, LPS barrier function and its synthesis pathway. In all-atom (AA) MD, the positions and velocities of each atom in the system are obtained using Newton’s laws of motion [38], [43], [44], [45]. Such AA description of the molecular models provides high level of detail of the system under investigation [37], [45], [46]. However, some complex biomolecular systems may not be explored through classical AA-MD simulations due to the computational demand of these simulations [38], [44]. Thereby, AA-MD simulations require short time steps (1–2 fs) in order to ensure numerical stability. Thus, the vast number of time steps involved in the simulations, along with the millions of interatomic interactions that are commonly evaluated during each time step, causes some simulations to be prohibitively expensive in terms of the required computational resources [38], [47]. Additionally, the efficient sampling of the conformational space is challenging due to the rough energy landscape of complex biomolecular systems, which is characterized by several metastable states separated by free-energy barriers well above thermal noise; thereby, high free-energy barriers make it difficult to escape from local minima, thus, hampering the visit of new conformational states. Since several biological processes take place on a time scale of seconds and beyond, facilitating the crossing of energy barriers is of paramount importance [37], [46], [48]. For that purpose, several enhanced sampling methods have been applied in LPS research, e.g. coarse-grained (CG) MD, umbrella sampling (US), replica-exchange umbrella sampling (REUS), steered MD (SMD), adaptive biasing force (ABF), and simulated annealing (SA). Additionally, the identification of appropriate reaction coordinates, which accurately quantify the progress between two thermodynamic states, is of paramount importance for analyzing and sampling the transitions between metastable states in complex molecular systems, as those that are involved in LPS research [49], [50], [51], [52], [53]. Moreover, in order to increase the computational speed and access to larger time scales, specialized supercomputers for MD simulations, such as MD-Engine, MD-GRAPE or Anton, can be used [38], [44], [54], [55], [56], [57], [58].

On the other hand, gaining insights into LPS phenomena not only calls for access to biologically meaningful length and time scales, but also could require the calculation of free-energy profiles, which enable the understanding of the thermodynamics of the event under investigation [59], [60], [61], [62]. In this regard, several methods, namely, solvated interaction energy (SIE), molecular mechanics Poisson-Boltzmann surface area (MM-PBSA) and molecular mechanics generalized Born surface area (MM-GBSA) have been applied for estimating the free energy of several phenomena in LPS research. Additionally, enhanced sampling methods such as ABF or US are also used to provide the free energy of the phenomena of interest along a reaction coordinate, that is, the potential of mean force (PMF) [48], [52], [63], [64].

It is worth mentioning that explaining in detail the theoretical basis of the above-mentioned enhanced sampling and free energy calculation methods is beyond the purpose of this review. Hence, these computational methods have been briefly summarized in the following subsections when their use for investigating different LPS phenomena is discussed.

Collectively, the complexity of the molecular systems involved in the investigation of the barrier function and synthesis pathway of LPS could require the coupling of MD simulations with different enhanced sampling methods and/or the use of specialized supercomputers for MD simulations, such as MD-Engine, MD-GRAPE or Anton, in order to access the time and length scales required to successfully examine these phenomena. Additionally, computing the free energy of key events related to LPS could also be of paramount importance in order to determine the propensity of such events to occur. In the following subsections, studies that address the investigation of the LPS synthesis, its barrier function, or strategies to surmount such barrier by combining MD simulations with different computational methods (i.e., enhanced sampling or free energy calculation approaches) and/or by resorting to supercomputers for running the simulations are reported and discussed.

2.1. LPS barrier function

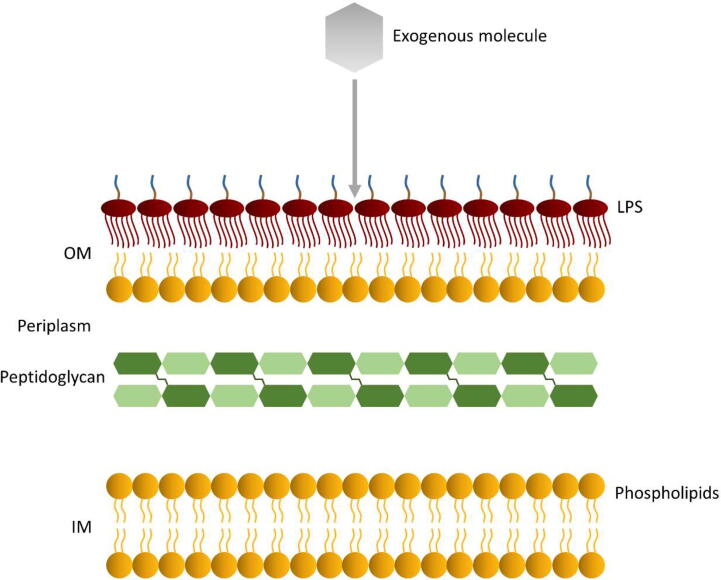
The OM of Gram-negative bacteria acts as a permeability barrier to prevent the influx of noxious agents into the cell, as seen in Fig. 2, which in turn results in the bacterial resistance to many antibiotics. LPS plays a crucial role in this barrier function; particularly, the low-permeability of LPS bilayers is influenced by regulatory pathways or by the interaction of LPS molecules with several membrane components [16], [17], [65], [66]. Therefore, exploring these mechanisms is crucial for elucidating the molecular basis of the bacterial resistance mechanism, and thus move a step forward in the discovery and development of novel antibiotics that effectively overcome such defense. Recent studies that tackle this investigation have been listed in Table 1. In this section, studies focused on the investigation of the aforementioned mechanisms are reviewed, highlighting the MD methods and the advanced computational resources that have been used to address such research.

Fig. 2.

Overview of the permeation of exogeneous agents through the multilayered structure of Gram-negative bacterial cell envelope.

Table 1.

Studies that use MD simulations to investigate phenomena related to the barrier function of LPS.^a,b

System	Production simulation software	Force field	Molecular representation	Enhanced sampling	Binding/ permeation free energy	Year	Ref.
Monophosphorylated lipid A membrane (in different salt concentration regimes: no salt, AlCl3, NaCl; one salt concentration per system)	GROMACS 2016.4	GROMOS 53A6 (*1)(*2)	AA	(-)	(-)	2021	[92]
Diphosphorylated lipid A membrane (in different salt concentration regimes: no salt, AlCl3, NaCl; one salt concentration per system)
Dihydrogen phosphate/Al3+, Na+, or Al3+ and NaCl (in different systems)
Bilayer (OL: LPS; IL: DOPC)/peptide VSAK	n.s.	MARTINI 22p (*1)	CG	(-)	(-)	2021	[93]
Symmetric bilayer (OL, IL: DOPC)/peptide VSAK
Bilayer (OL: re-LPS; IL: DMPC)/dimeric HD5	GROMACS 5.0	GROMOS 53A6	AA	SMDc	MM-PBSA	2021	[90]
Bilayer (OL: re-LPS; IL: DMPC)/dimeric HD5	GROMACS 5.0	GROMOS 53A6	AA	SMDc	(-)	2021	[89]
Symmetric V. cholerae S-LPS bilayers with different lipid A structures (one structure per system)	OpenMM 7.4.1	CHARMM36 (*2)	AA	(-)	(-)	2021	[94]
Asymmetric OM model (OL: Ra-LPS; IL: POPE, POPG, CDL)	GROMACS 5.1.2	MARTINI	CG	(-)	(-)	2021	[95]
Asymmetric OM model (OL: Ra-LPS; IL: POPE, POPG, CDL)/PMB (at different PMB/Ra-LPS ratios; one ratio per system)
Asymmetric OM model (OL: Ra-LPS; IL: POPE, POPG, CDL)/PMB (at 1:1 PMB/Ra-LPS ratio)					US (PMF, WHAM)c
Symmetric S. enterica re-LPS bilayer/Na+, K+, Ca2+, Mg2+ (one ion per system)	NAMD n.s.	CHARMM36NBFIX (*2)	AA	(-)	(-)	2020	[12]
Symmetric S. enterica re-LPS bilayer/OAH/Na+, K+, Ca2+, Mg2+ (one ion per system)					ABFc
C. crescentus O-antigen/monomeric protein RsaANTD	GROMACS 2019	CHARMM36m	AA	(-)	(-)	2020	[96]
Symmetric E. coli S-LPS bilayer	OpenMM n.s.	CHARMM36	AA	(-)	(-)	2020	[7]
Symmetric E. coli S-LPS/ECA (ECALPS, ECAPVPG, ECADPPG, ECAPSPG, ECAPG) bilayers (at different S-LPS/ECA ratios)
P. aeruginosa OM (OL: S-LPS; IL: DPPE)	GROMACS 4.6.5	GROMOS 53A6GLYC(*1) (*3)	AA	(-)	(-)	2020	[97]
P. aeruginosa OM (OL: S-LPS; IL: DPPE) OprM (embedded)
Pure POPC bilayer with OprM inserted
P. aeruginosa OM (OL: S-LPS; IL: DPPE)		MARTINI (*1) (*3)	CG
P. aeruginosa OM (OL: S-LPS; IL: DPPE) OprM (embedded)
Pure POPC bilayer with OprM inserted
Peptidoglycan-thymol	GROMACS 5.1.5	MARTINI 2.2 (*1)	CG	SMDc	US (PMF, WHAM)c	2020	[80]
		CHARMM36 (*3) CGenFF	AA
IM (DOPE, DOPG, TOCL1)	GROMACS 2018.2 and 5.1.4	CHARMM36 CGenFF	AA	(-)	(-)	2020	[33]
OM (OL: S-LPS; IL: DOPE, DOPG, TOCL1)
IM (DOPE, DOPG, TOCL1)-thymol (at different thymol/lipid ratios)				SMDc	US (PMF, WHAM)c
OM (OL: S-LPS; IL: DOPE, DOPG, TOCL1)-thymol
S. dysenteriae ShuA in DDM micelles	GROMACS 2018.2	CHARMM36m	AA	(-)	(-)	2020	[98]
S. dysenteriae ShuA in OM (OL: S. flexneri R-LPS; IL: PPPE, PVPG, PVCL2)
S. enterica Rc-LPS bilayer (lipid A phosphate groups charge: −2 or −1; one charge per system) Ca2+, K+, Mg2+, Na+, NBFIX Ca2+, CUFIX K+, CUFIX Na+ (one ion per system)	AMBER 18	CHARMM36 NBFIX CUFIX(*1) (*2) (*3)	AA	(-)	(-)	2020	[17]
S. enterica modified Rc-LPS bilayer (lipid A phosphate groups charge: −2 or −1; one charge per system) Ca2+, K+, Mg2+, Na+, NBFIX Ca2+, CUFIX K+, CUFIX Na+ (one ion per system)
S. enterica re-LPS bilayer (lipid A phosphate groups charge: −2 or −1; one charge per system) Ca2+, K+, Mg2+, Na+, NBFIX Ca2+, CUFIX K+, CUFIX Na+ (one ion per system)
S. enterica modified re-LPS bilayer (lipid A phosphate groups charge: −2 or −1; one charge per system) Ca2+, K+, Mg2+, Na+, NBFIX Ca2+, CUFIX K+, CUFIX Na+ (one ion per system)
S. enterica re-LPS bilayer (lipid A phosphate groups charge: −1) excess of Ca2+, K+, Mg2+, Na+ (one ion per system)
OM (OL: E. coli S-LPS; IL: POPE, POPG)	GROMACS 5.1.2	MARTINI 2.2 (*1)	CG	(-)	(-)	2019	[3]
OM (OL: E. coli S-LPS, R-LPS; IL: POPE, POPG)
OM (OL: E. coli S-LPS, POPE; IL: POPE, POPG)
OM (OL: E. coli S-LPS, R-LPS, POPE; IL: POPE, POPG)
Bilayer (OL: S. enterica LPS; IL: POPE)/LL-37	ANTON 2	CHARMM36(*1) (*2) (*3)	AA	(-)	(-)	2019	[66]
Bilayer (OL: S. enterica PhoPQ-modified LPS; IL: POPE)/LL-37
Bilayer (OL: S. enterica KDO2-lipid A; IL: POPE)/LL-37	AMBER 18
Bilayer (OL: S. enterica KDO2-modified lipid A; IL: POPE)/LL-37
OM bilayer (OL: hexa-acylated E. coli LPS; IL: PPPE, PVPG, PVCL2)/OmpE36	GROMACS 5.2	CHARMM36 NBFIX	AA	(-)	(-)	2019	[18]
OM bilayer (OL: hepta-acylated E. coli LPS; IL: PPPE, PVPG, PVCL2)/OmpE36
OM bilayer (OL: hexa-acylated E. coli LPS; IL: PPPE, PVPG, PVCL2)/OmpE36 (embedded)
Symmetric DMPC bilayer/OmpE36	GROMACS 4.6.5
OM (IL: POPE, POPG, CDL; OL: E. coli re-LPS)/OmpA, OmpX, OmpF, FhuA, EstA, BtuB (one protein per system)	GROMACS 2016	MARTINI 2.2 (*1) EN	CG	(-)	(-)	2019	[72]
OM (IL: POPE, POPG, CDL; OL: E. coli Ra-LPS)/OmpA, OmpX, OmpF, FhuA, EstA, BtuB (one protein per system)
OM (IL: POPE, POPG, CDL; OL: E. coli S-LPS)/OmpA, OmpX, OmpF, FhuA, EstA, BtuB (one protein per system)
OM (IL: POPE, POPG, CDL; OL: E. coli S-LPS, POPE)/OmpA, OmpX, OmpF, FhuA, EstA, BtuB (one protein per system)
DPPC membrane/OmpA, OmpX
P. aeruginosa OM (OL: re-LPS; IL: PPPE, PVPG, PVCL2)/OccK5	NAMD n.s.	CHARMM36	AA	(-)	(-)	2018	[99]
P. aeruginosa OM (OL: Ra-LPS; IL: PPPE, PVPG, PVCL2)/OccK5
P. aeruginosa OM (OL: S-LPS; IL: PPPE, PVPG, PVCL2)/OccK5
Symmetric S. enterica Rc-LPS bilayer	AMBER 16 ANTON 2	CHARMM36 (*2) (*3)	AA	(-)	(-)	2018	[67]
Symmetric S. enterica PhoPQ-modified Rc-LPS bilayer (3 modifications simultaneously)
LPS bilayer (OL: S. enterica Rc-LPS; IL: POPE)
LPS bilayer (OL: S. enterica PhoPQ-modifed Rc-LPS; IL: POPE) (3 modifications simultaneously)
Symmetric S. enterica PhoPQ-partially modified Rc-LPS bilayers
Membrane (OL: re-LPS; IL: DMPC)/dimeric and tetrameric HD5 (in different systems)	GROMACS 4.5.5	GROMOS 53A6	AA	(-)	(-)	2018	[88]
DMPC membrane/dimeric and tetrameric HD5 (in different systems)
E. coli OM (OL: re-LPS; IL: POPE, PVPG, CDL)	GROMACS 4.6.7	MARTINI 2.2 (*3) EN	CG	(-)	(-)	2017	[79]
E. coli IM (OL, IL: POPE, PVPG, CDL)
E. coli OM (OL: re-LPS; IL: POPE, PVPG, CDL) with TolC, OmpANTD monomer embedded and E. coli IM (OL, IL: POPE, PVPG, CDL) with AcrBZ, AqpZ embedded
E. coli OM (OL: re-LPS; IL: POPE, PVPG, CDL) with TolC, OmpAFL homodimer embedded and E. coli IM (OL, IL: POPE, PVPG, CDL) with AcrBZ, LacY embedded
OM (OL: P. aeruginosa or E. coli re-LPS; IL: PPPE, PVPG, CL, PVCL2) (in different systems)	NAMD n.s.	CHARMM36	AA	(-)	(-)	2017	[100]
OM (OL: P. aeruginosa or E. coli Ra-LPS; IL: PPPE, PVPG, CL, PVCL2) (in different systems)
OM (OL: P. aeruginosa S-LPS; IL: PPPE, PVPG, CL, PVCL2)
OM (OL: P. aeruginosa or E. coli re-LPS; IL: PPPE, PVPG, CL, PVCL2)/OprH (in different systems)
OM (OL: P. aeruginosa or E. coli Ra-LPS; IL: PPPE, PVPG, CL, PVCL2)/OprH (in different systems)
OM (OL: P. aeruginosa S-LPS; IL: PPPE, PVPG, CL, PVCL2)/OprH
PMB	GROMACS 4.5.4	GROMOS 54A7 GROMOS 53A6GLYCGROMOS 53A6 (*1)	AA	SA	(-)	2017	[40]
Symmetric penta-acylated lipid A /PMB				(-)
Symmetric hexa-acylated lipid A /PMB
Symmetric penta-acylated lipid AAra4N /PMB
Symmetric hexa-acylated lipid AAra4N /PMB
Symmetric penta-acylated re-LPS/PMB
TempL	GROMACS n.s.	GROMOS 53A6	AA	(-)	(-)	2017	[91]
Q3K-TempL
F5,8L-TempL
F5,8A-TempL
Lipid A bilayer/TempL				(-)	US (PMF, WHAM)c
Lipid A bilayer/Q3K-TempL

(*1) Modifications of the force field parameters were considered; check the original publication; (*2) Specific considerations for ions have been used; check the original publication;

(*3) Parameterization employed by other authors are used; check the original publication.

n.s.: Not specified.

^aFor the sake of clarity, the abbreviations and acronyms cited in this Table have been included and defined in the “List of abbreviations and acronyms” at the beginning of the manuscript.

^bThe force fields included in this Table encompass all of them used in the study, but the force fields used for each system have not been specified.

^cEnhanced sampling and/or free energy calculation methods are used to investigate the permeation of molecules into membranes.

The introduction of chemical modifications to LPS molecules represents a defense mechanism evolved in Gram-negative bacteria as a survival strategy in the host. In Salmonella enterica, the remodeling of the LPS structure is accomplished through the PhoPQ two-component regulatory system and involves the addition of a hydroxyl group, a positively charged aminoarabinose and a palmitoyl chain to the lipid A moiety; these modifications result in a stronger impermeability of the OM to several agents, such as large lipophilic drugs. Therefore, elucidating how LPS modifications enable the protection of Gram-negative bacteria from hostile environments has received outstanding attention [40], [66], [67], [68]. In this regard, Rice and Wereszczynski [67] investigated the influence of lipid A modifications on the LPS bilayer properties. For that purpose, they performed long-timescale AA-MD simulations of bilayers containing unmodified, partially modified or modified LPS with the three simultaneously added changes; these simulations were run on the Anton 2 supercomputer, thus enabling a total simulation time of 35 µs. Additionally, Martynowcycz and coworkers [66] also made use of Anton 2 for carrying out AA-MD simulations of the human antimicrobial peptide (AMP) LL-37 interacting with bilayers containing LPS with and without PhoPQ-mediated modifications in order to explore the resistance mechanism of S. enterica to LL-37. In this study, microsecond-scale simulations were also reported, with a total simulation time of 18 µs.

It should be pointed out that divalent cations bridging with LPS in order to stabilize LPS molecules in the OM of Gram-negative bacteria play also a pivotal role in limiting the penetration of external agents, such as, hydrophobic antibacterial molecules [12], [17], [69], [70]. In this regard, Rahnamoun et al. [12] explored the effect of the ionic environment (i.e. ionic radius and cation valency) on the structure and packing of LPS in the OM of Gram-negative bacteria, which in turn influences their resistance to bactericidal agents. For that purpose they coupled experiments and AA-MD [12]. Additionally, in order to move a step forward in the design of antibacterial materials, such as gold nanoparticles, they characterized the effect of different metal cations on the penetration into LPS bilayers of a model functionalization compound for coating the nanoparticles, namely oligo(allylamine hydrochloride) (OAH), since the coating of the nanoparticle surface governs LPS-nanoparticle interaction. To investigate the OAH intercalation into LPS bilayers, they carried out free energy calculations using the ABF method. This technique is based on calculating and averaging the instantaneous force exerted along the coordinate of interest; then, an external biasing force with the same modulus as the average force but opposite direction is adaptively applied [48], [64], [71].

Apart from the cation-LPS binding, tight interactions between outer membrane proteins (Omps) and LPS molecules are also involved in maintaining the low-permeability barrier that the OM of Gram-negative bacteria exhibits against toxicants, which in turn demonstrates the importance that the simulation of LPS-Omps systems has received. Nevertheless, it has been reported that investigating LPS-Omps interactions is hindered by the slow diffusion of LPS molecules in bilayers; hence, sampling LPS motions remains challenging on submicrosecond time scales [18], [72], [73]. In this regard, to improve the sampling, Shearer and coworkers [72] studied the orientations and interactions of six Omps (namely, OmpA, OmpX, BtuB, FhuA, OmpF and EstA) with several membrane environments, which differed in the LPS composition of the outer leaflet of OM models, by performing CG-MD simulations. Coarse-graining represents a popular approach to increase the time and length scales that are accessed by AA-MD simulations. Due to the simplification of the molecular models by embedding several atoms into a single bead, thus sacrificing atomistic details, the number of degrees of freedom is greatly reduced, which enables faster sampling in comparison to AA-MD simulations [37], [44], [45], [47], [74], [75]. Particularly, Shearer et al. [72] used an elastic network (EN) model for the coarse-grained modeling of the above-mentioned proteins. In EN models, proteins are represented as a network of point masses connected by springs; due to this simplified representation, MD results should be carefully interpreted when EN models are employed [76], [77], [78]. In their work, Shearer et al. [72] achieved simulation times of 30–40 µs per Omp/membrane system using coarse-grained representations of the molecules. However, they revealed that these time scales were not sufficient for the simulations to completely converge. Thereby, Shearer et al. [72] concluded that due to the slow diffusion rate of LPS molecules, simulation times longer than 60 µs may be needed to adequately sample LPS-containing membranes, and thus in order to access to such longer time scales, they suggested the use of enhanced sampling methods for future studies. Note, however, that the kinetics in CG models are not necessarily representative for the true kinetics of these systems, a fact that may be complicated further by the use of ENs.

It is worth mentioning that the study of Shearer et al. [72] was focused on providing insights into the role of Omps, and thus only the OM of Gram-negative bacteria was modeled in the simulations. However, both the IM and OM are populated by multiple proteins, which can influence their physical properties [79]. Despite the great significance of elucidating the complex relationship between both membranes and the proteins embedded in them, details are sparse due to the difficulties to perform simulations of such large systems and for carrying out experiments at the required resolution. Progress on this issue was made by Hsu and coworkers [79], who built models of the Escherichia coli cell envelope that included both the IM and OM, as well as, several membrane proteins, using a coarse-grained representation of the molecules. Specifically, these proteins were coarse-grained modeled using an EN model. From these models of the OM and IM without and with protein embedded and performing microsecond time scale CG-MD simulations, they gained insights into the effect of the number or type of membrane proteins on the dynamics of the IM and OM. However, they stated that a limitation of their work was the omission of the peptidoglycan cell wall, which came from the unavailability of CG models for peptidoglycan. Hence, future advances on the valuable study of Hsu et al. [79] rely on including the peptidoglycan cell wall in the coarse-grained model of the E. coli cell envelope. In this regard, Vaiwala et al. [80] developed a CG model for peptidoglycan; for that purpose, they used an AA model previously reported in the literature. Furthermore, they studied for the first time the interactions of the modeled peptidoglycan with thymol. To this end, they calculated the PMF of thymol insertion through the peptidoglycan layer, both at atomistic and coarse-grained levels, by performing USMD simulations; the initial configurations for such simulations were obtained from SMD simulations. In SMD simulations, the motion of selected atoms is guided by applying an external force with predefined direction through a harmonic spring [48], [81], [82], [83]. US enhances sampling by applying a biasing potential (so-called umbrella potential) to drive the system from one state to another. In USMD, independent simulations (named as windows) with different umbrella potentials are carried out to cover the pathway between these states; then, reweighting techniques such as the weighted histogram analysis method (WHAM) can be used to combine individual simulations and compute the PMF [46], [84], [85], [86], [87]. With this study, Vaiwala et al. [80] contribute to the understanding of the barrier properties of the peptidoglycan in Gram-negative bacteria, which is important for the development of novel antibiotics.

On the other hand, to gain insight into the barrier that Gram-negative bacteria exhibit for exogenous molecules, thus moving a step forward in the development of molecules to fight bacterial infections, exploring the interaction of molecules with bacterial membranes is of utmost importance. In this regard, Awang and coworkers aimed at elucidating at microscopic detail the interaction mechanism of the AMP human α-defensin 5 (HD5) and LPS; they addressed this investigation through different studies [88], [89], [90]. Specifically, they firstly analyzed both the role of LPS on HD5 activity and the effect of the common oligomeric states (dimer and tetramer) of HD5 on membrane interaction [88]. For these purposes, they examined the adsorption of dimeric and tetrameric HD5 on a LPS membrane compared to a bare phospholipid membrane (1,2-dimyristoyl-sn-glycero-3-phophocholine, DMPC, membrane) by performing AA-MD simulations. However, in this study Awang and coworkers did not observe the pore formation or the HD5 penetration into the membranes, which are crucial to advance in the elucidation of the HD5-LPS interaction, since according to the literature, the mechanism of HD5 to inactivate bacteria relies on disrupting the bacterial membrane by making a pore and penetrating into the cytoplasm [88], [89]. Thus, they conducted another study to explore the permeation of a dimeric HD5 into a LPS membrane model at atomic level. To address this investigation, they carried out SMD simulations [89]. Additionally, Awang et al. [90] studied how LPS membranes are destabilized by HD5 dimers, thus making further progress on the elucidation of key insights about the HD5-LPS interaction. For that purpose, they explored the dynamics of a dimeric HD5 along the membrane axis by simulating the HD5 dimer at different positions in a LPS membrane through AA-MD; these starting orientations were derived from SMD simulations. They concluded that despite the important insights they gained about the binding mechanism of HD5 and LPS membranes, permeation of HD5 was not observed, since this event occurs at the minute time scales. Hence, they highlighted the need of using advanced sampling techniques to elucidate the penetration mechanism of this AMP through MD simulations. It is worth mentioning that in these works of Awang and coworkers [88], [89], [90], a simplified LPS model, that is R-LPS, was used due to the complexity of bacterial LPS. In this regard, several studies have investigated the translocation of molecules (proteins, sugars, amino acids, etc.) into OMs. However, OM models with R-LPS molecules have been typically used. Although by considering OM containing R-LPS the computational complexity is reduced, the barrier that the O-antigen could offer is not investigated in these studies [33]. In order to address this issue, Sharma et al. [33] examined the interaction of thymol with bacterial S-LPS-containing OM and with the IM through AA-MD simulations, despite the challenge of modeling S-LPS atomistically because of the large number of atoms. It should be pointed out that thymol-OM and thymol-IM were simulated in different systems. Furthermore, Sharma and coworkers [33] derived the PMF of thymol insertion into the IM and S-LPS-containing OM by performing USMD simulations; SMD simulations were also carried out in order to obtain the initial configurations for US. It is noteworthy that the distance between the center of mass of the exogenous molecule and the center of mass of the bacterial membrane (e.g., the top of the OM’s OL, the IL, etc.) is typically used as the reaction coordinate to investigate the passage of molecules though the membrane [12], [33], [46], [80], [86], [89], [90], [91]. On the other hand, given that LPS is the major component of the outer leaflet of Gram-negative bacterial OMs, such leaflet had been modeled completely with LPS molecules, as indicated in Table 1. However, apart from LPS, OM's outer leaflets are also composed of other constituents that promotes the OM impermeability, such as the enterobacterial common antigen (ECA) in Gram-negative bacteria of the Enterobacteriaceae family (for instance E. coli or Klebsiella pneumoniae) [7]. Hence, including these constituents to the models of OM's outer leaflets is required in order to simulate more realistic OMs. Advances in this issue were addressed by Gao et al. [7], who modeled phosphatidyl-glycerol (PG)-linked ECA (ECA_PG) and LPS-associated ECA (ECA_LPS) molecules. They incorporated the developed ECA_PG and ECA_LPS models into symmetric E. coli S-LPS bilayers and performed AA-MD simulations to characterize several bilayers properties and the conformations of ECA and LPS. On the basis of the aforementioned computational procedures, it can be highlighted that the works of Shearer et al. [72], Hsu et al. [79], Vaiwala et al. [80], Sharma et al. [33], and Gao et al. [7] contributed to a great extent to the development of realistic models of the Gram-negative bacterial cell envelope, which are key to perform meaningful MD simulations.

In view of the studies that have been discussed throughout this section, it can be rationalized that three key issues should be considered for successfully shedding light into the barrier properties of the Gram-negative bacterial cell envelop, where LPS plays a pivotal role. These issues, which have been addressed below, are: (i) the complexity of the biological systems to be investigated and the challenge of sampling LPS motions on submicrosecond time scales, (ii) the need of using suitable representations of the bacterial cell envelope to perform meaningful MD simulations, and (iii) the importance of computing the energetics of translocation of exogenous molecules across the cell envelope to assess its barrier properties.

Investigating the mechanisms that influence the impermeability of LPS bilayers could be challenging due to the complexity of the biological systems that have to be explored and the difficulty of sampling LPS motions on submicrosecond time scales [18], [72]. Therefore, several strategies need to be adopted for successfully investigating several phenomena related to the barrier function of LPS, such as reducing the level of detail in the description of the molecules (i.e., use CG models for molecular representations), use enhanced sampling methods or resorting to specialized supercomputers to run the MD simulations. In this way, bridging the gap between the time scales at which biological processes occur and the accessible time scales of MD simulations could be addressed.

On the other hand, despite the importance of accessing to biologically relevant time scales, the cornerstone for understanding the molecular basis of the bacteria impermeability against exogenous agents is the use of suitable representations of the bacterial cell envelop to carry out meaningful MD simulations [33], [80]. Therefore, advances in modeling the cell envelope of Gram-negative bacteria have been fulfilled as it was previously detailed. Hence, developing a complete model that includes simultaneously as much elements as possible, namely, the IM, OM, peptidoglycan, and membrane proteins populating the IM and OM would lead to more meaningful insights. Additionally, as rationalized by Sharma et al. [33] and Gao et al. [7], OM models should comprise S-LPS (instead of R-LPS) as well as other molecules, such as, ECA or capsular polysaccharides, since these membrane constituents and the O-antigen units could also offer a barrier to the translocation of molecules into the bacteria. Hence, the works of Hsu et al. [79], Vaiwala et al. [80], Sharma et al. [33], and Gao et al. [7] could be used as a basis for the development of realistic models for the Gram-negative bacterial cell envelope. However, given the complexity of such realistic cell envelop, strategies, such as the use of special-purpose MD supercomputers and/or enhanced sampling methods would be required to obtain in-depth knowledge about the shield that Gram-negative bacterial cell envelope provides.

Finally, computing the energetics of translocation across the bacterial cell envelop enables identifying the barriers that hamper the passage of exogenous molecules (e.g., antimicrobial agents) through it, which is of paramount importance for gaining molecular insights into the interaction and transport of these molecules within the bacterial cell envelope. As described in the studies of Rahnamoun et al. [12], Sharma et al. [33], and Vaiwala et al. [80], the permeation free energies of several molecules into OM, IM or peptidoglycan models can be determined using different computational methods, such as, ABF or USMD.

2.2. LPS synthesis and transport

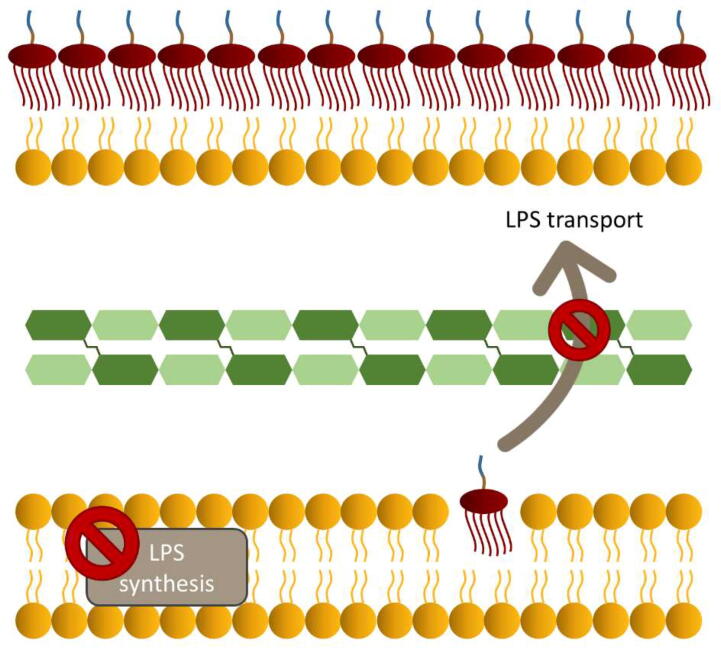
In order to tackle the antibiotic resistance challenge, not only the mechanisms that are involved in the Gram-negative bacteria protection by LPS molecules have been investigated, but the scientific community has also focused its efforts on disrupting the synthesis of the OM, as illustrated in Fig. 3. Specifically, molecules that take part in the biosynthesis pathway of LPS have been considered attractive targets for developing antimicrobial agents, since LPS is a crucial component for creating the OM and its absence makes bacteria more sensitive toward several exogenous agents, such as hydrophobic antibiotics [24], [34], [101], [102]. Hence, contributions to the design of inhibitors for such molecules have been made using MD simulations and free energy calculations, as reported in Table 2.

Fig. 3.

Representation of the tactics for disrupting the synthesis of Gram-negative bacterial OMs.

Table 2.

Studies that use MD simulations to investigate phenomena related to the synthesis and transport of LPS.^a,b

System	Production simulation software	Force field	Molecular representation	Enhanced sampling	Binding/process free energy	Year	Ref.
Apo K. pneumoniae LptDE embedded in bilayer (OL: re-LPS; IL: CDL, POPG, POPE)	GROMACS 2018.6 or 2019.1	MARTINI 2.2 EN CHARMM36	AA or CG/AA (*1)	With or without PLUMED(*2) (*3)	(-)	2021	[118]
Re-LPS-bound K. pneumoniae LptDE embedded in bilayer (OL: Re-LPS; IL: CDL, POPG, POPE)
Thanatin-bound K. pneumoniae LptDE embedded in bilayer (OL: re-LPS; IL: CDL, POPG, POPE)
A. baumanii KdsC/top 3 molecules from Asinex database	AMBER 16	AMBER ff03.r1 GAFF	AA	(-)	MM-GBSA MM-PBSA	2020	[24]
Apo S. flexneri LptDE embedded in DMPE bilayer	Anton 1 AMBER n.s.	CHARMM36	AA	SMD	REUS (PMF, WHAM)	2020	[4]
S. flexneri LptDE embedded in DMPE bilayer with LPS bound in the N-terminal domain of LptD
P. aeruginosa LptDE embedded in DMPE bilayer				(-)	(-)
P. aeruginosa LptDE embedded in OM model (OL: E. coli Ra-LPS; IL: POPE)
A. ferrooxidans GnnA/UDP-GlcNAc/NAD+	AMBER 18	GAFF2	AA	(-)	(-)	2020	[124]
Apo K. pneumoniae HEP-III	GROMACS 5.1.4	AMBER ff99SB	AA	(-)	(-)	2019	[34]
K. pneumoniae HEP-III/ADP					MM-PBSA
K. pneumoniae HEP-III/top 2 molecules from Asinex database
N. meningitidis KDO8P synthase/3 biphosphate inhibitors (one inhibitor per system)	AMBER 16	AMBER ff14SB	AA	(-)	MM-PBSA MM-GBSA SIE	2019	[101]
P. aeruginosa LpxH/Lipid X	AMBER 14	AMBER ff14SB GAFF	AA	(-)	(-)	2018	[125]
P. aeruginosa LpxH F82G/L83G mutant
Apo P. aeruginosa LpxH from apo and Lipid X bound crystal structures (in separate systems)
WT E. coli LptC dimer	Desmond n.s.	n.s.	AA	(-)	(-)	2018	[126]
Mutated E. coli LptC dimer
Apo E. coli HepI	Desmond n.s.	OPLS-AA 2005	AA	(-)	(-)	2017	[20]

(*1) The original publication does not explicitly indicate the molecular representation for each studied system. (*2) The original publication does not explicitly indicate in which of the studied systems PLUMED was used. (*3) When the PLUMED plugin was used, the specific enhanced sampling method has not been detailed. For specific information about the PLUMED plugin, the reader is directed to Ref. [127].

n.s.: Not specified.

^aFor the sake of clarity, the abbreviations and acronyms cited in this Table have been included and defied in the “List of abbreviations and acronyms” at the beginning of the manuscript.

^bThe force fields included in this Table encompass all of them used in the study, but the force fields used for each system have not been specified.

For instance, identifying inhibitory molecules for enzymes involved in the synthesis of KDO has received significant attention, due to the essentiality of this LPS constituent for the bacterial viability since the lack of KDO residues in LPS leads to the cease of cell growth [24], [101]. In this regard, Araújo et al. [101] attained a deeper understanding on the inhibition mechanism of Neisseria meningitidis 3-deoxy-d-manno-octulosonate 8-phosphate (KDO8P) synthase by several inhibitors. Two of these inhibitors were reported in the literature to be the top inhibitors for this enzyme; however, the molecular level details regarding their mode of action remained unknown. Additionally, the third inhibitor consisted of a molecule the authors hypothesized that resulted from the hydroxylation of one of the previous inhibitors. Araújo and coworkers [101] performed AA-MD simulations of N. meningitidis KDO8P synthase-inhibitor complexes and estimated their free energy of binding. For computing the enzyme-ligand binding free energy, they employed three methods, namely, MM-GBSA, MM-PBSA and SIE; according to their results, the same ranking for the potential inhibitors was obtained, which was in agreement with experimental data published previously, regardless of the considered method. MM-GBSA, MM-PBSA and SIE are end-point free energy methods, since they only sample the initial and final states of the system; thus, they offer a good compromise between accuracy and efficiency [103], [104], [105], [106], [107]. Other methods for providing more accurate free-energy calculations are the so-called alchemical methods, such as free energy perturbation (FEP) and thermodynamic integration (TI). However, the balance between the convergence of the free energy difference and the computational cost for big and flexible molecules hampers their use for computing the free energy in these systems. Specifically, achieving the convergence when the system under investigation involves slow structural transitions or large environmental reorganizations is difficult [105], [108], [109]. According to the MM-GBSA and MM-PBSA methods, the free energy of the free ligand, free receptor and ligand-receptor complex are calculated from the gas-phase molecular mechanics (MM) energy (that includes the internal, electrostatic and van der Waals energies), the polar and nonpolar solvation free energies, and the entropy upon ligand-receptor binding. The polar solvation free energy can be obtained using either the Poisson-Boltzmann equation (MM-PBSA) or a Generalized-Born model (MM-GBSA) [103], [105], [110], [111]. On the other hand, the SIE approach estimates the binding free energy from the intermolecular interaction energy in the bound state and the desolvation free energy. Both the interaction and desolvation contributions include a nonpolar and an electrostatic component [60], [107]. These methods, however, are approximate in the sense that important assumptions are made, e.g., concerning the validity of single-trajectory approaches [112], [113]. Additionally, Gulistan et al. [24] identified three potential inhibitors for Acinetobacter baumannii 3-deoxy-d-manno-octulosonate 8-phosphate phosphatase (KdsC) by combining several in silico methods. To this end, they shortlisted several hits from the Asinex database using a docking-based virtual screening approach. Subsequently, they performed AA-MD simulations of A. baumannii KdsC in complex with the filtered inhibitors that were neither toxic or mutagenic, and computed the enzyme-inhibitor binding free energy using the MM-GBSA and MM-PBSA methods. From these calculations, they determined the nature of the interactions (namely, electrostatic or van der Waals) that dominated the KdsC-inhibitor binding and ranked the potential hits according to the binding free energy value; they obtained similar trends with both end-point methods.

On the other hand, the enzyme heptosyltransferase-III (HEP-III) also plays an important role in the synthesis of LPS; particularly, HEP-III takes part in the transfer of the third heptose to the inner core oligosaccharide. Given that the truncation of LPS results in an increase of the sensitivity that Gram-negative bacteria exhibit to hydrophobic antibiotics, HEP-III has been considered an attractive drug target [34]. Panda and coworkers [34] identified hit compounds that could be further employed for the design of inhibitors against K. pneumoniae HEP-III. To this end, they performed a pharmacophore-based virtual screening of the Asinex database followed by molecular docking of the filtered compounds. In order to elucidate the molecular basis underlaying the K. pneumoniae HEP-III inhibition, they subsequently carried out AA-MD simulations of K. pneumoniae HEP-III bound to the top two hit molecules derived from the pharmacophore-based virtual screening and molecular docking, and also to adenosine diphosphate (ADP), which was considered as the reference ligand since it was used to develop the pharmacophore model. Finally, they assessed the propensity of the ligands to bind to the enzyme by estimating the binding free energy using the MM-PBSA method.

Due to the essentiality of the proteins that comprise the LPS transport (Lpt) machinery, which accomplish the transport of LPS molecules from the IM (where LPS is synthesized) to the OM, these proteins have also become potential targets for developing novel antibiotics [4], [114]. In this regard, Lundquist and Gumbart [4] elucidated the process of LPS insertion into the outer leaflet of the OM by the two-Omp complex LptDE. For that purpose, they employed the Anton 1 supercomputer for performing almost all the AA-MD simulations, although some of them were extended using the Amber simulation package on graphics processing units (GPUs), reaching a total simulation time greater than 14 µs. Apart from investigating the conformational dynamics of Shigella flexneri and Pseudomonas aeruginosa LptDE, that could be crucial for LPS insertion, they also gained insights into the formation of a lateral gate on S. flexneri LptD, which has been postulated to be a step required for LPS to enter into the OM. Particularly, they assessed the effect of the presence of a LPS molecule bound in the N-terminal domain of LptD on such gate opening by measuring the distance between the LptD N- and C-terminal β-strands over time and by computing the free energy of gate opening. In contrast to the above-mentioned studies where the interaction free energy was estimated for assessing the binding propensity between molecules, Lundquist and Gumbart [4] performed free energy calculations to determine the energetic cost for the separation of the β-strands involved in the gate opening. To obtain the open state, SMD simulations were performed. Free energy calculations of lateral gate opening for S. flexneri apo-LptD and LptD-LPS systems were computed using the REUS method and PMFs were derived from the REUS data using WHAM. Hence, to perform this investigation they defined the separation of the β1 and β26 strands from S. flexneri LptD in the apo and LPS-bound states as the reaction coordinate. In the REUS method, which is a generalization of the US approach, simulations differing in the temperature and/or in the umbrella potentials, are performed; during the simulation, the temperature and/or the umbrella potentials are exchanged between a pair of replicas. Afterwards, as with US simulations, data from REUS simulations are processed using WHAM [84], [87], [115], [116], [117].

On the other hand, further progress in the elucidation of the LPS insertion into the OM mediated by the LptDE complex was made by Fiorentino and coworkers [118]. Thereby, they explored how the binding of LPS and the AMP thanatin influence the conformational dynamics of K. pneumoniae LptDE coupling experiments and MD simulations. Specifically, they shed light into the mechanism by which bacterial LPS impacts LptDE dynamics by performing AA-MD simulations of the LptDE complex in its closed and open states. It should be pointed out that to insert the LptDE complex in the bilayer, they employed a serial multiscale approach, since this strategy has been recognized as powerful for incorporating proteins into lipid bilayers [119]. Hence, they firstly carried out CG-MD simulations of LptDE embedded in a bilayer; the final snapshot of the simulations was converted back to atomistic resolution and AA-MD simulations were run. This way, enhanced sampling by coarse-graining enables efficiently attaining the appropriate insertion of LptDE into the bilayer, whereas the AA-MD simulations provide the atomic details that are required to accurate investigate the system under study. This strategy is also known as backmapping or reverse mapping and makes possible merging the efficiency of CG models and the accuracy of AA ones, which in turn enables reaching larger time and length scales while ensuring atomic details [120], [121], [122], [123].

In light of the studies of Araujo et al. [101], Gulistan et al. [24], and Panda et al. [34], it can be rationalized that investigating the interaction of target enzymes and potential inhibitors can be addressed by AA-MD simulations. Hence, the use of enhanced sampling methods and/or special-purpose MD supercomputers is not needed, since these are simpler systems compared to those that are modeled for exploring phenomena related to the LPS pathway, which requires adopting the above-mentioned strategies. On the other hand, the works discussed throughout this section demonstrate that free energy calculations can be performed for different purposes. More specifically, the binding free energy to assess the binding ability of the inhibitors (ligands) towards the enzyme (receptor) may be estimated using end-point methods, which considerably reduces the computational cost of the calculations compared to alchemical free-energy methods [105]. However, determining the energetic cost of a stage (e.g., the lateral gate opening in LptD) requires calculating the free energy as a function of a reaction coordinate. For that purpose, methods such as US (or REUS) are used instead of end-point methods. This is similar to the calculation of the permeation free energy to determine the existence of barriers for the passage of exogenous molecules across bacterial membranes that was discussed in section 2.1, where the use of ABF or USMD for that purpose was pointed out.

On the basis of the strategies followed in the above-mentioned studies, which contribute to the design of molecules able to disrupt LPS synthesis, it can be recognized that the role of MD simulations in these investigations entails elucidating the molecular mechanism of the inhibition of enzymes involved in the LPS synthesis and unraveling the key steps of LPS synthesis. Hence, these works demonstrate that the coupling of MD simulations and free energy calculations provides valuable insights into the molecular basis of both the synthesis pathway of LPS molecules and the interaction mechanisms between the targets and hit compounds. Particularly, gaining insights into key steps of the LPS synthesis pathway facilitates the identification of enzymes as targets for inhibitors design. It is noteworthy that crucial knowledge for the design of these inhibitors is derived by combining MD simulations of the target-hit complex and free energy calculations. In this way, the nature of the binding and the residues that are key for the interaction can be identified, and the number of potential hits can be reduced by ranking them according to their affinity to the target. This information might be valuable for designing inhibitors with strong ability to target enzymes involved in LPS synthesis.

3. Force fields in LPS research

In the previous sections, one of the bottlenecks of MD simulations, namely, the access to biologically relevant time scales, has been addressed, and the use of several enhanced sampling methods to overcome this limitation has been discussed. However, the applicability of MD simulations is also limited by the accuracy of the force fields that are employed to describe the interactions between particles (i.e., atoms in AA or beads in CG simulations) [44], [45], [74]. Particularly, simulating LPS bilayers and OM systems, which is key for investigating and surmounting the barrier function of LPS as deduced from the systems included in Table 1, is hampered by the parameterization of LPS [17], [128]. Thereby, LPS parameterizations have been developed for several force fields (such as CHARMM36, and GROMOS) over the years; differences between these parameterizations include the LPS protonation state [17], [129]. It should be pointed out, however, that force-field parameters for LPS are typically transferred from the description of similar groups in the force fields rather than specifically parameterized from e.g. quantum–mechanical calculations on LPS. According to Table 1, GROMOS 53A6 and CHARMM36 are the force fields for LPS commonly used in AA-MD simulations, whereas the MARTINI force field is utilized when LPS is modeled at the CG level. The CHARMM LPS force field and corresponding CG models assign a charge of −2 to the lipid A phosphates, whereas the studies using GROMOS-based force fields and MARTINI models typically assign a charge of −1 to these groups [17]. Investigating how phosphate charge affects bilayer properties was addressed by Rice and coworkers [17] to characterize these differences of the force fields. They concluded that at or near physiological pH the charge of the lipid A phosphate groups should be −1 in order to obtain more reasonable results. Thereby, they recommended that LPS force field parameterizations should be updated to correct the charge of the lipid A phosphate groups.

Apart from LPS parameterization, appropriate ions parameterizations are also key to gain reliable insights from MD simulations of LPS systems, since simulations of charged lipid bilayers are seriously affected by the overbinding of ions to the lipid head groups [130], [131], [132]. For instance, Luna et al. [94] employed parameters for Ca²⁺ ions that were calibrated to match experimental data. On the other hand, Rahnamoun et al. [12] found that binding of cations (Na⁺ and K⁺) to LPS molecules was overestimated when simulations of LPS bilayers loaded with these monovalent cations were performed considering the standard CHARMM36 parameters. Therefore, they used a modified CHARMM36 force field with the non-bonded fix (NBFIX) parameters, which led them to in silico determined effective mean molecular areas per LPS that were in agreement with LPS mean molecular areas derived from Langmuir film balance experiments.

Overall, deriving reliable insights about the LPS barrier function from MD simulations requires the use of appropriate parameterizations for the LPS molecules and for the ions involved in the system. Hence, the considerations underlaying the different force fields should be carefully inspected so that the systems under investigation could be accurately simulated.

4. How are MD simulations and wet-lab experiments combined in LPS research?

The important role that MD simulations can play in the fight against antibiotic resistance, either shedding light into the barrier function and synthesis pathway of LPS or designing molecules for circumventing LPS defenses or disrupting its synthesis, has been demonstrated in previous sections. However, various of these reviewed studies do not use exclusively MD simulations, but they combine this in silico method with wet-lab experiments. Coupling MD simulations and experiments in different ways yields complementary views of the phenomena to be investigated. Understanding how MD and wet-lab experiments are combined for moving a step forward in LPS research is important in order to endorse the significance of this in silico method for tackling the challenge of antibiotic resistance. Therefore, we will now discuss representative examples of studies that combine MD and wet-lab experiments in order to move forward on the design of strategies to overcome antibiotic resistance, thus emphasizing the crucial implications that MD has on the experimental work.

MD is typically used to provide insights that promote the comprehension of the molecular basis of the investigated phenomena and to support the experimental findings. For instance, Schultz et al. [126] made use of different experimental techniques and MD simulations in order to characterize point mutations for disrupting the dimerization of the LPS transport protein LptC. While they elucidated the mutants responsible for disrupting the dimer and assessed the functional implications of monomeric LptC, MD simulations enabled them to unveil both the molecular interactions that guide LptC dimerization and how the mutations affect such interaction. Furthermore, Rahnamoun et al. [12] combined MD simulations and experiments to determine how the ionic environment affects LPS packing. Although MD simulations enabled them to gain a molecular view about these phenomena, they also determined the degree of LPS aggregation computational and experimentally. Thereby, they compared the LPS mean molecular area derived in silico and experimentally and found that both of them were in agreement.

Furthermore, MD simulations have been also used to study events that cannot been experimentally investigated, for example, due to experimental difficulties, the impossibility of experimentally measure some properties or because the process under investigation takes place in time scales where experimental observations could not be derived. Thus, since the rapidity at which the initial interactions between LPS and the human AMP LL-37 occur prevents them from being studied at the molecular level by experimental techniques, Martynowycz et al. [66] combined MD simulations and experiments in order to investigate how PhoPQ-mediated S. enterica LPS modifications change the bacterial susceptibility to LL-37. Specifically, they performed MD simulations in order to elucidate the initial stage of the LL-37/LPS association, whereas the equilibrium states of LPS monolayers both before and after their interaction with LL-37, which take place at longer time scales, were experimentally addressed. Additionally, experimental difficulties (e.g., low solubility in water of lipid A, or the inhomogeneity of lipid A preparations) may hinder the investigation of the mechanism by which polymyxins permeabilize the bacterial OM; however, MD simulations could enable the elucidation of such mechanism, as demonstrated by Santos and coworkers[40], who depicted the initial steps of PMB mechanism of action through AA-MD simulations. Similarly, molecular insights into the permeation of small molecules into bacterial IM and OM were provided by Sharma et al. [33] combining MD simulations and experiments. Specifically, they were unable to experimentally determine the location of the free-energy barrier for translocation; however, they found, through MD simulations and free energy calculations, the presence of a barrier to thymol insertion in the core oligosaccharide region.

Finally, MD simulations can drive experimental work when findings derived in silico are used for guiding the performance of experiments. In this regard, Bohl and coworkers [125] used MD simulations to disclose important knowledge about the substrate binding in the cap of LpxH, an enzyme involved in LPS synthesis. The simulations not only enabled them to provide evidence about the dynamic character of such binding cap, which was not apparent from the LpxH crystal structure, but also, to identify key residues for LpxH activity. Subsequently, the in silico predicted residues were experimentally mutated, and Bohl et al. [125] confirmed the importance of such residues for the LpxH activity.

Collectively, taking advantage of the microscopic details that MD provides and the evidence of wet-lab experiments is crucial for progressing on the development of strategies for fighting against antibiotic resistance. Particularly, in this section we have demonstrated that MD simulations can be combined with experiments in different ways. Thereby, MD can be used to study phenomena that cannot be experimentally accessed, thus complementing experimental findings. Additionally, when performed prior to experiments, MD insights can guide experimental work. On the other hand, some properties of the system under investigation can be both in silico and experimentally determined, thus supporting the validity of both results. All in all, regardless of how they are combined, the important knowledge that can be derived from the coupling of MD and experiments is key for shedding light into LPS phenomena, and thus contribute to overcome the challenge of Gram-negative bacteria resistance.

5. Summary and outlook

The role of LPS in the emergence of antibiotic resistance calls for the investigation of LPS phenomena that promote such barrier against the influx of exogenous molecules (e.g., antibiotics) intro Gram-negative bacteria. In this regard, due to the in-depth insights that MD provides, this in silico method, on its own or in combination with enhanced sampling and/or free energy calculation methods, has become a potential tool for shedding light into the mechanisms that underlie LPS synthesis and barrier function and for moving forward on the design of molecules for overcoming LPS defenses or disrupting its synthesis, as it has been demonstrated throughout this work. Particularly, the use of enhanced sampling approaches coupled with MD simulations has enabled bridging the gap between the biologically meaningful length and time scales and those that can be accessed by MD simulations. Despite the outstanding advances made in LPS research through MD simulations, further progress in the fight against antibiotic resistance relies on exploring phenomena that take place on time and length scales that could be beyond the reach of current day MD simulations. In this regard, the complexity of the Gram-negative bacterial cell envelope hampers the development of more realistic models of the bacterial envelope, that could include simultaneously the OM, IM and peptidoglycan cell wall, several components in the outer leaflet of the OM, apart from LPS, and proteins in both the inner and outer membranes, etc. Additionally, the system size makes it extremely challenging to simulate the whole Gram-negative bacterial membrane (e.g., E. coli has a radius of about 0.5 µm and is 1–2 µm long) [133] on relevant time scales; moreover, the slow diffusion of LPS molecules hinders the investigation of the equilibrium behavior of LPS systems. At the other end of the spectrum, quantum-level calculations are also required in order to procure a complete understanding about several LPS-related phenomena, such as, the enzymatic processes that take place in bacterial membranes and that can contribute to the antibiotic resistance of Gram-negative bacteria. Under those situations, performing multiscale MD simulations could be understood as a potential strategy to move forward on the elucidation of LPS phenomena that assist the surmounting of the resistance to antibiotics of Gram-negative bacteria.

On the whole, this work provides a comprehensive overview about the significance of MD simulations for exploring and understanding LPS phenomena, and demonstrates that this in silico method has become an essential tool for the rational design of strategies for surmounting the resistance to antibiotics of Gram-negative bacteria. We have reviewed articles that cover the last five years of LPS research, focusing specially on the use of MD combined with several computational methods (i.e., enhanced sampling and free energy calculation methods), and highlighting the possibility of using special-purpose MD supercomputers. We have also emphasized the role of MD simulations for influencing experimental work and the importance of appropriate LPS and ions parameterization to obtain reliable results. Despite the challenge of accessing to longer time scales and larger and more complex systems that MD is facing, this review highlights how deeply MD simulations are embedded in the fight against antibiotic resistance and foresees great hopes for MD in that field.

CRediT authorship contribution statement

Cristina González-Fernández: Investigation, Writing – original draft, Writing – review & editing, Visualization. Eugenio Bringas: Conceptualization, Supervision. Chris Oostenbrink: Writing – review & editing. Inmaculada Ortiz: Writing – review & editing, Supervision, Project administration, Funding acquisition.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.