Input integration by the circadian clock exhibits nonadditivity and fold-change detection

Significance

To optimize the cellular response, cells integrate information from diverse signals. The circadian clock is an internal mechanism that anticipates environmental daily changes, relying on various inputs to estimate the time of day. Yet, little is known regarding modes of input integration by the clock. Here, we show that a combination of different signals elicits a wide range of phase response, which often cannot be readily predicted based on the response to the individual signals. Additionally, we found that the response can follow the relative change in the signal strength, suggesting the potential involvement of a fold-change detection mechanism. Our study identifies principles of input integration by the circadian clock and promotes our understanding of clock resetting.

Abstract

Circadian clocks are synchronized by external timing cues to align with one another and the environment. Various signaling pathways have been shown to independently reset the phase of the clock. However, in the body, circadian clocks are exposed to a multitude of potential timing cues with complex temporal dynamics, raising the question of how clocks integrate information in response to multiple signals. To investigate different modes of signal integration by the circadian clock, we used Circa-SCOPE, a method we recently developed for high-throughput phase resetting analysis. We found that simultaneous exposure to different combinations of known pharmacological resetting agents elicits a diverse range of responses. Often, the response was nonadditive and could not be readily predicted by the response to the individual signals. For instance, we observed that dexamethasone is dominant over other tested inputs. In the case of signals administered sequentially, the background levels of a signal attenuated subsequent resetting by the same signal, but not by signals acting through a different pathway. This led us to examine whether the circadian clock is sensitive to relative rather than absolute levels of the signal. Importantly, our analysis revealed the involvement of a signal-specific fold-change detection mechanism in the clock response. This mechanism likely stems from properties of the signaling pathway that are upstream to the clock. Overall, our findings elucidate modes of input integration by the circadian clock, with potential relevance to clock resetting under both physiological and pathological conditions.

Circadian clocks are self-sustained biological oscillators with a period length of approximately 1 d. These clocks are ubiquitous among light-sensitive organisms and regulate various rhythmic activities in alignment with the geophysical daily cycles (1, 2). To remain aligned with the environment, circadian clocks are constantly synchronized by external signals, known as zeitgebers or timing cues, in the process of phase resetting (3, 4). In mammals, clocks are located in virtually every cell in the body, consisting of a molecular network of transcriptional-translational negative feedback loops. While the central clock in the suprachiasmatic nucleus in the brain is synchronized predominantly by light input from the eyes through the retino-ophthalmic tract, peripheral clocks are in general light insensitive and receive temporal information via numerous hormonal, neuronal, and metabolic routes (4).

Over the years, a wide variety of signaling molecules have been suggested to reset circadian clocks (5–9). In most cases, the effect of these signals on the clock was tested individually. However, in the body, circadian clocks are exposed to a multitude of potential timing cues with complex temporal dynamics (10). Hence, the response of the clock is likely shaped by the integration of multiple resetting inputs. However, the principles underlying input integration by the clock are largely unexplored, mostly due to technical challenges. A key feature of circadian resetting is that the extent and direction of the phase shift induced by a stimulus is time dependent. Therefore, composing a phase transition curve (PTC), namely a representation of the phase after the intervention as a function of the phase before the intervention, is necessary to thoroughly depict the resetting effect of a given signal (11). However, PTC experiments are usually low throughput and labor intensive, thus obtaining PTCs for combinations of signals was impractical. Recently, we established Circa-SCOPE, a method for high-throughput PTC reconstruction based on single-cell live microscopy (12). This system efficiently produces dozens of high-resolution PTCs simultaneously, and therefore enables the comprehensive dissection of the input integration of multiple signals by the circadian clock.

In this study, we examined how the clock integrates signals given either simultaneously or sequentially. We discovered that combinations of signals can give rise to complex nonadditive outcomes, which cannot be simply predicted based on the response to each of them individually. Moreover, we show that the background levels of an input can inhibit subsequent resetting by the same input. We further identified the involvement of signal specific fold-change detection (FCD) mechanism in clock resetting. Taken together, our results highlight the complexity of input integration by the circadian clock and unravel nonadditivity and FCD as underlying features.

Results

Experimental Design.

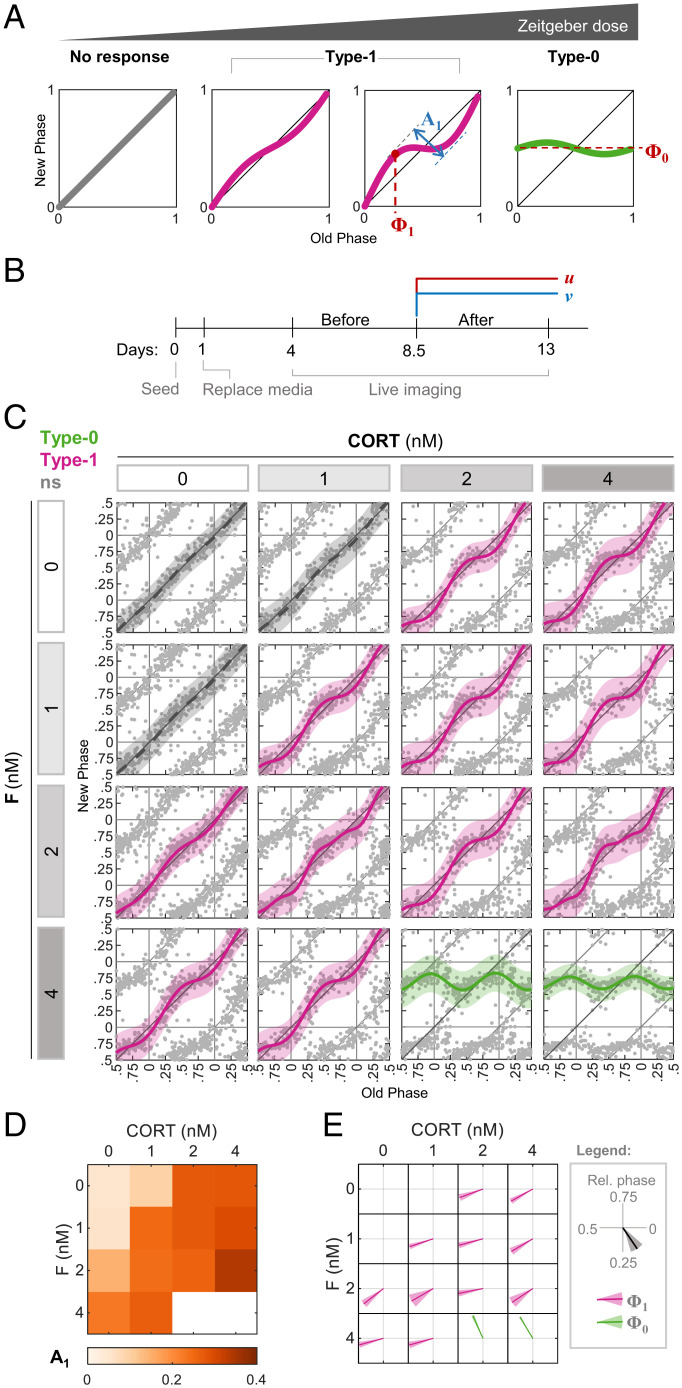
The characteristics of PTCs change in a typical dose-dependent manner (Fig. 1A) (11–15). A low dose of a signal normally elicits a “type 1” response, in which the mean slope of the PTC is 1. As the dose increases, the maximal phase delay and advance (the “PTC amplitude,” A₁ = max delay − max advance) grow monotonically in a dose-dependent manner, until a discontinuous transition occurs from type 1 to a type 0 response, featuring a mean slope of 0, and maximal PTC amplitude. Type 1 and type 0 responses can be further characterized by the phase of maximal shift (denoted here as Φ₁) and the mean new phase (Φ₀), respectively (Fig. 1A). Often, Φ₁ and Φ₀ are signal specific. This multidimensional and discontinuous nature of PTCs should be taken into consideration when examining the response not only to each single input but also to combination of signals.

Fig. 1.

Effects of the simultaneous administration of combinations of stimuli on PTC characteristics. (A) Schematic depiction of the progressive change in PTC in response to increasing dose of the zeitgeber, from no response through type 1 topology to type 0. We define the following parameters for analysis: type 1 PTC amplitude (A₁) is the difference between the maximal phase advance and the maximal phase delay; type 1 PTC phase (Φ₁) is the old phase, in which the maximal phase delay is induced; and type 0 mean new phase (Φ₀) is the average new phase induced across all of the old phases. Across the study, phases are given in relative units (normalized to the period length). (B) Schematic depiction of the experimental design. At 1 d postseeding, media was replaced, and live imaging started after 3 additional days. Two treatments (u and v) were added simultaneously to the culture in different combinations 8.5 d postseeding. (C) PTC matrix of the response to CORT and F given in different concentrations, as reconstructed by Circa-SCOPE. Each point represents the phases of a single cell. Data are double plotted for clarity. Pink: type 1 resetting model ± 95% confidence interval, green: type 0 resetting model ± 95% confidence interval, ns: nonsignificant (P > 0.05) in bootstrapping test for response, n = 138 to 267 cells per concentration (SI Appendix, Dataset S1). (D) Type 1 PTC amplitude in each combination of CORT and F from (C). (E) Vector plot of the type 1 PTC phase (pink) and type 0 mean new phase (green) in each combination of CORT and F from (C). Vector direction represents the relative phase ± SD from bootstrapping.

To examine the combinatorial response to multiple inputs given simultaneously, we used murine fibroblasts expressing a dual reporter system (NIH 3T3 H2B-mCherry Reverbα-Venus-NLS-PEST [NR-RVNP]) along the circadian single-cell oscillators PTC extraction (Circa-SCOPE) protocol (12) (Fig. 1B). In short, 1 d after seeding, culture media was replaced, and cells were allowed to desynchronize for 3 d. Next, cells were imaged for a total of 9 d. In the middle of the recording period (8.5 d postseeding), the cells were treated with pharmacological resetting agents at various concentrations, within the active and nontoxic range (12), either individually or in combination.

Integration of Inputs Acting through the Same Signaling Pathway.

We studied the effects of compounds that act through the same signaling pathway. We tested the corticosteroids corticosterone (CORT) and hydrocortisone (F), both of which act through the activation of the glucocorticoid receptor. As expected, both compounds induced similar immediate responses of core clock gene expression, as evidenced by analysis of their transcript levels 3 and 6 h posttreatment (SI Appendix, Fig. S1). PTC analysis of each compound at different concentrations showed similar profiles (Fig. 1C). Analysis of the combinatorial effect of the two compounds showed that the effect on A₁ is mostly stronger in response to the combination compared to the corresponding individual doses (Fig. 1D). To compare the effects on Φ₁ and Φ₀, we used a vector representation (Fig. 1E) in which the phase for each combination is represented by the direction of the vector, and the shading around the vector marks the variance. In the case of CORT and F, the Φ₁ was relatively similar for all of the combinations (Fig. 1E).

To obtain a quantitative measure for these observations, we developed a bootstrapping-based method to classify the mode of interaction between the two compounds. Intuitively, the null hypothesis for the interaction between two compounds should be “additivity,” often defined as f(a+b) = f(a) + f(b), where f is the response to certain doses of inputs a and b. However, in the case of phase responses, the output of the system is multidimensional, and the dose curves are nonlinear, even per single input, especially in the vicinity of the transition to type 0. Given this complexity, we built upon an approach that was applied to quantify combinatorial effects in bone morphogenetic protein signaling (16). We defined “linear additivity” as PRC(a,0) + PRC(0,b) = PRC(a,b), where PRC is the phase response curve, and a and b are concentrations of two resetting agents (i.e., (a,0) is a without b and vice versa). In particular, the phase shift induced in each initial phase by the combination is the sum of the phase shifts induced by each compound individually. As mentioned above, this strict linearity often is not accomplished even in the case of the same compound (e.g., PRC(a)+PRC(a) ≠ PRC(2a)). However, because the dose curve of A₁ to a single agent usually increases monotonically, we used a relatively more “relaxed” definition of additivity: A_1,ex(a,b) ≥ A₁(a,b) ≥ max(A₁(a,0), A₁(0,b)); (A_1,ex − expected A₁, as derived from [PRC(a,0) + PRC(0,b)]). We defined cases below this range as antagonistic and above as synergistic. A similar test was applied for Φ_1. Due to the noncontinuous nature of the type 1 to type 0 transition, the test was applied only for type 1 PTCs as summarized in SI Appendix, Fig. S2A.

We used the additivity test on the data of CORT and F combinations and found that A₁ did not significantly deviate from additivity, except for 1 nM CORT together with 1 nM F, which presented synergism (SI Appendix, Fig. S2B). This is a trivial case of synergism, which likely stems from two subeffective doses that together cross the effective threshold. For Φ₁, we observed no case of significant nonadditivity (SI Appendix, Fig. S2C).

In summary, we found, as expected, that the combination of two activators of the same signaling pathway elicit a simple input integration, with a mostly additive effect on PTC amplitude and no major effect on the PTC phase.

Integration of Inputs Acting through Different Signaling Pathways.

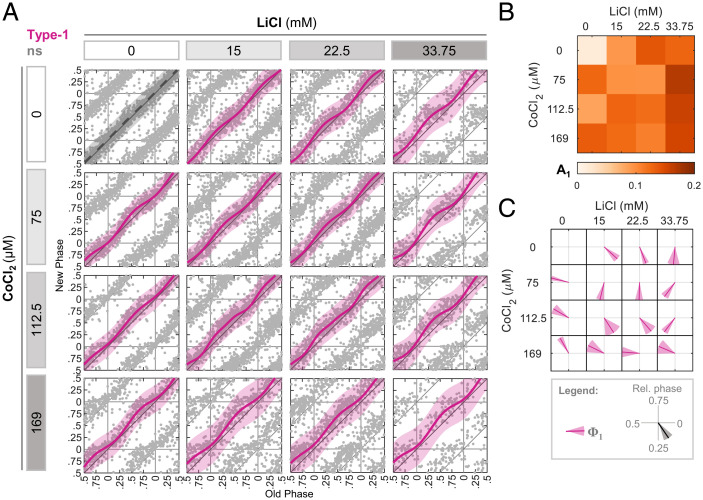
We next studied the effect of pairs of compounds that function via different signaling pathways. These include compounds that elicited either different or similar immediate clock gene response. We examined first LiCl and CoCl₂. The first inhibits glycogen synthase kinase-3β (GSK3β), a kinase known to phosphorylate several core clock proteins, and hence to affect clock parameters (17–22). CoCl₂ is known to stabilize hypoxia-inducible factor 1α (HIF1α), which was shown to affect clock genes through transcriptional activation (23–26). The immediate transcriptional response of the core clock genes to these compounds was considerably different (SI Appendix, Fig. S3). In line with our previous report (12), each of them elicited PTCs with distinct features that were almost opposite to one another (i.e., opposing Φ₁) (Fig. 2A). The response to different combinations of LiCl and CoCl₂ revealed several complex behaviors. Although it seemed that the A₁ of the combinations in general does not exceed the values of the individual treatments (Fig. 2 A and B), our additivity test revealed that it does not significantly deviate from additivity (SI Appendix, Fig. S2D). This is likely because the two compounds elicit very different Φ_1. In fact, one combination (169 μM CoCl₂ + 15 mM LiCl) showed increased A₁ and was classified as synergistic (SI Appendix, Fig. S2D). Regarding Φ₁, while in some combinations we detected an intermediate Φ₁ compared to the individual phases (Fig. 2C), in line with additive effect (SI Appendix, Fig. S2E), other combinations significantly deviated from this behavior (Fig. 2C and SI Appendix, Fig. S2E). However, these deviations showed no consistent dominant directionality (one case followed the individual administration of LiCl, while the other tended toward CoCl₂)_. Of note, some combinations resulted in a considerably wider peak of maximal phase delay, as also evident from the high SD of Φ₁ in many combinations (Fig. 2 A and C). Overall, our analysis shows that LiCl and CoCl₂ combinations give mostly additive results, with few exceptions in both A₁ and Φ_1.

Fig. 2.

Complex phase response upon combination of LiCl and CoCl₂. (A) PTC matrix of the response to LiCl and CoCl₂ given in different concentrations. Each point represents the phases of a single cell. Data are double plotted for clarity. Pink: type 1 resetting model ± 95% confidence interval, ns: P > 0.05 in bootstrapping test for response, n = 97 to 479 cells per concentration (SI Appendix, Dataset S2). (B) Type 1 PTC amplitude in each combination of LiCl and CoCl₂ from (A). (C) Vector plot of the type 1 PTC phase (pink) in each combination of LiCl and CoCl₂ from (A). Vector direction represents the relative phase ± SD from bootstrapping-based distribution.

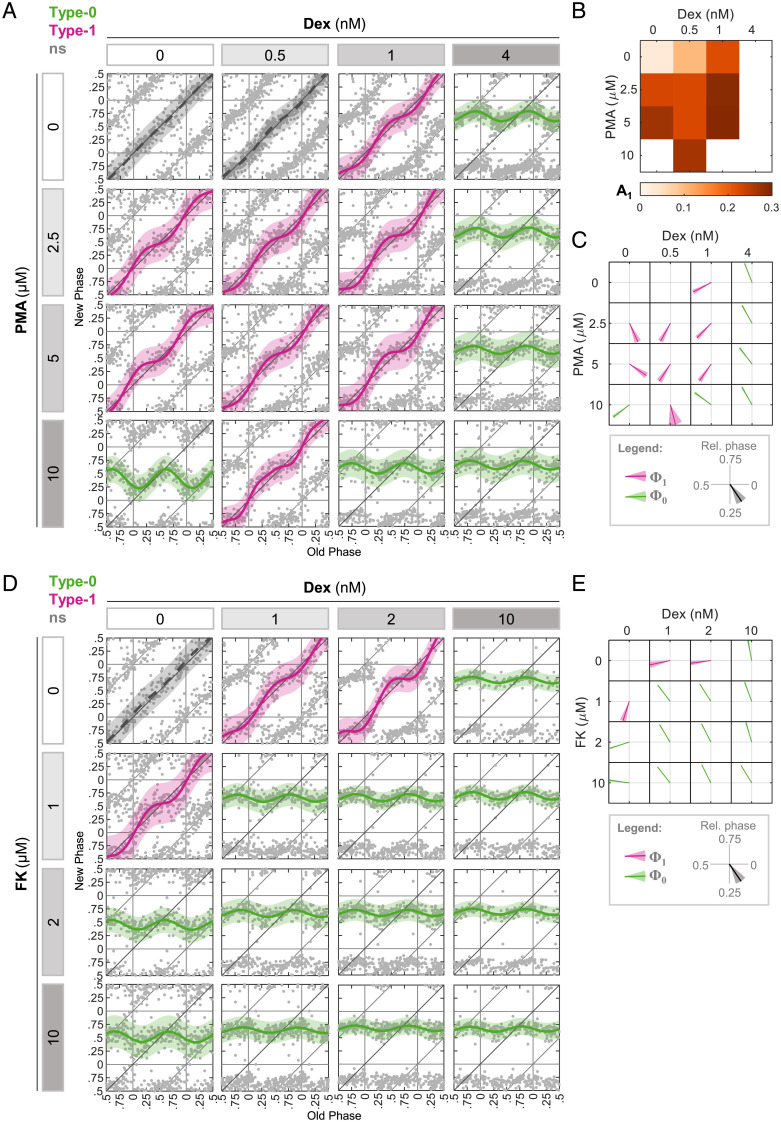
Next, we investigated pairs of compounds that present different PTC characteristics when administered individually, but elicit a comparable immediate response of clock gene expression. We tested dexamethasone (Dex), a potent glucocorticoid receptor activator, and phorbol-12-myristate-13-acetate (PMA), a protein kinase C activator (5, 6, 12, 27, 28). The immediate response of core clock gene expression was mostly comparable between the two (SI Appendix, Fig. S3). However, they elicited distinct PTC profiles with different PTC phases for both type 1 and type 0 responses when applied separately (Fig. 3A). The combination of different concentration ratios between the two showed that in most cases, PMA augmented the effect of Dex on A₁ (Fig. 3B) and was consistent with additivity assumption (SI Appendix, Fig. S2F). Apparently, Φ₁ and Φ₀ were largely dominated by Dex, because in most cases even low doses of Dex were sufficient to generate PTC with a Φ₁ typical of Dex (Fig. 3C and SI Appendix, Fig. S2G).

Fig. 3.

Dominance in phase response upon different zeitgeber combinations. (A) PTC matrix of the response to Dex and PMA given in different concentrations. Each point represents the phases of a single cell. Data are double plotted for clarity. Pink: type 1 resetting model ± 95% confidence interval, green: type 0 resetting model ± 95% confidence interval, ns: P > 0.05 in bootstrapping test for response, n = 151 to 328 cells per concentration (SI Appendix, Dataset S3). (B) Type 1 PTC amplitude in each combination of Dex and PMA from (A). (C) Vector plot of the type 1 PTC phase (pink) and type 0 mean new phase (green) in each combination of Dex and PMA from (A). Vector direction represents the relative phase ± SD from bootstrapping-based distribution. (D) PTC matrix of the response to Dex and FK given in different concentrations. Each point represents the phases of a single cell. Data are double plotted for clarity. Pink: type 1 resetting model ± 95% confidence interval, green: type 0 resetting model ± 95% confidence interval, ns: P > 0.05 in bootstrapping test for response, n = 91 to 208 cells per concentration (SI Appendix, Dataset S4). (E) Vector plot of the type 1 PTC phase (pink) and type 0 mean new phase (green) in each combination of Dex and FK from (D). Vector direction represents the relative phase ± SD from bootstrapping-based distribution.

Finally, we used Dex in combination with forskolin (FK), a potent inducer of cyclic adenosine monophosphate (cAMP) production (6, 7, 12, 29–31). Here again, although the two compounds act through different signaling pathways, the immediate response of the core clock gene expression was relatively similar (SI Appendix, Fig. S3). However, each of the compounds induced different PTC profiles, in which FK alone consistently showed earlier Φ₀ and Φ₁ compared to Dex (Fig. 3D). All of the tested combinations induced a type 0 response, and therefore were not qualified for our additivity test. Notably, the induced Φ₀ was typical for Dex and not for FK (Fig. 3E), pointing toward the dominance of Dex over FK in this respect.

Interestingly, we noticed some cases in which a subeffective dose of one compound had a notable effect when combined with another compound. Most strikingly, the lowest Dex concentration did not elicit significant phase shifts when administered alone, but it was sufficient to affect the PTC topology together with PMA (Fig. 3C). This was also evident even when combined with the highest PMA concentration, in which it reduced the response from type 0 to type 1.

In summary, our analyses demonstrated the ability of the combination of signals to affect the resetting strength and phase in complex manners, such as suppressing phase response or shifting the clock to a phase that was atypical of each of the signals alone.

Background Input Levels Attenuate Clock Resetting in a Pathway-Specific Manner.

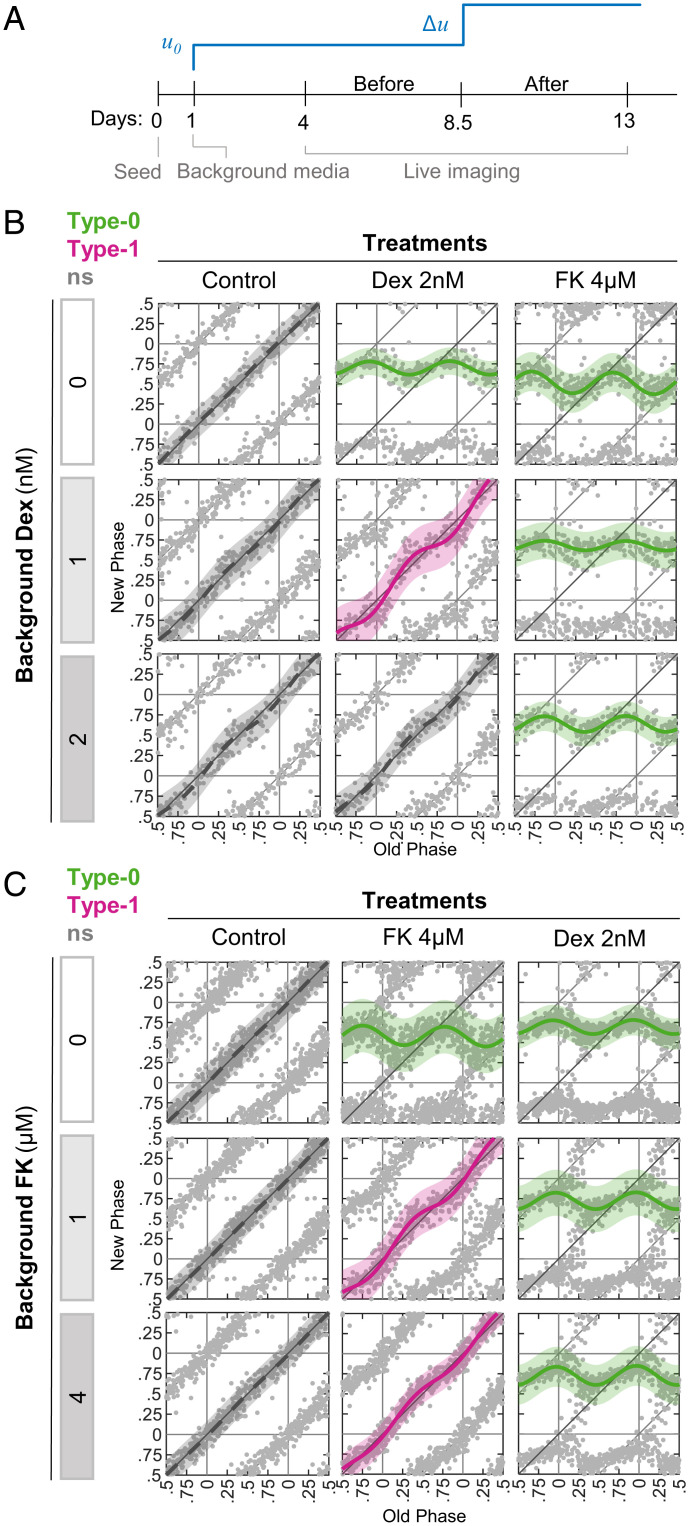
In the body, cells are not exposed to resetting signals in isolation, but rather in the context of existing signaling. This raises the question of whether the background levels of a signal will affect the response to a newly introduced stimulus. For example, studies in Neurospora showed that sequential exposure to light attenuates the clock response to a later exposure, a phenomenon known as photoadaptation (32–34). We therefore examined how the clock integrates signals sequentially. As a case study, we selected Dex and FK from the above combinations and adapted the Circa-SCOPE protocol as follows. One day postseeding, the media was replaced with media supplemented with either Dex or FK (“background media”). After 4.5 d of imaging, the cells were treated again with either Dex or FK (Fig. 4A). Based on previous reports, we assume that these two compounds are stable in the medium for several days (35–39). Intriguingly, we found that increasing concentrations of background Dex attenuated the response to Dex treatment in a dose-dependent manner (Fig. 4B). Similarly, background FK inhibited the response to FK treatment (Fig. 4C). We next examined whether the background effect is specific to treatment by the same intervention or represents a general repression of clock resetting. Importantly, we found that background Dex did not affect resetting by FK and vice versa (Fig. 4 B and C). However, Dex in the background attenuated the response to CORT, consistent with the fact that they both function through glucocorticoid receptor activation (SI Appendix, Fig. S4). The differences in the PTC profiles upon 2 nM Dex between Figs. 3 and 4 probably stem from the fact that this concentration elicits a response near the transition between type 1 and type 0.

Fig. 4.

Pathway-specific effect of signal background levels on phase response. (A) Schematic depiction of the experimental design. At 1 d postseeding, media was replaced and supplemented with background levels of the signal of choice (u₀) (“background media”). As a treatment, an additional dose of the signal (Δu) was given 8.5 d postseeding. (B) Increasing doses of Dex were added in background media, and then cells were treated with either Dex or FK. Depicted are the PTCs reconstructed from each background-treatment combination. Pink: type 1 resetting model ± 95% confidence interval, green: type 0 resetting model ± 95% confidence interval, ns: P > 0.05 in bootstrapping test for response, n = 116 to 201 cells per concentration (SI Appendix, Dataset S5). (C) Increasing doses of FK added in background media, and then cells were treated with either Dex or FK. Depicted are the PTCs reconstructed from each background-treatment combination. Pink: type 1 resetting model ± 95% confidence interval, green: type 0 resetting model ± 95% confidence interval, ns: P > 0.05 in bootstrapping test for response, n = 259 to 438 cells per concentration (SI Appendix, Dataset S6).

Together, our results indicate that background levels of a resetting signal inhibit the effect of a subsequent dose of the same signal, and this inhibitory effect depends on the reactivation of the same signaling pathway.

Fold-Change Detection Mechanism Participates in Clock Resetting.

The background effect on clock resetting can stem from several different mechanisms. While a simple explanation may be the saturation of the mediating receptor, a more exciting possibility is the existence of a FCD mechanism. In FCD, the design of the system renders it sensitive to the relative change in signal levels rather than to its absolute levels (40). The presence of background levels diminishes the response as the fold-change between the background and the final concentration is decreased. FCD was shown to increase the dynamic range and reduce intercellular variability in various sensory systems (40), and hence may be highly relevant for clock resetting.

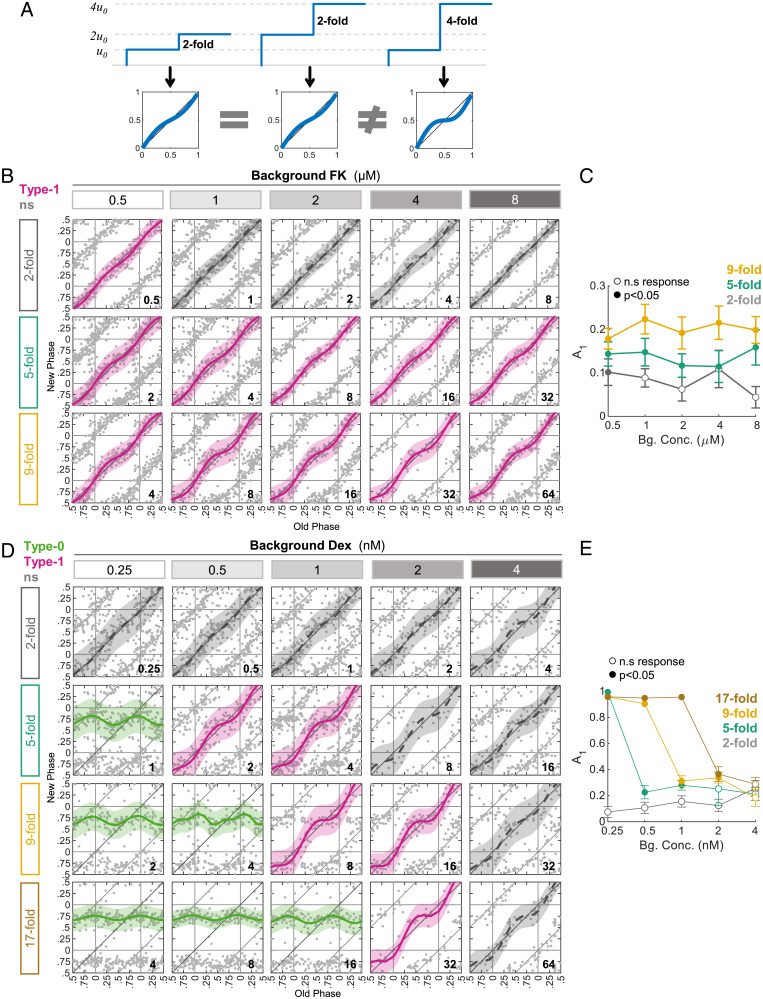
If phase resetting presents FCD, we expect that different conditions with the same fold-change between background and final concentration will show a similar response, while increasing the fold-change should increase the response (Fig. 5A). Here, we define X-fold as the final concentration divided by the background concentration—for example adding 1 μM to a background of 1 μM will give a final concentration of 2 μM, and hence a twofold increase. Hence, we exposed cells to FK in two-, five- and ninefold differences relative to various background levels. Remarkably, we found that the response to FK essentially followed the fold-change and not the absolute levels (Fig. 5B and C). We therefore concluded that the clock response to FK involves a FCD mechanism, a design feature that likely underlies the observed background inhibitory effect.

Fig. 5.

FCD in FK-induced phase resetting. (A) In FCD, the response to a signal is dependent on the relative change in the intensity of the signal, rather than the absolute level. Similar fold-changes from the background (u₀) should yield similar PTCs. (B) Cells were exposed to different background levels of FK and then were treated with an additional dose of FK. In each row, the FK treatment was administered in a concentration that gives the same fold-change from the corresponding background level (added concentration in micromolars is depicted in the bottom-right corner of each panel). Fold-change is defined as the final concentration (added + background) divided by the background concentration. Pink: type 1 resetting model ± 95% confidence interval, ns: P > 0.05 in bootstrapping test for response, n = 52 to 215 cells per concentration (SI Appendix, Dataset S7). (C) The PTC amplitudes as calculated from the data in (B). Open dots: ns; filled dots: significant response according to bootstrapping test; ± SD from bootstrapping-based distribution. (D) Cells were exposed to different background levels of Dex and then treated with an additional dose of Dex. In each row, the Dex treatment was administered in a concentration that gives the same fold-change from the corresponding background level (added concentration in nanomolars is depicted in the bottom-right corner of each panel). Pink: type 1 resetting model ± 95% confidence interval, green: type 0 resetting model ± 95% confidence interval, ns: P > 0.05 in bootstrapping test for response, n = 26 to 170 cells per concentration (SI Appendix, Dataset S8). (E) The PTC amplitudes as calculated from the data in (D). Open dots: ns; filled dots: significant response according to bootstrapping test; ± SD from bootstrapping-based distribution.

Similar experiments were conducted with Dex. However, the response was clearly not FCD-like, with the Dex background gradually hampering the response to additional Dex, even when administered with the same fold-change (Fig. 5D and E). The negative slope of A₁ (Fig. 5E) further suggests that the background effect is probably due to the saturation of one of the pathway components and not to FCD.

In conclusion, we identified FCD in the clock response to FK, which may play a role in the observed inhibitory background effect of FK.

Fold-Change Detection in FK- but Not Dex-Induced Gene Expression.

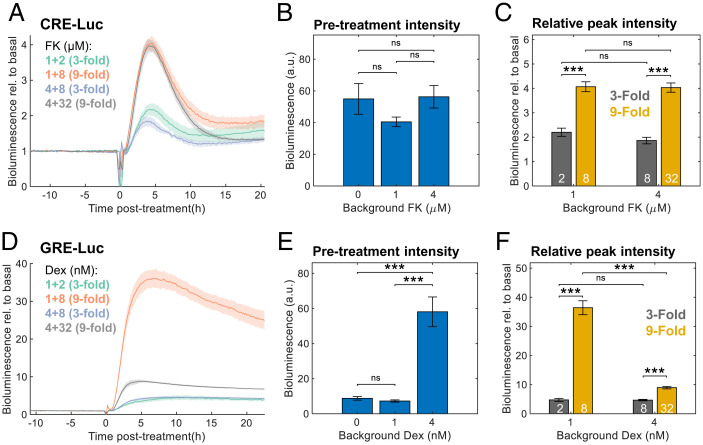
The FCD characteristics of FK-induced clock resetting may stem either from the properties of the signaling pathway upstream to the clock, or from the specific interaction with the circadian clockwork. In an attempt to discriminate between these two scenarios, we examined FCD in FK-induced gene expression using a reporter assay. To this end, we used a CRE-Luc (cAMP response element-luciferase) reporter, which responds to cAMP induction, as upon FK exposure. CREs are present in several clock gene promoters and are believed to play a role in the resetting response (30, 41). Cells transfected with CRE-Luc were exposed to different background levels and subsequent FK treatments, and their bioluminescence was continuously recorded (Fig. 6A and SI Appendix, Fig. S5A). We found no significant differences in the basal bioluminescence levels upon different background FK levels (Fig. 6B), which is indicative of exact adaptation. Moreover, the relative bioluminescence induction was similar to the fold-changes in FK concentrations, and not to the absolute levels (Fig. 6C). Therefore, we concluded that CRE-dependent regulation exhibits FCD properties and likely explains the FCD in clock response to FK.

Fig. 6.

Fold-change detection in FK- but not Dex-induced gene expression. (A) Cells were transfected with CRE-Luc reporter and treated with different background concentrations of FK. After 2 d of bioluminescence recording, different doses of FK were added. The bioluminescence data are presented relative to the pretreatment levels per sample; concentrations are given in micromolars (background + treatment). Means ± SEs, n = 4 plates per condition. (B) Average bioluminescence levels of CRE-Luc during 10 h of pretreatment with different background FK levels. Means ± SEs, n = 8 plates per condition; ns in two-sample Student’s t test. (C) Fold-change induction of CRE-Luc (maximal bioluminescence posttreatment divided by the pretreatment levels). White numbers: FK treatment concentrations in micromolars; means ± SEs, n = 4 plates per condition, ***P < 0.001, two-sample Student’s t test. (D) Cells were transfected with GRE-Luc reporter and treated with different background concentrations of Dex. After 2 d of bioluminescence recording, different doses of Dex were added. The bioluminescence data are presented relative to the pretreatment levels per sample; concentrations are given in nanomolars (background + treatment). Means ± SEs, n = 4 plates per condition. (E) Average bioluminescence levels of GRE-Luc during 10 h of pretreatment with different background Dex levels (means ± SEs, n = 8 plates per condition, ns in two-sample Student’s t test). (F) Fold-change induction of GRE-Luc (maximal bioluminescence posttreatment divided by the pretreatment levels). White numbers: Dex treatment concentrations in nanomolars; means ± SEs, n = 4 plates per condition, ***P < 0.001, two-sample Student’s t test.

Similar experiments were performed with GRE-Luc (glucocorticoid response element-luciferase) reporter to examine the response to Dex. GREs also inhabit several clock gene promoters (42–44). GRE-Luc transfected cells were responsive to Dex (Fig. 6D and SI Appendix, Fig. S5B); however, they neither showed adaptation (Fig. 6E) nor followed the fold-change in Dex levels (Fig. 6F). Hence, consistent with the Circa-SCOPE results (Fig. 5 D and E), the response of GRE-containing promoters to Dex did not exhibit FCD.

In summary, we identified FCD as a signal-specific feature of sequential input integration by the clock. Mechanistically, our results further suggest that this property stems from the properties of the input pathway (i.e., FK) rather than from its specific interaction with the core clock machinery.

Discussion

Temporal integration of multiple input signals by biological systems plays a central role in their “decision-making” and subsequent responses (45). The circadian clock is believed to enable the organism to anticipate and prepare in advance to challenges imposed by the cyclic environment. To this end, the intrinsic oscillator should be able to estimate the external time by processing timing information from the environment. This estimate is manifested in the phase of the oscillator and its relative alignment with the external cycle (46, 47). Presumably, the existence of multiple input pathways to the clock, and the modes in which the clock integrates the information from these inputs, is necessary to optimize phase alignment under different contexts. Previous studies on signal integration by the circadian clock mostly addressed the effect of conflicting light and temperature signals (48, 49) or light and feeding (50–52), primarily on animal models, while others took more generalized and theoretical approaches (53, 54). The present study uses systematic experimental methodologies to identify potential underlying principles in input integration by the circadian clock.

Overall, our results suggest that the circadian clock integrates multiple inputs through various modes, which can give rise to complex phenomena, such as dominance. The prevalence of these phenomena indicates that the effect of a combination of signals cannot be predicted merely from the effect of the individual signals. Hence, extracting specific predictions regarding in vivo resetting can benefit from cell culture assays alongside molecular-level modeling.

At the molecular level, additive effects can be simply explained by two signals sharing the same input pathway and hence affect the same core clock components and induce a similar response. However, complex interactions can stem from various mechanisms that can be broadly divided into upstream interaction, in which the two signaling pathways interact upstream to the core oscillator, or oscillator-intrinsic interaction, in which the two signals affect different nodes of the oscillator itself. While the former stems from extrinsic factors to the oscillator, the latter represents integration processes that stem from the internal structure of the core clock and the interactions between its components. For example, there are indications for potential crosstalk between GSK and HIF signaling pathways (55, 56) or between cAMP and glucocorticoid receptor pathways (57, 58), which may support an upstream interaction mechanism. Our immediate transcriptional response analysis of core clock genes (SI Appendix, Figs. S1 and S2) provides only a partial proxy to the mode of action of each drug on the clock, and therefore cannot serve to conclusively discriminate between the two models, especially in cases of dominance (Fig. 3).

Due to the nonlinearity and complex nature of PTCs, the selection of the specific doses for each compound in the combination experiments is not straightforward. Intuitively, a comparison can be made between categoric responses, namely, no response, type 1, or type 0 PTCs for each compound. However, a response denoted as type 1 is induced upon a wide range of concentrations, albeit with different characteristics (i.e., A₁ and Φ₁; see LiCl and CoCl₂ in Fig. 2). Whereas in type 0 the response does not change much with increasing concentrations due to saturation (e.g., see FK in Fig. 3D). Therefore, for the purpose of quantifying additivity, it is optimal to choose concentrations within the type 1 range (see CORT and F in Fig. 1 or LiCl and CoCl₂ in Fig. 2), which is also compatible with our statistical approach (SI Appendix, Fig. S2). However, dominance behaviors are better highlighted using an asymmetric design, whereby a concentration inducing a minor response to one drug is shown to overrule a strong response to the other drug (see combinations in Fig. 3). As noted above, other factors, such as cytotoxicity or drug solubility, impose additional limitations. Future studies with higher imaging capacity for simultaneously testing wider ranges of concentrations will enable better depiction of the effect of signal interactions.

More generally, our phenomenological classification method of interaction modes represents only one of the various ways to analyze the results. For simplicity, we chose to focus on two parameters of type 1 PTCs and one parameter of type 0. This choice neglects other aspects of the curves, such as the shape of type 0 curves. We included in the SI Appendix, Dataset S9, additional parameters that can be used for further analysis of these aspects. It also largely ignores nonsinusoidal shapes that are sometimes apparent in type 1 curves (e.g., Fig. 2). Technically, they result from fitting the data with a Fourier function with two components. However, in the case of combinations, they can hint at nonadditivity in a different manner, because such nonsinusoidal shapes cannot be the result of the summation of two perfect sine waves (with identical frequency). In the future, the establishment of a general theoretical framework for circadian input integration is expected to enable a more informative interpretation of our observations.

Our findings are highly relevant for clock resetting in natural systems. As mentioned earlier, mammalian peripheral clocks are exposed to multiple zeitgebers in parallel or sequentially through the blood serum or otherwise. It is well known that changes in the relative phase of certain zeitgebers, as in daytime restricted feeding, can differently affect the phase and amplitude of clocks in various peripheral tissues (59, 60). The consequences of misaligned and dysregulated zeitgebers are often considered deleterious (61, 62). In this regard, our results point toward the ability of some signals to antagonize or dominate others. In a physiological context, one can speculate on the possibility of hierarchy between signals, in which whenever the dominant signal (presumably a more reliable input) is present, the effect of the others is diminished.

We found that background levels of an input attenuate the response of the clock to subsequent inputs that function via the same signaling pathway. This phenomenon of context-dependent response is highly relevant for physiological and pathological conditions. For example, in the case of patients who are administered certain medications that can also reset the clock, such as steroids, the resetting by natural steroids is expected to be compromised, while resetting by other agents may still be effective.

Finally, we further demonstrated that, at least in the case of FK, the background-dependent response involves an FCD mechanism. FCD is an important design principle in many sensory systems and several signaling pathways (40, 63–65) and carries various advantages that are relevant for circadian clock function. First, it was shown that FCD can increase the dynamic range of responses to a signal. Second, sensitivity to a relative change in input provides robustness to absolute input levels. FCD can be beneficial, for example, when cell population is exposed to a concentration gradient of a signal, such as nutrient and waste gradients along blood capillaries. Without FCD, these cells are prone to be misaligned with one another due to differences in experienced zeitgeber strength. This can be prevented though an FCD mechanism, as the cells respond to the relative change in input intensity, which is more uniform, and hence respond similarly throughout the tissue. Thus, FCD can enhance intratissue synchrony, without any direct intercellular coupling, an attractive scenario that merits further investigation.

The observed FCD can be a property of the input pathway or its interaction with the core clock. Our reporter assays suggest that, at least in the case of FK, a FCD is already evident at the level of the input pathway, irrespective of the clock.

Taken together, our findings suggest design principles regarding input integration by the circadian clock, which raise exciting possibilities regarding their physiological and pathological implications.

Materials and Methods

Circa-SCOPE.

For the construction of PTCs, we used the Circa-SCOPE method as previously described (12). In short, NIH 3T3 NR-RVNP cells were seeded in 24-well plates and media was replaced the next day with FluoroBrite Dulbecco’s modified Eagle’s medium (DMEM) (Gibco) supplemented with 1% fetal bovine serum (FBS) (Gibco), 1 mM glutamine (Biological Industries), 100 U/mL penicillin, and 100 mg/mL streptomycin (Biological Industries). Cells were incubated for 3 additional days and then placed in the IncuCyte Zoom (Sertorius) incubated microscope and imaged for 9 consecutive days at 1-h intervals in red and green fluorescence channels as well as phase contrast. At 8.5 d postseeding, cells were treated with the agent of choice (SI Appendix, Table S1 for a list of agents and their sources). Upon imaging completion, images were extracted and analyzed based on our computational pipeline (66). A CellProfiler (version 3.1.9, Broad Institute (67)) pipeline was used for illumination correction, nuclei segmentation, tracking, and fluorescence quantifications. Subsequent analyses on the output were conducted with MATLAB (R2020b, MathWorks), including signal detrending, rhythmicity assessment before and after the treatment time, construction of PTCs, and statistical testing using bootstrapping methods. Cells that were trackable for the entire time course, and were rhythmic (R² > 0.5) both before and after the intervention, with a period between 22 and 29 h, were selected for PTC analysis. SI Appendix, Datasets S1–S8 include detailed results per cell. The phase in the before and after time frames was calculated and plotted in a PTC format.

PTC Statistical Evaluation.

PTC statistical analysis was performed as previously described (12). Briefly, the raw PTC data were fitted with two Fourier models for either type 1 or type 0 resetting. To test whether any phase response is present in a certain group, we bootstrapped from control (untreated) group samples in the size of the test group 10,000 times. In each iteration, a Fourier model was fitted, and the maximal shift was retrieved. The null hypothesis (namely, no phase shift) was rejected if the resampled maximal shift was higher than the observed maximal shift less than 5% of the times.

To select between type 1 and type 0 models, the root-mean-square deviation (RMSE) was calculated for each fit as a measure of goodness-of-fit (i.e., should be minimized for an optimal fit). We bootstrapped from the tested group 10,000 times. In each iteration, both models were fitted to the resampled data and RMSE was calculated for them. The type 1 RMSE should be larger than the type 0 RMSE 90% of the time to reject the null hypothesis of type 1 resetting. The different parameters of the fit, including A₁, Φ₁, and Φ₀, as well as other parameters and the bootstrapping-based P values, are summarized in SI Appendix, Dataset S9.

PTC Additivity Test.

Classification and tests for modes of interaction (SI Appendix, Fig. S2) were performed as follows. The PTC data were converted to PRC form, in which the y axis represent the phase shift induced per a specific initial phase (x axis). For each combination of agents a and b, the data of (a,0) and (0,b) were bootstrapped 10,000 times. In each iteration, the resampled data were fitted with a type 1 curve, and the PRC(a,0) + PRC(0,b) = PRC_ex(a,b) was calculated. Out of this PRC_ex, A₁ and Φ₁ were extracted (denoted A_1,ex(a,b), Φ_1,ex(a,b)). In addition, the resampled PRC(a,0) and PRC(0,b) were used to extract A_1,ex(a,0) and A_1,ex(0,b), respectively. The distributions of the expected parameters were then used to test against the observed A₁ and Φ₁ (denoted A_1,ob(a,b), Φ_1,ob(a,b)). For each null hypothesis, the observed parameter should differ from the expected distribution in more than 95% of cases to qualify as significant.

The null hypotheses for A₁ were tested hierarchically: (1) A_1,ob(a,b) = A_1,ex(a,b) (if retained: linear additivity); if rejected: (2) A_1,ob(a,b) > A_1,ex(a,b) (if retained: synergistic); if rejected: (3) A_1,ob(a,b) > max(A₁(a,0), A₁(0,b)) (if retained, “relaxed” additivity); or A_1,ob(a,b) < max(A_1,ex(a,0), A_1,ex(0,b)) (if retained: antagonistic). For Φ₁, we tested only the additivity null hypothesis Φ_1,ob(a,b) = Φ_1,ex(a,b). Note that our definitions of relaxed additivity or nonadditivity are well defined only when max(A_1,ex(a,0), A_1,ex(0,b)) < A_1,ex(a,b). While this is not necessarily true, we did not encounter in practice any case of nonadditivity that was in violation of it.

RNA Extraction and Quantitative PCR.

To measure the immediate transcriptional response to the treatments used, NIH 3T3 NR-RVNP cells were seeded in 6-cm plates (200,000 cells per plate). The next day, media was replaced with FluoroBrite DMEM (Gibco) supplemented with 1% FBS (Gibco), 1 mM glutamine (Biological Industries), 100 U/mL penicillin, and 100 mg/mL streptomycin (Biological Industries). At 8.5 d postseeding, cells were treated with the relevant agents. RNA was collected at 0, 3, and 6 h posttreatment. For RNA collection, each plate was washed once with phosphate-buffered saline (Biological Industries) and then incubated with 1 mL TRI-reagent (Sigma) for a few minutes. TRI-reagent homogenates were transferred to microtubes, snap frozen in liquid nitrogen, and stored at −80 °C until used. RNA was purified according to the standard TRI-reagent protocol. The RNA concentration was determined using the NanoDrop 2000 spectrophotometer (Thermo Fisher Scientific).

The synthesis of cDNA was performed using qScript cDNA SuperMix (Quanta Biosciences). Real-time-quantitative PCR assays were performed using SYBR Green (Roche) with a LightCycler II machine (Roche) and analyzed according to the 2^−ΔΔCt method. The first normalization was to the geometrical mean of three housekeeping genes: Hprt, Rplp0, and Tbp. The second normalization was to the mean expression of the untreated control at the 0 h time point. Log₂ transformation was applied to all of the data for presentation purposes. Primers’ sequences are detailed in SI Appendix, Table S2.

Real-Time Luminescence Assay.

For real-time luminescence measurements, NIH 3T3 NR-RVNP cells were seeded in 3-cm plates (80,000 cells per plate). At 1 d postseeding, cells were transfected with either CRE-Luc plasmid (Promega) or GRE-Luc plasmid (a kind gift from Yosef Yarden (68)) at 500 ng DNA per plate, using JetPRIME transfection reagent (Polyplus). After 5 h, the media was replaced with DMEM without phenol red (Gibco) supplemented with 1% FBS (Gibco), 1 mM glutamine (Biological Industries), 100 U/mL penicillin, 100 mg/mL streptomycin (Biological Industries), and 100 nM d-luciferin (Promega). Background concentrations of FK or Dex were added as indicated in Fig. 6 and SI Appendix, Fig. S5. The following day, cells were placed in the LumiCycle32 (Actimetrics) incubated luminometer, and their bioluminescence was continuously recorded. Two days from the start of recording, cells were supplemented with an additional dose of FK or Dex, as indicated in the relevant figures.

Statistics and Software.

All of the statistical analyses and data visualization were performed using MATLAB (R2020b, MathWorks).

Data, Materials, and Software Availability

All of the study data are included in the article and/or supporting information.