Morphological growth dynamics, mechanical stability, and active microtubule mechanics underlying spindle self-organization

Significance

The spindle is a microtubule-based, self-organized structure essential for equal segregation of chromosomes during cell division. The spindle’s bipolar shape is robustly maintained for the segregation accuracy but is occasionally disrupted, yielding multipolar phenotypes. How microtubules favor nonbipolar self-organization despite high bipolar stability is not known. Here, we find that this stems from the bistable nature of microtubule self-organization within the cytoplasm, which paves a separate route of multipolar organization from a bipolar phenotype. We also find that these two phenotypes infrequently switch upon maturation and by perturbed force, indicating the structure’s mechanical plasticity underlying the bistability. Our study thus reveals the mechanics governing the robust yet stochastic nature of spindle morphogenesis, which has relevance to tumors and unhealthy oocytes.

Abstract

The spindle is a dynamic intracellular structure self-organized from microtubules and microtubule-associated proteins. The spindle’s bipolar morphology is essential for the faithful segregation of chromosomes during cell division, and it is robustly maintained by multifaceted mechanisms. However, abnormally shaped spindles, such as multipolar spindles, can stochastically arise in a cell population and cause chromosome segregation errors. The physical basis of how microtubules fail in bipolarization and occasionally favor nonbipolar assembly is poorly understood. Here, using live fluorescence imaging and quantitative shape analysis in Xenopus egg extracts, we find that spindles of varied shape morphologies emerge through nonrandom, bistable self-organization paths, one leading to a bipolar and the other leading to a multipolar phenotype. The bistability defines the spindle’s unique morphological growth dynamics linked to each shape phenotype and can be promoted by a locally distorted microtubule flow that arises within premature structures. We also find that bipolar and multipolar spindles are stable at the steady-state in bulk but can infrequently switch between the two phenotypes. Our microneedle-based physical manipulation further demonstrates that a transient force perturbation applied near the assembled pole can trigger the phenotypic switching, revealing the mechanical plasticity of the spindle. Together with molecular perturbation of kinesin-5 and augmin, our data propose the physical and molecular bases underlying the emergence of spindle-shape variation, which influences chromosome segregation fidelity during cell division.

The spindle is a microtubule-based intracellular structure that segregates chromosomes during cell division. This structure comprises thousands to hundreds of thousands of microtubules in animal cells (1). The spindle’s typical shape is bipolar, which is crucial for equal partitioning of the replicated chromosomes between the two daughter cells. Despite the fundamental importance, the spindle’s bipolarity can be lost in a subset of a cell population. A prominent impaired phenotype is multipolar spindles, which can lead to chromosome segregation errors and are a hallmark of tumor cells (2). Multipolar spindles are also common in human oocytes, which are prone to aneuploidy (3, 4). Over the years, the understanding of genes and proteins that ensure spindle integrity has advanced significantly. However, the physical basis of how varied spindle-shape phenotypes arise remains mysterious.

The spindle’s bipolar architecture emerges through self-organization of microtubules. The organization requires no preloaded template that defines the structure’s overall morphology. Instead, the defined cell-sized architecture is built from integrated interactions of constituent molecules with microtubules as the basic building blocks. The main motive force organizing the spindle is generated by nanometer-sized motor proteins, such as kinesins and dynein, which collectively align microtubules with an antiparallel order and cluster their ends to form focused poles (5, 6). Furthermore, individual microtubules rapidly turnover with continued addition of new tubulin subunits as well as their loss from the assembled structure. Despite the marked instability of the polymers, a solid structural support that acts as a major site for microtubule nucleation, such as centrosomes, is not a prerequisite for spindle bipolarity (7–10). Also, more than two copies of centrosomes or multiple microtubule-organizing centers do not significantly influence spindle bipolarity in many organisms (8, 11–13). Thus, bipolar self-organization force can be predominant within the cytoplasm in shaping the spindle.

Despite the high potency of microtubules self-organizing into bipolar spindles, abnormally shaped spindles can arise in a subset of cells. Using sophisticated screening approaches, studies have demonstrated that the loss of key genes or proteins can result in loss of spindle bipolarity (14–17). However, nonbipolar spindles can also appear while cells naturally grow and proliferate. The intrinsic cellular mechanism of how microtubules occasionally favor nonbipolar self-organization is not known.

Regarding the spindle’s unstable nature in bipolarization, the spindle’s bipolar phenotype can be perturbed by mechanical force. For example, a kinesin-driven force that moves chromosomes toward the cell center disturbs spindle pole integrity, leading to multipolar spindle formation (18). Perturbation of the actomyosin-based intracellular force also influences spindle bipolarity (19). In the past, physical manipulation studies directly examined the impact of force on spindle integrity. Paradoxically, it is the spindle’s substantial bipolar stability that has been reported to date. For example, spindles undergo extensive deformation against externally applied stretching and compressing forces, but the structure can readily recover its size and shape after the force is removed (20–23). The spindle can also restore its bipolar shape after nearly half the mass of microtubules is mechanically dissected or when two spindles are fused together (24–26). Our previous microrheology analysis revealed that the bipolar spindle has substantial elasticity, the material property that enables the structure to restore its shape following perturbation by external force (27). The mechanical properties of the spindle that permit the structure to undergo persistent phenotypic changes in response to perturbing forces are not known.

Cell-free extracts prepared from unfertilized eggs of Xenopus laevis frogs (28) are an ideal model system to study the spindle self-organization mechanism, as it allows for assembling multiple spindles within a shared, nearly undiluted cytoplasm. The extracts exhibit intrinsic spindle shape variations (29, 30), allowing analysis of how individual structures grow and mature into different shape phenotypes. Owing to the cell-free nature, the assembled structures are amenable to controlled micromanipulation for examining their mechanical stability. External cues that can influence spindle bipolarity, such as cell shape and cell adhesion mechanics (14), are absent in this system.

Here, taking these advantages of the Xenopus system, we studied the morphological growth dynamics and mechanical stability of bipolar and multipolar spindles. By quantitatively analyzing the temporal growth dynamics of multiple spindles, we show that the structures self-organizing into bipolar and multipolar shapes take bistable, characteristic growth paths to attain the distinct shape phenotypes. Using high-resolution imaging and microneedle-based micromanipulation of spindles, we also find a distorted microtubule flow as a source of the growth path branching, and mechanical plasticity that permits the structures to switch their shape phenotypes. Together with molecular perturbation assays of kinesin-5 and augmin, we discuss how spindle-shape phenotypes become diverged and stabilized through self-organization of microtubules.

RESULTS

Tracking the Dynamics of Multiple Spindle Self-Organization Processes in a Bulk Cytoplasmic Extract.

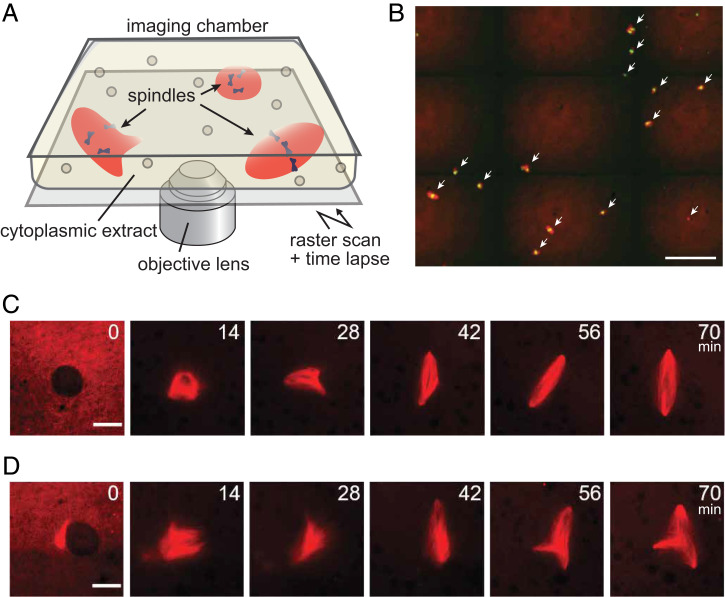
To examine the dynamics of microtubule self-organization into spindles, we started the assay by assembling thousands of interphase nuclei in a test tube by mixing cytoplasmic extracts of X. laevis eggs with purified sperm. The extract was then sealed in an imaging chamber soon after initiating mitosis, and the growth dynamics of microtubule-based structures, assembled around replicated chromosomes, were imaged using time-lapse spinning-disk confocal microscopy (Fig. 1A). Microtubules and chromosomes were visualized by adding X-rhodamine tubulin and SYTOX Green, respectively, to the extracts. The structures assembled were maintained at a low density by limiting the sperm number such that their frequent collisions could be prevented while the structures freely moved in the chamber. Long-term tracking of such highly mobile, sparsely distributed structures was achieved by raster scanning the sample stage while performing the time lapse (Fig. 1B). The interval of the imaging (1 min), magnification of the objective lens (×20), and the size of the scanning area (∼6 mm²) were such that several tens of spindle self-organization processes could be recorded with minimal phototoxicity (SI Appendix, Fig. S1A). The height of the imaging chamber (∼20 µm) was such that it could minimize the structures’ out of focus drift and three-dimensional (3D) rotation.

Fig. 1.

Tracking the dynamics of multiple spindle self-organization processes in a bulk cytoplasmic extract of Xenopus eggs. (A) Schematic of the assay. The temporal growth dynamics of spindles in the bulk cytoplasmic extract prepared from Xenopus eggs were imaged by time-lapse confocal fluorescence microscopy. Multiple spindle self-organization processes could be recorded in parallel by raster scanning the sample stage. (B) Representative fluorescence image (red: tubulin; green: DNA) cropped from the original large-field image data (2.7 × 2.3 mm²) acquired during the assay. White arrows highlight spindles. Scale bar, 200 µm. (C and D) Representative sequential snapshots cropped from the large-field, time-lapse image data (interval: 1 min), capturing the growth of microtubule-based structures from the nuclear envelope breakdown (t = 0 min) to the steady-state metaphase (t = 56 to 70 min). Bipolar (C) and tripolar (D) self-organization cases are shown. Time stamps indicate minutes. Scale bars, 25 μm.

Fig. 1 C and D show two series of sequential snapshots cropped from the large-field image series, revealing the rich dynamics of microtubule-based structures assembling into steady-state spindles (Movies S1 and S2). Specifically, following the nuclear envelope breakdown (defined as t = 0 min), microtubules started to massively polymerize to form nearly globular aggregates (t = 14 min). The aggregates then assumed more anisotropic shapes with premature poles, which dynamically grew, shrank, and changed their positions over time (t = 28 to 42 min). Eventually, these assembly intermediates matured into steady-state structures, with bipolar (Fig. 1C) and multipolar shapes (Fig. 1D) (t = 56 to 70 min). The overall self-organization process took 45 to 60 min with 60% to 80% of the matured spindles being bipolar (SI Appendix, Fig. S1B), which is comparable to the time and fraction that can be achieved with reactions performed in test tubes (20–22). Thus, we could track the dynamics of individual spindle self-organization processes with minimal interference associated with microscopy, compare multiple self-organization processes in parallel, and analyze the differences of how each structure matured into defined shape morphologies.

Bipolar and Nonbipolar Spindle Self-Organization Occurs Through Distinct Morphological Growth Paths.

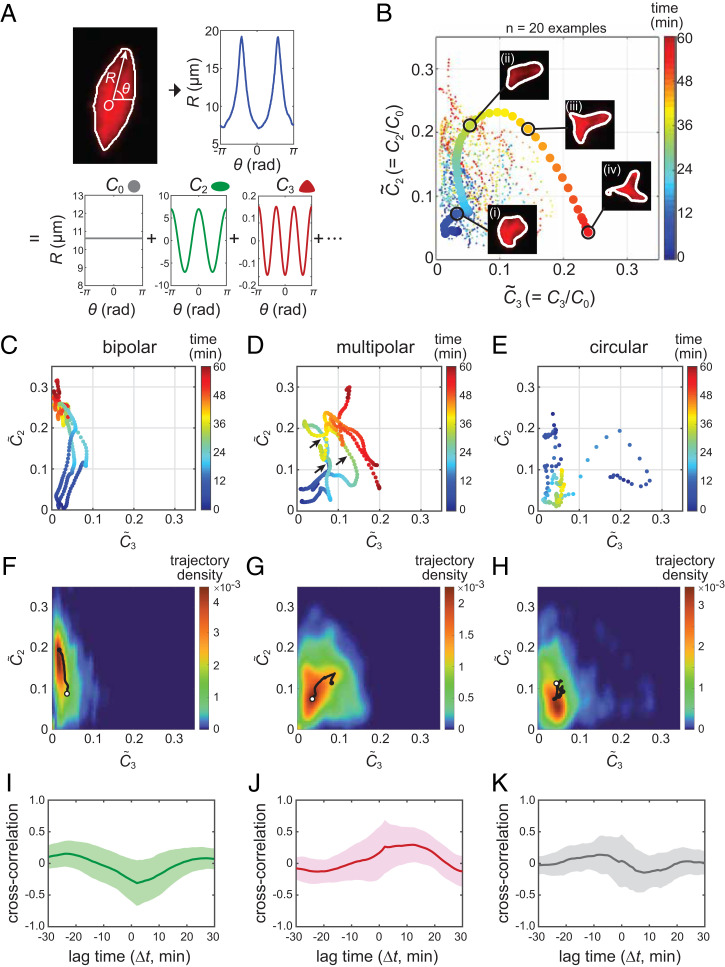
Having established the above imaging assay, we examined the morphological growth dynamics of individual spindles using a method called multipole expansion analysis (31) (Fig. 2A). This analysis enabled us to dissect the shape features of an imaged object by tracing its outline and then decomposing it into discrete Fourier modes. The coefficient of each Fourier mode, denoted as C_i (i = 0, 1, 2, …), is the measure of the structure’s i^-th order symmetry (the equation used for calculating C_i is provided in Materials and Methods). For example, a circular structure, such as one that is typical of an early growth phase (e.g., 14 min in Fig. 1C) and a monopolar aster composed of a radial array of microtubules (32), has a predominant 0th order symmetry and yielded a C₀ value significantly larger than C₂ and C₃ (SI Appendix, Fig. S2A). On the other hand, bipolar and tripolar structures have predominant second- and third-order symmetries, respectively, and each structure yielded large C₂ and C₃ values that were distinguishable from each other (SI Appendix, Fig. S2 B and C). The first order symmetry (C₁) is zero for any shape because the outline tracing vector (R in Fig. 2A) originated from the structure’s centroid. We assumed that the higher-order shape modes (i ≥ 4) were negligible to capture the spindle dynamics, as their magnitudes were small. We then obtained the normalized shape parameters, $\widetilde{C_2}$ = C₂/C₀ and $\widetilde{C_3}$ = C₃/C₀, whose magnitudes indicate the degree of bipolar and multipolar shape features, respectively, independent of the structure’s size (C₀). Finally, the values of $\widetilde{C_2}$ and $\widetilde{C_3}$ were calculated for each time-lapse frame and plotted in the $\widetilde{C_2}$–$\widetilde{C_3}$ plane. In this way, we could trace the morphological growth dynamics of spindles as single-line trajectories that travel across the two-dimensional “morphospace” (Fig. 2B).

Fig. 2.

Distinct morphological growth dynamics of bipolar versus multipolar spindle self-organization. (A) Schematic diagram of spindle-shape quantification. The spindle's shape feature was analyzed in each time-lapse frame by tracing its outline with the vector R originating from the structure’s centroid (O) (graph at Top Left). The angular profile of the traced outline (R(θ), blue line) was then decomposed into discrete Fourier modes with C_i (i = 0, 1, 2, …) (Lower panels). C₀ defines the structure's average radius. C₂ and C₃ are the measures of the structure’s bipolarity and multipolarity, respectively. (B) Example morphological growth trajectories of 20 spindles, obtained as in A and plotted in the two-dimensional morphospace. $\widetilde{C_2}$ and $\widetilde{C_3}$ are the degree of bipolarity and multipolarity normalized to spindle size by C₀. The spindle images (inset) are ones at the four selected time points (indicated by i, ii, iii, and iv) along the thick example trajectory. The corresponding profiles of R(θ) and C_i are provided in SI Appendix, Fig. S2F. (C–K) Representative morphological growth trajectories (C–E), the trajectory landscapes (F–H), and the cross-correlation profiles between $\widetilde{C_2}$ and $\widetilde{C_3}$ (I–K) for bipolar (C, F, and I), multipolar (D, G, and J), and circular (E, H, and K) self-organization cases. Data were sorted based on the final shape phenotype using a machine-learning–based algorithm. The growth trajectories presented (C–E) are three examples; additional examples are provided in SI Appendix, Fig. S2D (total n = 87, 39, and 19, respectively). The trajectory landscape (F–H), indicates the cumulative frequency of all-trajectories’ passages at each coordinate point. The black solid lines present the mean paths; the start and end points are marked with open and filled circles, respectively. The cross-correlation profile (I–K) was calculated based on the time courses of $\widetilde{C_2}$ and $\widetilde{C_3}$ for individual spindle samples (SI Appendix, Fig. S4A) and then averaged (solid lines). The shaded areas are SDs.

We performed this analysis for a total of 175 spindles and successfully obtained the growth trajectories of 145 spindles (SI Appendix, Fig. S2D). The remaining 30 spindles yielded short or interrupted trajectories due to low image contrast and were excluded from further analyses. We acknowledged that the spindles’ growth trajectories exhibited several characteristic patterns. For example, one trajectory persistently moved upward (along the $\widetilde{C_2}$ axis), whereas another trajectory exhibited large fluctuations across the morphospace. Notably, most of the trajectories that exhibited a strong upward movement reached a steady bipolar shape. In contrast, trajectories that exhibited large fluctuations tended to reach multipolar shapes.

To more objectively ascertain the link between the matured spindle-shape phenotypes and the trajectories they had followed, we performed machine-learning–based phenotype sorting. Briefly, we first trained an algorithm with 200 representative spindle images acquired separately from the time-lapse experiments. These images were manually classified into three categories: 1) circular, 2) bipolar, and 3) multipolar. The training image data were then mapped onto the $\widetilde{C_2}$−$\widetilde{C_3}$ morphospace, whereby the algorithm defined the borders between each shape category and created a phase map (SI Appendix, Fig. S2E). Finally, individual morphological growth trajectories obtained from time-lapse experiments were classified based on their final location in the phase map. The results agreed well with our prediction, showing that the characteristics of growth trajectories were distinctly different depending on the matured shape phenotypes (Fig. 2 C–E). Specifically, the majority of spindles that attained bipolarity had followed a path that predominantly traveled along the $\widetilde{C_2}$ axis with a slight deviation toward $\widetilde{C_3}$ (n = 87) (Fig. 2C). On the other hand, spindles that attained multipolarity followed a path that largely fluctuated between $\widetilde{C_2}$ and $\widetilde{C_3}$ (n = 39) (Fig. 2D). Importantly, many of the fluctuating trajectories for multipolar spindles displayed a transient upward movement toward $\widetilde{C_2}$ before turning to $\widetilde{C_3}$ (black arrows, Fig. 2D). The structure’s size (C₀) also changed over time and the multipolar spindles reached a smaller steady-state size than that of the bipolar spindles (30.0 ± 4.4 µm versus 33.5 ± 5.9 µm, respectively; mean ± SD; P = 0.002 by Mann–Whitney U test), whereas the overall temporal dynamics of C₀ was similar between the two cases (SI Appendix, Fig. S3). Circular structures, albeit observed less frequently, had trajectories that originated from a nonzero point and explored across the morphospace (n = 19) (Fig. 2E). We further calculated the likelihood of the trajectories’ passages at each coordinate point in the morphospace and generated the spindle’s growth landscape (Fig. 2 F–H), which shows the favored growth path of the microtubule-based structures. The landscapes were distinct from each other, suggesting the characteristic morphological growth path that leads to each spindle-shape phenotype.

Bipolar and Multipolar Spindles Exhibit Characteristic Shape Dynamics during Their Growth.

To further investigate the uniqueness of the spindle’s morphological growth features, we examined the temporal order and coordination between $\widetilde{C_2}$ and $\widetilde{C_3}$. Specifically, we calculated the cross-correlation between $\widetilde{C_2}$ and $\widetilde{C_3}$ and compared similarities in their time courses while applying a time delay against one another (denoted as Δt) (SI Appendix, Fig. S4A) (for the definition formula, see Materials and Methods). We found that the bipolar and nonbipolar self-organization cases yielded distinctly different temporal correlation patterns (Fig. 2 I–K). Specifically, for the bipolar self-organization cases, the cross-correlation profile revealed a prominent negative peak at Δt ∼ 0 min (Fig. 2I), indicating that the relationship between $\widetilde{C_2}$ and $\widetilde{C_3}$ is reciprocal. In other words, a growth of bipolar features occurs concomitantly with a shrinkage of multipolar features. In contrast, for the multipolar self-organization cases, a prominent positive peak was found at Δt ∼13 min (Fig. 2J), indicating that the emergence of bipolarity was followed by the growth of additional poles with several minutes delay. Circular (monopolar) self-organization cases also yielded a trend, but the magnitudes were less profound compared with the former two cases (Fig. 2K). Consistent results were obtained by employing different machine-learning algorithms (SI Appendix, Fig. S4B). Thus, bipolar spindle self-organization occurs while maintaining predominant bipolar growth features. Multipolar spindle self-organization occurs with temporally shifted growth of extra poles with large shape fluctuations.

Locally Distorted Microtubule Flow at an Early Self-Organization Phase Can Result in Delayed Extra Pole Growth.

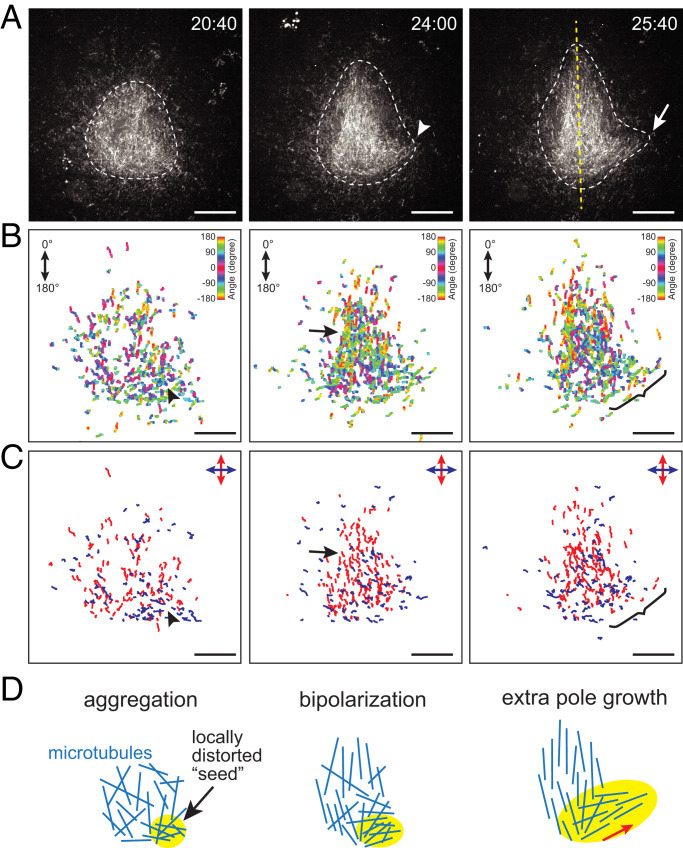
To understand local microtubule mechanics underlying the spindle’s morphological growth dynamics, we performed fluorescent speckle microscopy (Fig. 3). This method is based on a low concentration of dye-labeled tubulin added to extracts such that these tubulin subunits can be sparsely incorporated into the lattices of microtubules and form “speckles,” which can serve as fiduciary marks to track the motion and turnover of individual polymers (33). Of particular interest was the temporal delay of extrapole formation in multipolar spindles. Time-lapse imaging was performed over the course of spindle self-organization (interval: 1 to 2 s; total time: 45 to 60 min) with a high-magnification objective (×100), and individual speckles were tracked using an automated particle-tracking program. Fig. 3A shows sequential snapshots from a time-lapse recording that captured tripolar spindle self-organization (Movie S3). We observed that microtubules first formed a globular aggregate with minor deformations along the structure’s outline (white dashed line, t = 20 min:40 s). The aggregate then assumed an ellipsoidal shape with a bulge on one side (white arrowhead, t = 24:00). Eventually, a major bipolar symmetry was established (yellow dashed line, t = 25:40), while the protrusion grew into an extra pole (white arrow, t = 25:40). The overall morphological growth dynamics were consistent with those described earlier (Figs. 1 and 2).

Fig. 3.

Locally distorted microtubule flow within a premature structure can grow into an extra pole. (A) Sequential snapshots from time-lapse imaging data acquired using fluorescent tubulin speckle microscopy over the course of multipolar spindle self-organization (interval: 1.5 s). The structure assembled was initially globular (t = 20 min:40 s) and then became more ellipsoidal to establish bipolarity (t = 24:00 and 25:40), as outlined by white dashed lines. Meanwhile, a small bulge appeared (white arrowhead) and grew to an extra pole (white arrow). The yellow dashed line indicates the main bipolar axis that was established. (B and C) Speckle track maps. At each time point in A, ±50 successive frames were subjected to speckle motion tracking and the tracks generated (n ≥ 10 successive frames) were mapped in the image plane (B). The color codes indicate the mean motion orientation of each track, defined as indicated (Top Right). Individual speckle tracks were further split into two categories based on the orthogonally defined movement angle (C) such that the major bipolar-axis and off-axis movements of speckles could be clarified (red and blue, respectively). The black arrowheads indicate a location around which the speckles exhibited a distorted off-axis movement at an early growth phase. This fraction persisted and later grew to form an extra pole (brackets), while the majority of the speckles clustered around the structure’s center and contributed to bipolarization (black arrows), as outlined in D. Scale bars, 10 μm.

We then mapped individual speckle trajectories associated with the observed morphological dynamics and visualized their movement (Fig. 3B). The angle of each trajectory was color coded. We found that at an early time point (t = 20:40; Fig. 3B, Left), the speckle trajectories were largely scattered across the image plane with mixed colors, indicating a disordered arrangement of microtubules. A number of speckles then started to cluster at the center of the structure with complementary colors (t = 24:00; black arrow in Fig. 3B, Center), indicating the formation of an ordered, bipolar microtubule array. As time elapsed, the bipolar array expanded further to establish the major spindle axis while leaving a fraction of speckles moving off that axis around the location where the extra pole formed (t = 25:40; bracketed in Fig. 3B, Right). To examine the source of this off-axis movement, we traced the speckle track map back to earlier time points and found that there was a locally distorted polymer flow within the yet-to-polarize structure (black arrowhead, Fig. 3B). This distorted flow was more evident when the speckles were divided into two categories, either parallel or perpendicular to the bipolar axis (blue versus red tracks, Fig. 3C). Hence, a distorted microtubule flow arises at an early phase of spindle self-organization and persists as a “seed” while the structure establishes bipolarity; the seed then grows into an extra pole and a multipolar spindle can result (Fig. 3D).

Spindle Shape Is Independent of the Amount and Distribution of DNA.

Chromosomes stimulate a Ran-dependent signaling pathway to promote microtubule assembly in extracts (34). We thus examined the possible contribution of chromosomes to spindle shape by analyzing the amount and distribution of DNA within each structure (SI Appendix, Fig. S5 A and B). The amount of DNA was measured based on the integrated signal intensity of SYTOX dye in each spindle. The distribution of the DNA was quantified by generating an intensity profile of the dye around the spindle center and calculating the steepness of the profile (see schematic in SI Appendix, Fig. S5B). Our analysis revealed that both the amount and the distribution of the DNA exhibited broad distributions and showed no statistically significant differences between bipolar and multipolar spindles (n = 87 and 39, respectively; P  > 0.1 by Mann–Whitney U test).

Spindle Exhibits Mechanical Plasticity and Can Undergo Phenotypic Switching in Response to a Transient Force Perturbation Applied Near the Pole.

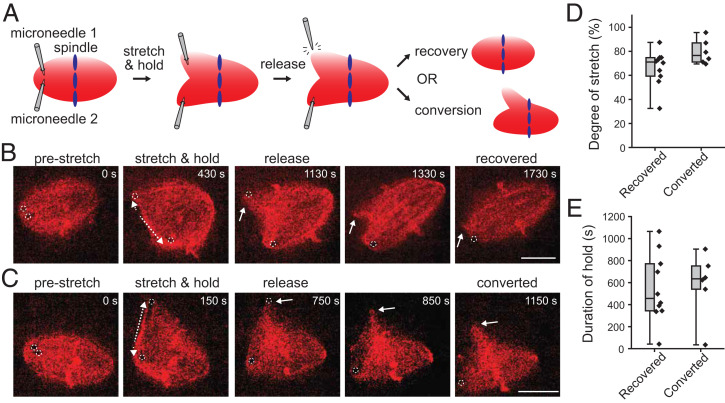
Our analyses suggested that varied spindle-shape phenotypes emerge through distinct paths of microtubule self-organization. Consistent with this, we observed that matured spindles stably maintained their bipolar and multipolar shape phenotypes over many minutes (SI Appendix, Fig. S6A). Interestingly, however, we also observed that the spindles infrequently switched their phenotypes between bipolar and multipolar shapes (5% ± 2% in 10 min for n = 245 spindles; mean ± SD; SI Appendix, Fig. S6B). To examine the mechanics underlying the spindle’s morphological multistability and stochasticity permitting phenotypic switching, we performed mechanical perturbation experiments (Fig. 4) (Movies S4–S6). Briefly, one pole of a bipolar spindle was captured using a pair of glass microneedles and then stretched such that the pole was mechanically split; the microneedle was then withdrawn from the spindle to free the captured pole, and the subsequent morphological changes were imaged by time-lapse microscopy (Fig. 4A). We found that out of 16 successfully stretched cases, 10 spindles recovered their initial bipolar morphology within 5 min; the freed pole gradually coalesced with the main spindle body to restore the bipolar shape (Fig. 4B and Movie S4). On the other hand, the remaining six spindles were converted into multipolar shapes; the extra poles created by micromanipulation were maintained over many minutes (>5 min; Fig. 4C and Movie S5). To explore the parameters that determine the probability of this phenotypic switching, we examined the magnitude and the duration of the applied stretch (Fig. 4 D and E). We found that the probability of the phenotypic switching largely depended on the magnitude of stretch (threshold: ∼70% of the initial spindle length) (Fig. 4D and SI Appendix, Fig. S7A). In these experiments, the manner in which the microneedles were moved varied among spindles (i.e., whether only one microneedle was moved or two microneedles were moved together); however, the procedure per se did not significantly influence the probability of the switching (SI Appendix, Fig. S7B). We did not observe that the multipolar spindles created by micromanipulation switched back to bipolar spindles, most likely because the probability of the spontaneous switching was substantially low (SI Appendix, Fig. S6B). Thus, the spindle can undergo plastic deformation in response to a transient force perturbation applied near the pole, permitting persistent phenotypic switching.

Fig. 4.

Spindle shape morphologies are stable but can be switched by acute mechanical perturbation. (A) Schematic showing our microneedle-based micromanipulation assay for examining a spindle’s morphological stability. The tips of two microneedles were inserted near one end of a bipolar spindle and moved apart to split the pole. One microneedle was then withdrawn from the structure and the resulting morphological change was observed. (B and C) Representative time-lapse images of spindles showing bipolar recovery (B) and multipolar conversion (C) in response to mechanical perturbation. In both cases, the left-side pole was captured by two microneedles (0 s) (the dotted circles indicate the positions of the tips) and then separated (dotted arrows) with a similar micromanipulation procedure. Soon after the upper microneedle was withdrawn, the freed pole (white arrow) either gradually coalesced to the proximal pole (1,130 to 1,730 s) (B) or remained in the new position (750 to 1,150 s) (C). (D and E) Frequencies of spindle-shape recovery and conversion depending on the magnitude (D) and the duration (E) of the applied stretch. A total of 16 spindles were examined (black diamonds). Box plots represent the median (horizontal lines) with interquartile ranges (box) and the smallest and the largest values (whiskers). Scale bars, 20 µm.

Kinesin-5 Provides the Spindle’s Characteristic Morphological Growth Dynamics Linked to Each Phenotype.

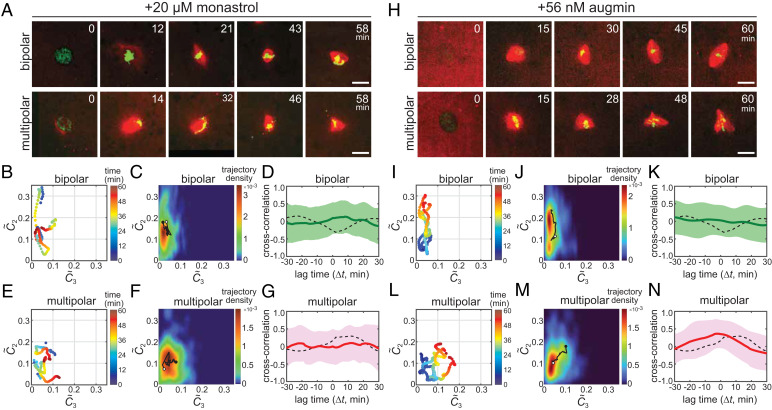
To explore the molecular mechanism underlying the spindle’s multistable self-organization properties, we performed molecular perturbation experiments (Fig. 5). Our first focus was on kinesin-5, as this motor protein is known to promote spindle bipolarity and multipolarity (9, 18, 32). We performed an identical imaging assay as described earlier but in the presence of monastrol, a chemical inhibitor of kinesin-5. At a saturated inhibition level (200 µM monastrol), we observed that >80% of the structures formed were monoasters (n = 24 of 28) (32, 35) (SI Appendix, Fig. S8A). On the other hand, at a moderate inhibition level (20 µM monastrol), monoaster formation was suppressed to ∼65% of 213 structures (n = 140); ∼20% of the structures were bipolar (n = 41) and the remaining ∼15% were multipolar (n = 32) (SI Appendix, Fig. S8B). Time-lapse imaging revealed several prominent differences in their morphological growth dynamics compared with untreated control, exhibiting highly unstable shape dynamics during their formations. For example, in the presence of monastrol, the structures assembled into bipolar were initially more disorganized and less compacted (t = 12 min; Fig. 5A) and their interpolar distance grew and shrank dynamically before reaching the steady-state (21 to 58 min; Fig. 5A) (Movie S7). Consistent with this, the morphological growth trajectories explored a broader morphospace as compared with the control (Fig. 5B). Such shape instabilities were also observed in the multipolar self-organization cases (Fig. 5E). Importantly, upon monastrol inhibition, the growth landscapes of bipolar and multipolar spindles, which show the structures’ favored growth paths, became overlapped with each other (Fig. 5 C and F). The cross-correlation profiles, which show the uniqueness of the spindle’s temporal shape dynamics, became also less distinguishable between the two cases (Fig. 5 D and G). We further noted that the cross-correlation peaks were much less pronounced compared with the control, indicating that the shape fluctuations were randomized (i.e., $\widetilde{C_2}$ and $\widetilde{C_3}$ became less temporally correlated) (solid versus dashed lines in Fig. 5 D and G). Together, kinesin-5 provides the spindle’s distinct self-organization paths and the morphological growth dynamics characteristic to each phenotype.

Fig. 5.

Kinesin-5 and augmin contribute to the spindle’s characteristic growth dynamics and shape stability. (A–G) Kinesin-5 inhibition assay results. (H–N) Augmin perturbation assay results. (A and H) Representative sequential snapshots from time-lapse imaging data showing bipolar (Upper panels) and multipolar (Lower panels) spindle self-organization in the presence of 20 µM monastrol (A) or 56 nM purified augmin holocomplex (H). Red: tubulin; green: DNA. Scale bars, 25 µm. (B, E, I, and L) Representative morphological growth trajectories of bipolar (B and I) and multipolar (E and L) spindles with partial monastrol inhibition (B and E) or with augmin addition (I and L) (n = 3 examples each). The trajectory landscapes (C, F, J, and M) and the cross-correlation profiles (D, G, K, and N) for the corresponding spindle phenotypes and perturbation conditions are also shown (n = 41, 32, 76, and 72, respectively). Additional examples of trajectories are provided in SI Appendix, Figs. S8C and S9G. The analysis methods and data presentation are as in Fig. 2.

Augmin Stabilizes the Growth Dynamics of Bipolar and Multipolar Spindles.

We next examined the contribution of augmin, an octameric protein that promotes microtubule nucleation in spindles (36). As our augmin inhibition assay did not yield stable shape phenotypes, we sought to perturb its activity by addition of purified augmin holocomplex (37) to extracts. We first tested the efficacy of the purified protein using a microtubule branching assay in extracts with a constitutively active mutant of Ran (RanQ69L) and EB1-GFP (38) (SI Appendix, Fig. S9 A and B). We observed that a nearly doubled amount of augmin in extracts [+56 nM versus the endogenous concentration of ∼60 nM (37)] promoted microtubule nucleation by approximately threefold (SI Appendix, Fig. S9 C and D) (n = 21 and 17 for control and augmin, respectively). We next examined the matured spindle phenotypes with the excess augmin (+56 nM) and found that there was robust formation of both bipolar and multipolar spindles, with shape morphologies similar to the control (SI Appendix, Fig. S9E). Notably, the distribution of the observed phenotypes was significantly biased toward multipolar structures (SI Appendix, Fig. S9F) (51.5% ± 7.4% versus 33.3% ± 5.6% for control; n = 286 and 283, respectively, mean ± SD from three independent preparations). We then analyzed the morphological growth dynamics of spindles using time-lapse imaging (Fig. 5H and Movies S8 and S9) (n = 172). We found that, in the presence of excess augmin, many of the growth trajectories became significantly less fluctuating and explored only a narrow region in the morphospace. This was observed both in bipolar and multipolar self-organization cases (Fig. 5 I, J, L, and M). The most drastic changes were noted in their cross-correlation profiles: For bipolar self-organization with excess augmin (n = 76), the negative peak that appeared at t ∼ 0 min in control spindles essentially disappeared and the profile became nearly flat as the growth of a multipolar feature ($\widetilde{C_3}$) was substantially suppressed (Fig. 5K). On the other hand, for multipolar self-organization with excess augmin (n = 72), the positive cross-correlation peak was maintained but its position in the horizontal axis was markedly shifted from t ∼13 min to t ∼ 0 min (Fig. 5N). This indicates that the growth of extra poles occurred nearly simultaneously with that of the other two poles and the spindle shape that transiently emerged grew progressively with little sampling of other shape morphologies. Thus, augmin stabilizes the structure’s characteristic shape dynamics and promotes the robust growth of both bipolar and multipolar spindles.

DISCUSSION

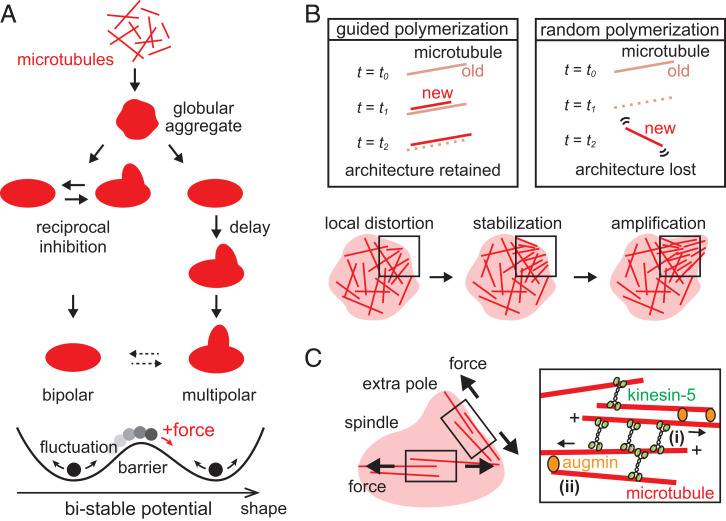
Using our long-term, large-field, live fluorescence imaging, quantitative shape analysis, and the bulk cytoplasmic extract of Xenopus eggs, we have revealed the characteristic morphological growth dynamics that lie in the process of spindle self-organization. Our data revealed that microtubule-based structures growing into bipolar and multipolar spindles undergo nonrandom, unique shape fluctuations and follow the distinct growth paths that lead to each phenotype (Fig. 6A). Speckle microscopy identified a local defect in the early microtubule networks, whereby the path to each spindle-shape phenotype is branched. We further showed that bipolar and multipolar phenotypes are stochastically switched at the steady-state in bulk and upon force perturbation, revealing the mechanical plasticity underlying the phenotypic multistability. Our findings on the stability and stochasticity of spindle morphogenesis can be expressed as a bimodal energy potential, which separates the growth paths of bipolar and multipolar spindles while permitting the occasional, plastic phenotypic change (Fig. 6A, Bottom).

Fig. 6.

Model for spindle self-organization multistability. (A) Schematic showing the characteristic morphological growth dynamics of bipolar and multipolar spindles. Microtubules first form a globular aggregate soon after nuclear envelope breakdown and then follow distinct growth paths for maturation. The paths to individual shape phenotypes are multistable, depicted as a bimodal energy potential (Bottom). The shape fluctuation occurs within each potential trough (black arrows); a transient large fluctuation or an external force perturbation can override the potential barrier separating the two stable shapes, leading to plastic phenotypic change (red arrow). (B) Model of the microtubule mechanics that govern the spindle’s mechanical plasticity. A defined cytoskeletal architecture can persist despite rapid microtubule turnover, when new microtubules progressively polymerize along preexisting, old microtubules before they depolymerize (labeled “guided polymerization”). On the other hand, the architectural information is lost when old microtubules depolymerize before the formation of new microtubules (labeled “random polymerization”). The guided polymerization mechanism may stabilize a local structural distortion within premature spindles and direct multipolar growth (Bottom). (C) Multistable spindle self-organization promoted by kinesin-5 and augmin. Kinesin-5 crosslinks and pushes apart pairs of microtubules [(i) in Inset], between the spindle’s two major poles and between pairs of other poles (black arrows). This mechanical activity promotes both spindle bipolarity and multipolarity, generating the characteristic shape fluctuation with opposing forces and separating the paths of self-organization. Augmin guides the orientation of newly generated microtubules and stabilizes the dynamic polymer architecture, making the structure more plastic [(ii) in Inset].

One of our prominent findings is the spindle’s morphological plasticity, in that multipolar spindles can be created by mechanical perturbation of bipolar spindles (Fig. 4). This is in stark contrast to studies that use genetic and cell biological approaches in which abnormally shaped spindles arise upon depletion or inhibition of key molecules (39). Given the rapid turnover of microtubules (40) and the extract’s overall potency to assemble bipolar spindles (29, 30), how can this plasticity be achieved? In the presence of these mechanochemical activities, microtubules that are misaligned or dislocated within the steady-state structure could be readily disassembled, and a more favorable bipolar architecture could be restructured. We propose that this is overridden by a mechanism which we refer to as “guided polymerization.” Namely, newly generated microtubules preferentially polymerize along preexisting old microtubules, or those that polymerize in random orientation immediately align with preexisting microtubules (Fig. 6B, Top Left panel). This should allow new microtubules to take over the position and orientation of old microtubules, whereby architectural information that is supposed to be lost due to polymer disassembly can be retained over many minutes, longer than the average lifetime of individual polymers. Otherwise, the position and orientation of the new microtubules are randomized, and the architectural information is not efficiently relayed from old to new microtubules (Fig. 6B, Top Right panel). Mitotic cytoplasm has a high microtubule-nucleation activity around chromosomes (41–43), and thus the generation of new microtubules should predominantly occur before the shrinkage of old microtubules. Furthermore, diverse microtubule crosslinking activities, such as motor and nonmotor microtubule-associated proteins, can crosslink adjacent microtubules (44–46) and readily align them into a nematic-like array (47). Experimental support for this comes from our micromanipulation experiments with speckle microscopy (Movie S6), wherein tubulin speckles that appeared immediately after spindle deformation followed the direction to which the preexisting microtubules were oriented. We predict that the guided polymerization operates at the steady-state as well as during the growth phase of spindles. Based on this mechanism, a local defect in the microtubule network, which arises within a premature structure (Fig. 3) most likely due to fluctuations in microtubule nucleation or stochasticity of motor protein forces, can be stabilized and the unfavored architecture is “locked” accordingly (Fig. 6B, Bottom panel). This stabilized network then grows into an additional pole such that spindle multipolarity is promoted. Bipolar spindles can form when such distorted flow is absent or disappears rapidly.

The observed mechanical plasticity of the spindle and its previously known elasticity (20–22) appear to be incompatible with each other because the plasticity is the property that allows the deformed shape to persist, whereas the elasticity is the property that restores the deformed shape. However, these two features can be mediated by considering the spindle’s characteristic material properties. Specifically, we have previously shown that the spindle is solid-like over a range of timescales from minutes to subseconds, whereas it fluidizes at an intermediate timescale (27). This transient fluidization should allow the spindle to undergo viscous deformation against a force perturbation while dissipating elastic energy that is otherwise used to restore its shape. The deformed structure should be mechanically unstable due to the fluidity but can regain overall stability as the long-timescale elasticity emerges (i.e., the structure becomes solid-like), allowing for a new shape that persists for many minutes. As the spindle’s plasticity was more prominent at larger deformations, the fluidization should take place in a strain-dependent manner.

A previous study reported that depletion of augmin promotes the formation of multipolar spindles (48). Our present study demonstrated that excess augmin also increases multipolar spindles (SI Appendix, Fig. S9 E and F). Importantly, the increase in multipolar spindles appeared in association with the enhanced bistability of bipolar and multipolar spindle formations, rather than by destabilization of bipolar spindles (Fig. 5). This enhanced bistability is consistent with the guided polymerization mechanism described earlier. Given the branched nucleation activity of augmin, this protein may promote the generation of new microtubules with shallow angles from old microtubules within the spindle [see (ii) Inset in Fig. 6C] and stabilize the polarity of the dynamic polymer network, bringing the plasticity to the microtubule-based structure and allowing the robust growth of varied spindle shape morphologies.

Our molecular perturbation assay also demonstrated that kinesin-5 creates the spindle’s characteristic shape dynamics and contributes to the distinct paths of microtubule self-organization (Fig. 5). In vitro, kinesin-5 crosslinks overlapping antiparallel microtubules and pushes them apart with their minus-end leading (49) [see (i) Inset in Fig. 6C]. This pushing force may act between the two major poles bridged by antiparallel microtubules and promote the structure’s uniaxial growth to establish bipolarity, as well as to push other assembled poles and bias the structure’s growth toward multipolar (black arrows, Fig. 6C). Within the cytoplasm, activities of other motor proteins, such as dynein and kinesin-14, may counteract this kinesin-5 pushing force and pull the poles together. A stochasticity in the pushing and pulling should result in the generation of the fluctuating shape dynamics. The paths to bipolar and multipolar spindles could be branched when the balance of these pushing and pulling forces is tipped, that is, the poles are pulled together when they are nearby (for bipolarity) whereas they are pushed apart when they are distant (for multipolarity). Taken all together, we propose that augmin increases the plasticity of the microtubule network and kinesin-5 deforms it to shape bipolar and multipolar spindles.

Many existing models have formulated spindle mechanisms by focusing on its size control (39, 50). On the other hand, the relation of spindle size to spindle shape (i.e., the pole numericity) is understood less well. Our data suggest that smaller spindles favor a multipolar over a bipolar shape phenotype (SI Appendix, Fig. S3). We infer that the impact of the shape fluctuation is larger for smaller spindles and thus causes multipolarity, especially given our finding of the prominent correlation between the spindle’s transient shape dynamics and the final shape morphologies. Our present analysis involved normalization of the shape amplitudes C₂ and C₃ with spindle size C₀, as the scaled values are maintained constant for structures of different sizes with the same geometry. However, as the mechanical properties of the spindle can differ depending on spindle size (e.g., larger spindles are less deformable) (30), the intrinsic shape dynamics may also depend on the size, and our analysis highlighted those of the majority of the spindle population. A recent study underscored the importance of 3D analysis for spindle size measurement (51). Implementing fast 3D scanning of spindles, which is currently limited in our analysis due to photostability and time resolution, should allow for identifying the mechanics that link the size and the shape of this self-organizing structure.

Spindles share layers of similarities with other subcellular organelles, such as centrosomes and nucleoli, in that the structures are micrometer sized, membrane-less, and undergo dynamic exchange of components. Whereas these are typical characteristics of phase-separating biomolecular droplets whose form is largely spherical and uniform (52), the spindle’s shape morphology diverges. Our study highlights the mechanical means that cause the morphological diversity and plasticity of the dynamic cytoskeletal structure, adding a layer to the principles of subcellular self-organization.

MATERIALS AND METHODS

A full description of the materials and methods is provided in the SI Appendix, Extended Materials and Methods.

Spindle Assembly and Imaging.

The spindle assembly reactions were performed using X. laevis egg extracts (53). For each reaction, freshly prepared, cytostatic factor–arrested extract was first cycled into interphase by the addition of Ca²⁺ with demembranated sperm (at 800 nuclei/µL) to assemble nuclei in test tubes. The extract was then cycled back into mitosis by dilution with an equal volume of fresh cytostatic factor–arrested extract and subsequently sealed in an imaging chamber (volume: 5 µL) for time-lapse imaging (interval: 1 min). Image acquisition was performed using spinning-disk confocal optics with two excitation lasers, a ×20 objective lens, and a scientific CMOS camera. A large-field image (2.7 × 2.3 mm²) was acquired at each time-lapse frame by raster scanning the sample stage. To visualize microtubules and chromosomes, X-rhodamine tubulin (200 nM) and SYTOX Green (1 nM) were added to the extracts. The experiments were performed at 19 ± 1 °C. The prepared extracts were stored on ice and used within 6 h. For speckle imaging, the microscope setup identical to that described above was used but with the following modifications: dye-labeled tubulin was added at 30 nM, the objective lens used was ×100, and the time-lapse interval was 1.5 s.

Micromanipulation.

Spindle micromanipulation experiments were performed using a dual-microneedle-based setup (27). We placed 5 µL of extracts in an open-top imaging chamber and covered them with mineral oil; then the tips of microneedles were inserted near one pole of a spindle and moved to split the pole by stirring a pair of low-drift, three-axis micromanipulators. The objective lens of ×60 or ×100 was used. The time-lapse interval was 1 s.

Proteins.

Augmin was expressed in an insect cell system and purified by tandem affinity chromatography according to a modified method from the originally published protocol (37) (His-tag was removed; the GST-tag was replaced with a ZZ tag). RanQ69L and EB1-GFP were prepared essentially as described previously (24, 54).

Molecular Perturbation.

Reagents were added to extracts at the start of spindle assembly. Monastrol was added to a final concentration of 20 µM or 200 µM with 0.5% (vol/vol) DMSO. The purified augmin was added to a final concentration of 56 nM.

Data Analysis.

Morphological growth trajectory.

Spindles’ morphological growth trajectories were generated by analyzing microtubule channel images acquired by time lapse. Each image was first processed for noise reduction and banalization. The contour of each highlighted structure was then traced using the outline tracing vector R, which was drawn from the structure’s centroid and rotated over 360° (−π ≤ θ ≤ π). The spindle’s shape profile, R (θ), obtained in this manner, was then decomposed into discrete Fourier modes according to the following equation:

$$R\left(\theta \right)={\displaystyle \sum }_{n=0}^{+\infty }{C}_n{e}^{-in\theta }$$ [1]

The amplitude of each Fourier coefficient C_n in Eq. 1 was calculated as follows:

$$C_n=\frac{1}{2\pi }\underset{-\pi }{\overset{\pi }{{\displaystyle \int }}}R\left(\theta \right)e^{-in\theta }d\theta ,$$ [2]

where C₀ is the measure of the structure’s size and C₂ and C₃ are the measures of the structure’s bipolarity and multipolarity, respectively. C₁ is zero for any shape, as the origin of R is fixed at the structure’s centroid. The values of C₂ and C₃ were then scaled by size with C₀ (defined as $\widetilde{C_2}$ and $\widetilde{C_3}$, respectively) and plotted onto a $\widetilde{C_2}-\widetilde{C_3}$ coordinate plane (referred to as the morphospace). The analysis was performed for every time-lapse frame such that the spindle’s entire growth trajectory was reconstituted.

Phenotype sorting.

The classification of spindle time-lapse data using machine learning was performed based on a linear discriminant analysis model (55, 56). The model was first trained with 200 spindle still images acquired independently from the time-lapse experiments. Each training image was manually labeled with one of the three shape classes (i.e., circular, bipolar, or multipolar) and linked to the $\widetilde{C_2}$ and $\widetilde{C_3}$ values calculated as above. All the labeled training images were then mapped onto the single plane of $\widetilde{C_2}-\widetilde{C_3}$, whereby the model created a phase map (SI Appendix, Fig. S2E) for discriminating spindle images based on the combination of ($\widetilde{C_2},\widetilde{C_3}$). After testing the performance of the trained model, spindle time-lapse data were sorted based on the trajectory’s final destination in the phase map.

Trajectory landscape.

The spindle’s morphological growth landscape was generated by projecting onto a single $\widetilde{C_2}-\widetilde{C_3}$ plane all the trajectory data pooled in each shape class and counting the number of trajectory segments that passed each coordinate point. A two-dimensional histogram was generated based on the numbers counted, normalized by the total number of trajectory segments, and then color coded for visualization.

Cross-correlation.

The cross-correlation profile was obtained using the following equation:

$$Cr(\mathrm{\Delta }t)=\frac{\langle {\tilde{C}}_2\left(t\right)-\langle {\tilde{C}}_2\rangle \rangle \cdot \langle {\tilde{C}}_3\left(t+\mathrm{\Delta }t\right)-\langle {\tilde{C}}_3\rangle \rangle }{\sqrt{\langle {\left({\tilde{C}}_2\left(t\right)-\langle {\tilde{C}}_2\rangle \right)}^2\rangle \langle {\left({\tilde{C}}_3\left(t\right)-\langle {\tilde{C}}_3\rangle \right)}^2\rangle }},$$ [3]

where Δt is the time shift between $\widetilde{C_2}$ and $\widetilde{C_3}$. The profile was generated for individual spindle time-lapse data and averaged across all the data pooled in each shape class.

Speckle tracking.

Speckle tracking was performed using a particle-tracking program as described previously (57). Successive time-lapse images of −50 to 50 frames from the time point of interest were subjected to the analysis. Speckles successfully tracked ≥10 frames were mapped onto a plane and color-coded based on the mean movement angle calculated.

Spindle deformation.

The extent of spindle deformation induced by microneedles was determined by measuring the distance over which the manipulated pole was stretched and then calculating its ratio to the prestretched spindle length. The duration of hold was determined as the time from when the microneedles reached a maximal separation to when the microneedle tips were withdrawn.

DNA amount and distribution.

The amount of DNA was determined by measuring the total fluorescence intensity of SYTOX dye within each spindle after background subtraction. The distribution of the DNA was analyzed by setting a polar coordinate with its origin at the spindle’s centroid, generating the intensity profile of the dye along the coordinate axis and calculating the slope of the profile by linear regression.

Data, Materials, and Software Availability

The original image data, analyzed trajectory data, and program codes have been deposited in Figshare (DOI: 10.6084/m9.figshare.20495262 (58); 20346882 (59); 20346894 (60); 20438892 (61); 20439000 (62); 20438889 (63); 20438988 (64)).