Modeling and optimization of pressure and water age for evaluation of urban water distribution systems performance

Abstract

Water loss has become increasingly critical as the severity of the water shortage situation has grown in recent decades. One of the options for reducing water loss in urban water distribution networks is pressure management. The study aimed to evaluate and optimize the existing water distribution system in the city. The proposed methodology is an interactive combination process between an optimization algorithm and WaterGEMS V8i to evaluate the performance of the distribution system. It was observed that, 43.80% of nodes (15–60 mH₂O), 5.10% of nodes (15 mH₂O), and 51.10% of nodes (>60 mH₂O) received pressure during peak hour demand. During low demand periods, only 4.4% of nodes (15–60 mH₂O) and 95.60% of nodes (>60 mH₂O) received pressure. The water age simulation results revealed that, 51.70% of the pipes were received water age <4.8 h, whereas the other 48.3% of the pipes were received water age <8.6 h during peak hour demand. During low demand periods, 45.58% of the pipes had a water age of less than 4.8 h while the other 54.42% of the pipes had water age of 4.8–20 h. The optimization result showed that after optimization, 4.4% of the nodes with optimum pressure increased to 75.18%, and 95.6% of the nodes decreased to 24.82%. Changing the size of the pipe based on the optimization result, and dividing an area into different pressure zones (adding more reservoirs at the far end of the distribution system) are all ways to improve or upgrade the distribution system.

Highlights

• •The amount of pressure and age of the water were higher at low demand periods than at peak demand.
• •One way to see how well a distribution system works is to look at how much pressure and how old the water is.
• •Through optimization, pressure can be kept at an optimum level in the distribution system.
• •Subsequent monitoring is very important for the sustainability of urban water distribution systems.

Optimization; Pressure; Simulation; Water age; Water distribution networks.

1. Introduction

In modern communities, water distribution networks play a critical function, as their proper operation is directly related to the population's well-being (Desta and Befkadu, 2020). The distribution network is an essential part of all water supply system (Sarbu and Ostafe, 2016). Water distribution systems are composed of nodes and links, and the nodes include: junction, tank, reservoir, while the link consists of: pipes, valves, and pumps (Liu and Yu, 2014). During their lifetime, most designed water distribution systems (WDSs) in urban areas are subjected to different internal and external development pressures, and they must be continuously updated to ensure a sufficient high level of service at all times (Zischg et al., 2017). As a result, the future of water use is exceedingly uncertain. It depends on numerous elements, such as changes in population and consumption habits, climate change, variations of land use, tourism and economic developments (Desta and Befkadu, 2020). All of these global influences can have a substantial impact on existing WDS's performance over their lifetime, which can be evaluated via a scenario analysis (Zischg et al., 2017). According to (Li and Han, 2020), the International Water Association (Alegre et al., 2016; Kun et al., 2007), the Office of Water Services (OFWAT), and Portugal's ERSAR have all developed water supply performance evaluation systems to assess the management performance of water supply systems, water firms, and they've all had a lot of success (Cabrera and Cabrera, 2016). Performance assessment, defined as "any approach that allows for the evaluation of the efficiency or effectiveness of a process or activity through the development of performance measures," is the key to long-term sustainability (Desta and Befkadu, 2020; Muranho et al., 2014). Pressure and water age are the most important parameter that should be considered while evaluating the performance water distribution system. Transient occurrences are characterized by variable pressures and velocities, which can be severe enough to break or damage pipes or equipment, while transient low pressures might cause delivery conditions to be disrupted (Ghorbanian et al., 2016). There are two types of water losses in water distribution systems (WDSs): real and apparent losses. Leaks at network fittings, pipe joints, breaks and/or bursts in pipes are the main causes of real losses, whereas apparent losses are caused by inaccurate meters and/or unauthorized consumption (Dai, 2021; Lambert A.O., 2002; Puust et al., 2010). Due to low or even negative pressure situations, high water losses can cause service interruptions, energy losses, and pollutant ingress (AL-Washali et al., 2020; Dai, 2021; Kouchi et al., 2017). With increased retention time in the water distribution system, water quality will decline, resulting in problems such as disinfection by-product generation, disinfectant decay, corrosion, taste, and odor (Cheng et al., 2015). This side effect has to do with the water age (i.e., the total amount of time the water spends inside the pipes before reaching the customer's tap), which can be significantly increased after a pressure management strategy is successfully implemented (Menelaos et al., 2020; Chondronasios et al., 2017; Shamsaei et al., 2013a, Shamsaei et al., 2013b). Water age is very significant for the water quality of a water distribution system, and it is mostly determined by the design and demands of the system (Cheng et al., 2015). A water distribution system consists of hydraulic components sources, pipes, pumps, and control elements (Perelman et al., 2008). Authorities are obliged to establish water supply systems from various available sources in order to provide safe drinking water to the entire population in a sustainable manner due to restricted water availability. The study used WaterGEMs V8i for modeling, evaluation and optimization process. In optimization process, genetic algorithms were widely adapted for calculation and evolutionary programing (Kadu et al., 2008; Marchi et al., 2014; Martin-candilejo et al., 2020). Genetic algorithms are used in many areas to solve optimization problems such as optimal parameter estimation (Abdelsalam and Gabbar, 2021; Demiroren et al., 2019; Selem et al., 2021). Economic aspects indicate that benefits should be maximized or expenses should be minimized (Song et al., 2019; Xu et al., 2020) while optimization of water distribution systems. This research focuses on analysis and optimizing the urban water supply system to ensure that the city’s water supply remains secure, reliable, and economical, as well as assuring long-term access to water of appropriate quality. This paper also discusses some of the issues surrounding pressure and water age criteria that are most relevant to developed countries where water supply reliability is generally assumed.

2. Materials and methods

2.1. Study area

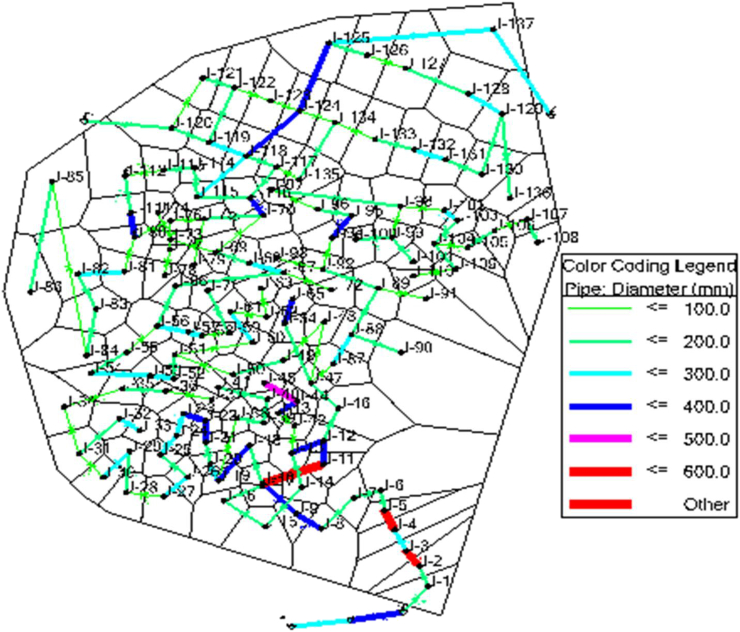
The study area considered in this study is Adama city, which is located in Oromiya Regional State, Ethiopia. Adama is characterized by very flat and low land surrounded by a lot of mountains (Desta and Befkadu, 2020). As regards to the proposed expansion, most of the areas are characterized by flat and undulated plains as well as mountain natural barriers (Desta and Befkadu, 2020). Adama has been one of the rapidly growing towns in the region of Oromiya as well as in the country since the period of 1964 (Yonas, 2010). According to the Central Statistical Agency of Ethiopia (CSA, 2007), this city has a total population of 220,212, a 72.25% increase over the population recorded in the 1994 census, with 108,872 males and 111,340 females. Average daily production of water from the treatment plant, which is the city's principal water supply source, was 36,000 m³/day, or 416 l/s. The research area network for analysis is depicted in Figure 1. The Thiessen polygons were defined by setting the total junction presence in the networks that supplies water to the community in Bentley water Gems’ tools toolbar.

Figure 1.

Map of study networks.

2.2. Base demand calculation on node

Demand allocation and projection are made much easier with Load Builder. Load Builder is accessed from tools toolbar in Bentley water Gems. Demand allocation and projection are substantially simplified with Load Builder, although data preparation with ArcGIS is required. There are different Load Builder Methods used to estimate the nodal demand. Some Load Builder methods employ the service area layer to distribute loads depending on areas associated with nodes. The Nearest Node technique is used to apply loading data from a shape file to the model’s closest junction or hydrant. The Nearest Pipe technique assigns loading data to the nearest pipe, which is then distributed among nodes depending on user-defined parameters. Proportional Distribution by Area: Combines a service area layer (usually created with the Thiessen polygon tool) with billing meter polygons with a single demand value to represent the service area around each junction. Overestimation of demand is a fundamental shortcoming of this method because it uses area to calculate nodal demand. Thiessen polygons were defined by setting the total junction presence in the networks in Bentley water Gems’ tools toolbar. The mechanism for calculating and assigning the expected to the model demand nodes is determined by the data provided. According to (Lippai and Wright, 2014) new developments rely on demand estimates based on land use data or surrogate information, while models of the existing developments rely on actual water production or customer metering. According to (Neha mangesh, 2009), the following formula was adopted to evaluate the nodal demand of the area. The population supplied by a supply node divided by the total population and times the town's total water production equals base demand for that node. Because the water supply distribution system should be analysed during this period in order to provide adequate water to consumers, the simulation period was chosen at peak hour demand. So, for this study population based method was selected which gives the accurate value of demand at each node. The numbers of population cover each supply node data obtained from Adama water supply and sewerage enterprise.

2.3. Hydraulic model analysis

WaterGEMS V8i was used to model the data, and the procedures were as follows: Data entry into Microsoft Excel; initial setup (units are set to SI); network schematic; model construction; model simulation; extended period analysis; problem analysis; Using the basic working equation, conservation of energy (head loss continuity) and conservation of mass (flow continuity) the WaterGEMS V8i program solves the distribution of flows and hydraulic grades. The values can be used to describe the difference in head loss or gain between two points. The conservation of energy principle implies that at each point in the system, the head loss must balance. Any head loss between two nodes must be in the same direction as the expected flow direction. Any widely known formula can be utilized in hydraulic calculations.

2.4. Optimization process

During the simulation period of continuous network operation, optimization is critical to minimizing the objective function. Darwin Designer is accessed from Bentley water Gems' analysis toolbar. Darwin Designer is a time-saving tool for creating new pipe layouts and rehabilitating existing ones. It allows the user to create pipes for an existing model either manually or automatically using efficient genetic algorithms. It provides for the presentation of numerous design candidates in order to find the best possible solution for a given system. In addition, solutions can be transferred into a new scenario for usage in an existing water system. There are some occasions where an optimization model, such as WaterGEMS′ Darwin Designer, can be useful, but only if the optimization assumptions perfectly match your design problem. It's preferable to have less pipe groups in Darwin designer since optimization takes a lot of computer time for a generic algorithm, therefore the more pipe groups you have, the longer it takes to find a solution. If you have a huge system, you might consider developing distinct parts of it using multiple runs. Bentley WaterGEMS CONNECT Edition assists in the correction of the most critical genetic algorithm parameter ranges. Population Size: 40 to 200; Cut Probability: 0.5–2.5%; Splice Probability: 50–80% Mutation Probability: 0.5–2%; Maximum Era Number: 4 to 10; Era Generation Number: 50 to 200. From those range we have adopted; Cut Probability: 1.7%; Splice Probability: 60% Mutation Probability: 1.5%; Maximum Era Number: 6; Era Generation Number: 150; Population Size 50; random speed 0.5; penalty factor 1,000,000; maximum trial 250,000 and non-improvement generation 600 on the basses of Darwin designer default criteria. Darwin designer uses Eqs. (1), (2), (3), (4), (5), and (6) for optimizing the parameters. The optimum pressure at the node was satisfied utilizing the Darwin Designer model with incorporated generic algorithm by setting the minimum and maximum pressure and velocity depending on local criteria. For the entire WDS, the optimization process assumed four general restrictive conditions: a minimum pressure head of 10 m H₂O in the water system, a maximum pressure head of 70 m H₂O in the water system, and a maximum and minimum acceptable flow velocity of 0.5 and 3.5 m/s for distribution pipes, respectively.

2.4.1. Objective function

The objective function is minimizing the total cost of installation pipe, C_T;

$$C_T=\sum _{X=1}^{X}0.254L_X{D}_X^{1.834}$$ (1)

where L_x is the length of the link x, in m and D_X is the diameter of the link x in mm.

Constraint: there are four constraints to fulfilled by the objective function;

• a.Node flow continuity constraint

$$\sum _{Xincidentonj}{Q}_X+q_j=0,\mathrm{j}=1,\cdots \mathrm{N}$$ (2)

where and Q_X the flow in link x to the node j; q_j is the demand at node j and; N is the total number of nodes in the network.

• b.Loop head constraints

$$\sum _{X\epsilon c}A{L}_X{Q}_X^p{D}_X^{-r}=0,c=1,...c$$ (3)

where A is a constant that varies depending on the connection material and unit of distinct terms; P and r are exponents of 2 and 5 for the Darcy-Weisbach formula, respectively; 1.85 and 4.87 for the Hazen-William formula.

$$A=\frac{\alpha }{C_{HW}^{1.85}}$$ (4)

where $\alpha =2.234\times {10}^{12}$; and C_HW = 130 for UPVC pipes; then, $A=\frac{\alpha }{C_{HW}^{1.85}}=2.74\times {10}^8$

• c.Path head loss constraints

$$\sum _{X\epsilon pj}A{L}_X{Q}_X^p{D}_X^{-r}\le h_j^{mn},j=1,...N$$ (5)

where $h_j^{mn}$ is the minimum residual pressure allowed at node j.

• d.Non-negative constraints

$$D_X\ge D^{mn},Q_X\ge Q^{mn}$$ (6)

where; D^mn and Q^mn the minimum link diameter and flow allowed in the network respectively.

3. Results and discussion

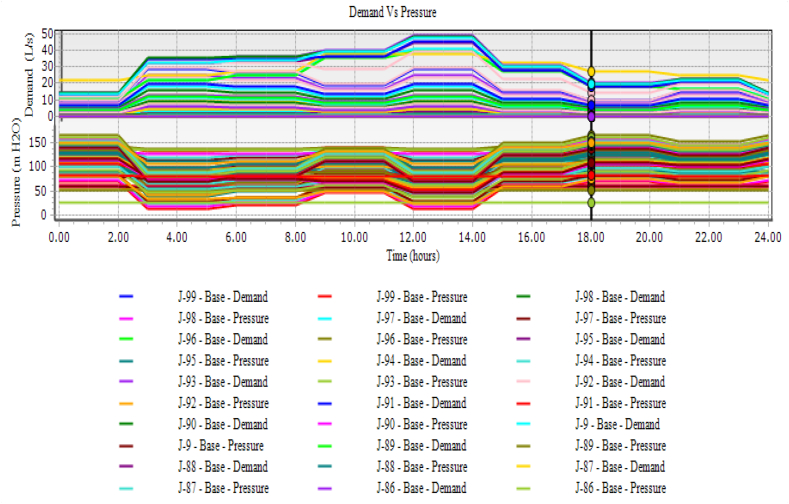
For the case of Adama city, WaterGEMs V8i was used to model the water distribution system. 147 connectors, 137 pipes, 1 pump, and 3 reservoirs were used to create the distribution system. For the case of pressure evaluation, the model was simulated with a setup time of 24 h. This is due to the fact that hydraulic parameters including pressure, velocity, and head loss change with time. The running period for determining water age was set at 288 h to ensure precise findings. Nodal pressure was far more relevant than the other two peak and average water demand hours since leakage and water quality worsened significantly during this low consumption hour. Figure 2 depicted the variation in demand and pressure across a 24-hour simulated period. As observed from Figure 2 the demand and pressure at each node have inverse relationship. When the demand was higher the pressure becomes reduced and vice versa. At 18:00 PM, the simulation is illustrated by a bolded vertical line demand and pressure relationship. As can be seen from this vantage point, demand was low but pressure was high. Because no water flow occurred in the distribution system at this time, maximum pressure, maximum water residence time (water age in the pipe), minimum velocity, and leakage rate were expected to be high at night (18:00 PM).

Figure 2.

Demand and pressure curve at extended period simulation.

3.1. Pressure at high demand

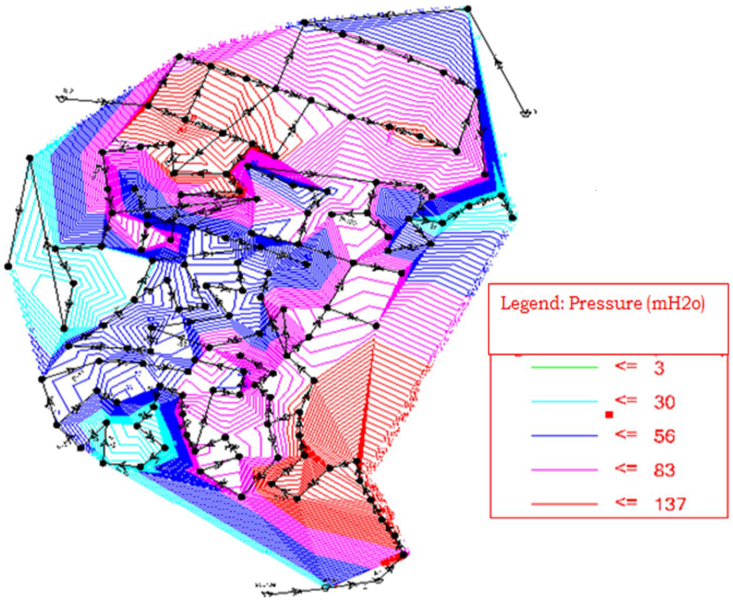
Figure 3 shows that the area covered by the red-colored counter is under a lot of pressure (less than or equal to 137 m mH₂O). The area highlighted by the purplish red counter has a water pressure of less than or equal to 83 mH₂O. This means that the distribution system could experiences bursts and leakages in the area with high pressure (Awe et al., 2020). This high water losses can cause service interruptions, energy losses, and pollutant ingress (Dai, 2021). Here, pressure reducing valves and zoning are very important to minimize such problems. The blue-black color counter emphasized places with a water head of less than or equal to 56 mH₂O, which was within (MoWR, 2006) standards. The blue-hued area had a water pressure of less than or equal to 30 mH₂O, which was within (MoWR, 2006) acceptable limits. This means that there was a balanced water distribution system, optimum pressure, and minimum water loss in those areas based on these local standards. In general, the area closest to the supply source received high pressure, while the area farthest away received low pressure. Table 1 was formulated based on normal conditions to show the pressure distribution throughout the entire area.

Figure 3.

Analysis of pressure at peak hour demand.

Table 1.

Pressure distribution result over the entire area at high demand.

Pressure range (mH2O)	Node count	Percentage
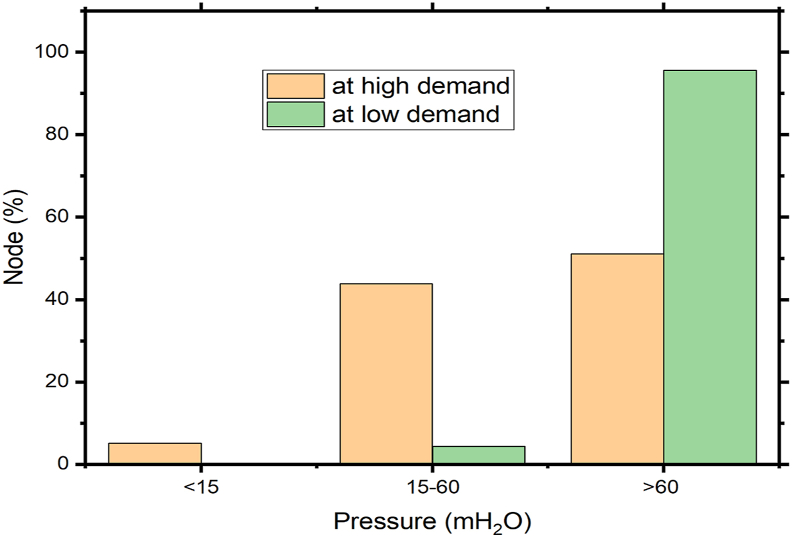
<15	7	5.109
15–60	60	43.796
>60	70	51.100

As observed from Table 1, 5.109% of the nodes received pressure less than the recommended minimum pressure (MoWR, 2006). The water supply problem here is caused by insufficient node pressure and water shortages in certain areas of the system (Awe et al., 2020). 43.796% of the nodes received pressure within acceptable range (MoWR, 2006). While the last pressure range greater than 60 mH₂O of water and was above the recommended maximum pressure (MoWR, 2006); this covered 51.100% from the total area. This means that maximum of the node in under stress in bursts and leakage. This causes increasing of water loss and unstable distribution of water in the system.

3.2. Pressure at low demand

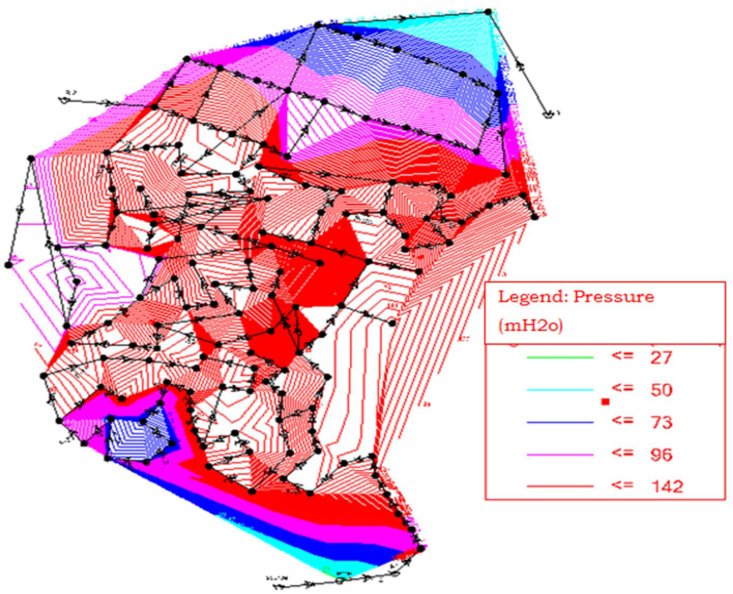
Because leakage and water quality deteriorated significantly during this low consumption hour, nodal pressure was much more important than the other two peak and average water demand hours. At night (18:00 PM), maximum pressure, maximum water residence time (water age in the pipe), minimum velocity, and leakage rate were expected to be high because at this time, no water flow occurred in the distribution system. As shown in Figure 4, the red counter map, which has a high pressure range (less than or equal to 142 m) which was above (MoWR, 2006) standards. The pressure range of the blue-black, blue, and magenta color counters was medium (50–96 m). Generally, as observed from Figures 3 and 4, the amount of pressure at low demand (Figure 4) was higher than at peak hour demand (Figure 3). This was due to decreasing velocity at low consumption times, which produces higher pressure in the distribution system. This causes increasing leakage and burst of pipe. For this reason, in order to reduce the existing leakage in the region active leakage control method should be applied so as to get the whole reported data for further investigation (Özdemir et al., 2021). The existing system is excessively imbalanced and inefficient in delivering water to meet demand in all sections of the system, as shown in Figure 4 (Awe et al., 2020). This unbalanced and inefficient water distribution system motivated us to optimize the system.

Figure 4.

Analysis of pressure at low hour demand.

As portrayed in Table 2, 95.6% of nodes were failed to satisfy desirable minimum pressure (MoWR, 2006) during the low demand situation. There was no node less than minimum allowable pressure of 15 m. While only 4.4% of nodes were in the permissible pressure ranges of minimum 15 m and maximum 60 m (MoWR, 2006). From Table 2 results 95.6% should be improved to be within the pressure design criteria in the water supply system.

Table 2.

Pressure distribution result over the entire area at low demand.

Pressure range (mH2O)	Node count	Percentage
<15	0	0.0
15–60	6	4.4
>60	131	95.6

3.3. Comparison of simulated pressures at peak hour and low demand period

Figure 5 shows a comparison of pressure distribution during peak and low-hour demand. As seen in this Table, at low demand, no nodes received pressure less than 15 mH₂O. During a moment of high demand, however, 5.11 % nodes were subjected to pressures of up to 15 mH₂O. During the low demand time, only 4.40 % nodes were received between 15 and 60 mH₂O pressure, which is the national suggested range. During a period of high demand, 43.9 % nodes were received between 15 and 60 mH₂O pressure. 95.60 % nodes got pressure greater than 60 mH₂O during low demand, while 51.10 % nodes received pressure greater than 60 mH₂O during high demand. In general, the pressure was higher during low demand periods than during peak demand periods. This is owing to the fact that water does not flow out of the system during low demand periods. This is because of at the night time most of the customers sleep and industries are shutdown (Jacobs and Strijdom, 2009).

Figure 5.

Pressure distribution at peak and low hours' demand.

3.4. Water age at peak hour and low hour flow

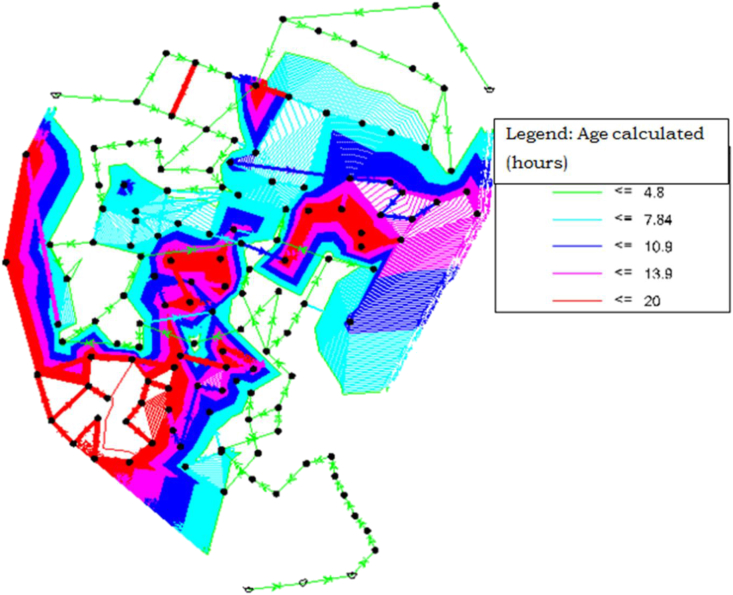
The cumulative residence time of water in the system, or water age, has come to be regarded as a reliable replacement for water quality. Figure 6 shows the water age analysis at a low demand hour. The analysis for water age was based on the assumption that the distribution system was loaded with continuous flow. Thus, any findings for this parameter were limited to this assumption. Water quality simulation requires a series of runs to understand the movement of water and water quality transformation in the system. Specific simulations included in this study were: water age. There was a variation in water quality in the distribution system from hour to hour of a particular day. This hourly variation of water quality was mainly related to demand patterns. As observed from Figure 6, the far end of the area received high water age, which is indicated by the red color, compared to the area situated near to the supply source. According to (World Health Organization (WHO), 2014), the age of water in the distribution system should be set as a minimum because of its high health impact.

Figure 6.

Simulated water age at low hour flow.

As it was illustrated in Table 3 at low hour flow majority of pipes 54.12% received water with age exceeding 4.8 h. So, according to (World Health Organization (WHO), 2014), the water age in the area should be minimized. This water age occurred in an area far from the reservoirs, which were located in the system's downstream section or at a lower elevation. The other 45.58% received by pipes were near the supply source. In general, at low demand periods at the far end point of the distribution system, the pressure was high and the velocity was low. This provided a high residence time of water in the distribution systems. The calculation of Table 3 was done based on the simulated result that was obtained from the software.

Table 3.

Water age distribution at low hour flow.

Water age (h)	Pipe count.	Percentage
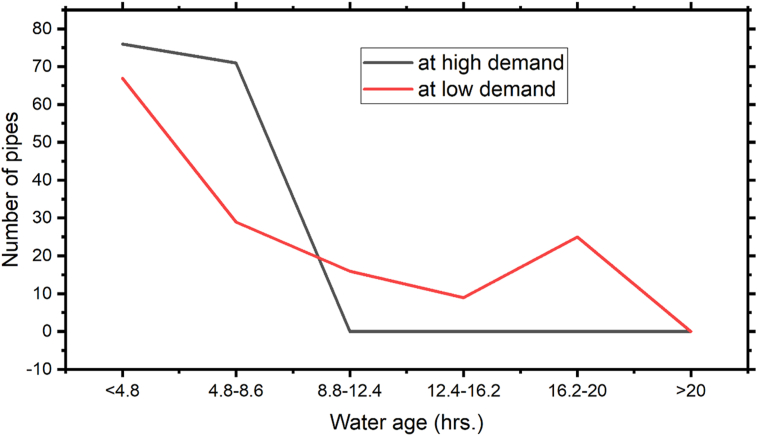
<4.8	67	45.580
4.8–8.6	29	19.730
8.8–12.4	16	10.880
12.4–16.2	9	6.122
16.2–20	25	17.010
>20	0	0.000

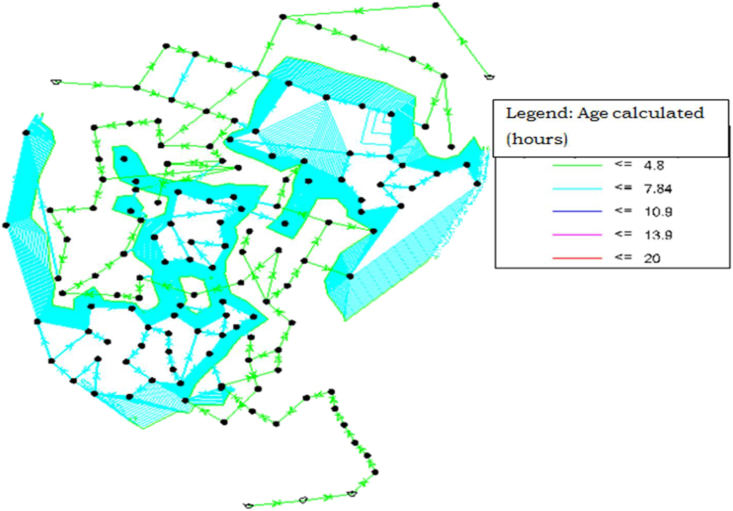
As depicted in Figure 7, water age was distributed over the area. But the value was different. The end point of the distribution system received more water than the area that was situated near to the source, which is indicated by the blue color.

Figure 7.

Simulated water age at peak hour flow.

Table 4 shows that at peak hour flow, 51.70% of pipes had a water age of less than 4.8 h, above 8.6 h, the age was reduced to zero. As observed from these two different simulated results (Figures 6 and 7), there was a significant difference between the age of the water reaching pipes at high water consumption time and low water consumption time. This is because water age in the distribution system is highly related to pressure and velocity. The average water age was reduced when the velocity increased (48.30% greater than 4.8 h), but increased when the velocity decreased at low demand (54.12% greater than 4.8 h).

Table 4.

Water age distribution at peak hour flow.

Water age (h)	Pipe count.	Percentage
<4.8	76	51.70
4.8–8.6	71	48.30
8.8–12.4	0	0.00
12.4–16.2	0	0.00
16.2–20	0	0.00
>20	0	0.00

3.5. Comparison of simulated water age at peak hour and low demand period

Figure 8 illustrates a comparison of water age distribution during peak and low-hour demand. During a moment of high demand, 76 pipes were exposed to water age of up to 4.8 h. The remaining 71 pipes have a water age of 4.8–8.6 h, with no pipes having a water age of more than 8.6 h. This is owing to the fact that the system was leaking more water. Of the total pipes in the system, 67 pipes were exposed to water age of up to 4.8 h during the low demand period. The remaining 29 pipes were between 4.8 and 8.6 h, 16 pipes were between 8.8 and 12 h, 9 pipes were between 12.4 and 16.2 h, and 25 pipes were between 16.2 and 20 h. During low demand periods, the average water age was generally higher than during peak demand periods. This is owing to that, there is no flow of water out of the system during low demand period. This favors increasing of residence time, decreasing water quality and increasing bacterial growth (Shamsaei et al., 2013). In spite of such increment, the value was within the standards. An average distribution system retention time of 1.3 days and a maximum retentiontime of 3.0 days (World Health Organization (WHO), 2014).

Figure 8.

Water age comparison at high and low demand period.

3.6. Model calibration

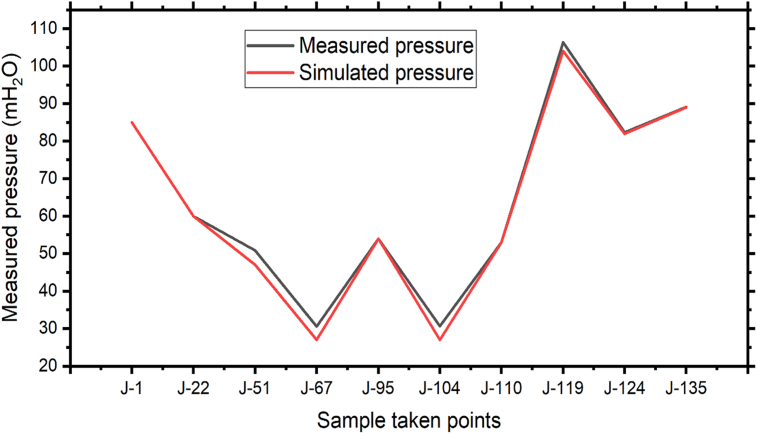
For the calibration, ten representative sample measurement locations were chosen based on the location of node to be representative of the distribution network. The measurements were collected nearer to the supply main nodes at residential faucets than at the direct connection to the water mains. The observed data was collected using water pressure gauge instrument (SKU61038). The head loss between the supply main nodes and the pressure measurement point was taken into account during the calibration. Figure 9 depicts the measured and simulated pressure calibration during peak hour demand. During the comparison of the measured pressure value with the simulated one, gaps of up to 10 m head were recorded at junctions 104, 110, and 119, and they were outside of the pressure standard and limitations suggested by Walski et al. (2003). Therefore, the simulated pressure value during peak demand time was calibrated until the result was approach to the measured pressure value.

Figure 9.

Graphical representation of the Measured and simulated pressure value during peak demand period.

3.7. Model validation

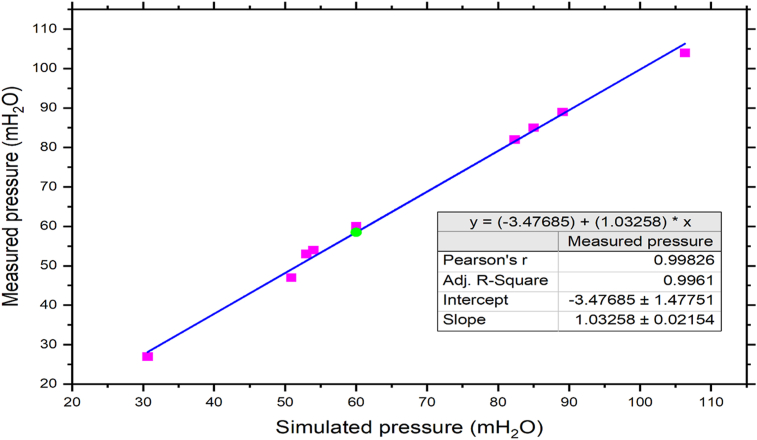
Model validation was carried out after calibration as observed from Figure 10, and an independent computed data set was employed to ensure that the model was properly calibrated. The calibrated model was run under settings different from those used for calibration in the validation step, and the results were compared to computed data. The calibrated model was then declared validated after the model results were closely approximated to the calculated results for an adequate time period. The correlation plot was developed after adjusting for the C-factor. So, after adjusting for pipe roughness, the resulting coefficient of determination (R²) accounted for 99.61% of the variance. Figure 10 shown that the simulated and computed pressure have a strong linear relationship at the validation phase according to Walski et al. (2003).

Figure 10.

Correlated plot during pressure calibration for peak demand time.

3.8. Process optimization

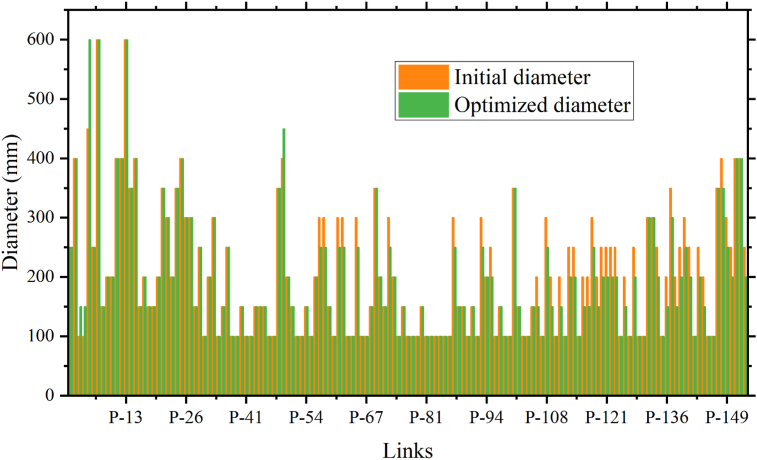
The diameter and length of a pipe have an impact on hydraulic parameters, such as head loss, pressure and velocity (Awe et al., 2020; Bong et al., 2007). The diameters of sub-main lines in the water distribution system at the post service housing scheme are more than 100 mm. As observed from Figure 11, the proportion of pipes that actually supply water to end users was: 51.11% of pipe diameters were 100 mm, 39.29% of pipe diameters were 150 mm, 45.45% of pipe diameters were 200 mm, 53.12% of pipe diameters were 250 mm, 76% of pipe diameters were 300 mm, 50% of pipe diameters were 350 mm, 56.25% of pipe diameters were 400 mm, 50% of pipe diameters were 450 mm and 40% of pipe diameters were 600 mm. This figure was changed after optimization to: 48.89% of pipe diameters were 100 mm, 60.71% of pipe diameters were 150 mm, 54.55% of pipe diameters were 200 mm, 46.88% of pipe diameters were 250 mm, 24% of pipe diameters were 300 mm, 50% of pipe diameters were 350 mm, 43.75% of pipe diameters were 400 mm, 50% of pipe diameters were 450 mm and 60% of pipe diameters were 600 mm. As the result of reduction in pipe sizes of the optimized design the cost reduction was brought (Gajghate et al., 2021). This optimization of pipe diameter of water distribution system was done based on local commercially available pipe size. In addition to cost of reduction hydraulic loss and material failure was saved.

Figure 11.

Initial and optimized pipe diameter.

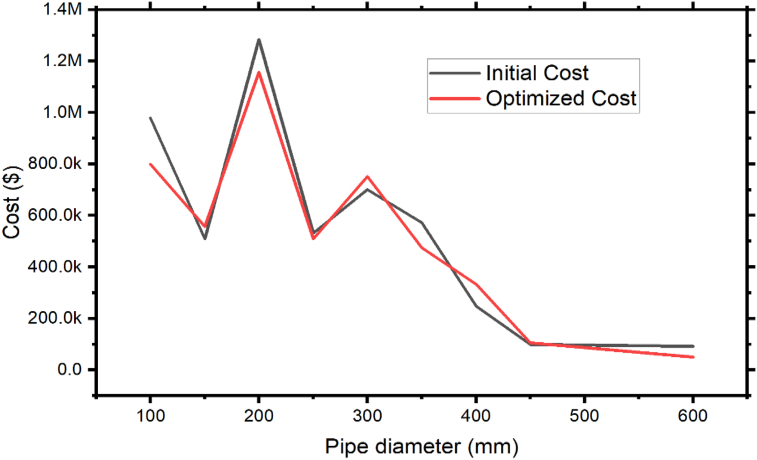
Figure 12 indicated that, the variation of cost before and after optimization process. As observed from Figure 10, the cost of 100 mm pipes was reduced by 18.39%, the cost of 150 mm pipes was increased by 9.27%, the cost of 200 mm pipes was reduced by 9.84%, the cost of 250 mm pipes was reduced by 4.11%, the cost of 300 mm pipes were increased by 7.25%, the cost of 350 mm pipes was reduced by 16.92%, the cost of 400 mm pipes was increased by 33.82%, the cost of 450 mm pipes was increased by 4.76%, and the cost of 600 mm pipes was reduced by 44.66%. After optimization, the overall cost of pipes was reduced by 5.56%.

Figure 12.

Initial and optimized cost.

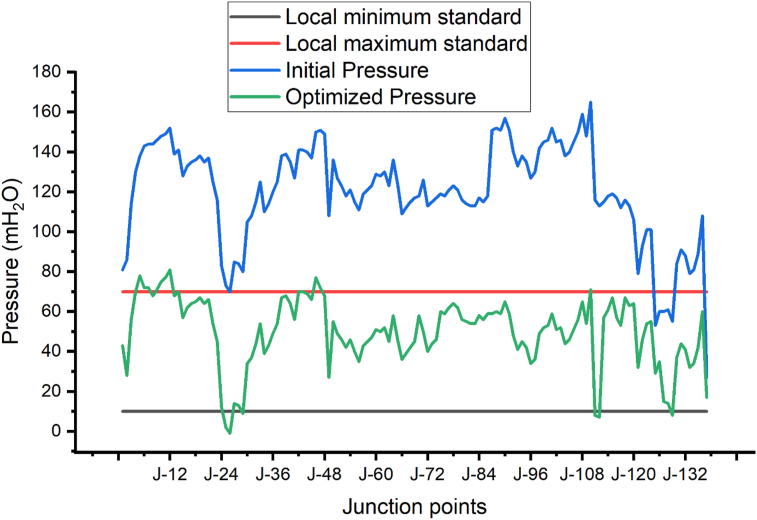
Figure 13 shows the pressure distribution before and after optimization. It also stated how far the starting and optimized pressure values differed from the local minimum and maximum standards. Before optimization, only 4.4% of the pressure met local regulations, while the remaining 95.6% was above the limit threshold. This indicated that, except for J-125, J-126, J-127, J-128, J-129, and J-137, the other junctions were affected by higher pressure. Pressure gauges should be installed at every point in a water distribution system to measure the amount of pressure in the system. The water distribution system had high and low-pressure points, indicating that the water supply was not stable. This means that, over time, the systems may experience bursts and leaks in high-pressure areas and water shortages in low-pressure areas. On the other hand, excessive pressure at night can cause or worsen the wear and tear of valves, including the problem of leaks or exposure to large breaks (Esberto and Orejudos, 2019). Following the optimization process, only 24.82% of the data did not match local criteria, while 75.18% was within the local limit value. The pressure of 24.82% was not far from the limit value; the minimum pressure was 1–14 mH₂O and the maximum pressure was 61–81 mH₂O. This indicated that the distribution system has a balanced pressure within the system. This means that pipe burst and leaks were kept to a minimum and that the consumer would have received enough water during each demand period. The condition is greatly improved in a well-designed model, where optimum pressures were detected in water distribution, which increases the level of hydraulic reliability, increases energy input storage, and system dissipation (Bonilla-Granados et al., 2021). In general as Figure 13 depicted that, after optimization process most of the nodal pressure in the distribution system fulfill the local design criteria (MoWR, 2006).

Figure 13.

Initial and optimized pressure.

4. Conclusion

The design, analysis, simulation, optimization, and other functions of water distribution networks are becoming increasingly dependent on computer applications. The WaterGEMS Vi8 has a higher level of acceptance in this regard. Pressure and water age were examined in this study at various times of high and low demand. During peak demand, the design criteria were only partially met, according to the results of the study. But despite this, the higher water-age value was acceptable to the locals. Results from this study show that water pressure did not meet design criteria for maximum and minimum pressure levels in the water distribution network. This was because the pressure was high and the velocity was low during the period of low demand, resulting in a long residence time. There were no changes in pipe size that resulted in changes in distribution system pressure. This variation of pressure initiated us to apply optimization process. The result of this study reveals that, after optimization process the pipe size was reduced and most of the pressure was with in the local standards. As a result, cost reduction, hydraulic loss and material failure was saved. In light of this information, Adama city's water sector will have to rethink their system and implement any necessary remediation measures as a result of this discovery. For Adama city's water distribution system to perform better, it requires both design and operational changes.

Declarations

Author contribution statement

Wendesen Mekonin Desta, Fekadu Fufa Feyessa (PhD), Seifu Kebede Debela: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

Data included in article/supp. material/referenced in article.

Declaration of interest’s statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.