Abstract
Deep learning techniques, in particular generative models, have taken on great importance in medical image analysis. This paper surveys fundamental deep learning concepts related to medical image generation. It provides concise overviews of studies which use some of the latest state-of-the-art models from last years applied to medical images of different injured body areas or organs that have a disease associated with (e.g., brain tumor and COVID-19 lungs pneumonia). The motivation for this study is to offer a comprehensive overview of artificial neural networks (NNs) and deep generative models in medical imaging, so more groups and authors that are not familiar with deep learning take into consideration its use in medicine works. We review the use of generative models, such as generative adversarial networks and variational autoencoders, as techniques to achieve semantic segmentation, data augmentation, and better classification algorithms, among other purposes. In addition, a collection of widely used public medical datasets containing magnetic resonance (MR) images, computed tomography (CT) scans, and common pictures is presented. Finally, we feature a summary of the current state of generative models in medical image including key features, current challenges, and future research paths.
Keywords: Generative adversarial networks, Variational autoencoders, Convolutional neural networks, Medical imaging, Computer vision, Artificial neural networks
Introduction
Since the appearance of machine learning (ML) as a part of artificial intelligence (AI) in the 1950s, the advances on data processing have achieved extraordinary achievements. Early machine learning techniques were unable to process data as it was gathered from its source due to high dimensionality; hence, the pattern identification ability that characterizes them was totally dependent on feature extraction methods. It required high expertise and careful fine tuning of the system to transform raw data into a different representation from which the algorithm could detect or classify patterns.
Nowadays, ML systems have a huge impact on the modern society and generate important benefits to many institutions along multiple industries, including the biomedical field. Among their many uses are recognizing objects in images, speech translation, and user profiling: these being extremely helpful utilities in the medical field. The present survey focuses on the specialized and leading edge subfield of generative models in deep neural networks (DNNs) applied in medical imaging. These models are based on the assumption that the features of an object in an image can be learned, and then a synthetic image could be generated so the differences between a real and a fake one are almost unnoticeable for human perception.
The main motivation for reviewing and explaining how artificial neural networks (NNs) and deep generative models work in medical imaging is to encourage its use in medical works. Surveys and reviews as those of authors like Akazawa and Hashimoto [1], De Siqueira et al. [2], Fernando et al. [3], Chen et al. [4], Sah and Direkoglu [5], and Abdou [6] cover a significant amount of works that apply deep learning to medical image analysis. Regarding generative models, Zhai et al. [7] review numerous autoencoder variants, while Kazeminia et al. [8] focus on the application of GANs for medical image analysis. Despite the fact that the reviews and studies above offer a broad representation of the works currently under way, they show a very technical report that requires an in-depth knowledge of how neural networks work to completely understand certain aspects of the covered subjects. We feel that important areas are left behind since many studies assume that the reader already has extensive knowledge of the fundamental internal workings of the models. This can lead to its usage as a “black box” instead of as an understandable and reliable tool. This situation can further cause opposition to its use by non computer science technical authors, who may not trust a not well-known tool that they are unable to account.
This survey includes recent applications of generative models in medical image processing, comprehensive explanations of its main architectures, and several lists of datasets consisting of medical images of different types. The rest of this paper is structured as follows. Section 2 shows an overview of the deep learning predecessors and outlines the main components and techniques used in many of the state-of-the-art models. Section 3 introduces the concept of generative models focusing on generative adversarial networks and variational autoencoders. Section 4 lists widely used medical and general images datasets. Finally, Sect. 5 discusses the main key features and challenges of generative models in medical image processing.
Deep learning
The aim of deep learning models is to represent probability distributions over data, such as natural images or natural language. This kind of corpora has a large number of features that common and simple artificial intelligence techniques are not able to extract to correctly infer conclusions from the data. Deep learning models stand out when used as a discriminative tool, being able to map high-dimensional data to a class label thanks to multiple techniques as forward and backpropagation through activation and loss functions, complex architectures, and the incorporation of operations as convolution and pooling [9].
In this section, we present a theoretical analysis of artificial neural networks and the techniques that allow them to stand out from other AI models.
Artificial neural networks
Conventional artificial neural networks (NNs) consist of many simple nodes called neurons, each performing a very specific task. Neurons get values as input and perform a linear function previously specified in a manner that an inference is obtained as output. The input can be obtained from sensors perceiving the environment or previous neurons, depending on the problem and how many computational stages it would require to be solved [10].
As noted above, a neuron is responsible of processing the information in its input, being the base unit of a larger network. For an array of () inputs, one neuron (j) multiplies each value by a weight () and adds it to a bias (), then all obtained values are summed and an activation function () is applied to the result. This process is the so-called forward propagation which delivers a real number as output [11].
Forward propagation
As Goodfellow et al. [11] explain, each neuron (j) stores a weight () for each input and a bias (), both of which being real numbers and also known as trainable parameters. Formally, for each neuron j and considering N inputs, forward propagation can be expressed as follows.
First, it uses a linear function to compute z (Eq. 1). Next, it applies an activation function (Sect. 2.1.2) to convert z into a probability (Eq. 2).
| 1 |
| 2 |
As represented in Fig. 1, a NN does not only own one neuron, but a set of neurons. These sets of neurons are organized in layers. The neurons of each layer are connected to the previous and to the next layers as a chain.
Fig. 1.
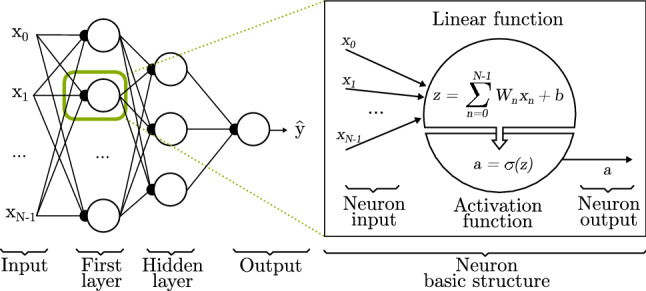
Basic artificial neural network structure. It consists of N inputs, ranging from to , and 3 layers; one input layer with one neuron for each input , one hidden layer that takes as input the previous layer output, and one output layer where the final result is deployed
During the training process, each data example with an associated label (y) is fed through the input layer. The final layer, called the output layer, yields an approximation of the label . The learning algorithm must decide how to update the W and b values of each intermediate layers to better approximate to y [11]. The intermediate layers are called hidden layers, and a more detailed explanation of its working is provided in Sect. 2.2. In this way, assuming N as the number of inputs in a layer and J as the number of neurons in a layer, W is a matrix of size equal to the number of neurons in a layer and its inputs ([J, N]), and the bias b is a vector of 1 and the number of neurons ([1, N]), since it is a single value in each neuron.
As the number of neurons increases and more layers are included in the NN, the number of operations needed to perform forward propagation is also greatly incremented. To reduce the operational burden, matrix operations can be used instead of an iterative process. This is the so-called vectorization technique, which offers a great leap forward in NN models since the matrix operations can be performed on graphic processing units (GPUs) achieving better performance, system optimization and reducing execution times. Eqs. 3 and 4 are vectorized alternatives to Eqs. 1 and 2.
| 3 |
| 4 |
Parameters a and relate to the same value, being common to name when it refers to the final output of a multiple layered NN, and a when it is an output of a neuron that will be part of the input of a different neuron on the next layer. Layers are covered in Sect. 2.2.
Since the probability value delivered in relies on the input, it is usually expressed as . Still, is not only affected by the inputs, but also considers the values found in the weights (W) and bias (b) of each neuron. Therefore, the neuron weight and bias can be updated considering the real value y and the predicted to make them as similar as possible, giving the neuron the ability to learn. The process of training (updating) the parameters W and b is done through backpropagation (Sect. 2.1.4) considering a loss function (Sect. 2.1.3).
Activation function
Before moving toward, it is worth focusing on the activation function and its goal. Generally, NN classification tasks require predicting the value of a variable y. As already seen before, this probability can be expressed as .
Activation functions take the real number value computed by the linear function (z) and transform it into a probability. Activation functions can be categorized depending on the number of values a class can take, and therefore, the system should predict. If class values are binary, the probability must lie between 0 and 1. In contrast, if the class is represented by a discrete variable with n possible values, the [0, 1] range is not suitable and a different function should be considered.
For binary classes, the most used activation functions are Sigmoid, Tanh, ReLU (Rectified Linear Unit), Leaky ReLU, and ELU (exponential linear unit) [11, 12]. Figure 2 shows a graphic representation of the activation functions.
Fig. 2.
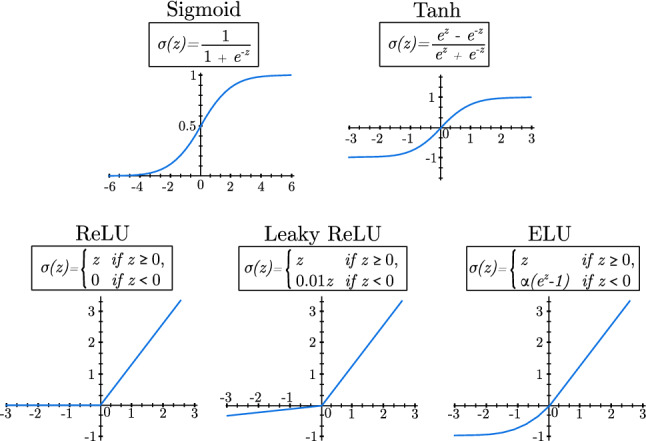
Most used activation functions
For multi-class classification, the most employed activation function is the so-called Softmax, a generalization of the sigmoid function in Fig. 2. It is able to represent the probability distribution over N different classes [11]. Softmax outputs a vector of N elements, each one storing a value between 0 and 1, and since the vector represents a valid probability distribution, the whole vector sums 1. In Eq. 5, and relate to the elements of the input vector z, and i refers to each position of the output vector:
| 5 |
Loss functions
In this section, a binary classification example is used to keep explanation complexity at a mininum as multi-class examples could be inferred the same way.
Loss function (L) provides a value of how correct was the prediction made by the NN for a specific example. Although initial NN uses the square error loss function, better choices appear later. One of the most used loss function is the binary cross-entropy (BCE) shown in Eq. 7. It is a special case of the cross-entropy (CE) function shown in Eq. 6, which was originally formulated to find the loss among C number of classes.
| 6 |
| 7 |
As can be seen in Fig. 3, the slope of the function can be calculated as a derivative. In this way, if the derivative is positive, hence a positive slope will be obtained. On the contrary, if the derivative is negative and its slope too. The derivatives help to know how correct the prediction was. Since this function returns a high value when the prediction is wrong and a low value when the prediction is correct, the trainable parameters of the neurons are changed over the training process to gradually improve the results.
Fig. 3.
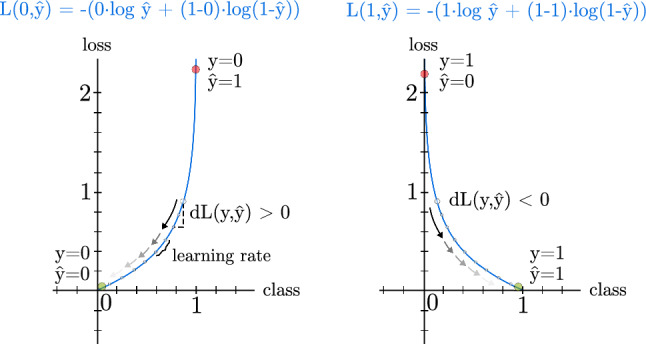
Loss function for an individual example throughout the training process. y is the label of an example of the training data, while is the predicted label of the same example. A steady learning rate is presented as example, but its value can be variable
Section 2.1.4 discusses backpropagation, explaining how derivatives affect trainable parameters W and b via a learning parameter .
BCE works well when used in a distribution-based scenario where an image must be classified as a whole into a category, but better options are available when the classification must be made at pixel level. An image is made up of square pixels, and groups of pixels define the different elements shown in it. Classifying these pixels depending on the element, they are part of is called semantic image segmentation [13], a subject that is extended in Sect. 3.2.
Selecting a loss function is very important when working in complex semantic segmentation. The most successful alternatives are focal loss [14], dice loss [15], Tversky loss [16], and shape-aware loss [17].
Focal loss [14] estimates the probability of belonging to a class as :
| 8 |
In this way, cross-entropy can be assessed as , and the focal loss function defined as:
| 9 |
Parameter works as a modulating factor to lower the weight of examples that are easier to classify, emphasizing on the hard negatives. The authors also propose the use of a balancing parameter () to improve accuracy. These conditions make the focal loss function perfect to work with highly imbalanced datasets.
Dice loss [15] is also useful when working with highly imbalanced data. It is defined as:
| 10 |
The main strength of dice loss lies on image to image comparison, being it particularly recommended when a set of images with their related classes, also known as ground truth, is available. Parameter ensures that the loss function avoids numerical issues when both y and equal 0.
Salehi et al. [16] build upon dice loss function and propose the Tversky Loss function, one of the loss functions for semantic segmentation of medical images that offers best results [13]. It adds weight to false positives and false negatives through the parameter, improving its reliability. Equation 11 shows its definition.
| 11 |
Lastly, the shape-aware loss function [17] considers the shape of the object; therefore, it is an excellent loss function in cases with difficult boundaries segmentation. It uses the cross-entropy (CE) loss function, and a coefficient of the average Euclidean distance (E) among i points around curves of predicted segmentation compared to the ground truth [13]. It is calculated as follows:
| 12 |
Building on the above loss functions, new alternatives arise combining them in such a way that results are improved. Examples of this are combinations of existing loss functions as combo loss [18] (combination of dice loss and BCE), and variants inspired in them as focal Tversky loss [19] and log-cosh dice loss [20].
Backpropagation
Early NNs were based on linear regression methods and were not able to learn. It was not until late 1900s when NNs benefited from backpropagation and gradient descent. As shown in the previous section, loss function and derivatives show how correct is the prediction. Thanks to backpropagation, a NN is able to learn from the accuracy of current predictions and update W and b values to improve it on the next iteration.
The goal is, therefore, to find the parameter values that minimize the loss, so when a new example is inputted to the system, it is classified correctly. To optimize this process, the values are not computed for each particular case, but the average of the loss functions of the dataset is calculated and used as a measure. This measure is called Cost function, and it is formally expressed as J(W, b), being M the number of examples in the dataset (see Eq. 13).
| 13 |
Considering that derivatives portray how much a value changes related to another variable, the derivative of the cost function related to the parameters W and b separately tells how much they should be changed. If predictions are accurate, then the loss values will be low; hence, parameters will be barely changed. Otherwise, high loss values lead to major changes. Also, a learning rate value () is used to control the update ratio so it does not escalate out of control. Eqs. 14 and 15 show the updating process of the trainable parameters.
| 14 |
| 15 |
Many authors succeeded at working with low layered NNs architectures. Bollschweiler et al. [21] implement a hidden layer NN for gastric cancer prediction before surgery. Dietzel et al. [22] study how a NN with a single hidden layer helps in breast cancer prediction through breast magnetic resonance images. Biglarian et al. [23] use a one hidden layer NN for early detection of distant metastasis in colorectal cancer.
Gardner et al. [24] train a NN consisting of only one hidden layer to detect diabetic retinopathy through 300 black and white retina pictures. When compared with an expert ophthalmologist judgment, the network achieved good accuracy for the detection of the illness. Years later, Sinthanayothin et al. [25] use a bigger set of colored retinal images (25,094) on a similar three layered NN. They conclude that working with colored RGB (red, green and blue) images improves the detection of retinal elements as optic disc, fovea, and blood vessels, which can be analyzed to detect sight threatening complications such as disc neovascularization, vascular changes, or foveal exudation.
NNs are not only used to analyze medical images, but other types of data collection can be also considered. Özbay et al. [26] introduce a new fuzzy clustering NN architecture (FCNN) for early diagnosis of electrocardiography arrhythmias. The NN consists of one hidden layer, achieving a high accuracy and improving previously reported works [27, 28].
Even after NN were generally dropped out and ignored for other techniques, many authors continued using them successfully. All presented models consisted on one input layer (100 - 400 nodes), one hidden layer (4 - 20 nodes) and a final output layer (1 - 10 nodes). It was not until the early 2000s that NN are brought again globally thanks, among other things, to the rising of fast graphics processing units (GPUs) and its convenient programming capabilities. They open a gate to what it is known today as deep neural networks (DNNs), offering a greater number of hidden layers and nodes.
Optimizer algorithms
As previously stated, the learning process is done through backpropagation in order to update the internal values of the network and decrease the loss, offering a more accurate prediction. This process is described in the previous section, and is known as gradient descent, one of the first optimizer algorithms. As the complexity of the data and the number of training cases increase, it is also more difficult to find the minima and its computational cost. Considering this fact, multiple optimization algorithms have risen over the years.
Stochastic gradient descent (SGD) is an iterative algorithm that follows a function until finding its lowest point as gradient descent. The only difference lies in that SGD updates the internal parameters of the network based on random examples instead of processing all of them. The process is computationally less expensive, but parameters have higher variance and larger fluctuation steps. Momentum algorithm aims to reduce the oscillations and variance of SGD using a parameter stored at each iteration that influences the next update in a way reminiscent of acceleration [29].
The previous optimizers use a constant learning rate, which is a problem when the gradients are sparse or small. Algorithms as AdaGrad [30] and its variants, such as RMSProp [31], Adam [32], or AdaDelta [33], introduce a parameter to modify it, achieving a variable learning rate. This variants aim to mitigate the decay of the learning rate that AdaGrad suffers using exponential moving averages of past gradients [34].
Evaluation metrics
Throughout the training process the optimizer algorithms work to minimize the loss function that the model uses as a tool to update its internal parameters, thus learning from the training dataset. However, these elements are not a reflection of the model performance, for which additional metrics are used depending on the task. When the output of the model is a discrete value, classification metrics must be taking into account. Conversely, if the output is a real value, regression metrics are the appropriate.
Classification metrics are based on the true and predicted condition of the training examples, being true positives (TP) or true negatives (TN) the instances that the model correctly predict, and false positives (FP) or false negatives (FN) the ones that it fails. While there are numerous metrics, the most common are accuracy, specificity, recall, precision, and F1 Score, a combination of the latter two [35]. Accuracy shows a percentage of the correct predictions over the total examples.
| 16 |
Specificity shows how well the model classifies true negatives.
| 17 |
Recall, also known as Sensitivity, is a metric representative of the correctly predicted samples. It is mainly used to know how well the model predicts true positives.
| 18 |
Precision is mainly used when one of the classes is under-represented, situation where the accuracy offers a high value that would not correctly represent reality.
| 19 |
Lastly, F1-Score combines precision and recall to provide a single metric in cases where both are important.
| 20 |
Furthermore, regression metrics use the predicted () and actual value (y) of each example to get the average deviation of the model predictions. One of the most extended metrics is the mean squared error (MSE), that can also be used as a root mean squared error (RMSE) to scale its value to be average deviation between the predicted and the real values.
| 21 |
Mean absolute error (MAE) is a regression metric that represents the absolute distance between the predicted and real values. It is a solid alternative to MSE, as outliers affect it to a lesser extent.
| 22 |
Deep neural networks
Numerous improvements to shallow NN have been proposed, but the groundbreaking advancement in this field is the evolution of NN to a deep architecture. They are called deep neural networks (DNNs), and their main characteristic is the inclusion of a high number of hidden layers. As seen in Fig. 1, a hidden layer is a set of neurons fully connected to the neurons of the previous (input) and next (output) layer.
DNNs composed of hidden layers replace hand-engineered feature detectors and are able to learn complex patterns. This type of multilayer architectures can be trained using simple stochastic gradient descent. As long as the linear functions of the neurons are relatively smooth functions of their inputs and of their internal weights (W) and bias (b), gradients can be computed using the backpropagation procedure [36].
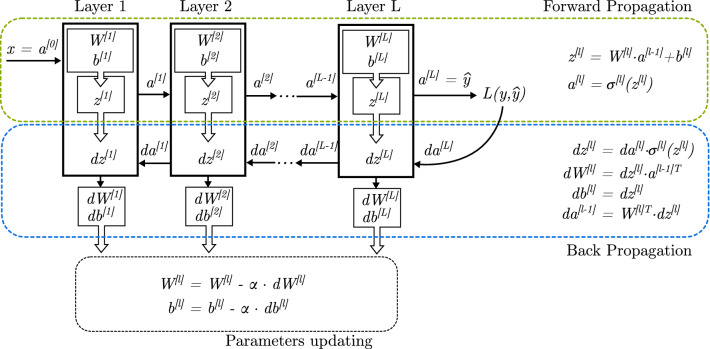
Through the forward propagation process, each layer l has an input vector x. It is represented as if it is an external input, or when it is the output of a previous layer (). Also, its output is expressed as , or when it is the final output layer.
During the Backward Propagation procedure, each layer l computes derivatives , , and . First two values are used to update (train) and , while the last one is served as input to the previous layer so the process can continue until reaching the input layer.
Figure 4 shows the forward and backward propagation processes. Because of the derivatives chain rule, the backpropagation equation can be applied to propagate gradients through all layers of the DNN. It starts on the output given by the forward propagation process, and continues layer by layer until it reaches the first layer (also called input layer).
Fig. 4.
Deep neural network training through forward and backward propagation. In this figure, the layer boxes represent a layer of artificial neurons fully connected with the previous and next layers
A great number of authors have capitalized on the possibilities that DNNs with fully connected layers offer, achieving key milestones in deep learning applied to medical studies. Clarke et al. [37] compare a backpropagation artificial neural network with two hidden layers (14 and 8 nodes each) to maximum likelihood method (MLM), and k-nearest neighbors (k-NN) algorithms over magnetic resonance (MR) image segmentation. They show that NN performs considerably better than MLM and similar to k-NN, providing improved boundary definition between tissues of similar MR parameters such as tumor and edema.
Cancer illness is an important subject of study whose pace has quickened thanks to NN since its early adoption. Veltri et al. [38] use a 2-3 hidden layers NN to detect prostate cancer, giving a significantly higher overall classification accuracy than logistic regression. Kan et al. [39] findings confirm that a NN with two hidden layers have superior potential in comparison with other methods of analysis for the prediction of lymph node metastasis in esophageal cancers. Nigam and Graupe [40] describe a method for automated detection of epileptic seizures from scalp-recorded electroencephalograms. They train a 4 layered NN where the input layer is connected simultaneously to both hidden layers. Darby et al. [41] use two hidden layers in a NN to predict which lymph nodes have a highest percentage of being metastasized in head and neck cancer.
In spite of the good results obtained with DNN architectures, their computation process is highly demanding. Moreover, as medical images with better quality and resolution appear, DNN fall behind as new models specifically crafted for image processing arise. This leads out to one of the most used and studied technique in recent works called convolution.
Convolutional neural networks
As can be inferred from Sect. 2.2, training and use of DNNs, where each layer has a high number of neurons, leads to a very computational demanding process. Moreover, the use of a high number of parameters as input (e.g., pixels of an image), makes it even more computationally demanding.
As colored images become an important subject of study, research focuses on processing data formed by multiple arrays of data. Considering one RGB (red, green, and blue) image as input of the NN, it could be disassembled into three 2D arrays, one for each color layer and one element for each pixel value. This is why convolution operations, which are specifically designed to work with matrices, are introduced as an alternative to fully connected layers. Multiple works [36, 42, 43] have demonstrated that convolutional networks (ConvNets or CNNs) offer similar or better results than DNNs with far less trainable parameters, resulting in less computation operations and smaller size architectures.
Trainable operations: convolution
The role of a convolution is to detect features found as patterns from the input. To achieve this, as Fig. 5 shows, a convolutional operation makes use of kernels, also called filters. From a mathematical point of view, a convolution operation is the result of an element-wise multiplication between a segment of the input and the filter, and the addition of the results. The process is repeated shifting the position of the segment a number of times set by the stride until the full surface of the input is covered. In this way, a single value for each segment is computed, shaping a new output matrix [44].
Fig. 5.
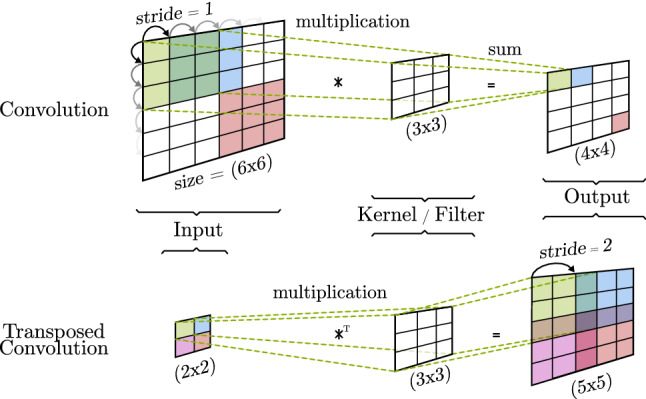
Basic convolution and transposed convolution
Basic convolutions can reduce (valid convolution) or keep (same convolution) the size of the input as output, while transposed convolutions (also called deconvolutions) take a small input and output a new matrix of greater size. The first type creates an abstract representation of the input, allowing feature extraction and classification techniques to be executed. The second alternative upsamples the input to increase its dimensions [45]. The size of the output matrix can be calculated using the input matrix size (n), the number of excluded cells on the edge of the output (), the number of positions that the filter is moved (), the filter size (f), and the number of filters (F). Eqs. 23 and 24 show the high width number of channels of the convolution and transposed convolution, respectively. It must be noted that many variants of the transposed convolutions are used as up-sample techniques, each one having its own output size calculation.
| 23 |
| 24 |
Originally, the values contained on the filters were fixed and manually crafted to detect a specific feature. LeCun et al. [36] applied backpropagation to convolutional operations, which enabled the training of the filters, automatically updating their values to gain new and better patter recognition values. Figure 6 shows how the convolution components can be associated with components of fully connected neural layers, making the back-propagation procedure very similar to what it is explained in Sect. 2.1.4. In this example, each filter of the two groups of filters has different values and each group of filters is trained separately. Moreover, each group of filters consists of 3 channels, meaning that each one is applied to a channel of the input and all values are summed together. At the end of this process, each group of filters outputs a one-dimensional matrix, so the final output is formed by two channels.
Fig. 6.
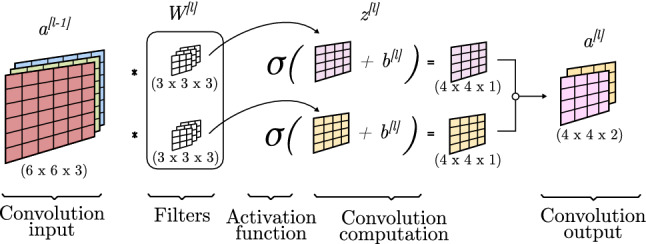
Convolution propagation
For the forward propagation process, a convolution operation is applied to the input of the l convolution block (Sect. 2.3.3) considering the trainable filters . A bias () is element-wise added to the matrix and is obtained. Finally, this new matrix is passed through an activation function and is obtained.
For the backward propagation process, gradients are propagated and the values of the bias and filters are updated as matrices as seen in Eqs. 14 and 15. To compute the calculations, dW and db are obtained as the addition of all the gradients of dZ (Eqs. 25 and 26):
| 25 |
| 26 |
These presented techniques are very basic alternatives used as explanation examples. As many authors have covered, problems like vanishing gradients [46, 47] or checkered patterns [45, 48] (caused by transposed convolutions as seen in Fig. 5) require additional techniques to be applied so convolutional operations can optimally work.
Non trainable operations: pooling
In contrast to convolutions, pooling is used to merge semantically similar features into one. They are fixed and not trainable operations that associate neighbor values reducing the dimension of the representation and creating an invariance to small shifts and distortions [36].
Multiple variants of pooling techniques (Fig. 7) are available depending on the intended outcome. The main difference between techniques is denoted by its application over a portion (window) of the input (Normal Pooling) or over all its values at the same time (Global Pooling).
Fig. 7.
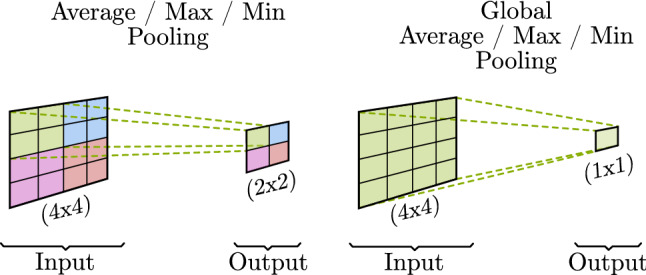
Pooling operations
The most used variants are: max or min pooling (higher or lower value goes to the input unmodified) and average pooling (an average value of all the input values affected is obtained as output). Nirthika et al. [49] perform an empirical study of pooling operations in CNN for medical image analysis. They conclude that choosing an appropriate pooling technique for a particular job is related to the size and scale of the images and its class-specific features.
CNN models
Although convolutions are known since late 1970s [50], it was not until 1995 that they were applied to medical images [51], and in 1998 in a real-world application in LeNet [36] for hand-written digit recognition. Eventually, Krizhevsky et al. [52] proposed the AlexNet, a CNN able to classify high-resolution images [53] that established the foundations to many modern models.
As pointed by LeCun et al. [36], CNNs offer four key advantages: local connections, shared weights, pooling, and the use of many layers. Convolutional neural networks consist of consecutive convolution and pooling layers, also called convolutional blocks. The way a convolutional block is built can be changed, allowing highly personalized architectures to fit multiple case studies. Many authors discuss how the the different layers can be combined, but the most relevant aspect of this architecture is the way the first convolutional layers specialize in recognizing simple patters (e.g., vertical or horizontal lines), while final layers are able to classify more complex layouts (types of objects, faces, etc.) [43].
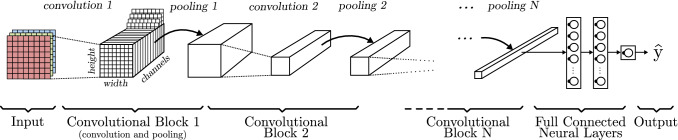
Figure 8 shows a typical CNN model that consists of a high number of convolutional blocks containing different convolution and pooling layers with multiple sizes, strides and padding. Generally, each consecutive convolutional block decreases the high and width of the representation, and increases the number of channels (depth) but, as seen in Sect. 2.3.1, the output size and number of channels is totally dependant on the internal parameters of the convolution operation (stride, filter size, number of filters, etc.). Right before the output layer, some fully connected layers are located. These layers, also known as dense layers, are identical in function and have the same structure as the ones addressed in Sect. 2.1. Their objective is to take the features extracted by the convolutional layers and learn a function to perform a classification of the data.
Fig. 8.
Convolutional neural network basic model based on AlexNet [52] architecture
Throughout the reviewed works, a set of CNN models stands out being embraced by the majority of authors as a base work to create their own models. They are broadly known and were originally created to solve the intrinsic problems of CNN architectures (e.g., overfitting and vanishing gradients) while achieving satisfactory results. AlexNet [52] was the largest CNN to date, it contains five convolutional and three fully connected layers. It is the first big CNN which showed that computer vision systems do not need to be carefully hand-designed, but can be trained to automatically learn from a labeled dataset as it did from ImageNet (Fig. 9). Several authors adjusted the AlexNet model to either improve the results or make them equal with a smaller model. The VGG-19 CNN [54], proposed by Simonyan and Zisserman, uses very small and convolution filters building a deeper model (19 layers) able to achieve better accuracy for localization and classification than the state-of-the-art models. They highlight the relevance of depth in vision systems. Moreover, SqueezeNet [55] achieves AlexNet-level accuracy on ImageNet with 50x fewer parameters. To accomplish this, Iandola et al. present a convolutional block named Fire. It replaces filters with filters and decreases the number of input channels to filters to drastically reduce the number of parameters in the CNN. Finally, they use large strides through the model to prevent the shrinking of the convolutional blocks output and therefore delaying downsampling leading to higher classification accuracy.
Fig. 9.

Convolutional neural network (CNN) based on AlexNet [52] and the VGG-19 [54]
Increasing the CNN models depth also leads to a degradation of the accuracy caused by the inclusion of new convolutional layers. He et al. [46] introduce the residual connection concept in its ResNet model (Fig. 10). They insert shortcut connections from a previous layer onto a later layer without any extra parameter nor computation complexity. The authors achieve high accuracy results even with very deep models, thereby avoiding vanishing gradients issues.
Fig. 10.
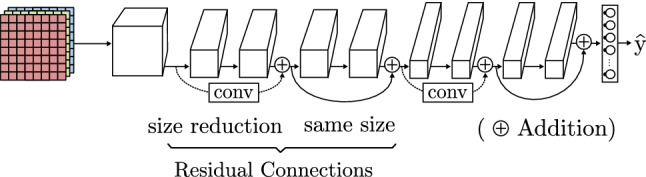
Residual CNN architecture based on ResNet [46]
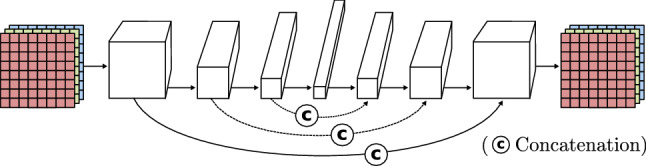
Huang et al. [56] suggest a more brute solution to the degradation of information based on the ResNet. They propose a model, called DenseNet, composed of dense blocks (Fig. 11). Each dense block is formed by many convolution operations and a final pooling. The most distinguishing feature is that every input is concatenated to the output of the convolutions inside the block. These dense residual connections allow to build deeper architectures avoiding data loss.
Fig. 11.
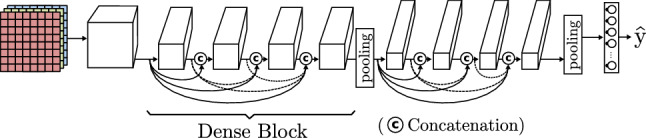
Dense CNN based on DenseNet [56]
Drawing inspiration from ResNet, Szegedy et al. introduce the inception-V4 model [57] (Fig. 12). It comes from previous inception models (v1 or GoogLeNet [42], v2-v3 [47]), and the ResNet previously seen. A basic inception block uses various size convolutions with different filters and pooling, which are, finally, concatenated to obtain the next layer input. The authors improve this model through versions optimizing both accuracy and computation time.
Fig. 12.
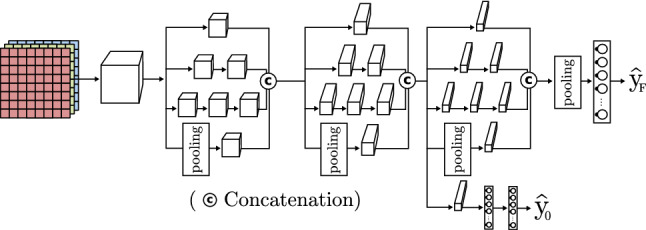
Inception CNN based on inception model [42]
When analyzing CNN architectures is far from clear that if the objective is to process high-quality images, the number of computational operations is very large. This implies the use of high-end computers and long run times. To address this problem, the MobileNetV3 proposed by Howard et al. [58] is specifically tuned to achieve high accuracy on mobile hardware with low specifications as mobile phones and on-board computers, with priority given to fast analysis of images. The MobileNet introduces the use of a separable convolution operation that is able to achieve similar results as basic convolution with far less number of operations. As can be seen in Fig. 13, a separable convolution executes two operations: first, it performs a depthwise convolution where each filter is applied to only one of the input channels. The number of output channels is the same as the input, but the height and width of the feature map is changed depending on the convolution characteristics. Secondly, a pointwise convolution is executed through all the channels. In this time, the output height and width are the same as the input, but the number of channels is equal to the number of filters.
Fig. 13.
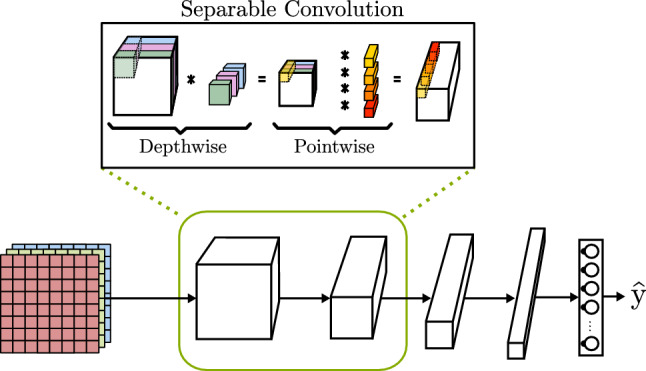
CNN with separable convolution block based on MobileNet [58]
To conclude, convolutions are a very important component of widely known systems specialized in segmentation [59] and object localization [58, 60]. One of the first and most important is the U-Net [59]. It uses a collection of convolutions and transposed convolutions without fully connected layers to obtain a segmented image of the input (Fig. 14), establishing a starting point in encoder-decoder architectures (Sect. 3.5).
Fig. 14.
Encoder-decoder model based on U-Net [59]
All above models propose new CNN architectures for image classification or image generation. In recent years, a collection of models appeared that focus on optimal detection and classification of objects in images. The most popular are Fast-RCNN [61] using a VGG CNN, DetectNet [62] through an inception CNN, SSD (Single Shot Detector) [63] with a MobileNet CNN, and YOLO (You Only Look Once) [60] which uses multiple CNNs in different versions, among others. These models use already existent CNNs to get a classification of the objects in an image, then with all this information they propose different techniques to add them to the original images (i.e., squares pointing the location of the image or coloring the pixels according to the object that they shape). Table 1 collects the most relevant CNN models and their main features.
Table 1.
Overview of convolutional neural networks. The models are ordered from an initial simpler model to the most sophisticated ones. Each model offers an improvement and capitalizes on the previous models advancements. C Classification, IR Image Recognition, SS Semantic Segmentation, IM Image Modification, OD Object Detection, and OP Object Positioning
| Model | Main features | Application |
|---|---|---|
| VGG-19 [54] | Use of smaller convolution filters in order to achieve a deeper model. The authors apply a combination of convolutions and poolings as feature extractors followed by three fully connected layers. | C, IR |
| ResNet [46] | Connection of convolution layers to further layers through a matrix addition. When the connection is done between matrices of different size, the model performs a convolution to adjust its height and width. | |
| DenseNet [56] | Introduction of Dense Blocks containing multiple convolutions and pooling steps. Thanks to the use of the same convolutions, the feature map size does not change inside the block, allowing to concatenate the channels of the input of the block with all its inside convolution outputs. This model achieves deeper architectures avoiding the data loss related to very deep models. | |
| Inception [42] | Introduction of inception block where different filters are applied to the same input, concatenating all their outputs. The model is able to extract features using a lower depth and incorporates multiple model outputs. In this way, it is able to evaluate the result in an intermediate state. | |
| MobileNet [58] | Use of depthwise separable convolution, a convolution operation that splits the operation, reducing the computational costs. This model is designed to run on low-powered devices as mobile phones and on-board computers, with priority given to fast analysis of images. | |
| U-net [59] | Introduces an encoder-decoder structure. First, the model performs a set of convolutions to extract features from an input image (encoder). Second, a collection of transposed convolutions tries to reconstruct the input image while including new information (decoder). To do so, the convolutions output is concatenated to the matching transposed convolution input. | SS, IM |
| Fast-RCNN [61] | These architectures use a convolutional neural network as main tool to detect objects. Their value is not in offering a new CNN model, but using its output to better detect objects and point at its location in a picture. | OD, OP |
| DetectNet [62] | ||
| SSD [63] | ||
| Yolo [60] |
CNNs are successfully applied in many medical fields, focusing on those areas where images are the main asset for diagnosis and analysis. Many techniques are used to adapt a convolutional architecture to different data input. The most common input are 2D images [64–66], but also 2.5D (slice-based) [67, 68] and 3D [69–71] representations are used, extracting a more useful representation across all three axis [72].
The authors in [64] train a CNN to classify images of suspect lesions as melanoma or atypical nevi, outperforming dermatologists of different hierarchical categories of experience. Kather et al. [65] evaluate the performance of five CNN models applied to colorectal cancer tissue images. The evaluated models are AlexNet [52], SqueezeNet [55], GoogLeNet [42], Resnet50 [46], and VGG19 [54], the latter having the best performance. In [66], the inceptionV3 model [47] is used together with a set of feature extraction and classifying techniques for the identification of pneumonia caused by COVID-19 in X-ray images.
Yun et al. [67] use a 2.5D CNN for pulmonary airway segmentation in volumetric CT. The authors employ three images for each spatial point they want to analyze. These images are taken from different angles (axial, sagittal, and coronal), where the center of the images corresponds to the same point. This way, the system can analyze three dimensions without having the computational requirements of using complete 3D images. It represents a major development on the early detection of obstructive lung disease. Similarly, Geng et al. [68] use three parallel slices in each of the three views as input of 3 different CNN (one for each input) fused by a fully connected layer. Their model is able to effectively detect lung diseases as atelectasis, edema, pneumonia, and nodule.
As 2D filters are applied to 2D images, 3D filters can be used to perform 3D convolutions. Multiple models can be used together with 3D convolutions increasing the computational cost but also being able to put together more information. In [69], 3D CT scans are used along with a modified U-Net model [59]. In order to process the 3D models, the authors have to subsample them, worsening the quality of the images, while 2D model could use high resolution examples. They are not able to offer quantitative comparisons between 2D and 3D models, but as GPU computation power and memory capacity continue to grow, future research could focus on employing high resolution 3D scans. Nair et al. [70] train a 3D U-Net able to detect Multiple Sclerosis lesion from multi-sequence 3D MR images. Last, Zhang et al. [73] build a model that merge together 2D and 3D CNN for pancreas segmentation that could be applied to tumor detection. Their progress improves the state-of-the-art segmentation algorithms and helps reducing the input size of the 3D CNN, decreasing the computational cost while maintaining the accuracy.
Generative models
Neural networks have played a key role in analyzing and classifying data. As already seen, many authors have demonstrated how deep models are capable of learning main attributes of different data (e.g., images) to achieve some specific goal (e.g., tumor detection). However, NN capabilities are not limited to data analysis, but they are able to generate new data in a way that can even seem real to human observers. Generative models are being used increasingly by authors for tasks like semantic segmentation, object detection or localization, image quality improvement, and data augmentation, among others.
Image generation
Although fully connected networks are able to generate images, CNNs have demonstrated that they are able to obtain high-quality images with far less training time and computational requirement. Image generation models can be separated into two types depending on their input: a vector or an image.
A decoder (Fig. 15) is a collection of transposed convolutional blocks arranged in a way that increases the width and height while reducing the number of channels until reaching the desired image size and the required number of channels, three for colored images and one for black and white images. The internal trainable parameters of the convolution (known as filters in Sect. 2.3.1) shape the image layer by layer. Through forward and backward propagation, this model is able to learn how to generate realistic images and it is controlled by the input vector, which can be a class definition vector or noise to add variation to the generation process. More details can be seen in Sect. 3.4.2.
Fig. 15.
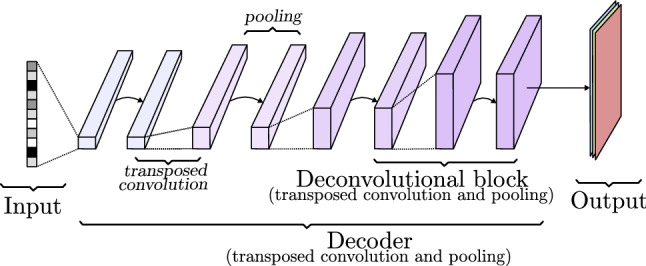
Decoder model based on transposed convolutions
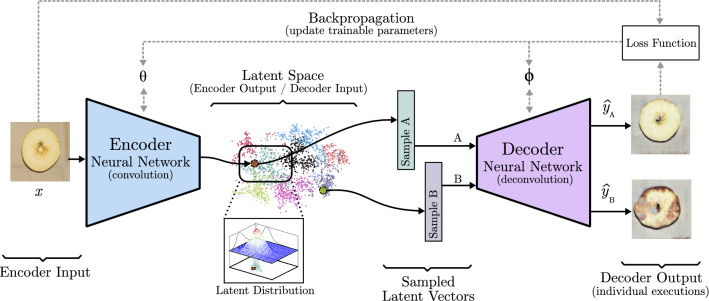
If the goal is to generate a new image from an already existing one, a model like the one represented in Fig. 16 is the way to go. It is composed of a decoder, like previously seen, but its input is the output of a convolutional network called encoder. This encoder-decoder architecture is able to extract the features of one image (input) like a normal CNN. Instead of relying on a few last fully connected layers to output a conclusion, it removes them and creates a new image (output) from the output of the last encoder convolutional block through the decoder. Each layer of the decoder takes the last pooling output of the encoder counterpart layer and concatenates it to the convolution output, this is known as skip connection. In this way, encoding information is transferred to the image creation process. During the training process, the output image is compared to the input image or to a paired image of the input, depending on whether the aim of the model is to rebuild the original image or to change its content. The internal parameters of the encoder and the decoder are changed considering how similar the target and the output image are. This basic idea is further developed in models like U-Net [59] (Sect. 3.4), and variational autoencoders (VAE) (Sect. 3.5).
Fig. 16.
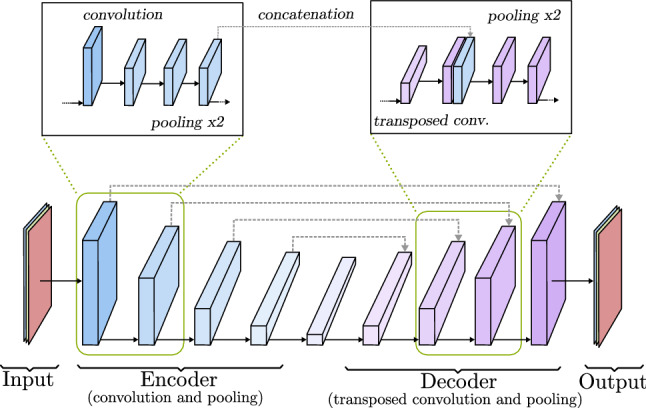
Encoder-decoder model based on U-Net [59]
Over the years, multiple generative models have emerged achieving even more reliable results. Although techniques as autorregresive models [74] or flow models [75] perform relatively well, the most used models nowadays are the variational autoencoders (VAEs) [76, 77] and generative adversarial networks (GANs) [9].
In this section, both VAE and GAN are analyzed, emphasizing on their main differences and similarities. Considering that the main internal parts of these networks are convolution, deconvolution, pooling layers (Sect. 2.3), and forward and backward propagation (Sects. 2.1, 2.2) are still used as training method, only main architecture characteristics are included. The main goal of these sections is to gather comprehensive knowledge of the models architecture, their capabilities, and how they influence the medical field.
Semantic image segmentation
A great number of works in medical and health-care field aim to locate certain elements in an image, not only to know where they are, but to also visualize their shape. Thanks to models as the U-Net, that generate an image from an existing one, it is possible to analyze each one of the input image pixels, classifying them according to the object that are part of. This process is known as Semantic Image Segmentation and, as can be seen in Fig. 17, the output is a matrix with the same size as the original image that contains a predicted class to each of the pixels. This information can be used to generate a completely new image, or merge it with the original as a mask to point out the classification of the objects in the image [78]. The training process of semantic segmentation models is based on the use of ground truth segmentation. The predicted class of each pixel is compared to the real class, updating the internal values of the model based on one of the loss functions described in Sect. 2.1.3.
Fig. 17.
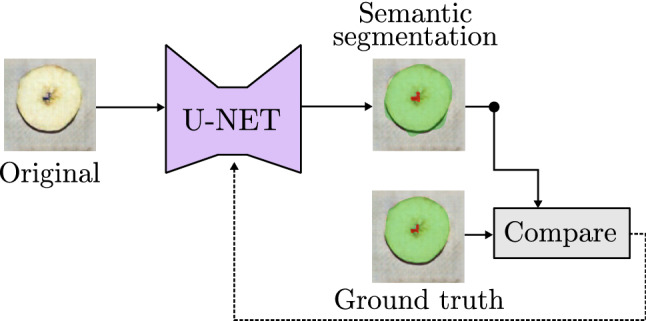
Example of image segmentation model based on U-Net [59]
Image segmentation has important applications in medical image analysis with multiple models rising along last years. Minaee et al. [79] and Asgari et al. [80] gather and review an extensive collection of works focusing on image segmentation.
In the medical field, several architectures to classify each pixel of an image have been proposed by different authors as, for example, full convolutional networks or adversarial training (Sect. 3.4). But, regarding medical works, the most extended architectures are encoder-decoder models and attention models.
When working with full convolutional networks (FCN), as seen in Section (Sect. 2.3), final layers do not match the size and shape of the input image. Because of it, after the last layers, new deconvolutional ones are introduced to reach the original size following a similar process as decoder models. Ben-Cohen et al. [81] propose to use FCN to detect liver metastases in CT examinations. The authors obtain good results, but nowadays this approach is being abandoned in favor of encoder-decoder models with a larger decoder network, and techniques as skip connections that help to achieve better quality segmentation.
Regarding adversarial training, works as the one presented by Daiqing et al. [82] rely on discriminative networks to train a generative model. The authors build their architecture on the StyleGAN [83], introducing an encoder network as a feature extractor of the input image. Doing so, the generation process is much closer to encoder-decoder networks than plain generative adversarial networks, although adversarial principles are still present.
Encoder-decoder architectures are the most commonly employed, in particular U-Net [59]-based models. Imtiaz et al. [84] apply an encoder-decoder model to screen glaucoma disease from retinal vessel images. Their model outperforms accuracy and processing time of other state-of-the-art works by using a pre-trained VGG16 [54] network as encoder. Rehman et al. [85] modify the skip connections of the U-Net introducing a feature enhancer block that adds more detail to the extracted features, helping the architecture to identify small regions. In a similar way, Zunair and Ben [86] introduce a sharp block in each skip connection of the U-Net in order to prevent the fusion of different features through the encoder convolution process and its merge with the decoder blocks. The sharpening process is performed by high pass kernels that infuse more relevance to distinct features. Su et al. [87] also improve the feature extraction process introducing the MSU-Net (Multi-Scale U-Net) to medical image processing. Specifically, the authors introduce separate convolution sizes in the same block in order to explore the input features at different levels, then each scale output is concatenated in order to be processed by the next convolutional block. To test their model, multiple datasets are used, including breast ultrasound images to detect cancer-harmed tissue, chest X-ray images showing tuberculosis cases and skin lesions pictures. Isense et al. [88] develop the nnU-Net tool, an auto-configurable architecture that adapts its internal parameters to work with multiple medical image datasets of different body parts. The authors use variations of U-Net including 2D U-Net, 3D U-Net, and 3D U-Net cascade to work with low-resolution images whose size is increased over time.
Despite the overall good performance of U-Net models, the very nature of the convolutional networks that build the encoder and decoder networks make them weak when working with high variable shape objects. This situation is very common in medical datasets, as the shape of target organs varies among different patients [89]. In order to overcome this drawback, recent works suggest to use Attention mechanisms that do not rely solely in the shape of the objects, highlighting the position where the main object that must be identified is located. This technique is drawn from natural language processing networks [90], where it is used as a method to check the connection between words using the weights that the model assigns to each word regarding the other terms of the text.
When working in computer vision, Attention mechanisms are usually introduced to existing semantic segmentation models as Attention blocks. These blocks divide the output features of a convolutional block in patches and explore how they are related to each other. This process helps to emphasize salient features, better locate objects of interest, and remove not useful elements by considering the relation to their neighbor area through trainable weights for the extracted features of each convolutional block [91].
Recently, multiple authors propose models that introduce Attention techniques in semantic segmentation tasks for medical images. Ouyang et al. [92] improve the diagnosis of pneumonia caused by COVID-19 by training two models, the first one using the whole lung dataset, and the second one using images with small infection area. While the second model gains more attention on the minority classes at the expense of possible over-fitting, the first one learns the feature representation from the original data distribution, thus addressing the fitting problems. The authors claim that attention mechanisms help the models to focus on important regions and improve affected area localization. This affirmation is also stated and demonstrated by Pang et al. [93] in liver tumor segmentation; Zuo et al. [89], also working with liver tumor images skin lesions, and retinal vascular segmentation; and Sinha and Dolz [94] which, using different resolutions of the same image to extract features at multiple scales, are able to better segment liver and brain tumor images.
Evaluation
Image generation models output a complete image, not a real or a discrete value. This change of the output nature causes evaluation metrics as described in Sect. 2.1.6 to be unsuitable. When working in semantic segmentation tasks, the objective is to compare the output of the model to the ground truth, checking which pixels were correctly predicted. The most common metrics are Pixel Accuracy, Intersection-Over-Union (IOU), and Dice Coefficient [35].
Pixel Accuracy shows which percentage of pixels are classified correctly. This method may be troublesome when studying images with one predominant class as it shows a high accuracy value even when many pixels of the smaller class are not correctly classified.
| 27 |
Intersection-over-Union (IoU) shows how the prediction and the ground truth overlap, thus taking into account even classes represented by few pixels.
| 28 |
Dice Coefficient (F1 Score) is very similar to IoU, and its results are equivalent. Both are common in medical studies, being author preference the main reason for choosing one over the other.
| 29 |
When a ground truth does not exist, as in realistic image generation tasks, above metrics lie pointless as a comparison can not be possible. In those cases metrics as inception score, Frechet inception distance, peak signal-to-noise ratio (PSNR), and structural similarity index (SSIM) must be adopted.
Inception score (IS) [95] and Frechet inception distance (FID) [96] focus on analyzing how realistic and variable the generated images are. To get these metrics, the authors use a pretrained inception model [42] to classify the generated images and compare its label distribution to the real examples. IS merges the probability of correctly classify an image, as a metric of its quality, and its distribution to check its diversity. FID introduces the usage of a multivariate Gaussian distribution to calculate the distance between real and fakes images distribution, making it a better option to analyze image diversity.
Generative adversarial networks
Generative adversarial networks, also known as GANs, were introduced by Goodfellow et al. [9] as a new framework for estimating generative models via an adversarial process. GANs consist of two different neural networks that are trained separately. One of the two models is a generator (G), a deconvolutional NN that captures the data distribution and generates a fake image. The other is a discriminator (D), which works as a classifier telling if its input is a real or fake image.
Following the work of the original authors [9], GANs can be formally described as two models based on a minimax game, as shown in Eq. 30. The objective is to train D using real data (x) to maximize the probability of assigning the correct label to images generated by G given noise variable z, while minimizing the chance of generating images in G that not look real to D. This means that GANs optimal end would be the distribution of real data () equal to the distribution of generated images ().
| 30 |
In Eq. 30, the first addend computes the probability of D predicting that real images (x) are authentic, while the second addend estimates the probability of D predicting that the generated images from G giving a noise z are not real.
Figure 18 shows the basic structure of a GAN, where and represent the trainable parameters of the generator and discriminator, respectively. A GAN is trained using a set of real images, where each one is represented as x features. Moreover, a fake example generated by G is represented as . The fake and real images are feed separately into the discriminator, whose job is to tell if they are fake () or real (x). D output is depicted as (like in Sects. 2.1 and 2.2). In order to prevent that the generator always generates the same output, a random noise vector is used as input. At the first, it was only used as a seed to generate different outputs, but as models become more complex, the noise turned into a way of controlling the content of the fake image. It can be combined with different data to select image characteristics or which class is represented in its content. To do so, different techniques have been proposed, such as the inclusion of a one-hot class vector to select the image class in the conditional GAN model [97], or the modification of the noise to select what the image shows in controllable GAN model [98].
Fig. 18.
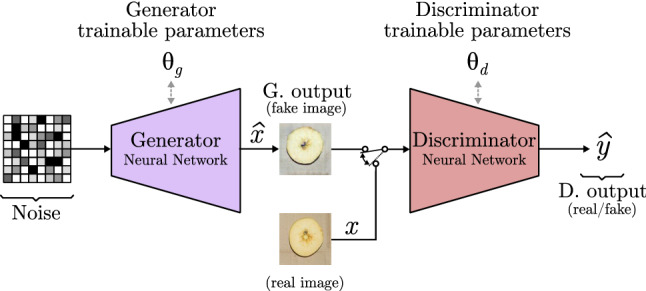
Generative adversarial network model based on deep convolutional GAN [99]
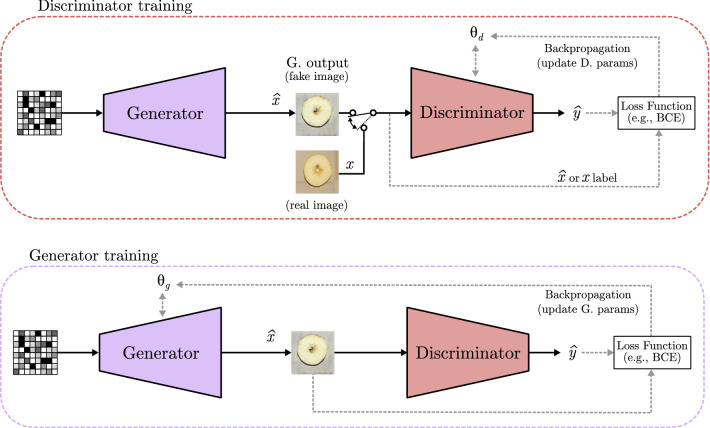
The training process of a GAN corresponds to a minimax two-model game, where each of the models is trained separately but needs to learn at same pace. On the one hand, if a completely trained generator is used while a naive discriminator is employed as classifier, the discriminator will be not able to distinguish whether it is a real or a fake image because the generator is doing a very good job generating images that seem real, thus not being able to learn. On the other hand, if a completely trained discriminator is used with an untrained Generator, the classifier will detect all the fake images and the generator will be not able to learn how to “trick” the discriminator. This is why the training process is done separately by batches, where G learns how to produce very good fake images, and then D learns how to detect them. Figure 19 shows how a GAN is trained. In both cases, the discriminator output is compared to the real label of the image, starting the backpropagation process of the trainable parameters or , depending on the model being trained. The training process is repeated until desired results are achieved. Finally, the discriminator model can be discarded and the generator is used to create the fake images as final output.
Fig. 19.
Generative adversarial networks training
GANs convergence
The GAN backpropagation procedure is the same as seen in Sect. 2.2, the only difference being the loss function implementation. Initially, the BCE loss function is implemented independently in each model, updating the parameters individually based on a discrete value returned by D depending on the prediction of the input image (real or fake). A high discriminator loss and low generator loss mean that the model generates images that it is not able to detect as fake, which is a desirable output. Specifically, the training point where G reaches the lowest point and D the highest is called convergence. Previous model states would generate low-quality images that are easily detected as fakes, and following steps would possibly introduce noise in the images, decreasing its quality. This shows that generative models do not necessarily benefit from long training procedures.
This process can lead to multiple problems. One of the main issues is the inability to converge, meaning that the model does not learn to generate images that look real. But still, achieving to trick the discriminator to not detect fake images is not sign of success, as the generator might be producing always the same almost real image as output, situation known as mode collapse. In order to sort out these problems, the loss function evolved to quantify the similarity between generated images and real data distributions based on the assumption that the more similar the distributions are, the better the models generation accuracy is, meaning more diverse and realistic fake images.
Arjovsky et al. [100] analyze and define different ways to measure the distance between two data distributions and propose the Wasserstein GAN (W-GAN). W-GAN swaps the discriminator for a new model known as “critic.” The critic model outputs a real value pointing out how real an image is, instead of a discrete one only stating if it is a real or a fake picture. Furthermore, W-GAN introduces the use of Wasserstein metric, an indicative measure of the cost of transforming one data distribution into another given an specific Earth-Mover distance. These changes to classic GANs help to train a model more gradually, avoiding mode collapse.
GANs noise manipulation
As previously stated, GANs are able to produce fake images that seem real. However, random or single class generation would heavily constrain GANs potential. This is why many authors worked on methods to control what the GAN is generating. Mirza and Osindero [97] propose a model called conditional GAN, represented in Fig. 20, that generates fake images of different classes. The class selection is done through a one-hot encoded vector concatenated to the noise vector. This class vector points out which class must be generated (1), while the other remains as (0), and the noise vector provides randomness.
Fig. 20.
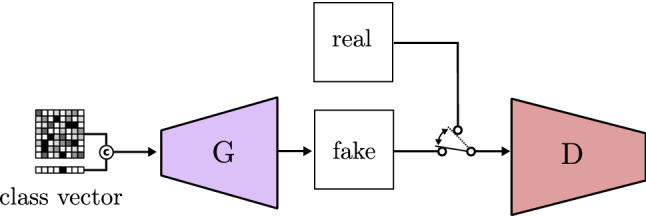
Conditional GAN based on CGAN [97]
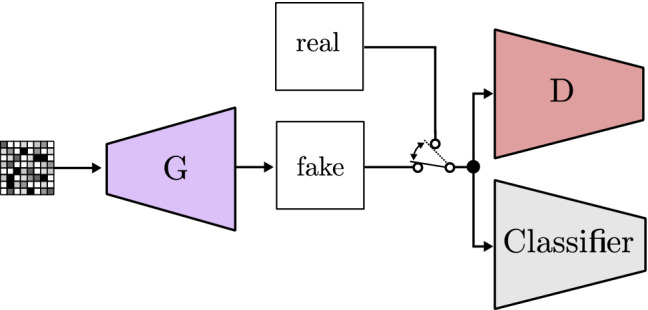
Lee and Seok [98] improve the model and propose the controllable GAN. The authors show how noise manipulation can influence which features are included in the fake image. As can be seen in Fig. 21, they add a third neural network working as a classifier whose main job is to help updating the noise, in order to produce more of the desired feature. In contrast to previously seen updating processes, the noise modification is done through gradient ascent, so the feature is maximized.
Fig. 21.
Controllable GAN based on CGAN [98]
Lastly, Shen et al. [101] review how the modification of the noise to control image features is related to a latent space. The authors claim that GANs are able to encode different semantics inside the latent space across multiple latent variables, being each of the variables a different feature. For instance, if the study focuses on human faces, the features would include eyes color, gender, and smiling, and others. To prove this, they propose the InterFaceGAN, a framework to explore how single or multiple semantics are encoded in the latent space of GANs that enables semantic face editing with any fixed pre-trained GAN model.
GANs applied to biomedical works
Multiple GAN models have been used as tools, inspiration, or as a starting point to develop new models applied to medicine. Some of them (Conditional GAN [97] and Controllable GAN [98]) are addressed in Sect. 3.4.2, but GANs have been on a continuous evolution since those models were proposed by their authors. Some of the most popular and widespread models are outlined below.
Radford et al. [102] propose a new model called deep convolutional GAN (DCGAN), and a set of guidelines to improve GANs including convolutional layers. They conclude that the elimination of the fully connected layers for convolutional layers, the use of ReLU activation in all generator layers except the output (which uses a tanh function), and the LeakyReLU activation in discrimination layers, among others, improve the quality of the generated images.
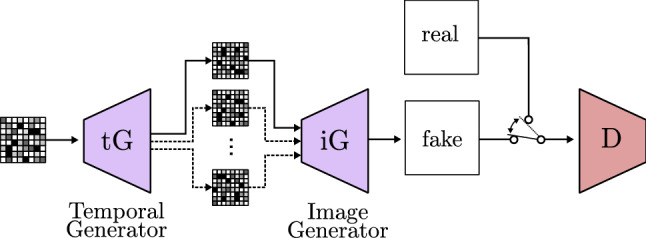
Saito et al. [103] propose a new model, called T-GAN (temporal GAN), able to generate sequences of images. They report the possibility to analyze video frames to train a model which generates consecutive images that together give the impression of movement (video). It first uses a temporal generator to build a collection of noises, one for each image of the sequence. As Fig. 22 shows, the noises are individually used to generate images through the GAN. Unfortunately, this model requires a lot of computation power, meaning that it is still not viable to use for many other authors, but as GPUs power keeps increasing, future works could benefit from this study.
Fig. 22.
Temporal GAN based on TGAN [103]
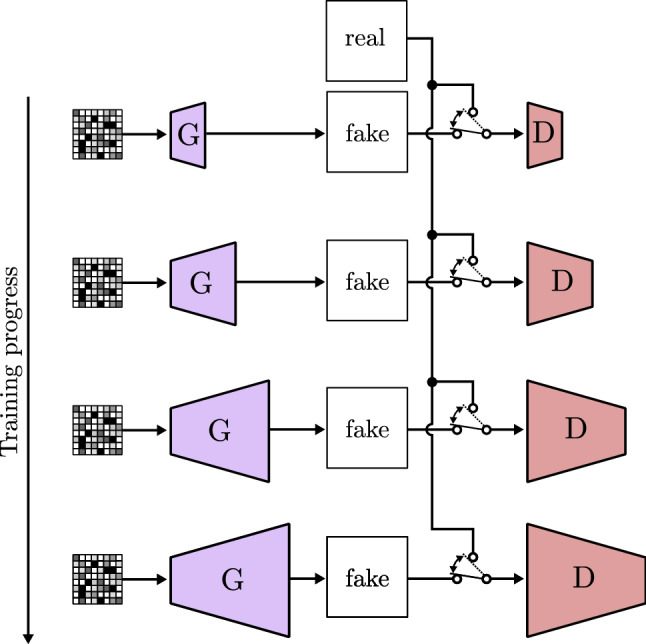
In recent years, many authors look forward to find new techniques in order to improve generated images resolution and quality, as well as to improve images variability to make GANs broader in scope. Karras et al. [104] advocate the use of progressive growing GANs (PGGAN). This model makes the generator and the discriminator bigger as training progresses, starting from low resolution and finally ending with a high resolution image (Fig. 23). The authors add new increased size layers allowing the training process to first find large-scale structures and then switch to finer details as new layers are included. PGGAN achieves training time reduction, more stable training, and high-resolution image generation with never obtained before quality.
Fig. 23.
Progressive growing GAN based on PGGAN [104]
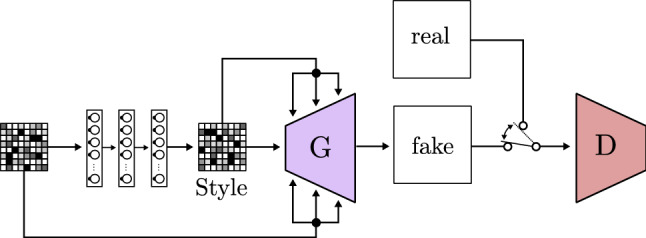
In a later paper [83], Karras et al. study how to transfer the style of an image to generate a variation of another image thanks to the proposed model StyleGAN. The authors introduce a fully connected network that transforms the input of the generator and feeds it in different entry points. This architecture, shown in Fig. 24, is based on a block called AdaIN (Adaptive Instance Normalization), which merges the intermediate latent space, the noise, and the convolution layer output/input to improve image generation.
Fig. 24.
Style GAN based on StyleGAN [83]
Finally, a rising number of models focuses on image to image translation. This technique consists of taking one image as input and transforming it to a different image that is still related to it. Isola et al. [105] assess this task and propose a model based on CGAN called Pix2Pix (Fig. 25). It uses the U-Net structure as a generator, offering great results in image semantic segmentation. Furthermore, Pix2Pix loss learning is adapted to the data used for its training, which makes it suitable for a wide variety of fields.
Fig. 25.
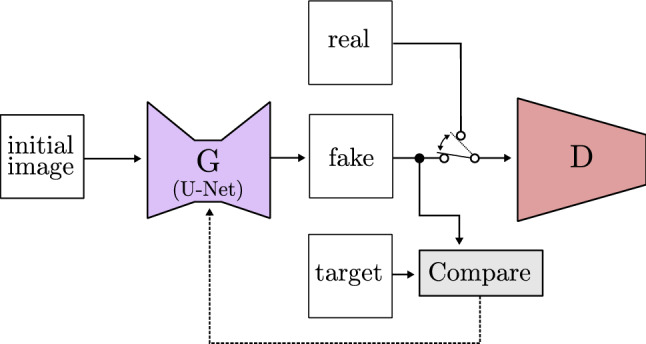
Image to image GAN based on Pix2Pix [105]
Zhu et al. [106] work with the Pix2Pix framework presented by Isola et al. [105] and the StyleGAN proposed by Karras et al. [83]. Their model, called cycle-consistent adversarial network(CycleGAN), is able to automatically translate an image into another and viceversa without a paired dataset used for training. As can be seen in Fig. 26, the authors achieve this by using two generators and two discriminators. First, it transforms the real image obtaining the output (fake A), then the process is reversed to get the original image (fake B) through a different generator, thus creating a cycle. Finally, different losses acquired through the comparison of different outputs of the model are combined together and used as learning loss. This is one of the most complex models to date, but results are evidence of its effectiveness.
Fig. 26.
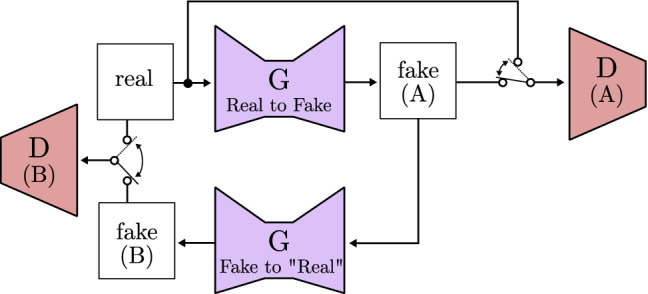
Cycle consistent GAN based on CycleGAN [106]
Among the recent models gathered in Table 2 is the VQ-GAN (vector quantized GAN) proposed by Esser et al. [107]. It draws inspiration from transformers structures used in models applied to text analysis. The authors suggest to use transformers to learn a distribution of the different labeled characteristics of the images. The model, shown in Fig. 27, uses an encoder to represent the image as a vector of image features merged with the transformer data. In this way, the image is represented by a rich feature vector instead of the values of the pixels. Finally, this new vector is fed to a GAN following the conventional path.
Table 2.
Overview of generative adversarial models. The models are ordered from an initial simpler model to the most sophisticated ones. Each model offers an improvement and capitalizes on the previous models advancements
| Model | Main features | Application |
|---|---|---|
| GAN [9] | First model that introduces the adversarial philosophy to generate synthetic images. It faces two different neural networks: the generator and the discriminator. The generator captures the data distribution and generates a new image, while the discriminator tries to categorize images as fake or real. The conditional GAN (CGAN) [97] was developed along the GAN. It is the first GAN model able to select and control the class of the generated image. | Image generation |
| CGAN [98] | (Controllable GAN) It extends the basic GAN functionality by adjusting the no| values to control the generated image content. It is able to generate images using more detailed labels that the basic GAN thanks to the introduction of a classifier. The generator keeps generating images and the fiscriminator categorizes them as fake or real, while the Classifier detects if the target class is depicted in the image. | Image generation using detailed labels |
| DCGAN [102] | (Deep convolutional GAN) Unsupervised model that introduces the use of convolutions in all layers, removing the last full connected layers that previous models included. It also uses Batch Normalization to stabilize learning, achieving better feature detection and images of higher resolution than previous models using less trainable parameters. | High resolution image generation, unsupervised learning |
| Pix2Pix [105] | The authors introduce the use of a U-Net model as a henerator instead of an encoder, and a dataset of paired images for the training process. This model, in addition to the discriminator, compares the fake image with the target image paired to the input. In this way, it is able to learn how to translate images to images with different features. | Image to image translation, semantic segmentation |
| TGAN [103] | (Temporal GAN) This model uses a temporal generator to build one noise matrix for each frame of the sequential image from the initial noise. Each of these new noises is sent to another generator that creates the images. | Generation of image sequences |
| CycleGAN [106] | It uses two generators, one to transform a real image to a fake one, and the other to transform the fake to another fake image that must be as close as possible to the real image. CycleGAN uses two different discriminators, and combine all the losses to obtain a cycle loss in order to be trained. | Image to image translation |
| PGGAN [104] | (Progressive growing GAN) A model that increases the number of layers of the generator and discriminator along the training process. It first detects large features structures and then shifts to discover finer scale details. | Production of high-quality images |
| StyleGAN [83] | This models uses a fully connected neural network to extract the style of an image, and a convolutional block called AdaIN to insert it in an input image. This style is inserted in multiple points of the model. | Merging of images |
| BigGAN [108] | It proves that GANs benefit from increasing the size of the model. BigGan establishes a threshold and re-samples the noise matrix in order to increase the number of trainable parameters, and as a result obtaining images with better fidelity and variety. | Generation of a great variety of high-quality images |
| VQ-GAN [107] | (Vector quantized GAN) It uses the transformer block, commonly used in natural language processing, to analyze the interaction between different parts of the image. First, an encoder synthesizes the image and represents it semantically as a collection of features. Then, this feature matrix is fed to the generator, from there, the standard GAN path is followed. | High resolution images |
Fig. 27.
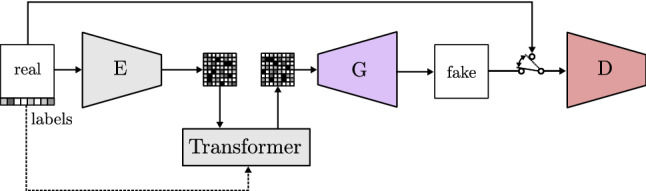
Vector featured GAN based on VQ-GAN [107]
Although GANs are used along multiple areas, they have a great influence over the biomedical field, where the analysis and the generation of images play a very important role. They take advantage of the recent increase of computational power and massive medical data availability. A big part of the data generated is applied to neuroimaging and neuroradiology, brain segmentation, stroke imaging, neuropsychiatric disorders, breast cancer, chest imaging, imaging in oncology, and medical ultrasound, among others [99].
Ghassemi et al. [99] propose a DCGAN to produce MR images of the brain. The authors train the GAN so the discriminator can detect fake MR images and extract their main features. Then, the fully connected layers of the Discriminator are replaced by a softmax layer which is trained again. In this way, they use it as a classifier able to detect meningiomas, gliomas, and pituitary tumors with high accuracy. Nema et al. [109] also study how GANs can be applied to unlabeled MR images. They propose an enhanced version of CycleGAN, called RescueNet, which offers excellent results regarding brain tumor segmentation. Klages et al. [110] evaluate CT image generation for head and neck cancer patients using Pix2Pix and Cycle-GAN models. The generated image is used together with MR imaging, which provides superior soft tissue contrast showing improvements in tumor delineation, segmentation and treatment outcomes in neck and head cancer. The authors conclude that the Pix2Pix model requires near perfect alignment between CT and MR images, while CycleGAN relaxes the constraint of using aligned images or even images acquired from the same patient.
In spite of being a widely known technique, MR images generation can be degraded due to patient motion, leading to increased cost and patient inconveniences. Do et al. [111] propose two GAN models (X-net and Y-net) able to rebuild downsampled MR images to speed up the process with no quality loss. Both models were firstly implemented as basic U-Nets, but the inclusion of a GAN discriminator improved the results and contributed to obtain more realistic images. Furthermore, certain procedures require more representative images, adding techniques to basic MR images. Positron Emission Tomography (PET) is often used along MR images (PET-MRI) and CT (PET-CT). PET-CT provides better results in scan time, costs, and patient comfort, but PET-MRI reduces the patient exposure to radiation [112]. This is one of the reasons why Pozaruk et al. [113] study how GANs can improve prostate cancer PET-MRI. They propose a GAN model to generate pseudo PET-CT images from PET-MR scans, meaning that a safer method is used to obtain high-quality images. Results show improved quantitative accuracy of PET-MR measurements, enabling its use in clinical lesion grading in a non-invasive manner. It leads to better prognostication and reduce or remove the need for biopsy or re-biopsy. Zhou et al. [114] also propose a GAN to enhance MR images of the brain for Alzheimer disease classification. They use 2.5D and 3D scans along with 3D-GAN which uses 3D convolutions to generate a better quality MR images. Then, a classifier analyzes the synthetic image to tell if the patient may suffer Alzheimer disease or not.
Skin lesion detection is a challenging task due to the large variations and scale differences of lesion areas shown in dermoscopy images. Lei et al. [115] use a GAN architecture including two discriminators for skin lessions segmentation. Even though the proposed model has problems detecting problematic areas on low contrast examples, the authors conclude that their model improves state-of-the-art methods and can also be extended to other medical image segmentation tasks. GANs are used by Qin et al. [116] as well. They propose a lesion classification method using a ResNet50 fed by synthethic images generated by a GAN. The authors compare four different GAN models, basic GAN[9], DCGAN[102], StyleGAN[83], and the proposed method SL-StyleGAN (Skin Lesion - StyleGAN). Their proposal, which is a modification of the base StyleGAN model, offers higher resolution in diverse skin lesion images. Furthermore, it provides a reliable artifact elimination method (e.g., hair, tick marks). This unintended effect is caused because the images are generated calculating the mean and variance of the feature map of one image, and then applying them to another input image.
The recent emergence of COVID-19 disease also motivated a lot of authors to apply GANs for its detection. The main area of study is the effects of COVID to lungs by means of pneumonia and lung inflammation. One of the most common diagnosis procedure is done through X-ray, MR and CT images, most of which, as previously seen, can be used as GAN input. Rasheed et al. [117] propose a diagnosis method based on X-ray images fed to a CNN classifier and the use of a GAN for data augmentation. Albahli [118] also analyzes X-ray images of the chest to distinguish COVID-19 from other chest diseases. The author employs a GAN to generate synthetic examples of COVID-19 X-ray chest images and solve unbalancing problems. Zhang et al. [71] generate multiple synthetic images using a DenseGAN to obtain higher quality images, and improve generalization and accuracy of a U-Net model used for image segmentation. In this way, the authors are able to obtain a bigger dataset and better segmentation accuracy of COVID-19 pulmonary CT images. Lastly, Li et al. [119] propose an architecture for COVID-19 diagnosis on CT scan images. The main objective of their proposed method is to generate new synthetic examples for data augmentation. Then, a CNN classifier automatically diagnoses the presence of COVID-19.
As many authors state [116–118], one of the main problems they face is the lack of specific data when studying a particular disease. GANs are able to generate synthetic images that can be used as real data, this is called data augmentation. One of many examples is provided by Pang et al. [120], who use a GAN to generate new examples of breast ultrasound images applied to breast cancer patients. The synthetic images generated by the GAN, alongside the real images, are fed into a CNN that classifies the masses found in the image as benign and malignant. This process allows the CNN to learn from a bigger dataset, thus obtaining better results.
Variational autoencoders
Introduced by Kingma and Welling [76] and Rezende et al. [77], the VAEs combine two different models, an encoder and a decoder. Both models are separate convolutional neural networks working together to learn different distributions that represent the input and to transform the found distributions in fake images, so when the training is over, the decoder can be used independently to generate new examples [121].
VAEs share the same encoder-decoder architecture as autoencoders, but the training process is regularized in order to achieve good generation properties and avoid overfitting. This is accomplished through the encoding of the input as a distribution over the latent space. Then, a point is sampled from that distribution to be decoded and the reconstruction error is computed.
The complete architecture can be seen in Fig. 28. The encoder is a CNN whose goal is to encode high-dimensional data into a low-dimensional representation. It is able to find a representation of the image and places it in a latent space (Sect. 3.5.1). A sample from the latent space consists of an array of means and standard deviations. This is taken as input for the decoder, where data are reconstructed from the low-dimensional representation. It is a transposed convolutional (or deconvolutional) neural network which takes the sample vector and produces a fake image. This fake image is then compared to the real one introduced as input for the encoder through a loss function (e.g., reconstruction loss [121]) from which the gradient is calculated. Finally, the backpropagation step is carried out from the last layer of the decoder to the first layer of the encoder.
Fig. 28.
Variational autoencoder model [52] architecture
Despite the great similarities with encoder-decoder models like U-Net, VAEs are distinguished by the fact that they do not learn only from the input data, but from the input distribution. In order to do so, the layer between the encoder and the decoder is replaced with two different layers, one for mean and the other one for standard deviation. Then, the decoder takes a sample (latent vector z) from this layer distribution to reconstruct it.
The latent vector should not be taken in a non deterministic way, as backpropagation would be impossible to fulfill. Kingma and Welling [76] and Rezende et al. [77] propose to take the samples using a “reparameterization trick” (Eq. 31), that consists in generating a latent vector z using two trainable parameters, being the mean, the standard deviation, and an auxiliary noise variable . This technique allows to backpropagate from the output of the decoder to the first layers of the encoder.
| 31 |
Figure 29 shows how VAEs internal structure differentiates from encoder-decoder structures.
Fig. 29.
VAE internal architecture
As mentioned above, the output of the decoder () is compared with the input of the encoder (x). The loss function of VAEs checks the divergence between both samples through a variation of evidence lower bound (ELBO), and Kullback-Leibler (KL) divergence between real and reconstructed image, thus measuring how similar are the real and generated example and how much information is lost. ELBO is maximized with respect to the encoder model parameters and the decoder parameters , so the reconstruction is as similar as possible to its original image. In Eq. 32 the VAE loss function is formally described, where represents the encoder model generating a latent vector z from real example x, and the decoder model reconstructing a new image from latent vector z [122].
| 32 |
VAEs latent space
The encoder of the VAEs draws new features from the input and represents them as encoded data. This means that the initial distribution is changed due to the encoding processing, and a new distribution called latent space (encoding distribution) is generated. This conversion usually implies the loss of data that can not be recovered by the decoder. The latent space consists of latent variables that are part of the model but are not observable [122].
Many authors proposed techniques to reduce data loss. As Davidson et al. [121] demonstrated, the latent space distribution (Gaussian distribution), used in Fig. 28, can be replaced by a von Mises-Fisher (vMF) distribution. In this way, a spherical representation of the latent space (hyperspherical) is employed instead of an hyperplanar representation, improving the latent representation and hence obtaining better results.
Figure 30 shows the main difference between the distributions. This change significantly improved VAE and its usage as a generative model.
Fig. 30.
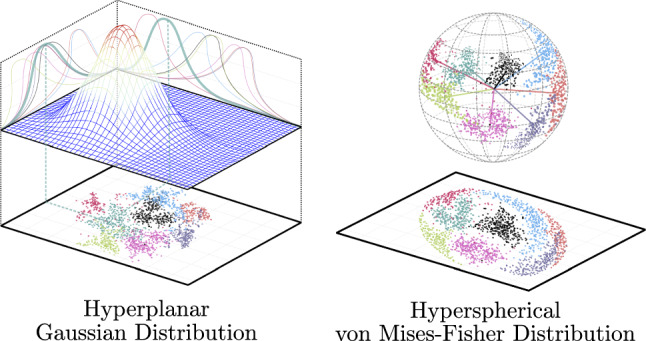
Visual comparison of hyperplanar and hyperspherical latent spaces
VAEs in the biomedical field
Image segmentation is one of the most intended purposes when using VAEs in medicine. The main purpose of these models is to generate a new image referencing the original in the input and highlighting areas of interest. The “fake” image has new information identifying specific objectives like abnormal characteristics or parts differentiation. Uzunova et al. [123] use conditional variational autoencoders (CVAEs) [124] together with 2D and 3D medical datasets as an unsupervised approach for pathology detection. They conclude that CVAEs are able to learn a proper representation of data applied to pathology detection in 2D images, while the complex representation of the 3D data handicap the reconstruction process. That is, the proposed model is able to enrich the 3D representation but is unable to properly reconstruct the input.
Akrami et al. [125] analyze how VAE models are affected by a pre-training process applied to brain lesion detection through 2D MR images of the brain. The authors come to the conclusion that their suggested model (Robust VAE), which uses a new loss function, achieves a higher performance using transfer learning through pre-training than base VAE. Marimont and Tarroni [126] also use MR images of the brain and abdominal area to study the performance of the VAE model called VQ-VAE. This specific model uses a dictionary of keys mapped to a discrete number of features of the latent space, working as a kind of embedding. The authors conclude that their unsupervised anomaly detection and localization method achieves better results than existing standard VAE approaches. They state that results improved when brain footage were used. This is often caused by a higher variance in the abdominal dataset. Wei et al. [127] mix MR and contrast-enhanced computed tomography (CECT) images, and raw data (clinical features) for risk prediction in hepatocellular carcinoma patients treated with stereotactic body radiation therapy using a model that combines two VAEs and one CNN. The proposed model accomplishes better performance than previous models showing promising predictive power, which can be used to personalize future liver cancer treatment.
Kou et al. [128] analyze high-resolution manometry (HRM) images, for esophageal motility disorders diagnosing. Their VAE model includes a different loss function and hyper-parameter tuning motivated by domain knowledge. In this way, the proposed model offers a reliable alternative to the current diagnosis method based on the analysis of the images by a large group of experts.
In view of the above, it is hereby confirmed that the GANs are more widespread in medicine works than VAEs. As pointed out by authors like [104, 129–131], GANs and VAEs are complementary, GANs advantages being VAEs disadvantages and vice versa. This is the reason many authors choose to not pick a particular model, but instead use an hybrid model that takes the best of GANs and VAEs simultaneously.
Larsen et al. [129] add a discriminator to a VAE structure, changing it to a VAE-GAN. The VAE is used as a generator which output goes through the discriminator to detect if it is a real image or not. The proposed model achieves high-quality image generation with the possibility of working over the latent space features. Bao et al. [130] analyze multiple hybrid models like VAE/GAN [129], CVAE [124], and PPGN [132]. The authors also propose a new model called CVAE-GAN by which superior performance and enhanced image quality is achieved. As can be seen in previous sections, these models can be directly applied to medical images, one of many examples being the work of Nakao et al. [131]. They combine a VAE and a GAN to build an unsupervised chest radiography anomaly detection system. Their proposal is able to detect anomalies with high precision, but it is not able to diagnose them. As the authors say, this approach does not replace the human doctor, but is rather a tool to help detect lesions and prevent oversights. Finally, in addition to the collection of VAEs and hybrid models, presented in Table 3, it is worth mentioning Baur et al. [133] comparative study since it offers a detailed analysis of both base and hybrid models applied to different datasets.
Table 3.
Overview of variational autoencoders and hybrid models VAE-GAN models
| Model | Main features | General Application |
|---|---|---|
| VAE [76, 77] | (Variational autoencoder) First model that introduces the use of a latent space to merge an encoder and a decoder. The Encoder learns the data distribution while the decoder learns how to rebuild the input image from a sample of the distribution. | Image generation and image compression. |
| CVAE [124] | (Conditional VAE) It takes an incomplete image as input and builds the missing areas of the image, and is able to generate an image from a specific class label. To achieve it, this model introduces a new variable and uses it to map multiple distributions to each of its values. The authors also propose a multi-scale output prediction to be able to use the model with large scale images. | Image reconstruction, labeling, and semantic segmentation. |
| VQ-VAE [134] | (Vector quantized VAE) This model introduces the use of image embedding vectors as input of the decoder to improve the quality of the generated images. | High-quality image and video generation. |
| VAE-GAN [129] | Hybrid model that includes a discriminator to the VAE architecture and collapses the decoder and the generator as the same CNN. It is able to take advantage of the complex data distribution of the VAE while generating high fidelity images as GANs. | Image generation. |
| PPGN [132] | (Plug & play generative networks) This hybrid model collapses the decoder and the generator and adds a classifier and a discriminator to analyze the generated images. | High-quality image generation |
| CVAE-GAN [130] | (Conditional VAE-GAN) The authors of this work propose to expand the PPGN model and use a class label to be able to better select which class must be generated. | Class selection of image generation |
| BiGAN [135] | (Bidirectional GAN) This model is able to extract semantic features and project the data into the latent space through the use of an encoder. This implies that, in contrast to base GANs, BiGAN is able to map latent samples to generate data and also perform the inverse process, from generated data to latent representation. It improves results in discrimination tasks and image generation with respect to the contemporary unsupervised and self-supervised models. | Feature extraction and discrimination tasks |
Datasets
Over the literature, different sets of images are used as training and test for the developed models. It is important to distinguish general images datasets from medical specific collections. The first are easier to collect since there is no personal sensitive data that must be anonymized. Medical images are difficult to gather because few patients that are suffering from a very specific illness are accessible to take the images, which need to be analyzed by medical staff to associate a label to the picture. It is a slow process that takes a lot of effort, and in many cases, high economic cost. This is one of many reasons why a lot of collections are private or require a payment to access them. Many authors opt to cooperate with a medical institution and gather their own images collection directly from patients, this being a slow process that not everyone is able to achieve.
To address this issue, free use collections can be found online along with challenges and competitions. Table 4 shows different collections of images including pictures, magnetic resonance (MR) images, computed tomography (CT) scans, and X-Ray images. The collections are grouped by the body area from which the images are taken (brain, breast, lungs/chest, and other).
Table 4.
Overview of medical datasets ordered by body area. Application column contains the most common usage of the dataset including: classification (C), detection and localization (D), and semantic segmentation (S)
| Area dataset | Overview | Application | Size | Refs. |
|---|---|---|---|---|
| Brain | ||||
| ADNI [136] | (Alzheimer’s Disease Neuroimaging Initiative) Includes Alzheimer’s disease patients, mild cognitive impairment subjects, and elderly controls. | C | 850k | [114, 137, 138] |
| OASIS-3 [139] | (Open Access Series of Imaging Studies) MR images data from 1098 individuals aged 42 to 95 years. Dataset focused on the study of dementia. | C / D | 2k+ | [99, 138] |
| BT [140] | (Brain Tumor dataset) MR images dataset that includes 3064 slices from 233 patients, containing 708 meningiomas, 1426 gliomas, and 930 pituitary tumors. It also includes tumor area annotations. | C / D | 3k+ | [99, 141] |
| BRATS [142] | (Brain Tumor Image Segmentation) It contains 285 brain tumor MR images scans, with four MR images modalities and full masks for brain tumors. | S | 285 scans | [109, 123] |
| MOOD [143] | (Medical Out-of-Distribution) Brain MR images-dataset divided in train (no anomalies cases) and test (both anomalies and no anomalies examples). Abdominal CT-scans (550) are also available. | D | 800 scans | [126] |
| Breast | ||||
| Camelyon [144] | Lymph node sections of breast cancer patients. It contains whole slide images of stained lymph node sections. Ground truth is provided on a lesion-level or patient-level depending on the dataset (Camelyon16 / Camelyon17). | C / D / S | 1k | [72] |
| DDSM [145] | (Digital Database for Screening Mammography) The dataset includes approximately 2,5k studies. Each study includes two images of each breast and patient information. | C / D | 10k | [146] |
| InBreast [147] | It is composed of 115 cases of breast cancer patients. It includes mass, calcification, asymmetry, and distortion lesions. Contours made by specialists are also provided. | C / D / S | 410 | [146] |
| BCS-DBT [148] | (Breast Cancer Screening-Digital Breast Tomosynthesis) It includes normal, actionable, biopsy-proven benign, and biopsy-proven cancer cases. The dataset also offers DICOM images, a spreadsheet indicating which group each case belongs to, annotation boxes, and image paths. | C / D / S | 22k+ | [149] |
| Lungs / COVID-19 | ||||
| ChestX-ray [150] | (Chest X-Ray Images (Pneumonia)) The set contains 5,232 chest X-ray images from children, including 3,883 characterized as depicting pneumonia (2,538 bacterial and 1,345 viral) and 1,349 normal, from a total of 5,856 patients. | C. / D / S | 5k+ | [117, 131, 151, 152] |
| ChestX-ray-NIHCC [153] | (National Institutes of Health Clinical Center) The dataset (also known as ChestX-ray-8 and ChestX-ray-14) includes X-ray images with disease labels (e.g., atelectasis, infiltration and pneumonia) from 30,805 unique patients. | C / D | 112k+ | [66, 71, 118] |
| CIDC [154] | (COVID-19 Image Data Collection) X-ray and CT images of patients which are positive or suspected of COVID-19 or other viral and bacterial pneumonias. | C / D | 600+ | [66, 152] |
| LIDC-IDRI [155] | (Lung Image Database Consortium and Image Database Resource Initiative) Lung CT images with marked-up annotated lesions as benign, malign, metastatic lesion or unknown. Each lesion also includes how the diagnosis was established (unknown, radiological images, biopsy and surgery). | C / D / S | 1k+ | [72] |
| COVID-19-NY-SBU [156] | (New York - Stony Brook University) The collection includes radiograph images of COVID-19 pulmonary disease patients. It also contains diagnoses, procedures, lab tests, and symptoms data of each patient. | C / D | 562k+ | – |
| Other | ||||
| ISIC [157] | (International Skin Imaging Collaboration) Compilation of patient-level sets of skin lesion images. It includes malignant, benignant images and contextual information of the same patient. | C / D / S | 40k+ | [64, 115, 116] |
| Pancreas-CT [158] | Abdominal contrast enhanced 3D CT scans of patients aged 18 to 76 years. A slice-by-slice segmentation of the pancreas performed by a medical student and verified by an experienced radiologist is provided as ground-truth. | C / S | 18k+ | [69] |
Table 5 gathers general topics image collections including faces, scenery, animals, common objects, numbers, etc. This datasets are usually used in object detection and classification task, but can also be used as training for generative models or semantic segmentation. As mentioned above (Sect. 4.1), the usage of these collections can help obtaining better results in medical studies. Through the use of transfer learning, a general topic collection can be used to train a model and learn how to detect basic shapes. Then, all layers, except the last ones, are frozen, so they do not learn anything and the unfrozen ones are trained again to detect specific features from a medical dataset.
Table 5.
Overview of general datasets ordered alphabetically. Size referring to number of images. Application column contains the most common usage of the dataset including: image generation (G), classification (C), detection and localization (D), and semantic segmentation (S). All collections can be used as data augmentation datasets
| Area / Dataset | Overview | Application | Size | Refs. |
|---|---|---|---|---|
| CelebA [159] | (CelebFaces Attributes) Face attributes dataset covering different poses and background. | G | 200k+ | [75, 83, 98, 101, 104, 129] |
| CIFAR-10 [160] | (Canadian Institute For Advanced Research-10) A 10 classes dataset that includes color images of birds, cats, dogs, trucks, automobiles, etc. A 100 class dataset (CIFAR-100) is also available. | C / G | 60k | [9, 42, 46, 74, 75, 77, 104] |
| Cityscapes [161] | Urban street images dataset labeled using 30 classes (e.g., road, person, and terrain). This dataset is widely used in semantic segmentation works. | S | 25k | [58, 105] |
| COCO [162] | (Common Objects in Context) This dataset contains more than 200k labeled images (2.5 million labeled instances) of common objects including household items, vehicles, animals, food, etc. | C / D / G | 330K | [46, 58, 60] |
| CUB [163] | (Caltech-UCSD Birds) Images of 200 bird species with 312 binary attributes and 15 part locations each. | C / D / G | 11k+ | [124] |
| Faces [164] | Facial expressions in younger, middle-aged, and older women and men. | G | 2,052 | [48, 77, 102] |
| Flickr25k [165] | (Multimedia Information Retrieval Flickr 25k) Social media images paired with annotations. More 30k, 50k, and 1 million versions are also available. | D / G | 25k | [97] |
| ImageNet [166] | This dataset contains 1000 object classes. It is one of the most commonly used in computer vision. | C / D / G | 1M+ | [42, 43, 47, 48, 52, 54, 55, 57, 59, 74, 75, 97, 102] |
| LFW [167] | (Labeled Faces in the Wild) Face photographs of more than 7k people. | G | 13k+ | [124] |
| LSUN [168] | Scene pictures divided in 10 separate scene categories containing 20 object categories as bird, boat, dog, etc. | C / D / S | 69M | [48, 75, 83, 98, 102, 104] |
| MNIST [169] | (Modified National Institute of Standards and Technology) Handwritten digits black and white images. | C / G | 70k | [9, 76, 77, 97, 103, 121] |
| VOC [170] | (Visual object classes) It contains labeled objects including different subclasses of person, animal (e.g., cow, dog), vehicle (e.g., boat, bus) and indoor (e.g., bottle, chair). Multiple variations of the dataset are accessible in different PASCAL VOC challenges. | D / G / S | 10k | [46] |
Transfer learning
Previously discussed models are not only used as an architectural starting point, but can also be used as already trained models through transfer learning (TL). TL is based on the use of a model trained with a different corpus, learning to detect basic shapes and objects. From this trained model, the last layers are trained again to learn a specific purpose. This way, the training time is reduced drastically while object detection accuracy remains almost intact. Several authors have successfully used this technique for medical purposes [65, 141]. Many other professionals took advantage of TL for diagnosis and handling of COVID-19 [151, 152, 171], Alzheimer Disease detection and stage classification [137, 138], breast cancer analysis [146, 149, 172, 173], and many other applications.
Among the research, ImageNet dataset [166] stands out because of its importance and its widespread use. It is used as a pre-train dataset from which general object characteristics can be learned. Section 4 addresses it together with more general and specific datasets.
Discussion
Even though neural networks and convolution operations are known since mid 1900s, it was not until 2015 that they broadly expanded in medical image analysis. CNNs feature extraction capabilities are an extremely useful tool that can be included in multiple models as an alternative to fully connected layers, reducing the size of the deep learning models and allowing their use by a wider general public. Pre-trained models facilitate their use as “black boxes” as they can be directly applied to medical images without requiring much effort. However, as knowledge about CNNs, GANs, and VAEs models increase, an end-to-end approach where the whole model is handcrafted and trained is preferred. This gives the authors the ability to adapt the model to the specific task requirements and to use different data types depending on the illness being studied.
Key features
The recent popularity of generative models causes a high number of models to appear, many of them pursuing the same objective and using nearly identical data. However, it is not possible to conclude which model is the best. Groups and researchers that choose to implement generative models tend to use well known models (e.g., Pix2Pix [105], Stylegan [104], and CVAE [123]) that offer positive results in different areas. Despite this, extremely varied results are obtained, proving that the architecture is not the key factor to get good results. Expert knowledge about the job to be done, like using the right activation functions and normalization, can provide great advantages. One of the best examples is the change from an hyperplanar to an hyperspherical latent space proposed by Davidson et al. [121], improving VAEs performance. Another example is the inclusion of an U-Net as a generator in GANs by Isola et al. [105], showing how the overall adversarial architecture can be kept and still makes significant changes to considerably improve the output.
Even when using the same model, authors can stand out from the others by the way they manipulate the data. Several researches show how image preprocesing and data augmentation through generative models improve different classification models. Being able to generate new fake examples that seem real even to expert medical staff, gives researchers the ability to generate a bigger dataset with which train any other system keeping the same data distribution as the original.
Yet even using the same dataset and model as other authors, hyper-parameter optimization can make a big difference in a model outcome. Internal parameters as normalization type, layers dropout, learning rates, and training time impact performance in a big way. Unfortunately, there are no hyper-parameter tuning rules to get the best model, only an empirical process can tell which ones work best in each scenario.
Generative models outlook
In view of the above, and considering that deep learning is continually under development, it is safe to say that new models and improved architectures are going to come to light in future years offering even better results. Nowadays, most authors in medical works choose generative models to increase the amount of data to train a model [71, 117, 120] or to highlight points of interest in images (e.g., classification and image semantic segmentation) [83, 123, 124].
The option that is most frequently observed in medical works is the use of GANs. This is due to the great empirical results and the ability to obtain high image resolution that eases the work of doctors and medical staff, where good image quality is an essential requirement. GANs are also supported by a increasing number of authors and corporations, making them a viable option for long-term projects.
VAEs are gaining ground thanks to the last improvements in image quality [123, 126] and its stable training property. The main reason most authors do not choose VAEs is the complexity of using latent spaces. But, in spite of such complexity, the latent space is what makes VAEs so powerful and further research could exploit its potential.
So far, GANs are the most commonly used models, but authors like [130, 131] report that good results can be achieved using hybrid models that merge GANs and VAEs. The most common practice is to use the VAE encoding capabilities to locate each example in the latent space, and then use GAN ability to produce a high-quality image from the VAE encoding. After all, much remains to be done in terms of generative models, and the combination of different models could offer a huge boost to medical investigation.
Challenges and future progress
After reviewing the internal work of different NN, CNN, GAN, and VAE models, and analyzing multiple works of different authors, it is clear that deep learning algorithms provide high benefits to medical image analysis. However, new challenges and obstacles are emerging. Many authors point out that the lack of large specific illness image datasets singularly complicates the job of training a model. Added to this is the complex, time-consuming task of labeling each one of the images. This process can only be done by expert medical staff, greatly limiting the amount of data that can be generated in a small span of time.
So far, generative models have proven to be useful in fake image generation for data augmentation, semantic segmentation, and even classification tasks, but they must continue adapting to emerging challenges and opportunities while maintaining their unique characteristics. As of yet, these models are used as support for medical staff, cutting down analysis times and undercutting the number of tedious chores that must be done by clinicians, also improving the quality of life of the patients. As more deep learning algorithms and generative models are accepted as clinical tools, entirely new approaches open up. Barely explored tasks as image reconstruction, image prediction, or the inclusion of text and diverse medical data over generative architectures will have an enormous impact in medical image analysis.
For the near future, as well as improving existing architectures, new techniques are being implemented to keep expanding the application of deep learning models and allow for better outcomes. One of the last advances in computer vision in medicine is the inclusion of Transformers, as previously seen in [107]. Transformers were first introduced in natural language processing as a way to introduce the word context in the mathematical representation used by the learning models. They are based on the self attention mechanism proposed by Vaswani et al. [90] and offer an alternative to sheer convolutional and recurrent neural networks by tokenizing groups of pixels that represent a semantic concept of the image, and later linking them to classify larger features [174]. In recent publications, Transformers have proven to obtain promising results when working with medical images in detection and classification of skin lesions applying semantic segmentation [175], and improving MR images quality [176].
Furthermore, new alternatives to GANs and VAEs as Diffusion models [177] are being developed. Diffusion models are a scored-based technique where they are trained by gradually adding noise following a Gaussian distribution to images and learning how to reverse it. Recent works in the medical field follow this approach obtaining better results than other state-of-the-art works. Jalal et al. [178] and Chung and Chul [179] make use of diffusion models to improve the quality of MR scans, while Wang et al. [180] apply it to low-dose CT images, thus being able to improve their quality and level of detail. In future works, hybrid models could take benefits from Diffusion models merging it with other generative alternatives previously presented in this work.
Lastly, the recent appearance of data collections with an evolutive point of view, as the one developed by Gomez et al. [181], proves that generative models could not only focus on a single image, but also to cover different states through a period of time. This process is similar to the generation of videos and sequences of images through LSTM blocks and 3D Convolutions, as proposed in [103], but further research could develop this field and offer great benefits in the medical field.
Conclusions
Looking at current deep learning trends, generative models are identified as the most used emerging techniques in medical imaging. Two main models, variational autoencoders (VAEs) [76, 77] and generative adversarial networks (GANs) [9], made the biggest impact in the field. Both are generative networks that can be trained end-to-end without a fully labeled training images, making it easier to bring together a suitable dataset. On one hand, VAEs merge two complementary neural networks (encoder/decoder) learning how to locate individual examples in a latent space, and then, rebuild them from particular samples. On the other hand, GANs handle two opposing convolutional neural networks where one generates artificial data and the other divides real from fake samples.
Finally, deep learning methods as CNNs and generative models as VAEs and GANs are often described in medicine as “black boxes.” This is a major problem, as in medicine all tools must be accountable. It is critically important to understand how they work and which are the potential legal consequences. In this work, we aim to explain and lift the veil of complexity that surrounds the most used deep learning methods in medicine imaging. A simple but detailed explanation of the diverse elements that can be found in a deep learning project: from the functioning of a single neuron to the complete architecture of a generative model. This study is expected to encourage the use of deep learning techniques in medical works and help medical staff to understand how they work and how can they be beneficial to their work.
Acknowledgements
This study was supported by MCIN/AEI/ 10.13039/501100011033 under the scope of the CURMIS4th project (Grant PID2020–113673RB-I00), the Consellería de Educación, Universidades e Formación Profesional (Xunta de Galicia) under the scope of the strategic funding of ED431C2018/55-GRC Competitive Reference Group, the “Centro singular de investigación de Galicia” (accreditation 2019–2022), and the European Union (European Regional Development Fund - ERDF)- Ref. ED431G2019/06. SING group thanks CITI (Centro de Investigación, Transferencia e Innovación) from the University of Vigo for hosting its IT infrastructure.
Funding
Pedro Celard is supported by a pre-doctoral fellowship from Xunta de Galicia (ED481A 2021/286). The funders had no role in study design, data collection and analysis, the decision to publish, or the preparation of the manuscript.
Declarations
Conflict of interest
Authors declare that there is not conflicts of interest.
Consent to participate
Authors have consented to the submission of this survey to the journal.
Consent for publication
Authors have consented to the publication of this survey to the journal.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
P. Celard, Email: pedro.celard.perez@uvigo.es
E. L. Iglesias, Email: eva@uvigo.es
J. M. Sorribes-Fdez, Email: sorribes@uvigo.es
R. Romero, Email: rrgonzalez@uvigo.es
A. Seara Vieira, Email: adrseara@uvigo.es.
L. Borrajo, Email: lborrajo@uvigo.es
References
- 1.Akazawa M, Hashimoto K. Artificial intelligence in gynecologic cancers: current status and future challenges - a systematic review. Artif Intell Med. 2021;120:102164. doi: 10.1016/j.artmed.2021.102164. [DOI] [PubMed] [Google Scholar]
- 2.de Siqueira VS, Borges MM, Furtado RG, Dourado CN, da Costa RM. Artificial intelligence applied to support medical decisions for the automatic analysis of echocardiogram images: a systematic review. Artif Intell Med. 2021;120:102165. doi: 10.1016/j.artmed.2021.102165. [DOI] [PubMed] [Google Scholar]
- 3.Fernando T, Gammulle H, Denman S, Sridharan S, Fookes C. Deep learning for medical anomaly detection - a survey. ACM Comput Surv. 2021;54:7. doi: 10.1145/3464423. [DOI] [Google Scholar]
- 4.Chen J, Li K, Zhang Z, Li K, Yu PS. A survey on applications of artificial intelligence in fighting against covid-19. ACM Comput Surv. 2021;54:8. doi: 10.1145/3465398. [DOI] [Google Scholar]
- 5.Sah M, Direkoglu C. A survey of deep learning methods for multiple sclerosis identification using brain mri images. Neural Comput Appl. 2022;34(10):7349–7373. doi: 10.1007/s00521-022-07099-3. [DOI] [Google Scholar]
- 6.Abdou MA. Literature review: efficient deep neural networks techniques for medical image analysis. Neural Comput Appl. 2022;34(8):5791–5812. doi: 10.1007/s00521-022-06960-9. [DOI] [Google Scholar]
- 7.Zhai J, Zhang S, Chen J, He Q (2018) Autoencoder and its various variants. In: 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), pp. 415–419. IEEE, Miyazaki, Japan. 10.1109/SMC.2018.00080
- 8.Kazeminia S, Baur C, Kuijper A, van Ginneken B, Navab N, Albarqouni S, Mukhopadhyay A. Gans for medical image analysis. Artif Intell Med. 2020;109:101938. doi: 10.1016/j.artmed.2020.101938. [DOI] [PubMed] [Google Scholar]
- 9.Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y. Generative adversarial nets. Adv Neural Inf Process Syst. 2014;27:2672–2680. [Google Scholar]
- 10.Schmidhuber J. Deep learning in neural networks: an overview. Neural Netw. 2015;61:85–117. doi: 10.1016/j.neunet.2014.09.003. [DOI] [PubMed] [Google Scholar]
- 11.Goodfellow I, Bengio Y, Courville A. Deep learning. Cambridge: MIT Press; 2016. [Google Scholar]
- 12.Clevert D-A, Unterthiner T, Hochreiter S (2016) Fast and accurate deep network learning by exponential linear units (elus). In: 4th International Conference on Learning Representations, ICLR 2016 - Conference Track Proceedings. ICLR, San Juan, Puerto Rico
- 13.Jadon S (2020) A survey of loss functions for semantic segmentation. In: 2020 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), pp. 1–7. IEEE, Región Metropolitana, Chile. 10.1109/cibcb48159.2020.9277638
- 14.Lin T, Goyal P, Girshick RB, He K, Dollár P (2017) Focal loss for dense object detection. In: 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, pp. 2999–3007. 10.1109/ICCV.2017.324
- 15.Sudre CH, Li W, Vercauteren T, Ourselin S, Jorge Cardoso M (2017) Generalised dice overlap as a deep learning loss function for highly unbalanced segmentations. In: Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support. Springer, Québec City, Canada, pp 240–248 [DOI] [PMC free article] [PubMed]
- 16.Salehi SSM, Erdogmus D, Gholipour A. Tversky loss function for image segmentation using 3d fully convolutional deep networks. In: Wang Q, Shi Y, Suk H-I, Suzuki K, editors. Machine Learning Medcine in Imaging. Cham: Springer; 2017. pp. 379–387. [Google Scholar]
- 17.Hayder Z, He X, Salzmann M (2017) Boundary-aware instance segmentation. In: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 587–595. 10.1109/CVPR.2017.70
- 18.Taghanaki SA, Zheng Y, Zhou SK, Georgescu B, Sharma PS, Xu D, Comaniciu D, Hamarneh G. Combo loss: handling input and output imbalance in multi-organ segmentation. Computerized Medi Imag Gr: Off J Computerized Med Imag Soc. 2019;75:24–33. doi: 10.1016/j.compmedimag.2019.04.005. [DOI] [PubMed] [Google Scholar]
- 19.Abraham N, Khan NM (2019) A novel focal tversky loss function with improved attention u-net for lesion segmentation. In: 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), pp. 683–687. IEEE
- 20.Berman M, Triki AR, Blaschko MB (2018) The lovász-softmax loss: A tractable surrogate for the optimization of the intersection-over-union measure in neural networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 4413–4421
- 21.Bollschweiler EH, Möonig SP, Hensler K, Baldus SE, Maruyama K, Hölscher AH. Artificial neural network for prediction of lymph node metastases in gastric cancer: a phase ii diagnostic study. Annal Surg Oncol. 2004;11:506–511. doi: 10.1245/ASO.2004.04.018. [DOI] [PubMed] [Google Scholar]
- 22.Dietzel M, Baltzer PAT, Dietzel A, Vag T, Gröschel T, Gajda M, Camara O, Kaiser WA. Application of artificial neural networks for the prediction of lymph node metastases to the ipsilateral axilla - initial experience in 194 patients using magnetic resonance mammography. Acta Radiologica. 2010;51:851–858. doi: 10.3109/02841851.2010.498444. [DOI] [PubMed] [Google Scholar]
- 23.Biglarian A, Bakhshi E, Gohari MR, Khodabakhshi R. Artificial neural network for prediction of distant metastasis in colorectal cancer. Asian Pacific J Cancer Prevent. 2012;13:927–930. doi: 10.7314/APJCP.2012.13.3.927. [DOI] [PubMed] [Google Scholar]
- 24.Gardner GG, Keating D, Williamson TH, Elliott AT. Automatic detection of diabetic retinopathy using an artificial neural network: a screening tool. Br J Ophthalmol. 1996;80:940–944. doi: 10.1136/bjo.80.11.940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sinthanayothin C, Boyce JF, Cook HL, Williamson TH. Automated localisation of the optic disc, fovea, and retinal blood vessels from digital colour fundus images. Br J Ophthalmol. 1999;83:902–910. doi: 10.1136/bjo.83.8.902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Özbay Y, Ceylan R, Karlik B. A fuzzy clustering neural network architecture for classification of ecg arrhythmias. Computers Biol Med. 2006;36:376–388. doi: 10.1016/j.compbiomed.2005.01.006. [DOI] [PubMed] [Google Scholar]
- 27.Osowski S, Linh TH. Ecg beat recognition using fuzzy hybrid neural network. IEEE Trans Biomed Eng. 2001;48:1265–1271. doi: 10.1109/10.959322. [DOI] [PubMed] [Google Scholar]
- 28.Ozbay Y, Karlik B (2001) A recognition of ecg arrhythmias using artificial neural networks. In: 2001 Conference Proceedings of the 23rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society, vol. 2, pp. 1680–1683. IEEE, Istanbul, Turkey. 10.1109/IEMBS.2001.1020538
- 29.Sutskever I, Martens J, Dahl G, Hinton G (2013) On the importance of initialization and momentum in deep learning. In: Dasgupta S, McAllester D (eds) Proceedings of the 30th International Conference on Machine Learning. Proceedings of Machine Learning Research, vol 28. PMLR, Atlanta, Georgia, USA, pp 1139–1147
- 30.Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization. J Mach Learn Res. 2011;12(61):2121–2159. [Google Scholar]
- 31.Tieleman T, Hinton G. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA: Neural Netw Mach Learn. 2012;4:26–31. [Google Scholar]
- 32.Kingma DP, Ba J (2015) Adam: A method for stochastic optimization. In: Bengio Y, LeCun Y (eds.), 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings
- 33.Zeiler MD (2012) ADADELTA: an adaptive learning rate method. CoRR http://arxiv.org/abs/1212.5701
- 34.Reddi SJ, Kale S, Kumar S (2018) On the convergence of adam and beyond. In: 6th International Conference on Learning Representations, ICLR 2018 - Conference Track Proceedings, Vancouver, Canada
- 35.Rahman T, Khandakar A, Qiblawey Y, Tahir A, Kiranyaz S, Abul Kashem SB, Islam MT, Al Maadeed S, Zughaier SM, Khan MS, Chowdhury MEH. Exploring the effect of image enhancement techniques on covid-19 detection using chest x-ray images. Computers Biol Med. 2021;132:104319. doi: 10.1016/j.compbiomed.2021.104319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521:436–444. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- 37.Clarke LP, Velthuizen RP, Phuphanich S, Schellenberg JD, Arrington JA, Silbiger M. Mri: stability of three supervised segmentation techniques. Magnetic Resonan Imag. 1993;11:95–106. doi: 10.1016/0730-725X(93)90417-C. [DOI] [PubMed] [Google Scholar]
- 38.Veltri RW, Chaudhari M, Miller MC, Poole EC, O’Dowd GJ, Partin AW. Comparison of logistic regression and neural net modeling for prediction of prostate cancer pathologic stage. Clin Chem. 2002;48:1828–1834. doi: 10.1093/clinchem/48.10.1828. [DOI] [PubMed] [Google Scholar]
- 39.Kan T, Shimada Y, Sato F, Ito T, Kondo K, Watanabe G, Maeda M, Yamasaki S, Meltzer SJ, Imamura M. Prediction of lymph node metastasis with use of artificial neural networks based on gene expression profiles in esophageal squamous cell carcinoma. Annal Surg Oncol. 2004;11:1070. doi: 10.1245/ASO.2004.03.007. [DOI] [PubMed] [Google Scholar]
- 40.Nigam VP, Graupe D. A neural-network-based detection of epilepsy. Neurol Res. 2004;26:55–60. doi: 10.1179/016164104773026534. [DOI] [PubMed] [Google Scholar]
- 41.Darby E, Nettimi T, Kodali S, Shih L (2005) Head and neck cancer metastasis prediction via artificial neural networks. In: 2005 IEEE Computational Systems Bioinformatics Conference - Workshops (CSBW’05), pp. 43–44. IEEE, Stanford, CA, USA. 10.1109/CSBW.2005.70
- 42.Szegedy C, Liu W, Jia Y, Sermanet P, Reed S, Anguelov D, Erhan D, Vanhoucke V, Rabinovich A (2015) Going deeper with convolutions. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 1–9. IEEE, Boston, MA, USA
- 43.Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Commun ACM. 2017;60:84–90. doi: 10.1145/3065386. [DOI] [Google Scholar]
- 44.Dumoulin V, Visin F (2018) A guide to convolution arithmetic for deep learning. 10.48550/arXiv.1603.07285
- 45.Shi W, Caballero J, Theis L, Huszar F, Aitken A, Ledig C, Wang Z (2016) Is the deconvolution layer the same as a convolutional layer?. 10.48550/arXiv.1609.07009
- 46.He K, Zhang X, Ren S, Sun J (2016) Deep residual learning for image recognition. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 770–778. IEEE, Las Vegas, NV, US
- 47.Szegedy C, Vanhoucke V, Ioffe S, Shlens J, Wojna Z (2016) Rethinking the inception architecture for computer vision. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2818–2826. IEEE, Las Vegas, NV, US
- 48.Odena A, Dumoulin V, Olah C (2016) Deconvolution and checkerboard artifacts. Distill. 10.23915/distill.00003
- 49.Nirthika R, Manivannan S, Ramanan A, Wang R. Pooling in convolutional neural networks for medical image analysis: a survey and an empirical study. Neural Comput Appl. 2022;34(7):5321–5347. doi: 10.1007/s00521-022-06953-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Fukushima K. Neocognitron: a self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol Cybern. 1980;36:193–202. doi: 10.1007/BF00344251. [DOI] [PubMed] [Google Scholar]
- 51.Lo S-CB, Lou S-LA, Lin J-S, Freedman MT, Chien MV, Mun SK. Artificial convolution neural network techniques and applications for lung nodule detection. IEEE Trans Med Imag. 1995;14:711–718. doi: 10.1109/42.476112. [DOI] [PubMed] [Google Scholar]
- 52.Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Adv Neural Inf Process Syst. 2012;25:1097–1105. [Google Scholar]
- 53.Litjens G, Kooi T, Bejnordi BE, Setio AAA, Ciompi F, Ghafoorian M, van der Laak JAWM, van Ginneken B, Sánchez CI. A survey on deep learning in medical image analysis. Med Image Anal. 2017;42:60–88. doi: 10.1016/j.media.2017.07.005. [DOI] [PubMed] [Google Scholar]
- 54.Simonyan K, Zisserman A (2015) Very deep convolutional networks for large-scale image recognition. In: 3rd International Conference on Learning Representations, ICLR 2015 - Conference Track Proceedings. ICLR, San Diego, California
- 55.Iandola FN, Han S, Moskewicz MW, Ashraf K, Dally WJ, Keutzer K (2016) SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and 0.5MB model size. 10.48550/arXiv.1602.07360
- 56.Huang G, Liu Z, van der Maaten L, Weinberger KQ (2017) Densely connected convolutional networks. In: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2261–2269. 10.1109/CVPR.2017.243
- 57.Szegedy C, Ioffe S, Vanhoucke V, Alemi A (2016) Inception-v4, inception-resnet and the impact of residual connections on learning. In: 31st AAAI Conference on Artificial Intelligence, AAAI 2017. AAAI press, San Francisco, California, pp 4278–4284
- 58.Howard A, Sandler M, Chen B, Wang W, Chen L-C, Tan M, Chu G, Vasudevan V, Zhu Y, Pang R, Adam H, Le Q (2019) Searching for mobilenetv3. In: 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, pp. 1314–1324. 10.1109/ICCV.2019.00140
- 59.Ronneberger O, Fischer P, Brox T (2015) U-net: Convolutional networks for biomedical image segmentation. In: Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015, pp. 234–241. Springer, Cham. 10.1007/978-3-319-24574-4_28
- 60.Bochkovskiy A, Wang C-Y, Liao H-YM (2020) YOLOv4: Optimal Speed and Accuracy of Object Detection. 10.48550/arXiv.2004.10934
- 61.Girshick R (2015) Fast r-cnn. In: 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, pp. 1440–1448. 10.1109/ICCV.2015.169
- 62.Tao A, Barker J, Sarathy S (2016) DetectNet: Deep Neural Network for Object Detection in DIGITS. https://developer.nvidia.com/blog/detectnet-deep-neural-network-object-detection-digits/. Accesed 2021-10-26
- 63.Liu W, Anguelov D, Erhan D, Szegedy C, Reed S, Fu C-Y, Berg AC. Ssd: Single shot multibox detector. Lect Notes Computer Sci. 2016;9905:21–37. doi: 10.1007/978-3-319-46448-0_2. [DOI] [Google Scholar]
- 64.Brinker TJ, et al. Deep learning outperformed 136 of 157 dermatologists in a head-to-head dermoscopic melanoma image classification task. Eur J Cancer. 2019;113:47–54. doi: 10.1016/j.ejca.2019.04.001. [DOI] [PubMed] [Google Scholar]
- 65.Kather JN, Krisam J, Charoentong P, Luedde T, Herpel E, Weis C-A, Gaiser T, Marx A, Valous NA, Ferber D, Jansen L, Reyes-Aldasoro CC, Zörnig I, Jäger D, Brenner H, Chang-Claude J, Hoffmeister M, Halama N. Predicting survival from colorectal cancer histology slides using deep learning: a retrospective multicenter study. PLOS Med. 2019;16:1–22. doi: 10.1371/journal.pmed.1002730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Pereira RM, Bertolini D, Teixeira LO, Silla CN, Costa YMG. Covid-19 identification in chest x-ray images on flat and hierarchical classification scenarios. Computer Methods Progr Biomed. 2020;194:105532. doi: 10.1016/j.cmpb.2020.105532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Yun J, Park J, Yu D, Yi J, Lee M, Park HJ, Lee J-G, Seo JB, Kim N. Improvement of fully automated airway segmentation on volumetric computed tomographic images using a 2.5 dimensional convolutional neural net. Med Image Anal. 2019;51:13–20. doi: 10.1016/j.media.2018.10.006. [DOI] [PubMed] [Google Scholar]
- 68.Geng Y, Ren Y, Hou R, Han S, Rubin GD, Lo JY. 2.5d cnn model for detecting lung disease using weak supervision. In: Hahn HK, Mori K, editors. Medical imaging 2019: computer-aided diagnosis. San Diego, California, US: SPIE; 2019. pp. 924–928. [Google Scholar]
- 69.Schlemper J, Oktay O, Schaap M, Heinrich M, Kainz B, Glocker B, Rueckert D. Attention gated networks: learning to leverage salient regions in medical images. Med Image Anal. 2019;53:197–207. doi: 10.1016/j.media.2019.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Nair T, Precup D, Arnold DL, Arbel T. Exploring uncertainty measures in deep networks for multiple sclerosis lesion detection and segmentation. Med Image Anal. 2020;59:101557. doi: 10.1016/j.media.2019.101557. [DOI] [PubMed] [Google Scholar]
- 71.Zhang J, Yu L, Chen D, Pan W, Shi C, Niu Y, Yao X, Xu X, Cheng Y. Dense gan and multi-layer attention based lesion segmentation method for covid-19 ct images. Biomed Signal Process Control. 2021;69:102901. doi: 10.1016/j.bspc.2021.102901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Hesamian MH, Jia W, He X, Kennedy P. Deep learning techniques for medical image segmentation: achievements and challenges. J Digital Imag. 2019;32:582–596. doi: 10.1007/s10278-019-00227-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Zhang Y, Wu J, Liu Y, Chen Y, Chen W, Wu EX, Li C, Tang X. A deep learning framework for pancreas segmentation with multi-atlas registration and 3d level-set. Med Image Anal. 2021;68:101884. doi: 10.1016/j.media.2020.101884. [DOI] [PubMed] [Google Scholar]
- 74.van den Oord A, Kalchbrenner N, Vinyals O, Espeholt L, Graves A, Kavukcuoglu K (2016) Conditional image generation with pixelcnn decoders. In: Advances in Neural Information Processing Systems, vol. 29. Curran Associates, Inc., Barcelona, Spain
- 75.Kingma DP, Dhariwal P (2018) Glow: Generative flow with invertible 1x1 convolutions. Advances in neural information processing systems 31. 10.48550/arXiv.1807.03039
- 76.Kingma D, Welling M (2014) Efficient gradient-based inference through transformations between bayes nets and neural nets. In: Proceedings of the 31st International Conference on Machine Learning, vol. 32, pp. 1782–1790. PMLR, Beijing, China
- 77.Rezende DJ, Mohamed S, Wierstra D (2014) Stochastic backpropagation and approximate inference in deep generative models. In: Proceedings of the 31st International Conference on Machine Learning. Proceedings of Machine Learning Research, vol. 32, pp. 1278–1286. PMLR, Bejing, China
- 78.Lateef F, Ruichek Y. Survey on semantic segmentation using deep learning techniques. Neurocomputing. 2019;338:321–348. doi: 10.1016/j.neucom.2019.02.003. [DOI] [Google Scholar]
- 79.Minaee S, Boykov Y, Porikli F, Plaza A, Kehtarnavaz N, Terzopoulos D. Image segmentation using deep learning: a survey. IEEE Trans Pattern Anal Mach Intell. 2022;44(7):3523–3542. doi: 10.1109/TPAMI.2021.3059968. [DOI] [PubMed] [Google Scholar]
- 80.Asgari Taghanaki S, Abhishek K, Cohen JP, Cohen-Adad J, Hamarneh G. Deep semantic segmentation of natural and medical images: a review. Artif Intell Rev. 2021;54(1):137–178. doi: 10.1007/s10462-020-09854-1. [DOI] [Google Scholar]
- 81.Ben-Cohen A, Diamant I, Klang E, Amitai M, Greenspan H (2016) Fully convolutional network for liver segmentation and lesions detection. In: Deep Learning and Data Labeling for Medical Applications. Springer, Cham, pp 77–85
- 82.Li D, Yang J, Kreis K, Torralba A, Fidler S (2021) Semantic segmentation with generative models: Semi-supervised learning and strong out-of-domain generalization. In: 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 8296–8307. 10.1109/CVPR46437.2021.00820
- 83.Karras T, Laine S, Aila T (2019) A style-based generator architecture for generative adversarial networks. In: 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, Canada, pp. 4396–4405. 10.1109/CVPR.2019.00453 [DOI] [PubMed]
- 84.Imtiaz R, Khan TM, Naqvi SS, Arsalan M, Nawaz SJ. Screening of glaucoma disease from retinal vessel images using semantic segmentation. Computers Electr Eng. 2021;91:107036. doi: 10.1016/j.compeleceng.2021.107036. [DOI] [Google Scholar]
- 85.Rehman MU, Cho S, Kim J, Chong KT. Brainseg-net: Brain tumor mr image segmentation via enhanced encoder-decoder network. Diagnostics. 2021;11:2. doi: 10.3390/diagnostics11020169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Zunair H, Ben Hamza A. Sharp u-net: Depthwise convolutional network for biomedical image segmentation. Computers Biol Med. 2021;136:104699. doi: 10.1016/j.compbiomed.2021.104699. [DOI] [PubMed] [Google Scholar]
- 87.Su R, Zhang D, Liu J, Cheng C. Msu-net: Multi-scale u-net for 2d medical image segmentation. Front Genet. 2021;12:58. doi: 10.3389/fgene.2021.639930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Isensee F, Jaeger PF, Kohl SAA, Petersen J, Maier-Hein KH. nnu-net: a self-configuring method for deep learning-based biomedical image segmentation. Nature Methods. 2021;18(2):203–211. doi: 10.1038/s41592-020-01008-z. [DOI] [PubMed] [Google Scholar]
- 89.Zuo Q, Chen S, Wang Z. R2au-net: Attention recurrent residual convolutional neural network for multimodal medical image segmentation. Security Commun Netw. 2021;2021:6625688. doi: 10.1155/2021/6625688. [DOI] [Google Scholar]
- 90.Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, Kaiser LU, Polosukhin I. Attention is all you need. In: Guyon I, Luxburg UV, Bengio S, Wallach H, Fergus R, Vishwanathan S, Garnett R, editors. Advances in neural information processing systems. Long Beach, California: Curran Associates Inc; 2017. [Google Scholar]
- 91.Mnih V, Heess N, Graves A. Recurrent models of visual attention. In: Ghahramani Z, Welling M, Cortes C, Lawrence N, Weinberger KQ, editors. Advances in neural information processing systems. Quebec, Canada: Curran Associates Inc; 2014. pp. 2204–2212. [Google Scholar]
- 92.Ouyang X, Huo J, Xia L, Shan F, Liu J, Mo Z, Yan F, Ding Z, Yang Q, Song B, Shi F, Yuan H, Wei Y, Cao X, Gao Y, Wu D, Wang Q, Shen D. Dual-sampling attention network for diagnosis of covid-19 from community acquired pneumonia. IEEE Trans Med Imag. 2020;39(8):2595–2605. doi: 10.1109/TMI.2020.2995508. [DOI] [PubMed] [Google Scholar]
- 93.Pang S, Du A, Orgun MA, Wang Y, Yu Z. Tumor attention networks: Better feature selection, better tumor segmentation. Neural Netw. 2021;140:203–222. doi: 10.1016/j.neunet.2021.03.006. [DOI] [PubMed] [Google Scholar]
- 94.Sinha A, Dolz J. Multi-scale self-guided attention for medical image segmentation. IEEE J Biomed Health Inf. 2021;25(1):121–130. doi: 10.1109/JBHI.2020.2986926. [DOI] [PubMed] [Google Scholar]
- 95.Salimans T, Goodfellow I, Zaremba W, Cheung V, Radford A, Chen X, Chen X. Improved techniques for training gans. In: Lee D, Sugiyama M, Luxburg U, Guyon I, Garnett R, editors. Advances in neural information processing systems. Barcelona, Spain: Curran Associates Inc; 2016. pp. 2234–2242. [Google Scholar]
- 96.Heusel M, Ramsauer H, Unterthiner T, Nessler B, Hochreiter S (2017) Gans trained by a two time-scale update rule converge to a local nash equilibrium. NIPS’17, pp. 6629–6640. Curran Associates Inc., Red Hook, NY, USA
- 97.Mirza M, Osindero S (2014) Conditional Generative Adversarial Nets. 10.48550/arXiv.1411.1784
- 98.Lee M, Seok J. Controllable generative adversarial network. IEEE. Access. 2019;7:28158–28169. doi: 10.1109/ACCESS.2019.2899108. [DOI] [Google Scholar]
- 99.Ghassemi N, Shoeibi A, Rouhani M. Deep neural network with generative adversarial networks pre-training for brain tumor classification based on mr images. Biomed Signal Process Control. 2020;57:101678. doi: 10.1016/j.bspc.2019.101678. [DOI] [Google Scholar]
- 100.Arjovsky M, Chintala S, Bottou L (2017) Wasserstein generative adversarial networks. In: Precup D, Teh YW (eds.) Proceedings of the 34th International Conference on Machine Learning. Proceedings of Machine Learning Research, vol. 70, pp. 214–223. PMLR, Sydney, Australia
- 101.Shen Y, Gu J, Tang X, Zhou B (2020) Interpreting the latent space of gans for semantic face editing. In: 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, Washington, pp. 9240–9249. 10.1109/CVPR42600.2020.00926
- 102.Radford A, Metz L, Chintala S (2016) Unsupervised representation learning with deep convolutional generative adversarial networks. In: 4th International Conference on Learning Representations, ICLR 2016 - Conference Track Proceedings, p. 149803. ICLR, San Juan, Puerto Rico
- 103.Saito M, Matsumoto E, Saito S (2017) Temporal generative adversarial nets with singular value clipping. In: 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, pp. 2849–2858. 10.1109/ICCV.2017.308
- 104.Karras T, Aila T, Laine S, Lehtinen J (2018) Progressive growing of gans for improved quality, stability, and variation. In: 6th International Conference on Learning Representations, ICLR 2018 - Conference Track Proceedings, p. 149806. ICLR, Vancouver, Canada
- 105.Isola P, Zhu J-Y, Zhou T, Efros AA (2017) Image-to-image translation with conditional adversarial networks. In: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, Hawaii, pp. 5967–5976. 10.1109/CVPR.2017.632
- 106.Zhu J-Y, Park T, Isola P, Efros AA (2017) Unpaired image-to-image translation using cycle-consistent adversarial networks. In: 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, pp. 2242–2251. 10.1109/ICCV.2017.244
- 107.Esser P, Rombach R, Ommer B (2021) Taming transformers for high-resolution image synthesis. In: 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 12868–12878. 10.1109/CVPR46437.2021.01268
- 108.Brock A, Donahue J, Simonyan K (2019) Large scale gan training for high fidelity natural image synthesis. In: 7th International Conference on Learning Representation 2019. ICLR, New Orleans
- 109.Nema S, Dudhane A, Murala S, Naidu S. Rescuenet: an unpaired gan for brain tumor segmentation. Biomed Signal Process Control. 2020;55:101641. doi: 10.1016/j.bspc.2019.101641. [DOI] [Google Scholar]
- 110.Klages P, Benslimane I, Riyahi S, Jiang J, Hunt M, Deasy JO, Veeraraghavan H, Tyagi N. Patch-based generative adversarial neural network models for head and neck mr-only planning. Med Phys. 2020;47:626–642. doi: 10.1002/mp.13927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Do W, Seo S, Han Y, Ye JC, Choi SH, Park S. Reconstruction of multicontrast mr images through deep learning. Med Phys. 2020;47:983–997. doi: 10.1002/mp.14006. [DOI] [PubMed] [Google Scholar]
- 112.Carreras-Delgado JL, Pérez-Dueñas V, Riola-Parada C, García-Cañamaque L. Pet/mri: A luxury or a necessity? Revista Española de Medicina Nuclear e Imagen Molecular (English Edition) 2016;35:313–320. doi: 10.1016/j.remnie.2016.07.002. [DOI] [PubMed] [Google Scholar]
- 113.Pozaruk A, Pawar K, Li S, Carey A, Cheng J, Sudarshan VP, Cholewa M, Grummet J, Chen Z, Egan G. Augmented deep learning model for improved quantitative accuracy of mr-based pet attenuation correction in psma pet-mri prostate imaging. Eur J Nucl Med Mol Imag. 2021;48:9–20. doi: 10.1007/s00259-020-04816-9. [DOI] [PubMed] [Google Scholar]
- 114.Zhou X, Qiu S, Joshi PS, Xue C, Killiany RJ, Mian AZ, Chin SP, Au R, Kolachalama VB. Enhancing magnetic resonance imaging-driven alzheimer’s disease classification performance using generative adversarial learning. Alzheimer’s Res Ther. 2021;13:60. doi: 10.1186/s13195-021-00797-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Lei B, Xia Z, Jiang F, Jiang X, Ge Z, Xu Y, Qin J, Chen S, Wang T, Wang S. Skin lesion segmentation via generative adversarial networks with dual discriminators. Med Image Anal. 2020;64:101716. doi: 10.1016/j.media.2020.101716. [DOI] [PubMed] [Google Scholar]
- 116.Qin Z, Liu Z, Zhu P, Xue Y. A gan-based image synthesis method for skin lesion classification. Computer Methods Progr Biomed. 2020;195:105568. doi: 10.1016/j.cmpb.2020.105568. [DOI] [PubMed] [Google Scholar]
- 117.Rasheed J, Hameed AA, Djeddi C, Jamil A, Al-Turjman F. A machine learning-based framework for diagnosis of covid-19 from chest x-ray images. Interdisciplinary Sci: Comput Life Sci. 2021;13:103–117. doi: 10.1007/s12539-020-00403-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Albahli S. A deep neural network to distinguish covid-19 from other chest diseases using x-ray images. Curr Med Imag Formerly Curr Med Imag Rev. 2021;17:109–119. doi: 10.2174/1573405616666200604163954. [DOI] [PubMed] [Google Scholar]
- 119.Li Z, Zhang J, Li B, Gu X, Luo X. Covid-19 diagnosis on ct scan images using a generative adversarial network and concatenated feature pyramid network with an attention mechanism. Med Phys. 2021;48:4334–4349. doi: 10.1002/mp.15044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Pang T, Wong JHD, Ng WL, Chan CS. Semi-supervised gan-based radiomics model for data augmentation in breast ultrasound mass classification. Computer Methods Progr Biomed. 2021;203:106018. doi: 10.1016/j.cmpb.2021.106018. [DOI] [PubMed] [Google Scholar]
- 121.Davidson TR, Falorsi L, Cao ND, Kipf T, Tomczak JM (2018) Hyperspherical variational auto-encoders. In: 34th Conference on Uncertainty in Artificial Intelligence 2018, vol. 2, pp. 856–865. Association For Uncertainty in Artificial Intelligence, Monterey, California
- 122.Kingma DP, Welling M. An introduction to variational autoencoders. Foundations Trends Mach Learn. 2019;12(4):307–392. doi: 10.1561/2200000056. [DOI] [Google Scholar]
- 123.Uzunova H, Schultz S, Handels H, Ehrhardt J. Unsupervised pathology detection in medical images using conditional variational autoencoders. Int J Computer Assist Radiol Surg. 2019;14:451–461. doi: 10.1007/s11548-018-1898-0. [DOI] [PubMed] [Google Scholar]
- 124.Sohn K, Lee H, Yan X. Learning structured output representation using deep conditional generative models. Adv Neural Inf Process Syst. 2015;28:3483–3491. [Google Scholar]
- 125.Akrami H, Joshi AA, Li J, Aydore S, Leahy RM (2020) Brain lesion detection using a robust variational autoencoder and transfer learning. In: 2020 IEEE 17th International Symposium on Biomedical Imaging (ISBI), pp. 786–790. IEEE, Iowa City, IA, USA. 10.1109/ISBI45749.2020.9098405 [DOI] [PMC free article] [PubMed]
- 126.Marimont SN, Tarroni G (2021) Anomaly detection through latent space restoration using vector quantized variational autoencoders. In: 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI), pp. 1764–1767. IEEE, Nice, Italy. 10.1109/ISBI48211.2021.9433778
- 127.Wei L, Owen D, Rosen B, Guo X, Cuneo K, Lawrence TS, Haken RT, Naqa IE. A deep survival interpretable radiomics model of hepatocellular carcinoma patients. Phys Medica. 2021;82:295–305. doi: 10.1016/j.ejmp.2021.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Kou W, Carlson DA, Baumann AJ, Donnan E, Luo Y, Pandolfino JE, Etemadi M. A deep-learning-based unsupervised model on esophageal manometry using variational autoencoder. Artif Intell Med. 2021;112:102006. doi: 10.1016/j.artmed.2020.102006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Larsen ABL, Sønderby SK, Larochelle H, Winther O (2016) Autoencoding beyond pixels using a learned similarity metric. In: Balcan MF, Weinberger KQ (eds.), Proceedings of The 33rd International Conference on Machine Learning. Proceedings of Machine Learning Research, vol. 48, pp. 1558–1566. PMLR, New York, New York, USA
- 130.Bao J, Chen D, Wen F, Li H, Hua G (2017) Cvae-gan: Fine-grained image generation through asymmetric training. In: Proceedings of the IEEE International Conference on Computer Vision (ICCV), pp. 2764–2773. IEEE, Venice, Italy. 10.1109/ICCV.2017.299
- 131.Nakao T, Hanaoka S, Nomura Y, Murata M, Takenaga T, Miki S, Watadani T, Yoshikawa T, Hayashi N, Abe O. Unsupervised deep anomaly detection in chest radiographs. J Digital Imag. 2021;34:418–427. doi: 10.1007/s10278-020-00413-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Nguyen A, Clune J, Bengio Y, Dosovitskiy A, Yosinski J (2017) Plug & play generative networks: Conditional iterative generation of images in latent space, Honolulu, Hawaii, pp. 3510–3520. 10.1109/CVPR.2017.374
- 133.Baur C, Denner S, Wiestler B, Navab N, Albarqouni S. Autoencoders for unsupervised anomaly segmentation in brain mr images: a comparative study. Med Image Anal. 2021;69:101952. doi: 10.1016/j.media.2020.101952. [DOI] [PubMed] [Google Scholar]
- 134.van den Oord A, Vinyals O, Kavukcuoglu K (2017) Neural discrete representation learning. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. NIPS’17, pp. 6309–6318. Curran Associates Inc., Red Hook, NY, USA
- 135.Donahue J, Krähenbühl P, Darrell T (2017) Adversarial Feature Learning. 10.48550/arXiv.1605.09782
- 136.Petersen RC, Aisen PS, Beckett LA, Donohue MC, Gamst AC, Harvey DJ, Jack CR, Jagust WJ, Shaw LM, Toga AW, Trojanowski JQ, Weiner MW. Alzheimer’s disease neuroimaging initiative (adni): clinical characterization. Neurology. 2010;74(3):201–209. doi: 10.1212/WNL.0b013e3181cb3e25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Ramzan F, Khan MUG, Rehmat A, Iqbal S, Saba T, Rehman A, Mehmood Z. A deep learning approach for automated diagnosis and multi-class classification of alzheimer’s disease stages using resting-state fmri and residual neural networks. J Med Syst. 2020;44:37. doi: 10.1007/s10916-019-1475-2. [DOI] [PubMed] [Google Scholar]
- 138.Puente-Castro A, Fernandez-Blanco E, Pazos A, Munteanu CR. Automatic assessment of alzheimer’s disease diagnosis based on deep learning techniques. Computers Biol Med. 2020;120:103764. doi: 10.1016/j.compbiomed.2020.103764. [DOI] [PubMed] [Google Scholar]
- 139.LaMontagne PJ, Benzinger TL, Morris JC, Keefe S, Hornbeck R, Xiong C, Grant E, Hassenstab J, Moulder K, Vlassenko AG, Raichle ME, Cruchaga C, Marcus D (2019) OASIS-3: Longitudinal Neuroimaging, Clinical, and Cognitive Dataset for Normal Aging and Alzheimer Disease. Cold Spring Harbor Laboratory Press. 10.1101/2019.12.13.19014902
- 140.Cheng J, Huang W, Cao S, Yang R, Yang W, Yun Z, Wang Z, Feng Q. Enhanced performance of brain tumor classification via tumor region augmentation and partition. PLOS ONE. 2015;10(10):1–13. doi: 10.1371/journal.pone.0140381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Deepak S, Ameer PM. Brain tumor classification using deep cnn features via transfer learning. Computers Biol Med. 2019;111:103345. doi: 10.1016/j.compbiomed.2019.103345. [DOI] [PubMed] [Google Scholar]
- 142.Menze BH, et al. The multimodal brain tumor image segmentation benchmark (brats) IEEE Trans Med Imag. 2015;34(10):1993–2024. doi: 10.1109/TMI.2014.2377694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143.Zimmerer D, Petersen J, Köhler G, Jäger P, Full P, Roß T, Adler T, Reinke A, Maier-Hein L, Maier-Hein K (2021) Medical out-of-distribution analysis challenge 2021. Zenodo. 10.5281/zenodo.4573948
- 144.Bándi P, et al. From detection of individual metastases to classification of lymph node status at the patient level: The camelyon17 challenge. IEEE Trans Med Imag. 2019;38(2):550–560. doi: 10.1109/TMI.2018.2867350. [DOI] [PubMed] [Google Scholar]
- 145.Heath M, Bowyer K, Kopans D, Moore R, Kegelmeyer P (2000) The digital database for screening mammography. Proceedings of the Fourth International Workshop on Digital Mammography 13. 10.1007/978-94-011-5318-8_75
- 146.Agarwal R, Díaz O, Yap MH, Lladó X, Martí R. Deep learning for mass detection in full field digital mammograms. Computers Biol Med. 2020;121:103774. doi: 10.1016/j.compbiomed.2020.103774. [DOI] [PubMed] [Google Scholar]
- 147.Moreira IC, Amaral I, Domingues I, Cardoso A, Cardoso MJ, Cardoso JS. Inbreast. Acad Radiol. 2012;19:236–248. doi: 10.1016/j.acra.2011.09.014. [DOI] [PubMed] [Google Scholar]
- 148.Buda M, Saha A, Walsh R, Ghate S, Li N, Swiecicki A, Lo JY, Yang J, Mazurowski MA (2020) Data from the breast cancer screening – digital breast tomosynthesis (bcs-dbt). 10.7937/e4wt-cd02
- 149.Nogay H, Akinci TC, Yilmaz M. Comparative experimental investigation and application of five classic pre-trained deep convolutional neural networks via transfer learning for diagnosis of breast cancer. Adv Sci Technol Res J. 2021;15:1–8. doi: 10.12913/22998624/137964. [DOI] [Google Scholar]
- 150.Kermany DS, et al. Identifying medical diagnoses and treatable diseases by image-based deep learning. Cell. 2018;172:1122–1131. doi: 10.1016/j.cell.2018.02.010. [DOI] [PubMed] [Google Scholar]
- 151.Khan AI, Shah JL, Bhat MM. Coronet: a deep neural network for detection and diagnosis of covid-19 from chest x-ray images. Computer Methods Progr Biomed. 2020;196:105581. doi: 10.1016/j.cmpb.2020.105581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152.Minaee S, Kafieh R, Sonka M, Yazdani S, Soufi GJ. Deep-covid: predicting covid-19 from chest x-ray images using deep transfer learning. Med Image Anal. 2020;65:101794. doi: 10.1016/j.media.2020.101794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Wang X, Peng Y, Lu L, Lu Z, Bagheri M, Summers RM (2017) Chestx-ray8: Hospital-scale chest x-ray database and benchmarks on weakly-supervised classification and localization of common thorax diseases. In: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 3462–3471. IEEE, Honolulu, HI, US. 10.1109/CVPR.2017.369
- 154.Cohen JP, Morrison P, Dao L (2020) COVID-19 image data collection. 10.48550/ARXIV.2003.11597
- 155.Armato SG, III, et al. The lung image database consortium (lidc) and image database resource initiative (idri): a completed reference database of lung nodules on ct scans. Med Phys. 2011;38(2):915–931. doi: 10.1118/1.3528204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 156.Saltz J, Saltz M, Prasanna P, Moffitt R, Hajagos J, Bremer E, Balsamo J, Kurc T (2021) Stony Brook University COVID-19 Positive Cases [Data set]. 10.7937/TCIA.BBAG-2923
- 157.Rotemberg V, Kurtansky N, Betz-Stablein B, Caffery L, Chousakos E, Codella N, Combalia M, Dusza S, Guitera P, Gutman D, Halpern A, Helba B, Kittler H, Kose K, Langer S, Lioprys K, Malvehy J, Musthaq S, Nanda J, Reiter O, Shih G, Stratigos A, Tschandl P, Weber J, Soyer HP. A patient-centric dataset of images and metadata for identifying melanomas using clinical context. Scientif Data. 2021;8:34. doi: 10.1038/s41597-021-00815-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158.Roth HR, Farag A, Turkbey EB, Lu L, Liu J, Summers RM (2016). Data From Pancreas-CT. 10.7937/K9/TCIA.2016.tNB1kqBU
- 159.Liu Z, Luo P, Wang X, Tang X (2015) Deep learning face attributes in the wild. In: 2015 IEEE International Conference on Computer Vision (ICCV), pp. 3730–3738. IEEE, Santiago, Chile. 10.1109/ICCV.2015.425
- 160.Krizhevsky A, Hinton G, et al (2009) Learning multiple layers of features from tiny images, 32–33
- 161.Cordts M, Omran M, Ramos S, Rehfeld T, Enzweiler M, Benenson R, Franke U, Roth S, Schiele B (2016) The cityscapes dataset for semantic urban scene understanding. In: Proc. of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 3213–3223. IEEE, Las Vegas, NV, USA
- 162.Lin T-Y, Maire M, Belongie S, Bourdev L, Girshick R, Hays J, Perona P, Ramanan D, Zitnick CL, Dollár P (2014) Microsoft coco: Common objects in context. In: Computer Vision - ECCV 2014. Springer, Cham, pp 740–755
- 163.Wah C, Branson S, Welinder P, Perona P, Belongie S (2011) The Caltech-UCSD Birds-200-2011 Dataset. Technical Report CNS-TR-2011-001, California Institute of Technology
- 164.Ebner NC, Riediger M, Lindenberger U. Faces–a database of facial expressions in young, middle-aged, and older women and men: development and validation. Behav Res Methods. 2010;42:351–362. doi: 10.3758/BRM.42.1.351. [DOI] [PubMed] [Google Scholar]
- 165.Huiskes MJ, Lew MS (2008) The mir flickr retrieval evaluation. In: MIR ’08: Proceedings of the 1st ACM International Conference on Multimedia Information Retrieval. MIR ’08, pp. 39–43. Association for Computing Machinery, New York, NY, USA. 10.1145/1460096.1460104
- 166.Deng J, Dong W, Socher R, Li L-J, Li K, Fei-Fei L (2009) Imagenet: A large-scale hierarchical image database. In: 2009 IEEE Conference on Computer Vision and Pattern Recognition. IEEE, Miami, FL, US, pp 248–255
- 167.Huang GB, Ramesh M, Berg T, Learned-Miller E (October 2007) Labeled faces in the wild: A database for studying face recognition in unconstrained environments. Technical Report 07-49, University of Massachusetts, Amherst
- 168.Yu F, Seff A, Zhang Y, Song S, Funkhouser T, Xiao J (2016) LSUN: Construction of a Large-scale Image Dataset using Deep Learning with Humans in the Loop. 10.48550/arXiv.1506.03365
- 169.LeCun Y, Cortes C (2010) MNIST handwritten digit database
- 170.Everingham M, Gool L, Williams CK, Winn J, Zisserman A. The pascal visual object classes (voc) challenge. USA: Kluwer Academic Publishers; 2010. [Google Scholar]
- 171.Apostolopoulos ID, Mpesiana TA. Covid-19: automatic detection from x-ray images utilizing transfer learning with convolutional neural networks. Phys Eng Sci Med. 2020;43:635–640. doi: 10.1007/s13246-020-00865-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Yap MH, Goyal M, Osman F, Martí R, Denton E, Juette A, Zwiggelaar R. Breast ultrasound region of interest detection and lesion localisation. Artif Intell Med. 2020;107:101880. doi: 10.1016/j.artmed.2020.101880. [DOI] [PubMed] [Google Scholar]
- 173.Papanastasopoulos Z, Samala RK, Chan H-P, Hadjiiski L, Paramagul C, Helvie MA, Neal CH. Explainable ai for medical imaging: deep-learning cnn ensemble for classification of estrogen receptor status from breast mri. In: Hahn HK, Mazurowski MA, editors. Medical imaging 2020: computer-aided diagnosis. Houston, Texas, US: SPIE; 2020. pp. 228–235. [Google Scholar]
- 174.Han K, Wang Y, Chen H, Chen X, Guo J, Liu Z, Tang Y, Xiao A, Xu C, Xu Y, Yang Z, Zhang Y, Tao D (2022) A survey on vision transformer. IEEE Transactions on Pattern Analysis and Machine Intelligence 1–1. 10.1109/TPAMI.2022.3152247 [DOI] [PubMed]
- 175.Wu H, Chen S, Chen G, Wang W, Lei B, Wen Z. Fat-net: feature adaptive transformers for automated skin lesion segmentation. Med Image Anal. 2022;76:102327. doi: 10.1016/j.media.2021.102327. [DOI] [PubMed] [Google Scholar]
- 176.Korkmaz Y, Dar SUH, Yurt M, Özbey M, Çukur T. Unsupervised mri reconstruction via zero-shot learned adversarial transformers. IEEE Trans Med Imag. 2022;41(7):1747–1763. doi: 10.1109/TMI.2022.3147426. [DOI] [PubMed] [Google Scholar]
- 177.Song Y, Ermon S. Generative modeling by estimating gradients of the data distribution. In: Wallach H, Larochelle H, Beygelzimer A, d’ Alché-Buc F, Fox E, Garnett R, editors. Advances in neural information processing systems. Vancouver, Canada: Curran Associates Inc; 2019. [Google Scholar]
- 178.Jalal A, Arvinte M, Daras G, Price E, Dimakis AG, Tamir J (2021) Robust compressed sensing mri with deep generative priors. In: Advances in Neural Information Processing Systems, vol. 34, pp. 14938–14954. Curran Associates, Inc., Virtual Conference
- 179.Chung H, Ye JC. Score-based diffusion models for accelerated mri. Med Image Anal. 2022;80:102479. doi: 10.1016/j.media.2022.102479. [DOI] [PubMed] [Google Scholar]
- 180.Wang L, Liu Y, Wu R, Liu Y, Yan R, Ren S, Gui Z. Image processing for low-dose ct via novel anisotropic fourth-order diffusion model. IEEE Access. 2022;10:50114–50124. doi: 10.1109/ACCESS.2022.3172975. [DOI] [Google Scholar]
- 181.Gomez T, Feyeux M, Boulant J, Normand N, David L, Paul-Gilloteaux P, Fréour T, Mouchère H. A time-lapse embryo dataset for morphokinetic parameter prediction. Data in Brief. 2022;42:108258. doi: 10.1016/j.dib.2022.108258. [DOI] [PMC free article] [PubMed] [Google Scholar]