Skip to main content
PMC home page
The Innovation logoLink to The Innovation
. 2022 Oct 18;3(6):100341. doi: 10.1016/j.xinn.2022.100341

Achieving metal-like malleability and ductility in Ag2Te1-xSx inorganic thermoelectric semiconductors with high mobility

Huiping Hu 1, Yuechu Wang 1, Chenguang Fu 1,∗, Xinbing Zhao 1, Tiejun Zhu 1,∗∗
PMCID: PMC9638828  PMID: 36353674

Abstract

Inorganic semiconductor Ag2Te1-xSx has been recently found to exhibit unexpected plastic deformation with compressive strain up to 30%. However, the origin of the abnormal plasticity and how to simultaneously achieve superb ductility and high mobility are still elusive. Here, we demonstrate that crystalline/amorphous Ag2Te1-xSx (x = 0.3, 0.4, and 0.5) composites can exhibit excellent compressive strain up to 70% if the monoclinic Ag2Te phase, which commonly exists in the matrix, is eliminated. Significantly, an ultra-high tensile elongation reaching 107.3% was found in Ag2Te0.7S0.3, which is the highest one yet reported in the system and even surpasses those achieved in some metals and high-entropy alloys. Moreover, high mobility of above 1000 cm2 V−1 s−1 at room temperature and good thermoelectric performance are simultaneously maintained. A modified Ashby plot with ductility factor versus carrier mobility is thereby proposed to highlight the potential of solid materials for applications in flexible/wearable electronics.

Keywords: thermoelectric materials, thermoelectric performance, silver chalcogenides, plastic deformability, carrier mobility

Graphical abstract

graphic file with name fx1.gif

Public summary

  • •

    Phase structure plays a crucial role in determining the mechanical properties of inorganic semiconductors Ag2Te1-xSx

  • •

    Metal-like malleability and ductility with a record-high tensile elongation of 107.3% are achieved in Ag2Te1-xSx

  • •

    The plastic Ag2Te1-xSx with decent thermoelectric performance could exhibit promising applications in the field of flexible/wearable electronics

Introduction

Over the last decade, the Internet of Things (IoT) and wearable electronics have experienced rapid growth owing to the demand for an intelligent society. Semiconductors with good thermoelectric (TE) properties have been found to be promising for powering IoT nodes1 and wearable electronics, such as wearable medical monitoring sensors and handheld devices.2 TE semiconductor devices,3,4 which have the advantages of being small in size, noise free, pollution free, and reliable long term, can realize the direct conversion of heat energy to electricity based on the Seebeck effect if a temperature difference exists. In human society, temperature difference exists everywhere, for instance, between the inside and outside of buildings or heat pipes or between the human body and the ambient environment, providing heat sources for powering IoT nodes and wearable electronics by TE devices.5 The TE performance can be evaluated by the materials’ dimensionless figure of merit zT, zT = S2σT/κ, where S, σ, T, and κ are the Seebeck coefficient, electrical conductivity, absolute temperature, and total thermal conductivity, respectively.6 TE materials are usually brittle and are typically designed to be a cuboid structure with two flat surfaces attaching to the heat source and sink for applications. However, in practical scenarios, the temperature difference can also exist in objects with curved surfaces, such as heat pipes and human body skin. These drive the ever-increasing demand for high-performance TE semiconductors with both superior deformability and high carrier mobility, facilitating mechanical processability and high carrier transport.

Conventional good TE materials are usually found in inorganic semiconductors, which are inherently brittle, limiting their applications for heat sources with curved surfaces.7,8 Organic conducting polymers have been used for fabricating flexible TE devices due to their mechanical flexibility and low thermal conductivity.9 Nevertheless, the power factor (PF), PF = S2σ, of organic materials is usually too low, only about 10−6–10−4 W m−1 K−2, and the carrier mobilities are between ∼1 and 10 cm2 V−1 s−1, leading to poor TE performance.10,11 By combining the flexibility of organic materials and the good TE performance of inorganic materials, hybrid flexible TE generators have been fabricated by depositing the thin film of inorganic semiconductors, such as Bi2Te312 and Ag2Se,13 atop flexible organic substrates, which could exhibit better TE performance than pure organic conducting polymers. However, the organic substrates induce additional thermal resistance and lower the actual temperature difference across TE materials, which is adverse to the power output of hybrid flexible TE devices.

Recently, an inorganic semiconductor, α-Ag2S, was found to exhibit an unexpectedly good malleability with a compressive strain above 50% at room temperature, which was thought to be owing to the continuous formation of Ag–S bonds during the slipping process.14,15 The intrinsically ductile Ag2S makes it a good candidate for application in full-inorganic flexible TE devices from the view of machinability and ductility. However, the zT value of pristine Ag2S is less than 0.02 at 300 K.16 A delicate balance between the high TE performance and good ductility of Ag2S-based materials was achieved in the alloying system, e.g., Ag2S0.5Se0.5 and Ag2S0.7Te0.3, and the zT at 300 K was improved to 0.26 and 0.3, respectively, without impairing the plasticity.17,18 The introduction of Se and/or Te into Ag2S not only optimizes the carrier concentration but also decreases the phase transition temperature from monoclinic phase to cubic superionic conductor phase with highly disordered Ag+ distribution.19,20 Ag2S0.7Te0.3 with a body-centered cubic structure shows both the lower Young’s modulus and nano hardness compared with monoclinic α-Ag2S.18 Density functional theory calculations indicate that the lower generalized stacking fault energy and the larger cleavage energy in cubic Ag2S0.7Te0.3 are responsible for its good ductility.18 These results suggest the cubic superionic conductor phase is the origin of good ductility in the S-rich Ag2Te1-xSx (x ≥ 0.7).

Unexpectedly, in the Te-rich Ag2Te1-xSx materials (x = 0.3 and 0.4), the amorphization was observed by He et al.21 Nevertheless, the studied amorphous Ag2Te0.6S0.4 sample can still exhibit large plastic deformability with a maximum compressive strain up to 25% and tensile strain to 12.5%. The formation and extending of shear bands, which are the primary process accounting for the ductility of bulk metallic glasses,21,22 were thought to be responsible for the exceptional plastic deformability. Distinct from the ductile Ag2Te0.6S0.4, the studied Ag2Te0.7S0.3 sample, which also exhibits amorphization, was brittle in the compressive test.21 More recently, Ag2Te0.5S0.5, which was thought to exhibit an amorphous/crystalline composite structure, was reported to display larger plastic deformation with a compressive strain of 30%.23 These results suggest that Ag2Te1-xSx compounds are promising candidates for power generation applications in scenarios with curved surfaces. However, the relationship between plastic deformability and the phase structure, particularly the amorphization, in Ag2Te1-xSx remains elusive. The revelation of this relationship is crucial for promoting both the understanding of the deformation mechanism and the practical applications of ductile inorganic semiconductors.

In this study, the amorphous Ag2Te1-xSx (x = 0.3, 0.4, and 0.5) samples were fabricated by directly quenching the molten ingots into cold water and subjecting them to different heat treatment processes to systematically investigate the correlation between phase structure and plastic deformability. Compared with the quenched ingots, the annealed Ag2Te1-xSx specimens with cubic-crystalline/amorphous structure exhibit the coexistence of metal-like malleability, superb ductility, high carrier mobility (∼1000 cm2 V −1 s−1 at 300 K), and decent TE performance. All the annealed Ag2Te1-xSx specimens exhibit large compressive strain up to 70% without fractures. Meanwhile, the maximum ductility was found in the Ag2Te0.7S0.3 sample with a maximum elongation of 107.3% under a relatively low ultimate stress of 46.7 MPa, the highest one yet found in the Ag2Te1-xSx system. These results pave the way for applying ductile and high-mobility Ag2Te1-xSx TE semiconductors in the field of flexible and wearable electronics.

Results and discussion

Coexistence of superb ductility and carrier mobility

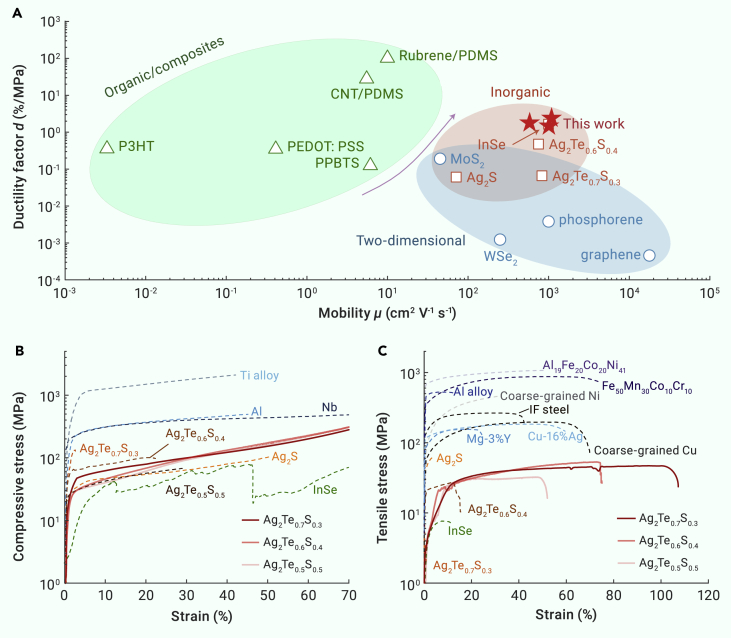
Both higher carrier mobility and mechanical ductility are prerequisites for the implementation of flexible/wearable devices. For TE devices, high carrier mobility can guarantee low power consumption. For flexible electronics, higher carrier mobility can enable a faster switching speed and higher operating frequencies of transistors. Meanwhile, ductility is required to optimize the mechanical behavior and facilitate the manufacture of the devices. Aimed at simultaneously evaluating these two parameters, a modified Ashby plot at ambient temperature is presented in Figure 1A. We define a ductility factor d = l/σu to quantitatively reflect the material’s ability to be stretched, where l is the total elongation at break (%) and σu is the ultimate tensile strength (MPa). Specifically, a large ductility factor d suggests that the materials can exhibit a large elongation at low tensile strength.

Figure 1.

Figure 1

Open in a new tab

Superb ductility in high-mobility inorganic semiconductor Ag2Te1-xSx (x = 0.3, 0.4, and 0.5)

(A) Ductility factor d versus carrier mobility μ for the annealed Ag2Te1-xSx specimens and those candidates that could be used in flexible electronics, including organic materials,24,25,26,27,28,29,30 two-dimensional nanomaterials,31,32,33,34,35,36,37,38 and plastic inorganic semiconductors.14,21,39,40 Note that the mobility for whole two-dimensional nanomaterials and partial organic films in (A) is field-effect mobility.

(B and C) Compressive (B) and tensile (C) tests at room temperature. Reported materials such as plastic inorganic semiconductors,14,21,23,39 metals, metallic alloys,41,42,43,44,45,46,47,48 IF steels,49 and high-entropy alloys50,51 are shown for comparison.

As shown in Figure 1A, organic semiconductors such as polydimethylsiloxane24,25 and poly(3,4-ethylenedioxythiophene) poly(styrene sulfonate),26,27 which have been widely used in fabricating flexible devices,52 show the highest ductility factor with the large elongation value at extremely low stress. However, the low carrier mobility of organic semiconductors limits their application to low-frequency flexible electronics.53,54,55,56 The emergence of two-dimensional (2D) nanomaterials, which are demonstrated to exhibit high device mobility (about 104 cm2 V−1 s−1 for graphene), promotes the flexible technology transformation from electronics for sensors and display to integrated flexible nanoelectronics.55,57 The low ductility factor for 2D nanomaterials, as shown in Figure 1A, is mainly due to their high modulus (for instance, 1000 GPa Young’s modulus for graphene57). Nevertheless, large-scale, reproducible synthesis of 2D nanomaterials has been still difficult to achieve so far.58 The values of the ductility factor for Ag2Te1-xSx specimens in this work are between organic semiconductors and 2D nanomaterials, sufficient to meet the required mechanical properties for flexible electronics. Besides, the carrier mobility of Ag2Te0.7S0.3 and Ag2Te0.6S0.4 around 1000 cm2 V−1 s−1 is comparable to traditional silicon material (1400 cm2 V−1 s−1 for electrons) and superior to organic semiconductors and ductile binary Ag2S, which shows significant advantages for applications in the fields of flexible electronics.

Figures 1B and 1C show the mechanical properties of the previously reported plastic inorganic semiconductors, metals, metallic alloys, steels, and high-entropy alloys. The metal-like malleability of cubic-crystalline/amorphous structure Ag2Te1-xSx is displayed in Figure 1B. The compressive strain reaches 70%, which is larger than that of plastic inorganic semiconductors14,21,23 and comparable to typical metals.41,42 Furthermore, the ductility for our crystalline/amorphous Ag2Te1-xSx is much higher than that of the previously reported monoclinic Ag2S, amorphous Ag2Te0.6S0.4, and van der Waals layered InSe, of which the elongation values are 4.2%,14 12.5%,21 and 12%39 respectively. Additionally, the tensile strain above 50% is also comparable to that for coarse-grained metals.43,44 High-entropy alloys display significantly improved mechanical properties compared with conventional engineering alloys, which overcome the strength–ductility trade-off and show not only high strength but also high tensile plasticity.59,60 As displayed in Figure 1C, the studied Ag2Te0.7S0.3 and Ag2Te0.6S0.4 samples show superior ductility to the state-of-the-art high-entropy alloys and exhibit a high uniform tensile elongation of about 100%. By further considering the relatively small tensile stress applied, the studied Ag2Te0.7S0.3 and Ag2Te0.6S0.4 samples exhibit excellent machinability for potential wearable/flexible applications on curved surfaces.

The detrimental role of monoclinic Ag2Te to plasticity

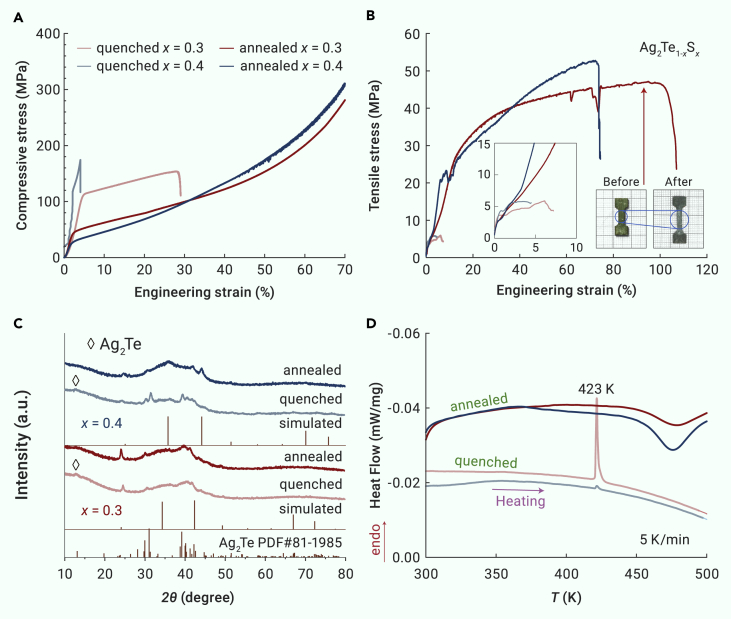
In the first set of our experiments, Ag2Te1-xSx (x = 0–0.5) ingots were synthesized by using a water-quench method to facilitate the formation of more amorphous phases. When x ≤ 0.2, the Ag2Te1-xSx samples crystallize in a monoclinic α-Ag2Te structure and exhibit brittle fracture in the compressive tests (Figure S1). The compressive and tensile properties of the quenched ingots (x ≥ 0.3) are displayed in Figures 2 and S2. Unexpectedly, only the Ag2Te0.7S0.3 sample is plastic, exhibiting a significant strain hardening process and around 27% compressive strain. Conversely, the compressive stress–strain curve of the Ag2Te0.6S0.4 sample displays linear elastic deformation behavior at the beginning of their stress–strain curves, and then the sample breaks at the maximum compressive strain of 4% without yielding (Figure 2A). This suggests a typical compressive failure of brittle materials, which is much different from the previous reports,21,23 in which the compressive strain for Ag2Te0.6S0.4 and Ag2Te0.5S0.5 samples could reach 20%. These differences make us aware that the various phase structures, relating to the different preparation methods, might have significant impacts on the plastic deformability of Ag2Te1-xSx materials and even result in a brittle–to–plastic variation. However, the factors that cause a considerable difference in the plastic deformability of Ag2Te1-xSx samples with the same nominal composition were previously not studied.

Figure 2.

Figure 2

Open in a new tab

Elimination of monoclinic Ag2Te phase in inorganic semiconductor Ag2Te1-xSx (x = 0.3 and 0.4)

(A and B) Stress–strain diagrams for quenched and annealed Ag2Te1-xSx specimens in the compressive test (A) and the tensile test (B). The inset in (B) shows the outer appearance of the tensile samples before and after the tensile test.

(C) Room temperature bulk XRD patterns of the quenched and annealed Ag2Te1-xSx samples. The simulated patterns by VESTA are displayed for comparison.

(D) DSC heating curves for quenched and annealed Ag2Te1-xSx samples with a heating rate of 5 K/min. The curve of the quenched x = 0.4 sample has been shifted down along the y axis to avoid overlapping with other measured curves

In the second set of our experiments, the quenched ingots were subjected to an annealing process at 723 K for 7 days. The X-ray diffraction (XRD) patterns of bulk Ag2Te1-xSx (x = 0.3, 0.4, and 0.5) obtained by quenching and annealing are displayed in Figures 2C and S2A. Firstly, it should be noted that the XRD patterns of samples with x = 0.3 and x = 0.4 in Figure 2C are different from those of Ag2Te0.7S0.3 and Ag2Te0.6S0.4 reported previously,21 which contain no sharp diffraction peak in the 2θ range of 30° to 50° and exhibit an amorphous phase-dominated structure. A small diffraction peak at 2θ = 12.5° is detected for all quenched samples, corresponding to the diffraction peaks of the monoclinic Ag2Te (space group P21/c). Furthermore, the whole differential scanning calorimetry (DSC) curves for the quenched and annealed Ag2Te1-xSx specimens during the heating and cooling process are displayed in Figure S3. The second heating cycle for quenched Ag2Te1-xSx and the first heating cycle for annealed Ag2Te1-xSx are displayed in Figures 2D and S2B for comparison. As can be seen, the DSC curves for quenched Ag2Te1-xSx indicate the phase transition of Ag2Te at 423 K from the monoclinic phase to the face-centered cubic phase,61 confirming the existence of monoclinic Ag2Te in the quenched samples. However, the electron probe microanalysis (EPMA) imaging and energy dispersive spectroscopy (EDS) mapping for the quenched Ag2Te0.6S0.4 sample (Figure S4) do not indicate the existence of monoclinic Ag2Te phases, probably owing to their crystallization in the nanoscale.

After annealing at 723 K for 7 days, the diffraction peak of Ag2Te at 2θ = 12.5° disappears in all annealed samples (Figures 2C and S2A). Meanwhile, no endothermic peak is observed in the DSC measurement for the annealed samples, further verifying the elimination of the Ag2Te phase during the annealing process. In addition, a slight dip, which is only observed in the first heating cycle of the thermal scan for all quenched and annealed Ag2Te1-xSx samples as displayed in Figure S3, might be due to the crystallization of the amorphous phase.

The sharp XRD peaks in the 2θ range of 20° to 55° are similar to those observed in cubic Ag2S0.7Te0.3.18 Thus, the body-centered cubic structure, similar to the middle-temperature phase of Ag2S with freely migrating Ag+,16 was adopted for the structure analysis. That is, Te and S atoms fully occupy the (0, 0, 0) site in which the atomic occupancy of S is 0.3, 0.4, and 0.5 for the x = 0.3, x = 0.4, and x = 0.5 samples, respectively, while Ag atoms are partially distributed over (0, 0.5, 0.5) and (0.25, 0, 0.5) sites. The simulated XRD peaks by VESTA62 software are displayed in Figures 2C and S2A, and the lattice parameters of x = 0.3, 0.4, and 0.5 are set to be 5.224, 5.020, and 5.013 Å for the simulation. The simulated XRD patterns are partly consistent with the experimental results, particularly for the annealed samples, confirming the partial formation of cubic structure in the studied Ag2Te1-xSx (x ≥ 0.3) samples. Moreover, the signature of partial amorphization of the Ag2Te1-xSx materials (x ≥ 0.3), that is, a broad hump appearing around 2θ = 30°–50°, was verified from the XRD pattern (Figure 2C), similar to previous reports.21,22,23,63 Moreover, the submicroscale vein-like dimple patterns with different depths are observed in the fracture surface of the brittle quenched x = 0.4 sample and the ductile annealed x = 0.4 sample (Figures 3A and 3B), showing a typical fracture morphology of BMGs, which indicates plastic flow on the microscale.64,65 Accordingly, we think that the main phase of the studied quenched and annealed Ag2Te1-xSx samples is a crystalline/amorphous composite and that the annealed ones exhibit the elimination of monoclinic Ag2Te. Additionally, Figures 3C–3F show that the EDS mappings performed on the polished surface of annealed Ag2Te0.6S0.4, indicating all elements, Ag, Te, and S, are distributed homogeneously.

Figure 3.

Figure 3

Open in a new tab

Microstructure of quenched and annealed Ag2Te0.6S0.4 samples

(A and B) SEM image of the fracture surface of the quenched Ag2Te0.6S0.4 (A) and the annealed Ag2Te0.6S0.4 (B).

(C) SEM images of the polished surface of the annealed Ag2Te0.6S0.4. (D–F) Ag (D), Te (E), and S (F) elemental distribution in (C).

As shown in Figure 2A, all annealed Ag2Te1-xSx (x = 0.3 and 0.4) specimens show mechanical characteristics of typical ductile materials in the compressive test. The large-strain deformation under compressive loading reflects the excellent plastic deformability of Ag2Te1-xSx materials. To comprehensively evaluate the mechanical properties of plastic materials, here tensile tests were also performed to determine the ductility.66,67 Tensile stress–strain curves of the quenched and annealed Ag2Te1-xSx are shown in Figures 2B and S2D, where the tensile plasticity (ductility) has been enhanced in annealed specimens compared with quenched Ag2Te1-xSx. All the annealed specimens exhibit large tensile strain above 50% with significant work hardening, and serrations are found in stress–strain curves for the annealed Ag2Te0.7S0.3 and Ag2Te0.6S0.4, resulting in larger tensile strain. Significantly, the annealed Ag2Te0.7S0.3 exhibits an extremely good ductility with total elongation of 107.3% under a relatively low ultimate stress of 46.7 MPa (Figure 2B), and the inset presents dog-bone-shaped tensile samples before and after the tensile test, indicating large tensile deformation in the deformation region. The tensile strain can reach 75.1% for annealed Ag2Te0.6S0.4 in Figure 2B and decreases to ∼51.8% for annealed Ag2Te0.5S0.5 in Figure S2D.

To examine the reproducibility of the plastic deformability in the Ag2Te1-xSx system, three cuboids and two dog-bone-shaped specimens were cut from various regions of the ingot for both quenched and annealed samples, and the stress–strain curves for compressive and tensile tests are shown in Figure S5. For quenched Ag2Te0.7S0.3, the compressive strain values range from 28.1% to 70%. Both brittle fracture and plastic deformation are observed in Ag2Te0.6S0.4 samples, while all the quenched Ag2Te0.5S0.5 cuboids exhibit brittle fracture. The inhomogeneity and uncontrollability of plastic deformability can be ascribed to the inhomogeneous distribution of the monoclinic Ag2Te phase in quenched Ag2Te1-xSx specimens. In contrast, when the quenched Ag2Te1-xSx is subjected to an annealing process at 723 K to eliminate the Ag2Te phase as discussed above, an enhanced plastic deformation behavior is observed in annealed Ag2Te1-xSx specimens, and, more importantly, the reproducibility of ductility for different pieces is pretty good. Distinctly, all annealed Ag2Te1-xSx specimens show mechanical characteristics of typical ductile materials in both the compressive and tensile tests. A large tensile strain above 50% is observed in all annealed Ag2Te1-xSx (x = 0.3, 0.4, and 0.5) specimens, which is larger than that in the previous reports (a tensile strain of around 12.5% in Ag2Te0.6S0.421), suggesting the importance of the elimination of monoclinic Ag2Te to obtain superb ductility.

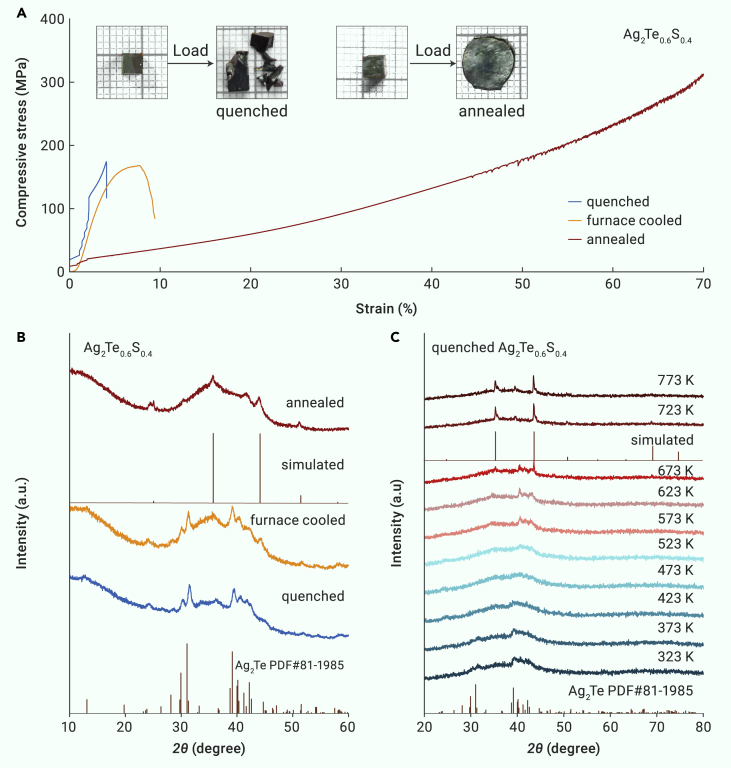
As discussed above, the plastic deformability of Ag2Te1-xSx materials is significantly affected by the heat treatment process. To further explore the effect of the heat treatment on the mechanical properties, Ag2Te0.6S0.4 samples were melted at 1273 K and then followed by different heat treatments to obtain the final ingots: water quenching, furnace cooling, and annealing (annealing at 723 K within 7 days). Figure 4A displays the compressive property for Ag2Te0.6S0.4 ingots with different heat treatments. The quenched and furnace-cooled Ag2Te0.6S0.4 samples, of which the XRD patterns in Figure 4B suggest the existence of the monoclinic Ag2Te phase, exhibit relatively weak deformability with a compressive strain smaller than 10% (Figure 4A). In contrast, the compressive strain–stress curves for annealed Ag2Te0.6S0.4 indicates a superior plastic deformation with a compressive strain up to 70%. The quenched and annealed specimens before and after compressive loading are shown in the inset of Figure 4A, and the quenched cuboid broke directly at the maximum load while the annealed cuboid can be eventually pressed into a plate without fracture. Moreover, the variable temperature XRD measurement for the quenched Ag2Te0.6S0.4 is shown in Figure 4C. Three XRD reflections, appearing around 2θ of 40°–45°, can be indexed to the monoclinic Ag2Te phase in a temperature range from 323 to 673 K. Above 723 K, the monoclinic structure disappears while the cubic structure appears. This is also the reason why the annealed temperature of the quenched sample was determined to be 723 K to eliminate the monoclinic Ag2Te phase. To conclude, the existence of the monoclinic Ag2Te phase is responsible for the weak deformability in Ag2Te1-xSx materials, and the heat treatment of annealing at 723 K is crucial to achieving good plastic deformability, which promotes the phase transformation into the cubic phase and eliminates the brittle Ag2Te phase simultaneously. Consequently, excellent plastic deformability can be achieved in Ag2Te1-xSx samples with the coexistence of cubic-crystalline and amorphous phases.

Figure 4.

Figure 4

Open in a new tab

Enhancement of the plastic deformability in Ag2Te0.6S0.4

(A and B) Compressive stress-strain curves (A) and room temperature bulk XRD patterns (B) for Ag2Te0.6S0.4 obtained by different heat treatment processes. The inset in (A) shows quenched and annealed cuboids before and after the compressive test.

(C) Powder XRD patterns of the quenched Ag2Te0.6S0.4 at different temperatures.

TE properties

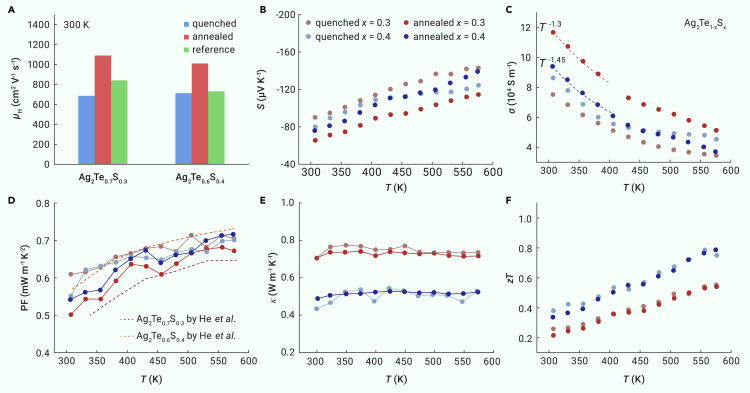
The Hall carrier mobility μH of quenched and annealed Ag2Te1-xSx (x = 0.3 and 0.4) is shown in Figure 5A. The μH for annealed Ag2Te0.7S0.3 and Ag2Te0.6S0.4 reaches above 1000 cm2 V−1 s−1 at ambient temperature, which is about 40% higher than the quenched samples as well as the previously reported ones.21 The Seebeck coefficient S and the electrical conductivity σ for quenched and annealed Ag2Te1-xSx (x = 0.3, 0.4, and 0.5) under a temperature range of 300 to 575 K are shown in Figures 5B, 5C, S6A, and S6B. All specimens display a typical conducting behavior of a degenerate semiconductor without the occurrence of intrinsic excitation. The σ follows a T−1.3∼T−1.5 dependency, implying that the acoustic phonon scattering dominates the charge transport. Notably, good electrical performance can be maintained in annealed specimens for Ag2Te0.6S0.4 and Ag2Te0.5S0.5 while enhancing the material’s ductility. As shown in Figure 5D, the PF values at 300 K are slightly reduced from 0.61 × 10−3 W m−1 K−2 for quenched Ag2Te0.7S0.3 to 0.50 × 10−3 W m−1 K−2 for annealed Ag2Te0.7S0.3 and have no change in the quenched and annealed samples for Ag2Te0.6S0.4, which are also comparable to the data reported.21 The electrical transport properties of Ag2Te1-xSx were analyzed by a single parabolic band (SPB) model (Note S1). In Ag2Te1-xSx materials, the density of states’ effective mass m∗ at 300 K, estimated by the theoretical Pisarenko curves presented in Figure S6C, gradually increases with the increasing S content, from m∗ = 0.12 me (where me is the free electron mass) for Ag2Te0.7S0.3 to m∗ = 0.20 me for Ag2Te0.3S0.7,18 implying that alloying S at Te sites might alert the shape of the conduction band minimum and yield to a larger m∗. This could explain why the annealed Ag2Te0.5S0.5 sample has a relatively low carrier mobility μH of 580 cm2 V−1 s−1 compared with other ductile annealed specimens. Based on the SPB model, the calculated PF as a function of carrier concentration nH is presented in Figure S6D, indicating that the electrical performance of Ag2Te1-xSx can be further enhanced by decreasing nH.

Figure 5.

Figure 5

Open in a new tab

Temperature dependences of thermoelectric properties for Ag2Te1-xSx (x = 0.3 and 0.4)

(A) Room temperature carrier mobility μH for quenched and annealed Ag2Te1-xSx specimens, and the reference data are presented for comparison.21

(B–F) Temperature dependence of (B) Seebeck coefficient S, (C) electrical conductivity σ, (D) power factor, (E) total thermal conductivity κ, and (F) zT values for quenched and annealed Ag2Te1-xSx (x = 0.3 and 0.4) specimens.

Figures 5E and S6E show the temperature dependence of the total thermal conductivity κ for all the Ag2Te1-xSx (x = 0.3, 0.4, and 0.5) samples. The κ values are in the range of 0.4 to 0.8 W m−1 K−1 and are independent of the temperature, which shows a typical thermal transport property of superionic conductors and amorphous solids as previously reported.68,69,70 The elimination of the Ag2Te phase in annealed specimens does not significantly affect the κ compared with the quenched one. The lattice thermal conductivity κL can be calculated by κ = κL + κe, in which the electronic thermal conductivity κe is evaluated via the Wiedemann–Franz law κe = LσT, where the Lorenz number L can be estimated according to the measured Seebeck coefficient using the SPB model. But it turns out that the values of κL for most of the quenched and annealed Ag2Te1-xSx samples are even negative near room temperature. This was also reported in other typical superionic conductors, such as Cu2Te-based71 and Ag2Te-based72 materials. The unphysical determination of κL can be ascribed to the overestimation of κe using the Wiedemann–Franz law in the superionic conductor phase since the mobile cations may also contribute to the electrical conductivity. The accurate determination of κL in Ag2Te1-xSx materials with migrating Ag+ needs further investigation in future studies.

The dimensionless figure of merit zT of all quenched and annealed Ag2Te1-xSx (x = 0.3, 0.4, and 0.5) is presented in Figures 5F and S6F. Finally, the annealed Ag2Te0.6S0.4 exhibits the highest zT in the range of 300 to 573 K, and a zT of about 0.3 at 300 K and a maximum zT of ∼0.8 at 573 K were obtained. It is worth noting that the temperature-dependent zT does not differ significantly for the quenched and annealed Ag2Te1-xSx samples. This value is comparable to other ductile TE materials at room temperature, in which zT values of 0.26 for Ag2S0.5Se0.5,17 0.20 for Ag2Te0.6S0.421 and 0.30 for Ag2S0.7Te0.3 were achieved.18 At 573 K, this value is also comparable with that of the brittle n-type commercial Bi2Te2.7Se0.3 TE materials,73 suggesting the potential of Ag2Te1-xSx for TE applications. In addition, the room temperature electrical properties of the annealed Ag2Te0.6S0.4 sample remain unchanged (Figure S7), while the κL increases after the compressive deformation. This anomalous trend suggests that the plastic deformation mechanism of Ag2Te1-xSx materials is independent of the movement of dislocations, as reported in plastic α-Ag2S.74

Conclusions

We have systematically investigated the processing–microstructure–property relationship of Ag2Te1-xSx plastic inorganic semiconductors. It was found that the precipitation of the monoclinic Ag2Te phase is the major cause of the brittleness in the Ag2Te1-xSx materials. Through long-term annealing at an appropriate temperature to eliminate the monoclinic Ag2Te phase, a large compressive strain of 70% and an excellent tensile elongation of 107.3% at room temperature are achieved in the cubic-crystalline/amorphous Ag2Te1-xSx composites. Meanwhile, a high carrier mobility of 1000 cm2 V−1 s−1 is also achieved at room temperature for the annealed Ag2Te1-xSx (x = 0.3 and 0.4) samples, which is 40% higher than that of the quenched ones. Moreover, the TE performance of Ag2Te1-xSx is not impaired by the elimination of the monoclinic Ag2Te phase. Consequently, a room temperature zT of 0.3 and a maximum zT of 0.8 at 573 K are achieved in annealed Ag2Te0.6S0.4. This study demonstrates that high-mobility Ag2Te1-xSx TE semiconductors with cubic-crystalline/amorphous structures can exhibit superb plasticity and thus have great potential in the field of flexible/wearable electronics.

Material and methods

See the supplemental information for details.

Acknowledgments

The authors acknowledge fruitful discussions with Prof. Yanhui Liu from the Institute of Physics, CAS. This work was supported by the National Science Fund for Distinguished Young Scholars (no. 51725102), the National Natural Science Foundation of China (nos. 92163203 and 52101275), the Key Research and Development Program of Zhejiang Province (2022C01131 and 2021C01026), and Zhejiang Provincial Natural Science Foundation of China (no. LD22E020005).

Author contributions

H.H., C.F., and T.Z. designed the project. H.H. prepared the samples, characterized structures, and conducted the physical and mechanical properties measurements. Y.W. performed the XRD characterization and provided discussions. H.H. and C.F. analyzed the data and wrote the original manuscript. T.Z. proposed valuable advice for revising the manuscript. T.Z. and X.Z. supervised the research work. All the authors reviewed and edited the manuscript.

Declaration of interests

The authors declare no competing interests.

Published Online: October 18, 2022

Footnotes

Supplemental information can be found online at https://doi.org/10.1016/j.xinn.2022.100341.

Contributor Information

Chenguang Fu, Email: chenguang_fu@zju.edu.cn.

Tiejun Zhu, Email: zhutj@zju.edu.cn.

Lead contact website

C. Fu.: https://person.zju.edu.cn/chenguang_fu

T. Zhu.: https://person.zju.edu.cn/msezhutj

Supplemental information

Document S1. Supplemental materials and methods, Figures S1–S7, and Note S1
mmc1.pdf (1.5MB, pdf)
Document S2. Article plus supplemental information
mmc2.pdf (3.8MB, pdf)

References

  • 1.Haras M., Skotnicki T. Thermoelectricity for IoT – a review. Nano Energy. 2018;54:461–476. [Google Scholar]
  • 2.Patel S., Park H., Bonato P., et al. A review of wearable sensors and systems with application in rehabilitation. J. NeuroEng. Rehabil. 2012;9:21. doi: 10.1186/1743-0003-9-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Shi X.L., Zou J., Chen Z.G. Advanced thermoelectric design: from materials and structures to devices. Chem. Rev. 2020;120:7399–7515. doi: 10.1021/acs.chemrev.0c00026. [DOI] [PubMed] [Google Scholar]
  • 4.Sun P., Kumar K.R., Lyu M., et al. Generic Seebeck effect from spin entropy. Innovation. 2021;2:100101. doi: 10.1016/j.xinn.2021.100101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Nozariasbmarz A., Collins H., Dsouza K., et al. Review of wearable thermoelectric energy harvesting: from body temperature to electronic systems. Appl. Energy. 2020;258:114069. [Google Scholar]
  • 6.Zhu T., Liu Y., Fu C., et al. Compromise and synergy in high-efficiency thermoelectric materials. Adv. Mater. 2017;29:1605884. doi: 10.1002/adma.201605884. [DOI] [PubMed] [Google Scholar]
  • 7.Li G., An Q., Duan B., et al. Fracture toughness of thermoelectric materials. Mater. Sci. Eng. R Rep. 2021;144:100607. [Google Scholar]
  • 8.Fan Z., Zhang Y., Pan L., et al. Recent developments in flexible thermoelectrics: from materials to devices. Renew. Sustain. Energy Rev. 2021;137:110448. [Google Scholar]
  • 9.Bahk J.H., Fang H., Yazawa K., et al. Flexible thermoelectric materials and device optimization for wearable energy harvesting. J. Mater. Chem. C. 2015;3:10362–10374. [Google Scholar]
  • 10.Zhang Q., Sun Y., Xu W., et al. Organic thermoelectric materials: emerging green energy materials Converting heat to electricity directly and efficiently. Adv. Mater. 2014;26:6829–6851. doi: 10.1002/adma.201305371. [DOI] [PubMed] [Google Scholar]
  • 11.Russ B., Glaudell A., Urban J.J., et al. Organic thermoelectric materials for energy harvesting and temperature control. Nat. Rev. Mater. 2016;1:16050. [Google Scholar]
  • 12.Kim S.J., We J.H., Cho B.J. A wearable thermoelectric generator fabricated on a glass fabric. Energy Environ. Sci. 2014;7:1959–1965. [Google Scholar]
  • 13.Ding Y., Qiu Y., Cai K., et al. High performance n-type Ag2Se film on nylon membrane for flexible thermoelectric power generator. Nat. Commun. 2019;10:841. doi: 10.1038/s41467-019-08835-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Shi X., Chen H., Hao F., et al. Room-temperature ductile inorganic semiconductor. Nat. Mater. 2018;17:421–426. doi: 10.1038/s41563-018-0047-z. [DOI] [PubMed] [Google Scholar]
  • 15.Chen H., Wei T., Zhao K., et al. Room-temperature plastic inorganic semiconductors for flexible and deformable electronics. InfoMat. 2021;3:22–35. [Google Scholar]
  • 16.Wang T., Chen H.Y., Qiu P.F., et al. Thermoelectric properties of Ag2S superionic conductor with intrinsically low lattice thermal conductivity. Acta Phys. Sin. 2019;68:090201. [Google Scholar]
  • 17.Liang J., Wang T., Qiu P., et al. Flexible thermoelectrics: from silver chalcogenides to full-inorganic devices. Energy Environ. Sci. 2019;12:2983–2990. [Google Scholar]
  • 18.Yang S., Gao Z., Qiu P., et al. Ductile Ag20S7Te3 with excellent shape-Conformability and high thermoelectric performance. Adv. Mater. 2021;33:2007681. doi: 10.1002/adma.202007681. [DOI] [PubMed] [Google Scholar]
  • 19.Blanton T., Misture S., Dontula N., et al. In situ high-temperature X-ray diffraction characterization of silver sulfide, Ag2S. Powder Diffr. 2011;26:114–118. [Google Scholar]
  • 20.Peng L., Yang S., Wei T.-R., et al. Phase-modulated mechanical and thermoelectric properties of Ag2S1-xTex ductile semiconductors. Journal of Materiomics. 2021;8:656–661. [Google Scholar]
  • 21.He S., Li Y., Liu L., et al. Semiconductor glass with superior flexibility and high room temperature thermoelectric performance. Sci. Adv. 2020;6:eaaz8423. doi: 10.1126/sciadv.aaz8423. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Liu Y.H., Wang G., Wang R.J., et al. Super plastic bulk metallic glasses at room temperature. Science. 2007;315:1385–1388. doi: 10.1126/science.1136726. [DOI] [PubMed] [Google Scholar]
  • 23.Liang X., Chen C. Ductile inorganic amorphous/crystalline composite Ag4TeS with phonon-glass electron-crystal transport behavior and excellent stability of high thermoelectric performance on plastic deformation. Acta Mater. 2021;218:117231. [Google Scholar]
  • 24.Danial N.S., Ramli M.M., Halin D.S.C., et al. Conference on Green Construction and Engineering Education. GCEE); 2017. Incorporation of Polydimethylsiloxane with reduced graphene oxide and zinc oxide for tensile and electrical properties. [Google Scholar]
  • 25.Micolich A.P., Bell L.L., Hamilton A.R. An improved process for fabricating high-mobility organic molecular crystal field-effect transistors. J. Appl. Phys. 2007;102:084511. [Google Scholar]
  • 26.Lang U., Naujoks N., Dual J. Mechanical characterization of PEDOT:PSS thin films. Synth. Met. 2009;159:473–479. [Google Scholar]
  • 27.Liu C., Lu B., Yan J., et al. Highly conducting free-standing poly(3, 4-ethylenedioxythiophene)/poly(styrenesulfonate) films with improved thermoelectric performances. Synth. Met. 2010;160:2481–2485. [Google Scholar]
  • 28.Kim H.J., Lee M.Y., Kim J.S., et al. Solution-assembled blends of regioregularity-Controlled Polythiophenes for coexistence of mechanical resilience and electronic performance. ACS Appl. Mater. Interfaces. 2017;9:14120–14128. doi: 10.1021/acsami.6b16703. [DOI] [PubMed] [Google Scholar]
  • 29.Kang Y.H., Bae E.J., Lee M.H., et al. Highly flexible and durable thermoelectric power generator using CNT/PDMS foam by rapid solvent evaporation. Small. 2022;18:2106108. doi: 10.1002/smll.202106108. [DOI] [PubMed] [Google Scholar]
  • 30.Zhang T., Li K., Li C., et al. Mechanically durable and flexible thermoelectric films from PEDOT:PSS/PVA/Bi0.5Sb1.5Te3 nanocomposites. Adv. Electron. Mater. 2017;3:1600554. [Google Scholar]
  • 31.Lee G.H., Yu Y.J., Cui X., et al. Flexible and transparent MoS2 field-effect transistors on hexagonal boron nitride-graphene heterostructures. ACS Nano. 2013;7:7931–7936. doi: 10.1021/nn402954e. [DOI] [PubMed] [Google Scholar]
  • 32.Li P., Jiang C., Xu S., et al. In situ nanomechanical characterization of multi-layer MoS2 membranes: from intraplanar to inter-planar fracture. Nanoscale. 2017;9:9119–9128. doi: 10.1039/c7nr02171b. [DOI] [PubMed] [Google Scholar]
  • 33.Fang H., Chuang S., Chang T.C., et al. High-performance single layered WSe2p-FETs with Chemically doped Contacts. Nano Lett. 2012;12:3788–3792. doi: 10.1021/nl301702r. [DOI] [PubMed] [Google Scholar]
  • 34.Li J., Medhekar N.V., Shenoy V.B. Bonding charge density and ultimate strength of monolayer transition metal Dichalcogenides. J. Phys. Chem. C. 2013;117:15842–15848. [Google Scholar]
  • 35.Li L., Yu Y., Ye G.J., et al. Black phosphorus field-effect transistors. Nat. Nanotechnol. 2014;9:372–377. doi: 10.1038/nnano.2014.35. [DOI] [PubMed] [Google Scholar]
  • 36.Wei Q., Peng X. Superior mechanical flexibility of phosphorene and few-layer black phosphorus. Appl. Phys. Lett. 2014;104:251915. [Google Scholar]
  • 37.Tao L., Lee J., Li H., et al. Inductively heated synthesized graphene with record transistor mobility on oxidized silicon substrates at room temperature. Appl. Phys. Lett. 2013;103:183115. [Google Scholar]
  • 38.Yu M.F., Lourie O., Dyer M.J., et al. Strength and breaking mechanism of multiwalled carbon nanotubes under tensile load. Science. 2000;287:637–640. doi: 10.1126/science.287.5453.637. [DOI] [PubMed] [Google Scholar]
  • 39.Wei T.R., Jin M., Wang Y., et al. Exceptional plasticity in the bulk single-crystalline van der Waals semiconductor InSe. Science. 2020;369:542–545. doi: 10.1126/science.aba9778. [DOI] [PubMed] [Google Scholar]
  • 40.Bandurin D.A., Tyurnina A.V., Yu G.L., et al. High electron mobility, quantum Hall effect and anomalous optical response in atomically thin InSe. Nat. Nanotechnol. 2017;12:223–227. doi: 10.1038/nnano.2016.242. [DOI] [PubMed] [Google Scholar]
  • 41.Rashad M., Pan F., Tang A., et al. Effect of Graphene Nanoplatelets addition on mechanical properties of pure aluminum using a semi-powder method. Prog. Nat. Sci.: Mater. Int. 2014;24:101–108. [Google Scholar]
  • 42.Lovato M.L., Stout M.G. Compression testing techniques to determine the stress-strain behavior of metals subject to finite deformation. Metall. Trans. A. 1992;23:935–951. [Google Scholar]
  • 43.Wang Y., Chen M., Zhou F., et al. High tensile ductility in a nanostructured metal. Nature. 2002;419:912–915. doi: 10.1038/nature01133. [DOI] [PubMed] [Google Scholar]
  • 44.Ma E., Zhu T. Towards strength-ductility synergy through the design of heterogeneous nanostructures in metals. Mater. Today. 2017;20:323–331. [Google Scholar]
  • 45.Zhang L., Chen L. A review on biomedical titanium alloys: recent progress and prospect. Adv. Eng. Mater. 2019;21:1801215. [Google Scholar]
  • 46.Liddicoat P.V., Liao X.Z., Zhao Y., et al. Nanostructural hierarchy increases the strength of aluminium alloys. Nat. Commun. 2010;1:63. doi: 10.1038/ncomms1062. [DOI] [PubMed] [Google Scholar]
  • 47.Wu Z., Ahmad R., Yin B., et al. Mechanistic origin and prediction of enhanced ductility in magnesium alloys. Science. 2018;359:447–452. doi: 10.1126/science.aap8716. [DOI] [PubMed] [Google Scholar]
  • 48.Tian Y.Z., Zhang Z.F. Microstructures and tensile deformation behavior of Cu-16 wt.% Ag binary alloy. Mater. Sci. Eng. 2009;508:209–213. [Google Scholar]
  • 49.Weng Y., Han D., Yong G. Springer Science & Business Media; China: 2011. Advanced Steels: The Recent Scenario in Steel Science and Technology. [Google Scholar]
  • 50.Shi P., Li R., Li Y., et al. Hierarchical crack buffering triples ductility in eutectic herringbone high-entropy alloys. Science. 2021;373:912–918. doi: 10.1126/science.abf6986. [DOI] [PubMed] [Google Scholar]
  • 51.Li Z., Pradeep K.G., Deng Y., et al. Metastable high-entropy dual-phase alloys overcome the strength-ductility trade-off. Nature. 2016;534:227–230. doi: 10.1038/nature17981. [DOI] [PubMed] [Google Scholar]
  • 52.Zou M., Ma Y., Yuan X., et al. Flexible devices: from materials, architectures to applications. J. Semicond. 2018;39:011010. [Google Scholar]
  • 53.Hu P., He X., Jiang H. Greater than 10 cm2 V-1 s-1: a breakthrough of organic semiconductors for field-effect transistors. InfoMat. 2021;3:613–630. [Google Scholar]
  • 54.Nathan A., Ahnood A., Cole M.T., et al. Flexible electronics: the next ubiquitous platform. Proc. IEEE. 2012;100:1486–1517. [Google Scholar]
  • 55.Gao L. Flexible device applications of 2D semiconductors. Small. 2017;13:1603994. doi: 10.1002/smll.201603994. [DOI] [PubMed] [Google Scholar]
  • 56.Guo C.F., Ding L. Integration of soft electronics and biotissues. Innovation. 2021;2:100074. doi: 10.1016/j.xinn.2020.100074. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 57.Akinwande D., Petrone N., Hone J. Two-dimensional flexible nanoelectronics. Nat. Commun. 2014;5:5678. doi: 10.1038/ncomms6678. [DOI] [PubMed] [Google Scholar]
  • 58.Chang C., Chen W., Chen Y., et al. Recent progress on two-dimensional materials. Acta Phys.-Chim. Sin. 2021;37:2108017. [Google Scholar]
  • 59.George E.P., Curtin W.A., Tasan C.C. High entropy alloys: a focused review of mechanical properties and deformation mechanisms. Acta Mater. 2020;188:435–474. [Google Scholar]
  • 60.Ye Y.F., Wang Q., Lu J., et al. High-entropy alloy: challenges and prospects. Mater. Today. 2016;19:349–362. [Google Scholar]
  • 61.Hu H., Xia K., Wang Y., et al. Fast synthesis and improved electrical stability in n-type Ag2Te thermoelectric materials. J. Mater. Sci. Technol. 2021;91:241–250. [Google Scholar]
  • 62.Momma K., Izumi F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011;44:1272–1276. [Google Scholar]
  • 63.Demetriou M.D., Launey M.E., Garrett G., et al. A damage-tolerant glass. Nat. Mater. 2011;10:123–128. doi: 10.1038/nmat2930. [DOI] [PubMed] [Google Scholar]
  • 64.Xi X.K., Zhao D.Q., Pan M.X., et al. Fracture of brittle metallic glasses: brittleness or plasticity. Phys. Rev. Lett. 2005;94:125510. doi: 10.1103/PhysRevLett.94.125510. [DOI] [PubMed] [Google Scholar]
  • 65.Sun B.A., Wang W.H. The fracture of bulk metallic glasses. Prog. Mater. Sci. 2015;74:211–307. [Google Scholar]
  • 66.Barry J., Goodno J.M.G. 9 edn. Cengage Learning; 2018. Mechanics of Materials. [Google Scholar]
  • 67.Zhu Y.T., Wu X.L. Ductility and plasticity of nanostructured metals: differences and issues. Mater. Today Nano. 2018;2:15–20. [Google Scholar]
  • 68.Zhao K., Eikeland E., He D., et al. Thermoelectric materials with crystal-amorphicity duality induced by large atomic size mismatch. Joule. 2021;5:1183–1195. [Google Scholar]
  • 69.Wang T., Zhao K., Qiu P., et al. Aguilarite Ag4SSe thermoelectric material: natural mineral with low lattice thermal conductivity. ACS Appl. Mater. Interfaces. 2019;11:12632–12638. doi: 10.1021/acsami.8b22741. [DOI] [PubMed] [Google Scholar]
  • 70.Xiao C., Xu J., Li K., et al. Superionic phase transition in silver chalcogenide nanocrystals realizing optimized thermoelectric performance. J. Am. Chem. Soc. 2012;134:4287–4293. doi: 10.1021/ja2104476. [DOI] [PubMed] [Google Scholar]
  • 71.Qiu Y., Liu Y., Ye J., et al. Synergistic optimization of carrier transport and thermal conductivity in Sn-doped Cu2Te. J. Mater. Chem. 2018;6:18928–18937. [Google Scholar]
  • 72.Wu R., Li Z., Li Y., et al. Synergistic optimization of thermoelectric performance in p-type Ag2Te through Cu substitution. Journal of Materiomics. 2019;5:489–495. [Google Scholar]
  • 73.Zhang Q., Lin Y., Lin N., et al. Enhancing the room temperature thermoelectric performance of n-type Bismuth-telluride-based polycrystalline materials by low-angle grain boundaries. Mater. Today Phys. 2022;22:100573. [Google Scholar]
  • 74.Liang X., Chen C., Dai F. Effect of plastic deformation on phonon thermal conductivity of α-Ag2S. Appl. Phys. Lett. 2020;117:253901. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. Supplemental materials and methods, Figures S1–S7, and Note S1
mmc1.pdf (1.5MB, pdf)
Document S2. Article plus supplemental information
mmc2.pdf (3.8MB, pdf)

Articles from The Innovation are provided here courtesy of Elsevier

RESOURCES