Abstract
Brain computer interface (BCI) systems were initially developed to replace lost function; however, they are being increasingly utilized in rehabilitation to restore motor functioning after brain injury. In such BCI-mediated neurofeedback training (BCI-NFT), the brain-state associated with movement attempt or intention is used to activate an external device which assists the movement while providing sensory feedback to enhance neuroplasticity. A critical element in the success of BCI-NFT is accurate timing of the feedback within the active period of the brain state. The overarching goal of this work was to develop a reliable deep learning model that can predict motion before its onset, and thereby deliver the sensory stimuli in a timely manner for BCI-NFT applications. To this end, the main objective of the current study was to design and evaluate a Multi-layer Perceptron Neural Network (MLP-NN). Movement-related cortical potentials (MRCP) during planning and execution of ankle dorsiflexion was used to train the model to classify dorsiflexion planning vs. rest. The accuracy and reliability of the model was evaluated offline using data from eight healthy individuals (age: 26.3 ± 7.6 years). First, we evaluated three different epoching strategies for defining our 2 classes, to identify the one which best discriminated rest from dorsiflexion. The best model accuracy for predicting ankle dorsiflexion from EEG before movement execution was 84.7%. Second, the effect of various spatial filters on the model accuracy was evaluated, demonstrating that the spatial filtering had minimal effect on model accuracy and reliability.
I. Introduction
Non-invasive mobile Brain Computer Interface (BCI) systems are reaching greater technological maturity resulting in faster and more reliable detection of the target brain activity. These advances improve their potential for all applications; particularly, the ability to quickly and reliably detect movement intention has greatly expanded use of BCI systems in rehabilitation applications where timing may play a critical role in producing neuroplasticity. In rehabilitative and restorative BCI systems, also referred to as neurofeedback training (BCI-NFT), the aim is to link brain activity during motor imagery or motor attempt to an external sensory stimulus to strengthen adaptive neural connections and thereby restore motor capabilities. The most common external devices used to provide contingent proprioceptive feedback to the central nervous system are functional electrical stimulation (FES) or a robot. Additionally, these devices may assist the subject in executing the motor task which further provides reward and visual feedback to the participants, and thereby improves the functional outcome. Due to its accessibility and high temporal resolution, electroencephalography (EEG), is the most common mobile brain imaging technique deployed in these applications.
In associative rehabilitative BCI paradigms, an endogenous task-specific brain-state as detected by low frequency movement related cortical potentials (MRCP) or event-related desynchronization (ERD) in the mu or beta bands during motor imagery or execution is coupled to time-correlated sensory feedback. According to the principle of Hebbian association [1], synapses strengthen through associative and causal inputs to post synaptic neurons. Unlike operant conditioning neurofeedback, in the associative paradigm the delivery of the feedback does not depend on modulation of the brain activity, but instead activation of an external device based on rapid detection of the planning or execution of the target movement from the EEG data. Although in both paradigms the timing of receiving feedback is important, in Hebbian association, the timing plays a more critical role in enhancing plasticity because in order to create the required neural association the feedback must arrive during the most active phase of the brain-state. In the case of MRCP, there is a narrow window of 300 ms [2] before the execution of the intended motor task. A potential advantage of the Hebbian association paradigm in BCI-NFT is that a lower training dose may be needed to produce meaningful functional improvement [3]. This has been supported by Mrachasz-Kersting et al. where small but significant improvements in lower limb functionality were reported after only 20 minutes (30 pairings of brain-state and sensory stimuli) [4]. There is a positive correlation between induced plasticity and detection accuracy as demonstrated by Niazi et al. [5]. Thus, implementation of an optimal classification algorithm that can provide a reliable, fast activation command to the external device is of utmost importance in BCI-NFT systems.
MRCP, detected in low frequency bands, e.g. from 0.05 to 10 Hz, have been considered as valid signals for controlling rehabilitative BCI systems [6, 7] and are generated during both imagined or attempted movements [5]. Peak negativity (PN) of MRCP has been specifically linked to the neurophysiological mechanism of motor planning and execution [4], which happens within 500ms prior to the movement onset [3]. Using an open-loop control strategy, Mrachasz-Kersting et al has used the mean PN, calculated offline using data collected during the calibration phase, to activate an electrical stimulation device. The electrical stimulation was applied to the tibialis anterior. Using this cue-based neurofeedback protocol they showed significant and clinically meaningful changes in the Fugl-Meyer Assessment (FMA) score in two randomized clinical trials in the stroke population [4, 8]. The timing of applying sensory feedback is fixed with respect to the cue, as calculated during the calibration phase; this timing of peak negativity with respect to the cue, however, may change during the online training sessions and may require re-calibration [9].
There have been some efforts to detect movement intention using the MRCP online, for self-paced and closed-loop BCI-NFT, to potentially cope with the time variability in EEG signals. In self-paced BCI-NFT systems the feedback can be applied by the user at their own preferred pace, and thereby provide a more engaging experience [5]. Niazi et al. proposed a simple matched filter for supervised detection of MRCP [6]. However, the uncertainty and time variant nature of the EEG signal are not ideal for matched filters [7]. Xu et al proposed a manifold learning algorithm followed by linear discriminant analysis (LDA) showing 200–400 ms of detection delay and >80% detection accuracy for classifying motor execution. Niazi et al. introduced an optimal spatial filter and improved the detection timing by 66.6 ± 121 ms with 82.5% detection accuracy [6].
Our aim was to evaluate the capability of a deep learning model to provide a superior method for classification of a motor task versus rest using MRCP features of EEG. Deep learning has recently demonstrated promising results in the classification of brain activity for applications such as hand movement classification [10], virtual reality based BCI-NFT [11] and exoskeleton-based BCI-NFT [12].
The main objective of this study was to evaluate the classification performance of a multi-layer perceptron neural network (MLP-NN) in identification of rest vs ankle dorsiflexion in healthy adults using MRCP components of EEG signals recorded from sensorimotor cortex. To this end we investigated: 1) the effect of rest and motor planning/execution on detection accuracy; and 2) the effect of spatial filtering on accuracy.
II. METHODS
A. Participants and Data Collection
Eight healthy subjects (4 females, 4 males; age: 26.3 ± 7.6 years; height: 171 ± 7 cm; weight: 75.6 ± 10.5 kg) with no history of neurological disease participated in this study to investigate brain activity during event-related motor tasks. Collecting ankle motion data was part of a larger experiment involving four different movements: walking, cycling, ankle dorsiflexion, and hand grasping. EEG data collection was synchronized with electromyography and motion capture. The data collection protocol was approved by the NIH Institutional Review Board (#13-CC-0110), and the participants provided informed consent.
Each study session was divided into 60 trials. At the beginning of each trial the subjects were seated in a recumbent position with their knees flexed and supported on a firm pillow and their feet suspended over the edge of the foam block, with a computer monitor in front of them which cued them when to move or rest (Fig.1). For the rest command, they were instructed to keep their lower extremity muscles relaxed and avoid motion of their eyes, head or body for 3 seconds (rest period from −3000 ms to 0 ms). At the end of the rest period a visual and audio cue instructed the subjects to dorsiflex their ankles repeatedly at approximately a 1 Hz pace, for 3 seconds. At time 0, the subject started to move their ankles. (Motor execution period from 0 ms to +3000 ms). EMG activity of dorsiflexor and plantarflexor muscles were recorded during the trial. The movement initiations were labeled using the motion capture system.
Figure 1.

Subjects were seated in recumbent position in front of a monitor. They were instructed to dorsiflex when a graphical cue appeared on the monitor. 64-channel EEG was recorded simultaneously.
B. EEG data collection and preprocessing
A 64-channel wireless active EEG system (Brain Products) with electrodes positioned using the 5% 10–20 international system (Easy Cap) with FCz as the reference collected EEG data at 1000 Hz. The EEG data were band pass filtered (0.01 to 10 Hz) to MRCP range then down-sampled to 500 Hz. Then 21 channels over the sensorimotor cortex encompassing the FC, C, and CP channels (FC5, FC3, FC1, FCz, FC2, FC4, FC6, C5, C3, C1, Cz, C2, C4, C6, CP5, CP3, CP1, CPz, CP2, CP4, CP6), which are associated with motor planning and execution, were used for generating the required datasets for training and testing our MLP-NN classifier. To optimize and evaluate this classifier, we conducted two analyses: 1) epoching analysis, where different epoch timings for defining our rest and motion classes were tested; 2) spatial filtering analysis, where we analyzed the effect of commonly used spatial filters versus no filter on the accuracy of the MLP-NN classifier. See Fig. 2 for the diagram of our analyses.
Figure 2.

The block diagram of the two analyses. Epoching analysis: where the effect of three time-epochings strategies for defining the rest and motion classes were evaluated. Spatial Filtering analysis: where the effect of commonly used spatial filtering techniques on the accuracy of the model were evaluated. Six combination of spatial filtering, i.e., six conditions (no-Filter, CAR, CSP, CAR+CSP, Lap and CAR+Lap), were applied to the Motor planning_2 and their accuracies were evaluated. Then the condition with the highest accuracy, no-Filter, were used for additional analysis, i.e., trial-based, subject based and individualized model evaluation.
C. Epoching Analysis
At this stage, the effects of rest and motion periods on classification accuracy were evaluated. Note that if the time period associated with class 2, motion, was before the onset of movement, time 0, it was called motor planning and if it was after motion onset it was called motor execution. Although the main objective of this study was predicting ankle dorsiflexion before the onset of movement, a dataset based on motor execution was added to compare its accuracy with predicting the motion using motor planning datasets. Three datasets were generated for this analysis:
Motor Execution: time point −1000 ms to 0 ms (500 samples) as Rest (class 1) and 0 to 1000 ms (500 samples) as motor execution (class 2).
Motor Planning_1: time point −2000 ms to −1000 ms as rest (class 1) and −1000 ms to 0 ms as motor planning (class 2). As both periods are prior to movement initiation, unlike the previous dataset, the second period is called motor planning.
Motor Planing_2: −2500 ms to −1500 ms as rest (class 1) and −1000 to 0 ms motor planning (class 2). Note that there is a 500 ms time-gap between rest and motor planning period in this dataset, unlike the other two datasets. We hypothesized that the earlier the rest period (the further away the rest period is from the movement initiation, i.e. time 0) the less chance there is a motor planning related desynchronization or MRCP in the EEG signals, and therefore, a more pronounced feature can be identified for differentiating between the two classes, rest and motion.
Each dataset included 22 columns; 21 sensorimotor channels (i.e., 21 features), and a label column, L1, indicating each class, class 1 (rest)=0 and class 2 (motion)=1. Note that each trained classifier was a two-class problem. The length of each dataset was 480,000 data points (8 subjects × 60 trials × 1000 data points (1 s, 500 samples of rest, and 1 s, 500 samples of motion)); resulting in a 480000 × 22 matrix. At each step of the model optimization a batch of 8 data points was used. The model was trained in 20 iterations (training epochs).
For epoching analysis, in addition to the aforementioned preprocessing steps, i.e., channel selection, bandpass filter, and down sampling to 500Hz, all of these three datasets were referenced to common average reference (CAR).
D. Spatial Filtering Analysis
Next, the effect of spatial filtering was evaluated on the MLP-NN classification accuracy, using CAR, Laplacian and common spatial pattern (CSP). These spatial filters are commonly used in MRCP-based BCI systems [4, 5]. The Motor Planning_2 dataset was used for this analysis. Six spatial filtering methods were applied to this dataset resulting in six conditions: 1) no spatial filtering (no-Filter), 2) CAR, 3) common spatial pattern (CSP) [13], 4) the combination of CAR and CSP, 5) Laplacian, and 6) combination of CAR and Laplacian. Laplacian filter was applied using Current Source Density (CSD) toolbox version 1.1 in MATLAB. The CAR and Laplacian have been previously shown to be superior spatial filters over single channel referencing [14]. Additionally, Niazi et al. [5] demonstrated the superiority of Laplacian to CSP.
A fivefold evaluation was conducted using 80% of the dataset as training and 20% for testing the accuracy. The training and testing samples were extracted randomly from the entire dataset.
In addition, trial-based, subject-based, and individualized model evaluations were conducted only on the no-Filter condition, i.e., the Motor planing_2 dataset with no spatial filtering. For trial-based evaluation, 20% of trials from each subject (96 total trials, 12 from each of 8 subjects, with each trial consisting of 500 samples, 1 s, of rest and 500 samples, 1 s, of motion) were randomly selected as the test data. For the subject-based evaluation, the entire dataset of two subjects (25% of the subjects) was randomly chosen as the test data. Finally, for the individualized model, 60% of the data of each subject were used as the test data and the model was trained using the remaining 40% of each subject’s data; thus, the model was trained and tested individually. Note that for the trial-based and subject-based test data, the model was trained with the remaining data that were not included in the test data. The mean and standard deviation (std) of detection accuracies across the five evaluation iterations were reported.
E. MLP Structure
The MLP was designed in Python 3.3 using Pytorch. The initial structure consisted of two hidden layers, with a dimension of 10 and ReLu activation function [15]. The optimizer used for training the MLP was Stochastic Gradient Descent (SGD) [16], with a learning rate of 1 and batch size of 8. Using a grid search strategy, the parameters of the MLP were optimized. The number of batches, i.e. the number of training time points (rows of the datasets) used for each optimization step, and hidden layers had a minimal effect on accuracy. In contrast, the number of hidden dimensions had a prominent effect on the accuracy. The dimension of 20 for each hidden layer was identified as optimal. Adam optimizer was also evaluated, showing a minimal effect on the accuracy. The learning rate, however, has a substantial effect on both optimizers; lr=0.001 and lr=0.01 work optimally for Adam and Stochastic Gradient Descent (SGD), respectively. The final model had three hidden layers used with 20 dimensions, batch size of 8, learning rate of 0.01, and used SGD optimizer.
For model accuracy, true positive (TP) was defined as correctly detecting the motion class and true negative (TN) was defined as correctly identifying the rest class. The model accuracy, was calculated as the rate of correct detections (TP + TN) over all of classification attempts. In addition, TP rate and FP rate were reported. A repeated measures ANOVA with Tukey’ HCD post-hoc test for multiple comparison was used to evaluate significant differences in accuracy. The statistical significance was set to p < 0.05.
III. Results & discussion
A. Epoching Analysis
As can be seen in Fig. 3 the detection accuracy was significantly higher for the motor execution (post movement onset, time 0) (p<0.001) dataset, with 89.2% ±0.5% (mean ± std) accuracy, when compared with the two motor planning datasets. In the motor planning datasets, as we hypothesized, the dataset with a time-gap between rest and motor planning period, Motor planning_2, resulted in a significantly higher detection accuracy, 84.7% ±0.7 (p<0.001).
Figure 3.
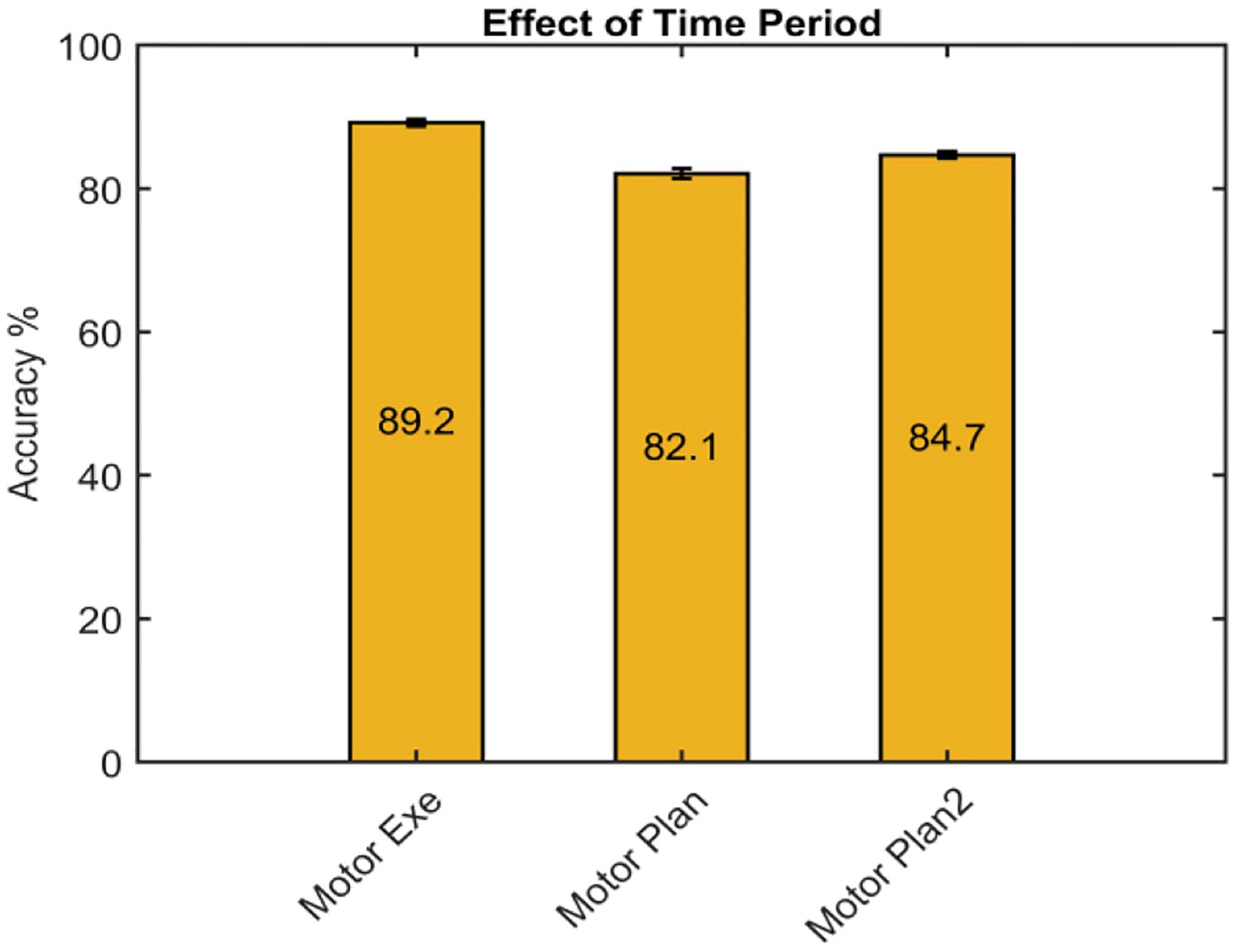
Effect of rest and motion execution/planning time periods on the classification accuracy. The standard deviations are [0.5,0.7,0.5], for the first, second and third bars, respectively. Motor Exe showed significantly higher accuracy than the other two datasets. The accuracy of Motor Plan2 dataset was significantly higher than Motor Plan.
B. Spatial filter analysis
Spatial filtering had minimal effect on detection accuracy of the model using the Motor planing_2 dataset (Fig. 4), and the condition with no spatial filtering, no-Filter, demonstrated the highest accuracies, 84.8% ± 0.7% and was significantly higher than the Laplacian and CSP filtering condition (p<0.001). Applying the Laplacian filter, on the other hand, decreased the accuracy to 79.8% ±1.2%; and it was significantly lower than all of the other datasets. Combining CAR with CSP and Laplacian did not significantly change their accuracies. The effect of spatial filtering is also demonstrated in Fig.5; no-Filter condition showed the highest true positive rate (TPR) and one of the lowest false positive rate (FPR). The true positive and false positive rates are presented in Table I. Note that TPR indicates the accuracy of the system in triggering the sensory feedback in BCI-NFT applications. On the other hand, false positive rate (FPR) is of the highest importance as triggering the feedback during the rest periods of training may create false association.
Figure 4.

The effect of spatial filtering on MLP-NN classification accuracy. No-Filter shows the detection accuracy with no spatial filter. CAR shows the effect of re-referencing by Common Average Reference (CAR). CAR & Lap shows the effect of both re-referencing by CAR and applying the Laplacian filter. The standard deviations are [0.7,0.5, 0.6, 0.5,1.2,0.6] for the 1st to 6th bar, respectively. The accuracy of no-Filter dataset was significantly higher than those of CSP dataset and Laplacian dataset. The accuracy of CSP was significantly higher than Laplacian. Adding CAR did not changed the accuracies significantly.
Figure 5.

The mean true positive vs false positive rate of spatial filtering across five-fold validation.
Table 1.
True positive rates (TPR) and false rates (FPR).
| Motor Exe | Motor Plan | Motor Plan 2 | no-Filter | CAR | CSP | CAR & CSP | Laplacian | CAR & Lap | |
|---|---|---|---|---|---|---|---|---|---|
| %TPR | 85.4 | 76.0 | 77.1 | 78.9 | 77.1 | 74.8 | 78.4 | 71.7 | 73.4 |
| %FPR | 8.0 | 13.4 | 9.5 | 10.7 | 9.5 | 12.7 | 14.7 | 14.1 | 14.6 |
The condition with the highest accuracy, i.e., the Motor planning_2 dataset with no spatial filtering (no-Filter in Fig. 4), was then used for the additional evaluations (trial-based, subject-based, and indvidualized model). The results of our subject-based and trial-based evaluations showed decreased accuracy of the model to 60.6%±1.4% and 64.8%±1.9%, respectively. The indvdualized model however substantially imporved the accuracy to 91.5%±3.2%. These results demonstrated the need for a subject-specific model or a transfer-learning approach, which will be a future direction of this work.
The proposed MLP-NN requires minimal preprocessing by eliminating the need for spatial filtering, which potentially can result in a higher detection speed. The detection speed will be investigated in future work. We will also evaluate this model online using healthy individuals and those with neurological disorders such as cerebral palsy. Additionally, we will compare the proposed MLP-NN model with convolutional neural CNN to potentially improve the TPR.
IV. Conclusion
The accuracy of MLP-NN in predicting ankle dorsiflexion was evaluated in this study. The detection accuracy was comparable to that of prior literature. The effect of spatial filtering on detection accuracy, however, was minimal, unlike previously proposed classifiers. This accurate detection model may minimize the preprocessing steps, thus the latency of detecting motor intention. Therefore, the proposed MLP-NN shows great potential in BCI neurofeedback systems for optimizing both the efficiency and effectiveness of motor rehabilitation and achieving desired neuroplastic effects.
Table 2.
The % accuracy (mean ±SD of the fivefold evaluation) of individually trained MLP-NN model.
| Subject # | |||||||
|---|---|---|---|---|---|---|---|
| 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 |
| 93.0±2.9 | 89.6±1.3 | 90.3±5.0 | 95.0±0.5 | 87.7±1.6 | 87.2±0.9 | 93.7±0.6 | 95.6±0.4 |
Acknowledgments
This work was supported by the Intramural Research Program of the NIH Clinical Center (Protocol 13-CC-0110).
References
- [1].Hebb DO, The organization of behavior: a neuropsychological theory. Science editions, 1949. [Google Scholar]
- [2].Grosse-Wentrup M et al. , “Using brain–computer interfaces to induce neural plasticity and restore function,” Journal of neural engineering, vol. 8, no. 2, p. 025004, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Mrachacz-Kersting N et al. , “Towards a mechanistic approach for the development of non-invasive brain-computer interfaces for motor rehabilitation,” The Journal of physiology, vol. 599, no. 9, pp. 2361–2374, 2021. [DOI] [PubMed] [Google Scholar]
- [4].Mrachacz-Kersting N et al. , “Efficient neuroplasticity induction in chronic stroke patients by an associative brain-computer interface,” Journal of neurophysiology, vol. 115, no. 3, pp. 1410–21, Mar 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Niazi IK, Mrachacz-Kersting N, Jiang N, Dremstrup K, and Farina D, “Peripheral electrical stimulation triggered by self-paced detection of motor intention enhances motor evoked potentials,” IEEE transactions on neural systems and rehabilitation engineering, vol. 20, no. 4, pp. 595–604, Jul 2012. [DOI] [PubMed] [Google Scholar]
- [6].Niazi IK et al. , “Detection of movement intention from single-trial movement-related cortical potentials,” (in eng), Journal of neural engineering, vol. 8, no. 6, p. 066009, Dec 2011. [DOI] [PubMed] [Google Scholar]
- [7].Xu R et al. , “Enhanced low-latency detection of motor intention from EEG for closed-loop brain-computer interface applications,” IEEE transactions on bio-medical engineering, vol. 61, no. 2, pp. 288–96, Feb 2014. [DOI] [PubMed] [Google Scholar]
- [8].Mrachacz-Kersting N et al. , “Brain state–dependent stimulation boosts functional recovery following stroke,” Annals of neurology, vol. 85, no. 1, pp. 84–95, 2019. [DOI] [PubMed] [Google Scholar]
- [9].Jochumsen M et al. , “Self-Paced Online vs. Cue-Based Offline Brain-Computer Interfaces for Inducing Neural Plasticity,” Brain sciences, vol. 9, no. 6, Jun 1 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Zhang G et al. , “Classification of hand movements from EEG using a deep attention-based LSTM network,” IEEE Sensors Journal, vol. 20, no. 6, pp. 3113–3122, 2019. [Google Scholar]
- [11].Karácsony T et al. , “Brain computer interface for neuro-rehabilitation with deep learning classification and virtual reality feedback,” in Proceedings of the 10th Augmented Human International Conference 2019, 2019, pp. 1–8. [Google Scholar]
- [12].Chowdhury MSN et al. , “Deep neural network for visual stimulus-based reaction time estimation using the periodogram of single-trial eeg,” Sensors, vol. 20, no. 21, p. 6090, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Ramoser H et al. , “Optimal spatial filtering of single trial EEG during imagined hand movement,” IEEE transactions on rehabilitation engineering, vol. 8, no. 4, pp. 441–446, 2000. [DOI] [PubMed] [Google Scholar]
- [14].McFarland DJ et al. , “Spatial filter selection for EEG-based communication,” Electroencephalography and clinical Neurophysiology, vol. 103, no. 3, pp. 386–394, 1997. [DOI] [PubMed] [Google Scholar]
- [15].Craik A et al. , “Deep learning for electroencephalogram (EEG) classification tasks: a review,” Journal of neural engineering, vol. 16, no. 3, p. 031001, 2019. [DOI] [PubMed] [Google Scholar]
- [16].Djamal EC et al. , “Identification of post-stroke EEG signal using wavelet and convolutional neural networks,” Bulletin of Electrical Engineering and Informatics, vol. 9, no. 5, pp. 1890–1898, 2020. [Google Scholar]


