Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Oct 21;126(43):18511–18519. doi: 10.1021/acs.jpcc.2c05816

Thermal Transport through Polymer-Linked Gold Nanoparticles

Xingfei Wei †, Ewa Harazinska †, Yinong Zhao ‡, Yi Zhuang †, Rigoberto Hernandez †,‡,¶,*
PMCID: PMC9639611  PMID: 36366755

Abstract

graphic file with name jp2c05816_0007.jpg

Polymer–nanoparticle networks have potential applications in molecular electronics and nanophononics. In this work, we use all-atom molecular dynamics to reveal the fundamental mechanisms of thermal transport in polymer-linked gold nanoparticle (AuNP) dimers at the molecular level. Attachment of the polymers to AuNPs of varying sizes allows the determination of effects from the flexibility of the chains when their ends are not held fixed. We report heat conductance (G) values for six polymers—viz. polyethylene, poly(p-phenylene), polyacene, polyacetylene, polythiophene, and poly(3,4-ethylenedioxythiophene)—that represent a broad range of stiffness. We address the multimode effects of polymer type, AuNP size, polymer chain length, polymer conformation, system temperature, and number of linking polymers on G. The combination of the mechanisms for phonon boundary scattering and intrinsic phonon scattering has a strong effect on G. We find that the values of G are larger for conjugated polymers because of the stiffness in their backbones. They are also larger in the low-temperature region for all polymers owing to the quenching of segmental rotations at low temperature. Our simulations also suggest that the total G is additive as the number of linking polymers in the AuNP dimer increases from 1 to 2 to 3.

1. Introduction

Polymer-linked nanoparticle network systems are of great interest for many applications, such as molecular electronics,1,2 phononics,3−5 thermoelectric devices,6−8 and autonomous computing materials.9−11 They also represent a complex system with heterogeneity at multiple scales which is challenging for typical bottom-up approaches and thus requires multiscale techniques to properly capture the so-called middle scales.12 These materials have been used in phononic devices to manipulate heat flow and perform simple logic operations analogous to those in standard electronic devices.13−15 Recently, Volz and co-workers16 reviewed theoretical and experimental progress in the use of nanostructured phononic devices to control thermal transport. However, it remains a big challenge to develop phononic devices that can perform data storage and computing.9

Nanoparticle networks can potentially emulate neuronal networks and perform brainlike computing.10,11 For example, Kathmann et al.17 demonstrated NOT, OR, NOR, AND, and NAND logical operations by controlling the radiative heat transfer between networks of nanoparticles (made of SiC, SiO2 , and VO2). Xiong et al.18 demonstrated the thermal-siphon effect and its potential application in thermoelectric applications using a simple 2D square array lattice network. Our recent work10 also employed networks using a 2D square array of polymer-linked nanoparticles to realize brainlike computing. Another recent work by Li and co-workers19 showed that heat transfer in a 1D chain network with a self-coupled loop can be affected by the loop length and coupling strength, which may be important in controlled thermal information processing.

Resolving the mechanism of heat transfer through a single polymer chain is thus critical to developing complex polymer-linked nanoparticle networks for phononic applications. Fermi et al.20 first discovered that energy transfer along a 1D chain can be divergent using a simple mathematical model in 1955. Using molecular dynamics (MD) simulations, Henry and Chen21 later found that the thermal conductivity of a single polyethylene (PE) chain can be above 100 W/(m·K) and even divergent. This is much larger than the thermal conductivity values in amorphous polymers, which usually range between 0.1 and 0.5 W/(m·K).22 Meanwhile, high thermal conductivity PE nanofibers were fabricated by Shen et al.,23 who found that ultradrawn PE nanofibers can reach conductivities as high as 104 W/(m·K). Recently, heat flux rectification—viz. a thermal diode—has been realized using a PE nanofiber containing both crystalline and disordered regions.24,25 Ma and Tian26 also showed that a design strategy using a bottlebrush polymer can lead to a thermal rectification ratio ∼70%.

In a single polymer chain, it has been reported that the thermal transport mechanism is related to polymer chain stiffness (dihedral torsion and angular bending energy), chain length, and application of strain in the chain.22,27−32 Liu and Yang28 concluded that when the polymer chain is short (e.g., <50 repeating unit PE), the phonon-boundary scattering mechanism dominates and heat flux increases with increasing chain length. This anomalous phenomenon has been quantitatively demonstrated through experiments by Cui et al.33 For thermal transport in a single polymer chain, in both simulations and experiments reported in the literature,21,27,28,31,33 the two heads of a polymer chain are typically held fixed. However, in polymer nanocomposites and polymer–nanoparticle networked materials, the nanoparticle shape and size can change and do affect heat transfer. This suggests a need to resolve the thermal transport mechanism in polymer-linked nanoparticle systems, where the mobile nanoparticles can influence the polymer property.

In this work, we use all-atom MD simulations to calculate the heat flux across different types of polymers linked between two gold nanoparticles (AuNPs). Each head of the polymer chain is connected to a corresponding AuNP at a (100) facet. The effects of polymer chain length, polymer type, AuNP size, temperature, polymer conformation, and number of polymer links are reported here. The correlations between heat conductance and all of these properties open up a design space that can be optimized for given applications in the development of new phononic devices using polymer–nanoparticle networks.

2. Simulation Models and Methods

2.1. Model

Simulation Model

The heat flux through a single polymer chain is calculated from a simplified model consisting of two AuNPs, each linked to different heads of a polymer; see Figure 1. The AuNP size is varied in diameter D across lengths 2, 4, and 8 nm. The polymer chain length is defined by the number of carbons in the backbone, NC, and varied from 12 to 400 across the simulations. Six different types of polymers are used in this work—viz. PE, poly(p-phenylene) (PPP), polyacene (ACE), polyacetylene (PA), poly(3,4-ethylenedioxythiophene) (PEDOT), and polythiophene (PT)—shown in Figure 1. The polymer models are built using Moltemplate.34,35 The Optimized Potentials for Liquid Simulations (OPLS)36,37 all-atom force field (with explicit hydrogens) is used to describe all interactions in the polymers. The Au–Au interactions in AuNPs are described by the Lennard-Jones (LJ) potential.10,11,38 Typically, each polymer chain is terminated by a thiol group (−S) at each head. The exceptions to this parametrization are the following: (i) in the ACE chain model, there are two thiol groups at each end; and (ii) in both PEDOT and PT models, each monomer unit has a sulfur atom that can bond to AuNPs, and the polymer chain is consequently not terminated with thiol groups. The Au–S bond is used to connect the polymer with the AuNP, which can then be described by the Morse potential.39 The other organic element interactions with Au atoms are described by the LJ potential with a small energy constant.11,39 All force field parameters are listed in Tables S1–S4 in the Supporting Information.

Figure 1.

Figure 1

Open in a new tab

Top panel: the scheme employed here modeling heat transfer from a hotter (left) AuNP to a colder (right) AuNP through a polymer chain—with a 100-carbon PE chain shown here—attached to the (100) facets of both 4 nm diameter AuNPs. Below the top panel, the chemical structures and names of six different types of polymers used in this work are shown so as to highlight the corresponding repeat unit. Sulfur, oxygen, carbon, and hydrogen atoms are rendered in yellow, red, black, and white, respectively, in color, and in light gray, dark gray, black, and white, respectively, in grayscale.

Simulation Protocol

All MD simulations in this work are propagated using the Large-scale Atomic Molecular Massively Parallel Simulator (LAMMPS) package.40 The simulation time step is 0.25 fs, as the hydrogen atoms are explicitly simulated in our model and modeling high-frequency C–H vibrations requires a short time step. The LJ and Coulombic potential cutoffs are both at 10 Å with an additional neighbor bin setting of 2.5 Å. The long-range pairwise interactions are not included. The simulation is performed in vacuum in a periodic box of dimensions 1000 × 1000 × 1000 Å3. The motion of the center of mass of the dimer is used to define the moving frame, and the box is placed on this frame. The center of mass of the dimer is placed in the center of this box and consequently has no drift. The size of the dimer is ∼200 Å along the long dimension, and it has a total number of atoms equal to ∼1244, ∼4836, and ∼33 372 for AuNPs with diameters, 2, 4, and 8 nm, respectively.

Initially, the polymer chain is placed in a straight line conformation aligned along the x-axis. A AuNP is placed near the head of each end of the polymer. For convenience, the polymer chain is placed perpendicular to the AuNP (100) facet, and the connections emerge naturally with the AuNPs. Additional details related to the making of the dimer structure can be found in our previous work,11 where we reported dimers, trimers, and tetramers built by poly(allylamine hydrochloride) (PAH)-linked AuNPs. The slow motion of the AuNPs—arising from their large mass—also leads to the stability of the polymer-linked AuNP dimers during the simulation time window of 10–100 ns.11 We find that when a PE chain length has six carbons, the two AuNPs can collide each other. Such collisions are rarely observed when the PE chain length is 12 carbons, with no collision at 24 carbons or longer chains. However, in PEDOT and PT chains, each monomer has a sulfur atom, which tends to drive the polymer chain to wrap a given AuNP. In turn, the decrease in the length of the chain connecting the dimers increases the likelihood of collision between them. We find that the PEDOT- and PT-linked AuNP dimers give rise to many different structures. We find that the local stability of the PEDOT and PT dimer structures has more uncertainty during the 10–100 ns observation window than the other polymer-connected dimers addressed here.

The heat flux across the polymer chain between the AuNPs is measured numerically in nonequilibrium MD (NEMD) simulations and is obtained for the various polymers listed in Figure 1. Typically, the entire system is first relaxed at T0 for more than 10 ns within a NVT ensemble constrained by a Langevin thermostat. Then, one AuNP is connected to a heat source at (T0 + 40 K), and the other AuNP is connected to a heat sink at (T0 – 5 K), while each is represented by a NVT Langevin thermostat at the respective temperature. These temperatures were selected in correspondence with those in the experiments reported in ref (33) at T0 = 300 K. The observed energy input at the source and energy output at the heat sink are recorded every 10 000 steps by the Langevin thermostat during the simulation. The total NEMD simulation time is 5–20 ns. The initial ∼2 ns of the NEMD run is used to reach steady state, which is not used in the heat flux calculation. In the 2 nm AuNP models, the simulation speed is fast, and we can access up to 20 ns of integration in less than 1 week of computing time. In the 8 nm AuNP models, the simulation speed is slow and accommodated only 5–6 ns of total NEMD trajectory integration. In the 4 nm AuNP models, the simulation speed is in the middle of these, with 5–10 ns of integration time. We can therefore use the last 5–10 ns of each integration to obtain the heat conductance (G) in 2 and 4 nm AuNP models. For 8 nm AuNP models, only the last 2 ns of the NEMD run are used to obtain G. At steady state, G is calculated by averaging the absolute power input (Pin) and output (Pout) and then dividing by the temperature gap (ΔT): G = (Pin + Pout)/(2ΔT); see Figure 1. We average more than 3–5 independent trajectories to calculate the final values of G reported below.

3. Results and Discussion

3.1. Chain Length and AuNP Size Effects on Heat Flux through a Single PE Chain

Meyhofer and co-workers33 showed that the thermal conductance (G) through a single PE chain increases from 15 to 30 pW/K with the chain length NC from 2 to 10 as reproduced in Figure 2 for comparison with our data. In ref (33), the strained chains reported there are stable because they are under tension between the gold surface and TEM tip. Polymers can hardly retain stability when they are freely connecting two AuNPs. In our simulations, the smallest consistently stable PE chain is at chain length NC = 12, while those dimers at NC = 6 always collapse. Representative schemes of PE-linked AuNP dimers from NC = 6 to 200 and D = 2, 4, and 8 nm are available in Figure S1 (Supporting Information). Here, we report primarily the heat conductance across a free chain within a AuNP dimer with lengths from NC = 12 to 200. While the setups for the strained chains of ref (33) and the free chains in the current work are not the same, it is notable that the order of magnitude in G is comparable. The rise in G across the strained chains from their experiments is visible in the smaller of the free chains connecting the heaviest of the AuNPs (with diameter equal to 8 nm) and also when the 8 nm chains are strained between dimers that are further apart. However, for free chains as they become longer, the general trend is G decreasing. This can be anticipated from Liu and Yang28 who found that G increases with increasing chain length for short polymer chains when phonon-boundary scattering dominates and G decreases with increasing chain length for longer polymer chains when intrinsic phonon scattering dominates. We find that there is a transition region lying between NC = 12 and 24 where G is optimal.

Figure 2.

Figure 2

Open in a new tab

Heat conductance G across a single PE chain in the AuNP dimer model of Figure 1 with variable chain lengths and AuNP sizes (circle, D = 2 nm; diamond, D = 4 nm; square, D = 8 nm). Experimental measurements (stars) by Meyhofer and co-workers33 for a single PE chain attached between a gold plane and a gold tip are shown for comparison.

The polymer thermal conductivity is directly related to the polymer chain stiffness and conformation.22,41−43 We characterized the conformation and stiffness for each model using the radius of gyration (Rg), AuNP–AuNP edge-to-edge distance (L), and backbone dihedral angle distribution; see Figures S2 and S3 in the Supporting Information. The Rg and dihedral angle distribution at NC = 12 (Figures S2b and S3a) show that the PE chain is more stretched in the D = 2 and 4 nm AuNP models. As a consequence, their values in G are higher than those for the D = 8 nm AuNPs; see Figure 2 at NC = 12. When the chain length NC is 24–200, we find similar values in G at D = 2, 4, and 8 nm (Figure 2). This is due to the similarity in their chain conformations, which is visible in Rg and in the dihedral angle distributions in Figures S2 and S3. In this work, we focus on heat flow through free polymers that are loosely connected between two AuNPs and where no stretching force is applied. This defines the sense in which the polymer between the AuNPs is said to be free. However, at NC = 12, the D = 2 and 4 nm models exhibit higher values in G than the D = 8 nm model (Figure 2), which is due to the slight stretches of the polymer chain arising from higher mobility in the smaller sized AuNPs. This can be confirmed from the dihedral angle distribution in Figure S3a, where the peaks at ∼180° for D = 2 and 4 nm are slightly higher than for D = 8 nm. We also find that for D = 8 nm dimers, the PE chain is stable in both strained (larger in L, Rg, and G) and free (smaller in L, Rg, and G) conformations in response to the change of distance L; see Figures S4 and S5.

For comparison with earlier reports,27,44,45 the heat conductance (G in pW/K) is converted to thermal conductivity [k in W/(m·K)] using estimates of the PE cross-sectional area S = 18.3 Å2 and k = G × L/S;46 see Table S5 in the Supporting Information. For AuNPs with D = 8 nm and PE at NC = 200, we found k = 3.11 W/(m·K), which is close to the lowest value—viz. 3.69 W/(m·K)—reported for a negative strain by Zhang and Luo.27 Meanwhile, we also converted the thermal conductance values to thermal conductivity values using both the AuNP–AuNP distance L and the PE contour length Lc; see Table S5. We can see that the thermal conductivity decreases with reducing PE chain length, and it is not affected by the AuNP size. As the PE thermal conductivity significantly increases under a stretch,27,44,45 we can confirm that our free PE chains—with their corresponding low k values—match the no stretching regime.

3.2. Heat Flux through Different Types of Polymers

The effect of chain length on electrical conductance in PPP, PEDOT, and PT has been extensively reported by several groups.7,47,48 However, the effect on heat conductance in conductive polymers remains unclear. Here, we model heat flow through a single chain of five different conjugated polymers—viz. PPP, ACE, PA, PEDOT, and PT—linked to AuNPs of different sizes and use the heat flow through PE—elaborated on in the previous section—as a reference. The G values of the five selected conjugated polymers with varying nanoparticle diameter are shown in Figure 3 and can be compared to those of PE in Figure 2. For PPP, ACE, and PA, the thiol functionalization and Au–S bonding are at both ends of the chain. For PEDOT and PT, each repeating unit instead contains an S atom, and the chains can attach entirely to the AuNP; see schemes in Figure 1 and representative structures in Figure 3f. The G values of PPP, ACE, and PA (G ∼ 40, 70, and 50 pW/K, respectively) reported in Figures 3a, 3b, and 3c are higher than those for PE (G ∼ 30 pW/K) owing to their stronger backbones. The variation of AuNP size in PPP, ACE, and PA does not appreciable affect G because the chain conformations and their properties—e.g., Rg and L—remain similar; see Figures S6 and S7 in the Supporting Information. For NC = 50–200 with 8 nm AuNPs, we also find that as the chain length increases, G of PA monotonically decreases, G of PPP first increases and then decreases, and G of ACE monotonically increases. This finding that aromatic backbones are better heat conductors and the interfacial thermal conductance decreases with increasing chain length agrees with reports on the thermal transport across polymer-linked carbon nanotubes by Liu et al.29 The trends in G differ as a consequence of stiffness differences in corresponding polymers. The phonon mean free path increases with increasing polymer chain stiffness. In turn, it can extend the region dominated by the phonon-boundary scattering mechanism leading to the trend with increasing G at longer chain lengths.28 We thus find that ACE is the stiffest of the polymers investigated here; PPP is more stiff than PA; and PA and PE are similar in stiffness. The two Au–S bonds at the ACE head/tail (Figure 1) increase the number of heat transfer channels, further enhancing G and leading to G = 60–80 pW/K (Figure 3b).

Figure 3.

Figure 3

Open in a new tab

Single chain heat conductance G of the polymers in Figure 1 except for PE—(a) PPP, (b) ACE, (c) PA, (d) PEDOT, and (e) PT—with varying chain lengths (NC = 50–200) and different AuNP sizes (D = 2, 4, and 8 nm). Note that the PE results are shown in Figure 2. Representative schemes of D = 4 nm AuNP dimers linked by PE, PPP, ACE, PA, PEDOT, and PT at NC ∼ 100 are shown in panel (f). In panels (a)–(e), the symbol size represents different AuNP sizes as indicated in the legend at the top left of panel (a). In panel (d), the PEDOT results also include G at NC = 400.

The G value of PEDOT and PT linked to 8 nm AuNPs first increases from NC = 50 to 100 and then slightly decreases after NC > 100; see Figures 3d and 3e. These trends are similar to those of PPP and suggest that the chain stiffness of PEDOT and PT is similar to that of PPP. However, for PEDOT dimers the two AuNPs will collapse, at D = 4 nm, NC = 50 and at D = 2 nm, NC = 50–100. For PT dimers the two AuNPs will also collapse, at NC = 50 with D = 2 and 4 nm AuNPs. When NC > 100, both PEDOT and PT dimers will not collapse with D = 2 and 4 nm AuNPs, but these dimer structures have much higher uncertainties than other types of polymers; see Rg and L results in Figures S4 and S5 (Supporting Information). Because the 8 nm AuNPs are much heavier than the 2 and 4 nm ones, the PEDOT and PT dimers are more stable than those with D = 2 and 4 nm. Figures S5d and S5e show that when using the same chain length of PEDOT and PT, the distance L between 2 nm AuNPs is shorter than 4 nm AuNPs, and both are shorter than 8 nm AuNPs. The distance L indicates that the D = 2 nm model has the shortest heat flow path, the most Au–S binding sites (or heat flow channels), and the highest G. We can therefore rank the AuNP models using G as G2nm > G4nm > G8nm which is directly related to the PEDOT and PT structures; see Figures 3d and 3e. Schemes of all different polymer-linked AuNP dimer models are provided in Figures S8, S9, and S10 for D = 2, 4, and 8 nm AuNPs, respectively.

In conductive polymers, it is important to rule out the contribution of hot electron flow to thermal heat transfer. The heat flux contribution induced by electrical conductance can be calculated by the Wiedemann–Franz law,49k/σ = LZT, where k is thermal conductivity, σ is electrical conductivity, the Lorenz number LZ = 2.44 × 10–8 V2 K–2, and T is temperature. When the transport path and cross-sectional area are the same for heat and electron, the Wiedemann–Franz law is written as Gh/Ge = LZT, where Ge is the electrical conductance and Gh is the heat conductance induced by electrons. For PT using Ge < 10–8 S47,50 at a chain length of 12 monomers (NC = 48), we calculate Gh = 0.07 pW at T = 300 K. The values of Gh for PPP, PA, PEDOT, and ACE are similarly as small as Gh of PT, and all are negligible. For PE at NC = 12, according to ref (33), we estimate Ge ∼ 6.2 × 10–8 S, and then we calculate Gh = 0.45 pW at T = 300 K, which is also small. According to the scaling rule in ref (51): 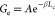Inline graphic, Ge exponentially decreases with increasing chain length; here A and β are constant values, and Lc is polymer contour length. The contribution to Gh will be much smaller with increasing NC.

3.3. Temperature Effect

In PE-linked AuNP dimers, the heat conductance decreases monotonically with increasing temperature; see the circle symbols in Figure 4a. This decreasing trend in G is directly related to decreasing polymer chain stiffness, which is confirmed by the polymer backbone dihedral angle distribution in Figure S11a (Supporting Information). We find that when T increases, dihedral angle peaks near 60° and 300° arise, which correspond to the two gauche conformations of the PE chain, and peaks at 180° and 360° become broader; see Figure S11a. Meanwhile, because PPP and ACE are more rigid, their G values stay constant up to T ∼ 600 K, and at T > 600 K, polymers become softer and G decreases; see Figure 4a. The dihedral angle distributions from all the aromatic backbone carbons in PPP and ACE also confirm that when T increases, dihedral angle peaks at 180° and 360° become broader, but no peaks appear near 60° or 300°; see Figures S11b and S11c. The absence of peaks near 60° or 300° indicates that PPP and ACE are very stiff polymers.

Figure 4.

Figure 4

Open in a new tab

Heat conductance G of single-polymer-linked AuNPs with D = 4 nm for PE, PPP, and ACE at NC ∼ 100 as a function of (a) the system temperature from T = 100 to 700 K and (b) the temperature gap from ΔT = 25 to 65 K.

To explore the temperature gap (ΔT) effect on G, the heat source temperature is varied from T1 = 320 to 360 K, while the heat sink temperature is kept constant at T2 = 295 K; see the scheme in Figure 1. We find that ΔT has no effect on G in all three of our models, viz. PE, PPP, and ACE; see Figure 4b. For PE at ΔT = 25 K, the polymer chain is slightly more rigid and G is slightly higher, but from ΔT = 35 to 65 K, G values remain the same; see Figure 4b. We also report Rg and distance L results at different temperatures and temperature gaps in Figure S12. We find that the dihedral angle distribution provides a useful measure of the stiffness of different polymer types; see more discussion in Section 3.4.

3.4. AuNP–AuNP Distance Effect

By moving AuNPs closer to each other, the polymer Rg and AuNP edge-to-edge distance L can be easily adjusted. Figure 5a shows that upon decreasing the distance L, the heat conductance is not changed for PE, PPP, or ACE in general. Earlier reports found the polymer heat conductance remaining nearly constant at a minimum value either when applying a negative strain on the PE chain27 or when the ratio Rfrac of the polymer’s end-to-end distance Lee to its contour length Lc, Rfrac = Lee/Lc, is below a threshold.31 For example, for a PE polymer with NC = 100 and a typical monomer diameter of ∼1.53 Å, LC ∼ 153 Å, which leads to the flat-behavior region seen in ref (31) for Rfrac in the range (0.26, 0.78). PPP and ACE have a monotonic increasing trend in potential energy with decreasing L in Figure 5b, indicating the persistence of a negative strain in the polymer. However, we see an exception that G starts to increase with decreasing L at a distance between 40 and 80 Å, and the potential V drops at that transition because the polymer partially collapses; see Figures 5a and 5b. The polymer conformation can be inferred through Rg in Figure 5c and the representative schemes of Figures 5d and 5e. We find that although Rg changes significantly in Figure 5c, G does not change when L decreases from 120 to 40 Å. The dihedral angle distributions exhibit similar histograms at different L distances (Figure S13 in the Supporting Information), which means the polymer stiffness is constant. In polymer-linked nanoparticle systems, Rg and the thermal conductance are not in one-to-one correspondence—that is, the polymer chain stiffness is not directly related to Rg or Lee—because the vibrational modes are confined by the nanoparticles. Instead, it appears that the polymer backbone dihedral angle distribution is a better reporter of polymer stiffness.

Figure 5.

Figure 5

Open in a new tab

Effects of the AuNP–AuNP edge-to-edge distance L on (a) heat conductance G, (b) shifted potential energy V – V0, and (c) Rg of a single PE, PPP, and ACE chain at NC ∼ 100. (V0 = −159 051 kcal/mol and panels (a)–(c) share the same legend). Representative schemes of (d) PE, (e) PPP, and (f) ACE at different L, where L is the center-to-center distance minus two AuNP radii.

3.5. Varying the Number of Polymer Linkers 1, 2, and 3

In composite materials and networked materials, the number of polymers linked between two nanoparticles can be more than one. Figure 6a shows that when changing the number of linking polymers, NL, from 1 to 2 to 3, G increases almost linearly (for PE, PPP and ACE at constant NC). Figure 6a also shows that G decreases with increasing chain length (for the same polymer type and NL). Figure 6b also shows that the average heat conductance per polymer chain value (G per chain) is very similar (within error bar difference) for PE and PPP at the same NC. This helps confirm a linear increase of G with the number of linkers NL. The only exception is that for ACE NL = 1 has a higher G per chain value than the NL = 2 or 3 systems; see the last panel in Figure 6b. This appears to be caused by the phonon mean free path of ACE being longer than that of PE and PPP because ACE has the most rigid backbone. Also, ACE chains have the largest interchain interactions, owing to the π–π stacking interactions in phenyl rings. Consequently, the interchain phonon scattering is the strongest and can cause more reduction in G per chain in ACE. On the other hand, for PE and PPP, the interchain interaction interference is not strong, and G per chain values remain almost the same with increasing the number of polymers from 1 to 2 to 3; see the first and second panels in Figure 6b. Representative schemes of two and three polymers—of either PE, PPP, or ACE—linking 4 nm AuNPs are provided in Figures S14 and S15.

Figure 6.

Figure 6

Open in a new tab

Dependence of (a) G and (b) G per polymer chain on the number of polymer chains, NL, linking the 4 nm AuNPs at three different chain lengths NC, ca. 50, 100, and 200, with precise values noted in the corresponding legends. Representative schemes for the structures are available in Supporting Information Figures S14 and S15.

4. Conclusions

In this work, we use MD simulations to calculate the heat conductance G through single-polymer-chain-linked AuNP dimers for six different types of polymers, viz. PE, PPP, ACE, PA, PEDOT, and PT, and three differently sized AuNPs, viz. 2, 4, and 8 nm in diameter. In the limit of the rigid attachment of the polymer ends, we found agreement between the results of our simulation of a PE chain linked to large 8 nm AuNPs and previous reports using bulk gold.27,33 We show that polymer thermal conductivity is directly related to polymer chain conformation and stiffness, and conjugated polymers (PPP and ACE) generally have larger G values. We found that AuNPs affect soft polymer structures (e.g., PE) but do not affect rigid polymers as the latter are necessarily already stiff. We also found in our atomistic simulations that at chain length NC ∼ 100, PE: G ∼ 30 pW/K, PPP: G ∼ 40 pW/K, PA: G ∼ 50 pW/K, and ACE: G ∼ 70 pW/K; for PEDOT- and PT-linked 8 nm AuNPs, dimer models remain stable, which has similar G as PPPA, while PEDOT- and PT-linked 2 and 4 nm AuNPs dimers are not stable. We observed that when T decreases from 700 to 100 K, the polymer stiffness increases. In particular, over this range in T, G increases from ∼20 to 38 pW/K for PE, from ∼40 to 50 pW/K for PPP, and from ∼60 to 80 pW/K for ACE.

The nature of the linking polymer and the nanoparticles to the heat conductance inside dimers was seen to effect conductivity as can be expected from prior work with rigidly held polymers. Interestingly, G remains constant upon a reduction of the AuNP–AuNP distance—L drops from 120 to 40 Å and Rg drops from 35 to 25 Å—which is due to the invariance of the heat flow contour path. Consequently, we found that for PE, PPP, and ACE, G is additive when NL increases from 1 to 2 to 3. In this work, we have thus demonstrated the atomistic mechanism of thermal transport through polymer chains in polymer-linked AuNP dimers.52−54 This finding may be of use in the design of flexible electronics and nanophononic devices. In future work, we will consider complex polymer–nanoparticle networks, such as the materials whose stability we described in ref (11), which offer potential applications to address data storage and computing needs.

Acknowledgments

We dedicate this article to Michael R. Berman for his leadership and guidance of innovations in physical chemistry over several decades, and for his previous support of our research group through the AFOSR program on Molecular Dynamics and Theoretical Chemistry. This work was initially supported by the National Science Foundation (NSF) through Grant No. OAC-1940152 and more recently by Grant No. CHE-2102455. The computing resources necessary for this research were provided in part by the National Science Foundation through XSEDE resources under grant number CTS090079 and the Advanced Research Computing at Hopkins (ARCH) high-performance computing (HPC) facilities supported by the NSF MRI Grant (OAC-1920103).

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcc.2c05816.

  • Detailed information about simulation model force field parameters, additional results, and schemes (PDF)

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry virtual special issue “Honoring Michael R. Berman”.

Supplementary Material

jp2c05816_si_001.pdf (6.2MB, pdf)

References

  1. Nitzan A.; Ratner M. A. Electron Transport in Molecular Wire Junctions. Science 2003, 300, 1384–1389. 10.1126/science.1081572. [DOI] [PubMed] [Google Scholar]
  2. Aradhya S. V.; Venkataraman L. Single-Molecule Junctions Beyond Electronic Transport. Nat. Nanotechnol. 2013, 8, 399–410. 10.1038/nnano.2013.91. [DOI] [PubMed] [Google Scholar]
  3. Pop E. Energy Dissipation and Transport in Nanoscale Devices. Nano Res. 2010, 3, 147–169. 10.1007/s12274-010-1019-z. [DOI] [Google Scholar]
  4. Li N.; Ren J.; Wang L.; Zhang G.; Hänggi P.; Li B. Colloquium: Phononics: Manipulating Heat Flow with Electronic Analogs and Beyond. Rev. Mod. Phys. 2012, 84, 1045. 10.1103/RevModPhys.84.1045. [DOI] [Google Scholar]
  5. Segal D.; Agarwalla B. K. Vibrational Heat Transport in Molecular Junctions. Annu. Rev. Phys. Chem. 2016, 67, 185–209. 10.1146/annurev-physchem-040215-112103. [DOI] [PubMed] [Google Scholar]
  6. Cui L.; Miao R.; Jiang C.; Meyhofer E.; Reddy P. Perspective: Thermal and Thermoelectric Transport in Molecular Junctions. J. Chem. Phys. 2017, 146, 092201. 10.1063/1.4976982. [DOI] [Google Scholar]
  7. Cui L.; Miao R.; Wang K.; Thompson D.; Zotti L. A.; Cuevas J. C.; Meyhofer E.; Reddy P. Peltier Cooling in Molecular Junctions. Nat. Nanotechnol. 2018, 13, 122–127. 10.1038/s41565-017-0020-z. [DOI] [PubMed] [Google Scholar]
  8. Wang K.; Meyhofer E.; Reddy P. Thermal and Thermoelectric Properties of Molecular Junctions. Adv. Funct. Mater. 2020, 30, 1904534. 10.1002/adfm.201904534. [DOI] [Google Scholar]
  9. Bathe M.; Hernandez R.; Komiyama T.; Machiraju R.; Neogi S. Autonomous Computing Materals. ACS Nano 2021, 15, 3586–3592. 10.1021/acsnano.0c09556. [DOI] [PubMed] [Google Scholar]
  10. Wei X.; Zhao Y.; Zhuang Y.; Hernandez R. Engineered Nanoparticle Network Models for Autonomous Computing. J. Chem. Phys. 2021, 154, 214702. 10.1063/5.0048898. [DOI] [PubMed] [Google Scholar]
  11. Wei X.; Zhao Y.; Zhuang Y.; Hernandez R. Building Blocks for Autonomous Computing Materials: Dimers, Trimers and Tetramers. J. Chem. Phys. 2021, 155, 154704. 10.1063/5.0064988. [DOI] [PubMed] [Google Scholar]
  12. Clark A. E.; Adams H.; Hernandez R.; Krylov A. I.; Niklasson A. M. N.; Sarupria S.; Wang Y.; Wild S. M.; Yang Q. The Middle Science: Traversing Scale in Complex Many-Body Systems. ACS Cent. Sci. 2021, 7, 1271. 10.1021/acscentsci.1c00685. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Li B.; Wang L.; Casati G. Thermal Diode: Rectification of Heat Flux. Phys. Rev. Lett. 2004, 93, 184301. 10.1103/PhysRevLett.93.184301. [DOI] [PubMed] [Google Scholar]
  14. Wang L.; Li B. Thermal Logic Gates: Computation with Phonons. Phys. Rev. Lett. 2007, 99, 177208. 10.1103/PhysRevLett.99.177208. [DOI] [PubMed] [Google Scholar]
  15. Paolucci F.; Marchegiani G.; Strambini E.; Giazotto F. Phase-Tunable Thermal Logic: Computation with Heat. Phys. Rev. Appl. 2018, 10, 024003. 10.1103/PhysRevApplied.10.024003. [DOI] [Google Scholar]
  16. Nomura M.; Anufriev R.; Zhang Z.; Maire J.; Guo Y.; Yanagisawa R.; Volz S. Review of Thermal Transport in Phononic Crystals. Mater. Today Phys. 2022, 22, 100613. 10.1016/j.mtphys.2022.100613. [DOI] [Google Scholar]
  17. Kathmann C.; Reina M.; Messina R.; Ben-Abdallah P.; Biehs S.-A. Scalable Radiative Thermal Logic Gates Based on Nanoparticle Networks. Sci. Rep. 2020, 10, 1–11. 10.1038/s41598-020-60603-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Xiong K.; Liu Z.; Zeng C.; Li B. Thermal-Siphon Phenomenon and Thermal/Electric Conduction in Complex Networks. Natl. Sci. Rev. 2020, 7, 270–277. 10.1093/nsr/nwz128. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Wang S.; Zeng C.; Yang F.; Xiong K.; Li B. Energy Diffusion of Simple Networks under the Spatiotemporal Thermostats. Eur. Phys. J. B 2021, 94, 1–8. 10.1140/epjb/s10051-021-00247-z. [DOI] [Google Scholar]
  20. Fermi E.; Pasta P.; Ulam S.; Tsingou M.. Studies of the Nonlinear Problems; Document LA-1940; Los Alamos National Laboratory: Los Alamos, NM, 1955.
  21. Henry A.; Chen G. High Thermal Conductivity of Single Polyethylene Chains Using Molecular Dynamics Simulations. Phys. Rev. Lett. 2008, 101, 235502. 10.1103/PhysRevLett.101.235502. [DOI] [PubMed] [Google Scholar]
  22. Wei X.; Wang Z.; Tian Z.; Luo T. Thermal Transport in Polymers: A Review. J. Heat Transfer 2021, 143, 143. 10.1115/1.4050557. [DOI] [Google Scholar]
  23. Shen S.; Henry A.; Tong J.; Zheng R.; Chen G. Polyethylene Nanofibres with Very High Thermal Conductivities. Nat. Nanotechnol. 2010, 5, 251–255. 10.1038/nnano.2010.27. [DOI] [PubMed] [Google Scholar]
  24. Zhang T.; Luo T. Giant Thermal Rectification from Polyethylene Nanofiber Thermal Diodes. Small 2015, 11, 4657–4665. 10.1002/smll.201501127. [DOI] [PubMed] [Google Scholar]
  25. Shrestha R.; Luan Y.; Luo X.; Shin S.; Zhang T.; Smith P.; Gong W.; Bockstaller M.; Luo T.; Chen R.; et al. Dual-Mode Solid-State Thermal Rectification. Nat. Commun. 2020, 11, 1–7. 10.1038/s41467-020-18212-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Ma H.; Tian Z. Significantly High Thermal Rectification in An Asymmetric Polymer Molecule Driven by Diffusive Versus Ballistic Transport. Nano Lett. 2018, 18, 43–48. 10.1021/acs.nanolett.7b02867. [DOI] [PubMed] [Google Scholar]
  27. Zhang T.; Luo T. Morphology-Influenced Thermal Conductivity of Polyethylene Single Chains and Crystalline Fibers. J. Appl. Phys. 2012, 112, 094304. 10.1063/1.4759293. [DOI] [Google Scholar]
  28. Liu J.; Yang R. Length-Dependent Thermal Conductivity of Single Extended Polymer Chains. Phys. Rev. B 2012, 86, 104307. 10.1103/PhysRevB.86.104307. [DOI] [Google Scholar]
  29. Liu J.; Alhashme M.; Yang R. Thermal Transport Across Carbon Nanotubes Connected by Molecular Linkers. Carbon 2012, 50, 1063–1070. 10.1016/j.carbon.2011.10.014. [DOI] [Google Scholar]
  30. Subramanyan H.; Zhang W.; He J.; Kim K.; Li X.; Liu J. Role of Angular Bending Freedom in Regulating Thermal Transport in Polymers. J. Appl. Phys. 2019, 125, 095104. 10.1063/1.5086176. [DOI] [Google Scholar]
  31. Dinpajooh M.; Nitzan A. Heat Conduction in Polymer Chains with Controlled End-to-End Distance. J. Chem. Phys. 2020, 153, 164903. 10.1063/5.0023085. [DOI] [PubMed] [Google Scholar]
  32. Dinpajooh M.; Nitzan A. Heat Conduction in Polymer Chains: Effect of Substrate on the Thermal Conductance. J. Chem. Phys. 2022, 156, 144901. 10.1063/5.0087163. [DOI] [PubMed] [Google Scholar]
  33. Cui L.; Hur S.; Akbar Z. A.; Klöckner J. C.; Jeong W.; Pauly F.; Jang S.-Y.; Reddy P.; Meyhofer E. Thermal Conductance of Single-Molecule Junctions. Nature 2019, 572, 628–633. 10.1038/s41586-019-1420-z. [DOI] [PubMed] [Google Scholar]
  34. Ponder J. W.; Richards F. M. An Efficient Newton-Like Method for Molecular Mechanics Energy Minimization of Large Molecules. J. Comput. Chem. 1987, 8, 1016–1024. 10.1002/jcc.540080710. [DOI] [Google Scholar]
  35. Rackers J. A.; Wang Z.; Lu C.; Laury M. L.; Lagardere L.; Schnieders M. J.; Piquemal J.-P.; Ren P.; Ponder J. W. Tinker 8: Software Tools for Molecular Design. J. Chem. Theory Comput. 2018, 14, 5273–5289. https://dasher.wustl.edu/tinker/ 10.1021/acs.jctc.8b00529. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Jorgensen W. L.; Maxwell D. S.; Tirado-Rives J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. 10.1021/ja9621760. [DOI] [Google Scholar]
  37. Kaminski G. A.; Friesner R. A.; Tirado-Rives J.; Jorgensen W. L. Evaluation and Reparameterization of the OPLS-AA Force Field for Proteins via Comparison with Accurate Quantum Chemical Calculations on Peptides. J. Phys. Chem. B 2001, 105, 6474–6487. 10.1021/jp003919d. [DOI] [Google Scholar]
  38. Heinz H.; Vaia R. A.; Farmer B. L.; Naik R. R. Accurate Simulation of Surfaces and Interfaces of Face-Centered Cubic Metals Using 12–6 and 9–6 Lennard-Jones Potentials. J. Phys. Chem. C 2008, 112, 17281–17290. 10.1021/jp801931d. [DOI] [Google Scholar]
  39. Ahn Y.; Saha J. K.; Schatz G. C.; Jang J. Molecular Dynamics Study of the Formation of a Self-Assembled Monolayer on Gold. J. Phys. Chem. C 2011, 115, 10668–10674. 10.1021/jp200447k. [DOI] [Google Scholar]
  40. Plimpton S. J. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. https://www.lammps.org 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
  41. Luo T.; Chen G. Nanoscale Heat Transfer–From Computation to Experiment. Phys. Chem. Chem. Phys. 2013, 15, 3389–3412. 10.1039/c2cp43771f. [DOI] [PubMed] [Google Scholar]
  42. Wei X.; Zhang T.; Luo T. Chain Conformation-Dependent Thermal Conductivity of Amorphous Polymer Blends: The Impact of Inter- and Intra-Chain Interactions. Phys. Chem. Chem. Phys. 2016, 18, 32146–32154. 10.1039/C6CP06643G. [DOI] [PubMed] [Google Scholar]
  43. Wei X.; Luo T. Chain Length Effect on Thermal Transport in Amorphous Polymers and a Structure–Thermal Conductivity Relation. Phys. Chem. Chem. Phys. 2019, 21, 15523–15530. 10.1039/C9CP02397F. [DOI] [PubMed] [Google Scholar]
  44. Ma H.; Tian Z. Chain Rotation Significantly Reduces Thermal Conductivity of Single-Chain Polymers. J. Mater. Sci. 2019, 34, 126–133. 10.1557/jmr.2018.362. [DOI] [Google Scholar]
  45. Zhu M.-X.; Song H.-G.; Yu Q.-C.; Chen J.-M.; Zhang H.-Y. Machine-Learning-Driven Discovery of Polymers Molecular Structures with High Thermal Conductivity. Int. J. Heat Mass Transfer 2020, 162, 120381. 10.1016/j.ijheatmasstransfer.2020.120381. [DOI] [Google Scholar]
  46. Boyer R. F.; Miller R. L. Polymer Chain Stiffness Parameter, σ, and Cross-Sectional Area per Chain. Macromolecules 1977, 10, 1167–1169. 10.1021/ma60059a053. [DOI] [Google Scholar]
  47. Capozzi B.; Dell E. J.; Berkelbach T. C.; Reichman D. R.; Venkataraman L.; Campos L. M. Length-Dependent Conductance of Oligothiophenes. J. Am. Chem. Soc. 2014, 136, 10486–10492. 10.1021/ja505277z. [DOI] [PubMed] [Google Scholar]
  48. Kang S. D.; Snyder G. J. Charge-Transport Model for Conducting Polymers. Nat. Mater. 2017, 16, 252–257. 10.1038/nmat4784. [DOI] [PubMed] [Google Scholar]
  49. Craven G. T.; Nitzan A. Wiedemann–Franz Law for Molecular Hopping Transport. Nano Lett. 2020, 20, 989–993. 10.1021/acs.nanolett.9b04070. [DOI] [PubMed] [Google Scholar]
  50. Yamada R.; Kumazawa H.; Noutoshi T.; Tanaka S.; Tada H. Electrical Conductance of Oligothiophene Molecular Wires. Nano Lett. 2008, 8, 1237–1240. 10.1021/nl0732023. [DOI] [PubMed] [Google Scholar]
  51. Su T. A.; Neupane M.; Steigerwald M. L.; Venkataraman L.; Nuckolls C. Chemical Principles of Single-Molecule Electronics. Nat. Rev. Mater. 2016, 1, 16002. 10.1038/natrevmats.2016.2. [DOI] [Google Scholar]
  52. Li N.; Ren J.; Wang L.; Zhang G.; Hänggi P.; Li B. Colloquium: Phononics: Manipulating Heat Flow with Electronic Analogs and Beyond. Rev. Mod. Phys. 2012, 84, 1045. 10.1103/RevModPhys.84.1045. [DOI] [Google Scholar]
  53. Ding Y.-F.; Zhu G.-M.; Shen X.-Y.; Bai X.; Li B.-W. Advances of Phononics in 2012–2022. Chin. Phys. B 2022, 10.1088/1674-1056/ac935d. [DOI] [Google Scholar]
  54. Malhotra A.; Maldovan M. Phononic Pathways Towards Rational Design of Nanowire Heat Conduction. Nanotechnology 2019, 30, 372002. 10.1088/1361-6528/ab261d. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp2c05816_si_001.pdf (6.2MB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES