The population genomics of multiple tsetse fly (Glossina fuscipes fuscipes) admixture zones in Uganda

Abstract

Understanding the mechanisms that enforce, maintain or reverse the process of speciation is an important challenge in evolutionary biology. This study investigates the patterns of divergence and discusses the processes that form and maintain divergent lineages of the tsetse fly Glossina fuscipes fuscipes in Uganda. We sampled 251 flies from 18 sites spanning known genetic lineages and the four admixture zones between them. We apply population genomics, hybrid zone and approximate Bayesian computation to the analysis of three types of genetic markers: 55,267 double-digest restriction site-associated DNA (ddRAD) SNPs to assess genome-wide admixture, 16 microsatellites to provide continuity with published data and accurate biogeographic modelling, and a 491-bp fragment of mitochondrial cytochrome oxidase I and II to infer maternal inheritance patterns. Admixture zones correspond with regions impacted by the reorganization of Uganda's river networks that occurred during the formation of the West African Rift system over the last several hundred thousand years. Because tsetse fly population distributions are defined by rivers, admixture zones likely represent both old and new regions of secondary contact. Our results indicate that older hybrid zones contain mostly parental types, while younger zones contain variable hybrid types resulting from multiple generations of interbreeding. These findings suggest that reproductive barriers are nearly complete in the older admixture zones, while nearly absent in the younger admixture zones. Findings are consistent with predictions of hybrid zone theory: Populations in zones of secondary contact transition rapidly from early to late stages of speciation or collapse all together.

INTRODUCTION

Genetic divergence occurs when the forces of mutation, genetic drift and local adaptation cause differences in genotype frequencies between isolated populations. Although divergence occurs most often during periods of geographic isolation (Coyne & Orr, 2004), periods of potential gene flow (secondary contact) are also common during speciation (Davison, Chiba, Barton, & Clarke, 2005; Martin, Dasmahapatra, Nadeau, Salazar, & Walters, 2013). Secondary contact can alter the evolutionary trajectory of the divergent lineages by enforcing, maintaining or even reversing divergence (Barton, 2001; Grant & Grant, 2008) by a balance between gene flow and the strength of selection against hybrids (Barton & Bengtsson, 1986; Barton & Hewitt, 1985; Collins & Rawlins, 2013; Mullen, Dopman, & Harrison, 2008; Turelli, Barton, & Coyne, 2001). The ecological and evolutionary processes underlying this balance appear to be contingent on the environmental, demographic and genomic context of secondary contact (reviewed in Gompert, Mandeville, & Buerkle, 2017) and remain an important question in speciation research and population genetics in general. Patterns of hybridization and introgression (gene flow among divergent lineages) across such regions of secondary contact provide an opportunity to elucidate the ecological and evolutionary processes important in divergence.

Tsetse flies (genus Glossina) are a promising system to investigate secondary contact because of their extensive population structure and evidence of admixture. The species Glossina fuscipes fuscipes is particularly well-suited for this line of questioning because there is evidence of admixture across multiple genetic breaks representing different stages of divergence (Beadell et al., 2010; Echodu et al., 2013; Opiro et al., 2017). Furthermore, G. f. fuscipes offers the advantage of being the object of intense applied research in population structure, ecology, genetics and physiology because of their epidemiological relevance as the obligate vectors of animal and human African trypanosomiasis (Aksoy, Caccone, Galvani, & Okedi, 2013; Kleine, 1909; Riley & Johannsen, 1932).

Previous research described four genetic clusters of G. f. fuscipes centred in the northwest, northeast, west and south of the country, with evidence of admixture between these clusters (Figure 1; Beadell et al., 2010; Opiro et al., 2017). We use the term “admixture zones” instead of “hybrid zones” in the context of this system because it is not clear whether they represent regions of secondary contact between reproductively isolated lineages. Instead, admixture zones could be regions undergoing primary divergence with gene flow or they could represent the remnants of old collapsed hybrid zones (e.g., in North American ravens, Webb, Marzluff, & Omland, 2011; in Galapagos giant tortoises, Garrick et al., 2014; in Galapagos finches, Grant & Grant, 2006).

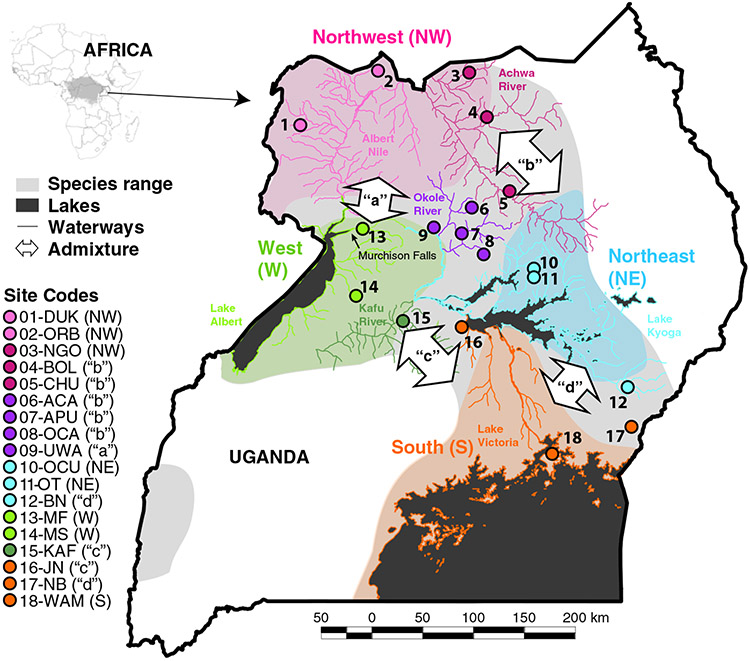
FIGURE 1.

Map of Uganda and the location of the 18 sampling sites of Glossina fuscipes fuscipes used in this study. Each sampling site marker indicates its placement relative to the distribution of the four pure genetic backgrounds (northwest: shaded pink, northeast: shaded blue, west: shaded green, south: shaded orange), and is color-coded by the watershed it falls within (Albert Nile: pink, Achwa River: magenta, Okole River: purple, Lake Kyoga: blue, Lake Albert: light green, Kafu River: dark green, Lake Victoria: orange). The species distribution of G. f. fuscipes beyond the distribution of the four pure genetic backgrounds is shown in light grey, and admixture zones (“a”, “b”, “c” and “d”) within this shading are indicated with arrows pointing to the genetic backgrounds in putative secondary contact in each zone.

The multiple admixture zones in this system provide an opportunity to compare the genetic structure, biogeographic context, and patterns of hybridization and introgression among them. One expectation established in the hybrid zone literature is that the context-dependent nature of reproductive isolation can create an array of introgression patterns in multiple hybrid zones (Coyne & Orr, 2004; Gompert et al., 2017), even within the same system (Bierne, Bonhomme, & David, 2003). Understanding introgression patterns can shed light on the evolutionary and ecological processes important in the process of speciation. For example, a long-standing question in speciation research is the relative importance of alternative forms of postzygotic reproductive barriers (i.e., intrinsic Dobzhansky–Muller incompatibilities vs. extrinsic ecological barriers: Barton, 2001, Schluter, 2000; Coyne & Orr, 2004; Funk, Nosil, & Etges, 2006; Gompert et al., 2017; Gross & Rieseberg, 2005; Rundle & Nosil, 2005). Recent theoretical work suggests that extrinsic and intrinsic barriers may not work in isolation, but instead can work synergistically in zones of secondary contact (i.e., the “coupling hypothesis”; Bierne, Welch, Loire, Bonhomme, & David, 2011). Under a model of divergence with gene flow, the coupling of multifarious barriers can rapidly advance the process of speciation from early to late stages (Gompert et al., 2017). One prediction of this hypothesis is the rare occurrence of stable long-lasting hybrid zones (Gompert et al., 2017), which implies rarity of first-generation hybrids as well as intermediate levels of introgression in nature. Here, we investigate this prediction with a comparison of introgression patterns found in G. f. fuscipes, a unique system with four admixture zones that exist within a ~40,000 km² region in Uganda (Beadell et al., 2010; Echodu et al., 2013; Opiro et al., 2017; Saarman et al., 2018). Our goal was to investigate the biogeographic context and patterns of introgression in this unique system (Figure 1) to provide insight on the evolutionary and ecological processes important in diversification.

In this study, we genotyped 251 individuals from 18 sites (Figure 1; Supporting Information Table S1) at 55,267 SNPs scored from double-digest restriction site-associated DNA (ddRAD) sequencing, 16 microsatellite markers and a 491-bp fragment of mitochondrial DNA (mtDNA) sequence from the cytochrome oxidase I and II (COI and COII) genes. We chose to use these three data types as each provides unique insight into hybrid zone dynamics. ddRAD data provided a genome-wide analysis of hybridization and introgression. Microsatellites offered continuity with previous studies and reliable models of recent evolutionary history because of their well-documented mutation rates, high molecular diversity and high minor allele frequencies (Beadell et al., 2010; Echodu et al., 2013; Hyseni et al., 2012; Opiro et al., 2016, 2017; Saarman et al., 2018). mtDNA sequences supplied inference of maternal inheritance, which can help distinguish asymmetrical reproductive barriers (Coyne & Orr, 2004) and past colonization patterns in hybrid zones (Currat, Ruedi, Petit, & Excoffier, 2008). Findings suggest that the coupling of multiple isolating barriers may play an important role in speciation in tsetse flies. This work lays the groundwork for more detailed investigation of the ecological and evolutionary processes critical to speciation and of the genetic basis for these processes.

2 ∣. METHODS

2.1 ∣. Samples and study area

Figure 1 shows the 18 sampling sites included in this study (details in Supporting Information Table S1). Tsetse flies were collected using bi-conical traps (Challier & Laveissiere, 1973) set out in groups of 10–15 traps within a radius of 2 km, a field protocol that reliably traps unrelated individuals (Echodu et al., 2013; Opiro et al., 2017). Sampling sites are a subset of sites from previous studies (Beadell et al., 2010; Echodu et al., 2013; Hyseni et al., 2012; Opiro et al., 2017) and were selected to represented the genetic diversity of the four geographic regions of genetically distinct populations found in Uganda (Figure 1: northwest, northeast, west and south; Beadell et al., 2010; Opiro et al., 2017) and the four admixture zones between them (Figure 1: “a” between the northwest and west, “b” between the northwest and northeast, “c” between the west and south, and “d” between the northeast and south).

Previous work has shown that watersheds facilitate dispersal in G. f. fuscipes (Bouyer et al., 2009) and thus play an important role in shaping genetic structure observed (Beadell et al., 2010; Hyseni et al., 2012; Opiro et al., 2017). To capture this geographic aspect, sampling was distributed across the seven major watersheds, and all descriptive analysis (i.e., genetic diversity, heterozygosity and structure) used the natural boundaries created by the watersheds (Figure 1, Table 1). We chose to define groups for descriptive analysis by watershed rather than by genetic cluster because either some sampling sites did not fall neatly within a single genetic cluster (Figure 1; Table 1; Beadell et al., 2010; Opiro et al., 2017).

TABLE 1.

Sample details and summary statistics for the 55,267 ddRAD SNPs for each sample organized and summarized by watershed

	Geographic region (admixture zone)	N	Pi	H O	H E	P LD	P HWD	F IS
Albert Nile
01-DUK†-NW	Northwest	20	0.177	0.207	0.172	0.200	0.121	−0.1691,2,3
02-ORB†-NW	Northwest	12	0.175	0.163	0.167	0.186	0.037	0.0811,2,3
		32	0.179	0.189	0.176	0.192	0.117	−0.0501,2,3
Achwa River
03-NGO	Northwest	12	0.169	0.139	0.162	0.176	0.093	0.2061,2,3
04-BOL	Northwest/Northeast (“b”)	20	0.162	0.180	0.158	0.174	0.051	−0.1041,2,3
05-CHU	Northwest/Northeast (“b”)	13	0.145	0.133	0.139	0.140	0.042	0.0951,2,3
		45	0.162	0.155	0.160	0.138	0.141	0.0551,2,3
Okole River
06-ACA	Northwest/Northeast (“b”)	18	0.163	0.175	0.158	0.167	0.053	−0.0711,2,3
07-APU	Northwest/Northeast (“b”)	10	0.170	0.190	0.161	0.199	0.026	−0.1151,2,3
08-OCA	Northwest/Northeast (“b”)	20	0.163	0.172	0.158	0.159	0.047	−0.0521,2,3
09-UWA	Northwest/West (“a”)	15	0.185	0.153	0.178	0.222	0.057	0.1901,2,3
		63	0.172	0.171	0.170	0.158	0.178	0.0141,2,3
Lake Kyoga
10-OCU†-NE	Northeast	20	0.146	0.148	0.142	0.132	0.048	0.000
11-OT†-NE	Northeast	14	0.143	0.142	0.137	0.121	0.024	0.0091,2,3
12-BN	Northeast/South (“d”)	12	0.161	0.154	0.154	0.144	0.040	0.0591,2,3
		46	0.156	0.148	0.155	0.130	0.103	0.0671,2,3
Lake Albert
13-MF†-w	West	10	0.155	0.147	0.147	0.185	0.021	0.0631,2,3
14-MS†-w	West	11	0.160	0.129	0.153	0.134	0.085	0.2301,2,3
		21	0.165	0.137	0.160	0.164	0.120	0.1861,2,3
Kafu River
15-KAF	West/South (“c”)	20	0.158	0.129	0.154	0.114	0.117	0.2121,2,3
Lake Victoria
16-JN	West/South (“c”)	5	0.108	0.106	0.096	0.056	0.004	0.0311,2,3
17-NB	Northeast/South (“d”)	5	0.100	0.101	0.089	0.048	0.004	0.003
18-WAM†-s	South	14	0.132	0.137	0.127	0.074	0.020	−0.0351,2,3
		24	0.134	0.122	0.131	0.087	0.043	0.1011,2,3

Geographic region of origin and assignment to admixture zones “a”–“d” if applicable (Beadell et al., 2010; Echodu et al., 2013; Opiro et al., 2017), sample size (N) and statistics from stacks v.1.34 software (Catchen et al., 2013) including sample-wide nucleotide diversity in the 55,267 representative SNPs (Pi; one SNP per ddRAD fragment), sample-wide observed heterozygosity (H_O), and sample-wide expected heterozygosity (H_E), statistics from plink version 1.9 (Purcell et al., 2007) including the proportion of locus pairs in linkage disequilibrium in this sample (P_LD) and the proportion of loci in Hardy–Weinberg disequilibrium in this sample (P_HWD), and sample-wide inbreeding fixation index (F_IS) calculated in the “hierFSTAT” R package (Goudet and Jombart, 2015). F_IS values are marked with ¹ if significantly different from zero with p < 0.02 based on 1,000 bootstrap replicates, with ^1,2 if p < 0.02 after Benjamini–Hochberg correction for multiple testing, and with ^1,2,3 if p < 0.02 after Bonferroni correction for multiple testing (Supporting Information Table S4). Samples that were used to represent the four pure genetic backgrounds are marked † followed by the abbreviation of the genetic cluster it represents (northwest: NW, northeast: NE, west: W, south: S).

From the northwest cluster (Table 1; Beadell et al., 2010; Opiro et al., 2017), we sampled from the Albert Nile watershed, which is characterized by lowland woodlands and gallery forest. This habitat extends north into South Sudan and west into the Democratic Republic of the Congo (DRC).

From the northeast cluster (Table 1; Beadell et al., 2010; Opiro et al., 2017), we sampled from the Lake Kyoga watershed, which is characterized by marsh and swampland. This region is bordered to the north and east by the edge of the G. f. fuscipes distribution where it is too dry to support the vector.

From the west cluster (Table 1; Beadell et al., 2010), we sampled the Lake Albert and the Kafu River watersheds, which contain patchy gallery forest along the major rivers. This region is bordered to the west by protected forests (Masindi National Park), where ecological competitors G. pallidipes, G. palpalis and G. brevipalpis are dominant (Abila et al., 2008), and to the west and south by elevation that is too high and temperatures that are too cool for G. f. fuscipes.

From the south cluster (Table 1; Beadell et al., 2010), we sampled from the Lake Victoria watershed, where urbanization has greatly reduced the available habitat down to a small strip of habitat along the lake and river shorelines. This region is bordered to the east and south by the edge of the G. f. fuscipes distribution where savannah habitat favours the ecological competitor G. pallidipes (Abila et al., 2008; Ciosi, Masiga, & Turner, 2014).

We also sampled from the Achwa and the Okole River watersheds, which are geographically intermediate to the centres of the northwest and northeast genetic clusters (Figure 1; Table 1; Beadell et al., 2010; Opiro et al., 2017). These watersheds were problematic to assign to a single genetic cluster because flies from these watersheds are a mix of the northwest, northeast and west genetic backgrounds (Figure 1: admixture zones “a” and “b”; Opiro et al., 2017; Saarman et al., 2018). The habitat in these watersheds is a mix of lowland woodlands characteristic of the northwest and swampland characteristic of the northeast.

2.2 ∣. DNA extraction and ddRAD sequencing library preparation

DNA for the ddRAD protocol was extracted from the heads, thorax, wings and legs of 254 G. f. fuscipes starting individuals (later reduced to 251 after removing individuals with low-quality sequence data) using Qiagen DNeasy blood and tissue extraction kits (Qiagen, Valencia, CA), with a preliminary step added for tissue pulverization using the Qiagen Bead-beater system. We then quantified DNA extractions with a Qubit 2.0 Fluorometer (Invitrogen, Carlsbad, CA, USA) and proceeded with only individuals having higher than 500 ng total yield of genomic DNA.

ddRAD sequencing libraries were prepared following Gloria-Soria et al. (2016, 2018) using a modified version of the Peterson et al. (2012) protocol with restriction enzymes NlaIII and MluCI and a size selection step that isolated 95- to 105-bp DNA fragments. We created eight ddRAD sequencing libraries of 32 pooled individuals each, which were sent to the Yale Center for Genome Analysis for 75-bp paired-read sequencing with the Illumina Hi-Seq platform under the “high-output” mode and were sequenced in lanes shared with randomly sheared libraries. The final data set includes 251 individuals (5–20 individuals per populations for 18 populations; Supporting Information Table S1). ddRAD-based paired-end short-read sequences for each of the final 251 individuals included in this study are available on NCBI via BioProject Accession no. PRJNA498097.

2.3 ∣. ddRAD sequence processing and SNP calling

The ddRAD library raw sequence reads were de-multiplexed, quality filtered and filtered for unambiguous barcodes using the “process_radtags” script from the stacks v.1.34 software (Catchen, Hohenlohe, Bassham, Amores, & Cresko, 2013). Processed reads were aligned to the 2,395 scaffolds available in the G. fuscipes GfusI1 reference assembly (Giraldo-Calderon, Emrich, MacCallum, Maslen, & Dialynas, 2014) with Bowtie2 v. 2.1.0 (Langmead & Salzberg, 2012) with the default settings, sorted with SAMtools v. 0.1.19 (Li et al., 2009), and analysed for SNPs with stacks. A VCF file of all SNPs was created by using the stacks cstacks script with a training set of 36 individuals from each of the four genetic backgrounds, and then, using pstacks, sstacks and the population script with all of the 251 final individuals in such a way that only SNPs with more than 5X coverage, a minor allele frequency greater than 0.2% and a genotyping rate greater than 80% were retained. Details of this are available in the Supporting Information Appendix S1. Read depth statistics were estimated using VCFtools version 0.1.13 (Danecek, Auton, Abecasis, Albers, & Banks, 2011; flag --geno-depth). Other necessary conversions between file formats (e.g., from VCF format to GenePop format) were performed using PGDSpider v. 2.0.5.2 (Lischer & Excoffier, 2012). The final VCF file contained 55,267 SNPs and 251 individuals from 18 sites that passed all filters.

We used plink version 1.9 (Purcell et al., 2007) to exclude physically linked SNPs with variance inflation factors (VIF) greater than 2 in 100-kb sliding windows (plink flag --indep 100 10 2), which was a far larger window size than the average distance of LD decay estimated at ~3 kb (Gloria-Soria et al., 2016). This reduced the ddRAD data set to 33,057 unlinked SNPs for the population structure analyses, and other analyses wherever noted because these benefit from using physically unlinked loci (Purcell et al., 2007).

2.4 ∣. Microsatellite genotyping

New genotypic data were collected from the 16 microsatellite loci for individuals present in the 251 individual ddRAD data set (Supporting Information Tables S1 and S2) that did not have existing data available from https://doi.org/10.5061/dryad.20b01 (Brown et al., 2008; Beadell et al., 2010; Opiro et al., 2017), using the same protocol as Opiro et al. (2017), which is detailed in Supplementary Methods. In several cases, because there was not enough DNA left to fill missing data gaps, we used different individuals from the same sampling site for the different data sets (Supporting Information Table S2). Thus, the total data set included new genotypic data for 16 loci from 25 new individuals from 5 sites, new data for 5 loci from 27 individuals from 3 sites already analysed at 11 loci by Beadell et al. (2010) and Echodu et al., (2013), and existing data for 16 loci from 194 individuals from 13 sites already analysed at all 16 loci by Opiro et al., (2017), which all together created a data set of 16 loci, 251 individuals, and 18 sites (Supporting Information Tables S1 and S2). 88% of the ddRAD and microsatellite data sets shared the same individuals (222 out of 251; Supporting Information Table S2). All genotypic data included in this study were deposited to Dryad (https://doi.org/10.5061/dryad.98rf2f1).

2.5 ∣. mtDNA sequencing

A 570-bp fragment of the mtDNA spanning the COI and COII genes was PCR-amplified for any individuals present in the final data set of 251 individuals (Supporting Information Tables S1 and S2) that did not have existing data available from GenBank (Accession nos. GU296746-GU296786; Beadell et al., 2010; Opiro et al., 2017). We used the same protocol as Opiro et al. (2017), which are detailed in Supplementary Methods. We were able to include only a subset of the individuals screened for nuclear markers (Supporting Information Table S2) because of low quantity and quality of older DNA extractions. In total, we sequenced 177 additional flies with 5–20 individuals per site and combined these with data for the same fragment from Beadell et al., 2010, Echodu et al., 2013 and Opiro et al., 2017 (Supporting Information Table S2). The total mtDNA data set consisted of 228 mtDNA sequences from 18 sites (Supporting Information Table S1). 82% of all three of the data sets (i.e., the ddRAD, microsatellites and mtDNA data sets) shared the same individuals (206 out of 251; Supporting Information Table S2). All haplotype sequences included in this study were deposited to GenBank (Accession nos. MK094112-MK094173).

2.6 ∣. Genetic diversity and population structure

2.6.1 ∣. ddRAD SNP genetic diversity

For the 55,267 ddRAD fragments, genetic diversity statistics were estimated with the stacks population script. The script was run once to obtain nucleotide diversity (Pi_A) estimates among all sites at both variable (158,537 SNPs at an average density of ~2.85 SNPs per ddRAD fragment) and invariable positions in the 55,267 ddRAD fragments scored. They were also scored a second time considering only a single representative SNP from each of the 55,267 polymorphic ddRAD fragments. This second run provided per-sample estimates of the number of polymorphic sites (PS), the number of private alleles observed (PA), the mean frequency of the major (most frequent) allele at each locus (P), observed heterozygosity (H_O) and expected heterozygosity (H_E). Diversity statistics were summarized by watershed after confirming the relevance of watersheds with an analysis of molecular variance (AMOVA; Supporting Information Appendix S1).

To help interpret the level of secondary contact among genetic units observed in the data, Hardy–Weinberg disequilibrium (HWD) was estimated in all loci (SNPs) as well as linkage disequilibrium (LD) among locus pairs. Relative HWD levels were determined as the proportion of loci in HWD in each sample below the p-value threshold of 0.05 (P_HWD; plink flag --hwe 0.05). Relative levels of LD were estimated with a plink command that determined the proportion of locus pairs in each sample over the D’ threshold of 0.5 (P_LD; plink flag --r2 inter-chr dprime with-freqs gz --ld-window-r2 0.01). The individual inbreeding coefficient relative to the sample (F_IS) was estimated with the Weir and Cockerham's (1984) method using R (R Core Team, 2016) and the “hierFSTAT” R package (Goudet & Jombart, 2015) and assessed for significance with 1,000 bootstrap samplings with corrections for multiple testing with the Benjamini–Hochberg (BH; Benjamini & Hochberg, 1995) and the Bonferroni (BF) methods (Dunn, 1961) in the “stats” R package (R Core Team, 2016).

2.6.2 ∣. ddRAD SNP population structure

We used the LD filtered data set of 33,057 unlinked SNPs to assess ddRAD population structure. Pairwise differentiations among samples were estimated with Wright's F-statistic (F_ST; Wright, 1951) in the “StAMPP” R package (Perrbleton, Cogan, & Forster, 2013) and assessed for significance with 1,000 bootstrap replicates with corrections for multiple testing using BH and BF methods in the “stats” R package. Wright's F_ST was chosen to allow for comparisons with previous G. f. fuscipes studies and among our different data sources. Pairwise F_ST values were used to test for isolation by distance (IBD), as implemented in the “adegenet” R package v. 2.0.1 (Jombart, 2008; Jombart & Ahmed, 2011). Geographic distances were generated using the Java-based “geographic matrix generator” version 1.2.3 (Ersts, downloaded November 2017). The significance of the regression was tested by a Mantel test with 10,000 randomizations (Goudet, Raymond, & Meeüs, 1996; Jombart, 2008; Jombart & Ahmed, 2011; Mantel et al., 1967). We applied the Mantel test to estimates from the full data set, from the northwest and northeast clusters, and from the west and south clusters. We split the samples into two larger clusters instead of the four units and four admixture zones (total of eight groups) for this analysis to allow for large enough sample size for statistical power.

We ran a principal component analysis (PCA) using the “adegenet” R package, which is a multivariate, model-free method that makes no assumptions about absence of HWD and LD. We performed clustering analyses with structure version 2.3.4 (Pritchard & Stephens, 2000) in “adegenet” in R. For structure, we used K (number of clusters) ranging from 1 to 18 (the total number of sites) and ran ten independent replicates with 250,000 iterations and 50,000 burn-in steps were run. The most informative K was assessed with the ad hoc statistic “ΔK” (Earl & Von Holdt, 2012; Evanno, Regnaut, & Goudet, 2005). Results from the ten replicates were combined using clumpak version 1.1 (Kopelman, Mayzel, Jakobsson, Rosenberg, & Mayrose, 2015). We also applied discriminant analysis of principal components (DAPC) as an alternative model-free clustering method and estimated pairwise co-ancestry coefficients with the program finestructure v. 2.0.7 (Lawson, Hellenthal, Myers, & Falush, 2012; Scheet & Stephens, 2006). Details of the DAPC and finestructure methods are available in the Supporting Information Appendix S1.

2.6.3 ∣. Microsatellite genetic diversity

In order to provide a link between the new ddRAD results and the previous estimates from the literature, we estimated observed heterozygosity (H_O), expected heterozygosity (H_E) and allelic richness (A_R). These estimates were made using the R libraries poppr v. 2.3.0 (Kamvar, Brooks, & Grünwald, 2015; Kamvar, Tabima, & Grünwald, 2014), PopGenReport v. 1.0.2 (Adamack & Gruber, 2014; Gruber & Adamack, 2015) and “adegenet.” The SNP and microsatellite-based estimates of diversity were compared with a linear regression, using the “stats” R package. In this analysis, microsatellite allelic richness was regressed against both nucleotide diversity Pi_A (Supporting Information Table S1) and Pi (Table 1).

2.6.4 ∣. Microsatellite population structure

F_IS and pairwise F_ST estimates were made in fstat 2.9.3 (Goudet 1995), and significance was assessed using p-values calculated from 1,000 randomizations. IBD was tested with the pairwise F_ST values, using a Mantel test with 10,000 randomizations implemented with the “adegenet” R package. SNPs and microsatellite F_ST estimates were also compared using a Mantel test with 10,000 randomizations in the “adegenet” R package. As with the ddRAD data set, the microsatellite principal components analysis (PCA) was implemented in the “adegenet” R package, and structure and DAPC analyses were performed with K ranging from 1 to 18.

2.6.5 ∣. mtDNA genetic diversity

To investigate maternal inheritance patterns in the admixture zones, we assessed the genetic diversity and population structure of mtDNA COI sequence data using the program arlequin (Excoffier & Lischer, 2010). Genetic diversity within populations was estimated by computing haplotype (H_d) and nucleotide diversity (N_d; Nei, 1987) in DnaSP version 5.0 (Librado & Rojas, 2009).

2.6.6 ∣. mtDNA population structure

Haplotype relationships were inferred by constructing a parsimony network using TCS (Clement, Snell, Walker, Posada, & Crandall, 2002) implemented in PopART (http://popart.otago.ac.nz/). The distribution of groups of related haplotypes (haplogroups) was visualized by watershed.

2.7 ∣. Biogeographic and demographic history of the admixture zones

2.7.1 ∣. Phylogenetic relationships

We evaluated evolutionary relationships among the sampled populations with the software TreeMix (Pickrell & Pritchard, 2012; Sukumaran & Mark, 2010). We used the ddRAD data set for this analysis because of the three data sets available, this marker type contained the greatest number of phylogenetically informative sites, and because the software is designed to deal with a great number of loci that have variation in their allele frequencies and evolutionary histories. The benefit of this method is that it allows for both population splits and gene flow, which has been long recognized to be the more accurate representation of relationships between populations with potential gene flow (Cavalli-Sforza & Piazza, 1975; Felsenstein 1982; Pickrell & Pritchard, 2012). Details of the TreeMix methods are provided in the Supporting Information Appendix S1.

2.7.2 ∣. Biogeographic and demographic models

We modelled the population history of the major genetic clusters found in Uganda (Figure 1) with approximate Bayesian computation (abc) in diyabc version 2.0.4 (Cornuet et al., 2014) and with migraine version 0.5.2 software (http://kimura.univ-montp2.fr/~rousset/Migraine.htm; Peery et al., 2012; Supporting Information Appendix S1) for comparison. The models focused on northern Uganda where alternative explanations for the patterns of divergence and diversity observed in each genetic cluster are in debate (Beadell et al., 2010; Echodu et al., 2013; Hyseni et al., 2012; Opiro et al., 2016, 2017; Saarman et al., 2018). Both abc and migraine simulations assume panmictic populations unless explicitly specified otherwise, so we used samples from the four watersheds that fell squarely within one of the four major genetic clusters (Figure 1; Table 1; Supporting Information Table S2). The northwest cluster was represented by two sites from the Albert Nile (01-DUK and 02-ORB), the northeast cluster was represented by two sites from Lake Kyoga (10-OCU and 11-OT), the west cluster was represented by two sites from Lake Albert (13-MF and 14-MS), and the south cluster was represented by a single site from Lake Victoria (18-WAM). We also included a sample from admixture zone “b” from the Okole River (Table 1; Supporting Information Table S2) in the abc analysis to allow us to distinguish alternative hypotheses of the formation of this admixture zone.

We used the microsatellite data set for abc and migraine simulations because of the three data sets available, it represented the best balance between being well-characterized (e.g., in terms of mutation model) and having high enough genetic diversity to provide statistical power. We also attempted to run the same analyses with the ddRAD data set, but were unsuccessful in parameterizing the mutation models because of lack of user control of the mutation priors in the case of diyabc, and insufficient compute power in the case of migraine. Details of the unsuccessful ddRAD-based abc analyses are available in Supplementary Methods.

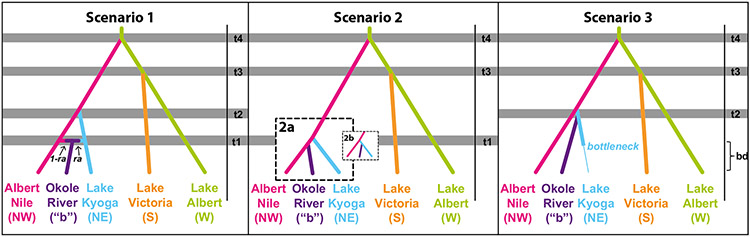
The ABC method is limited by joint estimates of timing of divergences, population size, mutation rate and the mutation model, making it impossible to accurately model simulated data sets based on these interdependent unknown parameters without informed priors. For this reason, priors for ABC models (Supporting Information Table S3) were based on independently derived estimates wherever possible. Mutation priors were based on estimates of microsatellite mutation rates in other insects (Chapuis, Plantamp, Streiff, Blondin, & Piou, 2015) and results from a published ABC analysis in a closely related species, Glossina pallidipes (Ciosi et al., 2014). Population size and bottleneck priors were based on previous population genetics estimates (Beadell et al., 2010; Echodu et al., 2013; Hyseni et al., 2012; Opiro et al., 2016, 2017). Time priors considered average generation time of G. f. fuscipes of 8 per year (45 days; Krafsur, 2009) and were based on the geologic history. We applied these time priors with caution using a three-step preliminary analysis (Supporting Information Appendix S1). In the first step of the preliminary analysis, the time priors were minimally restricted (<650 ka; Supporting Information Table S3) based on independent records of geologic events (Supporting Information Figure S1) that are well established to have driven patterns of tsetse population connectivity in Uganda at ~400, ~20–40 and ~10–20 ka (Supporting Information Figure S1; Beadell et al., 2010; Opiro et al., 2017). However, from the first step of the preliminary analysis, posterior estimates were unrealistically recent and truncated by zero. Thus, considering that all priors were interdependent, to make the models more realistic we performed two more steps of the preliminary analysis with increased specificity based on more detailed biogeographic scenarios that were built from independent records of geologic events (Supporting Information Figure S1) and published population genetics data (Beadell et al., 2010; Opiro et al., 2017; Saarman et al., 2018). There were three major river reorganizations in the region that would have impacted tsetse distribution and connectivity: (a) Lake Victoria formed ~400 ka and reversed the direction of flow of the major river systems from west to north (Supporting Information Figure S1a; Williams, Adamson, Prescott, & Williams, 2003; Danley et al., 2012), (b) the outflow from Lake Victoria altered its course to connect through Kafu River to Lake Albert ~20–40 ka (Supporting Information Figure S1b; Bishop, 1969) and (c) the outflow from Lake Victoria altered its course a third time to bypass the Kafu River and to connect directly to Albert Nile through Murchison falls (Supporting Information Figure S1c; Talbot & Williams, 2009). We used these timings of geologic events to refine the time priors during the preliminary analysis stage and then compared three alternative scenarios in the final ABC analysis:

Scenario 1 modelled the possibility that divergence among the four genetic backgrounds in Uganda was created during geologic events ~400 (Figure 2 and Supporting Information Figure S2a: t4), ~20–40 (Figure 2 and Supporting Information Figure S2b: t3) and ~10–20 ka (Figure 2 and Supporting Information Figure S2c: t2) and that the admixture zone “b” represents secondary contact between the northwest and northeast lineages, which is an idea proposed by Opiro et al. (2017).

FIGURE 2.

Schematic of competing scenarios 1–3 tested in diyabc (Cornuet et al., 2014) to evaluate the relative probability of (a) divergence followed by secondary contact (Scenario 1), (b) ongoing gene flow or very recent and incomplete divergence (Scenario 2) with the alternative topologies 2a and 2b, (c) and the role of a bottleneck (shown with the transition from a thick to thin line; Scenario 3) in shaping the patterns of genetic variation observed in G. f. fuscipes populations in Uganda. Each panel shows the topology and population fluctuations specified in the scenario, wherein Ne was free to vary 100–30,000, or 100–5,000 during a bottleneck. Time priors are shown in shading (not to scale) and are labeled on the right of each scenario (t4 = 340–360 ka, t3 = 20–40 ka, t2 = 10–20 ka, t1 = 5–135 years ago). “ra” refers to rate of admixture, and was allowed to vary from 0 to 1. “bd” refers to the bottleneck duration, and was allowed to vary from 1.25 to 5,000 years ago (Supporting Information Table S3), which corresponds to a final desiccation event that was thought to occur in the Lake Kyoga region (Danley et al., 2012).

Scenario 2 modelled the possibility that divergence among the four genetic backgrounds in Uganda was created during geologic events ~400 (Figure 2 and Supporting Information Figure S2a: t4) and ~20–40 ka (Figure 2 and Supporting Information Figure S2b: t3) and that the admixture zone “b” represents ongoing divergence with gene flow or incomplete divergence between the northwest and northeast (Figure 2 and Supporting Information Figure S2a: t1), which is an idea proposed by Saarman et al. (2018) and is based on theoretical considerations (Falush, VanDorp, & Lawson, 2016; Frantz, Cellina, Krier, Schley, & Burke, 2009; Meirmans, 2012).

Scenario 3 modelled the possibility that divergence among the four genetic backgrounds in Uganda was created during geologic events ~400 (Figure 2 and Supporting Information Figure S2a: t4), ~20–40 (Figure 2 and Supporting Information Figure S2b: t3) and ~10–20 ka (Figure 2 and Supporting Information Figure S2c: t2) and that the signal of admixture is a false one caused by a bottleneck event in one of two closely related lineages, a scenario outlined in Falush et al. (2016). We modelled the time of the possible population bottleneck at 0–5 ka, as this is the time frame that could have allowed for some divergence to accumulate between the northwest and northeast, before changing environmental conditions due to the final desiccation event in the Lake Kyoga region ~5 ka (Danley et al., 2012) and/or anthropogenic effects (Rinderpest, population displacement and recent vector control campaigns) of the past 135 years or so (Van Acker, 2004; Carmichael, 1938; Egeru et al., 2014; Gorsevski, Kasischke, Dempewolf, Loboda, & Grossmann, 2012) may have triggered dramatic shifts in population sizes.

2.7.3 ∣. Biogeographic and demographic parameter estimates

We estimated summary statistics from the simulated data to allow for comparison among the three final alternative scenarios and the observed microsatellite data. We recorded the number of alleles, mean heterozygosity and the M-index (Garza & Williamson, 2001; Excoffier, Estoupe, & Cournuet, 2005) for each lineage, and the mean pairwise F_ST distances (Weir & Cockerham, 1984) for each pair of lineages, for a total of 25 summary statistics. PCA was then performed on these 25 summary statistics to compare posterior estimates and to choose the scenario that had the closest match with the observed microsatellite data using the weighted logistic regression method described by Fagundes, Ray, Beaumont, Neuenschwander, and Salzano (2007). We also estimated the posterior predictive error with the method described by Cornuet et al., (2014) to confirm reliability of the model. For the ABC parameter estimates (Ne, timing of divergence events, admixture rates and mutation rates), the mean, median and 95% confidence intervals were drawn from the linear regression of the 1% of the simulations of the winning scenario that were closest to the observed microsatellite data.

For comparison, migraine analysis modelled demographic history assuming an exponential change in population size from the ancestral time point continuing until the current time point, which is the basic coalescence model (Leblois et al., 2014). This provided estimates of genetic diversity of the current sample (θ) and the hypothetical ancestral sample (θ_anc), and estimates of Ne (Supporting Information Appendix S1).

2.8 ∣. Characterization of genome-wide introgression in admixture zones

To understand the degree of allele frequency divergence and hybridization occurring in each of the four admixture zones, we used the LD filtered data set of 33,057 unlinked SNPs to characterize the absolute delta allele frequency, ∣Δp∣, across each admixture zone “a,” “b,” “c” and “d,” using the “introgress” R package v. 1.2.3 (Gompert & Buerkle, 2009). The ddRAD SNPs were the most appropriate genetic marker type to use in this analysis because they are randomly distributed at high density (~1 SNP per ~210 bp) across the genome. To establish the allele frequencies of each parental type, we used the same representatives of each of the four pure genetic clusters (Table 1 and Supporting Information Table S2) as used in the ABC analysis after confirming that each individual had high assignment (q-values >0.8) to a single cluster in the current study. For admixture zones “a,” “c,” and “d,” we maximized accuracy by only considering SNPs with ∣Δp∣ greater than 0.8 to estimate “interspecific” heterozygosity and “hybrid index,” a practice recommended by the authors of introgress (Gompert & Buerkle, 2009). For admixture zone “b” there were no ∣Δp∣ values >0.8, so we only considered SNPs with ∣Δp∣ > 0.5.

For comparison with the patterns of ∣Δp∣, we also estimated locus-by-locus F_ST values and tested for F_ST outlier loci using the R package OutFLANK version 0.2 (Whitlock & Lotterhos, 2015) with the same ddRAD data set used for the introgress analysis. Overlap of loci with F_ST with a right-tailed p-value >0.02 among the four admixture zones was assessed using the free online Venn diagram bioinformatics tool http://bioinformatics.psb.ugent.be/webtools/Venn/.

3 ∣. RESULTS

3.1 ∣. ddRAD sequencing statistics

Sequencing and diversity statistics of the ddRAD fragments indicated adequate coverage in all samples included in the final analyses (Supporting Information Figure S2; Table S1). Read depth per individual averaged 85.9 (range, 32.7–269.3) with its standard deviation averaging 650 (range, 62–1,446; Supporting Information Table S1). The majority (92.8%) of the aligned ddRAD fragments contained polymorphisms, as only 3,938 ddRAD fragments (7.2%) were removed during the stacks pipeline because they were invariant. The retained variant 55,267 ddRAD fragments contained 2.85 SNPs on average. Considering only the first SNP per fragment (to avoid scoring highly linked SNPs), the number of polymorphic sites (PS) per sample averaged 28,093 (range, 13,739–36,395; Supporting Information Table S1). This estimate appeared to be driven in large part by the sample number, because the lowest estimates of polymorphic sites were at sites with small sample sizes (Supporting Information Figure S2). The number of private alleles (PA) per sample averaged 348 (range, 46–1,025; Supporting Information Table S1). The mean of the major (most frequent) allele (P) at each locus averaged 0.89 (range, 0.87–0.93; Supporting Information Table S1). Among all sites, including both variant and invariant sites in the 55,267 ddRAD fragments scored, nucleotide diversity (Pi_A) averaged 0.006 (range, 0.004–0.007; Supporting Information Table S1). This equates to a genome-wide density of about 1 SNP per 150–270 bp after accounting for the 7.2% of ddRAD fragments that did not contain polymorphism.

3.2 ∣. Genetic diversity and population structure

3.2.1 ∣. ddRAD SNP diversity

Among the 55,267 SNPs in the ddRAD data set, sample-wide nucleotide diversity (Pi) averaged 0.15 (range, 0.10–0.19; Table 1). Sample-wide observed (H_O) and expected (H_E) heterozygosity averaged 0.15 with similar ranges (range, 0.10–0.21 and 0.09–0.18, respectively; Table 1). The proportion of loci in HWD in this sample (P_HWD) averaged 0.05 (range, 0.00–0.12; Table 1). The proportion of locus pairs in linkage disequilibrium in this sample (P_LD) averaged 0.15 (range, 0.05–0.22; Table 1). Sample-wide inbreeding F_IS averaged 0.04 (range, −0.17 to 0.23; Table 1). Bootstrap resampling indicated that most samples were slightly but significantly different from zero after BH and BF correction for multiple testing (Supporting Information Table S4), indicating slight HWD. The AMOVA results confirmed that there was significant partitioning of molecular variance among the seven watersheds (p-value <0.001), with 68.9% of the variation found among watersheds, 12.9% found among sites, and 20.3% found within sites (Supporting Information Table S5).

3.2.2 ∣. ddRAD SNP population structure

Pairwise F_ST indicated substantial population differentiation at small spatial scales of less than 50 km (Supporting Information Table S6). All but one of the SNP-based pairwise estimates of differentiation were significantly greater than zero (Supporting Information Table S6, above the diagonal), even after correcting for multiple comparisons (Supporting Information Table S7). The Mantel test for IBD indicated a significant effect of geographic distance on level of differentiation (p-value=0.047), as well as among the northwest and northeast (p-value=0.022), but not among the west and south (p-value=0.711; Supporting Information Figure S3a).

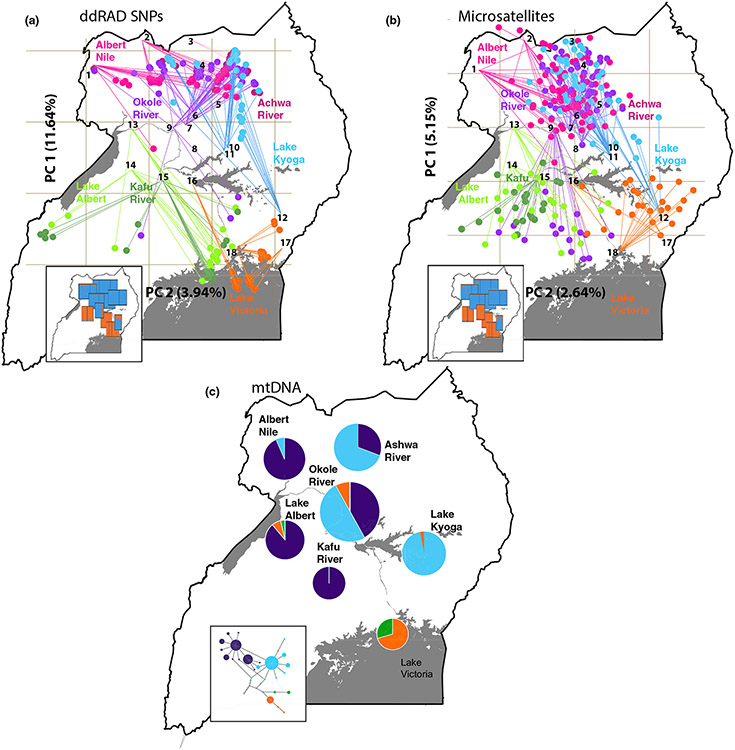
The results of the PCA on the SNPs data set identified genetic structure with a clear geographic component (Figure 3a; Supporting Information Figure S4). The first PC explained 11.64% of the total variance and separated samples north to south. The northwest and northeast (Albert Nile, Achwa River, Okole River and Lake Kyoga) and the south and west (Lake Albert, Kafu River and Lake Victoria) largely grouped together. The second PC explained 3.95% of the total variance and separated samples west to east (Figure 3a), highlighting differentiation between the west and south (i.e., Lake Albert and Kafu River from Lake Victoria) but not between the northwest and northeast ones (i.e., Albert Nile from Lake Koga). The results of structure and DAPC clustering analyses indicated an optimal K-value of two (Supporting Information Figure S5). They agree with the clustering pattern from the PCA, finding structure between the west and south, but no structure between the northwest and northeast (Supporting Information Figures S6 and S7; Table S8).

FIGURE 3.

Genetic structure of Glossina fuscipes fuscipes in Uganda, including (a) principle components analysis (PCA) plots for 55,267 ddRAD SNPs, (b) PCA plots for 16 microsatellites, and (c) the frequency of groups of related mtDNA COI-COII haplotypes. In (a) and (b) each individual is indicated with a point connected by a line to the site of origin, and are colored by watershed of origin (Albert Nile in pink, Ashwa River in magenta, Okole River in purple, Lake Kyoga in blue, Lake Albert in light green, Kafu River in dark green and Lake Victoria in orange; see Supporting Information Table S4) for PCA plots of PC1-PC4 without the map), and the insets display structure version 2.3.4 (Pritchard & Stephens, 2000) results at K=2 (see Supporting Information Table S6) for full size). In (c), groups of related haplotypes are shown in the same colors (Haplogroup A in purple, Haplogroup B in blue, Haplogroup C in orange, and Haplogroup D in green), and the inset displays the TCS haplotype network (see Supporting Information Table S11) for full size).

finestructure identified 10 and 75 major and minor clusters, respectively (Supporting Information Figure S8; horizontal lines numbered 1–10 along the top). The 10 major clusters identified the same groups as the PCA and clustering analysis. Major clusters c1–c7 contained northwest and northeast samples only, whereas the major clusters c8–c10 contained west and south samples only (Supporting Information Figure S8; Table S9).

3.2.2 ∣. Microsatellite diversity

Genotypic diversity of the 16 microsatellite loci (Supporting Information Table S10) was strongly correlated with the results from the SNP-based estimates (p-value <0.001; Supporting Information Figure S9). Allelic richness averaged 3.02 (range, 2.38–3.59; Supporting Information Table S10), observed heterozygosity averaged 0.55 (range, 0.45–0.64 (Supporting Information Table S10), and expected heterozygosity was generally higher than the observed one (average = 0.60, rage, 0.47–0.70; Supporting Information Table S10). F_IS averaged 0.08 (range, −0.07 to 0.21; Supporting Information Table S10). Bootstrap resampling indicated that seven of the 12 samples from the north (northwest, admixture zone “b,” or northeast) were significantly different from zero after BH correction for multiple testing (Supporting Information Tables S4), indicating HWD. In contrast, none of the west or south samples had F_IS values significantly different from zero (Supporting Information Table S10). The AMOVA results on this data set confirmed that there was significant partitioning of molecular variance among the seven watersheds (p-value <0.001), with 7.1% of the variation found among watersheds, 8.3% found among sites, and 84.6% found within sites (Supporting Information Table S5).

3.2.4 ∣. Microsatellite population structure

Pairwise F_ST values indicated significant population differentiation (Supporting Information Table S11) even after correcting for multiple testing (Supporting Information Table S7). The Mantel test for IBD indicated a significant effect of geographic distance on level of differentiation among all samples (p-value 0.047), as well as among the northwest and northeast (p-value 0.016), but not among the west and south (p-value 0.248; Supporting Information Figure S3b). These estimates were also strongly correlated with the results from the SNP-based estimates (p-value <0.001; Supporting Information Figure S3c), and all were significant after BH correction but non-significant after BF correction (Supporting Information Table S7).

Principal component analysis with the 16 microsatellites (Figure 3b) corroborates the strong geographic component in the genetic structure found with the SNPs, with strong north-to-south, and weak west-to-east differentiation. The clustering analysis assigned individuals to two genetic clusters (K = 2; Supporting Information Figure S5), with the same general groups found in the SNP-based analysis but with several differences (Figure 3b; Supporting Information Figures S6b and S10). Differences included grouping of the admixture zone “a” sample with the west (Lake Albert and Kafu River) rather than with the other Okole River (Supporting Information Figure S6), and substructure between the northwest and the northeast (Albert Nile from Lake Kyoga) at K = 4 (Supporting Information Figure S6b).

3.2.5 ∣. mtDNA genetic diversity

Sequencing identified 25 mtDNA haplotypes (Supporting Information Table S10) representing four groups of related haplotypes (haplogroups) in the TCS network (Supporting Information Figure S11). The number of haplotypes at each sampling site ranged from one to six (Supporting Information Table S10). Sixteen haplotypes were singletons (8 were haplogroup A, seven were haplogroup B, one was Haplogroup C, and one was haplogroup D). Haplotype diversity averaged 0.52 and ranged from 0.20 to 0.80, and nucleotide diversity averaged 0.0028 and ranged from 0.0011 to 0.0071 (Supporting Information Table S10). The mtDNA-based AMOVA results confirmed that there was significant partitioning of molecular variance among the seven watersheds (p-value = 0.012), with 28.2% of the variation found among watersheds, 27.6% found among sites, and 20.3% found within sites (Supporting Information Table S5).

3.2.6 ∣. mtDNA population structure

The distribution of haplogroups indicated spatial structuring (Figure 3c). Haplogroup A (purple) was most frequent in the northwest (Albert Nile, 94.4%) and west (Lake Albert and Kafu River; 79.1%, and 93.2%), occurred less commonly in admixture zone “b” (Achwa and Okole River; 17.2% and 24.0%), rarely in the northeast (Lake Kyoga; 4.8%), and not all in the south (Lake Victoria). Haplogroup B (blue) showed the opposite pattern, with high frequency in the northeast (Lake Kyoga; 95.2%) and low frequency in the northwest (Albert Nile, 5.6%; Figure 3c). Haplogroup C occurred only in the west (Lake Albert and Kafu River; 21.1%, 6.8%) and south (Lake Victoria; 95.2%). Haplogroup D occurred only once in the south (Lake Victoria; 4.8%).

3.3 ∣. Biogeographic and demographic history of the admixture zones

3.3.1 ∣. ddRAD SNP phylogenetic trees

Results from TreeMix confirmed the clustering found in the PCA, structure and DAPC analysis, with strong support for a split between the north (northwest, admixture zone “b” and northeast) samples and the combined west and south samples, but no support for separation of the northeast from the northwest (Supporting Information Figure S12a). This analysis identified migration and subsequent introgression across admixture zones “a” and “d.” Migration was predicted from the west (Kafu River) into the northeast (Albert Nile; 15-KAF to 01-DUK; Supporting Information Figure S12a) and from the south (Lake Victoria) into the northeast (Lake Kyoga; 17-NB to 12-BN; Supporting Information Figure S12a). In addition, the residual fit (Supporting Information Figure S12b) indicated positive values across admixture zone “c,” suggesting admixture beyond the two migration events identified in the tree. These positive residuals occurred between the south (Lake Victoria) and the west (Lake Albert and Kafu River; between 16-JN and 14-MS/15-KAF). There was no signal of migration or admixture across admixture zone “b.”.

3.3.2 ∣. Biogeographic scenarios modelled by ABC

The step 1 preliminary ABC analysis yielded time parameter estimates that were unrealistically low and truncated atzero (Supporting Information Figure S13). To resolve this problem, we included two more preliminary analyses (step 2 and step 3) that restricted the priors to increasingly narrow timings (Supporting Information Table S3) consistent with what is known of the geologic history of the region (Supporting Information Figure S1; Williams et al., 2003; Bishop, 1969; Danley et al., 2012). We then used the posterior distribution from step 3 of the preliminary analysis to inform the priors in the final analysis.

The final microsatellite-based ABC analysis indicated that Scenario 2 (Figure 2b) had the highest posterior probability (0.999) regardless of the topology used (Table 2). This scenario simulated the hypothesis that the signal of admixture in northern G. f. fuscipes populations was caused by ongoing gene flow or incomplete divergence between the northwest and northeast. Summary statistics from simulations under Scenario 2 (Supporting Information Table S13c) were the closest match to the observed data as compared to the other scenarios (Supporting Information Figure S14c) and were a close fit to the observed data in general (Supporting Information Figure S14). Results from the similar analysis attempted with the ddRAD SNPs did not show the same match of simulations with real data (Supporting Information Figure S14), but they did in fact indicate agreement with the microsatellite-based ABC analysis (Supporting Information Table S14). However, these results were unreliable because the only SNP mutation model available in diyabc (Cornuet et al., 2014) did not provide a good match of the modelled data with the observed SNP data under any preliminary settings or final scenarios modelled (Supporting Information Figure S14a) and could not be improved because of the lack of user choices in the diyabc interface (Cornuet et al., 2014).

TABLE 2.

Results from the ABC analysis on northern Uganda implemented in diyabc (Cornuet et al., 2014) based on the main topology 2a (Figure 3). (a) Posterior probabilities of competing scenarios by the polychotomic weighted logistic regression method (Cornuet et al., 2008), and 95% confidence interval for the microsatellite data set. (b) Parameter estimates based on the winning Scenario 2 including the mean, 95% confidence interval (CI), median and mode of the posterior distribution, and the description of each parameter estimated

(a)
Data set	Scenario 1	Scenario 2	Scenario 3	Error	Best scenario
Microsatellites	0.000 [0.000–0.000]	0.999 [0.999–1.000]	0.000 [0.000–0.000]	0.000	2
(b)
Parameter	Mean	CI	Median	Mode	Description
t1 (yrs)	95	40–128	102	118	Northwest/admixture zone “b” divergence
t2 (yrs)	123	101–135	126	135	Northwest/northeast divergence
t3 (yrs)	22,625	20,125–31,000	21,125	20,125	West/south divergence
t4 (yrs)	416,250	353,750–457,500	423,750	457,500	West/northwest divergence
N1	23,800	16,800–28,700	24,300	25,500	Ne of northwest lineage
N2	14,000	6,860–28,400	13,100	9,780	Ne of admixture zone “b”
N3	16,600	2,950–22,800	16,100	14,900	Ne of northeast lineage
N4	12,600	5,020–21,600	12,000	11,900	Ne of west lineage
N5	11,500	3,700–15,900	11,100	10,700	Ne of south lineage
μ	1.13E–04	1.00–1.58E–04	1.06E–04	1.00E–04	Mutation rate
p	0.1940	0.1340–0.2780	0.1930	0.1850	Geometric distribution of change in repeat length

Time estimates (t1, t2, t3 and t4) are expressed in years (yrs), effective population size estimates (N1, N2, N3, N4, N5) are expressed in number of breeding individuals. We also report estimates of the microsatellite mutation rate (μ) and geometric distribution of change in repeat length (P). See Figure 2 for schematics of the three scenarios and Supporting Information Table S3 for details of the priors used.

3.3.3 ∣. Biogeographic and demographic parameter estimates

The final microsatellite-based ABC simulations under the winning Scenario 2 indicated a mutation rate of ~1.15E-4 (Tables 1 and Supporting Information Table S13), and a geometric distribution of change in repeat length of ~0.2 (Tables 1 and Supporting Information Table S13). With this scenario, divergence between the northwest and northeast was estimated at ~61–123 years ago, divergence between the south and the west was estimated at ~22–23 ka, and divergence between the northwest/northeast and the south/west was estimated at ~390–416 ka (Tables 1 and Supporting Information Table S13). Ne was modelled at an average of 15,082, and ranged from a low of 8,780 in the south cluster to a high of 23,800 in the northwest cluster (Tables 1 and Supporting Information Table S13).

In the migraine simulations, Ne averaged 4,933, and ranged from a low of 2,465 in the south to highs of ~6,000 in the northeast and northwest (Supporting Information Table S12). The only significant change in population size detected in the migraine simulations was in the west, with an estimated doubling from 2,530 to 5,632 since the time of coalescence of all microsatellite diversity observed in the contemporary sample (Supporting Information Table S12).

3.4 ∣. Characterization of introgression in the admixture zones

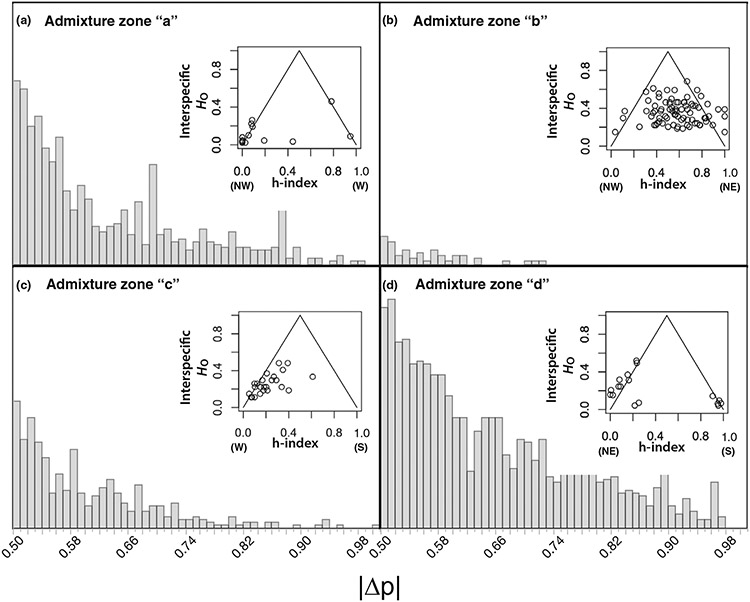
The INTROGRESS analysis indicated greater divergence in allele frequency (∣Δp∣) between parental samples for admixture zones “a,” “c,” and “d” than for admixture zone “b” (Figure 4). Of the 33,057 SNPs that passed the filters for unlinked loci, 797, 54, 605 and 1,451 SNPs had ∣Δp∣ > 0.5, and only 89, 0, 20 and 108 SNPs had ∣Δp∣ greater than 0.8 across admixture zones “a,” “b,” “c” and “d,” respectively (Figure 4a,c,d).

FIGURE 4.

Characterization of the Glossina fuscipes fuscipes admixture zones in Uganda using INTROGRESS v. 1.2.3 (Gompert & Buerkle, 2009) for (a) admixture zone “a”, (b) admixture zone “b”, (c) admixture zone “c”, and (d) admixture zone “d”. The main plots show the histograms of the absolute allele frequency difference (∣Δp∣) estimated from 33,057 unlinked ddRAD SNPs. Insets show triangle plots of the “interspecific” heterozygosity (H_O) against “hybrid index” (h-index) estimated with a subset of SNPs with high ∣Δp∣ (0.8 for admixture zones “a”, “c”, and “d”; 0.5 for admixture zone “b”), wherein first generation hybrids appear at the apex, advanced generation hybrids occur in the center, and parental types occur in the bottom left/right, with the genetic cluster that represents that parental type indicated with abbreviations: northwest (NW), northeast (NE), west (W), south (S).

Estimates of ∣Δp∣ and introgression suggested two general patterns. In the admixture zones “a” and “d,” most individuals were classified as parental types (h-index 0 or 1 with H_O < 0.5; insets of Figure 4a,d). In contrast, in the admixture zones “b” and “c,” individuals were classified as a wide range of advanced generation hybrids and backcrosses (h-index 0–1 and H_O < 0.5; insets of Figure 4a,d), suggesting many generations of interbreeding.

No matter the admixture zone, results indicate there are no first-generation (F1) hybrids in this study, as there is a gap in data points at the apex of each of the triangle plots (h-index of 0.5 and H_O > 0.5; insets of Figure 4). The single individual with an h-index close to 0.5 in admixture zone “a” had a very low estimated H_O value (much lower than 0.5, indicating it was not a true F1; Figure 4a). Instead, this outlier may be caused by incomplete characterization of the “parental” samples for this admixture zone, which is especially likely because of the geographic proximity of admixture zones “a,” “b” and “c” to the representative sampling site (09-UWA) in central Uganda (Figure 1). We also found some asymmetry in h-index scores in admixture zone “c,” where more individuals had h-index scores closer to the west (Lake Albert) genetic background (ranging from 0 to 0.5; inset of Figure 4c) than the other way around. This could reflect a biological reality, but might also be caused by sparse sampling across admixture zone “c.” More samples from this zone, especially to the east of the current samples, are needed to resolve the biological reality.

The distribution of F_ST values across each of the admixture zones (Supporting Information Figure S15) mirrored the distribution of ∣Δp∣. However, after appropriate corrections for multiple testing, outlier tests failed to identify statistically significant F_ST outliers in any of the admixture zones (Supporting Information Figure S16; Table S15), presumably because of small sample sizes (Table 1).

4 ∣. DISCUSSION

Our goal was to investigate the genetic structure, biogeographic context, and rates of hybridization and introgression in four G. f. fuscipes admixture zones in Uganda (Figure 1) to provide insight on the evolutionary and ecological processes important in diversification in this group of flies. We demonstrate that three of the four admixture zones were likely caused by hybridization during secondary contact, but that the third admixture zone “b” could instead be the outcome of ongoing divergence with gene flow, very recent divergence, or represent the remnants of an old collapsed hybrid zone. We find no F1 hybrids in any of the admixture zones and a dichotomous pattern of introgression (Figure 4) that could reflect weak reproductive barriers and early-stage speciation or nearly complete reproductive barriers and late-stage speciation. These findings provide preliminary support for the hypothesis that coupling of multiple isolating barriers may have accelerated the transition from early to late stages of speciation in G. f. fuscipes admixture zones.

4.1 ∣. Genetic structure

The SNP-based PCA (Figure 3a), clustering analyses (Figure 3a, Supporting Information Figures S6a and S7) and finestructure analysis (Supporting Information Figure S8) generally supported K = 2, with clear substructure between the west (Lake Albert) and the south (Lake Victoria), and less consistent substructure between the northwest (Albert Nile) and the northeast (Lake Kyoga) samples (Figure 3). There was a stronger signal of substructure in the microsatellites than in the SNPs. Stronger substructure could be the result of higher mutation rates in the microsatellites than in the average SNP scored across the entire genome. This is supported by the AMOVA results (Supporting Information Table S5), which indicated that the majority of the microsatellite variance occurred within sites (84.3%), while the majority of the SNP variance occurred among watersheds (68.9%; Supporting Information Table S5). This high within-site variation in the microsatellites is likely a consequence of recent mutations that arose within the last hundreds of generations and have remained at low frequency in the individuals at their site of origin because of limited exposure to the effects of genetic drift and migration. In contrast, the high among-watershed variation in the SNPs is likely a consequence of some ancient mutations that have diverged in allele frequency because of prolonged exposure to the effects of genetic drift and migration within watersheds and have caused a lower genome-wide estimate of within-site variation in the SNPs relative to the microsatellites.

Genetic structure was slightly different in the mtDNA than the nuclear markers. The major genetic break between the northeast/northwest and west/south samples occurred much further south. One possible cause of discordance could be the spatial dynamics of a moving contact zone (Barton & Turelli, 2011; Currat et al., 2008). A moving hybrid zone can result in preferential introgression of organelle genes from the local into the expanding population because of the higher probability of a hybrid backcrossing with the expanding population and the smaller Ne of organelle than nuclear genomes (Currat et al., 2008). Thus, the incongruence of mtDNA and nuclear genetic structure could suggest that there have been recent range expansions northwards of the west and south clusters. This hypothesis is supported by migration estimates from previous studies (Beadell et al., 2010; Echodu et al., 2013) as well as the TreeMix results in this study, which identified migration events from admixture zone “c” (Kafu River) into the northeast (Albert Nile; Supporting Information Figure S12a) and from the south (Lake Victoria) into the northeast (Lake Kyoga; Supporting Information Figure S12a). This hypothesis is also supported by the population expansion in the west supported by the demographic estimates from the migraine analyses (Albert Nile; Supporting Information Table S12), which could also indicate range expansion.

Another possible cause of discordance between the mitochondrial and the nuclear markers is asymmetrical isolation. One cause of asymmetrical isolation could be maternally inherited intracellular parasite Wolbachia, which can cause cytoplasmic incompatibility (CI) in G. f. fuscipes (Aksoy et al., 2013; Alam et al., 2012). Cytoplasmic incompatibility impacts the reproductive success and inheritance patterns because Wolbachia can prevent the formation of viable offspring in crosses of infected with uninfected individuals. Wolbachia infections in G. f. fuscipes are associated with the most common mtDNA haplotypes in Uganda (Symula et al., 2013), suggesting a potential fitness advantage of individuals with Wolbachia. If this is true, then Wolbachia would more strongly influence the inheritance patterns of the G. f. fuscipes mitochondrial genome than it would the nuclear genome. This implies that Wolbachia could have aided in the spread of the most common mitochondrial haplotypes beyond their original native range, thus accounting for discordance in the geographic placement of the genetic break in mitochondrial vs. nuclear markers in this study (Figure 3). In this case, since the boundary between northern and southern mitochondrial haplotypes (Figure 3c) falls further south than the boundary between the major nuclear genetic clusters (Figure 3a,b), Wolbachia-induced CI may have caused the southward spread of the mitochondrial haplotypes originating in northern Uganda. Since the resulting pattern would look much the same as the result of the alternative hypothesis (i.e., preferential introgression southwards of organelle genes during range expansion of nuclear genotypes northwards), more data are needed to test this hypothesis. Future research that examines the maternal transmission efficiency of Wolbachia in G. f. fuscipes and CI expression will provide insights into which mechanisms may have established the observed G. f. fuscipes mitochondrial/nuclear discordance in central Uganda.

4.2 ∣. Genetic diversity and linkage and Hardy–Weinberg disequilibrium

Estimates from the SNP and the mitochondrial data sets generally showed the same patterns of genetic diversity and aligned with previous studies of the nuclear genome (Beadell et al., 2010; Echodu et al., 2013; Hyseni et al., 2012; Opiro et al., 2016, 2017). SNP diversity (nucleotide diversity) and microsatellite diversity (allelic richness) shared a general trend (Supporting Information Figure S9), with higher estimates in the north than in the south (Table 1; Supporting Information Table S10). This latitudinal gradient was observed and shown to be statistically significant by Beadell et al. (2010) and Opiro et al., (2017), and it has been suggested that this pattern reflects higher connectivity of northwestern populations of G. f. fuscipes to the rest of the G. f. fuscipes geographic distribution to the north in South Sudan and west in the Demographic Republic of the Congo (DRC) and beyond, where most of its range lies. This gradient of genetic diversity could also reflect larger population sizes and or more long-term demographic stability in the northwest than other parts of Uganda. The mtDNA results did not show a latitudinal gradient, but instead showed slightly elevated diversity in the admixture zones (Supporting Information Table S10). This is expected because maternal inheritance of mitochondrial genomes prevents recombination, making haplotype and nucleotide diversity additive in localities that contain descendants from multiple lineages.

Elevated LD and HWD, specifically heterozygote deficit, are a distinguishing feature of geographic regions where there are secondary contact and interbreeding between divergent lineages (Gompert et al., 2017). We found positive F_IS and elevated LD and HWD in admixture zones “a” (09-UWA), “d” (12-BN and 17-NB) and “c” (15-KAF and 16-JN), with the exception of the estimates made in 16-JN and 17-NB, perhaps because of insufficient sample size of just five individuals in these samples (Table 1). Positive F_IS and elevated LD and HWD indicate heterozygote deficit, suggesting these admixture zones contain descendants from a mix of divergent lineages and were formed by secondary contact. In contrast, admixture zone “b” (04-BOL, 05-CHU, 06-ACA, 07-APU and 08-OCA) showed a different pattern, with variable F_IS estimates (Table 1), suggesting admixture zone “b” contains descendants of a more homogenous ancestral background.

4.3 ∣. Biogeographic and demographic history of the admixture zones

SNP-based results from TreeMix supported a history of divergence and subsequent gene flow in zones “a” (ancestral migration from west to northwest; Supporting Information Figure S12a), “c” (admixture between west and south; Supporting Information Figure S12b) and “d” (ancestral migration from south to northeast; Supporting Information Figure S12a), but there was no support for divergence across admixture zone “b” (between the northeast and northwest; Supporting Information Figure S12). This biogeographic pattern was further supported in microsatellite-based ABC simulations that most closely matched the observed data under Scenario 2, where divergence between the northwest (Albert Nile) and west (Lake Albert) samples occurred ~400 ka, and divergence between the west (Lake Albert) and south (Lake Victoria) occurred ~23 ka (Table 2). These modelled timings are similar to previous estimates based on mtDNA (Beadell et al., 2010). Simulations also suggested divergence between the northeast and northwest was very recent (during the 1900s; Table 2), making it possible that the signal of admixture could represent divergence with gene flow, the remnants of an old and now collapsed hybrid zone, or a signal of very recent population contraction and expansion caused by anthropogenic changes.

One possible cause for the weak signal of divergence between the northwest and northeast in the TreeMix results (Supporting Information Figure S12) and the recent timing of divergence in the winning ABC scenario (Table 2) could be that the genetic structuring found among populations in northern Uganda (Figure 2) was caused by recent demographic fluctuations rather than by sustained divergence. Introduction of the Rinderpest virus in the late 1800s led to large mammal die offs with up to 80% mortality (Carmichael, 1938), which likely reduced tsetse populations because they depend on blood meals for reproduction. Recent divergence between the northwest and northeast could also be due to more modern processes than the Rinderpest outbreak, such as habitat change that resulted from the insurgence of the Lord's Resistance Army in northern Uganda in the 1990s through 2009 (Van Acker, 2004), or very recent vector control efforts since 2009. The insurgence of the Lord's resistance army in northern Uganda displaced hundreds of thousands of people and their livestock, and left millions of acres of northwestern Uganda fallow for over a decade (Egeru et al., 2014; Gorsevski et al., 2012). This disruption of the agricultural system likely indirectly caused tsetse population crashes when livestock—and the blood meals they generally provide to tsetse flies—were removed. During this same period, vector control in northern Uganda ceased for almost 20 years (Egeru et al., 2014). Since 2009, vector control activities have resumed in northern Uganda, and there is evidence that these activities have left signals of population bottlenecks, especially in the northeast (Opiro et al., 2016, 2017). Thus, Uganda's recent history of sever livestock die offs during the Rinderpest outbreak and civil unrest could have caused tsetse population fluctuations that played a role in the apparent divergence between the northwest and northeast (Figure 2).

4.4 ∣. Characterization of introgression in the admixture zones

INTROGRESS results indicated variable levels of divergence and hybridization in the four G. f. fuscipes admixture zones found in Uganda (Figure 1) that fell into one of two patterns: either displaying high genome-wide divergence (∣Δp∣) and mostly parental types, or low genome-wide divergence (∣Δp∣) and highly variable ancestry (Figure 4). In the first case, results suggest that admixture zones “a” and “d” have well-established reproductive barriers and that successful reproduction across the admixture zone was rare (insets of Figure 4a,d). In the second case, results suggest that admixture zones “b” and “c” have very few reproductive barriers and that successful reproduction across the admixture zone and among offspring from these crosses was common (insets of Figure 4b,c). The possible physiological, behavioural, mechanical or ecological mechanisms of reproductive barriers in admixture zones “a” and “d” are difficult to interpret from the current data (Coyne & Orr, 2004), especially since there is so little previous knowledge of the mating system and ecological interactions between the different lineages in secondary contact (Aksoy et al., 2013; Krafsur, Marquez, & Ouma, 2008). Nonetheless, the observed genome-wide pattern of low introgression levels (insets of Figure 4a,d) in these two admixture zones indicates strong reproductive barriers that block introgression in a large portion of the G. f. fuscipes nuclear genome. On the other hand, the observed genome-wide pattern of high introgression levels (insets of Figure 4b,c) in the other two admixture zones indicates incomplete reproductive barriers.

Possible drivers of the dichotomous pattern in introgression are the coupling of multiple exogenous and endogenous barriers across geographic space (i.e., the “coupling hypothesis” Bierne et al., 2011), or the coupling of prezygotic and postzygotic barriers (Butlin, 1989; Rundle & Nosil, 2005). The accumulation of associations of genotypes (coupling) in barrier loci across geographic space is a well-documented phenomenon that has been only recently recognized as an important component in speciation (Bierne et al., 2011). Associations among barrier loci are expected to create feedback between selection and gene flow (Gompert et al., 2017), and thereby either rapidly enhance the overall barriers to gene flow, or can lead to a sudden collapse of barriers (Bimova, MacHolan, Baird, Munclinger, & Dufkova, 2011; Flaxman, Wacholder, Feder, & Nosil, 2014; Gompert et al., 2017; Schilling et al., 2018; Servedio & Noor, 2003). At one extreme, assortative mating can cause build-up of associations between genotypes and can rapidly enhance reproductive barriers. At the other extreme, gene flow and non-assortative mating can cause disassociation among genotypes at barrier and non-barrier loci and can rapidly erode reproductive barriers. It remains an open question whether feedback caused by coupling of barrier loci is often a critical component of speciation. A prediction of this feedback hypothesis is that most hybrid zones would fit the description of either extreme: hybrid zones should either contain mostly parental types with little variability in introgression because of strong barriers to gene flow that have accumulated by this feedback, or they should contain hybrid types with highly variable ancestry and introgression because of their young age or history of barrier collapse.

Other possible explanations for the dichotomous pattern in introgression include reinforcement (Butlin, 1989) or ecological speciation (Rundle & Nosil, 2005). Although both alternatives include the coupling of multiple barriers, they also specifically involve both prezygotic and postzygotic factors, while the "coupling hypothesis" involves only postzygotic factors. Untangling which prezygotic and postzygotic factors are involved in reproductive isolation in this system will require more locus-by-locus analysis and breeding experiments. More locus-by-locus analysis to identify the genomic regions involved is not possible with the current results because low statistically power prevented detection of non-neutral introgression or F_ST outliers (Supporting Information Table S13; Gompert & Buerkle, 2010). Breeding experiments to distinguish prezygotic from postzygotic barriers—such as mating behaviour and egg–sperm incompatibilities—are also not possible until methods are developed to breed this species in an experimental setting. Future work that includes further molecular surveys with the same markers but with larger sample sizes and breeding experiments can elucidate the specific isolating mechanisms at play and allow tests of specific hypotheses on the contribution and contingency of prezygotic and postzygotic (intrinsic and extrinsic) isolating barriers.

4.5 ∣. Conclusion and future directions

Our findings provide insight into the evolutionary processes that generated multiple G. f. fuscipes admixture zones in Uganda (Figure 1). This system provides a unique opportunity to draw from more than 10 years of study and multiple genetic markers in a species that displays a range of evolutionary histories and multiple stages of divergence. Results provide preliminary support for the "coupling hypothesis" and set the stage for a more detailed analysis of variable introgression across these admixture zones. Detailed analysis of introgression can inform the genes involved in reproductive isolation and can more directly test predictions of hypotheses like the “coupling hypothesis”. Specifically, a second prediction of the “coupling hypothesis” that hybrid zones should either display little or extensive variability in introgression among loci (Gompert et al., 2017) could not be tested with this data set because we did not have adequate samples sizes to identify significant outlier loci in the zones with evidence of secondary contact (admixture zones “a,” “c” and “d”). To fill this knowledge gap, we need denser and more even geographic sampling across the admixture zones, especially for zone “a” (Figure 1).

DATA ACCESSIBILITY

ddRAD sequencing data, NCBI BioSample, PRJNA498097. Microsatellite genotypes, Dryad, https://doi.org/10.5061/dryad.98rf2f1. Mitochondrial DNA sequences, Genbank Accession nos. MK094112-MK094173