The Linkage-Disequilibrium and Recombinational Landscape in Daphnia pulex

Abstract

By revealing the influence of recombinational activity beyond what can be achieved with controlled crosses, measures of linkage disequilibrium (LD) in natural populations provide a powerful means of defining the recombinational landscape within which genes evolve. In one of the most comprehensive studies of this sort ever performed, involving whole-genome analyses on nearly 1,000 individuals of the cyclically parthenogenetic microcrustacean Daphnia pulex, the data suggest a relatively uniform pattern of recombination across the genome. Patterns of LD are quite consistent among populations; average rates of recombination are quite similar for all chromosomes; and although some chromosomal regions have elevated recombination rates, the degree of inflation is not large, and the overall spatial pattern of recombination is close to the random expectation. Contrary to expectations for models in which crossing-over is the primary mechanism of recombination, and consistent with data for other species, the distance-dependent pattern of LD indicates excessively high levels at both short and long distances and unexpectedly low levels of decay at long distances, suggesting significant roles for factors such as nonindependent mutation, population subdivision, and recombination mechanisms unassociated with crossing over. These observations raise issues regarding the classical LD equilibrium model widely applied in population genetics to infer recombination rates across various length scales on chromosomes.

Significance.

Surveys of linkage disequilibrium (LD) between nucleotide sites in natural populations reveal the degree to which recombination influences patterns of molecular/genomic evolution. Focused on hundreds of whole-genome sequences of the microcrustacean Daphnia pulex, this study yields an overview of the imprint of variation of recombinational activity among populations and within and among chromosomes at an unprecedentedly high level of refinement. The results reveal patterns of decline of LD with increasing physical distance between chromosomal sites in the study species that are inconsistent with conventional population-genetic theory, and consistent with disparities previously found in other species.

Introduction

Recombination plays numerous roles in evolutionary processes, providing a path to the joint appearance of independent mutations in the same haplotype, while also freeing beneficial mutations from background deleterious mutations at linked sites (Charlesworth and Charlesworth 2010). Despite these presumed advantages of recombination, one of the most conserved genetic features across the entire eukaryotic domain is the occurrence of just one to two crossovers per chromosome arm per meiotic event, which results in an inverse relationship between the average crossover rate per nucleotide site and genome size (Lynch 2007). This relationship exists because, on average, chromosome numbers do not increase with genome size, and when variation in such numbers is taken into consideration, almost all of the interspecific variation in average site-specific crossover rates is accounted for (Lynch et al. 2011). In principle, recombination rates between closely spaced sites can be much higher than expectations based on random crossovers if, for example, a substantial fraction of recombination events involves gene conversion with nonreciprocal exchange, as seems to be the case (Andolfatto and Nordborg 1998; Lynch et al. 2014). Assuming recombination-drift equilibrium, in the absence of gene conversion, the amount of linkage disequilibrium (LD) between sites separated by $d$ nucleotides is expected to scale like $1/(1+4N_e{c}_{0}d)$, where $N_e$ is the effective population size, and $c_0$ is the recombination rate per nucleotide site (Walsh and Lynch 2018). Although this model is commonly assumed in a wide array of population-genetic analyses, it is violated in the presence of gene conversion, which magnifies the recombination rate between closely spaced sites, but has no influence on the rate between sites separated by distances exceeding conversion-tract lengths. Moreover, recombination rates can vary among chromosomes if these vary substantially in length, and in some vertebrates recombination events are highly concentrated into relatively small fractions of the genome, so that some gene regions experience much higher rates of both gene conversion and crossing over than others (Auton et al. 2012; Lam and Keeney 2015; Singhal et al. 2015). Thus, there is a need for large-scale studies of recombination in natural populations to guide future work on the general interpretation of patterns of LD.

Population-genomic data offer a way to greatly refine our understanding of the recombinational landscape and its degree of heterogeneity across chromosomal regions and among species. Gene conversions and recombinational hotspots (arbitrarily defined as local regions with rates inflated $>10\times$) are not easily revealed by conventional meiotic genetic maps, which generally capture only crossover events and typically not very many of them. However, patterns of LD in samples from natural populations have the potential to illuminate fine-scale recombinational features, as cumulative effects reflect time scales (in generations) roughly equivalent to the effective population size, and because the intervals between markers are substantially reduced. Of course, LD approaches themselves have limitations, as they average across generations, sexes, and can be affected by selective sweeps.

Here, we take advantage of substantial population-genomic data sets derived from several populations of the aquatic microcrustacean Daphnia pulex to reveal the basic recombinational features in this model species. Although some D. pulex have evolved obligate asexuality (Hebert et al. 1988; Tucker et al. 2013), all of the isolates in this study are cyclical parthenogens from ephemeral ponds. Owing to habitat desiccation, sexual reproduction is enforced on an annual basis, with typically just three to five intervening asexual generations per year, and populations are persistently very close to Hardy–Weinberg equilibrium for molecular markers (Lynch 1984; Maruki et al. 2022). Some gene-conversion-like processes can occur during asexuality, but crossovers are unobserved in the absence of meiosis (Omilian et al. 2006; Keith et al. 2016). Prior work has shown that even after including the asexual generations, the average rate of crossing over per nucleotide site per generation is $\sim$60% higher in D. pulex than in the well-studied insect Drosophila, owing to the smaller chromosome number and the absence of male recombination in the latter (Lynch et al. 2017).

With analyses based on genomic sequences of hundreds of individuals, this study has exceptionally high power for revealing aspects of the recombinational landscape and contrasting the observed patterns with theoretical expectations from population-genetic theory, an enterprise that has been historically difficult owing to the large sampling variance of linkage-disequilibrium measures. Three approaches are used to estimate genome-wide patterns of LD: the conventional population-genetic parameter ($r^2$) involving allelic correlations between sites; a measure based on the distribution of heterozygous sites within individuals; and an estimate based on temporal sampling. In addition, more fine-scale analyses are applied in the search for heterogeneity of recombination rates across chromosomes.

The results indicate a relatively uniform recombinational landscape across the D. pulex genome, both among populations and among chromosomes. As in other eukaryotic species (Langley et al. 2000; Frisse et al. 2001; Malkova et al. 2004; Mancera et al. 2008; Yin et al. 2009; Yang et al. 2012; Padhukasahasram and Rannala 2013; Lynch et al. 2014), the majority of recombination events appear to occur without crossing over. The relationship between linkage disequilibrium and physical distance between sites, estimated by three different methods, reveals a rate and pattern of decline that is inconsistent with the standard model in which mutations arise in a spatially independent manner and recombination rates increase linearly with physical distance between sites.

Results

Population-level Linkage Disequilibrium

To guard against the innate limitations of all statistical measures of LD, resulting from both large sampling variance and statistical bias (Walsh and Lynch 2018), the genome-wide average scaling of LD with physical distance between sites was evaluated in three ways. First, population-level LD was quantified with the squared correlation ($r^2$, corrected for sampling bias) involving the joint distribution of pairs of SNPs across individuals within populations. Although this measure of LD is the conventional parameter used in nearly all population-genetic analyses, it has the undesirable property that the upper bounds of possible values depend on the underlying allele frequencies, with maximum values of 1.0 only possible when allele frequencies at both sites are identical (VanLiere and Rosenberg 2008). The latter condition is approached as analyses are confined to specific bins of allele-frequency classes, but is still not entirely satisfied even if analyses are restricted to very high-frequency alleles.

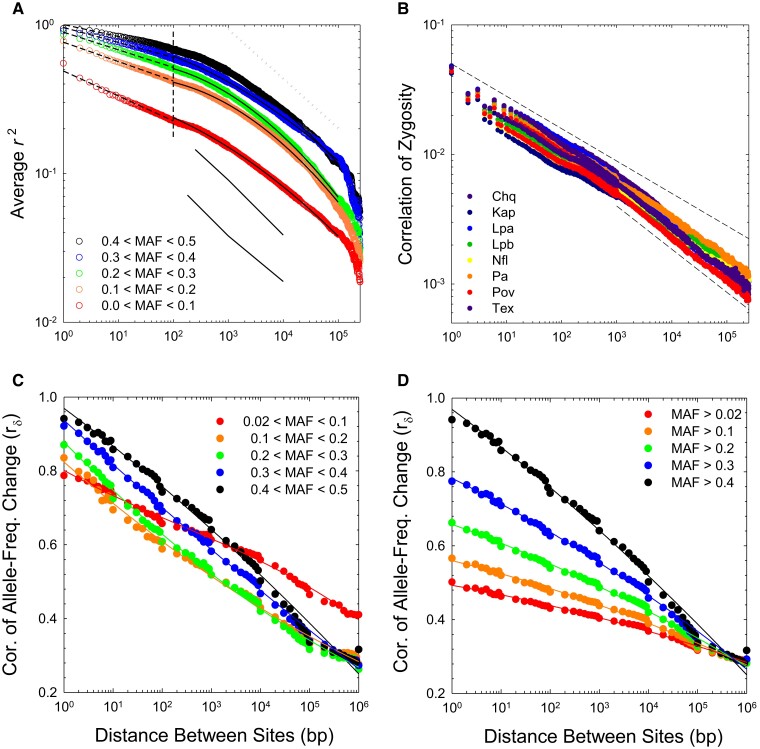
To clarify this effect, we subdivided the data into five bins restricted to various ranges of minor-allele frequencies. As the pattern of LD is quite similar among populations (below), the results are simply summarized by averaging over all eight populations (fig. 1A). As expected, the heights of the curves decline with decreasing minor-allele frequencies (MAFs). However, all five analyses exhibit consistent scaling behavior. For sites separated by $d\le 100$ bp, there is a power-law decline of $r^2$ with increasing physical distance between sites (revealed as a least-squares linear regression on a log–log plot), but for $d>100$ bp, there is a slow quadratically increasing rate of decline of $r^2$ on a log scale (again, as identified by least-squares analysis). Together, these two fits almost perfectly describe the scaling behavior of average $r^2$ values within all classes of MAFs, accounting for >99% of the variance in the distance-dependent measures of $r^2$ up to a distance of ${10}^5$ bp between sites (supplementary table 1, Supplementary Material online), beyond which sample-size limitations start to reduce the reliability of the data. With the large numbers of genotypes analyzed in this study, even at a distance of 250 kb (the maximum to which we extended the analyses), LD is still discernible, although the values are very low ($\sim$5% of the magnitude for adjacent sites).

Fig. 1.

(A) Response of average population-level $r^2$ to increasing distance between sites. The vertical dashed line at $d=100$ bp denotes the approximate break point in the scaling behavior of LD with physical distance between sites; fitted least-squares regression parameters above and below this threshold are given in supplementary table 3, Supplementary Material online. The upper dashed line provides a reference for $-$1/3 power-law scaling. The lower, thin lines give the average estimates of $r^2$ for D. melanogaster taken from figure 1 in Garud and Petrov (2016); upper and lower lines denote data for samples from Raleigh and Zambia, respectively. (B) Response of individual-level $\mathrm{\Delta }$ to increasing distance between sites for the eight study populations. Upper and lower dashed lines denote power-law scaling behavior with slopes of $-1/4$ and $-1/3$, respectively. (C,D) Average correlations of allele-frequency changes between adjacent years in the series of samples from population PA, plotted with two different binnings of frequencies.

Individual-level Linkage Disequilibrium

The second approach, the correlation of zygosity, $\mathrm{\Delta }$ (Lynch 2008; Lynch et al. 2014), provides an individual-based measure of LD, defined by the spatial distribution of pairs of heterozygous sites. The decline of $\mathrm{\Delta }$ with physical distance among sites is qualitatively similar among all populations, with the full range of values at any particular distance varying by a factor of no more than two between populations (fig. 1B, and supplementary fig. 2, Supplementary Material online). Again, it can be seen that the distance-dependence of this measure of LD is best described by two phases—on a logarithmic scale, an approximately linear decline of $\mathrm{\Delta }$ with distance between sites $d<1$ kb, and weakly quadratic behavior at larger distances (supplementary table 1, Supplementary Material online). As with population-level LD, these simple summary regressions explain >99% of the variance in mean distance-dependent LD measures.

As noted in Lynch et al. (2014), $\mathrm{\Delta }$ and $r^2$ are expected to exhibit similar scaling with $d$ under the assumption of a population in drift-mutation-recombination equilibrium, as both are expected to be proportional to the squared disequilibrium coefficient. Although average $r^2$ scales more weakly with $d$ than does $\mathrm{\Delta }$ for $d<1,000$ bp, this is at least in part a natural artifact of the former being mathematically constrained by allele frequencies, whereas $\mathrm{\Delta }$ is not. As in most species, the vast majority of polymorphic sites in these populations have minor-allele frequencies (MAFs) $\ll$0.1 (Maruki et al. 2022), and as can be seen in figure 1A, as the utilized allele frequencies become increasingly confined to this range, the scaling of $r^2$ with distance becomes more similar to that for $\mathrm{\Delta }$, as expected. As a first-order approximation at large $d$, for both average $r^2$ and $\mathrm{\Delta }$, the negative scaling of LD with physical distance approaches a power-law relationship with exponent $\simeq -1/4$, that is, an $\sim$1.8-fold decline in LD with a 10-fold increase in $d$, far from the inverse scaling expected if the recombination rate between sites were to increase linearly with $d$.

Correlation of Allele-Frequency Changes in Sequential Samples

The third approach is based on the idea that a natural manifestation of LD is an expected decline of the correlation in temporal allele-frequency changes between loci with increasing physical distance between sites. Such behavior is simply a consequence of the repeatability of samples—sites exhibiting more LD are expected to show more consistent directional deviations in allele frequencies in pairs of samples following a bout of recombination. To quantify this type of scaling using information from eight single-generation intervals in population PA, we phased the alleles at pairs of polymorphic sites into coupling and repulsion states (using the unambiguous information from all but double heterozygotes), and then estimated the average correlation in the changes in frequencies of alleles in coupling phase ($r_{\delta }$) for each specific distance between sites.

Again, to deal with the frequency-dependence of the upper limit to LD estimates, the results are displayed in two ways (in fig. 1C with both participating alleles within the same narrow window in frequency; and in fig. 1D with MAFs cumulative from a variable lower bound to the upper frequency of 0.5). Either way, it is clear that there is a strong negative decline in the average joint sampling deviations of allele-frequency change for loci up to ${10}^6$ bp apart, with $\sim$50% of the decline occurring by the point at which sites are 10 kb apart.

The quantity $r_{\delta }$ can be thought of as a measure of the sampling correlation of allele frequency estimates at two sites. The expected value of the numerator (the covariance of allele-frequency change) should be a function of LD only, as sampling error within sites alone will not lead to covariance between sites not in LD. However, the denominator of $r_{\delta }$ is a function of the sampling variances of allele frequencies, some of which is a function of the sample size (as is also true for $r^2$ estimates). Thus, although the absolute values of $r_{\delta }$ are not necessarily fully quantitatively consistent with single-sample $r^2$, the scaling of $r_{\delta }$ with physical distance is expected to reflect the true genomic pattern of long-term LD.

Fine-scale Patterns

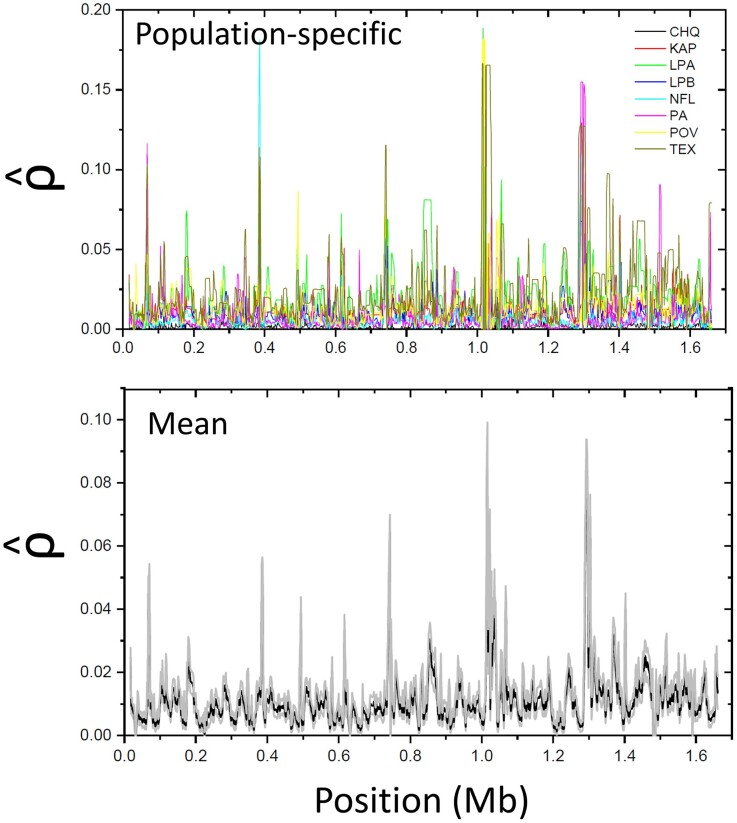
To obtain an approximate view of the landscape of recombination intensity along chromosomal regions, we employed LDhat (McVean and Auton 2007) to estimate the spatial pattern of the population recombination rate $\rho =4N_e{c}_0$ (where $N_e$ is the effective population size, and $c_0$ is the rate of recombination between adjacent sites) across assembled scaffolds. We cannot expect this approach to yield completely unbiased estimates of region-specific recombination rates in any organism, for as with all other methods, the general procedure assumes a linear relationship between the local recombination rate and the distance between sites as well as a single panmictic population experiencing no admixture. However, there is still expected to be a monotonic relationship, on average, between the estimate $\hat{\rho }$ and the population parameter $\rho =4N_e{c}_0$, and all prior studies have proceeded with this in mind. As can be seen in figure 2 for the largest D. pulex scaffold, there is an approximate order-of-magnitude range in $\hat{\rho }$ among sites and populations, although much of this is due to sampling error, with the amplitude of spatial fluctuations being muted by $\sim$50% when averages are taken across populations. The mean of the estimated population recombination rate over all genomic sites is $\hat{\rho }=0.0124$ per nucleotide site per generation (SE $<{10}^{-6}$ based on 2-kb nonoverlapping windows). Using a much smaller subset of data (from population KAP (Maruki et al. 2022) only) and somewhat different settings with LDhat, Urban (2018) independently obtained the estimate $\hat{\rho }=0.0153$.

Fig. 2.

Estimated pattern of recombination-rate variability over the length of the largest D. pulex scaffold (1). The top panel overlays the $\hat{\rho }$ profiles for each of the eight study populations, whereas the bottom panel gives the mean (black) $\pm$1 one standard error (gray) over all populations.

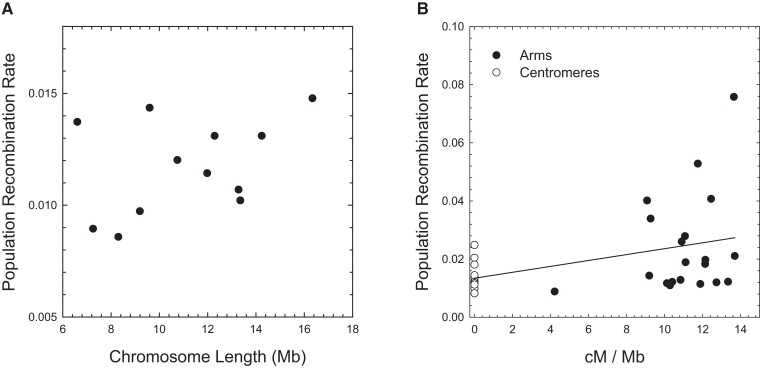
By use of scaffolds that have been uniquely anchored to the genetic map (Molinier et al. 2021), average chromosome-specific estimates of $\hat{\rho }$ were found to fall in the narrow range of 0.0086–0.0148 (with average $\mathrm{SE}=0.0004$; supplementary table 2, Supplementary Material online). Owing to the typical eukaryotic pattern of $\sim$1 crossover per chromosome arm, one might expect the per-site recombination rate to decline with increasing chromosome length (Jensen-Seaman et al. 2004; Lynch 2007; Smeds et al. 2016). However, the estimated physical lengths of D. pulex chromosomes fall in the narrow range of 6.6–16.3 Mb (and genetic-map lengths in the range of 70–130 cM, with 6.5–12.8 cM/Mb; supplementary table 2, Supplementary Material online), and averaged across all populations, chromosome-specific $\hat{\rho }$ are not significantly correlated with the physical length of chromosomes (fig. 3A).

Fig. 3.

(A) Absence of a significant relationship between the population recombination rate ($\rho$), averaged across populations, and physical length of chromosomes (least-squares regression slope $=$ 0.00027 (0.00021); $r^2=0.14$; $P=0.22$). (B) Weak relationship between the population recombination rate ($\rho$) and the crossover intensity for chromosomal regions obtained from the genetic maps (regression slope $=$ 0.00101 (0.00044); $r^2=0.15;$$P=0.031$). The SEs of individual estimates of all plots are on the order of the widths of the points or smaller.

From the high-resolution genetic maps for this species (Molinier et al. 2021), we were able to estimate average $\hat{\rho }$ for each well-defined centromeric region (which have essentially no observed crossovers in $F_1$ crosses; supplementary table 2, Supplementary Material online) and chromosome arm, with the former constituting an average $\sim$40% of individual chromosome lengths. Although it is generally thought that recombination is strongly repressed in centromeric regions (Petes 2001), cases of weak suppression are known (True et al. 1996; Stukenbrock and Dutheil 2018), and here it is found that average $\hat{\rho }$ in putative centromeric regions, 0.0144 (0.0015), is $\sim$60% that on chromosome arms, 0.0241 (0.0028). However, the correlation between $\hat{\rho }$ and crossover intensity per physical distance is weak (fig. 3B). Aside from the high sampling variance of LD-based estimates of the recombination rate, this weak correlation may be largely a consequence of the failure of crossover-based maps to account for the much more frequent gene-conversion events unaccompanied by crossovers.

There is approximately five-fold variation in $\hat{\rho }$ among populations (supplementary table 3, Supplementary Material online). To determine whether this is a consequence of variation in actual recombinational activity (as opposed to simple differences in local effective population sizes), the population-specific $\hat{\rho }$ (rough estimates of $4N_e{c}_0$) were normalized by dividing by the average diversities at neutral sites (estimates of $4N_{e}u$, where $u$ is the base substitution rate per nucleotide site; from Maruki et al. 2022). This further reduces the disparity between populations. The resultant ratios (supplementary table 3, Supplementary Material online) are all within a factor of $\sim$2 of each other, with the exception of population Tex, which appears to have $\sim$4-fold higher recombinational activity relative to the remaining populations. The sources of the elevation in population Tex are unclear, but might arise if this population has historically undergone more frequent bouts of sexual reproduction than the others.

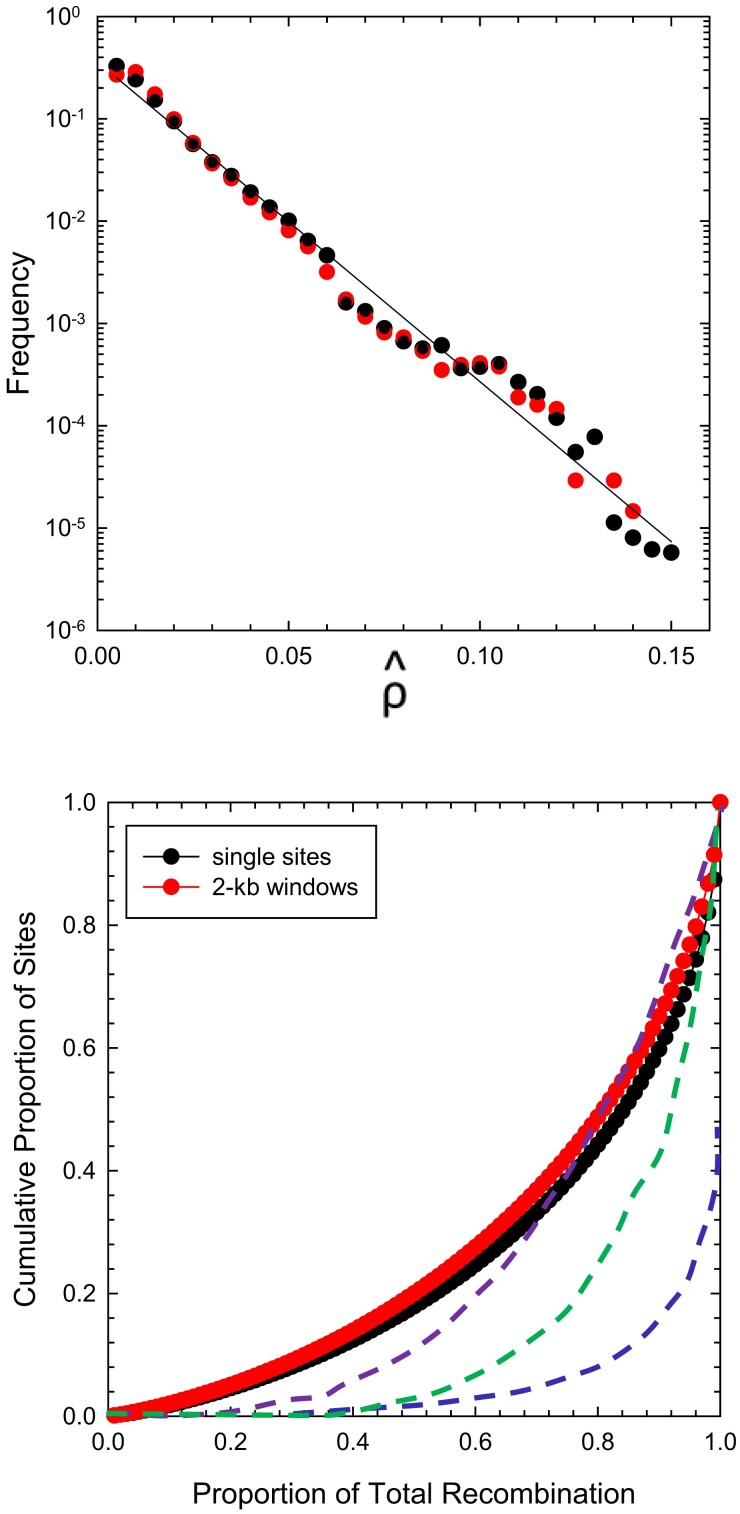
Although $\hat{\rho }$ may yield a biased estimate of true $\rho$, spatial variation in the former should still provide insight into differences in recombinational activity across chromosomal regions. The distributions of the site-specific rate estimates (as well as those for 2-kb windows) are nearly exponential, as expected under a pattern of random recombination (fig. 4). Some mild recombination hotspots appear to be present (below), but they do not account for much of genome-wide recombination. Rather, 20% of the total recombination is accounted for by $\sim$5% of the sites (or windows), 50% by $\sim$20% of the sites, and 90% by $\sim$65% of the sites. This is a strong contrast with the situation in humans, where $\sim$85% of total recombination is accounted for by $\sim$10% of the sites (Auton et al. 2012).

Fig. 4.

(Above) Frequency profiles of the $\hat{\rho }$ estimates of the population-averaged scaled recombination rate on a per-nucleotide and a per 2-kb window basis, based on 137,643,518 sites and 68,821 windows. The least-squares regression of log (frequency) on $\hat{\rho }$ has intercept $-0.44$ and slope $-31.3$ ($r^2=0.979$). (Below) Cumulative distributions for the data in the upper panel (which utilizes the same red/black color scheme for Daphnia). In ascending order, the dashed blue line is the function derived for European human populations (taken from fig. 2 in Auton et al. 2012), green for mouse (Paigen et al. 2008), and purple for Drosophila pseudoobscura (Smukowski Heil et al. 2015).

As an additional way to quantify such evenness, we calculated Gini coefficient, which measures the level of inequality in cumulative frequency distributions, such as in figure 4, and ranges from 0 (for no variation in recombination rates among sites) to 1 (for a single hotspot). The estimated coefficient for D. pulex is 0.11, lower than any other recorded estimate, for example, 0.35 for C. elegans (Bernstein and Rockman 2016), 0.50 for Drosophila pseudoobscura (Smukowski Heil et al. 2015), and 0.8 for mammals (Paigen et al. 2008; Kong et al. 2010). In summary, there is less variance in the D. pulex recombinational landscape than in any other species for which such data are available (fig. 4).

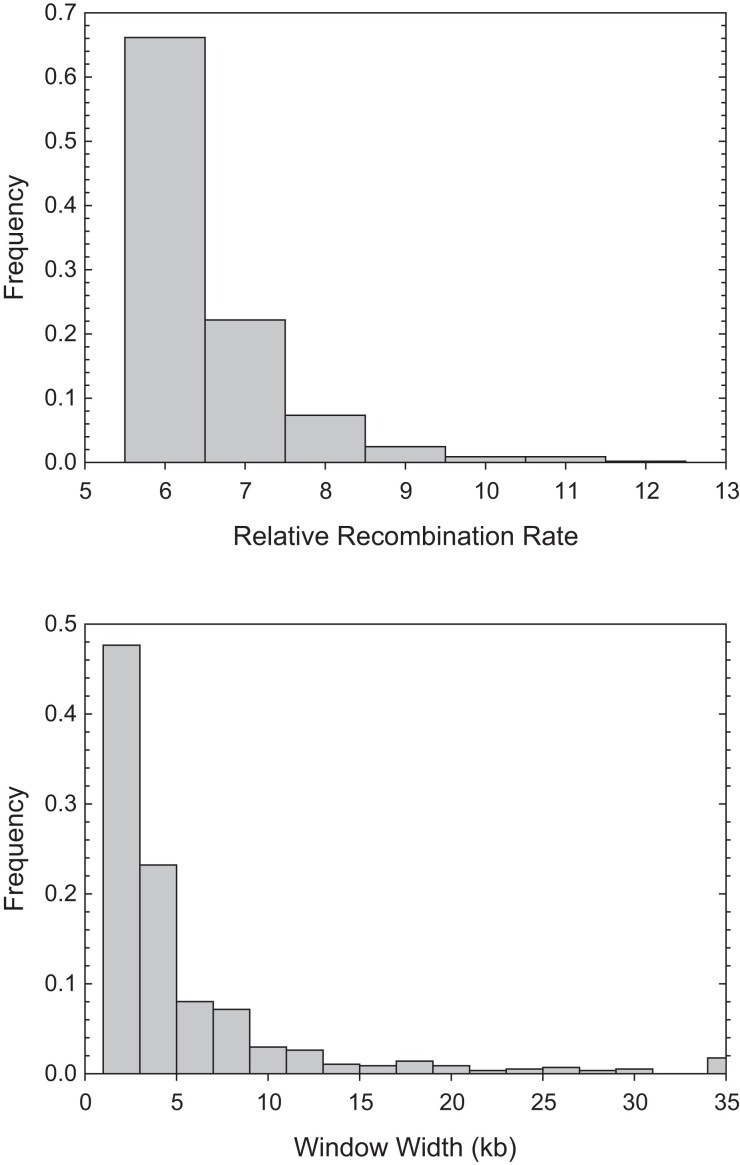
To further evaluate whether a small subset of chromosomal regions is associated with exceptionally high recombination rates, we searched for such locations by applying a procedure to more closely scrutinize the average recombination profiles over the eight populations. Validated by computer simulations applied to the KAP study population (Urban 2018), the method simply flags as significant any region >500 bp in length with an inflation in $\hat{\rho }$ in excess of $5\times$ relative to the genome-wide background level. These threshold criteria successfully identify >92% of hotspots with a $>10\times$ effect, with just a 2% false-positive rate (Urban 2018). In total, we identified 573 candidate hotspots, with average recombination-rate inflation (relative to background levels) of $6.0\times$ ($\mathrm{SD}=1.0$) and average window width of 5.7 (7.8) kb (fig. 5). Of these candidate hotspots (which might be more appropriately labeled warmspots), 88% had elevations in recombination rates in the range of $5$–$7\times$, with the maximum value being $12\times$.

Fig. 5.

Estimated elevations of recombination rates (relative to background levels) for 573 candidate recombination hotspots and the widths of the associated chromosomal regions (the two measures are only weakly positively correlated, $r^2=0.11$).

As a second approach, we applied the program LDhot (Auton et al. 2014), using the output derived from LDhat as input files and simulating 1,000 random data sets as null expectations. This analysis revealed 536 hotspot regions, with average length 6.0 kb and average inflation of the recombination rate of $21.5\times$ relative to background levels. Together, the two approaches only yielded 37 overlapping candidate hotspots, having an average $6.0\times$ ($\mathrm{SD}=0.9$; range of 5.0–8.2) inflation of the recombination rate and average window width of 5.0 (7.0) kb.

This lack of concordance between results using two approaches is likely in large part a consequence of the very large sample variance of LD combined with error in inference associated with the underlying statistical analyses. For example, the false-positive rate in hotspot detection using LDhot is 0.24–0.56 with human data (Auton et al. 2014), and it is likely worse when the background recombination rate is only a few times lower than that in potential hotspots, as in this study. This potential for false positives can be further seen by noting that before Bonferroni correction to the 5% level, both approaches yielded $\sim$11,600 candidate hotspots, with this declining to just $\sim$550 after correction. If correction is further reduced to the 2% level, a further 230 events are eliminated, showing that there are very few locations where excess recombination rates can be confidently inferred. Finally, we note that the four genetic maps for D. pulex (Molinier et al. 2021) provide no evidence of cM/Mb dichotomies within chromosome arms.

Using MEME 4.12.0 (Bailey et al. 2009), an attempt was made to determine whether this subset of putatively high-recombination regions was enriched for specific nucleotide-sequence motifs. The only potential motif found across both methods was a largely homopolymeric run of As (Ts on the opposite strand). Although this same motif is also enriched in non-hotspot regions, it has been implicated as hotspot-associated in birds (Singhal et al. 2015), Arabidopsis (Wijnker et al. 2013), and to some extent in yeast (Pan et al. 2011). The effect may be a simple consequence of A:T being weaker than G:C bonds, and hence more conducive to local chromosome breaks. Taken together, these data, along with the cumulative recombination profiles in figure 4, indicate that although some localized regions with elevated recombinational activity may exist in D. pulex, the effects are not large.

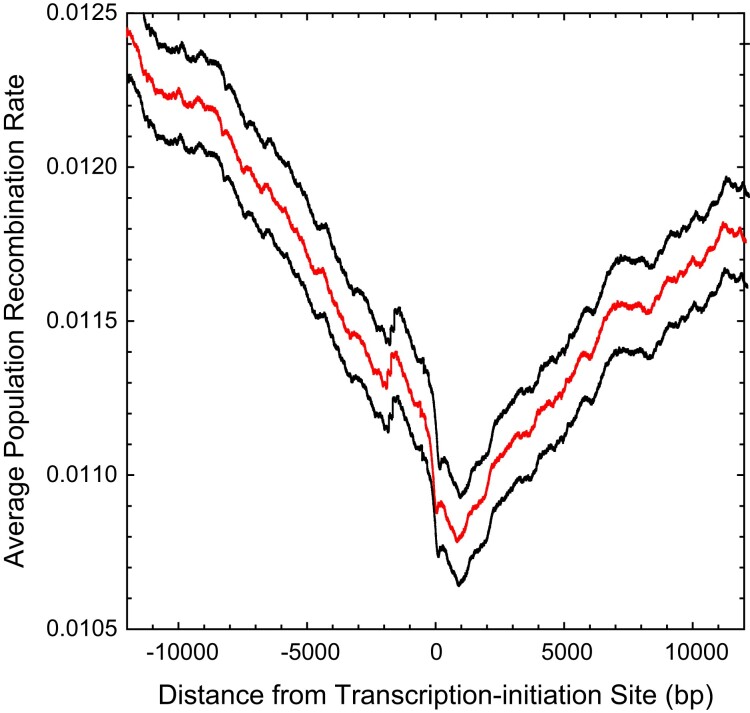
To determine whether recombination rates are influenced by factors associated with gene bodies, we estimated how the average recombination rate per nucleotide site varied as a function of the distance from the known transcription–initiation sites in this species (Raborn et al. 2016). Although there is a general pattern of depressed recombination towards the beginning of genes (fig. 6), the magnitude of reduction is only $\sim$13% relative to the genome-wide average. Such suppression has been noted in Drosophila (Chan et al. 2012; Smukowski Heil et al. 2015) with a somewhat higher amplitude (20–50%), although studies in yeast (Lam and Keeney 2015) and birds (Singhal et al. 2015) suggest the opposite pattern.

Fig. 6.

Average population-scaled recombination rate, $\hat{\rho }$ as estimated by LDhat, as a function of the distance from the transcription–initiation sites of all genes for which such positions are known; the black lines denote $\pm$2 standard errors of the means (intermediate line). The horizontal dashed line denotes the genome-wide average recombination rate.

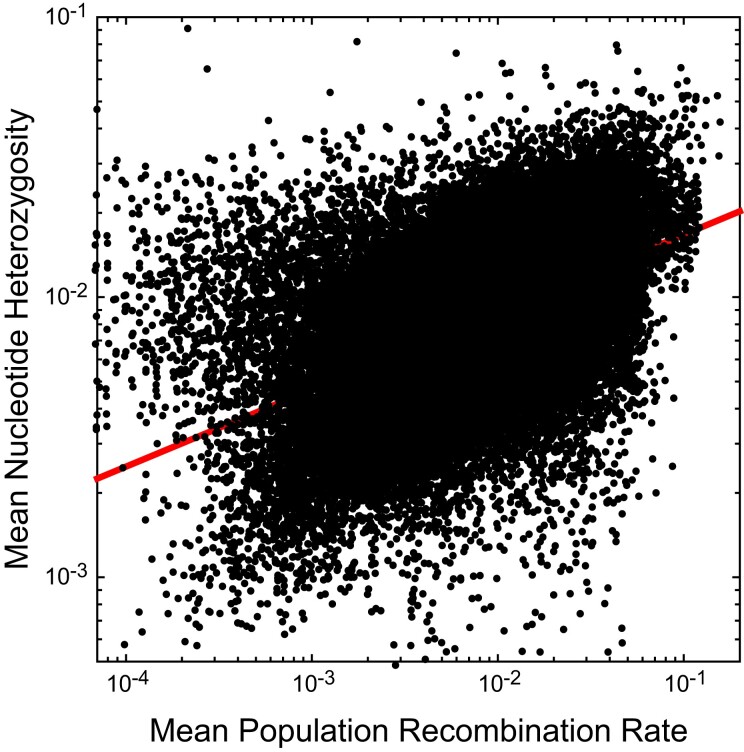
Finally, there is a positive relationship between standing heterozygosity within nucleotide sites and the population-level recombination rate (fig. 7). Such a pattern suggests that recombination reduces the rate of loss of local variation by background selection and/or selective sweeps, that recombination is mutagenic, or both. However, with a slope of 0.276 (0.002) on a log scale, the relationship is far from linear.

Fig. 7.

Relationship between average nucleotide heterozygosity and population recombination rate, $\hat{\rho }$, as estimated by LDHat. Small black points are based on windows of 2-kb width. The least-squares regression is $\log (\pi )=-1.50+0.276\log (\hat{\rho })$, with $r^2=0.244$.

Discussion

Based on very large population-genomic data sets and a diversity of analytical approaches, this comprehensive study suggests a fairly homogeneous recombinational landscape in D. pulex, with average patterns and rates of recombination being similar among populations and within and among chromosomes. The results also highlight a number of methodological and interpretative limitations in studies of LD in natural populations, raising caveats about the use of such information to derive inferences about recombinational differences among study species.

For example, most studies simply report global patterns of the population-LD coefficient $r^2$, ignoring the underlying allele-frequency distribution. As shown in figure 1A, absolute magnitudes and patterns of decline of $r^2$ with physical distance among sites are highly sensitive to the utilized frequencies of alleles, although this is not the case for the individual-based LD measure $\mathrm{\Delta }$, which simply relies on the incidence of heterozygous sites. As a consequence, samples from populations with different site-frequency spectra can lead to biased inferences about the scaling of LD with physical distance, as well as to erroneous localizations of recombination hotspots (Dapper and Payseur 2018). In addition, almost all prior studies report plots of $r^2$ vs. $d$ on an arithmetic scale and/or fail to correct for sample-size bias, obscuring the still real (and meaningful) pattern of decline of LD at large physical distances between sites once $r$ has dropped below 0.1.

Violations of the Standard Model for Population LD

Under drift-mutation-recombination equilibrium in a panmictic population, the squared correlational measure of LD is expected to scale with physical distance $d$ between sites as

$$r^2\simeq \frac{1}{1+4N_{e}c}$$ (1a)

(Ohta and Kimura 1971; Hill 1975). It is often assumed that $c=c_{0}d$, where $c_0$ is the rate of recombination per nucleotide site, and $d$ is the distance between sites (in bp), which ignores the contribution from gene conversion. Allowing for gene conversion,

$$c\simeq c_0[xd+(1-x)L(1-e^{-d/L})]$$ (1b)

where $x$ is the fraction of recombination events accompanied by crossovers, and $L$ is the mean conversion-tract length (in bp, assumed to be exponentially distributed) (Andolfatto and Nordborg 1998; Langley et al. 2000; Frisse et al. 2001; Lynch et al. 2014). If $x=1$ and/or $d\ll L$, $c\simeq c_{0}d$, whereas for $d\gg L$, $c\simeq c_{0}xd$. Thus, except for an order of magnitude range of $d$ in the vicinity of the mean conversion-tract length, under the assumptions of the standard model, LD as measured by $r^2$ or $\mathrm{\Delta }$ is expected to scale inversely with $d$, which is far from the case with observed data.

The estimate $x\simeq 0.1$ for the fraction of recombination events accompanied by crossovers in D. pulex (Lynch et al. 2014) is similar to estimates in Drosophila, humans, many other vertebrates, and land plants (reviewed in Lynch et al. 2014). Thus, assuming that $\hat{\rho }$ reflects $4N_{e}x{c}_0$, the total population-level recombination rate ($4N_e{c}_0$, which is equivalent to the expected recombination rate for sites more closely spaced than the average conversion-tract length) in the study species $\simeq 0.124$, averaging over sexual and asexual generations. Considering the lower and upper bounds of estimates of $x$ for multicellular species, 0.05 and 0.2 (Lynch et al. 2014), $4N_e{c}_0$ would be bounded by 0.248 and 0.062, respectively.

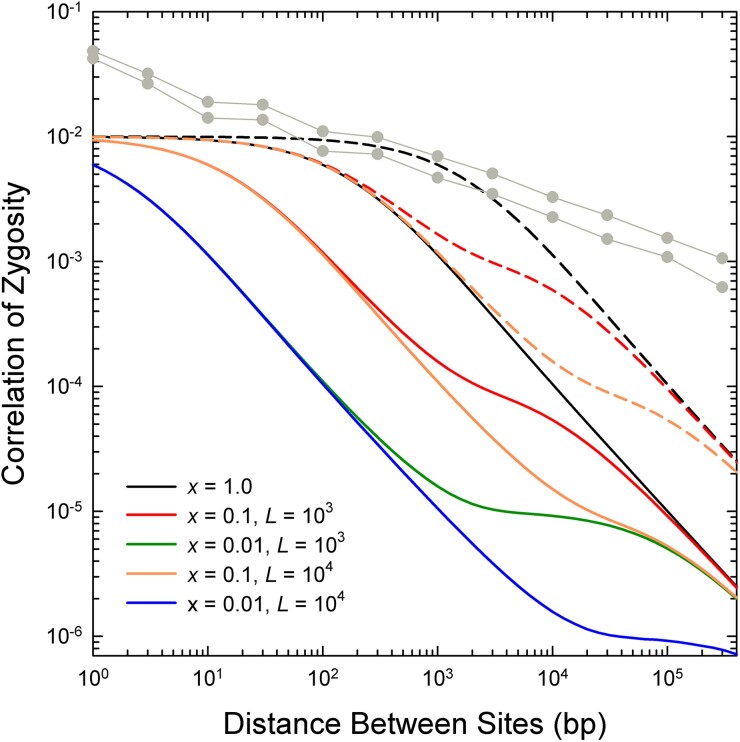
Using the expected parameters for D. pulex, and accounting for sexual reproduction every 3–10 generations, the expected magnitude of negative scaling of $\mathrm{\Delta }$ with $d$ based on equations (1a,b), shown in figure 8, can be seen to be far stronger than revealed by the actual data at distances >1 kb (figs. 1 and 8). Even at physical distances exceeding 10 kb, the observed negative scaling approaches a maximum of $d^{-1/3}$, whereas conventional theory predicts proportionality to $d^{-1}$. In addition, for physical distances up to $\sim$1 kb, there is substantially more observed LD than predicted by theory.

Fig. 8.

Expected pattern of decline of the correlation of zygosity ($\mathrm{\Delta }$) with increasing physical distance between sites as a function of $x$, the fraction of recombination events resulting in a crossover, and $L$, the mean length of a gene-conversion tract (in bp), under the assumption of an exponential length distribution of the latter. Derived using equation (8) in Lynch et al. (2011), based on equilibrium theory of Ohta and Kimura (1971) and Hill (1975), and equation (1) in Frisse et al. (2001). It is assumed that the population mutation rate is $4N_{e}u=0.01$, as observed in Maruki et al. (2022), and that the population recombination rate per site per generation is $4N_e{c}_0/\delta =0.01$, as described in the text. Solid and dashed lines denote results for a periodicity between sexual bouts of $\delta =3$ and $10$ generations, respectively. From Lynch et al. (2014), the same scaling is expected for the squared linkage disequilibrium coefficient, $r^2$, which is approximately equal to $\mathrm{\Delta }/\pi$. The light gray lines with data points give the upper and lower bounds of $\mathrm{\Delta }$ for the actual genomic analyses in figure 1B.

Similar discrepancies between theory and observation have been seen in many other metazoans (Lynch et al. 2014). For example, the negative scaling of $r^2$ with physical distance in both the North American and Zambian populations of D. melanogaster is similar in the range of $d={10}^2$–${10}^4$ bp to that for D. pulex (fig. 1A), although the absolute values of average $r^2$ differ (presumably owing in part to different ranges of allele frequencies applied). More extensive analyses of D. melanogaster summarized in Lynch et al. (2017; their fig. 9), including results from fully sequenced genomes, further support the unexpectedly slow decline of LD with physical distance in this species. Similarly weak scalings have been observed consistently in humans and other great apes (Reich et al. 2001; Lynch et al. 2014). Thus, there appears to be broad and consistent discordance between the scaling of LD with physical distance between sites expected under conventional theory and that actually observed.

Under the conventional population-genetic model, LD is also expected to be nearly unresponsive to distances between chromosomal sites at the shortest scales, as the likelihood of any recombination between sites is then very low relative to the power of drift (fig. 8). Yet as can be seen in figure 1, regardless of the metric employed, the negative scaling of LD with distance on a scale of 1–100 bp is very similar to that on a scale of 100–1,000 bp, that is, LD increases with decreasing $d$ more rapidly than expected under the conventional model. As reviewed previously (Lynch et al. 2014), one likely contributor to the excess LD at short distances is the simultaneous appearance of multiple mutations on short spatial scales, which creates more LD than expected by chance.

However, a second likely source of elevated short-distance LD and a reduced rate of decay with distance involves population subdivision (Ohta 1982; Wakeley and Lessard 2003; De and Durrett 2007), which few (if any) species are completely free of. Population subdivision causes excess LD by trapping pairs of alleles in local demes, in effect reducing their effective population sizes, until sufficient time elapses for migration across the metapopulation (similar to the time lag needed to dissipate the effects of nonindependent mutations). Such effects are relevant to D. pulex, as the mean $F_{ST}$ for the study populations is $\simeq$0.3 (Maruki et al. 2022), which implies fewer than one migration event per population per generation. Theory predicts that with $F_{ST}$ in the range of 0.25–0.5, the magnitude of $r^2$ is increased and the scaling rate of decay with $d$ is substantially decreased, especially in the case of a stepping-stone (isolation-by-distance) model (Ohta 1982; Wakeley and Lessard 2003; De and Durrett 2007). Historical changes in population size can also influence the distance-dependent pattern of LD (Lynch et al. 2014), but the data for D. pulex suggest that $N_e$ has changed by factors of no more than a few fold in the history of these samples (Lynch et al. 2017, 2020), which is inadequate to generate the patterns seen herein.

Finally, as shown in figure 8, under the conventional model with gene conversion (equations 1a,b) a shoulder in the LD-distance profile is expected at length scales on the order of the mean conversion-tract length. However, no such pattern is seen in the actual data (fig. 1), although gene-conversion-like processes are known to occur in D. pulex even in the absence of meiosis. By observing the loss of heterozygosity in asexually propagated lines, Omilian et al. (2006) and Keith et al. (2016) found that nonmeiotic homogenizing events occur at rates on the order of ${10}^{-6}$–${10}^{-4}$ per nucleotide site per generation in the study species, with many spans with lengths in the range of 100–1,000 bp (as expected for gene-conversion events) but others extending up to 1 Mb (and probably involving other types of events, such as break-induced replication). The signature of such events in LD vs. distance profiles may be obscured by the other effects noted above and/or by a higher variance in the length distribution of conversion events than assumed in equation (1b).

Using LD to Infer the Incidence of Sexual Reproduction

In principle, a comparison of estimates of population-wide LD with that expected based on genetic crosses might reveal the incidence of sexual reproduction in the nature. As the program LDhat assumes a linear relationship between the recombination rate and the physical distance over a range of sites, $\hat{\rho }$ might be expected to approximate the population-level crossover rate per nucleotide site, which in our case is equivalent to $4N_{e}x{c}_0/\delta$, where $\delta$ is the number of generations between periods of sexual reproduction. Using this logic, Tsai et al. (2008) compared the genetic-map based estimate of $x{c}_0$ with that obtained by factoring out the estimated $N_e$ from $\hat{\rho }$, and concluded that the yeast S. cerevisae undergoes sexual reproduction only every 1,000–3,000 cell divisions in the wild. Depending upon how much $\hat{\rho }$ overestimates $x{c}_0$ by ignoring gene-conversion-like events, these estimates of $\delta$ could be underestimated by a factor as large as $1/x$.

This kind of interpretation also ignores the possibility of pre- and post-meiotic events that might influence LD, for example, nonindependent mutation and/or migration. As an example of why these issues might be a concern, consider the situation in Drosophila melanogaster, where fine-scale genetic maps imply an average $x{c}_0\simeq 2.3\times {10}^{-8}$ per nucleotide site for female meiosis on the two major autosomes (Singh 2005), which must be reduced by 50% to account for the absence of crossing over in males. For the Raleigh population, $\rho \simeq 0.0118$ (Chan et al. 2012), and by setting silent-site heterozygosity to its equilibrium expectation of $4N_{e}u$ and factoring out the known mutation rate, $u=5.2\times {10}^{-9}$ (Schrider et al. 2013), an $N_e$ of 800,000 is inferred. Assuming that 0.0118 estimates $4N_{e}x{c}_0$, the estimated population recombination rate ($\rho$) then implies $x{c}_0\simeq 3.7\times {10}^{-9}$, which is $\sim 3.1\times$ lower than the map-based estimate of $1.15\times {10}^{-8}$. In other words, even though D. melanogaster is an obligately sexual species, explanation of the standing level LD requires that the effective rate of crossing over be $\sim 3.1\times$ lower than that observed in laboratory crosses. Again, if $\hat{\rho }$ overestimates $x{c}_0$ by failing to account for gene-conversion processes, this discrepancy would be even greater.

Extending this type of analysis to D. pulex, we note that from the average genetic maps from several crosses, $x{c}_0\simeq 8.5\times {10}^{-8}$ per nucleotide site (Molinier et al. 2021). From Maruki et al. (2022), the long-term average $N_e$ from these populations $\simeq 6.4\times {10}^5$, which under the assumption that $\hat{\rho }=0.0124\simeq 4N_{e}x{c}_0/\delta$, implies that $x{c}_0/\delta \simeq 4.8\times {10}^{-9}$ for the natural populations. Thus, taken at face value, comparison of these two measures implies an average of $\delta \simeq 18$ generations per sexual episode, which is $\sim$3 to $6\times$ longer than the intervals expected in these temporary-pond populations (see Introduction), not greatly different from the inflation observed in D. melanogaster. Aside from the potential influence of nonindependent mutations and population subdivision, this apparent reduction in the effective frequency of recombination in these D. pulex populations might be a function of very rare years in which such ponds never dry up, in which case a maximum of 20 consecutive clonal generations could occur. There is also the possibility that there has been a several-fold reduction in recent $N_e$ in these populations, as suggested by the temporal analysis in Lynch et al. (2020), which would bring the population-genomic data and ecological observations in closer alignment. Mating between close relatives can also reduce the effective recombination rate, but this seems unlikely here, given that all of these populations have genome-wide profiles of genotype frequencies close to Hardy–Weinberg expectations (Maruki et al. 2022).

Recombination Hotspots

Finally, although hotspots account for very large fractions of the total recombinational activity in humans (Myers et al. 2005), chimpanzees (Auton et al. 2012), mouse (Paigen et al. 2008), and birds (Groenen et al. 2009; Kawakami et al. 2017), this appears not to be the case in Daphnia. Strong recombination hotspots are also lacking in Drosophila (Chan et al. 2012; Comeron et al. 2012; Manzano-Winkler et al. 2013; Smukowski Heil et al. 2015) and in C. elegans (Kaur and Rockman 2014), although there does appear to be more rate heterogeneity in these species than in D. pulex (fig. 4). Keeping in mind that the types of genetic and population-structural factors that deviate from the assumptions of underlying computational programs such as LDhat may render the search for recombination hot spots conservative and result in the false identification of recombination cold spots, the current data suggest that, among animals, recombination hotspots may largely be confined to vertebrates.

Closing Comments

Given that the use of spatial patterns of LD to infer selection is a major enterprise (Walsh and Lynch 2018), the future acquisition of unbiased inferences will require the development of proper null models based on an understanding of the recombinational, mutational, and population-subdivision mechanisms that generate baseline LD profiles. The quantitative relationships presented here provide a start by identifying the types of problems that need to be resolved, but these are purely statistical expressions. A fuller understanding of the mechanisms underlying general patterns of LD will require further development of population-genetic theory and empirical study of the chromosome-level features of gene conversion and other homogenizing processes.

Materials and Methods

Sample Collection, DNA Sequencing, and Data Preparation

Methods involving data acquisition are outlined in detail in Maruki et al. (2022), and are only recapped briefly here. In addition to reporting on samples from eight temporary-pond populations distributed in the midwest and eastern portions of North America, we include an evaluation of one of the populations (PA) sampled annually from 2013 to 2021. Each established genotype is a hatchling from a unique sexually-produced resting egg, collected shortly after pond refilling each year. Almost all such hatchlings are expected to be products from a mating in the immediately preceding year, as long-term resting-egg survival seems unlikely in the highly oxidized surface soil of the study sites. Consistent with the absence of such spill-over (which would cause a Wahlund effect), all population samples were in near Hardy–Weinberg equilibrium proportions (Maruki et al. 2022).

All sequence reads were mapped to the reference genome for D. pulex (PA42 3.0; Ye et al. 2017) derived from a clone from one of the study populations (PA), again as outlined in Lynch et al. (2017) and Maruki et al. (2022). A very high degree of synteny between this genome and those recently generated with long reads for the closely related species D. pulicaria indicates that the PA42 reference has minimal assembly problems (Jackson et al. 2021). As more fully detailed in Maruki et al. (2022), prior to analysis, the resultant clone-specific data within each population were screened to: (1) mask out any sites discordant with a goodness-of-fit test; (2) remove any potentially contaminated isolates; (3) remove clones with $<3\times$ average coverage per site; (4) mask repetitive regions; and (5) remove sites with sequencing error-rate estimates <0.01 (see Lynch et al. 2017). The resultant numbers of mapped sites and individuals analyzed per population are noted in Maruki et al. (2022, e.g., supplementary table S1, Supplementary Material online); sample sizes for multiple years for population PA ranged from 72 to 94 clones.

Estimation of Broad-scale Patterns of Linkage Disequilibrium

Site-specific allele and genotype frequencies and individual genotype calls were determined using the maximum likelihood (ML) procedures of Maruki and Lynch (2015, 2017). Population-level linkage disequilibrium ($D$) was estimated using the ML method of Maruki and Lynch (2014), which is designed for populations in Hardy–Weinberg equilibrium, a condition fulfilled by the study populations (Maruki et al. 2022). These methods are easy to implement, requiring as input the simple read quartets (numbers of inferred A, C, G, and T nucleotides) at each filtered site in each individual, and factor out the contributions from all sources of sequencing errors (not simply quality scores) by ML. Given the mean sequence coverages and numbers of individuals deployed in this study, these methods yield estimates that are essentially unbiased, with sampling variance close to the minimum theoretical possibility, and hence perform as well as (and in many cases better than) other existing methods (Maruki and Lynch 2015, 2017). To minimize any potential alignment issues, all such analyses were confined to all pairs of sites within scaffolds, provided there were no more than 10 undefined intervening nucleotides.

Although the ML estimator of $D$ is essentially unbiased (see also Ragsdale and Gravel 2020), estimates extrapolated to $r^2$, the squared, normalized LD coefficient, are upwardly biased by sampling error. With large sample sizes and high LD, the bias is relatively small, and is ignored in most prior studies, leading to the impression that the LD stabilizes at nonzero values at large physical distances between sites. With whole-genome data, where there is interest in the decline of LD out to very large physical distances, it is desirable to eliminate the bias, and this can be done by subtracting from estimates of $r^2$ the sampling variance of $r$ estimated as ${\sigma }_r^2\simeq (1-{\rho }^2{)}^2/n$, (eq. A1.20b, from Lynch and Walsh 1998), where $\rho$ is the parametric correlation coefficient, $n$ is the number of individuals in the sample (Weir and Hill 1980), and the average value of $r$ derived from two-locus, phased genotypes is substituted for $\rho$. As $r\to 0$, the expected value of $r^2$ becomes equivalent to the sampling variance, $\simeq 1/n$, and the bias correction leads to $r^2$ estimates converging on 0.

Individual-level disequilibrium (correlation of zygosity) was estimated with the methods of Lynch (2008) as implemented in Haubold et al. (2010). Results reported for each population are averages for each of the ten individuals with the highest sequence coverage, over a range of physical distances between sites of 1 and 250,000 bp. For the first 1,000 bp, estimates were obtained for increments of single nucleotides, whereas to offset the increased sampling variance with declining numbers of more distant pairs, for intersite distances of 1,000 to 20,000 bp, the data were binned into windows of 10-bp in width, and for larger distances into 100-bp bins.

For the PA population, we estimated the covariance of allele-frequency change between pairs of linked sites in samples from adjacent years. The idea here is that although sampling error associated with finite numbers of individuals will result in variance of allele-frequency estimates across years, correlated changes among linked sites requires the presence of linkage disequilibrium. For each pair of polymorphic sites, the alleles were first phased into coupling configurations using information from all individuals other than double heterozygotes. Then, for all pairs of sites separated by a particular distance $d$, for the minor allele frequencies, the temporal deviations were calculated as ${\delta }_{i1}=p_{i1,t+1}-p_{i1,t}$ and ${\delta }_{i2}=p_{i2,t+1}-p_{i2,t}$, where $i1$ and $i2$ denote the sites for the ith pair, and $p_{x,y}$ denotes the allele frequency at site $x$ in year $y$. Given the two $\delta$ values for all pairs of sites separated by distance $d$, the correlation of allele-frequency change was then calculated using the standard expression (covariance in the numerator, and the square root of the products of the variances from the first and second years in the denominator). Averaging over eight annual comparisons (spanning a total of $\sim$30 generations) provided a pooled estimate of $r_{\delta }$ for each distance $d$.

Fine-scale Patterns of Linkage Disequilibrium

To evaluate spatial variation within and among chromosomes in the population recombination rate per generation per base pair ($\rho =4N_e{c}_0$, where $N_e$ and $c_0$ are the effective population size and recombination rate per generation per base pair) in each population, we applied the LDhat program of McVean and Auton (2007) to each individual population, averaging the site-specific measures across all populations to minimize background sampling noise. To minimize uncertainties, we ignored all pairs of sites separated by gaps containing >10 nucleotide sites, as well as any sites within 1-kb flanking regions of such regions. This conservative approach still left available thousands of spans of SNPs in excess of 10 kb in length (supplementary fig. 1, Supplementary Material online). All analyses were restricted to sites with minor-allele frequency estimates that were found by maximum-likelihood to be significantly >0.01 at the $0.05$ probability level (Maruki et al. 2022).

Our choice of parameter settings for these analyses was based on extensive sensitivity analyses using the known distribution of polymorphic sites in one of the study populations, KAP (Urban 2018). For the sample sizes and rates of crossover recombination reported here, computer simulations showed that: (1) estimates of $\rho$ are nearly unbiased for uninterrupted length spans of at least 10 kb, with the variance in estimates declining dramatically when lengths exceed 50 kb; (2) substantial missing data (>30% missing alleles) can cause elevated sampling variance and upwardly biased $\rho$ estimates; and (3) the use of block penalties ranging from 5 to 50 gives nearly identical results. Thus, to be conservative in our analyses, we focused on 323 scaffolds/blocks with lengths >100 kb, with all clones within each population having $>7\times$ sequence coverage, which left $\sim$130 million sites in the final analysis. Prior to running the interval program (part of the LDhat package), we phased the alleles within each population using fastPHASE version 1.4.8 with default settings (Scheet and Stephens 2006). Then, guided by the simulations in Urban (2018), we used the program lkgen (in the LDhat package) to modify the LDhat lookup table (setting the population mutation rate $=$ 0.01 (informed by the analyses in Maruki et al. 2022), which is appropriate for D. pulex); and in running the interval program, we used the parameters known to be efficient for D. pulex data (i.e., block penalty $=$ 5; number of iterations $=$ 1,000,000; and number of updates between samples $=$ 3,500).

An alternative maximum-likelihood approach to estimating $\rho$ is the program LDhelmet (Chan et al. 2012), which the authors argue yield more precise estimates than LDhat, although this seems not to always be the case (Hermann et al. 2019). LDhelmet is very highly demanding in terms of computational time, and would require $>3\times {10}^6$ CPU hours to complete a study of the magnitude herein. However, to obtain some insight into the robustness of our analyses, we did use LDhelmet to perform a parallel analysis of one population, Tex. Averaging over the results for 323 scaffolds, we obtained estimates of $\rho$ equal to 0.0805 ($\mathrm{SE}=0.0035$) and 0.0742 (0.0027) with LDhat and LDhelmet, respectively, which are not significantly different. Estimates using LDhat exceed those with LDhelmet when the former is high, but are lower than those with LDhelmet when the former is low, that is, LDhat yields more extreme values, although the differences between the two, which occur at the most extreme values, are less than two-fold (supplementary fig. S3, Supplementary Material online).

Supplementary Material

Supplementary data are available at Genome Biology and Evolution online.

Data Availability

The FASTQ files of the raw sequencing data for the contemporary population samples are available at the NCBI Sequence Read Archive (accession numbers SAMN06005639 and SRP155055), and for the annual samples from population PA are deposited under project ID PRJNA684968.