Energy Cost Expression for a Youth Compendium of Physical Activities: Rationale for Using Age Groups

Abstract

Purpose:

This study compared the accuracy of physical activity energy expenditure (PAEE) prediction using two methods of accounting for age dependency versus one standard (single) value across all ages.

Method:

PAEE estimates were derived by pooling data from five studies. Participants, 6–18 years (n=929), engaged in 14 activities while in a room calorimeter or wearing a portable metabolic analyzer. Linear regression was used to estimate the measurement error in PAEE (expressed as MET_y) associated with using age-groups (6–9, 10–12, 13–15, and 16–18 years) and age-in-years (each year of chronological age (e.g., 12=12.0–12.99 years)) versus the standard (a single value across all ages).

Results:

Age-groups and age-in-years showed similar error, and both showed less error than the standard method for cycling, skilled and moderate-to-vigorous intensity activities. For sedentary and light activities, the standard had similar error to the other two methods. Mean values for root mean square error ranged from 0.2–1.7 MET_y across all activities. Error reduction ranged from −0.2–21.7% for age-groups and −0.23–18.2% for age-in-years, compared to the standard.

Conclusion:

Accounting for age showed lower errors than a standard (single) value; using an age-dependent model in the Youth Compendium is recommended.

Introduction

The Compendium of Physical Activities standardized the coding of physical activity energy expenditure (PAEE) by activity type and intensity (METs) for adults (2). According to the Adult Compendium, a MET is the activity metabolic rate divided by the resting metabolic rate (2). Updated in 2000 (3) and in 2011 (1), the Compendium is intended to be used in adults without physical limitations. Energy expenditure estimates from the Compendium are not recommended for children and adolescents.

Despite the fact that evidence has shown adult MET values both underestimate and overestimate PAEE for youth, depending on activity (7), many individuals have used the adult Compendium for youth (11, 15). To address the lack of PAEE estimates for youth, Ridley et al. introduced the Compendium of Energy Expenditures for Youth (12). In the youth Compendium, when youth data were not available, adult values that adjusted for differences in basal metabolic rates between adults and youth were used (13). In addition, walking and running PAEE were derived from youth data using modeling techniques. The Youth Compendium was an important starting point to provide MET values for youth, but was limited because about two-thirds of the values were actually adult-based and only one MET value was provided for all age groups (12).

To update the Youth Compendium with youth-based values, a method is needed that expresses the energy cost of physical activities and considers: 1.) children’s resting energy expenditure is higher than adults’ and declines with age on a mass-specific basis (7, 14) and 2.) the energy cost of performing submaximal activities increases with age when expressed as kcal/min (LO₂/min) but decreases with age when expressed relative to body mass (mlO₂/kg/min) (14), meaning that children become more efficient in their movements over time (14). The differences in PAEE between youth and adults for rest and physical activity highlight the need to take into account age-related changes when estimating youth PAEE.

Previously, our work group examined expressions of energy cost and suggested that the Youth MET (MET_y; energy cost of the activity divided by (estimated) basal energy expenditure) was the most practical metric to use in an updated Youth Compendium (10). However, using MET_y does not completely ameliorate age-related changes in energy expenditure. Thus, given the wide range of energy equivalences for one MET over childhood and adolescence, choosing one standard MET value to apply to all ages may be challenging. Alternatively, employing several values to represent MET_y across the age spectrum may be unwieldy in practice. The method of expressing the energy cost of physical activities should provide the smallest error possible while considering age-related differences in energy cost in children and adolescents. Therefore, the purpose of this study was to compare the measurement error for two methods of accounting for age dependency in MET_y, age-groups (6–9, 10–12, 13–15, and 16–18 years) and age-in-years (e.g., 12=12.0–12.99), to a standard for all ages. This is necessary because the development of an updated Youth Compendium is underway.

Methods

Design.

Investigators from five sites contributed the data included in this manuscript: Baylor College of Medicine (4), Michigan State University (MSU) (17), Oregon State University (OSU) (17), University of Massachusetts – Boston (UMB) (5, 6), and University of North Carolina at Chapel Hill (UNC) (7). All studies contributing data were cross-sectional in design. Each site obtained approval from its own Institutional Review Board, and all parents and youth provided written informed consent and assent, respectively. Due to the use of secondary, de-identified data for analyses, none of the IRBs required further permission. Because this study involved secondary analysis of existing data, the precise EE measurement methods were not perfectly standardized across sites. To ensure the data were representative of a metabolic steady state, all laboratories collected data for at least 5 minutes. MSU and OSU collected data for 5 min. UNC collected data for 7 min. UMB collected data for 8 min, and Baylor for 20 minutes. The VO₂ measurement system used also differed by study site: MSU and OSU (Oxycon portable metabolic analyzer), UMB and UNC (Cosmed portable metabolic analyzer), and Baylor (room calorimeter). All systems were calibrated with tanks containing known concentrations of O₂ and CO₂, and flow rates were calibrated with a 3-L syringe in the case of portable metabolic systems or infusion of N₂ and CO₂ into the room calorimeters to simulate human respiration. Data collected with portable metabolic analyzers were collected breath-by-breath and averaged over 1-min time intervals. Data collected with the room calorimeter were also averaged over 1-min time intervals.

In the combined data set, there were 43 activities with measured values. Fourteen activities with ≥ 100 participants and an age range of at least 6 to 18 years were selected for analysis. The 14 activities included were computer games, television viewing, housework, sweeping, Wii play, cycling, aerobics, dance, walking at 2 and 3 mph, running at 4 and 5 mph, basketball, and rope skipping. Specific details regarding exactly how activities were performed can be found in the original manuscripts from each site (4, 6, 7, 17). Activities represented different intensity levels, from sedentary (e.g., computer games) to vigorous (e.g., running). Lifestyle (e.g., dance), household (e.g., sweeping), and skilled activities (e.g., basketball) were included, and children performed some activities at a prescribed pace and others at self-selected pace.

Participants.

Across all studies, participants ranged from 5 to 19 years (overall mean 12 ± 3 y (mean ± SD)). The total sample included 1060 youth. However, 112 individuals did not have VO₂ data for any of the 14 activities or were missing key variables such as age, height, or body mass, and were excluded from analyses. Additionally, the research team excluded data from 19-year-olds (n=2) and five-year-olds (n=17). The final sample included 505 boys and 424 girls, for a total of 929 youth. Data from MSU and OSU included participants 6–15 years old. UNC included 8–18 year-olds. UMB included 11–15 year-olds, and Baylor included 6–18 year-olds. All activities included in analyses involved participants 6–18 years old, with the exception of basketball (7–16 years) and rope skipping (8–18 years). See Tables 1 and 2 for further information regarding number of participants and ages for each activity and demographic characteristic. The racial/ethnic distribution was as follows: 61% Caucasian, 21% African American, 11% Hispanic, and 7% other races/ethnicities. The majority of the sample (43%) was from the UNC. The Baylor and UMB sites contributed 17% and 18%, respectively, and the MSU and OSU sites contributed 22%.

Table 1.

Number of participants included in activities by age group

Activity	6–9 years	10–12 years	13–15 years	16–18 years
Sedentary
Computer games	102	136	95	30
Television viewing	101	125	110	89
Light-intensity
Housework	68	99	61	5
Sweeping	124	170	133	74
Wii® Play	44	58	49	20
Non-weight bearing
Cycling ~10 mph	59	67	75	75
Moderate- to vigorous-intensity
Aerobics	114	118	92	21
Dance	45	62	48	25
Walk - 2 mph	132	132	138	107
Walk - 3 mph	120	47	7	98
Run - 4 mph	78	83	84	70
Run - 5 mph	44	29	12	23
Skilled
Basketball	105	89	61	8
Rope Skipping	49	77	72	65

Table 2.

The number of participants (and percentage) for demographic characteristics by age group

Participant	6–9 years		10–12 years		13–15 years		16–18 years		6–18 years
Characteristics	(n=241)		(n=329)		(n=242)		(n=117)		(n=292)
Sex
Boys	124	(51.5)	178	(54.1)	147	(60.7)	56	(47.9)	505	(54.4)
Girls	117	(48.5)	151	(45.9)	95	(39.3)	61	(52.1)	424	(45.6)
Race/Ethnicity
African American	31	(12.9)	90	(27.4)	57	(23.6)	18	(15.4)	196	(21.1)
Caucasian	169	(70.1)	175	(53.2)	141	(58.3)	79	(67.5)	564	(60.7)
Hispanic	30	(12.4)	38	(11.6)	27	(11.2)	10	(8.5)	105	(11.3)
Other	11	(4.6)	26	(7.9)	17	(7.0)	10	(8.5)	64	(6.9)
Body Mass Index Category*
Underweight	5	(2.1)	8	(2.4)	3	(1.2)	1	(0.9)	17	(1.8)
Normal Weight	170	(70.5)	189	(57.4)	157	(64.9)	84	(71.8)	600	(64.6)
Overweight	28	(11.6)	64	(19.5)	34	(14.0)	17	(14.5)	143	(15.4)
Obese	38	(15.8)	68	(20.7)	48	(19.8)	15	(12.8)	169	(18.2)

^*Body mass index for age is based on measured height and weight. Underweight = <5th percentile, healthy weight = 5 - <85^th percentile; overweight ≥85^th - < 95^th percentile; obese = ≥95^th percentile (http://www.cdc.gov/growthcharts/cdc_charts.htm).

Note: All column percentages may not add up to 100% because of rounding

Data Management.

Variables included demographic characteristics (age, sex), anthropometric characteristics (height, body mass), and (absolute) VO₂ values (in ml∙min⁻¹) for all activities. Height and body mass were used to calculate body mass index (BMI) and BMI percentile according to reference values from the Centers for Disease Control and Prevention (CDC) growth charts (http://www.cdc.gov/nccdphp/dnpao/growthcharts/resources/sas.htm).

Dependent variable.

The Youth MET (MET_y) was calculated for each participant for each activity as EE (kcal∙kg⁻¹∙hr⁻¹) divided by basal metabolic rate (BMR), which was determined using the Schofield equation (16). The Schofield equation takes into account age, sex, height and weight.

Statistical Analyses.

We compared the error associated with the age-groups and age-in-years methods to a method with a standard value across ages (which was the referent group; Table 3). Sensitivity testing was conducted to determine if there were significant differences between the sites for each activity. For consistency, we used a regression approach and sample-dependent values to estimate the error for the three approaches. In order to examine error relative to the standard method, we calculated the percent reduction in residual variance (root mean square error) for age-groups and age-in-years regression methods (10). Data analyses were conducted with a statistical software package (SAS 9.3 version; SAS, Cary, NC). The standard method resembled the approach in the Adult Compendium, in which a single MET_y value, representing the sample’s mean age, was assigned to a specific activity, regardless of age.

Table 3.

Results from comparison of estimated youth METs from standard, age-groups, and age-in-years models

Activity	N	Model Descriptive Statistics				Model Root Mean Square Error (RMSE)			Percent Reduction in RMSE from Standard
		All Models	Standard*	Age-Groups	Age-in-Years	Standard	Age-Groups	Age-in-Years	Age-Groups	Age-in-Years
		Mean	(SD)	(SD)	(SD)	RMSE (RSD)	RMSE (RSD)	RMSE (RSD)	%	%
Sedentary
Computer games	363	1.40	(0.23)	(0.01)	(0.03)	0.23 (0.31)	0.23 (0.31)	0.23 (0.32)	1.59	0.56
Television viewing	425	1.20	(0.26)	(0.05)	(0.03)	0.26 (0.34)	0.25 (0.33)	0.25 (0.33)	1.76	0.65
Light-intensity
Housework	233	3.00	(0.57)	(0.04)	(0.05)	0.57 (0.83)	0.57 (0.81)	0.57 (0.81)	−0.22	0.22
Sweeping	501	3.32	(0.63)	(0.06)	(0.08)	0.63 (0.79)	0.62 (0.80)	0.62 (0.80)	1.22	0.82
Wii® Play	171	2.63	(0.72)	(0.11)	(0.03)	0.72 (1.08)	0.70 (1.03)	0.72 (1.08)	1.37	−0.23
Cycling
Cycling ~10 mph	276	5.76	(1.30)	(0.43)	(0.65)	1.29 (1.51)	1.09 (1.31)	1.12 (1.29)	15.26	13.52
Moderate- to vigorous-intensity
Aerobics	345	3.83	(0.98)	(0.21)	(0.36)	0.98 (1.12)	0.92 (1.06)	0.92 (1.07)	6.16	6.65
Dance	180	3.55	(0.98)	(0.16)	(0.25)	0.97 (1.23)	0.91 (1.12)	0.94 (1.17)	5.68	3.11
Walk - 2 mph	509	3.56	(0.66)	(0.23)	(0.17)	0.66 (0.84)	0.61 (0.77)	0.64 (0.80)	7.25	3.08
Walk - 3 mph	272	4.41	(0.92)	(0.46)	(0.57)	0.92 (1.66)	0.92 (1.62)	0.92 (1.64)	0.67	0.41
Run - 4 mph	315	8.16	(1.56)	(0.62)	(0.90)	1.56 (1.92)	1.22 (1.47)	1.27 (1.61)	21.66	18.25
Run - 5 mph	108	8.21	(1.61)	(0.11)	(0.08)	1.60 (2.43)	1.53 (2.26)	1.50 (2.21)	4.26	6.51
Skilled
Basketball	263	6.77	(1.63)	(0.71)	(0.91)	1.62 (1.85)	1.35 (1.55)	1.35 (1.58)	16.21	16.95
Rope Skipping	263	8.10	(1.66)	(0.18)	0.64)	1.66 (2.04)	1.50 (1.87)	1.53 (1.85)	8.71	7.60

^*Standard Deviation (SD) from sample, SD for model with constant is zero

Note: RMSE is the root of the mean square errors; percent reduction reflects the relative reduction in the root mean square error (RMSE) from the model that is constant across all ages compared to the models that include age. For example, percent reduction from Standard to Age-in-years is (RMSE_constant- RMSE_ageyrs)/RMSE_constant x 100%. Positive % indicates a decrease in error and a negative % indicates an increase in error when including age.

Standard (metric constant): Metric = b0

For the age-groups method, a MET_y value was assigned to each of the four age-groups using an average age for each age group: 6–9 year olds, 10–12 year olds, 13–15 year olds, and 16–18 year olds. The four age-groups were chosen to represent pre- (middle childhood), early, mid- and late adolescence (9), The World Health Organization classifies adolescence as 10–18 years (http://www.who.int/topics/adolescent_health/en/).

Age-groups (metric standard within age-groups): Metric = b0 + b1*10–12 years + b2*13–15 years + b3*16–18 years, referent group is 6–9 years

The age-in-years method allowed the metric to vary for each year of age (e.g., 12-yr-olds were 12.0–12.99 years). The predicted value is a standard plus an incremental value for each additional year.

Age-in-years (metric varies with age): Metric = b0 + b1*Age (years)

Following the analyses, the team developed an example layout for the Youth Compendium (Table 4). For comparative purposes, the standard value is shown in the first column, age-groups in the middle four columns, and age-in-years regression equations in the last column.

Table 4.

Youth MET (MET_y) values for ages 6–18 years based on regression analysis

Activity	Standard METya	METy by Age Groupb				Age-in-years: Equation (METy=b0 + b1*age)
	6–18 years	6–9 years	10–12 years	13–15 years	16–18 years
Sedentary
Computer games	1.40	1.44	1.41	1.38	1.35	1.51 + −0.01 x age
Television viewing	1.20	1.16	1.19	1.22	1.25	1.08 + 0.01 x age
Light-intensity
Housework	3.02	2.92	3.00	3.06	3.13	2.76 + 0.02 x age
Sweeping	3.32	3.44	3.35	3.26	3.18	3.66 + −0.03 x age
Wii® Play	2.63	2.59	2.62	2.65	2.67	2.53 + 0.01 x age
Cycling
Cycling ~10 mph	5.60	4.75	5.41	5.98	6.54	3.34 + 0.19 x age
Moderate- to vigorous-intensity
Aerobics	3.95	3.38	3.82	4.20	4.58	2.44 + 0.13 x age
Dance	3.56	3.19	3.48	3.72	3.97	2.57 + 0.08 x age
Walk - 2 mph	3.56	3.34	3.51	3.66	3.81	2.96 + 0.05 x age
Walk - 3 mph	4.40	4.27	4.37	4.46	5.55	4.04 + 0.03 x age
Run - 4 mph	8.10	6.89	7.83	8.64	9.45	4.86 + 0.27 x age
Run - 5 mph	8.27	7.33	8.06	8.69	9.32	5.75 + 0.21 x age
Skilled
Basketball	7.28	5.79	6.95	7.94	8.93	3.31 + 0.33 x age
Rope Skipping	7.93	7.01	7.73	8.34	8.96	5.46 + 0.21 x age

^aMid-point of age range is 12 years

^bMid-points for age-groups are 7.5 years, 11 years, 14 years, and 17 years

Results

Average height of the sample was 152 ± 17 cm (mean ± SD), and average body mass was 49 ± 20 kg. BMI averaged 21 ± 7 kg∙m⁻², with 67% of the sample classified as normal weight (5^th-84^th percentile), 15% overweight (85^th-94^th percentile), and 18% obese (≥95^th percentile), according to Centers for Disease Control and Prevention growth charts (https://www.cdc.gov/growthcharts/cdc_charts.htm). Approximately 3% to 9% (depending on activity) of the pooled data had values that were deemed as outliers, meaning they were excluded from the analyses. The team performed extensive evaluation of outliers (based on weight-relative VO₂ values) and only removed those values that were deemed biologically implausible (which in all cases were more than two standard deviations from the age- and sex-specific mean for that activity). Basketball was the only activity for which there was a significant (p˃0.01) site by age interaction. Upon further investigation, it appeared the difference was due to differences in sample site characteristics. One site had an equal number of boys and girls whereas the other site had twice as many boys as compared to girls. An additional examination involved fitting the basketball activity models with a site main effect and a site by age interaction. The results yielded even smaller error, similar to the model without site, with <1% difference in the percent reduction of error between the two models accounting for age.

There was a greater reduction in error for MET_y using age-groups or age-in-years for activities such as cycling and more vigorous intensity/skilled activities (Table 3), as compared to a standard (single) value. Across all activities, using age-groups resulted an average of 6.6% less error than using a standard value, while using the age-in-years method resulted in 5.6% less error than using the standard. Mean standard errors indicated that all three methods had low error for predicting energy expenditure (EE) accurately (mean differences ranged from 0.2 to 0.7 MET_y) for sedentary and light activities. Error for cycling, moderate-to-vigorous, and activities requiring complex motor skills (e.g., basketball) was higher (0.6 to 1.7 MET_y). Additionally, for all cycling, moderate-to-vigorous, and skilled activities (with the exception of walking at 3 mph), age-groups and age-in-years methods had lower error relative to the standard method.

Figures 1 and 2 show visual representations of error reduction across methods for two activities, walking at 2 mph and basketball. Illustrations of these two activities were chosen since walking represents a light-to-moderate intensity, and basketball represents a skilled, moderate-to-vigorous activity. Less error across methods occurs for walking (Figure 1) than for basketball (Figure 2). There is greater disparity in MET_y in older children compared to younger children for basketball than for walking.

Figure 1.

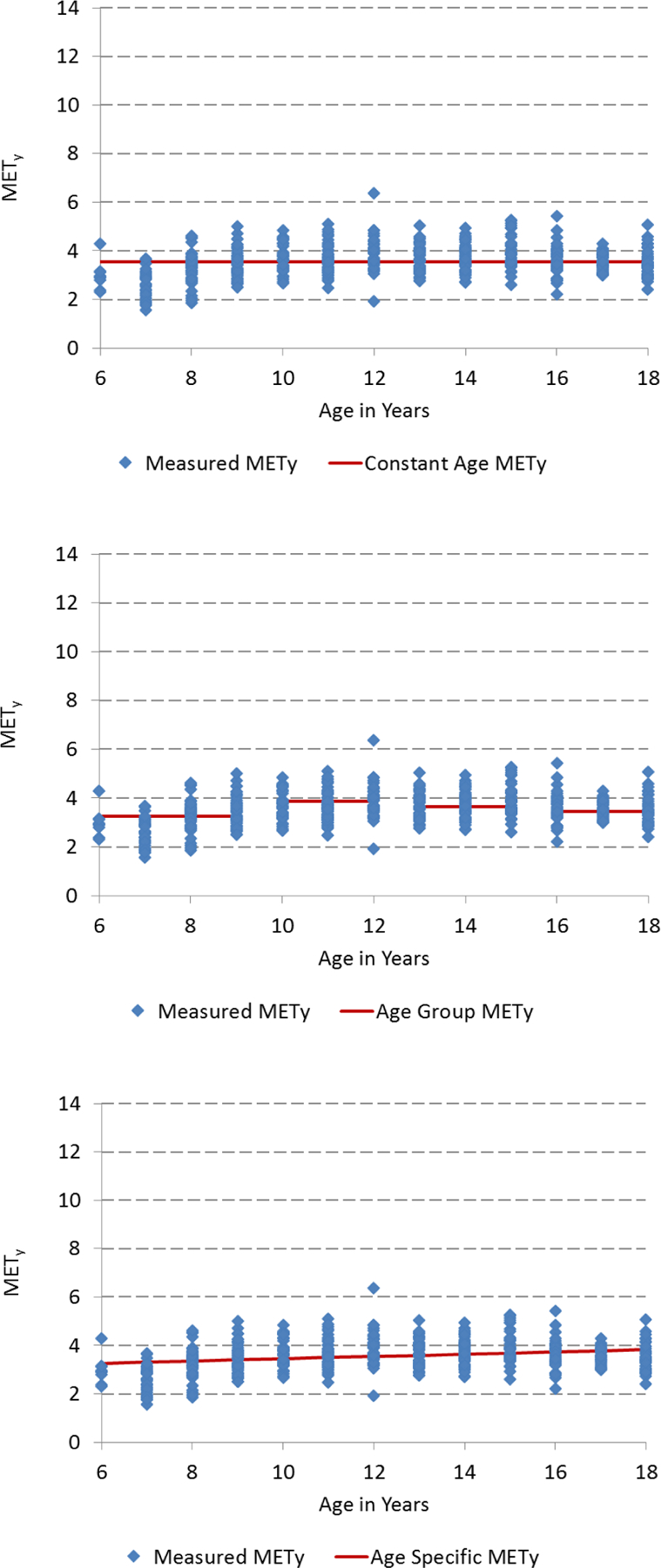
Visual representation of the three models used to examine the additional reduction in error in Youth METs (MET_y) for walking 2 mph when accounting for age: standard MET_y across all ages (top), standard MET_y for age-groups (middle), and age-in-years MET_y (bottom).

Figure 2.

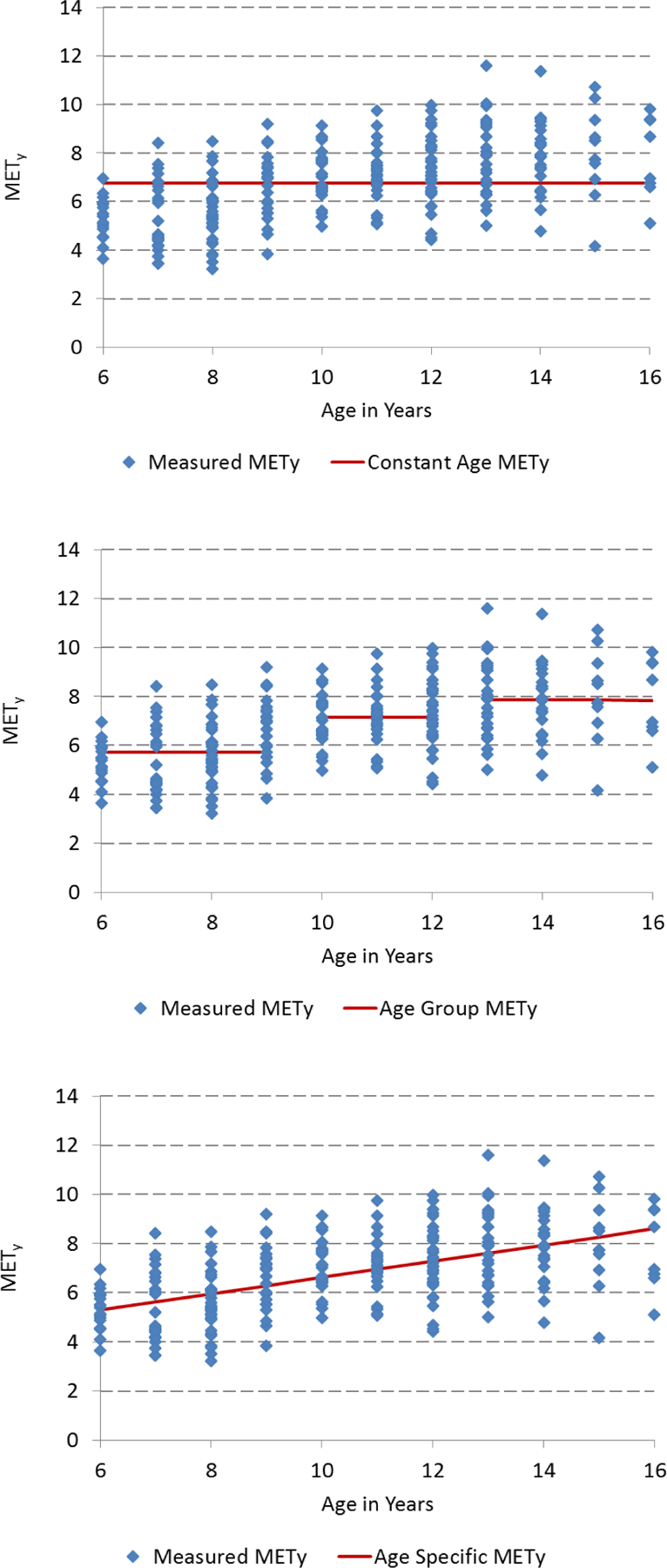
Visual representation of the three models used to examine the additional reduction in error in Youth METs (MET_y) for basketball when accounting for age: standard MET_y across all ages (top), standard MET_y for age-groups (middle), and age-in-years MET_y (bottom). Note data were not collected for 17–18 year olds.

Table 4 highlights the contrast in MET_y between the standard and age-groups methods. Using a standard MET_y value for all ages (6–18 y) results in overestimation of EE for younger age-groups and underestimation of EE for older age-groups for most activities. For some activities, such as sedentary and light, differences across age-groups were less than one MET_y. However, for skilled activities, differences across age-groups could be as much as 2–3 MET_y, illustrating that the use of MET_y by age-groups would result in less over- and under-estimation than the use of a standard MET_y value.

Discussion

Our findings showed that using MET_y values that accounted for age resulted in less error in energy expenditure prediction than using one standard value across all ages, particularly for cycling, moderate-to-vigorous, and skilled activities. Thus, a single value, like in the Adult Compendium (1,2,3) is not the best approach for estimating energy cost for youth. These findings have relevance for the development of an updated Youth Compendium of physical activities. An updated Compendium will provide energy cost values for many activities over a wide range of ages. The use of age-groups or age-in-years approaches would reduce the error to a similar degree. Obtaining values for each year of age would be difficult and time-consuming; obtaining energy expenditure estimates for age-groups may be a more feasible approach.

The original Ridley Compendium provides a single, standard MET_y value for all ages (12). When comparing standard MET_y values from the current study to the Ridley Compendium, the values appear to be similar for sedentary and light activities, but some values are higher and some are lower for locomotor activities and bicycle riding. Regardless, the approach of using one value across ages is problematic given the known energy expenditure differences at rest and during activity across ages. For example, an 8-year-old child has a BMR of approximately 1.7 kcal.kg^−1.h⁻¹ while a 16-year-old adolescent has a BMR of approximately 1.1 kcal.kg^−1.h⁻¹ (16). Therefore, youth of these two ages riding a bicycle at approximately six MET_y would have energy expenditures of 10.2 kcal.kg^−1.h⁻¹ and 6.6 kcal.kg^−1.h⁻¹ for the 8- and 16-year-old, respectively, which is a difference of 3.6 kcal.kg^−1.h⁻¹ or approximately 35% less for the 16 year old. If one assumes the body mass of a 10-year-old is 35 kg then the child would expend ~357 kcal for an hour of bicycle riding, whereas a 60 kg, 16-year-old would expend ~396 kcal doing the same activity. This amounts to approximately an 11% higher PAEE for the 16-year-old adolescent compared to the 8-year-old child. Additionally, younger children are less efficient when performing many activities because they have higher EE per unit mass compared to an adolescent (14) or lack experience with the activity. Our findings illustrate how, especially for activities in the moderate-to-vigorous and skilled categories, use of a standard value would overestimate energy cost for younger children and underestimate energy cost for adolescents. The combination of differences in basal metabolic rate and PAEE can result in large age-related differences (4.75 vs. 6.5 MET_y in the 6-yr-old vs. 16-yr-old, respectively) in activities such as cycling. Using the methods that take age into account reduces error up to 15–20% compared to the standard. Thus, we do not recommend a single, standard MET_y value for activities included in the Compendium.

The age-groups and age-in-years methods provide similar energy expenditure estimates for most activities. Since BMR changes significantly as the child grows, a specific age-related methodology would be optimal, especially for research purposes. However, the age-in-years approach may be difficult for some users of the Compendium, such as practitioners in an applied setting. The age group approach has been used previously by Harrell et al. (7), but the authors had only three age groups that were sex-specific. Our research team considered many different approaches for age-groups. For example, Harrell et al. devised puberty-related groups and then developed age-groups based on those pubertal differences. We chose age over puberty due to the lack of such information on the majority of subjects and the better generalizability of age over puberty. In addition, a closer examination of the Harrell data shows that the largest difference in REE between any of their three age-groups was 32%, while the largest difference between any of the five pubertal developmental stages was 37%. Thus, there was little improvement in error when using pubertal development over age, especially given the difficulty with obtaining accurate assessment of pubertal development. Although it seems intuitive that the age-in-years approach might outperform the age-groups approach, this was not the case. One reason is that it is possible that the relationship between age and energy expenditure is not completely linear. Another reason is that there were not data for particular activities at certain ages. Overall, using age-groups is likely the best approach to accounting for age in a Youth Compendium.

This study had several strengths and weaknesses. One weakness was a small number of younger or older children for some activities. Rope skipping and cycling included fewer 6–9 year-olds than other age-groups, while housework and basketball included fewer 16–18 year-olds. This may have resulted in less variability in the results because of more similar BMR and metabolic efficiency in the remaining age-groups. Another weakness was use of the Schofield equation to estimate BMR, rather than using measured values. Although the different data collection sites collected pre-exercise (resting) data, the protocols varied and all measures were taken immediately pre-exercise. True measures of BMR are difficult to obtain in children, and although it would be preferable to have them the team considered it better to standardize based on the equation. Similarly, most studies that would need to use a Youth Compendium would not be likely to assess true BMR.

We did not present values separately by sex. The Adult Compendium does not distinguish between sexes, either, and when sex differences were examined in the current sample, they comprised less than two percent of the variance in energy expenditure values after correcting for age and body mass. Also, some may view lack of accounting for body composition as a limitation. However, the adult Compendium does not make a weight/body composition-based adjustment. The purpose is to apply on a population-level basis, meaning that many types of individual differences are not accounted for in a Compendium. However, if researchers or practitioners desire to use an individualized approach, a corrected MET adjustment procedure is available for the adult Compendium (8). This approach is comparable to the age-groups approach used here. The strengths of the study include a large sample size, a large range of ages included, and a variety of activity intensities.

Use of age-groups or age-in-years MET_y values produces estimation errors that are similar and acceptable. However, assigning a standard MET_y value to represent energy cost of a given activity for all ages of children and adolescents is not optimal. Using age-groups to express energy expenditure in an updated youth Compendium may be a feasible alternative that also provides acceptable accuracy.