Abstract
We introduce an extended generalised logistic growth model for discrete outcomes, in which spatial and temporal dependence are dealt with the specification of a network structure within an Auto-Regressive approach. A major challenge concerns the specification of the network structure, crucial to consistently estimate the canonical parameters of the generalised logistic curve, e.g. peak time and height. We compared a network based on geographic proximity and one built on historical data of transport exchanges between regions. Parameters are estimated under the Bayesian framework, using Stan probabilistic programming language. The proposed approach is motivated by the analysis of both the first and the second wave of COVID-19 in Italy, i.e. from February 2020 to July 2020 and from July 2020 to December 2020, respectively. We analyse data at the regional level and, interestingly enough, prove that substantial spatial and temporal dependence occurred in both waves, although strong restrictive measures were implemented during the first wave. Accurate predictions are obtained, improving those of the model where independence across regions is assumed.
Keywords: COVID-19, Conditional Auto-Regressive, Stan, Generalised logistic growth
1. Introduction
Several approaches for modelling and forecasting COVID-19 incidence, prevalence, and related outcomes have been recently proposed. When high-quality data are available, compartmental models such as SIR/SEIR (Diekmann et al., 2013) are well known to describe the contagion dynamics satisfactorily and lead to scenario evaluation. However, high-quality data are unlikely to be collected for the current epidemic, leading to the failure of most forecasts based on those approaches (Ioannidis et al., 2020). Italy is not an exception. Indeed, public Italian data are gathered for mere descriptive and surveillance purposes, and present several issues that severely affect their quality. Coherency, comparability, and consistency have been largely overlooked. Measurement errors and systematic biases are common. Data collection systems are not standardised nor necessarily supported by proper digital or electronic devices and infrastructures. Late notifications, corrections, and adjustments to the daily cases occur repeatedly. In this context, empirical direct data modelling seems to be a more viable option than mechanistic compartmental models, allowing the researcher to deal with measurement error and restrict prediction to a short term (Girardi et al., 2020, Cabras, 2020, Alaimo Di Loro et al., 2021). An approach of this kind, as proposed by Alaimo Di Loro et al. (2021), involves the specification of an appropriate parametric distribution for the available aggregated data (e.g., Poisson or Negative Binomial for counts), perhaps meaningful predictors and offsets, and a logistic-type time trend. One of the limitations of this approach is that indicators in each area are modelled independently. That is clearly only a working assumption, as mobility have occurred across Italian regions also during the hard lockdown of Spring 2020. Even sick people with COVID-19 have been sometimes transferred from one region to another. Furthermore, it is likely that regions close to each other culturally, economically, or geographically (e.g., sharing borders) present similar features as people experience similar climates, pollution and have similar lifestyles. For these reasons, this work aims to overcome this limitation by explicitly taking into account the spatial dependence across regions and the temporal dependence within regions. We make this extension for different specifications of the generalised growth model of Alaimo Di Loro et al. (2021), in a Bayesian framework. The Bayesian formulation by itself is already a notably additional advancement, regardless of the model specification. We report here that posterior summaries, in our experience, seem to be more stable compared to the maximum likelihood estimates, possibly due to difficulties in finding a global optimum for the likelihood of an inherently non-linear model. Furthermore, exploiting hierarchical models’ flexibility in a Bayesian context, we replace the Negative Binomial assumption in Alaimo Di Loro et al. (2021) with the Poisson distribution. The still present over-dispersion and unobserved heterogeneity are accounted for by including observation-specific random effects. If the random effects were assumed to be gamma-distributed, the corresponding marginal would indeed be a Negative Binomial and the method would be analogous to the original modelling framework. However, we rather consider normally distributed random effects on the log scale. Gaussianity allows for a more straightforward specification of prior information and inclusion of possible dependence structures in the process governing such effects. While temporal correlation is dealt with an Auto-Regressive (AR) structure, spatial dependence is included by specifying a suitable Conditional Auto-Regressive (CAR) prior, where the covariance matrix is identified using two possible networks: one based on geographic proximity and one built on historical data of transport exchanges between regions (taken from Della Rossa et al., 2020). The advantage of introducing this dependence structure is twofold. On the one hand, the resulting simultaneous model provably gives more accurate description of the true pandemic evolution than separate models for each region. On the other hand, it can be expected that parameter estimates of characteristics of interest (e.g., peak time and height) can benefit from the pooling information from multiple regions. We separately evaluate the first and the second wave of Sars-CoV-2 in Italy. Similarly to Bartolucci and Farcomeni (2021), we consider weekly incidence, even if observed cases are made available daily. That is done in order to mitigate the issues with erratic daily fluctuations due to late reporting. Even though we are aware that this does not solve the data issues, it sufficiently alleviates them, as testified by the smoother time series obtained at the weekly level. The remainder of the article is organised as follows: Section 2 gives the necessary background, with some information about the available data and the growth curve models proposed in a frequentist framework by Alaimo Di Loro et al. (2021). The hierarchical structure of our model proposal is described in Section 3, while further details about the inclusion of the spatial and temporal dependence are given in Section 3.1. Section 4 describes our Bayesian sampling strategy for approximating the posterior distribution of the model, and give insights on how to modify the CAR specification to gain in computational efficiency. Results of our modelling options for the first and second wave of COVID-19 in Italy are reported in Sections 5, 5.1. Concluding remarks can be found in Section 6.
2. Setup
Public data about COVID-19 in Italy are published every day by the Civil Protection Department, since February 24th, 2020.1 For each of nineteen regions and two provinces (Trento and Bolzano, forming the region of Trentino Alto Adige), these include (i) prevalence indicators (currently positive, Intensive Care Unit (ICU) occupancy, hospital occupancy) and (ii) incidence indicators (e.g. newly diagnosed positives, deceased, new admissions to ICU, swabs, subjects tested). For a more technical description refer to Dicker et al. (2006) and Alaimo Di Loro et al. (2021). For any of the incidence indicators in a given area, the number of new cases at time can be obtained as the first difference of its cumulative counterpart as where and are the number of new and cumulative cases at time , respectively, and where we may assume without loss of generality. Cumulative indicators present some peculiarities: they are monotone non-decreasing and their behaviour usually follows a logistic-type growth curve. These curves have been widely used to describe various biological processes (Werker and Jaggard, 1997). More recently, they have also been adapted in epidemiology and biostatistics for modelling the onset and the spreading of epidemics (Hsieh, 2009, Hsieh and Chen, 2009, Hsieh, 2010).
Alaimo Di Loro et al. (2021) proposed a modified Richards’ curve (Richards, 1959), also known as the Generalised Logistic Function, for modelling cumulative incidence indicators. The generalised logistic function can accurately model various monotone processes and include other widely-used logistic growth curves as special cases (Tsoularis and Wallace, 2002, Gompertz, 1825). In Alaimo Di Loro et al. (2021) a parametric model is specified for region-specific incidence indicators (e.g., Poisson or Negative Binomial), where the cumulative indicators are assumed to follow a five-parameters Richards’ curve. The classical formulation of Richards’ curve can be expressed as:
| (1) |
where represents a lower asymptote (or baseline), is the distance between the upper and the lower asymptote, represents the growth rate, determines the point of inflection (when it corresponds exactly to the peak position), and is an asymmetry parameter regulating differences in the behaviour of the ascending and descending phase of the curve. Due to the monotone behaviour of cumulative incidence indicators, growth rate and asymmetry parameter are constrained to be positive. However, a maximum of is foreseen for the Richards’ curve as . This implies that the virus would be eradicated at some point, an option which seems unlikely so far. In order to allow the model to reach an endemic state in which there is a constant (hopefully, small) growth, we generalise Eq. (1) by considering a linear trend on the baseline :
| (2) |
This is similar to the use of an endemic parameter for the first differences as pursued in Alaimo Di Loro et al. (2021).
Assuming that the expected value of (cumulative incidence indicator at time ) can be modelled with a (possibly modified) Richards’ curve, i.e. , the expected value for the innovation can be straightforwardly obtained as:
| (3) |
where:
| (4) |
3. Generalised Logistic Growth Curve model with space–time dependence
Let denote the time-series of number of new cases in area , for , such that
The main assumption of our model is that arises from a Poisson distribution with mean . This can be expressed as:
where is an offset term that accounts for region-specific exposures levels.
When the offset is present, all other parameters impacting the overall rate become dimensionless, regardless of the scale of the corresponding region. In other words, the term can be interpreted as a relative measure of the risk of region at time with respect to the considered offset .
Different specifications of lead to different models, each with its own characteristics. We decompose the log-risk in three main components:
| (5) |
where is a specific random effect for the th area at time , is a deterministic function denoting the general time trend, with possibly region specific parameters as for Eq. (4), and a linear predictor based on covariates with associated regression coefficients .
3.1. The spatio-temporal CAR model
The observation-specific random effects are included to account for unobserved heterogeneity in the data. At each time, possibly correlated random effects allow regional curves to deviate from their global average. Besides, their presence corrects for the evident over-dispersion (with respect to the Poisson assumption) present in the time-series.
These random effects can either be completely independent, present temporal dependence, spatial dependence, or spatio-temporal dependence. In a Bayesian framework, the covariance structure can be induced hierarchically by specifying a suitable prior on the complete set of random effects. In order to simplify the formulation of the random effects prior, we collect all of them in a set of time-varying vectors .
Spatial dependence at each time point can be introduced by using a CAR prior (Besag, 1974) over some network, that under Gaussianity produces a so-called Gaussian Markov Random Field (GMRF, Rue and Held, 2005). This approach falls into the wide range of methods related to disease mapping (see Waller and Carlin, 2010 and Lawson, 2018 for a review). Such CAR prior specification allows incorporating the undeniable spatial correlation at the second level of the model hierarchy, avoiding analytical complications inherent in modelling spatial correlation within non-Gaussian distributions with inter-related mean and variance structures (Gelfand et al., 2010). This form of dependence is valid on discrete domains arranged over a network, where neighbouring relationships are determined by an adjacency matrix (possibly weighted). The matrix is a symmetric matrix with all diagonal elements equal to (as no region/area/unit is its own neighbour), and where off-diagonal elements are greater than if and only if areas and are connected (): the larger the connection strength , the closer the two random effects are pulled together. The original expression of this prior starts from the consideration of the full conditional of each random effect given all the others. For the generic , the full conditional has mean equal to the weighted combination of the random effects in its neighbourhood:
where and is the overall variance of the random effect. This induces smooth variations over close regions, as determined by . Following Brook’s lemma, for a fully connected graph (i.e. with no “islands”), this local specification implies a very specific global multivariate prior on the vector , centred at and with precision matrix which depends on the network structure. Under row-wise normalisation of the weights in , and introducing a spatial smoothing parameter , this global prior can be expressed as:
| (6) |
where and the matrix is a diagonal matrix containing the row sums of the weights of each region on the diagonal. This simply ensures that the weights of each region are properly normalised over all its neighbours (i.e. the row-wise normalisation). The spatial smoothing parameter regulates the amount of spatial dependence: values close to approximate independence (no impact of ) and values close to strong spatial dependence (full impact of ). This spatial CAR expression introduces spatial dependence among random effects belonging to connected regions at the same time-point. Nevertheless, we cannot neglect the indisputable temporal correlation which characterises such kind of data. Following the original work by Rushworth et al. (2014), we induce such dependence by imposing a temporal Auto-Regressive structure over the vectors . This yields a spatio-temporal CAR model (CAR-AR) whose only difference in this work from the original version is that, instead of the mixed specification of Leroux et al. (2000), we here consider the typical CAR of Besag (1974). In particular, we also extend the original AR(1) formulation introduced in Rushworth et al. (2014) to order . The extended specification amounts to the following prior for the collection of time-varying spatial vectors:
| (7) |
where is the set of coefficients governing the amount and direction of temporal dependence at different lags. Such a complex AR structure may be very useful to catch dependence and seasonality patterns at different temporal scales. For instance, we may expect to observe a strong weekly seasonality at the daily level, which may be well-captured by an AR(7) specification (potentially with some of the lower order coefficients set to zero). Remark that AR(J) processes are stationary only if the characteristic polynomial has the reciprocal of its roots lying inside the unit circle. This property is desirable as it favours the identification of all the considered space–time components. This is not easily enforced for arbitrary values of . A general prior choice in this sense is provided in Huerta and West (1999), where the process is reparametrised in terms of ’s and other auxiliary latent components. Section 5 focuses on the analysis of weekly data that do not show any cyclic behaviour. Therefore, we only expand on the case , where stationarity is guaranteed by simply enforcing . In the time series literature the first time points are usually ignored, and just conditioned upon. Eq. (7) makes a simplifying working assumption of independence of the first time points to obtain a marginal parameterisation. This clearly is irrelevant for the case , while in the other cases we recommend checking the goodness of fit of the initial joint distribution, and maybe adjust the assumptions. All abovementioned hyperparameters are then ascribed standard hyperpriors, commonly found in the literature:
where the latter has been coded as with (see Algorithm 1 in the Appendix).
3.2. The logistic growth trend
In Section 2, we state that we want to model the general trend of COVID-19 counts (of positives) in a single outbreak by using the first differences of the Richards’ curve as in Alaimo Di Loro et al. (2021). The first differences in Eq. (4) do not present an elegant expression and are slightly cumbersome to work with. Since data are collected at equally spaced time intervals, we propose to linearly approximate with the derivative of the Richards’ curve, as follows:
| (8) |
where . In our implementation, we initially considered both the exact and the linearised version of Eq. (4), (8), respectively. In the final results, differences were negligible, but the latter provided improved numerical stability and convergence of the chains. Thus, we decided to stick to this version, which is also used to produce the final results included in Section 5.1.
The expression in Eq. (5) implicitly considers a very highly parametrised model, where each region is allowed its own vector of parameters , hence its own Richards’ curve, to drive the trend of the regional outbreaks. In the sequel, we alternatively envision the existence of one common single Richards’ curve governing the spread of the epidemic in all the Italian regions, which then deviate from this global average as an effect of specific characteristics (observed or unobserved). This is obtained as a particular case of the former, where .
There is an essential difference between these two specifications, especially in terms of the role of the space–time random effects. The first one is a local model, where the random effects represent temporal variations of the mean underlying each regional counts-series from the region-specific trend. In the second case, they instead represent the spatio-temporal deviations of each region’s means, at each time, from the common curve. From a dependence interpretation standpoint, in the first case we are assuming that if region and region are connected, when region deviates from its trend , then region will likely have similar deviation from its own trend as well. In the second case, we are assuming that if region and region are connected, when region deviates from the general trend , then region will also deviate from the general trend similarly.
Let us recall that the parameters governing the differences of the Richards’ curve are constrained on the positive domain . In order to favour the elicitation of diffuse priors and the Bayesian estimation process, these have been parametrised on the log-scale as . The first two have been assigned a prior, while the last two a one. These correspond to very vague priors on the log-scale, where the second are assigned a lower variance given their double-exponentiated nature in Eq. (8). One may argue that the same prior specification for and does not reflect the natural intuition about being some order of magnitude lower than . However, while this may seem obvious in the case of COVID-19 pandemic waves, we here want to point out that this is not necessarily true in general. For instance, in the case of an endemic disease, we may observe a relatively high baseline (endemic rate) with only small seasonal waves of infections that could be rapidly contained. However, we performed some preliminary runs embedding such prior belief before proceeding to the final analysis of Section 5. The results were indistinguishable to the ones obtained using vague priors and therefore we opted for the latter in order to let the data drive the final estimates.
The parameter , unlike the others, belongs to the whole real line and, more importantly, is not dimensionless. Its magnitude is indeed related to the dimension of the analysed time window. It can be loosely interpreted as the lag-phase of the outbreak (for it represents precisely the point of maximum of the curve), which is the point in time when the exponent becomes negative. It is not well-identified for varying , and hence it has been given a prior to help it move inside the observed time interval (included in with 95% probability).
3.3. The linear predictor
The linear predictor describes the effect of covariates on the log-risks. Since the dimension of the region is already accounted for in the offset term, such covariates shall account for exogenous factors that affect the spread of the virus, or the ability to detect the infected people in each area at different times. In practice, this term shall represent all the meaningful observed heterogeneity between regions and within regions over time.
For instance, the population density is a region-specific and constant over time feature that can likely impact on the rate of infection. This covariate has been considered in the recent work by Jalilian and Mateu (2021) and proved to be valid for both explanation and prediction purposes. Another interesting variable to study may be the number of daily swabs. Its inclusion accounts for the effort in detecting positive cases carried out by a region at a specific time.
If covariates are considered, then the vector is associated to a vector of coefficients . In our Bayesian machinery, this vector is assigned a multivariate Normal prior with independent components , which corresponds to a fairly diffuse prior considering the log-linear link.
It is here important to highlight that we are not including the intercept in the linear predictor. In the case of region-specific Richards’ curves, the intercept is implicitly defined by the parameters and already, and its inclusion would introduce a non identifiable parameter and jeopardise proper convergence of the estimation algorithms. In the case of a common single Richards’ curve, one may want to include region-specific intercepts . These would have the effect of moving the whole region-specific curve up or down with respect to the global average, again accounting for unobserved heterogeneity among regions. However, the goal is to have this heterogeneity explained by the spatio-temporal random effects : the inclusion of such individual intercepts would add an unwanted player in the game and make the interpretation of the final results intricate.
4. Estimation
Estimation has been carried out using Stan,2 which is a probabilistic programming language for statistical modelling and high-performance statistical computation (Carpenter et al., 2017, Stan Development Team, 2021). It interacts with R and can be called directly from RStudio (Allaire, 2012) through the rstan package (Stan Development Team, 2020). Among its many capabilities, it allows to get full Bayesian inference by drawing from the posterior density by a specific Markov Chain Monte Carlo (MCMC) sampling method known as Hamiltonian Monte Carlo (HMC, Betancourt, 2017). The HMC techniques provide an efficient sampling scheme based on the simulation of Hamiltonian dynamics for approximating the target distribution (Neal et al., 2011). Its functioning relies on the analogy between the parameter value and the trajectory of a fictitious particle subject to a potential energy field, preserving its total energy (the Hamiltonian), obtained as the sum of potential and kinetic energy. In practical terms, given the chain’s current value and the corresponding log-density, it picks the new value of the chain by proposing a random shift in the log-density value and then moving arbitrarily far away from that point along the corresponding contour line. The latter allows for fast and complete exploration of the whole density that does not negatively affect the acceptance rate, minimising the risk of wasting time (or even getting stuck) in local high-density areas. Unlike the Metropolis–Hastings (Metropolis et al., 1953) or Gibbs sampler (Geman and Geman, 1984), it provides robust performances and easily reaches convergence even for very complex models, e.g.: posterior density characterised by complex geometries, multi-layered hierarchical models with many parameters, models depending on large sets of latent variables, etc. One of the advantages of Stan is that it allows for an easy implementation of the No U-Turn Sampler (NUTS, Hoffman and Gelman, 2014). NUTS proved to perform at least as efficiently as the standard HMC but, generally, does not require any tuning of the hyperparameters governing the proposals. Hence, it sensibly reduces the computational burden and averts any user intervention or wasteful runs. Another advantage of the NUTS algorithm is that situations in which the sampling cannot thoroughly explore the whole posterior distribution are easily detectable. Indeed, when the approximation of the Hamiltonian dynamic fails to reach specific areas without departing from the original Hamiltonian value, the so-called divergent transitions arise. For more details we refer to Betancourt (2016). The Stan interface reports divergences as warnings and provide ways to access which iterations encountered them. The bayesplot package (Gabry et al., 2019) can be used to visualise them and locate the areas in which the exploration failed. If no divergences occur, we can be confident that the chain was able to explore the whole domain of interest of the log-posterior density.
After few warm-up iterations, during which the NUTS automatically adapts its future behaviour to the shape of the posterior density, chain convergence and desirable accuracy are usually reached even in few iterations (). Nevertheless, doing more iterations does not harm and longer chains lead to more robust result. When the log-posterior density is computationally intensive to compute or the geometry of the posterior is particularly complex, the approximation of the Hamiltonian dynamics can be significantly slowed down and negatively impact on the total run-time. For instance, for the model in Section 3, there are spatial vectors of random effects that contribute to the overall density. The evaluation of the contribution of each of these requires the computation of the corresponding prior, which in turn involves the computation of inverse and determinant of the matrix . It is clear how the naive implementation of such a model is all but efficient. Nevertheless, we can exploit two facts in order to ease computations. First, the spatial covariance structure does not vary over time, especially along iterations; this implies that we can compute the inverse and determinant only once in advance without doing the same calculations repeatedly. Second, each region has only a few neighbours, and the matrix is not full, paving the way for efficient algebraic solutions. In practice, many efficient strategies can be adopted in order to alleviate the computational burden by speeding up linear algebra operations. Here, we based ours on the Exact-sparse CAR elaborated in Joseph (2016), which accrues significant computational efficiency by more than halving the needed run-time.3 The original code has been slightly modified in order to include the temporal AR structure of our spatio-temporal CAR. The core of the Stan program needed to update the CAR-AR random effects is presented in Algorithm 1 of the Appendix. The full codes to reproduce the results presented in Section 5 are available in a public GitHub repository accessible at https://github.com/minmar94/Covid19-Spatial.
5. Application to COVID-19 incidence in Italy
We test and compare our proposals defined in Sections 3, 4 on the data described in Section 2. We consider the time series of the weekly positives at the regional () level, for the first and the second wave of the epidemic. From an epidemiological perspective, there is no strict definition for what is or is not an epidemic wave (or phase). However, the scientific community agrees on the fact that the word wave implies a natural pattern of peaks and valleys, suggesting that even during a lull, future outbreaks of the disease are possible. Our proposal is able to model only one epidemic wave at a time, since the Richards’ curve entails a single peak time and height. The latter implies that the start and end date of each wave must be set by the researcher. Albeit this is a drawback of our approach, it can be easily seen through sensitivity analyses that results do not drastically depend on this choice. We mention here the work by Bartolucci and Farcomeni (2021), which can flexibly model more than one wave at a time, but at the price of not being able to explicitly estimate important characteristics of each wave (e.g., peak time, onset time, etc.). Similarly, Farcomeni et al. (2021) do not require to identify a time frame for waves, but it is restricted to short term predictions.
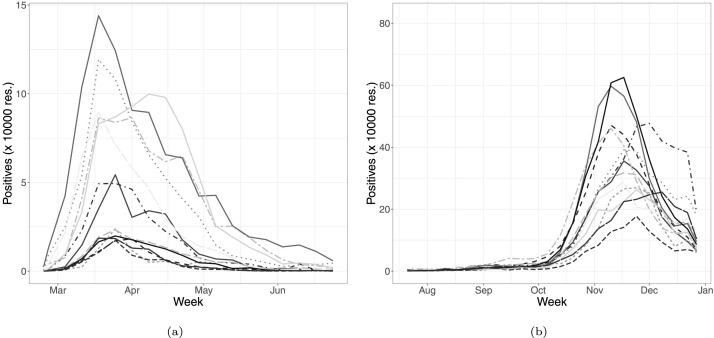
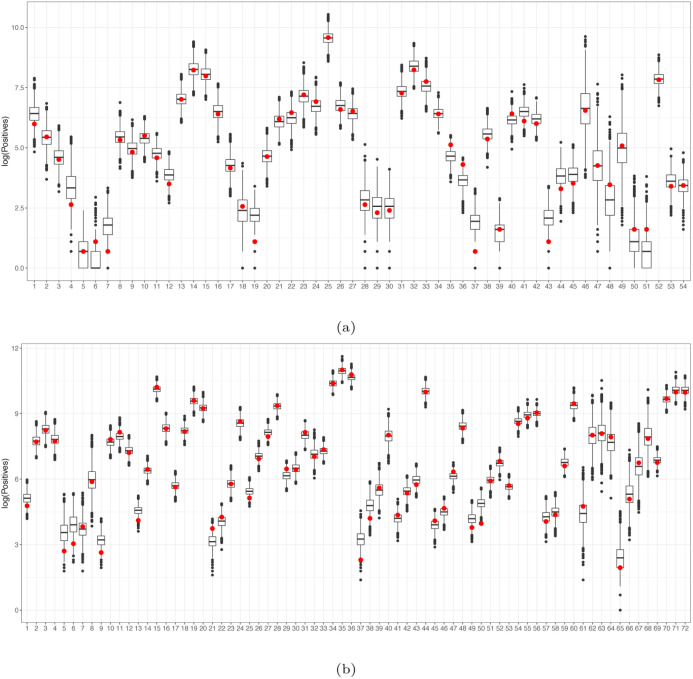
In our application, we set the 24th of February 2020, as the start date of the first wave, namely when systematic data recording started, while the 19th of July 2020 is set as the end date. That is the day in which discos and pubs were re-opened after the lockdown period (a total of 22 weeks). For the second wave, the 20th of July 2020 was set as the start date, while the 27th of December 2020 was set as the end date (for a total of 24 weeks), which corresponds to the end of the last week of the year and, more importantly, is the day the vaccine campaign began in all Europe (a.k.a. V-day). The regional time series of the weekly positives for both waves are reported in Fig. 1(a) and Fig. 1(b), respectively. It can be seen that the second wave had a slower onset (due to the seasonality of infections in early Summer) but a much higher peak for most regions. That is not only due to a larger number of infected with respect to the first wave (which has mostly hit only the northern part of Italy) but also to the much larger proportion of identified cases.
Fig. 1.
Regional weekly time series for positives during the first (a) and second (c) waves.
We recall that we used the logarithm of the number of residents scaled by a factor of as an offset, essentially studying the number of positives per 10,000 residents rather then crude incidence. This is necessary in order to be able to compare different regions, which can have very different number of infected only due to a very different number of residents. We also included the number of total weekly swabs (standardised) as covariate, to take into account different contact tracing efforts. The number of positive swabs can be assumed to be negatively associated to the proportion of undetected cases, and is one of the official indicators of the World Health Organisation.
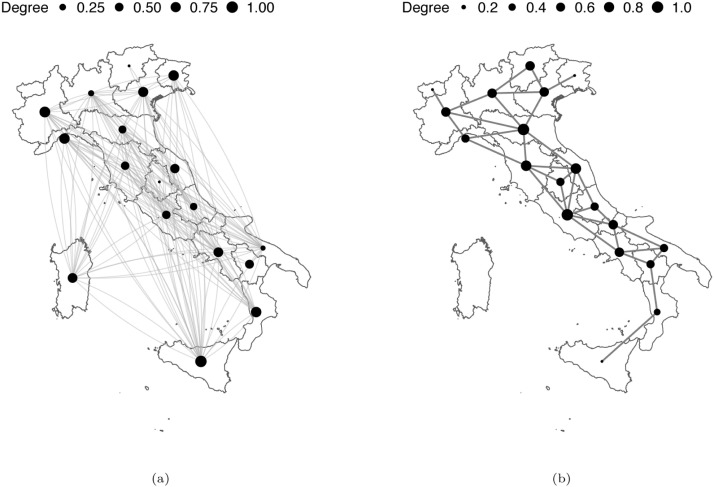
We also compared two different specifications for the adjacency matrix in the CAR-AR model. The first matrix, which we refer to as , specifies a neighbourhood structure based on proximity flows and the availability of direct train, flights, and ferry connections. This matrix has been also used in Della Rossa et al. (2020), and can lead to distant regions to be neighbours because of, for instance, frequent internal flight connections. The original matrix is a weighted measure of commuters’ flow and is not symmetric since exchanges may have different magnitudes in the two directions. As a fast and viable solution to symmetrise the matrix in this application, we decided to dichotomise it. We set if there exists a positive flow in at least one of the two directions. The second adjacency matrix, which we refer to as , is the most typically adopted network defined on regions’ mutual geographical position. In our application, we considered a first-order structure, where only pairs of regions sharing at least one land border are considered as neighbours.
The two different neighbourhood structures are shown in Fig. 2(a) and Fig. 2(b), respectively. In particular, we report the number of edges (connections) and the (scaled) degree of each region. We notice that using we end up with 18 out of 20 regions that have at least one connection (Molise and Valle d’Aosta have none), three of them having 12 neighbours (which is the mode), and where Sicilia is the most connected area with 15 neighbours. On the other hand, using we end up with seven regions that have 3 neighbours; two regions that have 6 neighbours, while Sardegna, which is an island, has no connections. For Sicilia, which is also an island, we selected Calabria as the only neighbour. The two regions are separated by very few kilometres of sea (the Strait of Messina), with extremely frequent ferry connections.
Fig. 2.
Network structure of the two adjacency matrices considered: (a) and (b).
As a baseline model for comparison, we also considered the possibility of a completely disconnected graph , hence assuming complete spatial independence between regions. Nevertheless, being temporal dependence undeniably present in the observed series, we always retain the temporal AR structure between subsequent vectors . As a matter of fact, preliminary runs that neglected this feature of the date produced way worse results (especially in terms of out-of-sample performances) that will not be reported in the sequel.
5.1. Main results
For the sake of brevity, we will refer to the model ignoring spatial dependence with the fully disconnected graph as , and as and to the models including spatial dependence using and as adjacency matrices, respectively. We considered these three dependence structures for the model with one common Richards’ curve, which we name common, and the model with region-specific Richards’ curves, which we name regional.
For all models considered, we ran two separate chains for 10,000 iterations, allowing Stan to perform 5000 warm-up iterations each, which were discarded for inferential purposes.
We computed several metrics in order to compare the goodness-of-fit and predictive performance of the model’s alternatives. The large flexibility of the space–time random effects specification easily makes the model fit the observed set of data almost perfectly. This feature exposes the typical in-sample metrics to over-fitting, flawing any sensible interpretation of the results, and would inevitably favour the highly parametrised regional model. Therefore, we decided to avert the over-fitting issues by artificially subtracting 15% randomly selected points from each region’s time series. These are treated as missing data in the estimation process, and the ability to reconstruct the missing pieces properly is then verified in terms of various metrics: Coverage, Root Mean Squared Error (RMSE) and Predictive Interval Width (PIW). Comparison of these three metrics for the three dependence structures, with common and regional Richards, for the two waves, are presented in Table 1.
Table 1.
Out-of-sample predictive performances of our proposals with a common or region-specific Richards’ curve in the first and the second wave.
| Wave | Metric | Common |
Regional |
||||
|---|---|---|---|---|---|---|---|
| I | Coverage | 0.98 | 0.98 | 0.98 | 0.96 | 1 | 0.96 |
| PIW | 1535 | 1178 | 1144 | 3311 | 846 | 1017 | |
| RMSE | 423 | 184 | 272 | 399 | 331 | 314 | |
| II | Coverage | 0.96 | 0.97 | 0.92 | 0.97 | 0.96 | 0.92 |
| PIW | 33393 | 4497 | 4046 | 16900 | 3131 | 3121 | |
| RMSE | 12841 | 910 | 995 | 3669 | 1008 | 1038 | |
We can clearly observe how the out-of-sample performances are comparable across the common and regional specifications. The coverage is close (actually larger in most cases) to the 95% nominal level in both cases, for all the dependence structures. and , under both the common and regional specification of the logistic trend, show equivalent coverage and similar PIWs. However, the common specification provides more accurate out-of-sample predictions in terms of RMSE, whenever the random-effects account for the spatial dependence ( and ). Therefore, given the comparable out-of-sample performances and the more parsimonious specification of the common model, we chose this one as the preferred option. All future results will then be referred to this specification.
Parameter estimates for the spatial () and temporal () auto-correlation, together with the swabs’ effect () are reported in Table 2. Here, we want to first highlight that there is a clear evidence of strong dependence both spatial and temporal, with values of in all models for both waves. It is instead notable how the transport based graph detects low spatial dependence () during the first wave, and a large spatial dependence during the second wave (). This change in the spatial correlation parameter between the first and the second wave for , highlights the different type of non-pharmaceutical measures that were adopted to contain the spread of the contagion and the estimated values are completely reasonable, given the harder block to inter-regional movements that characterised the first wave as compared to more liberal mobility policies that accompanied the second one. On the contrary, the geographic vicinity effect is stable across the two waves, probably capturing similarities between close regions that depend on shared unobserved characteristics more than on people exchange.
Table 2.
Comparison of parameters’ estimates for the spatial () and temporal () auto-correlation, and for the swabs’ effect in the first and the second wave.
| Wave | Param. | |||
|---|---|---|---|---|
| I | – | 0.14 (0.02, 0.21) | 0.76 (0.71, 0.81) | |
| 0.89 (0.87, 0.91) | 0.88 (0.90, 0.93) | 0.86 (0.85, 0.89) | ||
| 0.36 (0.26, 0.44) | 0.34 (0.25, 0.42) | 0.21 (0.14, 0.29) | ||
| II | – | 0.93 (0.92, 0.95) | 0.87 (0.85, 0.90) | |
| 0.88 (0.86, 0.90) | 0.87 (0.85, 0.89) | 0.82 (0.80, 0.85) | ||
| 0.42 (0.38, 0.46) | 0.27 (0.24, 0.30) | 0.13 (0.09, 0.16) | ||
The parameter represents the effect of additional swabs on the number of detected positives. Being the swabs variable standardised, this does not allow for a trivial interpretation. However, we can observe a positive effect which was more evident during the first wave than the second wave. This happens unsurprisingly, since the testing efforts were not yet at full capacity during the first outbreak, with many undetected cases, detected as soon as additional testing hubs were made available.
Table 3 shows the estimated parameters of the common Richards in all settings. We here recall that represents the baseline (endemic rate), the final size of the outbreak (in terms of cases every 10,000 residents), the contagion speed, the lag-phase and the asymmetry. We can clearly observe how the second wave is characterised by a larger final outbreak size, a larger endemic rate and a longer lag-phase (meaning the curve approximates exponential growth for a longer time window) in all cases. Furthermore, while the first outbreak was characterised by positive asymmetric behaviour (with a fast and sudden growth followed by a long descending phase) the second wave presented a negative asymmetric evolution, probably because of the softer lockdown measures undertaken. Indeed, the positive asymmetry characterising the first wave reflects the hard containment measures implemented by the Italian government at the beginning of the epidemic (March 2020), which were gradually loosened. On the contrary, the second wave experienced a negative asymmetry as the prevention policies were mild at the beginning of the second outbreak (mid Summer 2020) and were suddenly strengthened following the abrupt increase of positive cases in late November 2020.
Table 3.
Parameters’ estimates of the Richards’ curve for the first and the second wave.
| Wave | Model | |||||
|---|---|---|---|---|---|---|
| I | 0.05 (0.04, 0.06) | 23 (20, 27) | 0.62 (0.60, 0.64) | 2.0 (1.5, 2.5) | 7.8 (6.3, 9.9) | |
| 0.06 (0.05, 0.07) | 20 (17, 22) | 0.62 (0.59, 0.65) | 2.2 (1.7, 2.8) | 7.9 (5.5, 9.3) | ||
| 0.05 (0.04, 0.06) | 26 (21, 31) | 0.61 (0.58, 0.65) | 2.2 (1.5, 2.9) | 7.8 (5.2, 9.3) | ||
| II | (, ) | 158 (143, 172) | 3.46 (3.26, 3.63) | 23.2 (23.1, 23.3) | 0.06 (0.05,0.07) | |
| (, ) | 178 (127, 215) | 2.72 (2.33, 3.08) | 22.9 (22.8, 23.2) | 0.09 (0.07,0.10) | ||
| (, ) | 194 (163, 220) | 3.50 (3.20, 3.70) | 23.1 (22.9, 23.2) | 0.06 (0.05, 0.07) | ||
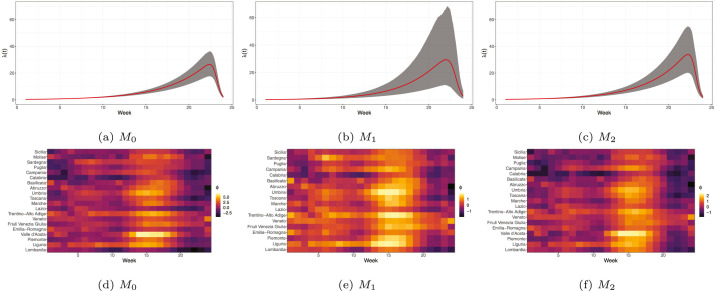
Fig. 3(a)–3(c) and Fig. 4(a)-4(c) show the estimated common Richards’ curves (red solid line) by the proposed models with the associated uncertainty (grey areas represent the 95% credible intervals) for the first and the second wave, respectively. In Fig. 3(d)–3(f) and Fig. 4(d)–4(f) we instead report the heatmaps of the estimated spatio-temporal effect for each model specification for the first and the second wave, respectively. The estimated common Richards’ curve and random effects during the first wave highlight how deviations from the global average presented a strong geographic clustering effect, as the number of positive cases increased from the South to the North of Italy. On the contrary, there is relative homogeneity in the deviations of each region from the national epidemic at each time point during the second wave. This means that all regions experienced a similar epidemic trend in terms of shape but different in terms of relative magnitude. Notably, some peculiar regional behaviours are highlighted very clearly. For example, a sudden surge in the contagion between October and November 2020 experienced by Trentino Alto Adige and Umbria. In general, we notice that a larger uncertainty characterises the common Richards’ estimated by for the second wave compared to the other two models. Considering that the PIWs (see Table 4) do not vary much across the proposed dependence structures, this implies a stronger identification of the random effects, i.e. less variability of the random effects. We can then assume that this model provides a better description of the regional heterogeneity in the data.
Fig. 3.
Common Richards’ curve for the first wave for the different specifications of the random effect (top panels); Posterior mean of the random-effect (bottom panels).(For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Fig. 4.
Common Richards’ curve for the second wave for the different specifications of the random effect (top panels); Posterior mean of the random-effect (bottom panels).(For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Table 4.
Validation metrics for the estimated models for the first and the second wave: coverage and rmse out-of-sample (in-sample), WAIC and LOO.
| Wave | Model | Coverage | RMSE | WAIC | LOO |
|---|---|---|---|---|---|
| I | 0.98 (1) | 423 (2.1) | 2869 | 3087 | |
| 0.98 (1) | 184 (2.3) | 2650 | 2849 | ||
| 0.98 (0.99) | 272 (2.5) | 2774 | 2982 | ||
| II | 0.96 (0.99) | 12841 (2.8) | 4112 | 4393 | |
| 0.97 (0.99) | 910 (4.6) | 3820 | 4080 | ||
| 0.92 (0.99) | 995 (4.1) | 3971 | 4252 | ||
In order to fully compare the different dependence structures on the space–time random effects for the common model, we also evaluated the overall fitting performances in terms of two wide-scope indicators: the Watanabe–Akaike Information Criterion (WAIC) (Watanabe and Opper, 2010), and the Leave-One-Out (LOO) score as in Vehtari et al. (2017). These two metrics shall be considered as a proxy of the out-of-sample prediction accuracy, but can be directly computed from the fitted Bayesian model by retaining the log-likelihood values at the different steps of the chain (Vehtari et al., 2017). Results of the estimated validation metrics for the three models for both the first and the second wave are reported in Table 4. We notice that results are comparable, with performing slightly better in terms of RMSE, WAIC and LOO for both waves, guaranteeing a greater or equal coverage in both scenarios. Furthermore, comparing the in-sample and out-of-sample RMSE, we can see how the independent model strongly overfits on the training set. On the other hand, limiting and driving the behaviour of the random effects through a spatial structure (such as and ) strongly improves the predictive power of the model and leads to way more reliable results. All things considered, is then chosen as the best dependence structure, also in light of the appealing interpretation of the varying spatial dependence strength as expressed by in the two waves (see Table 2). Hence, the following results will be referred to this model.
Fig. 5(a)–5(b) show the map of the temporal averages of the space–time effects of each region: . These values can be interpreted as the effect of the over-dispersion on the contagion’s spread due to the interactions with the neighbourhood and the auto-regressive term. That allows to verify which regions generally presented an infection rate larger than the national average along the two waves. As already pointed out, we can notice a stronger geographical clustering during the first wave, which is even more evident looking at the maps than at the heatmaps. Given the low value of the estimated in the first wave, this effect is not really linked to the superimposed networking structure, but is an inherent characteristic of the data at regional level: the pandemic initially hit stronger the North of Italy and only later slowly spread to the South. On the contrary, the geographic clustering effect vanishes during the second wave and the colouring of the map looks smoother. Regions similarity is actually explained by people exchange and transportation between regions (larger value of ). It is crucial to notice that, differently from what was often reported by the news in Italy, Lombardia did not perform worse in terms of positive cases with respect to the rest of the country along the second wave (net of the tracking effort and regional offset). We added the maps obtained using for comparison in Fig. 7, Fig. 7 of the Appendix, and we only report here that differences were negligible.
Fig. 5.
Average estimated spatial random effect by for the first (a) and the second (b) wave.(For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Fig. 7.
Average estimated spatial random effect by for the first (a) and the second (b) wave.
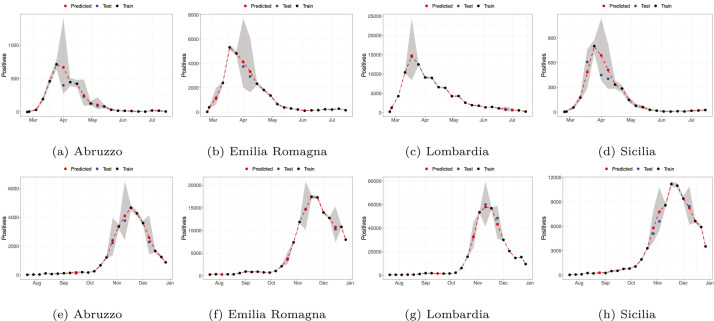
We argue that the chosen model is able to reconstruct the true evolution of the incidence curve, also at missing points in the series. Some examples are in Fig. 6(a)–6(h). The fit along all time points (in sample and out-of-sample) are plotted together with the 95% posterior predictive intervals for four randomly selected regions (Abruzzo, Emilia Romagna, Lombardia and Sicilia), for the first and the second wave of the epidemic. We can clearly notice how the random effect allows the model to capture the wiggly behaviour of the observed data, and how almost all the observed data fall into the prediction intervals in spite of the large over-dispersion of the observed counts. More importantly, the predictive intervals obviously widen in correspondence of the missing observations, and practically always include the true value, even when this deviates from a typical, expected behaviour (see again Fig. 6(a)–6(h)). Given the homogeneity assumptions for Richards’ curve for all regions, this must be mainly due to the dependence structure induced by . Fig. 8 in the Appendix shows specifically the out-of-sample predictive performances, where values in the test set are plotted on the log-scale. Appendix includes an evaluation of the forecasting performances (i.e. prediction of future outcomes) of the model, yielding results very coherent to the ones included in this section.
Fig. 6.
Observed time series (red dots) and model fit (black solid) with 95% prediction intervals (black dashed) for 4 randomly chosen regions in the first (top panels) and the second wave (bottom panels).(For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Fig. 8.
Observed points (red) and simulated predictions (boxplots) for the first (a) and the second wave (b) test sets.(For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
6. Discussion
Modelling incidence cases poses several issues, ranging from the discrete nature of the observations to the dependence structure of the data across times and neighbouring regions. The proposed generalised logistic growth curve accommodates the main data features, and provides a satisfactory solution for data analysis and prediction under a spatially heterogeneous framework. The proposal is applied to Italian regional data, but it can be applied to data from any other country. Similarly, if data were available at the province and/or municipality level, within-region spatial dependence could be explored, promptly identifying clusters of positive cases.
The spatio-temporal dependence is modelled through the inclusion of region-specific random effects. The inclusion of random effects relaxes the working assumption used in Alaimo Di Loro et al. (2021), where independence was assumed. Failure of the independence-assumed model to fit the data could be due to misspecification of any of the elements defining the linear predictor. Here, not all possible covariates, such as population density or pollution exposure levels, were considered in model specification. Their joint effect is, however, summarised by latent variables, i.e. the random effects. On the one side, the additional computational burden can be dealt with Stan within a Bayesian framework with minor efforts. On the other side, the improvements in the goodness of fit and predictions are evident. As shown in Section 5, the dependence network plays a crucial role and gives useful insights. Here, we analysed two separate waves in Italy. During the first wave, strict restrictions were applied, strongly limiting mobility across the country, mainly allowing for transportation routes only. As a result, the spread of the contagion was mostly influenced by geographic proximity, with northern regions being more affected by the epidemic than those in the Centre and South of Italy. During summer, instead, people took the chance of less restrictive travelling constraints and enjoyed the summer season having holidays far from their region of residence. This led to a completely different spatial association. The country was not anymore divided into three geographical macro-regions, but a more uniform development of the epidemic was observed. Regions’ colouring Fig. 5(b) reflects both the type of regional policy in terms of screening and the type of non pharmaceutical measures taken. For example, Calabria did not develop a consistent screening activity, and hence was subject to more strict restrictions than other regions.
These results, together with the considerations about the data collection procedures implemented in Italy and their impacts on data quality in Section 1, have important consequences in terms of public health policies. In particular, they make even more clear that the ability to monitor, predict and hence govern a pandemic is directly linked to the availability of high quality data, fully harmonised at regional level. Although in a country like Italy, with a high level of regional autonomy, the data collection procedures are necessarily decentralised, the COVID-19 pandemic has shown the need of an integrated system of health data collection, transmission, storage and dissemination, which must be necessarily centralised in order to avoid the heterogeneity, time misalignment and lack of quality which have characterised the available data in this critical period, and have hampered the possibility to obtain from the data the best possible information to support public decisions. Moreover, all our results also point out that in a country with marked geographical, environmental, social and economic regional differences, like Italy, the management of a pandemic must be coordinated at national (and perhaps even at supranational) level, but implemented through specific measures that take into account regional heterogeneity. At the same time, inter-regional mobility should always be considered as crucial, since it can jeopardise the effectiveness of restrictions imposed at regional level, as shown by the different role played by the spatial component in the second wave compared with the first wave in Italy.
The latent dependence structure consistently aids interpretation. However, it may induce some bias in the predictions if the underlying network is misspecified. To avoid such bias, the network might be explicitly modelled, and estimated together with all other parameters in the MCMC machinery. There are some examples of this approach in the recent literature (Rushworth et al., 2017, Ejigu and Wencheko, 2020, Corpas-Burgos and Martinez-Beneito, 2020), and it is a possible further development for our model. In the future we will also consider weighted spatial structures as in Della Rossa et al. (2020), by specifying as . Indeed, using weighted adjacency matrices may better reflect the underlying similarity among geographical units and either boost or mitigate the neighbourhood effect on the mean of each one of them. However, this was not pursued in this paper in order to directly compare unweighted versions of the two spatial graphs. We do not generally expect results to differ extremely when applying the weighted matrix. However, we are aware that the specification of the spatial weights matrix can both affect model fitting and parameter estimation. More importantly, in a recent paper by Duncan et al. (2017), where different specifications of have been compared to perform spatial smoothing, the model using binary, first-order adjacency weights proved to be an optimal choice for achieving a good model fit. Another important extension would be the development of a space–time model capable of capturing the entire evolution of an epidemic, fitting all waves within the same model specification. That could be done by developing a model based on a mixture of Richards’ curves, each capable of describing individual epidemic waves. In particular, a change-point model, in the spirit of Girardi et al. (2021), could be specified under our framework. The unknown change point, which could be in principle more than one, could be estimated along with all other model parameters. The resulting model is a (constrained) finite mixture model that could be implemented in future research, whose computational burden is not much different from the one considered here. Similarly, assessing the effectiveness of the Italian risk-zones policy during the different waves (Pelagatti and Maranzano, 2021) could also be implemented under the proposed framework, providing further insights to the decision-makers to govern the epidemic spread better. Eventually, to exploit the general idea of dependence in both space and time, we may imagine defining a space–time neighbourhood structure linking neighbouring regions at different time points. In all mentioned developments, we have to remember that swabs play a crucial role. Hence, we have to imagine a nested, hierarchical model structure where a proper predictive model is added if the prediction of cases becomes a crucial feature.
Further results (e.g. chain diagnostics) are available from the authors upon request and we point again the reader to the public GitHub repository available at https://github.com/minmar94/Covid19-Spatial.
Acknowledgements
The authors wish to thank an anonymous referee and the associate editor for their suggestions that considerably helped in improving the paper from its previous version. This work has been partially supported by Fondo integrativo speciale per la ricerca (FISR) , grant number FISR2020IP_00156.
Footnotes
GitHub repository: https://github.com/pcm-dpc/COVID-19.
Webpage at https://mc-stan.org/.
The computational gain is inversely proportional to the degree of the network defining neighbourhoods.
Appendix.
Exact-sparse CAR algorithm
Estimated average spatial random effect
See Fig. 7.
Posterior distribution of out-of-sample predictions
See Fig. 8.
Forecasting performances
As pointed out by an anonymous referee, during the COVID-19 pandemic the objective of authorities and researchers was to predict the future incidence. Hence, it would be interesting to see which of the proposed models performs “better” when that is the objective in mind.
We would like to remark that this model has been originally conceived as an explanatory tool, not as a forecasting tool. That is why the prediction performances have been assessed on values occurring within the waves in the main text. This conceptual limitation depends on a number of factors, listed here below.
-
•
The expression of the mean depends on the number of weekly swabs, which is not known in advance at future times. In order to provide valid and accurate forecasts (together with the corresponding uncertainty) the number of weekly swabs and positives shall be modelled jointly. This is something worth of exploration in the future.
-
•
The model includes a complex and highly parametrised spatio-temporal structure. Hence, it likely need a relative large number of time-points to estimate its components without introducing bias.
-
•
The main focus on the paper is on identifying the most informative spatial structure in the observed data. In principle, spatial dependence is much more helpful when predicting the counts of some regions at some time , when other regions’ counts at the same time are available. On the contrary, the impact of spatial dependence can rapidly fade when considering future outcomes, where temporal dependence shall dominate the process behaviour (unless suitable space–time neighbouring structure is considered). In any case, when there is no information from other regions at the same time, the spatial dependence shall propagate through time and its effect is inevitably diminished week after week.
All things considered, we still believe the proposed model may provide reasonable predictions up to 15 days (2 weeks) ahead, as for all our other works on this topic (please see Farcomeni et al., 2021 and Alaimo Di Loro et al., 2021). Hence, in this section, we show predictions at one- and two-weeks ahead, comparing the different specifications of . We only did this for the common Richards’: the best model, as discussed in Section 5.1. Issue 1 is overcome by assuming constant tracing effort: the weekly number of swabs used to predict the positive cases for the weeks ahead is assumed to be the same as the previous (in sample) week. This is a very strong (and possibly wrong) working assumption, which is particularly ill-suited for the first wave when the tracing was improving its capabilities week after week. Therefore, forecasts shall be interpreted only in relative terms as a comparison between the three dependence structures and not in absolute terms. The prediction experiment was developed as follows.
First wave. We estimate four examples building training sets up to April 12-19-26 and May 03, 2020. We predict the following first and second week counts in each case.
Second wave. We estimate four examples building training sets up to November 22–29 and December 06–13, 2020. We predict the following first and second week counts in each case.
Fig. 9 shows an example of posterior predictive distribution. Notice how this is strongly skewed, hence we also considered posterior medians as point estimates for the forecasts.
Fig. 9.
Density and traceplot of a predicted value.
Performances are evaluated in terms of root mean square predictive error (RMSPE), whose distribution by wave, window, and dependence structure can be observed in Fig. 10. The errors are ultimately averaged over the various regions and fitting windows, keeping 1-week and 2-weeks ahead as separate objects, and the resulting estimates are reported in Table 5.
Table 5.
Average (Median) RMSPE for each model specification for the first and the second wave at different steps ahead.
| Wave | Model | Week(s) ahead |
|
|---|---|---|---|
| 1 | 2 | ||
| I | 244 (47) | 259 (54) | |
| 242 (46) | 256 (53) | ||
| 267 (49) | 282 (45) | ||
| II | 1670 (728) | 2544 (1522) | |
| 1388 (496) | 2189 (1005) | ||
| 1749 (825) | 2578 (1543) | ||
Fig. 10.
Prediction error (on the log scale) at different steps ahead, for each specification of and for each wave.
Eventually, what is found in terms of fit quality in the original application is also confirmed for these forecasts. Along the first wave, there is no clear dominance of one dependence structure over the others: apparently, the most of the information is carried by the temporal process. Instead, along the second wave, the transport flows dependence structure provides clearly better forecasts than all its competitors. Note that the two-weeks-ahead prediction error is uniformly larger than the one-week-ahead as expected, for both waves and for each specification of .
Some examples of the point forecasts, together with the corresponding uncertainty, are shown in Fig. 11.
Fig. 11.
Observed time series: black dots are in-sample, grey dots are out-of-sample. Predicted values (red dots) with 95% prediction intervals (red dashed) for 2 randomly chosen regions in the first (top panels) and the second wave (bottom panels). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
References
- Alaimo Di Loro P., Divino F., Farcomeni A., Jona Lasinio G., Lovison G., Maruotti A., Mingione M. Nowcasting COVID-19 incidence indicators during the Italian first outbreak. Stat. Med. 2021;40(16):3843–3864. doi: 10.1002/sim.9004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allaire J. Citeseer; Boston, MA: 2012. RStudio: Integrated Development Environment for R, Vol. 770; p. 394. [Google Scholar]
- Bartolucci F., Farcomeni A. A spatio-temporal model based on discrete latent variables for the analysis of COVID-19 incidence. Spat. Stat. 2021 doi: 10.1016/j.spasta.2021.100504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Besag J. Spatial interaction and the statistical analysis of lattice systems. J. R. Stat. Soc. Ser. B Stat. Methodol. 1974;36(2):192–225. [Google Scholar]
- Betancourt M. 2016. Diagnosing suboptimal cotangent disintegrations in Hamiltonian Monte Carlo. arXiv preprint arXiv:1604.00695. [Google Scholar]
- Betancourt M. 2017. A conceptual introduction to Hamiltonian Monte Carlo. arXiv preprint arXiv:1701.02434. [Google Scholar]
- Cabras S. 2020. A Bayesian Deep Learning model for estimating COVID-19 evolution in Spain.arXiv:2005.10335 [Google Scholar]
- Carpenter B., Gelman A., Hoffman M.D., Lee D., Goodrich B., Betancourt M., Brubaker M.A., Guo J., Li P., Riddell A. Stan: a probabilistic programming language. Grantee Submiss. 2017;76(1):1–32. doi: 10.18637/jss.v076.i01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corpas-Burgos F., Martinez-Beneito M.A. On the use of adaptive spatial weight matrices from disease mapping multivariate analyses. Stoch. Environ. Res. Risk Assess. 2020;34(3):531–544. [Google Scholar]
- Della Rossa F., Salzano D., Di Meglio A., De Lellis F., Coraggio M., Calabrese C., Guarino A., Cardona-Rivera R., De Lellis P., Liuzza D., et al. A network model of Italy shows that intermittent regional strategies can alleviate the COVID-19 epidemic. Nature Commun. 2020;11(1):1–9. doi: 10.1038/s41467-020-18827-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dicker R.C., Coronado F., Koo D., Parrish R.G. 2006. Principles of epidemiology in public health practice; an introduction to applied epidemiology and biostatistics. [Google Scholar]
- Diekmann O., Heesterbeek H., Britton T. Princeton University Press; Princeton: 2013. Mathematical Tools for Understanding Infectious Disease Dynamics. [Google Scholar]
- Duncan E.W., White N.M., Mengersen K. Spatial smoothing in Bayesian models: a comparison of weights matrix specifications and their impact on inference. Int. J. Health Geogr. 2017;16(1):1–16. doi: 10.1186/s12942-017-0120-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ejigu B.A., Wencheko E. Introducing covariate dependent weighting matrices in fitting autoregressive models and measuring spatio-environmental autocorrelation. Spat. Stat. 2020;38 [Google Scholar]
- Farcomeni A., Maruotti A., Divino F., Jona-Lasinio G., Lovison G. An ensemble approach to short-term forecast of COVID-19 intensive care occupancy in Italian regions. Biom. J. 2021;63:503–513. doi: 10.1002/bimj.202000189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabry J., Simpson D., Vehtari A., Betancourt M., Gelman A. Visualization in Bayesian workflow. J. R. Stat. Soc. Ser. A. 2019;182(2):389–402. [Google Scholar]
- Gelfand A.E., Diggle P., Guttorp P., Fuentes M. Chapman and Hall/CRC Press; Boca Raton, FL: 2010. Handbook of Spatial Statistics. [Google Scholar]
- Geman S., Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 1984;(6):721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- Girardi P., Greco L., Mameli V., Musio M., Racugno W., Ruli E., Ventura L. Robust inference from robust Tsallis score: application to COVID-19 contagion in Italy. Statistics. 2020 doi: 10.1002/sta4.309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girardi P., Greco L., Ventura L. Misspecified modeling of subsequent waves during COVID-19 outbreak: A change-point growth model. Biom. J. 2021;63:In press. doi: 10.1002/bimj.202100129. [DOI] [PubMed] [Google Scholar]
- Gompertz B. XXIV. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. In a letter to Francis Baily, Esq. FRS &c. Philos. Trans. R. Soc. Lond. 1825;115:513–583. doi: 10.1098/rstb.2014.0379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman M.D., Gelman A. The No-U-Turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014;15(1):1593–1623. [Google Scholar]
- Hsieh Y.H. Modeling and Dynamics of Infectious Diseases. World Scientific; 2009. Richards model: a simple procedure for real-time prediction of outbreak severity; pp. 216–236. [Google Scholar]
- Hsieh Y.H. Pandemic influenza A (H1N1) during winter influenza season in the southern hemisphere. 2010;4:187–197. doi: 10.1111/j.1750-2659.2010.00147.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsieh Y.H., Chen C. Turning points, reproduction number, and impact of climatological events for multi-wave dengue outbreaks. Trop. Med. Int. Health. 2009;14(6):628–638. doi: 10.1111/j.1365-3156.2009.02277.x. [DOI] [PubMed] [Google Scholar]
- Huerta G., West M. Priors and component structures in autoregressive time series models. J. R. Stat. Soc. Ser. B Stat. Methodol. 1999;61(4):881–899. [Google Scholar]
- Ioannidis J.P., Cripps S., Tanner M.A. Forecasting for COVID-19 has failed. Int. J. Forecast. 2020 doi: 10.1016/j.ijforecast.2020.08.004. URL: http://www.sciencedirect.com/science/article/pii/S0169207020301199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jalilian A., Mateu J. A hierarchical spatio-temporal model to analyze relative risk variations of COVID-19: a focus on Spain, Italy and Germany. Stoch. Environ. Res. Risk Assess. 2021:1–16. doi: 10.1007/s00477-021-02003-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joseph M. 2016. Exact sparse CAR models in Stan, 2016. URL http://mc-stan.org/users/documentation/case-studies/mbjoseph-CARStan.html. [Google Scholar]
- Lawson A.B. CRC Press; 2018. Bayesian Disease Mapping: Hierarchical Modeling in Spatial Epidemiology. [Google Scholar]
- Leroux B.G., Lei X., Breslow N. Statistical Models in Epidemiology, the Environment, and Clinical Trials. Springer; 2000. Estimation of disease rates in small areas: a new mixed model for spatial dependence; pp. 179–191. [Google Scholar]
- Metropolis N., Rosenbluth A.W., Rosenbluth M.N., Teller A.H., Teller E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953;21(6):1087–1092. [Google Scholar]
- Neal R.M., et al. Handbook of Markov Chain Monte Carlo, Vol. 2, No. 11. 2011. MCMC using Hamiltonian dynamics; p. 2. [Google Scholar]
- Pelagatti M.M., Maranzano P. University of Milan Bicocca Department of Economics, Management and Statistics Working Paper; 2021. Assessing The Effectiveness of the Italian Risk-Zones Policy During the Second Wave of COVID-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richards F. A flexible growth function for empirical use. J. Exp. Bot. 1959;10(2):290–301. [Google Scholar]
- Rue H., Held L. CRC Press; 2005. Gaussian Markov Random Fields: Theory and Applications. [Google Scholar]
- Rushworth A., Lee D., Mitchell R. A spatio-temporal model for estimating the long-term effects of air pollution on respiratory hospital admissions in Greater London. Spat. Spatio-Tempor. Epidemiol. 2014;10:29–38. doi: 10.1016/j.sste.2014.05.001. [DOI] [PubMed] [Google Scholar]
- Rushworth A., Lee D., Sarran C. An adaptive spatiotemporal smoothing model for estimating trends and step changes in disease risk. J. R. Stat. Soc. Ser. C. Appl. Stat. 2017;66(1):141–157. [Google Scholar]
- Stan Development Team A. 2020. RStan: the R interface to Stan. R package version 2.21.2. URL: http://mc-stan.org/ [Google Scholar]
- Stan Development Team A. 2021. Stan modeling language users guide and reference manual, 2.26. URL: http://mc-stan.org/ [Google Scholar]
- Tsoularis A., Wallace J. Analysis of logistic growth models. Math. Biosci. 2002;179(1):21–55. doi: 10.1016/s0025-5564(02)00096-2. [DOI] [PubMed] [Google Scholar]
- Vehtari A., Gelman A., Gabry J. Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Stat. Comput. 2017;27(5):1413–1432. [Google Scholar]
- Waller L., Carlin B. In: Handbook of Spatial Statistics. Gelfand A.E., Diggle P., Guttorp P., Fuentes M., editors. Chapman and Hall/CRC Press; Boca Raton, FL: 2010. Disease mapping. [Google Scholar]
- Watanabe S., Opper M. Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. J. Mach. Learn. Res. 2010;11(12) [Google Scholar]
- Werker A., Jaggard K. Modelling asymmetrical growth curves that rise and then fall: Applications to foliage dynamics of Sugar Beet (Beta vulgaris L.) Ann. Botany. 1997;79(6):657–665. [Google Scholar]