Precision Requirements and Data Compression in CryoEM/CryoET

Abstract

With larger, higher speed detectors and improved automation, individual CryoEM instruments are capable of producing a prodigious amount of data each day, which must then be stored, processed and archived. While it has become routine to use lossless compression on raw counting-mode movies, the averages which result after correcting these movies no longer compress well. These averages could be considered sufficient for long term archival, yet they are conventionally stored with 32 bits of precision, despite high noise levels. Derived images are similarly stored with excess precision, providing an opportunity to decrease project sizes and improve processing speed. We present a simple argument based on propagation of uncertainty for safe bit truncation of flat-fielded images combined with lossless compression. The same method can be used for most derived images throughout the processing pipeline. We test the proposed strategy on two standard, data-limited CryoEM data sets, demonstrating that these limits are safe for real-world use. We find that 5 bits of precision is sufficient for virtually any raw CryoEM data and that 8–12 bits is sufficient for intermediate averages or final 3-D structures. Additionally, we detail and recommend specific rules for discretization of data as well as a practical compressed data representation that is tuned to the specific needs of CryoEM.

Introduction

Due to increasing detector speed and automation improvements, the size of CryoEM and CryoET datasets have been rapidly growing. As with any field, ideally it would be possible to routinely archive not only the original experimental data, but also all of the intermediate files associated with the analysis. In many analysis pipelines it is not uncommon for such intermediate data to significantly eclipse the original raw images in size. Further, many shared data collection sites limit their retention of raw collected data to only a few months to avoid the need to establish massive data archival capacity. As a secondary concern, file I/O time, rather than computation, can be rate limiting in many types of analysis. Simply opening a 4k × 4k × 1k tomogram for visualization can take several minutes on a workstation using a typical network mounted filesystem. If it were possible to store such data more compactly without impacting interpretation, then substantial savings in wasted time and resources could result.

Clearly this concept is not new to the field, and early discussions of this issue date back decades. Two publications have tackled the problem since the ‘resolution revolution’ inspired by direct detectors. The first (McLeod et al., 2018) tested 4 or 8 bit representations combined with compression using the Blosc (https://www.blosc.org/) metalibrary, but primarily targeted raw movie frames. The second (Eng et al., 2019) proposed the use of JPEG compression for long term archival as a sustainable alternative to simply deleting everything after some period of time. That is, they recognized that information loss would occur, but that lossy archival was still an improvement over discarding everything. This second manuscript did perform testing which demonstrated a surprising amount of information retention even with fairly aggressive JPEG compression. However, testing was performed using excess-data conditions, which would not be able to detect small levels of information loss.

Counting-mode detectors have improved the compression situation for archival of raw electron counting movie-mode data, through use of lossless compression in TIFF files as well as other novel strategies for high speed detectors (Guo et al., 2020). However, the derived aligned movie averages are still typically stored as 32 bit floating point images, retaining numerical precision far beyond the uncertainty of the pixel values. Extracted per-particle movie stacks are also conventionally stored uncompressed since gain normalization is required. Lossless compression is, of course, non-controversial, as it preserves the original uncompressed data bit-for-bit. However, such compression is also of limited value when the data being compressed has very high noise levels. Indeed, a typical corrected CryoEM movie average will still occupy 60–80% of its original size even after use of the best existing compression algorithms.

As we discuss below, theoretical arguments can easily be made that typical flat-fielded CryoEM images should not require more than 4–5 bits of precision, and in some cases, as few as 2–3 bits, with no loss of information. Without testing on real data, such statements have not been considered trustworthy by the community at large, and adoption of compression has largely been limited to the lossless compression described above. In this manuscript we consider the implementation-independent question of acceptable bit truncation levels on both theoretical and practical grounds as well as describe a standards-compliant compression methodology using the interdisciplinary HDF5 file format (https://www.hdfgroup.org/HDF5/ )(Dougherty et al., 2009).

Proposed Limits for Routine Bit Truncation

Our goal is to establish safe strategies for routine reduction of precision at all stages of CryoEM data processing after flat fielding, while maintaining results indistinguishable from the original data, thus reducing storage requirements and improving data processing throughput. We explicitly exclude raw direct detector movie frames from this discussion, as this data is already well served by existing, often manufacturer specific, methods, and bit truncation is of no practical value when the number of bits is very small.

One of the earliest concepts taught in experimental science is error estimation. When making a physical measurement, such as 247.482 mg, an estimate of the uncertainty of the value is required, representing the reproducibility of the measurement. If the uncertainty of the aforementioned mass were 0.1 mg, then we would instead record 247.4 ± 0.1 mg, irrespective of the precision of the instrument. Recording additional digits is statistically nonsensical if they represent true uncertainty (noise). A typical total electron dose in a CryoEM counting-mode movie-average might be ~20 e⁻/pixel and yet current practice is to store flat-fielded images as floating point numbers with 7 digits of precision. Performing gain correction/flat fielding does not change the fact that electron impacts are discrete events. Indeed, uncertainty in the gain correction images themselves increase the uncertainty in the corrected image, further reducing, if only slightly, the needed precision.

If perfect electron detectors were possible, the recorded electron count would represent the best theoretically achievable statistical certainty. Our goal is to identify acceptable limits for reduction of precision by establishing limits for theoretically perfect detectors. These limits will therefore also be guaranteed to be safe for any real-world detector, which necessarily will have higher noise levels, and thus greater uncertainty, requiring less precision. The associated quantum efficiency (DQE) (McMullan et al., 2009) is important in detector design, but it has no impact on our discussion, as it can only reduce, not increase, the required precision. Similarly, these are also valid limits for integrating mode detectors which clearly cannot provide greater accuracy than event counting detectors.

As electron events are independent, Poisson statistics apply. If the expectation value of a particular measurement is N counts, the standard deviation of the measurement is $\sqrt{N}$. This allows us to easily estimate the number of bits we need to preserve in any measurement based on the maximum number of electrons expected in a pixel. Note that this purely considers shot noise, and any additional noise sources in the imaging process would further reduce the required precision. Thus we are determining a safe bit retention level for a theoretically optimal experiment, so these recommendations will not change with future detector developments.

If the dose per pixel is M electrons, the expectation value can be exactly represented with ⌊log₂ M⌋ + 1 bits. Taking the Poisson distribution into account, adding an additional bit, thus doubling the maximum value, permits accurate representation of >99.5% of values for M>10. From the standard deviation, we can estimate the number of bits of pure noise as $⌊\mathrm{l}\mathrm{o}{\mathrm{g}}_2{M}^{1/2}⌋=\frac{1}{2}⌊\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}M⌋$. In theory, we should only need to preserve $\frac{1}{2}⌊\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}M⌋+1$ bits to retain all significant bits. So, even if we had an unusually high 256 e⁻/pixel dose, we should only need to retain 5 significant bits to properly record the measurement. For a typical 20 e⁻/pixel micrograph, only 3 bits would be required.

Note that this discussion assumes images with expectation values which vary in a relatively narrow dynamic range, but this is typical for biological CryoEM, and is unlikely to cause issues in realistic use-cases. An exception to this would be diffraction mode images for MicroED (Shi et al., 2013), which have an extremely large dynamic range, and would thus be unsuitable for the simple bit truncation proposed here. Related techniques, such as floating point bit truncation, in which trailing bits in the floating point significand are zeroed, could still be usable. However, floating point truncation produces a non-uniform distribution of discrete samples in value space, which can cause problems for some real-space CryoEM image processing. In testing, even with bitshuffling (Masui et al., 2015), floating point bit truncation provided substantially worse lossless compression than our proposed bit truncation with integer storage.

Averaging in Poisson statistics is quite straightforward, as the standard deviation is the square root of the total count irrespective of how the measurements are grouped prior to summing. Thus the derived data in CryoEM image processing, produced by averaging together many measurements, is substantially less noisy than the original data, and thus requires more precision to accurately record. Many effects, such as the variable gain in individual pixels in direct electron detectors, which necessitates flat fielding, can only be detected when averaging together sufficient numbers of images to produce an aggregate electron count large enough to detect the effect. This does not invalidate the fact that the precision of the individual images being averaged could be safely reduced. The averaging process itself produces the additional bits of precision necessary to represent the effects not observable in the individual images.

Due to this averaging effect, we must also consider the permissible level of bit truncation for derived images, which may represent the average of tens of thousands to millions of individual images. If 10,000 particle images were averaged in 2-D, each with 20 e⁻/pixel, using the same mathematics, we see that we would need up to 9 bits to represent the result with sufficient precision. Processes such as 3-D reconstruction, unfortunately, cannot be as easily characterized in real-space. While bit requirements could be computed for Fourier pixels, they would vary with location, and the wide dynamic range in Fourier space would raise significant issues. Real space uncertainties will depend heavily on the effective Fourier filtration applied to the map. As low-pass filtration is effectively a local averaging process, this further reduces the uncertainties of the (blurred) pixel values. Based on the size of typical single particle analysis (SPA) projects, and the minimal impact that precision of individual pixel values has on structural interpretation, we can empirically estimate that 12 bits is more than sufficient for any final filtered 3-D reconstruction in CryoEM, and that for the vast majority of cases 8 bits is sufficient. Having said that, the largest factor influencing file size when compressing typical 3-D volumes is masking. The region of interest in typical CryoEM maps usually represents only a tiny fraction of the full cubic volume, and all of the constant values outside the mask are extremely compressible. Even if we retain the maximum recommended 12 bits, if masking is performed, the final volume will readily compress to a small fraction of its original size. It is worth mentioning that the bit truncation process clearly also applies to the mask, such that the “soft” masks commonly used in CryoEM to reduce resolution exaggeration will become slightly less smooth due to discretization. With 8 or more bits, we have not found this to cause difficulties with resolution assessment or map interpretation.

Tomograms must be considered separately, as imaging parameters are vastly different. First, tomograms are often collected at lower magnifications to increase the field of view. Considering a typical cellular tomogram with 100 e⁻/Ų total dose and 4 Å/pixel sampling, one might conclude that M should be 1600. However, when a tomogram is reconstructed, the information is distributed over the Z axis. For a 200 nm thick section, we would have 500 slices in our reconstruction, or on average only 3 e−/voxel. Even with nonuniform density distribution along Z, it is easy to see that 3–4 bits should be theoretically sufficient to accurately represent a raw tomographic reconstruction. This situation may change drastically, however, if the reconstruction is further processed. Applying a low-pass filter to or denoising a tomogram will produce greatly reduced per-pixel uncertainties, theoretically requiring substantially more bits to represent with sufficient precision. Room temperature tomograms of stained sections could also require substantially more bits due to their large dynamic range. One could still raise the question of whether the additional per-pixel precision in either of these cases is actually useful in data interpretation. However, to ensure that the recommended compression levels are safe, we suggest 8 bits for raw tomograms, with the caveat that reasonable arguments for preserving only 4–5 bits could be made. Indeed, packages like IMOD (Kremer et al., 1996, Mastronarde and Held, 2017) have historically offered 8 bit representations for tomograms to conserve space and improve speed.

Limits of Discretization or Lossy Compression Error

Next, we consider whether the use of only a few possible discrete values for each pixel will itself be an issue. With decimal digits, the minimum number of discrete values preserved even with a single digit of precision is obviously 10. When considering data representations with 1–3 bits, the number of potential values each pixel may have is clearly quite small. This could conceivably have some impact on image processing. JPEG compression similarly introduces errors, but in spatially localized frequency space. That is, information is also lost in JPEG, but real-space histograms still span 8 bits.

We can characterize the maximum Fourier space errors due to either of these effects by performing either discretization or JPEG compression on an image, then computing the FSC between the original and reduced images (Fig. 1). We performed this test on an image containing pure Gaussian white noise. It is important to note that these curves are characterizing the representational error between the images and do not imply that these errors will propagate to any sort of derived analysis, such as SPA. If, for example, 4 images were averaged together, the average would immediately have two additional bits, with correspondingly reduced representational error. So, there are very few situations in which these observed differences would have an obvious impact on analysis.

Figure 1.

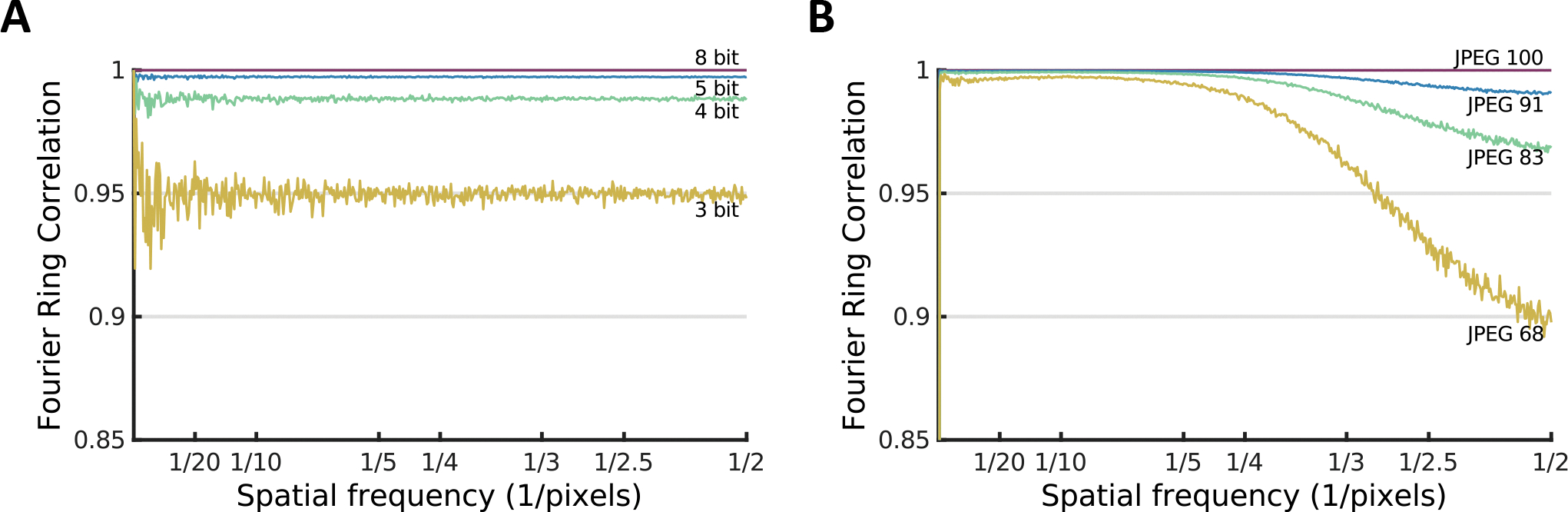
Measurement of the maximum potential impact of real-space representational error in Fourier space using FSC curves when compression is applied to random Gaussian noise. A) Bit truncation and B) JPEG compression.

Even in the worst-case scenario, bit compression to 3 bits, the mean FRC remains at roughly 0.95, implying that this issue is unlikely to have a substantial impact on CryoEM analysis, even of unaveraged images. We also observe that at similar data reduction levels (see Table 1) JPEG compression more strongly impacts high resolution information, but better preserves low resolution information. Given that in CryoEM data, the spectral signal to noise ratio (SSNR) declines rapidly with resolution, and high resolution is where we most need to recover information for a good reconstruction, this is an additional argument that JPEG compression is less suitable for use in CryoEM.

Table 1.

File size reduction and copy times for the set of frame-averaged micrographs in the β-gal test dataset. Bit truncations were performed as described under Implementation of Bit Truncation. Zstd and zlib compression were both level 1. System caches were cleared for all timing measurements.

Convention	Dataset	Dataset Size (MB / % of raw)		RAMDISK Copy Time 1 thread (s)	PCIe SSD Copy Time 30 threads (s)	SATA SSD Copy time 30 threads (s)
32 Bit Float
Raw	float	5469	100%	-	8.1 ± 0.2	52 ± 2
HDF5 zlib	float	4935	90%	161.8 ± 0.2	12.7	56
Blosc zstd	float	4901	90%	18.2	8.4	52
Bit Truncated
zlib	8 bit	1224	22%	39.4	5.4	37
zlib	5 bit	817	15%	28.7	4.9	34
zlib	4 bit	650	12%	26.9	4.5	36
zlib	3 bit	481	9%	25.3	4.9	35
zstd	5 bit	697	13%	13.0	4.2	32
zstd	5 bit + bitshuffle	860	16%	11.9	4.6	34
JPEG
	JPEG 100	1367	25%	-	-	-
	JPEG 91	815	15%	-	-	-
	JPEG 83	645	12%	-	-	-
	JPEG 68	485	9%	-	-	-

Data Compression

Compression algorithms can be divided into two broad classes: lossless and lossy. Lossless compression algorithms make use of patterns in the data to produce a reduced bit representation while preserving the exact original values. When using lossless compression, the decompressed data will match the original data bit-for-bit with no possibility of error. Lossless compression is entirely safe for scientific use, and the primary consideration in its use is the tradeoff between the computational resources required for compression and decompression versus the savings in storage and concomitant improvements in data input/output times. Pure noise, where every bit is randomly set to 0 or 1, is nearly incompressible, whereas patterned data, what we would consider “signal”, is typically reasonably compressible.

Lossy compression includes algorithms such as JPEG, which was recently proposed as a possible compression mechanism for long-term CryoEM data archival (Eng et al., 2019). Lossy compression prioritizes specific features of the data, and strives to preserve these while sacrificing lower priority features to achieve substantial file-size reductions. Notably for CryoEM, JPEG operates in a form of localized Fourier space, meaning compression has an impact on the spectral profile of the data, and tends to produce real-space artifacts. When considering lossy algorithms in science, it is critical to understand what is being lost, and data scientists generally suggest avoiding algorithms such as JPEG for scientific tasks (Cromey, 2010, Cromey, 2013). Other error-bounded lossy algorithms more appropriate for scientific data do exist, such as SZ3 (Zhao et al., 2021) and ZFP (Lindstrom, 2014), and could be considered for specific purposes. Without the properties described in Table 2, however, adaptations would be required for use in CryoEM/ET.

Table 2.

Table of conditions and corresponding value maps used during bit truncation to preserve necessary image properties for CryoEM analysis. min() and max() are the minimum and maximum pixel values in the image.

Image Test	Integer Mapping	Representative Image Types
All pixels are integers, max()-min() < 2nbits	Subtract min() and use integers directly.	Counting-mode image before flat fielding. Results of integer output image processing. Categorical images, which should always be stored with sufficient bits to be unchanged.
All pixels are integers, min()<0≤max()	Subtract min() and truncate necessary number of bits. Shift such that 0 maps to 0 on read.
All pixels are integers	Subtract min() and truncate necessary number of bits.
min()≤0≤max()	Integers span min() to max() shifted such that the integer closest to zero represents exactly 0	A masked image, other images spanning 0
None of the above are true	Integers span min() to max()	Generic image data

While our proposed use of bit truncation is lossy from an algorithmic perspective, it is not lossy from a scientific perspective; it is accurately representing each measurement to the precision required by statistical uncertainty. Simple bit truncation has well defined properties in both real and Fourier space and can be easily quantified and justified. The eliminated bits are demonstrably beyond the limits of measurement.

While we do not believe it represents an appropriate choice, JPEG compression is also considered in our tests, as it has previously been proposed (Eng et al., 2019) for long-term archival, while acknowledging its lossy nature. Due to the very low bit requirements we derived above, JPEG can be used to produce successful reconstructions even at high compression levels, but it also produces real-space artifacts which interfere with some common operations in CryoEM/ET data processing.

Testing Truncation Effects on SPA

To confirm that bit truncation at the proposed levels has no measurable impact on representative 3-D reconstructions, we performed extensive SPA testing. For testing to be valid it was critical that the reconstructions be limited by data quantity, not quality. A reconstruction with a very large number of particles will generally achieve a saturating resolution, beyond which significant resolution gains are not possible. Under such conditions removing even a significant fraction, say 25%, of the data may have no measured impact on the reconstruction quality. If bit truncation were to degrade the data in some small but measurable way, with an excess of data, the result may be similarly unaffected, despite actual information loss. So, for a valid test of data quality, we must work in a regime with few enough particles that any significant particle quality loss could be observed in the reconstruction.

For refinement we made use of the simplified SPA refinement tool in EMAN2.91 (e2spa_refine.py), which performs straightforward iterative reference-based angular assignment with 3-D Fourier reconstruction, in conjunction with canonical EMAN2 CTF correction. This avoids any class-averaging or maximum likelihood methods which might similarly act to conceal information loss in the data. Our goal is not to achieve the best conceivable structure, but rather to ensure that results are equivalent when the input data and intermediate files are bit truncated, so we target approaches which should be the most sensitive to such issues.

Two standard CryoEM data sets were selected from the 2015–2016 CryoEM Map Challenge (https://challenges.emdataresource.org/?q=2015_map_challenge) (Heymann et al., 2018) for testing. β-galactosidase (β-gal) is a stable enzyme which refines easily and consistently, producing results with predictable resolution, and has been a standard for microscope performance testing over the last decade. We used a 5,513-particle subset of this collection (EMPIAR-10012) (Bartesaghi et al., 2014) which demonstrates a clear reduced resolution as compared to the full data set, meeting the requirement for a data quantity limited test.

TrpV1 (Liao et al., 2013) is an integral membrane protein which was selected for testing due to its local flexibility in solution. This ensures that images of such flexible structures can also be truncated without degradation. We selected a subset of 15,982 particles from this data (EMPIAR-10005), again meeting the requirement for a data quantity-limited test. While the structure does refine reliably to reasonably high measured resolution, the refinements exhibit more variation than observed in a stable enzyme like β-gal (Fig 3E).

Figure 3.

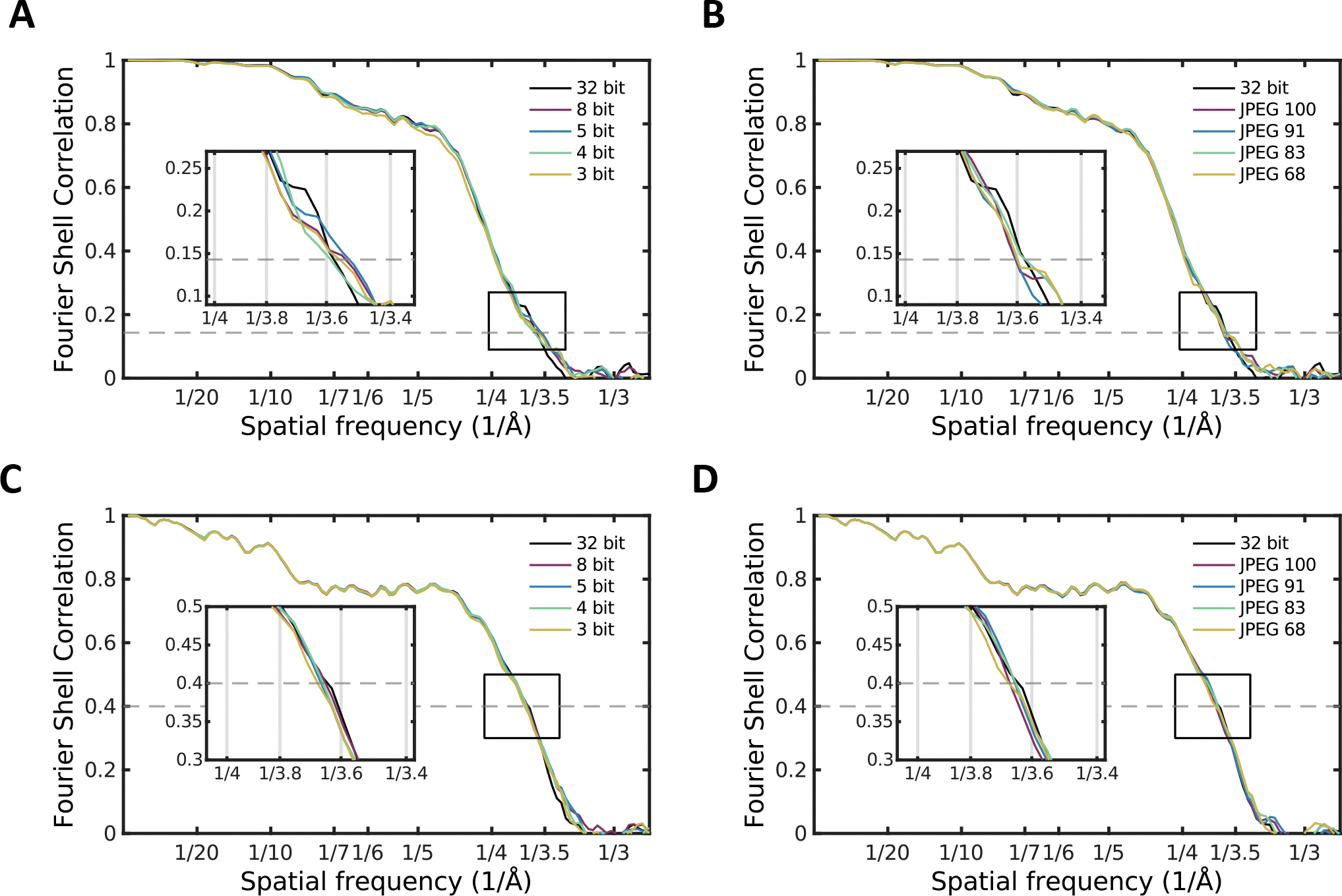
The effect of various levels of bit truncation and JPEG compression on even-odd Fourier shell correlation (FRC) of 3-D reconstructions for A) β-gal after different levels of bit truncation and B) β-gal after different levels of JPEG compression, and map vs model Fourier shell correlation curves of C) bit truncated and D) JPEG compressed β-gal dataset reconstructions. Inset plots show magnified views of the same curves intersecting with the corresponding FSC cut-off value as indicated by the rectangular annotation.

Prior to bit truncation, the flat-fielded micrographs were clamped at +/− 4 standard deviations from the mean. Pixels outside this range were clamped to the limiting value. This process eliminates outliers which may be present due to various experimental causes and is part of normal micrograph pre-processing as described in Implementation of Bit Truncation.

The 32 bit control was performed with bit truncation of intermediate files completely disabled in the entire refinement pipeline after import. For JPEG, which is not natively supported in EMAN2, micrographs were converted to 8 bit TIFF with JPEG compression at the specified quality level, then converted back to HDF5 retaining the reconstituted JPEG values. For all other compression test refinements (5, 4, and 3 bit), frame-averaged flat-fielded micrographs were truncated to the specified number of bits. Subsequent processing made use of the proposed compression levels for all intermediate files. Specifically: 12 bits for reconstructed 3-D volumes and 8 bits for masks. The same initial model was used for all refinements, and all refinement options were identical.

In both data sets, we show results for the original 32 bit floating point data and 8, 5, 4, and 3 bit compression. Based on our earlier discussion, we hypothesized that 5 bit compression is safe for virtually any SPA data set, and in some cases 3 or 4 bits may also suffice. For β-gal, where a complete high resolution structure is available for comparison, we also performed JPEG compression at levels selected to produce compressed file sizes comparable to bit truncation + zlib.

If bit truncated particles can achieve the same resolution, and further, produce equivalent FSC curves, within the limits of uncertainty of the FSC itself, this demonstrates that precision reduction truly did not degrade the data. Individual refinement runs were as close to identical as possible. As portions of the orientation determination process incorporate randomness, runs are equivalent but not truly identical, and this is responsible for the variability observed among multiple identical runs (Fig. 4B).

Figure 4.

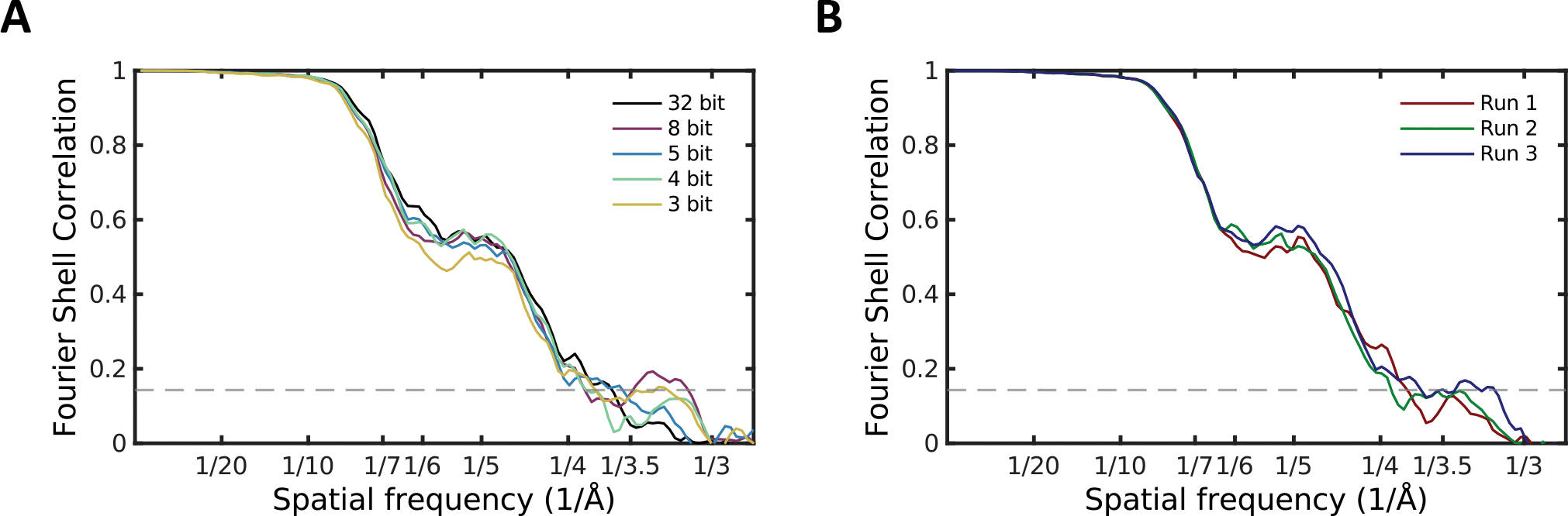
TrpV1 reconstruction FSC curves. A) The effect of various levels of bit truncation on internal Fourier shell correlation. B) The run-to-run variation of TrpV1 even-odd FSC curves when performing a sequence of 3 identical reconstructions of the uncompressed data.

Four of the final refined maps for each of the two data sets are shown in Fig. 2. Slight visible differences among the maps are all within the range of variability among identical refinements. The magnified regions in the bottom of Fig. 2A–D are overlaid on local density from PDB 5A1A (Bartesaghi et al., 2015), which is also used for the map vs. model FSC curves in Fig. 3C, D. The magnified regions of Fig. 2E–H are overlaid on PDB 3J9J (Barad et al., 2015), which is locally accurate even if not complete enough to use for map vs. model FSC calculations.

Figure 2.

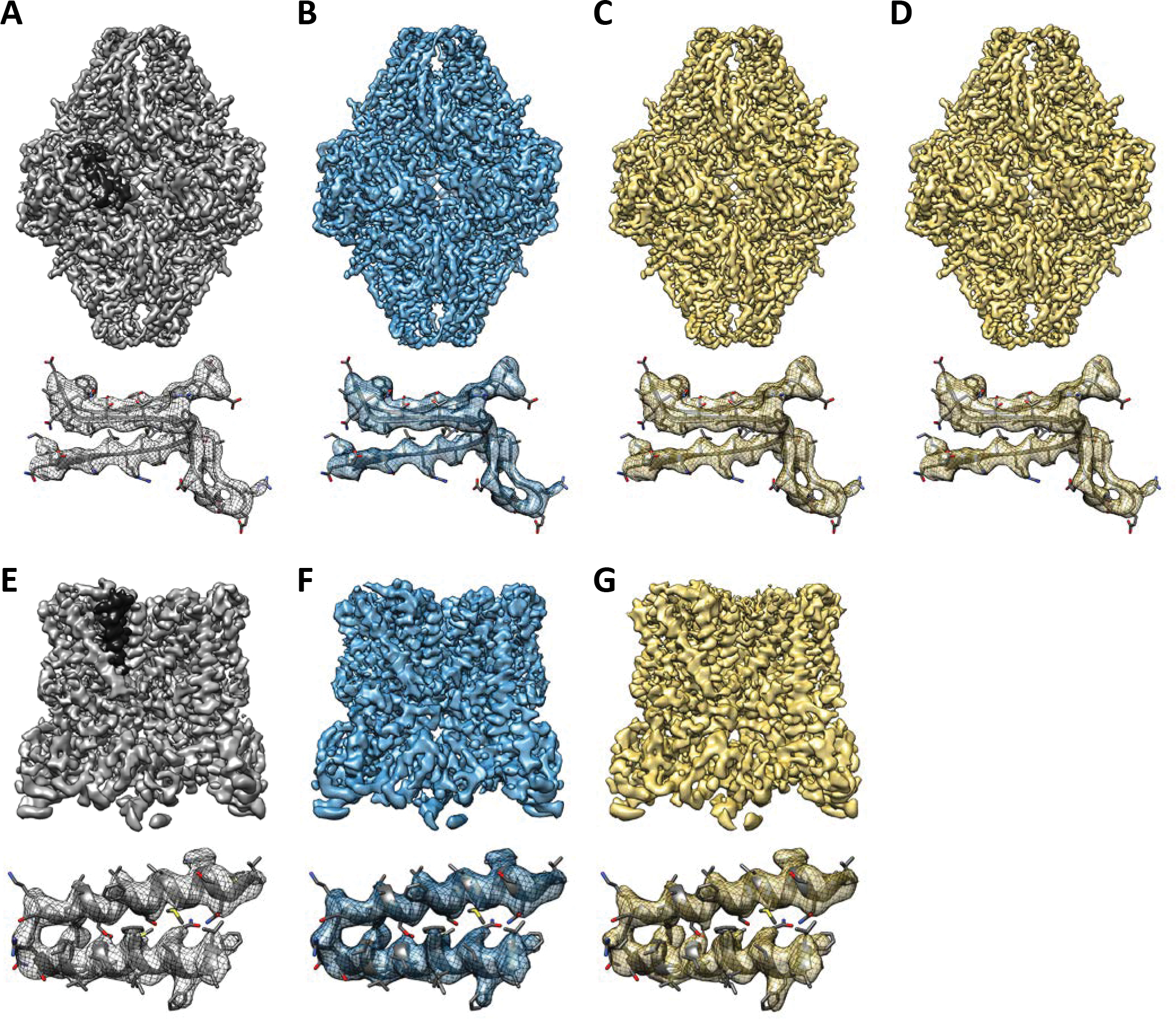
Comparison of full reconstruction volumes (upper) and a selected subarea (lower) with previously published atomic model of β-gal from reconstructions with micrographs after A) no compression, B) 5 bit discretization, C) 3 bit discretization, and D) JPEG 68 compression. Comparison of full reconstruction volumes (upper) and a selected subarea (lower) from TrpV1 reconstructions with micrographs after E) no compression, F) 5 bit discretization, and G) 3 bit discretization. The black-colored surfaces indicate the location of the sub-volume in the full map. Iso-surface colors correspond to the line colors in Fig. 3–4.

FSC curves for all runs on β-gal are shown in Fig. 3. Fig. 3A–B shows the even/odd FSC curves for all of the tested compression levels. Fig. 3C–D shows map vs. model FSC curves for each of the final averaged maps. While it could be argued that the 3 bit compression produces measurable, if very slightly lower FSC based on the internal test, when compared to a high resolution reference map, any differences become truly negligible and well within the variance of the FSC curves themselves.

Results for the even-odd FSC test at different bit compression levels for the TrpV1 data set are shown in Fig 4. more variability is observed in this test, and at intermediate resolution, again, the 3 bit curve appears slightly lower than the others, though this does not continue at high resolution. For comparison, the uncompressed data was run 3 times with identical data and parameters (Fig 4B). It is clear that the natural variability of this data, without classification, is simply larger than β-gal, and we would argue that there are no scientifically important differences among the various bit truncated runs.

Compression Performance

In Table 1 we compare file storage sizes and speeds for the flat-fielded frame averages used in the β-gal test, with a range of compression and storage options, including bit truncation followed by lossless compression as well as JPEG compression. Copy time is the time required to read the uncompressed float-32 images and write using the stated parameters to the same storage. The HDF5 file format supports the zlib deflate algorithm natively. For comparison we also tested the Blosc implementation of zstd, a newer alternative to zlib which leverages modern multithreaded CPUs to improve speed with some other optimizations (https://github.com/facebook/zstd). For the 5 bit case we also include results for bitshuffle followed by zstd as it has been suggested (Masui et al., 2015, McLeod et al., 2018) that shuffling should improve compression levels. Extensive testing with bitshuffle (not shown) yielded no consistent size reductions other than a slight reduction for floating point data. In performance testing, the RAMDISK column assesses time for a single thread where storage performance is not a factor. PCIe and SATA SSD columns demonstrate that for many typical situations, compression times are storage bandwidth limited rather than CPU limited. SATA SSD results are somewhat comparable to systems with high performance storage mounted via a typical gigabit network connection. In all cases, system disk buffers were flushed prior to each test to ensure data caching did not influence performance scores.

The key results we focus on in this table is that the vast majority of the file size reduction is provided by bit truncation. While this table shows only zlib and zstd compressors, basic testing with other algorithms such as SZIP, LZW and BZIP2 (not shown) demonstrated that the relative contribution of a specific algorithm to compressed size is minimal compared to the dramatic file size reductions produced by precision reduction. Further, in common use-cases, the relative speed of various algorithms is generally overshadowed by storage performance. That is not to say that making use of a carefully selected compression algorithm is without merit, simply that using the correct level of precision is significantly more impactful. The zlib compression used in HDF5 is known to be quite slow compared to other algorithms, and this is discussed below.

Implementation of Bit Truncation

In addition to determining the number of bits to retain, the mathematical process for mapping floating point pixel values to small bit integer representation is critical for typical CryoEM image processing algorithms to function correctly. To make the best use of the available values a linear transform is applied to the image prior to truncating bits. When reading the image, the inverse transform is applied to restore values to the original range.

It is quite common in CryoEM for zero to be considered a special value in images, often associated with masking/solvent flattenting. It is thus critical that one discrete value represent exactly zero in such cases, so this information is not completely lost. This immediately means that 1 bit representations are not possible, since it would be impossible, then, to have both positive and negative values, and even 2 bit representations would have strong sign asymmetry. When zero is included in the data range, bit truncation may cause some additional values close to zero to become exactly zero during compression, and while this is not generally a problem, users should be aware of this effect.

If the original data is already in an integer representation, we wish to avoid remapping the data to integers again, as this may produce combing artifacts. Instead, the existing integers should be directly truncated to the desired number of bits, reducing the integer precision, but retaining the fact that values are integers. If the data already requires fewer than the specified number of bits, then no rescaling is required at all. Indeed, certain classes of images, such as multi-level masks, where integer pixel values represent categories, must not be truncated at all, as this would drastically alter the interpretation of the data.

Frequently, CryoEM data will have a small number of extreme outliers, which are purely artifactual. These range from x-ray pixels on integration mode detectors to flat fielding issues in specific pixels and even software artifacts. If such extreme outliers are included in the integer mapped range, then the bulk of the pixel values near the mean value of the image will be represented by an improperly small number of integer values. Values in CryoEM are typically ‘clamped’ beyond 3–5 standard deviations from the mean to combat the impact of outliers. Clearly, this process must not be repeated, or each time an image went through a read-write sequence the range of values might become narrower. To avoid this, this process is not part of the bit truncation itself, but should be part of standard workflows when appropriate, prior to any bit truncation. Ideally this would take place as part of the flat fielding procedure.

Table 2 summarizes the complete set of rules we propose for bit truncation of arbitrary CryoEM/ET image data. The rules take into account peculiarities and common use cases in this field. The tests are performed in order. The first successful test defines the applied mapping. Each image must thus be analyzed as part of the image saving process, but this requires only a single pass in RAM, and is negligible computationally. A pseudocode implementation is provided in Appendix 1.

Few file formats, and no CryoEM-specific formats, readily support representation as an arbitrary number of bits. However, when excess zero bits are stored, the storage is recovered by virtually any lossless compression algorithm. Thus, if the targeted number of bits is 8 or fewer, the native representation used for storage will be 8 bits. If greater than 8 but <= 16, a 16 bit representation is used. The most significant unused bits are set to zero. In cases where more than 16 bits are requested, numbers remain in floating point format and are losslessly compressed.

HDF5 Implementation

EMAN2 has used the interdisciplinary HDF5 as a native file format for nearly 15 years. The format is also supported by the widely-used Chimera visualization application (Goddard et al., 2007) and recent versions of IMOD, as well as many generic scientific data processing software packages. HDF5 supports gzip compression natively and transparently, meaning that gzip-compressed data can be read by any HDF5 compatible program without modification, or even direct knowledge that the data is compressed, with caveats discussed below. While a wide range of newer algorithms are available as plugins for HDF5, after fairly extensive testing (partial results in Table 1), we found that, unsurprisingly, virtually all of the effective compression is provided by the bit truncation process itself, and that experimentation with various compression algorithms and bit or byte shuffling did not produce any truly compelling improvements. The one improvement alternative algorithms does offer is better performance, but at this point in time we believe broader compatibility is a higher priority.

Our argument for using the dated, but standard zlib compression is that this compressor is distributed with standard HDF5 binaries, and thus can be used with virtually any HDF5 supporting software without modification. While other compression algorithms such as those in Blosc are available, and are straightforward to install for an experienced programmer, they would be far from trivial to install for the typical software user in the CryoEM community, particularly if they were faced with installing it into a binary distribution of some specific software package. Typical users would not even understand why the HDF5 compatible software was apparently unable to read their data to recognize that a plugin was required. If, in the future, the standard HDF5 library begins including some of these newer plugins as standard, or if a more automated solution for HDF5 plugins becomes available, then we may revisit this decision for EMAN2. At present, we believe that making HDF5 as broadly usable as possible is the more critical factor for potential future adoption by other CryoEM software.

Gzip compression permits specification of a compression level from 0 to 9. Unlike with lossy compression methods such as JPEG, this choice has no impact on the restored data, which remains identical irrespective of level, but does impact compression time. Time scaling is quite dramatic, for example, a typical 1k × 1k × 512 tomogram is 2150 MB as a 32 bit volume. Compressed to 5 bits this falls to 256 MB with level 1 compression and 234 MB with level 8 compression, but compression time rises from 9 s for level 1 to almost a minute for level 8. The level 1 compression time is substantially less than the roughly 20 seconds it would take to write the uncompressed file to 1 GbE attached network storage. Time for decompression, however, is relatively unaffected by compression level, requiring roughly 2 s for a volume of this size. The overall compression time clearly depends on the speed and capacity of the underlying storage, but even on slower storage there seems little practical advantage in using higher compression levels, so the default is compression level 1.

The detailed organization used by EMAN2 within HDF5 files is documented at http://eman2.org/Hdf5Format. The mapping from the reduced integer values to floating point values is linear. This is similar to the “floatint” concept used in earlier CryoEM file formats, such as the Purdue Image Format (PIF). When images have been bit truncated, four header values are stored for each image: stored_rendermin, stored_rendermax, stored_renderbits, and stored_truncated. Stored integer values can be converted to the original floating point values as follows:

$$\text{result}=\left(\text{storedvalue}/\left(2^{\text{renderbits}}-1\right)\right)*\left(\text{rendermax}-\text{rendermin}\right)+\text{rendermin}$$

stored_truncated is not required to restore the original values, but simply stores a count of the number of pixel values which were outside the rendermin/rendermax range during the storage process. At the time of writing, these parameters are not recognized by UCSF Chimera (Goddard et al., 2007) or IMOD (Kremer et al., 1996), meaning compressed images can still be read by these packages, but the integer representation will be recovered, rather than the adjusted values. This will, for example, influence the isosurface thresholds when such an HDF5 volume is read into Chimera, but otherwise no changes are required to read these files in any package offering HDF5 support. As the transformation is purely linear, no changes in represented structure will result, and in most CryoEM applications, an arbitrary linear transformation of density values is already assumed. Appendix 2 includes details of how to control bit truncation and compression when using EMAN2.

Conclusions

The primary purpose of this manuscript is to establish standards for matching the precision of CryoEM data to the associated uncertainties, providing, as a side effect, substantial reduction in file sizes, with no impact on scientific interpretation. These standards, including the methodology for mapping different types of image data to an integer range in a CryoEM compatible way, are not file format specific, and could be adopted with any file format with native support for lossless compression.

Storing the complete raw data and all intermediate refinements, along with processing notes could be viewed as equivalent to preserving physical lab notebooks in terms of maintaining complete records of scientific projects. Given the size of intermediate files generated during CryoEM processing, often this is viewed as prohibitive, and storing the raw data with an ostensibly complete record of the processing that was performed is considered sufficient. It is not clear that repeating the process with this information would produce truly identical results, with the additional need to replicate the precise set of software used at that time. The 5–10 fold size reductions provided by the proposed methods on intermediate 3-D volumes and other files should make it significantly more practical for such long-term archives of complete projects to be maintained. The relative impact of a specific choice of lossless compression algorithm is small compared to that provided by the reduction of precision, so specific choice of algorithm can be driven by priorities other than simply compression efficiency.

As a secondary issue, we consider the question of file formats. Having developed CryoEM software for over 25 years, which supports more than 30 file formats used in the field, we have encountered a wide range of issues, from widely used formats with no published specifications, to software that violates the published specifications, to intentional deviation from published standards for specific purposes. Many files produced 20 years ago can now only be read because of packages like EMAN2 (Tang et al., 2007) and EM2EM (https://www.imagescience.de/em2em.html). To ensure long-term readability of archived data, the use of open file formats which do not require esoteric algorithms to read should be strongly favored. Naturally, innovation is sometimes still required, as, for example the detector-specific data stored in the new EER format (Guo et al., 2020), could not be efficiently represented in other existing formats. However, for images with more separation from the raw detector data, standardization is a laudable, if elusive goal. The secondary goal of this manuscript is not to propose a final standard for the community, but to explain the decisions made in EMAN2 and the rationale for them.

The revised MRC format (Cheng et al., 2015) has become a broad standard in the CryoEM community, but it is also heavily abused, with different companies making different uses of the “extended header”, often in poorly defined and incompatible ways, compromising the future recovery of data and metadata. Indeed, there are cases where existing MRC files cannot be unambiguously interpreted without human-provided context. In EMAN2, the code implementing the “simple” MRC format is arguably the most complicated of the 32 formats it supports. The entire purpose in using a standard file format is its usability across software packages and the prospects for it remaining readable in future. If a standard format requires dramatic alterations to meet some specific need, adopting a different format, which already meets those needs, would seem the better strategy. For this reason, we feel the MRCX proposal (McLeod et al., 2018) is not an optimal approach.

There are a limited number of existing file formats which readily achieve all of the archival needs of the CryoEM community: support for arbitrary metadata headers, multidimensional image data, a range of data storage types, large numbers of images in a single file, compression support and very large file sizes. The two most widely used formats meeting most of these goals are TIFF and HDF5.

TIFF would seem to be an attractive option given its existing use for compressed direct detector movies and use of the OME-TIFF variant in the optical microscopy community. It has native compression, supports multiple images and representations, has mechanisms for metadata storage, and is clearly a widely used standard. However, it lacks direct support for multidimensional data, requiring interpreting stacks of 2-D images as volumes, and making stacks of volumes awkward. TIFF also uses 32 bit pointers, effectively limiting file sizes to 4 GB, and making them very challenging to use in the broader CryoEM context. BigTIFF (http://bigtiff.org) proposes changes to the format which would support large image files, but it has not achieved the sort of widespread support enjoyed by TIFF, so while not unreasonable, it may be premature to establish as a community standard.

At present, this leaves us with HDF5 (https://www.hdfgroup.org/solutions/hdf5), which is widely used across scientific disciplines, is professionally supported, has a 20+ year history, and was originally designed to solve exactly the sort of problems the CryoEM community currently faces. It supports all of the features required by the CryoEM community, including compression. It offers open source libraries for a range of languages, and has extensive capabilities. Unfortunately, these extensive capabilities have given the HDF5 libraries a significant learning curve, which has dissuaded many programmers from trying. On the other hand, the HDF5 implementation in EMAN2 is dramatically simpler and far more logical than the implementation required for the MRC format.

While the current practice of retaining excess precision in CryoEM data is arguably harmless from a scientific perspective, neither is there a scientific rationale for doing so. The approach we have explored in this manuscript, of determining limiting uncertainties based on common image types at use in the field, should be, as we have demonstrated, completely safe from an information loss perspective, and offers numerous advantages to the field. As we have demonstrated, five retained bits is a completely safe precision level for typical CryoEM images, and 8–12 bits should be adequate for 3-D maps and class-averages. While we have not demonstrated this via testing, these limits should hold even for methods such as phase plates which enhance low resolution contrast, so long as the number of e⁻/pixel remains in the discussed range. From our tests it appears that even 5 bits is an overly conservative estimate for many situations, as additional noise sources are clearly present in typical CryoEM imaging. However, with 3 or fewer bits, discretization issues may become non-negligible, and the permissible image dynamic range is reduced. It would be quite reasonable for users to make use of fewer bits if specific conditions produce appropriate levels of uncertainty, but we expect that most users will elect to simply follow the general guidelines.

While JPEG compression does provide perfectly acceptable reconstructions in our testing, mirroring previous results (Eng et al., 2019), it is far harder to justify scientifically. Information loss in JPEG is based on perceptual standards rather than noise estimates. Further, as it operates on discrete cosine transforms in 8×8 pixel blocks, it can produce positional artifacts, as well as poorly defined Fourier changes. The general behavior of JPEG compression vs. bit truncation was presented in Fig. 1, and it is clear that while JPEG sacrifices high resolution information before low resolution information, at the very modest compression levels being discussed here, these effects simply don’t have a measurable impact on reconstructions. Finally, CryoEM makes fairly extensive use of specific per-pixel values, ranging from exactly 0 representing masked regions to looking at specific per-pixel electron counts. As JPEG alters individual pixel values in an unpredictable way, such analysis is impossible. Given that there is no clear advantage to JPEG compression with file sizes comparable to the proposed bit truncation approach, and it has been argued that JPEG is simply inappropriate for scientific use (Cromey, 2010, Cromey, 2013), we would argue against its use in the CryoEM/CryoET fields.

Irrespective of arguments about file formats, which are admittedly controversial, the use of reduced bit representations should greatly reduce storage issues and permit long term archival at substantially lower cost than required by current methods. The recommendations presented in this manuscript have been adopted within EMAN beginning with version 2.91, and we encourage other software developers in the field to consider making similar strategies available.

Appendix 1: Bit Truncation Pseudo-Code

Abstracted from EMAN2:

https://github.com/cryoem/eman2/blob/master/libEM/emutil.cpp - EMUtil::getRenderLimits

https://github.com/cryoem/eman2/blob/master/libEM/io/hdfio2.cpp

#Reading and Writing Bit Truncated Data
#Designed for flat-fielded images and intermediate files (not low dose movie frames)
#definitions:
#
# ceil(num)      = value rounded to next larger whole number
# floor(num)        = value rounded to next smaller whole number
# round(num)        = Traditional rounding to whole number: 2.5 -> 3, −2.5 -> −3
# count0s(image)    = number of data values in the array which are exactly 0
# length(array)     = returns the length of array
# maximum(array)    = returns the largest value in the array
# minimum(array)    = returns the smallest value in the array
#
# rendermin = smallest float value represented in the bit truncated range
# rendermax = largest float value represented in the bit truncated range
# renderbits = desired number of non zero bits to preserve
# These values are stored in HDF files as stored_rendermin, stored_rendermax, stored_renderbits
#
# For image objects:
# image[data] refers to a one dimensional array of values in the image/volume
# image[“name”] refers to a header value stored with the image
#
# TO values are considered exclusive, stopping before the specified value
# Python style blocks indicated by indentation without explicit END statements
##############################
# READING BIT TRUNCATED DATA #
##############################
#Reading (restoring) truncated data is a simple linear mapping using
#   header-stored values. It is assumed that the input array is floating point
#   containing integer values when renderbits>0
FUNCTION read_image(name)
    image = read_image_data_and_header(name)
    # if renderbits is not set or is zero, then no data modification is required
    IF image[“stored_renderbits”] > 0 THEN
        scale = (image[“stored_rendermax”]-image[“stored_rendermin”])/(2**image[“stored_renderbits”]-1)
        FOR index = 0 TO length(image[data])
            image[data][index] = image[data][index] * scale + image[“stored_rendermin”]
    RETURN image
##############################
# WRITING BIT TRUNCATED DATA #
##############################
# Before calling truncate_image: Clamp/threshold image (if needed)
# If there are outlier values in the image, values near the mean
#   may be compressed into a small number of bins, reducing the
#   effective compression. If necessary, perform outlier removal, but
#   never do this more than once on a given image.
#   (for typical floating point data we often clamp to +/− 4 std dev)
# This will take a floating point array as input and
# return an 8 or 16 bit array suitable for lossless compression
# image - input floating point array
# number_bits - desired number of truncated bits in the range of 3 – 16
FUNCTION truncate_image(image, number_bits)
    IF number_bits<3 or number_bits>16 THEN EXCEPTION
    # this represents the range of values represented by a given number of bits
    # when the minimum and maximum value in a range must both be represented
    max_steps = 2**number_bits − 1
    # Step size between integer bins in the original floating point values
    # note that this value may be modified in appropriate situations below
    step = (maximum(image[data])-minimum(image[data])) / max_steps
    count_int=0
    FOR value IN image[data]
        IF value == floor(value) THEN count_int += 1
    # Allocate the output array
    IF number_bits <= 8 THEN outimage = new_8bit_array(length(image[data]))
    ELSE outimage = new_16bit_array(length(image[data]))
    # This section determines:
    # rendermin = smallest floating point value represented in the truncated integer range
    # rendermax = largest “
    # these values may be adjusted from the actual image minimum and maximum to achieve
    # specific targets as described in table 2
    # if all values in the floating point image are integers
    IF count_int == length(image[data]) THEN
        # integer data should remain integers when read, which requires some adjustments
        IF image.range() < 2 ** truncimage[“renderbits”] THEN
            # if the integer data already fits into the desired number of integer bits
            # set the max to the maximum value possible for number_bits
            rendermin = minimum(image[data])
            rendermax = minimum(image[data]) + max_steps
        ELSE # if bits must be truncated
            # first calculate the fewest bits needed to preserve the original data
            neededbits = ceil( log(image.range() + 1 , base=2) )
            # calculate the step size using the number of bits being truncated
            # this guarantees that the step size will be an integer when restoring
            step = 2 ** (neededbits - number_bits)
            # set rendermin
            IF minimum(image[data]) < 0 < maximum(image[data]) THEN
                # if the data spans 0, we automatically enforce a bin at 0.
                #   To do this, the minimum must be an exact multiple of
                #   the step for 0 to be included as a restored value. So round the
                #   minimum to the nearest value that is a multiple of the step. It is
                #   guaranteed to be moved by less than the precision being truncated
                rendermin = round( minimum(image[data]) / step ) * step
            ELSE
                # if the data does not include both positive and negative values
                # use the actual minimum
                rendermin = minimum(image[data])
            # set rendermax such that the resulting range will be
            #   an exact multiple of the step when it is calculated during reading.
            #   This ensures that integers will be read as integers
            rendermax = rendermin + step * max_steps
    # in this block, the image contains non-integer values
    ELSE
        IF minimum(image[data]) < 0 < maximum(image[data]) THEN
            # if the data spans 0, we select rendermin/max such that one integer represents exactly 0
            # first, check if min() is already a multiple of the step
            IF minimum(image[data]) == floor( minimum(image[data]) / step ) * step THEN
                #then keep the range where it is
                rendermin = minimum(image[data])
                rendermax = maximum(image[data])
        ELSE
            # We must reserve one bin for values of 0. First, calculate the
            #   step of the integer bins as if there were one fewer bin.
            step = (maximum(image[data])-minimum(image[data])) / (max_steps - 1)
            # the minimum must be an exact multiple of the step for 0 to be
            #   included as a restored value. So move the rendermin down
            #   (toward negative infinity) to the next multiple of the step.
            rendermin = floor( minimum(image[data]) / step ) * step
            # calculate (and set) the max using the full number of steps
            #   but with the new step size
            rendermax = rendermin + step * max_steps
    ELSE
        #if the data starts or stops at 0, or otherwise does not span 0
        rendermin = minimum(image[data])
        rendermax = maximum(image[data])
# Actual data remapping using rendermin & rendermax
FOR index = 0 TO length(image[data])
    IF value <= rendermin THEN outimage[data][index] = 0
    ELIF value >= rendermax THEN outimage[data][index] = max_steps
    ELSE outimage[data][index] = round((value - rendermin) * max_steps / (rendermax-rendermin))
outimage[“stored_rendermin”]=rendermin
outimage[“stored_rendermax”]=rendermax
# 8 or 16 bit array ready for writing
RETURN outimage

Appendix 2: Using EMAN2 for bit truncation and format conversion

In development versions of EMAN2/3 after June 2022, a new syntax is available for specifying bit truncation in any output file in any EMAN2 program. These filename specifications override any default compression or other command-line arguments discussed below. This will be supported for all appropriate file formats, with an updated list maintained on the EMAN2 Wiki:

https://eman2.org/ImageFormats

The new specification permits:

<filename>:<bits>

<filename>:<bits>:f

<filename>:<bits>:<min>:<max>

<filename>:<bits>:<minsig>s:<maxsig>s

For example:

myfile.mrcs:5 – which will produce an 8 bit MRC stack file with 5 bits of precision, covering the full range of values after extreme outliers have been removed

myfile.hdf:12:3s:3s – will produce a compressed16 bit hdf5 file, with 12 bits of precision, using values extending from mean-3*sigma to mean+3*sigma

mymask.mrc:8:f – will produce an 8 bit MRC volume with 8 bits of precision, covering the full range of values in the original image, with no outlier removal

The original mechanism for HDF5 compression is available in EMAN2.91 and later. There are several command-line methods to compress files:

e2compress.py will compress a set of input images, volumes or stacks in any format EMAN2 can read. The result will be a set of correspondingly named set of HDF5 files. If the input files are uncompressed HDF5, the input files will be overwritten by default. Multithreaded compression is available when compressing multiple files. For example:

e2compress.py im1.mrc im2.mrc im3.mrc im4.mrc --bits 5 --threads 4 --nooutliers

e2compress.py --help will provide details on all options

Many programs, including the ubiquitous e2proc2d.py and e2proc3d.py take the --compressbits=<bits> command line option. This will govern the number of retained bits in the main output images produced by the program. In certain programs specific output files are hardcoded to compress in a specific way.

Decompression and/or conversion to other file formats is normally accomplished using e2proc2d.py or e2proc3d.py, which can read or write any file format supported by EMAN2 (https://eman2.org/ImageFormats). Use --help for details on available options.

For example:

e2proc2d.py mystack.hdf mystack.mrcs

e2proc2d.py mystack.hdf mystack.spi

e2proc3d.py myvolume.hdf myvolume.mrc

Simple Python examples:

from EMAN2 import *
# read the first image from file.mrcs
image=EMData(“file.mrcs”,0)
# convert to numpy, example, not required for write_compressed
ary=image.numpy()
# manipulate ary (numpy) or image (EMData), data shared
# write image to first position (0) in file.hdf with 5 bits
image.write_compressed(“file.hdf”,0,bits=5)
# write image to first position of SPIDER file without compression
image.write_image(“file.spi”,0)
# read all images from stack file into a Python list
images=EMData.read_images(“file.mrcs”)
# write all images to a compressed HDF5 file, starting at position 0
EMData.write_compressed(images,”file2.hdf”,0,bits=5)
# The full calling syntax is:
im_write_compressed(self, filename, n, bits=8, minval=0, maxval=0, nooutliers=False, level=1, erase=False)

where:

n is the number of the image/volume in a stack file

bits is the number of bits to retain after truncation

minval and maxval permit overriding the range of float values to map to the truncated integers

nooutliers (should not be specified with minval/maxval) will clamp up to 0.01% of outliers

level specifies the zlib compression level

erase will cause the existing image file to be erased prior to writing

It is important to note that unlike uncompressed images, when overwriting compressed images in HDF5 files, the space used by the original image is not recovered. For example, if you write 5 compressed images to an HDF5 file, then overwrite image #2 with a new compressed image, the file will behave as expected, but the file will be larger than it should be, by the size of the original compressed image #2. It is thus advisable when writing compressed HDF5 files, to avoid overwriting existing images. Writing images in arbitrary order, however, does not have this problem.