Uncovering the biological basis of control energy: Structural and metabolic correlates of energy inefficiency in temporal lobe epilepsy

Abstract

Network control theory is increasingly used to profile the brain’s energy landscape via simulations of neural dynamics. This approach estimates the control energy required to simulate the activation of brain circuits based on structural connectome measured using diffusion magnetic resonance imaging, thereby quantifying those circuits’ energetic efficiency. The biological basis of control energy, however, remains unknown, hampering its further application. To fill this gap, investigating temporal lobe epilepsy as a lesion model, we show that patients require higher control energy to activate the limbic network than healthy volunteers, especially ipsilateral to the seizure focus. The energetic imbalance between ipsilateral and contralateral temporolimbic regions is tracked by asymmetric patterns of glucose metabolism measured using positron emission tomography, which, in turn, may be selectively explained by asymmetric gray matter loss as evidenced in the hippocampus. Our investigation provides the first theoretical framework unifying gray matter integrity, metabolism, and energetic generation of neural dynamics.

The structural and metabolic basis of control energy in the brain is uncovered by leveraging epilepsy as a human lesion model.

INTRODUCTION

Human brain function emerges from continuous neural dynamics that give rise to diverse activation states and rich rules for transitioning between states (1–3). Understanding the mechanisms governing these dynamical processes remains a core focus of inquiry in neuroscience (3). Recent developments have demonstrated that network control principles underlie the dynamical repertoire of many complex systems (4, 5). In formalizing those principles, network control theory (NCT) serves as a powerful approach from systems engineering that is typically deployed to design and manage technological, robotic, and communication systems. However, its nascent application to neural systems has proven remarkably productive, both across species (6, 7) and more particularly in humans (8–10). In these studies, NCT is used to model dynamic processes, such as the attainment and maintenance of brain states, and transitions between them, as a function of the underlying structural network architecture measured using diffusion magnetic resonance imaging (MRI). For example, one can simulate the activation of a given brain circuit by modeling the transition to a state when regions from this circuit are selectively active. Moreover, NCT can be used to quantify the energetic costs, or control energy, needed to facilitate these simulated state dynamics (11).

Control energy, as typically defined in engineering, refers to the input required to drive the system from one state to another along a trajectory of intermediate states (12). When modeling the temporal dynamics of brain activity, such an input can take the form of endogenous costs associated with internal cognitive demand or mental load (13, 14) or can take the form of direct external manipulations such as brain stimulation (15) or medication (14). In the former context, the need for control energy to support designated brain dynamics can also be conceptualized as a measure of energetic efficiency, which is determined in part by dynamics and in part by the topological organization of the underlying structural network. As a marker of efficiency, it is notable that control energy decreases over development, suggesting enhanced efficiency with age (16), and is heightened in psychiatric disorders, suggesting decremented efficiency in disease (17, 18). These prior investigations lay important groundwork for the use of NCT to model the structurally constrained energetic processes that guide brain state transitions; collectively, these studies support its feasibility, ensure its methodological rigor, and underscore its neuroscientific relevance.

However, a key remaining question is whether and how control energy relates to biological forms of energy that are measurable in vivo or in vitro. One way to address this issue is to quantify how the aforementioned energetic efficiency, measured as control energy, cofluctuates with unrelated measures of energy consumption. It is well known that the brain poses marked energetic demands, consuming 20% of the body’s energy while comprising merely 2% of the body’s weight (19). Notably, neural dynamics and their energetic sequelae are disrupted in neurological and psychiatric disorders, with devastating consequences for cognitive function and behavior. One prototypical example of a dynamical energetic disruption is an epileptic seizure. As transient periods of hypersynchronous neuronal activity (20), seizures consume substantial energy and instantly disrupt ongoing brain dynamics, causing marked behavioral disturbances (21, 22). Despite their transience, the impact of seizures on brain function can linger well beyond seizure termination, especially in patients with drug-resistant focal epilepsy, such as the common temporal lobe epilepsy (TLE). Neuropsychological assessments in patients with TLE during the interictal period, i.e., when they are not suffering from seizures, reveal persistent deficits across multiple cognitive and affective domains (23–25), indicating the presence of prominent disruptions to normal brain dynamics.

TLE is also characterized by widespread alterations in brain structure, which extends beyond the seizure foci in the temporal lobes (26, 27). Concordantly, epileptogenic regions evince persistent hypometabolism during interictal periods (28). The severity of both structural damage and hypometabolism is associated with cognitive decline in patients with TLE (29–31), suggesting that chronic neural dysfunction might be rooted in a reduced baseline metabolism underpinned by compromised structural integrity. Regional hypometabolism could hamper the attainment and maintenance of healthy activation levels, in turn, decrementing the brain’s dynamic repertoire and clamping cognitive function. Examples of such altered dynamics in TLE abound, spanning reduced language network flexibility (i.e., fewer state transitions) (32), reduced memory network flexibility (33), delayed information flow, and slower activation spreading times (34).

Leveraging these pervasive alterations in dynamics, metabolism, and structure, here, we consider TLE as a lesion model and capitalize on NCT to assess how damage to structural connectivity disrupts the energetic generation of brain dynamics and its metabolic underpinning. We begin by stipulating a dynamical model whereby activity is constrained to spread along structural connections (Fig. 1A). Using this model, we quantify the control energy required to move between any two states or patterns of activity (11). Although a generic artificial system could hypothetically visit any state, evidence suggests that the brain preferentially visits some states more often than others (2, 35, 36). These preferential states can be defined by the coactivation of regions that are functionally coupled at rest (37, 38). These so-called intrinsic connectivity networks (ICNs) can also be detected during task performance and have been shown to support a range of cognitive processes (37, 39, 40). Here, we study the efficient attainment of eight such preferential states (9, 38), whereby only regions in a given ICN are active (Fig. 1B). Then, we use NCT to simulate transitions among preferential states and to estimate the associated energy costs, thereby probing the brain’s efficiency and integrity in the presence of TLE. Our simulations evaluate two transition types: (i) reaching transitions, where the brain moves from a theoretical baseline to a preferential state (Fig. 1C), and (ii) switching transitions, where the brain moves between two preferential states (Fig. 1D). By estimating the control energy for reaching transitions, we determine which preferential states are difficult to reach; that determination informs our understanding of the ICNs affected by TLE. Subsequently, we compute control energy for switching transitions, which allows us to identify the regions that tend to carry the greatest energetic burdens in supporting the brain’s dynamical repertoire. Last, we dig deeper into the neurophysiological underpinnings of control energy by leveraging fluorodeoxyglucose (FDG)–positron emission tomography (PET) images, which are commonly obtained as part of the presurgical evaluation in patients with TLE, to measure baseline brain metabolism. These data allow us to verify whether regions that show altered energetic efficiency in facilitating brain state transitions also present with metabolic anomalies and to determine how both the theoretical and empirical measures of energy costs are related to the underlying structural integrity of those regions. Our analyses thus provide two contributions of major significance that substantially advance the extant literature. First, we demonstrate how control energy tracks changes in the energetic efficiency of the brain, which, in turn, emerge as a consequence of epilepsy-related pathology. Second, we provide a data-driven, biological interpretation of control energy by systematically probing its relationship with the brain’s underlying glucose metabolism and structural integrity.

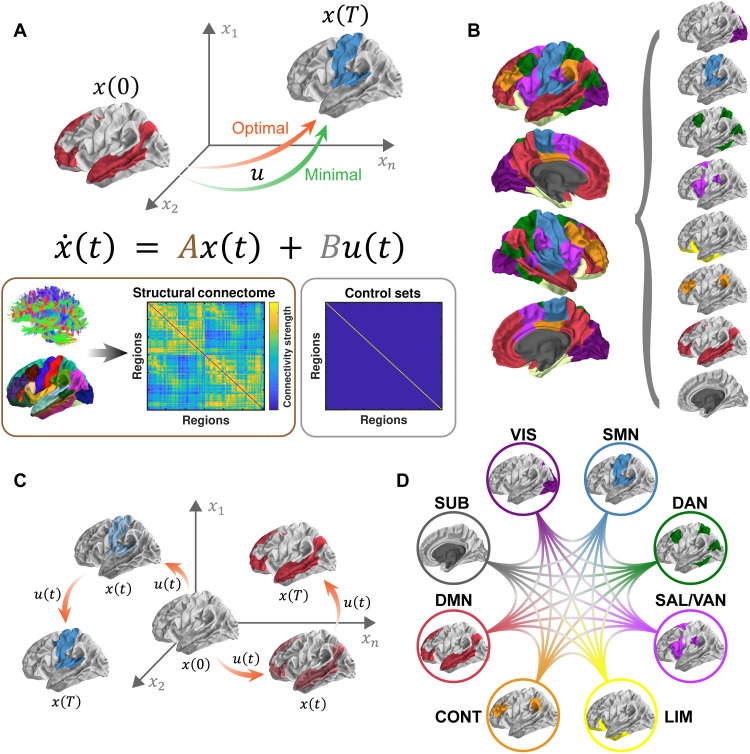
Fig. 1. Schematic of methods.

(A) On the basis of a simplified noise-free, linear, continuous-time, and time-invariant model of neural dynamics, we simulate energetic processes during brain state transitions instantiated upon and constrained by the structural connectome (matrix A). Two types of control energy (a quadratic function of u) are depicted: the minimal control energy (MCE) required to drive the brain from an initial state [x(0)] to a final state [x(T)] using a specific set of control nodes (whole brain, matrix B) and the optimal control energy (OCE) additionally constrains the length of the trajectory between states. (B) Eight preferential brain states are defined according to the known ICNs (37, 38). Within each state, regions from a specific ICN are activated at a magnitude of 1, whereas the rest of the brain remains at 0 (inactivated). These preferential brain states constitute the initial and final states of our simulations. (C) We then simulate the energetic inputs required to activate each of the preferential brain states from a theoretical baseline (i.e., activity magnitude of 0). Next, we estimate the OCE consumed during each of the activation processes across the whole brain for each individual. (D) We also simulate transitions between preferential brain states and estimate the MCE consumed at each brain region for each individual. VIS, visual network; SMN, somatomotor network; DAN, dorsal attention network; SAL/VAN, salience/ventral attention network; LIM, limbic network; CONT, executive control network; DMN, default mode network; SUB, subcortical network.

In this study, we enrolled 60 patients with TLE and 50 demographically matched healthy controls (HCs) (Table 1), who underwent an MRI scanning session including both a high–angular resolution diffusion imaging (HARDI) scan and a T1-weighted (T1w) anatomical scan. Among the enrolled patients, 50 also received an FDG-PET scan as part of their presurgical evaluation. From each participant’s HARDI data, we generated a structural connectome and estimated the control energy required to perform all reaching and switching transitions. Then, we tested for energetic inefficiency in TLE by comparing control energy between patients and HCs. We showed that patients with TLE present with an energetic inefficiency in reaching a preferential state predominantly composed of limbic regions. This inefficiency was due to excessive energy costs associated with activating the limbic network ipsilateral to the patients’ seizure focus. When considering switching transitions, we found that the mesial and inferior parts of the ipsilateral temporal lobe demanded greater energy consumption in TLE than in HCs. These increased costs of regulating brain dynamics incurred by patients with TLE limit their capacity to activate and maintain desired brain states, potentially leading to dysfunction. Furthermore, we found that this energetic imbalance between ipsilateral mesial and inferior temporal regions and their contralateral counterparts were accompanied by similar asymmetries in metabolic patterns. Specifically, a mediation analysis focused on the hippocampus showed that such association may be rooted in a corresponding asymmetry of underlying gray matter volume loss.

Table 1. Sample demographic and clinical characteristics.

Continuous variables were presented as means ± SD. TLE, patients with TLE; HC, healthy controls; HARDI, high–angular resolution diffusion imaging; FIAS, focal impaired awareness seizure; FAS, focal aware seizure; FBTCS, focal to bilateral tonic-clonic seizure; ASM, antiseizure medication. The quality of T1w images was assessed with an image quality rating and the total intracranial volume produced with the Computational Anatomy Toolbox (CAT12). The quality of HARDI data was assessed with a neighboring correlation index (74), which quantified the similarity between low b volumes with similar gradient directions, and with the mean framewise displacement (73) as a measure of head motion. Seizure focus was classified as left temporal (LT) and right temporal (RT). Temporal pathology was diagnosed by neuroradiologists on the basis of presurgical MRI scans as normal brain MRI (NB), hippocampal sclerosis (HS), and other pathologies (other), such as tumor, focal cortical dysplasia, and encephalocele. FBTCS history was sorted as follows: none, patients who had never had any FBTCS events during their lifetime; remote, patients who had experienced FBTCS in the past, but none for 1 year or more before scanning; and current, patients who had recurrent FBTCS within 1 year before scanning (46). For continuous variables, independent t tests were conducted. For categorical variables, chi square tests were conducted. Significant differences were highlighted in bold.

Experimental group (N)	TLE (60)	HC (50)	T/χ2	P
Age (year)	41.13 ± 14.41	37.98 ± 11.78	1.24	0.218
Sex (male/female)	34/26	26/24	0.24	0.625
Handedness (right/left)	51/9	42/8	0.02	0.885
T1-weighted image quality
Image quality rating	0.858 ± 0.006	0.859 ± 0.006	−1.13	0.260
Total intracranial volume (cm3)	1417 ± 150	1416 ± 143	0.04	0.969
HARDI image quality
Neighboring correlation	0.795 ± 0.013	0.795 ± 0.015	−0.31	0.754
Mean framewise displacement	0.375 ± 0.155	0.343 ± 0.132	1.16	0.251
Structural network properties
Matrix density	0.895 ± 0.045	0.911 ± 0.045	−1.79	0.076
Matrix total weight (log10( ∙ ))	7.078 ± 0.018	7.086 ± 0.014	−2.58	0.011
Seizure focus (LT/RT)	38/22
Age at epilepsy onset (year)	25.28 ± 15.59
Duration of epilepsy (year)	15.85 ± 16.46
Temporal pathology (NB/HS/ other)	15/27/18
Frequency of FIAS (number per month)	9.28 ± 16.41
FBTCS history (none/remote/ current)	19/16/25
Seizure type
FIAS	9
FAS	1
FIAS/FAS	9
FIAS + FBTCS	22
FAS + FBTCS	1
FIAS/FAS + FBTCS	14
FBTCS	4
Number of current ASMs (1/2/3)	27/26/7

RESULTS

We started our analyses by verifying that the imaging data quality was comparable between the two experimental groups (Table 1). Next, for each participant, we reconstructed a structural white matter network as a weighted undirected adjacency matrix composed of 122 cortical and subcortical regions (see details in Materials and Methods), which formed the basis of our NCT analyses (e.g., matrix A in Fig. 1A). We observed that patients with TLE presented lower matrix density and total weight (i.e., sum of all edge weights) than HCs (Table 1), which is in accord with the well-recognized white matter abnormalities in TLE (41, 42). To minimize the influence of demographic and data quality metrics on our subsequent statistical analyses, we regressed them out from all imaging derivates using linear regression (see Materials and Methods).

Simulated activation of ICNs

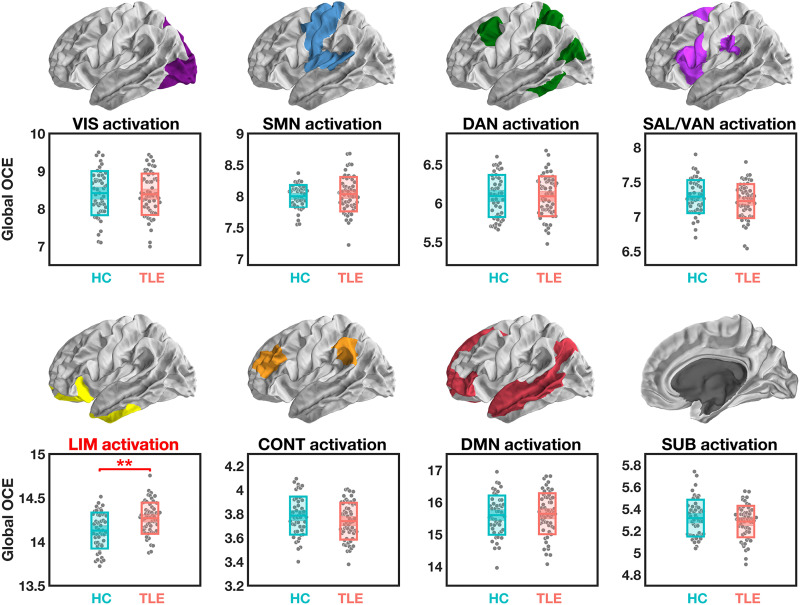
Our first research question pertained to the energetic costs associated with reaching each preferential brain state. Specifically, we examined the extent to which patients with TLE may exhibit energetic abnormalities during the activation of eight canonical ICNs (9, 38), including the visual, somatomotor, dorsal attention, salience/ventral attention, limbic (encompassing amygdala and hippocampus), executive control, default mode, and subcortical networks (Fig. 1B). We used the optimal control framework (9, 10, 15, 16) to model how the brain’s underlying structural network facilitated transitions from an initial baseline state to each preferential (final) state. Here, the initial state was set at a theoretical baseline with activity magnitude in all regions at 0. For each of our eight preferential states, the activity magnitude of regions within a specific ICN was set to 1, while the rest of the brain remained at 0 (16). Thus, these reaching transitions simulated the rise of activity in the target ICN from a mean-centered baseline, mimicking the activation process triggered by specific cognitive operations. For this model, an optimal solution of the control energy needed at each region can be produced by constraining both the energy costs and the length of the transition trajectory based on the underlying network topology (13). As previously reported (13), we referred to this solution as the optimal control energy (OCE) and summarized it globally as a measure of the brain’s energetic efficiency (Fig. 1C; see details in Materials and Methods). For each participant, we estimated the global OCE during each reaching transition. We regressed the confounding variables out of these global OCE estimates and compared the residuals between our two groups using a permutation-based t test (43), an approach that simultaneously corrects for multiple comparisons by controlling the family-wise error rate (44). We found that patients with TLE required greater global OCE to activate the limbic network compared to HCs (Welch’s t₁₀₈ = 3.80, P_corr = 0.002). The global OCE needed to activate other ICNs did not significantly differ between the two groups (Welch’s |t₁₀₈| < 1.55, P_corr > 0.609) (Fig. 2). This finding suggested that it was energetically more challenging for patients with TLE to specifically activate the limbic network.

Fig. 2. Global OCE estimated during simulated activation of ICNs.

After correction for multiple comparisons, significant group differences were only found for the simulated activation of the LIM, which demanded more global OCE in patients with TLE compared to HCs. **P_corr < 0.01. The central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively.

In the above analysis, our preferential states were defined with ICNs extended into both hemispheres. However, seizures in our enrolled patients with TLE were exclusively of unilateral origin, i.e., from either the left or the right temporal lobe. This laterality of seizure focus prompted the question of whether the energetic inefficiency that we observed in these patients may be asymmetric, especially regarding the limbic network, which included both the epileptogenic temporal lobe and its contralateral counterpart. To probe this asymmetry, we resimulated the reaching transition for the limbic network twice, once to activate the limbic regions in the left hemisphere only and once to activate regions in the right hemisphere. Although such a hemispheric restriction of activation is unlikely to occur in the brain, the simulation offers an opportunity to assess the laterality of the pathological burden observed in patients with TLE. When examining the lateralized global OCE, we found a significant hemisphere-by-group interaction (F_2,107 = 15.20, P = 2 × 10⁻⁶) (Fig. 3), demonstrating that patients with TLE required more energy to activate the limbic network ipsilateral to the seizure focus. More specifically, patients with TLE with a left-sided seizure focus required more energy to activate the left hemispheric limbic network [versus right TLE (RTLE): P_Bonferroni = 0.048; versus HC: P_Bonferroni = 4 × 10⁻⁵], whereas patients with TLE with a right-sided seizure focus required more energy to activate the right hemispheric limbic network [versus left TLE (LTLE): P_Bonferroni = 0.007; versus HC: P_Bonferroni = 2 × 10⁻⁴]. By contrast, we observed no significant differences between patients with TLE and HCs regarding the energy needed to activate the contralateral limbic network (P_Bonferroni > 0.588). Thus, the extra energetic costs associated with limbic network activation in TLE can be attributed to the increased energetic needs of the ipsilateral hemisphere but not of the contralateral one.

Fig. 3. Global OCE estimated during a simulated transition from the baseline to a final state where only one side of the LIM is activated.

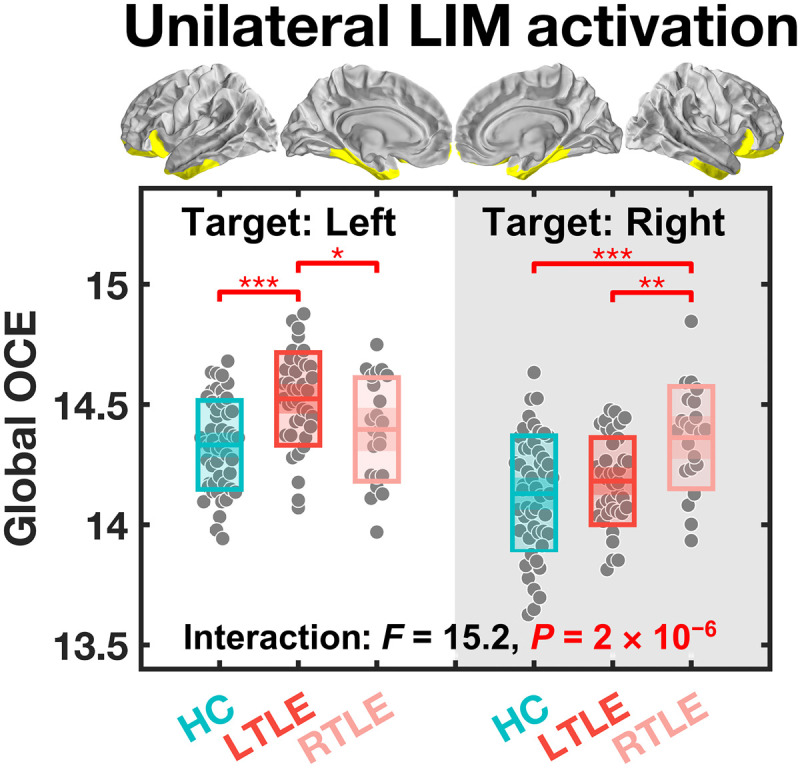
When the target was set to the left hemispheric LIM, only patients with left TLE (LTLE) needed more energy than the other two groups. When the target was set to the right hemispheric LIM, only patients with right TLE (RTLE) needed more energy than the other two groups. *P_Bonferroni < 0.05, **P_Bonferroni < 0.01, and ***P_Bonferroni < 0.001. The central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively.

Regional energetic efficiency in supporting brain state transitions

Empirical brain dynamics depend not only on the attainment of different states but even more on the flexible transitions among them, supported by brain regions consuming energy with different efficiency. While our reaching transition simulations have enabled us to identify global energetic inefficiency during limbic network activation in patients with TLE, these transitions are not necessarily representative enough, i.e., the brain does not revisit a specific baseline each time but, rather, continuously transitions between different states. Thus, to better profile regional energetic efficiency, we extended our investigation to examine switching transitions among our preferential states, as a closer approximation of empirical brain dynamics (9). For each individual, we modeled a total of 64 pairwise transitions, including both reciprocal-state transitions and single-state persistence, i.e., transitions that start and end at the same state, among the eight ICN-defined preferential states (Fig. 1D). To allow for maximal flexibility during the simulated transitions, we estimated the minimal control energy (MCE), which can be obtained by only constraining the control input to facilitate the designated transition, regardless of its trajectory (13). For each region, we averaged the MCE across all 64 transitions as a region-specific metric of energetic efficiency at the individual level. As in prior work (41, 45, 46), we mirror-flipped the regional MCE of the patients with RTLE to group metrics according to the laterality of the seizure focus, to enhance statistical power (41, 46). This procedure was done after confound regression and Z-standardization of each patient’s regional MCE relative to HC data. Thus, instead of comparing raw values of regional MCE from mixed hemispheric origin between patients and HCs, we performed a permutation-based one-sample t test on patients’ Z scores of the 122 regions to identify abnormal regional energetic efficiencies within ipsilateral and contralateral hemispheres, respectively (see Materials and Methods for further details).

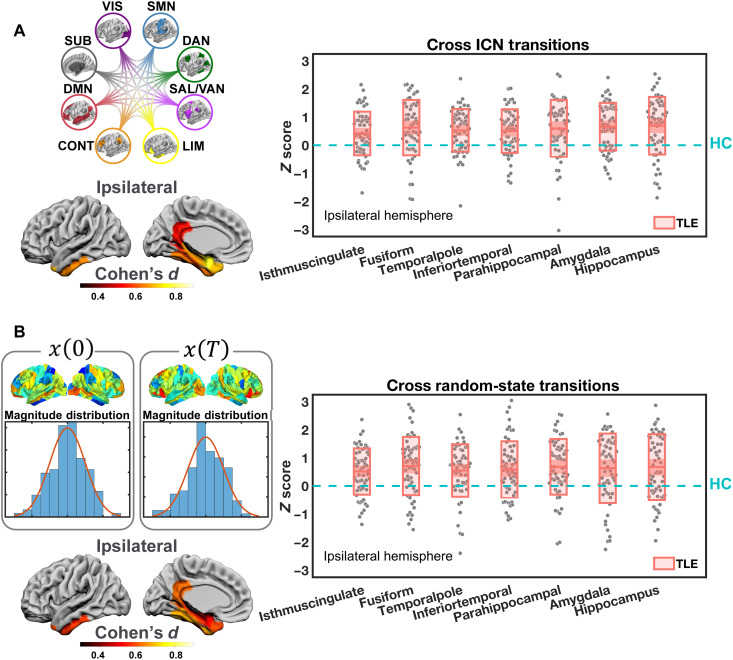
After correcting for multiple comparisons, we found that regional MCE was significantly elevated in patients with TLE within the hemisphere ipsilateral to the seizure focus only. This elevation occurred specifically in regions such as the temporal pole (t₅₉ = 5.40, P_corr = 1 × 10⁻⁴), inferior temporal gyrus (t₅₉ = 5.03, P_corr = 5 × 10⁻⁴), amygdala (t₅₉ = 6.01, P_corr = 1 × 10⁻⁵), hippocampus (t₅₉ = 5.24, P_corr = 2 × 10⁻⁴), parahippocampal gyrus (t₅₉ = 4.54, P_corr = 0.003), and fusiform gyrus (t₅₉ = 4.93, P_corr = 7 × 10⁻⁴), as well as the isthmus of the cingulate gyrus (t₅₉ = 4.17, P_corr = 0.011; rest of the brain: |t₅₉| < 3.41, P_corr > 0.114) (Fig. 4A). No significant effects were observed in the contralateral hemisphere. In TLE, these regions required more energy to facilitate the same brain state transitions than in HC. Furthermore, this energetic inefficiency was largely located in the ipsilateral temporolimbic regions, consistent with our previous results showing costly activation of the limbic network in patients with TLE.

Fig. 4. Regional energy efficiency differences between patients with TLE and HCs.

(A) We estimated the minimal control energy (MCE) consumption of each region during all transitions between the brain states defined by ICNs. In the hemisphere ipsilateral to the seizure focus, we found significantly higher energy consumption in patients with TLE than in HC among several temporolimbic regions. (B) We then estimated the MCE consumption of each region during transitions between 100,000 pairs of initial [x(0)] and final states [x(T)] with randomly generated activity magnitudes. Concordant results were found, showing that the patients needed significantly higher control energy in the ipsilateral temporolimbic regions. The boxplots depict the deviation scores (Z) of energy consumption of patients with TLE in reference to HC. Only regions with significant group differences after multiple comparison corrections are displayed, including the isthmus of the cingulate gyrus (Isthmuscingulate), fusiform gyrus (Fusiform), temporal pole (Temporalpole), inferior temporal gyrus (Inferiortemporal), parahippocampal gyrus (Parahippocampal), amygdala, and hippocampus.

It remains to be determined, however, whether simulating transitions among ICN-defined brain states can provide a representative overview of all possible brain state transitions. Thus, we stringently assessed the robustness of the above findings by comparing them to MCE values derived from transitions between 100,000 pairs of random initial and final states. These random states were generated following a Gaussian distribution of activity magnitude across the 122 regions with a mean of 1 and an SD of 0.1 as previously done (16). This finite repository serves as an approximation of all possible state transitions when no a priori brain states are explicitly defined. We adopted the same minimal control framework as above and obtained Z-transformed regional energy estimates. Consistent with our primary findings, we found significantly higher MCE in the ipsilateral hemisphere only, encompassing regions such as the temporal pole (t₅₉ = 4.57, P_corr = 0.003), inferior temporal gyrus (t₅₉ = 4.45, P_corr = 0.004), amygdala (t₅₉ = 3.96, P_corr = 0.022), hippocampus (t₅₉ = 4.44, P_corr = 0.004), parahippocampal gyrus (t₅₉ = 5.33, P_corr = 2 × 10⁻⁴), and fusiform gyrus (t₅₉ = 5.30, P_corr = 2 × 10⁻⁴), as well as the isthmus of the cingulate gyrus (t₅₉ = 4.83, P_corr = 0.001; rest of the brain: |t₅₉| < 3.30, P_corr > 0.156) (Fig. 4B). Thus, analysis of randomly generated brain states yielded results matching those observed from ICN-defined brain states, supporting the notion that our preferential states appropriately represented the repertoire of empirical brain dynamics.

Biological validation of the brain’s energetic inefficiency in TLE

Through NCT, we have established that TLE is associated with energetic inefficiency during simulated brain dynamics, not only with respect to attaining preferential states but also in relation to transitions among them. Next, we sought to validate our findings using an independent measure of neurophysiological energy consumption, FDG-PET. FDG-PET is a common clinical investigation used for seizure focus localization and allows probing brain metabolism in vivo by measuring regional glucose uptake. Here, FDG-PET was acquired in a subset of 50 patients with TLE during their presurgical evaluation. In the absence of HC data as baseline, we used data from the contralateral hemisphere in the same patient as a reference (47). After confound regression, we generated a laterality index (LI) of glucose uptake for each region (see Materials and Methods for details). A negative LI indicated lower ipsilateral metabolism than contralateral, whereas a positive LI indicated higher ipsilateral metabolism than contralateral. This relative definition of hypometabolism versus hypermetabolism is commonly used in clinical settings (48). Leveraging this measure of metabolic integrity, we sought to identify the neurophysiological basis of the energetic inefficiency observed in our patients with TLE.

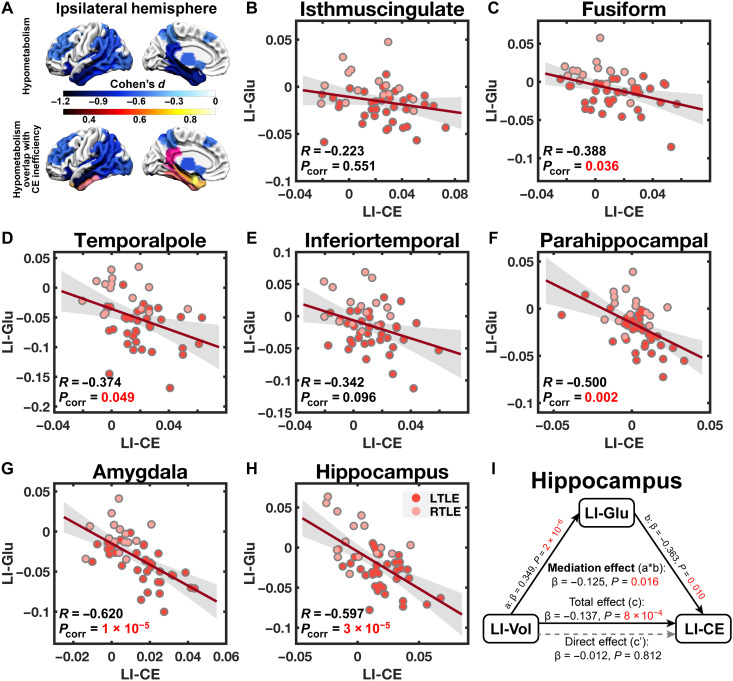
Our first and most straightforward observation was that all the regions with disrupted energetic profiles captured by our NCT analyses—ipsilateral temporal pole, inferior temporal gyrus, amygdala, hippocampus, parahippocampal gyrus, fusiform gyrus, and isthmus of cingulate gyrus—also exhibited ipsilateral hypometabolism (permutation-based one-sample t test correcting for multiple comparisons; Fig. 5A and table S1). To expound on this observation, we also calculated LIs of the regional MCE in these regions and tested bivariate correlations between the seven pairs of LIs (i.e., one for MCE and one for glucose uptake) with a permutation-based product-moment correlation controlling for multiple comparisons. We found significant correlations between LIs pairs at the temporal pole (R₄₉ = −0.37, P_corr = 0.049), amygdala (R₄₉ = −0.62, P_corr = 8 × 10⁻⁶), hippocampus (R₄₉ = −0.60, P_corr = 3 × 10⁻⁵), parahippocampal gyrus (R₄₉ = −0.50, P_corr = 0.002), and the fusiform gyrus (R₄₉ = −0.39, P_corr = 0.036) but not within the inferior temporal gyrus (R₄₉ = −0.34, P_corr = 0.096) or isthmus of cingulate gyrus (R₄₉ = −0.22, P_corr = 0.551) (Fig. 5, B to H). These results suggest that the regions where patients with TLE show greater control energy needs also show greater hypometabolism (i.e., lower metabolic baseline) with respect to their contralateral counterparts.

Fig. 5. Regional control energy consumption is associated with glucose metabolism in patients with TLE.

(A) Multiple comparisons–corrected one-sample t tests on LIs (with RTLE mirror-flipped to match the ipsilateral versus the contralateral side) of regional glucose uptake revealed widespread ipsilateral hypometabolism in reference to the metabolic levels in the contralateral hemisphere (top). Notably, all the ipsilateral temporolimbic regions with atypical energetic profiles also presented with hypometabolism (bottom). (B to H) Pearson correlations corrected for multiple comparisons revealed significant associations between the laterality of glucose uptake and control energy consumption during all the transitions between the states defined by ICNs, most prominently in the limbic regions, whereas the side with lower glucose metabolic baseline consumed more control energy. Note that LIs were not mirror-flipped for RTLE for the correlation analyses. Corrected P values (P_corr) are depicted. (I) A mediation analysis was performed on the hippocampus, where the association between the laterality of gray matter volume (LI-Vol) and control energy (LI-CE) was also found to be significant. We found that the laterality of glucose uptake (LI-Glu) provided a full mediation of the association between the former two variables. The significance of the mediation effect was assessed using bootstrapped confidence intervals.

One common reason for a region to exhibit hypometabolism is the loss of local structural integrity, as manifested by gray matter atrophy (49, 50). Accordingly, within the abovementioned regions, we also examined whether the LI of control energy was correlated with the LI of gray matter volume. We found a significant correlation between energy and volume LIs in the hippocampus only (R₄₉ = −0.47, P_corr = 0.005; all other regions had |R₄₉| < 0.32 and P_corr > 0.167). This finding indicated that greater gray matter volume loss in the hippocampus was associated with greater control energy needs. A bootstrapped mediation analysis focusing on the hippocampus found that the LI of glucose uptake provided full mediation of the association between the LI of gray matter volume and the LI of control energy (β = −0.125, P = 0.016; Fig. 5I). Thus, the loss of local structural integrity may serve as a substrate leading to a decline in baseline regional metabolism, which, in turn, engenders inefficient energetic control of brain dynamics.

Sensitivity analyses on the contributions of control energy in characterizing the brain’s energetic efficiency

Last, we conducted several sensitivity analyses to verify the contributions of control energy in characterizing the brain’s energetic efficiency. First, we evaluated the impact of the overall white matter health on our obtained results. White matter lesions are commonly detected with specific T2-weighted imaging sequences in the form of white matter hyperintensity (WMH). In the absence of these data, however, estimation of global WMH volume can still be obtained from the T1w image using the Computational Anatomy Toolbox (CAT12). Accordingly, we extracted estimates of WMH for each individual and regressed those estimates out of our control energy metrics. We then repeated our main analyses and found consistent results at every step (result S1). Therefore, changes to control energy metrics are mainly driven by changes to the dynamics occurring atop altered structural networks rather than being driven by overall white matter health.

Second, we explored whether similar findings can be obtained from conventional derivatives of the structural connectome and whether control energy provided unique information by comparison. We began by replacing the global OCE needed to activate each ICN with the connectivity strength of each ICN (i.e., the sum of all edge weights connected to all regions within each ICN) and compared the latter between patients with TLE and HCs, as we had in Fig. 2. We then replaced nodal MCE with nodal degree and strength and performed the same statistical analyses as those presented in Figs. 4 and 5. We found that, compared to the control energy findings, parallel results can be largely reproduced with the connectivity strength of the ICN, and with nodal strength but not with nodal degree (result S2 and tables S2 to S4). To determine whether control energy metrics accounted for unique variance, we formulated stepwise linear regression models and confirmed that, compared to these conventional connectomic metrics, control energy generally confers superior explanatory power both in differentiating patients from controls and in predicting the asymmetry of glucose metabolism (result S2 and table S5).

Third, we tested whether similar findings could be produced with other NCT metrics, such as average and modal controllability, and whether control energy provided unique information compared to them. Here, we replaced nodal MCE with average and modal controllability and performed the same statistical analyses reported in Figs. 4 and 5. We found significant patient-control differences in both average and modal controllability, which were in line with our control energy findings (result S3 and tables S6 and S7). However, only the laterality of modal controllability showed significant associations with the laterality of glucose metabolism (result S3 and table S8). Again, through stepwise linear regression models, we confirmed that the control energy is more sensitive to the effects of pathology and is a better predictor of brain metabolic asymmetry compared to controllability (result S3 and table S9).

DISCUSSION

NCT is a powerful approach to studying the brain’s energy landscape, as both supported and constrained by the underlying white matter connectivity architecture (6–10). In the absence of any external input (e.g., brain stimulation), the brain consumes metabolic resources to facilitate neural dynamics, and that process can be theoretically simulated by the NCT metric of control energy. However, the precise relation between biological energy and control energy remains to be elucidated. Here, we conceptualized TLE as a lateralized lesion model and investigated how disruptions in energetic efficiency during simulated brain state transitions are associated with pathological changes in regional glucose metabolism and structural integrity, thereby providing a neurophysiological correlate for control energy. We began by showing that patients with TLE required more control energy to activate the limbic network compared to HCs. In particular, this increased energy was localized to the limbic network ipsilateral to the patients’ seizure focus. Furthermore, we quantified regional energy profiles during transitions between different brain states and found that the mesial and inferior parts of the ipsilateral temporal lobe in TLE consumed more control energy on average than HCs. Intuitively, the extra energetic demands in these patients may result in suboptimal dynamics and inadequate activation, which, in turn, may eventually impair function. We demonstrated that the imbalance of energetic costs between the ipsilateral and contralateral mesial and inferior temporal regions was also mirrored in their asymmetric metabolic patterns, whereby regions with lower baseline metabolic levels also had higher energetic demands. Specifically, for the hippocampus, we found significant associations between lateralization of energy costs, glucose uptake, and gray matter volume, with hypometabolism fully mediating the increase in energy demand pertaining to volume loss on the ipsilateral side. In excavating these relations, our study uncovers the neurophysiological correlates of control energy, thereby paving the way for further application of this powerful framework in both health and disease.

In this study, we focused on two main categories of simulated brain state transitions. The first one probed the efficiency with which patients’ brains could attain each of eight ICN-defined preferential brain states from a common baseline. Compared to HCs, patients with TLE needed greater global control energy to activate the limbic network, especially its ipsilateral side. Thus, it is plausible that failing to meet these increased energy demands may underpin inadequate limbic activation and dysfunction. Considering the overlap between the limbic network and the seizure focus in TLE, dysfunction within this network may be expected in these patients. For instance, episodic memory deficits and affective comorbidities are commonly reported in TLE (23, 25) and can be reasonably attributed to limbic dysfunction. Previous imaging studies have shown that some limbic regions, such as the epileptogenic hippocampus, are less activated during episodic memory encoding in TLE (51–53). Last, altered functional connectivity seeded from the amygdala is also associated with comorbid psychiatric symptoms in these patients (54). In line with this evidence, our findings suggest that TLE is associated with compromised energetic efficiency of ipsilateral limbic regions.

Brain function depends on the ability to both reach desired brain states and swiftly transition among them. Therefore, our second set of analyses focused on modeling the brain’s capacity to transition between pairs of ICN-defined preferential states. Across all possible pairwise transitions, we found that patients with TLE exhibited elevated control energy requirements compared to HCs, again rooted in ipsilateral temporolimbic regions. These results suggest that disruption to the underlying structural networks of patients with TLE not only affects the activation of the limbic network but also leads to greater energy demands of ipsilateral temporolimbic regions during transitions among all ICN-defined states. Last, we sought to further validate our findings by testing 100,000 pairs of random brain states that were not a priori rooted in functional neuroanatomy. In doing so, we found near-identical results, demonstrating that the increased energy costs in the ipsilateral temporolimbic regions represent a general signature of dysfunctional control of neuronal dynamics in patients with TLE. Collectively, our study provides evidence that altered brain dynamics in TLE, as a pathological trait, are underpinned by energetic inefficiency that mostly affects areas in proximity or closely connected to the seizure focus and may represent a substrate of enduring brain dysfunction.

After establishing the validity of NCT for identifying energetic inefficiency rooted in the topology of the structure connectome and dynamics thereupon, we sought to provide further clarification regarding the neurophysiological basis of this trait. We know that the brain consumes energy via glucose metabolism (19), and previous studies have linked control energy to cognitive effort (14). Therefore, we hypothesized that the magnitude of control energy may reflect the extent of local metabolism needed to instantiate the desired neural dynamics. Using FDG-PET, we showed that regional energetic inefficiency coexists with altered metabolism in TLE. Specifically, we observed that reduced baseline glucose intake (i.e., hypometabolism) aligned, as clinically expected, with the side of seizure focus. Taking the contralateral hemisphere as reference, we found that greater ipsilateral hypometabolism was associated with greater ipsilateral energetic inefficiency. We thus highlight a formal link between theoretical control energy and a physiological measure of brain metabolism and suggest that the compromised metabolic baseline in affected regions may lead to greater energetic challenges in supporting desired brain dynamics. Regardless, we advocate for future work to establish whether glucose expenditure during a specific cognitive process can also be successfully tracked by control energy estimated during a simulation of the same dynamic process.

A common cause of metabolic alterations may be the loss of underlying structural integrity. For instance, concomitant gray matter volume loss and hypometabolism are reported in patients with TLE, especially in epileptogenic regions such as the hippocampus (55). In our patients with TLE, we found that gray matter volume asymmetry was also associated with energy asymmetry in the hippocampus. Through a mediation analysis, we formally demonstrated that the asymmetry of baseline metabolism fully mediates the association between the asymmetry of gray matter volume and energy costs. That is, greater volume loss may lead to greater baseline hypometabolism, thereby increasing energy demands during brain state transitions in the ipsilateral hippocampus. These results deliver a unifying framework, linking independently measured regional volumetrics, glucose metabolism, and network control properties derived from structural networks. Our work thus captures both the metabolic and volumetric bases of control energy, further supporting its application in modeling the endogenous resources consumed during brain dynamics in the absence of external stimulation. In addition, our work suggests that the magnitude of control energy is modulated not only by the transition trajectory (13–15) but also by the integrity of the underlying structure. Specifically, regions harboring pathology, such as the hippocampus in TLE, can exhibit different degrees of neural loss, causing a metabolic resource gap that, in turn, affects brain state transitions. Nonetheless, regional structural integrity may not be the only determinant of local metabolism and energetic demands. Local inhibitory circuitry (28, 56), or diaschisis due to connections from the pathological regions (56, 57), may affect local metabolism and energy consumption as well, even in the absence of local volume loss.

Prior work has demonstrated that NCT can provide insights unattainable by graph theory metrics, particularly regarding how the brain’s topological organization supports brain function (15, 16, 18, 58, 59). In line with these prior studies, here, we show through a series of sensitivity analyses that, compared to conventional descriptive connectomic metrics, control energy offers superior sensitivity to the effects of pathology and metabolic asymmetry. One likely explanation for this finding is that variation of degree and strength only reflects local topology, while control energy metrics capitalize on modeling the spread of dynamics and can thus better quantify the complex patterns of interindividual variations emerging from the full topology of the structural connectome (18). In addition, we find consistent associations between the lateralities of glucose metabolism and modal controllability, which further confirms our primary hypothesis that brain metabolism may serve as a biophysical substrate for network control. Notably, control energy and controllability capture distinct dimensions of variance, and control energy accounts for greater variance in brain metabolism than controllability.

Several methodological considerations are pertinent to this study. First, the structural connectome obtained via diffusion tractography used in our study is an approximation of the real structural scaffold of functional brain dynamics. Implementing other forms of structural connectivity, such as a spatial adjacency network, may provide added value to our model (13). Second, we modeled the neural dynamics under assumptions of linearity and time invariance, following previous studies (9, 10, 13, 15, 16). Recent research has shown that these simplified models can provide useful first-order approximations of brain dynamics (60, 61) and even outperform nonlinear models when predicting the macroscopic brain activity measured by functional MRI and intracranial electrocorticography (62). Nonetheless, further adaptations are expected to incorporate advanced features such as nonlinearity (63, 64) and time dependence (65). Third, as in previous studies (9, 10, 16), we defined a discrete set of brain states on the basis of ICNs known to underpin cognition (37, 39, 40). Alternatively, the magnitude of brain states could also be defined via empirically measured neurophysiological signals (14, 15, 17). However, the estimated energy costs in our model depend not only on the network structure but also on the distance between the initial and final states (15). Thus, by setting binary states uniformly, we ensured a consistent transition distance across all participants. Accordingly, the extent of energy costs only reflects the efficiency of the underlying network structure (or the lack thereof) during the same designated dynamic process. However, we acknowledge that epilepsy may not only compromise the brain dynamics that we seek to simulate here but also alter how brain regions coactivate and influence patterns of regional clustering into cohesive functional networks. Future NCT work capitalizing on personalized functional network topography (66) may provide more fine-grained, subject-specific descriptions of how the energetic processes are compromised in patients with epilepsy. Fourth, in the absence of PET data in HCs, we focused on ipsilateral hypometabolism relative to the contralateral hemisphere in patients. However, we note that imbalances might be attributed to metabolic abnormalities in either or both hemispheres. Future work should capitalize on HCs’ PET data to better disentangle hemisphere-specific associations between control energy and brain metabolism. Fifth, our TLE cohort was heterogeneous in etiology, which may raise the possibility of subgroup-specific energetic characteristics that were not addressed in the current study. Last, some antiseizure medications (ASMs) may affect brain dynamics (67); however, because of the heterogeneous regimen of ASM history in our patients, we did not focus on the relationship between ASMs and control energy profiles here. Similarly, while interictal epileptic discharges (IEDs) can transiently influence brain dynamics, their relevance to control energy warrants further investigation, as quantitative measures of IEDs were not available in this study.

In summary, our study capitalized on TLE as a disease model to deliver a unifying framework linking loss of structural integrity, alterations of local metabolism, and greater energetic demands to attain desired brain state transitions, leading to altered brain dynamics. By providing a neurophysiological basis of control energy, our work paves the way for further applications of NCT in the field of neuroscience.

MATERIALS AND METHODS

Participants

Sixty patients with refractory unilateral TLE (38 left-sided and 22 right-sided) were recruited from the Thomas Jefferson Comprehensive Epilepsy Center. Diagnosis was determined by a multimodal evaluation including neurological history and examination, interictal and ictal scalp video–electroencephalography, MRI, FDG-PET, and neuropsychological testing. Localization was determined after confirming that the testing was concordant for unilateral TLE, as described previously (68). Patients were excluded from the study for any of the following reasons: previous brain surgery, evidence for extratemporal or multifocal epilepsy by history or testing, contraindications to MRI, or hospitalization for any axis I disorder listed in the DSM-5 (Diagnostic and Statistical Manual of Mental Disorders V). Depressive disorders were admissible, given the high comorbidity of depression and epilepsy (69). The demographic and clinical characteristics of the patient groups are presented in Table 1, along with the demographic information of 50 age-, sex-, and handedness-matched HCs. All HCs were free of psychiatric or neurological disorders based on a health screening measure. This study was approved by the Institutional Review Board for Research with Human Subjects at the Thomas Jefferson University. All participants provided informed consent in writing.

Imaging acquisition

All participants were scanned on a 3-T X-series Philips Achieva clinical MRI scanner (Amsterdam, the Netherlands) at the Thomas Jefferson University Hospital. The data acquisition session included both a HARDI scan and a high-resolution T1w anatomical scan. The HARDI scan was 61-directional with a b value of 3000 s/mm² and repetition time (TR) = 7517 ms, echo time (TE) = 98 ms, in addition to 1 b0 images. The matrix size was 96 by 96 with a slice number of 52. The field of view (FOV) was 230 mm by 230 mm, and the slice thickness was 2.5 mm. Participants lay in a foam pad to comfortably stabilize the head and were instructed to remain still throughout the scan. Before collection of the HARDI scan, T1w images (180 slices) were collected using an magnetization-prepared rapid gradient-echo sequence (256 by 256 isotropic 1-mm voxels; TR = 640 ms, TE = 3.2 ms, flip angle = 8°, FOV = 256 mm by 256 mm) in identical positions to provide an anatomical reference. The in-plane resolution for each T1 slice was 1 mm³ (axial oblique).

As part of their presurgical evaluation, 50 patients also underwent on-site PET scans. The other 10 patients who received PET scans from other facilities (off-site), and HCs who did not receive PET scans, were excluded from the FDG-PET–related analysis. All PET scans were performed during interictal periods using a standard protocol. Preinjection blood glucose level was less than 150 mg/dl for all patients (range, 61 to 128 mg/dl). An intravenous catheter was inserted under local anesthesia, and a dose around 5.9 ± 1.4 mCi of radioactive FDG (100 mg/liter) was injected. The scan was initiated about 42 ± 15 min after the injection. Participants’ eyes were open, and their ears were nonoccluded. Ambient noise and light were kept to a minimum. Thirty-one patients (62% of patients; 20 LTLE and 11 RTLE) were scanned on a Siemens Biograph 1080 PET/CT, with data consisting of 109 axial slices, 3 mm thick, and 1 mm by 1 mm in resolution. The remaining 19 patients (38% of patients; 15 LTLE and 4 RTLE) were scanned on a Siemens Biograph 20 mCT PET/CT, with data consisting of 110 axial slices, 3 mm thick, and 1.6 mm by 1.6 mm in resolution. Attenuation-corrected PET images were iteratively reconstructed by standard vendor-provided software. There was no significant difference in the proportion of patients with LTLE and RTLE acquired with either scanner (χ² = 1.17, P = 0.28). Furthermore, we obtained asymmetry indices that use the same participant as reference, therefore reducing potential scanner-specific bias, as reported previously (47). This procedure also avoids confounds related to demographic factors, such as age, medication history, and epilepsy history (70, 71). Nevertheless, the scanner model was also used as a categorical nuisance regressor during the data analysis along with demographic information.

Imaging processing

The T1w and HARDI data were analyzed through QSIprep (v0.8.0; https://qsiprep.readthedocs.io) (72), which is based on Nipype 1.4.2. QSIprep automates diffusion MRI data preprocessing and reconstruction using well-recognized neuroimaging tools including Advanced Normalization Tools (ANTs), Analysis of Functional NeuroImages, FMRIB Software Library (FSL), DSI Studio, MRtrix3, and fMRIprep.

Anatomical data preprocessing

The T1w image was corrected for intensity nonuniformity using N4BiasFieldCorrection (ANTs 2.3.1) and was used as a T1w reference throughout the workflow. The T1w reference was then skull-stripped using antsBrainExtraction.sh (ANTs 2.3.1), using OASIS as the target template. Spatial normalization to the International Consortium for Brain Mapping (ICBM) 152 Nonlinear Asymmetrical template version 2009c was performed through nonlinear registration with antsRegistration (ANTs 2.3.1), using brain-extracted versions of both T1w volume and template. Brain tissue segmentation of cerebrospinal fluid, white matter, and gray matter was performed on the brain-extracted T1w using FMRIB’s Automated Segmentation Tool (FSL 6.0.3).

Diffusion data preprocessing

The HARDI image was first denoised using a Marchenko-Pastur principal components analysis method, underwent Gibbs-ringing artifacts removal, and then was spatially bias-corrected through MRtrix3. Subsequently, it was corrected for head motion and eddy current distortions via eddy_openmp (FSL 6.0.3). A deformation field to correct for susceptibility distortions was estimated on the basis of fMRIprep’s fieldmap-less approach. The deformation field was that resulting from co-registering the b0 reference to the same-subject T1w reference with its intensity inverted. Registration was performed with antsRegistration (ANTs 2.3.1), and the process was regularized by constraining the deformation to be nonzero only along the phase-encoding direction and was further modulated with an average fieldmap template. On the basis of the estimated susceptibility distortion, an unwarped b = 0 reference was calculated for a more accurate co-registration with the T1w reference, and then a final preprocessed HARDI image was produced in the native space of the T1w reference with an isotropic voxel size of 2 mm³. Two quality metrics were calculated on the basis of the preprocessed data, including framewise displacement (73) and neighboring correlation (74).

Diffusion data reconstruction and tractography

The preprocessed HARDI image was reconstructed via MRtrix3. Multitissue fiber response functions were estimated using the Dhollander algorithm, during which fiber orientation distributions (FODs) were estimated via constrained spherical deconvolution (CSD) using an unsupervised multitissue method. Specifically, a single-shell optimized multitissue CSD was performed using MRtrix3Tissue (https://3Tissue.github.io), a fork of MRtrix3. FODs were intensity-normalized using mtnormalize. Subsequently, an anatomically constrained probabilistic tractography was performed using the iFOD2 probabilistic tracking method, in which the white matter FODs were used for tractography and the T1w segmentation was used for anatomical constraints. For each participant, we generated 10⁷ streamlines with a maximum length of 250 mm, minimum length of 30 mm, and FOD power of 0.33. Weights for each streamline were calculated using a spherical deconvolution-informed filtering of tractograms (SIFT2) (75), which was then used to estimate the structural connectivity matrix.

Brain parcellation customization

Consistent with previous work (9), we chose the Lausanne parcellation scheme including n = 129 cortical and subcortical parcels (76) to build the structural network. This parcellation scheme is established by subdividing the Desikan-Killiany anatomical atlas. Specifically, to enable the proposed asymmetry analysis, we needed the parcellation to be symmetric. However, we noted that six regions have been subdivided asymmetrically, whereas the medial orbitofrontal gyrus, inferior parietal gyrus, and lateral occipital gyrus have one more subdivision in the right hemisphere, and the rostral middle frontal gyrus, precentral gyrus, and postcentral gyrus have one more subdivision in the left hemisphere. These additional subdivisions were subsequently merged with their corresponding neighbor to match their cross-hemisphere counterpart, producing a symmetric version of the parcellation constituted by 61 pairs of cortical and subcortical parcels (excluding brainstem; details in table S10). This parcellation was then inversely warped onto the native space of the T1w reference and resampled at 2-mm³ voxel resolution. Using tck2connectome (MRTrix3), allowing a 2-mm radial search from each streamline end point to locate the nearest node, we built a 122 by 122 undirected adjacency matrix for each participant with the SIFT2 weighted streamline counts representing interregional structural connectivity.

To define neurobiologically meaningful brain states, we capitalized on an established functional brain parcellation (77) of ICNs, which was defined by clustering the resting-state functional connectivity data from 1000 healthy participants (38). This parcellation is constituted by seven cortical ICNs that are commonly seen during both resting and task conditions (37, 39), including visual, somatomotor, dorsal attention, salience/ventral attention, limbic, executive control, and default mode networks. As in prior work (9), we mapped both parcellations to a common surface space (fsaverage) and calculated the proportional overlap of vertices between each parcel and each of the seven ICNs. Using a winner-take-all strategy, we assigned each parcel to the ICN with highest overlap proportion (Fig. 1B). In addition, subcortical regions were summarized into an eighth, subcortical network, except for the hippocampus and amygdala, which were assigned to the limbic network following the common clinical definition. These eight nonoverlapping networks were used as representative brain states during simulations of brain state transitions. The rationale of defining brain state with these ICNs is discussed in method S1.

FDG-PET data preprocessing

PET images were preprocessed with Statistical Parametric Mapping 12 (SPM 12; www.fil.ion.ucl.ac.uk/spm/software/spm12). Briefly, the PET image was first co-registered to the T1w reference image, smoothed with a 6-mm kernel, and intensity-normalized by the global mean uptake estimated on the basis of a skull-striped brain mask derived from the T1w reference image. Regional mean glucose uptake was subsequently estimated on the basis of the same parcellation. As stated, in the absence of PET data from HC, we calculated the LI (${\text{LI}}_i=\frac{L_i-R_i}{L_i+R_i}$) of regional glucose uptake from the aforementioned 61 pairs of parcels for the subsequent analyses.

Regional gray matter volume estimation

Last, we obtained regional mean gray matter volumes using the CAT12 (v12.7; www.neuro.uni-jena.de/cat/). The T1w image was first denoised with a spatial adaptive nonlocal means denoising filter, followed by internal resampling to properly accommodate low-resolution images and anisotropic spatial resolutions. Subsequently, the data were bias-corrected and affine-registered followed by the standard SPM “unified segmentation.” The brain was then parcellated into left and right hemispheres, subcortical areas, and the cerebellum. Furthermore, local white matter hyperintensities were detected to be later accounted for during the spatial normalization. Subsequently, a local intensity transformation of all tissue classes was performed, and a final adaptive maximum a posteriori segmentation was then refined by applying a partial volume estimation, which effectively estimated the fractional content for each tissue type per voxel. Last, the tissue segments were spatially normalized to a common reference space using Geodesic Shooting registration, so that the regional gray matter volume could be estimated on the basis of the same parcellation. In addition, the total intracranial volume and a summary image quality rating for each T1w image were exported and were used as covariates.

Brain state transitions simulated through linear NCT

Theoretical framework of linear NCT

To investigate whether TLE is associated with compromised efficiency of common brain dynamics, we leveraged recent developments of linear NCT and explored the energetic efficiency of the structural brain network in facilitating designated brain state transitions. The following equations have been derived and reported in previous work (9, 10, 13, 15, 16); we report them here to clarify precisely how NCT was used in our analyses and simulations.

As in previous work (9, 10, 13, 15, 16), we used a simplified noise-free linear and time-invariant network model to describe the dynamics of the brain

$$\stackrel{·}{x}=\mathit{Ax}(t)+\mathit{Bu}(t)$$ (1)

Here, x(t) is an N × 1 vector that represents the state (i.e., activity level) of each node of the system at time t (N = 122). A is an N × N adjacency matrix denoting the relationship between the system elements, which can be operationalized as the structural brain network. To ensure the stability of the system, A is normalized as follows (13)

$$A_{\text{norm}}=\frac{A}{\Vert \mathrm{\lambda }{(A)}_{\text{max}}\Vert +1}-I$$ (2)

whereas λ(A)_max denotes the largest positive eigenvalue of the system and I denotes the N × N identity matrix. Subtracting this identity matrix ensures that internal dynamics decay for each node, thereby stabilizing the system to prevent its infinite growth. B is the input matrix that identifies the nodes in the control set. Here, we set B to be the N × N identity matrix to set all the brain parcels as control nodes where energy can be consumed to facilitate brain state transitions. Last, u(t) denotes the amount of energy injected into each control node at each time point t. Intuitively, u(t) can be summarized over time to represent the total energy consumption during transition from an initial state to a final state.

Simulation I: Individual ICN activation

In our first simulation, we considered the scenario that the brain transits from an initial baseline state (x₀ = x(t = 0)) to a final state (x_T = x(t = T)) when a specific ICN is predominantly activated. We modeled this control task by setting

$$x_i(t=0)=0,i=1,\dots ,122$$

and

$$x_i(t=T)=\{\begin{array}{cc}0,& \text{if} i\notin {\text{ICN}}_k\\ 1,,& \text{if} i\in {\text{ICN}}_k\end{array}, k=1,\dots ,8$$

Note that, theoretically, setting the initial state to full zeros does not necessarily mean that the brain is globally inactive, which is biologically impossible. Rather, it can be viewed as a mean-centered baseline, and the final state has additional activations within the specific ICN than other regions by 1 arbitrary unit. This setting is analogous to task functional MRI analyses, where contrasts are commonly set between a condition of interest (1) and a baseline (0) (16).

To explore the energetic efficiency of the structural brain network in facilitating the activation of specific ICNs, we adopted the optimal control framework to estimate the control energy required to optimally steer the brain through these state transitions (15, 16). Against a naturalistic trajectory, when the brain state drifts without any control input, the proposed state transition commonly relies on the additional control input u(t) to reach the desired final state. This control effort can be intuitively understood as an internal cognitive control process (or as external brain stimulation in other patient scenarios), and it is based on both the energy costs and the length of the transition trajectory (13). Therefore, an optimal solution can be described as the minimized combination of both the length of the transition trajectory and the required control energy, during the state transition from an initial state (x(0) = x₀) to the final state (x(T) = x_T) over the time horizon T [see (10, 78)]

$$\begin{array}{cc}\hfill u(t)*& =\underset{u}{\text{argmin} J(u)}\hfill \\ & =\underset{u}{\text{argmin}}{\displaystyle {\int }_0^T}({(x_T-x(t))}^{\top }S(x_T-x(t))+\mathrm{\rho }u{(t)}^{\top }u(t))\mathit{dt}\hfill \end{array}$$ (3)

where (x_T − x(t))^⊤(x_T − x(t)) is the distance between the state at time t and the final state x_T, T is the finite amount of time given to reach the final state, and ρ is the relative weighting between the cost associated with the length of the transition trajectory and the input control energy. Following a previous benchmarking study (13), we set T = 3 and ρ = 1, allowing 1000 steps of transition from the initial state to the final state. To minimize the unintended energy cost on regulating the regions of no interest (i.e., those outside of the target ICN), we applied a constraint matrix S, which is an N × N binary diagonal matrix that selects only regions that are members of the target ICN. Accordingly, the term (x_T − x(t))^⊤S(x_T − x(t)) specifically constrains the trajectories of all regions within the target ICN, and the term u(t)^⊤u(t) constrains the amount of control energy used to reach the final state. The cost function J(u(t)*) is used to solve the unique optimal control input u(t)*. Specifically, we define a Hamiltonian as

$$H(p,x,u,t)={(x_T-x)}^{\top }S(x_T-x)+\mathrm{\rho }{u}^{\top }u+p(\mathit{Ax}+\mathit{Bu})$$ (4)

According to the Pontryagin minimization principle (78), if u* is a solution with the optimal trajectory x*, then there exists a p* such that

$$\begin{array}{c}\frac{\mathrm{\partial }H}{\mathrm{\partial }x}=-2S(x_T-x^{*})+A^{\top }{p}^{*}=-{\stackrel{·}{p}}^{*},\\ \frac{\mathrm{\partial }H}{\mathrm{\partial }p}={\mathit{Ax}}^{*}+\mathit{Bu},\\ \frac{\mathrm{\partial }H}{\mathrm{\partial }u}=2\mathrm{\rho }{u}^{*}+B^{\top }{p}^{*}=0\end{array}$$ (5)

From this set of equations, we can derive that

$$u^{*}=-\frac{1}{2\mathrm{\rho }}{B}^{\top }{p}^{*}$$ (6)

$${\stackrel{·}{x}}^{*}={\mathit{Ax}}^{*}-\frac{1}{2\mathrm{\rho }}{\mathit{BB}}^{\top }{p}^{*}$$ (7)

which can be reduced to

$$\left[\begin{array}{c}{\stackrel{·}{x}}^{*}\\ {\stackrel{·}{p}}^{*}\end{array}\right]=\left[\begin{array}{cc}A& -\frac{1}{2\mathrm{\rho }}{\mathit{BB}}^{\top }\\ -2S& -A^{\top }\end{array}\right]\left[\begin{array}{c}{x}^{*}\\ p^{*}\end{array}\right]+\left[\begin{array}{c}0\\ 2S\end{array}\right]x_T$$ (8)

If we denote

$$\tilde{A}=\left[\begin{array}{cc}A& -\frac{1}{2\mathrm{\rho }}{\mathit{BB}}^{\top }\\ -2S& -A^{\top }\end{array}\right]$$

$$\tilde{x}=\left[\begin{array}{c}{x}^{*}\\ p^{*}\end{array}\right]$$

$$\tilde{b}=\left[\begin{array}{c}0\\ 2S\end{array}\right]x_T$$

then this reduced Eq. 8 can be rewritten as

$$\dot{\tilde{x}}=\tilde{A}\tilde{x}+\tilde{b}$$

and can be solved as

$$\tilde{x}(t)=e^{\tilde{A}t}\tilde{x}(0)+{\tilde{A}}^{-1}(e^{\tilde{A}t}-I)\tilde{b}$$ (9)

Then, by fixing t = T, we arrive at

$$\tilde{x}(T)=e^{\tilde{A}T}\tilde{x}(0)+{\tilde{A}}^{-1}(e^{\tilde{A}T}-I)\tilde{b}$$ (10)

We let

$$c={\tilde{A}}^{-1}(e^{\tilde{A}T}-I)\tilde{b}$$

$$e^{\tilde{A}T}=\left[\begin{array}{cc}{E}_{11}& E_{12}\\ E_{21}& E_{22}\end{array}\right]$$

so that Eq. 10 can be rewritten as

$$[\begin{array}{c}{x}^{*}(T)\\ p^{*}(T)\end{array}]=\left[\begin{array}{cc}{E}_{11}& E_{12}\\ E_{21}& E_{22}\end{array}\right]\left[\begin{array}{c}{x}^{*}(0)\\ p^{*}(0)\end{array}\right]+\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right]$$

from which we can obtain

$$x^{*}(T)=E_{11}{x}^{*}(0)+E_{12}{p}^{*}(0)+c_1$$ (11)

Moreover, if we let $\overline{S}=I-S$, then as a known result in optimal control theory (11), $\overline{S}{p}^{*}(T)=0$. Therefore

$$\overline{S}{p}^{*}(T)=\overline{S}{E}_{21}{x}^{*}(0)+\overline{S}{E}_{22}{p}^{*}+\overline{S}{c}_2=0$$ (12)

Last, p*(0) can be solved for as follows

$$p^{*}(0)={\left[\begin{array}{c}{\mathit{SE}}_{12}\\ \overline{S}{E}_{22}\end{array}\right]}^{+}(-[\begin{array}{c}{\mathit{SE}}_{11}\\ \overline{S}{E}_{21}\end{array}]x^{*}(0)-[\begin{array}{c}{\mathit{Sc}}_1\\ \overline{S}{c}_2\end{array}]+[\begin{array}{c}\mathit{Sx}(T)\\ 0\end{array}\left]\right)$$ (13)

where [∙]⁺ indicates the Moore-Penrose pseudo-inverse of a matrix. Now that we have obtained p*(0), we can use it and x(0) to solve for $\tilde{x}$ via forward integration based on Eq. 9. To solve for u^*, we take p* from our solution for $\tilde{x}$ and solve Eq. 6. In particular, the OCE injected at each region i can be defined as

$$E_i^{*}={\displaystyle {\int }_0^T}{\Vert u_i^{*}(t)\Vert }^2\mathit{dt}$$ (14)

or given in total

$$E_{\text{opt}}^{*}={\displaystyle \sum _{i=1}^m}{E}_i^{*}={\displaystyle {\int }_0^T}{u}^{*}{(t)}^{\top }{u}^{*}(t)\mathit{dt}$$ (15)

This total OCE consumption $E_{\text{opt}}^{*}$ is then used as a measure of efficiency of the structural brain network during specific ICN activations.

Simulation IIa: Between ICN transitions

In our second simulation, we investigated the regional energetic consumption associated with facilitating brain dynamics. While it is computationally impossible to simulate all brain transitions, we considered two sets of finite repositories instead. First, we used the eight ICN-defined representative brain states (i.e., the x_T in the “Simulation I: Individual ICN activation” section) and explored all the possible transitions among them (9). Counting scenarios of both reciprocal transitions and single-state persistence (i.e., x₀ = x_T), this simulation resulted in a total of 64 control tasks. Considering the linear nature of our dynamical model, theoretically, any possible transition can be written as a linear combination of the proposed transitions (9). Thus, this simulation is generally relevant to all transitions represented during common brain dynamics.

We further alleviated the constraint on the length of the transition trajectory in our model to allow the brain to travel more freely across different intermediate states. Specifically, we adopted a subform of the optimal control framework, namely, the MCE, which can be obtained by letting ρ → ∞ in Eq. 3, so that the cost function J accounts only for the control input to facilitate the designated transition regardless of the trajectory (13). Accordingly, the MCE during the state transition from an initial state (x(0) = x₀) to the final state (x(T) = x_T) over the time horizon T can be described as (2, 13, 17)

$$u(t)*=\underset{u}{\text{argmin} J(u)}=\underset{u}{\text{argmin}}{\displaystyle {\int }_0^T}u{(t)}^{\top }u(t)\mathit{dt}$$ (16)

To solve the MCE u(t)* this time, we compute the controllability Gramian W for controlling the network A from the control node set B in Eq. 1 as

$$W={\displaystyle {\int }_0^T}{e}^{\mathit{A}(\mathit{T}-\mathit{t})}{\mathit{B}\mathit{B}}^{\top }{\mathit{e}}^{{\mathit{A}}^{\top }(\mathit{T}-\mathit{t})}\mathit{dt}$$ (17)

where, as defined previously, A is the normalized N × N structural brain network, B is an N × N identity matrix setting all the brain parcels as control nodes, and T is the finite time horizon of the transition trajectory. Similarly, we set T = 3 and allow for 1000 steps of transition from the initial state to the final state following (13). Then, the u(t)* can be computed as

$$u(t)*={\mathit{B}}^{\top }{e}^{{\mathit{A}}^{\top }(T-t)}{W}^{-1}(x(T)-e^{\mathit{A}\mathit{T}}x(0))$$ (18)

and the MCE injected at each region i can be calculated on the basis of Eq. 14. Last, for each brain region, we averaged their MCE across the 64 control tasks as a measure of their individual energetic consumption during dynamics among known ICNs.

Simulation IIb: Random brain state transitions

The second set of finite repositories of brain states included 100,000 pairs of randomly generated initial and final brain states x_rand with a Gaussian distribution at mean(x_rand) = 1 and std(x_rand) = 0.1 (16). Accordingly, this simulation resulted in a total of 100,000 control tasks, which served as an approximation of all transitions when no prior preference of brain states is explicitly defined. On the basis of our previous argument of the linear nature of the model, we were not expecting significant difference between our previous simulation IIa and this simulation IIb. Rather, we expected to observe a consistency between the two, which would serve as a validation of simulation IIa. Similarly, we adopted the same minimal control framework, and for each brain region, we calculated and summarized their MCE across the 100,000 control tasks as the measure of their individual energetic consumption during brain dynamics among randomly organized brain networks.

Statistical inferences

Comparisons for common demographic and clinical information were made with standard parametric tests such as an independent t test or chi square test, conducted using IBM SPSS v25. The α level was set at P < 0.05 for both parametric and nonparametric tests.

Confounding factor regression

To minimize the influence of individual variances of the demographic characteristics and imaging data qualities (Table 1), confounding factor regressions were applied before statistical inferences on our neuroimaging data. Specifically, for derivates from all imaging modalities, four potential confounding factors were identified and included in the models: age, sex, handedness, and total intracranial volume. Furthermore, additional confounding factors were added to the models for different modalities: (i) for HARDI derivates (i.e., control energy), the neighboring correlation, mean framewise displacement, matrix density, and total weight were added; (ii) for T1w derivates (i.e., regional gray matter volume), the image quality rating was added; and (iii) for FDG-PET derivates (i.e., regional glucose uptake), the PET scanner model was added. For each modality, all confounding factors were regressed out from their derivates with one linear regression model, and the residuals were taken for subsequent statistical analyses.

Permutation-based nonparametric statistical testing

To minimize the bias of the data distribution to our statistical inference and to correct for multiple comparisons, we implemented a permutation-based method as our main statistical strategy (43). Individual permutation-based statistical testing allows inference of the probability of the observed statistic (e.g., t value and r value), from a distribution of the same statistic estimated from massive instances of the same samples with their group identities permuted (79). In many cases, we wish to apply a permutation-based test to scenarios with multiple comparisons, i.e., comparing multiple within-subject variables across the same groups of subjects. In this case, we can expand the traditional approach by applying a “t_max” principle to adjust the estimated P values of each variable for multiple comparisons by controlling the family-wise error rate (44). Briefly, the observed statistic for each variable is compared to the distribution of the most extreme statistic across the entire family of tests for each possible permutation. This procedure corrects for multiple comparisons, because the distribution of the most extreme statistics automatically adjusts to reflect the increased chance of false discoveries due to an increased number of comparisons (43). We performed 1,000,000 permutations each time to ensure high precision during P value estimation (46). This strategy was applied on all analyses (i.e., t tests and product-moment correlations) when multiple comparison correction was required.

To increase statistical power (41, 45, 46), the regional control energy values of the patients with RTLE were flipped left to right, allowing all statistical analyses to be conducted in accordance with the site of ictal onset (left, ipsilateral; right, contralateral). However, as there was no way to flip HC data to match the ipsilateral versus contralateral side in the patients with RTLE, we instead calculated the deviation score of regional energy [Z_pat = (E_pat − μ_con)/σ_con, where μ_con and σ_con were the mean and SD of the same regional energy from the HC] for each patient at each hemisphere and flipped the Z score of RTLE afterward (41, 46). Then, Z scores were evaluated via a permutation-based one-sample t test.

Permutation-based mediation analysis

To disentangle the associations among regional gray matter volume change, glucose metabolism, and control energy consumption in the hippocampus, we applied a mediation analysis to test the hypothesis that the regional metabolic baseline, as a measure of functional integrity, mediated the relationship between local structural integrity and energetic efficiency. After confound regression, we generated the laterality indices for gray matter volume, glucose uptake, and MCE estimated during cross-ICN transitions. We then evaluated the significance of the indirect effect using bootstrapped confidence intervals via the MediationToolbox (https://github.com/canlab/MediationToolbox). Specifically, we examined (i) path c: the total effect of the LI of gray matter volume on the LI of MCE; (ii) path a: the relationship between the LI of gray matter volume and the LI of glucose uptake; (iii) path b: the relationship between the LI of glucose uptake and the LI of MCE; and (iv) path c′: the direct effect of the LI of gray matter volume on the LI of MCE while controlling for the mediator (LI of glucose uptake). The mediation/indirect effect a*b is the effect size of the relationship between the LI of gray matter volume and the LI of MCE that was reduced after controlling for the mediator (LI of glucose uptake). For each path, we calculated the β coefficient, which reflected the changes of the outcome for every one-unit change in the predictor. A bootstrap analysis (i.e., resampled 1,000,000 times) was implemented to estimate the confidence intervals for the indirect effect.

Citation diversity statement

Recent work in several fields of science has identified a bias in citation practices such that papers from women and other minority scholars are undercited relative to the number of such papers in the field (80–88). Here, we sought to proactively consider choosing references that reflect the diversity of the field in thought, form of contribution, gender, race, ethnicity, and other factors. First, we obtained the predicted gender of the first and last author of each reference by using databases that store the probability of a first name being carried by a woman (84, 89). By this measure (and excluding self-citations to the first and last authors of our current paper), our references contain 11.56% woman (first)/woman (last), 22.12% man/woman, 22.12% woman/man, and 44.2% man/man. This method is limited in that (i) names, pronouns, and social media profiles used to construct the databases may not, in every case, be indicative of gender identity and (ii) it cannot account for intersex, nonbinary, or transgender people. Second, we obtained predicted racial/ethnic category of the first and last authors of each reference by databases that store the probability of a first and last name being carried by an author of color (90, 91). By this measure (and excluding self-citations), our references contain 11.17% author of color (first)/author of color (last), 14.42% white author/author of color, 25.78% author of color/white author, and 48.64% white author/white author. This method is limited in that (i) names and Florida voter data to make the predictions may not be indicative of racial/ethnic identity and (ii) it cannot account for Indigenous and mixed-race authors or those who may face differential biases because of the ambiguous racialization or ethnicization of their names. We look forward to future work that could help us to better understand how to support equitable practices in science.

Supplementary Materials

This PDF file includes:

Supplementary Methods S1

Supplementary Results S1 to S3

Tables S1 to S10

References

View/request a protocol for this paper from Bio-protocol.