Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2022 Nov 9;12:19141. doi: 10.1038/s41598-022-22058-7

The first space-filling polyhedrons of polymer cubic cells originated from Weaire-Phelan structure created by polymerization induced phase separation

Naofumi Naga 1,2,✉, Masumi Jinno 2, Yuting Wang 3, Tamaki Nakano 3,4,✉
PMCID: PMC9646714  PMID: 36351975

Abstract

The Weaire–Phelan structure is a three-dimensional structure composed of two different polyhedra having the same volume, i.e., pyritohedron and truncated hexagonal trapezohedron. It was proposed by Weaire and Phelan in 1993 as a solution of the Kelvin problem of filling space with no gaps with cells of minimum surface area and equal volume. It was found in physical systems including liquid foam and a metal alloy while it has never been constructed as organic materials. We report herewith the first polymeric Weaire–Phelan structure constructed through phase-separation of a single polymer species that is synthesized by simple polyaddition between tetrakis(3-mercaptopropionate) and 1,6-diisocyanatohexane. The structure has the order of micrometers and is amorphous unlike reported crystal structures similar to the Weaire–Phelan structure.

Subject terms: Chemistry, Materials science

“Tessellation of space into cells of equal volume with the least surface area” has been referred to as the Kelvin problem from the nineteenth century. In 1887, Lord Kelvin proposed a convex uniform honeycomb formed by a bi-truncated octahedron1. This form is called “Kelvin structure” and has been widely believed as the most efficient form in tessellation2. After more than 100 years later, Weaire and Phelan discovered a more efficient form, so called “the Weaire-Phelan structure”, by computer simulations3. The Weaire-Phelan structure is composed by two kinds of cells with equal volume. One is a tetrakaidecahedron with two hexagonal and twelve pentagonal phases, and the other is an irregular dodecahedron with pentagonal faces. The arrangement of 3/4 of the tetrakaidecahedron cells and 1/4 of the dodecahedron cells in a specific way forms the Weaire-Phelan structure.

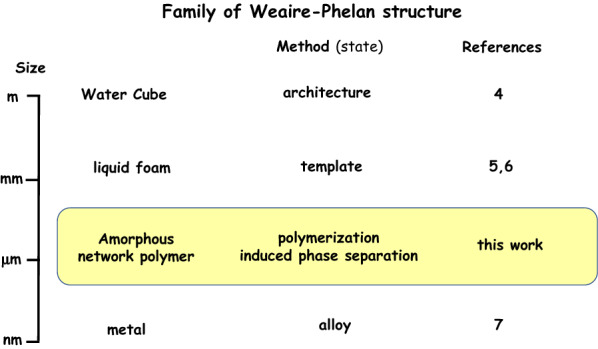
The family of the Weaire-Phelan structure is summarized in Fig. 1. The Weaire-Phelan structure inspired the architecture design of Beijing National Aquatics Center, called ‘Water Cube’, for the 2008 Summer Olympics4. The Weaire-Phelan structure has been found in physical materials only in two cases, i.e., liquid foam with the order of millimeters in size made from a detergent solution5,6 and a Pd-Pb alloy7. However, it has never been constructed for organic materials including polymer, especially, single-component polymeric material. The highly ordered three-dimensional structure in polymeric materials could open a way to novel function. In this work, we successfully constructed a Weaire-Phelan structure using a network polythiourethane through polymerization-induced phase separation forming closely packed uniform particles of the order of micrometer for the first time. The polymer was synthesized by simple polyaddition reaction between tetrakis(3-mercaptopropionate) (PEMP), a multi-functional primary thiol compound as a “joint” source monomer, and hexamethylene diisocyanate (HDI), a diisocyanate as a “linker” source monomer, in the presence of triethyl amine (TEA) as a base catalyst in toluene (Fig. 2a).

Figure 1.

Figure 1

Open in a new tab

Family of Weaire-Phelan structure.

Figure 2.

Figure 2

Open in a new tab

(a) Synthetic scheme of network polymers through the addition reaction of PEMP and HDI in toluene, and photos and images of the polymers, (b) Photos of PEMP-HDI network polymers from the reaction systems at monomer concentrations in the reaction systems of sample 1 (left): 25 wt%, sample 2 (center): 30 wt%, and sample 3 (right): 35 wt%, SEM images of PEMP-HDI network polymers (c) 25 wt% (sample 1), (d) 30 wt% (sample 2), and (e)–(g) 35 wt% (sample 3).

Crystal or mesophase structures with some similarity to the Weaire-Phelan structure and with sizes of tens of nanometers are known, for examples, Type I clathrate structure for alkali metal silicides and germanides8 and for gas hydrates composed of methane, propane and carbon dioxide9, and a Frank-Kasper phase (FK A15) of some self-assembled organic molecules such as dendritic liquid crystals, block copolymers, and giant surfactants10–15. However, organic amorphous materials having the Weaire-Phelan structure are unprecedented. The polymer Weaire-Phelan structure we report here is characterized by amorphousness and the size of the order of micrometers prepared by very facile synthetic procedures.

The synthetic methodology employed in this work is based on the “joint-and-linker” concept. The addition reaction between a multi-functional monomer as a source of “joint” (“joint”-source monomer) and α,ω-bifunctional monomer as a source of “linker” (“linker-source monomer) forms polymer network16–24. The joint-and-linker synthesis so far reported often preferentially yielded porous polymers by polymerization-induced phase separation via spinodal decomposition. When the porous structure is fixed at an early stage of spinodal decomposition, a monolithic structure composed of co-continuous structure of polymer backbone and vacant space is produced. While isolated particles are generated at a later stage, and aggregated particles are formed upon an increase in the polymerization rate. The size and morphology of porous structure are decided by the ratio of the polymerization (network formation) rate to the phase separation rate. The relative ratio can be controlled by designing monomers and catalysts to tune reactivity and by considering miscibility between the polymer network and the solvent25–34.

The addition reaction between PEMP and HDI was conducted at monomer concentrations of 25, 30, and 35 wt%, {(PEMP + HDI)/(PEMP + HDI + Toluene)}*100 = 25, 30, and 35 wt% ([PEMP] = 0.28, 0.34, and 0.40 M), resulting in samples 1, 2, and 3, respectively, in toluene in the presence of TEA as catalyst at room temperature at a feed ratio of [PEMP]/[HDI] = 1/2 ([–NCO] = [–SH]) and at a ratio of [TEA]/[–SH] = 1/100. All the reaction mixtures quickly turned opaque within a few minutes of the catalyst addition and yielded network polymers as shown in Fig. 2b. In the FT-IR spectra of the PEMP-HDI network polymer, the absorption peak based on –NCO group at 2250 cm-1 almost completely disappeared and a peak based on thiol-urethane bond emerged at 3300 cm-1 (Fig. S1), supporting the intended reaction mechanism. Wide-angle x-ray diffraction patterns of the polymers showed only broad halo profiles, revealing that the polymers are amorphous.

The scanning electron microscopy (SEM) images of the PEMP-HDI network polymers are shown in Figs. 2c–e. The polymer obtained at a monomer concentration of 25 wt% (sample 1) showed a morphology composed of particles with spherical shapes and fused spherical shapes with a diameter of about 1.5 µm (Fig. 2c). The reaction at a monomer concentration of 30 wt% also produced spherical particles with slightly larger diameters than those in sample 1 (sample 2, Fig. 2 d) where the particles appeared more densely accumulated than those in sample 1. It is noteworthy that the surface of the particles sample 2 were slightly truncated. On the other hand, the sample obtained at a monomer concentration of 35 wt% (sample 3) clearly exhibited space-filling polyhedron particles with pentagon and hexagon faces on the surface which may correspond to the polyhedrons the Weaire-Phelan structure. Isolated particles of the PEMP-HDI network polymer of sample 3 appeared distorted tetrakaidecahedron and dodecahedron units of the Weaire-Phelan structure, in (Figs. 2 e,f,g and Fig. 3). The bulk density of the PEMP-HDI network polymer increased with an increase in the monomer concentration of the reaction system, i.e., 0.808 g/cm3 (sample 1), 0.861 g/cm3 (sample 2), and 1.094 g/cm3 (sample 3), respectively.

Figure 3.

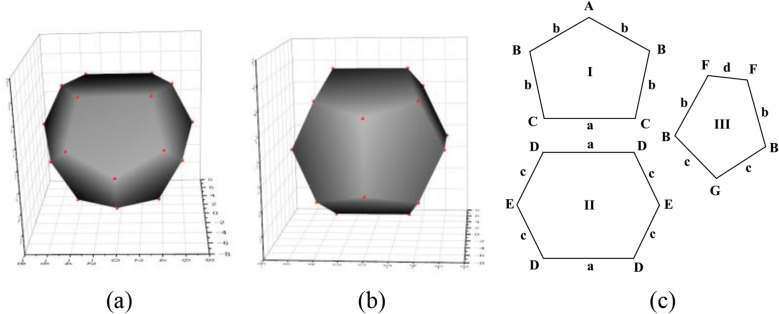
Figure 3

Open in a new tab

(a) Tetrakaidecahedron, (b) dodecahedron polyhedrons, and (c) pentagon and hexagon structures in the theoretical Weaire-Phelan structure.

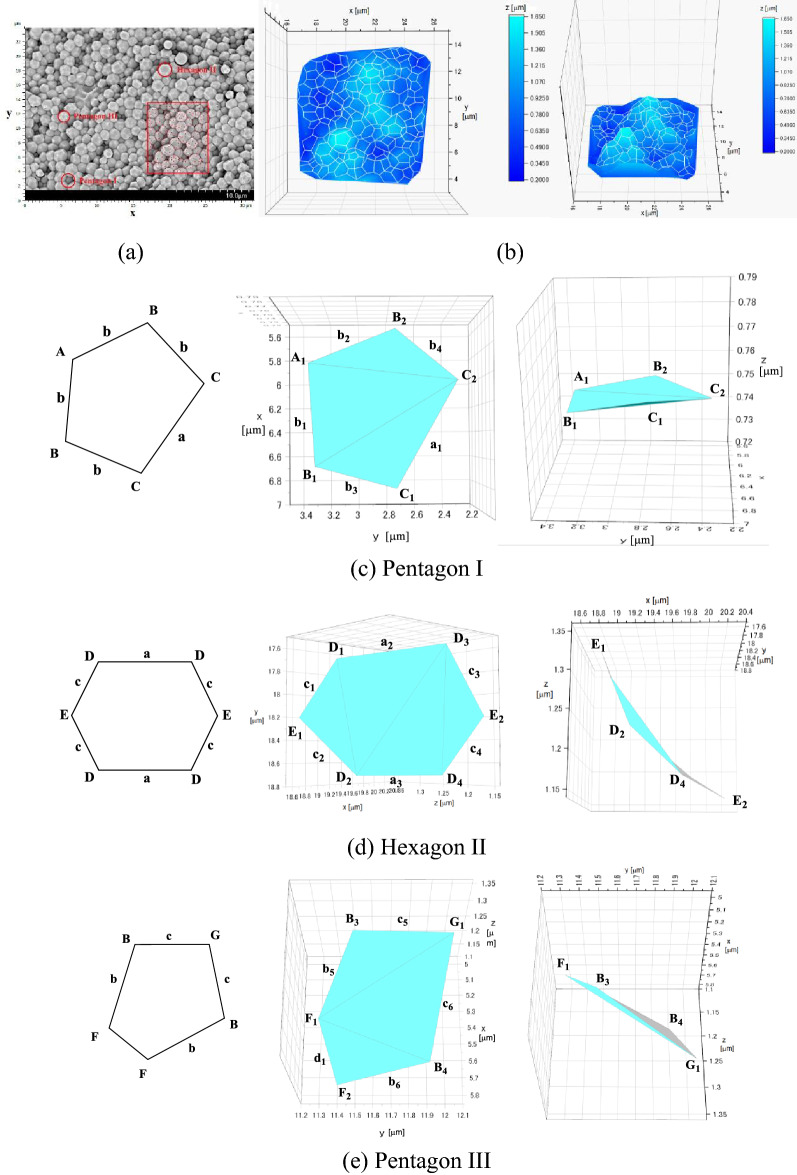
The polyhedron structure of sample 3 was further studied by 3D SEM in more detail (Fig. 4). Space-filling polyhedrons with structures exactly matching those of the polyhedrons of the Weaire-Phelan structure were clearly detected. Figure 4b shows the plots of the structures reproduced based on the three-dimensional coordinates of the vertices of particles, observed in the rectangular frame of the 3D SEM image (Fig. 4a) of the surface of the PEMP-HDI polymer sample 3. The bird's eye views of PEMP-HDI polymer clearly indicated that the three-dimensional polyhedron particles with micrometer-order sizes were formed over the surface of sample 3.

Figure 4.

Figure 4

Open in a new tab

(a) A 3D SEM image, (b) bird’s eye views of the PEMP-HDI polymer of sample 3, 3D plots of (c) Pentagon I, (d) Hexagon II, and (e) Pentagon III.

The theoretical Weaire-Phelan structure without any anisotropy is composed of two pentagons and one hexagon structures as shown in Fig. 3c. From this view, the structures of the polyhedrons observed on the surface of sample 3 were quantitatively examined. Figures 4c–e compare the pentagon structure I, hexagon structure II, and pentagon structure III extracted from the 3D SEM image as marked in red in Fig. 4a with the corresponding theoretical structures in Fig. 3c. The side lengths and angles of the polygons in Fig. 4 were calculated from the coordinate points in the 3D SEM image, which are available in supporting information. The numerical data of the side lengths and angles of the polygons from the observed structures and those from the theoretical structures are summarized in Table. 1.

Table 1.

Structure comparison of polyhedrons observed in 3D SEM with theoretical structure in the Weaire-Phelan structure.

Sides & angles a Side length µm Length ratio b Theoretical
length ratio		 Angle
º		 Theoretical
angle º		 Error
%
Pentagon I
a1 (µm) 0.92 1.07a’ 1a  + 7.1
b1 (µm) 0.79 0.92a’ 0.76a  + 21.0
b2 (µm) 0.64 0.75a’ 0.76a − 1.3
b3 (µm) 0.55 0.64a’ 0.76a − 15.8
b4 (µm) 0.57 0.66a’ 0.76a − 13.2
A1 (º) 110.5 121.6 − 9.1
B1 (º) 113.0 106.6  + 6.0
B2 (º) 110.4 106.6  + 3.6
C1 (º) 105.7 102.6  + 3.0
C2 (º) 100.3 102.6 − 2.2
Hexagon II
a2 (µm) 0.80 0.89a’’ 1a − 11.0
a3 (µm) 0.82 0.91a’’ 1a − 8.8
c1 (µm) 0.54 0.60a’’ 0.66a − 9.1
c2 (µm) 0.59 0.66a’’ 0.66a  ± 0.0
c3 (µm) 0.78 0.87a’’ 0.66a  + 31.4
c4 (µm) 0.64 0.71a’’ 0.66a  + 7.6
D1 (º) 119.5 116.6  + 2.5
D2 (º) 121.4 116.6  + 4.1
D3 (º) 122.5 116.6  + 5.1
D4 (º) 128.8 116.6  + 10.5
E1 (º) 125.7 126.9 − 1.0
E2 (º) 101.4 126.9 − 20.0
Pentagon III
b5 (µm) 0.43 0.79b’ 1b − 21.3
b6 (µm) 0.51 0.93b’ 1b − 6.7
c5 (µm) 0.53 0.97b’ 0.86b  + 12.8
c6 (µm) 0.53 0.97b’ 0.86b  + 12.8
d1 (µm) 0.35 0.64b’ 0.58b  + 10.3
B3 (º) 101.5 106.6 − 4.8
B4 (º) 107.0 106.6  + 0.4
F1 (º) 135.3 112.2  + 20.6
F2 (º) 101.4 112.2 − 9.6
Open in a new tab

a: Coordinate points are available in supporting information, b: a1 + b1 + b2 + b3 + b4 = 4.04a’, b5 + b6 + c5 + c6 + d1 = 4.3b’, a2 + a3 + c1 + c2 + c3 + c4 = 4.64a’’.

As for pentagon I (Fig. 4c and Table. 1 (i)), the observed angles were in good agreement with the theoretical values while the ratios of the observed side lengths slightly deviated from those of the theoretical lengths. A relatively large deviation was detected in a side length (c3) in hexagon II (Fig. 4 d and Table. 1 (ii)), and the other the side lengths and all angles showed relatively good agreement between the observed and theoretical values. The structure of hexagon II appears very close to that of the corresponding theoretical structure. Pentagon III structure fairly well coincided with the theoretical structure with at most 20% errors both in the side lengths and angles (Fig. 4 e and Table. 1 (iii)).

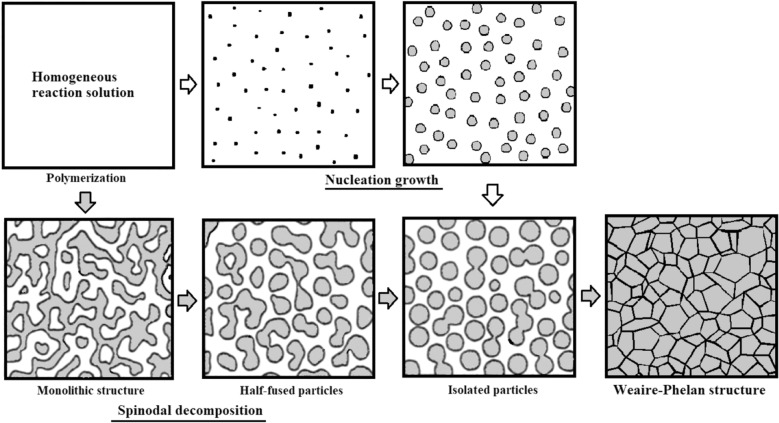
The formation process of the space-filling polyhedrons of the PEMP-HDI network polymer is proposed as follows. The porous structures in samples 1 and 2 were formed by the phase separation induced by the polyaddition between PEMP and HDI in toluene. Thereafter, two types of phase separation process are possible, i.e., nucleation growth and spinodal decomposition as shown in Fig. 5. Although, monolithic structure was not detected in the SEM images of the present research (Figs. 2 c,d), phase separation should preferentially occur via spinodal decomposition, as previously observed in other porous polymers prepared by the “joint-and-linker” method21,23.In the SEM image of sample 1 (Fig. 2c), half-fused particles were detected which should be formed via spinodal decomposition. At an early stage of spinodal decomposition, co-continuous monolithic structure should be formed, and further phase separation transforms the monolithic structure to the structure with dispersed droplet-type morphology by interfacial tension, which forms the connected particles. The formation of the half-fused particles in sample 1 (Fig. 2c should be completed at this transition state of the phase separation35–37.A further progress of the phase separation forms isolated spheres accompanied by their growth. The surface morphology in sample 2 should be completed at this stage, as shown in Fig. 2d. An increase in monomer concentration in the present reaction systems would increase the phase separation rate, which should finalize the phase-separated structure at later stages of phase separation. As described above, the small circle planes, which were derived from the truncated structures, were detected on the surface of the particles in sample 2 (Fig. 2d). Contact between particles may possibly play a key role in the formation of the polyhedral shapes. An increase in monomer concentration in the reaction increased the space occupancy in the porous polymer by the polymer network, leading to the slightly more transparent appearance of sample 3 than samples 1 and 2 (Fig. 2b). The polyhedrons observed in sample 3 (Fig. 2e) can be formed by 3D occupation of vacant space in the porous polymer by the spheres. The polyhedrons may be formed on an increase in the number of particles per unit space at the highest monomer concentration used in this work where the spheres changed into the polyhedrons in order to facilitate the densest (most dense) packing in space without leaving any gaps. In this process, truncation seems to be indispensable in reducing gaps between particles, and the spheres eventually took the shapes of tetrakaidecahedron and dodecahedron which can completely fill up the space without any gaps left.

Figure 5.

Figure 5

Open in a new tab

Phase separation models via nucleation growth and Spinodal decomposition to form Weaire-Phelan structure.

The cubic honeycomb proposed by Kelvin was thus formed for the Weaire-Phelan structure in this work. This is the first example of Weaire-Phelan structure made from a polymer species and of solid-polymer cubic honeycomb created by polymerization-induced phase separation. The material synthesized in this work may be potentially applicable as photonic38–40, separation, catalytic, nano-medical and structural materials based on the new synthetic methodologies and structural concepts.

While there still are slight deviations in specification between the theoretical polyhedrons of the perfect Weaire-Phelan structure, further investigations are ongoing targeting to minimize the deviations. Control of space filling and tessellation should be useful not only from a basic view but also from views of development of advanced materials with unforeseen functions.

Supplementary Information

Supplementary Information. (141.9KB, docx)

Acknowledgements

The authors would like to thank Hitachi High-Tech Corporation for technical assistance with the 3D SEM image of the polymer. This research was partially supported by JSPS KAKENHI grant number 24550261, MEXT/JSPS KAKENHI grant number JP 19H02759, and Japan Science and Technology Agency grand number JPMJTMl9E4.

Author contributions

N.N. and T.N. conceived the idea. N.N, M.J., Y.W., and T.N. designed the experiments. For the experimental work, N.N. and J.M. focused more on the synthesis and SEM observation, Y.W. and T.N. helped perform some of the experiments and data analysis. N.N. and T.N. wrote the paper. All the authors discussed the experiments, edited the paper and gave consent for this publication under the supervision of N.N. and T.N.

Data availability

Data generated and analyzed during this study are provided as source data with this paper or included in the Supplementary Information. Further data are available from the corresponding authors on reasonable request.

Competing interests

The authors declare no competing interests.

Footnotes

Publisher's note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Contributor Information

Naofumi Naga, Email: nnaga@sic.shibaura-it.ac.jp.

Tamaki Nakano, Email: tamaki.nakano@cat.hokudai.ac.jp.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-022-22058-7.

References

  • 1.Kelvin L. On the division of space with minimum partitional area. Phil. Mag. 1887;24:503. doi: 10.1080/14786448708628135. [DOI] [Google Scholar]
  • 2.Hales TC. The honeycomb conjecture. Discret. Comput. Geom. 2001;25:1–22. doi: 10.1007/s004540010071. [DOI] [Google Scholar]
  • 3.Weaire D, Phelan R. A counter-example to Kelvin’s conjecture on minimal surfaces. Phil. Mag. Lett. 1994;69:107–110. doi: 10.1080/09500839408241577. [DOI] [Google Scholar]
  • 4.Fountain, H. A Problem of bubbles frames an olympic design. New York Times (2008).
  • 5.Gabbrielli R, Meagher AJ, Weaire D, Brakke KA, Hutzler S. An experimental realization of the Weaire-Phelan structure in monodisperse liquid foam. Phil. Mag. Lett. 2012;92:1–6. doi: 10.1080/09500839.2011.645898. [DOI] [Google Scholar]
  • 6.Ball P. Scientists make the ‘perfect’ foam. Nature. 2011 doi: 10.1038/nature.2011.9504. [DOI] [Google Scholar]
  • 7.Yuhara J, He B, Matsunami N, Nakatake M, Le Lay G. Graphene’s latest cousin: Plumbene epitaxial growth on a “nano watercube”. Adv. Mater. 2019;31:1901017. doi: 10.1002/adma.201901017. [DOI] [PubMed] [Google Scholar]
  • 8.Kasper JS, Hagenmuller P, Pouchard M, Cros C. Clathrate structure of silicon Na8Si46 and NaxSi136 (x < 11) Science. 1965;150(3704):1713–1714. doi: 10.1126/science.150.3704.1713. [DOI] [PubMed] [Google Scholar]
  • 9.Cros C, Pouchard M, Hagenmuller P. Sur une nouvelle famille de clathrates minéraux isotypes des hydrates de gaz et de liquides, interprétation des résultats obtenus. J. Solid State Chem. 1970;2:570–581. doi: 10.1016/0022-4596(70)90053-8. [DOI] [Google Scholar]
  • 10.Frank FC, Kasper JS. Complex alloy structures regarded as sphere packings. I Definitions and basic principles. Acta Crystallogr. 1958;11:184–190. doi: 10.1107/S0365110X58000487. [DOI] [Google Scholar]
  • 11.Frank FC, Kasper JS. Complex alloy structures regarded as sphere packings. II. Analysis and classification of representative structures. Acta Crystallogr. 1959;12:483–499. doi: 10.1107/S0365110X59001499. [DOI] [Google Scholar]
  • 12.Reddy A, Buckley MB, Arora A, Bates FS, Dorfman KD, Grason GM. Stable frank-kasper phases of self-assembled, soft matter spheres. PNAS. 2018;115:10233–10238. doi: 10.1073/pnas.1809655115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Lachmayr KK, Wentz CM, Sita LR. An exceptionally stable and scalable sugar-polyolefin frank-kasper A15 phase. Angew. Chem. Int. Ed. 2020;59:1521–1526. doi: 10.1002/anie.201912648. [DOI] [PubMed] [Google Scholar]
  • 14.Lachmayr KK, Sita LR. Small-molecule modulation of soft-matter frank-kasper phases: A method for adding function to form. Angew. Chem. Int. Ed. 2020;59:3563–3567. doi: 10.1002/anie.201915416. [DOI] [PubMed] [Google Scholar]
  • 15.Huang M, Hsu CH, Wang J, Mei S, Dong X, Li Y, Li M, Liu H, Zhang W, Aida T, Zhang WB, Yue K, Cheng SZD. Selective assemblies of giant tetrahedral via precisely controlled positional interactions. Science. 2015;348:424–428. doi: 10.1126/science.aaa2421. [DOI] [PubMed] [Google Scholar]
  • 16.Naga N, Michida R, Kudo S, Nagami Y, Moriyama K, Nageh H, Furukawa H, Nakano T. Synthesis of joint-linker type gels and porous polymers by addition reactions of multi-functional thiol and alkyl diacrylate, diisocyanate compounds. Mater. Today Commun. 2019;18:153. doi: 10.1016/j.mtcomm.2018.11.013. [DOI] [Google Scholar]
  • 17.Naga N, Hasegawa K, Nageh H, Nakano T. Synthesis and properties of degradable gels and porous polymers including acetal group in the network structure by addition reaction of multi-functional phenols and divinyl ether compounds. Polym. Bull. 2019;77:5631–5645. doi: 10.1007/s00289-019-03033-1. [DOI] [Google Scholar]
  • 18.Naga N, Fujioka S, Inose D, Ahmed K, Nageh H, Nakano T. Synthesis and properties of porous polymers synthesized by Michael addition reactions of multi-functional acrylate and diamine, dithiol compounds. RSC Adv. 2020;10:60–69. doi: 10.1039/C9RA09684A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Naga N, Miyanaga T, Wang Y, Nakano T. Synthesis and properties of σ-π conjugated porous polymers obtained with Mizoroki-Heck reaction of tetra vinyl cyclic siloxane with dibromo fluorene. J. Polym. Sci. 2020;58:2301–2309. doi: 10.1002/pol.20200268. [DOI] [Google Scholar]
  • 20.Miyanaga T, Naga N. Phase and morphology control of organic-inorganic hybrid network polymer by means of hydrosilylation reaction of cubic silsesuquioxane or cyclic siloxane and divinyl or diallyl compounds. Chem. Lett. 2020;49:1236–1239. doi: 10.1246/cl.200421. [DOI] [Google Scholar]
  • 21.Naga N, Sato M, Mori K, Nageh H, Nakano T. Synthesis of network polymers by means of addition reactions of multifunctional-amine and poly(ethylene glycol) diglycidyl ether or diacrylate compounds. Polymers. 2020;12:2047. doi: 10.3390/polym12092047. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Naga N, Ito M, Mezaki A, Tang HC, Chang TFM, Sone M, Nageh H, Nakano T. Morphology control and metallization of porous polymers synthesized by michael addition reactions of a multi-functional acrylamide with a diamine. Materials. 2021;14:800. doi: 10.3390/ma14040800. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Naga N, Inose D, Ishida T, Kubota K, Nageh H, Nakano T. Synthesis of polymer networks by means of addition reactions of tri-amine and poly(ethylene glycol) diacrylate or diglycidyl ether compounds. Polym Bull. 2021;78:2745–2763. doi: 10.1007/s00289-020-03241-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Naga N, Yamada K, Moriyama K, Kudoh S, Nagami Y, Nageh H, Nakano T. Synthesis of network polymers by photo-initiated thiol-ene reaction between multi-functional thiol and poly(ethylene glycol) diacrylate. Polym. Bull. 2021 doi: 10.1007/s00289-021-03643-8. [DOI] [Google Scholar]
  • 25.Chan PK, Aljendro Rey D. Polymerization-Induced Phase Separation. 1. Droplet Size Selection Mechanism. Macromolecules. 1996;29:8939–8941. [Google Scholar]
  • 26.Chen W, Kobayashi S, Inoue T, Ohnaga T, Ougizawa T. Polymerization-induced spinodal decomposition of poly(ethylene-co-vinyl acetate)/methyl methacrylate mixture and the influence of incorporating poly(vinyl acetate) macromonomer. Polymer. 1994;18:4015–4021. doi: 10.1016/0032-3861(94)90289-5. [DOI] [Google Scholar]
  • 27.Zhang G, Qiao G. Polymerization-induced spinodal decomposition of ethylene glycol/phenolic resin solutions under electric fields. J. Chem. Phys. 2013;139:134903. doi: 10.1063/1.4822295. [DOI] [PubMed] [Google Scholar]
  • 28.Wang F, Ratke L, Zhang H, Altschult P, Nestler B. A phase-field study on polymerization-induced phase separation occasioned by diffusion and capillary flow-a mechanism for the formation of porous microstructure in membranes. J. Sol Gel Sci. Technol. 2020;94:356–374. doi: 10.1007/s10971-020-05238-7. [DOI] [Google Scholar]
  • 29.Higuchi T, Yano Y, Aita T, Takami S, Adschiri T. Phase-field simulation of polymerization-induced phase separation: II. Effect of volume fraction and mobility of network polymer. J. Chem. Eng. Japan. 2017;50:79–85. doi: 10.1252/jcej.16we037. [DOI] [Google Scholar]
  • 30.Liu Y. Polymerization-induced phase separation and resulting thermomechanical properties of thermosetting/reactive nonlinear polymer blends: A review. J. Appl. Polym. Sci. 2012;127:3279–3292. doi: 10.1002/app.38721. [DOI] [Google Scholar]
  • 31.Luo K. The morphology and dynamics of polymerization-induced phase separation. Euro. Polym. J. 2006;42:1499–1505. doi: 10.1016/j.eurpolymj.2006.01.019. [DOI] [Google Scholar]
  • 32.Kimura N, Kawazoe K, Nakanishi H, Norisuye T, Miyata QTC. Influence of wetting and shrinkage on the phase separation process of polymer mixtures induced by photopolymerization. Soft Matter. 2013;9:8428–8437. doi: 10.1039/c3sm51203g. [DOI] [Google Scholar]
  • 33.Kyu T, Lee JH. Nucleation initiated spinodal decomposition in a polymerizing system. Phys. Rev. Lett. 1996;76:3746–3749. doi: 10.1103/PhysRevLett.76.3746. [DOI] [PubMed] [Google Scholar]
  • 34.Lee JC. Polymerization-induced phase separation. Phys. Rev. E. 1999;60:1930–1935. doi: 10.1103/PhysRevE.60.1930. [DOI] [PubMed] [Google Scholar]
  • 35.Cahn JW, Hilliard JE. Free energy of a nonuniform system. I Interfacial free energy. J. Chem. Phys. 1958;28:258–267. doi: 10.1063/1.1744102. [DOI] [Google Scholar]
  • 36.Cahn JW. Phase separation by spinodal decomposition in isotropic systems. J. Chem. Phys. 1965;42:93–99. doi: 10.1063/1.1695731. [DOI] [Google Scholar]
  • 37.Inoue T. Reaction-induced phase decomposition in polymer blends. Prog. Polym. Sci. 1995;20:119–153. doi: 10.1016/0079-6700(94)00032-W. [DOI] [Google Scholar]
  • 38.Cai Z, Li Z, Ravaine S, He M, Song Y, Yin Y, Zheng H, Teng J, Zhang A. From colloidal particles to photonic crystals: Advances in self-assembly and their emerging applications. Chem. Soc. Rev. 2021;50:5898–5951. doi: 10.1039/D0CS00706D. [DOI] [PubMed] [Google Scholar]
  • 39.Gu X, Liu Y, Chen G, Wang H, Shao C, Chen Z, Lu P, Zhao Y. Mesoporous colloidal photonic crystal particles for intelligent drug delivery. ACS Appl. Mater. Interfaces. 2018;10:33936–33944. doi: 10.1021/acsami.8b11175. [DOI] [PubMed] [Google Scholar]
  • 40.Paquet C, Kumacheva E. Nanostructured polymers for photonics. Mater. Today. 2008;11:48–56. doi: 10.1016/S1369-7021(08)70056-7. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information. (141.9KB, docx)

Data Availability Statement

Data generated and analyzed during this study are provided as source data with this paper or included in the Supplementary Information. Further data are available from the corresponding authors on reasonable request.

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES