Systematic literature review of the performance characteristics of Chebyshev polynomials in machine learning applications for economic forecasting in low-income communities in sub-Saharan Africa

Abstract

Chebyshev polynomials have unique properties that place them in a class of functions that are highly efficient in the approximation of non-linear functions. Machine learning techniques are being applied to solve complex non-linear problems in the financial markets where there is a proliferation of financial products. The techniques for valuing diverse portfolios of these products can be time consuming and expensive. Formal research has been conducted to determine how machine learning can considerably reduce the computational effort without losing accuracy. The objective of this systematic literature review is to discover evidence of research on the optimal use of Chebyshev polynomials in machine learning and neural networks that may be used for the estimation of generalized financial outcomes of large clusters of small economic units in low-income communities in sub-Saharan Africa. Scopus, ProQuest, and Web of Science databases were queried with search criteria designed to recover peer-reviewed research articles that addressed this objective. Many articles discussing broader applications in engineering, computer science, and applied mathematics were found. Several articles provided insights into the challenges of forecasting stock price outcomes from unpredictable market activities, and in investment portfolio valuations. One article addressed specific environmental issues relating to energy, biology, and ecological situations, and presented encouraging results. While the literature search did not find any similar articles that address economic forecasting for low-income communities, the applications and techniques used in stock market forecasting and portfolio valuations can contribute to formative theory on sustainable development. There is currently no theoretical underpinning of sustainable development initiatives in developing countries. A framework for small business structures, data collection, and near real-time processing is proposed as a potential data-driven approach to guide policy decisions and private sector involvement.

Supplementary Information

The online version contains supplementary material available at 10.1007/s43546-022-00328-w.

Introduction

The World Bank (2021) estimated that in 2017 approximately 689 million people globally were living below their poverty threshold of US$1.90 per day. This situation is now far worse because of climate change, armed conflict, population growth, and disease. The World Bank (2021) have estimated that the number of people living under the poverty line could increase by up to 150 million in 2021 due to COVID-19, and by as many as 132 million by 2030 due to climate change. Sub-Saharan Africa (S-SA) and South Asia are the most vulnerable of all global regions (World Bank 2021).

Small to medium enterprises (SMEs) are community-based initiatives with a relatively small service area operating in diverse sectors with wide geographic diversity (Abisuga-Oyekunle et al. 2020; Azunu and Mensah 2019; GSMA 2020). Well-organized and managed SMEs could improve the wellbeing of these communities and reduce poverty in S-SA (Abisuga-Oyekunle et al. 2020; Anetor et al. 2020). This would give rise to potentially millions of SMEs in S-SA requiring a systematic approach to determining the collective economic, social, and environmental value of these SMEs, potential risks, and generalization characteristics. However, the research literature does not provide the depth and breadth of ideas and techniques required for the design, implementation, analysis, and visualization of generalizable programs for economic, social, and environmental wellbeing (Aftab and Ismail 2015; Khavul and Bruton 2013; Manzoor et al. 2019; Mazambani and Mutambara 2018). There is an absence of research relating to theoretical frameworks from which strategies for sustainable development leading to poverty alleviation can be derived. A well-developed business approach to poverty alleviation does not exist (Khavul and Bruton 2013). The absence of performance evaluation frameworks that inform economic and social performance initiatives precludes any systematic strategic approach to sustainable development (Mazambani and Mutambara 2018). There is no consensus in the field of development studies nor any established theory on how sustainable development should proceed (Aftab and Ismail 2015). Further, there is no systematic approach to bridging the digital and information divides with equitable access to the Internet (Urquhart et al. 2008).

The modelling of large numbers of SMEs requires the continuous collection of data covering a wide range of social, economic, and environmental measures, and sophisticated data analysis techniques to estimate local, regional, and national growth, prosperity, and wellbeing. The computational cost of such analysis could become burdensome. Some insights to this cost can be drawn from recent developments in financial market forecasting and portfolio valuations (Laris and Ruiz 2018). The complexity of investment portfolios has resulted in significant computational burdens when undertaking risk assessments and portfolio revaluations (Laris and Ruiz 2018). The challenge of modelling large numbers of SMEs under different risk scenarios is similar. Data analytics techniques and machine learning (ML) have made it possible to study sustainability phenomena on a large scale. As well as drawing analytical conclusions of historical performance, it is possible to develop predictive and even prescriptive assessments of social, economic, and environmental development initiatives with high levels of granularity.

The purpose of this systematic literature review (SLR) was to discover formal research into the development of efficient ML algorithmic models that may be suitable for the processing of large non-linear datasets expected from SMEs in S-SA, and the role of Chebyshev polynomials in reducing computational effort and hence costs. The search results were very limited with a few articles that focused on time series forecasting of financial market prices. A 2020 literature review of the application of ML to financial market forecasting revealed more than 150 articles (Ryll and Seidens 2019). This survey concluded that ML techniques generally outperformed traditional financial market forecasting models. A 2019 literature review reported that deep learning models significantly outperformed other techniques in ML but there was a lack of published research in the application of deep learning in time series forecasting in finance (Sezer et al. 2020). Examples of financial and stock market forecasting using various ML techniques claim more accurate outcomes compared with “traditional” models and techniques for more computationally efficient valuations of investment portfolios are being developed (Maciel and Ballini 2010; Mohapatra et al. 2018; Parida et al. 2017; Rout et al. 2017; Siddique et al. 2017; Vlasenko et al. 2019). As financial products become more complex the methods for undertaking comprehensive near real-time risk assessment are becoming computationally intensive (Mohapatra et al. 2018; Ryll and Seidens 2019). Chebyshev interpolation techniques have been shown to exhibit exponential convergence for many non-linear functions (Boyd and Petschek 2014), potentially leading to faster computation of investment portfolios and financial forecasting. Research into the application of Chebyshev polynomials in a neural network trained by differential evolution in a specific ecological/environmental case study produced encouraging results compared with other ML techniques (Troumbis et al. 2020). In this case study the highly non-linear nature of environmental data was recognized, and a Chebyshev series expansion was found suitable for approximation of this data. Further, the research acknowledged the complex nature of environmental data which included climate, economics, environment management, ecology, and biology datasets (Troumbis et al. 2020).

Neural networks with fast optimization may provide a useful tool for developing multiple “what-if?” scenarios and hence lead to more informed policy and resource planning decisions. Chebyshev, Legendre, and Jacobian polynomials are used in many fields of engineering, mathematics, and computer science (Boyd and Petschek 2014, Table 1). With the increased use of big data analytics and ML in social sciences, including economics and environmental science, many situations have arisen where the fast optimization of models for the sustainability of economic, environmental, and social outcomes is required. Chebyshev polynomials are well known as a class of polynomials that produce very efficient outcomes in the approximation of arbitrary functions (Boyd and Ong 2011; Boyd and Petschek 2014) and can be used in the non-linear approximation of large datasets (Troumbis et al. 2020). The selection of Chebyshev polynomials for further investigation was based upon encouraging results in ML. Are these polynomials optimum for use in neural networks that aim to predict the outcomes of large numbers of financial stimulus programs for low-income communities and their impact on GDP and other measures of wellbeing?

Table 1.

Database queries

Title only			Title, abstract, and keywords*
Research question 1
	Chebyshev	AND	Machine learning	AND	Economic
		OR	Neural networks	OR	Financial
Sub-question 1
	Chebyshev	AND	Approximation function
		OR	Curve fitting
		OR	Interpolation
Sub-question 2
	Chebyshev	AND	Convergence	AND	Gradient descent
Sub-question 3
	Chebyshev	AND	Activation function	AND	Machine learning
				OR	Neural networks
Sub-question 4
	Chebyshev	AND	Jacobi
Sub-question 5
	Chebyshev	AND	Legendre

*All variants of the keywords/phrases were searched

These objectives are encapsulated in the following research questions:

Research Question 1—Can Chebyshev polynomials improve computational efficiency in ML models for financial or economic portfolio valuations or predictions?

Sub-Question 1—How are Chebyshev polynomials used in the approximation of non-linear functions?

Sub-Question 2—Can Chebyshev polynomials improve the rate of convergence in gradient descent?

Sub-Question 3—Are Chebyshev polynomials useful as activation functions in machine learning?

Sub-Question 4—Chebyshev polynomials versus Jacobi polynomials in optimization problems?

Sub-Question 5—Chebyshev polynomials versus Legendre polynomials in optimization problems?

The significance of this research is embedded in the development of new computational techniques that can more readily provide responsive analyses of community-led initiatives covering a wide range of social, economic, and environmental issues related to wellbeing. The ability to engage sophisticated and highly granular analyses will provide researchers with views on the sustainability and generalizability of these initiatives, and the impact of collaborative efforts between SMEs in product development, marketing, and sales. Rapid insights into poverty alleviation strategies across all spatial and cultural domains may be derived through classification of the complex social structures that characterize low-income communities. This SLR draws upon observations made in other disciplines to construct a potential framework for optimizing sustainability models for social wellbeing. A contribution is also made in the development of an organizational structure for community-led initiatives based on the design science research methodology. A final dividend of the research is potentially from the development of procedures for the rapid reporting of progress towards the United Nations sustainable development goals (United Nations 2022).

The next section describes a comprehensive, reproducible, and rigorous methodological process for the discovery of relevant research from published literature. This is followed by discussion on the results of the literature search, an assessment of the quality and relevance of the research articles, an analysis of research findings, and finally a discussion on the application of the research findings in sustainable development and future research. This SLR follows the Prisma (2020) structure and content recommendations for systematic literature (PRISMA 2020).

Methodology

The search for relevant articles requires an approach that demands rigorous attention to detail. An iterative process to obtain an optimum collection of the most relevant and credible research articles is used. The challenge is to extract these articles from the large research repositories, each with proprietary query definitions. The combination of the bibliographic capabilities of EndNote and the qualitative search capabilities of NVivo facilitate meta-analysis and good record keeping at each iteration. There are multiple tools for the visualization of the search outcomes including Excel, Tableau, and custom code. In this SLR, Excel is used to represent 2 dimensional results. Figure 1 illustrates the search process of this SLR.

Fig. 1.

Search Process

Table 1 lists keywords, phrases, and Boolean structures that were used for each research question. Scopus, Web of Science, and ProQuest databases were searched. Google Scholar does not have the capability to distinguish between data sources and hence returns many references that are secondary sources of information and is used in this SLR for verification purposes only. The search criteria require articles to be peer reviewed, published in journals or conference proceedings, English language, and published during or after 2010.

The search capabilities of each of the databases were used to undertake high-level searches on the broadest scope for each research question. EndNote was used to aggregate the search results into one database to create a single project library. The search and collation capabilities of EndNote were then used to identify relevant research articles for further examination. NVivo is an analytic tool for qualitative research on unstructured data in many different forms. The final step in this process was to present the outcomes of the search in a manner that can be readily visualized and understood. NVivo has some of this capability, but other applications have such as Excel and Tableau have greater flexibility, and data presentations are more readily changed to add greater power to the interpretive outcomes of the search process. This procedure can be readily shared with researchers and practitioners for authentication and collaboration purposes. It inherently records an audit trail, and it can be easily updated without having to recreate the project library each time.

ML is increasingly being used in many areas of social science (Franco and Santurro 2020) but much of this work has not been reported in formal academic research (Ryll and Seidens 2019; Sezer et al. 2020). Hence the limitations of the methodology can be discussed at the following levels:

• Choice of databases to be queried. The databases for recovery of research articles were chosen purposively. Other databases may have contained publications that would have captured additional perspectives on the research questions.

• The scope of the database search. In this SLR, the searches were limited to peer-reviewed articles presented for publication in journals or in conference proceedings. This excludes research notes, book chapters, institutional reports, dissertations, aid agency reports, and contributions by various other government and private sector organizations.

• Choice of search terms and phrases. The primary goal of this SLR was to discover research in the applicability of Chebyshev polynomials in computational methods for financial forecasting of sustainable development initiatives in low-income communities. This approach may have precluded other more effective computational methods for this purpose. However, Chebyshev polynomials are well understood for their role in approximating non-linear data, a characteristic of social science phenomena in the context of sustainability studies in low-income communities. Further, search related to Research Question 1 was predicated on the mandatory presence of the terms “machine learning” and “neural networks” appearing in the title or abstract of the research article. This may have precluded other more effective techniques in statistics or econometrics.

The next section presents the results of the extensive database search using the criteria defined in this section and the manual selection process to refine the list to articles that are deemed most likely to contribute to the research questions.

Search results

Table 2 records the number of research articles returned for each query on each database. Eighteen files were created, 6 for each of Web of Science, ProQuest, and Scopus. The queries returned in Table 2, except for Google Scholar, were uploaded to Endnote. Endnote was used to create a single consolidated repository for each of the research questions. The Endnote upload process eliminated some duplicates while appending some of the research articles.

Table 2.

Database query results

Query	Web of Science	ProQuest	Scopus	Google
Research question 1	6	2	3	1,600*
Sub-question 1	134	13	169	Not queried
Sub-question 2	1	0	3	Not queried
Sub-question 3	2	3	7	Not queried
Sub-question 4	40	9	41	Not queried
Sub-question 5	73	8	62	Not queried

*Some articles were selected from the Google Scholar results

EndNote searches for the PDFs of the articles and, if successful, attaches them to the article references. Otherwise, the PDFs were extracted manually from the journal databases and attached to the article record in EndNote. EndNote queries, together with manual reading of the article abstracts, were used to further reduce the library. Many articles were eliminated because of subtle differences in author names, or the title not being detected by Endnote. Others were eliminated because they were deemed not highly relevant to the research questions even though they satisfied the search criteria. Typically, these articles were in areas of engineering or science that were very application specific. The manually selected article counts are listed in Table 3 and the details of each article are listed in Tables 1–6 of Appendix A.

Table 3.

Final number of articles selected

Query	Endnote merge	After manual selection
Research question 1	22	14
Sub-question 1	250	24
Sub-question 2	3	3
Sub-question 3	10	5
Sub-question 4	49	4
Sub-question 5	87	12

The next section describes the qualitative approach undertaken with the aid of NVivo to further identify the core articles that will be analyzed and discussed in the analysis section.

Assessment

Each of the files for the research questions were exported from EndNote to NVivo for further analysis. The purpose of this step was to provide a very high-level assessment of the frequency of occurrences of the primary and associated keywords in the articles to give a broad view of the quality and relevance of their content to the research questions. Other textual searches were performed to test for the presence of omitted relevant keywords/phrases.

Research question 1

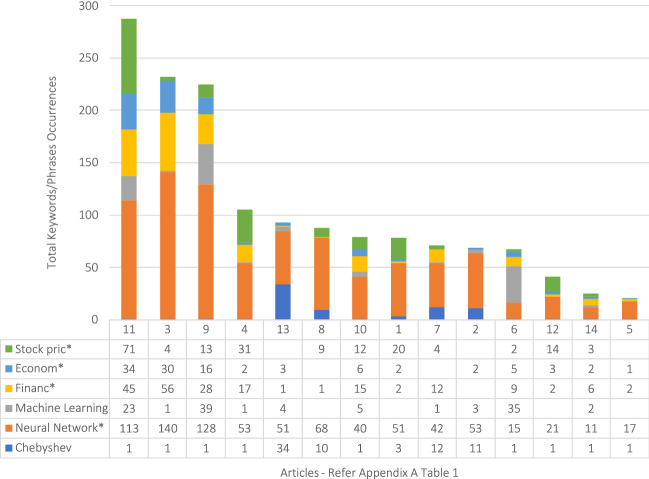
Appendix A Table 1 lists the articles for Research Question 1. During the search process for Research Question 1 only a few articles were discovered that related somewhat to the search criteria. The final selection of 14 articles was compiled from the results of the searches returned from Scopus, Web of Science, and ProQuest to which some manually selected articles were added from Google Scholar searches. Because Research Question 1 is interested in the role of Chebyshev polynomials in neural network implementations to study financial and economic forecasting, the results in Fig. 2 show the distribution of variants of the search criteria such as “stock price*” as a proxy for “finance*” and “economic*”.

Fig. 2.

Occurrences of keywords/phrases in all articles for research question 1

Sub-question 1

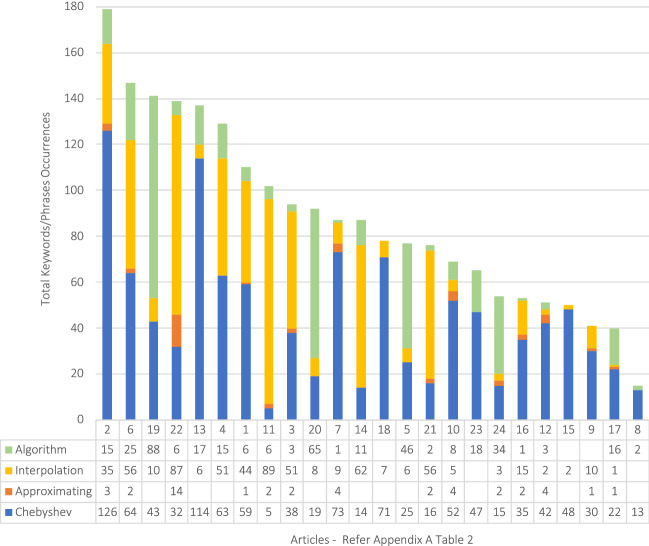
Appendix A Table 2 lists the articles for Sub-question 1. The keywords/phrases makeup of Sub-Question 1 are plotted in Fig. 3. The word “algorithm” appeared frequently in the NVivo analysis and was included in overall counts. Interpolation is the focus of the algorithm, with accuracy as a key determinant of predictive analysis. Examination of Fig. 3 reveals an expectation that Chebyshev interpolation is a frequent topic.

Fig. 3.

Occurrences of keywords/phrases in all articles for sub-question 1

Sub-question 2

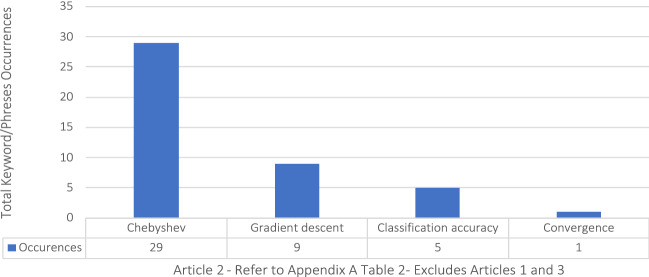
Appendix A Table 3 lists 3 articles for Sub-question 2, but only one article could be uploaded to NVivo for technical reasons. Article 2 was processed by NVivo, and Fig. 4 shows the occurrences of the search words and the additional phrase “classification accuracy”.

Fig. 4.

Occurrences of keywords/phrases in article 2 in sub-question 2

This article was published in 2017 in the Journal for Advances in Intelligent Systems and Computing which has an impact factor of 0.570 and a H index of 34.

Sub-question 3

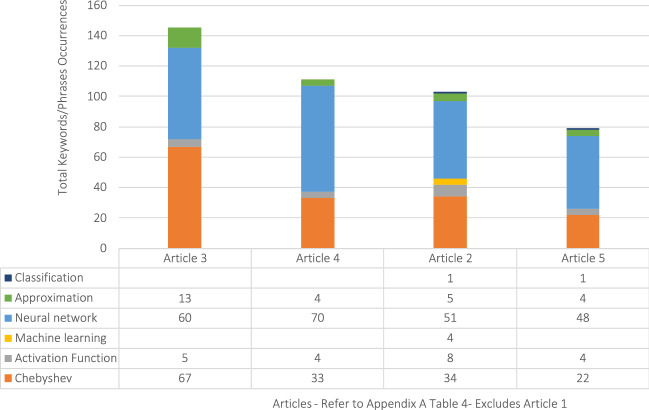
Appendix A Table 4 lists 5 articles for Sub-Question 3. This sub-question addresses the potential for Chebyshev polynomials to describe almost any non-linear activation function in neural networks. Non-linear activation functions facilitate the functional computation of any process. They enable efficient back propagation because their derivatives can be calculated. Observation of the frequency of “activation function” with “Chebyshev” in Fig. 5 suggests that the 4 articles are relevant to Sub-Question 3. One article was eliminated from the Appendix A Table 4 search results because it could not be imported to NVivo for technical reasons. The additional search terms “approximation” and “classification” relate to specific tasks in neural networks.

Fig. 5.

Occurrences of keywords/phrases in all articles in sub-question 3

Sub-questions 4 and 5

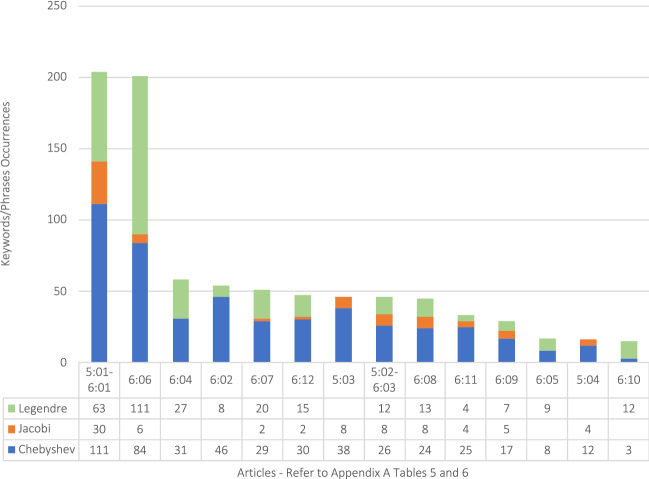
Appendix A Tables 5 and 6 list 6 articles for Sub-Questions 4 and 5. Analysis of the searched literature revealed that these two questions can be combined, and a single high-level appraisal made. Figure 6 is the outcome of the merger of Appendix A Tables 5 and 6 and presents a good visualization of the scope of literature that shows the relationships between the various polynomial families of which Chebyshev polynomials belong. Article 1 from Appendix Tables 5 and 6, and article 6 from Table 1 indicate good potential for the discussion on the relative benefits of the three classes of polynomials, Chebyshev, Jacobi, and Legendre. The X axis of Fig. 6 denotes Table-Article, e.g., 5-01 means Table 5 Article 1.

Fig. 6.

Occurrences of keywords/phrases in all articles in sub-questions 4 and 5

Table 5.

Design science research model for action plan for low-income community development

Design phase	Description
Problem recognition	Failings of current efforts to reduce poverty
Idea for a resolution	Solution based on community empowerment, capital, and technology
Design of trial solution	Design a model for creating a microeconomic cell that addresses social, environmental, and economic issues one community at a time
Implementation of trial	Implement a trial to measure the goals of the model, and to collect data
Evaluation	Evaluate the data, refine the model
Information	Provide metrics for poverty reduction and sustainable development

Quality appraisal

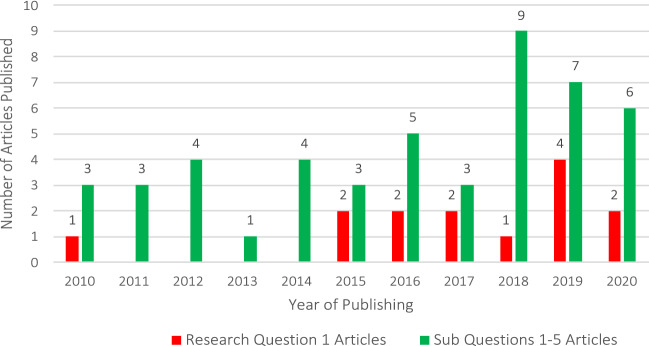
Appendix B Tables 1 lists 14 journals from which 14 articles were recovered for Research Question 1. Appendix B Table 2 lists 32 journals and 8 proceedings from which 44 articles were recovered for Sub Questions 1–5. Overall, only 4 journals contained no more than 2 articles returned from the searches. The journals and proceedings cover mathematics, engineering, financial, economic, and computer science. This high-level assessment reveals a good spread of research as reflected in the diversity of the publications. Figure 7 is a chronological profile of the articles recovered for each year since 2010. Journals for Research Question 1 are shown separately from the journals for Sub-Questions 1–5. Both categories show an upwards trend. This aligns with an observed increase in discussions and development activities in the informal media on a wide range of applications for neural networks across all disciplines, including social sciences.

Fig. 7.

Articles published per year

There is considerable diversity in the sources of articles. The reasons for this were not researched, but one intuitive view is that this is good because the articles are drawn from a broader base of scientific thinking and possibly less biased. However, had a lot more articles been recovered by the search process then this might have provided a more compelling view. On the other hand, the lack of depth across many journals might also indicate a lack of concentrated research on the application of neural networks and data analytics in the social sciences and information systems disciplines. The proliferation of journals is taken as a positive indicator of intellectual diversity but there is a potential gap in the literature on this subject. The journals are considered credible because all articles, with two possible exceptions, are peer reviewed. The impact factors for some journals were not available.

Over the past decade, the number of articles published per year has exhibited an upward trend but there are few research articles in this field, indicating a potential research gap. However, it is noted that the application of neural networks in social sciences is a relatively new field of research and, while there is significant research activity, this has not been reflected in high numbers of peer-reviewed articles. This SLR mainly reflects peer-reviewed research and hence the risk of exclusion of early-stage research is acknowledged.

Journal impact factors (# times cited/Number of articles published over a specific period) or other journal ranking strategy would most likely give a misleading ranking result (Smith 2013). The depth of peer-reviewed research pertaining to Research Question 1 seems limited. The number of citations for each article was examined. As expected, these generally conform inversely with year of publication. Older well-cited articles are indicative of credibility, but the number of citations would also fail under any attempt to rank them. Year of publication has a little more promise with the most recent articles likely to share contemporary thinking on neural network applications in social sciences.

Quantitative ranking of the articles was facilitated through the textual search capabilities of NVivo. A simple ranking of articles based upon the frequency of the search criteria was adopted and the articles were sorted in highest to lowest order of the sum of the number of occurrences of the search keywords and phrases for each research question. Figures 2, 3, 4, 5, and 6 depict these rankings. Figure 6 shows a combination of the search results for Sub-questions 4 and 5. This is appropriate because of the interrelated nature of these two questions. A more sophisticated ranking might apply weights to each of the search criteria.

The approach to qualitative assessment of the articles was to read each article and to encode relevant text and mathematical formulae using NVivo. This produced a searchable index of the different classes of information. This is a highly organized way of discovery and retention of qualitative material which was then searched looking for specific themes. A final potential qualitative measure was simply, how readable was the article? However, readability as a ranking criterion may lead to bias and was not attempted in this SLR. The next section summarizes the key findings from the research articles.

Analysis

The field of computational social science aided by the availability of large datasets and data analytics is expanding rapidly. There is an on-going debate at the intersection of social theory and computational science with one view attempting to discredit social theory, while another view foresees a blend (Radford and Joseph 2020). The sheer volume of data from finely granular social environments can be processed to provide highly nuanced visualizations of the human condition, the natural environment, the economic environment, and the social structures. Hence, there is a compelling view that an inductive evidence-based approach is less biased and speaks dispassionately and directly to the actual social condition. The following analysis attempts to highlight the key outcomes of those research articles that are most likely to address this approach. Large medium velocity datasets, cultural diversity, spatial diversity, and highly variable environmental factors characterize the challenge of managing large numbers of SMEs into sustainability.

Analysis of qualified search results

This SLR investigates formal research in the application of ML techniques that may be used for determining the future likelihood of sustainable livelihoods in low-income communities in the presence of some artefact promoting social wellbeing. The artefact is an economic stimulus mitigated by a wide range of external factors such as climate change, political stability, threats of terrorism, fertility rates, disease, education levels, and more. In this context, the literature search did not expose any significant depth of articles and the observations of Sezer et al. (2020) and Ryll and Seidins (2019) were supported.

Research Question 1 seeks to discover the role of Chebyshev polynomials in the construct of efficient neural network designs for economic forecasting purposes. The research sub-questions are a series of primers on the characteristics of Chebyshev polynomials and their role in developing efficient computational techniques. The scale of the social initiatives that may realize a sustainable direction for poverty alleviation is very large. Low-income communities dominate the landscape in S-SA and the computational models will process potentially millions of community datasets.

Research question 1

Appendix A Table 1 lists the articles returned from the literature search for Research Question 1. Troumbis et al. (2020) describe a differential evolution trained feed-forward neural network that utilizes Chebyshev polynomials to model non-linear environmental data. The purpose of this neural network closely aligns with Research Question 1. Troumbis et al. (2020) identify datasets covering energy consumption, biomass production, and ecological measures. The Chebyshev polynomials model the non-linear input data. A unique feature of the modelling is, instead of a single polynomial being used to characterize the input variables, it encodes a polynomial series to obtain precise series expansions of the input variables for greater accuracy. The neural network utilizes several layers to estimate the output derived from weighted sums of the Chebyshev series expansions. Differential evolution is used to train the model to minimize the squared error of the design parameters. Troumbis et al. (2020) used several data sets to test the efficiency of the model and concluded that, while the network performed well, the outcomes offered insights to pathways for future research. Troumbis et al. (2020) provide some thoughts on how the nature of the datasets impact on network design and performance. Domain specific data may present challenges that need to be thoroughly investigated before any conclusions can be reached on the validity of any network design.

Troumbis et al. (2020) pose a future research path to investigate neuro-fuzzy networks as an extension of their neural network model. Vlasenko et al. (2019), Dash and Dash (2016), and Parida et al. (2017) explore the potential of applying neuro-fuzzy networks in financial time series forecasting. Time series forecasting deals with datasets that exhibit greater volatility and non-linear characteristics than many other datasets. This further emphasizes the sensitivity of neural network models to domain specific data. Neuro fuzzy networks may use Chebyshev polynomials to increase the dimensionality of approximating functions to provide improved non-linear expansion of the input variables to help deal with the high volatility of the input data. This then appears to be where the Troumbis et al. (2020) network model could be extended to deal with different characteristics of the input data.

The remainder of the articles in Appendix A Table 1 relate to variants on time series financial forecasting and do not specially relate to the research questions in respect of Chebyshev polynomials. However, articles such as by Maciel and Ballini (2010), Mohapatra et al. (2018), Rout et al. (2017), Ryll et al. (2019), Sahoo et al. (2015), and Siddique et al. (2017) confirm the importance of ML or artificial neural networks (ANNs) to stock market forecasting and confirm the nonlinear highly volatile nature of financial markets data. Stock prices may serve as a proxy for the financial performance of small business entities in low-income communities and issues of model selection, and these articles provide valuable insight into the model designs. Rout et al. (2017) concluded that ML algorithms using the multi-layer perceptron do not converge to a solution as fast as ANNs. They also noted that Chebyshev polynomials can be used to improve computational efficiency.

Sezer et al. (2020) undertook a comprehensive literature review to address the relevance of deep learning to financial time series forecasting and concluded that recurrent neural networks are commonly used, and they performed better than ML models. It can also be reasonably concluded that Chebyshev polynomials have important roles in the implementation of feed forward ANNs where the input data space describes non-linear variables. Further, the use of Chebyshev polynomials in back propagation ANNs has the potential of improving the rate at which outputs converge. The ability to differentiate Chebyshev polynomials over the input space makes them ideal in this situation.

The following discussion on each research sub-question is intended to create a broad understanding of the characteristics of Chebyshev polynomials with examples of how they can be applied to new and innovative use of these important mathematical techniques.

Sub-question 1

The ability of Chebyshev polynomials to approximate arbitrary functions is well known. While not included in the literature search, the definitive work of Mason and Handscomb (2003) is an important reference. Appendix A Table 2 lists a small sample of research articles that were published from 2010 to 2020. They reflect the importance of Chebyshev polynomials across many sectors of interest. Boyd and Ong (2011) illustrate the fascination in defeating the Runge phenomenon which may cause attempts to approximate smooth functions with equidistant interpolation points to fail near the endpoints. Boyd and Ong (2011) point out that the Runge phenomenon is eliminated when the interpolation points are the roots of Chebyshev polynomials. They then go on to prove that the dissection of the interpolation interval [− 1,1] into sub domains and then applying Lagrangian polynomial interpolation methods for the sub-domains that lie close to the endpoints of the interval results in exponential convergence as the number of interpolation points increases. Ibrahimoglu (Ibrahimoglu 2020) illustrates the continued and more recent interest in showing how Chebyshev interpolation defeats the Runge phenomenon. This has important ramifications in the approximation of social science data where the behavior of the data near the extremities of the interpolation interval are unknown. The research shows that various techniques in neural networks that engage Chebyshev polynomials for the approximation of non-linear input data can be applied to ensure reliable and computationally efficient convergence to an accurate output function.

Lamichhane et al. (2016) presents a method using Chebyshev interpolants to solve partial differential equations in 2 and 3 dimensions where there are large numbers of interpolation points. This is particularly useful in solving flow, diffusion, and convection problems in engineering. There are potential situations, for instance, in social science where the data may characterize a diffusion phenomenon resulting from a policy intervention addressing poverty alleviation in rural communities. How do such interventions impact the migratory flow of people from rural to urban environments? This is of particular interest in computational social science which is developing understandings of such phenomena from nuances in large datasets.

The diversity of the importance of Chebyshev polynomials in social science is illustrated by Glau et al. (2019) with a new method for stock option pricing in the USA. The method is a 2-stage approach wherein certain model-dependent computations are performed offline using a variety of methods including Monte Carlo, partial differential equations, or Fourier transforms. The online backward induction giving rise to forward predictions of option pricing is performed on a Chebyshev grid. How this work may be utilized in the forecasting of other economic models that are subject to high volatility such as experience in stock option pricing is uncertain. However, volatility in option pricing offers investment opportunities. It is conceivable that volatility in other social phenomena may also present mitigation opportunities such as in the control of disease outbreaks in agribusiness. While this might sound far-fetched, option pricing takes into consideration past market trends and shocks to predict future outcomes.

Appendix A Table 2 includes other examples of the prevalence of Chebyshev polynomials to solve problems which have potential influence in computational social science, and the increased interest in neural networks to gain insights from large social datasets. For instance, Xia et al. (2014) and Babic (2013) discuss the modelling of analog circuits in electronics using Chebyshev polynomials. Natural phenomena are analog and convey information in continuous form. Techniques for the approximation of arbitrary analog representation in any field have a natural fit with other fields. In this sense the importance of excellent approximating abilities of Chebyshev polynomials is ubiquitous.

Sub-question 2

This sub-question intends to highlight the potential use of Chebyshev polynomials in ML that otherwise use learning optimization by the method of gradient descent. Appendix A Table 3 lists the articles retrieved for this purpose.

Iqbal and Ghazali (2017) developed a multilayer perceptron neural network for classification with Chebyshev polynomials used to functionally expand the input data to a higher dimension. The inputs are transformed from a lower feature space to a higher feature space in the first layer of the neural network. Levenberg–Marquardt back propagation performs the learning part of the neural network. Iqbal and Ghazali (2017) were able to show that, for classification purposes, this method was superior in terms of computational cost and accuracy over other methods including those that use gradient descent methodologies. They also claim that the transformation of the input data to a higher feature space avoids the potential local minima dilemma of gradient descent methods.

Han et al. (2018) developed an approach using Chebyshev polynomials to improve the efficiency of computing unbiased estimates of stochastic gradients for spectral functions. The research undertaken by Han et al. (2018) involves random selection of unbiased Chebyshev expansions and then applying a novel approach to minimize the variance of the estimates. According to Han et al. (Han et al. 2018) this resulted in considerable speed and accuracy improvements in the computation of spectral sums. Spectrum in this context refers to the set of eigen values of a matrix. ML techniques often encounter optimization challenges when confronted with spectral functions of parametric matrices (Han et al. 2018).

Lin et al. (2015, 2010) discuss how an application for a Chebyshev neural network was implemented to adjust permanent magnet synchronous motor control performance under conditions of nonlinear load characteristics. The Chebyshev neural network in this application demonstrated faster convergence and hence the neural network was more responsive to nonlinear load variations and “time varying behaviors”. This further demonstrates the persuasiveness of using Chebyshev polynomials in industrial applications where speed and accuracy is vital.

Sub-question 3

This sub-question relates to the potential use of Chebyshev approximations as activation functions in neural networks for classification tasks. Activation functions commonly used in classification neural networks include binary step function, linear function, sigmoid function, tanh/hyperbolic tangent function, rectified linear unit function (ReLU), leaky ReLU and parametric ReLU. Appendix A Table 4 lists articles that use the non-linear approximation capabilities of Chebyshev polynomials in several applications.

Jin et al. (2019) presented a method for classifying wine regions using activation functions based on a combination of Chebyshev polynomials that was able to accurately model the input variables (such as the characteristics of the wine regions). The classification neural network in this application is described by Jin et al. (2019) as a modified multi-output Chebyshev polynomial feedforward neural network. The classifier is a 3-layer neural network in which the hidden layer performs the summation of the normalized weighted inputs and transforms them using the Chebyshev basis function. Jin et al. (2019) used cross validation to measure the quality of the neural network and they optimized the weights that are used between the hidden layer and the output layer. Jin et al. (2019) tested their neural network design with data from several wine regions in Italy and concluded that the classification accuracy rates were superior to 9 other classification methods and the complexity was reduced.

Rigos et al. (2016) developed a neural network design using Chebyshev polynomials for the determination of shoreline position from coastal images. In this design the Chebyshev polynomial coefficients describe transformed input data (non-linear regression approximation of image histograms), and various thresholds were then set to meet shoreline position criteria at the output. The feed-forward neural network is trained by back propagation. Rigos et al. (Rigos et al. 2016) claim that the use of 3rd and 4th order Chebyshev polynomials in this application outperformed all other methods of shoreline position approximation.

Zhiqi et al. (2016) used Chebyshev polynomials as the activation function in a back propagation neural network to improve the accuracy of gestures that are important in the development of human–computer interaction technology. The network design employed a 3-layer neural network with the hidden layer using gradually increasing order of Chebyshev polynomials as the activation function. The output layer conforms with the classification criteria and performs the summation of the weighted outputs of the hidden layer. Zhiqi et al. (2016) claim superior performance over “ordinary backpropagation neural networks”. Li and He (2010) also used Chebyshev polynomials as the activation function in a neural network design for nonlinear system identification and similarly concluded that the network performance was “superior to those of conventional neural networks”. The conclusions by Troumbis et al. (2020) are previously discussed and support the performance claims of the other authors in this section in respect of the use of Chebyshev polynomials within the network design.

Sub-questions 4 and 5

Discussion on sub-questions 4 and 5 is combined because of the independently observed interrelationships between Chebyshev, Jacobi, and Legendre polynomials. Appendix A Table 1 5 and 6 list articles on these relationships, with Boyd and Petschek (2014) being the dominant reference in these search lists. The intent of these research sub-questions is to highlight discussion on the relative performance of the 3 polynomial classes in the approximation of arbitrary non-linear functions that might be encountered in datasets for social science. For the purposes of the following discussion, Boyd and Petschek (2014) refer to Gegenbauer polynomials that include Chebyshev and Legendre polynomials as special cases of Jacobi polynomials that are orthogonal on the interval [− 1,1] with respect to the weight function ${(1-x^2)}^{\alpha -\frac{1}{2}}$. Boyd and Petschek (2014) acknowledge that there are various measures under which any comparisons of the polynomial types can be undertaken. However, while there are some stated exceptions, Chebyshev coefficients usually decrease $\sqrt{n}$ faster than Legendre coefficients. The exceptions noted by Boyd and Petschek (2014) are summarized in Table 1 of their article under certain criteria. This table states that under some of these criteria other polynomials may produce greater optimality and it is a useful guide when designing neural networks. In their summary of the extensive evaluation of the different classes of polynomials, Boyd and Petschek (2014) (Boyd and Petschek 2014) state:

The relative merit of Chebyshev polynomials versus other members of the Jacobi family is shown to be complicated. Particular Jacobi or Gegenbauer polynomials are better than Chebyshev for the following situations: (i) functions f (x) with endpoint singularities (ii) the radial dependence of functions f (r, θ) on a disk and (iii) the latitudinal dependence of functions f (λ, θ) on a sphere. Otherwise, it is generically true that the Legendre coefficients bn converge more slowly than the corresponding Chebyshev coefficients an in the sense that bn ∼ O(√n)an. It is impossible to give the proportionality constant in the ratio bn/an precisely as this is function-dependent even within the class of entire functions.

The foregoing analysis has shown that techniques using ML algorithms with Chebyshev activation functions are potentially efficient computational platforms for stock market and portfolio valuations under complex scenarios of risk and historical performance. The next section describes how these techniques may be useful in the construction of a computational platform that can address questions of sustainability and generalizability of SME initiatives in S-SA.

Discussion

A portfolio of financial assets is conceptually similar to a portfolio of sustainable development initiatives in the form of SMEs. It is postulated that the computational techniques used in financial markets to value investment portfolios and investment decisions can be applied to valuing sustainable development initiatives and guide private sector investment and policy decisions. The core of the SME artefact is a financial asset that is influenced by a wide range of social, economic, and environmental factors. In any given region of a developing country there may be numerous SMEs and their collective performance is a measure of the growth and prosperity of the region. Portfolio managers in financial markets strive to maximize portfolio value through various asset allocations and risk balancing techniques. In the sustainable development of low-income communities, the objective is for SME management and policy directives to collaborate to maximize economic growth to reduce poverty and improve wellbeing. As with portfolios of financial market assets, collections of SMEs face individual and market related challenges. The ability to respond to these challenges in near real-time is essential under both scenarios. However, unlike the financial markets where there is a plethora of data for sophisticated analytics, there is realistically no comparable data generated from sustainable development initiatives. Further, there are no organizational frameworks or any established theory for sustainable development leading to poverty alleviation (Aftab and Ismail 2015; Khavul and Bruton 2013; Manzoor et al. 2019; Mazambani and Mutambara 2018). Census and other household survey data is not readily available in developing countries (Blumenstock et al. 2015; Njuguna and McSharry 2017; Xie et al. 2016). Further, how information and communication technology (ICT), which has been transformative in Western countries, can be used in developing countries is not well-developed (Urquhart et al. 2008). There is considerable scope for future research in organizational theory to gain greater insights into the interrelationships between the genuine needs of low-income communities and the types of commercial and policy structures needed to best serve these communities.

Research gaps

There is an absence of research into efficient computational frameworks for the calculation of social, economic, and environmental risk mitigated measures of wellbeing. The search for research articles was confined to those which contributed to the design and implementation of frameworks which used ML structures and Chebyshev polynomials to assist in computational efficiency and accuracy. While these confining criteria are acknowledged, the broader literature, the activities of the United Nations in respect of the sustainable development goals, the work of large numbers of economists at the World Bank, and academic research in peripheral areas point towards artificial intelligence (AI) solutions. For instance, the task of identifying locations of extreme poverty engaged remote sensing in combination with ML to create fine resolution maps of likely areas (Engstrom et al. 2019). Other researchers are using ML techniques to predict areas of poverty using night light data from remote sensing satellites (Njuguna and McSharry 2017; Xie et al. 2016). It is reasonable to conclude there is a research gap in computational social science that focuses the analytical, predictive, and prescriptive potential of ML on the operationalization of low-income sustainable development initiatives for poverty alleviation. Emphasis instead is currently placed on the application of ML as an analytical tool.

Potential SME data generating framework

The lack of data for the continuous assessment of the social, economic, and environmental initiatives at the community level may be addressed under a comprehensive information systems structure for community SMEs. Design science research (DSR) is an information systems theoretical and practical approach to the systematic design, development, and refinement of artefacts that are applicable in social sciences (Peffers et al. 2008). DSR is described by Wieringa (2014) to be a solution-oriented research approach which incorporates the conceptualization of a solution to a research question. The design of an artefact which addresses this conceptual solution can then be constructed and implemented as an experiment. The design undergoes continuous iterative evaluation and refinement until the artefact performs to a defined level of quality (Peffers et al. 2008). Performance data are made available through formal API/SDK (Applications Programming Interface/Software Development Kits) semantics as input to the broader data collection process. Figure 8 depicts the structure of the design science research methodology (DSRM) (Peffers et al. 2008).

Fig. 8.

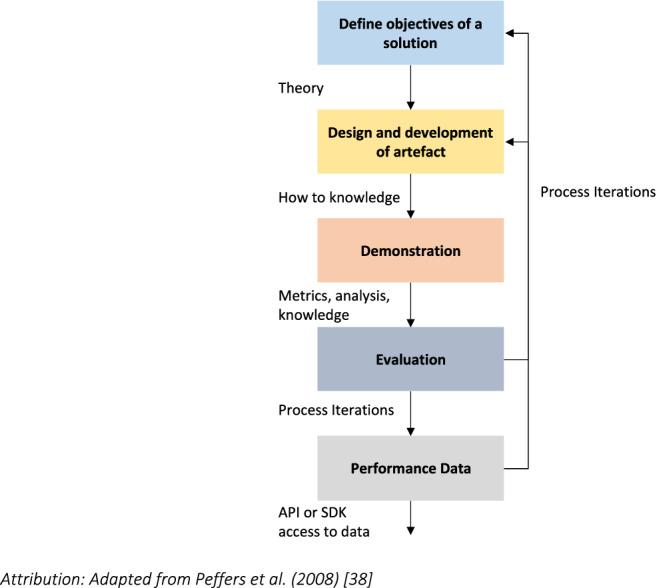
Design science research methodology

DSR has potential applicability in the design, experimentation, and implementation of SMEs for sustainable development projects, and in the on-going monitoring and management of these projects into a state of sustainability. It potentially serves to provide structure to innovation and to inform socio-technical transition theory (STTT) (Geels 2002). The DSRM is intrinsically computational and can be applied consistently across multiple domains. Hevner et al. (2004) established a set of seven guidelines for DSR as shown in Table 4.

Table 4.

Design science research model guidelines

Guideline		Design Science Research Action Plan Model
1	Design an artefact	DSR must produce a viable artefact in the form of a construct, a model, a method, or an instantiation
2	Problem relevance	The objective of DSR is to develop technology-based solutions to important and relevant business problems
3	Design evaluation	The utility, quality, and efficacy of a design artefact must be rigorously demonstrated via well-executed evaluation methods
4	Research contributions	Effective DSR must provide clear and verifiable contributions in the areas of the design artefact, design foundations, and/or design methodologies
5	Research rigor	DSR relies on the application of rigorous methods in the construction and evaluation of the design artefact
6	Design as a search process	The search for an effective artefact requires utilizing available means to research desired ends while satisfying laws in the problem environment
7	Communication of research	DSR must be presented effectively both to technology-oriented as well as management-oriented audiences

Attribution: Hevner et al. (2004)

Hevner et al. (2004) stress that these guidelines are meant to illustrate the requirements for effective DSR and are not meant to be used prescriptively. However, Hevner et al. (2004) emphasize the importance of addressing the principles of each of the guidelines. Peffers et al. (2008) developed a DSR methodology (DSRM) for an information systems (IS) artefact that emphasizes the importance of Guideline 1—creation of an innovative artefact, Guideline 2—such artefact is to address an unsolved business problem, and Guideline 3—its utility, quality, and efficacy must be demonstrable. This IS artefact can be further developed to embrace social, economic, and environmental aspects within an information technology (IT) (Leoz and Petter 2018). Table 5 describes the DSRM for the implementation of a socio-technical artefact postulated by De Leoz and Petter (2018) and depicted in Fig. 9. The artefact is the social, environmental, and economic model for the empowerment of a community to address poverty and sustainable development. Information on the social, economic, and environmental performance of the artefact is made available for analysis.

Fig. 9.

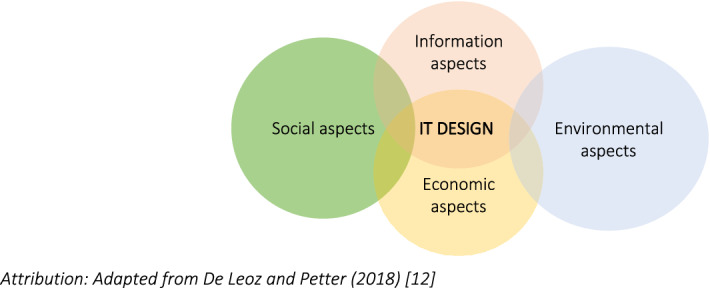
Social, economic, and environmental aspects in the design of a socio-wellbeing artefact

The practical implementation of Fig. 9 for SMEs involves the establishment of an IT infrastructure typically comprised of combinations of office computers, cloud-based computers and storage, and a wide range of Internet edge devices for data collection. The SME manages its business with financial accounting, inventory management, customer relationship management, production control systems (anything engaged in the manufacturing process), a commerce website, and social media. The SME can invest in social infrastructure such as schools and health services, and in environmental projects including waste management, sanitation, and water supply. Further, observations of community activities can be recorded at any accessible point of the IT platform, such as the SME website, to generate a comprehensive profile of the community. Participating community members can also be enabled with smartphones or other mobility devices to report household information (incomes, number of occupants, ages, gender, school attendance, health clinic visits, and more), smartphone airtime purchases, and other information. Weather information can be automatically made available from low-cost weather stations. This platform can accept any data format (video, text, images). Remote access to this platform is via an application program interface (API) or software development kit (SDK) which automatically streams data to a cloud repository for near real-time analysis and visualizations. This approach to data collection obviates the need for periodic surveys and provides a much richer information compilation that will give managers and policy makers current and relevant information for their decision support systems. It is potentially much less expensive than cumbersome census and survey procedures and can also greatly reduce the cost of compliance reporting under the United Nations sustainable development goals (United Nations 2022).

SMEs operating under this organizational structure will report large volumes of data. The processing of this data will be a computational challenge and ML techniques with fast optimization are required to present highly nuanced visualizations of SME performance. For instance, reports on the collective contribution of SMEs engaged in aquaculture projects in different regions to sustainable development objectives will provide valuable insights into the viability of this industry and highlight challenges in achieving growth targets, production levels, market share, and employment goals. Reporting on the progress of collaboration between SMEs to share information on production technologies and to develop marketing and branding strategies is another example. At the household level, comprehensive analysis of the impact of community-led sustainable development initiatives on household incomes, school attendance, gender inequality (school drop-out rates), and other factors can contribute to the development of data driven estimates of wellbeing.

Potential computational framework

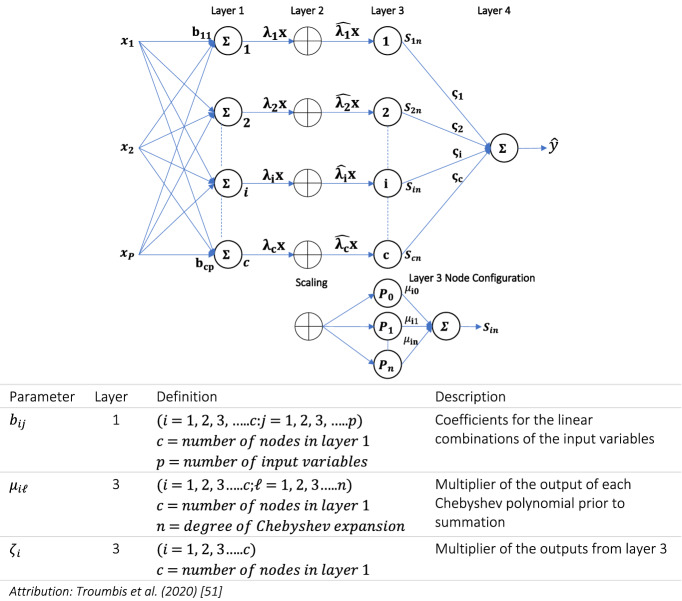
Research has indicated that an algorithmic approach to the processing of large datasets in social sciences is computationally efficient. Machine learning with fast optimization using Chebyshev expansions is worthy of further investigation. A simple feed-forward neural network with Chebyshev approximation of the input data and trained using differential evolution is a potential starting point for research into optimal processing of the data generated by the SMEs (Troumbis et al. 2020). Figure 10 illustrates a 4-layer design comprising:

• Input layer – a layer that sums the product of the network design parameter $b_{\mathit{ij}}$ with the p-dimensional input data, $y=f\left(x_1,\cdots ,.,x_p\right)$.

• Scaling layer – this layer scales the input data to the interval [-1, 1] which is the interval required by the activation layer.

• Activation layer – which employs Chebyshev series expansion, $P_n\left(x\right),$ for approximating the nonlinear characteristics of the input data. Chebyshev polynomials are orthogonal over the interval [-1, 1], hence the need for the scaling layer.

• Output layer – which sums the weighted outcomes of the activation layer to give $\widehat{y}-y\cong 0,$ as an indicator of the accuracy of the model calculated by minimizing the squared error of the output with differential evolution.

Fig. 10.

Neural network design

The neural network in Fig. 10 is seeking to find an optimal representation of the input data through regression. For this purpose, the network training involves the minimization of the squared error represented by:

$$J_{\mathit{SE}}=\sum _{k=1}^N{{|y}_k-\widehat{y_k}|}^2$$

and the objective function for minimization is:

$$J_{\mathit{SE}}=\sum _{k=1}^N{\left|y_k,-,\sum _{i=1}^c,\sum _{\ell =1}^n,{\zeta }_i,{\mu }_{\mathit{ik}},P_k,\left(r,\sum _{j=1}^p,b_{\mathit{ij}},x_j,-,g\right)\right|}^2$$

r and g are Layer 2 scaling factors, and ${\zeta }_{i,}{\mu }_{\mathit{ik}},\mathrm{and}{b}_{\mathit{ij}}\mathrm{are}\mathrm{the}\mathrm{network}\mathrm{design}\mathrm{parameters}.$

The objective function can be minimized by adjusting the network design parameters at each of the layers. The most common way of doing this is to use backpropagation and gradient descent. However, this requires the activation function at each hidden layer to be differentiable and can lead to complexities when high orders of the Chebyshev polynomials are utilized. A potentially more effective way of determining the network design parameters is to employ a technique that is based upon a one-to-one mapping of these design parameters with each point in the optimization space using differential evolution (DE). DE is inspired by the natural processes of selection, mutation, and crossover (also called genetic recombination) that results in a new genotype (individuals, creatures, or phenotypes) that may or may not have improved fitness compared with others in the optimization space (Baioletti et al. 2020; Storn and Price 1997). Genotypes with greater fitness replace those with lower fitness. In any given population, this may evolve to result in a genotype that has the best or optimum fitness. Optimization problems are characterized by the search space over which optimization is required, an objective function (e.g., minimization of squared errors), and a set of constraints (Lin et al. 2018). Differential evolution operates to find solutions in the search space that are successively improved through multiple generations or iterations (Baioletti et al. 2020). Troumbis et al. (2020) discuss an implementation of DE that was successfully used with complex non-linear environmental data. Eltaeib and Mahmood (2018), Lin et al. (2018), and Baioletti et al. (2020) show how other variations of DE provide a potentially powerful approach to optimizing neural networks for social science applications involving large datasets.

Other optimization methods include particle swarm optimization (PSO) (Poli et al. 2007) and agent-based modelling (ABM) (Barbati et al. 2012). PSO is a heuristic approach based on the observation of the movements of identities in a swarm, such as birds in a flock (Poli et al. 2007). It is the combined interactions of these identities that determines the direction and velocity of the swarm. In optimization problems, identities or particles are distributed on the search space of the function for which a global optimum is being sought as defined by the objective function. In a D-dimensional search space each particle is defined by three D-dimensional vectors that describe the current position, the previous best position, and its velocity. The objective is to determine the best positions to guide the swarm to an optimum location (Poli et al. 2007). In ABM, identities or agents are characterized by specific attributes, such as in a socio-economic environment. The agents interact with each other and the environment under a rules-based paradigm (Barbati et al. 2012). ABM is also inspired by the flocking phenomena of birds and fish, and agents can be any physical or virtual entity. ABM has been used in human biology to study the spread of cancers and the COVID-19 pandemic, supply chain characteristics, manufacturing procedures, and robotics and engineering applications (Barbati et al. 2012). ABM has been shown to successfully model large complex nonlinear problems where there are many decision variables, parameters, and constraints, and where the environment is dynamic (Shen et al. 2006). Hence, there is potential for optimization of the objective function described for the neural network shown in Fig. 10 using ABM. Some techniques for the optimization of neural networks using PSO and DE were modeled by Troumbis et al. (2020) using environmental and ecological datasets. There is no known application of ABM to the optimization problem for the large nonlinear datasets envisaged for sustainable development by SMEs in S-SA.

The data generating process described in this SLR for sustainable development initiatives continuously captures large volumes of data. This data generation is partly automated and partly manual, and it is not known how well these optimization techniques will perform under these conditions. Research into variations of optimization algorithms along with efficient and relevant data generation and preprocessing of the input data will be required.

Managerial implications

The goal of the computational frameworks is to inform both business and policy decisions. The types of reports and analysis are like those employed in stock and financial markets to assist investment decisions in near real-time. In these situations, the performance of all assets is scrutinized and adjusted under different operational, market, and risk scenarios. It is envisaged that future computational frameworks will be cloud-based with data collection and analysis being performed in near real-time. The following summarizes the implications from both business and policy perspectives.

Business implications

It is generally recognized that SMEs offer potential for more diverse activities over a broader demographic than the highly location-centric activities of extractive and other large industries (Abisuga-Oyekunle et al. 2020; Azunu and Mensah 2019; Hambayi and Vedanthachari 2017; Manzoor et al. 2019). Large commercial operations play a significant role in the overall economy, but SMEs are central to strategies for low-income community development and poverty alleviation. For SMEs to achieve success across multiple industry sectors (agribusiness, manufacturing, construction, and retail, services) organizational structures must be put in place that facilitate funding, business management, job creation, marketing (including brand development), access to information (farming techniques and production quality management), and performance reporting. SME entrepreneurs and innovators will be able to receive continuous reports on the performance of their business operations including forward forecasts relative to budget expectations, comparative performance against other similar industry SMEs, results of collaborative efforts and market trends, regional economic trends, and contributions to national economic outcomes.

Policy implications

Policy-based initiatives to help facilitate social, economic, and environmental development can be continuously monitored and reported for effectiveness. Such initiatives may include infrastructure (roads, energy, water, and telecommunications) or more focused support for SMEs including tax incentives, grant funding, employment incentives, training programs, health, and education services. The forward-looking capabilities will inform policy decisions and capacity planning. Another benefit may result from the ability to transition people who are working in the informal sector into the formal sector and hence become visible for taxation purposes and government support programs.

Theoretical contributions

The theoretical contributions of this article may be viewed in terms of originality and utility. While this article is a review of existing literature, there are contributions to originality in developmental theory for sustainable development in low-income countries and in the utility for automated and semi-automated data collection as follows.

Originality

The hypothesis that Chebyshev polynomials can play an important role in the implementation of efficient computational frameworks for application in financial or economic valuations and forecasting is supported by existing literature in stock market and financial market examples. It can be reasonably concluded from the research question analyses that accuracy and speed of calculations is enhanced when Chebyshev polynomials are used to approximate non-linear data sets in ML models. This SLR has drawn parallels with the dynamics of developmental initiatives in low-income communities and the role of SMEs in support of social, economic, and environmental imperatives. This maybe a foundational contribution to the theory for low-income community sustainable development for poverty alleviation where potentially none currently exists (Aftab and Ismail 2015; Mazambani and Mutambara 2018; Urquhart et al. 2008; Manzoor et al. 2019). Further, this SLR has introduced the concept of an integrated data collection, analysis, and visualization computational framework that may be optimized to provide continuous near real-time perspectives on sustainable development initiatives in low-income communities. This associates the data generation process more closely to the computational domain and meaningful visualizations of the real-life phenomena, and advances knowledge for AI inspired social science experiments.

Utility

This SLR has highlighted constraints in accessing reliable census and survey data in S-SA. It has also introduced the idea that, under formal operational structures, SMEs can automatically report a wide range of data encompassing financial performance, job creation, and investment in local infrastructure. Reporting by individuals can also be supported with an appropriate mobile phone application. By extension, the framework supports any source of data collection for any type of data (text, image, video, audio, sensors, and the Internet of things). This is a whole-of-system approach that can be implemented as a cloud-based service with reports and visualizations accessible anywhere in a browser.

Conclusions

Policy support for large numbers of SMEs across S-SA requires the continuous collection and near real-time processing of large quantities of data. This requires significant computational effort to evaluate the performance of SMEs operating in different markets, climates, geographic areas, cultural diversity, and risk scenarios. The analysis may be highly nuanced so that SMEs can be visualized as individual entities or groups of entities operating in the same market segment. It is perceived that trends in climate change, internal conflicts, policy changes, and national security challenges can impact SME performance.

This requires new tools for analytical and predictive computations and visualizations. Machine learning using deep learning techniques with fast optimization may contribute to this objective. Chebyshev interpolation at neural network layers have been shown to enable accurate quantitative modeling of large non-linear datasets in social sciences. Further, techniques for the rapid optimization of neural networks exhibited improvements in computational speed and hence lower costs. This SLR specifically targets research that has been undertaken in the development of these machine learning techniques. No research was discovered that addressed the performance evaluation of large clusters of SMEs. However, some research in the evaluation of stock market prices and investment portfolios provides valuable insights to SME performance modeling. A potential data generating model was introduced for the SMEs together with a basic computational neural network framework that could be used as a starting point for developing more comprehensive and efficient models in future research.

Future research

The ability of the SMEs to consistently generate reliable data is a key area for research. At the heart of each SME, there are several business operations that must be quantified and reported. These include information on production status, human resources, financial allocations for overheads, and investments in community social and environmental programs It is envisaged that advanced information systems will be required, and research needs to be undertaken to assess the most appropriate implementations of the business infrastructure. Heavy reliance will be placed on access to the Internet.

The computational framework introduced in this SLR will require considerable research to determine the most appropriate implementations of neural networks to address different datasets for different social scenarios. What are the optimum neural networks architectures? What accuracy is required in the approximation of the input data? These questions directly relate to the computational resources needed for the desired outcomes. Higher accuracies may require higher orders of Chebyshev polynomials and hence more computational resources. Fast optimization of the neural network may require research into more advanced algorithmic techniques.

The field of computational social science is at an early stage and the foregoing is just a glimpse of the challenges and opportunities for more proactively driven policy initiatives for poverty alleviation. Many of the tools for computational social science have already been developed but have been deployed in the search for knowledge of social behavior that leverages commercial advantage for large companies. These same tools may be applied to address systemic poverty on a much larger scale.

Supplementary Information

Below is the link to the electronic supplementary material.

Authors contributions

DC is the principal author with technical support and review from SL and GM.

Funding

No external funding has been used for this research.

Availability of data and materials

All database search results are available in Endnote library format.

Code availability

No code was generated for this article.

Declarations

Conflict of interest

There are no known conflicts of interest.