Efficient Implementation of Density Functional Theory Based Embedding for Molecular and Periodic Systems Using Gaussian Basis Functions

Abstract

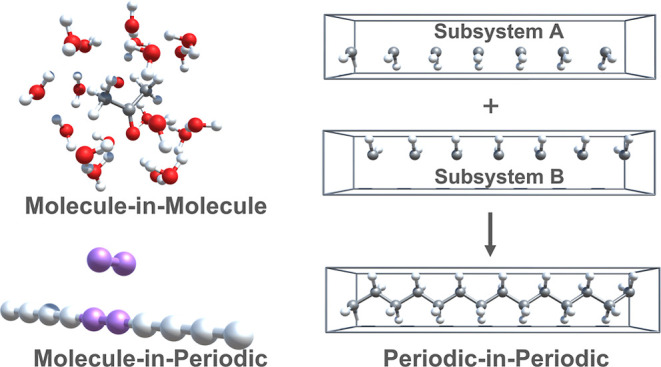
A practical and effective implementation of density functional theory based embedding is reported, which allows us to treat both periodic and aperiodic systems on an equal footing. Its essence is the expansion of orbitals and electron density of the periodic system using Gaussian basis functions, rather than plane-waves, which provides a unique all-electron direct-space representation, thus avoiding the need for pseudopotentials. This makes the construction of embedding potential for a molecular active subsystem due to a periodic environment quite convenient, as transformation between representations is far from trivial. The three flavors of embedding, molecule-in-molecule, molecule-in-periodic, and periodic-in-periodic embedding, are implemented using embedding potentials based on non-additive kinetic energy density functionals (approximate) and level-shift projection operator (exact). The embedding scheme is coupled with a variety of correlated wave function theory (WFT) methods, thereby providing an efficient way to study the ground and excited state properties of low-dimensional systems using high-level methods for the region of interest. Finally, an implementation of real time–time-dependent density functional embedding theory (RT-TDDFET) is presented that uses a projection operator-based embedding potential and provides accurate results compared to full RT-TDDFT for systems with uncoupled excitations. The embedding potential is calculated efficiently using a combination of density fitting and continuous fast multipole method for the Coulomb term. The applicability of (i) WFT-in-DFT embedding, in predicting the adsorption and excitation energies, and (ii) RT-TDDFET, in predicting the absorption spectra, is explored for various test systems.

1. Introduction

Hybrid systems, such as molecules adsorbed on or attached to metallic and semiconducting surfaces or nanostructures, constitute a particular challenge to electronic structure calculations because both the extended (periodic) character of the surface and the localized (aperiodic) molecular properties and spectroscopic observables need to be described properly. For example, metals and semiconductors are typically well described, applying density functional theory (DFT) and functionals based on the local density approximation (LDA) or generalized gradient approaches (GGAs). However, for molecules, in many cases, computationally more challenging hybrid or range-separated hybrid functionals are necessary for a proper description of the electronic structures. This may be even more important for molecules adsorbed on metallic surfaces, as new (charge-transfer) states of the combined hybrid system may build up, the proper description of which may require reaching for wave function-based quantum chemical methods. In addition, imposing the usual periodic boundary conditions in electronic structure calculations may result in a periodic pattern of molecules with much higher surface coverage than encountered in experiments, which may lead to spurious interactions between neighboring molecules. Using larger supercells can help to reduce the interactions but significantly increases the computational demand.

One of the major challenges in the application of state-of-the-art wave function theory (WFT) methods to such hybrid chemical systems is their unfavorable N^3–8 scaling with respect to system size. Therefore, the choice of the method used is usually based on a reasonable trade-off between speed and accuracy. However, because the region of interest in such systems is usually small, it is desirable to use embedding-based strategies that allow using different levels of theory for different portions of the system. Embedding techniques rely on partitioning the total system into active and environment subsystems based on wave function or density.

Kohn–Sham DFT (KS-DFT) provides a theoretically exact framework for density functional theory based embedding that relies on partitioning the real space electronic density ρ(r). The most common way to realize DFT-in-DFT embedding is via frozen density embedding (FDE), wherein the total energy is minimized with respect to the active subsystem density, while the environment density is kept frozen. The theory and methodology was introduced by Wesolowski and Warshel¹ based on earlier work by Cortana.² Within FDE, the influence of the environment on the active subsystem is considered through an effective embedding potential which, for the most part, depends on the environment density. This allows different levels of treatment for active and environment subsystems. Despite the desirable nature, FDE is impaired by the need for approximate kinetic energy density functionals (KEDFs), rendering it useful only for weakly interacting subsystems. This can be addressed by using potential inversion techniques³⁻⁶ or projection operators.⁷⁻⁹ The projection operator enforces the Pauli exclusion principle between subsystems and eliminates the need for KEDFs.

Extension of DFT-based embedding to time-dependent DFT (TDDFT) for the study of excited states has been explored by several groups.^10,11 It is also known as subsystem TDDFT or FDE-TDDFT. While most of the works are based on the linear-response TDDFT (LR-TDDFT) formalism, only the implementations by Krishtal et al.¹² and De Santis et al.¹³ have investigated the coupling of FDE to real time-TDDFT (RT-TDDFT). The former is implemented in Quantum ESPRESSO¹⁴ and is based on plane waves, while the latter employs Gaussian basis functions (BFs). Both the implementations are approximate in nature due to the use of KEDF-based embedding potentials. RT-TDDFT allows the study of the non-linear matter–radiation interactions at the femtosecond time-scale and can be used to monitor the electron-dynamics in real-time.

Coupling of DFT-based embedding with correlated WFT methods such as coupled-cluster singles and doubles (CCSD) has consistently been shown to improve the DFT description of both ground and excited state properties of hybrid systems, even with the approximate KEDF-based embedding potential.^6,15−19 The expensive correlated calculation is restricted to the active subsystem (region of interest) embedded in an environment described by DFT. This is extremely useful as it offers the best of both worlds, that is, the accuracy of WFT methods and the speed of DFT. Due to its tremendous success it has been used to accelerate the study of solute–solvent systems via molecule-in-molecule embedding, as well as molecules adsorbed on a surface via molecule-in-periodic embedding. Carter and co-workers have been the pioneers of molecule (WFT)-in-periodic(DFT) embedding; however, their implementations have usually relied on a plane-wave DFT calculation for the periodic system and localized basis calculation for the molecular subsystem.^6,15,20,21 Therefore, to construct the embedding potential for the molecular subsystem, a transformation from the plane-wave to localized basis is necessary which is not trivial. Recently, an implementation based on mixed Gaussian plane-wave basis has been reported using products of atomic orbital BFs.²² Chulhai and Goodpaster’s QSoME embedding software¹⁹ based on PySCF¹⁹ is a recent example of an implementation utilizing Gaussian basis for the periodic subsystem; however, PySCF calculates potential matrices in reciprocal space which leads to efficiency issues especially for the Coulomb term. Notable implementations supporting periodic systems are also found in KOALA²³ (Gaussian basis) and Quantum ESPRESSO^24,25 (plane-wave basis) programs. The former allows performing WFT-in-WFT calculations by combining wave function FDE with one-dimensional periodicity. The latter, on the other hand, allows FDE calculations of two or more subsystems where more than one subsystem can be periodic and has been successfully used to embed neutral and charged subsystems inside a periodic subsystem, thereby allowing the calculation of ionization potentials.²⁶

In this work, an efficient and flexible implementation of DFT-based embedding using only Gaussian BFs within the TURBOMOLE program package²⁷ is described. This allows us to treat the periodic and molecular systems at the same footing as well as easy construction of embedding potential. Both KEDF and projection operator-based embedding potentials are employed to perform molecule-in-molecule, periodic-in-periodic, and molecule-in-periodic embedding. The Coulomb term, in embedding calculations involving periodic systems, is computed entirely in the direct space using only Gaussian BFs. Successful application of WFT-in-DFT to study the van der Waals interaction between H₂ (molecular) and H₁₀ chain (periodic) is demonstrated, despite an approximate KEDF-based embedding potential. Next, the WFT-in-DFT excitation energies, using different embedding potentials, of organic solutes in water, as well as the adenine–thymine base pair are compared with the results obtained from WFT calculations on the entire system. A projection-operator-based exact periodic-in-periodic embedding implementation is also reported that supports k-point sampling. Finally, the applicability of the embedding scheme coupled with RT-TDDFT using approximate or exact embedding potentials with or without a supermolecular basis is explored.

2. Theory and Implementation Details

In the following, the various embedding methodologies on which the current DFT-based embedding implementation is based on are described shortly.

2.1. Frozen Density Embedding

Only the key concepts of FDE are discussed in the following, while the readers are referred to the review by Wesolowski et al.²⁸ for a detailed overview on FDE. For the sake of simplicity, only the closed-shell case is considered here. However, the formalism can straightforwardly be generalized for the open-shell case and is outlined in detail in ref (29). Within the FDE¹ formalism, the total electron density ρ^tot of the system is partitioned into active and environment subsystem densities, ρ^act and ρ^env, such that ρ^tot = ρ^act + ρ^env. For a given frozen ρ^env, the ρ^act is determined by solving the Kohn–Sham constrained electron density (KSCED) equations

1

where 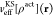is the usual KS effective potential of the isolated active subsystem, ϕ_i^act are the KS orbitals of the active subsystem, and v_emb is the embedding potential describing the effect of the environment subsystem. It is defined as

2

where the first and second potentials on the right hand side are due to the nuclei and electrons of the environment, respectively. The third term is the non-additive exchange–correlation potential and the last term is responsible for enforcing the Pauli exclusion principle between the subsystems^7,29 and is known as the non-additive kinetic potential

3

which is evaluated using an approximate KEDF. The embedding potential in eq 2 is exact in the limit of the exact KEDF. However, there are certain conditions that the densities are required to fulfill in order to recover the exact energy of the total system: (a) the environment density should be a non-negative function ρ^env(r) ≥ 0 and (b) the environment density should never be larger than the exact ground-state total density of the system ∀rρ^tot(r) ≥ ρ^env(r). Therefore, FDE can give only the upper bound of the ground state energy of the total system if ρ^env violates the above conditions. As a result, the quality of the results that one obtains is dependent on the choice of ρ^env. One possible choice is to use the isolated environment density without the active subsystem. Alternatively, freeze-and-thaw (FaT) cycles may be performed to obtain a relaxed ρ^env. FaT refers to the procedure where the roles of the active and environment subsystem are interchanged iteratively and was first introduced by Wesolowski and Weber.³⁰ Although, in principle, the partitioning of the total system is not unique, the FaT procedure yields unique subsystem densities as an artifact of approximate KEDFs (see discussions in refs (28) and (31)). Furthermore, due to the approximate KEDFs, the v_emb defined in eq 2 is suitable only for weakly overlapping subsystem densities.^32,33

2.2. Projection-Based Embedding for Molecular Systems

The need for approximate KEDFs within the FDE formalism stems from the fact that the KS orbitals of active and environment subsystems are not orthogonal with respect to each other. Therefore, the total kinetic energy of the system (T_s^tot) cannot be written as a simple sum of the kinetic energies of the subsystems 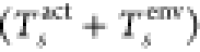but also requires a non-additive component (T_s). However, this orthogonality can be enforced by employing a level-shift projection operator introduced by Manby and Miller.⁷ Projection-based FDE is also known as “FDE with external orthogonality”.⁸ The level-shift projection operator is defined as P_B = μS^ABD^BS^BA, where S^AB is the overlap matrix of the active subsystem (A) BFs with the environment (B) BFs, D^B is the density matrix of the environment subsystem, and μ is the parameter that tends to infinity ideally and is taken to be 10⁶ in practical implementation. Essentially, the level-shift projection operator raises the energy of the ith environment orbital (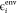) to a very high value 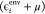for calculations on the active subsystem, thereby ensuring orthogonality between the subsystems and enforcing the Pauli exclusion principle. The embedding potential, in the matrix form, can therefore be written as

4

with the elements M_μν of the first three matrices on the right hand side 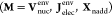defined as

5

where 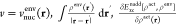and μ_act, ν_act are the BFs of the active subsystem. The method proposed by Manby and Miller⁷ requires a KS-DFT calculation on the entire system, and subsequently, the orbitals associated with the active and environment subsystems are identified for projection-based FDE. Alternatively, a more convenient procedure was proposed by Chulhai and Jensen,⁸ in which, starting from arbitrary subsystem KS orbitals, FaT cycles are performed to converge to the exact subsystem densities (KS orbitals). It should be noted here that projection-based FDE requires a supermolecular basis for the subsystems in order to achieve exact supermolecular DFT results and the approximate monomolecular basis results do not offer any significant improvement over the classic FDE with KEDFs (see Table S1 of the Supporting Information in ref (18)). An alternative to the level-shift projection operator is the Huzinaga operator³⁴ that provides better accuracy in the monomolecular basis.¹⁸

2.3. Projection-Based Embedding for Periodic Systems

For projection-based FDE to work for periodic systems, the only requirement is to make sure that the occupied Bloch orbitals of the active subsystem at a particular k-point are orthogonal to the occupied Bloch orbitals of subsystem B at the same k-point.¹⁹ The orthogonality of Bloch orbitals ψ_k at distinct k-points is ensured inherently. Therefore, the level-shift projection operator can be written as

6

where S_AB^k is the overlap matrix of the Bloch functions of A and B, with elements

7

To embed an active periodic subsystem in a periodic environment, the embedding potential is constructed analogously to eq 4, where all the terms are replaced by their periodic counterparts. In the matrix form, the embedding potential at a particular k-point can be written as

8

where V_nuc^k,env and J_elec are the Coulomb potential matrices due to the nuclei and the electrons of the periodic environment, respectively, and X_nadd^k is the non-additive exchange–correlation matrix. These are obtained from a Fourier transform of their real-space counterparts

9

where M_μν are the elements of the potential matrices, and L is the lattice vector. Similar to the molecular case, a supersystem basis along with FaT is required for exact results. This periodic-in-periodic framework can also be extended to perform a molecule-in-periodic embedding as shown in ref (19).

2.4. Extension to Correlated WFT Methods (WFT-in-DFT)

FDE can be coupled with higher level (WFT) methods using the frozen density embedding theory (FDET)²⁸ and the working equations can be found in ref (35) for variational WFT methods, and in ref (36) for non-variational WFT methods. In this work, however, the energy-error compensation ansatz, made popular by Carter and co-workers³⁷ is employed to perform WFT-in-DFT embedding. Using this approach, the molecular DFT embedding potentials can be used to perform WFT-in-DFT embedding (also known as high level-in-low level embedding¹⁹) in a straightforward and practical manner. This is done by adding the purely DFT-based v_emb to the Hartree–Fock (HF) core potential of the active subsystem and obtaining the converged HF reference orbitals. Any post-HF method can then be used to obtain an improved description of ground state and excited state properties. It should be noted that in some implementations, the embedding potential (or a part of it) may be updated self-consistently during the HF (variational) run, by updating ρ^act.^15,37,38 After the WFT-in-DFT calculation, the correction to the ground state DFT energy of the total system can be calculated as

10

where E_WFT^act and E_DFT are the WFT and DFT ground state energies, respectively, of the embedded active subsystem, obtained self-consistently in the presence of the embedding potential. The corrected energy of the total system is then given as

11

where E_DFT^tot is the low-level DFT energy of the total system. In principle, the doubly counted term ∫v_embρ_WFT/DFT dr, corresponding to the energy of interaction with the environment, should be subtracted from the energies E_WFT/DFT^act. This is because E_DFT already contains the interaction energy between the subsystems at the DFT level. Some strategies to deal with the double counting have been discussed in ref (6). In this work, the embedding potential is used only as a fixed additional one-electron potential in the Hamiltonian of the active subsystem to obtain E_WFT^act and E_DFT, and the explicit contribution due to the embedding potential ∫v_embρ_WFT/DFT^act dr is simply excluded from this quantity. Therefore, the influence of the environment is accounted for only implicitly during the optimization of HF reference orbitals.

This is in contrast to the exact FDET energy functional (eq 6 of ref (28)), as here (i) the total DFT energy of the system is being corrected by the 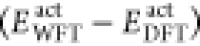term, (ii) there is an implicit assumption that the ρ^act from WFT is the same as ρ^act from DFT calculation; therefore, the energy contribution due to the embedding potential cancels out .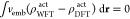

The calculation of excitation energies using WFT-in-DFT can be done using response-based³⁹ approaches or as the difference of the excited state energies¹⁷ of the embedded active subsystem. The latter approach is employed in this work. The polarization effects are neglected while calculating the WFT-in-DFT excitation energies of the active subsystem. That is, the excitations are assumed to be localized to the embedded active subsystem and the environment remains unperturbed (ρ^env unchanged). This means that most of the parts of the ground and excited state embedding potentials would be very similar; however, not exactly due to the additional dependence on ρ^act. This dependence on ρ^act can be circumvented by using the linearized FDET approach for excited states.^40,41 This has an added functionality of ensuring the orthogonality of embedded wavefunctions for each state.

Finally, it should be noted that even though the projection operator-based embedding potential allows us to perform exact DFT-in-DFT embedding, its use in WFT-in-DFT calculations may not always be computationally advantageous as it requires a supermolecular basis for a good representation of the embedding potential. Therefore, some works consider the possibility of using basis set reduction techniques,^42,43 absolute localization scheme,¹⁸ dual basis approach,⁴⁴ or truncation of virtual space⁴⁵ to address this issue. The approximate KEDF-based embedding potentials, however, can be used for WFT-in-DFT embedding straightforwardly (even with a monomolecular basis) without any additional steps and have been successfully employed for a number of applications, for example, correction to DFT adsorption energies of CO on Pd(111)¹⁵ and excitation energies of CO on Pd(111),³⁸ as well as solvated molecules.^16,17,46

2.5. Extension to Real Time–Time-Dependent Density Functional Embedding Theory

RT-TDDFT involves solving the single-particle time-dependent KS equations

12

where v_eff^KS[ρ](r,t) is the time-dependent effective KS potential that depends on the time-dependent electron density ρ(r,t). In implementations based on Gaussian BFs, the elements of the time-dependent single particle reduced density matrix D(t) can be evaluated as

13

where N_MO is the number of molecular orbitals (MO) and C_ν(μ)m(t) are the elements of the MO coefficient matrix C(t). The KS MOs are given as

14

where N_bf is the number of BFs (atomic orbitals) μ(r). The time evolution of the density matrix in the orthonormal basis is given by the Liouville–von Neumann (LvN) equation

15

where F(t) is the time-dependent KS matrix in the MO basis. The density matrix D(t) is propagated in time by numerically integrating the LvN equation using a plethora of methods⁴⁷ that ensure the idempotency of D(t). In this work, the Magnus expansion is used which is quite popular for its performance and stability. For further details on the RT-TDDFT implementation used in this work, the readers are referred to our previous work.⁴⁸

Coupling of DFT-in-DFT embedding with RT-TDDFT, hereafter referred to as real time–time dependent density functional embedding theory (RT-TDDFET), is quite straightforward. To propagate the electron density of the active subsystem embedded in an environment, the single-particle time-dependent KS equations (eq 12) need to be swapped with the KSCED equations (eq 1)

16

which include the embedding potential v_emb due to the environment. The propagation procedure remains the same.

Note, v_emb is a functional of both ρ^act and ρ^env (eqs 2 and 4) which are themselves dependent on time. Hence, as ρ^act(r,t) evolves in time, it would affect ρ^env(r,t), which in turn would also be needed to be evolved for a fully coupled RT-TDDFET. Consequently, for each time-step two RT-TDDFET calculations would need to be performed. This is also known as coupled FDE-TDDFT.

2.6. Implementation Considerations

The Coulomb contribution to the embedding potential (eqs 2 and 4) is evaluated efficiently using a combination of density fitting and continuous fast multipole method as described in ref (49). Furthermore, the KEDF and XC terms are calculated using the linear scaling hierarchical integration scheme.⁵⁰ The implementation also takes advantage of linear scaling direct space periodic DFT code for embedding calculations involving periodic systems.⁴⁹ The LibXC library is used for access to a large number of the exchange–correlation functionals and KEDFs.⁵¹

For WFT-in-DFT calculations, the modification is made only to the reference HF Hamiltonian (Fock matrix). This allows easy coupling with practically all the existing WFT methods in TURBOMOLE such as second-order approximate coupled-cluster singles and doubles (CC2), CCSD with perturbative triples CCSD(T), Møller–Plesset (MP2), and so forth. The embedding potential is calculated only once using DFT-based densities for ρ^act and ρ^env and kept fixed during the HF and WFT run similar to the linearization strategy proposed in ref (52). Additionally, in order to avoid complications of using a different embedding potential for ground and excited state, which requires v_emb to be updated with the excited ρ^act, the ground state v_emb is used for excited state WFT-in-DFT calculation as well.^40,41 This is denoted as “route A” in ref (17). The excitation energy can then be approximated using

17

where 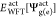are the WFT ground (excited) state energies evaluated in the presence of the ground state v_emb, however, do not contain the corresponding contribution ∫v_embρ_g(e)^act dr explicitly. The above equation is taken from ref (17) (eq 16) and follows from eq 15 of the same work by assuming that ρ_e ≈ ρ_g^act. Please note that the non-linear embedding potential never appears in the explicit evaluation of the energies in eq 17. Such a procedure, where the environmental polarization is neglected, has been also denoted as state-independent embedding (no differential polarization) in ref (17), although implicit polarization may occur when using a supermolecular basis.⁵³ Alternatively, the ground-state polarization of the environment may be performed by employing the FaT procedure discussed previously. This is in contrast to the state-specific¹⁷ and response theory³⁹-based approaches where the response of the environment can be accounted for. Such an approximation is valid when the non-additive kinetic and XC potentials of the ground and excited states are not much different. This approximation has been known to reproduce the experimental energies of local excitations of acetone-in-water,¹⁶ CO adsorbed on Pd(111),^15,38 and embedded MgO clusters²¹ with reasonable accuracy and is discussed in detail in ref (17).

For RT-TDDFET, ideally both ρ^act(r,t) and ρ^env(r,t) should be evolved in time to obtain the same results as a supermolecular calculation. In our implementation however, the environment density is kept fixed to its ground state value ρ^env(r,t₀), that is, the environment does not react to the excitations in the active region. This leads to savings in computation time with little to no loss of accuracy as long as there is no coupling between the excitations of the subsystems, that is, the excitations are localized to the active part and do not respond to the excitations of the other subsystem. Furthermore, it is also possible to use a frozen ground state embedding potential for RT-TDDFET, where even the active subsystem density is fixed to its ground state value, resulting in further cost-savings.

In the following, the exact strategies for constructing the embedding potential, based on the approximate KEDFs and the level-shift projection operator are discussed.

2.6.1. Method 1 (KEDF)

This is essentially the classic FDE strategy of constructing the embedding potential. The isolated environment density ρ^env is determined using DFT. This density is then plugged into the KEDF-based embedding potential v_emb (eq 2), and the active subsystem density ρ_emb^act is relaxed in the presence of this embedding potential. Because the embedding potential is also a functional of the active subsystem density, it is updated at each SCF iteration during the active subsystem DFT run. It is also possible to perform FaT by interchanging the active and environment subsystems, resulting in a converged embedding potential. The embedding potential so constructed can thereafter be used for correlated WFT or RT-TDDFET calculation on the active subsystem. The implementation supports both mono- and super-molecular basis calculations.

2.6.2. Method 2 (KEDF)

The second strategy is inspired by the long-existing implementations of Carter and co-workers.^15,38 Here, the total system density ρ^tot and the isolated active subsystem density ρ_iso^act are determined using a low level method such as DFT with LDA functional. Then, an approximation for the environment density 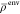is calculated as 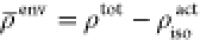. The KEDF-based embedding potential v_emb (eq 2) is then calculated by using the fixed 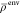and ρ_iso as environment and active subsystem densities, respectively. This means that v_emb remains constant during the active subsystem embedding run. Updating the v_emb with the embedded active subsystem density ρ_emb^act during the DFT-in-DFT embedding run resulted in convergence issues as also reported in refs (15) and (20).

Please note that while in ref (15), only the nadd KEDF term (eq 3) was kept fixed to avoid the convergence issue, here the entire embedding potential is frozen during the embedding calculation.

Although this method can be used to perform molecule-in-molecule embedding, it is especially effective for molecule-in-periodic embedding due to the fact that the KS matrix for periodic DFT is computed entirely in direct space using Gaussian BFs.

In our implementation, after the total periodic system DFT run, the total Coulomb J^tot, exchange–correlation X^tot, and kinetic T^tot potential matrices (in the basis of active subsystem), corresponding to the central unit cell, are saved on the disk. These are defined as

18

19

20

where μ and ν are the BFs of the active subsystem corresponding to the central unit cell, while ρ^tot and ρ_n^tot are the total periodic electron and nuclear charge density, respectively. Analogously, after the isolated active subsystem DFT run, the corresponding matrices J^act, X^act, and T^act are calculated and subtracted from their total system counterparts to form the embedding potential. This is very practical because all the required matrices are already calculated during the regular DFT run except the KEDF-based kinetic potentials. Both monomolecular and supermolecular basis calculations are supported via method 2; however, it is incompatible with the FaT procedure. It is worthwhile to note that the approximation for environment density 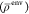, used here, can be negative, which violates the requirement of ρ^env to be a non-negative function as mentioned in Section 2.1. Therefore, the results are expected to contain additional error.

2.6.3. Method 3 (Projection Operator)

The third strategy is nearly the same as method 1, except that the need for the approximate KEDFs is circumvented by using a level-shift projection operator described in Section 2.2. In addition to the molecule-in-molecule embedding, it can also be used to perform periodic-in-periodic embedding. The isolated molecular (periodic) environment density and density matrix are determined using DFT and the embedding potential is constructed for the active molecular (periodic) subsystem using eq 4 (8). In our implementation, the FaT procedure is used to obtain exact results as proposed by Chulhai and Jensen.⁸ Only supermolecular basis is supported for periodic-in-periodic embedding calculations. The periodic-in-periodic embedding implementation is similar to the one reported in ref (19), with one major difference, that all the contributions to the embedding potential (eq 8) are calculated in direct space except the non-local projection operator. This allows for a much more efficient k-point sampling. Direct inversion of iterative subspace was employed to accelerate the slow convergence for periodic calculations.

3. Computational Details

In this section, the computational details of the various systems studied in this work are presented. All the calculations in this work are performed using TURBOMOLE unless stated otherwise.

3.1. H₂–H₁₀

The calculations on the H₂–H₁₀ system utilize the def2-TZVPP basis set and the Weigend (universal) auxiliary basis set for density fitting.^54,55 The DFT and embedding potential calculations are performed using the Slater exchange functional and the Perdew–Wang correlation functional (LibXC codes: x = 1, c = 12).^56,57 The LC94 KEDF is used for the calculation of the non-additive kinetic potential in v_emb (method 2) which is derived from the Perdew–Wang (PW91) exchange functional⁵⁸ (therefore also denoted as PW91K) with parameters adapted for the kinetic energy by Lembarki and Chermette (LC94)⁵⁹ and investigated in the context of FDE by Wesolowski et al.⁶⁰ The corresponding LibXC code is 521. The periodic γ-point CCSD(T) calculations are performed with PySCF.⁶¹ The python script used is provided in the Supporting Information.

3.2. Solvated Molecules: Acetone, Acrolein, and Methylenecyclopropene

The CC2^62,63 and CC2-in-DFT calculations on the solvated molecules are performed using the cc-pVDZ basis sets⁶⁴ and the corresponding auxiliary basis sets⁶⁵ for the resolution of identity (RI) approximation. For CC2-in-DFT, the solvated molecules are considered as the active subsystem and the water molecules are considered as the environment subsystem. The exchange–correlation functional is approximated using the Perdew–Burke–Ernzerhof (PBE) parametrization of the GGA.^66,67 For the calculation of the embedding potentials using methods 1 and 2, the LC94 KEDF was employed.⁵⁹

3.3. Adenine–Thymine

The DFT, CC2, and CC2-in-DFT calculations on adenine–thymine base pair were performed using the cc-pVDZ basis set and the corresponding auxiliary basis sets.⁶⁴ The embedding potential calculations made use of the PBE exchange–correlation functional, and LC94 KEDF.^59,66,67

3.4. Periodic Systems: Polyethylene, Neoprene, and Diamond

The basis sets and the k-mesh sizes used for the periodic calculations are shown in Table 3. Supersystem bases were used for both the subsystems. The PBE exchange–correlation functional (LibXC codes: x = 101, c = 130) was used. The embedding potential was calculated using method 3 with five FaT cycles.

Table 3. Calculation Details (k-Mesh Size and Basis Set) as Well as the Total DFT Ground State Energies (a.u.) and Periodic-in-Periodic Embedding Errors of Periodic Systems.

system	k-mesh size	basis set	EDFT	ΔE = Eemb – EDFT
polyethylene 1D	32 × 1 × 1	def2-SVP	–78.4571146	2.0 × 10–6
neoprene 1D	10 × 1 × 1	def2-SVP	–614.9723856	1.2 × 10–6
diamond 3D	10 × 10 × 10	def2-SVP	–304.3591154	2.1 × 10–6

3.5. LiH

For the calculations on LiH, the def2-TZVPPD basis set along with the Weigend (universal) auxiliary basis was employed.^54,55 For the exchange–correlation functional, a combination of Slater exchange (LibXC code: 1) and Vosko–Wilk–Nusair expression V (VWN5) correlation (LibXC code: 7) was used.^56,68 For RT-TDDFT and RT-TDDFET, the propagation time was 700 au (≈17 fs) with a time step of 0.1 au. For RT-TDDFET with method 1, the LDA Thomas–Fermi KEDF (LibXC code: 50) was used.⁶⁹ Five FaT cycles were used to determine the ground state subsystem densities for both methods 1 and 3.

3.6. Benzene–Fulvene

The calculations on the benzene–fulvene dimer are performed using the def2-TZVPPD basis and the Weigend (universal) auxiliary basis at the PBE level (LibXC codes: x = 101, c = 130).^54,55,66,67 The LC94 KEDF (LibXC code: 521) was employed for embedding potentials calculated using method 1.⁵⁹ The propagation time was set to 1000 au, with a time step of 0.1 au for RT-TDDFT and RT-TDDFET calculations.

4. Results and Discussion

4.1. WFT-in-DFT: Ground States

The applicability of molecule-in-periodic embedding is tested for ground state properties such as adsorption energies. As the test system, an H₂ molecule interacting with an H₁₀ periodic 1D chain is considered. The structures are provided in the Supporting Information. To perform the embedding calculations, the H₂ molecule as well as the two central H atoms of the H₁₀ chain are considered as the active subsystem and treated using the explicitly correlated CCSD(T) method. The rest of the H atoms are treated at the LDA-DFT level. This system has also been studied by Carter and co-workers previously; however, there are some subtle and obvious differences in our approach.⁶ The main difference being that, in contrast to a unique embedding potential used in their study, an approximate KEDF-based embedding potential is employed here, which is calculated using method 2 described in Section 2.6.2. Moreover, here, the adsorption energies are calculated instead of binding energies, and the LDA-DFT and WFT-in-DFT results are compared with periodic γ-point CCSD(T) calculations. It should be noted that unlike DFT calculations, the adsorption energies are not the same as the binding energies for CCSD(T) calculations as shown in Supporting Information, Figure S1. Therefore, a molecule-in-periodic embedding scheme is needed to correctly model the adsorption energy.

Figure 1 shows the adsorption energies of the H₂ molecule calculated for various separation distances from the H₁₀ chain using molecule-in-periodic embedding, periodic γ-point DFT, and periodic γ-point CCSD(T) methods. The DFT and CCSD(T) adsorption energies are calculated using the following formula

21

Figure 1.

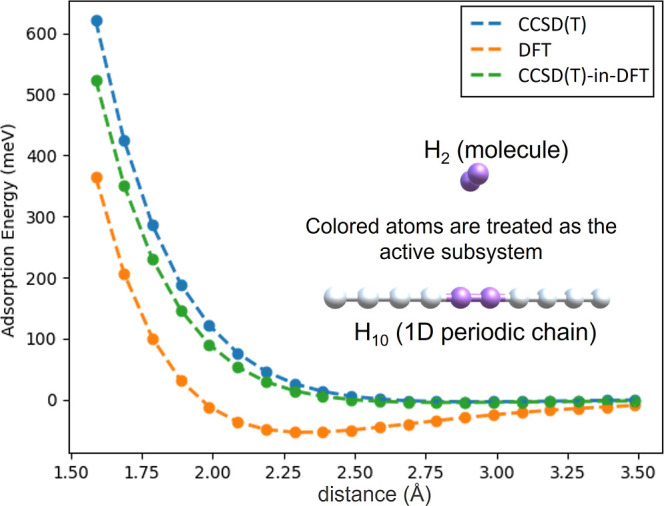
Adsorption energies of H₂ on the H₁₀ periodic chain at various separation distances calculated using periodic CCSD(T), LDA-DFT, and CCSD(T)-in-DFT.

As expected, DFT overbinds the H₂ molecule and predicts too short equilibrium distances. The periodic DFT calculation gives an adsorption energy of around −53.18 meV at the equilibrium separation of 2.29 Å. CCSD(T) predicts a very weak adsorption energy of −3.27 meV and a higher equilibrium distance of 2.89 Å. The CCSD(T)-in-DFT adsorption energies are calculated by correcting the DFT adsorption energies in the same way the total DFT energies were corrected in eq 11 (Section 2.4)

22

where

23

and

24

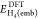and 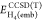are the DFT and CCSD(T) energies of the embedded active subsystem (H₂ and two central atoms of the H₁₀ chain) in the presence of the embedding potential (method 2), but without the ∫v_embρ_DFT/CCSD(T)^act dr term. Similarly, to calculate 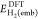and 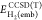, an embedding calculation is performed for the two central atoms of the H₁₀ chain. CCSD(T)-in-DFT gives an adsorption energy of −4.37 meV at an equilibrium distance of 2.78 Å. From Figure 1, it is observed that CCSD(T)-in-DFT is able to correct the LDA adsorption energies quite significantly reproducing the CCSD(T) results with negligible errors and significantly reduced computational cost.

4.2. WFT-in-DFT: Excited States

In order to illustrate the validity and applicability of the implementation, CC2-in-DFT excited state calculations are performed to study: (1) solvatochromic shifts in small molecules and (2) hydrogen-bonding-induced shifts in the adenine–thymine nucleic acid base pair.

4.2.1. Solvatochromic Shifts

Water solvent-induced shifts in the first excitation energies of acetone, acrolein, and methylenecyclopropene (MCP) are studied using the structures shown in Figure 2a–c, with 20, 19, and 17 water molecules, respectively (see the Supporting Information for atomic coordinates). It has previously been shown that WFT-in-DFT excited state calculations provide a very reasonable description of solvent (water)-induced shifts in the chosen molecules.¹⁷ Therefore, these systems were used to validate the implementation. Only the embedding potentials employing non-additive KEDFS are considered because they work well without a supermolecular basis for weakly interacting systems. This allows a significant reduction in the computational cost.

Figure 2.

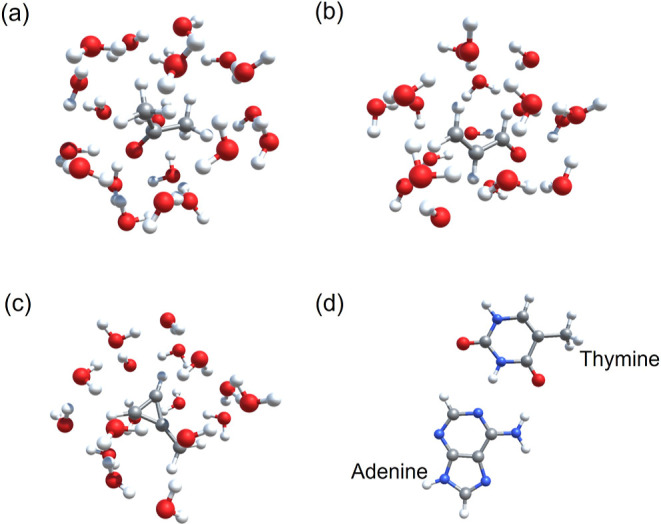
Structures of (a) acetone in water, (b) acrolein in water, (c) methylenecyclopropene in water, and (d) adenine–thymine base pair used for CC2-in-DFT excited state calculations. Gray: C, red: O, white: H, and green: N. Visualizations created using CrysX-3D Viewer.⁷⁰

In Table 1, the lowest excitation energies of the supermolecular CC2 calculation are compared with CC2-in-DFT calculations using method 1, with and without the FaT procedure, as well as with the method 2. Method 1, without FaT, fares the best with a maximum absolute error of just 0.03 eV with respect to the supermolecular CC2 calculation, probably due to beneficial error-cancellation. Method 2 performs the worst among all the methods, with the maximum absolute error of 0.62 eV, which is expected due to its simplistic nature. Applying the FaT procedure to calculate a self-consistent embedding potential, results in slightly inferior performance than without FaT. The results are in agreement with the similar studies performed in refs (17) and (71). The magnitude of error with method 1 is similar to the one reported by Zech et al.,⁷¹ although they used a supermolecular basis. The good performance of embedding potential calculated via method 1 is quite encouraging and also serves as a validation of the implementation. It should be noted that such a WFT-in-DFT approach dramatically reduced the computational requirements. As an example, consider the case of acetone-in-water, where the total number of BFs is 466, out of which, only 86 are for acetone. Therefore, only 86 BFs (<20% of total) were required to perform the CC2-in-DFT calculations.

Table 1. First Excitation Energies (eV) of the Solvated Molecules from Supermolecular CC2 and CC2-in-DFT Using Embedding Potentials Constructed via Methods 1 and 2.

system	CC2 isolated	CC2 supermolecular	CC2-in-DFTmethod 1	CC2-in-DFTmethod 1 FaT	CC2-in-DFTmethod 2
acetone + water	4.49	4.81	4.78	4.88	5.32
acrolein + water	3.71	4.10	4.10	4.20	4.72
MCP + water	4.61	5.15	5.12	5.26	5.18

4.2.2. Adenine–Thymine Base Pair

The performance of the embedding potentials calculated using methods 1 and 2 is examined for the CC2-in-DFT excitation energies of the adenine–thymine base pair. The structure was taken from ref (10) and is visualized in Figure 2d. This system has been studied before in the context of FDE-TDDFT.^10,72

The first six excitation energies of the total system calculated using various methods are reported in Table 2. Comparing the CC2 supermolecular results with the excitation energies of the isolated adenine and isolated thymine molecules, it is clear that the difference is not trivial. Furthermore, CC2 calculation on the isolated adenine molecule predicts the first π → π* transition of adenine to be of higher energy (5.56 eV) than the n → π* transition (5.38 eV). This ordering is reversed in the CC2 supermolecular calculation. All the CC2-in-DFT calculations using different embedding potentials were able to reproduce this behavior very well. Similar to the case of solvated molecules, CC2-in-DFT with v_emb calculated using method 1 performs the best for most of the excitations, with a maximum absolute error of only 0.05 eV. Method 1 with FaT gives very similar results to method 1 without FaT, with a few errors being slightly larger. FaT procedure results in self-consistent subsystem densities, and the converged v_emb thus generated is supposed to be more accurate in theory. However, this is only valid for DFT-in-DFT embedding. The performance of WFT-in-DFT embedding is also dependent on the ability of DFT to accurately describe the ground state of the system. The slightly inferior performance of v_emb obtained using method 1 with FaT suggests that the DFT description of the ground state of the system is not entirely accurate. Additionally, it has also been suggested that the variational relaxation of the environment density is problematic because, in addition to the meaningful electronic polarization, it is also an artifact of the error in the approximation used for the non-additive KEDF. This results in artificial charge redistribution or a wrong polarization of the active and environment subsystems (see discussion in refs (28)(31), and (53)). The maximum absolute error, however, is smaller at just 0.04 eV. Once again, method 2 gives the largest errors with respect to the reference supermolecular CC2 calculation.

Table 2. Calculated First Six Excitation Energies (eV) of the Adenine–Thymine Base Pair.

transition	CC2 isolated	CC2 supermolecular	CC2-in-DFTmethod 1	CC2-in-DFTmethod 1FaT	CC2-in-DFTmethod 2
thymine n → π*	5.20	5.34	5.34	5.38	5.51
adenine π → π*	5.56	5.52	5.55	5.54	5.55
adenine n → π*	5.38	5.58	5.56	5.60	5.60
thymine π → π*	5.74	5.65	5.70	5.69	5.73
adenine π → π*	5.79	5.74	5.76	5.76	5.78
adenine n → π*	6.01	6.13	6.14	6.17	6.24

4.3. Exact Periodic-in-Periodic Embedding

To illustrate and validate the working of the periodic-in-periodic embedding, the total energies of periodic systems using regular DFT and periodic-in-periodic embedding using the level-shift projection operator (method 3) have been calculated. Three periodic systems are considered. Neoprene (1D), polyethylene (1D), and diamond (3D). The structures are shown in Figure 3. The atomic positions as well as the lattice parameters are taken from ref (19) and also provided in the Supporting Information. The labeled and transparent atoms are treated as one subsystem and the remaining as the other subsystem.

Figure 3.

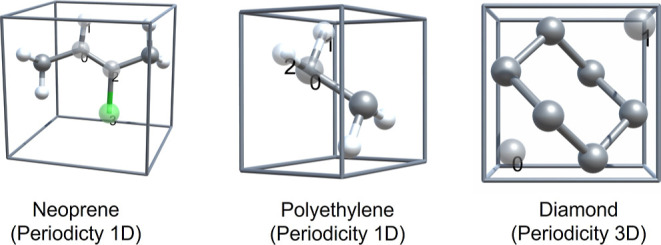
Structures of the periodic systems used for exact periodic-in-periodic embedding. Gray: C, white: H, and green: N. Subsystem I: labeled and transparent atoms; Subsystem II: opaque atoms. Visualizations using CrysX-3D Viewer.⁷⁰

Table 3 shows the reference DFT energies of the total periodic system as well as the errors obtained with DFT-in-DFT embedding (method 3) for the different systems considered. The errors are of the order of μHa, implying numerically exact embedding. A similar accuracy was also achieved in ref (19). This implementation does not offer any computational savings due to the need of a supersystem basis for exact results. However, this periodic-in-periodic embedding implementation can be extended to perform exact molecule-in-periodic embedding via projection operator (method 3) and serves as a stepping stone for that. An interesting use-case could be to study two different periodic structures stacked over each other, with each requiring a different exchange–correlation functional.

4.4. RT-TDDFT Coupled with DFT-Based Embedding

The implementation of RT-TDDFT coupled with DFT-in-DFT embedding (RT-TDDFET) is tested for systems with coupled and uncoupled excitations.

4.4.1. LiH

First, the LiH molecule with the closed shell Li⁺ and H⁻ subsystems at a separation of 2 Å is examined. It has been shown previously by Chulhai and Jensen¹¹ that the excitation energies of Li⁺ are greater than 48 eV at the LDA level and therefore uncoupled to the H⁻ excitations. This is also illustrated in Figure 4, where the RT-TDDFT absorption spectra of LiH, H⁻, and Li⁺ have been plotted. In their study, they were able to recover exact excitation energies using LR-TDDFT coupled with projection operator based embedding (our method 3). In this work, RT-TDDFET spectra of both the subsystems are calculated and their superposition is compared with the regular RT-TDDFT spectrum of the total system. Embedding potentials calculated via methods 1 and 3 are considered. Furthermore, the influence of monomolecular and supermolecular basis is examined. For an uncoupled system such as LiH, the absorption spectrum corresponding to method 3 (with FaT and supermolecular basis) is expected to reproduce the regular RT-TDDFT absorption spectrum exactly even though the environment density is kept frozen to the ground state density. Therefore, this would also serve as a validation of the implementation.

Figure 4.

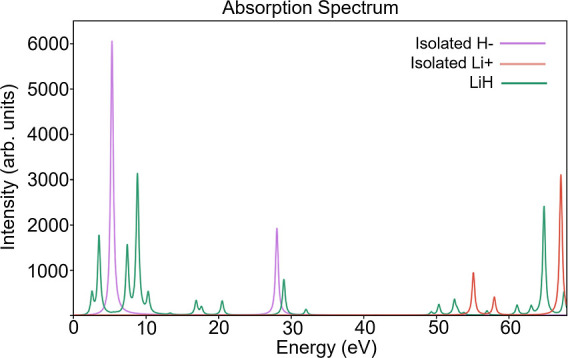
RT-TDDFT absorption spectra of LiH as well as isolated H⁻ and Li⁺.

Figure 5a,c shows the absorption spectra calculated with methods 1 and 3, respectively, with monomolecular bases for the subsystems. Both the methods show large errors in the absorption spectra, with method 3 being the worst with no qualitative similarity to the reference spectrum. This is expected as the level-shift projection operator is not meant for use with monomolecular basis. The supermolecular basis results are shown in Figure 5b,d. Spectra from both the methods show significant improvement over their monomolecular basis counterparts. Method 3 reproduces the reference spectrum exactly. This shows that, while KEDF-based embedding may be able to predict a few excitation energy shifts reasonably, a proper description of the entire absorption spectrum requires a projection operator + supermolecular basis treatment. It should be noted here that although the environment-density was frozen in the embedding potential, the active subsystem density was updated at each time-step. Therefore, the embedding potential was not independent of time. However, it was also checked that for the case of LiH, the absorption spectra were quite similar, even with a frozen embedding potential (see Figure S2 of the Supporting Information). Please note, a comparison of the binding energies with and without embedding has also been provided in Table S4 of the Supporting Information.

Figure 5.

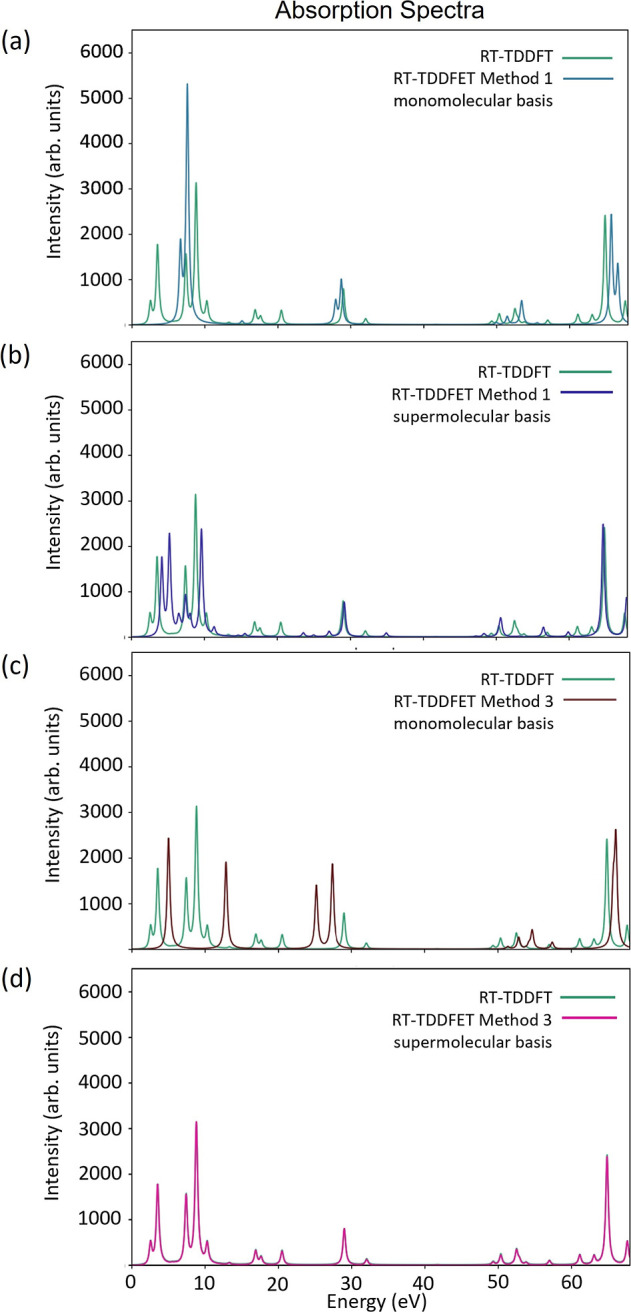
Comparison of the RT-TDDFET absorption spectra of the LiH molecule calculated using various embedding techniques with the reference RT-TDDFT absorption spectrum: (a) method 1 (monomolecular basis), (b) method 1 (supermolecular basis), (c) method 3 (monomolecular basis), and (d) method 3 (supermolecular basis).

4.4.2. Benzene–Fulvene Dimer

Next, the system of strongly coupled chromophores: benzene and fulvene at a separation of 4 Å is considered. A detailed analysis of this system in the context of RT-TDDFT and FDE has been performed in ref (12) using Quantum ESPRESSO.¹⁴ However, in that work, the authors used a plane-wave basis and only the KEDF-based embedding potential, corresponding to our method 1. Here, the effect of supermolecular or monomolecular basis as well as the type of embedding potential used is investigated. Furthermore, the effect of updating the embedding potential during the time evolution is also considered.

Figure 6a shows the comparison of RT-TDDFET absorption spectra, obtained using method 1 (without FaT), employing a monomolecular basis and keeping v_emb frozen in time, with the isolated and total RT-TDDFT spectra. Clearly, the RT-TDDFET spectrum is nowhere close to the reference total spectrum, where the peak corresponding to benzene is significantly suppressed. In fact, unlike the LiH case, method 1 produces a spectrum that is very similar to the spectra of isolated subsystems, indicating no effect of embedding. Therefore, to model the excitations in a better manner, a supermolecular basis treatment is required. In Figure 6b, the RT-TDDFET absorption spectra for methods 1 and 3, calculated using supermolecular basis and a frozen v_emb are reported. Note that five FaT cycles were used to calculate the ground state starting densities of the subsystems. The spectrum corresponding to method 1 shows slight improvement over its monomolecular counterpart by suppressing the benzene peak slightly further. This spectrum is similar to the one obtained in ref (12) using a plane-wave basis, which is equivalent to using a supermolecular basis. The RT-TDDFET spectrum corresponding to method 3 shows remarkable similarity to the reference total spectrum.

Figure 6.

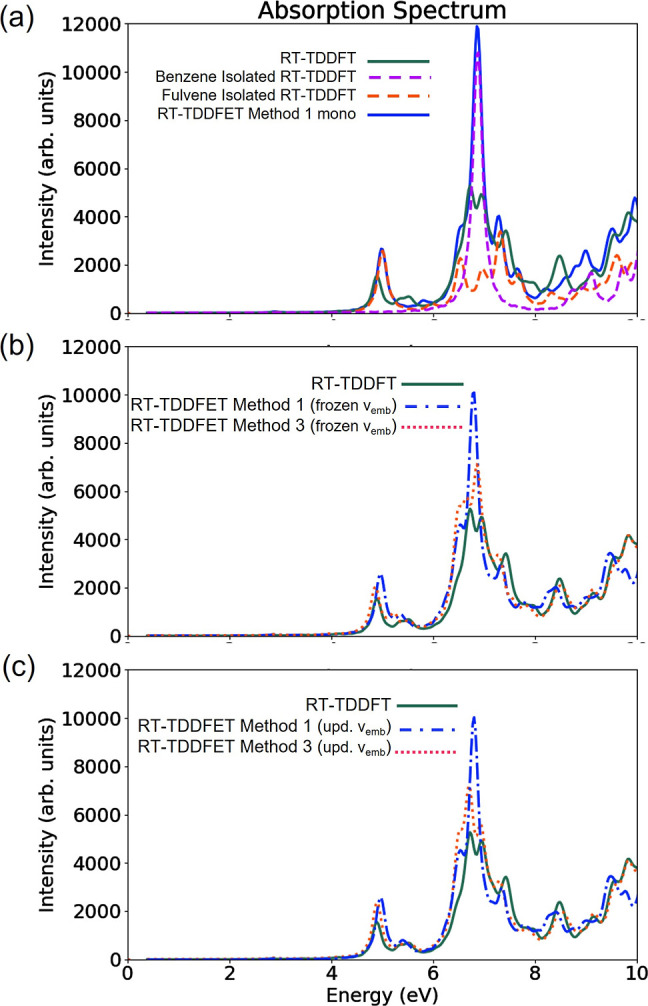
Comparison of the RT-TDDFET absorption spectra of benzene–fulvene dimer calculated using various embedding techniques with the reference RT-TDDFT absorption spectrum: (a) method 1 (monomolecular basis + frozen v_emb) along with the isolated RT-TDDFT absorption spectra of benzene and fulvene, (b) methods 1 and 3 (supermolecular basis + frozen v_emb), and (c) methods 1 and 3 (supermolecular basis + updating v_emb).

Thus far, the embedding potential was kept frozen during the RT-TDDFET procedure. That is, only the ground state densities were used for the active and environment subsystems in the formula of v_emb. Figure 6c shows the results when the active subsystem density, in the expression of v_emb, is allowed to be updated with time, as in the LiH case. There is no notable difference in the RT-TDDFET (method 1) spectrum; however, RT-TDDFET (method 3) does benefit from this added flexibility and matches the reference total RT-TDDFT absorption spectrum even more, reproducing almost all the qualitative features. Unlike the LiH case with uncoupled excitations, it is not possible to reproduce the reference RT-TDDFT spectrum completely even with method 3 and updating embedding potential. This is because the environment density is still not evolved in time, and hence does not react to the excitations of the active subsystem. However, reasonable accuracy is achieved nonetheless because the chromophores are 4 Å apart. Therefore, the improvement gained from updating embedding potential may or may not justify the added computational cost of updating embedding potential and must be decided on a case-by-case basis. For a more detailed analysis of the effect of updating the embedding potential, the readers are referred to ref (13).

5. Summary and Conclusions

An efficient implementation of DFT-based embedding for molecules and periodic systems using Gaussian-type orbitals as BFs is described. The implementation is flexible and supports various flavors of embedding: molecule-in-molecule, molecule-in-periodic, and periodic-in-periodic. Embedding potentials based on KEDFs and projection operator are implemented. Furthermore, the implementation is coupled with a variety of quantum chemistry methods such as CCSD(T), CC2, RT-TDDFT, and so forth.

Consistent with previous studies, it is showed that KEDF-based WFT-in-DFT calculations with monomolecular basis offer a significantly improved description of ground^15,38 and excited^17,53,71 state properties over DFT at only a fraction of the computational cost. Furthermore, a real-space implementation of exact periodic-in-periodic embedding using projection operator, supermolecular basis, and FaT procedure is reported. While this does not lead to any computational advantage yet, it can be improved in the future by employing basis set truncation techniques or using a smaller basis for the environment. Lastly, a detailed analysis of RT-TDDFT coupled with DFT-in-DFT embedding is presented, describing the influence of supermolecular basis, as well as the time dependence of the embedding potential. For systems with uncoupled excitations, RT-TDDFET with projection operator-based embedding potential and supermolecular basis is able to reproduce the reference RT-TDDFT spectrum exactly, even though the environment density is kept frozen. Additionally, it offers reasonable accuracy for coupled chromophores as well.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.2c00380.

• Atomic coordinates of the investigated systems; Python script for periodic HF, DFT, CCSD(T), and CCSD(T); molecular binding energy versus adsorption energy of H₂–H₁₀ chain; comparison of DFT-in-DFT and DFT binding energies for LiH and benzene–fulvene dimer; and RT-TDDFET absorption spectrum of LiH using a frozen versus updating embedding potential (ZIP)

The authors declare the following competing financial interest(s): Marek Sierka has an equity interest in TURBOMOLE GmbH and serves as its chief executive officer.