Overconfidence bias in the Indian stock market in diverse market situations: an empirical study

Abstract

Market situations affect investors’ sentiments. Sudden and sharp changes in the market may make investors adjust their beliefs and change their viewpoints. To quote, such sharp changes include the stock market crash of 2008 and the COVID-19 pandemic, which significantly impacted investors' emotions. In this direction, this study attempts to find investors’ overconfidence bias in different market situations, i.e., precrash period (2006–2008), crash period (2008–2010), and post-crash period (2010–2015, 2015–2020, 2020–2021). We have obtained secondary data for this study from the BSE 100 index (as a proxy of the Indian stock market). Econometric techniques used for data analysis include Vector Auto Regression (VAR), Granger causality VAR/Block Exogeneity Wald Test, and Impulse Response Function (IRF). The study finds that the investors were overconfident during pre-crash periods, i.e., before the global market crash of 2008 and the duration between 2015 and March 2020. In postcrash periods, i.e., during 2008–2010, 2010–2015, and 2020–2021, investors were not overconfident.

Introduction

One basic assumption of standard finance theories is investor rationality (Titan 2015). It assumes investors to be utility-maximizing machines that take investment decisions on a risk-return trade-off basis, but it is practically impossible (Simon 1955). Investors do not always consider risk-return trade-offs before investing. Sometimes they invest in trying their luck, sometimes to follow their investment gurus, sometimes in proximate companies’ stocks, and so on. In essence, it is not always rationality that guides the investors’ decisions; often, it is feelings, heuristics, and instinct (Tversky and Kahneman 1974). These feelings/heuristics/instincts are termed behavioral biases in the subject of behavioral finance.

Overconfidence is a robust behavioral bias in the Indian stock market (Statman et al. 2006). We can break overconfidence as over + confidence. More than appropriate confidence is overconfidence. Individuals’ too much confidence in their knowledge, accuracy, capabilities, and luck make them overconfident (Oskamp 1965; Koriat et al. 1980; Lichtenstein et al. 1977). Similarly, stock market information, past successes, capability to access information, and capability to analyze information turn an investor into an overconfident investor (Daniel et al. 1998; Barber and Odean 2001; Gervais and Odean 2001). Similarly, Berthet (2022) states that overconfidence bias affects professionals’ decision-making processes in four areas: management, finance, medicine, and law.

Developed and developing stock markets have shown the presence of overconfident investors (Charles and Kasilingam 2015; Choudhary et al. 2021). Odean (1999), Barber and Odean (2000), Statman et al. (2006), Du and Budescu (2017), and Meier (2018) find the existence of overconfidence bias among investors of the United States. Similarly, Glaser and Weber (2007) confirm overconfidence bias among the investors of Germany. Likewise, Grinblatt and Keloharju (2009) find overconfidence bias among the investors of the Finland stock market. Furthermore, Metwally and Darwish (2015) evidence overconfident investors in the Egyptian stock market in different market situations. In this context, Zia et al. (2017) and Qasim et al. (2019) find overconfidence bias amongst Pakistani investors. In the Indian stock market, De et al. (2010), Prosad et al. (2013), and Mushinada and Veluri (2018) find the investors overconfident.

Overconfidence is an emotional bias, and emotions change with market conditions. Bull periods bring joy and happiness, while bear periods bring sadness to the market. Feelings of happiness and sadness affect the stock market also. Metwally and Darwish (2015) study the Egyptian stock market in different upward and downward periods and found that the market conditions affect the trading activity. There is minimal research in the Indian context that studies the effect of market situations on trading activity except for Mushinada (2020). To bridge this gap, we study overconfidence bias among Indian investors in different market situations at the market level. We study the data for the period 2006–2021 consisting of the pre-crash period (2006–2008), crash period (2008–2010), and post-crash periods (2010–2015, 2015–2020, 2020–2021). The reason for the sub-division of the period 2010–2021 is the presence of structural breaks around 2015 and the COVID-19 outbreak in 2020. Another reason for sub-dividing the post-crash period is to make the results generalizable, as we cannot generalize the research results, which studies heterogeneous data in one go.

This research is unique as it is one of the scarce studies to check the effect of market conditions on trading activity, especially in the case of the Indian stock market. Earlier, De et al. (2010), Prosad et al. (2013), and Prosad et al. (2017) have also found instances of overconfident investors in the Indian stock market at the market level. What prompts us to carry out this research is that we cannot generalize the results from the data, which comes from heterogeneous market conditions, analyzed in one go. Therefore, first, we segregate data into several sub-periods to match similar market conditions and explore it accordingly to match the generalizability criterion.

The leftover parts of the article are presented in the following manner: Sect. 2 discusses the review of relevant literature, and Sects. 3 and 4 discuss research objectives and methodology, respectively. Section 5 depicts data analysis and discussion of results. Finally, Sect. 6 concludes the findings of the study.

Review of relevant literature

We have reviewed various studies published in reputed journals for this paper regarding the foundations of overconfidence, the impact of demographic factors on overconfidence, the influence of overconfidence on the stock market, and the change in investors' overconfidence level.

Foundations of overconfidence

Most studies report that the incidences of past success, i.e., good returns in the past, make investors overconfident and pursue them to trade more. Daniel et al. (1998) reveal that the shareholders who gain wealth through successful investments fall prey to self-attribution and become overconfident. They also find overconfident investors to overweight personal information and under weigh public information, which increases market volatility. Likewise, Gervais and Odean (2001) note that investors become overconfident when they get wealth from their investment decisions. Talking from another view, Glaser and Weber (2007), and Liu et al. (2016) find that when investors feel that they are better in investment skills, they can earn superior returns than others, then they become overconfident. Investors are more overconfident when the markets are in the bull phase (Chen, 2012; Kudryavstev, 2017). However, Huang and Goo (2008) name the incidences of past success as a happy investment atmosphere, which makes the investors overconfident. Likewise, Abdin et al. (2022) find that illusion of control, optimism, and self-attribution are reasons for investors’ overconfidence.

Through their empirical research, Daniel et al. (1998) find that self-attribution bias is a key determinant of investors’ overconfidence. Overconfident investors trade more insistently and invite more market volatility, turnover, and trading volume. It is further confirmed by Odean (1998), Statman et al. (2006), Chuang and Susmel (2011), Prosad et al. (2013), Daniel and Hirshleifer (2015), Mushinada and Veluri (2018), Huang et al. (2022), Jain et al. (2022), etc. In this context, Meier (2018) mediates the association between overconfidence and trading volume with risk appetite. They state that overconfidence increases investors' risk appetite, becoming overconfident. However, more risk-taking by investors makes them prone to suffer losses in the future (Ritika and Kishor 2020). Due to aggressive trading, trading strategies of overconfident investors fail, and they earn inferior returns (De et al. 2010; Ho 2011; Tekce and Yilmaz 2015; Bao and Li, 2020; Bregu, 2020), and the rational investors get the benefit of it (Hirshleifer and Luo 2001).

Impact of demographic factors on overconfidence

Demographic factors also play a role in determining investor overconfidence. For example, many studies on overconfidence find male investors to be more overconfident than their counterparts, i.e., female investors (Barber and Odean, 2001; Bhandari and Deaves, 2006; Davar and Gill, 2007; Mishra and Matilda, 2015; Prosad et al., 2015; Banerjee et al., 2018; Mushinada and Veluri, 2019; and Paisarn et al. 2021). Studies also find that educated investors are more overconfident than uneducated investors (Li et al., 2006; Qasim et al., 2019). Inexperienced investors are more overconfident, but as the experience increases, the overconfidence quotient of investors decreases (Gervais and Odean, 2001; Kansal and Singh, 2018). Similarly, Renu and Christie (2019) find an association between income and overconfidence. They find a positive association between income level and overconfidence quotient.

Influence of overconfidence on the stock market

The first empirical study in this field is by Odean (1999). He studied the data on a brokerage firm's purchase and sale of securities from 1987 to 1993. He found that overconfident investors trade more and earn lesser returns (by selling a set of securities and buying another). Further, Barber and Odean (2000) scrutinize the data of position statements and trading activities of 65,000 retail investors from 1991 to 1997 and confirm the results of Odean (1999). Similarly, the study of Statman et al. (2006) is an essential contribution to the field of overconfidence that establishes an association between market returns and market turnover to find investor overconfidence. Investors are overconfident if there is a significant positive relation between lagged market returns and current market turnover. Glaser and Weber (2007), Griffin et al. (2007), Chuang and Susmel (2011), Prosad et al. (2013), Metwally and Darwish (2015), Zia et al. (2017), and Alsabban and Alafraj (2020), Zhou et al. (2022) follow the methodology of Statman et al. (2006) to examine investor overconfidence. In this context, Huang et al. (2022) find an increase in stock market turnover when investors are overconfident and a decrease in stock market turnover when investors are non-overconfident in China’s share market.

Change in investors’ overconfidence level

Some studies discuss the change in the overconfidence level of investors with a shift in market situations. Mushinada (2020) says that as the market conditions change, investors become irrational, but they adapt to changing market situations and gradually achieve equilibrium. Metwally and Darwish (2015) study the overconfidence levels of investors in the Egyptian stock market separately in upward and downward trending periods. However, Namouri et al. (2018) conclude that stock return dynamics produce curvilinear and time variation effects. Additionally, investors' belief has a significant impact on stock return—the result of investors' belief on stock return changes with the change in market condition.

Research gap

Most studies under review analyze investor overconfidence for a long time without considering the market situation. For example, the global stock market witnessed a crisis in 2008, which greatly affected investor sentiments. Therefore, this study examines investor overconfidence before, during, and after the global crisis to bridge the knowledge gap.

Hypotheses of the study

Based on the literature review and research gap, we formulate the following two hypotheses for this study:

H₁: Investors are overconfident, i.e., current market turnover is directly related to past market returns.

H₂: Overconfidence level of investors changes with changes in market situations.

Research objectives

This paper examines Indian equity investors’ overconfidence for the 16-year periods 2006–2021, which is clustered into sub-periods: 2006–2008, 2008–2010, 2010–2015, 2015–2020, and 2020–2021. We take 2006–2008 as a pre-crash period and 2008–2010 as a crash period. The period post-2010 is the post-crash period, but there was a structural break in August 2015 and, again, the COVID-19 outbreak in 2020. Therefore, we segregate the post-crash period into three segments; 2010–2015, 2015–2020, and 2020–2021. Overconfidence changes with changes in market conditions (Metwally and Darwish 2015), which is why we choose to study overconfidence bias in different market conditions. Covid-19 has significantly affected India (Vig and Kaur 2022). Therefore, we studied overconfidence bias separately in 2020–21.

Research methodology

We have selected the S&P BSE 100 index of the Bombay Stock Exchange (BSE) as representative of the Indian equity market for testing investors’ overconfidence. The reason for selecting BSE 100 as the Indian equity market proxy is its broad coverage and inclusion of companies of all sectors.

We checked overconfidence by establishing an association between index returns and index turnover using the methodology of Statman et al. (2006) and Metwally and Darwish (2015). Authors have used Vector Auto Regression (VAR), Granger causality, and Impulse Response function (IRF) to test the association between returns and turnover. The periods 2006–2008, 2008–2010, 2010–2015, 2015–2020, and 2020–2021 are represented hereafter as P1, P2, P3, P4, and P5.

Unit root test

The initial condition for time series analysis is the stationarity of the series. Only if the series of analyses are stationary will the results be able for generalization. We used Augmented Dickey-Fuller (ADF) unit root test to test whether the series under study is stationary or not (market return and market turnover). The null hypothesis of the ADF test assumes that the series has a unit root (non-stationary time series) against the alternate hypothesis that there is no unit root (stationary time series). If the observed p-value of the ADF test is less than 0.05, the null hypothesis is rejected, and it can be said with 95% confidence that the series is stationary and vice versa.

Vector autoregression (VAR)

SIMS (1980) developed a VAR model for situations where a set of variables are assumed to be on the same level without distinguishing between endogenous and exogenous variables. The term auto regression implies the presence of an endogenous variable on the right side of the equation, and the word vector denotes two (or more) variables (Gujarati et al. 2009).

VAR follows the following equations using ordinary least square regression:

$${\text{LogT}}_{\text{t}}=\alpha +{\sum }_{j=1}^n{\beta }_j{\text{LogT}}_{\text{t - j}}+{\sum }_{j=1}^n{\lambda }_j{\text{Rm}}_{\text{t - j}}+{\epsilon }_1$$

$${\text{Rm}}_{\text{t}}=\alpha +{\sum }_{j=1}^n{\beta }_j^{\prime }{\text{LogT}}_{\text{t - j}}+{\sum }_{j=1}^n{\lambda }_j^{\prime }{\text{Rm}}_{\text{t - j}}+{\epsilon }_2$$

where,

LogT = Natural logarithm of index turnover.

Rm = Daily market return.

α and α’ = Constant.

β and β’ = Coefficients of Log T.

λ and λ’ = Coefficients of Rm,

j = Lag length, and.

ε₁ and ε₂ = Error terms.

The selection of lag length j comes before equation estimation. Too many lags result in less control, and very few lags result in specification errors (Gujarati et al. 2009). Akaike lag length criterion has been used in this study, i.e., a model with the lowest value of the Akaike coefficient is selected.

VAR Granger causality/Block exogeneity Wald test

Granger causality VAR shows modest proof of a lead-lag connection between series. Causality implies that the movements in the series are chronologically ordered. Granger VAR returns the same number of panels as dependent/endogenous variables, i.e., one for each dependent variable. The panel for each dependent variable shows whether we can remove lags of any independent/exogenous variable from the VAR model (because of its insignificant impact on the dependent variable) or not.

Impulse response function (IRF)

B*rooks (2014) states that IRF traces out the responses of endogenous variables of VAR to shocks in each variable. For finding impulse response for each equation variable, a unit shock is applied to the error term, and its effect on the VAR system is noted over time. If there are n variables in a VAR model, n² number of impulse responses generated. For example, in our VAR model, we have two variables, turnover and return; we will get 2² = 4 impulse responses: response of turnover to return, response of turnover to turnover, response of return to return, and response of return to turnover. Response of turnover to return implies how turnover will change with shock in the error term; the response of turnover to turnover shows the change in turnover with shock in the error term of turnover. Similarly, the response of return to return shows changes in return due to shock in the error term of return; the response of return to turnover shows the change in return due to shock in the error term of turnover.

Data

We take daily data for BSE 100 open, high, low, close, and turnover from the CMIE (Centre for Monitoring Indian Economy) database of the Indian economy. We compute index returns as changes in the natural log of the closing value of the index with the following formula:

$${\text{Return}}_{\text{t}}=\text{Ln}\left({\text{P}}_{\text{t}}/{\text{P}}_{\text{t}-1}\right)=\text{Ln}({\text{P}}_{\text{t})}-\text{Ln}\left({\text{P}}_{\text{t}-1}\right)$$

where Return_t denotes market return (calculated daily), P_t represents the close price of day t, and P_t-1 represents the close price of the preceding day (t-1).

We use log turnover in the equation instead of turnover because the return is a ratio of data. To make variables at par, we use log values of turnover for analysis.

Results and discussion

Descriptive statistics

First, we performed a descriptive analysis of the data deployed in the study. It simply gives an overview of the variables of the study. Description of index returns and turnover data for periods 2006–08, 2008–2010, 2010–2015, 2015–2020, and 2020–2021 is in Table 1.

Table 1.

Descriptive Statistics.

Source: Authors’ calculations

2005–2008		2008–2010		2010–2015		2015–2020		2020–2021
Return	Turnover	Return	Turnover	Return	Turnover	Return	Turnover	Return	Turnover	Mean
27,228.8	0.1	31,430.0	0.0	12,721.5	0.0	15,534.3	0.0	24,308.6	0.2	Median
23,135.5	0.2	31,064.4	0.2	11,671.2	0.1	12,514.4	0.1	19,409.5	0.3	Maximum
76,440.6	4.4	88,879.9	7.0	111,245.4	3.0	528,780.6	5.9	367,534.1	8.1	Minimum
9237.6	− 4.5	8707.3	− 11.7	804.0	− 3.0	1711.1	− 13.9	3383.7	− 5.8	Std. Dev
12,577.2	1.6	9767.6	2.2	5516.8	1.0	26,953.8	1.0	27,361.4	1.4	Skewness
1.2	− 0.5	1.0	− 0.4	6.7	0.0	16.7	− 2.7	9.4	0.2	Kurtosis
4.3	4.0	6.6	5.2	101.8	3.2	309.4	35.7	108.9	8.9	Jarque–Bera
89.9	23.5	340.5	109.6	6834.1	508,792.9	4,873,178.0	56,380.5	120,118.2	367.7	Probability
0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	Mean

The descriptive analysis outline of the data. All turnover and return series depict a kurtosis value greater than 3, which implies a leptokurtic distribution: a characteristic of financial time series data (Mushinada and Veluri 2018). Jarque–Bera probability values of all series indicate the non-normality of all the series under consideration at a 5% significance level. As per the Central Limit Theorem, violation of normality has no issue if the sample size is more than 100 (Mishra et al. 2019).

Unit root test

We applied the ADF test to check the stationarity of the time series. ADF test of all present study series rejected null hypothesis at 1% confidence level, meaning thereby, all the series under study were stationary and fit for further analysis.

Market return and turnover relationship during P1

We applied the VAR model on returns and logged turnover in e-views with automatic lag length 2. After that, we checked the lag length criteria for the VAR model. Table 2 shows the results of lag length criteria.

Table 2.

Optimal lag selection for a turnover during P1.

Source: Authors’ calculations

Lag	Log L	LR	FPE	AIC	SC	HQ
0	− 313.5073	NA	0.533852	5.048117	5.09337	5.0665
1	− 220.6267	181.3030*	0.128772*	3.626027*	3.761786*	3.681179*
2	− 218.0094	5.025247	0.131662	3.64815	3.874415	3.740069
3	− 216.9062	2.082699	0.137929	3.6945	4.011271	3.823187
4	− 213.3865	6.532564	0.139029	3.702185	4.109462	3.86764
5	− 211.831	2.837293	0.144635	3.741296	4.239079	3.943519
6	− 207.3256	8.073688	0.143555	3.73321	4.321499	3.9722
7	− 206.0082	2.318584	0.149973	3.776131	4.454927	4.05189
8	− 203.9535	3.550544	0.15488	3.807256	4.576557	4.119783
9	− 202.2188	2.942073	0.160814	3.843501	4.703308	4.192795
10	− 199.6863	4.213988	0.164912	3.866982	4.817295	4.253044

^*Indicates lag order selected by the criterion

The starred values in the table are appropriate lag lengths according to different criteria. The two most common criteria used for lag length selection are AIC (Akaike information criterion) and SC (Schwarz information criterion). Both criteria suggested a VAR model with two lags; therefore, we run the VAR model with 2 lags on the data for 2006–2008; Table 3 shows the results.

Table 3.

VAR model for turnover and return in P1.

Source: Authors’ calculations

		Coefficient		Std error	T statistic	P-value
Turn
Return(-1)		0.013		0.009	1.426	0.155
Return(-2)		0.018		0.009	2.046	0.0413*
Turn(-1)		0.661		0.071	9.290	0**
Turn(-2)		0.224		0.071	3.170	0**
R2					0.759
Adjusted R2					0.755
Durbin-Watson stat					1.917
Return
Turn(-1)	1.041		0.465		2.239	0.026
Turn (-2)	− 1.151		0.467		− 2.466	0.014*
Return(-1)	0.159		0.064		2.487	0.0132*
Return(-2)	− 0.020		0.065		− 0.311	0.756
R2					0.043
Adjusted R2					0.028
Durbin-Watson stat					1.965

*Significant at 5% confidence level. **Significant at 1% confidence level. Turn denotes the natural logarithm of turnover; return denotes daily index return

The first section of Table 3 shows the effect of two lags of turn and two lags of return on the current turn. A significant p-value of the second lag of return (-2) implies a significant effect of the market return of second lag on the current turn giving the imprints of the presence of overconfident investors in the market. The second part of Table 3 shows that the market return’s own lagged value and second lag of turn affect it significantly.

The authors applied VAR Granger causality and Impulse Response Function (IRF) to support the VAR results and robust check. Table 4 shows the results of the VAR Granger causality test.

Table 4.

Results of VAR Granger causality during P1.

Source: Authors’ calculations

VAR Granger Causality/Block Exogeneity Wald Tests
Excluded	Chi-sq	DF	Prob
Dependent variable: Turn
Return	7.496885	2	0.0236*
All	7.496885	2	0.0236*
Dependent variable: Return
Turn	6.479163	2	0.0392*
All	6.479163	2	0.0392*

^*Significant at 5% confidence level. **Significant at 1% confidence level. Turn denotes the natural logarithm of turnover; return denotes daily index return

The VAR Granger Causality test results indicate that we cannot exclude return (sig. value 0.0236) from an equation with a turn as the dependent variable. Similarly, we cannot exclude turn (sig. value 0.0392) from an equation with return as the dependent variable. The VAR Granger causality test's results complement the VAR model’s results implying a significant effect of lagged market return on the turn, which proves the presence of overconfident investors in the market during the pre-crash period.

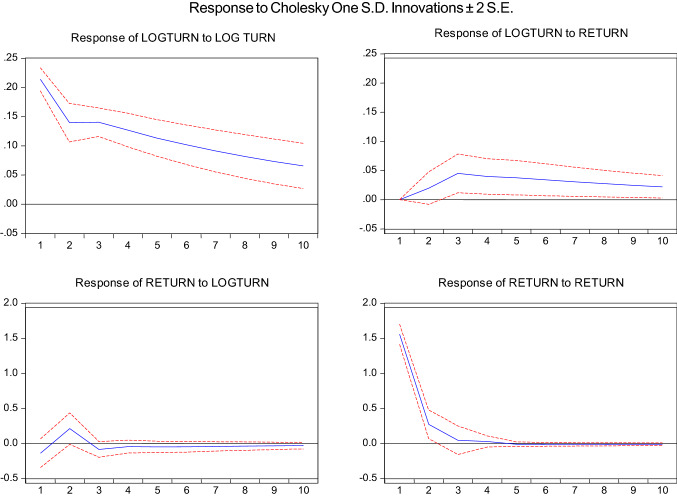
To further check the results of the VAR model, we run IRF on the results of VAR estimation. Figure 1 shows how one standard deviation shock in each variable (impulse) affects the dependent variable.

Fig. 1.

IRF of turnover and return during P1

Source: Authors’ calculations

Figure 1 shows that one standard deviation shock affects market turnover for 10 lags. More particularly, this effect is not evident for lag 1; it significantly affects the 2nd and 3rd lag, diminishes after the 3rd lag up to the 10th lag, and dies after that. IRF also proves the presence of overconfident investors in the Indian stock market before the global crash of 2008.

Market return and turnover relationship during P2

We first find appropriate lag length using Lag length criteria for applying the VAR model on time series data of 2008–2010. Table 5 shows the results of lag length criteria.

Table 5.

Optimal lag selection for turnover and return during P2.

Source: Authors’ calculations

Lag	LogL	LR	FPE	AIC	SC	HQ
0	− 753.8366	NA	0.316704	4.525967	4.548789	4.535067
1	− 625.9127	253.5497	0.150793	3.783908	3.852372	3.811206
2	− 10.9994	29.38017	0.141255	3.718559	3.832665*	3.764055*
3	− 606.2625	9.27525	0.140634	3.714147	3.873895	3.77784
4	− 601.933	8.425562	0.140359	3.712174	3.917565	3.794066
5	− 594.0656	15.21657*	0.137149*	3.708524	3.940049	3.789106
6	− 593.3235	1.42656	0.139855	3.689016*	4.005199	3.826812
7	− 592.4087	1.747411	0.142468	3.716998	4.069316	3.863485
8	− 587.8972	8.563796	0.142041	3.723935	4.111896	3.87862
9	− 584.9424	5.573398	0.142942	3.730194	4.163797	3.903077
10	− 582.8216	3.97485	0.144572	3.741447	4.220692	3.932528

*Indicates lag order selected by the criterion

Based on the AIC criterion, we selected 6 lags for applying the VAR model during 2008–2010. Table 6 shows the results of VAR for P2.

Table 6.

VAR model for turn and return in P2.

Source: Authors’ calculations

	Coefficient			Std error	T statistic		P-value
Turn
Return(-1)	0.009			0.005	1.919		0.0554
Return(-2)	0.009			0.005	1.726		0.0847
Return(-3)	− 0.001			0.005	− 0.258		0.797
Return(-4)	0.005			0.005	0.956		0.339
Return(-5)	0.000			0.005	0.042		0.967
Return(-6)	− 0.005			0.005	− 1.074		0.283
Turn(-1)	0.440			0.053	8.378		0**
Turn(-2)	0.110			0.057	1.918		0.055
Turn(-3)	0.117			0.056	2.098		0.0363*
Turn(-4)	0.039			0.056	0.696		0.487
Turn(-5)	0.141			0.055	2.552		0.0109*
Turn(-6)	0.038			0.053	0.728		0.467
R2					0.615
Adjusted R2					0.602
Durbin-Watson stat					1.946
Return
Turn(-1)		− 0.350	0.565			− 0.619		0.536
Turn(-2)		0.141	0.617			0.228		0.819
Turn(-3)		0.668	0.605			1.104		0.270
Turn(-4)		− 1.157	0.599			− 1.931		0.0539
Turn(-5)		0.283	0.599			0.473		0.636
Turn(-6)		0.342	0.553			0.617		0.537
Return(-1)		0.096	0.052			1.847		0.0652
Return(-2)		− 0.033	0.053			− 0.618		0.537
Return(-3)		0.052	0.055			0.947		0.344
Return(-4)		− 0.050	0.055			− 0.909		0.364
Return(-5)		0.007	0.054			0.124		0.902
Return(-6)		0.030	0.054			0.564		0.573
R2								0.025
Adjusted R2								0.434
Durbin-Watson stat								1.952

*Significant at 5% confidence level. **Significant at 1% confidence level. Turn denotes the natural logarithm of turnover; return denotes daily index return

Part one of the above table depicted turn as the dependent variable and lagged values of return and turn as independent variables. Insignificant p values of all lagged values of return denote that market return did not significantly affect turn during 2008–2010, implying the absence of overconfidence bias among investors during this period.

The second part of the above table shows that the return's own lagged values and turn lagged values also did not significantly affect it (return) in this period. For robust testing, we run the VAR Granger causality test on the results of the VAR model; Table 7 shows the results.

Table 7.

Results of VAR Granger causality during P2.

Source: Authors’ calculations

VAR Granger Causality/Block Exogeneity Wald Tests
Excluded	Chi-sq	df	Prob
Dependent variable: Turn
Return	9.600084	6	0.1425
All	9.600084	6	0.1425
Dependent variable: Return
Turn	4.309485	6	0.6349
All	4.309485	6	0.6349

Turn denotes the natural logarithm of turnover; return denotes daily index return

The results of VAR Granger causality are in tune with the results of the VAR model. We can exclude return (sig. value 0.1425) from an equation with turnover as a dependent variable implying that market return does not significantly affect turnover. We can also exclude turnover (sig. value 0.6349) from an equation with return as the dependent variable.

Now, we apply IRF to the results of the VAR model. Figure 2 shows the results of IRF.

Fig. 2.

IRF of turn and return during P2.

Source: Authors’ calculations

For this paper's objective, we focus on the response of turnover to return. It is evident from Fig. 2 that shock in the error term of return did not affect turnover for any of the lags. The results of IRF are also complementary to the results of VAR estimation.

Market return and turnover relationship during P3

We checked lag length before applying the VAR model to the time series data. Table 8 shows different criteria for leg length selection.

Table 8.

Optimal lag selection for a turnover during P3.

Source: Authors’ calculations

Lag	LogL	LR	FPE	AIC	SC	HQ
0	− 2142.66	NA	0.134877	3.672359	3.681029	3.675629
1	− 2048.22	188.392	0.115526	3.517499	3.543507	3.527309
2	− 1993.69	108.5841	0.105952	3.430982	3.474330*	3.447333
3	− 1984.7	17.88649	0.105049	3.422426	3.483113	3.445316
4	− 1968.63	31.88095	0.102901	3.401768	3.479794	3.431199
5	− 1954.6	27.80152*	0.101149*	3.384588*	3.479954	3.420559*
6	− 1951.88	5.384172	0.10137	3.386776	3.49948	3.429287
7	− 1948.66	6.343803	0.101507	3.388123	3.518167	3.437175
8	− 1944.74	7.731312	0.10152	3.388255	3.535638	3.443847

*Indicates lag order selected by the criterion

AIC criterion recommended selecting 5 lags for applying VAR on time series data of 2010–2015. Table 9 shows the results of VAR.

Table 9.

VAR model for turn and return in P3.

Source: Authors’ calculations

Column1	Coefficient	Std error	T statistic	P-value
Turn
Return(-1)	0.002184	0.009311	0.234538	0.8146
Return(-2)	0.001035	0.009423	0.10987	0.9125
Return(-3)	0.004913	0.009421	0.521509	0.6021
Return(-4)	− 0.01299	0.009464	− 1.37204	0.1702
Return(-5)	0.025222	0.009331	2.703095	0.0069
Turn(-1)	0.191027	0.028868	6.617279	0
Turn(-2)	0.210035	0.029169	7.200566	0
Turn(-3)	0.054677	0.029746	1.838098	0.0662
Turn(-4)	0.13905	0.029701	4.681647	0
Turn(-5)	0.125355	0.029369	4.268328	0
R2				0.267699
Adjusted R2				0.261477
Durbin-Watson stat				2.02366
Return
Turn(-1)	0.05176	0.090357	0.572836	0.5668
Turn(-2)	0.040153	0.091191	0.440319	0.6597
Turn(-3)	− 0.02179	0.093117	− 0.23396	0.815
Turn(-4)	0.022189	0.091079	0.243619	0.8075
Turn(-5)	− 0.152	0.09194	− 1.65321	0.0984
Return(-1)	0.100604	0.029076	3.460067	0.0005
Return(-2)	0.01397	0.029347	0.476024	0.6341
Return(-3)	− 0.01102	0.029466	− 0.37401	0.7084
Return(-4)	0.006806	0.02954	0.230402	0.8178
Return(-5)	0.004987	0.029192	0.170825	0.8644
R2				0.01343
Adjusted R2				0.005091
Durbin-Watson stat				2.001612

*Significant at 5% confidence level. **Significant at 1% confidence level. Turn denotes the natural logarithm of turnover; return denotes daily index return

It is clear from the above table that during 2010–2015, the 5th lag of return and 1–2, 4th and 5th lag of its own (turnover) significantly and positively affected turnover. Return’s first lag affected it (return). These results indicate the presence of overconfident investors in the Indian stock market during the post-crash period.

We tested the results of the VAR model using the VAR Granger causality test. Table 10 shows the results.

Table 10.

Results of VAR Granger causality during P3.

Source: Authors’ calculations

VAR Granger Causality/Block Exogeneity Wald Tests
Excluded	Chi-sq	Df	Prob
Dependent variable: Turn
Return	8.714436	5	0.121
All	8.714436	5	0.121
Dependent variable: Return
Turn	3.156274	5	0.6759
All	3.156274	5	0.6759

Turn denotes the natural logarithm of turnover; return denotes daily index return

Table 10 shows that we can exclude return (sig. value 0.121) from an equation with a turn as the dependent variable. We can also exclude turn (sig. value 0.6759) from an equation with return as the dependent variable. The results of the Granger causality test are not in harmony with the results of VAR estimation.

Finally, we perform IRF on VAR estimation to test the turnover response to shock in the error term of return. Figure 3 shows the results of IRF.

Fig. 3.

IRF of turnover and return during P3.

Source: Authors’ calculations

Results of IRF support the results of Granger causality VAR but are inconsistent with the results of the VAR model. It is apparent from turnover response to return that the error term of return did not significantly affect turnover in any of the lags. The above analysis shows that Indian investors were not significantly overconfident during 2010–2015.

Market return and turnover relationship during P4

We first find appropriate lag length using lag length criteria for applying the VAR model on time series data for 2015–2020. Table 11 shows the results of lag length criteria.

Table 11.

Optimal lag selection for a turnover during P4.

Source: Authors’ calculations

Lag	LogL	LR	FPE	AIC	SC	HQ
0	− 2480.71	NA	0.198747	4.060032	4.068387	4.063177
1	− 2383.07	194.7988	0.170529	3.906903	3.931968	3.916336
2	− 2355.58	54.75452	0.164102	3.868489	3.910264	3.884211
3	− 2307.35	95.91494	0.152651	3.796153	3.854638	3.818163
4	− 2302.16	10.30042	0.152355	3.79421	3.869405	3.822509
5	− 2289.23	25.62267	0.150147	3.77961	3.871515	3.814198
6	− 2253.46	70.7891	0.142544	3.727648	3.836263*	3.768524
7	− 2242.9	20.85392*	0.141024*	3.716926*	3.842251	3.764091*
8	− 2241.05	3.653474	0.14152	3.720438	3.862473	3.773891

*Indicates lag order selected by the criterion

AIC criterion recommended selecting 7 lags for applying VAR on time series data of 2015–2020. Table 12 shows the results of VAR.

Table 12.

VAR model for turn and return in P4.

Source: Authors’ calculations

Column1	Coefficient	Std error	T statistic	P-value
Turn
Return(-1)	0.007005	0.010251	0.683277	0.4945
Return(-2)	− 0.01084	0.010136	− 1.06899	0.2852
Return(-3)	0.004247	0.010104	0.420284	0.6743
Return(-4)	− 0.01958	0.010251	− 1.90963	0.0563
Return(-5)	0.013371	0.010446	1.280023	0.2007
Return(-6)	− 0.01135	0.010454	− 1.08568	0.2777
Return(-7)	− 0.02471	0.011536	− 2.14209	0.0323
Turn(-1)	0.235574	0.028691	8.210738	0
Turn(-2)	0.104722	0.029245	3.580855	0.0003
Turn(-3)	0.224728	0.029729	7.559245	0
Turn(-4)	− 0.02115	0.030432	− 0.69511	0.4871
Turn(-5)	− 0.00762	0.029995	− 0.25418	0.7994
Turn(-6)	0.145054	0.029984	4.83777	0
Turn(-7)	0.045005	0.029419	1.529777	0.1262
R2				0.268111
Adjusted R2				0.259636
Durbin-Watson stat				1.998526
Return
Turn(-1)	− 0.03805	0.080094	− 0.4751	0.6348
Turn(-2)	0.010559	0.08164	0.129338	0.8971
Turn(-3)	− 0.09311	0.082991	− 1.12192	0.262
Turn(-4)	0.140635	0.084954	1.655412	0.098
Turn(-5)	− 0.08839	0.083734	− 1.05555	0.2913
Turn(-6)	− 0.03993	0.083702	− 0.47702	0.6334
Turn(-7)	− 0.03163	0.082126	− 0.38509	0.7002
Return(-1)	− 0.00571	0.028618	− 0.19957	0.8418
Return(-2)	0.02372	0.028296	0.838296	0.4019
Return(-3)	0.047041	0.028206	1.667751	0.0955
Return(-4)	0.031215	0.028616	1.090812	0.2755
Return(-5)	0.111198	0.029161	3.813247	0.0001
Return(-6)	− 0.18584	0.029183	− 6.36814	0
Return(-7)	0.115544	0.032205	3.587775	0.0003
R2				0.072409
Adjusted R2				0.061668
Durbin-Watson stat				1.990232

*Significant at 5% confidence level. **Significant at 1% confidence level. Turn denotes the natural logarithm of turnover; return denotes daily index return

It is clear from the above table that during 2015–2020, the 7th lag of return and 1–3 and 6th lag of its own (turnover) significantly and positively affected turnover. Return’s 5-7th lag affected it (return). These results indicate the presence of overconfident investors in the Indian stock market during 2015–2020.

We tested the results of the VAR model using the VAR Granger causality test. Table 13 shows the results.

Table 13.

Results of VAR Granger causality during P4.

Source: Authors’ calculations

VAR Granger Causality/Block Exogeneity Wald Tests
Excluded	Chi-sq	Df	Prob
Dependent variable: Turn
Return	15.05459	7	0.0353
All	15.05459	7	0.0353
Dependent variable: Return
Turn	5.846007	7	0.5578
All	5.846007	7	0.5578

Turn denotes the natural logarithm of turnover; return denotes daily index return

Table X shows that we cannot exclude return (sig. value 0.0353) from an equation with a turn as a dependent variable, but we can exclude turn (sig. value 0.5578) from an equation with return as the dependent variable. The results of the Granger causality test are in harmony with the results of VAR estimation.

Finally, we perform IRF on VAR estimation to test the turnover response to shock in the error term of return. Figure 4 shows the results of IRF.

Fig. 4.

IRF of turnover and return during P4.

Source: Authors’ calculations

The results of IRF support the Granger causality VAR but are inconsistent with the results of the VAR model. It is apparent from turnover response to return that the error term of return significantly affects turnover. It is clear from the above results that Indian investors were overconfident during 2015–2020.

Market return and turnover relationship during P5

We first find the appropriate lag length using Lag length criteria for applying the VAR model on time series data for 2020–2021. Table 14 shows the results of lag length criteria.

Table 14.

Optimal lag selection for a turnover during P5.

Source: Authors’ calculations

Lag	LogL	LR	FPE	AIC	SC	HQ
0	− 533.855	NA	0.298108	4.465456	4.494461*	4.477143
1	− 525.586	16.33079*	0.287691	4.429883	4.516899	4.464944*
2	− 521.158	8.671795	0.286669*	4.426315*	4.571342	4.48475
3	− 519.849	2.54167	0.293176	4.44874	4.651777	4.530549
4	− 516.781	5.905318	0.295474	4.456509	4.717557	4.561692
5	− 512.475	8.217185	0.294739	4.453959	4.773018	4.582517
6	− 509.929	4.816781	0.298356	4.466073	4.843143	4.618005
7	− 507.913	3.779314	0.303365	4.48261	4.91769	4.657915
8	− 507.655	0.480562	0.313019	4.513788	5.006879	4.712468

*Indicates lag order selected by the criterion

AIC criterion recommended selecting 2 lags for applying VAR on time series data of 2010–2015. Table 15 shows the results of VAR.

Table 15.

VAR model for turn and return in P5.

Source: Authors’ calculations

Column1	Coefficient	Std error	T statistic	P-value
Turn
Return(-1)	0.014019	0.020045	0.699377	0.4847
Return(-2)	0.019978	0.020023	0.997731	0.3189
Turn(-1)	0.198949	0.063449	3.13559	0.0018
Turn(-2)	0.162472	0.063258	2.568394	0.0105
R2				0.090156
Adjusted R2				0.075055
Durbin-Watson stat				2.028331
Return
Turn(-1)	0.225781	0.189054	1.19427	0.233
Turn(-2)	− 0.12481	0.188486	− 0.66218	0.5082
Return(-1)	− 0.01298	0.059726	− 0.21732	0.8281
Return(-2)	0.005767	0.059661	0.09667	0.923
R2				0.006773
Adjusted R2				− 0.00971
Durbin-Watson stat				1.982778

*Significant at 5% confidence level. **Significant at 1% confidence level. Turn denotes the natural logarithm of turnover; return denotes daily index return

It is clear from the above table that during 2020–2021, 1–2 lag of its own (turnover) significantly and positively affected turnover. Neither the return’s own lagged values nor the turnover is lagged values affect it (return). These results indicate the absence of overconfident investors in the Indian stock market during 2020–2021. We tested the results of the VAR model using the VAR Granger causality test. Table 16 shows the results.

Table 16.

Results of VAR Granger causality during P5.

Source: Authors’ calculations

VAR Granger Causality/Block Exogeneity Wald Tests
Excluded	Chi-sq	Df	Prob
Dependent variable: Turn
Return	1.417364	2	0.4923
All	1.417364	2	0.4923
Dependent variable: Return
Turn	1.574068	2	0.4552
All	1.574068	2	0.4552

Turn denotes the natural logarithm of turnover; return denotes daily index return

Table X shows that we can exclude return (sig. value 0.4923) from an equation with a turn as the dependent variable, and we can exclude turn (sig. value 0.4552) from an equation with return as the dependent variable. The results of the Granger causality test are in harmony with the results of VAR estimation.

Finally, we perform IRF on VAR estimation to test the turnover response to shock in error terms of return. Figure 5 shows the results of IRF.

Fig. 5.

IRF of turnover and return during P5.

Source: Authors’ calculations

Results of IRF support the results of Granger causality VAR and VAR model. It is apparent from the response of turnover to return that the error term of return did not significantly affect turnover in any of the lags. The above analysis shows that Indian investors were not significantly overconfident during 2020–2021.

Discussion

The results of data analysis show that during 2005–2008, lagged market returns significantly affected the turnover, showing investors’ overconfident behavior. During 2008–2010 and 2010–2015, past returns did not significantly affect the turnover indicating the non-overconfident behavior of investors. We may attribute the global crash of 2008 to the reason behind this phenomenon of investors turning overconfident to non-overconfident. When we checked the effect of lagged return on the turnover during 2015–2020, we found a significant effect, indicating towards overconfident behavior of investors. Again, in 2020–2021, returns did not significantly affect turnover, indicating non-overconfident investors. We attribute the COVID outbreak to why investors turned non-overconfident this time. The results of this study are beneficial for investors, brokers, and other stakeholders of the capital market because they may try to avoid overconfidence and loss of confidence during investment decisions. Investors may reflect on rational behavior during investment decisions and protect themselves from the probable losses due to overconfidence and lack of confidence. Alkhatib et al. (2022) also find a significant effect of Covid-19 on various stock markets.

Conclusion

The paper gives empirical facts regarding overconfidence bias during the pre-crash and lack of confidence after-crash period. The study demonstrates that turnover is positively related to past returns due to overconfidence in pre-crash periods (2006–2008, 2015–2020). This is consistent with the findings of Prosad et al. (2017) and Mushinada and Veluri (2018). On the other hand, based on experience and events like the global stock market crash of 2008 and the COVID-19 outbreak, investors lose their confidence and adapt to the changing market conditions; therefore, we see no signs of overconfident behavior during post-crash periods (2008–2015, 2020–2021). These findings are consistence with the results of Hiremath and Kumari (2014), Hiremath and Narayan (2016), and Mushinada (2020).

The crash of 2008 and the COVID-19 outbreak in 2020 show the investors of the whole world that nothing can be predicted about the stock market; the most gaining stock today may become the most losing stock tomorrow. As the market situations change, disequilibrium arises, investors adapt to changing market conditions until a new equilibrium is restored.

Biographies

Jitender Kumar

Neha Prince

Appendixes Full form of abbreviations used in optimal lag selection for turnover and return during P1, P2, P3, P4, and P5

LR	Sequential modified LR test statistic (each test at 5% level)
FPE	Final prediction error
AIC	Akaike information criterion
SC	Schwarz information criterion
HQ	Hannan-Quinn information criterion

Unit root test

Unit root test determines whether a series have a unit root (non-stationary) or not (stationary). Null hypothesis defines unit root and alternate hypothesis defines stationarity of series.

Vector auto regression (VAR)

A VAR model examines the cross sectional time series. Since it is difficult to measure overconfidence directly as a lot of variables affect it. Therefore, we infer overconfidence from the hypothesis if lagged returns affect trading volume or not. If, there is a significant positive effect of lagged returns on market turnover, we infer overconfidence to exist and vice-versa.

Granger causality test

Granger causality test determines whether a series forecasts another or not. A time series A_t granger causes time series B_t if lagged values of A i.e. A_t-1, A_t-2, A_t-3 (along with lagged values of B_t) significantly affect B_t.

Impulse response function (IRF)

Impulse response functions describe the effect of independent variables on dependent variables at the time of shock and over succeeding points in time.

Declarations

Conflict of interest

To the best of our knowledge no potential financial and non-financial conflict.

Human or animal rights

No human participants and/or Animals are involved in this research.