Building Force Fields - an Automatic, Systematic and Reproducible Approach

Abstract

The development of accurate molecular mechanics force fields is a significant challenge that must be addressed for the continued success of molecular simulation. We developed the ForceBalance method to automatically derive accurate force field parameters using flexible combinations of experimental and theoretical reference data. The method is demonstrated in the parameterization of two rigid water models, yielding new parameter sets (TIP3P-FB and TIP4P-FB) that accurately describe many physical properties of water.

Graphical Abstract

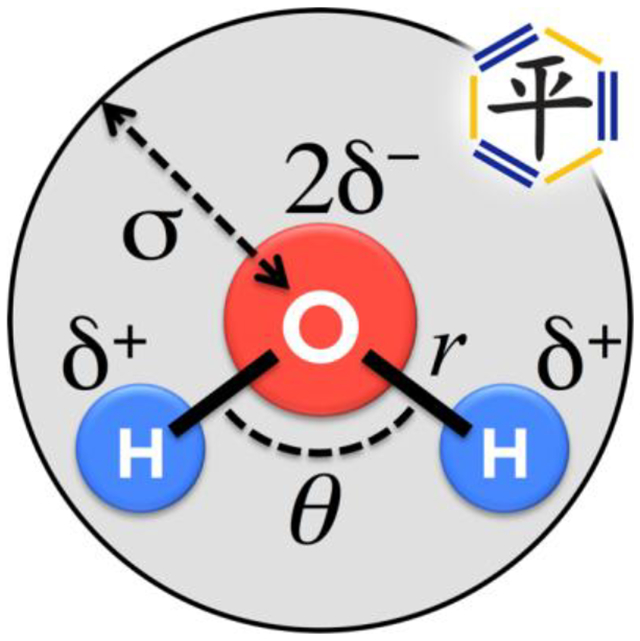
Schematic of a rigid three-point water model with names of some adjustable parameters shown (partial charge δ, bond angle θ, van der Waals radius σ). The ForceBalance method (top right) is applied to parameterize rigid four-point and three-point water models in this work.

Molecular mechanics (MM) is the simulation method of choice in many areas of chemistry, biochemistry and condensed matter physics because it provides an atomic-resolution picture of molecular processes at low computational cost. The predictive power of MM simulation depends on improving the accuracy and reliability of force fields; indeed, more accurate force fields have been shown to improve model resolution in protein structure refinement.^1–2 In order to make rapid developments in force field accuracy, force field construction needs to be systematic, reproducible, and statistically driven – but the task is commonly considered to be a “black art” due to its immense practical complexity.³ To address this challenge, we developed the ForceBalance method to automatically derive accurate force field parameters using flexible combinations of experimental and theoretical reference data.⁴ In this work, ForceBalance is used to develop two highly accurate yet simple models for liquid water; the model parameters are highly reproducible, with the calculation converging reliably to the same result starting from different initial parameter sets. The new models comprise a sound foundation for constructing biomolecular force fields that are fast, accurate, and reproducible.

ForceBalance is an optimization program with unique features for efficiently building accurate force fields. The calculation input is a labeled force field file with initial parameters and a reference data set consisting of experimental measurements and/or high-level ab initio calculations; the output is a set of optimized parameters and simulated properties (Figure 1).

Figure 1.

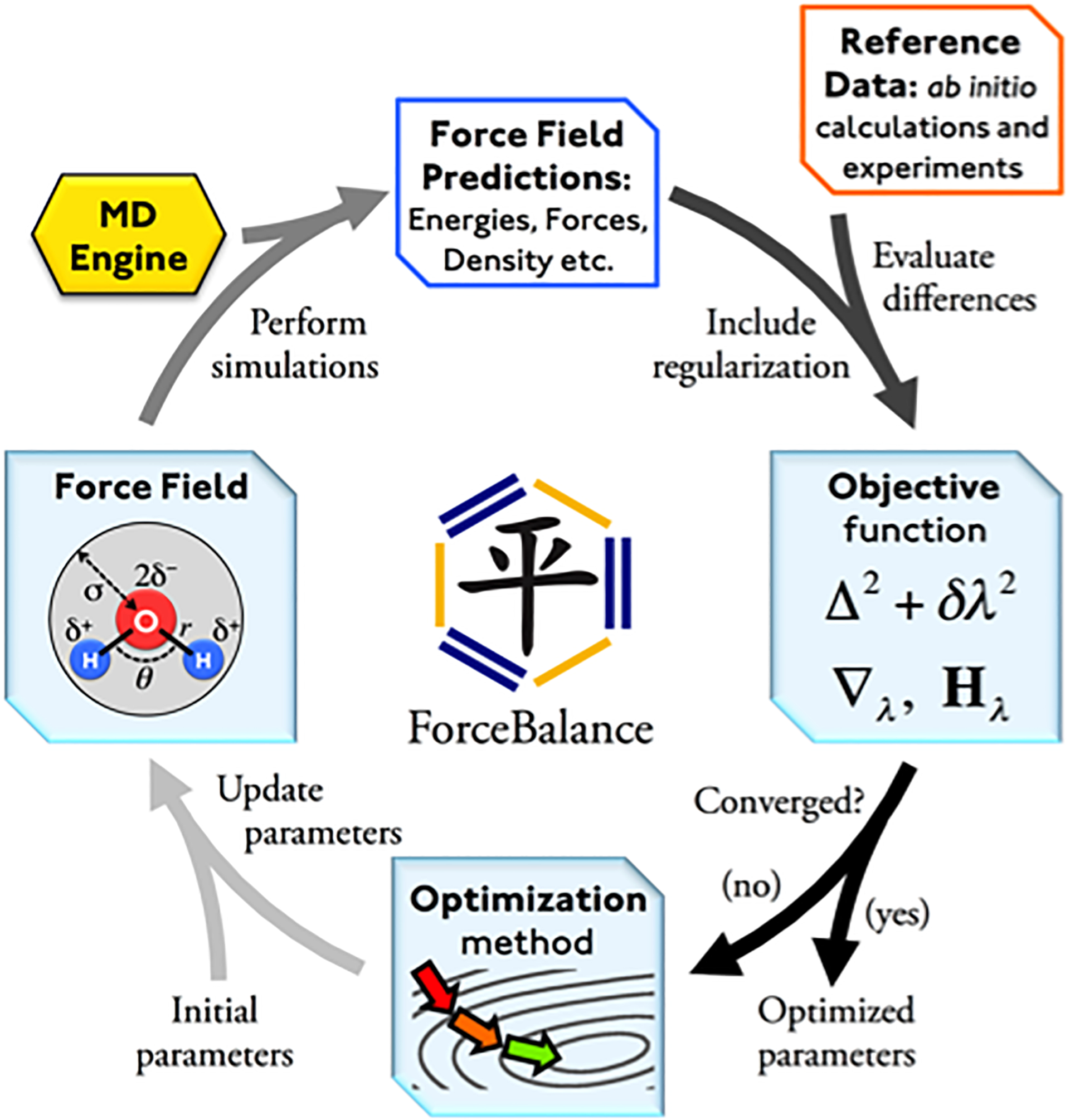
ForceBalance procedure. The calculation begins with an initial set of force field parameters (lower left) used to generate a force field and perform simulation using molecular dynamics (MD) software (upper left). The objective function and its derivatives are computed from differences between the simulation results and reference data (upper right), with a regularization term that prevents overfitting. The optimization method updates the parameters in order to minimize the objective function, and provides optimized parameters at the end of the calculation (lower right).

The objective function for optimization is a sum of squared differences between simulated properties and reference data, normalized to the variance of the reference data. The simulations are automatically executed using interfaces to molecular dynamics (MD) simulation engines (e.g. GROMACS⁵, TINKER⁶, or OpenMM⁷). The parameter search is performed using internal optimization routines capable of both semilocal (gradient-based) and stochastic minimization.

Force field parameterization presents significant challenges that set it apart from other parameter fitting calculations. Since the introduction of the concept in the 1960’s, parameterization calculations have grown to be as diverse as the scientific ideas that underlie them.^8–11 The calculations differ along three main axes - the functional form, the reference data, and the optimization algorithm; ForceBalance modularizes these aspects of the calculation and allows them to be freely interchangeable. For example, some research groups focus on matching microscopic interactions from ab initio calculations,¹² while others build effective potentials to reproduce experimental physical properties; ForceBalance allows exploration of both directions and enables hybrid approaches¹³ that combine ab initio and experimental data. Different force fields can be parameterized using the same data set for making objective comparisons between functional forms. The researcher may choose to employ gradient-based algorithms when good initial parameters are available, or stochastic methods when initial values are lacking or where the objective function is rugged or nonlinear.

Another major challenge in force field parameterization is the significant complexity of the optimization problem, characterized by a computationally expensive objective function containing significant statistical noise. The noise comes from the statistical sampling of properties to be matched to experiment, and can only be reduced by increasing the simulation length and cost. The parameter dependence of properties is even more difficult to evaluate because numerical differentiation requires running multiple simulations and evaluating small differences between statistically noisy estimates. ForceBalance uses thermodynamic fluctuation formulas to calculate accurate parametric derivatives of simulated properties without running expensive multiple simulations;^14–15 furthermore, it adaptively adjusts the simulation length so that long simulations are performed only at the end of the optimization where the highest precision is required.

The complexity of the force field parameter space presents a third major challenge, since parameters have different physical units and nontrivial interdependencies. ForceBalance implements a mapping function that connects the mathematical optimization parameters to the physical force field parameters in order to ensure that the minimization problem is well-behaved with variables of order unity; this also allows the physical parameters to be arbitrary functions of one another to satisfy constraints such as charge neutrality. The onerous problem of overfitting is treated by regularization (penalty function), which corresponds to imposing a prior distribution of parameter probabilities in a Bayesian interpretation. The prior widths reflect the expected variations of the parameters during the optimization, which may be chosen heuristically or sampled over in an empirical Bayes approach.

In order to maximize the efficiency of simulating properties, ForceBalance interfaces with several powerful and complementary technologies. ForceBalance includes an interface to OpenMM 6.0,⁷ a graphics processing unit (GPU)-accelerated MD engine. The Work Queue library¹⁶ allows ForceBalance to parallelize multiple simulations across compute nodes in different physical locations. ForceBalance analyzes the data from finished simulations using the multistate Bennett acceptance ratio estimator (MBAR)¹⁷ which allows multiple simulations at different thermodynamic phase points to statistically contribute to one another. These methods are open source and freely available on the Web.

Here we demonstrate the utility of ForceBalance by parameterizing two rigid water models. These models are most commonly used for protein simulations in explicit solvent; the most commonly used example is the TIP3P three-point model, which was published over thirty years ago.¹⁸ As theoretical and computational methods have improved and new experimental data have become available over the years, there is a need for new model parameters that give improved agreement with experiment. Furthermore, improving water models carries significant promise for protein force fields, which are currently inaccurate for temperature-dependent properties such as peptide melting curves.¹⁵ To meet these needs, we developed improved parameterizations of rigid 4-point and 3-point water models, which we call TIP4P-FB and TIP3P-FB respectively (FB stands for ForceBalance). Below we discuss the parameterization of the individual models followed by a brief comparison.

The TIP4P water model consists of four interacting particles per molecule in a rigid geometry – three particles representing the O and H atoms, and a fourth massless particle (virtual site) located on the HOH angle bisector. The H atoms and virtual site carry positive and negative charge, and the O atoms interact via a Lennard-Jones potential. The three widely used parameter sets for this model (TIP4P¹⁸, TIP4P-Ew¹⁹, and TIP4P/2005²⁰) vary significantly in their accuracy for describing different properties, and none of them are able to reproduce the static dielectric constant of the liquid.

We ran ForceBalance calculations starting from the existing parameter sets using a large data set consisting of the temperature and pressure dependence of six key liquid properties, the densities of several phases of ice, and over 100,000 high-level ab initio energy and force calculations. In three separate calculations that started from the three existing parameter sets, the optimizations converged toward the same point in parameter space despite their disparate initial values (Figure 2). We call the newly optimized parameter set TIP4P-FB. The convergence behavior is a strong indicator of the reproducibility of force field parameterization using ForceBalance, and also indicates that the optimization problem is convex in the explored region of parameter space.

Figure 2.

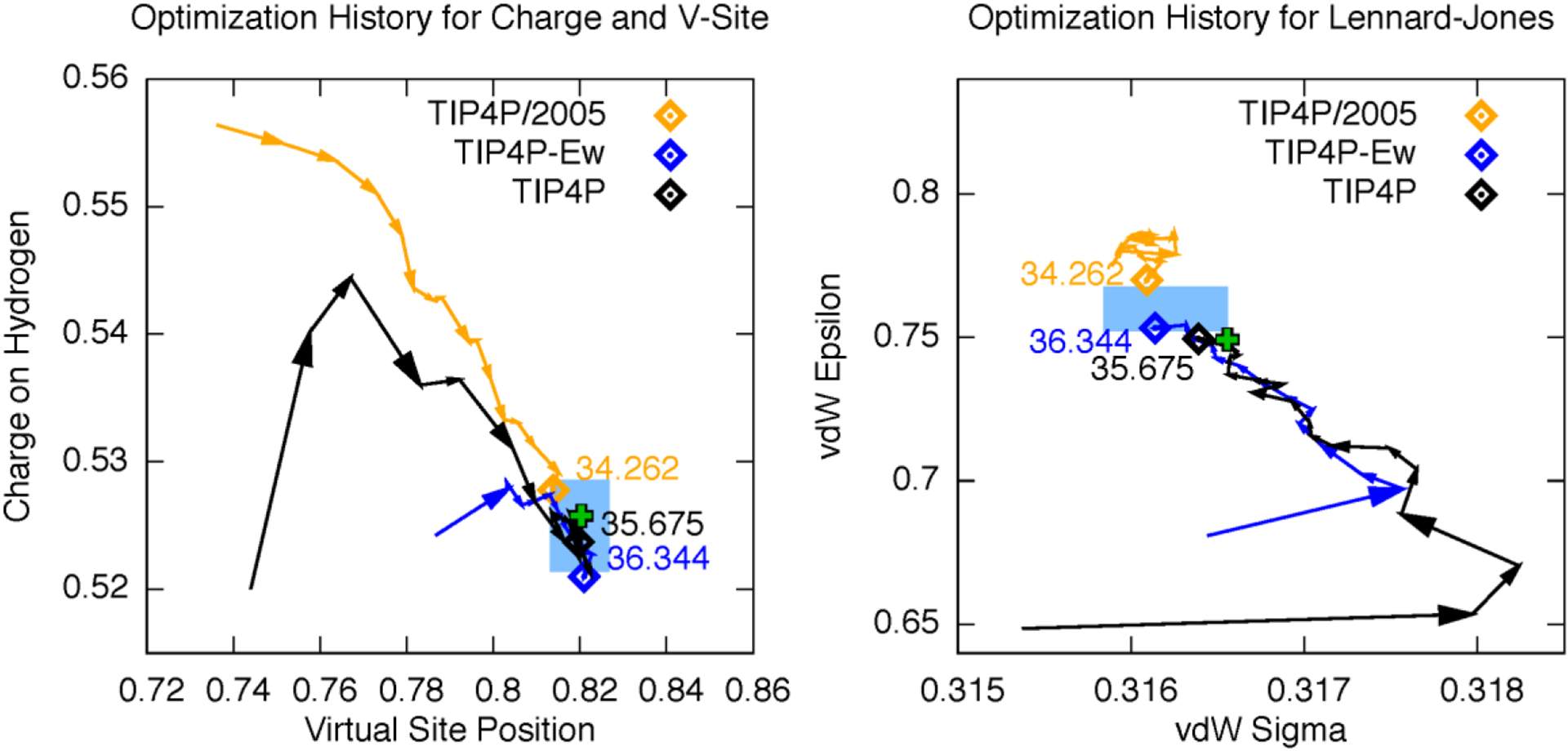
Parameter convergence in ForceBalance optimization. Colored lines represent the evolution of TIP4P model parameters starting from original TIP4P values (black), TIP4P-Ew (blue), and TIP4P/2005 (orange). The optimization converges toward the same region of parameter space from all three initial parameter sets. The light blue rectangle indicates a range of parameter uncertainty where the objective function deviates by ±3. The green cross shows the final TIP4P-FB parameter values.

In contrast to the three starting parameter sets, TIP4P-FB accurately reproduces the dielectric constant across a wide temperature and pressure range; at ambient conditions the simulated value is 77.3 ± 0.4 (experimental 78.4). This level of agreement is achieved without sacrificing accuracy in the other thermodynamic properties such as the equation of state (Figure 3). Remarkably, these results are highly reproducible – multiple calculations at different starting values converged to the same result. Moreover, the final parameters agree closely with a recently published model (TIP4P-ε), where the parameterization was performed using a manual and more specialized procedure.²¹

Figure 3.

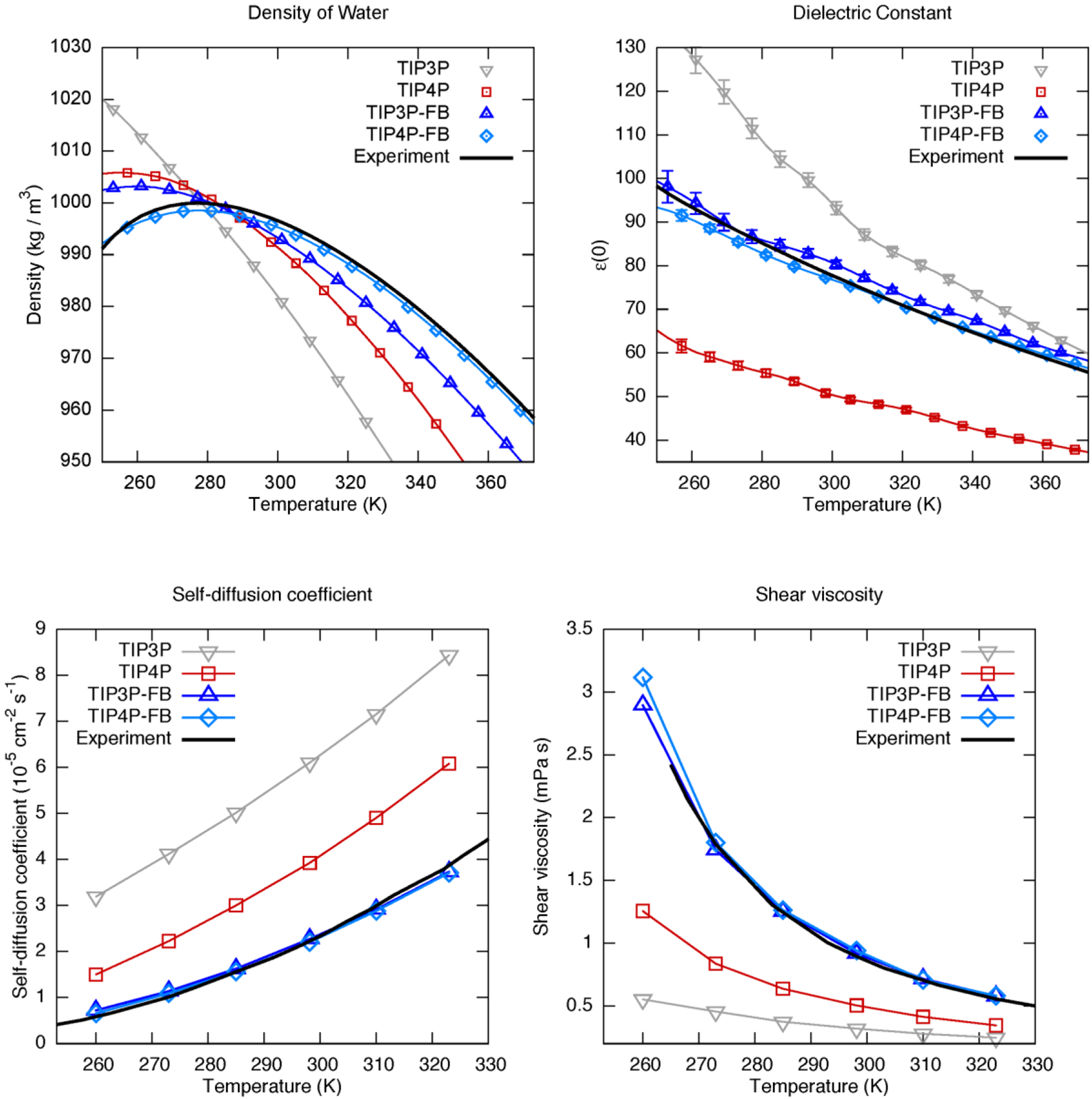
Performance of ForceBalance-optimized TIP3P-FB and TIP4P-FB water models (blue triangles, blue diamonds) compared to TIP3P (gray triangles) and TIP4P (red squares). The ForceBalance-optimized models improve the accuracy of the density (top left) and provide a qualitatively accurate description of the liquid dielectric constant (top right); kinetic properties not used to optimize the model, such as the self-diffusion coefficient (bottom left) and shear viscosity (bottom right), are also much improved. Comparisons with a greater number of models and properties are provided in Supporting Figures 1–9.

Three-point water models are simpler and computationally less expensive than four-point models, though they also tend to be less accurate from having one less interaction site. The development of more realistic 3-point water models is highly desirable because, for the reasons above, we may expect that the 3-point models will continue to be the most used. We thus applied ForceBalance to develop an improved 3-point model called TIP3P-FB, using the existing TIP3P and SPC/E models as starting points. We added two more free parameters corresponding to the geometry of the rigid molecule after determining that preserving the SPC/E or TIP3P geometry led to poor results. The optimized model had a bond length of 1.01 Å and a bond angle of 108.1 degrees – intermediate between the TIP3P and SPC/E bond angles.

The quality of fit for TIP3P-FB is shown in Figure 3, compared with TIP4P-FB and other models in the literature. TIP3P-FB is accurately fit to the experimental density at ambient and higher temperatures, but it begins to deviate from experiment at low temperatures with a maximum difference of ~1%. This contrasts with TIP4P-FB which fits the temperature dependence of the density more accurately. The quality of fit is comparable to TIP4P-FB for other properties such as the dielectric constant and heat of vaporization (Supporting Figure 2).

We experimented with different choices of weights for physical properties to see if an improved fit for the density could be achieved for the 3-point model; indeed, a more accurate fit can be achieved by by greatly increasing the weight of the density relative to other properties, but doing so introduces severe errors in the heat of vaporization, radial distribution functions and self-diffusion coefficient. We interpret this as a cautionary example against overfitting a single property. Thus, the TIP3P-FB parameters represent the best compromise between the density and other properties for a rigid 3-point model that is presently achievable by ForceBalance.

Table 1 shows several physical properties of water computed for the TIP3P-FB and TIP4P-FB models compared with experiment and several existing rigid water models in the literature. Also included for comparison is the iAMOEBA flexible polarizable model,¹⁴ which was parameterized using ForceBalance and a similar data set; while highly accurate, it is also much more expensive than the other models in this table (by a factor of 5 or more).

Table 1.

Comparison of water model performance at 298.15 K, 1.0 atm.

Property	Expt.	TIP3P	SPC/E	TIP4P	TIP4P-Ew	TIP4P/2005	TIP3P-FB (This work)	TIP4P-FB (This work)	iAMOEBA
ρ / g cm−3	0.997	0.98	0.994	0.992	0.995	0.993	0.995	0.996	0.997
ΔHvap / kcal mol−1	10.52	10.05	10.43	9.90	10.58	10.93	10.71	10.80	10.94
α / 10−4 K−1	2.56	9.2	5.0	4.4	3.2	2.8	4.1 (1)	2.5 (1)	2.5 (1)
κT / 10−6 bar−1	45.3	57.4	46.1	60	48	46	44.5 (3)	45.2 (2)	41.1 (4)
Cp / cal mol−1 K−1	18.0	18.74	18.3	18.9	19.2	19.0	19.1 (1)	19.0 (1)	18.5 (2)
ε(0)	78.5	94	68	53	62	58	81.3 (9)	77.3 (4)	80.7 (11)
D0 / 10−5 cm2 s−1	2.29	6.05	2.97	4.05	2.83	2.59	2.28 (2)	2.21 (2)	2.54 (2)
η / mPa s	0.896	0.321	0.729	0.494	0.72	0.855	0.91 (2)	0.94 (3)	0.85 (2)
σ / mJ m−2	71.8	52	63	59	65	69	64 (1)	70 (1)	69 (1)
TMD (°C)	+4	−91	−36	−20	+1	+5	−12	+4 (1)	+4 (1)

Properties listed are: density ρ, heat of vaporization ΔH_vap, thermal expansion coefficient α, isothermal compressibility κ_T, isobaric heat capacity C_p, static dielectric constant ε(0), self-diffusion coefficient D₀, shear viscosity η, surface tension σ, and temperature of maximum density TMD. The polarizable and relatively complex iAMOEBA model (right column) is included for comparison because it was parameterized using ForceBalance and a similar data set.

Both the TIP3P-FB and TIP4P-FB models perform well in fitting the six thermodynamic properties of water, except TIP3P-FB falters at reproducing the density at low temperatures. Also, both models are equally accurate for several structural and kinetic properties that were not part of the optimization, such as the O-O radial distribution function (Supporting Figure 7), the self-diffusion coefficient and shear viscosity (Figure 3, also Supporting Figures 8–9). The comparison with existing models is highly favorable; in fact TIP3P-FB exceeds most four-point models in accuracy for many properties, except for the density behavior at low temperatures. We propose that the increased complexity of 4-point models is justified for applications that require accurate descriptions of the water density at low temperature.

Moving beyond water, ForceBalance is applicable to more complex systems such as organic molecules, lipid membranes and proteins; these investigations are ongoing in our lab and in collaborations with other groups, and we plan to carry out these parameterizations using either TIP4P-FB or TIP3P-FB as the solvent model. We are optimistic that the results presented here will encourage the wider adoption of ForceBalance and similar methods, which have the potential to transform the onerous task of force field development into a systematic and reproducible calculation in a unified framework.

ForceBalance is open source and freely available at https://simtk.org/home/forcebalance.

Computational Methods.

Reference data for force field parameterization can be both experimental and theoretical in origin; for water, we are fortunate that both experimental and theoretical reference data are plentiful.^22–23 Here we describe the different types of data used to parameterize TIP4P-FB and TIP3P-FB, summarized in Table 2. The experimental properties are tabulated in Supporting Tables 2 and 3, and the complete reference dataset is provided electronically. (https://simtk.org/home/tip3p-fb)

Table 2.

Data references for parameterization of TIP4P-FB (full tables in Supporting Tables 2 and 3.)

Reference Data	Scaling Factor
Liquid Density ρ	2 kg m−3
Heat of Vaporization ΔHvap	5 kJ mol−1
Thermal Expansion Coefficient α	10−4 K−1
Isothermal Compresibility κT	5×10−5 bar−1
Isobaric Heat Capacity cP	1 kg mol−1 K−1
Dielectric Constant ε(0)	2
Ice Density ρ	5 kg m−3
136,800 MP2/heavy-aug-cc-pVTZ Potential Energies and Atomistic Forces	stdev(EQM), PMΣ(|FQM|)

Orange: Liquid phase experimental data, 249 – 373 K (1 atm), 380 – 450 K (along liquid-vapor phase boundary), 1000 – 9000 bar (298 K). Green: Solid phase experimental data consisting of the densities of ice in the Ih, II, III, V, and VI phases, not used for TIP3P-FB. Blue: Theoretical reference data. The scaling factors for potential energies and atomistic forces are given by the standard deviations of the ab initio reference calculations. The objective function is a scaled sum of squared differences between the simulation results and the reference data; the scaling factors (equivalent to inverse weights) are given in the right column.

The dominant paradigm in water model development is to fit the parameters to reproduce a set of experimentally measured properties. In this work, we include six properties over a wide range of thermodynamic conditions: density, heat of vaporization, thermal expansion coefficient, isothermal compressibility, isobaric heat capacity, and dielectric constant. These properties are evaluated at 40 temperatures spanning a range of 249.15 – 450 K at the vapor-liquid phase boundary, and 9 pressures from 1000 – 9000 bar at 298.15 K (Supporting Table 2). Our simulations below 373.15 K were performed at atmospheric pressure rather than the true vapor-liquid phase boundary (< 1 atm), which introduces a negligible correction term. For the TIP4P-FB parameterization we also included the experimentally measured densities of ice, including ordinary ice Ih and several high pressure ice phases (II, III, V, and VI), listed in Supporting Table 3.

ForceBalance evaluates the simulated properties in the isothermal-isobaric (NPT) ensemble and calculates their parametric derivatives to use in the optimization. The derivatives are calculated using a fluctuation formula similar to Hamiltonian Gibbs-Duhem integration.²⁰ Our properties of interest originate from thermodynamic averages and fluctuation, and a generic thermodynamic average property A may be expressed as the following integral:

$$\begin{gathered} {\langle A\rangle }_{\lambda }=\frac{1}{Q\left(\lambda \right)}\int A\left(r,V;\lambda \right)\text{exp}\left(-\beta \left(E\left(r,V;\lambda \right)+PV\right)\right)drdV \\ Q\left(\lambda \right)=\int \text{exp}\left(-\beta \left(E\left(r,V;\lambda \right)+PV\right)\right)drdV, \end{gathered}$$ (1)

where A is the observable, r a given molecular configuration in a periodic simulation cell, λ the force field parameter, E the potential energy, β ≡ 1/k_bT the inverse temperature, k_B the Boltzmann constant, T the temperature, P the pressure, V the volume, Q the isothermal-isobaric partition function, and the angle brackets with a λ subscript represent an ensemble average in the thermodynamic ensemble of the force field parameterized by λ. In practice, this integral is evaluated numerically by sampling via molecular dynamics or Monte Carlo simulation. We can differentiate Equation 1 and obtain the analytic derivative of the property with respect to the parameter:

$$\begin{gathered} \frac{d}{d\lambda }{\langle A\rangle }_{\lambda }=\frac{1}{Q}\int \text{exp}\left(-\beta \left(E+PV\right)\right)\left[\frac{\partial A}{\partial \lambda }+A\left(-\beta \frac{\partial E}{\partial \lambda }\right)\right]drdV \\ -\frac{1}{Q^2}\frac{dQ}{d\lambda }\int A\text{exp}\left(-\beta \left(E+PV\right)\right)drdV \\ ={\langle \frac{\partial A}{\partial \lambda }\rangle }_{\lambda }-\beta \left({\langle A\frac{\partial E}{\partial \lambda }\rangle }_{\lambda }-{\langle A\rangle }_{\lambda }{\langle \frac{\partial E}{\partial \lambda }\rangle }_{\lambda }\right), \end{gathered}$$ (2)

where ∂A/∂λ and ∂E/∂λ are the partial derivatives of the property and potential with respect to the parameters, and independent variables in parentheses are omitted for clarity. The potential energy derivative is calculated in a post-processing step by reevaluating the potentials with perturbed parameter values after the simulation is complete.

Equation 2 shows that the derivative of an ensemble average property resembles a fluctuation property or second-order correlation function. The derivatives of thermodynamic response functions (i.e. fluctuation properties) may be derived in a similar manner; for example, the derivatives of the thermal expansion coefficient α, isothermal compressibility κ_T, isobaric heat capacity c_P, and dielectric constant ε(0) resemble third-order correlation functions. We remark that the derivative of a thermodynamic property is intrinsically more difficult to estimate than the property itself since it always manifests as a higher-order fluctuation.

In addition to experimental data, highly detailed ab initio calculations also provide valuable reference data for model development; they are impractical for many condensed-phase applications due to their high cost but provide valuable information on the microscopic interactions for smaller systems such as water clusters. In this work, the theoretical reference data includes energies and gradients calculated at the dual basis RI-MP2^24–26/heavy-aug-cc-pVTZ²⁷ level of theory for over 100,000 cluster geometries extracted randomly from simulations using the highly accurate iAMOEBA water model.¹⁴ These geometries are taken from simulations of liquid-vapor interfaces and liquid-solid interfaces over a wide temperature and pressure range; the full sampling protocol is given in the Supporting Information. The calculations were performed using Q-Chem 4.0;²⁸ the resolution of the identity (RI) approximation and the dual-basis (DB) approximation used their respective auxiliary basis sets corresponding to heavy-aug-cc-pVTZ as implemented in Q-Chem.

Although we included a very large amount of reference data into our optimization, there is still the danger of overfitting. Overfitting is treated by regularization, in which parameter values are penalized if they stray too far from their original values. Penalty functions have a natural interpretation in Bayesian statistics because they correspond to the negative logarithm of a prior distribution, analogous to how a potential energy function is the negative logarithm of a Boltzmann distribution.²⁹ For example, a harmonic penalty function corresponds to a Gaussian prior distribution:

$$P\left(\lambda \right)\propto e^{-\raisebox{1ex}{${\lambda }^2$}\!\left/ \!\raisebox{-1ex}{${\alpha }^2$}\right.}\leftrightarrow R\left(\lambda \right)=\frac{{\lambda }^2}{{\alpha }^2},$$ (3)

where P(λ) represents the prior probability distribution of the parameter λ, and R(λ) is the harmonic penalty function. The width of the prior distribution α (and corresponding inverse squared strength of the penalty function) represents our expectation of possible parameter values before introducing the parameterization data. The regularized objective function then corresponds to the posterior distribution. Thus, the regularized optimization alleviates the task of manually selecting the highly sensitive force field parameters, but still requires the prior widths to be specified using physical knowledge. Our optimization was regularized using a Gaussian prior specified in Supporting Table 1 corresponding to a parabolic penalty function.

In ForceBalance, the overall objective function is expressed as a weighted sum of squared residuals over the experimental and theoretical target data sets (inverse weights and data types in Table 2) with a regularization term added. The exact gradient and approximate Hessian matrix of the objective function is derived from the first derivatives of the properties using the Gauss-Newton approximation. The Levenberg-Marquardt algorithm^30–31 with an adaptive trust radius^32–33 is used to perform an iterative minimization of the nonlinear least squares objective function. Convergence of the objective function to within a standard error of 1–3 is typically achieved in less than 30 optimization cycles.