Development and validation of AMBER-FB15-compatible force field parameters for phosphorylated amino acids

Abstract

Phosphorylation of select amino acid residues is one of the most common tools for regulating protein structure and function. While computational modeling can be used to explore the detailed structural changes associated with phosphorylation, most molecular mechanics force fields developed for the simulation of phosphoproteins have been noted to be inconsistent with experimental data. In this work, we parameterize force fields for blocked dipeptide forms of the phosphorylated amino acids serine, threonine, and tyrosine using the ForceBalance software package with the goal of improving agreement with experiment for these residues. Our optimized force field, denoted as FB18, is parameterized using high-quality ab initio potential energy scans and is designed to be fully compatible with the AMBER-FB15 protein force field. When utilized in MD simulations together with the TIP3P-FB water model, we find that FB18 consistently enhances the prediction of experimental quantities such as ³J NMR couplings and intramolecular hydrogen-bonding propensities in comparison to previously published models. As was reported with AMBER-FB15, we also see improved agreement with the reference QM calculations in regions at and away from local minima. We thus believe that the FB18 parameter set provides a promising route for the further investigation of the varied effects of protein phosphorylation.

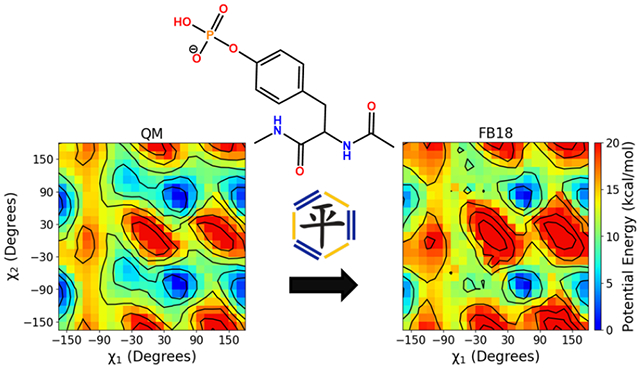
Graphical Abstract

Introduction

Protein phosphorylation, the enzyme-catalyzed reversible addition of a phosphate group to protein residues, represents one of the most ubiquitous post-translational modifications (PTMs); it has been estimated that approximately 30% of all proteins are phosphorylated at some point in their lifetimes.^1,2 Protein kinases catalyze the transfer of a phosphate group from molecules such as ATP to various amino acid residues, while phosphatases catalyze the reverse reaction.^3,4 This reversible PTM can cause changes to the local and/or global structure of proteins, which may serve to modify their activity in key cellular pathways.⁵ Many phosphorylation sites are located in intrinsically disordered proteins (IDPs); for such a protein, phosphorylation may alter its conformational ensemble and/or ability to bind to its biomolecular partners.^6–9 Because phosphorylation represents a strong chemical perturbation to a protein, it is perhaps unsurprising that it is used by the cellular machinery to regulate important processes such as metabolism, apoptosis, membrane transport, cell signaling, and a variety of other essential cellular processes.^2,10,11

Human genome mutations can result in improper function of the protein kinases and phosphatases that catalyze the addition and removal of phosphate groups from proteins, potentially leading to improper regulation of these key cellular pathways. This leads to diseases such as cancer, diabetes and various neurodegenerative disorders.^1,12–15 Due to the central role that the kinases and phosphatases play in the regulation of these diseased pathways, phosphorylated systems are increasingly becoming promising targets for drug development strategies, demonstrating the importance of this PTM for proper cell function.^16–22 Thus, the effects of protein phosphorylation must be studied thoroughly to understand how it modulates the regular functions of proteins and to understand how/why abnormal phosphorylation associated with disease disrupts these functions. The detailed study of these systems may significantly aid current drug development processes, in addition to furthering our basic understanding of cellular physiology.

Computational simulations are a valuable complement to experimental techniques that aim to characterize the changes in protein structure and function that occur upon phosphorylation (or dephosphorylation). This is especially true for IDPs, which exist as an ensemble of structures that may be difficult to deduce from experimental data that often consist of ensemble averages.²³ Molecular dynamics (MD) simulations in particular have been used to study a wide variety of protein properties in general, including protein folding and conformational change.^24–32 Numerous MD simulations have been performed for various phosphorylated systems in the past, such as tau protein, RNA polymerase III, smooth muscle myosin and others, with the goal to elucidate the conformational changes that phosphorylation introduces to these systems.^33–36 The accuracy of these simulations, however, is strongly determined by the classical force field used for the MD simulation.^37–40 Force fields for phosphorylated amino acids have been mainly developed for those relevant for eukaryotes: serine, threonine and tyrosine. These force field parameters are generally available for monoanionic and dianonic protonation states, as these are the relevant forms at physiological pH.⁴¹ In the AMBER force field, phosphorylated amino acid parameters were first created for AMBER ff99⁴² by Homeyer et al.⁴³ The partial charges were parameterized using RESP,⁴⁴ Lennard-Jones parameters were generally taken from phosphodiesters in the AMBER force field, and a variety of new bonded parameters were implemented. Validation was performed in order to ensure that torsional energies reproduced example ab initio calculations. As the Lennard-Jones (LJ) parameters were not optimized for the phosphorylated amino acids, Steinbrecher et al.⁴⁵ optimized the oxygen LJ radii on the phosphate group to reproduce solvation free energies computed using thermodynamic cycles, gas phase basicities, and other values from quantum chemistry (QM) calculations of phosphorylated amino acid analogues. There exist another set of force field parameters in AMBER 03 as part of Forcefield PTM, which was designed for a variety of post-translational modifications,⁴⁶ but parameters are only available for the dianionic species of the phosphorylated amino acids in this package. The AmberTools 20 distribution includes newly derived side chain-specific torsion parameters for phosphorylated residues that are compatible with the ff14SB and ff19SB force fields, but the parameterization and validation approaches have not yet been published. Parameters for phosphorylated residues have also been developed for the GROMOS and CHARMM force fields, with parameters either derived from nucleic acids or parameterized similarly to the AMBER force fields.^47–51

The validation of phosphorylated amino acid parameters by comparing simulation predictions to experiment is lacking in the literature, in contrast to the case of the canonical amino acids. A recent article by Vymětal et al.⁵² has pointed out inconsistencies in calculated quantities by the AMBER and CHARMM force fields for the phosphorylated amino acids over a wide range of properties related to their conformational ensembles, such as NMR ³J couplings, intramolecular hydrogen bonding propensities, conformational preferences, and more; inconsistencies in calculated conformational preferences by AMBER and CHARMM for larger IDPs have also been noted by Rieloff and Skepö⁵³. This raises questions about the suitability of current force field parameter sets for simulation of these systems.

The need to improve force field accuracy for phosphorylated residues can be met by leveraging recent methods that were used to reparameterize force fields for the canonical amino acids.^54–56 One of the well-established avenues for improving these force fields is to refit the bonded parameters, in particular those describing the dihedral angle degrees of freedom, by fitting to high-quality ab initio quantum chemistry calculations. The AMBER-FB15 protein force field is one example of this approach.⁵⁴ In the parameterization of AMBER-FB15, the parameters fit to a large data set consisting of RI-MP2/aug-cc-pVTZ level^57,58 calculations on blocked dipeptide versions of the 20 canonical amino acids in standard and alternate protonation states, including relative potential energies and gradients of constrained optimized structures on dense grids of main chain and side chain dihedral angle constraints, and vibrational frequencies at optimized geometries. The parameters were optimized in automated fashion using ForceBalance, a program which has been successfully used for systematic and reproducible force field parameterization for a variety of systems.^59–62 Although AMBER-FB15 produced notably improved predictions of equilibrium and temperature-dependent properties of proteins, the original work did not develop compatible parameters for PTMs such as phosphorylation.

The goal of this work is to create AMBER-FB15 compatible parameters for six phosphorylated amino acids: phosphoserine, phosphothreonine and phosphotyrosine in their monoanionic and dianonic protonation states. We first build a reference data set composed of accurate MP2-level QM data as was done for AMBER-FB15. ForceBalance is used to optimize bonded parameters starting from those created by Homeyer et al.⁴³ for the phosphorylated side chains in order to keep consistent parameters for the backbone atoms, with the nonbonded parameters unmodified from those implemented by Homeyer et al.⁴³ and Steinbrecher et al.⁴⁵ Detailed potential energy surface comparisons are made between parameters from AMBER ff99SB,⁶³ which we use as a starting point for the force field optimization, the “FB18” optimized parameters presented in this work and the QM reference data for validation of the energies predicted by the new parameters. Additionally, we compare the new force field to experimental data for blocked dipeptide forms of each of the amino acids parameterized here, similarly to the procedure performed by Vymětal et al.⁵² These are essentially the simplest phosphorylated systems possible, for which a multitude of data exists, such as ³J NMR couplings and chemical shifts, intramolecular hydrogen bond propensities, and backbone conformational preferences.^64–66 The simple nature of these systems allows for relatively straightforward comparison between MD simulation results and experiment.

We find that the parameters from AMBER ff99SB generally overestimate QM energetic barriers for these phosphorylated systems, consistent with what was observed in the parameterization of AMBER-FB15.⁵⁴ The FB18 parameters adjust these barriers to overall better agreement with the QM data, which we believe can lead to further improvement in the prediction of experimental observables. Indeed, we find that FB18 is able to significantly enhance force field predictions for quantities such as ³J NMR couplings in these systems, which is particularly promising as the force field was not explicitly parameterized to any experimental data of this nature. Moreover, comparisons between AMBER ff99SB and FB18 indicate that the latter yields improvements in the qualitative predictions from MD simulations with respect to experimental data on phosphate group-to-backbone hydrogen bonding. We therefore recommend the use of FB18 along with AMBER-FB15 for the further study and exploration of phosphorylation on the effects of protein structure.

Methods

Reference Data Set

The reference data used to parameterize AMBER-FB18 is comprised of QM single-point energies, gradients and vibrational modes, largely following the procedure described for canonical amino acids in parameterizing AMBER-FB15.⁵⁴ The single-point energies and gradients were computed for constrained energy-minimized structures where constraints were varied over 2-D grids of main chain or side chain dihedral angles. The TorsionDrive⁶⁷ procedure was employed to generate the grids of constrained optimized structures using a wavefront propagation method as illustrated in Figure 1. The procedure starts with a user-specified grid of dihedral angle constraints and one or more initial structures. In the first iteration, the initial structures are energy-minimized with the dihedral angle constraints set to the nearest grid point. Next, constrained energy minimizations are started from the minimized structures with new target constraint values set to the neighboring grid points (4 for a 2-dimensional scan), and the cycle is repeated. As the iterations proceed, multiple minimizations may be targeted at the same grid point starting from different neighboring points, or new minimizations may be targeted at a grid point that already has results from a previous iteration. When this occurs, the energies of the newly finished minimizations are compared with any previous results at that grid point, and new calculations are launched in the next iteration only if a new lowest-energy structure is found. Thus, at the end of the TorsionDrive procedure, the dihedral grid has an energy-minimized structure at each point with the property that no new constrained minimizations started from neighboring grid points could further lower the energy. While TorsionDrive is computationally more expensive than running the constrained minimizations separately, it has the advantage of producing a maximally continuous potential energy surface even when there are multiple local minima in the orthogonal degrees of freedom.

Figure 1:

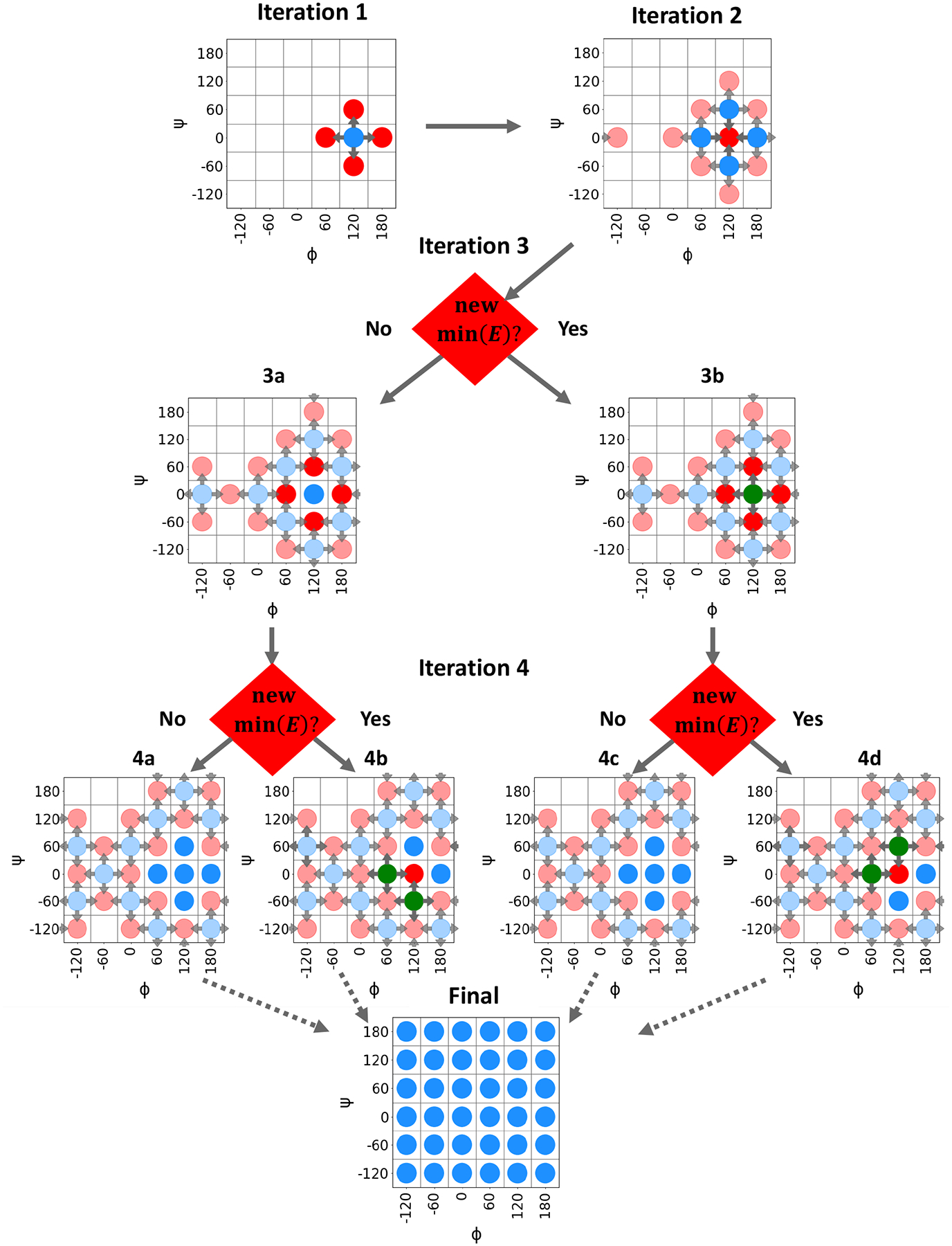
Illustration of TorsionDrive procedure. Grid points containing energy minimization data are represented by a circle; blue circles represent inactive grid points with data from previous iterations, red circles are grid points with active minimization(s), and green circles indicate a new lowest energy structure has been found at a grid point containing results from previous iterations. Arrows point from the initial to target constraint values.

Fig. 1 explains how the TorsionDrive iterations unfold for a hypothetical example with a 2-D grid of (ϕ,ψ) angles with 60° resolution. The individual iterations are described as follows:

Iteration 0: (not shown) The user-provided initial structure is energy-minimized with dihedral constraints set to the nearest grid point at (120°, 0°).

Iteration 1: Four new minimizations are started with constraints targeting the neighboring grid points (120°± 60, 0°± 60).

Iteration 2: Four new minimizations are started from each of the completed minimizations from Iteration 1, for a total of 16, including four targeting the original grid point at (120°, 0°). The five circles in the middle are highlighted for clarity.

Iteration 3: Four new minimizations are launched from the lowest-energy minimized structure at each of the eight blue circles on the perimeter (32 total). These include three new minimizations at each of the outer four points in the highlighted region (120°± 60, 0°± 60). The four energy minimizations at the center point (120°, 0°) from Iteration 2 are compared with the existing result from Iteration 0. If a new lowest-energy structure is found, then four new minimizations are started from this point (3b). Otherwise, this point becomes inactive (3a). Note that two minimizations are started at the grid point (−60°, 0°) from opposite ends of the propagating wavefront.

Iteration 4 : Four new minimizations are launched from the lowest-energy structures on the perimeter (40 total). The energy minimizations at (120°± 60, 0°± 60) from Iteration 3 are compared with the previous results from Iteration 1. If a new lowest-energy structure is found, then new minimizations are launched (4b, 4d). Otherwise, the points become inactive (4a, 4c).

Iteration N : The iterations continue until self-consistency, i.e. no new local energy minima are found with lower energy.

For each monoanionic phosphorylated amino acid, we performed two TorsionDrive calculations that scanned the backbone (φ, ψ) and side chain (χ₁, χ₂) dihedral angles respectively, each on a 2-D grid with 15° resolution. We observed that some of these minimizations led to proton transfer from a backbone N-H group to the phosphate, and rectified this by constraining the two N-H bond lengths to 1.01Å. These minimizations produce two 24×24 grids with an associated geometry at each point. As the constrained dihedral angles are varied over the grid, the orthogonal degrees of freedom can change significantly; this effect can be seen in Figure S1 in the Supporting Information, which shows the variation in the optimized ϕ/ψ as the χ₁/χ₂ angles are scanned. Because this procedure involves several times as many energy minimizations as grid points (i.e. thousands per dipeptide), they are carried out using a relatively inexpensive level of theory, B97-D3/6–31G*.^68,69 The lowest-energy structures on each grid point are then re-minimized with their constraints at the RI-MP2/aug-cc-pVDZ level of theory,⁵⁷ followed by a RI-MP2/aug-ccPVTZ gradient calculation and a RI-MP2/aug-cc-pV(T,Q)Z single-point energy calculation to estimate the MP2/CBS energy using Helgaker’s two-point extrapolation.⁷⁰ Because the TorsionDrive procedure was highly costly, we took a less expensive approach for the dianionic residues by removing the hydrogen on the phosphate group from each structure in the monoanionic grids and running the constrained minimizations independently; single-point energy and gradient calculations were then performed following the same procedure as the monoanionic case.

In addition to the dihedral potential energy surfaces, we also performed vibrational analyses to provide additional data for the bonded parameters. For each dipeptide in both protonation states, an unconstrained RI-MP2/aug-cc-pVTZ energy minimization was carried out for the overall lowest energy structure taken from the grids, followed by a RI-MP2/aug-cc-pVTZ numerical Hessian calculation and vibrational analysis for the vibrational frequencies and normal modes. Scaling factors for the vibrational frequencies were the same as those used for the AMBER-FB15 frequency calculations.^54,71

Despite our best efforts to scan over the relevant degrees of freedom when generating the QM data, the optimized MM force field often has spurious local energy minima that occur at structures not covered by the QM data set. To address this issue, we generated new QM data energies and gradients from molecular mechanics (MM) energy-minimized structures using the optimized force field and appended them to the training data set, then re-optimized the force field with the expanded data set. After we have optimized the initial force field using the dihedral potential energy surfaces and frequency calculations, each structure on the 2D QM grid is optimized using the new force field, and the resulting structures are clustered using heavy-atom root-mean-square deviation (RMSD) and a cutoff of 0.1 Å. The clustering produces 25–50 geometries per residue / protonation state, from which RI-MP2/CBS single-point energies and RI-MP2/aug-cc-pVTZ gradients are computed and added to the dataset. Because spurious minima have relatively high QM energies, adding this data to the parameter optimization creates a feedback loop to eliminate these minima in the “re-optimized” force field. This outer loop is repeated three times to reduce the occurrence of spurious local minima before producing the final FB18 parameter set.

Table 1 summarizes the total reference data in the parameter optimization. The TorsionDrive procedure used Q-Chem 4.4 to perform the energy minimizations and the Work Queue library to distribute the independent minimizations at each step of the wavefront propagations.^72,73 The final MP2 optimizations were carried out using Psi4 1.1 called from the geomeTRIC geometry optimization package;^74,75 Psi4 was also used for the single-point energy and gradient calculations as well as the vibrational analysis.

Table 1:

Reference Data types for the FB18 force field. The (φ, ψ) grids include five geometry optimizations that failed to converge as shown in Figures S20 and S21.

reference data	no. of calculations
grid of energies and gradients over (φ,ψ) for 6 protonation states	3451
grid of energies and gradients over (χ1,χ2) for 6 protonation states	3456
vibrational frequencies for each protonation state	6
energies and gradients of MM-optimized structures	405

Parameter Optimization

ForceBalance, a software package designed for systematic and reproducible force field development, was used for the parameter optimization. The underlying theory of ForceBalance is reviewed here, and the reader is directed to References 54,59,62 for a more comprehensive description.

ForceBalance seeks to minimize the difference between results predicted by the reference data and the force field represented as a least-squares objective function of the following form:

$$L_{\mathit{\text{tot}}}(\mathbf{\text{k}})=\sum _{T\in \mathit{\text{targets}}}{w}_T{L}_T(\mathbf{\text{k}})+w_{\mathit{\text{reg}}}{\left|\mathbf{\text{k}}\right|}^2$$ (1)

Here, L_tot refers to the total objective function and is dependent on the optimization variables k. The objective function has a hierarchical structure, and L_tot is comprised of individual objective functions for each target, L_T (k) individually weighted by w_T . A Tikhonov regularization term is also added, with a user-determined global regularization strength w_reg, here set to 1.0. In the context of this work, there are four targets for each residue / protonation state: the two QM dihedral scans, the vibrational frequency calculations, and the single-point energies and gradients from MM-optimized structures from the feedback procedure. The w_T applied to the QM dihedral scans and vibrational frequencies is set to 1.0 in this work, while a w_T of 4.0 was used for the MM-optimized structures to increase the contribution of this term focusing on elimination of spurious minima.

Each target objective function in ForceBalance consists of contributions representing one or more properties of a molecular system:

$$L_T(\mathbf{\text{k}})=\sum _{j\in \mathit{\text{properties}}}{w}_j^{(T)}{L}_j^{(T)}(\mathbf{\text{k}})$$ (2)

Here, the $w_j^{(T)}$ refers to the weight applied to the contributions from individual properties $L_j^{(T)}$. For the targets consisting of single-point energies and gradients (the dihedral potential energy surfaces and MM-optimized structures), $w_j^{(T)}$ was set to 1.0 for the energies and 0.1 for the forces, whereas for the vibrational frequencies there is only one property $\left(w_j^{(T)}=1.0\right)$. The lower weight for the forces was chosen because the QM forces for the constrained energy-minimized structures tend to be relatively small compared to if they had been sampled from a constant-temperature ensemble. As the (QM - MM) force deviations are normalized by the RMS of the (small) QM forces, the force deviation term in the objective function is artificially large.⁵⁴ Therefore, we choose $w_j^{(T)}=0.1$ to counteract this effect, so that the energy and force contributions to the objective function are roughly equal. The $L_j^{(T)}(\mathbf{\text{k}})$ are given by

$$L_j^{(T)}(\mathbf{\text{k}})=\frac{1}{{\left(d_j^{(T)}\right)}^2}\frac{{\sum }_{p\in \mathit{\text{points}}}{w}_{\mathit{\text{jp}}}^{(T)}{\left|y_{\mathit{\text{jp}}}^{(T)}(\mathbf{\text{k}})-y_{\mathit{\text{jp}},\mathit{\text{ref}}}^{(T)}\right|}^2}{{\sum }_{p\in \mathit{\text{points}}}{w}_{\mathit{\text{jp}}}^{(T)}}$$ (3)

This term computes the difference between the property predicted by the force field parameters on a specific data point p, $y_{\mathit{\text{jp}}}^{(T)}$, with that predicted by the reference data, $y_{\mathit{\text{jp}},ref}^{(T)}$. The $d_j^{(T)}$ variable is used to normalize and remove physical units for each property. Individual weights for data points within a property are given by $w_{\mathit{\text{jp}}}^{(T)}$, and are all set to one for the vibrational frequencies. For the dihedral grids, a weight function similar to the one implemented for the construction of AMBER-FB15 is used:⁵⁴

$$w_{\mathit{\text{jp}}}^{(T)}\left(E_{\mathit{\text{jp}}}\right)=\{\begin{array}{l}{D}^{-1}A\left(y_{\mathit{\text{jp}}}^{(T)}(\mathbf{\text{k}})-y_{\mathit{\text{jp}},ref}^{(T)}\right),E_{\mathit{\text{jp}}}\le D\hfill \\ {\left(D^2+{\left(E_{\mathit{\text{jp}}}-D\right)}^2\right)}^{-1/2}A\left(y_{\mathit{\text{jp}}}^{(T)}(\mathbf{\text{k}})-y_{\mathit{\text{jp}},ref}^{(T)}\right),E_{\mathit{\text{jp}}}>D\hfill \\ 0,E_{\mathit{\text{jp}}}>U\hfill \end{array}$$ (4)

$$A(\Delta )=\{\begin{array}{l}1,\Delta \ge 0\hfill \\ 100,\Delta <0\hfill \end{array}$$ (5)

The weight function is a decreasing function of the potential energy above the minimum, and has the effect of prioritizing the objective function towards low-energy structures that are statistically most probable during the MD simulations. For relative energies below D, the weight takes a constant value, then becomes inversely proportional to energy until the upper cutoff U is reached, where the weight drops to zero. The lower cutoff D is set to 5 kcal/mol in both AMBER-FB15 and this work. However, in contrast to the canonical amino acids where U is set to 20 kcal/mol, the dianionic residues have a substantial number of structures with relative energies greater than 20 kcal/mol (shown in the Supporting Information Figures S20–S22). Therefore, the cutoff energy was increased from U = 20 kcal/mol to U = 40 kcal/mol for the dianionic species. The $A\left(y_{\mathit{\text{jp}}}^{(T)}(\mathbf{\text{k}})-y_{\mathit{\text{jp}},ref}^{(T)}\right)$ term depends on the sign of the MM-QM energy difference, and is designed to heavily penalize force field predictions in which the MM energy is lower than the QM energy (see Ref. 54).

To compute y_jp(k) above, the mathematical parameters k are mapped to physical parameters K through a linear transformation:

$$K_{\lambda }=K_{\lambda }^{(0)}+p_{\lambda }{k}_{\lambda }$$ (6)

where is λ an index pertaining to individual force field parameters, K_λ is the current physical value of the parameter undergoing optimization, $K_{\lambda }^{(0)}$ is the original physical parameter, p_λ is the parameter prior width and k_λ is the mathematical parameter or optimization variable. The linear mapping between mathematical and physical parameters allows one to simultaneously optimize parameters that have different physical units and may vary across many orders of magnitude. The prior width is a hyperparameter that is user-specified for each parameter type, and controls the size of the variations of parameters of that type over the course of the optimization. For a fixed change in the physical parameter, the change in the mathematical parameter is inversely proportional to the prior width, therefore the prior width is proportional to the inverse square of the penalty function contribution. Due to a greater anticipated deviation in the initial parameters compared to those seen in AMBER-FB15, the prior widths for the bond and angle parameters were both increased by a factor of 5. The prior widths used for FB18 are shown in Table 2.

Table 2:

Prior Width Values for Each Parameter Type

parameter type	prior width
bond length	0.05 nm
bond force constant	5 × 105 kJ mol−1 nm−2
bond angle	25 °
angle force constant	500 kJ mol−1 rad−2
dihedral phase	π rad
dihedral amplitude	10 kJ mol−1

The AMBER-FB15 force field parameters for the backbone of each amino acid along with the AMBER ff99SB parameters (with some modifications detailed below) for the phosphorylated side chains was used as the starting point of the optimization.^43,45,54 As the purpose of this work is to add onto the existing AMBER-FB15 model, only bonded parameters pertaining to the side chain for each protonation state were optimized in order to maintain compatibility. Residue and protonation state specific β carbon atom types (and γ carbon atom types for monoanionic and dianionic phosphorylated threonine) were added in order to better fit the dihedral potential energy surfaces; the atom types for each residue are listed in the Supporting Information Tables S1–S6. Additionally, we found a sizeable discrepancy for the phosphorous-oxygen (linking the amino acid side chain to the phosphate group) equilibrium bond length parameter for the dianionic phosphorylated amino acids compared to the value produced from the QM optimizations and of model phosphorylated analogues (detailed in the Supporting Information §1.2). As the parameter optimization is sensitive to the initial parameter values through the penalty function, we altered these initial bond length values in order to produce a more reasonable starting point for ForceBalance. GROMACS 5.1.4 interfaced with ForceBalance was used for performing MM single-point energies/gradients, energy minimizations, and vibrational analysis for the parameter optimization process.⁷⁶

Molecular Dynamics Simulations

Unphosphorylated, protonated phosphorylated (charge: −1e), and deprotonated phosphorylated (charge: −2e) serine, threonine, and tyrosine dipeptides were built in extended conformations using the tleap program of AmberTools 18⁷⁷ and either the AMBER ff99SB⁶³ or FB18 force fields. We will use the three-letter identifiers SER, THR and TYR for unphosphorylated serine, threonine and tyrosine dipeptides, respectively; S1P, T1P and Y1P to refer to protonated phosphorylated serine, threonine and tyrosine dipeptides; and SEP, TPO and PTR to refer to deprotonated serine, threonine and tyrosine dipeptides. As outlined in the leap setup script leaprc.phosaa10 (contained in AmberTools 18), the partial atomic charges for the phosphorylated amino acids were obtained from Homeyer et al.,⁴³ and modified Lennard-Jones radii for the phosphate oxygens were obtained from Steinbrecher et al.⁴⁵ Each peptide was solvated in a truncated octahedron of 1380 to 1400 TIP3P⁷⁸ (for ff99SB) or TIP3P-FB¹² (for FB18) water molecules and neutralized by the addition of 1–2 sodium ions where applicable. The Joung-Cheatham monovalent ion parameters⁷⁹ for TIP3P were used with the ff99SB/TIP3P simulations, while the same authors’ monovalent ion parameters for SPC/E were used with the FB18/TIP3P-FB simulations, as the TIP3P-FB water model is closer in parameter space to SPC/E⁸⁰ than TIP3P.

All energy minimizations and MD simulations were performed using pmemd and pmemd.cuda⁸¹ programs of Amber 18. Periodic boundary conditions were used with a 9.0 Å cutoff for real space nonbonded interactions, PME for long-range electrostatics, and an analytic correction for long-range van der Waals interactions. First, each system was minimized with 250 steps of steepest descent minimization, followed by 250 steps of conjugate gradient minimization. During this phase of minimization, peptide atoms were restrained with a harmonic force constant of 10.0 kcal mol⁻¹ Å⁻². Next, the same amount of minimization was performed without restraints. The subsequent molecular dynamics simulations were performed using a 2.0 fs time step and with SHAKE to constrain all bonds with hydrogen atoms. First, the systems were heated linearly from 100 to 303.15K over 20 ps with an additional 20 ps of NVT equilibration using a Langevin thermostat with a coupling constant of 1.0 ps⁻¹. Next, 50 ps of NPT equilibration was performed at the same temperature and with a pressure of 1.013 bar using a Berendsen barostat with a coupling constant of 2.0 ps⁻¹. During the heating and equilibration steps, the peptides were again restrained with a harmonic force constant of 10.0 kcal mol⁻¹ Å⁻². A final NPT equilibration without constraints was performed for 200 ps using a Monte Carlo barostat, with volume swaps attempted every 100 steps (200 fs). Production simulations were performed for 1.5 μs, with trajectory snapshots saved every 10 ps.

We observed slow convergence of dihedral angle distributions and/or scalar couplings for some of the dipeptides. In particular we aimed for all systems to have uncertainties no larger than ~0.01 in terms of predicted probabilities of backbone conformational states and ~0.1 Hz in terms of predicted scalar couplings. For these systems (ff99SB: T1P and TPO; FB18: SER, THR, Y1P, and PTR) we performed replica exchange MD (REMD) simulations to improve the conformational sampling. The REMD protocol consisted of running 20 replicas in exponentially spaced temperatures between 303.15 K and 410 K. Replicas were first equilibrated (i.e., simulated without any exchange attempts) for 10 ns. After the equilibration period, REMD simulations were performed for 300 or 600 ns, with exchange attempts made every 0.2 ps (100 steps) and structures saved every 5 ps (25 swap attempts). The exchange success rate was between 22–25% for all replicas (and systems).

Data Analyses of MD simulations

A simple approach was used to generate uncertainty estimates for all of the numerical data obtained from the MD simulations. First, each production simulation was first split into two equally-sized blocks. Then, to create two quasi-independent simulation blocks, the first 10% of each block was discarded as a decorrelation period. The resulting numerical data from these blocks are presented as the mean of the two blocks ± the difference between the two blocks.

Backbone conformational preferences were categorized by binning ϕ/ψ angles according to the definitions of Vymětal et al.⁵² Backbone ³J_HN,Hα scalar couplings were calculated using the “ensemble” Karplus equation parameters given in Table 1 of Vögeli et al.⁸² The quality of agreement with experimental scalar coupling data was quantified using the following χ² statistic:⁸³

$${\chi }^2=\frac{1}{N}\sum _{i=1}^N\frac{{\left(\langle J_{i,\text{sim}}\rangle -J_{i,\text{expt}}\right)}^2}{{\sigma }_i^2}$$ (7)

Here we assume that the uncertainties ${\sigma }_i^2$ are dominated by the uncertainties inherent in the Karplus equation parameters (RMSD: 0.36 Hz), which are an order of magnitude larger than the reported experimental uncertainties (~0.05 Hz) or simulation uncertainties due to finite sampling. We also calculated these scalar couplings using the “rigid” Karplus equation parameters of Vögeli et al.⁸² to verify that our conclusions were robust with respect to the choice of parameters (Table S7 in the Supporting Information).

Side chain ³J_Hα,Hβ scalar couplings were calculated using the residue-specific Karplus equation parameters given in Table 2 of Pérez et al.⁸⁴ We used the residue-specific parameters as opposed to the “consensus” parameters because the scalar couplings for serine and threonine are systematically and significantly lower than all other residues due to the electron-withdrawing nature of the oxygen substituent attached to the Cβ atom in these residues.⁸⁴

Results and discussion

Optimized Parameter Values

Figures S2–S19 in the Supporting Information show the top 10 parameter value changes for each parameter type. While the equilibrium bond lengths and angles from the AMBER-FB15 optimization procedure changed by no more than 5%, the largest parameter changes noted for FB18 are slightly greater than 10%. The parameters describing the different phosphorous-oxygen bond and angle terms were, in general, changed the most as can be seen in Figures S2–S5. The equilibrium bond lengths were mainly increased for these atom types, with the exception of the OV-P bond length (oxygen linking to the phosphate group in PTR), which experienced a small reduction compared to the initial value we assigned from QM energy minimizations. The force constants for the bond and angle terms associated with the phosphate group were also largely modified, with a close to 25% reduction for the hydrogen-oxygen-phosphorous angle for the monoanionic species being the largest parameter change. The other large parameter changes are associated with the new beta carbon atom types that have been introduced. These parameters had greater changes for the dianionic residues compared to the monoanions.

Figures S6–S17 break down the dihedral angle parameter changes by multiplicity. The dihedrals involved with the newly introduced β carbons and the amino acid backbone were generally modified more than the dihedrals involving the phosphorous atom. The dihedral angle parameters belonging to the dianions changed more than the corresponding monoanions as in the bond and angle terms, although this varies by residue/multiplicity. As in AMBER-FB15, the equilibrium phase angles change by no more than approximately 30°, and the torsion amplitudes change by no more than 1 kcal/mol.

Quality of Fit

Figure 2 above displays an example potential energy surface for monoanionic phosphorylated tyrosine dipeptide (Y1P) with the (χ₁, χ₂) angles constrained, comparing the QM reference data with the ff99SB and FB18 force field predictions. As can be seen, ff99SB predicts a broad low energy region around the (χ₁) dihedral angle of −100° which is shown not to exist in the QM data. FB18 corrects this region, albeit with a slight overestimation of the energy at the higher energy peaks. It also manages to broaden low energy regions that ff99 predicts to be too high, such as at the regions of (50, 100) and (50, −100). We expect the better agreement with the QM potential energy surface to lead to a more accurate sampling of equilibrium structures in simulation and improved temperature-dependent properties as is observed in AMBER-FB15. Heat maps for all residues/dihedral angle combinations are shown in Figures S20–S22 in the Supporting Information. Similar agreement as shown in Figure 2 is observed, although the (ϕ, φ) grids for dianionic phosphorylated serine and threonine dipeptides appear to significantly overestimate the energy in some regions.

Figure 2:

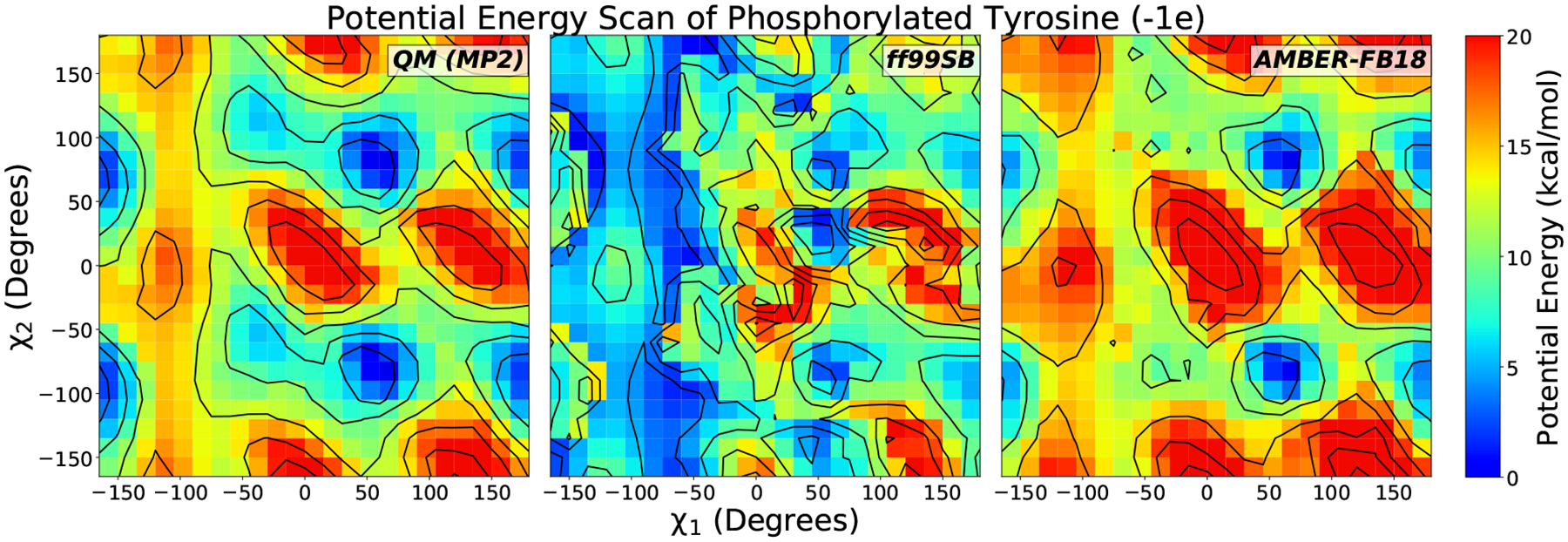
Potential energy surface for monoanionic phosphorylated tyrosine blocked dipeptide (Y1P). Left: QM relative energies calculated at the RI-MP2/CBS level at RI-MP2/aug-cc-pVDZ energy-minimized structures with constrained (χ₁, χ₂) dihedral angles. We compare the MP2 energies to the initial force field parameters (ff99SB, central panel) and the optimized parameters in this work (AMBER-FB18, right panel). The agreement with QM is markedly improved after the fit.

Figure 3 shows the results of re-optimizing the parameters after adding QM training data calculated at energy-minimized structures using the optimized force field, using monoanionic phosphorylated tyrosine (Y1P) as an example. The initial energies predicted in the first cycle have a RMSE of 9.08 kcal/mol, with the force field predicting MM energies that are too low compared to the QM data. The addition of these data points to the objective function in Equation 3 seeks to increase the energies of these spurious minima. In the second cycle, where the force field is re-optimized with the additional QM data, the RMSE for the energies calculated at the MM minimized structures significantly decreases to 1.54 kcal/mol. In the third cycle the RMSE has a minor decrease from Cycle 2 to 0.92 kcal/mol, indicating that the reoptimization procedure has essentially converged.

Figure 3:

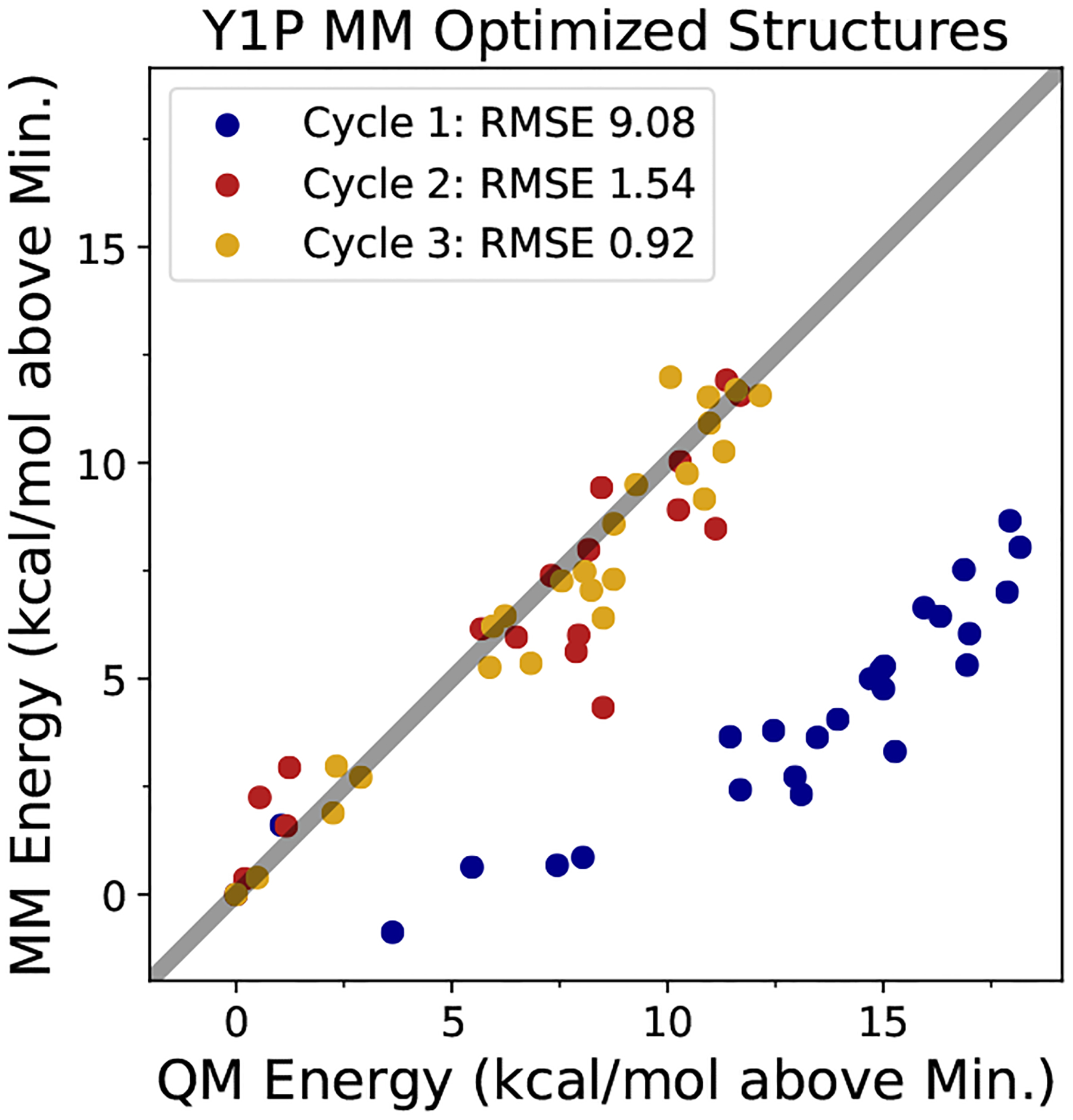
MM vs. QM predicted energies for phosphorylated tyrosine dipeptide (−1e). The points represent predicted minimum energy structures from the force field, which are eliminated through multiple cycles of adding the QM energies and gradients for these points back into the objective function.

Validation of Parameters: MD Simulations of Dipeptides

Intramolecular Hydrogen Bonding Propensities

NMR chemical shift data obtained for phosphorylated serine and threonine dipeptides at varying pH levels suggest that the oxygen atoms of the phosphate group are able to form hydrogen bonds with the two backbone amide protons of the capped dipeptides.⁶⁵ In the analysis that follows, we will refer to the amide nitrogen immediately N-terminal to the side chain as N_self and the amide nitrogen that belongs to the C-terminal capping group as N_cap.

For the phosphorylated serine dipeptides (in our nomenclature: S1P and SEP), the experimental data suggest that there is a substantial increase in hydrogen bond formation to the proton of N_self upon deprotonation of the phosphate group (i.e., when S1P becomes SEP), while there is no change in the hydrogen bond formation propensity for the proton of N_cap.⁶⁵ MD simulations performed with ff99SB yield nearly zero phosphate-to-backbone hydrogen bonding in either S1P or SEP (Table 3). Conversely, simulations performed with FB18 display hydrogen bonding to both amide protons for both S1P and SEP, with increases in hydrogen bonding propensities for both upon deprotonation of the phosphate group. Here it seems that neither force field offers an entirely satisfactory reproduction of the qualitative trends present in the experimental data, as ff99SB does not form these phosphate group-to-backbone hydrogen bonds enough and FB18 perhaps forms them too readily (at least to the proton of N_cap).

Table 3:

Phosphate Group to Backbone Hydrogen Bond Propensities

Residue	Donor	ff99SB	FB18	Expt. Trend
S1P	Nself	0.0180 ± 0.0009	0.186 ± 0.002	—
	Ncap	0.0095 ± 0.0005	0.090 ± 0.003	—
SEP	Nself	0.0022 ± 0.0001	0.318 ± 0.004	—
	Ncap	0.0003 ± 0.0001	0.338 ± 0.003	—
diff: SEP - S1P	Nself	−0.0158 ± 0.0009	0.132 ± 0.005	↑↑
	Ncap	−0.0092 ± 0.0005	0.248 ± 0.004	↔
T1P	Nself	0.080 ± 0.002	0.028 ± 0.002	—
	Ncap	0.252 ± 0.009	0.009 ± 0.002	—
TPO	Nself	0.127 ± 0.002	0.59 ± 0.02	—
	Ncap	0.146 ± 0.007	0.043 ± 0.005	—
diff: TPO - T1P	Nself	0.047 ± 0.003	0.56 ± 0.02	↑↑↑
	Ncap	−0.10 ± 0.01	0.034 ± 0.005	↑

Note: The “Expt. Trend” column represents a qualitative interpretation of chemical shift data given in Lee et al.⁶⁵

The experimental data for the phosphorylated threonine dipeptides (in our nomenclature: T1P and TPO) display a different trend, with a greater increase in hydrogen bond formation to the proton of N_self upon deprotonation of the phosphate group (i.e., when T1P becomes TPO) and a non-negligible increase in the hydrogen bond formation propensity for the proton of N_cap.⁶⁵ For these residues, ff99SB yields a slight increase in hydrogen bonding to N_self upon deprotonation of the phosphate group, but a decrease in hydrogen bonding to N_cap. FB18, however, is able to recapitulate the experimental trend, with a large increase in hydrogen bond formation to the proton of N_self and a modest increase in hydrogen bond formation to the proton of N_cap. In this case it appears that FB18 is able to more faithfully reproduce the hydrogen bonding trends than ff99SB.

Backbone Conformational Preferences

Backbone conformational preferences are a common method of validation for force field development because they play a key role in determining the secondary structure preferences of simulated proteins. Here we examined the backbone conformational preferences of all nine dipeptides, using the same definitions of secondary structure (i.e., “helical”, “PPII”, and “extended”) as Vymětal et al. to facilitate direct comparison with that work and additionally validate our own simulation results.⁵² We classify ϕ/ψ angles not corresponding to one of these three regions as “other”; such conformers would be considered as either αL or αr in Vymětal et al.⁵² For completeness we have included the ϕ/ψ free energy surfaces for all of the dipeptides in the Supporting Information (Figures S23–S25).

As in Vymětal et al., we find that phosphorylation and then deprotonation of the phosphate group successively increase the helical nature of the serine dipeptide when simulated using ff99SB (Figure 4). Likewise, phosphorylation causes a modest shift from PPII to extended conformations in threonine, whereas the opposite trend appears for tyrosine (Figure 4). With FB18, however, the shifts in conformational preferences are generally much larger, especially for the deprotonated phosphorylated residues. In particular, we see that deprotonated phosphorylated serine (SEP) has more helical content and greatly reduced extended and PPII content compared to neutral serine. (The missing ~50% of conformers are in the lower left of the α-helical (αr) region of the Ramachandran diagram and are therefore classified as “other” rather than “helical” according to the definitions of these regions (Figure S23).⁵²) The same is largely true for threonine under FB18, although more of the conformers remain in the “helical” region. In both cases, it is likely that FB18’s greater propensity to form phosphate group-backbone hydrogen bonds (due to the changes in torsion potentials and other bonded potentials relative to ff99SB) enables the stabilization of the “helical” or nearly helical “other” conformers of these dipeptides. Finally, for tyrosine we see that the deprotonated phosphorylated residue (PTR) has a much larger proportion of “extended” conformers than its neutral or protonated phosphorylated counterparts (Figure 4). As the phosphate group of PTR is unable to form hydrogen bonds with the backbone, it is difficult to attribute the stabilization of the “extended” conformation to changes in any specific nonbonded interaction.

Figure 4:

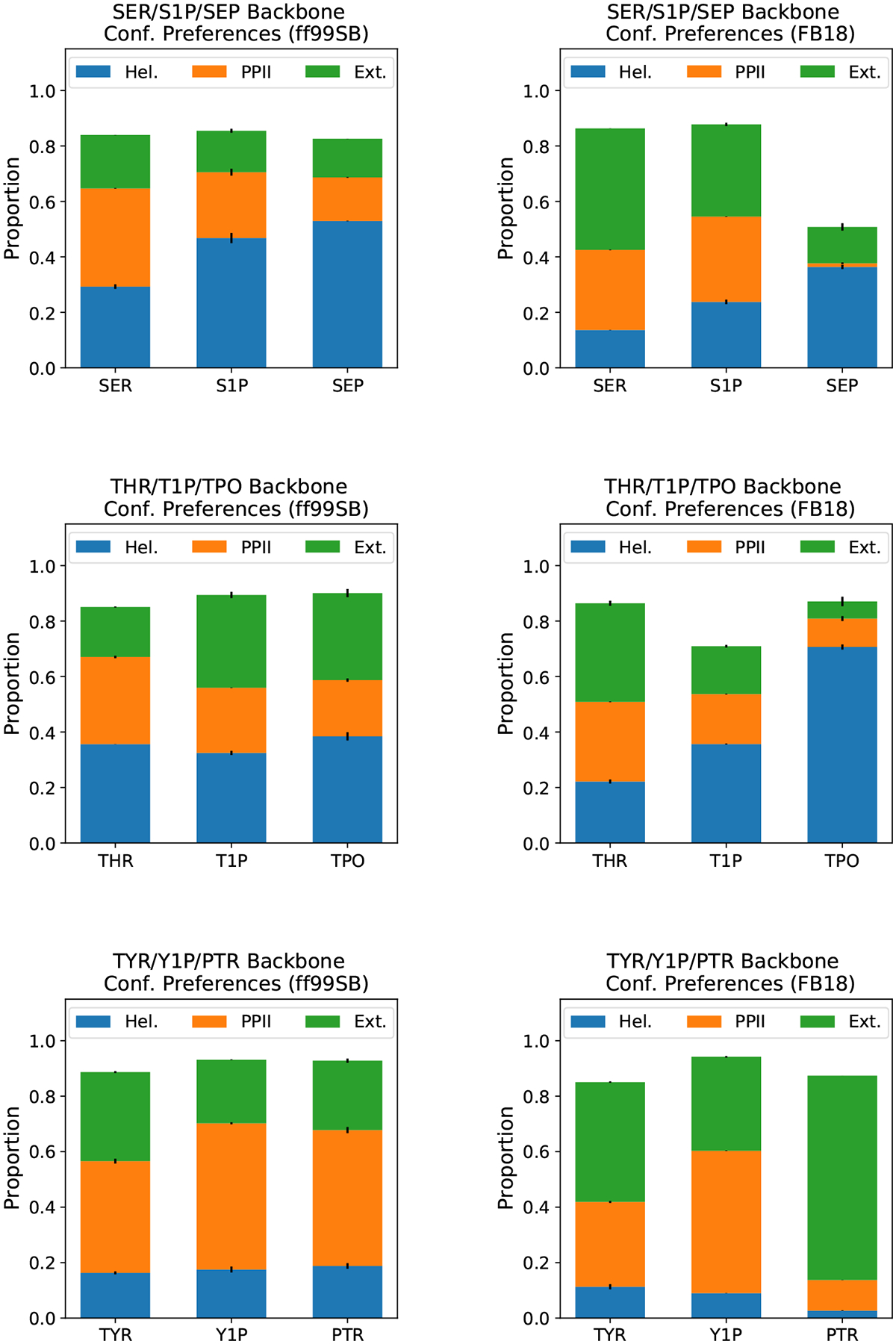
Comparison of backbone conformational preferences: results obtained with ff99SB (left) and FB18 (right). Conformers were classified as helical, polyproline II, or extended, according to the definitions used by Vymětal et al.⁵² Filled bars represent the averages between two halves of the simulations. Black whiskers show the differences between two halves of the simulations.

Overall, it appears that the predicted impacts of phosphorylation on backbone conformational preferences are quite different between ff99SB and FB18. One way to begin to address which force field is more accurate is to examine experimental data that reports on these preferences; in this case, ³J_HN,Hα scalar couplings report directly on the ensemble average of the ϕ angle distribution. Experimental ³J_HN,Hα scalar coupling data are available for both unmodified and phosphorylated (both protonation states) serine and threonine, but only unmodified tyrosine. As shown in Table 4 and Figure 5, ff99SB generates scalar couplings that are close to experiment for unmodified residues and protonated phosphorylated serine (S1P) and threonine (T1P), but the predicted scalar couplings for deprotonated phosphorylated serine (SEP) and threonine (TPO) are far from the experimental values (~1.5 Hz and ~2.5 Hz, respectively). Moreover, all of the predicted scalar couplings generated by ff99SB reside between approximately 6.9 Hz and 7.6 Hz, regardless of residue identity, phosphorylation, or protonation state. This can be rationalized by noting that the backbone conformational preferences, specifically the proportions of extended conformers (ϕ centered on −165°) vs. proportions of helical + PPII conformers (ϕ centered on −60°), are quite similar for all of these dipetides under ff99SB. As with the backbone conformational preferences, FB18 generates J-coupling predictions that are qualitatively different. In particular, FB18’s predictions agree with experiment to a level of ≤ 0.5 Hz for all of the simulated dipeptides.

Table 4:

Backbone ³J_HN,Hα Scalar Couplings (in Hz)

Residue	ff99SB	FB18	Experiment
SER	7.098 ± 0.005	6.687 ± 0.009	7.02
S1P	7.31 ± 0.01	6.338 ± 0.009	6.85
SEP	7.56 ± 0.02	6.06 ± 0.01	5.98
THR	7.608 ± 0.003	7.40 ± 0.02	7.35
T1P	7.623 ± 0.001	8.047 ± 0.005	7.55
TPO	7.767 ± 0.008	5.50 ± 0.02	5.23
TYR	7.45 ± 0.01	6.997 ± 0.003	7.13
Y1P	6.95 ± 0.01	5.86 ± 0.02	n/a
PTR	7.132 ± 0.008	6.686 ± 0.003	n/a

Figure 5:

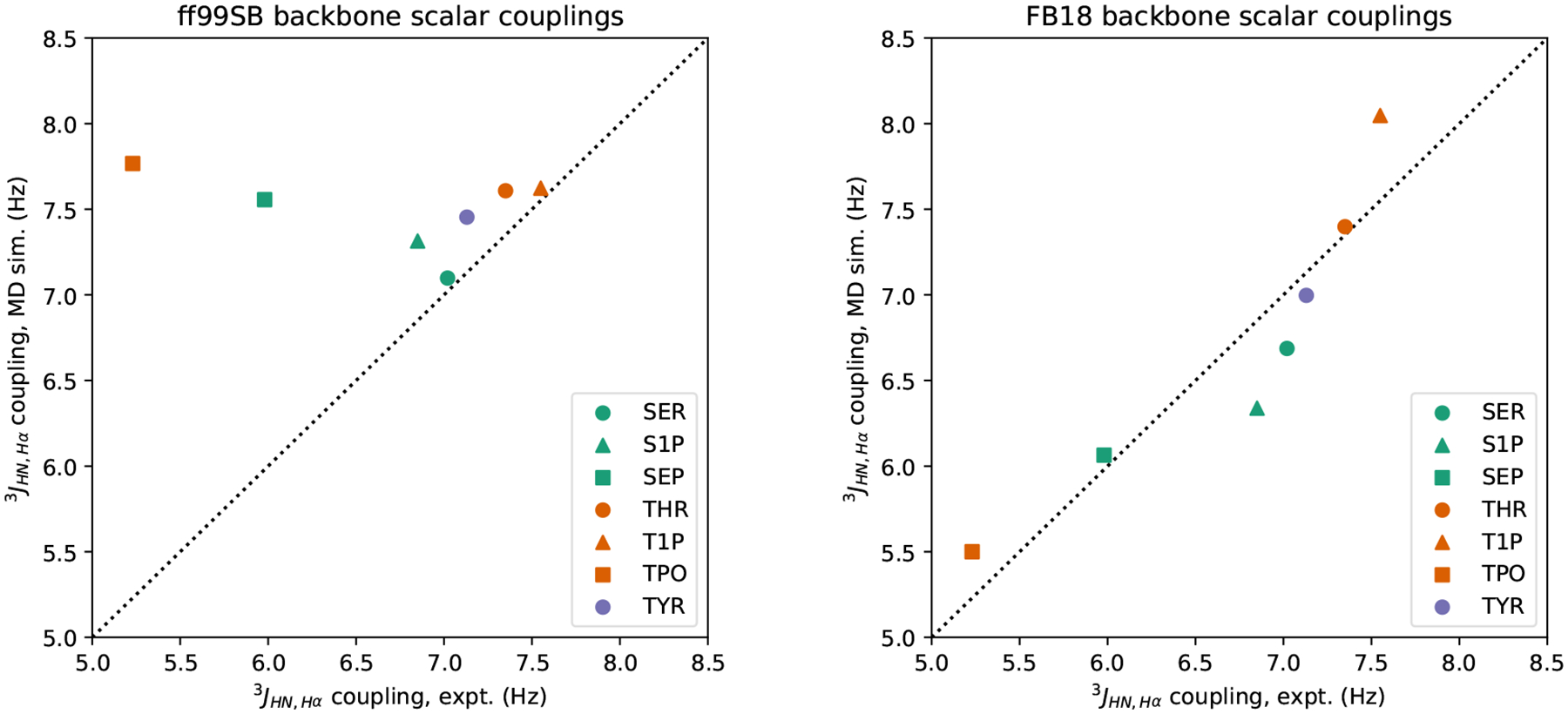
Comparison of experimental and simulated ³J_HN,Hα scalar couplings: results obtained with ff99SB (left) and FB18 (right). Scalar couplings are calculated from simulation structures using the “ensemble” Karplus equation parameters of Vögeli et al.⁸² Experimental data are taken from Avbelj et al. and Kim et al.^64,66

To quantify the agreement between the scalar couplings predicted from our simulations and the experimentally measured couplings, we computed both the χ² score, as in Best et al.,⁸³ and the (Pearson) correlation coefficient r for these data. Across all seven residues for which there are experimental data, we found that the χ² score for ff99SB was 10.27, while the χ² score for FB18 was 0.79. If we restrict the comparison to only the phosphorylated residues with experimental data (i.e., S1P, SEP, T1P, and TPO), then the χ² scores for ff99SB and FB18 are 17.63 and 1.14, respectively. We note that a χ² score of 1 or below suggests that the predicted couplings are comparable to the experimentally measured couplings, given all of the uncertainties present. Calculating the correlation coefficient r and its 95% confidence interval (CI) for the scalar coupling data of all residues under ff99SB yields −0.389 (95% CI: [−0.883, 0.515]), while for FB18 r is 0.916 (95% CI: [0.524, 0.988]). The former CI suggests that, despite the “clustered” appearance of Figure 5, there is little-to-no correlation between ff99SB’s predictions and the experimental data, whereas the latter CI suggests that FB18’s predictions have a moderate-to-strong correlation with these same data.

In short, FB18 generates accurate (i.e., within ~0.5 Hz) predictions of backbone scalar couplings across all residues examined, but especially for the deprotonated phosphorylated residues that have the largest charge perturbation relative to the unmodified residues. This gives us some confidence that the differences in backbone conformational preferences between ff99SB and FB18 that are shown in Figure 4 are meaningful and that FB18’s predictions are likely as accurate as – and in some cases substantially more accurate than – ff99SB.

Side Chain Conformational Preferences

We next examined the conformational preferences of the amino acid side chains by analyzing their χ₁ and χ₂ angle distributions. As can be seen in Figure 6, all of the residues appear to sample 3 states (with varying preferences for those states) that are either gauche or trans with respect to rotation about the Cα –Cβ bond. ff99SB yields nearly identical χ₁ distributions for each unmodified amino acid and its phosphorylated variants, with the greatest exception being unmodified threonine (THR) vs. phosphorylated threonine (T1P and TPO). In this case, the addition of a phosphate group appears to be the sole factor behind the change in conformational preferences, rather than the charge state of the phosphate group. In contrast, we find that FB18 yields χ₁ distributions that are generally quite distinct between the unmodified residues and their phosphorylated counterparts. Moreover, there are significant differences in side chain conformational preferences between the protonated (S1P, T1P, and Y1P) and deprotonated (SEP, TPO, and PTR) phosphorylated residues. In this sense, FB18 yields χ₁ distributions that are immediately distinguishable from those of ff99SB. We discuss how these differences might manifest themselves in experimental data further below.

Figure 6:

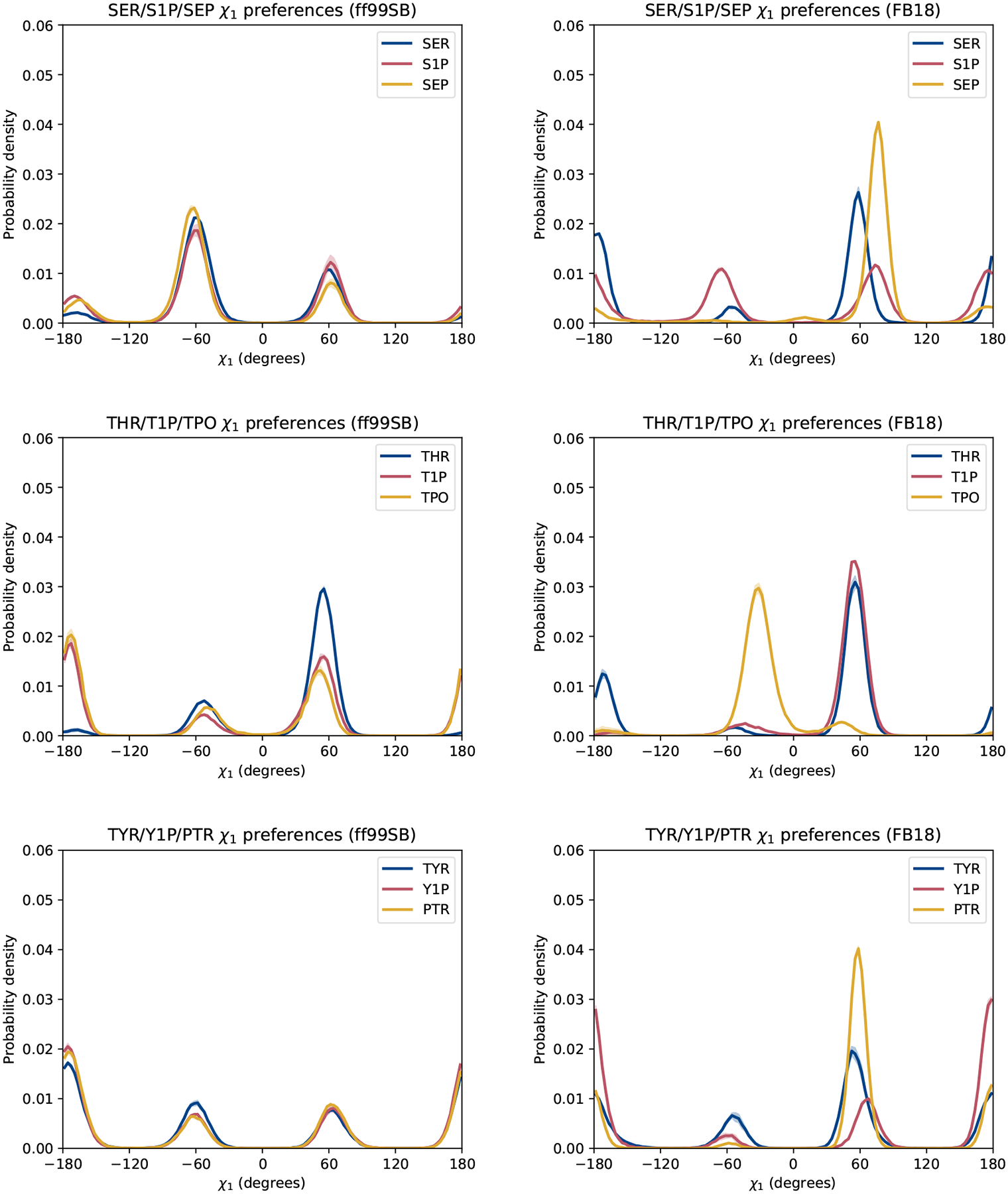
Comparison of χ₁ side chain conformational preferences: results obtained with ff99SB (left) and FB18 (right). Lines represent the average between two halves of the simulations. Shaded regions represent the differences between the two halves.

The χ₂ distributions generated by each force field, shown in Figure 7, also display striking differences, particularly for phosphorylated serine and threonine. In particular, ff99SB predicts nearly all trans conformations for phosphorylated serine (both S1P and SEP), whereas FB18 predicts sampling of all three states – with a preference for the gauche states – in S1P and a strong preference for gauche⁻ state in SEP. Likewise, ff99SB predicts a fairly broad distribution of χ₂ angles in T1P and TPO (between 60°and 180°), while FB18 predicts more strongly peaked distributions (albeit within the same general range). It is likely that the χ₂ distributions for phosphorylated threonine diverge from the usual gauche^±-trans paradigm due to the due to the fact that this dihedral angle is defined by rotation about the central Cβ-Oγ bond between the Cα and P atoms and both the steric effects and intrapeptide hydrogen bonding of the phosphate group. Both force fields are consistent, however, in predicting the ±90° preference of tyrosine residues, as expected for residues where the Cγ atom is sp²-hybridized.

Figure 7:

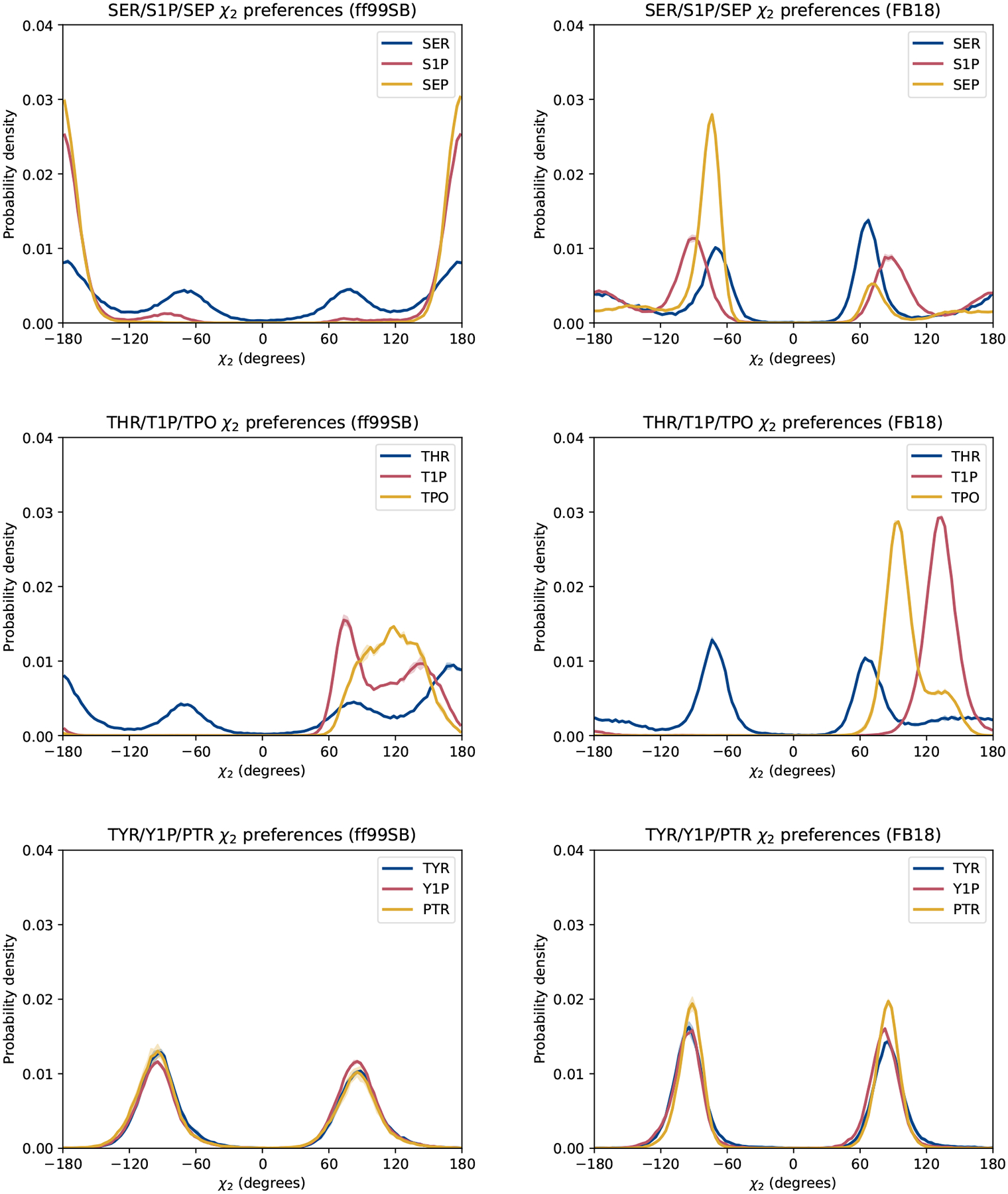
Comparison of χ₂ side chain conformational preferences: results obtained with ff99SB (left) and FB18 (right). Lines represent the average between two halves of the simulations. Shaded regions represent the differences between the two halves.

Finally, we briefly revisit the question of how the accuracy of these two force fields (and others) could be evaluated with respect to side chain conformational preferences. One direct reporter of the χ₁ distribution of a side chain is the ³J_Hα,Hβ scalar coupling. To that end, we calculated predicted ³J_Hα,Hβ coupling values for all of the residues we examined in this study to see what, if any, differences we might find. We observe that ff99SB and FB18 differ in their predictions by anywhere between 0.6 and 2.7 Hz for these residues. These differences are approximately an order of magnitude greater than the typical experimental uncertainties of ~0.05 Hz. Therefore we think that if NMR scalar coupling data could be obtained for the side chains of these dipeptides, it would almost certainly enable force field developers to discriminate between “less accurate” and “more accurate” when it comes to reproducing the intrinsic conformational preferences of phosphorylated residues.

Conclusion

Through a combination of the existing AMBER-FB15 protein force field and a systematic optimization of the intramolecular parameters for the side chains of phosphorylated serine, threonine, and tyrosine, we have built FB18, a new set of parameters for the simulation of phosphorylated peptides and proteins. We demonstrated that it was possible to generate a substantially improved fit to the QM data in both the low-energy and high-energy regions. As is observed in AMBER-FB15, we expect the better agreement to the QM scans to improve sampling of equilibrium structures and temperature-dependent properties for simulations of larger phosphoproteins, although such systems were not studied in this work.

Our model is validated by examining the conformational preferences of blocked dipeptides using comprehensive ensembles generated from either μs-long MD simulations or REMD and comparisons with available experiments. The validation simulations demonstrate significant improvements in the accuracy of predicted experimental quantities, particularly NMR scalar couplings and intramolecular hydrogen bonding propensities, in comparison to AMBER ff99SB. We identify this promising agreement as a result of the QM torsion scans performed using TorsionDrive, as both of these experimental quantities are related to the dihedral angle potentials; this further demonstrates the utility of the procedure for generating reference data for force field development. Further improvements in reproducing experimental data might be obtained by generating the QM reference data and performing the MM calculations using implicit solvent models, as in the AMBER ff19SB protein force field and several AMBER nucleic acid force fields.^85–88

We believe the performed benchmarks on the model dipeptide systems in this work indicate that FB18, along with AMBER-FB15, is a promising framework for the further investigation of phosphoprotein structural and functional properties. The more accurate prediction of the conformational ensembles provided by FB18 will likely play a crucial role in the simulation of IDPs, where individual amino acids may adopt a wide variety of conformations. Additionally, we anticipate the procedure we performed may be extended to add additional PTMs to AMBER-FB15, which should allow for the generation of an accurate and comprehensive parameter set for the simulation of a large variety of protein conformational states.

Table 5:

Side Chain ³J_{Hα ,Hβ} Scalar Couplings (in Hz)

Residue	ff99SB	FB18
SER	3.20 ± 0.02	5.41 ± 0.01
S1P	3.68 ± 0.05	4.62 ± 0.07
SEP	3.39 ± 0.03	2.75 ± 0.01
THR	2.80 ± 0.05	4.15 ± 0.10
T1P	5.42 ± 0.11	2.73 ± 0.05
TPO	5.90 ± 0.11	4.83 ± 0.08
TYR	7.032 ± 0.003	6.17 ± 0.07
Y1P	7.51 ± 0.11	8.42 ± 0.12
PTR	7.38 ± 0.09	5.43 ± 0.05

Note: Scalar couplings are calculated from simulation structures using the residue-specific Karplus equations of Pérez et al.⁸⁴