Strain-induced van der Waals gaps in GeTe revealed by in situ nanobeam diffraction

Abstract

Ordered germanium vacancies in germanium telluride thermoelectric material are called van der Waals (vdW) gaps, and they are beneficial for the thermoelectric performance of the material. The vdW gaps have been observed by atomic resolution scanning transmission electron microscopy, but their origin remains unclear, which prevents their extensive application in other materials systems. Here, we report that the occurrence of vdW gaps in germanium telluride is mainly driven by strain from the cubic-to-rhombohedral martensitic transition. Direct strain and structural evidence are given here by in situ nanobeam diffraction and in situ transmission electron microscopy observation. Dislocation theory is used to discuss the origin of vdW gaps. Our work here paves the way for self-assembling two-dimensional ordered vacancies, which establishes a previously unidentified degree of freedom to adjust their electronic and thermal properties.

Advanced electron microscopy discloses the origin of van der Waals gaps in GeTe.

INTRODUCTION

Defect engineering is widely used to tailor the physical properties of materials, from dislocations in work hardening, via dopants in laser optics and microelectronics, to surface defects in heterogeneous catalysis (1–11). Two-dimensional (2D) defects arouse extensive interest due to their unique physical properties (12). The most common 2D planar defects are grain boundaries, twin boundaries, and stacking faults (13). Beyond these well-studied 2D planar defects, 2D sheets of vacancies are attracting increasing attention, since this kind of defect changes not only the local atomic arrangement but also the local chemical bonding. However, this kind of defect does not even get an entry into classic textbooks of materials science, indicating our unfamiliarity and a lack of understanding.

In GeTe-based thermoelectric materials, Ge vacancies can form locally ordered structures, a kind of defect usually called the van der Waals (vdW) gap. These vdW gaps are reported to be beneficial for thermoelectric performance, since they can effectively reduce the lattice thermal conductivity by enhancing phonon scattering events (14, 15). Although the structure of vdW gaps has been studied by atomic resolution high-resolution transmission electron microscopy (HRTEM) and/or high-resolution scanning transmission electron microscopy (HRSTEM) (14, 16, 17), the origin of the ordering of Ge vacancies and the slip mechanism of the adjacent Te atom layers remains controversial. As the reported GeTe-based materials usually contain Bi or Sb doping and have the composition like (GeTe)_1−x(Bi₂Te₃)_x or (GeTe)_1−x(Sb₂Te₃)_x, some works assume that the vdW gaps are caused by the Bi₂Te₃ or Sb₂Te₃ layers, which make the vdW gaps in GeTe-based material similar to the vdW gaps in Bi₂Te₃ or Sb₂Te₃ (18–20). However, they did not offer solid evidence to prove their assumption. There is another possibility that the vdW gaps are ordered Ge vacancies, which are not part of the structure of Bi₂Te₃ or Sb₂Te₃. Which kind of hypothesis is correct needs to be proved by experimental evidence.

We get inspired by the formation process of the void in structural materials. The driving force is believed to be the tensile strain (21–25). These examples provide us hints that the origin of these vdW gaps may be linked to its strain environment.

In this work, we propose that the ordering and slip process in GeTe-based material is mainly driven by the strain from the cubic-to-rhombohedral martensitic transition. The composition of (GeTe)_0.975(Bi₂Te₃)_0.025 is used in this work. Our in situ nanobeam diffraction (NBED) and in situ TEM results offer experimental evidence on the strain and structural evolution. Dislocation theory is adopted to discuss the generation and slip of vdW gaps. We will show that the growth of vdW gaps can be described as the climbing of an edge dislocation, in which the normal strain drives the merger of isolated vacancies into a vdW gap. The resultant vdW gap can go through a slip process, which further releases the normal strain and results in a relative shear of the two adjacent parts of the vdW gap. The presented mechanism provides a way to control the generation of vdW gaps by adjusting the vacancy concentration and the annealing temperature, then optimizing the thermal conductivity, and lastly improving the thermoelectric performance. The orientation of vdW gaps can be controlled by compressive strain. Our work therefore paves the way to control self-assembling vdW structures, which establishes a previously unidentified degree of freedom for tuning their electronic and thermal properties.

RESULTS

Crystal structure of GeTe and vdW gaps

GeTe goes through a phase transition at around 700 K from the low-temperature (LT) rhombohedral phase to the high-temperature (HT) cubic rock salt phase (26). The LT rhombohedral phase can be treated as a pseudo-cubic phase. The lattice parameters of the LT pseudo-cubic phase and the HT cubic rock salt phase are listed in table S1. After the phase transition from the HT cubic phase to the pseudo-cubic phase, one body diagonal is elongated (10.67074 Å in contrast to 10.42695 Å), and the rest of the body diagonals are shortened (10.25538 Å in contrast to 10.42695 Å). We define [111]_PC as the elongated body diagonal, where PC denotes the crystallographic index of rhombohedral material in pseudo-cubic notation. The lengths of the elongated and the three shortened body diagonals are listed in table S2.

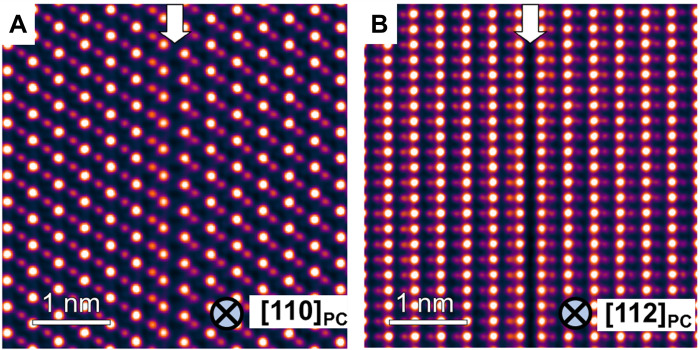
The vdW gap in GeTe is a 2D defect (27): A layer of Ge atoms is missing. High-angle annular dark-field (HAADF) STEM images along [110]_PC and [112]_PC are shown in Fig. 1. The positions of vdW gaps are indicated by the white arrows.

Fig. 1. The atomic structures of vdW gaps.

Colored STEM HAADF images of vdW gaps along with the [110]_PC and [112]_PC zone axes in (A) and (B). The position of vdW gaps is indicated by the white arrows.

Structure evolution before and after the annealing process

The original sample before annealing is quenched from the liquid phase. The quenched sample is then annealed at 300°C for 2 hours inside the TEM. The vdW gaps are generated during this process. This can be easily found by comparing TEM images of the sample before and after the annealing process (Fig. 2). One typical area before and after the annealing process is indicated by the red circle. The structure evolution is also confirmed by electron diffraction in fig. S1, in which the annealed sample shows the stripe-like reflections in fig. S1D, as the red arrow indicates, in contrast to the quenched sample (fig. S1B). This stripe-like reflection originates from the vdW gaps (28). Higher-magnification TEM images of vdW gaps are shown in fig. S2.

Fig. 2. TEM images of the same area before and after annealing.

(A) Pristine sample at room temperature. (B) Sample annealed at 300° for 2 hours and then cooled down to room temperature. The inserted image is the high-magnification image of the vdW gaps. The red circles in (A) and (B) indicate the same area, in which the structure change is obvious.

Strain evolution before and after the generation of vdW gaps

The strain distribution before and after the generation of vdW gaps is illustrated in Fig. 3, starting with a unit cell of the crystal structure. As mentioned, the LT pseudo-cubic phase is an elongated cubic structure (Fig. 3A). From the analysis of the deformation of a unit cell (Fig. 3B) and a great many unit cells (Fig. 3C), we find that to fill the 3D space, the arrangements of deformation should be like the way shown in Fig. 3D, which results in alternating strain fields (tension-compression-tension-etc.). We find this kind of strain field in our samples before annealing (Fig. 3, F and G) and after annealing (Fig. 3, H and I) by applying NBED (29). Figure 3 (H and I) are the strain result at room temperature. The figure panels show that strain fields are directed along [111] and [−111] directions, with the red and blue colors indicating the areas that are in tension or compression, respectively, along the noted directions. It can be seen that after the annealing process at 300°C for 2 hours, the strain fields have changed substantially; tension has clearly been released from most areas. This effect that is shown quantitatively in the line profiles in Fig. 3 (F to I) are shown in Fig. 3 (J and K); strain along [−111] and [111] directions has decreased, also indicating that the lattice has shrunk along these directions.

Fig. 3. Strain evolution due to the annealing process.

(A) 3D sketch of the phase transformation from HT cubic phase to LT pseudo-cubic phase. (B) 2D projection of the phase change of a unit cell. (C) Sketch of a group of unit cells after deformation. The deformation transforms the unit cells in this projection from rectangle to parallelogram. (D) A combination of unit cell groups. (E) The corresponding strain distribution along the [111] and [−111] directions. (F) and (G) are the strain results along [111] and [−111] directions before annealing. (H) and (I) are the strain results along [111] and [−111] directions after annealing at 300° for 2 hours and then cooled to room temperature. (F) to (I) share the intensity bar with (F). (J) Line profiles of the strain along [−111] direction before and after annealing, corresponding to the orange and purple boxes in (F) and (H). (K) Line profiles of the strain along [111] direction before and after annealing.

Orientation relationship of vdW gaps and the strain field

Figure 4A shows an area in which the strain along the [111] and [−111] directions is mapped in more detail, in Fig. 4 (B and C). The NBED patterns in Fig. 4 (D to G) from locations M, N, O, and P show that the vdW gaps are only generated in the red-colored areas (under tension) and that they are perpendicular to the direction of the elongated unit cell diagonal (see the stripe-like reflections between reflection points in Fig. 4, D and E, as indicated by white arrows). These results suggest a close relationship between the vdW gaps and the local strain fields.

Fig. 4. Orientation relationship of vdW gaps and the strain field.

(A) A STEM HAADF image taken after annealing. (B) and (C) are strain field results along the [111] and [−111] directions. (D) to (G) are NBED patterns at M, N, O, and P points in (A). All the diffraction patterns are taken along the [110]_PC.

Direct observation of the generation of vdW gaps

From room temperature to 250°C, the microstructure remains stable because of the low atomic diffusion rate. From 250° to 300°C, Ge gaps start to nucleate and grow gradually. As shown in Fig. 5A (indicated by the white dotted circle), there are no obvious vdW gaps in the sample before annealing. When the sample was heated to 250°C, the vdW gaps start to nucleate, which is evident by the contrast in Fig. 5B (red arrow indicated). At 300°C, the vdW gaps grow faster along (111)_PC planes, reaching much larger length (Fig. 5C). This dynamic growth process of the vdW gaps can also be seen in movie S1. The movie plays at 10 times the real speed for clearer visualization of the growth process. From our observation, we calculate the growth speed of the gaps to be about 6 nm/min or one atomic step every 4 s. As confirmation of the vdW structure, the stripe-like reflections (as the white arrows show) in a selected-area electron diffraction (SAED) pattern at 300°C are shown in Fig. 5D. The SAED pattern is taken from the circled area in Fig. 5C from the [110]_PC zone axis.

Fig. 5. The origin of vdW gaps.

(A to C) In situ TEM images taken at room temperature (RT) (250° and 300°C). (D) Electron diffraction pattern of the observed area at 300°C, taken along the [110]_PC zone axis. (E) A HRSTEM HAADF image taken along the [110]_PC. d₁, d₂, d₃ are the distances of adjacent Te layers at vdW gap, intermediate area and the intact area, which are indicated in E. (F) Schematic of the growth mechanism of vdW gaps, viewed along the [112]_PC.

DISCUSSION

The dominant driving force for the growth of the vdW gaps

The vdW gaps are thought of as superlattices of Bi₂Te₃ or Sb₂Te₃ in GeTe (18–20). Under this assumption, the formation of vdW gap needs additional elements such as Bi or Sb. However, we find that in a nonstoichiometric GeTe, such as the Ge₉₄Te₁₀₀, vdW gaps can be generated as well (fig. S3, as the white arrows indicate).

We propose that the structure of vdW gaps in GeTe is an ordering of Ge vacancies, terminated at two edge dislocations, beyond which the GeTe lattice recovers to intact. The Te-Te distance (0.278 nm) is much shorter in the vdW gap area than that in the perfect crystal area (0.367 nm; Fig. 5E). Furthermore, the growth of vdW gaps is found to be directly linked to the strain field perpendicular to it (Figs. 2 and 3). This phenomenon allows us to treat the vdW gaps as a stacking fault within an edge dislocation loop. The growth of vdW gaps can thus be treated as positive climbing of dislocations. In dislocation theory, positive climbing indicates that the dislocation loops are expanding (30).

There are two kinds of driving forces for positive climbing: mechanical and chemical (Fig. 5F) (30). The mechanical climbing force can be calculated by

$$\mathit{F}=-{\mathrm{\sigma }}_{\mathit{xx}}*\mathit{b}$$ (1)

where σ_xx is the normal stress in the x direction (perpendicular to the climbing direction) and σ_xx = ε_xx*G, ε_xx is the normal strain in the x direction; G is Young’s modulus; and b is the magnitude of the Burgers vector.

Taking G = 44.3 GPa (31), ε_xx = (10.67 − 10.43)/10.43 = 0.023 (10.67 and 10.43 Å are the length of body diagonals in LT pseudo-cubic and HT cubic phases), b = 0.367 − 0.278 nm = 0.089 nm, and the mechanical force is approximately F = 0.09 N/m (30).

In contrast to the mechanical force, the chemical force f is (32)

$$f=\frac{\mathit{bkT}}{\mathrm{\Omega }}\text{ln}(C/C_0)$$ (2)

where b is the Burgers vector; k is Boltzmann’s constant; T is the absolute temperature; Ω is the volume per atom; and C is the total concentration of vacancies, C = C₀ + C₁, where C₀ is the vacancy concentration in equilibrium at room temperature and C₁ is the vacancy concentration caused by adding Bi₂Te₃. The defect reaction is

$${\mathrm{Bi}}_2{\mathrm{Te}}_3\stackrel{3\text{GeTe}}{\to } 2{\text{Bi}}_{\text{Ge}}^{·}+V_{\text{Ge}}^{\prime \prime }+3{\text{Te}}_{\text{Te}}^{\times }$$ (3)

C₀ can be estimated by the carrier concentration. Considering that each Ge vacancy creates two carriers and the measured carrier concentration is 8.1 × 10²⁰ cm⁻³, the Ge vacancy concentration should be about 4.05 × 10²⁰ cm⁻³ (33).

C₁ can be calculated on the basis of Eq. 3. The composition can be written as (GeTe)₃₉(Bi₂Te₃)₁, which means that ¹/₄₂ of the Ge positions is occupied by the vacancies. The volume of a pseudo-cubic unit cell is about 2.16 × 10⁻²² cm³, each having four Ge positions, which gives C₁ = (4/42)/(2.16 × 10⁻²² cm³) = 4.4 × 10²⁰ cm⁻³. As b ≈ 0.089 nm and Ω = 4/3*π*(0.5a)³ = 0.11 nm³ (a = 5.98 Å, the lattice parameter of pseudo-cubic GeTe), then the chemical force according to Eq. 2 is ~0.0025 N/m. Because F > > f, we can conclude that the mechanical force here plays the dominant role in the generation of gaps. Note that mechanical stress is the reaction force caused by the elongation process (fig. S4).

The nucleation of the vdW gap

Ge vacancies introduce a compressive stress field (34), which tends to be attracted to domain boundaries (a typical large-scale 2D defect in GeTe). Around Ge vacancies, a local Cottrell atmosphere forms that can lower the total free energy of the stress field and point defects (35).

In a very simple model, assuming that the dislocation loop is a circle, if we neglect the extra interfacial energy due to the week vdW force, then the energy relationship for the driving force to overcome the resistance can be E(mechanical force) ≥ E(dislocation loop). That is

$$F*\mathrm{\pi }{r}^2⩾E(\text{edge})*2\mathrm{\pi }r$$ (4)

where E(edge) is the energy of edge dislocation of unit length and r is the radius of the dislocation loop. The energy of dislocation is mainly the elastic-strain energy [E_el(edge)] (30). Thus, E(edge) = E_el(edge). The strain energy can be calculated by

$$E_{\text{el}}(\text{edge})=\frac{G{b}^2}{4\mathrm{\pi }(1-\nu )}\text{ln}\left(\frac{R}{r_0}\right)$$ (5)

where G is the elastic modulus, b is the burgers vector, ν is the Poisson ratio, R is the influenced radius of the strain, and r₀ is the radius of the dislocation core. As G = 44.3 GPa, ν = 0.24 (36) and R = 10 r₀ (30). The calculated E_el(edge) = 8.46 × 10⁻¹¹ J/m. By replacing each term, we get r ≥ 1.88 nm, which is the critical radius for a stable dislocation loop. The E(mechanical force) will be always larger than the E(dislocation loop) upon r ≥ 1.88 nm, which means that the vdW gap will grow until reaching the domain boundaries. Note that the resistance is somewhat underestimated, because we omit the vdW binding energy and energy by dislocation core. In this way, the critical radius for a stable dislocation loop should be larger than 1.88 nm. Because the nucleation energy cannot be offered entirely by mechanical force when the radius is lower than 1.88 nm, the domain boundaries are the sites for nucleation due to the possible heterogeneous nucleation mechanism. We can find the nucleation of vdW gaps to take place at the domain boundaries, as can be seen in the image contrast in Fig. 5B (indicated by a red arrow).

Kinetic aspect of the growth process

The growth of the dislocation loop needs a continuing supply of vacancies, which are thermodynamically driven by the chemical potential gradient and kinetically driven by the relatively HT. The chemical potential can be calculated as (37)

$$\mathrm{\mu }=\mathit{kT}\text{ln}(C/C_{\text{vdW}})$$ (6)

Near the vdW gaps, the concentration of isolated vacancies is C_vdW, where the chemical potential approaches zero, while the area with a higher concentration C > C_vdW has positive chemical potential. The vacancies will continuously diffuse to the area of the vdW gaps, while μ > 0.

It is easy to understand that we cannot easily observe the generation of vdW gaps at an LT due to the limited diffusion velocity of the vacancies. The diffusion coefficient D_B can be calculated with the following equation (38)

$${\mathit{D}}_{\mathrm{B}}={\mathit{D}}_0\text{exp}(-\mathit{Q}/\mathit{RT})$$ (7)

where D₀ is a constant, Q is the energy barrier for the diffusion, R is the ideal gas constant R = 8.314 J/(mol·K), and T is the absolute temperature. According to this equation, we know that D_B increases with increasing temperature. At LT, although the thermodynamic condition (ΔG < 0) is achieved, the diffusion velocity of vacancies is so low that not enough vacancies could form vdW gaps.

The slip of Ge gaps

The slip process can release more strain energy. As the left and right inserts of Fig. 5E show, the vdW gap without slip has a width of 0.309 nm in contrast to the vdW gap with slip, which has a width of 0.278 nm. The slip has been indicated by a white arrow.

When heated above 300°C, the atomic slip of vdW gaps can be observed. Slip in this case indicates a simultaneous shear of the two adjacent sides of the vdW gap; the distance of adjacent Te-Te layers becomes smaller, and strain energy is released. Because of the inherent drift in heating TEM sample holders, we cannot observe this slip in situ at atomic resolution, but the corresponding moving strain contrast caused by this process has been captured. As indicated by the white circle in fig. S5 (A to C), the stress field–induced contrast moves along with the vdW gap. The speed is about 315 nm/min, which is much higher than that of the growth of gaps. This is because this process does not need long-range diffusion of atoms. Movie S2 shows the slip process of a vdW gap, which is increased to five times faster than the actual speed.

These slips originate from the relative displacements of two parts of the crystal adjacent to the gap (Fig. 1A). This process can further release the normal strain and thus is thermodynamically favorable. It should be pointed out that the slip may take place with dislocation climbing at the same time.

The difference of vdW gaps in GeTe and layered materials

Although shared with the same name, the vdW gaps in GeTe and layered materials such as Bi₂Te₃ and SnSe are different. The vdW gaps in GeTe are nonperiodical defects, which can be seen from the HRTEM images (fig. S2A). However, vdW gaps in layered materials are periodical structures. This difference makes the vdW gaps in GeTe tunable in terms of their spacings, which may be important freedom to tune the thermoelectric properties.

In conclusion, the dominant driving force for the generation and slip of the 2D vdW gaps is the mechanical force, which is induced by a cubic-to-rhombohedral phase transformation. The strain energy is released by forming the vdW gap structure (Fig. 6). This mechanism is more broadly applicable, e.g., to explain the strain results in (39), in which the direction of the ordered oxygen vacancies is perpendicular to the tensile strain.

Fig. 6. Schematic diagram of the formation of the vdW gap in GeTe.

(A) to (C) are the vacancies ordering process, while (D) and (E) show the slip process. Each step of structural change is accompanied by the corresponding release of normal strain.

The understanding of the vacancy nature of the vdW gap enables the materials scientist to control the number of gaps. For example, the number of vdW gaps can be increased by adding more group VA cations via Bi₂Te₃ or Sb₂Te₃. In addition, it may become possible to produce vdW gaps with a specific orientation by applying compressive stress in perpendicular directions.

The in situ NBED is a useful tool to study martensitic transitions, as they usually comprise the shear of a group of atoms to produce a strain change. In situ NBED offers a large viewing area, making it easy—despite thermal sample drift—to find the same area back after the phase transition for measuring the strain evolution.

2D vacancy ordering is a common phenomenon in many materials systems, with the most-reported compounds being the oxides: CeO₂ (40, 41), CaMnO₃ (42), SrMnO₃ (43), YMnO₃ (44), Bi_0.81Pb_0.19FeO_2.905 (45), BaCeO₃ (46), CaTiO₃-CaFeO_2.5 (47), Y₂O₃ (48), and La_0.5Sr_0.5CoO_3−x (49). In addition, it has recently been reported that Sn vacancies can form vdW gaps in the SnTe system (50). In 2D materials such as WS₂, the S vacancies can order into a chain (51). All these examples show that vacancies tend to order under appropriate conditions. The resulting modified bonding changes the local strain, charge distribution, and other electronic properties, offering previously unidentified freedom to adjust functional properties by controlling the ordering of defects.

MATERIALS AND METHODS

Synthesis

The nominal composition of the sample studied in this work is (GeTe)_0.975(Bi₂Te₃)_0.025. The 7-g raw materials with a nominal composition (GeTe)_0.975(Bi₂Te₃)_0.025 were evacuated (<5 × 10⁻⁴ Pa) and sealed in quartz tubes. The solid solution reaction recipe is as follows: The quartz tube was heated up to 1000°C in 12 hours and kept at that temperature for another 12 hours before being water-quenched to room temperature. The average quenching rate is estimated about 35°C per second. The obtained ingots were taken out from the quartz and hand-milled into powders for follow-up spark plasma sintering (Dr. Sinter, Japan). The sintering process took place at 550°C for 5 min under the uniaxial pressure of 50 MPa. The size of the sintered cylinder sample is φ10 by 14 mm. The material in Fig. 1 goes through a cycle heating process from room temperature to 500°C, which is a dynamic annealing process.

TEM sample preparation

The samples for TEM study were cut from the sintered cylinder samples. The specimens for TEM characterization were prepared by the standard cutting, grinding, polishing, and dimpling method. After mechanical thinning to a thickness of ~20 to 30 μm, the samples were further ion milled to electron transparency using a Gatan 695 ion polisher at the temperature of liquid nitrogen. During ion milling, the samples were milled with the beam voltage of 4.2 kV, a beam current of 65 μA, and a milling angle of ±5°. After the samples were perforated, a voltage of 0.5 kV, a beam current of 35 μA, and a milling angle of ±4° were used to optimize the thin area of the specimen. The samples were further milled at a voltage of 0.1 kV and a current of 15 μA to remove the surface-damaged layer. The average thickness of observed area for NBED is estimated about 46 nm using log-ratio method.

TEM observation

Structure characterization by TEM was performed with a Thermo Fisher Scientific Themis G2 60-300 in STEM mode. All the observations in this work are under 300 kV. Atomic resolution STEM HAADF images are acquired with a beam current of 50 to 100 pA, a convergence angle of ~25 mrad, and a collection angle of 63 to 200 mrad. The observed phenomena (generation and slip of gaps) happened slowly, so the recorded movies were speeded up to make the phenomena easier to be observed by the reader. In the in situ TEM experiments (Fig. 5, A to D), the TEM specimen was heated without irradiation of the electron beam (e-beam). Only when we take pictures of the local structure, we turn on the beam.

NBED experiment

The NBED experiment was conducted in Thermo Fisher Scientific Titan ETEM G2. For NBED experiment (Figs. 3 and 4), the sample was annealed for 2 hours at 300°C without e-beam irradiation. The strain mapping of the annealed state was conducted at room temperature after annealing at 300°C for 2 hours. A brief introduction of the NBED method is shown in the Supplementary Materials (section S1).

In situ heating experiment

The prepared TEM samples were heated by a Gatan heating holder at an average heating rate of 3°C/min. During the heating process and cooling process, the TEM specimen was kept intact for observation. The discussion about the sublimation behavior of the experimental material at elevated temperatures is shown in section S2 and fig. S6. To confirm that the generation of vdW gaps is not the result of the sublimation of TEM specimen, we conducted the ex situ heating experiment. The result and discussion can be found in section S3 and fig. S7.

Supplementary Materials

This PDF file includes:

Sections S1 to S3

Figs. S1 to S7

Tables S1 and S2

References

Other Supplementary Material for this manuscript includes the following:

Movies S1 and S2