Spontaneous beat synchronization in rats: Neural dynamics and motor entrainment

Abstract

Beat perception and synchronization within 120 to 140 beats/min (BPM) are common in humans and frequently used in music composition. Why beat synchronization is uncommon in some species and the mechanism determining the optimal tempo are unclear. Here, we examined physical movements and neural activities in rats to determine their beat sensitivity. Close inspection of head movements and neural recordings revealed that rats displayed prominent beat synchronization and activities in the auditory cortex within 120 to 140 BPM. Mathematical modeling suggests that short-term adaptation underlies this beat tuning. Our results support the hypothesis that the optimal tempo for beat synchronization is determined by the time constant of neural dynamics conserved across species, rather than the species-specific time constant of physical movements. Thus, latent neural propensity for auditory motor entrainment may provide a basis for human entrainment that is much more widespread than currently thought. Further studies comparing humans and animals will offer insights into the origins of music and dancing.

Neural dynamics conserved across species underlies the optimal tempo of beat synchronization to music within 120 to 140 BPM.

INTRODUCTION

Charles Darwin argued that humans inherit the perception of musical rhythm from their progenitors (1). Beat perception and synchronization are common in humans, typically within 120 to 140 beats/min (BPM) and most frequently used in musical compositions (2–4). However, beat synchronization is not common in some species (5). To understand this behavior in animals, we first raised two hypotheses underlying beat synchronization in humans.

In the first hypothesis, the optimal tempo is determined by the time constant of body structure and physical movement. This body-cause theory is evident by the step frequency of ~2 Hz (~120 BPM) during human walking (6) and by the relationship between movement and time perception (7, 8). This hypothesis predicts that the optimal tempo in small animals such as rats is much faster than that in humans, according to the power-law scaling of the step frequency and body weight (9, 10). Theoretical models (11, 12) also support the power-law scaling where physiological time scales—e.g., heartbeat (13), breathing rate (14), circulation time (15), and life span (16)—shorten with body size.

In the second hypothesis, the optimal tempo is determined by the time constant of the brain. This brain-cause theory is evident from the rhythm conservation of brain function across species (17) and neural entrainment by beats in humans (18, 19). Beats also entrain neural activities in the auditory cortex of rats (20), where the time constant of short-term adaptation possibly affects entrainment (21–23). Given that species share similar time constants of short-term plasticity in the auditory cortex, this hypothesis predicts that the optimal tempo for beat synchronization is preserved across species.

To test these hypotheses, we conducted behavioral and electrophysiological experiments in rats. Their movement time scale is several times faster than that of humans (9). To date, no study has reported beat synchronization in rats.

RESULTS

Beat synchronization in rats and humans

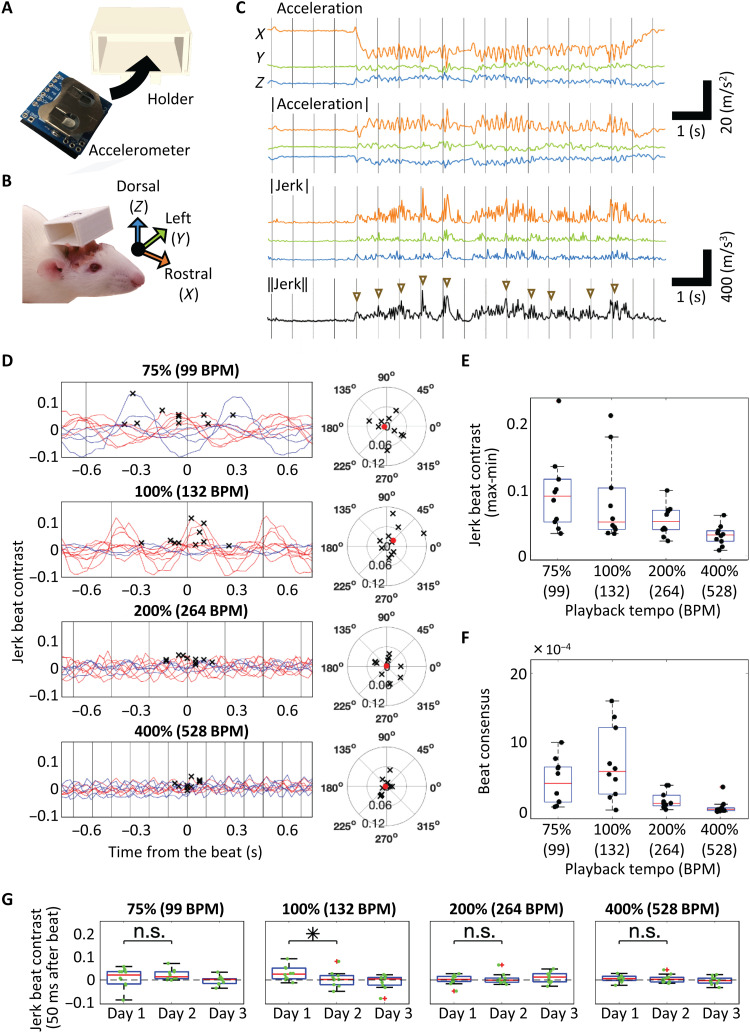
We measured rats’ head movements during music playback using a wireless, miniature accelerometer fixed to the head (Fig. 1, A and B). For three consecutive days, we recorded the accelerations along three axes while playing 60-s excerpts of “Sonata for Two Pianos” in D major, K.448, by Mozart at four different tempos, 99 (75%), 132 (100%), 264 (200%), and 528 (400%) BPM. We observed that the head movements synchronized to beats in some trials (movie S1) and that these movements were likely more visible in a bipedal stance (movie S2 and fig. S1). This beat synchronization was better characterized by the jerk (derivative of acceleration) than by the acceleration (Fig. 1C) (24, 25). Our experiments in humans also confirmed that the head jerk captured beat synchronization consistently as video motion analyses did (movie S3 and figs. S2 and S3). Note that, here, we use the term “beat” to refer to the metric position sometimes described as “tactus” or “pulse” [i.e., metric positions (pos.) 1, 2, 3, and 4 in the 4/4 meter shown in Figs. 2 and 3].

Fig. 1. Beat synchronization in rats.

(A) Wireless accelerometer and holder used in the experiment. (B) Rats with the holder and definition of the three axes. (C) Representative head movements during music playback at the original tempo. The acceleration vector, the absolute value of the acceleration vector, the jerk vector, and the Euclidean norm of jerk are shown. Triangles indicate the increase in jerk around the beat. Beat timings are indicated by gray lines. (D) Left: Mean jerk beat contrast values of days 1 and 2 calculated by shifting the window of the putative on-beat timing for each tempo. In-phase synchrony is plotted in red, whereas reverse-phase synchrony is plotted in blue. Gray vertical lines indicate actual beat timing. The crosses indicate the maximum jerk beat contrast in a cycle (n = 10). Right: The distribution of maximum jerk beat contrast is plotted in the phase field with 0° corresponding to a beat. Each cross indicates an animal, and the red dot indicates the average. (E) Amplitude of beat contrast variation (max-min) at each playback tempo. Each black dot indicates an animal. (F) Intersubject similarity of beat contrast is defined as $\text{beat consensu}\mathrm{s}{}_i=\mid {\sum }_{j\ne i}{\overrightarrow{r}}_i·{\overrightarrow{r}}_j\mid$, where i is the animal index and ${\overrightarrow{r}}_i$ is the maximum jerk beat contrast in the phase field. The beat consensus of animal i increases when ${\overrightarrow{r}}_i$ is in phase or in reverse phase with that of other animals. (G) Jerk beat contrast at beat (0°) on each day. Box plots here and hereafter show the median, 25th/75th percentiles, and maximum/minimum within the 1.5× interquartile range. n.s., not significant. *P < 0.05.

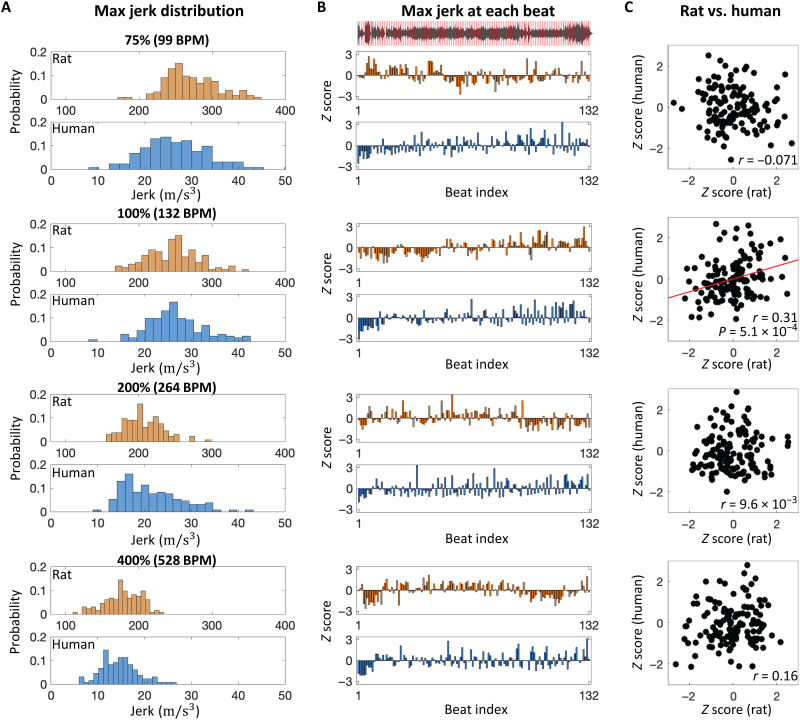
Fig. 2. Comparison of beat synchronization between rats and humans during music presentation (K.448).

(A) Distribution of maximum jerk between each putative beat as a function of playback tempos (75, 100, 200 and 400%). (B) Maximum jerk at each beat. Z scores of jerk were plotted at each beat index (1 to 132). The sound waveform of music with putative beat timings (red lines) are shown in the top inset. (C) Correlation of jerk at each beat index between rats and humans. The correlation coefficient (r) is indicated in each inset.

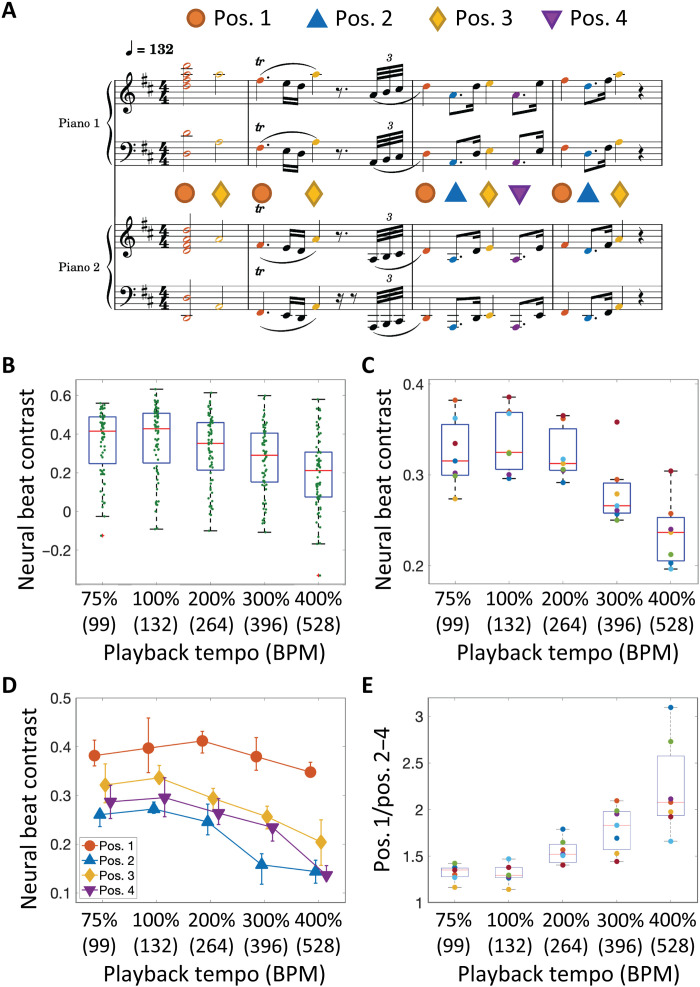
Fig. 3. Neural tuning of music beats.

(A) An excerpt of a musical piece was presented at five different tempos. Colored notes correspond to putative beats, each categorized into four positions (pos.1 to 4) in a bar. (B) Neural beat contrast in a representative animal. Each dot indicates a recording site in the auditory cortex. (C) Neural beat contrast with calculated mean for each animal (n = 7). (D) Neural beat contrast at each beat position. The error bar indicates the 25th and 75th percentiles of individual differences. (E) The ratio of neural beat contrast at the first beat with respect to those at other beats.

Synchronization to putative beats based on the score (i.e., red lines in the top inset in Fig. 2B) was quantified as below

$$\text{Jerk beat contrast} (\mathrm{a}.\mathrm{u}.)=\frac{X_{\text{on}}-X_{\text{off}}}{X_{\text{on}}+X_{\text{off}}}$$

where X_on is the Euclidean norm of the jerk vector averaged around beat (40% of the music playback) and X_off is that elsewhere (the remaining 60%). The average of the jerk beat contrast was derived in each rat by shifting the window of putative beat timing (Fig. 1D). The amplitude of beat contrast variation (max-min) significantly differed across the four tempos (Kruskal-Wallis test, P = 2.6 × 10⁻³; Fig. 1E). Of the 10 rats, the variation of beat contrast was significant for 6, 5, 3, and 1 rats for tempos at 75, 100, 200, and 400%, respectively, compared with the random condition (P < 5.0 × 10⁻²; see Material and Methods). In addition, the intersubject similarity of the jerk beat contrast differed across tempos (Kruskal-Wallis test, P = 2.8 × 10⁻⁴) and was maximum at the original tempo (Fig. 1F). At 132 BPM, beat synchronization was distinct on day 1 with a significant decay on day 2 (Mann-Whitney U test, P = 4.5 × 10⁻²; Fig. 1G).

Head movements in human participants during music listening exhibited similar trends of beat contrast and beat consensus to those in rats (Kruskal-Wallis test: beat contrast, P = 5.1 × 10⁻⁵; beat consensus, P = 1.3 × 10⁻⁸; fig. S4 and movie S3). In both species, the head movements decayed with a tempo increase in both acceleration (fig. S5A) and jerk (Fig. 2A). In rats and human participants that exhibited a significant beat contrast at the original tempo, i.e., 5 of 10 rats and all 12 human participants, we investigated the mean jerk as a function of the phase angle between metric positions of beats to address whether these beat synchronous movements were predictive or reactive and found that the beat synchronous movements in rats were more reactive than those in humans (i.e., the jerk at the original tempo was maximized at phase >0 in rats, while at phase <0 in humans) (fig. S3A). However, close inspection of our data did not rule out the possibility that the beat synchronous movements in rats were predictive at pos. 1 in the original tempo, because the jerk z score started to increase before the beat, and were significantly positive at the beat (fig. S3B). For beat perception and synchronization, the musical context was likely to play an important role because a click sequence of rasterized rhythm of the original piece induced a significantly smaller beat contrast and beat consensus than the original music excerpt in our human participants (Mann-Whitney U test: beat contrast, P = 1.7 × 10⁻²; beat consensus, P = 9.7 × 10⁻⁵; fig. S4, B and C). To test whether the musical context induced similar movements in rats and humans, we analyzed the temporal variation of jerks across a musical passage and found that the maximum jerk at each putative beat varied across the music passage (Fig. 2B) and that these patterns in rats were significantly correlated to those in humans only at the original tempo [r = 0.31, P = 5.1 × 10⁻⁴, t test; (see fig. S5 for acceleration); r = 0.37, P = 1.1 × 10⁻⁵ (Fig. 2C)]. This interspecies similarity supported our hypothesis of the brain-caused theory.

Beat tuning in the auditory cortex

To investigate whether the beat synchronization matched the time scale of neural beat processing, we measured multi-unit activities (MUAs) at the fourth layer of the auditory cortex and determined the core cortex (the primary and anterior auditory fields, or A1 and AAF) and the belt cortex (other higher-order auditory fields), based on the characteristic frequency (CF) and onset latency using a microelectrode array with 10 × 10 sites (26). We characterized the neural responses to putative beats during presentation of the music excerpt used in the behavioral experiment. The excerpt included 127 beat notes and 362 nonbeat notes and was played at different tempos, 75, 100, 200, 300, and 400% (Fig. 3A). Following a previous study (20), we quantified neural beat contrast as follows

$$\text{Neural beat contrast} (\mathrm{a}.\mathrm{u}.)=\frac{R_{\text{on}}-R_{\text{off}}}{R_{\text{on}}+R_{\text{off}}}$$

where R was the mean difference between the onset response of MUAs for 5 to 30 ms (MUA_onset) and the baseline level of MUAs for 0 to 5 ms (MUA_base) following the onset of beat (R_on) and nonbeat (R_off) notes. Neural beat contrast was derived for each recording site (Fig. 3B) and averaged for each animal (n = 7). Consequently, this contrast significantly differed among tempos (Kruskal-Wallis test, P = 7.0 × 10⁻⁴), with the original tempo displaying the highest contrast (Fig. 3C).

The beat tuning was different between fields: At all playback tempos, the neural beat contrasts in the belt were smaller than those in the core (fig. S6). The neural beat contrasts significantly differed across tempos in both the core (Kruskal-Wallis test, P = 6.5 × 10⁻³) and belt (P = 8.0 × 10⁻⁵). The neural beat contrast in the higher-order auditory cortex was maximized at a slower tempo than those in the core cortex, suggesting that the higher-order auditory cortex is critical to the tuning of beat perception and is similar to prosodic chunking in humans (27).

At the original tempo, the neural beat contrasts were different between beat positions (Kruskal-Wallis test, P = 2.9 × 10⁻⁴; Fig. 3D). Beat contrasts at pos.1 were significantly larger than those at either pos. 2 (P = 2.9 × 10⁻³) or pos. 4 (P = 2.9 × 10⁻³) but not at pos. 3 (P = 8.7 × 10⁻²), and beat contrasts at pos. 3 were significantly larger than those at pos. 2 (P = 2.9 × 10⁻³) but not at pos. 4 (P = 8.2 × 10⁻¹) (Mann-Whitney U test with Bonferroni correction), suggesting a (weak) downbeat effect on pos. 3. Although the notes at pos. 1 and 3 had a higher acoustic energy than those at pos. 2 and 4, these differences in acoustic energy did not purely reflect the neural response magnitudes (fig. S7), suggesting that the neural responses at each note were modulated by the preceding stimulus context.

The ratio of neural beat contrasts between the first position and other positions increased with tempo (Kruskal-Wallis test, P = 1.8 × 10⁻⁵; Fig. 3E). This result suggests that the auditory cortex rescaled the excerpts with high tempo into its optimal tempo, where notes at the first beat in the musical score were more underscored than those at other beats.

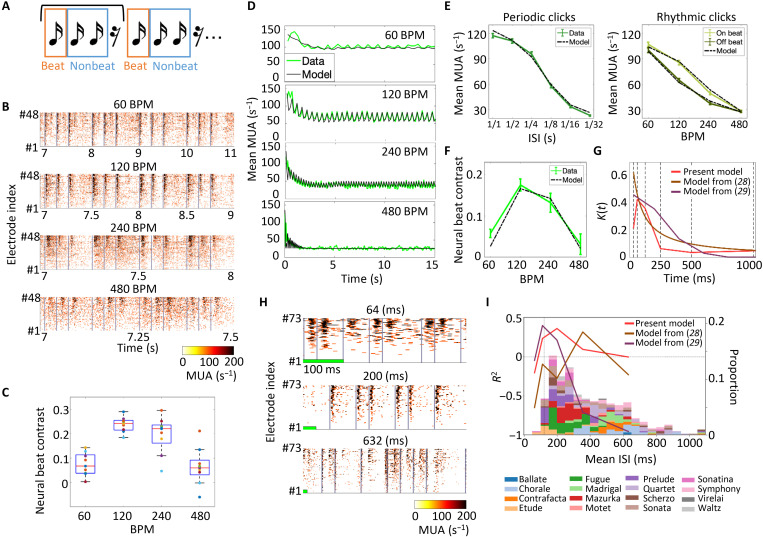
To further investigate the mechanism underlying this cortical tuning, we tested simplified rhythmic click sequences at four different tempos, 60, 120, 240, and 480 BPM (Fig. 4A). Because every click in the sequence was identical, a click at pos. 1 is the only distinct stimulus that had a longer interstimulus interval (ISI) than other positions, and therefore, pos. 1 was defined as a beat in this sequence, whereas pos. 2 and 3 were defined as nonbeats. We observed that the evoked responses significantly differed among metric positions in 120 BPM (Kruskal-Wallis test, P = 3.2 × 10⁻²) and marginally in 240 BPM (P = 6.7 × 10⁻²) (Fig. 4B and fig. S8) possibly due to the short-term adaptation to the preceding clicks. We also found that neural responses at a rest was significantly negative, i.e., MUA_onset < MUA_base, at 120, 240, and 480 BPM (one-sided t test, P = 1.7 × 10⁻³, P = 1.9 × 10⁻², and P = 3.2 × 10⁻³), suggesting that the auditory cortex encoded the rest in a predictive manner. Similar to the music stimulus, the beat contrast differed among tempos in this rhythmic click sequence (Kruskal-Wallis test, P = 9.1 × 10⁻⁵) with the highest contrast around 120 BPM (n = 9; Fig. 4C).

Fig. 4. Short-term adaptation model to explain neural tuning around 120 BPM.

(A) Rhythmic click sequences of 15 s (three clicks and one rest) played at four different tempos. Beat was defined as the first of three consecutive clicks. (B) Representative MUAs averaged among 10 trials. MUAs of 48 recording sites plotted according to mean MUA amplitudes. Each data is aligned at 7 s from stimulus onset and scaled. Gray lines indicate click presentation. (C) Neural beat contrasts of all animals (n = 9) calculated from their MUA responses to rhythmic click stimuli. Each dot represents the mean neural beat contrast of all recording sites per animal. (D) Simulated MUA responses to the rhythmic click stimuli. Green lines indicate the mean MUA responses of all recording sites with click-elicited responses; black lines indicate the simulation results. (E) Mean MUA responses to periodic and rhythmic clicks. Solid lines indicate the MUA data in electrophysiological experiments; dashed lines indicate the simulation results. The error bar indicates the SEM. (F) Neural beat contrast to rhythmic clicks in electrophysiology and simulation. (G) Outline of the kernel function predicted from the present experiments. The kernel functions of previous studies are also shown for reference. (H) Representative MUA in response to random click sequences with different mean ISIs. (I) Prediction accuracy of each model (solid lines). The distribution of mean ISI in a variety of music is shown for reference (bars).

We hypothesized that short-term adaptation underlies cortical tuning within 120 to 140 BPM. To quantify the short-term adaptation property of auditory cortex, we estimated the adaptation kernel in a data driven manner from MUA responses to periodic click sequences. On the basis of a previous study (28), we modeled neural responses to click sequences as follows

$$\text{MUA}(t)=\text{max}(M_0,M(s(t)-I(t)))$$

$$I(t)={\displaystyle {\int }_0^t}K(t-t\prime )·\text{MUA}(t\prime )\mathit{dt}\prime$$

where M₀ is the minimum MUA response to stimulus, M is a scaling parameter, s(t) is a binary function indicating the presence of the stimulus, I(t) is the short-term adaptation level, and K(t) is the temporal property of neural suppression after the sound presentation. The outline of K(t) was estimated from the MUA response to periodic clicks with an ISI ranging between 1/32 and 1 s and fitted to the response to rhythmic clicks at 60, 120, 240 and 480 BPM (see Materials and Methods). Consequently, our model explained rhythm-dependent MUAs across all tested tempos in terms of not only the global decrease but also the cyclic changes in MUAs (Fig. 4D). In addition, it explained the MUA response to both periodic and rhythmic clicks (Fig. 4E). According to our model, the neural beat contrast was maximum around 120 BPM (Fig. 4F). To obtain this tuning, the outline of K(t) suggests that neural activities in the auditory cortex are strongly suppressed for ~250 ms after the sound stimulus (Fig. 4G). The estimated effect of short-term adaptation lasted longer in the higher-order auditory cortex than in the core cortex, supporting the importance of the higher auditory cortex in the neural beat tuning (fig. S9).

Conventional models with different kernel functions (28, 29) failed to explain the above beat tuning properties (fig. S10). We also tested how well the kernel functions predicted the MUA response to random click sequences (Fig. 4H). Our model showed the highest prediction performance when the mean ISI was around 200 ms, while those by Zuk et al. (29) and by Drew and Abbott (28) performed better for faster and slower click sequences, respectively (Fig. 4I and fig. S11). To estimate which adaptation model best predicts neural activities to music stimuli, we examined the Humdrum Kern database (http://kern.humdrum.org) to characterize ISI distributions used in music (bars in Fig. 4I). Consequently, we found that the ISI range that our model predicted covered more music genres than the previous models. We also estimated the spatiotemporal receptive field (STRF) with a time window of 200 ms in a data-driven manner (20, 30), but this STRF failed to explain the beat tuning within 120 to 140 BPM (fig. S12) possibly because the temporal window in this STRF model was much shorter than that in our adaptation model, i.e., 5 s. Thus, the adaptation property we revealed herein in a data-driven manner is likely to underlie the perception and creation of musical rhythms.

DISCUSSION

In this study, we demonstrated that rats displayed spontaneous beat synchronization and neural tuning in the auditory cortex within 120 to 140 BPM, possibly due to short-term adaptation. Both subcortical and thalamocortical pathways are likely responsible for said adaptation (21, 31–35). These results suggest that the optimal tempo for beat synchronization depends on the time constant in the brain, which is conserved across species (17). Previous studies on beat synchronization in animals shaped this behavior through training or exposure to a musical environment (35–40). To the best of our knowledge, this is the first report on innate beat synchronization, except in humans (2).

Beat synchronization in nonhuman mammals has been characterized as reactive movements to an audible beat (35, 36), while humans commonly exhibit predictive beat synchronization. Our data also showed that the beat synchronization in rats was more reactive than that in humans (fig. S3A). However, the beat synchronization in rats could neither be characterized as being purely reactive nor be explained only by startles, because (i) the jerk increased significantly with the timing of beat at pos. 1 in the original tempo (fig. S3B), (ii) no synchronization was observed at pos. 3 despite the relatively large beat amplitude (figs. S3B and S7A), and (iii) the jerk increase was not aligned with beats at 75% playback tempo although beat amplitudes and evoked neural activities were larger than those in the original tempo (Fig. 1D and figs. S3A and S7). Future studies are still needed to fully identify whether and how the beat synchronization is predictive in rodents and other nonhuman animals.

Regardless of whether it is reactive or predictive, this spontaneous synchronization to beats in rodents might act as an evolutional precursor for predictive synchronization to musical beats in humans, perhaps being necessary but not sufficient for the development of voluntary predictive synchronization. Previous studies have also argued that the “bottom-up” processing of music in the auditory system even in rodents predisposes the human-like predictive properties of beat perception and synchronization (20, 21).

Spontaneous beat synchronization in rats and other animals has been overlooked thus far, probably because the movements were too small to be identified visually (41). Although beats within 120 to 140 BPM are appealing to the sensorimotor cortex, the smaller body structure of rodents with their quadruped posture, characterized as a higher resonance frequency than the human body, is one of the constraints in amplifying rhythmic movements. In future studies, rats in bipedal stance might address the bodily amplification of beat synchronization (movie S2 and fig. S1). However, our comparisons between rats and humans indicate that the head acceleration in humans while listening to music alone in a quiet room was comparable with that in rats (10 to 15 m/s²; fig. S5) and that the head jerk in humans (10 to 40 m/s³) was 10 times smaller than that in rats (100 to 300 m/s³; Fig. 2), due to the smaller mass of head. Thus, beat synchronization in humans is neither always larger than in rats nor large enough to be visible.

Another potential constraint in animals that do exhibit beat synchronization is the limited connectivity between the auditory and motor systems, which might underlie vocal learning and beat synchronization (5, 37, 42). As in humans, intricate interaction between the basal ganglia (19, 43–45), premotor cortex (19, 43, 46), supplementary motor cortex (18, 43), cerebellum (19, 45), and auditory system (19–21) underlies beat perception and its interspecies differences. Furthermore, this behavior disappeared after a few experimental trials in our study. The beat synchronization was unlikely to be reinforced because rats, unlike humans, had no motivation to move in synchrony to music. On the first day, stimulus novelty might amplify beat synchronization in rats through the dopaminergic system (47–49). Alternatively, to the extent that beat synchronization was partially caused by startles (i.e., in a reactive manner), rats might become accustomed to the music stimuli and gradually exhibit less startles over days.

Despite the small movements, our experiments demonstrated that both humans and rats showed consistent beat synchronization without any motivation to move while listening to music. How this innate beat synchronization is reinforced as voluntary large-scale rhythmic movements to a beat in humans goes beyond the scope of our study. Music-induced physical movement and music-induced physical social interactions might have intrinsic rewarding effects (50–53).

We used a mathematical model of short-term adaptation to explain the response properties in the auditory cortex, rather than the neural mechanism of beat processing. Some studies have used predetermined mathematical functions to model adaptation, e.g., an exponential and power-law decay (28), a specific temporal smoothing window (29), and the gammatone filters for temporal modulation (54). These models might be biologically realistic or plausible but have not been verified through neurophysiological experiments in the auditory cortex. Unlike these works, we determined the kernel function outline in a data-driven manner as a model of short-term adaptation. We believe that this complementary approach is one of the most important contributions of our work, and we reveal that the beat tuning within 120 to 140 BPM was obtained by the temporal window of ~250 ms, strongly suppressing neural activities after the sound stimulus. Considering that the STRF model could better explain the neural responses in the auditory midbrain (20) than in the auditory cortex (fig. S12) and that the long-lasting adaptation model better predicted the auditory cortical responses than the STRF model, the beat processing is possibly more temporally dynamic in the auditory cortex than in the midbrain. Similarly, the adaptation at the level of midbrain may influence the perceptual emergence of a beat (21). Moreover, since the higher-order auditory cortex had a longer time window of adaptation than the core cortex (fig. S9), the evolution of the adaptation time scale along the auditory pathway is likely to play a key role in the beat perception.

Our data suggest that sound patterns with energy peaks within 120 to 140 BPM produce the largest neural responses in the auditory cortex and trigger the largest head movements at this tempo. However, how the auditory information at each note is converted into motor commands, in a predictive manner rather than in a purely sequential manner, is beyond the scope of this study. Neural activity at layer 4 in the auditory cortex reflects auditory information and is hardly modulated by movement (55). Therefore, the auditory cortex is essentially reactive but is equipped with some prediction mechanisms before triggering the motor system (33–35). For example, we characterized temporally dynamic adaptation (Fig. 4), which might produce predictive activities in the auditory cortex. We also showed that the omitted stimulus slightly but significantly modulated MUA in the rhythmic click sequence (fig. S8B), suggesting that the auditory cortex in rats encoded the rest in a predictive manner, similar to the human auditory cortex exhibiting omitted stimulus potentials (56). Furthermore, the auditory cortex in rats exhibited human-like mismatch negativity (57), which is consistent with predictive processing. Neural oscillatory models beyond the auditory cortex (3, 58–61) might offer insights into predictive beat synchronous movements.

Thus, further studies into the behavioral and neural characterization of beat synchronization are still required to draw conclusions about its predictive mechanism in nonhuman animals. Comparing humans and other animals will open a new avenue to elucidate the mechanism of beat synchronization beyond the sensory system and possibly offer insights into the origins of music and dancing.

MATERIALS AND METHODS

Animals

This study was conducted in strict accordance with Guiding Principles for the Care and Use of Animals in the Field of Physiological Science published by the Physiological Society of Japan. The experimental protocol was approved by the Committee on the Ethics of Animal Experiments at the Graduate School of Information Science and Technology, the University of Tokyo (JA19-2). All efforts were made to minimize animal suffering or discomfort and to reduce the number of animals used. After the experiments, animals were euthanized with an overdose of pentobarbital sodium (160 mg/kg, intraperitoneally).

Wistar rats were used in the experiments. All rats were bought from Tokyo Laboratory Animals Science Co. Ltd. at 9 weeks old and were housed on a 12:12 light-dark cycle (light on at 7:00 p.m./light off at 7:00 a.m.).

Human participants

The experimental protocol was approved by the Committee on the Ethics at the Graduate School of Information Science and Technology, the University of Tokyo (UT-IST-RE-210708). Twenty healthy participants (mean age, 29.6 ± 10 years; seven females) participated in the experiment. All participants provided informed consent.

Acceleration measurement of beat synchronous movements

Accelerometer

To measure head movements of rats and human participants, we used a wireless accelerometer (TWELITE 2525A, Mono Wireless Inc., Japan) that weighed 6.5 g including the battery (Fig. 1A). To attach it to the rat skull, we designed a holder (Fig. 1B) and fabricated it using a three-dimensional printer (Replicator 2X, MakerBot Industries, Brooklyn, NY).

Ten rats aged 9 to 10 weeks were anesthetized by isoflurane inhalation (3 to 5%). Xylocaine (1%, 0.1 ml) was administered subcutaneously for local anesthesia. Atropine sulfate (5%, 0.5 ml) was administered intraperitoneally to reduce the viscosity of bronchial secretions. After the removal of tissues covering the parietal skull, five M1 × 3-mm screws were drilled into the skull. All were distributed posterior to the bregma. The accelerometer holder was fixed to the screws with two types of dental cement (Super-Bond C & B, Sun Medical, Shiga, Japan; Unifast II, GC Corporation, Tokyo, Japan). After the surgery, capisten (5 mg/ml, 0.2 ml) and viccillin (25 mg/ml, 0.2 ml) were injected intramuscularly into the left and right legs, respectively.

For human participants, the accelerometer was attached onto a headphone (ATH-AR3, Audio-technica, Tokyo, Japan). Data from 12 human participants were obtained and compared to those from rats.

Stimuli

A 60-s excerpt of “Sonata for two pianos (K.448)” by Mozart was used as stimulus in our behavioral experiment. Defining a beat as a quarter note in music score (Fig. 3A), 132 beats were included in the test excerpt. We modified the MIDI file for four different playback tempos, 75% (99 BPM), 100% (132 BPM), 200% (264 BPM), and 400% (528 BPM). In these test stimuli, the tempo was modified, but the pitch of each note was identical to the original excerpt. To align the sound pressure, each MIDI file was converted to a WAV file of 96-kHz sampling, and the squared amplitude was modified to be constant. To align the playback duration, 200 and 400% playback tempos were played two and four times in a row, respectively. In human experiments, a click sequence of rasterized rhythm of the original piece was also presented.

Data acquisition in rats

Following full recovery from the surgery, the rats were habituated to the experimental apparatus—dim-lit black box, 70 cm (W) × 70 cm (D) × 80 cm (H) in size—and allowed to freely explore inside the box for 20 min. The habituation was conducted for two consecutive days.

From the day after habituation was completed, recordings were conducted for three consecutive days. All sounds were played through a speaker placed above the experimental arena. The sound pressure level (SPL) was adjusted at approximately 70-dB SPL (with respect to 20 μPa) on the ground. The accelerometer was inserted in the holder just before the recording. The rats were placed in the experimental box and allowed to freely explore in silence for a minute. Then, music stimuli of four different tempos were played in a random order, interleaved with 1 min of silence. This procedure was repeated twice. Throughout the experiment, acceleration data and overhead video were recorded.

To control the rats’ physiological states, habituation and measurements were conducted between 13:00 and 15:00 every day. In addition, they were fed right after these procedures. The body weight at the time of measurement was maintained between 290 and 310 g by controlling the amount of food.

Data acquisition in humans

Human participants entered a soundproof room and were fitted with headphones. The participants adjusted the volume to a comfortable level by themselves while listening to a part of Mozart K.448 not used in the main experiment. After the adjustment, the participants were asked to move their head to the music presented through the headphone. The acceleration of head movements was monitored by the same setup used in the animal experiment.

Statistical significance of the jerk beat contrast

The null distribution of random jerk beat contrast was calculated. The 40% pseudo-beat time and 60% pseudo-nonbeat time were randomly selected from recorded data. Pseudo–jerk beat contrast was calculated using the mean jerk (Euclidean norm of the jerk vector) at each time. This manipulation was repeated 250 times for each tempo, and the null distribution of 1000 pseudo–jerk beat contrast in total was obtained for each animal. The top 1% of the null distribution was used as threshold of statistical significance. When the jerk beat contrast was larger than this threshold, the animal was considered to exhibit beat synchronization.

Visual characterization of beat synchronous movements

Experimental procedure

We reasoned that the quadruped posture of rats hampered amplification of beat synchronous head movements. Therefore, we attempted to investigate beat synchronous movements when rats maintained a biped stance during music presentation. To motivate rats to keep a biped stance, a water supplier in an experimental arena was raised gradually higher and lastly placed at a height a rat could not reach without standing bipedally and could not hold the filling port with its forelegs (62). To reinforce the reward effect, water was restricted for 24 hours before the training.

The experiment was conducted in a transparent box [30 cm (W) × 30 cm (D) × 36 cm (H)] with a height-adjustable ceiling, where a water supplier was placed. This box was placed in a soundproof room with a dim light. One training session lasted for about 30 min, and this session was repeated until a rat immediately stood up to seek a water bottle once put in the arena. Rats typically completed this training within a few days.

The main experiment was conducted in an identical arena as used for the training. Water was restricted for 5 hours before the experiments. To observe the bipedal standing motion while not drinking water, the water supplier was placed slightly higher than the height where rats could comfortably reach and drink water in the standing posture. During the experiment, rats could move freely in the arena. Five pieces of music were presented as follows: K.448 by Mozart, “Born This Way” by Lady Gaga, “Another One Bites the Dust” by Queen, “Beat It” by Michael Jackson, and “Sugar” by Maroon 5. Each music piece was randomly played through the speaker twice (approximately 45 min). All movements in the experimental session were recorded from a camera behind the arena.

Video analysis

DeepLabCut 2.1.10.4 (63) was used to analyses the beat synchronous movements of the standing rats. After manual annotation of 500 images for seven parts of the body (nose, right/left eye, right/left ear, neck, and the base of tail), the network was trained for 60,000 iterations.

The prominent frames of beat synchronization were extracted manually (see movie S2). The nose displacement in the extracted frames was calculated as

$$\text{displacement}=\text{norm} (P_{\text{nose}}-\text{mean}(P_{\text{eye},\text{ear}}))$$

where P_nose is the nose position and mean (P_{eye, ear}) is the mean position of the right/left eye and right/left ear. We quantified the displacement instead of jerk in this video analysis because the sampling rate of the video acquisition was not sufficiently high to reliably quantify the jerk. To quantify the beat synchronization, the local maximum and local minimum of nose displacement was calculated. The MATLAB function “findpeaks” was used to identify the upper and lower peaks with a prominence level between 2 and 50. A prominence level of >50 is considered as misdetection of body parts.

Data acquisition in humans

In 8 of 20 human participants, the head movements were monitored by a video camera from overhead during music listening. A red marker was attached on the top of the accelerometer holder for video tracking.

To quantify the head movement, the displacement of the accelerometer holder was tracked in the video using the manually wrote Python code. The video was first cropped around the accelerometer holder. Each video frame was then transformed into a binary image to extract the red marker attached on the accelerometer holder, and the marker contour was detected using “findCounters” function in the OpenCV library. The contour center was regarded as the head position (see movie S3).

Electrophysiology experiment

Surgery

Apart from the behavioral experiments, 13 naïve rats in total were used for electrophysiological experiments. Music stimuli were tested in seven animals, periodic and rhythmic click sequence in nine animals, and random click sequences in five animals.

Rats were anesthetized with urethane (1.2 g/kg) administered intraperitoneally. Xylocaine (1%, 0.1 ml) was administered subcutaneously for local anesthesia. Atropine sulfate (5%, 0.5 ml) was administered intraperitoneally to reduce the viscosity of bronchial secretions. The parietal and right temporal tissues were removed. Cerebrospinal fluid was drained to avoid edema. An M1 × 3-mm screw was drilled into the left parietal bone to contact the dura and was used as a reference electrode. A needle was inserted into the skin of the right forelimb and was used as a ground electrode. The right temporal bone and part of the dura mater were removed to expose the auditory cortex. To limit the sound presentation to the left ear, the right eardrum was ruptured, and a cotton swab was plugged into the right ear to ensure unilateral sound inputs from the ear contralateral to the exposed cortex.

Neural measurement

After surgery, an electrophysiological recording similar to the previous studies was conducted (26). The neural activities of the auditory cortex were recorded under anesthesia using a microelectrode array with 10 × 10 sites (96 active measurement electrodes) (ICS-96, Blackrock Microsystems, Salt Lake City, UT) in a 4-mm by 4-mm site. Using a custom-made spacer, we adjusted the recording depth at 700 μm from the pial surface. Neural activities were amplified 1000-fold, bandpass-filtered from 0.3 to 500 Hz and 250 to 7500 Hz, and measured at a sampling frequency of 1 kHz for local field potentials (LFPs) and 30 kHz for MUAs, respectively (Cerebus Data Acquisition System, Cyberkinetics Inc., Salt Lake City, UT).

To identify the location of the auditory cortex, click-evoked LFPs were measured on the cortical surface. Each click was a positive-first biphasic square pulse with a duration of 50 μs per phase. The array was positioned so as to cover the entire click-evoked activation and slowly inserted into the cortex. To confirm that the electrode reached the fourth layer of the auditory cortex, click-evoked LFP was constantly monitored. The LFP exhibited a positive deflection at the cortical surface but a negative one at the fourth layer. MUA recordings were initiated >30 min after insertion.

As previously described (26, 64, 65), we identified the auditory cortex and its subregions according to the tonotopic map and onset latency of tone-evoked MUA. Tone bursts with a 5-ms rise/fall time and 30-ms total duration were used to determine a CF at each recording site. From MUAs within 40-ms poststimulus latency, CF was determined as the frequency at which test tones evoked MUA at the lowest intensity or as the largest response at 20-dB SPL, i.e., the minimum intensity used in this experiment. The test frequencies ranged from 1.6 to 64 kHz with an increment of 1/3 octaves, and test intensities ranged from 20- to 80-dB SPL with an increment of 10 dB. Each test tone was repeated 20 times in a pseudo-random order with an intertone interval of 600 ms. The core (A1 and AAF) and belt (ventral, suprarhinal, and posterior, anterior ventral auditory fields) regions were then identified from CF map and MUAs onset latency.

When calculating the neural beat contrast (Fig. 3), we used the electrodes with identifiable CF. For the neural beat contrast of the rhythmic click stimuli (Fig. 4), the analysis was further limited to click-evoked MUAs, which were larger than the mean + 2SDs of spontaneous MUA (≥5 s after a previous sound stimulus). The mean and SD were derived as the temporal variance of spontaneous MUAs at each electrode.

Stimuli

In the electrophysiological experiment, neural activities in the auditory cortex were stimulated by identical musical excerpts (Mozart K.448) to those used in the behavioral experiment. In addition to the four playback tempos described above, a tempo of 300% (396 BPM) was added to the test conditions in electrophysiological experiments.

As simpler stimuli than the music excerpt, periodic, rhythmic, and random click sequences were prepared. In the periodic click sequence, clicks were repeated for 15 s with a fixed ISI of 1, 1/2, 1/4, 1/8, 1/16, and 1/32 s. The rhythmic click sequence comprised three consecutive clicks and a rest at equal intervals (Fig. 4A) repeated for 15 s at a fixed tempo of 60, 120, 240, or 480 BPM. Beat was defined as the first of the three consecutive clicks. Each stimulus was played randomly for 10 times. In the random click sequence, clicks were presented with an interval of 32, 56, 100, 178, and 316 ms at a probability of 0.5 for 5 min. Each click sequence was fixed across animals and presented once. Each stimulus was played through a speaker placed 10 cm from the left ear and the SPL was adjusted to 70 dB at the left ear.

Short-term adaptation model

We hypothesized that short-term adaptation played a role in the beat tuning in the auditory cortex and built a mathematical model to estimate the short-term adaptation property in a data-driven manner. On the basis of a previous study (28), the following model was used

$$\text{MUA}(t)=\text{max}(M_0,M(s(t)-I(t)))$$ (1)

$$I(t)={\displaystyle {\int }_0^t}K(t-t\prime )·\text{MUA}(t\prime )dt\prime$$

where MUA(t) is the mean MUA between 5 and 30 ms after the stimulus, M₀ is the minimum MUA response to stimuli, M is a scaling parameter adjusted to each data point, s(t) is a binary function that indicates the presence of a click sound, I(t) is the short-term adaptation level, and K(t) is the temporal properties of neural suppression after the sound presentation. To reduce the parameters, M₀/M is fixed to the ratio between the mean MUA response of the 10 to 15 s after the stimulus onset of the most frequent periodic click (ISI = 1/32 s) and that of the initial click.

In this study, we estimated the outline of kernel function (𝑡) from the MUA response to five periodic click sequences (MUA^P_τ(t)), where τ (in seconds) denotes the ISIs in the periodic clicks (τ = {τ₀, τ₁, τ₂, τ₃, τ₄} = {1,1/2,1/4,1/8,1/16}).

We posited that MUA(t) and s(t) converges to $\overline{\text{MUA}(t)}$ and α/M, respectively, under periodic input if t is long enough. From the Eq. 1, the mean MUA response to the periodic click (P_τ, given) is approximated as below

$$P_{\mathrm{\tau }}=\overline{\text{MU}{\mathrm{A}}^{P_{\mathrm{\tau }}}(t)}\backsimeq M(s(t)-I(t))\backsimeq \mathrm{\alpha }-M{\displaystyle {\int }_0^t}K(t-t\prime )\mathit{dt}\prime ·\overline{\text{MU}{\mathrm{A}}^{P_{\mathrm{\tau }}}(t)}$$

We approximated the integral of the kernel function with the summation of representative kernel values with a scaling parameter α and a linear correction parameter β as below

$$P_{\mathrm{\tau }}\backsimeq \mathrm{\alpha }-\mathrm{\beta }({\displaystyle \sum _{m=1}^{\mathrm{\tau }·m\le 1}}K(\mathrm{\tau }·m))·P_{\mathrm{\tau }}$$

The representative kernel values K(τ_n)(n ∈ {0,1,2,3,4}) was recursively estimated as below

$$\text{When} n=0,K({\mathrm{\tau }}_0)\simeq (\mathrm{\alpha }/P_{{\mathrm{\tau }}_n}-1)/\mathrm{\beta }$$

$$\text{When} n>0,K({\mathrm{\tau }}_n)\simeq (\mathrm{\alpha }/P_{{\mathrm{\tau }}_n}-1)/\mathrm{\beta }-{\displaystyle {\sum }_{m=2}^{1/\mathrm{\tau }}}K({\mathrm{\tau }}_n\bullet m)$$

Here, unknown K(τ_n ∙ m) is approximated by the mean value of known K(τ_n ∙ m) as below

$$K({\mathrm{\tau }}_n·m\prime )\simeq \left\{K\right({\mathrm{\tau }}_{n-1}·\frac{m\prime -1}{2})+K({\mathrm{\tau }}_{n-1}·\frac{m\prime +1}{2}\left)\right\}/2$$

Under the assumption that K(t ≤ 0,5 ≤ t) = 0, the whole K(t) was obtained by linear interpolation. The parameters α and β were optimized to fit the MUA responses to the rhythmic clicks. The identical K(t) was used for the simulation of MUA responses to the periodic clicks and random clicks.

We also tested the simulation with existing models by Drew and Abbott (28) and Zuk et al. (29). Drew and Abbott and Zuk et al. defined their kernel functions, K_D and K_Z, respectively, as expressed below

$$K_{\mathrm{D}}(t)=\frac{\mathrm{\alpha }}{\mathrm{\beta }+t}$$

$$K_{\mathrm{Z}}(t)=\mathrm{\alpha }{f}_{\mathrm{z}}(t)$$

where α and β are fitting parameters and f_z(t) is a temporal smooth window of Zuk et al. (29). Similar to the model above, α and β were optimized to fit the MUA responses to the rhythmic clicks. The identical K(t) was used for the simulation of MUA responses to the periodic clicks and random clicks.

Fitting the linear-nonlinear model with STRF

On the basis of previous studies (20, 30), MUA response to musical stimuli was fitted using a linear-nonlinear STRF model. First, a Mel spectrogram of Mozart K.448 with five different tempos (75, 100, 200, 300, and 400%) was calculated, using MATLAB function “melSpectrogram.” We used 31 log-spaced frequencies from 1 to 32 kHz (1/6 octave spacing) with 10-ms Hanning windows, overlapping by 5 ms. Then, we took the logarithm of the resulting values, and the values lower than 0 dB were set to 0 dB. The music spectrogram with 31 frequencies and 40 bins (200 ms in the past) was linearly fitted to the training dataset of MUA (the average of 8 trials of 10) using Ridge regression. Fivefold testing was used to determine the optimal parameters. We obtained the STRF kernel (fig. S12A) by averaging the STRF kernel of five different tempos. The output of the linear model z_t was calculated using the convolution of music spectral data and STRF kernel. The nonlinear model $\widehat{y}$ below was used to fit the MUA test dataset (the average of 2 trials of 10) y_t with 10-ms Hanning window, overlapping by 5 ms.

$${\widehat{y}}_t=a+\frac{b}{1+\text{exp}(-(z_t-c)/d)}$$

The parameters a, b, c, and d were fitted to the five musical excerpts respectively using MATLAB function “lsqcurvefit.” We obtained the result by changing the combination of training dataset and test dataset five times. The fitting result was evaluated by

$$R^2=1-\frac{\sum _t{(y_t-\widehat{y})}^2}{\sum _t{(y_t-\overline{y})}^2}$$

where $\overline{y}$ is the mean of y.

Music analysis

The distribution of the mean ISI of music was characterized using the Humdrum Kern database (http://kern.humdrum.org). Up to 30 music scores of 16 genres each (ballet, chorale, contrafacta, etude, fugue, madrigal, mazurka, motet, prelude, quartet, scherzo, sonata, sonatina, symphony, virelai, and waltz) were used. The mean ISI of each score was calculated using Humdrum toolkit and Python (Fig. 4I).

To quantify the amplitude of Mozart K.448 at each musical note, the waveforms of WAV files at the play speed ratio (X) of either 0.75, 1, 2, 3, or 4 were squared (96-kHz sampling), and the peak envelope of the squared waveform was calculated using the MATLAB function “envelope” (MathWorks, Natick, MA). The peak separation parameter was set to 3000/X. The local maximum of peak envelope around each musical note (0 to 0.1/X s) was regarded as the sound amplitude. The amplitude of musical notes at each beat position and nonbeat position was averaged.

Supplementary Materials

This PDF file includes:

Figs. S1 to S12

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S3

View/request a protocol for this paper from Bio-protocol.