Factors that Determine the Variation of Equilibrium and Kinetic Properties of QM/MM enzyme simulations: QM region, Conformation and Boundary Condition

Abstract

To analyze the impact of various technical details on the results of QM/MM enzyme simulations, including the QM region size, catechol-O-methyltransferase (COMT) is studied as a model system using an approximate QM/MM method (DFTB3/CHARMM). The results show that key equilibrium and kinetic properties for methyl transfer in COMT exhibit limited variations with respect to the size of the QM region, which ranges from ~100 to ~500 atoms in this study. With extensive sampling, local and global structural characteristics of the enzyme are largely conserved across the studied QM regions, while the nature of the transition state (e.g., secondary kinetic isotope effect) and reaction exergonicity are largely maintained. Deviations in the free energy profile with different QM region sizes are similar in magnitude to those observed with changes in other simulation protocols, such as different initial enzyme conformations and boundary conditions. Electronic structural properties, such as the covariance matrix of residual charge fluctuations, appear to exhibit rather long-range correlations, especially when the peptide backbone is included in the QM region; this observation holds when a range-separated DFT approach is used as the QM region, suggesting that delocalization error is unlikely the origin. Overall, the analyses suggest that multiple simulation details determine the results of QM/MM enzyme simulations with comparable contributions.

Graphical Abstract:

1. Introduction

Combined quantum mechanical (QM)/ molecular mechanical (MM) simulations have been widely employed in the characterization and understanding of enzymatic processes.^1–9 Systematically improving over the past few decades, QM/MM simulations have shown extensive success from drug discovery to enzyme engineering.^4,9–11 However, QM/MM simulations still suffer some pressing challenges and limitations.¹² For instance, in addition to the general concern in the accuracy of the QM method,^13–15 the quality of the MM force field,¹⁶ the QM/MM boundary scheme^17–19 and the QM/MM non-bonded parameters,^20–22 a systematic method for the identification of the appropriate QM region has historically been elusive.^23–26

The selection of a QM region is not a straightforward task and inappropriate choices, especially with inaccuracy in QM/MM interactions,^22,27 can lead to computational artifacts and thus abjectly different predictions from experiment. Although large QM regions should be able to more realistically describe a system, enlarging a QM region may scale to prohibitively expensive levels. It has been shown that QM regions on the order of several hundreds to thousands of atoms are required for a variety of chemical properties such as energies,^28–30 NMR shieldings,^31,32 and other spectroscopic properties.³³ This slowly converging nature of energy differences has prompted the analysis of QM region selection based on electronic structure properties such as the Fukui function²⁵ and bond critical point.³⁴ Some of these schemes suggest upwards of a couple of hundred atoms.^25,35,36

While it is unequivocal that extensively large QM regions are necessary for convergent energies and many other electronic properties, it is unclear if large QM regions are most essential (among all possible methodological considerations) for a meaningful understanding of the catalytic mechanism of enzymes, such as the nature of the transition state and its stabilization relative to uncatalyzed reaction in solution. In particular, disagreement exists regarding how the QM region size impacts computed QM/MM free energy profiles,^37,38 which require extensive sampling for convergent results.^7,39–42 For instance, it was shown in catechol-O-methyltransferase (COMT), where 200–300 atoms are required for converged energies,³⁵ that QM/MM free energy simulations using different QM choices can yield remarkably different if not opposite thermodynamic results while significantly affecting barrier heights.⁴³ Yet, for the same system, PM6/MM calculations have shown that the free energy surface is fairly robust, especially with respect to the predicted energy barrier,⁴⁴ although the reliability of the PM6 method used therein was questioned^43,45 for properly capturing electronic structure over an extended region.

In this work, using COMT as a test enzyme system, we analyze the catalytic properties (Scheme 1) across previously studied QM partition schemes.^43,45 Our work is complementary to previous studies^35,43–45 because of several reasons. First, we use a different QM approach (DFTB3⁴⁶), thus comparison to previous studies helps better understand whether key observations depend on the QM level. Second, our free energy simulations explore much more of the protein’s conformational ensemble, in terms of not only the extensive length of individual metadynamics simulations but exploring different initial structures, which include both the crystal structure and snapshots taken from long (~400 ns) classical molecular dynamics simulations. Third, we also compare results from spherical boundary (GSBP^47,48) and periodic boundary setups, for both the wild type enzyme and a more flexible variant (Y68A, see below) studied in previous experimental investigations,⁴⁹ so as to evaluate the impact of fluctuations of remote residues. Finally, we also compute two kinetic properties of the system: secondary kinetic isotope effect (KIE) for the methyl transfer and barrier crossing transmission coefficient, κ,⁵⁰ using path-integral⁵¹ and positive reaction flux^52,53 simulations, respectively.

Scheme 1:

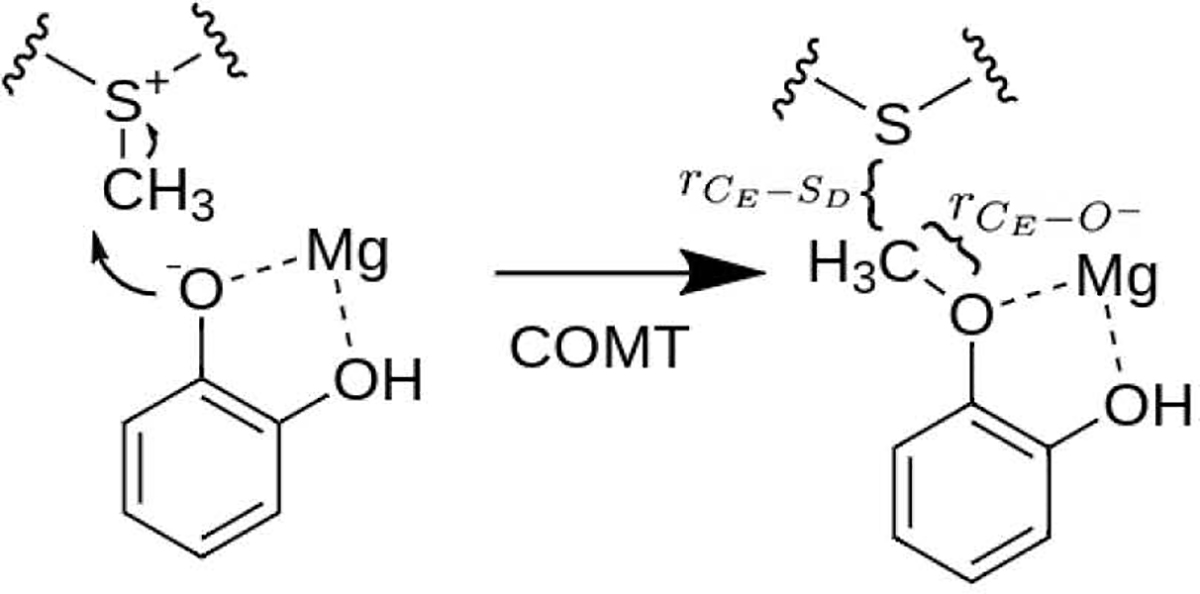
The methyl transfer reaction in catechol-O-methyltransferase (COMT).

The equilibrium and kinetic results make clear that the overall structural features, free energy landscape and nature of transition state exhibit limited variations across the different models with a QM region that ranges from ~100 atoms to more than 500 atoms, suggesting that the key catalytic features of the enzyme is largely conserved regardless of the extent of the QM region. Extensive sampling along with the addition of physical attributes such as dispersion interactions among the QM atoms, initial starting conformation, periodic vs. spherical boundary condition⁵⁴ and the QM/MM partitioning scheme play at least equally recognizable differences in the computed free energy profile. On the other hand, covariance of residual charge fluctuations⁴³ exhibits long-range correlation, especially when the QM region includes protein backbone atoms, suggesting that a large QM region is required to properly capture certain electronic structural properties; to probe whether charge delocalization error associated with popular GGAs⁵⁵ (on which the DFTB3 model is based^56,57), plays a major role in this observation, we have also conducted charge analysis using a range-separated Density Functional Theory (DFT) method enabled by recent developments of GPU based DFT approaches.^58–60

2. Computational Methods

Human catechol-o-methyltransferase (COMT) with 3,5-dinitrocatechol and S-adenosyl methionine substrates (PDB ID: 3BWM)⁶¹ is used to set up the calculation (Fig. 1a), in which 3,5-dinitrocatecholate is modified to catecholate. All simulations are conducted using CHARMM⁶² and the CHARMM36 force field,^63–65 along with the modified TIP3P model for water.^66,67 Protonation state of titratable groups is determined via PropKa^68,69 and hydrogen atoms are added with the HBUILD module of CHARMM. Four different QM partitions (M2–5, see illustration in Fig. 1b; also see Table S1 in the Supporting Information) previously studied⁴³ are recreated by placing QM link atoms at the C_α-C_β frontier while employing the Divided Frontier Charge (DIV) scheme.¹⁸ One partition (M5C) extends the QM region to include the backbone of most amino acids, leading to regions of contiguous peptide strands in line with the largest QM region in previous calculations.⁴³ The smallest QM region in the previous work⁴³ (M1) is not studied here as it does not include all the ligands of the Mg²⁺ in the QM region and therefore, in our opinion, does not represent a viable choice in realistic studies.

Figure 1:

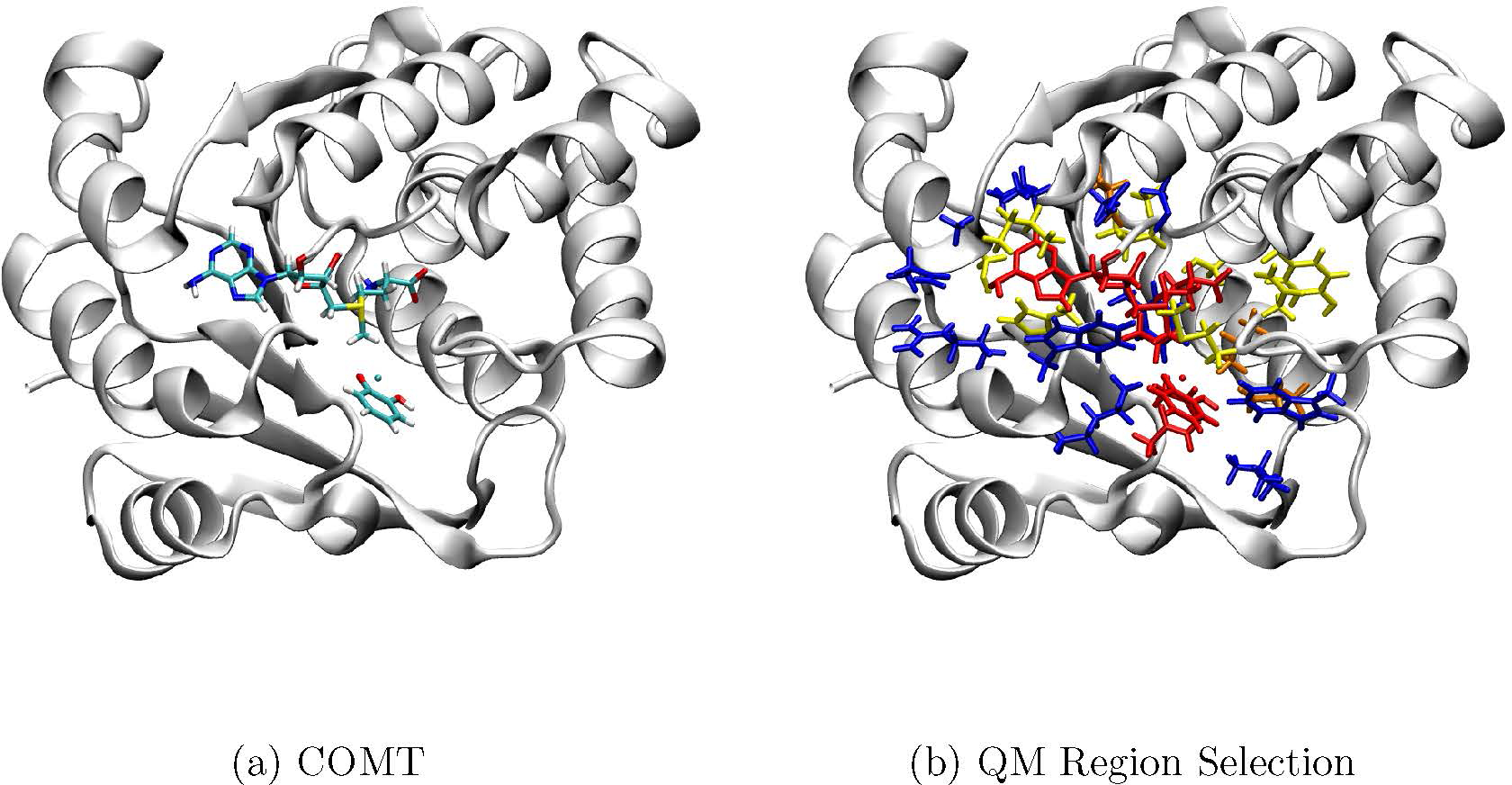
Illustration of the active site and QM region selections for the catechol-O-methyltransferase (COMT) system. (a) The active site that contains the co-factor, S-adenosyl methionine (SAM), the Mg²⁺ ion, the substrate catechol; (b) extending QM regions of M2 (red), M3 (+orange), M4 (+yellow), and M5 (+blue) where each region incorporates the previous colored regions. For amino acids, only the sidechains are included in the QM region in these partitioning scheme. In the M5C model, the QM region further includes the protein backbone atoms for residues in the M5 model, leading to a QM region consisting of 505 atoms.

The approximate Density Functional Tight Binding⁵⁶ up to 3rd Order (DFTB3)⁴⁶ with the 3OB parameterization,^70,71 is used as the QM method. DFTB3 has been shown to provide fairly reliable structures and energies in biomolecules while providing 10^2–3 speedup in comparison to traditional DFT methods,^57,72 making it particularly attractive for free energy simulations of biomolecules,⁷³ although system-specific calibration is always essential.⁷⁴ As shown in Fig. S1 in the Supporting Information, calculations for a gas-phase model system using trimethyl sulfide, catecholate, Mg²⁺ and coordinating waters find that DFTB3 underestimates the barrier while overestimating exergonicity for the methyl transfer reaction of interest as compared to two popular DFT methods; consistent with the larger exergonicity, the transition state is also earlier at the DFTB3 level compared to DFT results. For the model reaction in water (Fig. S2), similar to previous observations,⁷⁵ DFTB3/MM free energy simulations underestimate the methyl transfer barrier compared to the experimental estimate (see discussion in⁷⁶) by at least 4 kcal/mol. Nevertheless, the similarity in the general potential energy profiles in the condensed phase (Fig. S2b) supports the use of DFTB3 for the purpose of examining the impact of different methodological details, especially QM region size, on QM/MM results for COMT. Moreover, as noted below, DFTB3/MM simulations are able to capture the equilibrium and kinetic isotope effects for the methyl transfer in solution and COMT, further supporting the use of DFTB3 for describing the relevant transition state. To probe the effect of dispersion among DFTB3 atoms, each QM region is studied with and without Grimme’s D3 empirical dispersion model.⁷⁷ As discussed in a recent review of semi-empirical QM methods for the treatment of non-covalent interactions in the context of biomolecular simulations,⁷⁸ DFTB3, especially when supplemented with the D3 dispersion model, generally provides an adequate description of non-covalent interactions, although further improvements for highly charged interactions are warranted.

The primary set of systems is constructed based on the crystal structure (PDB code: 3BWM) using the Generalized Solvent Boundary Potential (GSBP) scheme, which has been shown to efficiently model long-range electrostatics in protein environments.^47,48 System setups follow general procedures previously used in our group.^22,74 In brief, the inner region has a radius of 27 Å and is explicitly solvated up to 25 Å about the center (chosen to be the active site Mg²⁺ ion); the inner-inner reaction field matrix, M_ij, is described with spherical harmonics up to 20th order, and the outer region electrostatic potential is represented with a grid of size 0.5 Å using a focusing scheme.⁷⁹ Non-bonded interactions are treated with extended electrostatics and a group-based cutoff scheme.⁸⁰ Each system is allowed to equilibrate for no less than 200 ps using a 1 fs integration step at 300 K after minimization and heating simulations.

To test the sensitivity of QM/MM results to the GSBP partitioning, as well as the GSBP framework itself, classical MD simulations are performed for both wild type (WT) and the Y68A COMT with periodic boundary condition (PBC). Both systems are setup using CHARMM-GUI⁸¹ using a 76 Å cubic box in a 0.15 M KCl solution. MD simulations were run at 300 K using a 2 fs integration step and PME⁸² electrostatics in OpenMM⁸³ for over 400 ns each, including an initial equilibration of 250 ps. Several snapshots from the classical simulations were then prepared for QM/MM PBC and GSBP simulations using the M2 QM selection based upon different protein configurations, leading to 8 additional systems (3 PBC and 5 GSBP, vide infra). Upon QM/MM conversion, each system is allowed to re-equilibriate for no less than 50 ps at 300 K using a 1 fs integration step. QM/MM PBC simulations employ PME electrostatics^84,85 while GSBP simulations employ extended-electrostatics⁴⁸ in the same fashion as described above.

Potentials of mean force (PMFs) for the methyl transfer reaction for the different QM/MM models are computed using well-tempered metadynamics with multiple walkers and the CHARMM-Plumed interface.^86–89 The reaction coordinate ξ is chosen as the anti-symmetric stretch between the catecholate nucleophilic O⁻ and the SAM sulfur/methyl group; i.e., $\xi =r_{C_E-S_D}-r_{C_E-O^{-}}$ (see Scheme 1). 28 walker seeds are generated along ξ from −1 to 2 Å for each system. Each walker is run for at least 200 ps each for a total of 5.6 ns of sampling for models M2–5(+D3), whereas 100 ps per walker is used for M5C. As shown in Fig. S3 in the Supporting Information, this level of sampling is found to be adequate for the convergence of PMF for the current system. Statistical analysis of the free energies were performed using block-analyzed reweighting of the resultant PMFs.⁹⁰

Kinetic isotope effects and transmission coefficients are computed to analyze the nature of the transition state and the quality of the approximate reaction coordinate.⁹¹ The maxima of the computed PMFs are used to construct putative transition state ensembles using constrained MD simulations; since the experimental KIE was measured⁴⁹ based on V/K_m, the reactant state in the KIE calculations is taken to be SAM in a 25 Å water sphere. The putative transition state and reactant state ensembles are constructed based on 200 ps of sampling, leading to over 200,000 configurations for each. Secondary tritium KIEs on the SAM methyl are then computed using a path-integral free energy perturbation (PI-FEP) method.⁵¹ Convergent results require 32 beads representing hydrogen and at least 15,000 evenly spaced frames from the transition state/reactant ensemble with at least 100 Monte Carlo steps per classical frame. In total, calculation of the KIE via the PI-FEP approach requires the equivalence of around 50–100 ns of sampling, and thus is limited to models M2-M4. The transmission coefficient, κ, is obtained via the plateau of the normalized reactive flux correlation function,^50,52,53,92 which is obtained from initiating 100 transition state frames, each with 100 randomized momenta along the reaction coordinate for M2–4.

3. Results and Discussion

3.1. Free Energy Profile

COMT has previously been extensively studied as a model system for methytransferases, which play a fundamental role in gene regulation^93,94 and neurotransmitter metabolism.⁹⁵ COMT inactivates catecholamines such as dopamine, norepinephrin and epinephrin through methylation donated by a SAM cofactor in a Mg²⁺-ligated active site.^76,96,97 As methyltransferases play a key role in post-translational modification, especially in the area of neurobiology, COMT has been studied extensively, providing a crucial model in the understanding of methyltransfers.⁴⁹ For instance, genetic polymorphism in COMT such as Val158Met has been shown to reduce COMT’s catabolic activity, leading to an apparent relationship to certain detrimental neuropsychiatric phenotypes.⁹⁸

As COMT provides a rich base for theoretical models, energy and free energy surfaces have been computed using multiple levels of theory, ranging from full ab initio quantum mechanical active site models to QM/MM free energy simulations.^{35,43,44,76,99–101} However, seemingly disparate results were obtained between different studies, leading to discussions of error sources between methods. To date, there has been much disagreement in how large the QM region should be for reliable free energy results.

To evaluate the (in)sensitivity of the free energy profile to QM size, we show the COMT methylation transfer PMFs after extensive sampling based on increasing QM region sizes using DFTB3/MM multi-walker well-tempered metadynamics (Fig. 2), with a summary of critical energetics and reaction coordinate values with different QM regions summarized in Table 1. Overall, the computed free energy barriers are in the range of 10.1–13.0 kcal/mol (the correction due to transmission coefficient is generally modest, see Table 3), substantially lower than the experimental free energy barrier of 18.1–19.2 kcal/mol.¹⁰² This is expected based on the gas-phase and solution-phase model calculations shown in the Supporting Information; for example, as noted above, the DFTB3/MM simulations underestimate the reaction barrier in solution by at least 4 kcal/mol.⁷⁵ It should be noted that although a recent DFTB3/MM study of COMT obtained a free energy barrier of 22.5 kcal/mol,¹⁰⁰ the study was done starting with a mono-chelating catecholate motif that significantly differs from the initial structure in the current and other previous studies.^35,43,44

Figure 2:

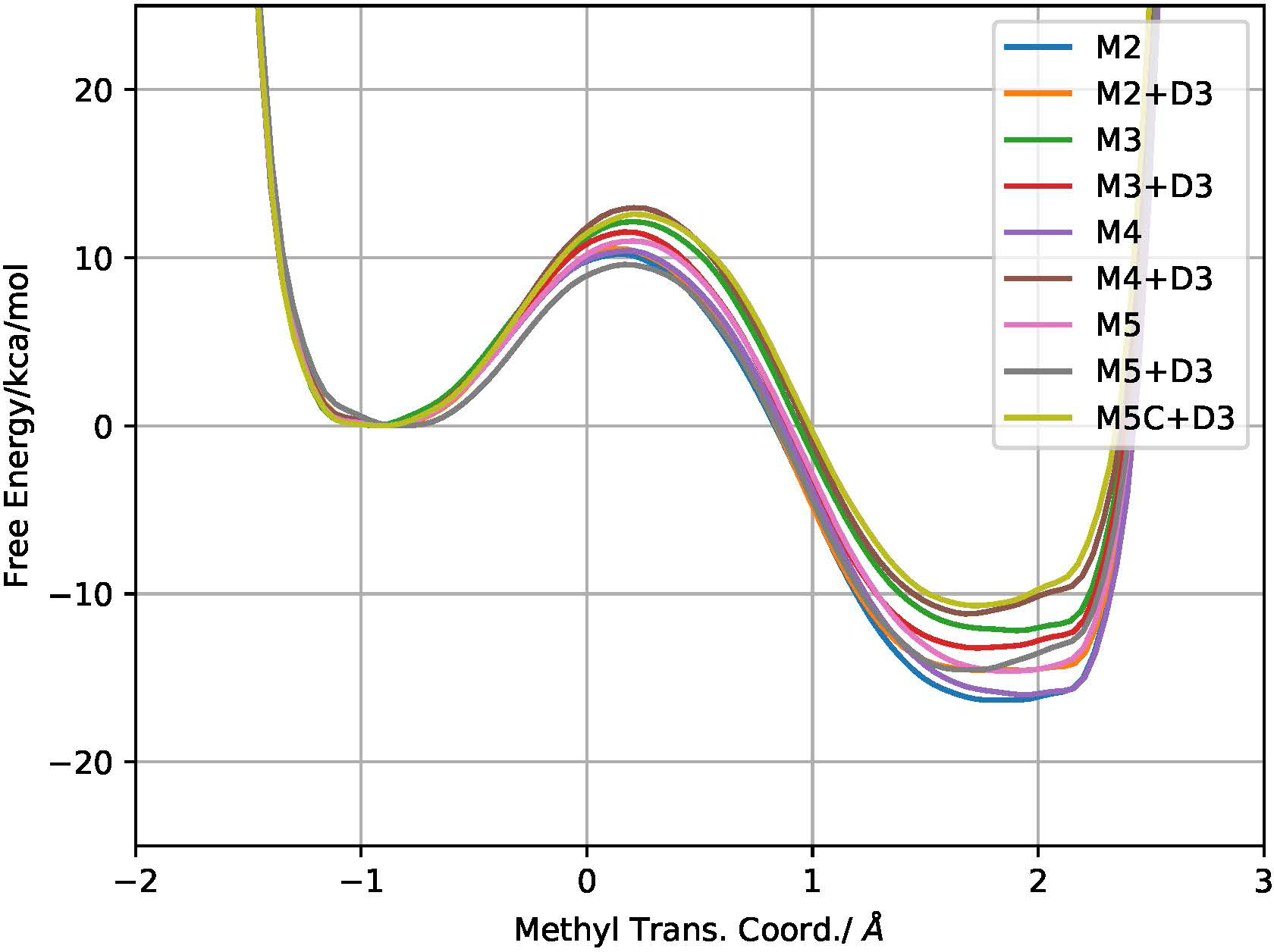
Free energy profiles from DFTB3/MM metadynamics simulations with different QM/MM models; ‘+D3’ results include the empirical dispersion contribution per respective model for the metadynamics simulations. Note that for M5C, due to the large QM region, only simulations including the empirical dispersion interactions among the QM atoms (M5C+D3) are conducted. Statistical errors along each surface are typically in the 0.1–0.3 kcal/mol range.

Table 1:

Key features for the computed free energy profiles shown in Fig. 2 of the main text; energetics (statistical uncertainty in parentheses) are in kcal/mol, and reaction coordinate values (RX: reactant; TS: transition state; PD: product) are in the unit of Angstrom.

Models	ξRX	ξTS	ΔG‡	${\mathrm{\Phi }}_{C{H}_3}^{‡}$	ξPD	ΔG
M2	−0.88	0.16	10.2(0.2)	46	1.77	−16.3(0.1)
M2+D3	−0.88	0.12	10.5(0.3)	49	1.92	−14.5(0.1)
M3	−0.93	0.20	12.1(0.2)	43	1.90	−12.2(0.1)
M3+D3	−0.88	0.16	11.5(0.2)	48	1.73	−13.2(0.1)
M4	−0.93	0.17	10.4(0.2)	47	1.90	−16.0(0.1)
M4+D3	−0.88	0.21	13.0(0.2)	42	1.68	−11.2(0.1)
M5	−0.92	0.25	11.7(0.2)	44	1.75	−12.5(0.1)
M5+D3	−0.81	0.12	10.1(0.2)	59	1.76	−13.4(0.1)
M5C+D3	−0.92	0.20	12.6(0.2)	42	1.71	−10.7(0.1)

^aThe planarity of the methyl group ${\mathrm{\Phi }}_{C{H}_3}^{‡}$ is given as the average absolute value of the H-C-H-H improper dihedral in degrees from each transition state ensemble with the standard deviation given in parentheses, defined such that 0 is perfectly planar.

Table 3:

Computed secondary equilibrium and kinetic isotope effects for the methyl group in SAM, along with other key transition state properties and the transmission coeffcient, κ; energetics are in kcal/mol, and reaction coordinates are in the unit of Angstrom.

Models	ξTS	ΔG‡	${\mathrm{\Phi }}_{C{H}_3}^{‡}$ a	2o Isotope Effect b	κ	Effective ΔG‡ c
Equil.				0.78
M2	0.16	10.2	46 (9.2)	0.77	0.61	10.5
M2+D3	0.12	10.5	49 (9.4)	0.82	0.59	10.8
M3	0.20	12.1	43 (9.0)	0.81	0.36	12.7
M3+D3	0.16	11.5	48 (9.4)	0.78	0.25	12.3
M4	0.17	10.4	47 (9.4)	0.80	0.39	11.0
M4+D3	0.21	13.0	42 (8.7)	0.86	0.31	13.7

^a).The planarity of the methyl group ${\mathrm{\Phi }}_{C{H}_3}^{‡}$ is given as the average absolute value of the H-C-H-H improper dihedral in degrees from each transition state ensemble with the standard deviation given in parentheses, defined such that 0 is perfectly planar.

^b).The first row gives equilibrium isotope effect for the reaction in solution, and the rest are kinetic isotope effects for the enzymatic reaction. The experimental values are 0.83 and 0.79, respectively. ^49,96,99,105

^c).The effective ΔG^‡ is the corresponding ΔG^‡ value corrected by the transmission coefficient (i.e., increased by an amount of k_BTln(κ⁻¹).

The issue of primary interest here is not the absolute barrier itself, but its variations due to various methodological details; thus no attempt was made to adjust the reaction barrier by refitting the DFTB model, such as repulsive potentials.¹⁰³ Along this line, we observe a modest level of sensitivity in both barrier and reaction exergonicity to the QM size with similar trends in barrier energy distributions (Fig. S4). With an overall spread of 2.9 kcal/mol in free energy barriers among the various models (as compared to ~8 kcal/mol for similar PM6/MM studies⁴⁴ and ~20 kcal/mol for DFT/MM⁴³), there is no apparent trend in the QM size dependence; the position of the barrier along the reaction coordinate is ~0.15 Å, with a minor variation of 0.13 Å among the different QM regions. Although the exergonicity is more liable to change (with a range of 5.6 kcal/mol), again the variations are much less severe than reported previously (~20 kcal/mol for similar PM6/MM studies⁴⁴ but ~25 kcal/mol for DFT/MM⁴³) while maintaining the qualitative exergonic nature of the reaction. Previous studies have noted that the sensitivity in exer/exogonicity can be attributed to the change from formally charged reactants to neutralized products.⁴⁴ An interesting observation is that for larger QM models the effect of dispersion becomes increasingly important. For instance, inclusion of dispersion for M5 shifts the transition state earlier by 0.13 Å while decreasing the height by 1.6 kcal/mol. Meanwhile, inclusion of dispersion in M4 decreases the exergonicity by ~6 kcal/mol.

As discussed in previous work,^17–19 partitioning schemes generally should avoid creation of the QM/MM boundary across polar covalent bonds to prevent over-polarization of the QM region. Even with this precaution, extra care must be taken to further prevent un-physical charge distribution through certain methods such as the DIV scheme used here.¹⁸ Nonetheless, in M5C+D3 we partition the QM region across peptide bonds to include the protein backbone so as to better compare to the recent study of Kulik and co-workers.^35,43 While M5C+D3 is still within range compared to all other models, it is noted that M5C+D3 produces somewhat larger differences from M5+D3 (ΔΔG^‡ = 2.5, ΔΔG = 2.7 kcal/mol).

All models discussed so far have been constructed in the GSBP framework based on the crystal structure, thus significant reorganization of the protein environment may not be captured due to the atoms fixed in the outer region of the GSBP setup.⁵⁴ To evaluate contributions from slower fluctuations that involve distal regions, we have conducted a battery of free energy simulations with starting structures taken from longer classical molecular dynamics simulations of both WT- and Y68A-COMT using QM/MM GSBP and PBC simulations; the Y68A mutant is chosen so as to compare the magnitude of free energy variation due to different simulation protocols with the impact of mutation, which is 1.6 kcal/mol according to experiment.¹⁰²

In classical molecular simulations, WT COMT stayed remarkably similar to the crystal structure except for a reorganization of Y38 and R201, while Y68A appeared to be more flexible, primarily due to a more mobile N-terminus with modest deviations in some key distances in the active site such as the methyl C-catecholate O distance, as well as rearrangements in the next shell (see Figs. S5–S8 in Supporting Information). This offers an excellent opportunity to verify the robustness of free energy results as a function of different structural models. For the WT enzyme, we initiate DFTB3/MM free energy simulations using GSBP with 190 ns (Y38-R201 elongation) and 250 ns (stabilized RMSD point for both WT & Y68A) snapshots. Similarly, we initiate GSBP simulations for Y68A starting with the 40 ns (SAM-Y143 elongation), 110 ns (N-Terminus leaves solution) and 250 ns snapshots from classical simulations. As further comparison, we perform PBC based DFTB3/MM free energy simulations for both WT and Y68A starting with the snapshot at 250 ns from the respective classical simulations.

Overall, as seen in Fig. 3 and Table S2, the PBC models do not differ substantially (sub k_BT) from their most direct complementary GSBP models, due to the lack of any highly mobile regions in COMT. For WT simulations, the minor structural changes after longer MD runs can produce free energy barrier differences on the order of 1.5–1.8 kcal/mol. For Y68A, the significant deviations from WT crystal structure can produce free energy barriers upwards of 3.7 kcal/mol. However, these variations are on the order of the deviations observed due to different QM regions and within the observed experimental increase in free energy upon mutation, making it challenging to robustly capture the effect of the Y86A mutation.

Figure 3:

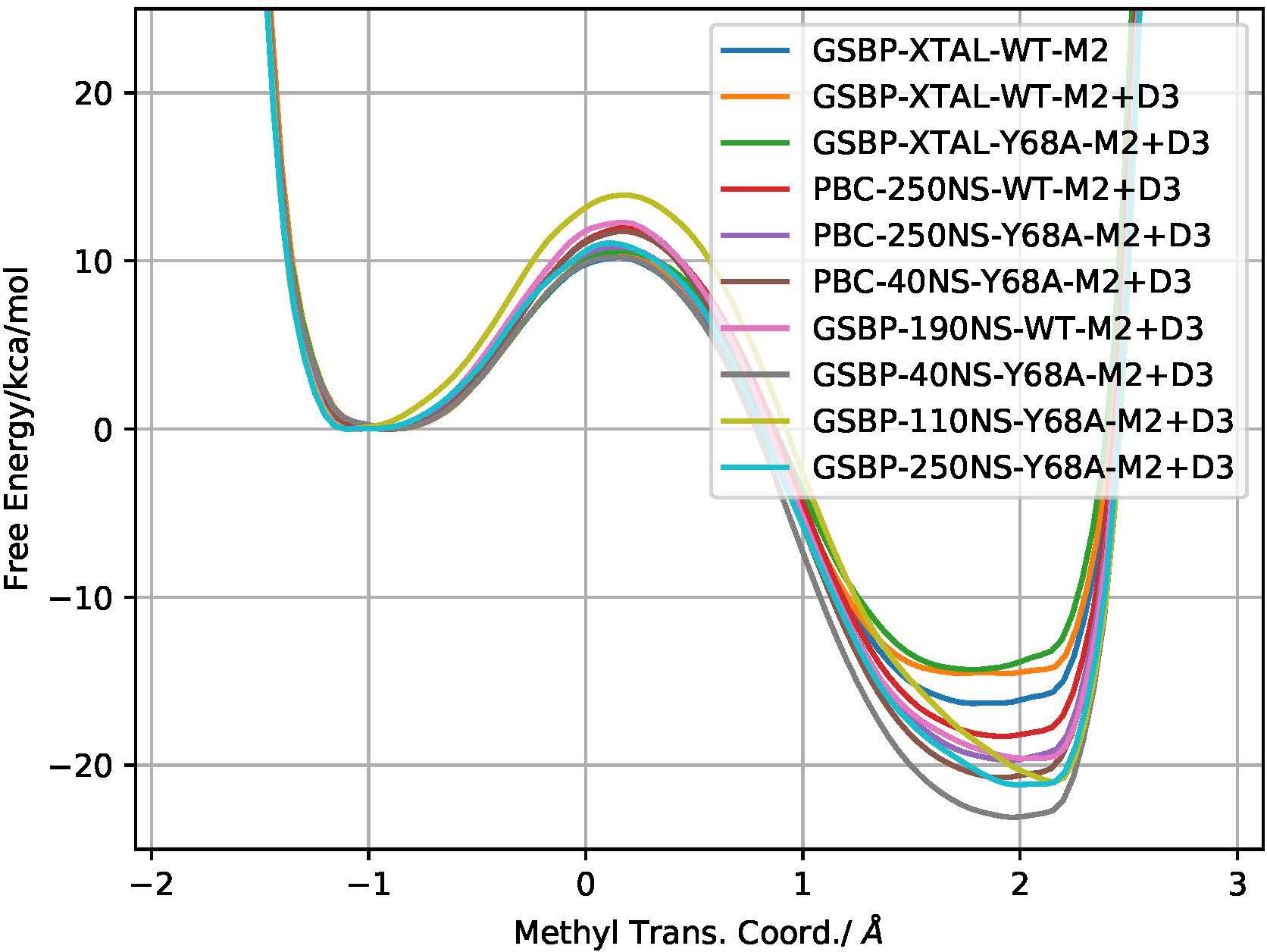
Free energy profiles from DFTB3/MM metadynamics simulations for different WT and Y86A models using the M2 QM region; ‘+D3’ results include the empirical dispersion contribution per respective model. Error along the PMF ranges typically from 0.1–0.3 kcal/mol. See Supporting Information Table S2 for tabulated form.

In short, compared to previous DFT/MM based umbrella sampling simulations,^35,43 the current study suggests that once adequate sampling is conducted, the free energy profile exhibits modest sensitivity to the QM region size. Other methodological choices such as dispersion among the QM atoms, QM/MM partitioning scheme and the starting structure of the free energy simulations are at least as important to the free energy results. These variations make it challenging to consistently capture modest contributions due to the mutation of second-shell residues, such as Y68A.

3.2. Structural Features

To determine how each subsequent expansion of the QM region affects the free energy surfaces, we investigate key local and global structural features. One of the most important features is the retention of the core active site distances, particularly coordination to the Mg²⁺ ion. Monitoring all amino acid/substrate coordination distances across the reaction reveals that the active site is structurally impervious to QM region choice (Fig. 4). For example, as the reaction progresses, catecholate charge becomes neutralized via methyl transfer (see Fig. S10 in the Supporting Information), thus one may expect a slight loosening of the CAT-O⁻-Mg distance. Indeed, all models capture this trend of CAT-O⁻-Mg coordination elongation along with a slight tightening of D141/D169-Mg coordination as the reaction progresses, and extending the QM region does not noticeably affect these trends. However, for some simulations, without the inclusion of dispersion, catecholate coordination at the product side becomes destabilized (Fig. 4), an effect not observed in any simulations including dispersion.

Figure 4:

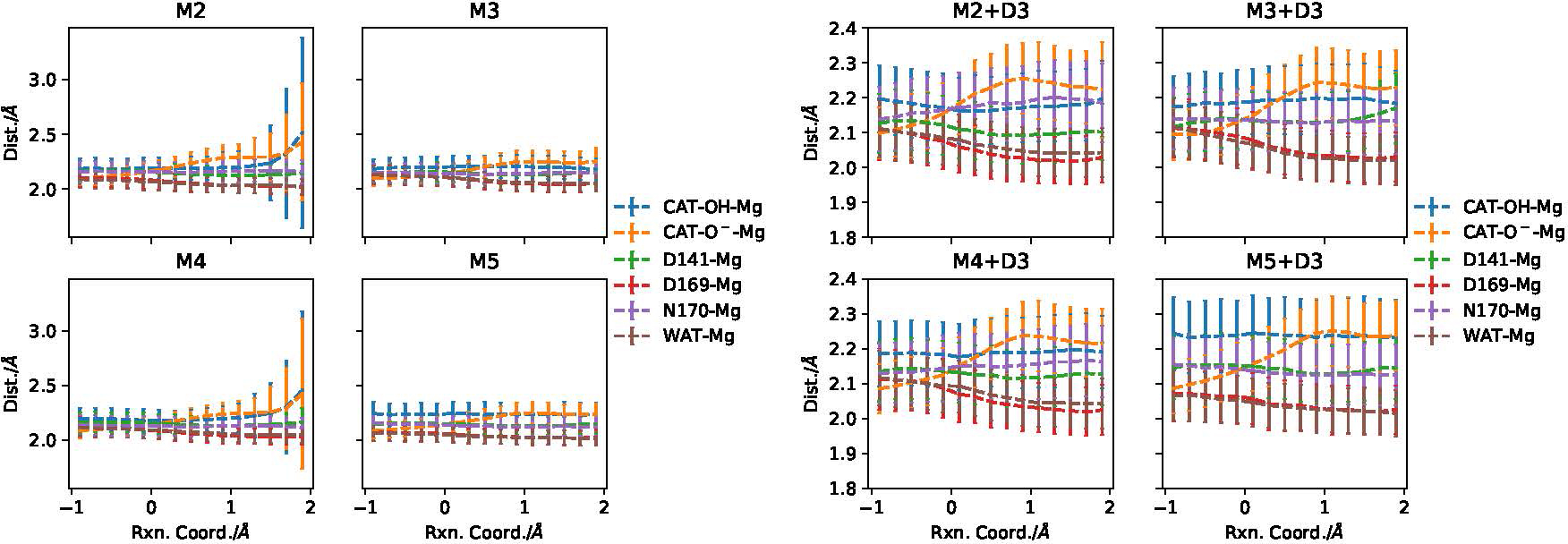
Evolution of O-Mg coordination distances in the active site across the reaction coordinate ξ for the QM/MM models with and without empirical dispersion (+D3). The main difference only lies in the destabilization of catecholate coordination at the product side in some of the simulations (M2 and M4) without the empirical dispersion.

With regards to other key active site structural characteristics, previously it was observed⁴³ that CAT-OH participates in a low-barrier hydrogen bond with E199, a feature that model M2 does not capture as E199 is in the MM region. Even with larger QM regions, SHAKE was applied to all bonds involving hydrogen, barring proton transfer between catechol and E199. To make a fair comparison to previous simulations, PMF calculations are repeated without the SHAKE constraint in catecholate for the M3 model, which includes E199 in the QM region; the free energy profile for the proton transfer between catechol and E199 is also explicitly computed (Fig. 5). These observations confirm that the preferred product state does exhibit an unusually shared proton between CAT and E199; however, the exergonicity is only increased by ~1.8 kcal/mol, and the effect on the barrier height is even smaller (~0.5 kcal/mol lower if the proton is shared). Thus the allowance of this unusually short hydrogen bond/sharing is unlikely to change the free energy surface between M3 and larger models.

Figure 5:

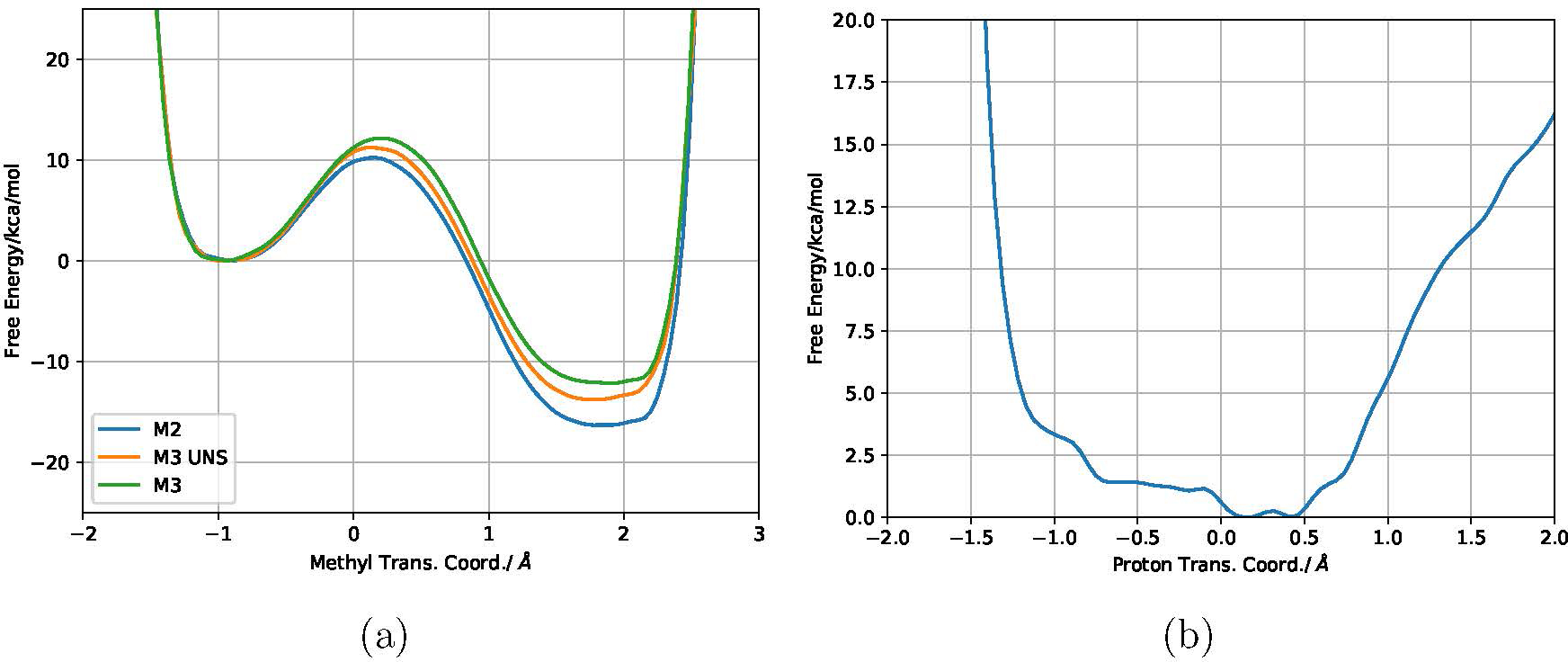
Effect of the strong hydrogen-bond between E199 and catecholate on the free energy surface (FES) in COMT. (a) FES of M2, M3 and M3 without the SHAKE protocol on the CAT-O-H bond (UNS). (b) FES of proton transfer given by the asymmetric stretch of the Catechol O, Catechol H, and an E199 acceptor oxygen.

Looking at more global structural characteristics, we determine the average number of inter-residue hydrogen bonds between different regions of COMT. As M2 is the minimalist model in this study, we next consider extending our structural analysis to the perseverance of hydrogen bonding networks within and outside the “core” M2 region. Using a distance and angular threshold of 3.0 Å and 20°, respectively, the number of core-core, core-outer, and outer-outer (not to confuse with the outer region in the GSBP setup) hydrogen bonds are computed for the reactant, transition state and product regions across the models; the M2 core selection includes only the M2 QM region, and the outer selection includes all protein atoms included in the M5 QM model. As shown in Table 1, hydrogen bonds are largely maintained throughout the reaction and between each model. Again, we see no significant structural change globally within variance in the protein regardless of the QM region size.

The lack of apparent structural changes between each model after extensive sampling reinforces the relative robustness of the free energy surfaces with regards to expanding QM regions. Similar analyses were done on select Y68A GSBP and PBC simulations due to Y68A’s relatively high flexibility (see Table S4 in Supporting Information). Compared to WT simulations, Y68A appears to have ~ one less hydrogen bond between the core and outer region, while the core-core/outer-outer regions are similar. Given that Y68, nominally in the region beyond the core, does not natively hydrogen bond with the core in WT, these results suggest that the Y68A mutation affects the active site in an indirect way, disrupting nearby hydrogen bonds instead. Further studies are necessary to explore these structural differences to firmly establish the mechanism for the reduced catalytic activity of Y68A.⁴⁹

3.3. Kinetic Isotope Effect and Transmission Coefficient

To evaluate DFTB3 for characterizing the methyl transfer transition state, we compute the secondary proton/tritium kinetic isotope effect (KIE) for the main systems studied (i.e., the GSBP setups based on the crystal structure) using a path-integral free energy perturbation approach,⁵¹ which has been applied to not only H/D/T KIEs but also heavy-atom KIEs such as ¹⁸O KIEs for phosphoryl transfer reactions.^79,104 As mentioned above, the cost of the path-integral simulations limited us to models M2-M4(+D3).

All models agree rather well with previous theoretically and experimentally observed inverse KIE (0.79) and equilibrium isotope effect (0.83).^49,96,99,105 As these calculations depend on the local configuration and vibrational modes of the transition state, a minimal QM region (M2, M2+D3) leads to reasonable estimates of the KIE likely because DFTB3 gives fairly accurate vibrational frequencies for sulfur containing compounds.¹⁰⁶ These results further support the use of DFTB3/MM for the characterization of methyl transfer transition state in COMT, and the conclusion that the key characteristics of the transition state does not change in any major way with respect to the QM size.

The transmission coefficients, κ, evaluated for different models (M2-M4, with and without D3) and the corresponding corrections to the effective activation free energy are also summarized in Table 3. For most models, the deviation of κ from unity is modest and in the range of 0.5–0.6, which is expected for a relatively simple methyl transfer reaction in the enzyme active site. With some models, however, the value of κ is smaller, suggesting perturbation in the active site structure, charge distribution and therefore the coupling of the transferring methyl group with the environment.⁵³ For example, it appears that κ generally decreases as empirical dispersion is included to each QM region. Nevertheless, the contribution of κ to the effective activation free energy is overall on the order of k_BT.

3.4. Electronic Structural Features: Charges and Charge Covariance

Finally, we discuss the dependence of electronic structural features of COMT on the QM region size. First, we note that the evolutions of the charges of Mg²⁺, the catechol and SAM during the reaction are generally insensitive to the QM region size (see Fig. S10 in the Supporting Information), again supporting that the overall feature of the catalyzed methyl transfer is preserved across different QM region selections. To probe the electronic structure at a more detailed level, we focus here on the covariance matrix of total charge amongst residues, as pioneered by Kulik and co-workers;^43,107 similar to Ref.,⁴³ for each amino acid residue (or co-factor), we compute the sum of Mulliken charges, and we monitor the charge covariance matrices in the reactant, transition state and product ensembles. The covariance matrices are organized based on the average distances to the Mg²⁺. Calculations for the M2 model suggest that the DFTB3/MM results based on the Mulliken analysis are generally consistent with higher level DFT/MM results based on the CM5 charge¹⁰⁸ (see Figs. S11–S12 in the Supporting Information).

With a large QM region as in M5+D3, while there is non-negligible coupling between charge fluctuations between the core M2 region and residues further away (Fig. 6), we note that the magnitudes of such coupling are markedly reduced compared to those within the M2 core. Indeed, mapping of the covariance matrices onto the protein structure (Fig. 7) further highlights that only nearby residues are significantly involved. Focusing on couplings within the M2 core (Fig. 8), all QM/MM models display overall similar degrees of charge covariance. As M3 includes some second shell amino acids, particularly E199, that engage in strong hydrogen bonds to the substrates, there are large fluctuations attenuated to M3. Notably, even with a somewhat destabilized catecholate geometry in the product, the charge covariance in M2 remains remarkably similar to the other models. Thus, it appears that even minimalistic models such as M2 or M3 can adequately capture and screen the charge fluctuations during the course of the reaction in COMT.

Figure 6:

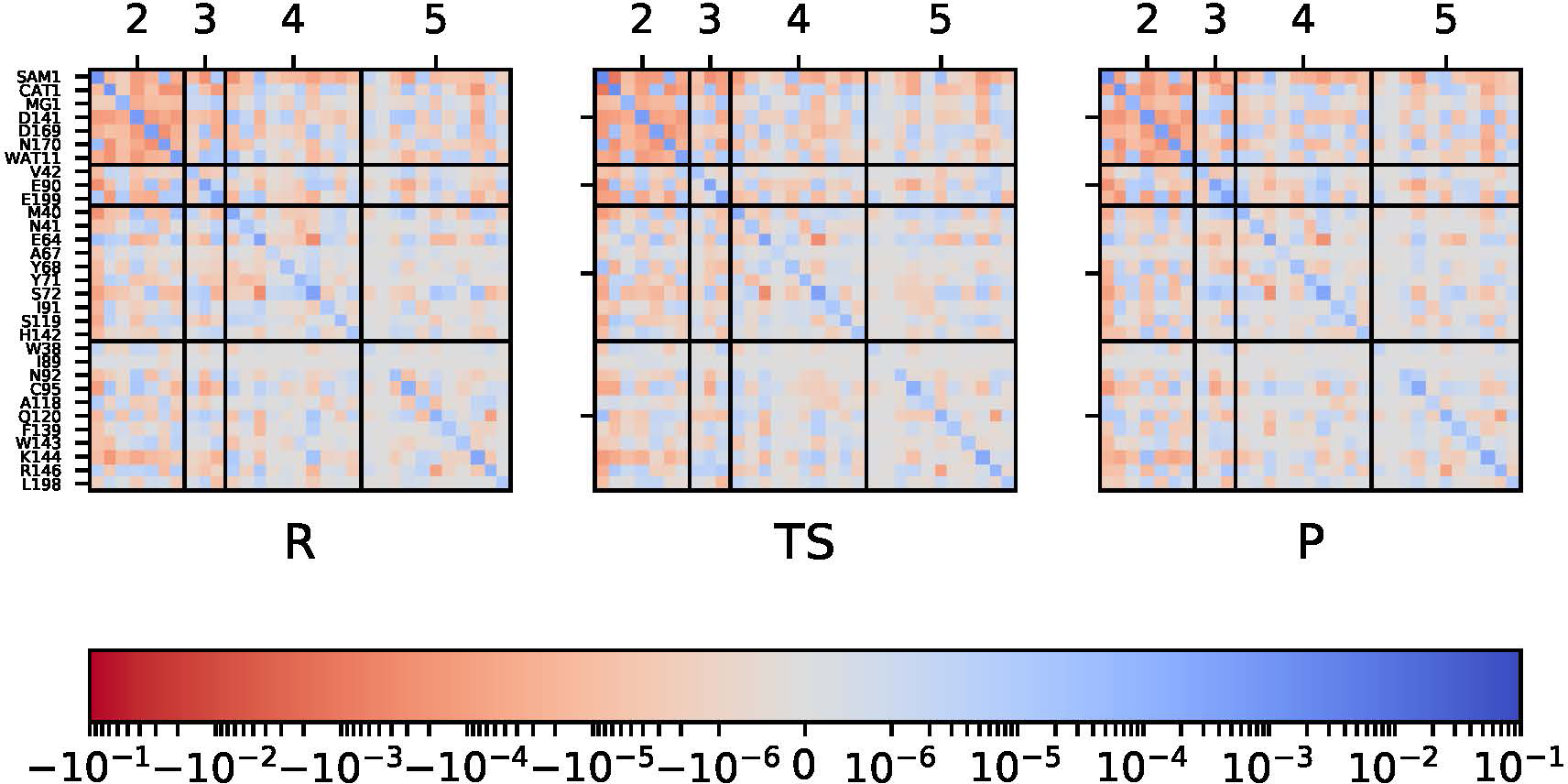
The charge covariance matrices at the DFTB3/MM level for the reactant, transition state and product bins (see Table 1) for the M5+D3 model. Grid spacing highlights the residues in different QM selection choices in the QM/MM models.

Figure 7:

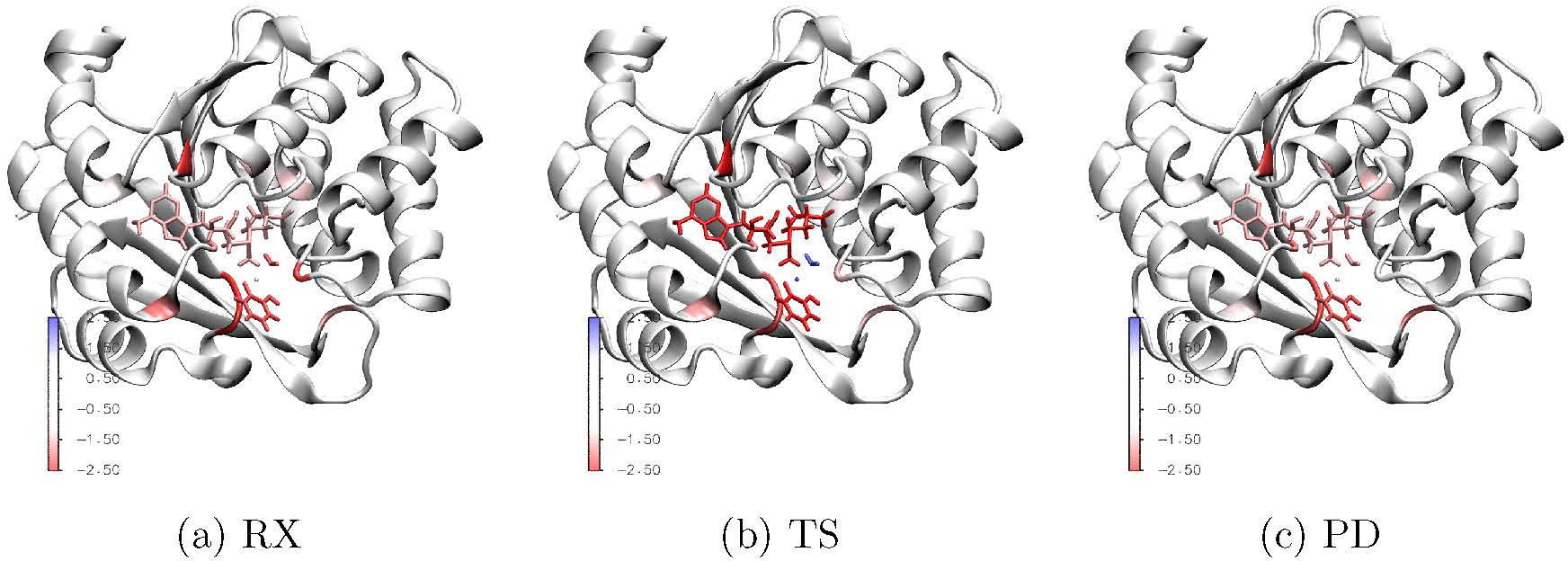
Max Covariance at the DFTB3/MM level (×10⁵ for visual clarity) between any residue to those in the M2 region computed for M5+D3 mapped onto the protein structure; for results for the M5C+D3 model, see Fig. S20 in the Supporting Information.

Figure 8:

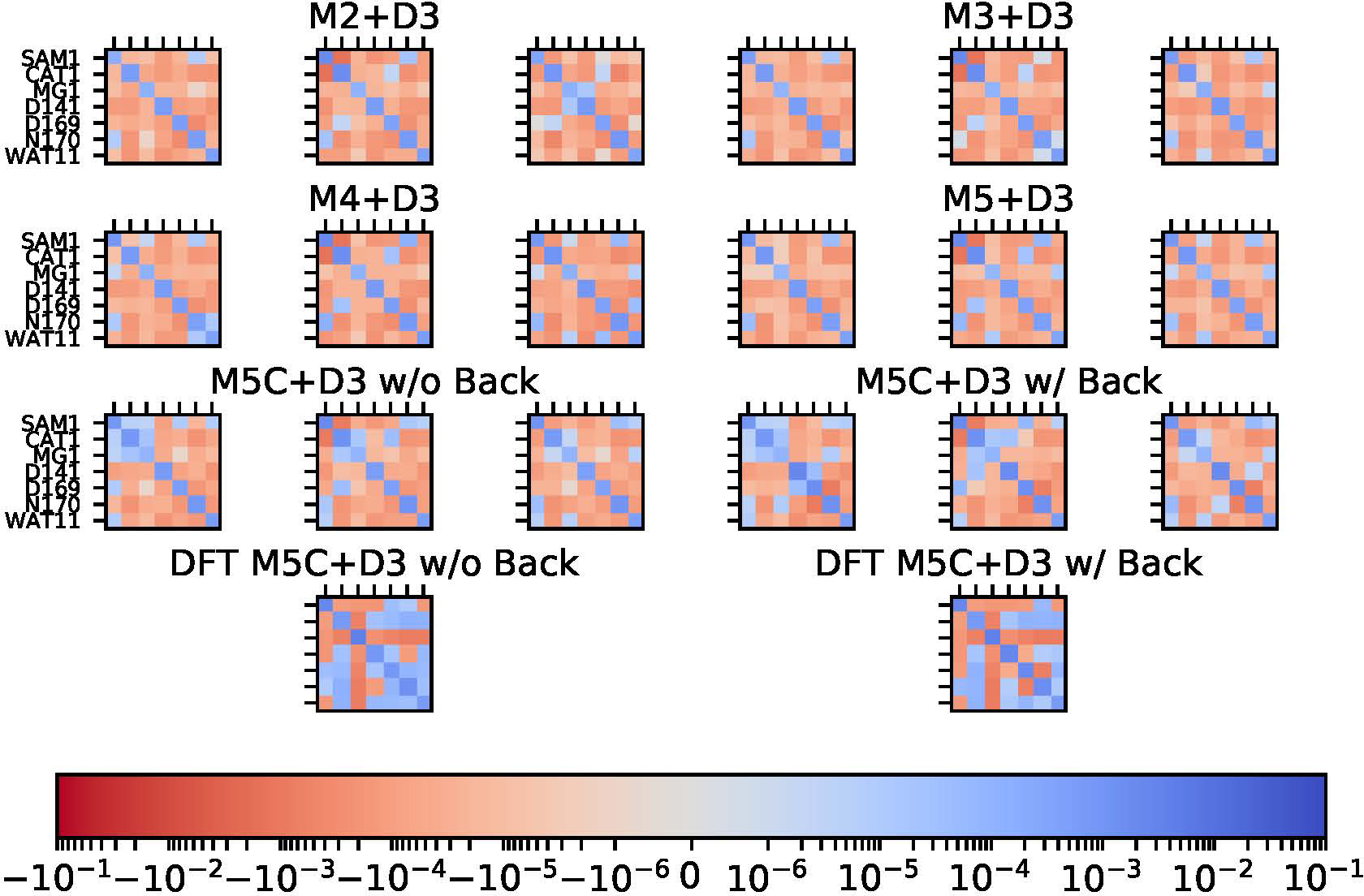
Charge covariance matrices at the DFTB3/MM level for the M2 region from different QM/MM simulations that include empirical dispersion; for each model, results for the reactant, transition state and product are shown separately. For the M5C+D3 model, charges are reported for each residue with those for the backbone atoms either included (‘w/Back’) or excluded (‘w/o Back’). Results for QM/MM simulations without the empirical dispersions are overall similar and thus not shown. For comparison, the last row shows the CM5 charges from DFT (ωPBEh/def2-SVP)/MM calculations using DFTB3/MM snapshots for the reactant state.

On the other hand, between M5C+D3 (Fig. 9, which does not include backbone charges) and M5+D3, we note several major differences in the charge covariance matrices. With M5C+D3, in the reactant state, there is a notable simultaneous charge movement amongst the charged center (SAM, CAT, MG). Moreover, the overall charge covariance seems shifted from the core M2/M3 regions and globally spread. For example, the ratio of extreme off-diagonal covariance values is 25 for M5+D3, while the ratios are generally much smaller and less than 5 with the M5C+D3 model (Fig. S13 in the Supporting Information), highlighting more uniform charge covariance across different regions. These observations are reinforced when including the backbone charges in the covariance calculations (Fig. S14 in the Supporting Information). Single-point charges using ωPBEh/def2-SVP and PBE/def2-SVP on the DFTB3 M5C+D3 structures reveal similar trends (e.g., Figs. S15 vs. S17, and Figs. S16 vs. S18 in the Supporting Information). While ωPBEh/def2-SVP modestly decreases the magnitude of charge covariances of residues in the outer compared to core residues, inclusion of the backbone leads to a more pronounced effect (Figs. S15 vs. S16, and Fig. S19 in the Supporting Information). Therefore, it appears that the electronic structure is perturbed substantially when the QM region includes protein backbone atoms to form contiguously bonded regions, and this trend is not due to the delocalization errors associated with typical GGA functionals.⁵⁵ This is further illustrated by the ranges of total charge for each residue in M5+D3 and M5C+D3 calculations. As shown in Fig. 10, the range is significantly expanded with the M5C+D3 model; similar to previous discussion,⁴³ the total charge of even non-polar residues such as Ile and Leu can fluctuate as much as 0.4 e once the protein backbone is included in the QM region.

Figure 9:

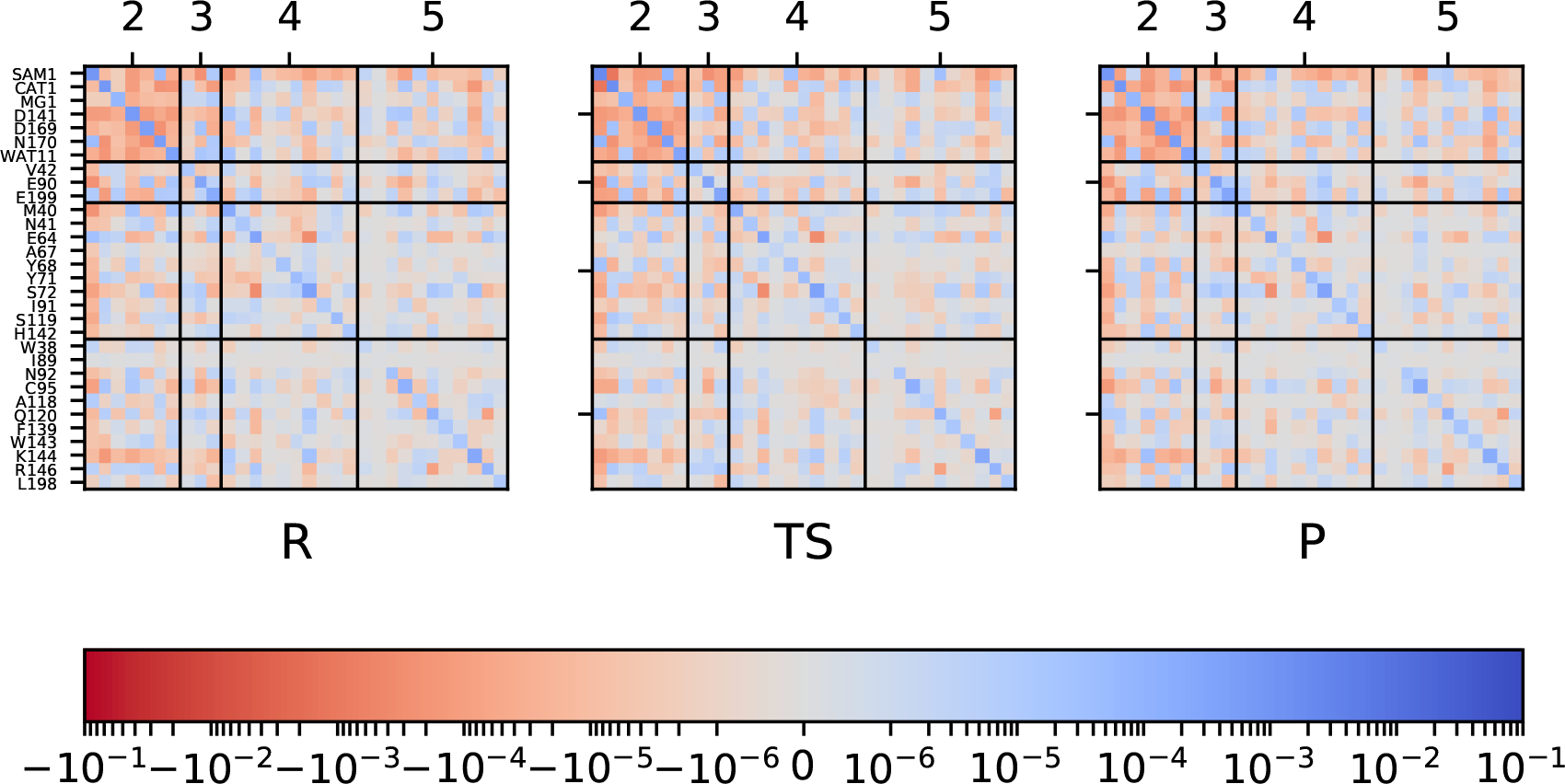
Similar to Fig. 6, but for the M5C+D3 model. To be consistent with Fig. 6, the results here only include charges for the sidechain atoms. Results include backbone charges for the M5C+D3 model are shown in Fig. S14 in the Supporting Information; results computed with DFT/MM single point calculations are also included in the Supporting Information (Figs. S15–S18).

Figure 10:

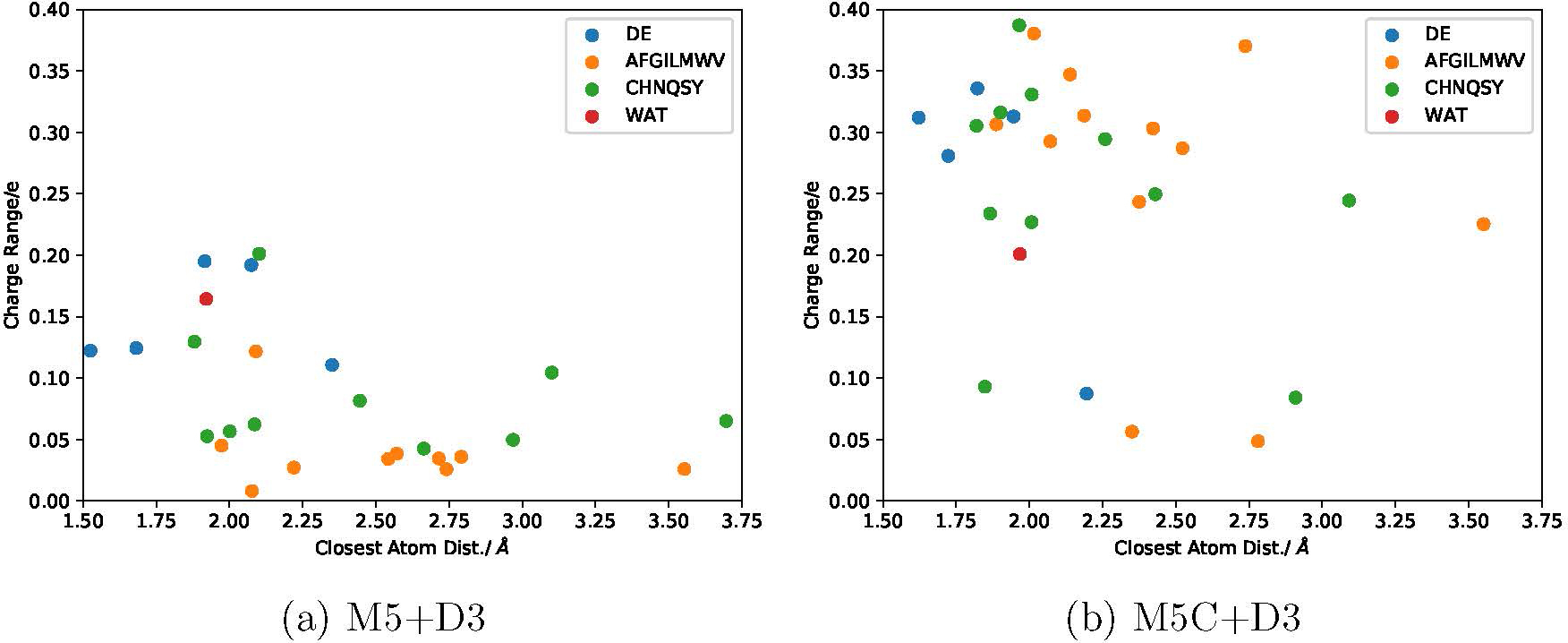
The range of total charge (i.e., maximum deviation from the integer reference) per residue from (a) M5+D3 and (b) M5C+D3 simulations; for the latter, the charges include backbone contributions. The charge range is plotted as a function of the closest distance of the residue to either SAM, CAT or MG. Charges are color coded into negatively charged (blue), non-polar (orange), polar (green), positively charged (red), and water (purple). All charges are DFTB3 Mulliken charges.

4. Concluding Remarks

Although the value of QM/MM simulations to mechanistic analysis of enzymes has been generally recognized, it remains non-trivial to balance computational accuracy and efficiency for arbitrary enzyme systems. One of the technical issues that has attracted much debate in recent years concerns the appropriate size of the QM region, with recommendations ranging from less than a hundred to several hundreds and approaching a thousand. It is an important issue since the proper QM size will also impact other methodological choices, such as multi-level free energy methods^6,10,109,110 and machine learning approaches^111,112 for improving the accuracy of low-level QM/MM energetics; if the proper QM region is routinely on the order of several hundreds, the applicability of these approaches will be substantially limited. Using COMT as a model system and an efficient but approximate DFT approach as the QM method, we aim to gain additional insights into this debate.

The most significant observation here is that the free energy profile, key structural/charge evolutions of the enzyme during the reaction as well as kinetic isotope effects show limited variations with respect to the QM region size, qualitatively similar to the observation from a previous semi-empirical QM/MM free energy study.⁴⁴ For example, the position and height of the barrier change by 0.13 Å and 2.9 kcal/mol as the QM region is enlarged by more than 400 atoms. Similarly, even electronic structural properties such as residual charge covariance matrix for the core residues (M2 region) appear to be rather insensitive to the variation of the QM region. There are larger variations in the exergonicity, which is consistent with the consideration that the methyl transfer reaction leads to neutralization of a pair of formal charges, thus polarization of the enzyme environment is expected to make larger contributions; still, the magnitude of variation observed here is substantially smaller than those reported in previous work.⁴³ Thus these results support the notion^38,44 that the key features of enzyme catalysis can be captured with a modest QM region size. The significant variations in energies observed in previous studies appear to be largely quenched once extensive conformational sampling is included. Whether this is yet another manifestation of the enthalpy-entropy compensation phenomena often observed for biological systems^113–115 deserves further analysis, although a preliminary analysis along the lines of previous studies¹¹⁶ (see Fig. S4 in the Supporting Information) does not indicate any such compensation effects. We note that without adequate sampling of dipolar relaxation in the enzyme environment, the effect of distant groups on the QM region can be overestimated. For example, when contributions from distant charged residues to the pK_a of a titratable group were analyzed in a perturbative fashion,^117,118 i.e., by computing the change of QM/MM interaction energies without re-sampling the MD trajectory after the MM partial charges on a charged residue are turned off, the effects were significantly overestimated (> 10 kcal/mol). For a similar reason, with limited sampling, the effect of altering the description (MM vs. QM) of distal residues can be exaggerated.

For large QM region calculations, in addition to the issue of dispersion, which evidently makes a notable contribution to the free energy profile in COMT, an important technical detail concerns the QM/MM partitioning scheme. While including only the sidechains in the QM region leads to rather short-ranged residual charge covariance, including the protein backbone into the QM region leads to significantly longer-ranged coupling in charge fluctuations. This observation can be explained by the fact that including protein backbone atoms leads to a larger set of contiguously bonded atoms. Therefore, it is plausible that the proper convergence of certain electronic structure properties indeed requires rather large QM regions, especially those that are highly sensitive to the charge density variation; indeed, according to the holographic electron density theorem,¹¹⁹ variation in the local charge density may impact charge density in remote regions since the electron density is analytic away from the nuclei. We note that the DFTB3 approach used here, due to the parameterization based on the PBE functional, suffers from delocalization error as other popular GGA functionals.^120,121 Therefore, the long-range residual charge covariance observed in the M5C(+D3) model might be an exaggerated effect, as observed in the early development of the charge fluctuation model for proteins.¹²² However, we note that the trends in the charge fluctuations are largely conserved when a range-separated DFT method is used as the QM. Thus these results strongly suggest that different properties likely require different QM region sizes, a feature often observed in the analysis of complex systems. It is therefore encouraging to see extensive efforts in systematically determining QM region dependence with respect to different observables.^{15,26,28–31,35,123}

While our computed KIEs for WT-COMT match experimental values rather well, investigation of the Y68A mutant offers a surprising challenge. On the one hand, although Y68A is more flexible, PBC and the more constrained GSBP boundary conditions lead to remarkably similar free energy results. On the other hand, the higher structural flexibility of Y68A offers different starting enzyme conformations that lead to deviations in the barrier height on the same order as experimentally measured effect of mutation (1.6 kcal/mol on the barrier height). More systematic analysis of the Y68A mutant is warranted to firmly establish the mechanism for the reduced activity induced by the second-shell mutation.

Finally, we recognize that the current study employs an approximate, semi-empirical approach (DFTB3) that has limitations in the description of both chemical and non-covalent interactions. For example, rather strong hydrogen bonds have been observed in recent analyses of high-resolution crystal structures,^124,125 which might demand more accurate QM methods for proper description. Therefore, it remains important to cross-validate the current observations with more accurate QM methods. However, we emphasize that such analysis requires extensive sampling to properly converge the free energy profile, and short QM/MM simulations using reactant state conformations equilibrated with long classical MD simulations,³⁶ while informative, are not replacement for proper free energy simulations. Moreover, as emphasized repeatedly in previous studies,^7,74,126,127 it is essential (and often straightforward) to calibrate semi-empirical QM method for the specific system of interest (e.g., using proton affinities of key reactive groups) to avoid unrealistic errors in computed free energy profiles.¹²⁸

Table 2:

The average number of hydrogen bonds (with standard deviations in parentheses) between atoms in different regions, where cc = core M2/core M2, co = core M2/M5 selection, oo = M5 selection/M5 selection.

Ensemble a	QM/MM Model	cc	co	oo
RX	M2+D3	0.43 (0.57)	4.50 (1.36)	3.28 (1.32)
	M3+D3	0.60 (0.64)	3.98 (1.41)	2.98 (1.32)
	M4+D3	0.72 (0.65)	3.92 (1.32)	2.79 (1.26)
	M5+D3	0.52 (0.63)	4.25 (1.42)	3.38 (1.24)
TS	M2+D3	0.64 (0.66)	3.56 (1.33)	3.16 (1.39)
	M3+D3	0.51 (0.62)	4.03 (1.45)	3.56 (1.28)
	M4+D3	0.55 (0.63)	3.71 (1.41)	2.64 (1.24)
	M5+D3	0.47 (0.60)	4.40 (1.44)	3.21 (1.25)
PD	M2+D3	0.55 (0.56)	4.16 (1.33)	3.23 (1.24)
	M3+D3	0.43 (0.55)	4.32 (1.45)	3.51 (1.27)
	M4+D3	0.46 (0.57)	3.80 (1.43)	2.57 (1.17)
	M5+D3	0.52 (0.60)	4.25 (1.40)	3.22 (1.25)

^a).A window size of 0.2 Å was used for the reactant (RX) and product (PD) while a window size of 0.1 Å was used for the transition state (TS).