Abstract
This work proposes to develop and evaluate a deep learning framework that jointly optimizes k-t sampling patterns and reconstruction for head and neck dynamic contrast-enhanced (DCE) MRI aiming to reduce bias and uncertainty of pharmacokinetic (PK) parameter estimation. 2D Cartesian phase encoding k-space subsampling patterns for a 3D spoiled gradient recalled echo (SPGR) sequence along a time course of DCE MRI were jointly optimized in a deep learning-based dynamic MRI reconstruction network by a loss function concerning both reconstruction image quality and PK parameter estimation accuracy. During training, temporal k-space data sharing scheme was optimized as well. The proposed method was trained and tested by multi-coil complex digital reference objects of DCE images (mcDROs). The PK parameters estimated by the proposed method were compared with two published iterative DCE MRI reconstruction schemes using normalized root mean squared errors (NRMSEs) and Bland-Altman analysis at temporal resolutions of Δt=2s, 3s, 4s, and 5s, which correspond to undersampling rates of R=50, 34, 25, and 20. The proposed method achieved low PK parameter NRMSEs at all four temporal resolutions compared with the benchmark methods on testing mcDROs. The Bland-Altman plots demonstrated that the proposed method reduced PK parameter estimation bias and uncertainty in tumor regions at temporal resolution of 2s. The proposed method also showed robustness to contrast arrival timing variations across patients. This work provides a potential way to increase PK parameter estimation accuracy and precision, and thus facilitate the clinical translation of DCE MRI.
Keywords: DCE MRI, Image reconstruction, Deep learning, Sampling pattern, Pharmacokinetic model
I. Introduction
Dynamic contrast-enhanced (DCE) MRI is an imaging technique that acquires a time-series of T1 weighted images before, during and after a bolus administration of a contrast agent (CA) to enable quantitative physiological parameter extraction from a pharmacokinetic (PK) model. The extracted parameters, e.g., blood volume and blood flow, could help assess the histological grade of tumors [1], differentiate tumors from normal tissue [2], and monitor as well as predict cancer response to therapy [3]. Despite these promises, DCE MRI still faces technical challenges that limit its utility for routine clinical use or even for application to multi-center clinical trials. Major challenges include: 1) a trade-off between spatial resolution and/or spatial volume coverage of anatomy of interest versus temporal resolution of the dynamic scan; and 2) accuracy and reproducibility of the quantified parameters that are sensitive to temporal resolution, PK model, pulse sequence and reconstruction method [4], [5].
To achieve adequately high temporal resolution of DCE MRI to yield accurate PK parameter estimation [4], parallel imaging [6] and different k-t space sampling trajectory designs [7]–[11] have been used. The challenge of simultaneously increasing spatial resolution, coverage volume and temporal resolution of DCE MRI requires optimizing the k-t sampling pattern (SP) by taking advantage of the spatiotemporal sparsity of dynamic signals as well as characteristics of anatomy being imaged. A few attempts have been made to optimize the SP to leverage similarity of the same body site assisted by prior knowledge for image reconstruction algorithms [12]–[16]. However, these works most relied on pattern search algorithms that lack computational efficiency. Most importantly, no currently known strategy considers the underlying quantitative PK parameter estimation model in the sampling optimization, even though an influence of the k-t SP on the variance of estimated PK parameters has been demonstrated [17]. We hypothesize that joint optimization of DCE MRI k-t SPs and PK parameter estimation has the potential to improve accuracy and reproducibility of the estimated parameters.
Nonlinear algorithms are needed to reconstruct high quality MR images from highly undersampled k-t space DCE data. Compressed sensing-based methods have been applied with hand-crafted constraints exploiting the spatial and temporal sparsity in DCE MRI [18]–[21]. Recently, deep learning has shown promise in MR image reconstruction by exploring data-driven constraints [22]–[26]. In deep learning-based frameworks, recurrent neural networks (RNNs) that processes temporal information in the dynamic data have shown superior performance in DCE MRI reconstruction [27], [28]. More recently, deep learning-based joint optimization of k-space SPs and reconstruction networks has been proposed [29]–[31], and shown improved quality of reconstructed MR images from optimized undersampled k-space data compared to compressed sensing-based methods with non-optimized sampling. However, existing investigations have primarily focused on the optimization for static MR image reconstruction.
In this work, we extend the use of RNNs further to jointly optimize k-t space SPs of DCE MRI acquisition and image reconstruction with an objective that combines image quality and parameter estimation accuracy. The dynamic MRI reconstruction network exploits the spatiotemporal sparsity of DCE MRI to optimize where in k-space and when in the dynamic time course to acquire the MR data. The PK parameter estimation l2 loss was integrated into the objective of the image reconstruction network to account for PK modeling information during network training. Realistic multi-coil digital reference objects (mcDROs) were created from PK parameter maps estimated from patient scans with head and neck cancers and used for network training and testing, which provided ground truth for quantitative evaluation. The proposed method was tested in a wide range of temporal resolutions of mcDROs, and showed reductions in PK parameter bias and uncertainty compared to two previous published works [21], [32].
II. Methods
Our proposed method consists of four major components: 1) k-t SP optimization, 2) k-t space data sharing optimization, 3) a dynamic MR image reconstruction network, and 4) a PK parameter estimation layer. The first three have learnable parameters and are jointly optimized during training. The last component, the PK parameter estimation layer, has no trainable parameters, but its gradient is passed on to the other components to provide feedbacks for the network learning. The overall workflow of the proposed approach is shown in Fig. 1. The details of each component and how they are combined to allow an end-to-end training are described in the following subsections.
Fig. 1.
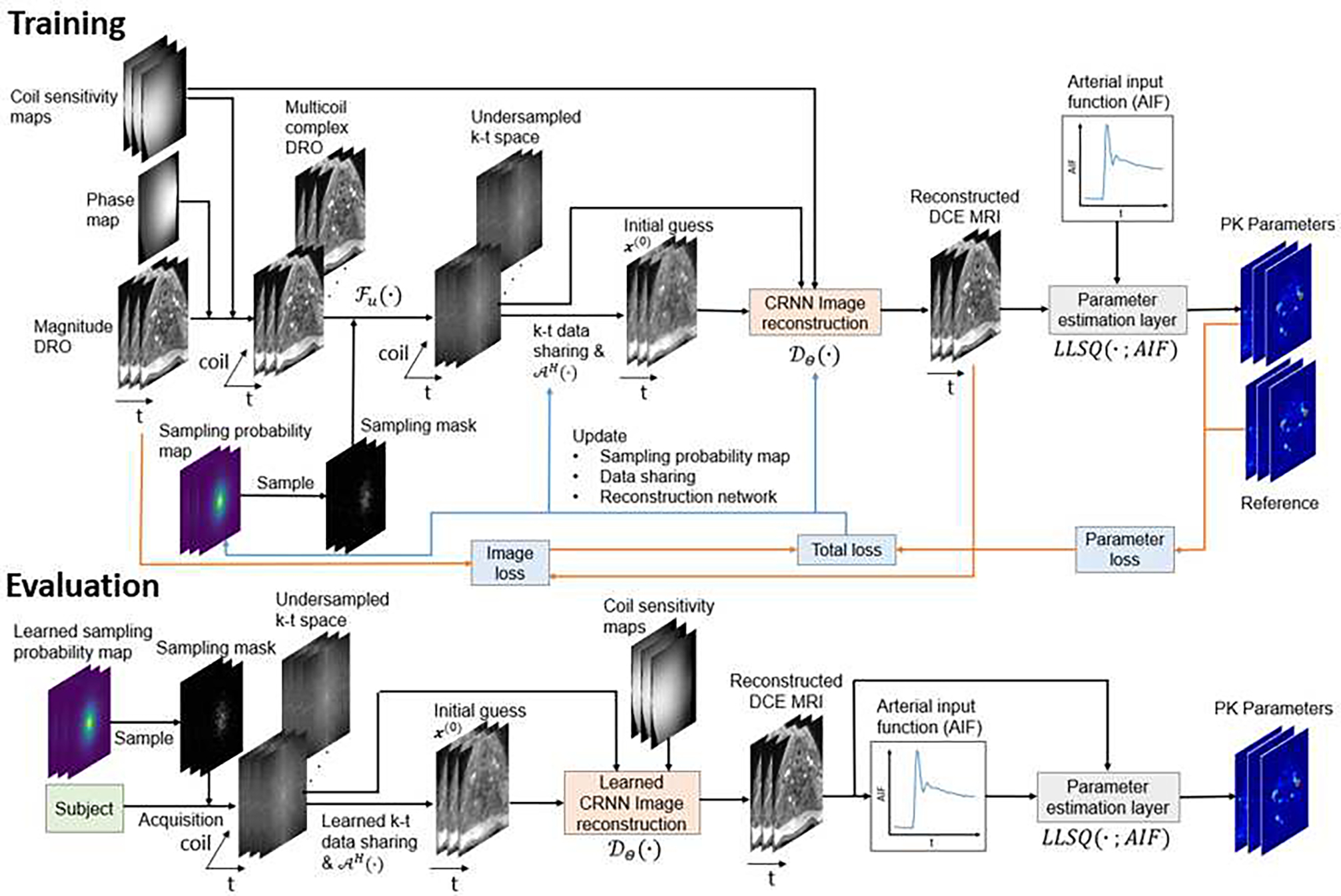
The training and evaluation workflows of the proposed method. The k-t sampling probability map, k-t data sharing, and image reconstruction network are jointly optimized with respect to both image and parameter reconstruction quality using fully sampled DCE MRI data in the training phase. In the evaluation phase, the learned sampling mask and reconstruction network are used to undersample and reconstruct real data.
A. k-t Sampling Pattern
In this work, the k-t space SP that represents 2D phase encoding locations along the time course of a DCE acquisition using a 3D T1 weighted spoiled gradient echo sequence is learned jointly with the reconstruction network. Frequency encodings are fully sampled due to their rapid sampling speed. We extended LOUPE [33] to the time domain by adding a temporal degree of freedom (TDoF) to learn dynamic SPs in the k-t space. Let denote a sequence of fully sampled images of a slice with width nx, height ny and nt time frames. The 2D Cartesian k-space SP in a kx-ky plane at time nt is denoted as where superscript u represents “undersampling”, which is formulated as a realization of random vector Mu containing independent Bernoulli random variables, i.e. , where denotes the subsampling probability to be learned. Therefore, the undersampled k-space data of the cth coil can be written as , where Cc is a diagonal matrix with the coil sensitivity values of the cth coil as the diagonal elements, F is the forward discrete Fourier transform matrix and Fu = diag(mu)F is the undersampling matrix. The first timeframe of the image slice is fully sampled to provide the anatomic baseline prior to the arrival of the injected contrast.
To implement LOUPE with a TDoF, a set of neural network weight parameters to be learned is regularized by an element-wise sigmoid function to produce a set of sampling probability maps . To create SPs from the sampling probability maps pu, a sigmoid function is used to approximate the operation so that mu = σv(u − pu), where is a realization of and is an element-wise sigmoid function with slope v. The sigmoid function ensures nonzero gradient when backpropagating through the sampling of Bernoulli random variables.
B. k-t Space Data Sharing
In DCE MRI, adjacent temporal frames share similar contrast enhancements among the same anatomy, and especially, dynamic changes are limited before starting contrast uptake and after reaching the uptake plateau. Sharing the k-space data among temporal frames within the same anatomy would reduce undersampling-caused aliasing in an initial image for reconstruction network training. Inspired by previous data sharing approaches [25], we propose a novel machine learning-based k-space data sharing (DS) scheme. A subset of frames is determined during training to share their k-space data with frame j, and represented by a data sharing mask where superscript s represents “sharing” and value 1 or 0 indicates sharing or not. The k-space data from other frames shared with frame j at coil c, , is described as follows:
| (1) |
where denotes the j′th frame of a MR slice and is the subsampling mask for frame j. If a k-space location in frame j has more than one frame for data sharing, a data average is taken. Then, the initial guess of the image of frame j at coil c is obtained by taking an inverse discrete Fourier transform (DFT) of the combined acquired and shared k-space data as:
| (2) |
where FH denotes the inverse DFT matrix. Finally, the coil-combined initial guess of the image is .
Similar to the approach that generates the SP, the data sharing mask is a realization of random vector containing independent Bernoulli random variables of which the probability is parameterized by network weights that are learned during training. The same σv(∙) is used to approximate the sampling of Bernoulli random variables.
C. Image Reconstruction
To take full advantage of temporal sparsity of DCE MRI, we adopted and modified the Convolutional RNN (CRNN) framework [34] to utilize RNN capability of extracting temporal correlations in dynamic data and to improve computation efficiency. In the modified CRNN, connections are over both temporal and iteration dimensions, which is not used in deep-learning methods for static image reconstruction.
In the typical compressed sensing (CS) framework, the MR image reconstruction problem is usually posed as a nonlinear optimization problem in a form:
| (3) |
where is the set of fully sampled images, A is the MRI system matrix including effects of coil sensitivity, Fourier encoding and undersampling, y is the measured k-space data and denotes a regularization term that represents our prior knowledge of x. The first l2 norm enforces the data-consistency (DC) between the reconstructed image and the acquired k-space data. For dynamic MR reconstruction, is often employed as spatiotemporal total variation (TV) [35] or low rank [36] constraints. By applying variable splitting and alternating minimization techniques, can be solved iteratively by:
| (4) |
| (5) |
where μ is a penalty parameter and z is an auxiliary variable. The x update is often called the DC term. We follow D-POCSENSE [37] to implement this step as
| (6) |
The z update is a proximal operator, which we follow previous works [25], [34] to solve with a CNN-based dealiasing network parameterized by Θ so that . We used a modified version of the CRNN framework as the de-aliasing network.
Our CRNN framework (Fig. 2) contains 5 components: 1) one bidirectional CRNN layer over both time and iterations (BCRNN-t-i), 2) one recurrent U-net (R-U-net-i), 3) one 2D CNN layer, 4) residual connection, and 5) multi-coil DC layers. Inspired by a previous work on multi-scale image deblurring [38], we replaced the second component, a CRNN layer over iterations (CRNN-i) of the original CRNN framework, with a compact U-net structure where a recurrent connection over iterations is placed on the bottleneck of the U-net, dubbed recurrent U-net (R-U-net-i). This modification largely reduces the GPU memory and training time, allowing other components being incorporated to the framework, e.g., the PK parameter estimation layer. The CRNN was also extended to multicoil settings by using a multicoil DC layer (6).
Fig. 2.
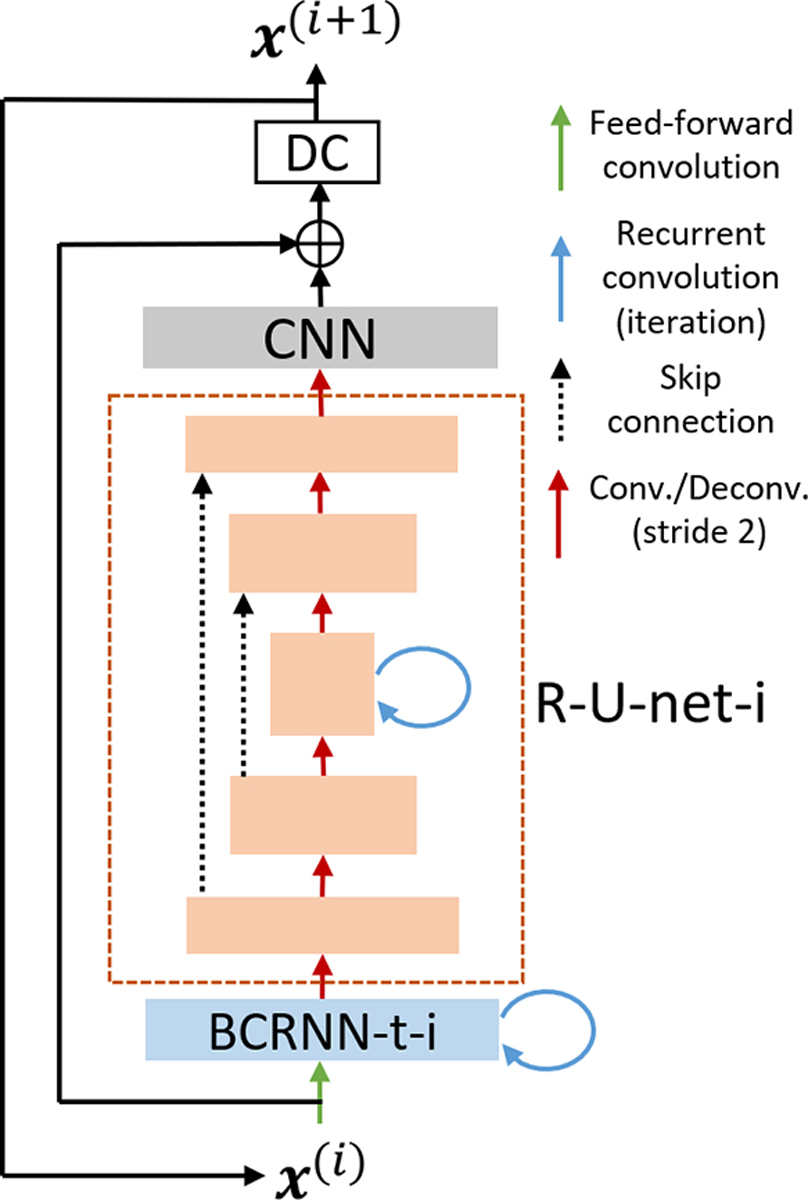
The overall structure of the image reconstruction network. The new R-U-net-i structure has 5 layers with 2 down sampling and up sampling paths. The bottleneck layer has a recurrent connection across iterations.
D. PK parameter estimation
The extended Tofts (eTofts) model [39] was implemented in this study which estimates the transfer constant Ktrans of the CA that diffuses from blood vessels to the interstitial space, the rate constant kep of the CA efflux from the interstitial space to blood plasma and the fractional volume of blood plasma vp voxel-by-voxel. Also, a voxel-wise contrast bolus arrival time, τBAT(r) is warranted for accuracy of PK parameter estimation [40]. Finally, we adopted a linear least squares (LLSQ) method for PK parameter estimation [41], which is more robust to the low SNR of DCE data and more computationally efficient than NLSQ fitting. Linear operations in LLSQ fitting can be easily incorporated into a deep learning framework. The eTofts model for LLSQ fitting is expressed as:
| (7) |
where Ktrans, kep, and vp are linearly related to the integral of Ct(r, t) (concentration of tissue contrast (CTC)), integral of Cp(t) (concentration of blood plasma contrast), and Cp(t). For a given τBAT(r), Ktrans, kep, and vp can been readily estimated using only linear operations. τBAT(r) can be estimated jointly with Ktrans, kep, and vp by minimizing the normalized root mean squared error (NRMSE) between the measured and the estimated CTCs. The τBAT(r) range can be determined by prior knowledge. In our implementation, we tested τBAT(r) values of {0, 1, …, 6} s for tissue in the head and neck region. The LLSQ method is wrapped as a layer denoted as LLSQ(∙ ; Cp) with the layer input as the reconstructed images .
E. Loss Function
The learning objective is formulated to include both l2 errors of reconstructed images and estimated PK parameters as the following:
| (8) |
where is the initial guess of an image as described by (2). represents ground truth values of Ktrans, kep and vp. nvox is the number of voxels in the anatomic region, and Cp is the ground truth CA concentration in plasma. The first term in the expectation represents the l2 norm between reconstructed PK parameter maps and corresponding ground truth values, called the parameter loss. The second term is the l2 norm between reconstructed and ground truth images, called the image loss. β controls weighting between the parameter loss and the image loss.
III. Experiments
A. Multi-coil Digital Reference Objects
mcDROs of DCE MRI data used for training and testing were synthesized using patient specific AIFs and PK parameter maps estimated from real DCE MRI data of 17 patients with head and neck cancers enrolled on a protocol approved by the Institutional Review Board.
The DCE MR images of the patients were acquired using a 3D dynamic scanning sequence (TWIST) with an injection of 0.149 cc/kg of gadobenate dimeglumine on a 3 Tesla MRI scanner (Skyra, Siemens Healthineers, Erlangen Germany). The scanning parameters were: flip angle = 10°, echo time (TE) = 0.97ms, repetition time (TR) = 2.73ms, 60 time frames, voxel size = 1.56mm×1.56mm×2.5mm, and matrix = 192×192. The dynamic images were interpolated to have spatial resolution of 1.56mm×1.56mm×1.56mm. Axial slices were used due to their small dimensions and relative anatomical symmetry compared to the anatomy along the cranial-caudal direction, which may allow more aggressive k-space undersampling. For all cases, the patient specific AIFs were extracted manually by averaging the signal intensity-time curves of 20 voxels from the carotid artery, which had maximum intensities at the time frame before the enhancement peak [42], and then subtracted and divided by the average pre-contrast signal intensities of the voxels. The PK parameter maps were estimated using LLSQ with joint estimation of τBAT(r) in {0, 1, …, 6}s. The voxels that had estimated parameters out of the physiologically reasonable range (Ktrans ∈ (0, 3)min−1, kep ∈ (0, 6)min−1, vp ∈ (0, 0.55)) were considered incompatible with eTofts model and excluded from the final estimated maps. These parameter maps were regarded as ground truth values for mcDRO creation, and network training and testing.
mcDROs with temporal resolutions of {2, 3, 4, 5}s and spatial resolution of 1.56mm×1.56mm×1.56mm were simulated. Using a TR of 2.73ms that can be achieved on this 3 T scanner yields undersampling rates (R) of {50, 34, 25, 20} for temporal resolutions of {2, 3, 4, 5}s, respectively. The undersampling rate is a reduction factor in the k-space subsampling relative to fully sampling of each frame. The mcDRO creation steps are: 1) Simulate CTCs Ct(r, t) from ground truth PK maps of Ktrans(r), kep(r), vp(r) using the eTofts model and patient specific AIF Ct(t), and τBAT(r) in the voxels where the eTofts model is applicable, 2) Add Gaussian noise to the simulated CTCs to have contrast-to-noise ratios (CNR) of 20 in each voxel to mimic the noise level present in real DCE data, 3) Convert the CTCs to signal intensity images using baseline signal intensities s0(r, 0) from the actual scan as: s(r, t) = [1 + Ct(r, t)]s0(r, 0), 4) Use the signal intensities from the real scan for the voxels where eTofts model is not applicable (e.g., vessels), 5) Estimate coil sensitivity maps from fully sampled high resolution (0.875mm×0.875mm×3.3mm) post Gd T1-weighted images acquired immediately following the DCE scans by using ESPIRiT [43] and compressing coils from 30 to 8 coils [44], 6) Create complex DCE images by using the real phase variation estimated from post Gd T1-weighted images of the same patient ϕ(r) as: s(r, t) = [1 + Ct(r, t)]eiϕ(r)s0(r, 0), 7) Create multi-coil DCE image series as well as multi-coil time-series of k-space data (see Fig. 1). Note that the simulated mcDROs used realistic PK parameter ranges, AIFs and anatomy provided from patients.
Of 17 patients, 8 were randomly selected for training, 3 for validation and 6 for testing. Note that during training, the ground truth patient specific AIF Cp(t) was used for PK parameter estimation, while during testing, a patient specific AIF was extracted from reconstructed MR images by a fully automated process that mimicked how an expert delineated an AIF [42]. As a brief, the anatomy surface was extracted by thresholding followed by closing operation. The contrast enhancement peak within the anatomy surface was detected after performing enhanced signal subtraction and division from baseline signals. The 20 voxels with the maximum enhancement in the dynamic frame of 3–10s prior to the peak of tissue enhancement was considered as an AIF. A 3×3 Gaussian filter was applied to the real scan for creation of mcDROs used for training and validation, but not for mcDROs set aside for testing in order to provide for better AIF characterization during testing.
B. Network Training
The R-U-net-i unit of the reconstruction network used in the experiment contains 3 convolutions and 3 deconvolutions with stride 2, where the number of filters (nf) are doubled or halved after each convolution or deconvolution. We used kernel size k=3. The number of filters of the BCRNN-t-i unit and the number of iterations were optimized and set to nf = 32 and N=5, respectively. The estimated PK parameters were clipped to the physiologically reasonable range to stabilize the network training. Adam optimizer [45] was used with learning rate 1e-3. We used batch size = 1 and terminated training when the validation error was not improved in 3 consecutive epochs. All codes were implemented in PyTorch, and the experiments were performed on an NVIDIA RTX A6000 GPU with 48GB memory.
C. Evaluation and Comparison
1). CRNN Network Architecture Hyperparameter Optimization:
First, we optimized nf and N across the combinations of nf ∈ {8,16,32,64} and N ∈ {3,5,10} using the mcDRO with spatial resolution 1.56mm×1.56mm×1.56mm and temporal resolution 3s. Fixed Poisson disk SP and image loss were used. The best nf and N were selected according to the average parameter NRMSE across the three PK parameters and were used in experiments thereafter. The Poisson disk SP was generated using SigPy package (https://github.com/mikgroup/sigpy).
2). Ablation Study of CRNN:
To demonstrate the effectiveness of CRNN for DCE MRI reconstruction, we next performed an ablation study to evaluate effects of recurrent connections in temporal and iteration dimensions in CRNN by removing each or both connections. The same training data, loss function, SP, and evaluation metrics were used as in Section C. 1).
3). Ablation Study of Learnable k-t Sharing:
The learnable k-t sharing was compared with fixed neighbor-frame sharing strategies [25] in which {0,2,4,6,8,10,12} neighbour-frames of a center frame were shared. The same training data, loss function, SP, and evaluation metrics were used as in Section C. 1).
4). Ablation Study of k-t Sampling Pattern Learning Module:
To demonstrate the benefit of k-t SP learning module, we removed it from the proposed framework, and used the fixed Poisson disk and uniform random samplings to train the network. The same training data, loss function, and evaluation metrics were used as in Section C. 1).
5). Weighting Parameter Optimization:
We optimized weighting parameter β in terms of the NRMSE of estimated PK parameters using the mcDRO with spatial resolution 1.56mm×1.56mm×1.56mm and temporal resolution 3s to search β in {0,0.01,0.1,0.3,0.7,1}. The optimized weighting parameter was used in the following experiments.
6). The Effect of Contrast Arrival Time Variation across Subjects:
One variation in the DCE signals across patients is the contrast arrival time (tCA), which needs to be tested for its effect on the network performance. Here, tCA was defined as the time when the DCE signal started rising from the baseline and calculated by the second time-derivative of the spatially averaged DCE signals, .
We first analyzed the tCA distribution in the training and testing datasets. Then, we aligned tCA to 35s for all data by shifting the DCE series along the time dimension. We compared performance of the model trained by the time shifted data but tested using the data with and without time shifting. This experiment was done under spatial resolution 1.56mm×1.56mm×1.56mm and temporal resolution 3s. The performance results were used to determine how to deal with the variation of contrast arrival time variation across subjects.
7). Comparison with Prior Works:
To demonstrate the advantages of joint optimization of k-t subsampling and reconstruction, we compared our method with two iterative dynamic MRI reconstruction methods. These two methods both explored spatiotemporal sparsity of dynamic MRI but did not optimize SPs, and instead used heuristic Poisson disk [46] and uniform random SPs. The first one is a dictionary learning-based indirect PK parameter estimation method [32] (DL) which was implemented based on open source code (https://github.com/sajanglingala/DCE_dictionary_recon). The ranges of PK parameters used for library learning were adjusted according to our data. As in the original paper, a population-based AIF was used in the test. The second method is a low-rank plus sparse model [21] (L+S) for which the open source code (https://github.com/JeffFessler/reproduce-l-s-dynamic-mri) is available. Proximal optimized gradient method (POGM) was used for optimization. We compared performances of the two methods with ours under different temporal resolutions of {2, 3, 4, 5}s and spatial resolution 1.56mm×1.56mm×1.56mm.
8). Evaluation Metrics:
The image reconstruction quality was measured using the structural similarity index measure (SSIM) and peak signal to noise ratio (PSNR) for different aspects of image similarity. The PSNR is calculated for each reconstructed slice as , where is the ground truth image time series. The PK parameter estimation accuracy was evaluated by NRMSE, defined as , where θi and stand for the ground truth and estimation of the ith parameter, respectively, and MSE(∙, ∙) represents mean squared error. The mean and standard deviation (SD) of the parameters were calculated across testing mcDROs. Bland-Altman analysis was performed to assess bias and uncertainty in reconstructed PK maps compared with ground truth.
IV. Results
A. CRNN network architecture hyperparameter optimization
In the grid search of nf and N of the CRNN architecture, nf=32 showed the best overall NRSMEs across three parameters, for which N=5 was better than 3 (Fig. 3).
Fig. 3.
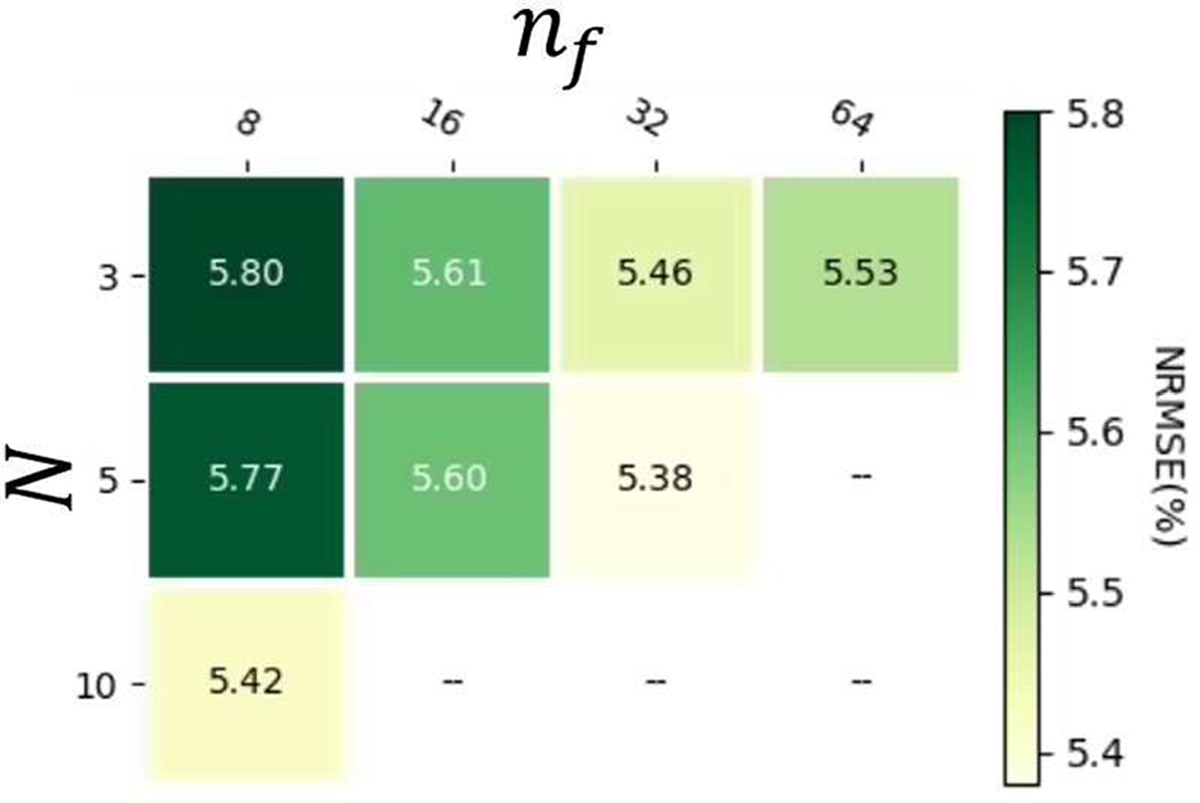
Grid search results of nf and N of the CRNN architecture. Blank blocks are due to the combinations of nf and N beyond the available GPU memory.
B. Ablation Study of CRNN
In the ablation study of the recurrent connections in the temporal and iteration dimensions in the CRNN, the temporal connections were crucial for the parameter reconstruction accuracy, and the iteration further reduced errors in the parameters, see NRMSEs in Table I.
TABLE I.
Mean NRMSEs of estimated PK parameters with (Y) or without (N) recurrent connections in temporal and iteration dimensions
| Temporal | Iteration | NRMSE (%) |
|---|---|---|
|
| ||
| Y | Y | 5.38 |
| N | N | 8.04 |
| Y | N | 5.61 |
| N | Y | 5.83 |
C. Ablation Study of Learnable k-t Sharing
The learned k-t sharing strategy was superior over fixed neighbor-frame sharing strategies in terms of NRMSEs of PK parameters (Fig. 4).
Fig. 4.
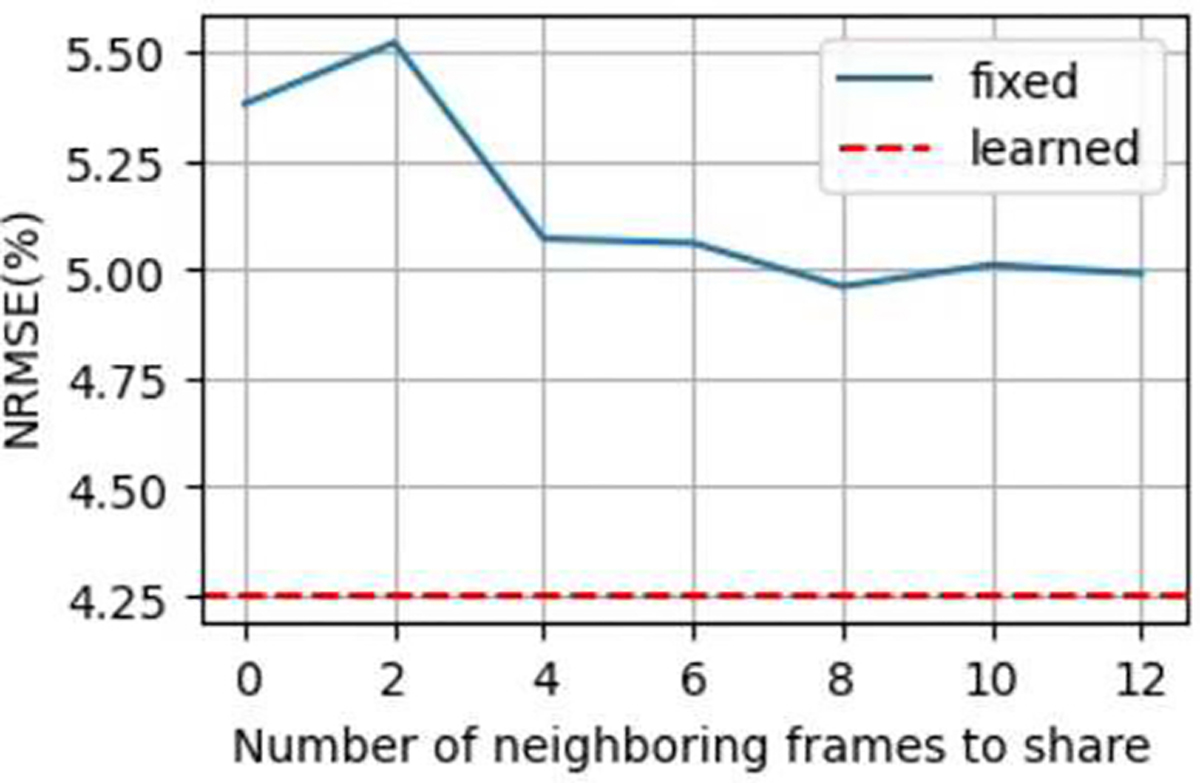
NRMSEs of PK parameter using fixed k-t sharing patterns (blue curve) over the number of shared neighboring frames. For comparison, NRMSE of learned k-t sharing is plotted as a red dashed line.
D. Ablation Study of k-t Sampling Pattern Learning Module
The learned k-t SP outperformed the fixed Poisson disk and uniform random samplings under the same CRNN reconstruction architecture in terms of NRMSEs of PK parameters (Table II).
TABLE II.
Mean NRMSEs of estimated PK parameters using the Poisson disk, uniform random, and learning-based samplings
| SP | NRMSE (%) |
|---|---|
|
| |
| Learned | 3.17 |
| Poisson | 4.69 |
| Uniform | 10.17 |
E. Weighting Parameter Optimization
Searching for the optimal weighting parameter β in {0,0.01,0.1,0.3,0.7,1} using the mcDRO yielded that β=0.1 had the best performance for PSNR of reconstructed images and NRMSE of PK parameters. The PSNR and SSIM of the reconstructed images and NRMSE of the estimated PK parameters of tested β values are shown in Table III. Note that when β = 1, where the loss function reduces to including the image loss l2 only and which was used commonly in deep learning-based reconstruction of MRI in the literature, the performance on image reconstruction was similar to β = 0.1 but the accuracy of estimated PK parameters was worse than β = 0.1. However, when β = 0, where the image loss was not included, both image quality and PK parameter estimation accuracy were worse than any β > 0 . In the subsequent experiments, the optimal weighting parameter was used.
TABLE III.
PSNR and SSIM (Mean ± σ) of reconstructed images and NRMSE of estimated PK parameters with different β values
| β | PSNR (dB) | SSIM | NRMSE (%) |
||
|---|---|---|---|---|---|
| Ktrans | kep | vp | |||
|
| |||||
| 0 | 24.66 ± 0.62 | 0.40 ± 0.01 | 3.75 ± 1.45 | 13.24 ± 5.76 | 16.76 ± 7.25 |
| 0.01 | 40.71 ± 0.39 | 0.89 ± 0.01 | 2.82 ± 1.50 | 7.72 ± 3.39 | 3.16 ± 1.57 |
| 0.1 | 41.55 ± 0.47 | 0.90 ± 0.00 | 1.92 ± 0.96 | 6.48 ± 2.69 | 2.55 ± 1.10 |
| 0.3 | 41.46 ± 0.48 | 0.90 ± 0.00 | 1.97 ± 1.02 | 6.82 ± 2.89 | 2.63 ± 1.10 |
| 0.7 | 41.22 ± 0.43 | 0.90 ± 0.01 | 2.49 ± 1.38 | 8.72 ± 4.19 | 3.53 ± 1.79 |
| 1 | 41.65 ± 0.51 | 0.91 ± 0.00 | 2.34 ± 1.50 | 7.46 ± 3.39 | 2.88 ± 1.62 |
F. The Effect of Contrast Arrival Time Variation across Subjects
Variations in tCA variations observed in both training and testing datasets, with tCA = 38.5 ± 3.6 in the training set and tCA = 40.5 ± 4.5 in the testing set. The proposed network trained using DCE data with the same tCA performed similarly well on testing data with the same tCA and different tCAs in terms of PK parameter NRMSEs (Table IV), indicating that the contrast arrival time differences among subjects did not have a significant effect on the PK parameter estimation accuracy for the proposed method.
TABLE IV.
The PK parameter estimation NRMSEs (Mean ± σ) of the proposed model trained on time shifted DCE data and tested on the data with and without time shifting
| Testing tCA | NRMSE (%) |
||
|---|---|---|---|
| Ktrans | kep | vp | |
|
| |||
| with | 2.16 ± 0.92 | 7.07 ± 2.88 | 3.08 ± 1.64 |
| without | 2.01 ± 0.91 | 6.94 ± 2.98 | 2.72 ± 1.14 |
G. Comparison with Prior Works under Different Temporal Resolutions
Based upon the results in Table IV, we trained the model using the data without time-shifting. The NRMSEs of the PK parameters estimated from the DCE data with different temporal resolutions and SPs by the proposed method compared to L+S and DL are summarized in Table V.
TABLE V.
PK parameter estimation NRMSEs (Mean ± σ) using the proposed method with learned sampling patterns (SP), L+S with Poisson disk and uniform random sampling, and DL with Poisson disk random sampling at Δt ∈ {2,3,4,5}s and corresponding R ∈ {50,34,25,20}
| Method | SP | Δt (s) | R | NRMSE (%) |
||
|---|---|---|---|---|---|---|
| Ktrans | kep | vp | ||||
|
| ||||||
| Proposed | Learned | 2 | 50 | 2.14 ± 1.01 | 6.71 ± 2.82 | 2.71 ± 1.21 |
| 3 | 34 | 1.92 ± 0.96 | 6.48 ± 2.69 | 2.55 ± 1.10 | ||
| 4 | 25 | 1.98 ± 0.90 | 6.46 ± 2.61 | 2.52 ± 1.05 | ||
| 5 | 20 | 2.21 ± 1.09 | 7.14 ± 3.13 | 3.77 ± 2.45 | ||
|
| ||||||
| L+S | Poisson | 2 | 50 | 3.40 ± 1.87 | 10.73 ± 4.35 | 7.74 ± 5.13 |
| 3 | 34 | 3.17 ± 1.75 | 10.22 ± 4.36 | 4.84 ± 2.15 | ||
| 4 | 25 | 3.03 ± 1.46 | 10.32 ± 4.37 | 4.88 ± 2.24 | ||
| 5 | 20 | 2.90 ± 1.17 | 10.62 ± 4.75 | 4.74 ± 2.12 | ||
|
| ||||||
| L+S | Uniform | 2 | 50 | 7.79 ± 7.00 | 12.62 ± 6.47 | 44.32 ± 20.80 |
| 3 | 34 | 6.45 ± 4.28 | 12.48 ± 6.32 | 41.79 ± 21.57 | ||
| 4 | 25 | 5.44 ± 4.08 | 12.76 ± 6.69 | 42.40 ± 19.59 | ||
| 5 | 20 | 6.59 ± 3.94 | 13.08 ± 6.29 | 23.56 ± 13.04 | ||
|
| ||||||
| DL | Poisson | 2 | 50 | 7.30 ± 3.57 | 10.57 ± 4.60 | 6.40 ± 2.43 |
| 3 | 34 | 7.31 ± 3.35 | 10.14 ± 4.30 | 6.51 ± 2.45 | ||
| 4 | 25 | 8.05 ± 4.29 | 10.21 ± 4.42 | 6.68 ± 2.59 | ||
| 5 | 20 | 8.02 ± 4.36 | 9.95 ± 4.25 | 6.90 ± 2.78 | ||
|
| ||||||
| DL | Uniform | 2 | 50 | 3.92 ± 1.66 | 13.46 ± 5.96 | 6.74 ± 2.83 |
| 3 | 34 | 4.10 ± 1.94 | 13.41 ± 5.95 | 6.75 ± 2.83 | ||
| 4 | 25 | 4.37 ± 2.33 | 13.15 ± 5.73 | 6.78 ± 2.86 | ||
| 5 | 20 | 4.44 ± 1.99 | 13.09 ± 5.81 | 6.80 ± 2.84 | ||
The proposed method consistently outperformed L+S and DL using both Poisson disk random sampling and uniform random sampling at all tested temporal resolutions by a factorof ~2 to 20 in NRMSE (%). The best performance achieved by the proposed method was at Δt=3s (R=34) for Ktrans and at Δt=4s (R=25) for kep and vp.
Examples of reconstructed PK images at temporal resolution of 2s of the proposed method, L+S using Poisson disk sampling, and DL using Poisson disk sampling as well as the ground truth PK maps are shown in Fig. 5. The proposed method generated the most perceptually similar PK maps to the ground truth maps and support the quantitative results. Note that the L+S method overestimated Ktrans and vp values and resulted in larger errors in kep estimation in this example slice. Also, the DL method showed overestimations in all three parameters.
Fig. 5.
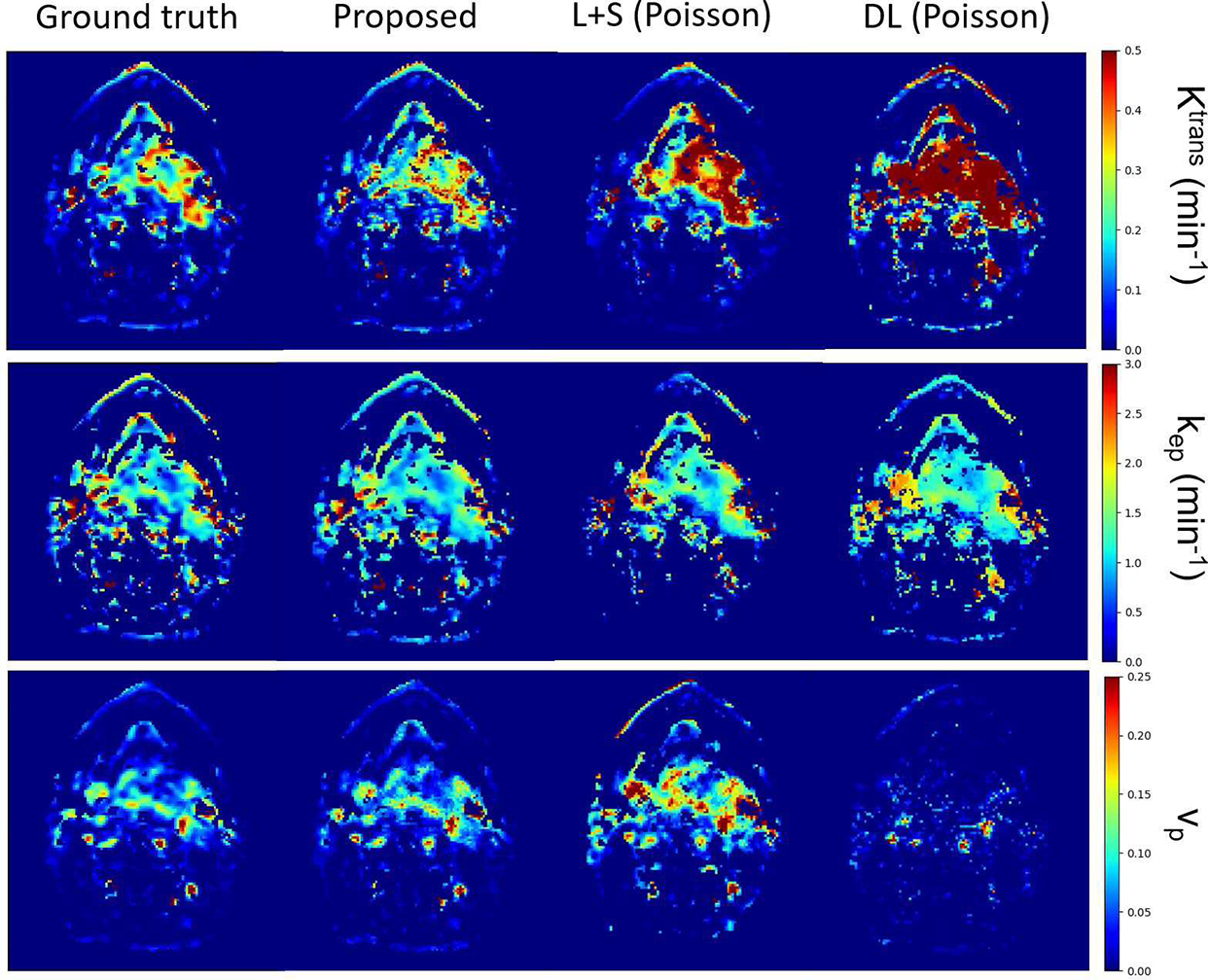
Example reconstructed PK parameter maps from one slice at temporal resolution of 2s (R =50) using the proposed method (second column), L+S with Poisson disk sampling (third column) and DL with Poisson disk sampling (forth column). The ground truth maps (first column) are also included for comparison.
The bias and uncertainty of the three PK parameters estimated from the DCE data at 2 s temporal resolution by the proposed method, L+S with Poisson disk sampling, and DL with Poisson disk sampling in gross tumor volumes of all 6 testing DROs are shown in the Bland-Altman plots in Fig. 6. For comparison, the plots of PK parameters estimated from fully sampled DCE data at the same temporal resolution were also included. The bias observed in the fully sampled data might be due to the added Gaussian noise [4], [41]. The proposed method showed comparable estimation bias and uncertainty to those from fully sampled DCE data, but reduced bias and uncertainty compared to DL and L+S methods. The proposed method improved the standard deviation of the PK parameter estimation errors by 0.10 (41%) and 0.19 (56%) compared to DL and L+S with Poisson disk sampling, respectively. A systematic bias on all three parameters was present in the L+S and DL methods.
Fig. 6.
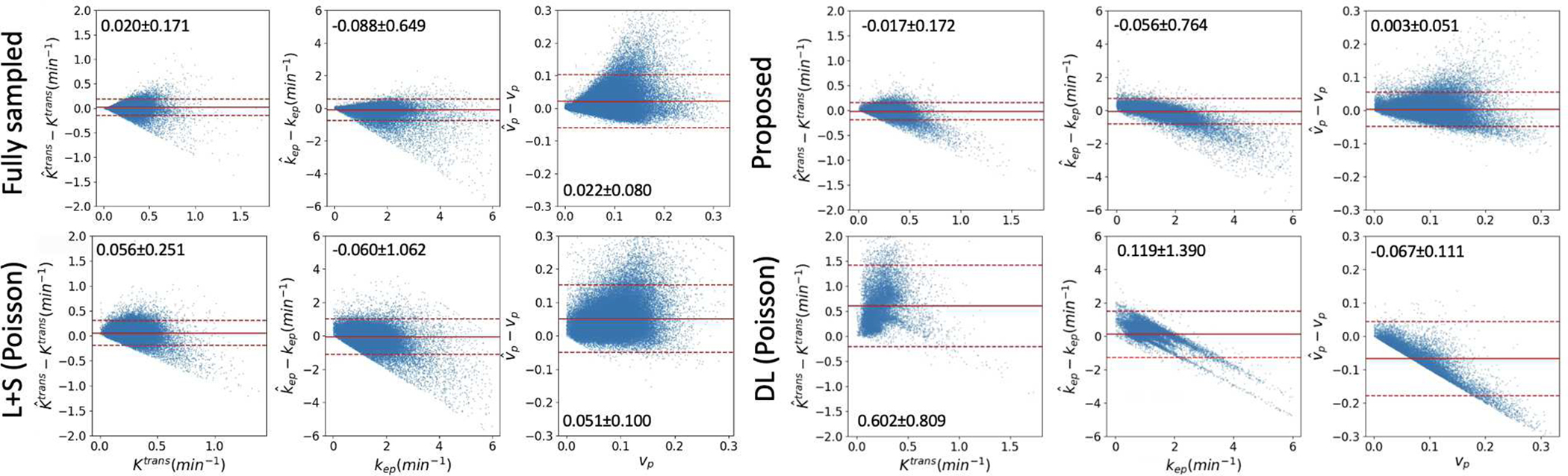
Bland-Altman plots of the difference between estimated , , and and reference values Ktrans, kep, and vp of fully sampled DCE data, the proposed method, L+S with Poisson disk sampling, and DL with Poisson disk sampling at temporal resolution of 2s (R=50). Each dot represents to one tumor voxel in 6 mcDROs. The mean and 1.96×SD were marked in each plot and represented by solid and dotted red lines, respectively.
The learned sampling probability maps and sampling masks at frame 20 and the ky-t plot of the central kx for the DCE temporal resolution Δt=2s compared to the Poisson disk and uniform random SPs are shown in Fig. 7. Note that the probabilities at the center of the k-space varied over the contrast uptake time course learned by the proposed method. The learned sampling mask had a lower sampling density in the k-space center than Poisson disk sampling.
Fig. 7.
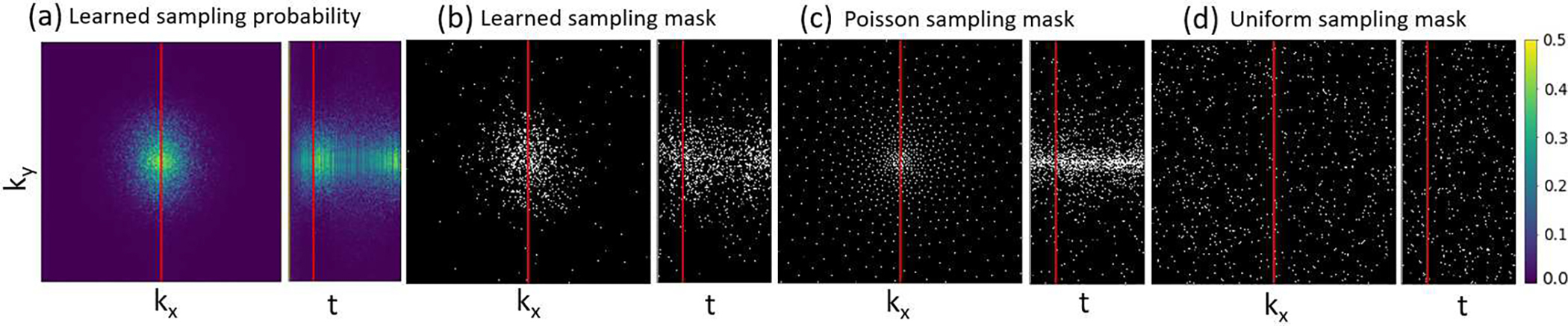
Illustration of learned phase encodings of kx vs ky at the 20th time frame and ky vs t at the central kx (respective left and right subpanels in each plot): (a) learned sampling probability maps by our method; (b) realization sampling masks by our method, (c) Poisson disk sampling masks, and (d) uniform random sampling masks. All maps were obtained at temporal resolution of 2s and R=50. White dots indicate locations of phase-encodings acquired in the kx-ky plane. Note that the first frame is fully sampled to provide baseline anatomy.
V. Discussions
In this work, we developed a deep learning-based framework to jointly optimize k-t SPs and image reconstruction for DCE MRI by minimizing a loss function including l2 errors of both image reconstruction and PK parameter estimation. A time series of sampling probability maps in the k-t space was optimally learned by the network to achieve rapid acquisition and accurate estimation of PK parameters. A PK parameter loss with optimal weighting, added into the objective function of image reconstruction, improved accuracy in the PK parameter estimation as well as quality of reconstructed images compared to using the image loss only. Overall, our proposed method performed superior and had reduced bias and uncertainty in the estimated PK parameters compared to two iterative dynamic MRI reconstruction methods. In addition, the proposed method was robust to patient-wise contrast arrival time variations. This method has the potential to increase spatial resolution of DCE MRI using a higher acceleration factor while providing accurate and precise PK parameter estimates. One possible extension of the current approach is to replace the LLSQ layer with a neural network that can simultaneously produce PK parameter estimations and corresponding uncertainties [47]. This may allow direct minimization of the uncertainty in PK parameters.
It is important to learn the optimal subsampling patten in the k-t space for dynamic image acquisition, instead of using a random SP following an assumed distribution, e.g., a Poisson distribution or uniform distribution of the k-space data. Similarly, temporal data sharing, although widely used in dynamic acquisitions, lacks optimization and is instead manually crafted [48], [49]. In this work, we extended LOUPE [33] to the time domain and added a TDoF to learn dynamic subsampling and data sharing in the k-t space. In the learned sampling probability maps, the sampling density near the k-space center was high during initial contrast uptake, but decreased over time, and then increased at the end of the temporal acquisition. This could be explained as the data near the k-space center are important to capture fast contrast dynamics for accurate estimation of PK parameters, and then became less important over the time course. Also, the spread of sampling probabilities in the k-space at the frames near the time course center could be due to fact that the spatiotemporal sparsity is well captured by the CRNN network. The increased density near the k-space center at the end of the acquisition could be because of the zero initializations of the hidden features of the BCRNN layer which may be removed by using learnable initializations.
We included the PK parameter loss in the objective for image reconstruction. The weighting of the PK parameter loss in the objective had a nonlinear effect on NRMSEs of estimated PK parameters [50]. We found that an optimal weighting between the image loss and parameter loss improved both image and PK parameter reconstruction qualities. While the image loss provided direct guidance on image reconstruction, the parameter loss distilled PK modeling knowledge that the image l2 loss might not be sensitive to in the model during training and in SP optimization. We observed that the sampling density was more concentrated in the k-space center when the model was trained with image loss only compared with that trained with combined image and parameter losses. This is possibly because the inclusion of parameter loss enabled the network to directly learn hemodynamics in the signal time courses that influence parameter maps, thereby sampling the k-space center less frequently.
In our comparison with two other methods under different temporal resolutions, we observed a nonlinear dependence of NRMSE on temporal resolutions, which could be due to the interplay of temporal resolution, signal to noise ratio (SNR) and SPs. While both high temporal resolution and SNR are beneficial for PK parameter estimation [4], [41], [51], in practice, there is usually a tradeoff between the two. The optimal temporal resolutions of 4s and 5s from the proposed method represented a balance of these factors. The AIF could be another factor contributing to the accuracy of PK parameter estimation [40]. Note that the proposed and L+S methods extracted patient-specific AIFs from the reconstructed images, while the DL method used a population-based AIF for PK parameter estimation which might contribute to, at least in part, the high bias observed in the Bland-Altman plot [52]. We also observed a generally higher instability in kep compared with Ktrans and vp as demonstrated in the corresponding NRMSEs (Table 4), which is consistent with prior reports [4].
In this work, the proposed method was validated using realistic multi-coil complex DROs to demonstrate its ability to reduce PK parameter estimation bias and uncertainty compared with iterative reconstruction methods using non-data driven SPs. One limitation of the current mcDROs simulation is that the real data was acquired using view sharing techniques at Δt=3s, which might reduce the temporal high frequency information in the subsequently derived AIFs used in the simulation for mcDROs at higher temporal resolutions (Δt<3s). High temporal resolution DCE MRI sequences [53], [54] could be utilized to create mcDROs at higher temporal resolutions in future works. Validating the proposed method in prospective studies in future investigations is also warranted. To facilitate these studies, realistic factors such as motion and native T1 can be easily incorporated into training data to make the network robust to these factors present in real scans. In future prospective studies, the learned SPs can be implemented as 2D phase encoding locations in a 3D T1 weighted spoiled gradient echo sequence without changing other sequence parameters. One of the challenges in applying the proposed method to prospective studies is that the timing of the contrast arrival may vary from patient to patient even with the same contrast injection timing due to patient-specific factors such as cardiac output [55]. This may cause the SPs trained with a specific contrast arrival timing to fail in fully capturing the contrast dynamics information, which may result in uncertainty in PK parameter estimation. Our simulation of clinically measured variations in mcDROs demonstrated that small variations normally encountered in clinical scans had almost no impact on the PK parameter NRMSEs. This demonstrates the apparent robustness of the network to the normal variations in contrast arrival times expected in clinical DCE MRI scans of the neck region. Direct estimation of PK parameters from k-t space data has shown promise for parameter reconstruction in DCE MRI [17], [20]. An interesting direction of future works will be to incorporate data-driven priors into these approaches by extending the proposed framework to direct PK parameter reconstruction.
VI. Conclusions
We have presented a jointly optimization framework for head and neck DCE MRI k-t SP and image reconstruction with a combined objective of image reconstruction quality and PK parameter estimation accuracy. Optimization of the k-t SP by learning the sparsity in the dynamic contrast enhanced images seems to enable a dramatic reduction in the k-space sampling to achieve accurate PK parameter estimations including in tumor regions. The proposed framework is general and can be applied to other quantitative MRI application, such as T1, T2, and apparent diffusion coefficient quantification, to improve the scan efficiency. Future study is warranted to validate the proposed method in in vivo experiments.
APPENDIX
A. Examples of Reconstructed Images and Time Courses of DCE Signals
Considering that DCE image series cannot be easily analyzed and comprehended by human brains, it is desirable to directly output parametric maps from a dynamic scan and omit intermediate reconstructed dynamic image series. Therefore, we optimized quality of parametric maps in this study. However, our proposed method resulted in more faithful reconstructed images and time courses of dynamic signals than DL and L+S methods (Fig. 8).
Fig. 8.
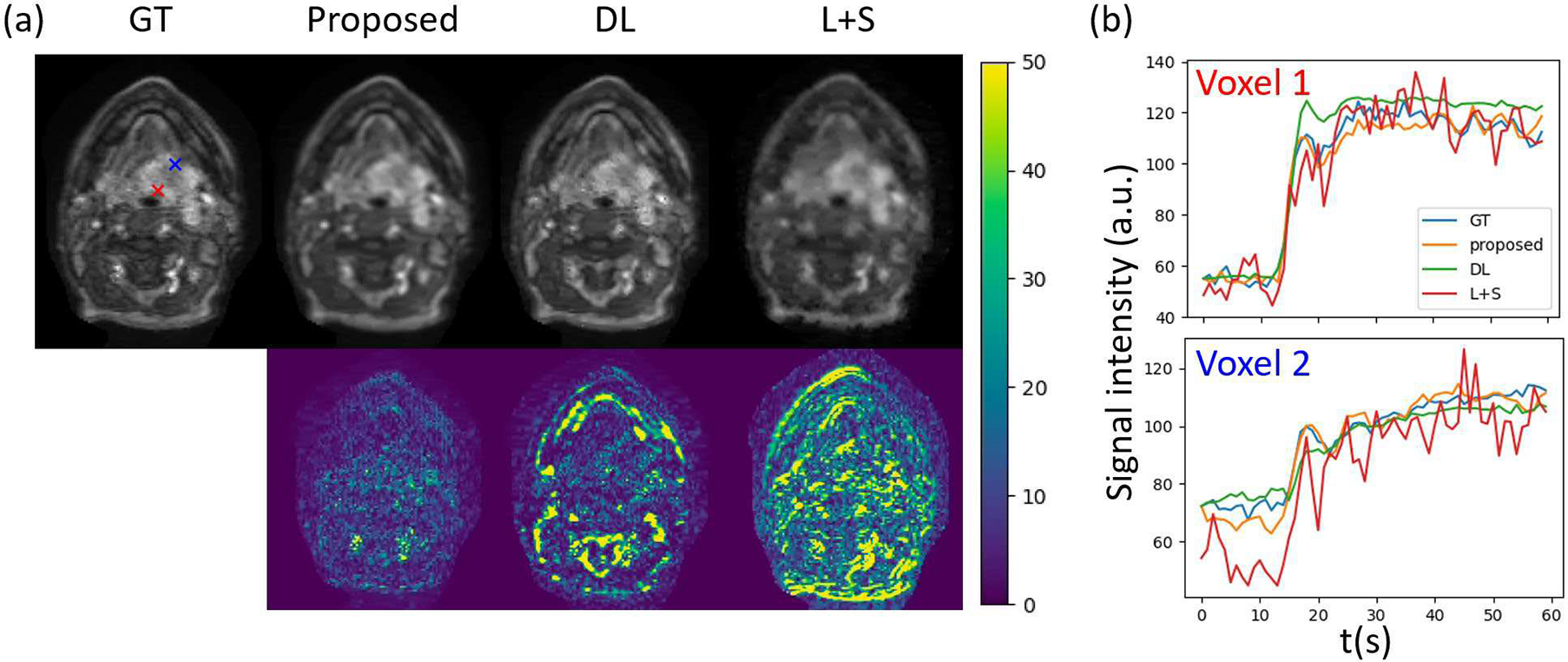
(a) Example reconstructed images at the 30th frame by different methods (first row) and their corresponding error maps (second row). (b) Time courses of dynamic signals at two example voxels within the tumor region reconstructed by different methods. The two voxels are marked by red and blue crosses in the Ground truth (GT) image in (a). In these examples, we used spatial resolution of 1.56×1.56×1.5mm and temporal resolution of 3s in mcDROs. Note large deviations and fluctuations in the DCE signals generated by DL and L+S methods, respectively.
B. Adaptation of the Learnable SPs to Specific Anatomies
The learned sampling probability maps depend upon trained DCE signals and anatomies, see Fig. 9. Note that different patterns were yielded from training on DCE time-series from different anatomic regions ((a) brain+neck, and (b) brain). Also, full width half maximums (FWHMs) of the probability density projections were different in kx and ky dimensions between anatomic regions. In contrast, empirical sampling patterns are one for all, which omit spatial sparsity and are not optimized for anatomy.
Fig. 9.
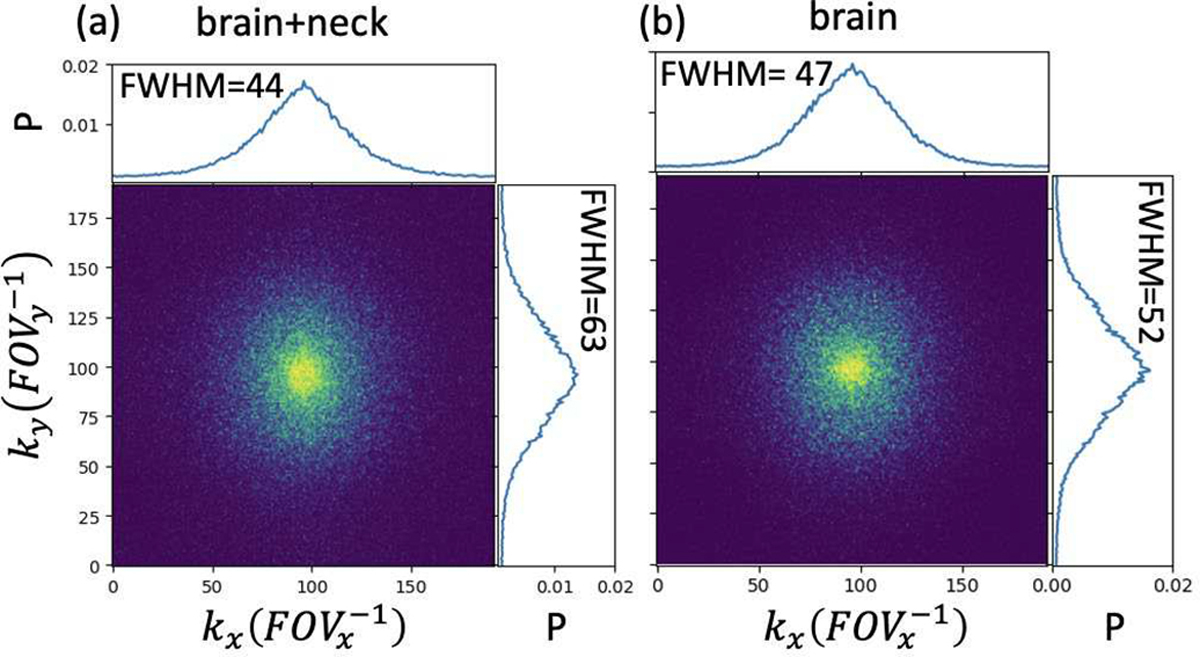
Learned sampling probability maps at the 30th frame trained with (a) full mcDROs including brain and neck slices and (b) brain slices only. Projections of the probability densities on the kx and ky dimensions are shown in the top and right plots of each probability map. The full width half maximum (FWHM) of each projection is shown in the top left corner of the plot. mcDROs with spatial resolution of 1.56×1.56×1.56mm and temporal resolution of 3s were used. GT=Ground truth; P=Probability; FOV=Field of view.
Contributor Information
Jiaren Zou, Department of Radiation Oncology, and the Department of Biomedical Engineering, University of Michigan, Ann Arbor, MI 48109, USA.
Yue Cao, Department of Radiation Oncology, the Department of Biomedical Engineering, and the Department of Radiology, University of Michigan, Ann Arbor, MI 48109, USA.
References
- [1].Vishwanath V, Jafarieh S, and Rembielak A, “The role of imaging in head and neck cancer: An overview of different imaging modalities in primary diagnosis and staging of the disease,” J. Contemp. Brachytherapy, vol. 12, no. 5, pp. 512–518, 2020, doi: 10.5114/jcb.2020.100386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Bisdas S, Baghi M, Wagenblast J, Vogl TJ, Choon HT, and Tong SK, “Gadolinium-enhanced echo-planar T2-weighted MRI of tumors in the extracranial head and neck: Feasibility study and preliminary results using a distributed-parameter tracer kinetic analysis,” J. Magn. Reson. Imaging, vol. 27, no. 5, pp. 963–969, 2008, doi: 10.1002/jmri.21311. [DOI] [PubMed] [Google Scholar]
- [3].Cao Y et al. , “Early Prediction of Outcome in Advanced Head-and-Neck Cancer Based on Tumor Blood Volume Alterations During Therapy: A Prospective Study,” Int. J. Radiat. Oncol. Biol. Phys, vol. 72, no. 5, pp. 1287–1290, Dec. 2008, doi: 10.1016/j.ijrobp.2008.08.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Cao Y, Li D, Shen Z, and Normolle D, “Sensitivity of Quantitative Metrics Derived from DCE MRI and a Pharmacokinetic Model to Image Quality and Acquisition Parameters,” Acad. Radiol, vol. 17, no. 4, pp. 468–478, Apr. 2010, doi: 10.1016/j.acra.2009.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Aryal MP et al. , “Real-time quantitative assessment of accuracy and precision of blood volume derived from dce-mri in individual patients during a clinical trial,” Tomography, vol. 5, no. 1, pp. 61–67, 2019, doi: 10.18383/j.tom.2018.00029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Griswold MA et al. , “Generalized Autocalibrating Partially Parallel Acquisitions (GRAPPA),” Magn. Reson. Med, vol. 47, no. 6, pp. 1202–1210, 2002, doi: 10.1002/mrm.10171. [DOI] [PubMed] [Google Scholar]
- [7].Van Vaals JJ et al. , “‘Keyhole’ method for accelerating imaging of contrast agent uptake,” J. Magn. Reson. Imaging, vol. 3, no. 4, pp. 671–675, 1993, doi: 10.1002/jmri.1880030419. [DOI] [PubMed] [Google Scholar]
- [8].Lim RP et al. , “3D time-resolved MR angiography (MRA) of the carotid arteries with time-resolved imaging with stochastic trajectories: Comparison with 3D contrast-enhanced bolus-chase MRA and 3D time-of-flight MRA,” Am. J. Neuroradiol., vol. 29, no. 10, pp. 1847–1854, 2008, doi: 10.3174/ajnr.A1252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Feng L et al. , “Golden-angle radial sparse parallel MRI: combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI,” Magn. Reson. Med, vol. 72, no. 3, pp. 707–717, 2014, doi: 10.1002/mrm.24980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Zhu Y, Guo Y, Lingala SG, Lebel RM, Law M, and Nayak KS, “GOCART: GOlden-angle CArtesian randomized time-resolved 3D MRI,” Magn. Reson. Imaging, vol. 34, no. 7, pp. 940–950, 2016, doi: 10.1016/j.mri.2015.12.030. [DOI] [PubMed] [Google Scholar]
- [11].Song T et al. , “Optimal k-space sampling for dynamic contrast-enhanced MRI with an application to MR renography,” Magn. Reson. Med, vol. 61, no. 5, pp. 1242–1248, 2009, doi: 10.1002/mrm.21901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Knoll F, Clason C, Diwoky C, and Stollberger R, “Adapted random sampling patterns for accelerated MRI,” Magn. Reson. Mater. Physics, Biol. Med., vol. 24, no. 1, pp. 43–50, 2011, doi: 10.1007/s10334-010-0234-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Choi J and Kim H, “Implementation of time-efficient adaptive sampling function design for improved undersampled MRI reconstruction,” J. Magn. Reson, vol. 273, pp. 47–55, 2016, doi: 10.1016/j.jmr.2016.10.006 [DOI] [PubMed] [Google Scholar]
- [14].Gözcü B et al. , “Learning-Based Compressive MRI,” IEEE Trans. Med. Imaging, vol. 37, no. 6, pp. 1394–1406, Jun. 2018, doi: 10.1109/TMI.2018.2832540. [DOI] [PubMed] [Google Scholar]
- [15].Zibetti MVW, Herman GT, and Regatte RR, “Fast Data-Driven Learning of MRI Sampling Pattern for Large Scale Problems,” Sci. Rep, no. 0123456789, pp. 1–19, 2020, doi: 10.1038/s41598-021-97995-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Sherry F et al. , “Learning the Sampling Pattern for MRI,” IEEE Trans. Med. Imaging, vol. 39, no. 12, pp. 4310–4321, 2020, doi: 10.1109/TMI.2020.3017353. [DOI] [PubMed] [Google Scholar]
- [17].Bliesener Y, Lingala SG, Haldar JP, and Nayak KS, “Impact of (k,t) sampling on DCE MRI tracer kinetic parameter estimation in digital reference objects,” Magn. Reson. Med, vol. 83, no. 5, pp. 1625–1639, 2020, doi: 10.1002/mrm.28024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Guo Y, Lingala SG, Bliesener Y, Lebel RM, Zhu Y, and Nayak KS, “Joint arterial input function and tracer kinetic parameter estimation from undersampled dynamic contrast-enhanced MRI using a model consistency constraint,” Magn. Reson. Med, vol. 79, no. 5, pp. 2804–2815, 2018, doi: 10.1002/mrm.26904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Lingala SG et al. , “Tracer kinetic models as temporal constraints during brain tumor DCE‐MRI reconstruction,” Med. Phys, vol. 47, no. 1, pp. 37–51, Jan. 2020, doi: 10.1002/mp.13885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Guo Y, Lingala SG, Zhu Y, Lebel RM, and Nayak KS, “Direct estimation of tracer-kinetic parameter maps from highly undersampled brain dynamic contrast enhanced MRI,” Magn. Reson. Med, vol. 78, no. 4, pp. 1566–1578, Oct. 2017, doi: 10.1002/mrm.26540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Lin CY and Fessler JA, “Efficient Dynamic Parallel MRI Reconstruction for the Low-Rank Plus Sparse Model,” IEEE Trans. Comput. Imaging, vol. 5, no. 1, pp. 17–26, 2018, doi: 10.1109/tci.2018.2882089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Qin C, Schlemper J, Hammernik K, Duan J, Summers RM, and Rueckert D, “Deep Network Interpolation for Accelerated Parallel MR Image Reconstruction,” vol. 2, pp. 1–6, 2020, [Online]. Available: http://arxiv.org/abs/2007.05993. [Google Scholar]
- [23].Aggarwal HK, Mani MP, and Jacob M, “MoDL: Model-Based Deep Learning Architecture for Inverse Problems,” IEEE Trans. Med. Imaging, vol. 38, no. 2, pp. 394–405, 2019, doi: 10.1109/TMI.2018.2865356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Aggarwal HK and Jacob M, “J-MoDL: Joint Model-Based Deep Learning for Optimized Sampling and Reconstruction,” IEEE J. Sel. Top. Signal Process, vol. 14, no. 6, pp. 1151–1162, Oct. 2020, doi: 10.1109/JSTSP.2020.3004094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Schlemper J, Caballero J, Hajnal JV, Price AN, and Rueckert D, “A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction,” IEEE Trans. Med. Imaging, vol. 37, no. 2, pp. 491–503, 2018, doi: 10.1109/TMI.2017.2760978. [DOI] [PubMed] [Google Scholar]
- [26].Hammernik K et al. , “Learning a variational network for reconstruction of accelerated MRI data,” Magn. Reson. Med, vol. 79, no. 6, pp. 3055–3071, 2018, doi: 10.1002/mrm.26977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Qin C, Schlemper J, Caballero J, Price A, Hajnal JV, and Rueckert D, “Convolutional Recurrent Neural Networks for Dynamic MR Image Reconstruction,” IEEE Trans. Med. Imaging, vol. 38, no. 1, pp. 280–290, Dec. 2017, doi: 10.1109/TMI.2018.2863670. [DOI] [PubMed] [Google Scholar]
- [28].Qin C et al. , “k-t NEXT: Dynamic MR Image Reconstruction Exploiting Spatio-Temporal Correlations,” Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), vol. 11765 LNCS, pp. 505–513, 2019, doi: 10.1007/978-3-030-32245-8_56. [DOI] [Google Scholar]
- [29].Bahadir CD, Wang AQ, Dalca AV, and Sabuncu MR, “Deep-Learning-Based Optimization of the Under-Sampling Pattern in MRI,” IEEE Trans. Comput. Imaging, vol. 6, pp. 1139–1152, 2020, doi: 10.1109/TCI.2020.3006727. [DOI] [Google Scholar]
- [30].Zhang J et al. , “Extending LOUPE for K-space Under-sampling Pattern Optimization in Multi-coil MRI,” pp. 1–11, 2020, [Online]. Available: http://arxiv.org/abs/2007.14450. [Google Scholar]
- [31].Weiss T, Senouf O, Vedula S, Michailovich O, Zibulevsky M, and Bronstein A, “PILOT: Physics-Informed Learned Optimized Trajectories for Accelerated MRI,” pp. 1–23, 2019, [Online]. Available: http://arxiv.org/abs/1909.05773. [Google Scholar]
- [32].Lingala SG et al. , “Tracer Kinetic Models as Temporal Constraints during DCE-MRI reconstruction,” 2017, [Online]. Available: http://arxiv.org/abs/1707.07569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Bahadir CD, Dalca AV, and Sabuncu MR, “Learning-Based Optimization of the Under-Sampling Pattern in MRI,” Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), vol. 11492 LNCS, pp. 780–792, 2019, doi: 10.1007/978-3-030-20351-1_61. [DOI] [Google Scholar]
- [34].Qin C, Schlemper J, Caballero J, Price AN, Hajnal JV, and Rueckert D, “Convolutional Recurrent Neural Networks for Dynamic MR Image Reconstruction,” IEEE Trans. Med. Imaging, vol. 38, no. 1, pp. 280–290, Jan. 2019, doi: 10.1109/TMI.2018.2863670. [DOI] [PubMed] [Google Scholar]
- [35].Wang C, Yin FF, Kirkpatrick JP, and Chang Z, “Accelerated Brain DCE-MRI Using Iterative Reconstruction With Total Generalized Variation Penalty for Quantitative Pharmacokinetic Analysis: A Feasibility Study,” Technol. Cancer Res. Treat, vol. 16, no. 4, pp. 446–460, 2017, doi: 10.1177/1533034616649294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Lingala SG, Hu Y, Dibella E, and Jacob M, “Accelerated dynamic MRI exploiting sparsity and low-rank structure: K-t SLR,” IEEE Trans. Med. Imaging, vol. 30, no. 5, pp. 1042–1054, May 2011, doi: 10.1109/TMI.2010.2100850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Schlemper J et al. , “Data consistency networks for (calibration-less) accelerated parallel MR image reconstruction,” vol. 1, pp. 2–7, 2019, [Online]. Available: http://arxiv.org/abs/1909.11795. [Google Scholar]
- [38].Tao X, Gao H, Shen X, Wang J, and Jia J, “Scale-Recurrent Network for Deep Image Deblurring,” in 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Jun. 2018, pp. 8174–8182, doi: 10.1109/CVPR.2018.00853. [Google Scholar]
- [39].Tofts PS, “Modeling tracer kinetics in dynamic Gd-DTPA MR imaging,” J. Magn. Reson. Imaging, vol. 7, no. 1, pp. 91–101, Jan. 1997, doi: 10.1002/jmri.1880070113. [DOI] [PubMed] [Google Scholar]
- [40].Singh A, Rathore RKS, Haris M, Verma SK, Husain N, and Gupta RK, “Improved bolus arrival time and arterial input function estimation for tracer kinetic analysis in DCE-MRI,” J. Magn. Reson. Imaging, vol. 29, no. 1, pp. 166–176, Jan. 2009, doi: 10.1002/jmri.21624. [DOI] [PubMed] [Google Scholar]
- [41].Murase K, “Efficient method for calculating kinetic parameters using T1-weighted dynamic contrast-enhanced magnetic resonance imaging,” Magn. Reson. Med, vol. 51, no. 4, pp. 858–862, Apr. 2004, doi: 10.1002/mrm.20022. [DOI] [PubMed] [Google Scholar]
- [42].Kim MM et al. , “Developing a Pipeline for Multiparametric MRI-Guided Radiation Therapy: Initial Results from a Phase II Clinical Trial in Newly Diagnosed Glioblastoma,” Tomogr. (Ann Arbor, Mich.), vol. 5, no. 1, pp. 118–126, 2019, doi: 10.18383/j.tom.2018.00035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Uecker M et al. , “ESPIRiT - An eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA,” Magn. Reson. Med, vol. 71, no. 3, pp. 990–1001, 2014, doi: 10.1002/mrm.24751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Zhang T, Pauly JM, Vasanawala SS, and Lustig M, “Coil compression for accelerated imaging with Cartesian sampling,” Magn. Reson. Med, vol. 69, no. 2, pp. 571–582, 2013, doi: 10.1002/mrm.24267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Kingma DP and Ba JL, “Adam: A method for stochastic optimization,” Dec. 2015, [Online]. Available: http://arxiv.org/abs/1412.6980. [Google Scholar]
- [46].Bridson R, “Fast poisson disk sampling in arbitrary dimensions,” ACM SIGGRAPH 2007 Sketches, SIGGRAPH’07, p. 2006, 2007, doi: 10.1145/1278780.1278807. [DOI] [Google Scholar]
- [47].Bliesener Y, Acharya J, and Nayak KS, “Efficient DCE-MRI Parameter and Uncertainty Estimation Using a Neural Network,” IEEE Trans. Med. Imaging, vol. 39, no. 5, pp. 1712–1723, 2020, doi: 10.1109/TMI.2019.2953901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Levine E, Daniel B, Vasanawala S, Hargreaves B, and Saranathan M, “3D Cartesian MRI with compressed sensing and variable view sharing using complementary poisson-disc sampling,” Magn. Reson. Med, vol. 77, no. 5, pp. 1774–1785, 2017, doi: 10.1002/mrm.26254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Le Y, Kroeker R, Kipfer HD, and Lin C, “Development and evaluation of TWIST Dixon for dynamic contrast-enhanced (DCE) MRI with improved acquisition efficiency and fat suppression,” J. Magn. Reson. Imaging, vol. 36, no. 2, pp. 483–491, 2012, doi: 10.1002/jmri.23663. [DOI] [PubMed] [Google Scholar]
- [50].Ulas C et al. , “Direct Estimation of Pharmacokinetic Parameters from DCE-MRI using Deep CNN with Forward Physical Model Loss,” vol. 11070 LNCS, pp. 39–47, Apr. 2018, doi: 10.1007/978-3-030-00928-1_5. [DOI] [Google Scholar]
- [51].Zou J, Balter JM, and Cao Y, “Estimation of pharmacokinetic parameters from DCE-MRI by extracting long and short time-dependent features using an LSTM network,” Med. Phys, vol. c, pp. 1–11, 2020, doi: 10.1002/mp.14222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Port RE, Knopp MV, and Brix G, “Dynamic contrast-enhanced MRI using Gd-DTPA: Interindividual variability of the arterial input function and consequences for the assessment of kinetics in tumors,” Magn. Reson. Med, vol. 45, no. 6, pp. 1030–1038, 2001, doi: 10.1002/mrm.1137. [DOI] [PubMed] [Google Scholar]
- [53].Georgiou L, Wilson DJ, Sharma N, Perren TJ, and Buckley DL, “A functional form for a representative individual arterial input function measured from a population using high temporal resolution DCE MRI,” Magn. Reson. Med, vol. 81, no. 3, pp. 1955–1963, Mar. 2019, doi: 10.1002/mrm.27524. [DOI] [PubMed] [Google Scholar]
- [54].Park JS, Lim E, Choi SH, Sohn CH, Lee J, and Park J, “Model-Based High-Definition Dynamic Contrast Enhanced MRI for Concurrent Estimation of Perfusion and Microvascular Permeability,” Med. Image Anal, vol. 59, p. 101566, 2020, doi: 10.1016/j.media.2019.101566. [DOI] [PubMed] [Google Scholar]
- [55].Ashton E, Raunig D, Ng C, Kelcz F, McShane T, and Evelhoch J, “Scan-rescan variability in perfusion assessment of tumors in MRI using both model and data-derived arterial input functions,” J. Magn. Reson. Imaging, vol. 28, no. 3, pp. 791–796, Sep. 2008, doi: 10.1002/jmri.21472. [DOI] [PubMed] [Google Scholar]


