Abstract
Heparins and heparan sulfate polysaccharides are negatively charged glycosaminoglycans and play important roles in cell-to-matrix and cell-to-cell signaling processes. Metal ion binding to heparins alters the conformation of heparins and influences their function. Various experimental techniques have been used to investigate metal ion-heparin interactions, frequently with inconsistent results. Exploiting the quadrupolar 23Na nucleus, we herein develop a 23Na NMR-based competition assay and monitor the binding of divalent Ca2+ and Mg2+ and trivalent Al3+ metal ions to sodium heparin and the consequent release of sodium ions from heparin. The 23Na spin relaxation rates and translational diffusion coefficients are utilized to quantify the metal ion-induced release of sodium ions from heparin. In the case of the Al3+ ion, the complementary approach of 27Al quadrupolar NMR is employed as a direct probe of ion binding to heparin. Our NMR results demonstrate at least two metal ion-binding sites with different affinities on heparin, potentially undergoing dynamic exchange. For the site with lower metal ion binding affinity, the order of Ca2+ > Mg2+ > Al3+ is obtained, in which even the weakly binding Al3+ ion is capable of displacing sodium ions from heparin. Overall, the multinuclear quadrupolar NMR approach employed here can monitor and quantify metal ion binding to heparin and capture different modes of metal ion-heparin binding.
Keywords: metal, sodium, heparin, NMR, diffusion, relaxation, quadrupolar nuclei
1. Introduction
Heparins and heparan sulfate polysaccharides are polydisperse linear glycosaminoglycans (GAGs) composed of repeating disaccharide units of D-glucosamine and uronic acid residues. The O- and N-sulfation of these disaccharide units lead to the high negative charge of these GAGs (Scheme 1) [1]. Heparins are commonly found in the granules of mast cells, and heparan sulfates are ubiquitously present in the extracellular matrix of a wide variety of animal tissues and organs [2,3]. These polyanionic GAGs interact with a diverse array of biomolecular and biological targets, including extracellular matrix and cell surface components, growth factors, proteases, protease inhibitors, and various pathogens [4,5,6]. They play significant roles in many pathophysiological processes, such as cell-to-cell and cell-to-matrix signaling, inflammation, cellular growth and differentiation, angiogenesis, blood coagulation, and host defense against pathogens [5,7,8]. In recent years, the pharmacological application of heparin and heparin-like GAGs has extended from their classic use as anti-coagulant and anti-thrombotic agents to potential anti-inflammation, neuroprotective, antiviral, and anti-cancer therapeutics [1,9,10].
Scheme 1.
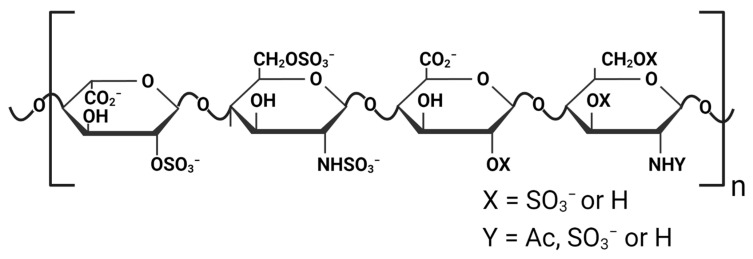
Chemical structure of heparin is shown as an example by two disaccharide units: the left disaccharide unit composed of 2-O-sulfated iduronic acid and 2-N- and 6-O-sulfated glucosamine, and the right disaccharide unit composed of glucuronic acid (with or without 2-O-sulfation) and glucosamine (with or without 2-N-acetylation or sulfation or 6-O-sulfation). Created with Biorender.com.
Due to the high concentration of negatively charged sulfate and carboxylate groups, heparin molecules exhibit high binding affinity to positively charged metal ions. It has been shown that heparin binds to monovalent cations such as Na+ and K+, divalent cations such as Ca2+ and Mg2+, and trivalent cations such as Al3+, among others [11]. Heparins can serve as a reservoir of metal ions in the extracellular environment and regulate metal ion-dependent biomolecular activities [12]. In addition, the binding of heparin to metal ions can alter the three-dimensional structure of heparin, hence modulating its interaction with various biomolecular targets [10,12,13].
The binding of metal ions to heparin has been previously studied through techniques such as infrared spectroscopy, atomic absorption, circular dichroism, optical polarimetry, NMR spectroscopy, and potentiometric titration [11,14,15,16]. These techniques require different sample conditions and are sensitive to various aspects of metal ion-heparin binding; hence the results have frequently been inconsistent. Here, we employ NMR spectroscopy, specifically 23Na NMR relaxation and diffusion methods, to investigate metal ion binding to sodium heparin through competition-based assays. The 23Na NMR has been used to study sodium ion binding to various biological macromolecules, including heparin [16,17]. More recently, it has been demonstrated that 23Na NMR, along with 35Cl and 17O NMR, can serve as a sensitive proxy to monitor ions and water dynamics in highly concentrated and crowded aqueous solutions and confined environments [18,19,20,21,22]. 23Na has a natural abundance of about 100% and a gyromagnetic ratio of 11.262 MHz.T−1, which is around 0.26 of 1H nuclei [23]. As a result, 23Na is a fairly sensitive nucleus in NMR experiments. It has a spin quantum number of 3/2 with a quadrupole moment (Q) of +0.104 Barn [24], which indicates a rather strong quadrupolar relaxation provided that there is a sizeable electric field gradient at the site of 23Na nuclei. Consequently, the 23Na NMR signals of sodium-containing complexes are often severely broadened due to the large electric field gradient and the resultant efficient quadrupolar relaxation [25,26]. This is the case for sodium heparin where the positively charged 23Na ions are bound through ionic interaction with the negatively charged sulfate and carboxylate groups. On the other hand, the hydrated sodium ions in aqueous solutions experience a nearly symmetrical electric environment with a near-zero electric field gradient and therefore possess a low quadrupolar relaxation rate and can lead to relatively narrow 23Na NMR signals [18,23]. Exploiting the difference in NMR behavior of heparin-bound sodium and free hydrated sodium ions, we determine the relative heparin-binding affinity of divalent cations Ca2+ and Mg2+, as well as the trivalent cation Al3+. In the latter case, we combine 23Na NMR with 27Al NMR measurements and simultaneously monitor the binding of Al3+ ions to heparin and the resultant release of Na+ ions from heparin. Our results demonstrate the presence of more than one metal ion-binding site on heparin and determine the order of binding affinity for the studied ions. More generally, this study highlights multinuclear quadrupolar NMR’s potential in quantifying metal ion binding to heparins and distinguishing various modes of binding.
2. Results
To begin with, a brief overview of the theory of 23Na NMR relaxation in solution is presented. As a quadrupolar nucleus, the NMR relaxation of spin-3/2 23Na is dominated by a quadrupolar relaxation mechanism. Energy fluctuations in the system cause quadrupolar NMR relaxation due to the anisotropic interaction between the electric quadrupole moment of the nucleus (eQ) and the electric field gradient (EFG) tensor present at the site of nuclei. The rate of quadrupolar relaxation is determined by the magnitude and timescale of fluctuations in the energy of this anisotropic interaction, mainly caused by stochastic rotational motions of molecules in solution and their associated EFG tensors. According to Redfield’s theory, the quadrupolar relaxation of a spin-3/2 nucleus is generally governed by a bi-exponential relaxation process where the low and high relaxation rates correspond respectively to the central transition () and one pair of satellite transitions (). However, if the rotational correlation time, τc, is much smaller than 1/ω0 (ω0, Larmor frequency of 23Na in rad. s−1, 1.5 ns in our study), the two relaxation rates of 23Na nuclei become identical, and a mono-exponential relaxation process is recovered. Consequently, under this so-called fast “extreme-narrowing” regime, the 23Na signal line shape becomes single-Lorentzian, and the 23Na longitudinal spin-lattice and transverse spin-spin relaxation times, T1 and T2, respectively, are identical, independent of ω0 (as long as it remains within the extreme-narrowing regime), and inversely proportional to τc. The 23Na relaxation times can therefore represent the rotational mobility of sodium ions in this regime. On the other hand, in the “slow motion” regime where or larger, the central and satellite transitions will experience distinct T1 and T2 relaxation times, which are field-dependent through dependence on spectral densities J(ω0) and J(2ω0). Due to different T2 relaxation times for the two central and satellite transitions, the 23Na signal line shape becomes double-Lorentzian. When increases due to an increase in ω0 and/or τc, the two T1 relaxation times decrease until they reach their minimum values and then monotonously increase afterward. The T2 relaxation time of the central transition follows a similar trend; however, the satellite transition exhibits a monotonous decrease with [17,25,26,27]. With further increase in τc when (ωQ is the quadrupolar coupling constant in angular frequency units), the system enters the so-called “ultraslow regime,” and its relaxation deviates from Redfield’s theory, which is outside the scope of the current study (see Methods for further description) [26,28].
2.1. Titration with Metal Ions Leads to Sodium Ion Release from Heparin
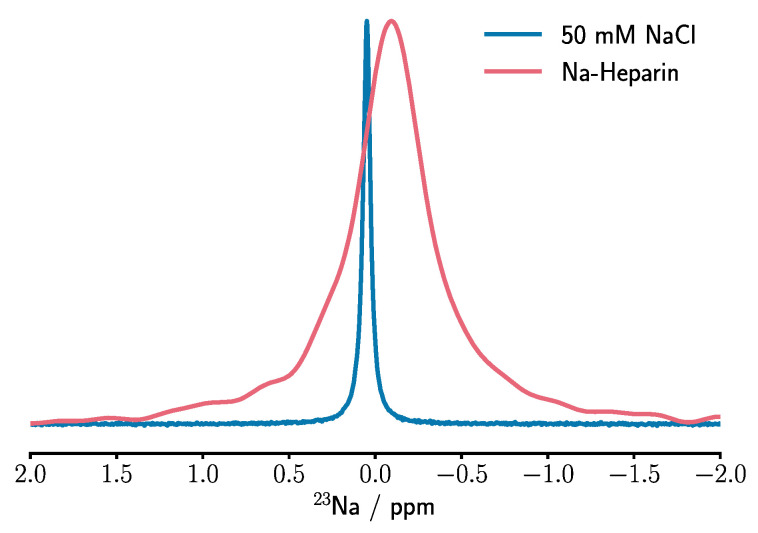
First, we measured the 1D 23Na NMR spectrum of a control sodium chloride solution in water (50 mM), which resulted in a single peak with an (apparent) chemical shift of 0.05 ppm (Figure 1). The peak was well fit by a single Lorentzian, and the linewidth obtained through the fit was ca. 5.3 ± 0.1 Hz. Then, the 1D 23Na NMR spectrum of an aqueous solution of sodium heparin (5 IU/mL) showed a single rather broad peak with an apparent linewidth of 48.3 ± 0.5 Hz at around −0.095 ppm, which was again well fit by a single-Lorentzian. As mentioned above, the almost ten-fold increase in the linewidth of the 23Na NMR signal is expected to have been caused by a combination of longer rotational correlation time and larger local EFG present in the place of heparin-bound sodium ions when compared to the free symmetrically hydrated sodium ions in the control solution. The slight upfield chemical shift change is likely to represent the relative shielding of 23Na nuclei in the heparin-bound form because of the nearby negative charges. The comparison with integrated signal intensities of known sodium chloride solutions (10 mM, 50 mM, and 1 M) indicated that around 44 ± 2 mM of sodium ions contributed to the signal in the measured sodium heparin samples.
Figure 1.
1D 23Na NMR spectrum of the sodium heparin sample (red), showing a significant signal broadening and a small displacement towards negative chemical shifts when compared to the reference NaCl sample (blue).
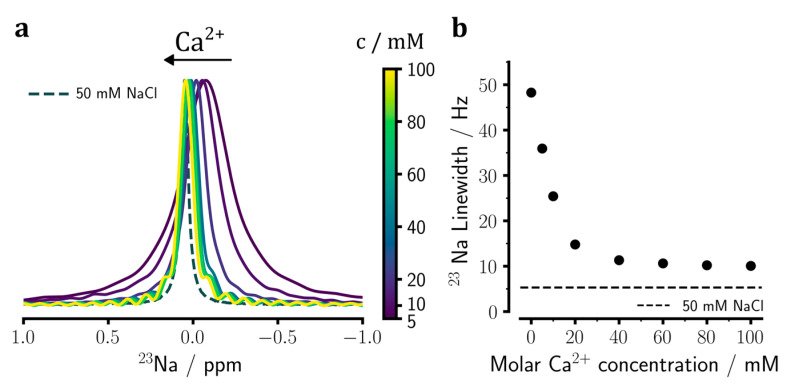
Next, we investigated the binding of divalent Ca2+ ions to heparin through titration of the sodium heparin sample with 0 to 100 mM CaCl2 and 23Na NMR measurements. After adding 5 mM Ca2+, a considerable reduction in 23Na signal linewidth was observed (Figure 2a). Through titration, a gradual change in the chemical shift and linewidth of the 23Na NMR signal towards those of the control sample was observed, indicating Ca2+ binding-induced release of sodium ions from heparin and exchange between the free and bound sodium ions occurring in the fast exchange regime with respect to NMR chemical shift timescale (kex >> Δω ≅ 96 s−1). Importantly, the Ca2+ concentration-dependent change in 23Na signal linewidth showed a limiting value of around 10.1 ± 0.1 Hz (Figure 2b), considerably larger than the value of 5.3 ± 0.1 Hz obtained for the control sample. The limiting linewidth value was almost fully achieved already at around 40–60 mM CaCl2 concentration and the further increase in CaCl2, concentration to 100 mM had little impact on 23Na signal linewidth. These data suggest the presence of at least two sodium-binding sites on heparin, one with a weak affinity that is readily substituted by added Ca2+ ions in the range up to ~ 50 mM concentration, the other(s) with a stronger affinity that remains occupied even at added Ca2+ concentrations as high as 100 mM.
Figure 2.
23Na NMR spectral changes of sodium heparin caused by the addition of Ca2+ ions and the consequent release of sodium ions from heparin. (a) Upon titration of sodium heparin with 0 to 100 mM CaCl2, the 23Na chemical shift gets narrower and moves downfield towards the chemical shift of the reference NaCl sample (see Figure 1). (b) Changes in the 23Na signal linewidth in dependence of added Ca2+ ion concentration, showing a monotonic decrease approaching a value slightly larger than the linewidth of the reference NaCl sample (represented by the dashed line). The spectra shown in (a) are re-scaled according to their peak intensities. The error bars in (b) are comparable in size to the symbols and, therefore, barely visible.
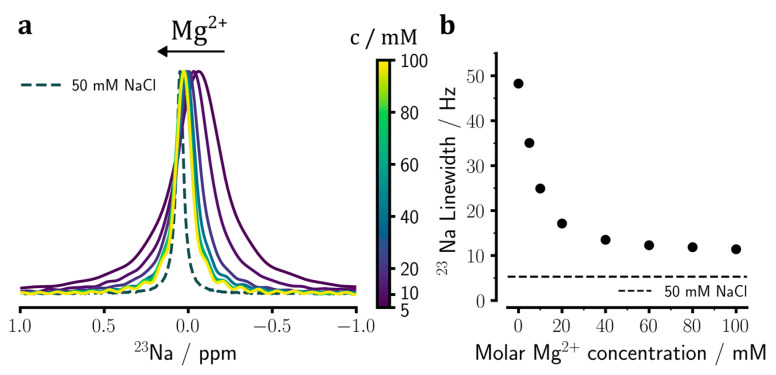
Subsequently, we studied the binding of divalent Mg2+ ions to heparin through similar 23Na NMR-based titration experiments with MgCl2 (Figure 3a). Titration with 0 to 100 mM Mg2+ ions led to changes in 23Na chemical shifts from −0.095 ppm to 0.026 ppm and in the linewidths from 48.3 Hz to 11.4 Hz. In line with Ca2+ ion titration data (Figure 2b), the Mg2+ concentration-dependent change in linewidth further supported the presence of more than one sodium-binding site on heparin (Figure 3b). Furthermore, the comparison between the limiting line widths (11.4 Hz for Mg2+ vs. 10.1 Hz for Ca2+) suggested that the affinity of Mg2+ ions for the weaker sodium ion-binding site on heparin was lower than that of Ca2+ ions. In the absence of titration data at much larger concentrations, however, the affinities of Ca2+ and Mg2+ ions for the stronger binding site(s) on heparin could not be compared.
Figure 3.
23Na NMR spectral changes of sodium heparin caused by the addition of Mg2+ ions and the consequent release of sodium ions from heparin. (a) Upon titration of sodium heparin with 0 to 100 mM MgCl2, the 23Na chemical shift gets narrower and moves downfield towards the chemical shift of the reference NaCl sample (see Figure 1). (b) Changes in the 23Na signal linewidth in dependence of added Mg2+ ion concentration, showing a monotonic decrease approaching a value slightly larger than the linewidth of the reference NaCl sample (represented by the dashed line). The spectra shown in (a) are re-scaled according to their peak intensities. The error bars in (b) are comparable in size to the symbols and, therefore, barely visible.
2.2. Rotational Mobility of Released Sodium Ions from Heparin
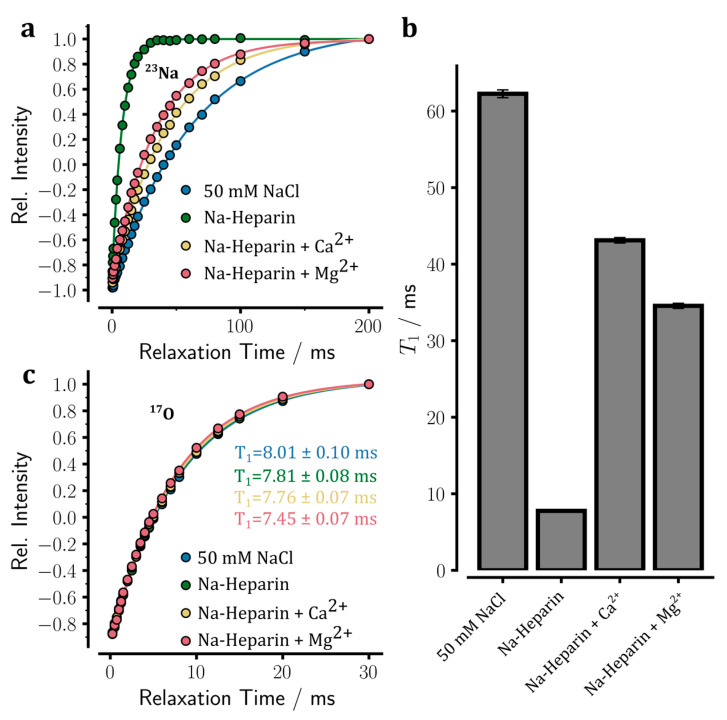
To further investigate how the addition of Ca2+ or Mg2+ ions affects sodium ion binding to heparin, the longitudinal spin-lattice (T1) relaxation times of 23Na were measured in sodium heparin samples in the absence or presence of added ions through standard inversion-recovery experiments.
In the control sample (50 mM NaCl), the intensity recovery obeyed a mono-exponential recovery curve consistent with Na+ ions in the fast extreme-narrowing regime (Figure 4a). Even in the sodium heparin sample in which the heparin-bound sodium ions are expected to have a much slower rotational correlation time than free sodium ions, the intensity recovery data did not show a clear deviation from the mono-exponential recovery curve either (Figure 4a). The 23Na T1 relaxation times obtained through fitting to a mono-exponential recovery function (see Equation (1) in Section 4) were 62.3 ± 0.5 ms in the control NaCl solution and 7.8 ± 0.0 ms in the sodium heparin sample (Figure 4b). Notably, the 23Na T1 relaxation time of 62.3 ms in the control NaCl sample was almost identical to the 23Na T2 of 60.2 ms estimated through the linewidth of the 23Na signal (see above, the corresponding relaxation rates were 16.1 and 16.6 s−1, respectively). The small difference of around 0.5 s−1 in relaxation rates are likely to be caused by B0 field inhomogeneity broadening and the inherent noise in the spectrometer frequency lock system. Unlike the control sample, however, a considerable difference was observed between the 23Na T1 relaxation time of 7.8 ms in the sodium heparin sample and the linewidth-based T2 of 6.6 ms: the corresponding relaxation rates were 128.2 and 151.7 s−1. The difference of around 23.5 s−1 in relaxation rates is too large to be entirely caused by the B0 field inhomogeneity and lock system noises. Instead, it suggests the possibility that the system is partially outside the extreme-narrowing regime. Indeed, the T1/T2 ratio of ~1.18 is consistent with a τc of ca. 0.88 ns. Under this condition where ω0τc is ~0.585, the difference in T1 or T2 relaxation times of the central and satellite transitions are too small to lead to a clear bi-exponential intensity recovery in T1 relaxation experiments or a double-Lorentzian signal line shape. Another possibility is that an exchange process between free and heparin-bound sodium ions occurring at tens of milliseconds timescale leads to exchange-mediated contribution to T2, but not T1, relaxation rates.
Figure 4.
Longitudinal spin-lattice (T1) relaxation of 23Na NMR signals in sodium heparin samples determined through standard inversion-recovery NMR experiments. (a) The 23Na inversion-recovery data are shown as relative intensity versus relaxation time (duration of relaxation delay) for the following samples: sodium heparin sample without added ion, sodium heparin samples with 100 mM CaCl2 or MgCl2 added, and a reference NaCl solution. Upon the addition of Mg2+ and especially Ca2+ ions, the relaxation-induced recovery of 23Na signals becomes slower and approaches but does not reach, that of the reference NaCl sample. (b) The obtained 23Na T1 relaxation times of the measured samples. The 23Na T1 data show partial Ca2+ or Mg2+ ion-dependent release of sodium ions from heparin, which is stronger in the case of Ca2+ ions. (c) The 17O inversion-recovery data of the above samples show only slight differences in the viscosity-dependent 17O T1 of water.
The almost eight-fold difference in 23Na T1 of these two samples potentially originated from two factors, (i) the slower rotational correlation time of heparin-bound sodium ions than free sodium ions, and (ii) the larger local electric field gradient present at the site of heparin-bound 23Na nuclei compared to free symmetrically-hydrated sodium ions. The possible contribution of viscosity changes to 23Na T1 can be excluded, as the viscosity-dependent 17O T1 times do not show any significant difference between these two samples (Figure 4c) [22]. If we assume a 23Na quadrupolar coupling constant (QCC, χ) of 500–2000 kHz, typical values reported for sodium carboxylate salts in literature [29,30], then the 23Na T1 of 7.8 ms in the sodium heparin sample would imply a τc of ~6–130 ps (longer τc values at smaller QCCs). Notably, the lower limit of 6 ps coincides with the reported τc of free sodium ions at the same temperature [31]. In comparison, the upper limit of 130 ps is too short of pushing the quadrupolar relaxation of sodium ions away from the extreme-narrowing regime. If we take τc of ca. 0.88 ns estimated above from the T1/T2 ratio, then a 23Na QCC of around 234 kHz would be needed to reproduce the (average) T1 and T2 values. These QCC values are unrealistically small for the sodium ions bound specifically to negatively charged carboxylate or sulfate groups of heparin [29,30]. On the other hand, they seem too large for sodium ions bound non-specifically to the negatively charged layer of the heparin surface. Instead, the estimated QCC of around 234 kHz could arise from a dynamic exchange of sodium ions between these two modes of binding to heparin.
Next, we investigated how the addition of Ca2+ or Mg2+ ions would affect the 23Na T1 relaxation in the sodium heparin sample. As shown in Figure 4b, the mono-exponetial pattern of intensity recovery was preserved upon the addition of 100 mM CaCl2 or MgCl2. However, the 23Na T1 rose from 7.8 ± 0.0 in the sodium heparin sample to 43.1 ± 0.4 and 34.6 ± 0.3 ms, respectively. Notably, the 23Na T2 relaxation rates estimated from linewidths were 25.7 and 30.9 s−1, respectively, after the addition of Ca2+ or Mg2+ ions, which were only slightly different from the corresponding T1 relaxation rates of 23.2 ± 0.2 and 28.9 ± 0.3 s−1. The 23Na T1 values obtained after the addition of Ca2+ or Mg2+ ions were smaller than the value of 62.3 ± 0.5 ms measured in the control NaCl sample, indicating that Ca2+ or Mg2+ ion-induced sodium release from heparin was incomplete. Assuming that the observed 23Na T1 relaxation rates were population-weighted averages of the relaxation rates of free and heparin-bound sodium ions, it was found that Ca2+ ions had released 93.6 ± 1.8% of the heparin-bound sodium ions, while the corresponding value for Mg2+ ions was 88.5 ± 1.8%. These results, therefore, support the higher strength of Ca2+ than Mg2+ ions in releasing sodium ions from heparin.
2.3. Translational Mobility of Released Sodium Ions from Heparin
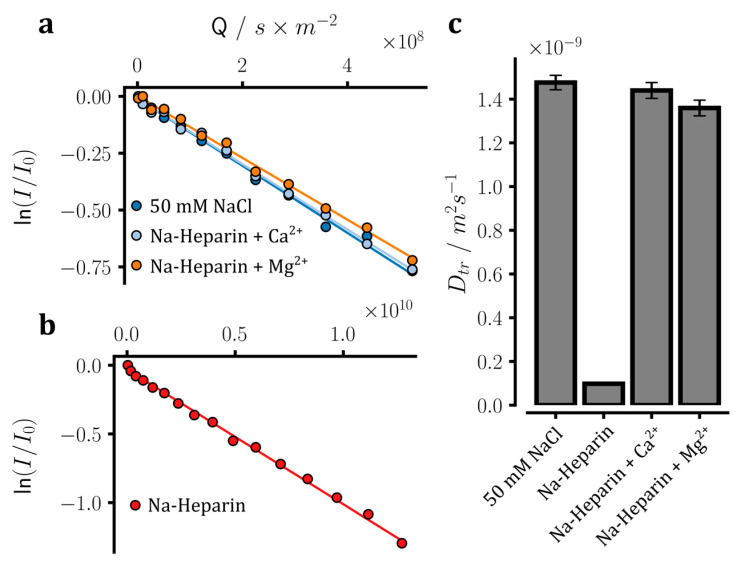
Subsequently, we investigated how the translational mobility of sodium ions is affected by the addition of Ca2+ or Mg2+ ions to sodium heparin. To this end, the diffusion coefficient of sodium ions was measured through the PFG-NMR diffusion method (Figure 5a,b). In these measurements, the z-axis gradient-dependent attenuation of NMR signal intensities during diffusion delays is interpreted as diffusive displacement of the underlying molecules/ions along the z-axis, and thereby diffusion coefficients of respective molecules/ions are determined [32]. The free sodium ions in the control NaCl sample showed a diffusion coefficient of 1.48 ± 0.03 × 10−9 m2·s−1, which is in good agreement with previous reports [18,19,31]. The heparin-bound sodium ions, however posed a challenge for NMR dffusion measurements as the relatively slow diffusion of the bound ions and the severe relaxation of the 23Na signal during the required tens of milliseconds-long diffusion delays would not leave any appreciable 23Na signal to be measured. Assuming that the heparin-bound sodium ions diffuse together with the heparin, it was possible to indirectly determine the diffusion coefficient of bound sodium ions through 1H-based PFG-NMR measurements (Figure 5b). In this way, the diffusion coefficient of heparin-bound sodium ions was determined at 9.80 ± 0.19 × 10−11 m2·s−1, which is almost 15 times smaller than the diffusion coefficient of free sodium ions. It is worth noting that the free and heparin-bound sodium ions showed a less marked difference in their 23Na T1 than their diffusion coefficients (eight-versus 15-fold, see above), which suggests that the sodium ions probably enjoy a considerable degree of local rotational mobility in the heparin-bound form.
Figure 5.
Translational diffusion of sodium ions measured in heparin samples through 23Na or 1H-based pulse field gradient NMR diffusion experiments. (a,b) Gradient-dependent decrease in the intensity of 23Na NMR signals in sodium heparin samples in the presence of 100 mM CaCl2 or MgCl2, as well as in the reference NaCl sample. Due to the fast relaxation of 23Na signals in the sodium heparin sample without added ions and the severe loss of 23Na signal intensity, no 23Na NMR diffusion experiment could be conducted for this sample. Instead, as shown in (b), the diffusion coefficient of sodium ions in the heparin-bound form was estimated through a 1H-based NMR diffusion experiment, assuming that the heparin molecules and sodium ions are rigidly bound and diffuse together. (c) The obtained translational diffusion coefficients (Dtr) of sodium ions in the measured samples. The diffusion data are consistent with the partial release of sodium ions from heparin after the addition of Mg2+ and especially Ca2+ ions.
Upon addition of 100 mM CaCl2 or MgCl2 to heparin, the diffusion coefficient of sodium ions increased to 1.44 ± 0.04 × 10−9 and 1.36 ± 0.04 × 10−9 m2·s−1, respectively. Assuming that the observed diffusion coefficients of sodium ions were population-weighted averages of the free and heparin-bound sodium ions, it was found that 97.1 ± 2.7% and 91.3 ± 2.9% of sodium ions were released by Ca2+ and Mg2+ ions, respectively. These results are in qualitative agreement with the above-mentioned 23Na T1 relaxation data and further support the higher strength of Ca2+ ions than Mg2+ ions in releasing sodium ions from heparin.
2.4. Rotational and Translational Mobility of Titrated Metal Ions, Case of 27Al Ions
The data presented above demonstrate the power of 23Na NMR-based competition assays in detecting and quantifying metal ion binding to heparin. To explore whether more direct NMR methods could be used to monitor metal ions binding to heparin, we turned our attention to the nuclei of binding metal ions. Unfortunately, the NMR-active calcium and magnesium isotopes like 43Ca and 25Mg are relatively rare in nature and have very low gyromagnetic ratios (γ), compromising the sensitivity of NMR experiments and demanding specific NMR probes suitable for low-γ nuclei. Therefore, we chose aluminum ions, of which the 27Al nucleus has a natural abundance of ca. 100% and a fairly large gyromagnetic ratio. The 27Al nucleus has a spin quantum number of 5/2; hence it is quadrupolar [24]. As a result, its relaxation rate is significantly contributed by the quadrupolar relaxation mechanism, which is highly sensitive to binding events and the resultant changes in the chemical environment.
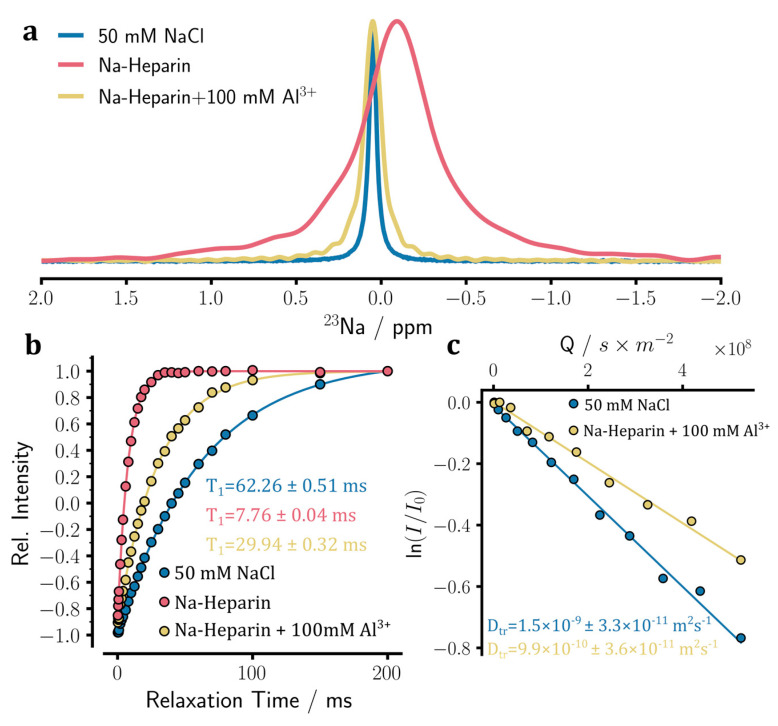
The addition of 100 mM aluminum sulfate resulted in the release of sodium ions from heparin, as reflected in changes in the 1D 23Na NMR spectra and an increase in 23Na T1 and diffusion coefficients (Figure 6a–c). The Al3+ ion-induced increase of 23Na T1 to 29.9 ± 0.3 ms indicates the release of ca. 85% of sodium ions from heparin, which is considerably smaller than the corresponding values for Ca2+ (ca. 94%) and Mg2+ (ca. 89%). The relatively small increase of the 23Na diffusion coefficient to 9.9 ± 0.4 × 10−10 m2·s−1 suggested an even lower amount of sodium ion release (ca. 65%). In qualitative agreement with previous reports [11], the 23Na T1 times and diffusion coefficients indicated that the trivalent Al3+ ions were less strong than the divalent Ca2+ and Mg2+ ions in releasing sodium ions from heparin (the strength order was Ca2+ > Mg2+ > Al3+). It is, however, notable that the Al3+ ion-induced release of sodium ions from heparin indicates a larger affinity of Al3+ than sodium ions for the respective binding site on heparins, which is not consistent with the order of affinities reported in ref. [11] based on atomic absorption experiments.
Figure 6.
Aluminum ion binding to sodium heparin was monitored through 23Na NMR experiments. (a) 1D 23Na NMR spectra of sodium heparin, before and after the addition of 100 mM Al2(SO4)3. The spectrum of the reference NaCl solution is also shown. The addition of Al3+ ion leads to 23Na signal narrowing and peak displacement towards the chemical shift of free sodium ions. (b) Longitudinal spin-lattice (T1) relaxation of 23Na signals measured through standard inversion-recovery experiments. The T1 relaxation data indicate the partial release of sodium ions from heparin caused by the addition of Al3+ ions. (c) Translational diffusion coefficient (Dtr) of sodium ions measured through pulse field gradient NMR diffusion experiments. The Dtr of sodium ions in the heparin with Al2(SO4)3 sample is larger than that of the heparin sample without added ions (see Figure 5c) but smaller than that of the reference NaCl sample. This is consistent with the partial release of sodium ions from heparin caused by added Al3+ ions.
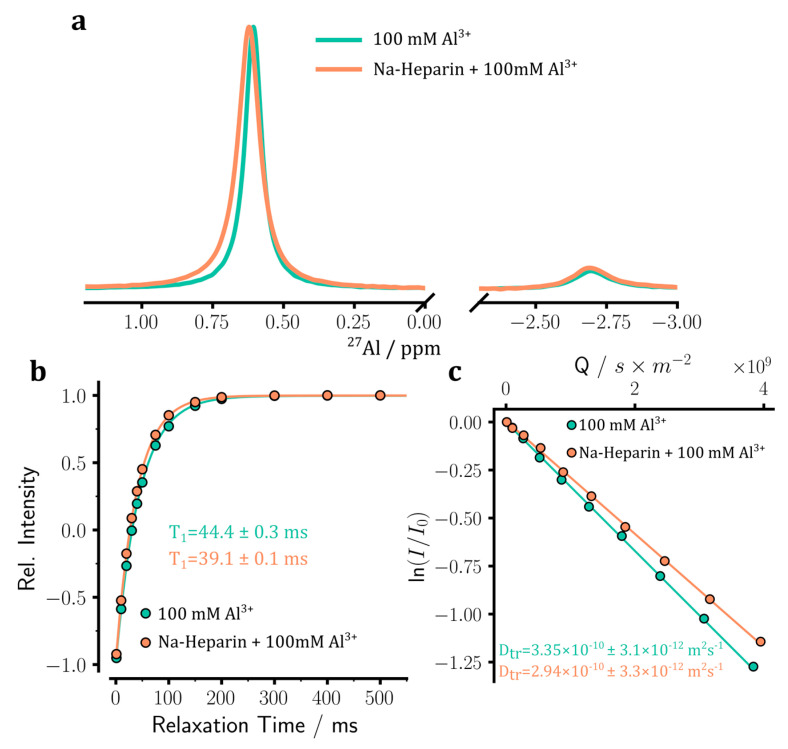
Finally, we measured the 1D 27Al NMR spectra of a 100 mM aluminum sulfate solution in the absence or presence of sodium heparin (5 IU/mL). As shown in Figure 7a, the 1D 27Al NMR spectrum of aluminum sulfate showed two peaks, a major peak (88.6 ± 0.2%) centered at around 0.9 ppm and a minor peak (11.4 ± 0.2%) around −2.4 ppm. A previous study has shown that the major peak corresponds to [Al(H2O)6]3+ species, while the minor peak has its origin in [Al(H2O)5SO4]+ species [33]. Upon the addition of heparin, the chemical shifts and linewidths of the two 27Al signals showed changes suggesting the binding of aluminum ion species to heparin. Further direct evidence for the binding of Al3+ ions to heparin was provided by 27Al T1 relaxation measurements. Upon addition of heparin, the 27Al T1 relaxation times decreased from 44.4 ± 0.3 ms to 39.1 ± 0.1 ms for the major peak (Figure 7b) and from 32.4 ± 0.1 ms to 30.5 ± 0.1 ms for the minor peak. The translational diffusion coefficient of Al3+ ions changed from 3.4 ± 0.03 × 10−10 m2·s−1 in the control sample to 2.9 ± 0.03 × 10−10 m2·s−1 in the heparin sample (Figure 7c). Assuming that the bound Al3+ ions diffuse together with heparin and have a diffusion coefficient identical to that of heparin, it is estimated that around 83% of Al3+ ions are in the free and only 17% are in the bound states. The 23Na and 27Al NMR provided complementary probes of binding/un-binding these metal ions to/from heparin.
Figure 7.
Aluminum ion binding to sodium heparin was monitored through 27Al NMR experiments. (a) 1D 27Al NMR spectra of 100 mM Al2(SO4)3 sample, in the absence or presence of sodium heparin. The major and minor peaks, respectively, corresponding to [Al(H2O)6]3+ and [Al(H2O)5SO4]+ species, are shown. The addition of sodium heparin leads to slight displacement and broadening of the 27Al signal. (b) Longitudinal spin-lattice (T1) relaxation of 27Al signals measured through standard inversion-recovery experiments. (c) Translational diffusion coefficient (Dtr) of Al3+ ions measured through pulse field gradient NMR diffusion experiments. Upon the addition of heparin, a small decrease in 27Al T1 relaxation time (b) and Dtr coefficient (c) is observed, indicating the partial binding of Al3+ ions to heparin.
3. Discussion
Our results showed that metal ion binding to heparin could be monitored through a 23Na NMR-based competition assay. The addition of Ca2+ (Figure 2), Mg2+ (Figure 3), and Al3+ (Figure 6) ions to sodium heparin led to the release of sodium ions from heparin, as revealed by metal ion-induced changes in 23Na chemical shifts and linewidths (Figure 2, Figure 3 and Figure 6), T1 relaxation times (Figure 4 and Figure 6) and diffusion coefficients (Figure 5 and Figure 6). Analysis of 23Na NMR data demonstrated the presence of more than one metal ion-binding site on heparin and supported the affinity order of Ca2+ > Mg2+ > Al3+ for the site with lower affinity. In the case of Al3+, complementary 27Al NMR experiments provided direct evidence for Al3+ ions binding to heparin (Figure 7).
Heparins have a high negative charge density because of carboxylate and particularly sulfate groups in their structure (see Scheme 1) [1]. It is therefore expected that heparins act as polyelectrolytes and in dilute solutions covered by a layer of positive counterions, as predicted by Manning’s counterion condensation model [34] or Poisson-Boltzmann theory [35]. In addition to this rather non-specific mode of counterion binding to heparin, the positively charged metal ions can be more specifically engaged in binding with negatively charged groups in heparin, where specific interactions beyond electrostatic interaction stabilize the ion-heparin binding. The 23Na NMR data reported here confirm the presence of more than one sodium ion binding site on heparin, in which the site with weaker binding affinity is substituted by added divalent Ca2+ and Mg2+ and trivalent Al3+ ions. Our data do not allow identifying the sodium binding sites on heparin. Nevertheless, the lower melting point and higher solubility of sodium acetate than sodium sulfate suggest that the lattice energy of sodium acetate is lower than sodium sulfate. Accordingly, it appears reasonable to speculate that the carboxylate groups may form the weak binding site, while the sulfate groups are more likely involved in the strong binding mode. The 23Na NMR-based competition data support the relative affinity order of Ca2+ > Mg2+ > Al3+ > Na+ ions for the weak binding site on heparin. Regarding the strong binding site, the data presented here does not provide a relative affinity order. It is, however, interesting to note that the addition of 100 mM Ca2+, Mg2+, or Al3+ ions did not displace the residual bound sodium ions at concentrations as low as 7 mM or lower (<15% of total Na+ concentration of mM, see above). As a result, the Na+ ion seems to have a larger affinity than the studied divalent and trivalent ions for the strong binding site on heparin. The suggested affinity orders for the weak and strong binding sites of heparin are partially consistent with a previous atomic absorption-based report [11], potentially because of its different sensitivity to various modes of ion-heparin binding. Our data highlights the importance of site-specific affinity data in ion-heparin binding studies, especially when contradictory results are obtained through various techniques.
In accordance with partial deviation from the extreme-narrowing regime, the 23Na T1 and T2 relaxation times of the sodium heparin sample were different from each other. The 23Na T1 and T2 relaxation rates could be explained by a τc of ~0.88 ns and a 23Na quadrupolar coupling constant of ~ 234 kHz. The latter value lies between the typical quadrupolar coupling constants of sodium carboxylate ions [29,30] and the values expected for sodium counterions non-specifically condensed on heparin undergoing dynamic exchange with the surrounding ionic atmosphere and bulk solution. Accordingly, we hypothesize that a sodium ion exchange process between the specific and non-specific binding sites of heparin partially averages the relaxation-active quadrupolar coupling constants and leads to an effective intermediate coupling constant. A complete analysis of this complex exchange process involves several unknown parameters and demands extensive relaxation rate measurements beyond the scope of the current study.
The ubiquitous presence of negatively charged proteoglycans in the extracellular space can act as buffers for positively charged metal and organic ions and thereby influence various physiological and pathophysiological processes outside the cells [12,13]. In addition, it is known that ions such as Ca2+ or Mg2+ can alter the conformation of heparin and consequently modulate their functions, e.g., in host defense against pathogens [10]. In neurodegenerative diseases, heparins are known to trigger pathogenic aggregation of proteins such as tau protein in a metal ion-dependent manner on the one hand [7,36,37,38] and act as neuroprotective agents on the other hand [9]. Considering various modes of ions binding to heparin, as shown here, it is interesting to explore the range of structural and activity changes in heparin in dependence on ion types and binding sites.
In summary, we present a multinuclear quadrupolar NMR study of metal ions binding to heparins. Using a 23Na NMR-based competition assay involving 23Na NMR relaxation and diffusion measurements, we detect and quantify the binding of metal ions Ca2+, Mg2+, and Al3+ to sodium heparin, support the presence of more than one ion binding site on heparin undergoing dynamic exchange and provide a relative affinity order for the studied ions. Combined with other methods of studying ion-heparin binding, the presented method can provide a more detailed picture of ion-heparin binding and its potential structural and functional consequences.
4. Materials and Methods
Magnesium chloride, MgCl2, calcium chloride, CaCl2, and aluminum sulfate, Al2(SO4)3, were purchased from Sigma. The unfractionated heparin (high-molecular-weight, ~10–20 kDa) at a concentration of 50,000 IU/mL was obtained from Ratiopharm (Ulm, Germany).
NMR experiments were conducted at a Bruker spectrometer with a proton Larmor frequency of 400.13 MHz equipped with a room-temperature triple resonance broadband (TBO) probe. Unless stated otherwise, the NMR samples contained 5 IU/mL sodium heparin dissolved at 99.95% D2O, to which MgCl2, CaCl2, or Al2(SO4)3 at specified concentrations were added. The deuteron signal was used for spectrometer frequency locking and chemical shift referencing (4.700 ppm). For natural abundance 23Na, 27Al, and 17O NMR experiments, the inner broadband coil of the TBO probe was tuned and matched at ~ 105.84, 104.26, and 54.24 MHz, respectively, corresponding to the Larmor frequencies of 23Na, 27Al, and 17O nuclei. NMR measurements were performed at 298 K, controlled to ±0.05 K by a Bruker VT unit calibrated using the residual proton signals of a standard deuterated methanol sample.
The longitudinal spin-lattice (T1) relaxation of 23Na, 27Al, and 17O was studied through standard inversion-recovery experiments. In 23Na T1 experiments, 26 relaxation delays (t) of 0.25, 0.5, 0.75, 1, 2, 3, 4, 6, 8, 10, 12.5, 15, 17.5, 20, 25, 30, 35, 40, 45, 50, 60, 70, 80, 100, 150 and 200 ms were used. The 16 relaxation delays used for 27Al T1 experiments were 1, 10, 20, 30, 40, 50, 75, 100, 150, 200, 300, 400, 500, 750, 1000, 2000 ms. The corresponding values for 17O T1 experiments were 0.25, 0.5, 0.75, 1, 1.25, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5, 6, 7, 8, 10, 12.5, 15, 20, 30 ms. In all T1 experiments, sufficiently long total recycle delays (d1 + acq.) were used in order to ensure complete Boltzmann magnetization of the studied nuclei. Assuming a fast “extreme narrowing” regime in which relaxation-dependent recovery of signal intensities of these quadrupolar nuclei obeys a single-exponential recovery equation (see below), the intensity (I) versus relaxation delay (t) data were fitted to:
| (1) |
through which the T1 relaxation times were obtained.
The (translational) diffusion coefficient (D) of sodium and aluminum ions was measured through the 23Na- or 27Al-based pulse-field-gradient (PFG) NMR diffusion method using the standard stebpgp1s pulse sequence. The known diffusion coefficient of residual HDO in 99.8% D2O at 25 °C (1.900 × 10−9 m2·s−1) was used for gradient calibration. The magnetic field z-gradient-based intensity attenuation data were fitted to the standard Stejskal-Tanner (ST) equation,
| (2) |
with , where γ is the gyromagnetic ratio of the corresponding nucleus, g is the gradient strength and Δ and δ are the big and little diffusion delays, respectively. The big and little diffusion delays were 20 and 5 ms for 23Na and 75 and 7 ms for 27Al NMR diffusion experiments, respectively. In the 1H-based PFG-NMR experiment used to determine the diffusion coefficient of heparin-bound ions, the big and little diffusion delays were 50 and 5 ms, respectively.
The 23Na, 27Al, and 17O nuclei have spins I = 3/2, 5/2, and 5/2, respectively. Nuclei with spins have non-zero electric quadrupole moment (eQ), and its anisotropic interaction with the local electric field gradient (EFG) leads to an additional NMR relaxation mechanism called quadrupolar relaxation. In general, the quadrupolar relaxation of half-integer spin contains components, of which one belongs to the single central transition (CT: ) and components belong to the corresponding pairs of satellite transitions (ST: for spin-3/2 23Na and and for spin-5/2 27Al and 17O). However, within the so-called fast “extreme-narrowing” regime where (ω0, Larmor frequency, τc, rotational correlation time associated with the stochastic reorientation of the EFG tensor), the relaxation rates of the central and satellite transitions become identical and, therefore a single-exponential relaxation pattern is recovered. Under this regime, the T1 and T2 relaxation times are identical and inversely proportional to τc, according to
| (3) |
where I is the spin quantum number, is the quadrupolar coupling constant (QCC, CQ), Q is the quadrupole moment, and η is the asymmetry parameter representing the deviation of the electric field gradient (EFG) tensor eq from axial symmetry. When τc and/or ω0 increase and the system enters the so-called “slow regime” where or larger, the T1 and T2 times corresponding to the CT and ST components become distinct. In the case of spin-3/2 nuclei such as 23Na, the two relaxation times are given by Equations (4)–(7) [17,23,25,26]:
| (4) |
| (5) |
| (6) |
| (7) |
The bi-exponential longitudinal spin-lattice and transverse spin relaxation of 23Na nuclei can be expressed as:
| (8) |
| (9) |
in which Mz and Mx,y are longitudinal and transverse magnetizations and M0 is the thermal equilibrium (Boltzmann) magnetization. For the calculation of 23Na relaxation rates in dependence of τc or χ on the basis of Equations (3)–(7), an asymmetry parameter η of 0.4 was assumed. With further increase in τc when (ωQ is quadrupolar coupling constant CQ in angular frequency units), the systems enter the so-called “ultra-slow” regime in which the spin relaxation deviates from Redfield’s relaxation theory [26,28]. The “ultra-slow” regime is not relevant in our study and therefore is not described further.
Acknowledgments
N.R.-G. acknowledges the Deutsche Forschungsgemeinschaft (German Research Foundation, DFG) for research grant RE 3655/2-3. The generous access to NMR measurement time provided by the Department of NMR-based Structural Biology, Max Planck Institute for Multidisciplinary Sciences, is gratefully acknowledged. We thank Anja Ehrhardt for providing us with the heparin sample and Sahithya PB Vemulapalli for initial help with sample preparation and NMR experiments.
Author Contributions
Conceptualization, methodology, N.R.-G.; investigation, D.S. and N.R.-G.; resources, C.G. and N.R.-G.; data curation, D.S. and N.R.-G.; writing—original draft preparation, N.R.-G.; writing—review and editing, D.S., C.G. and N.R.-G.; visualization, D.S.; supervision, N.R.-G. All authors have read and agreed to the published version of the manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data of this study can be shared upon reasonable request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Funding Statement
This research received no external funding, and the APC was waived by the IJMS editorial board.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Wang P., Chi L., Zhang Z., Zhao H., Zhang F., Linhardt R.J. Heparin: An old drug for new clinical applications. Carbohydr. Polym. 2022;295:119818. doi: 10.1016/j.carbpol.2022.119818. [DOI] [PubMed] [Google Scholar]
- 2.Stevens R.L., Fox C.C., Lichtenstein L.M., Austen K.F. Identification of chondroitin sulfate E proteoglycans and heparin proteoglycans in the secretory granules of human lung mast cells. Proc. Natl. Acad. Sci. USA. 1988;85:2284–2287. doi: 10.1073/pnas.85.7.2284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Seidel H., Hertfelder H.J., Oldenburg J., Kruppenbacher J.P., Afrin L.B., Molderings G.J. Effects of Primary Mast Cell Disease on Hemostasis and Erythropoiesis. Int. J. Mol. Sci. 2021;22:8960. doi: 10.3390/ijms22168960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Capila I., Linhardt R.J. Heparin-protein interactions. Angew. Chem. Int. Ed. 2002;41:391–412. doi: 10.1002/1521-3773(20020201)41:3<390::AID-ANIE390>3.0.CO;2-B. [DOI] [PubMed] [Google Scholar]
- 5.Hacker U., Nybakken K., Perrimon N. Heparan sulphate proteoglycans: The sweet side of development. Nat. Rev. Mol. Cell Biol. 2005;6:530–541. doi: 10.1038/nrm1681. [DOI] [PubMed] [Google Scholar]
- 6.Oduah E.I., Linhardt R.J., Sharfstein S.T. Heparin: Past, Present, and Future. Pharmaceuticals. 2016;9:38. doi: 10.3390/ph9030038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Snow A.D., Cummings J.A., Lake T. The Unifying Hypothesis of Alzheimer’s Disease: Heparan Sulfate Proteoglycans/Glycosaminoglycans Are Key as First Hypothesized Over 30 Years Ago. Front. Aging Neurosci. 2021;13:710683. doi: 10.3389/fnagi.2021.710683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Marques C., Reis C.A., Vives R.R., Magalhaes A. Heparan Sulfate Biosynthesis and Sulfation Profiles as Modulators of Cancer Signalling and Progression. Front. Oncol. 2021;11:778752. doi: 10.3389/fonc.2021.778752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ma Q., Cornelli U., Hanin I., Jeske W., Linhardt R., Walenga J., Fareed J., Lee J. Heparin oligosaccharides as potential therapeutic agents in senile dementia. Curr. Pharm. Des. 2007;13:1607–1616. doi: 10.2174/138161207780765918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mese K., Bunz O., Volkwein W., Vemulapalli S.P.B., Zhang W., Schellhorn S., Heenemann K., Rueckner A., Sing A., Vahlenkamp T.W., et al. Enhanced Antiviral Function of Magnesium Chloride-Modified Heparin on a Broad Spectrum of Viruses. Int. J. Mol. Sci. 2021;22:10075. doi: 10.3390/ijms221810075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Stevic I., Parmar N., Paredes N., Berry L.R., Chan A.K. Binding of heparin to metals. Cell Biochem. Biophys. 2011;59:171–178. doi: 10.1007/s12013-010-9129-5. [DOI] [PubMed] [Google Scholar]
- 12.Williams R.J.P. Biochemistry of Sodium, Potassium, Magnesium, and Calcium. Q. Rev. Chem. Soc. 1970;24:331–365. doi: 10.1039/qr9702400331. [DOI] [Google Scholar]
- 13.Zhang F., Liang X., Beaudet J.M., Lee Y., Linhardt R.J. The Effects of Metal Ions on Heparin/Heparin Sulfate-Protein Interactions. J. Biomed. Technol. Res. 2014;1 doi: 10.19104/jbtr.2014.101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rabenstein D.L., Robert J.M., Peng J. Multinuclear magnetic resonance studies of the interaction of inorganic cations with heparin. Carbohydr. Res. 1995;278:239–256. doi: 10.1016/0008-6215(95)00263-4. [DOI] [PubMed] [Google Scholar]
- 15.Grant D., Long W.F., Moffat C.F., Williamson F.B. The effect of Cu(II) ions on the optical rotation of heparin. Biochem. Soc. Trans. 1992;20:1S. doi: 10.1042/bst020001s. [DOI] [PubMed] [Google Scholar]
- 16.Lerner L., Torchia D.A. A multinuclear NMR study of the interactions of cations with proteoglycans, heparin, and Ficoll. J. Biol. Chem. 1986;261:12706–12714. doi: 10.1016/S0021-9258(18)67149-2. [DOI] [PubMed] [Google Scholar]
- 17.Cesare Marincola F., Casu M., Saba G., Lai A. 23Na NMR relaxation studies of the Na-DNA/drug interaction. ChemPhysChem. 2001;2:569–575. doi: 10.1002/1439-7641(20011015)2:10<569::AID-CPHC569>3.0.CO;2-S. [DOI] [PubMed] [Google Scholar]
- 18.Fuentes-Monteverde J.C., Becker S., Rezaei-Ghaleh N. Biomolecular phase separation through the lens of sodium-23 NMR. Protein. Sci. 2021;30:1315–1325. doi: 10.1002/pro.4010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.D’Agostino C., Davis S.J., Abbott A.P. (23)Na NMR T1 relaxation measurements as a probe for diffusion and dynamics of sodium ions in salt-glycerol mixtures. J. Chem. Phys. 2021;154:224501. doi: 10.1063/5.0051672. [DOI] [PubMed] [Google Scholar]
- 20.Nimerovsky E. New experimental observations of the behavior of sodium ions in saturated rock samples. J. Magn. Reson. 2019;302:72–87. doi: 10.1016/j.jmr.2019.04.002. [DOI] [PubMed] [Google Scholar]
- 21.Rezaei-Ghaleh N. Water Dynamics in Highly Concentrated Salt Solutions: A Multi-Nuclear NMR Approach. ChemistryOpen. 2022;11:e202200080. doi: 10.1002/open.202200080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Rezaei-Ghaleh N., Munari F., Becker S., Assfalg M., Griesinger C. A facile oxygen-17 NMR method to determine effective viscosity in dilute, molecularly crowded and confined aqueous media. Chem. Commun. 2019;55:12404–12407. doi: 10.1039/C9CC06124J. [DOI] [PubMed] [Google Scholar]
- 23.Madelin G., Lee J.S., Regatte R.R., Jerschow A. Sodium MRI: Methods and applications. Prog. Nucl. Magn. Reson. Spectrosc. 2014;79:14–47. doi: 10.1016/j.pnmrs.2014.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Stone N.J. Table of nuclear electric quadrupole moments. Atom. Data Nucl. Data Tables. 2016;111:1–28. doi: 10.1016/j.adt.2015.12.002. [DOI] [Google Scholar]
- 25.Hubbard P.S. Nonexponential Nuclear Magnetic Relaxation by Quadrupole Interactions. J. Chem. Phys. 1970;53:985–987. doi: 10.1063/1.1674167. [DOI] [Google Scholar]
- 26.Gerothanassis I.P., Tsanaktsidis C.G. Nuclear electric quadrupole relaxation. Concept Magnetic Res. 1996;8:63–74. doi: 10.1002/(SICI)1099-0534(1996)8:1<63::AID-CMR5>3.0.CO;2-N. [DOI] [Google Scholar]
- 27.Shekar S.C., Tang J.A., Jerschow A. Dynamics of I=3/2 Nuclei in Isotropic Slow Motion, Anisotropic and Partially Ordered Phases. Concept. Magn. Reson. A. 2010;36:362–387. doi: 10.1002/cmr.a.20195. [DOI] [Google Scholar]
- 28.Shen J.H., Terskikh V., Wu G. Observation of the Second-Order Quadrupolar Interaction as a Dominating NMR Relaxation Mechanism in Liquids: The Ultraslow Regime of Motion. J. Phys. Chem. Lett. 2016;7:3412–3418. doi: 10.1021/acs.jpclett.6b01530. [DOI] [PubMed] [Google Scholar]
- 29.Lerner L., Torchia D.A. An Analysis of Non-Lorentzian Na-23 Line-Shapes in 2 Model Systems. J. Am. Chem. Soc. 1986;108:4264–4268. doi: 10.1021/ja00275a004. [DOI] [Google Scholar]
- 30.Bonekamp J., Eguchi T., Jonas J. Na-23 Nmr-Study of Ionic Mesophases in Molten Sodium Carboxylates. Chem. Phys. Lett. 1980;75:360–362. doi: 10.1016/0009-2614(80)80531-8. [DOI] [Google Scholar]
- 31.Price W.S., Chapman B.E., Kuchel P.W. Correlation of Viscosity and Conductance with Na-23+ Nmr T1 Measurements. B Chem. Soc. Jpn. 1990;63:2961–2965. doi: 10.1246/bcsj.63.2961. [DOI] [Google Scholar]
- 32.Johnson C.S. Diffusion ordered nuclear magnetic resonance spectroscopy: Principles and applications. Prog. Nucl. Magn. Reson. Spectrosc. 1999;34:203–256. doi: 10.1016/S0079-6565(99)00003-5. [DOI] [Google Scholar]
- 33.Berger S., Nolde J., Yuksel T., Tremel W., Mondeshki M. Al-27 NMR Study of the pH Dependent Hydrolysis Products of Al-2(SO4)(3) in Different Physiological Media. Molecules. 2018;23:808. doi: 10.3390/molecules23040808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Manning G.S. The molecular theory of polyelectrolyte solutions with applications to the electrostatic properties of polynucleotides. Q. Rev. Biophys. 1978;11:179–246. doi: 10.1017/S0033583500002031. [DOI] [PubMed] [Google Scholar]
- 35.Sharp K.A. Polyelectrolyte Electrostatics—Salt Dependence, Entropic, and Enthalpic Contributions to Free-Energy in the Nonlinear Poisson-Boltzmann Model. Biopolymers. 1995;36:227–243. doi: 10.1002/bip.360360210. [DOI] [Google Scholar]
- 36.Dong X., Qi R., Qiao Q., Li X., Li F., Wan J., Zhang Q., Wei G. Heparin remodels the microtubule-binding repeat R3 of Tau protein towards fibril-prone conformations. Phys. Chem. Chem. Phys. 2021;23:20406–20418. doi: 10.1039/D1CP02651H. [DOI] [PubMed] [Google Scholar]
- 37.Mukherjee S., Panda D. Contrasting Effects of Ferric and Ferrous Ions on Oligomerization and Droplet Formation of Tau: Implications in Tauopathies and Neurodegeneration. ACS Chem. Neurosci. 2021;12:4393–4405. doi: 10.1021/acschemneuro.1c00377. [DOI] [PubMed] [Google Scholar]
- 38.Mizoroki T., Meshitsuka S., Maeda S., Murayama M., Sahara N., Takashima A. Aluminum induces tau aggregation in vitro but not in vivo. J. Alzheimers Dis. 2007;11:419–427. doi: 10.3233/JAD-2007-11401. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data of this study can be shared upon reasonable request from the corresponding author.