Flexible integration of continuous sensory evidence in perceptual estimation tasks

Significance

Accumulating sensory information over time is crucial for making accurate judgments when acting in the face of noisy or ambiguous sensory information. For example, a hunting predator needs to compute the net direction of motion of a large group of prey (e.g., shoals of fish or birds flying in flock). Here, we study the underlying neural mechanisms by developing a neural network model that can average angular sensory input near-optimally and also signal the reliability of the estimated average direction. Moreover, the network can flexibly give larger weight to either initial or more recent sensory information, as we observe in humans performing an estimation task. Our findings shed light on the neural circuit mechanisms underlying continuous perceptual judgments.

Abstract

Temporal accumulation of evidence is crucial for making accurate judgments based on noisy or ambiguous sensory input. The integration process leading to categorical decisions is thought to rely on competition between neural populations, each encoding a discrete categorical choice. How recurrent neural circuits integrate evidence for continuous perceptual judgments is unknown. Here, we show that a continuous bump attractor network can integrate a circular feature, such as stimulus direction, nearly optimally. As required by optimal integration, the population activity of the network unfolds on a two-dimensional manifold, in which the position of the network’s activity bump tracks the stimulus average, and, simultaneously, the bump amplitude tracks stimulus uncertainty. Moreover, the temporal weighting of sensory evidence by the network depends on the relative strength of the stimulus compared to the internally generated bump dynamics, yielding either early (primacy), uniform, or late (recency) weighting. The model can flexibly switch between these regimes by changing a single control parameter, the global excitatory drive. We show that this mechanism can quantitatively explain individual temporal weighting profiles of human observers, and we validate the model prediction that temporal weighting impacts reaction times. Our findings point to continuous attractor dynamics as a plausible neural mechanism underlying stimulus integration in perceptual estimation tasks.

Integrating information over time is a fundamental computation that neural systems need to perform in perceptual decision and continuous estimation tasks. While a categorical perceptual decision usually requires discriminating stimuli in order to select between several options [e.g., left vs. right motion of an random dot stimulus (1)], in stimulus-estimation tasks, participants report a continuous stimulus feature—for example, the average motion direction in degrees (2–5). Specifically, here, we consider tasks that require estimating, as an analog quantity, the temporal average of a circular feature, such as the direction of a time-varying stimulus. There is currently no neural network model that can perform this computation.

Evidence integration in categorical decision tasks is thought to rely on slow recurrent dynamics and competition between neural populations, each encoding one of the categorical choice options (6–9). The architecture of these discrete attractor neural network models thus directly reflects the categorical nature of the decision task. By design, these models do not maintain information about continuous features of the integrated stimulus, as required in estimation tasks.

The optimal representation of continuous sensory stimuli in neural population codes has been studied extensively using neural coding models (10–15). These models can explain how to combine different cues in a single representation (10, 12) and how to read-out the population for optimal stimulus discrimination (11, 14). However, these studies have investigated neither the computations involved in temporal stimulus averaging nor the underlying neural circuit mechanisms.

A potential candidate for such a circuit mechanism is the well-known continuous attractor dynamics observed in recurrent neural networks (16–21). Continuous line attractor models can integrate and represent a continuous feature in the graded firing rate of a neural population (19–22). However, these rate-code-based models are not suited for optimal integration of a circular feature (e.g., the average stimulus direction). First, it is unclear how an angular quantity could be mapped onto the different levels of neural population activity. Second, as we will show here, a single continuous variable is insufficient to optimally integrate a circular feature because this computation unfolds in a two-dimensional (2D) manifold, similar to the computation of a vector sum, which requires keeping track of the vector length and direction. No model that represents only a single variable (including rate-code-based line attractors) can perform this operation in an optimal way. We thus do not consider rate-code-based models here and, instead, focus on continuous bump attractor networks (16–18).

Bump attractor networks have a topological ring architecture, and, due to strong recurrent coupling, they can show localized activity in a subset of neurons with a bell-shaped pattern (bump) that persists even in the absence of tuned external input. Because all states along the ring are energetically equal, the bump can be centered anywhere along the network. The bump location thus provides a substrate for encoding a continuous variable, such as an orientation or a spatial location. Moreover, while intrinsically, the bump position is stable, external inputs can drive the bump to move. Due to these features, bump attractor networks have been proposed as the neural mechanism underlying a variety of sensory and cognitive computations: the emergence of contrast-invariant orientation tuning in visual cortex (17); the identification of the direction of a weak motion stimulus (23); multiple-choice decision making (24); the maintenance of spatial working memory in prefrontal cortex (25, 26); and the representation of spatial orientation and angular path integration in the mammalian head-direction system (27–30), in the fly’s heading-direction system (31), and in grid cells (32). None of these previous studies has investigated in detail how a bump attractor network can accumulate sensory information to estimate the time average of a continuous stimulus, as required in perceptual estimation tasks, and under which conditions this accumulation is optimal.

Here, we show that the ring attractor model can accurately compute the average of a time-varying circular stimulus feature. By virtue of the transient dynamics during the slow formation of the bump state, the network approximates a perfect vector integrator (PVI), such that the phase of the activity bump tracks the running circular average of the stimulus. Moreover, the temporal weighting of sensory evidence can be flexibly controlled by the overall excitatory drive that determines the internally generated bump dynamics. To illustrate the relevance of our theoretical results, we analyze data from psychophysical experiments, in which human observers integrated a stream of eight oriented stimulus frames. We show that the continuous attractor model can quantitatively fit the observed heterogeneity of temporal weighting regimes across subjects and confirm a model-predicted relationship to the subjects’ reaction times (RTs).

Results

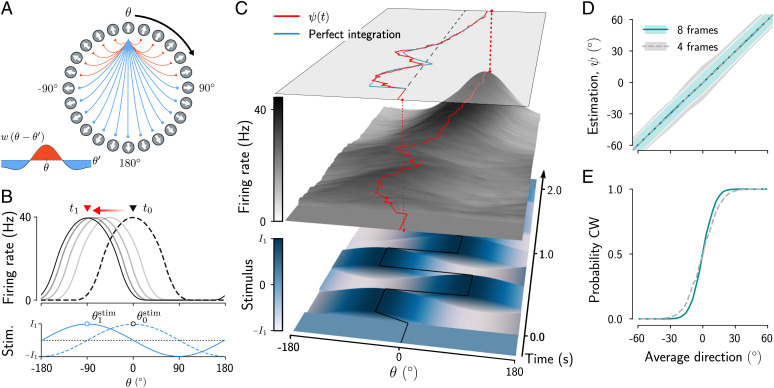
We start by simulating the integration of stimuli in a continuous ring attractor model, as in experimental tasks that require estimating, as an analog quantity, the average direction of motion of a noisy random dot stimulus (2, 3) or of a sequence of oriented Gabor patches (33–35). The network model has a ring architecture and Mexican-hat connectivity (Fig. 1A), and its firing-rate dynamics are described by Eq. 3 (Materials and Methods). Due to strong recurrent connectivity, a localized bump of activity emerges in the network (Fig. 1B). As has been shown previously (17), a fast change of the stimulus to a new direction does not lead to an instantaneous extinction and reappearance of the bump at the new direction, but, rather, initiates a continuous translation of the activity along the ring network, directed toward the new stimulus direction (Fig. 1B). Thus, the bump position at a given time depends on the current input to the network and on the previous bump position.

Fig. 1.

Stimulus integration in the bump attractor network. (A) Ring network with Mexican-hat connectivity— that is, strong local excitation (red connections) and broader inhibitory coupling (blue). (B) Network activity for neurons arranged according to their position in the ring (A). Due to strong recurrent connectivity, a bump of activity emerges in this network at a position determined by the external input and persists when the input is removed. For time-varying inputs, the activity bump (dashed line) moves toward a new position (solid black line). (C) Network activity in a single trial. The initial activity of the network (Middle) is spatially homogeneous and evolves into a bump while integrating a time-varying stimulus composed of eight oriented stimulus frames (Bottom). (C, Top) The phase of the bump (red) as a function of time closely tracks the running average of the orientations of the stimulus frames (blue). (D and E) Continuous stimulus estimate (D) and probability of clockwise choices (E) as a function of the average stimulus direction for stimulus durations of 1 s (four stimulus frames of 250 ms) and 2 s (eight stimulus frames). Categorical choices were obtained by converting positive angles to clockwise reports and negative angles to counterclockwise reports. Error bars indicate SD. Stim., stimulus.

We wondered whether through this mechanism the position (phase, ψ) of the activity bump could track the average of a time-varying stimulus. We simulated a task that required estimating the average direction of eight successive oriented stimulus frames with constant strength (e.g., stimulus contrast) and directions distributed between $-{90}^{°}$ and $+{90}^{°}$. As illustrated in a representative trial (Fig. 1C), we found that the evolution of the bump phase closely approximated the cumulative running average of the stimulus—that is, the time average of the stimulus up to a given time point (Fig. 1 C, Top). Indeed, estimation curves, obtained by simulating many trials, show that, on average, the bump phase closely tracks a continuous estimate of the averaged sensory input (Fig. 1D). The estimation accuracy improves with the stimulus duration, as expected from an integration process (error bars in Fig. 1D). This improvement can also be seen in psychometric curves obtained by converting the analog estimate to a categorical choice (Fig. 1E). In sum, these simulations show that the bump attractor network can integrate the stimulus over times much larger than the neural time constant ($\tau =20$ ms, stimulus duration $T_{\text{stim}}=2$ s).

Optimal Stimulus Integration with Bump Attractor Dynamics.

Motivated by the observation that the phase of the bump can track the average of the stimulus with striking precision (Fig. 1), we next sought to identify and characterize the neural network mechanisms underlying stimulus integration in the bump attractor network. To study the dynamics of the movement of the bump, we applied a standard perturbation method (ref.  36; SI Appendix) and reduced the network model (Eq. 3) to a 2D differential equation for the amplitude, R(t), and the phase of the bump, $\psi (t)$:

$$\tau \frac{\partial R}{\partial t}={\tilde{I}}_1\cos \left(\psi -{\theta }^{\text{stim}}\right)+{\tilde{I}}_{0}R-c{R}^3+{\xi }_1(t),$$ [1a]

$$\tau \frac{\partial \psi }{\partial t}=-\frac{{\tilde{I}}_1}{R}\sin \left(\psi -{\theta }^{\text{stim}}\right)+\frac{{\xi }_2(t)}{R},$$ [1b]

where τ is the neural time constant, and the time-varying stimulus input is characterized by its strength ${\tilde{I}}_1$ and its orientation ${\theta }^{\text{stim}}(t)$. The additional excitatory drive ${\tilde{I}}_0$ is proportional to the global excitatory drive to each neuron, relative to its critical value at the onset of the bump (${\tilde{I}}_0\propto I_0=I_{\text{exc}}-I_{\text{crit}}$; SI Appendix). The constant c depends on the synaptic connectivity profile and the nonlinear neural transfer function (SI Appendix, Eq. S3). In the absence of stimulus input (${\tilde{I}}_1=0$), the bump dynamics is determined by the terms ${\tilde{I}}_{0}R$ and $-c{R}^3$ in Eq. 1a, and we refer to them as the “internally generated bump dynamics.” Finally, the noise terms ${\xi }_1(t)$ and ${\xi }_2(t)$ are related to the internal stochasticity and to fluctuations in the stimulus realized as independent noise inputs to each neuron in the full model (Eq. 3). Note that such reduced models have been long studied in physics (37) and that they are universally valid near the bifurcation, independent of the details of the original network model. This reduced model allows us to study the dynamics of the bump analytically.

Perfect vector integration.

A key insight of this paper is gained by comparing the 2D model (Eq. 1) with the optimal computation of the running average of the stimulus direction. This implies keeping track of the circular mean of the time-varying stimulus direction ${\theta }^{\text{stim}}(t)$, which requires computing the vector sum of the stimulus vectors, each defined by their strength I₁ and their direction ${\theta }^{\text{stim}}$ (SI Appendix, Fig. S1 A and C; Materials and Methods). To compare this optimal solution with the bump attractor network, we derived a dynamical system that continuously tracks the cumulative circular average, the PVI. Optimal integration in the PVI unfolds on a 2D manifold, with an angular variable representing the stimulus average and a radial variable representing stimulus uncertainty. The corresponding 2D equation (Eq. 4) turned out to be nearly identical to the amplitude equation, but without the intrinsic dynamics of the bump amplitude (the two terms depending on R in Eq. 1a). This remarkable equivalence indicates that—when the internally generated bump dynamics are negligible—the bump attractor model achieves optimal integration by tracking the stimulus average in the phase and the stimulus uncertainty in the amplitude of its population activity. In the following, we will develop an intuition for this result and investigate the additional properties of the bump attractor model that originate from its nonlinear amplitude dynamics.

Dynamics of the bump.

From Eq. 1b, it directly follows that the rate of change of the phase (the angular speed $d\psi /dt$) depends on the ratio of the stimulus strength I₁ and the bump amplitude R. Thus, for a given stimulus strength I₁, the higher the amplitude of the bump, the smaller the angular speed—that is, larger bumps are more sluggish (SI Appendix, Fig. S2B). The steady-state bump amplitude is determined by the global excitatory drive I₀ ($R_{\infty }\propto \sqrt{I_0}$; SI Appendix), indicating the key role of this parameter for the integration dynamics.

A deeper understanding about how a time-varying stimulus impacts the phase of the bump can be gained if we visualize the dynamics of the amplitude equation, Eq. 1, as a three-dimensional potential well $\mathrm{\Theta }\left(R,\psi \right)$, given by (SI Appendix)

$$\mathrm{\Theta }\left(R,\psi \right)=-R{\tilde{I}}_1\cos \left(\psi -{\theta }^{\text{stim}}\right)-\frac{{\tilde{I}}_0}{2}{R}^2+\frac{c}{4}{R}^4.$$ [2]

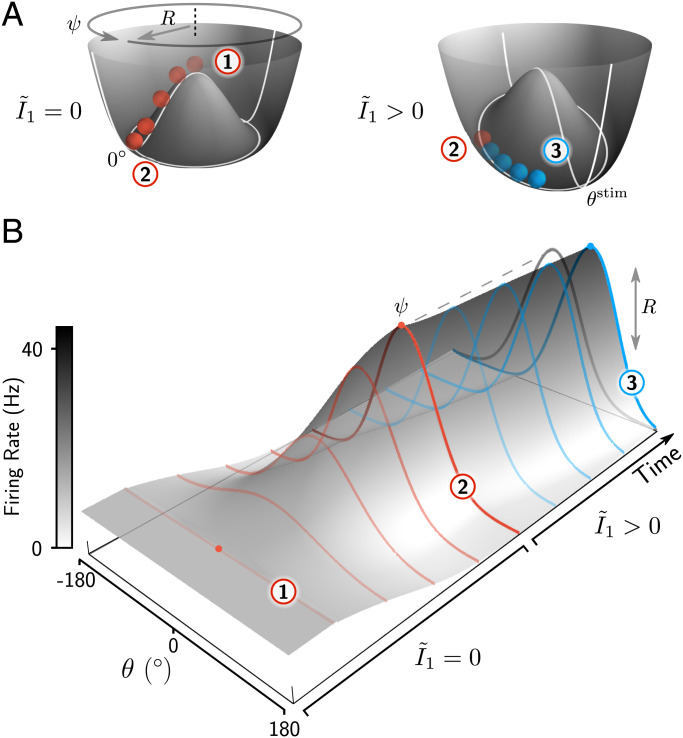
This allows us to describe the mechanism underlying the evolution of the bump graphically as a heavily damped ball sliding down the walls of the potential (Fig. 2). In the absence of stimulus input ($I_1=0$), the potential $\mathrm{\Theta }\left(R,\psi \right)$ resembles a juice-squeezer-shaped surface with a circular well representing bump attractor states (R  >  0) that are neutrally stable along the angular dimension ψ (Fig. 2A). The unstable fixed point at the center of the manifold corresponds to a bump with zero amplitude (R = 0) (Fig. 2, point 1)—i.e., the uniform activity state.* The formation of the bump is described by the movement of the ball that rolls downward toward the stable manifold, while increasing its distance to the center, R (Fig. 2 A and B, transition from point 1 to point 2). When presenting a stimulus to the network ($I_1>0$), the radial symmetry of the potential is broken, and a deeper region arises at the location of the stimulus ${\theta }^{\text{stim}}$ (Fig. 2 A, Right). If the ball has already reached the stable manifold, the stimulus will force it to move toward this deeper state along the manifold (Fig. 2A, transition from point 2 to point 3), corresponding to a movement of the bump toward ${\theta }^{\text{stim}}$, accompanied by only slight changes in bump amplitude (Fig. 2B). In contrast, if the ball has not yet reached the stable manifold—i.e., when a stimulus is applied during the initial bump formation, as in Fig. 1C—it will cause both a change in bump phase and, together with the internally generated bump dynamics, a change in bump amplitude.

Fig. 2.

Dynamics of the bump attractor network in the potential landscape. (A) Geometrical representation of the potential corresponding to the dynamics of the bump attractor (Eq. 2). The surface of this potential represents the dynamical 2D manifold of Eq. 1, such that a point on this surface is a possible state of the activity bump, characterized by its amplitude R and phase ψ. The movement of the red ball in each potential corresponds to the dynamics of bump formation and translation shown in B. (B) Evolution of the network activity from the unstable homogeneous state 1 to the stable bump state 2 in the absence of external stimuli (${\tilde{I}}_1=0$), followed by a translation of the bump (transition from state 2 to state 3) toward the location of the stimulus ${\theta }^{\text{stim}}$ when the external stimulus is present (${\tilde{I}}_1>0$). Note that for ${\tilde{I}}_1=0$, the bump forms at an arbitrary angle ψ, determined by noise fluctuations.

In general, successive stimulus frames of a time-varying stimulus drag the bump toward their respective orientations in a continuous fashion (Fig. 1C), with an angular displacement that depends on the current bump amplitude (SI Appendix, Fig. S2B). We can distinguish two distinct stages of the bump dynamics: 1) the transient regime, in which the bump amplitude is growing continuously; and 2) a fully formed bump. The integration properties of the bump in these two stages are qualitatively different. In the first stage, during the transition from homogeneous network activity to a persistent bump state, the bump grows in amplitude, driven by the internal dynamics and the stimulus, and successive stimulus frames become less and less effective in moving the bump. In the second stage, when the bump amplitude has reached its steady state, it cannot grow further, and the impact of subsequent stimuli becomes constant over time. Equipped with the theoretical insights gleaned from our analysis of Eqs. 1 and 2, we can now study different stimulus-integration regimes in the network.

The Ring Model Shows a Variety of Temporal Evidence-Integration Regimes.

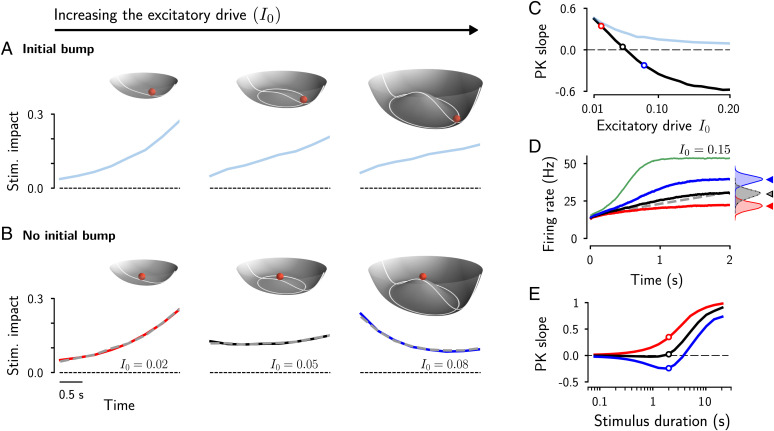
Our theoretical results showed that the changes in bump phase caused by a time-varying stimulus critically depend on the bump amplitude, suggesting its key role in the integration of sensory stimuli. To investigate this, and to confirm the validity of the analytical results in a wide parameter range, we ran simulations in which networks with different steady-state bump amplitudes had to estimate the average direction of a sequence of oriented frames, distributed between $-{90}^{°}$ and $+{90}^{°}$, as in Fig. 1C. The bump amplitude was set by varying the global excitatory drive to the network I₀ and keeping all other parameters fixed. To quantify the dynamics of evidence integration, we used the psychophysical kernel (PK), which measures the impact of each stimulus frame on the final direction estimate (i.e., the bump position at the end of the trial) using a regression model (Materials and Methods).

We first considered the simpler case, where a trial starts with an initial bump (i.e., the ball is in the circular attractor well; point 2 in Fig. 2). This is relevant because spontaneous bump states have been observed in prefrontal and visual cortex (38–40), and we elaborate on the potential impact on perceptual judgments further below. The PKs we obtained for different values of I₀ are qualitatively similar (Fig. 3A): They all rise, indicating that the stimulus frames later in the trial have more impact on the final estimate (i.e., the bump phase ψ at the end of the trial) than early stimulus frames. This commonly called “recency” effect becomes weaker as I₀ increases, yielding a decrease of the PK slope (Fig. 3C). The reason for the general overweighting of late stimulus information (leaky integration) in the bump attractor model is not trivial, but can be understood by comparison with the PVI (Eq. 4) and, more specifically, by comparing their corresponding potentials. The potential of the PVI (Eq. 5) takes the form of a plane going through the origin and tilted toward the stimulus direction ${\theta }^{\text{stim}}$. Thus, the evolution of R in the PVI only depends on the particular combination of the directions of stimulus frames in each trial, and, on average, R will grow because of a net movement in the direction of the mean of the stimulus distribution ${\overline{\theta }}^{\text{stim}}$ (SI Appendix, Fig. S1D shows how the growth rate depends on the width of the stimulus distribution). As R grows, the angular updates become smaller with each stimulus frame (in other words, as the number of samples grows, the running average direction increasingly relies on the already-accumulated information). This is in contrast to the integration process in the bump attractor network with a formed bump, in which the bump amplitude is fixed (determined by the shape of the potential; Fig. 2A), and integration occurs only in the angular direction. Because of this, the network gives equal weight to the angular updates over time, thus partly erasing the accumulated stimulus information, while overweighting late stimulus information. The strength of the recency effect depends on the bump amplitude. As described in the previous section, the smaller the I₀, and, thus, the bump amplitude, the larger the angular displacement for a given stimulus strength I₁ and the faster the bump can track the orientation of incoming stimuli, resulting in a PK with increasing recency effect (Fig. 3 A and C and SI Appendix, Fig. S2).

Fig. 3.

The global excitatory drive ${\mathbf{I}}_{\mathbf{0}}$ determines the integration regime of the network. (A) PKs for increasing values of I₀ (Lower; from left to right, $I_0=0.02$, 0.05, and 0.08) with a fully formed bump as the initial condition. The PKs describe the impact of each stimulus frame on the estimated average orientation. (A, Upper) For small values of I₀, the potential takes the form of a steep paraboloid, where the bump has little space to grow (Upper Left). Intermediate values of I₀ transform the potential into a wide surface similar to a dish with a relative flat central area (A, Upper Center). Increasing I₀ widens the potential and gives rise to an increasingly deeper circular manifold at the bottom of the juice squeezer (A, Upper Right). (B) PKs as in A, but with spatially homogeneous initial conditions (flat network activity; ball at the center of the potential). PKs were obtained from numerical simulations of the ring attractor network (colored lines) and from simulating the amplitude equation (dashed gray lines; Eq. 1). (C) PK slope as a function of the excitatory drive I₀, for the spatially homogeneous (black line) and inhomogeneous (blue line) initial conditions. (D) Evolution of the bump amplitude for different values of I₀. Colored lines correspond to values of I₀ used in B. The evolution of the vector length in the PVI is shown for comparison (dotted gray line). (D, Inset) Distribution of the bump amplitude at the end of the trial. The histograms for $I_0=0.05$ and for the PVI (in black) perfectly overlap. (E) PK slope as a function of the stimulus duration, with stimuli composed of eight frames of varying duration between 10 ms and 2.5 s (i.e., a total stimulus duration of up to 20 s). Corresponding PKs are shown in SI Appendix, Fig. S4A. Stim., stimulus.

Strikingly, when we ran simulations in which the network had to estimate the average stimulus direction starting the trials in the homogeneous network state, with no bump formed (i.e., at the unstable center position on the potential; point 1 in Fig. 2; see SI Appendix for details on the initial conditions), we observed three qualitatively distinct integration regimes, depending on the global excitatory drive to the network I₀ (Fig. 3B and Movies S1–S3). In the first regime, a small I₀ yields again a recency PK (Fig. 3 B, Left). Here, the steady-state bump amplitude is relatively small, and the bump can only grow very slightly over time (Fig. 3D, red line). Thus, stimulus integration is limited by the small bump amplitude, as in the previously considered case with the bump formed from the beginning of the trial (Fig. 3 A, Left).

Second, for large I₀, the networks showed a “primacy” effect—that is, early stimulus information now had a higher impact on the final estimation than later stimulus information (Fig. 3 B, Right and Movie S3). This can be understood by considering that in this regime, the bump amplitude is small at the beginning of the trial, but then quickly grows to a large amplitude (Fig. 3D, blue line). Thus, the bump can quickly follow the stimulus direction early in the trial during the formation of the bump, but while growing, it becomes increasingly sluggish, and stimulus information becomes comparably less effective in displacing the bump. Compared to the PVI, the bump amplitude grows too quickly because it is driven by the internally generated dynamics in addition to the stimulus (i.e., the potential is not flat as for the PVI, but has a peak in the center; Fig. 3 B, Top Right). The resulting down-weighting of later stimulus frames only occurs while the bump is growing (transition from point 1 to point 2 in Fig. 2). Once the steady-state bump amplitude has been reached (corresponding to the attractor well of the potential), the model starts to overweight incoming evidence, and, as a consequence, for very long stimulus durations, the model will eventually show a recency PK (Fig. 3E, blue line).

Third, for intermediate values of I₀, primacy and recency effects balance out, and we obtained an almost perfectly uniform PK (Fig. 3 B, Center and Movie S1). Thus, in this regime, all stimulus frames had the same impact on the final estimate over the whole trial (PK slope $=0$; Fig. 3C). In this case, the potential has only a relatively small peak at the center, approximating the flat potential of the PVI (Fig. 3 B, Center Upper). The growth rate of the bump amplitude is mainly driven by the stimulus, as in the PVI (SI Appendix, Fig. S1D). The value of I₀ in which the model best approximates the PVI depends on the stimulus strength, the stimulus duration, and the distribution of the stimulus directions (SI Appendix, Fig. S4). Approximately perfect integration is only possible as long as the bump amplitude can be strongly shaped by the external stimulus (before the well of the potential is reached)—that is, perfect integration relies on the transient dynamics during the transition from spontaneous activity to a persistent bump state. For long stimulus durations, the bump state will eventually be reached, and integration again becomes leaky, as indicated by a recency PK (Fig. 3E, positive PK slopes). In contrast, for very short stimulus durations, the internally generated bump dynamics become negligible, and the PKs approach uniform integration in all cases (Fig. 3E). Thus, primacy, uniform, and recency PKs are robustly observed for small and intermediate stimulus durations ($T_{\text{stim}}$ in the range of hundreds of milliseconds up to several seconds).

Accuracy of Stimulus Estimation.

We next quantified the estimation accuracy in the different temporal integration regimes of the bump attractor model (shown in Fig. 3B). We computed stimulus-estimation curves by reading out the bump phase from the network activity at the end of the trial, averaging the estimates across trials, and plotting them as a function of the actual mean orientation ${\overline{\theta }}^{\text{stim}}$ (Fig. 4A).

Fig. 4.

Dependence of estimation accuracy on the global excitatory drive ${\mathbf{I}}_{\mathbf{0}}$ and the noise ${\mathbf{\sigma }}_{\text{OU}}$. (A) Estimated average (Avg.) direction as a function of the true average of a 2-s stimulus composed of eight oriented frames, for increasing values of I₀. Solid lines indicate the average across trials, and the shadings indicate SD. (A, Insets) Corresponding PKs from Fig. 3B. (B) The rms error (SI Appendix) of the ring attractor network with noise (${\sigma }_{\text{OU}}=0.15$) and without noise (${\sigma }_{\text{OU}}=0$) as a function of the global excitatory drive I₀. The estimation error for ${\sigma }_{\text{OU}}=0.15$ (black line) corresponds to the estimations shown in A. The estimation error for a perfect weighted average of the stimulus directions (with the same temporal weighting as the network model, but otherwise optimal; SI Appendix) is shown for comparison. Note that the curve corresponding to ${\sigma }_{\text{OU}}=0$ has been shifted such that for both conditions the critical value of $I_{\text{exc}}$ at the bifurcation point is aligned. (C) Dependence of the estimation error on the stimulus duration and the noise amplitude ${\sigma }_{\text{OU}}$. Stimuli had eight frames of varying durations, as in Fig. 3E, and the excitatory drive was $I_0=0.05$. Estimation error curves for other values of I₀ are shown in SI Appendix, Fig. S4C.

Estimation bias.

When varying the bump amplitude through a change in excitatory drive I₀, we found that the estimation curves always stayed close to the identity line (Fig. 4A). We quantified this by computing the estimation bias (SI Appendix) and obtained $b_{\text{est}}<2^{°}$ for all values of I₀ (SI Appendix, Fig. S5E, red line). Unbiased estimation in the bump attractor model^† is a direct consequence of starting the integration process in the neutral center of the potential and the symmetry of the potential (Fig. 2, point 1). The direction of the first stimulus frame determines the initial phase of the forming bump in an unbiased manner. Subsequently, the bump moves and grows, but as long as the directions of the stimulus frames are drawn independent and identically distributed from some underlying distribution, clockwise and counterclockwise bump displacements are equally likely, and the trial average of the estimates remains unbiased, irrespective of the temporal weighting regime (SI Appendix, Fig. S5A). We also investigated the estimation bias in the network with an initially formed bump (Fig. 3A and SI Appendix, Fig. S5). In psychophysical experiments, this initial bump position could be determined by a reference line shown before the onset of the stimulus (3, 4), or it could be related to the subject’s prior expectation before the start of the stimulus (5). In the network, we found an attractive bias of the estimates toward the initial condition that decreases over time as the stimulus is integrated (SI Appendix, Fig. S5D). Moreover, for a fixed stimulus duration, its magnitude increased with the global excitatory drive I₀ to the network (SI Appendix, Fig. S5E, blue line). The reason is that a higher I₀ yields larger bumps that are more sluggish and, thus, need more time to overcome the bias caused by the initial bump position.

Estimation error.

We found that the trial-to-trial variability of the estimates depended on the integration regime (Fig. 4A, shaded areas; Fig. 4B). Several factors could give rise to estimation errors in the attractor model and may thus contribute to this dependence: 1) internal noise and stimulus fluctuations of magnitude ${\sigma }_{\text{OU}}$ (Materials and Methods); 2) suboptimal evidence integration due to nonuniform evidence integration (i.e., nonuniform PKs); and 3) additional impact of the nonlinear internally generated bump dynamics on evidence integration not captured by the PK. We first considered the impact of the noise by running simulations of the network without noise (${\sigma }_{\text{OU}}=0$) and obtained, as expected, a general decrease of the estimation errors (Fig. 4B, orange line). We next tested to what degree the remaining estimation errors could be accounted for by the nonuniform evidence weighting in the primacy and recency regimes. To show this, we compared the dependency of the estimation error on I₀ of the attractor model, with the estimation error obtained by computing the true average of the stimulus directions with the PVI, but weighted with the PKs from the bump attractor model (Fig. 4B, dashed line). The obtained estimation errors are almost indistinguishable from the errors of the noiseless bump attractor network. Thus, the increase of estimation errors for nonoptimal I₀ can be attributed to the suboptimal, nonuniform, temporal weighting captured by the PK. Because the nonlinear internally generated bump dynamics of the ring model can only yield an approximately uniform PK, the estimation errors are nonzero, even for the best I₀ for a given stimulus distribution (particularly for wide distributions; SI Appendix, Fig. S4D). We confirmed that the estimation errors for the noiseless bump attractor network were low for the entire range of stimulus durations for which uniform weighting is achieved (Fig. 4C, dashed line; Fig. 3E, black line). Furthermore, we found that the relative contribution of noise and suboptimal evidence integration to the estimation error depends on the stimulus duration (Fig. 4C). For short stimulus durations, the noise cannot be averaged out, and it becomes the dominant factor. For very long stimulus durations, the noise is essentially averaged out, and estimation errors are primarily caused by suboptimal weighting, as indicated by converging estimation error curves in Fig. 4C. Finally, we found that temporal gaps in the stimulus stream increased the estimation errors due to noise-driven bump diffusion during the gap periods and changes in evidence weighting caused by longer total integration times (SI Appendix, Fig. S6). Together, these results show that the estimation accuracy in the bump attractor network is limited by noise and by the internally generated bump dynamics causing nonuniform evidence integration, whereas further contributions of nonlinearities (not captured by the PK) are negligible.

Robustness of stimulus estimation to noisy connectivity.

All simulations so far were obtained from ring attractor networks with idealized, rotation-invariant, and noiseless connectivity profiles. It is well known that even small noise in the weight profiles destroys the neutrally stable ring attractor manifold and leads to a few discrete attractor states (28). The drift of the bump toward one of the few stable positions can be disastrous for working memory, where one wants to store a localized, cue-specific activity pattern over a prolonged time interval (41). However, we reasoned that stimulus integration in the transient regime during the formation of the bump may be more robust against heterogeneous connectivity. To test this, we ran simulations with different noisy connectivity matrices and found that this leads to systematic deviations of the stimulus-estimation curves from the identity line (i.e., estimation biases) and increased estimation errors (SI Appendix, Fig. S7). Nevertheless, even for relatively large noise in the connectivity matrices, the estimation curves were monotonic functions of the stimulus average in all cases, and all networks showed primacy, uniform, and recency PKs, as observed for noiseless connectivity (SI Appendix, Fig. S7).

The Ring Model Explains Heterogeneity in Integration Dynamics in Humans.

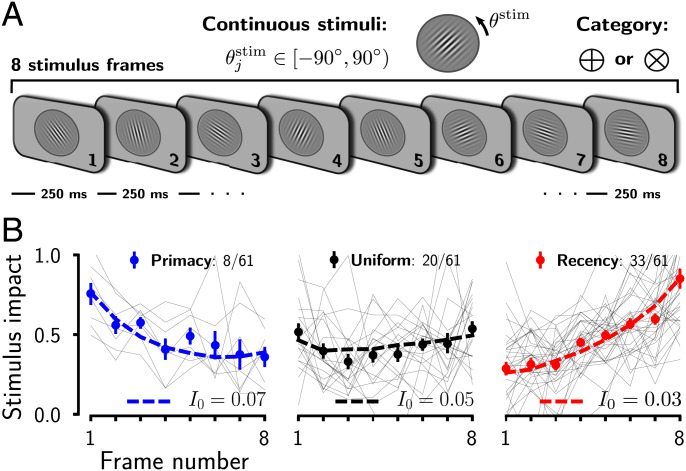
We tested whether human subjects show variations in their integration dynamics in a stimulus-averaging task and whether the ring model could parsimoniously account for those variations (Fig. 5). In this task, a visual stream of eight oriented Gabor patters was presented to participants (Fig. 5A; ref. 33). Each frame had an orientation between $-{90}^{°}$ and ${90}^{°}$ and a fixed duration of 250 ms. At the end of the stream, participants reported whether, on average, the tilt of the eight frames fell closer to the cardinal or diagonal axes. Participants were able to combine the evidence favoring either option, improving their accuracy in trials with higher evidence (33–35).

Fig. 5.

The ring attractor model accounts for experimentally observed PKs. (A) Category-level averaging task (33–35). Participants reported whether, on average, the tilt of eight oriented Gabor patterns fell closer to the cardinal $\left\{0^{°},{90}^{°}\right\}$ or diagonal $\left\{-{45}^{°},{45}^{°}\right\}$ axes. (B) PKs obtained from human subjects were heterogeneous. Thin lines represent the PKs of individual subjects and data points with error bars the group averages. We fit the ring model to the experimental data by varying the excitatory drive I₀ (dashed lines).

We merged the data from three studies (33–35) carried out using very similar experimental conditions (n = 61 subjects; Materials and Methods). We computed their individual PKs and classified the subjects according to their temporal weighting behavior (primacy, uniform, and recency) (Materials and Methods). As previously reported (34), across participants, there was a tendency for late temporal weighting (recency). However, subject-by-subject analysis revealed a broad range of integration dynamics (Fig. 5B and SI Appendix, Fig. S8). The majority of participants weighted more the sensory evidence during the late periods of the stimulus (33/61), yet a substantial proportion of the participants weighted the evidence approximately uniformly (20/61). Finally, a minority of participants (8/61) weighted early frames of the stimulus more than late frames, showing a primacy PK. Qualitatively, the ring model could capture these different temporal integration dynamics observed in the psychophysical experiments (Fig. 3). To assess whether the model could explain the data in a quantitative manner, we performed simulations with the same stimulus statistics as in the behavioral experiment. We systematically adjusted both the global excitatory drive to the network, I₀, and the noise level, ${\sigma }_{\text{OU}}$, such that the ring network reproduced, on average, the experimental results (Fig. 5B), characterized by the slope of the across-subjects PKs and the average performance for each integration regime (primacy, uniform, and recency). The intersubject heterogeneity in temporal evidence weighting could thus parsimoniously be explained by varying the overall excitatory drive that determines the amplitude of the bump, while adjusting the noise fluctuations to match the performance of the subjects.

It is conceivable that the global excitatory drive does not only differ between individuals, but that it could also be modulated on a trial-to-trial basis, such that it may therefore change the time course of evidence integration, depending on the current task conditions. Such a task-driven change has previously been observed in a similar task as in Fig. 5 that studied the mechanisms of perceptual choices under focused and divided attention (35). In that task, two spatially separated stimulus streams were presented simultaneously, and subjects had to integrate either a single or both streams in a trial-to-trial basis. We built a network model consisting of two ring circuits (SI Appendix) and found that the results of this experiment can be explained by a change in the excitatory drive that controlled the allocation of a fixed amount of resources between the two circuits (SI Appendix, Fig. S9). In sum, our model suggests that the overall excitatory drive determines the integration regime. Control signals, like top-down attention signals or neuromodulatory gain changes, can impact the dynamics of evidence integration, and the model makes specific predictions about the underlying changes in neural activity.

Bump Attractor Dynamics Links Integration Dynamics and RTs.

Finally, to derive specific predictions from the model that go beyond the shape of the PK, we extended the model by coupling the ring-integration circuit to a canonical decision circuit (6, 7) and studied the decision build-up in the different evidence-integration regimes (Fig. 6 and SI Appendix, Fig. S10). In this two-circuit model (Fig. 6A and SI Appendix), evidence about the average stimulus direction is integrated in the phase of the activity bump in the integration circuit and then converted to a categorical choice in the decision circuit. The model architecture is similar to previous models that incorporate a decision read-out circuit (14, 42), and it is consistent with experimental evidence suggesting that premotor cortex shows discrete attractor dynamics in binary decision tasks (43, 44). However, we would like to note that, while our two-circuit model is broadly consistent with existing data, a direct validation of our specific architecture must await future experiments, ideally from simultaneous multiarea recordings.

Fig. 6.

Dependence of RTs on the shape of the PK. (A) Ring integration circuit coupled to a categorical decision circuit (SI Appendix). Left (L) and right (R) excitatory populations in the decision circuit receive inputs, I_L and I_R, from their corresponding side of the ring. The inhibitory population (I) promotes winner-take-all competition (6). At the end of the stimulus presentation, the decision process is triggered by the activation of an urgency (or choice commitment) signal that initiates the competition. (B) Dependence of RTs on the excitatory drive I₀ in the model. (B, Upper) Average activities of the L and R populations for low (dashed) and high (solid) I₀ and stimuli with average direction of 15^∘. RT is measured from the onset of the urgency signal (at t = 2 s; shaded area) until one of the firing rates reaches the threshold $r_{\mathrm{th}}=50$ Hz. B, Upper, Inset shows the summed bottom-up inputs, I_L and I_R. (B, Lower) Average activity of the integration circuit at the end of the stimulus presentation. (C) Average RTs as a function of the PK slope. (D) RTs of human subjects (n = 47) vs. their PK slopes show a significant correlation (r = 0.39, P = 0.006, t test). Subjects’ RTs were z-scored for each dataset (SI Appendix).

Specifically, we were interested in how the dynamics of the bump impacts the RT, from stimulus offset to reaching a categorical choice. We found that the model predicts a direct relationship of RTs and the shape of the PK (Fig. 6C). Different PKs in the model are obtained by varying the excitatory drive to the network (Fig. 5). Increasing the excitatory drive leads to an increase of the bump amplitude and a transition from recency over uniform to primacy weighting (Fig. 3 B and C). The bump amplitude, in turn, affects the RT in the two-circuit model (Fig. 6B). RTs are larger for small bump amplitudes because the decision circuit receives weaker input and, therefore, takes longer to reach the decision threshold. Taken together, the model predicts that primacy temporal weighting should be accompanied by shorter RTs and recency weighting by longer RTs—i.e., RT should increase with the slope of the PK (Fig. 6C). Note that we would obtain the same prediction if we replaced the decision circuit with a different mechanism (e.g., a drift-diffusion model), as long as the RT is a function of the firing rate in the integration circuit. We tested this nontrivial prediction in the experimental data and indeed found a significant correlation between the subjects’ RTs and PK slopes (Fig. 6D). It is unlikely that the differences in RTs could be explained by a different fraction of correct trials depending on the PK slope because we did not find a correlation between PK slope and the fraction of correct trials (Fig. 6D; $r=0.04,\hspace{0.17em}P=0.774,\hspace{0.17em}n=47$, t test). Moreover, we found that RTs in human subjects decreased with the average stimulus evidence for correct trials and increased for incorrect trials, which is also captured by the network model (SI Appendix, Fig. S10). In sum, the two-circuit model provides a mechanistic link between neural population activity, evidence-integration dynamics, and RTs that can be further validated experimentally.

Discussion

We investigated the neural network mechanisms underlying the integration of a time-varying stimulus (e.g., a sequence of visual gratings with different orientation) for continuous perceptual judgments. Analytically and through simulations, we showed that the classical continuous ring attractor model (17, 25, 28) can nearly optimally compute the time integral of stimulus vectors defined by the strength and the direction of the stimulus. As required by optimal integration of a circular feature, the population activity of the network unfolds on a 2D manifold with an angular and a radial latent variable. The angular variable corresponds to the circular average of the stimulus directions and is represented by the position of the network’s activity bump. The radial variable evolves, depending on the dispersion of the stimulus directions, and it is represented by the amplitude of the activity bump. Thus, the network simultaneously tracks the running average of the stimulus and the uncertainty of sensory information. The precise dynamical regime in which the model closely approximates perfect vector integration depends on the stimulus statistics, as well as the stimulus strength and duration (SI Appendix, Fig. S4). It is characterized by a relatively wide and shallow potential, so that the evolution of the bump is dominated by the stimulus, and not by the internally generated bump dynamics (Fig. 3).

A key finding here is that optimal stimulus averaging relies on the transient dynamics during the formation of the bump, whereas evidence weighting in a network with a fully formed bump becomes suboptimal. The limiting factor imposed by the internal dynamics of the network is that the bump amplitude cannot grow beyond a maximum value that depends on the model parameters and is proportional to the overall excitatory drive to the network. When the maximum bump amplitude is reached, which will eventually happen for long stimulus durations, the model has reached the neutrally stable ring attractor and can still track the average stimulus phase. However, the model is then overweighting later stimulus frames, similar to a leaky integrator. In addition to this recency effect, the model can also show primacy temporal weighting when the internal network dynamics contributes to a rapid initial growth of the bump, and initial stimulus frames have a relatively higher impact on the evolution of the bump phase. In sum, we have uncovered the fundamental mechanism underlying stimulus integration in the phase and the amplitude of the bump of the ring attractor model.

Flexibility of Temporal Integration.

The internally generated bump dynamics endow the bump attractor network with a variety of integration kernels, ranging from early (primacy) over uniform to late (recency) temporal weighting. The key parameter that controls the integration dynamics is the global excitatory drive to all neurons in the network, I₀ (Fig. 3). Keeping all other parameters fixed, I₀ determines the depth and the width of the potential (SI Appendix, Fig. S2) and, thus, the maximal bump amplitude and the intrinsic network dynamics. We showed that by varying I₀, the model could account for the heterogeneity in how human observers weighted sensory evidence across a stream of oriented stimulus frames (Fig. 5), as well as for their RTs (Fig. 6 and SI Appendix, Fig. S10). In addition to a different level of global excitatory drive, subjects are likely to show other differences as well—for example, a different E/I ratio or a different gain of the neural circuits involved in evidence integration. Effectively, in the model, these intersubject differences can be captured by different values of I₀. In particular, it can be shown that a change in the slope of the neuronal transfer function is mathematically equivalent to a change in I₀. The global cortical gain can also be modulated in a task-dependent manner across time in individual subjects—for example, controlled by top-down control signals or neuromodulation (45–47). This provides a mechanistic explanation for attention-driven differences in evidence integration (SI Appendix, Fig. S9). Moreover, a time-varying neural gain or excitatory drive in the model can switch the network from an integration regime into a working-memory regime that has different requirements. During stimulus estimation, the excitatory drive should be moderate, so that the network has a relatively shallow potential and would act as a PVI. Subsequently, after stimulus presentation, an increase of I₀ can make the potential wider and deeper and, thus, increase the stability of the bump against noise and against further incoming stimuli, as is needed for distractor-resistant working memory (25, 48). Such a transition could also be gradual—for example, caused by a ramping I₀ (49).

Mechanisms Underlying Biases in Perceptual Estimation and Categorization Tasks.

Independent of the temporal weighting regime, the average orientation estimates of the model were always unbiased, as long as the integration process starts with homogeneous network activity (Fig. 4). Starting the integration process with a formed activity bump shifts temporal integration toward recency and can introduce estimation biases toward the initial bump position (Fig. 3 and SI Appendix, Fig. S5). The existence of bump states before stimulus presentation is supported by neural population recordings (38–40). A recent paper (5) investigated how prior expectations influence motion-direction estimation in humans and found attractive biases toward the predictive cued direction and a correlation between reported directions and directions decoded from magnetoencephalography (MEG) activity that emerged before stimulus onset. These findings are consistent with the initial bump condition in our model (SI Appendix, Fig. S5).

Moreover, it has been shown in combined discrimination and estimation tasks that stimulus estimation is influenced by a categorical decision causing postdecision biases (3, 4, 15, 50). It has been suggested that these bias effects are mediated through selective attention signals and through changes in global gain (4, 50). Our bump attractor model allows for testing these hypotheses. For example, in the seminal work of Jazayeri and Movshon (3), subjects showed a repulsive bias of direction estimates (away from a reference) while performing a fine-motion-discrimination task. In contrast, subjects showed an attractive bias (toward a reference) in a similar coarse discrimination task, in which they had to report whether the dots moved toward or 180^∘ away from the reference. In the model, a spatially modulated attention signal, targeting the location of the two possible choices in the ring, could potentially reproduce the experimentally observed biases. During the fine-discrimination task, the attention signal would attract the bump toward the clockwise or counterclockwise directions away from the reference, causing a repulsive bias, and the same mechanism would cause the attraction bias during the coarse-discrimination task. Overall, our network model provides a comprehensive computational framework for investigating the neural mechanisms underlying stimulus estimation and perceptual categorization and their interaction in future studies.

Comparison with Other Models.

Bump attractor models have previously been used to model angular path integration in the head-direction system (27–30, 51). This involves the integration of angular head velocity (at which the animal’s head turns), such that the bump position tracks the current direction of the head (52). This integration process relies on a different mechanism than stimulus integration in our model. Head-direction models translate a velocity signal into a rotation of the bump by introducing an asymmetry in the attractor dynamics. This can be realized through populations of right- and left-rotation cells that are selectively activated by rightward and leftward angular head-velocity inputs and are connected to head-direction cells with a spatial offset (27, 51). As a result, in these models, the angular head velocity controls the speed of the bump, such that a constant angular head velocity yields a constant bump rotation. In contrast, our model does not include a rotation mechanism, and the bump moves with an angular speed that is determined by the sine of the difference of the current bump position ψ and the stimulus direction ${\theta }^{\text{stim}}$ (Eq. 1b). Furthermore, nearly optimal computation of the stimulus average is only possible in the transient regime, while head-direction models operate in the regime in which the bump is already fully formed.

Furthermore, bump attractor networks have previously been used to model multiple-choice decision making, with several activity bumps representing discrete choice options (24). Evidence accumulation in this model relies on competitive dynamics between the bumps, which lead to ramping up of the firing rate of the winning bump. This is in stark contrast to the stimulus averaging carried out jointly in the amplitude and the phase of a single activity bump in our model.

Mathematically, our bump attractor model can be viewed as a generalization of the discrete attractor model of two-choice perceptual decision making (6, 7, 9, 53). However, the dynamics of evidence integration in the two models are fundamentally different. Discrete attractor models have a double-well potential that usually leads to a primacy temporal weighting because once the system settles into one of the two attractors, it remains there until the end of the trial. Recently, we have described how uniform and recency weighting can be obtained when fluctuations in the stimulus together with the internal noise are strong enough to overcome the categorization dynamics and cause transitions between the attractor states (53). In contrast to this, in the bump attractor model, a continuous integration process—without abrupt transitions—is realized in the amplitude and phase of the bump, and the stimulus always impacts the bump phase, yielding recency without the need for strong fluctuations.

A previous model proposed that populations of Poisson-spiking neurons can represent probability distributions, with the amplitude of a bump-shaped population activity related to the variance of the distribution (12, 14). In our model, bump amplitude and stimulus variability are also related, but as a consequence of the optimal computation of the circular mean. A further substantial difference is that the two models solve a very different task: Our model computes the circular average of stimuli with time-varying orientation based on attractor dynamics, whereas the model from Beck et al. (14) computes the posterior distribution of accumulated noisy stimulus information for optimal decision making by means of near-linear integration.

Several previous models of categorical decision making can explain primacy and recency effects in evidence accumulation based on different mechanisms (53–57). Here, we have shown that the global excitatory drive or a global gain change provides a parsimonious explanation for different PK shapes in continuous estimation tasks. How a change in evidence integration is realized in the brain is an interesting open question that needs to be addressed experimentally (e.g., ref. 58).

Experimental Predictions Provided by Our Model.

Our model accounts for the heterogeneity in PKs observed in humans (Fig. 5), and we have confirmed the model prediction of a relationship between PKs and RTs (Fig. 6). To further validate the dynamical mechanisms that we propose, we derived several specific predictions that can be tested in human or monkey experiments.

First, our model predicts characteristic changes of the evidence-integration dynamics when changing the strength, the duration, or the statistics of the stimulus. PKs should shift toward recency for longer stimulus durations (Fig. 3E) and for higher stimulus contrast, which could be tested in a psychophysical experiments with randomly interleaved trials. Additionally, the model predicts that broader distributions of the stimulus directions would shift the PK toward primacy and also increase the estimation error (SI Appendix, Fig. S4D). These predictions are constrained by the fundamental mechanisms that govern the integration dynamics in the bump attractor network, which are fully captured by the amplitude equation (Eq. 1).

Second, the dynamics of evidence integration crucially depends on the global excitatory drive or gain of the model (Fig. 3), and this could be tested experimentally by using pharmacological or optogenetic manipulations. A recent study has compared stimulus integration in human participants in sessions where they have been administered the N-methyl-d-aspartate receptor antagonist ketamine or a placebo (59). Reduced excitability under ketamine led to more recency PKs (more leaky integration), consistent with a reduction in excitatory drive in our model.

Third, the central prediction of our model is a systematic relationship between the amplitude of the population response and the rate of change of its phase (SI Appendix, Fig. S2B). This could be validated in simultaneous multiunit recordings from parietal or frontal areas in monkeys performing an orientation-averaging task. It would require decoding the current estimate of the average direction during evidence integration and measure the impact of individual stimulus frames on this estimate. The change of phase in response to the same orientation difference (between stimulus frame and current average) should decrease in a manner inversely proportional to the population firing rate. Neural recordings would also allow for testing whether neural firing rates and the estimates reported by the subject are related, as predicted by the bump attractor model, as in prefrontal cortical neurons during spatial working memory (26). Thanks to recent advances in fine-grained decoding of sensory and decision information across multiple brain areas from MEG activity (60), it may be possible to test the same prediction noninvasively in humans.

Finally, our work suggests that the same neural circuits that are involved in working memory may also be able to carry out stimulus averaging in perceptual estimation tasks. Bump attractor dynamics may thus be a versatile and unifying neural mechanism underlying both working memory and evidence integration over prolonged timescales.

Materials and Methods

Ring Model.

The dynamics of the bump attractor model are described in terms of the effective firing rate, $r\left(\theta ,t\right)$, of a neural population arranged in a ring, $\theta \in \left[-\pi ,\pi \right)$ (Fig. 1A), obeying the integro-differential equations (17, 18, 61).

$$\begin{array}{l}\tau \frac{\partial r}{\partial t}=-r+\mathrm{\Phi }(\frac{\tau }{2\pi }{\displaystyle {\int }_{-\pi }^{\pi }w}\left(\theta -\theta \prime \right)r\left(\theta \prime ,t\right)d\theta \prime \\ \hspace{1em}+I_{\text{exc}}+I_{\text{stim}}\left(\theta ,t\right)+\xi \left(\theta ,t\right)),\end{array}$$ [3]

where τ is the neural time constant and $\mathrm{\Phi }(·)$ is the quadratic/square-root current-to-rate transfer function (ref. 62; SI Appendix, Eq. S3). The synaptic input to a neuron with preferred orientation θ consists of a recurrent current due to the presynaptic activity at a location $\theta \prime$ with a weight $w\left(\theta -\theta \prime \right)$ and external currents $I_{\text{exc}}+I_{\text{stim}}\left(\theta ,t\right)$ plus fluctuations $\xi \left(\theta ,t\right)$. The connectivity profile, $w(\theta )$, is written in terms of its Fourier coefficients, w_k ($k=0,1,2,\dots$), and represents the effective excitatory/inhibitory coupling and can therefore include both positive and negative interactions. Fig. 1A shows an example of Mexican-hat-type connectivity with strong recurrent excitation and broad inhibition. External inputs are divided into a global net excitatory drive $I_{\text{exc}}$ that modulates the excitability of the network and a time-varying input $I_{\text{stim}}$ that represents the sensory stimulus. In general, the sensory stimulus can be written in terms of its Fourier coefficients I_k, $k=1,2,\dots$, with directions ${\theta }_k(t)$. Throughout this work, we will focus on an input of the form $I_{\text{stim}}(\theta ,t)=I_1\cos \left(\theta -{\theta }^{\text{stim}}(t)\right)$ to model a stimulus with constant strength I₁ and a time-varying orientation ${\theta }^{\text{stim}}(t)$, but our derivations are equally valid for time-varying stimulus strengths I₁. A detailed description of the stimuli used in the simulations is given in SI Appendix. Finally, the fluctuation term $\xi \left(\theta ,t\right)$ reflects the joint effect of the internal stochasticity of the network and temporal variations in the stimulus. For simplicity, we model these fluctuations as independent Ornstein–Uhlenbeck processes for each neuron, with amplitude ${\sigma }_{\text{OU}}=0.15$ and time constant ${\tau }_{\text{OU}}=1$ ms. SI Appendix, Table S1 summarizes the values of the model parameters.

PVI.

In order to understand the integration process carried out by the ring attractor model, we derived a dynamical system that perfectly integrates a circular variable to compute the circular average. In general, the optimal strategy to keep track of the average, $\overline{z}(t)$, of a time-varying stimulus, z(t), is to compute the cumulative running average. For discrete-time stimuli, the cumulative running average can be computed iteratively as: ${\overline{z}}_t={\overline{z}}_{t-1}+\frac{1}{t}\left(z_t-{\overline{z}}_{t-1}\right),\hspace{0.17em}t=1,2,\dots$, where t represents discrete time points. If we assume that the updates ${\overline{z}}_t-{\overline{z}}_{t-1}$ are small enough, and taking $z(t)\in ℂ$ to be a stimulus vector with strength I(t) and direction ${\theta }^{\text{stim}}(t)$, the cumulative running average can be written as $\overline{z}(t)=\frac{1}{t}R(t)e^{\psi (t)}$ (SI Appendix), and its dynamics obey

$$\frac{dR}{dt}=I(t)\cos \left(\psi -{\theta }^{\text{stim}}(t)\right),$$ [4a]

$$\frac{d\psi }{dt}=-\frac{I(t)}{R}\sin \left(\psi -{\theta }^{\text{stim}}(t)\right).$$ [4b]

We refer to this 2D equation as the PVI. The corresponding potential landscape is a plane going through the origin and tilted toward the stimulus direction ${\theta }^{\text{stim}}$:

$${\mathrm{\Theta }}^{\text{PVI}}\left(R,\psi \right)=-RI\cos \left(\psi -{\theta }^{\text{stim}}\right).$$ [5]

The angular variable ψ of the PVI (Eq. 4b) exactly describes the evolution of the circular average of the orientations of the stimulus frames—i.e., the PVI computes the cumulative circular average (SI Appendix, Fig. S1 A and C).

The radial variable R of the PVI has several interpretations. First, R(t) is the magnitude of the integrated vectors (i.e., the length of the resulting vector), and the average magnitude of $\overline{z}(t)$ can be computed as $|\overline{z}(t)|=\frac{1}{t}R(t)$. Second, from this geometric interpretation, it is easy to see that R(t) measures the dispersion of the directions ${\theta }^{\text{stim}}$, with R(t) growing linearly with t if ${\theta }^{\text{stim}}(t)$ is a constant. If ${\theta }^{\text{stim}}(t)$ is sampled from some underlying distribution, the growth will be slower and depends on the width of the distribution (SI Appendix, Fig. S1 B and D). Third, if we assume that ${\theta }^{\text{stim}}(t)$ is sampled from a von Mises distribution with mean μ and concentration κ, the running circular mean $\psi (t)$ will also be distributed according to a von Mises distribution, with concentration proportional to $R(t)\kappa$. In a Bayesian framework, $\psi (t)$ and R(t) thus track the mean and the concentration of the posterior distribution (63).

PK.

To quantify temporal evidence weighting, we measured the impact of individual stimulus frames during the course of the trial on the eventual direction estimate using a regression model. Because we are considering circular features (i.e., estimation of the average stimulus direction), linear regression is not well suited, and we define the PK as the weights of a circular regression model instead (SI Appendix). To quantify the overall shape of a PK, we define the PK slope (53). It is the slope of a linear regression of the PK, with negative values indicating a decaying PK (primacy), zero indicating uniform integration, and positive values indicating an increasing PK (recency). Formally, we fit the PK with a linear function of time, $\text{PK}(t)={\beta }_0+k{\beta }_{1}t,$ where β₁ is the PK slope and $k=\frac{1}{2\text{var}(t)}$ is a factor that normalizes the PK slope to the interval $(-1,1)$.

Psychophysical Data and Data Analysis.

We used published data from three studies carrying out psychophysical experiments, in which human subjects had to categorize the average direction of a stream of eight oriented Gabor patterns with orientations uniformly distributed in the range between $-{90}^{°}$ and ${90}^{°}$. (Fig. 5A; refs. 33–35). In each trial, participants reported whether, on average, the orientation of the eight samples [each sample with a duration 250 ms (33, 34), respective 333 ms (35)] fell closer to the cardinal or diagonal axes. In total, we analyzed the data of 71 subjects. A detailed description of the data is given in SI Appendix.

PKs of each participant were obtained as the weights of logistic regression (SI Appendix, Fig. S8). To characterize the shape of individual PKs, we used logistic regression with the constraint that the PK is either uniform (constant) or a linear function of time. We compare the model fits using the Akaike information criterion and classify each PK as uniform (best model has a constant PK), primacy (linear model with negative slope), or recency (linear model with positive slope) (SI Appendix, Fig. S8).

Data, Materials, and Software Availability

The psychophysical data and analysis scripts and the code of the computational models are available at GitHub (https://github.com/wimmerlab/flexbump) (64). Previously published data were used for this work (33–35).