Abstract.
Purpose
Breast conserving surgery (BCS) is a common procedure for early-stage breast cancer patients. Supine preoperative magnetic resonance (MR) breast imaging for visualizing tumor location and extent, while not standard for procedural guidance, is being explored since it more closely represents the surgical presentation compared to conventional diagnostic imaging positions. Despite this preoperative imaging position, deformation is still present between the supine imaging and surgical state. As a result, a fast and accurate image-to-physical registration approach is needed to realize image-guided breast surgery.
Approach
In this study, three registration methods were investigated on healthy volunteers’ breasts () with the supine arm-down position simulating preoperative imaging and supine arm-up position simulating intraoperative presentation. The registration methods included (1) point-based rigid registration using synthetic fiducials, (2) nonrigid biomechanical model-based registration using sparse data, and (3) a data-dense three-dimensional diffeomorphic image-based registration from the Advanced Normalization Tools (ANTs) repository. Additionally, deformation metrics (volume change and anisotropy) were calculated from the ANTs deformation field to better understand breast material mechanics.
Results
The average target registration errors (TRE) were , , and (mean ± standard deviation) and the average fiducial registration errors (FRE) were , , and for the point-based rigid, nonrigid biomechanical, and ANTs registrations, respectively. The mechanics-based deformation metrics revealed an overall anisotropic tissue behavior and a statistically significant difference in volume change between glandular and adipose tissue, suggesting that nonrigid modeling methods may be improved by incorporating material heterogeneity and anisotropy.
Conclusions
Overall, registration accuracy significantly improved with increasingly flexible and data-dense registration methods. Analysis of these outcomes may inform the future development of image guidance systems for lumpectomy procedures.
Keywords: breast cancer, lumpectomy, surgical guidance, registration, finite element modeling, deformable image registration
1. Introduction
Breast conserving surgery (BCS) is recommended for the majority of patients with early-stage breast cancer, and a successful surgical outcome depends on achieving negative tumor margins to prevent reoperation and the likelihood of recurrence.1 Breast magnetic resonance (MR) imaging has high sensitivity and accuracy for tumor size estimation and has been used for preoperative planning of BCS procedures.2 Additionally, MR imaging with the patient in the supine position has been shown to more closely represent tumor extent in surgery compared to prone positioning (breast pendant), which is subject to large gravity-induced deformations.3,4 In recognition of this, the feasibility of using preoperative MR supine imaging combined with optical tracking and ultrasound imaging for assisting intraoperative navigation is under investigation.5–7 Going further, work on the use of intraoperative MR imaging to assist directly during the procedure by reimaging is also being explored.8
While direct re-imaging of the tissue with MR is an attractive direction, workflow encumbrance and high cost are likely to prohibit intraprocedural adoption. Alternatively, using preoperatively acquired, well-resolved supine MR imaging data to guide lumpectomy procedures is a more viable option but would be highly dependent on calculating an accurate three-dimensional (3D) image-to-physical registration.9 Registration for BCS is particularly challenging since the imaging and surgical presentations differ. In the case of acquiring a supine preoperative MR for assisting breast surgery, the ipsilateral arm would typically be positioned either in the arm-down or arm-up configuration to conform to a closed bore MRI scanner. In comparison, lumpectomy is typically performed with the ipsilateral arm extended laterally in a T-shape. An image-to-physical registration is needed to account for positional changes between the imaging and surgical states.
When considering registration, rigid techniques are fast but fail to capture large soft-tissue deformations that occur from changes in position.10,11 Affine transformations can improve registration accuracy but only represent a global transformation. Nonrigid registration methods that utilize elastic biomechanical models can capture local deformations yet are nontrivial in implementation.6,12 For example, developing biomechanical models that accurately capture large nonrigid breast deformations is challenging due to the variation in breast material properties and anatomical body forces.13 It is also unclear how patient-specific ligament structure including suspensory Cooper’s ligaments and the superficial fascia may affect breast deformations.14 Nonrigid registration methods for image-to-image registration are less applicable for the surgical problem (which requires image-to-physical registration), but a wide range of deformation models for capturing small and large deformations has been proposed including elastic, viscous fluid flow, optical flow, and deep learning models.15 One advantage of image-to-image registrations (compared to sparse data registrations) is the resulting dense displacement mapping between the moving and fixed images, which can be used for investigating deformation characteristics with voxel-level specificity.
Quantifying breast mechanical properties such as stiffness and anisotropy is valuable for informing both image-to-physical and image-to-image nonrigid registration methods. However, there are large measurement variations that depend not only on the patient’s physiology but also on the measurement technique.16 Both ex vivo mechanical tests and in vivo techniques such as MR elastography (MRE) have been used to measure the Young’s Moduli of adipose, glandular, and tumor tissue with stiffness value estimates ranging widely (1.2 to 24 kPa for adipose tissue) depending on the technique.17,18 Anisotropy in the breast has been investigated with acoustic radiation force impulse (ARFI) imaging and with MRE, and both techniques have been correlated with tissue type and fiber orientation.19,20 Other noninvasive quantification techniques —such as analyzing the displacement field derived from an image-to-image nonrigid registration—may be of interest to provide additional insight into tissue mechanical properties.21,22
Another aspect to consider with registration methods is the nature of the data that enables the alignment process. Ultimately, both rigid and nonrigid registration methods depend on acquiring sparse geometric or image intensity data in the intraoperative environment to establish correspondence between the preoperative image and the intraoperative breast state. In the work reported here, supine MR imaging was acquired in an arm-down and arm-up presentation to represent preoperative and a mock intraoperative breast state. In some respect, this represents a more rigorous challenge than the laterally extended (T-shape) arm positioning used in typical lumpectomy procedures. Nevertheless, this allowed for a gold standard by providing full 3D volumetric visualization of the breast in a pre- and post-deformation state. Image-to-image registration was utilized to provide a best comparator of the volumetric transformation. Additionally, a sparse set of geometric features and points was extracted from the imaging data to mimic realistic available intraoperative digitization data using conventional methods (e.g. tracked ultrasound and surface fiducials). With digitization data completely realized with varying levels of density, registration methods were evaluated and compared. In particular, rigid and sparse-data nonrigid registration methods were compared to the best comparator which was a symmetric diffeomorphic image-to-image registration algorithm with B-spline regularization available in the Advanced Normalization Tools (ANTs) repository.23 Although many algorithms are available, this method in the ANTs repository was selected for image-to-image registration because of its ease of use, ability to capture large deformations, and robustness in many different medical imaging applications. This best comparator deformation field was then used to analyze volume change and anisotropy for the entire breast and for adipose and glandular tissue independently to better understand the underlying material mechanics associated with breast deformations. Important findings on the fidelity of sparse-data-driven approaches are reported as well as future directions in breast biomechanical modeling and advanced registration techniques for BCS. Contributions of this work include (1) evaluating the performance of a nonrigid image-to-image registration algorithm on an intrasubject supine breast MR imaging dataset, (2) comparing accuracy of registration methods with varying levels of data and complexity, and (3) extracting biomechanical insights from the nonrigid image-to-image deformation field.
2. Methods
2.1. Image Acquisition and Preprocessing
Supine breast MR imaging was performed on the left and right breasts of seven healthy volunteers using a Phillips 3T closed-bore scanner and a 16-channel torso coil. Volunteers were enrolled with informed consent in a study approved by the Institutional Review Board at Vanderbilt University. T1 High Resolution Isotropic Volume Excitation (THRIVE) sequence scans were obtained with one of two voxel sizes ( or ) with the ipsilateral arm down by the torso to mimic preoperative positioning and with the ipsilateral arm up by the head to mimic intraoperative positioning. The field of view included the entire breast volume, and the primary image slice was acquired in the axial direction. While true intraoperative positioning usually extends the arm to a T-shape pose, the arm-up configuration represents a more challenging configuration that enables quantitative image-to-image comparison. Twenty-six MR visible synthetic fiducials (IZI Medical Products, Owing Mills, Maryland) were placed on the surface of each breast prior to imaging. Two of the 14 breast images were omitted due to imaging artifacts, and for one subject, only the left breast was imaged, leaving 11 () breasts from seven individuals with ages ranging from 25 to 57 years included in the study.
3D breast volumes were manually segmented from the MR images along the boundary between the chest wall and breast parenchyma. The surface fiducial markers were manually labeled and used as corresponding points in the mock preoperative and intraoperative positions. For each volunteer,18–26 corresponding subsurface features were manually picked in the mock preoperative and intraoperative images for target evaluation. Breast tissue was labeled as either adipose or glandular tissue semi-automatically using Otsu thresholding with manual correction. Volunteer breast segmentation volumes and glandular tissue percentages are reported in Table 1. Custom mesh generation software was used to generate 3D breast meshes of the segmentations with 4 mm edge length tetrahedral elements.24
Table 1.
Volunteer breast volume and glandular tissue percentage. Each roman numeral denotes one volunteer with (a,b) indicating an individual breast.
| Case | Volume () | % Glandular |
|---|---|---|
| I | 1198 | 4 |
| II.a | 701 | 9 |
| II.b | 682 | 9 |
| III.a | 672 | 36 |
| IV | 649 | 15 |
| V | 629 | 50 |
| III.b | 611 | 44 |
| VI.a | 596 | 60 |
| VI.b | 519 | 42 |
| VII.a | 444 | 32 |
| VII.b | 398 | 37 |
| Mean ± std | 645 ± 208 | 31 ± 19 |
2.2. Registration Methods
Three registration methods were evaluated. The first method consisted of a rigid registration calculated from the surface fiducials using a conventional least-squares singular value decomposition point-based registration method.25 The surface fiducials were labeled on the arm-down and arm-up MR images to simulate the image-to-physical registration problem. The data used for this registration, specifically the surface fiducials in blue, are shown in Fig. 1.
Fig. 1.
Visualization of the data used in the mock preoperative position and the mock intraoperative position for registration. Rigid registration used MR-visible skin fiducials (blue), nonrigid model-based registration used MR-visible skin fiducials (blue), skin surface (yellow), and chest wall surface (red), and ANTs registration used the 3D image volumes.
The second method utilized a nonrigid FEM-based registration based on the methodology proposed in Heiselman et al. and implemented for breast registration in Richey et al.26–28 Briefly, 45 control points were placed on the surface of the preoperative 3D breast mesh excluding the skin surface and individually perturbed in the , , and directions to create a basis of displacement modes which were solved as forward homogeneous isotropic linear elastic boundary value problems with Young’s Modulus and Poisson ratio . These material properties were chosen based on previous implementations of this method and to model breast tissue as nearly incompressible.26–29 After perturbation, the local boundary region displacements surrounding each control point were recomputed to determine a statically equivalent, locally distributed load to eliminate single-point displacement artifacts in the deformation modes. Levenberg–Marquardt optimization was used to solve for a linear combination of these modes that minimized the distances between the deformed and intraoperative MR-visible skin fiducials, intrafiducial skin surface, and sparsely sampled chest wall surface while also incorporating a strain energy penalty to constrain deformations. This optimization is represented in the equation
| (1) |
where is the objective function, is the parameter vector representing the linear combination of displacement modes plus a rigid translation and rotation, is the error between the deformed and intraoperative point , is the number of points within a feature , is the weight of the feature , is the strain energy of the deformation, and is the strain energy weight which was set to . The strain energy weight parameter was chosen empirically to balance between the deformability of the organ and the strain energy imparted on the system. It should be noted that because the displacement modes are calculated using a linear elastic model with displacement boundary conditions only, the stiffness of the tissue is controlled by both the Young’s Modulus value the strain energy weight parameter (more detail is available in Heiselman et al.26). In this registration, three data features—the MR-visible skin fiducial points, the intra-fiducial skin surface point cloud, and the sparsely sampled chest wall surface point cloud—were included in the objective function and weighted equally to optimize the registration parameter vector . The data features for this registration were extracted from the arm-down and arm-up MR images to simulate the image-to-physical registration problem and are shown in blue, yellow, and red in Fig. 1. It should be noted that in this framework, sparse chest wall surface sampling represents equivalent data that would be acquired using tracked ultrasound imaging demonstrated in previous work.6,11 Registration was performed on a single thread of a 3.6 GHz AMD Ryzen 7 3700X CPU.
The third method was a 3D image-to-image registration that registered the arm-down and arm-up MR images (Fig. 1). This approach registered the mock preoperative and intraoperative images using a symmetric diffeomorphic image registration algorithm with explicit B-spline regularization available in the ANTs repository.23 Images were masked using a dilated breast volume segmentation mask so that the MR visible fiducials were included in the masked volume. The registration was initialized with the rigid point-based registration method, i.e., the initial comparator in this study, and followed by the deformable B-spline symmetric normalization method. Registration was performed using multithreading on 2.3 GHz Intel Xeon (E5-4610 v2) CPUs. The optimal parameters used for ANTs registration are reported in Table 2.
Table 2.
ANTs registration parameters used for optimal breast MR image registration.
| ANTs Registration Parameters | |
|---|---|
| ANTs Script | antsRegistrationSyN.sh |
| Initialization | Rigid point-based registration |
| Stages | Deformable b-spline symmetric normalization |
| Similarity metric | Cross-correlation |
| Multiresolution sampling levels | 5 |
| Histogram bins | 32 |
| Histogram matching | Yes |
| Spline distance | 26 |
| Gradient step size | 0.1 |
2.3. Evaluation of Registration Accuracy
The resulting deformations were applied to the preoperative skin fiducials and subsurface targets and compared to their true intraoperative locations. To evaluate registration accuracy at the skin surface, fiducial registration error () was calculated as the root mean squared error between corresponding fiducial points
| (2) |
where is the distance between the deformed ’th fiducial and the corresponding ’th intraoperative fiducial. Similarly, target registration error () was calculated as the root mean squared error between targets
| (3) |
where is the distance between the deformed ’th target and the corresponding intraoperative ’th target. and were compared across registration methods using paired -tests at a significance level of .
2.4. Tissue Characterization
Mechanics-based metrics representing volume change and directional preference in volume change were calculated as a means of interpreting the ANTs best comparator deformation field as described in Amelon et al.21 and utilized for breast in Jahani et al.22 The Jacobian determinant index () to measure volume change and the anisotropic deformation index (ADI) to measure anisotropy were computed using the following formulas:
| (4) |
where is the eigenvalues, or the principal stretches, of the deformation gradient tensor with for material that has anisotropic behavior in all three principal directions and for isotropic materials. indicates volume contraction, indicates no volume change, and indicates volume expansion. ADI = 0 indicates isotropic deformation and indicates increasingly anisotropic deformation.21 , , and ADI were calculated at every element in the breast mesh using the data provided by the ANTs deformation field. The eigenvalues and metrics were averaged within segmented adipose tissue and within segmented glandular tissue. Average metrics were compared across tissue types using paired -tests ().
3. Results
3.1. Registration Performance Comparison
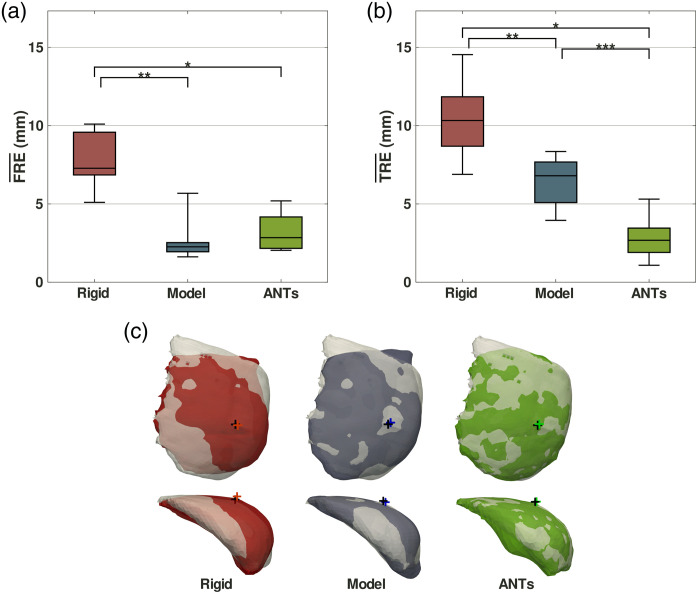
The distribution of FREs for each registration method is shown in Fig. 2(a). The average of the root mean squared error FRE values across all breasts was , , and for the rigid, model-based nonrigid, and ANTs registration methods respectively (mean ± standard deviation). When compared to rigid registration, nonrigid model-based registration resulted in a 68% improvement in FRE () and ANTs resulted in a 60% improvement in FRE (). There was no significant difference in FRE between the nonrigid model-based registration and the ANTs registration ().
Fig. 2.
Registration methods performance comparison showing (a) fiducial registration error () and (b) target registration error () from 11 breasts. Whiskers represent minimum and maximum and values. Statistical significance is denoted with asterisks (*,** and *,**,***). (c) Coronal (top row) and axial (bottom row) overlay views of registered breast meshes from one case (V) on the ground truth mock intraoperative breast meshes in gray with crosses marking the deformed (red, blue, green) and ground truth (black) nipple locations.
The distribution of TREs for each registration method is shown in Fig. 2(b). The average of the root mean squared error TRE values across all breasts was , , and for the rigid, model-based nonrigid, and ANTs registration methods respectively (mean ± standard deviation). When compared to rigid registration, nonrigid model-based registration resulted in a 38% improvement in TRE () and ANTs resulted in a 73% improvement in TRE (). ANTs registration improved TRE by 56% compared to nonrigid model-based registration ().
Overlays of the deformed (red, blue, green) and ground truth (light gray) mock intraoperative breast meshes from the three registration methods for one example case (V) are shown in Fig. 2(c). The deformed mesh more closely matches the ground truth mock intraoperative mesh with increasing data density—the sparse-data model-based registration outperforms rigid registration and the dense-data ANTs image registration outperforms the model-based registration. Additional quantitative registration metrics such as Dice coefficients or Jaccard indices were not included for this study because breast segmentation is subjective and variable between the arm-down and the arm-up images. This can be seen in the discrepancy between the deformed and ground-truth meshes in the upper left corner of the coronal views in Fig. 2(c).
Computation time varied for each registration method. Rigid registration computation time was trivial () and would be feasible for real-time surgical applications. Model-based nonrigid registration took 12.1 s on average for each case and would be feasible for near real-time implementation. ANTs registration took 7.4 h on average for each case and would not be feasible for real-time applications.
3.2. Image Registration Analysis
The ANTs image registration results and deformation field were further analyzed for insights into breast deformation patterns. Subsurface target distributions and errors from three example cases are shown in Fig. 3(a). The target locations were distributed evenly throughout the breast volume. The maximum target errors were 1.7, 6.6, and 5.9 mm for the low (VII.b), medium (V), and high (I) volume exemplar cases, respectively. For all 237 targets aggregated across the cases, the average absolute error in the inferior–superior direction was slightly yet significantly higher than in the medial–lateral and anterior–posterior directions (). This result is likely because the inferior–superior direction corresponds to the image acquisition direction with the larger voxel dimension. There were no observable correlations between error directionality and anatomical target location. The mesh deformations generated from the ANTs image registration are shown in Fig. 3(b) as the signed deformation distance on the mesh surface. In the coronal view, outward extension was seen in the upper outer quadrant and inward compression was seen around the nipple although there was variation in different cases. Overall, the ANTs image registration deformation revealed stretching in the superior–inferior direction and flattening in the anterior–posterior direction occurring with arm-down to arm-up motion. While qualitative, the results agree with anticipated behavior.
Fig. 3.
ANTs image registration results from a large (I), medium (V), and small (VII.b.) breast volume case. Coronal (top row) and axial (bottom row) views of the mock preoperative breast meshes are shown with a gray cross marking the nipple location. (a) Spheres indicate subsurface target locations and are colored according to individual target error. (b) Mesh color indicates the signed distance from ANTs image registration deformation moving from arm-down to arm-up with warm colors representing outward surface extension and cool colors representing inward surface compression.
Image registration was also evaluated by comparing deformed and ground truth image volumes shown in Fig. 4(a). The glandular features were similar in corresponding axial slices of the deformed and target image volumes indicating an accurate image registration. Example images are shown with four targets from four different cases. For each quartile, one target is shown with error within 0.1 mm of the quartile median target error. Although the fourth quartile target shown has a larger error distance, the glandular image features in the deformed and target images still show strong agreement. 75% of all target errors were below 3 mm as shown in the histogram in Fig. 4(b), implying that the ANTs image registration was accurate throughout the image volume for all cases.
Fig. 4.
Target error distribution and image results from the ANTs image registration. (a) Image registration results from four cases where axial slices show a target with error within 0.1 mm of the median target error of each quartile are shown and target error is reported in the upper left corner. The deformed image (top row) breast segmentations and targets are in yellow, and the ground truth image (bottom row) breast segmentations and targets are in green. The insert shows axial projections of the overlayed deformed and ground truth targets. (b) Target error histogram of 237 subsurface targets from all cases with quartiles shown in blue, yellow, green, and red.
3.3. Mechanics-based Metrics Analysis
The average eigenvalues, or principal stretches, of the deformation gradient tensor computed at each mesh element deformed by the ANTs deformation field and stratified by tissue type are reported in Table 3. These average eigenvalues suggest that the breast exhibits orthotropic behavior and that the three eigenvalues vary in magnitude. There is also consistency in the eigenvalue magnitudes exhibited across all cases.
Table 3.
Average eigenvalues from the deformation gradient tensor for adipose and glandular tissue.
| Case | Adipose | Glandular | Adipose | Glandular | Adipose | Glandular |
|---|---|---|---|---|---|---|
| I | 1.27 | 1.54 | 0.98 | 0.96 | 0.76 | 0.70 |
| II.a | 1.28 | 1.42 | 0.97 | 0.99 | 0.78 | 0.74 |
| II.b | 1.27 | 1.52 | 0.97 | 0.94 | 0.78 | 0.71 |
| III.a | 1.23 | 1.20 | 1.01 | 1.01 | 0.81 | 0.82 |
| IV | 1.31 | 1.46 | 1.00 | 1.01 | 0.72 | 0.69 |
| V | 1.32 | 1.35 | 0.99 | 1.00 | 0.71 | 0.73 |
| III.b | 1.29 | 1.37 | 0.97 | 0.99 | 0.73 | 0.74 |
| VI.a | 1.38 | 1.40 | 0.99 | 1.00 | 0.70 | 0.72 |
| VI.b | 1.31 | 1.37 | 0.97 | 1.00 | 0.73 | 0.75 |
| VII.a | 1.30 | 1.31 | 1.04 | 1.04 | 0.73 | 0.75 |
| VII.b | 1.27 | 1.28 | 1.00 | 0.99 | 0.74 | 0.81 |
| Mean ± std | 1.29 ± 0.04 | 1.39 ± 0.10 | 0.99 ± 0.02 | 0.99 ± 0.03 | 0.74 ± 0.03 | 0.74 ± 0.04 |
The distribution of the average and ADI values computed from the ANTs deformation field and stratified by tissue type are shown in Fig. 5, and the metric values for each individual case are reported in Table 4. The average value for adipose tissue was across all cases (mean ± standard deviation). Comparatively, the average value for glandular tissue was , which was slightly yet statistically significantly higher than adipose tissue (). This difference indicates that on average, ANTs predicted a minor contraction of adipose tissue and a minor expansion of glandular tissue during the deformation from arm-down to arm-up positions. The average ADI value for adipose tissue was across all cases, and the average ADI value for glandular tissue was (mean ± standard deviation). There was no statistically significant difference in ADI value between adipose and glandular tissue (). This finding suggests that ANTs registration predicts both tissue types to have anisotropic behavior.
Fig. 5.
Distribution of average (a) Jacobian - and (b) anisotropic deformation index - ADI values for adipose and glandular tissue calculated from the ANTs deformation field. Whiskers represent minimum and maximum index values. Statistical significance is denoted with asterisks ().
Table 4.
Average Jacobian and anisotropic deformation index values for adipose, glandular, and total tissue.
| Case | ADI | |||||
|---|---|---|---|---|---|---|
| Adipose | Glandular | Total | Adipose | Glandular | Total | |
| I | 0.95 | 1.00 | 0.96 | 0.48 | 0.81 | 0.49 |
| II.a | 0.97 | 1.03 | 0.97 | 0.44 | 0.64 | 0.46 |
| II.b | 0.96 | 1.00 | 0.96 | 0.45 | 0.79 | 0.48 |
| III.a | 1.01 | 1.00 | 1.01 | 0.38 | 0.34 | 0.37 |
| IV | 0.95 | 1.00 | 0.96 | 0.60 | 0.73 | 0.61 |
| V | 0.93 | 0.99 | 0.96 | 0.64 | 0.58 | 0.61 |
| III.b | 0.93 | 1.00 | 0.96 | 0.53 | 0.57 | 0.55 |
| VI.a | 0.96 | 1.02 | 0.99 | 0.68 | 0.66 | 0.67 |
| VI.b | 0.94 | 1.05 | 0.98 | 0.57 | 0.58 | 0.57 |
| VII.a | 1.01 | 1.02 | 1.01 | 0.57 | 0.54 | 0.56 |
| VII.b | 0.93 | 1.03 | 0.97 | 0.57 | 0.40 | 0.51 |
4. Discussion
This comparison of three registration methods demonstrated significant improvement with increasing method complexity and data extent. The nonrigid model-based registration method performed significantly better than the rigid registration method in both FRE and TRE, which is consistent with the fact that there are large nonrigid deformations that occur between arm-down to arm-up positions.11 This result suggests that a BCS image guidance system would benefit from nonrigid registration to better localize subsurface breast tumors. However, the nonrigid model-based registration performance was limited, and possible explanations for this may be the need for additional geometric data, the lack of heterogeneity or anisotropy in the model, or the lack of anatomic structural components in the model such as the suspensory Cooper’s ligaments of the breast.30 Additionally, the ANTs 3D image registration method performed significantly better than both the rigid and nonrigid model-based registration methods when considering TRE and significantly better than the rigid registration when considering FRE. This difference is expected given that ANTs registration is intensity-based and utilizes dense image data with volumetric voxel-to-voxel matching of image intensity features, while the nonrigid model-based registration is driven with sparse point-cloud data consistent with the limitations and practices of standard surgical suites. As a point of comparison, the nonrigid model-based registration method used between 840 and 1110 data points as seen in the image-to-physical registration data description of Fig. 1, while the respective image-to-image registration data description used by the ANTs registration method used 1000-fold more data (approximately over 1 million voxels depending on dimensions of the masked image volume). Emphasizing the comparison even further, the rigid registration used only the 26 MR-visible skin fiducials as data points. Given the differences in data extent and its relationship to registration performance, the results are somewhat anticipated; however, based on the investigation here, variations in registration methodology to include anatomical complexity and alternative material properties and boundary conditions are likely to play an important role in improving the fidelity of the nonrigid model-based registration.
Another key difference between registration methods was computation time, with rigid registration runtime being trivial (), nonrigid model-based registration taking 12.1 s on average, and ANTs registration taking 7.4 h on average. While ANTs registration computation time could be improved by down-sampling the image volumes or using deep-learning based methods such as VoxelMorph or SynthMorph, the impact of those choices on target fidelity remains to be investigated.31,32 As with most processes, improving speed often comes at the price of accuracy. In the current realizations above, the rigid and nonrigid model-based registrations reported would be preferable for the surgical problem given that they could be used for real or near-real-time registrations. While it is unlikely that any nonrigid sparse-data registration method could outperform ANTs given the discrepancy in the amount of input data in this experiment, the nonrigid model-based registration is preferable when considering the procedural workflow, the registration runtimes, and the significantly worse performance of rigid point-based registration. Additionally, the encumbrance of intraoperative MR imaging data compromises the practical use of ANTs for procedural updates. Despite being less accurate than the best comparator, the reduced data acquisition requirement of the model-based approach is a significant advantage and enables an easier translational pathway that would allow for near-continuous registration updates.
Another contribution of this work is the utilization of the ANTs registration package for breast MR supine-to-supine image registration and analysis. While ANTs registration has been used extensively on neuroimaging data, its application for breast image registration is more limited. The specific method used here was the ANTs symmetric image normalization method with explicit B-spline regularization (a directly manipulated free-form deformation algorithm) with cross-correlation as the similarity metric. Using Gaussian smoothing regularization instead of explicit B-spline regularization was explored, but the explicit B-spline regularization method performed significantly better () in terms of TRE. This behavior likely arose because B-spline regularization can better capture the large deformations present in the breast. Using mutual information instead of cross correlation as the similarity metric was also explored, and there was no significant difference () in TRE results when using the different similarity metrics. However, cross-correlation was selected as most applicable similarity metric for this dataset because it can be assumed that both the fixed and moving images have similar intensity profiles given that they are both MR images of the same subject. Other diffeomorphic image registration packages and algorithms have been applied to breast images previously including Elastix, Thirion’s demons algorithm, and the DRAMMS algorithm.33,34 While more analysis is needed to evaluate ANTs registration performance compared to other available image registration packages, the ANTs registration parameters reported here may be applicable for additional breast image registration applications including longitudinal studies, intersubject comparisons when studying tumor treatment responses, and performing multimodal registrations.35,36
With respect to understanding breast biomechanics and its material properties, the average value across all cases was suggesting, as expected, nearly no volume change () in breast tissue between arm-down and arm-up positioning. However, examining the average value within adipose and glandular tissue types separately showed statistically significant differences. While very modest, the value for glandular tissue was slightly higher than the value for adipose tissue. This suggests a variable response to different arm positions between adipose and glandular tissue, with glandular tissue expanding slightly more than adipose tissue. Additionally, the average ADI value across all cases was suggesting that the breast undergoes anisotropic deformation () between arm-down and arm-up positions. It should be noted that ADI values in this range express modest stretch behavior ratio differences among principal axes. Interestingly, no significant difference was found between adipose and glandular tissue. This may suggest an underpinning anisotropic structure that supports the entire breast volume such as Cooper’s ligaments. Both and ADI value differences imply that nonrigid modeling methods may benefit from incorporating material properties reflecting heterogeneity and anisotropy.
With respect to limitations, all conclusions drawn from the biomechanical indices assume that the ANTs deformation field is correctly representing the true local deformation field that occurs between arm-down and arm-up positioning. It is important to note that the ANTs deformation field is subject to method-specific bias from the image-to-image registration algorithm and not necessarily constrained by mechanics. The TRE results show that the ANTs registration is more accurate than rigid and nonrigid model-based registration and achieves a registration accuracy lower than 3 mm for 75% of targets in all volunteers. However, the average maximum target registration error across all cases is 8.9 mm for ANTs registration, with the error from an individual target from one case being as high as 20.8 mm. This implies that there are some regions of the image volumes where ANTs registration is not accurate. This may be because of poor image quality in those regions, MRI image artifacts, or a lack of distinguishable image features. These inaccuracies should be considered when using the biomechanical indices to make inferences about tissue properties. Additionally, breast tissue properties fluctuate with age, and cancerous tumors are typically stiffer than adipose and glandular tissue.16 Further study on a cohort of breast cancer patients rather than healthy volunteers would more conclusively assess the viability of the proposed registration and analysis methods for image-guided breast surgery.
5. Conclusion
This work evaluated three registration methods—a rigid method, a nonrigid model-based method, and an ANTs 3D image diffeomorphic method—for registering arm-down to arm-up supine breast MR images on eleven healthy volunteer breast cases while also providing an analysis of breast tissue biomechanical properties based on the image registration deformation field. On average, nonrigid model-based registration driven with sparse data localized subsurface target points with TRE, which was 38% better than rigid registration and compatible with real-time registration goals for lumpectomy. In contrast, although not practical intraoperatively, ANTs localized subsurface points with TRE when driven with full volumetric images and was 73% better than rigid registration. The FRE also significantly improved when comparing rigid to nonrigid model-based registration and when comparing rigid to ANTs registration, although there was no significant difference in FRE between the nonrigid model-based and ANTs registration. Biomechanical indices calculated from the ANTs deformation field suggest that adipose and glandular tissue vary in terms of volume change and that the breast undergoes anisotropic deformation during the arm-down to arm-up motion. This investigation suggests that model-based registration may improve with approaches that incorporate anisotropic material properties and heterogeneous tissue types, with the potential for more accurate patient-specific material properties as elastography imaging methods continue to improve. It also demonstrates the utility of image-to-image registration in uncovering soft-tissue mechanical properties, which is an underemphasized application of image-to-image registration compared to its use for longitudinal and intersubject comparisons. Overall, this investigation into supine breast image registration lays the groundwork for future model-based registration methods for surgical guidance systems that rely on accurate registration for intraoperative tumor localization during lumpectomy procedures.
Acknowledgments
The authors would like to acknowledge the support of the National Institutes of Health through Grant Nos. R01EB027498 and T32EB021937, the National Science Foundation for a Graduate Research Fellowship awarded to M.J.R., and the Vanderbilt Center for Human Imaging supported by Grant No. 1S10OD021771-01 for the 3T MRI. This manuscript is an expansion of an SPIE Proceedings paper.37
Biography
Biographies of the authors are not available.
Disclosures
The authors have no potential conflicts to disclose.
Contributor Information
Morgan J. Ringel, Email: morgan.j.ringel@Vanderbilt.edu.
Winona L. Richey, Email: winona.richey@vanderbilt.edu.
Jon S. Heiselman, Email: jon.s.heiselman@vanderbilt.edu.
Ma Luo, Email: m.luo92@outlook.com.
Ingrid M. Meszoely, Email: ingrid.meszoely@vanderbilt.edu.
Michael I. Miga, Email: michael.miga@vanderbilt.edu.
References
- 1.Waljee J. F., et al. , “Predictors of re-excision among women undergoing breast-conserving surgery for cancer,” Ann. Surg. Oncol. 15(5), 1297–1303 (2008). 10.1245/s10434-007-9777-x [DOI] [PubMed] [Google Scholar]
- 2.Mann R. M., Cho N., Moy L., “Breast MRI: state of the art,” Radiology 292(3), 520–536 (2019). 10.1148/radiol.2019182947 [DOI] [PubMed] [Google Scholar]
- 3.Carbonaro L. A., et al. , “Contrast enhanced breast MRI: spatial displacement from prone to supine patient’s position. Preliminary results,” Eur. J. Radiol. 81(6), e771–e774 (2012). 10.1016/j.ejrad.2012.02.013 [DOI] [PubMed] [Google Scholar]
- 4.Joukainen S., et al. , “Feasibility of mapping breast cancer with supine breast MRI in patients scheduled for oncoplastic surgery,” Eur. Radiol. 29(3), 1435–1443 (2019). 10.1007/s00330-018-5681-y [DOI] [PubMed] [Google Scholar]
- 5.Pallone M. J., et al. , “Supine breast MRI and 3D optical scanning: a novel approach to improve tumor localization for breast conserving surgery,” Ann. Surg. Oncol. 21(7), 2203–2208 (2014). 10.1245/s10434-014-3598-5 [DOI] [PubMed] [Google Scholar]
- 6.Conley R. H., et al. , “Realization of a biomechanical model-assisted image guidance system for breast cancer surgery using supine MRI,” Int. J. Comput. Assist. Radiol. Surg. 10(12), 1985–1996 (2015). 10.1007/s11548-015-1235-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Barth R. J., et al. , “A randomized prospective trial of supine MRI-guided versus wire-localized lumpectomy for breast cancer,” Ann. Surg. Oncol. 26(10), 3099–3108 (2019). 10.1245/s10434-019-07531-4 [DOI] [PubMed] [Google Scholar]
- 8.Mallory M. A., et al. , “Feasibility of intraoperative breast MRI and the role of prone versus supine positioning in surgical planning for breast conserving surgery,” Breast J. 23(6), 713–717 (2017). 10.1111/tbj.12796 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Alam F., et al. , “Medical image registration in image guided surgery: issues, challenges and research opportunities,” Biocybern. Biomed. Eng. 38(1), 71–89 (2018). 10.1016/j.bbe.2017.10.001 [DOI] [Google Scholar]
- 10.Gombos E. C., et al. , “Intraoperative supine breast MR imaging to quantify tumor deformation and detection of residual breast cancer: preliminary results,” Radiology 281(3), 720–729 (2016). 10.1148/radiol.2016151472 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Richey W. L., et al. , “Impact of deformation on a supine-positioned image guided breast surgery approach,” Int. J. Comput. Assist. Radiol. Surg. 16(11), 2055–2066 (2021). 10.1007/s11548-021-02452-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ebrahimi M., et al. , “Using surface markers for MRI guided breast conserving surgery: a feasibility survey,” Phys. Med. Biol. 59(7), 1589–1605 (2014). 10.1088/0031-9155/59/7/1589 [DOI] [PubMed] [Google Scholar]
- 13.Eder M., et al. , “Comparison of different material models to simulate 3-D breast deformations using finite element analysis,” Ann. Biomed. Eng. 42(4), 843–857 (2014). 10.1007/s10439-013-0962-8 [DOI] [PubMed] [Google Scholar]
- 14.McGhee D. E., Steele J. R., “Breast biomechanics: what do we really know?” Physiology 35(2), 144–156 (2020). 10.1152/physiol.00024.2019 [DOI] [PubMed] [Google Scholar]
- 15.Wang M., Li P., “A review of deformation models in medical image registration,” J. Med. Biol. Eng. 39, 1–17 (2019). 10.1007/s40846-018-0390-1 [DOI] [Google Scholar]
- 16.Ramião N. G., et al. , “Biomechanical properties of breast tissue, a state-of-the-art review,” Biomech. Model. Mechanobiol. 15, 1307–1323 (2016). 10.1007/s10237-016-0763-8 [DOI] [PubMed] [Google Scholar]
- 17.Xydeas T., et al. , “Magnetic resonance elastography of the breast: correlation of signal intensity data with viscoelastic properties,” Invest. Radiol. 40(7), 412–420 (2005). 10.1097/01.rli.0000166940.72971.4a [DOI] [PubMed] [Google Scholar]
- 18.Krouskop T. A., et al. , “Elastic moduli of breast and prostate tissues under compression,” Ultrason. Imaging 20(4), 260–274 (1998). 10.1177/016173469802000403 [DOI] [PubMed] [Google Scholar]
- 19.Zhou J. Q., et al. , “Anisotropic properties of breast tissue measured by acoustic radiation force impulse quantification,” Ultrasound Med. Biol. 42(10), 2372–2382 (2016). 10.1016/j.ultrasmedbio.2016.06.012 [DOI] [PubMed] [Google Scholar]
- 20.Sinkus R., et al. , “Imaging anisotropic and viscous properties of breast tissue by magnetic resonance-elastography,” Magn. Reson. Med. 53(2), 372–387 (2005). 10.1002/mrm.20355 [DOI] [PubMed] [Google Scholar]
- 21.Amelon R., et al. , “Three dimensional characterization of regional lung deformation,” J. Biomech. 44(13), 2489–2495 (2011). 10.1016/j.jbiomech.2011.06.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jahani N., et al. , “Prediction of treatment response to neoadjuvant chemotherapy for breast cancer via early changes in tumor heterogeneity captured by DCE-MRI registration,” Sci. Rep. 9(1), 1–12 (2019). 10.1038/s41598-019-48465-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tustison N. J., Avants B. B., “Explicit B-spline regularization in diffeomorphic image registration,” Front. Neuroinf. 7, 39 (2013). 10.3389/fninf.2013.00039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sullivan J. M., Charron G., Paulsen K. D., “A three-dimensional mesh generator for arbitrary multiple material domains,” Finite Elem. Anal. Des. 25(3–4), 219–241 (1997). 10.1016/S0168-874X(96)00027-3 [DOI] [Google Scholar]
- 25.Arun K. S., Huang T. S., Blostein S. D., “Least-squares fitting of two 3-D point sets,” IEEE Trans. Pattern Anal. Mach. Intell. PAMI-9(5), 698–700 (1987). 10.1109/TPAMI.1987.4767965 [DOI] [PubMed] [Google Scholar]
- 26.Heiselman J. S., Jarnagin W. R., Miga M. I., “Intraoperative correction of liver deformation using sparse surface and vascular features via linearized iterative boundary reconstruction,” IEEE Trans. Med. Imaging 39(6), 2223–2234 (2020). 10.1109/TMI.2020.2967322 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Richey W. L., et al. , “Tumor deformation correction for an image guidance system in breast conserving surgery,” Proc. SPIE 12034, 120340K (2022). 10.1117/12.2611570 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Richey W. L., et al. , “Computational imaging to compensate for soft-tissue deformations in image-guided breast conserving surgery,” IEEE Trans. Biomed. Eng. (2022). 10.1109/TBME.2022.3177044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Griesenauer R. H., et al. , “Breast tissue stiffness estimation for surgical guidance using gravity-induced excitation,” Phys. Med. Biol. 62, 4756–4776 (2017). 10.1088/1361-6560/aa700a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rajagopal V., Nielsen P. M. F., Nash M. P., “Modeling breast biomechanics for multi-modal image analysis—successes and challenges,” Wiley Interdiscip. Rev.: Syst. Biol. Med. 2(3), 293–304 (2010). 10.1002/wsbm.58 [DOI] [PubMed] [Google Scholar]
- 31.Balakrishnan G., et al. , “VoxelMorph: a learning framework for deformable medical image registration,” IEEE Trans. Med. Imaging 38(8), 1788–1800 (2019). 10.1109/TMI.2019.2897538 [DOI] [PubMed] [Google Scholar]
- 32.Hoffmann M., et al. , “SynthMorph: learning contrast-invariant registration without acquired images,” IEEE Trans. Med. Imaging 41(3), 543–558 (2022). 10.1109/TMI.2021.3116879 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mehrabian H., et al. , “Deformable registration for longitudinal breast MRI screening,” J. Digit. Imaging 31(5), 718 (2018). 10.1007/s10278-018-0063-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ou Y., et al. , “Deformable registration for quantifying longitudinal tumor changes during neoadjuvant chemotherapy,” Magn. Reson. Med. 73, 2343–2356 (2015). 10.1002/mrm.25368 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Li X., et al. , “A nonrigid registration algorithm for longitudinal breast MR images and the analysis of breast tumor response,” Magn. Reson. Imaging 27(9), 1258–1270 (2009). 10.1016/j.mri.2009.05.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Guo Y., et al. , “Breast image registration techniques: a survey,” Med. Biol. Eng. Comput. 44(1), 15–26 (2006). 10.1007/s11517-005-0016-y [DOI] [PubMed] [Google Scholar]
- 37.Ringel M. J., et al. , “Breast image registration for surgery: insights on material mechanics modeling,” Proc. SPIE 12034, 1203411 (2022). 10.1117/12.2611787 [DOI] [PMC free article] [PubMed] [Google Scholar]