Bendable long graded index lens microendoscopy

Abstract

Graded index (GRIN) lens endoscopy has broadly benefited biomedical microscopic imaging by enabling accessibility to sites not reachable by traditional benchtop microscopes. It is a long-held notion that GRIN lenses can only be used as rigid probes, which may limit their potential for certain applications. Here, we describe bendable and long-range GRIN microimaging probes for a variety of potential micro-endoscopic biomedical applications. Using a two-photon fluorescence imaging system, we have experimentally demonstrated the feasibility of three-dimensional imaging through a 500-µm-diameter and ∼11 cm long GRIN lens subject to a cantilever beam-like deflection with a minimum bend radius of ∼25 cm. Bend-induced perturbation to the field of view and resolution has also been investigated quantitatively. Our development alters the conventional notion of GRIN lenses and enables a range of innovative applications. For example, the demonstrated flexibility is highly desirable for implementation into current and emerging minimally invasive clinical procedures, including a pioneering microdevice for high-throughput cancer drug selection.

1. Introduction

Optical imaging of live tissues at cellular resolution is of high interest in cancer, immunology, neuroscience and inflammatory disease research, among others. Current approaches are typically limited to confocal or multiphoton imaging at the surface of tissues, for example, the outermost 300-600 µm of tissue using tumor windows [1]. Furthermore, in clinical settings, minimally invasive (interventional) procedures require precise image-guided placement of needles and catheters into the body for applications including tissue biopsy and tumor ablation for cancer treatment [2,3]. Such approaches can be performed through tiny (sub-2 mm) skin incisions as short outpatient procedures and provide a less invasive, lower risk method to diagnose and treat disease compared to surgery. Real-time fluorescence microscopy at the tip of a needle or catheter has the potential to significantly improve the capabilities of such procedures – for example by confirming that a needle is within a tumor target during biopsy [4], providing early cancer detection [5,6], and identifying tumor heterogeneity [7].

There are technical issues that need to be addressed before microscopy-guided needle placement can be considered viable for interventional procedures. Interventional needles are thin, with its inner working channel having a typical diameter of <1.5 mm. Most interventional needles bend upon insertion into deep tissues; a recent study demonstrated more than 1 mm deflection of over 50% of interventional needles during liver ablation procedures [8]. Large diameter and rigid optical probes are not compatible with such needles and procedures. Existing flexible fluorescence imaging systems that can be placed into interventional needles have not provided spatial resolution or three-dimensional (3D) imaging capability required for detailed intra-procedural tissue characterization [9]. Therefore, there is a need to develop microendoscopy systems with probes that can be placed through a thin working channel, accommodate needle deformations, and provide a highly spatially resolved characterization of adjacent tissues in real time.

An immediate novel application for such deep-tissue, high-resolution optical imaging directly in patients is in measuring drug responses and immune infiltration in cancer patients. A pioneering biomedical microdevice [10], which carries up to 20 drugs and is implantable in situ in diseased tissue, has been demonstrated in cancer patients to provide high throughput evaluation of drug efficacy in tumoral microenvironments [11–15], as well as directly in the brain for applications in neurodegenerative disease [16]. While the drug-tissue interaction is generated in vivo, this technology currently requires the sample be removed from the body and relies on traditional ex vivo histology for analysis, which only provides static information and misses key time-dependent processes of drug-tumor and tumor-immune interactions. Efforts are ongoing to develop an in situ histology laboratory where tumor drug responses are measured directly without the need of biopsy [17,18]. This research uses a graded index (GRIN) lens endoscope that is integrated with the microdevice as an in situ microimaging tool. In this development, GRIN lenses serve as a viable and so far the only practically available microendoscopic probe for 3D fluorescence imaging that does not need distal optomechanical elements for depth scanning. The optomechanical element free design, which keeps the miniature footprint of the imaging probe itself, is key for integration with the microdevice. While continuous 3D imaging of drug diffusion dynamics has been successfully demonstrated by the microimaging-microdevice system [18], a current limitation to the development of a more clinically impactful interventional system for deeper tissues (e.g., liver and kidney) lies in the short length and rigidity of all existing GRIN probes. Therefore, bendable or flexible long GRIN probes are desired for next-generation developments.

Many other flexible fluorescence imaging probes have been around for decades. One popular design is the combination of a single mode fiber (SMF) [19,20] or fiber bundle [21,22] with a rigid and short GRIN lens at the probe tip. In this design, the SMF or fiber bundle is the flexible element, which delivers the excitation laser to a high numerical aperture (NA) GRIN lens for high resolution imaging and collects the returned fluorescence signal. Lateral two-dimensional scanning is realized by vibrating the SMF or switching illumination between individual cores of the fiber bundle. Imaging at different depths to obtain 3D information further requires changing the physical or optical distance between the fiber (or fiber bundle) and the GRIN lens. The 3D imaging capability is desired by the biomedical microdevice for optical sectioning of heterogeneous drug distributions and characterization of immune cell responses with cellular resolution. However, the optomechanical element needed for 3D imaging greatly increases the device’s size, which precludes utilization in minimally invasive applications such as the biomedical microdevice. Over the last decade, the development of flexible endoscopes based on a single multimode optical fiber (MMF) has received increasing attention [23–27]. In those systems, instead of using optomechanical elements for 3D scanning, wavefront shaping is used to generate and scan the focus for imaging from the proximal end. Although this single MMF endoscopy concept is attractive because it retains a small footprint, a pre-calibration of the transfer matrix of fiber modes is required from the distal end and this calibration becomes invalid easily when the MMF deforms. For example, intensity of the pre-calibrated focus dropped obviously if the distal end of a ∼1.5 m long step-index MMF was translated by only 3 mm, but the tested GRIN MMFs showed much better resilience [24]. Efforts are being proposed to combat the deformation-induced degradation [28–31].

Here we describe and demonstrate a bendable, long thin GRIN endoscope that may enable high-quality 3D microscopy through curved needles and more. This flexible endoscope does not require calibration from the distal end and thus preserves the small spatial footprint of the probe itself required for minimally invasive clinical integration. This development challenges the conventional notion that GRIN lenses are limited to being used as rigid imaging probes only [32]. The demonstrated bendable microimaging probe is attractive for many applications that are currently not feasible with a traditional rigid GRIN lens.

2. Bendable GRIN lenses and experimental setup

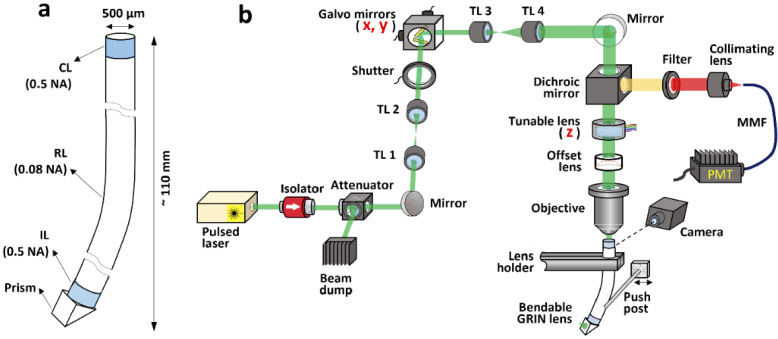
To demonstrate imaging through bendable long GRIN lenses, a bare 500-µm-diameter and ∼110 mm long triplet GRIN lens was custom designed (GRINTECH GmbH). The lens is semi-bendable because of its thin diameter, large length, and lack of a rigid outer casing, as shown in Fig. 1(a). Although it has been shown that a GRIN rod lens with the same diameter was able to withstand a minimum bend radius of 105 mm without breaking [33], this bare lens is only supposed to work in laboratory settings where bending is controllable and does not lead to break. In future clinical developments, the mechanical robustness can be much improved by a thin polymer coating which only marginally affect the bendability (see more later in the Discussion section). The length of the coupling lens (CL) and imaging lens (IL) was 852 µm and 537 µm, respectively, and both lenses had a nominal NA of 0.5. The relay lens (RL) was 108.444 mm long and had a NA of 0.08. The detailed index profiles are given in the Supplemental Methods section 1.3. A right-angle prism is attached on the distal end for side-view imaging, which is favoured for integration with our biomedical microdevice with side opening for imaging [18]. The investigation in this work is also applicable to lenses without the side-view prism. The nominal working distance was 200 µm in water on the object side and 200 µm in air on the image side. Due to the short lengths of CL and IL, only the RL lens was bent during all testing. A laser scanning two-photon microscopy system schematically depicted in Fig. 1(b) was built for testing of 3D imaging through the bendable lens. The 3D imaging was implemented through two galvo mirrors for lateral scan (x and y directions) and an electronically tunable lens for depth scan (z direction). A detailed description of the two-photon imaging system is found in the Supplemental Methods section 1.1. To simulate real-world bending in deeper tissues, the lens was held vertically by a holder, and a level post mounted on a translational stage was used to push the lens at a certain point below the holder to introduce a cantilever beam-like deflection to the lens, as that found in the interventional needles [8].

Fig. 1.

Bendable long GRIN lenses and the testing setup. (a) Geometry of the custom bendable long triplet GRIN lens. CL, coupling lens; RL, relay lens; IL, imaging lens. (b) Schematic of the experimental setup used to demonstrate two-photon imaging through the bendable lens. TL, tube lens; MMF, multimode fiber; PMT, photomultiplier tube.

For reliable characterization of imaging, it is critical to make sure that there is no bending-induced mechanical displacement to the proximal end of the lens. Therefore, a camera monitoring the lens top from a direction perpendicular to the bending direction was set up. Because of the great rigidity of the thick stainless-steel holder relative to the small diameter of the lens, no visible displacement during the lens bending was observed (see Supplementary Figure S1).

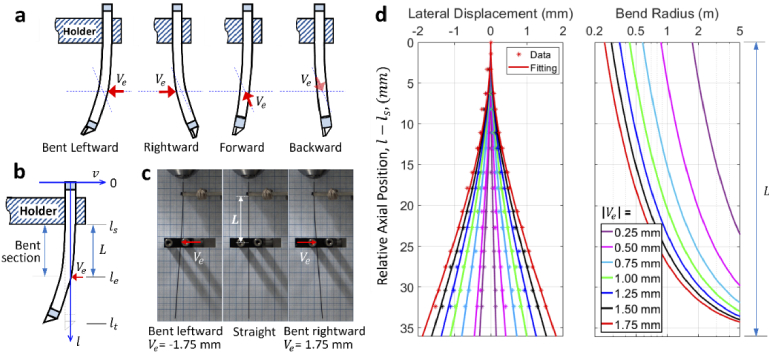
Four representative bending directions were tested, which are defined schematically in Fig. 2(a). While direction of the leftward and rightward bending was perpendicular to the prism surface, direction of the forward and backward bending was parallel to the prism surface. Real-world lens deflection can be described as a linear combination of the four tested bending. A parametric description of the lens bending (depicted by the curvature of the lens axis) is illustrated by the schematic in Fig. 2(b). A displacement of $V_e$ was introduced at the axial location of $l_e$ , resulting in a cantilever beam-like deflection starting from the axial position of $l_s$ which was the bottom end of the lens holder. Except the bent region between $l_s$ and $l_e$ , the other parts of the lens were straight. In all experiments and theoretical simulations in this work, the length of the bent section, L, was kept constant (=36.1 mm) so that the lens curvature was the same (for the same $V_e$ ) for more convenient comparison. The theoretical description of the lens deflection and calculation of the location dependent bend radius (i.e., radius of curvature) is detailed in Supplemental Methods section 1.2.

Fig. 2.

Characterization of lens deflection. (a) Definition of the four tested bending directions, (b) schematic illustrating the parameters used for describing the cantilever beam-like deflection, (c) images of the lens being straight or bent, (d) measured lens shape and the corresponding curve fitting (left) and theoretical bend radius (right).

Three images of the lens when it was bent leftward, straight, and bent rightward are shown in Fig. 2(c). Using a grid paper placed behind the lens, shape of the bent section was measured and fitted to the theoretical equation describing deflection of a cantilever beam (Eq. (S1) in the Supplemental Methods section 1.2), the results are shown in the left panel of Fig. 2(d). We observed excellent agreement between the measured distribution of the data points and the theoretical equation, which confirmed that the lens indeed deformed as a cantilever beam. The leftmost and rightmost curves in the left panel of Fig. 2(d) (both red) correspond to the lens bending shown in the left and right images of the Fig. 2(c), respectively. For this cantilevered lens, the minimum bend radius occurs at the bend start location (i.e., axial position $l_s$ ), and the bend radius increases exponentially and reaches infinity (i.e., lens being straight) as it approaches the bend end location (i.e., axial position $l_e$ ), as is shown in the right panel of Fig. 2(d). Therefore, the major perturbation to the optical rays comes from the bend start position (with the largest curvature) and the influence gradually reduces to zero as the bend end position (no curvature) is reached. The minimum bend radius was calculated to be 248.2 mm when the displacement $V_e$ was 1.75 mm (using Eq. S2 in the Supplemental Methods section 1.2). In this case, displacement of the lens’ distal end was ∼6 mm, which is larger than the maximum deflection (<3 mm) of 93% of image-guiding needles [8]. This distal displacement is also larger than the tested translation (3 mm) for a pre-calibrated single MMF based imaging [24]. The calculated varying bend radius along the lens axis is used for simulation of ray trajectories in the bent section of the GRIN lens.

3. Theoretical investigation of bend-induced perturbation to ray trajectories

As will be shown later experimentally, the most notable change after the lens was bent is the lateral shift of the field of view (FOV). This is due to the perturbation of ray trajectories by bending, which is first investigated theoretically here. GRIN lenses can be described as essentially a kind of MMF with GRIN profile, and ray tracing can be used to predict the optical trajectories within an MMF.

For simplicity, only the ray paths within the meridional plane containing the centre of the bend are simulated, which is straightforward and provides intuitive insight for the investigation of FOV shift. In an GRIN MMF, the ray path is determined by the generalized Snell’s law which reduces to ray invariants [34]. As schematically illustrated in Fig. 3(a), within the straight section of the GRIN lens, the ray invariant $\beta$ is given as [34]

$$\beta =n(r)\cos \theta (r),$$ (1)

where r is the radial position, $n(r)$ is the refractive index (RI) profile, $\theta (r)$ is the angle between the path tangent and the axial direction. In the bent section, the ray invariant $\overline{\beta }$ becomes [34]

$$\overline{\beta }=\frac{R+r}{R+\rho }[n(r)+\mathrm{\Delta }n(r)]\cos \theta (r),$$ (2)

where R is the bend radius, $\rho$ is the radius of the GRIN lens, and $\mathrm{\Delta }n(r)$ is the bend-induced RI modification given by [35]

$$\mathrm{\Delta }n(r)=-\frac{n^3(r)}{2}[p_{12}-\mu (p_{11}+p_{12})]\frac{r}{R},$$ (3)

where $p_{11}$ and $p_{12}$ are the elasto-optic coefficients and $\mu$ is the Poisson’s ratio of the lens material. The above equations govern the ray trajectories within the investigated meridional plane of the lens. Without bending, the rays follow sinusoidal-like paths. When the lens is bent leftward, the rays drift toward the outer interface of the bend (the right side of Fig. 3(a)), following curved sinusoidal-like paths. This drift can be attributed to two effects: the purely geometric deformation and the RI modification due to elasto-optic effects.

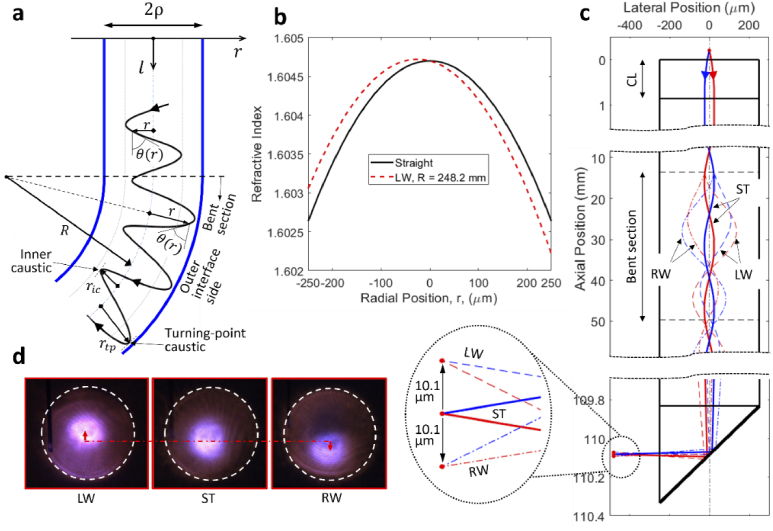
Fig. 3.

Perturbed ray paths due to lens bending. (a) Schematic showing the shift of ray trajectories toward the outer interface on the bend, (b) RI profiles of the RL with and without bending, (c) simulated ray trajectories with and without lens bending, inset showing enlarged view of the focus position, (d) experimental observation of bend induced focus shift. LW, bent leftward; RW, bent rightward; ST, straight.

For pure bending of a GRIN lens, the dominant strain is the axial normal strain (i.e., $r/R$ in Eq. (3)) [36], which leads to a slight increase in RI of the inner layers (compressive stress) and slight decrease in RI of the outer layers (tensile stress). Because of the linear dependence of axial normal strain on the radial position, the RI modification is also linearly dependent on the radial position. RI profiles of the relay lens when it is straight and bent leftward with a bend radius of 248.2 mm (the minimum tested bend radius mentioned earlier) are shown in Fig. 3(b). From the view of modal analysis, shift of modal fields toward the outer interface of a bent step-index fiber has been observed both theoretically and experimentally [35,37]. Although their results are for step-index fibers, the shift direction agrees with that of our ray optics analysis for GRIN MMFs.

Using the ray invariants defined in Eqs. (1) and (2), ray trajectories within the GRIN lens can be solved numerically. A more detailed description of the numerical simulation can be found in the Supplemental Methods section 1.3. Figure 3(c) shows the simulated trajectories of two symmetric incident rays making an initial angle of 3° with the lens axis. For the close-up view of the ray trajectories, the curved GRIN lens axis is mapped to a straight shape such that the radial position of the ray paths is clearly visible. As discussed earlier, the lens undergoes a cantilever beam-like deflection with $ls=12.7mm$ , $L=36.1mm$ , and $|V_e|=1.75mm$ , and the bent section lies between the two horizontal broken lines. Without bending, the ray paths (solid curves) are symmetric about the lens axis. When the lens is bent leftward, the ray paths (dashed lines) shift toward the right side of Fig. 3(c) (the outer interface side for leftward bending), agreeing with the qualitative demonstration in Fig. 3(a). When the lens is bent rightward, the ray paths (dot dashed lines) shift toward the left side of Fig. 3(c) (the outer interface side for rightward bending). Inset of Fig. 3(c) shows position of the focus (represented by the intersection point). In comparison with the case when the lens is straight, the focus shifts upward and downward by the same amount of 10.1 µm when the lens is bent leftward and rightward, respectively.

The bend-induced shift of focus was experimentally verified using an infrared detector card placed a few centimetres in front of the lens prism (see Fig. 3(d)). The white dashed circle represents the boundary of all rays exiting the GRIN lens, the brightest spot is the focus position. An upward and downward shift of focus was clearly observed for the leftward and rightward bending, respectively, which agrees with the theoretical predictions.

4. Shift of FOV

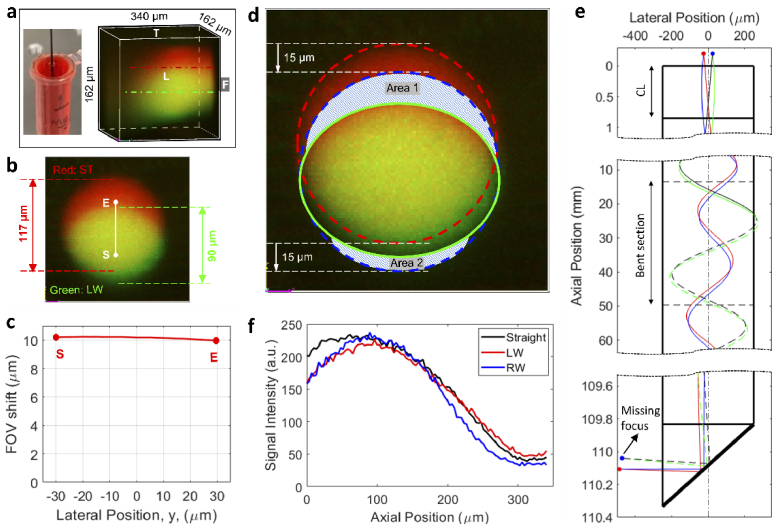
The shift of the focus induced by the lens bending leads to a shift of the FOV. To test the FOV shift, a small cube of cured polydimethylsiloxane (PDMS) with imbedded 1 µm diameter fluorescent beads was attached to the prism surface (see the left part of Fig. 4(a)), fixing the beads relative to the lens prism. The orientation and coordinates of the FOV are defined in the right part of Fig. 4(a). An overlaid 3D image of fluorescent beads in the PDMS with a straight (red) and bent leftward (green) GRIN lens is shown in Fig. 4(b). Because of the anisotropic point spread function, the spherical beads are imaged as ellipsoid. A notable lateral shift of bead positions toward the bottom side of the FOV was observed after lens bending.

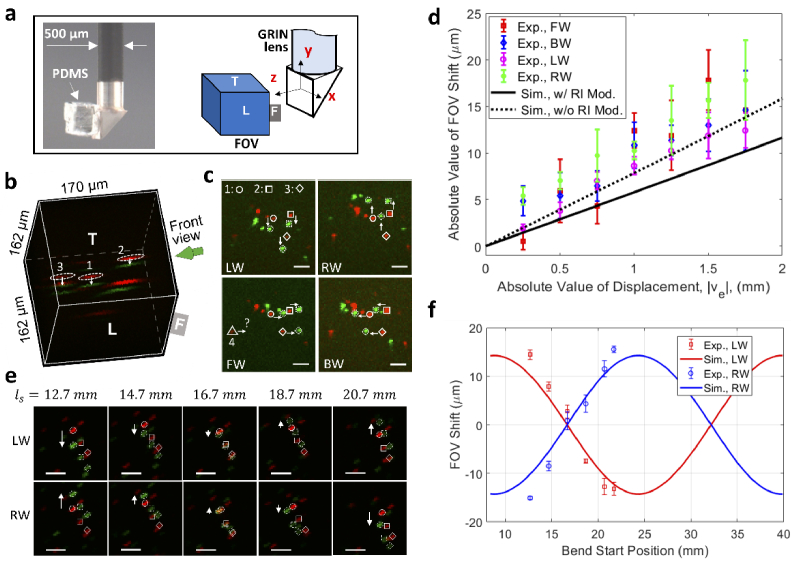
Fig. 4.

Demonstration of bend induced FOV shift. (a) An image of the fluorescent bead-imbedded PDMS attached to the prism surface for testing of FOV shift (left) and definitions of orientation and coordinates of the FOV (right), (b) an overlaid 3D image of fluorescent beads in PDMS, (c) front view of bead positions for different bending directions, (d) measured and simulated FOV shift as a function of the displacement, (e) front view of bead positions when the lens is bent at different locations, (f) measured and simulated FOV shift as a function of the bend location (represented by the bend start location, $l_s$ ). All scale bars: 20 µm. In all images of b, c, and e, red is for straight lens and green is for bent lens. LW, bent leftward; RW, bent rightward; FW, bent forward; BW, bent backward. For b and c, $l_s=12.7mm$ , $V_e=-1.75mm$ (leftward bending).

To quantify the FOV shift more precisely, the front view of the bead positions in the FOV is examined. The front view is defined as the view direction perpendicular to the front (F) face of the FOV (see Fig. 4(b)). Figure 4(c) shows images of the same beads when the lens was subject to the four different bending directions defined in Fig. 2(a). The three beads denoted by the dashed ellipses in Fig. 4(b) are tracked and denoted, respectively, by the open circle, square, and diamond. Since the FOV shifts upward when the lens is bent leftward, as illustrated earlier in Fig. 3(c), the bead position shifts downward in the FOV, which is in agreement with the experimental observation as shown in the top left corner of Fig. 4(c). On the contrary, the bead positions shifted upward when the lens was bent rightward (see the top right image of Fig. 4(c)), which again agrees with the theoretical predictions for rightward bending in Fig. 3(c). For the other two bending directions, the bead positions shifted rightward and leftward when the lens was bent forward and backward, respectively. These results suggest that, with the same bending curvature, the FOV undergoes a shift toward different directions for different bending directions. Also note that all the beads shifted by similar amounts, indicating a uniform shift across the FOV.

Figure 4(d) summarizes the experimental and theoretical absolute FOV shift as a function of the absolute displacement $|V_e|$ . The experimental data were obtained from shifts of the three designated beads. The simulated FOV shift with the bending induced RI modification considered (solid line) generally agrees with the experimental results, though we note that the agreement is better when the RI modification is not considered (dashed line). Note that the elasto-optic coefficients ( $p_{11}$ =0.121, $p_{12}$ =0.270) used for calculating the RI modification in Eq. (3) are evaluated at a wavelength of 630 nm [38], and that the coefficients at the actual wavelength of 1040 nm, which are currently unavailable, are expected to be smaller due to the smaller RI of fused silica at longer wavelengths. This implies that the simulated FOV shift would agree more closely with the experimental results if more accurate elasto-optic coefficients were available. The results also imply that the FOV shift depends virtually linearly on the displacement within the tested range. Detailed evolution of ray trajectories when $V_e$ varies between −1.75 mm (leftward bending) and 1.75 mm (rightward bending) is recorded in Visualization 1 ^{(3.7MB, avi)} .

Next, the dependence of FOV shift on the bend location was investigated. Due to the periodic feature of ray trajectories (solid curves in Fig. 3(c)), it is anticipated that the FOV shift is location dependent. Figure 4(e) shows the front view of shift of bead positions when the same bend was applied at several different locations represented by the varying bend start position $l_s$ (with fixed $V_e$ and $L$ ). Note that a different piece of bead embedded PDMS was used in this testing. Figure 4(f) summarizes the FOV shift as a function of the bend location. The experimental FOV shifts were obtained by the shifts of the three beads denoted by the open circle, square, and diamond in Fig. 4(e). The simulated $l_s$ ranging from 8.4 mm to 39.9 mm covers a whole pitch length of the relay lens, but the experimental $l_s$ ranging from 12.7 mm to 21.7 mm is narrower. In our case, the experimental range was limited by the travel range of the translation stages applied, but it covered a range with both positive and negative FOV shifts. In general, we observe excellent agreement between the experimental and theoretical results. As expected, these results imply that the FOV shift is a periodic function of the bend location, which follows the periodicity of the ray trajectories. Changes in ray trajectories as the bend start location varies are recorded in Visualization 2 ^{(3.9MB, avi)} .

5. FOV deformation and signal amplitude characterization

In the above investigation, FOV shift was measured by discrete beads which are easy to be identified and tracked but occupy only a small random portion of the FOV. A complete characterization of FOV should be done by using a uniform target that covers the whole FOV. A 1 mg/mL doxorubicin solution was used as the uniform signal intensity target for such characterization (left part of Fig. 5(a)). Doxorubicin is a water-soluble anti-cancer drug with red autofluorescence and is widely used clinically and in research settings [10]. An overlaid 3D image captured in the solution when the lens was straight (red) and bent leftward (green) is shown in the right panel of Fig. 5(a), and front view of the overlaid 3D image is displayed in Fig. 5(b). While the fluorescence signal can be excited and collected within the whole 162 × 162 × 340 µm³ volume, it is observed that the signal amplitude decreases at positions away from the center and deep within the sample. If the effective FOV is defined as the volume that is clearly visible in Fig. 5(a) (above ∼20% of the maximum intensity), then the FOV has a diameter of ∼117 µm and a depth of ∼300 µm before bending. After bending, there was a change to the overall shape (i.e., from circle to ellipse) as well as a clearly observable downward shift. As discussed earlier in Fig. 4(c), FOV shift was virtually uniform across the FOV. More evidence can be found in Supplementary Figure S2 which records the shifts of additional fluorescent beads across a wider area of the FOV. As a theoretical verification, the shift of points composing line SE in Fig. 5(b) is calculated and presented in Fig. 5(c). The theoretical result also suggests that the FOV shift remains largely constant.

Fig. 5.

FOV characterization using a uniform fluorescent solution. (a) Testing of FOV using a uniform doxorubicin solution (left), and an overlaid 3D image obtained in the solution (right), (b) characterization of FOV deformation from the front view, (c) simulated FOV shift versus location along the line SE shown in (b), (d) illustration of the FOV deformation, (e) simulated missing of focus as ray trajectories hit the lens boundary when the lens is bent leftward, (f) signal distribution along the axial line comprising the highest signal intensity. For all experiments and simulations involving lens bending, $l_s=12.7mm$ and $|V_e|=1.75mm$ .

With the characteristics of FOV shift known, the FOV deformation (front view) is illustrated in Fig. 5(d). The original shape when the lens is straight is a circle (dashed red curve), which shifted downward by ∼15 µm to the dashed blue circle. However, the focus that scans the top part of the FOV, as designated by the shadowed Area 1, is missing because the shifted ray trajectories hit the edge of the lens and are refracted or absorbed (dashed black and green curves in Fig. 5(e)). This missing focus contributed to the missing top part of the FOV, i.e., Area 1. The absence of bead 4 in the lower left image of Fig. 4(c) (designated by the open triangle) after the lens was bent forward was due to the missing Area 1 of the FOV. Note that, in this case, the missing Area 1 was on the left side of the FOV due to a different bending direction. The absence of beads 1 and 2 in Supplementary Figure S2 when the lens was bent leftward is another example of the missing Area 1 of the FOV. On the contrary, the bottom part, i.e., Area 2, was missing due to the inherent limit of the lens FOV. The ray trajectories for this area are still within the lens boundary with bending (solid blue and red curves in Fig. 5(e)), thus the missing Area 2 does not originate from the bend. These two missing areas lead to a final FOV shape enclosed by the solid green ellipse in Fig. 5(d), i.e., while the horizontal FOV does not change, the vertical FOV reduces. The measured values in Fig. 5(b) suggest that circa 76.9% (= 90 µm / 117 µm) of the lateral FOV was preserved in the vertical direction. This FOV deformation was not observed if the lens is only translated (Supplementary Figure S3) which provides further evidence that the FOV deformation is caused by lens bending (rather than displacement of the lens top). We want to mention that, while the FOV size is adequate for many applications of our drug-screening microdevice, a larger FOV is preferred in many other cases so that a wider range of targets (e.g., cells or particles) can be monitored. A straightforward way to increase the FOV is to use a GRIN lens with a larger diameter, but with the cost of reduced flexibility. Another approach may be to take multiple images continuously across the tissue and then stitch them together to generate an image with a much larger combined FOV.

In addition to the FOV deformation, the signal amplitude is further characterized. Because bend introduces attenuation not only to the excitation laser but also the collected fluorescent signals, it is expected that bending would result in signal losses. Figure 5(f) shows the intensity distribution along an axial line that comprises the point with the highest signal amplitude. The dot dashed lines in Fig. 5(a) show the positions of the axial line for the straight lens and the lens bent leftward. These results suggest that the tested bending did not introduce meaningful losses to the signal amplitude, which is consistent with the neglectable losses theoretically predicted for a GRIN MMF with a relative bend radius of $R/\rho \approx 1000$ [34].

6. Resolution

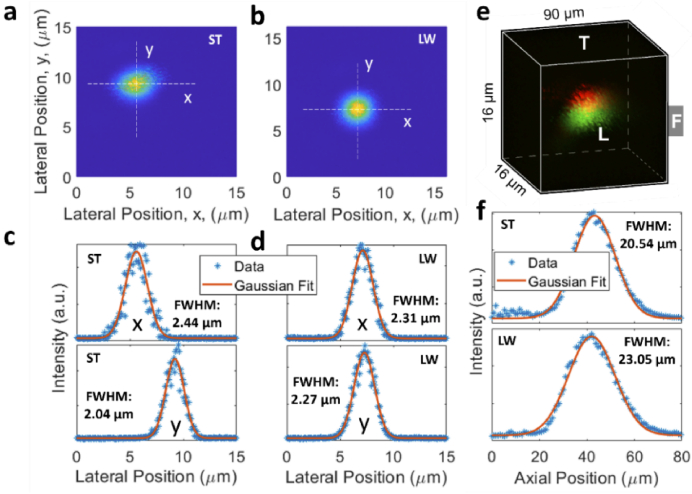
Lastly, it is of interest to characterize resolution when the GRIN lens is bent. Figure 6 shows the experimental results tested by bead #1 in Fig. 4(b). Fine lateral scan of the fluorescent bead when the lens is straight and bent leftward is shown in Fig. 6(a) and 6(b), respectively, and the corresponding signal distribution along the horizontal (i.e., x) and vertical (i.e., y) directions is displayed in Fig. 6(c) and 6(d), respectively. Using Gaussian curve fitting, the resolution defined by the full width at half maximum (FWHM) was 2.44 µm (x direction) and 2.04 µm (y direction) for the straight lens. The resolution changed to 2.31 µm (x direction) and 2.27 µm (y direction) when the lens was bent leftward. The axial resolution was obtained by acquiring a high-resolution 3D image of the fluorescent bead, as seen in Fig. 6(e), and the axial data points along with the Gaussian curve fitting are shown in Fig. 6(f). The axial resolution was 20.54 µm and 23.05 µm, respectively, for the straight and bent lens. Note that the axial resolution was about ten times that of the lateral resolution. The above results suggest a resolution change of −5.3%, 11.2%, and 12.2% for the x, y, and z direction, the minus sign suggests reduction in FWHM after the lens is bent. More experimental characterization of resolution was also conducted using the beads #2 and #3 designated in Fig. 4(b), the results are similar and summarized in Supplementary Table S1. Taken together, these results suggest that there was no significant degradation in resolution for the lens subject to the tested bending. We believe that the resolution is limited by other inherent aberrations of the GRIN lens itself, additional aberration caused by the tested bending may not significantly affect the overall resolution and thus be negligible. It is worth mentioning that other published work also reveals the robustness of wavefront enabled imaging through a deformed GRIN MMF [39].

Fig. 6.

Characterization of resolution. (a), (b) Lateral image of the same bead when the lens was straight or bent leftward, (c), (d) the respective intensity distribution along the x and y directions, (e) overlaid 3D image of the bead without (red) and with (green) bending for axial (i.e., z) resolution characterization, (f) intensity distribution along the z direction. ST, straight; LW, bent leftward. For the bent lens, $l_s=12.7mm$ and $V_e=-1.75mm$ .

Note that the above resolutions were tested using the beads closer to the FOV center. Although we did not observe a significant change in resolution across the whole effective FOV, we believe the resolution would deteriorate as the off-axis distance increases further, which is intrinsic to many practical imaging applications [40]. Causes of this behaviour include off-axis aberrations (e.g., astigmatism) and a decrease in effective NA with increasing axial offset and working distance [25].

7. Discussion and conclusions

In this work, we have demonstrated the feasibility of imaging through a bendable GRIN lens. We tested cantilever beam-like deflection as would be expected during passage through an interventional needle or other working channels. Distinct location dependent FOV shift as well as FOV deformation after the lens is bent are discovered. Note that it is the bend radius that plays the key role in causing the FOV change through altering the ray invariant (i.e., Eq. (2)), and a smaller bend radius leads to a larger FOV shift. The minimum bend radius tested was slightly less than 25 cm. This should be sufficient for the majority of needle-based interventional procedures [8]; however, for less rigid catheter-based procedures, this may be insufficient. In practice, more complicated deformations to the lens are expected in clinical settings, such as a combination of bends toward different directions, which may lead to a combinative FOV shift toward a direction not included in this work. In terms of mechanical durability, GRIN lenses are made of similar materials as silica optical fibers which may have a much tighter bend with the protective coating. In a similar fashion, the mechanical robustness of bendable GRIN lenses can be much enhanced by a similar polymer coating for long-term applications, while the bendability may be virtually all preserved.

Two-photon imaging was used to demonstrate 3D imaging through the ∼11 cm long bendable GRIN lens. For longer GRIN lenses, intermodal and chromatic dispersions may contribute to additional aberrations, leading to both resolution degradation and signal drop (due to pulse broadening). Techniques may be applied to potentially alleviate or eliminate these issues. For example, confocal imaging [41,42] can be used to eliminate chromatic dispersion by using a single wavelength laser (as opposed to a wealth of wavelengths of the pulsed laser for two-photon imaging). Wavefront shaping can be used to eliminate resolution degradation originating from intermodal dispersions [24,43]. Furthermore, although only fluorescence imaging is demonstrated through the bendable GRIN lens, it can be applicable to other microscopy techniques, such as Raman imaging.

In summary, our studies show that long-range, high-resolution deep tissue imaging using bent GRIN lenses is feasible, and we quantitatively describe the effects of bending on ray trajectories, FOV, and resolution. This proof-of-concept demonstration of imaging through bendable long GRIN lenses challenges the conventional notion that GRIN lenses are limited for use as rigid imaging probes. The long-range flexibility demonstrated here, which is desirable for many previously unattainable applications, is expected to expand the impact of GRIN lens microendoscopy in both research and clinical settings.

Funding

National Institutes of Health10.13039/100000002 (5P41EB015871, 5P41EB028741, 5R37CA224144); BWH Radiology Department Research Pilot Grant.

Disclosures

O.J. is a consultant to Kibur Medical, Inc. His interest was reviewed and is managed by BWH and MGB Healthcare in accordance with their outside interest policies.

Data availability

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.

Supplemental document

See Supplement 1 ^{(3.8MB, pdf)} for supporting content.