Abstract
Free energy calculations are rapidly becoming indispensable in structure-enabled drug discovery programs. As new methods, force fields, and implementations are developed, assessing their accuracy on real-world systems (benchmarking) becomes critical to provide users with an assessment of the accuracy expected when these methods are applied within their domain of applicability, and developers with a way to assess the expected impact of new methodologies. These assessments require construction of a benchmark—a set of well-prepared, high quality systems with corresponding experimental measurements designed to ensure the resulting calculations provide a realistic assessment of expected performance. To date, the community has not yet adopted a common standardized benchmark, and existing benchmark reports suffer from a myriad of issues, including poor data quality, limited statistical power, and statistically deficient analyses, all of which can conspire to produce benchmarks that are poorly predictive of real-world performance. Here, we address these issues by presenting guidelines for (1) curating experimental data to develop meaningful benchmark sets, (2) preparing benchmark inputs according to best practices to facilitate widespread adoption, and (3) analysis of the resulting predictions to enable statistically meaningful comparisons among methods and force fields. We highlight challenges and open questions that remain to be solved in these areas, as well as recommendations for the collection of new datasets that might optimally serve to measure progress as methods become systematically more reliable. Finally, we provide a curated, versioned, open, standardized benchmark set adherent to these standards (protein-ligand-benchmark) and an open source toolkit for implementing standardized best practices assessments (arsenic) for the community to use as a standardized assessment tool. While our main focus is benchmarking free energy methods based on molecular simulations, these guidelines should prove useful for assessment of the rapidly growing field of machine learning methods for affinity prediction as well.
1. Overview
This guide focuses on recommended best practices for benchmarking the accuracy of small molecule binding free energy (FE) calculations. Here, we define benchmarking as the assessment of expected real-world performance relative to experiment. We contrast this with the assessment of methods or tools intended to arrive at the same target free energy, which we refer to as validation (Figure 1), the comparison of the computational efficiency or speed of these methods, or mapping of effort-accuracy trade offs, all of which also play essential roles in dictating real-world usage. Importantly, validation calculations are often performed on systems selected for tractability, rather than intended to be representative of real-world applications [1–3].
Figure 1. Illustration of the definitions of Validation, Application, and Benchmarking used in this guide.
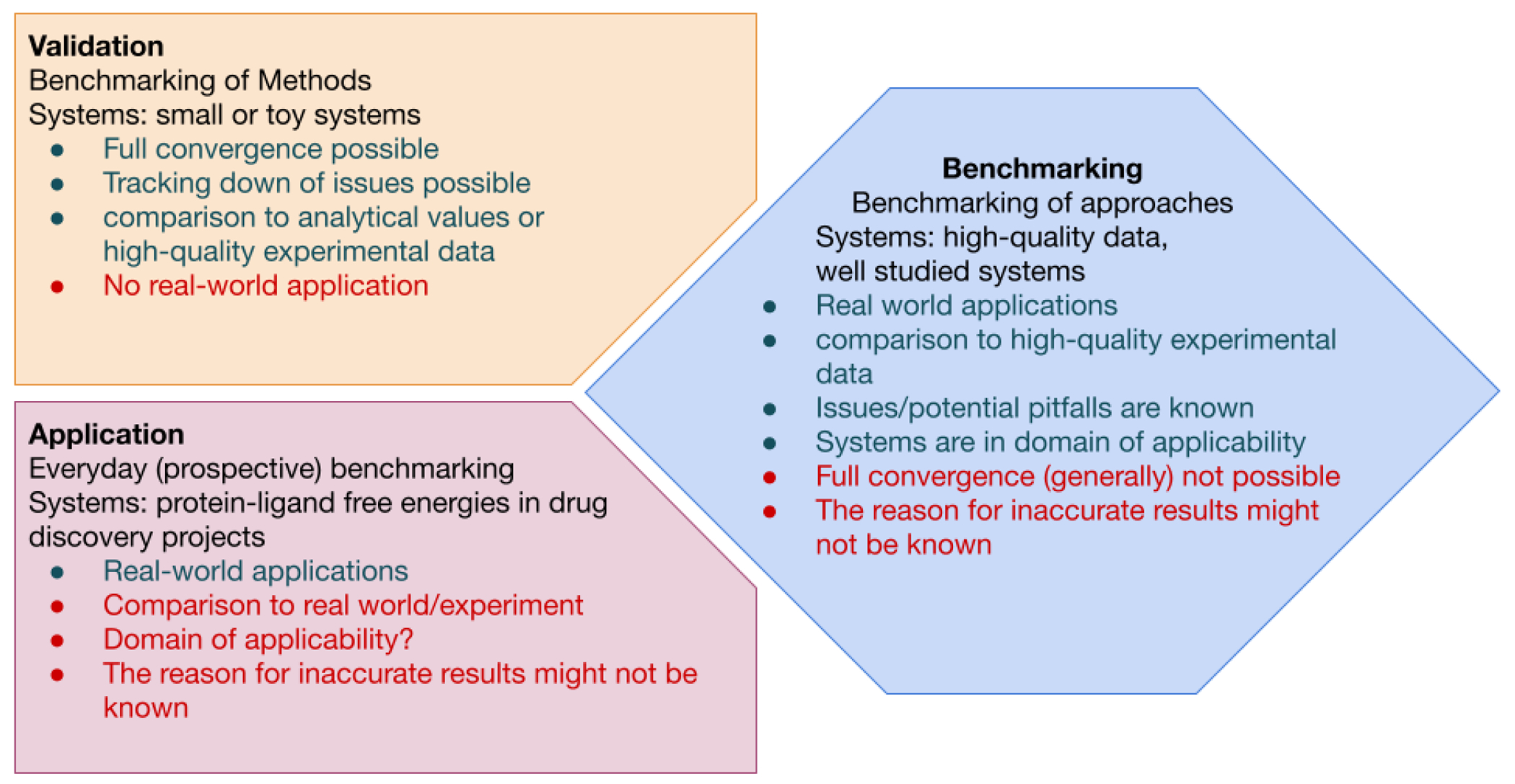
For each term, the definition, advantages (green) and potential short-comings (red) in terms of method evaluation are listed in the three panels. Validation (top left panel) uses systems that will confidently converge, the expected results are known, and the underlying issues are well understood. Validation sets allows robust development and improvement of methods. Application (bottom left panel) of a method, on the other hand, uses real-world systems and enables methods to be continuously evaluated on real-world applications of interest. Because the systems may not be well understood, it is possible for methods to fail in new ways that are difficult to detect. Benchmarking (right panel) bridges validation and application by aiming to assess the accuracy of real-world applications relative to experiment in cases where experimental data quality is not limiting and the method is known to be applied within its domain of applicability. Compared to validation, the size and complexity of the system may introduce challenges to producing robust, repeatable results.
As illustrated in Figure 1, benchmarking against experiment would ideally be performed on high quality data in order to provide an accurate assessment of expected performance under conditions where structure or assay deficiencies do not limit performance. In good benchmark sets, the potential pitfalls and complications in the data are well understood, but these systems may still challenge methodologies to produce reproducible, consistent predictions due to conformational sampling timescales–unlike simpler systems selected for methodology validation. We also differentiate benchmarking from application (Figure 1), where one is often constrained by the availability of experimental data and limited to a particular target, which may not always fall within the domain of applicability of the methodology. We aim to construct benchmarks that provide a good predictor of the expected accuracy in applications that fall squarely within the domain of applicability and for which good experimental data is available.
Organization:
This best practices guide is organized as follows: First, we give a brief overview of protein-ligand binding free energy methods and their use with the goal of highlighting key concepts that guide the construction of a meaningful benchmark. Next, we discuss recommendations for the construction of a high-quality experimental benchmark dataset, which must consider the availability of high-quality structural and bioactivity data as well as the expected domain of applicability. Next we provide recommendations on preparing structures for free energy calculations in a manner that will enable the benchmark dataset to be widely and readily usable by practitioners and developers, incorporating best practices for carrying out free energy calculations. We then discuss recommendations for the statistical analysis of both retrospective benchmarks and blind prospective challenges in order to derive robust conclusions about the accuracy of these methods and insights into where they fail. To address the absence of a standard community-wide benchmark, we provide a curated, versioned, open, standardized benchmark set adherent to these standards (protein-ligand-benchmark). In addition, we provide an open source toolkit that implements standardized best practices for assessment and analysis of free energy calculations (arsenic). Finally, we conclude with recommendations for data collection and curation to guide the systematic improvement of available benchmark sets and drive the expansion of the domain of applicability of free energy methods.
2. Introduction
The quantitative prediction of protein ligand binding affinity is a key task in computer-aided drug discovery (CADD). Accurate predictions of ligand affinity can significantly accelerate preclinical stages of drug discovery programs when used to prioritize compounds for synthesis with the goal of improving or maintaining potency [4, 5]. Binding free energy calculations–particularly alchemical binding free energy calculations–have emerged as arguably the most promising tool [6]. Alchemical methods, which include a multitude of approaches such as free energy perturbation (FEP) [7, 8] and thermodynamic integration (TI) [9–11], have a substantial legacy, with the original theory dating back many decades. Seminal work in the 1980’s and 90’s demonstrated that molecular dynamics (MD) and Monte Carlo (MC) simulation packages could carry out these calculations for practical applications in organic and biomolecular systems [12–18].
Alchemical perturbations in binding free energy calculations involve the transformation of one chemical species into another, or its complete creation or deletion, via a chemically unrealistic pathway (alchemical) that can only be achieved in silico by manipulating its interactions in a defined way. This is achieved by changing an atom from one chemical element to another. Alchemical calculations are often classified as either relative (RBFE) or absolute (ABFE) binding free energy calculations. While the underlying theory is similar, the implementation differs in how the thermodynamic cycle is constructed and which quantities can be computed: In RBFEs, a generally modest alchemical transformation of the chemical substructures that differ between the ligands is performed to compute the difference in free energy of binding between the related ligands (ΔΔG). By contrast, ABFEs alchemically remove an entire ligand, enabling the absolute binding free energy of a ligand (ΔG) to be computed and directly compared to experiment. A detailed review of commonly-used alchemical methodologies and best practices for their use is provided in a separate best practices guide [19].
In drug discovery, lead optimization (LO) typically involves the synthesis of hundreds of close analogues, often differing by only small structural modifications, in order to identify the optimal leads that show a good balance of target potency and other properties. This makes it an ideal scenario for RBFE, where small differences in structure are well suited to alchemical perturbation.
A number of recent studies have highlighted the good performance of RBFE for LO tasks. An early influential publication from Schrödinger [20] reported mean unsigned errors of < 1.2 kcal/mol on a curated set of 8 protein targets, 199 ligands, and 330 perturbations using their commercial implementation of FEP. Minimal discussion was devoted to how these targets were selected, other than their diversity and the availability of published structural and bioactivity data for a congeneric series for each target; notably, some ligands appearing in the published studies from which the data were curated were omitted due to the presence of presumed changes in net charge and the potential for multiple binding modes that would fall outside the domain of applicability. Schrödinger utilized the same benchmark set to assess subsequent commercial force field releases (OPLS3 [21] and OPLS3e [22]). In the absence of other significant efforts to curate benchmark sets, this set (often called the “Schrödinger JACS set”) has become the de facto dataset for most large scale RBFE reports, used to compare the performance of Amber/TI calculations [23], Flare’s FEP (a collaboration between Cresset and the Michel group) [24], and PMX/Gromacs [25], as well as machine learning studies [26, 27]. By contrast, ABFE calculations have not been studied on datasets of similar scale to date, although individual reports have shown success accurately predicting binding affinities [28, 29].
Despite the reported success of RBFE calculations on these benchmark sets, there are many reports demonstrating that RBFE calculations still struggle in scenarios [30] such as with scaffold modifications [31], ring expansion [32], water displacement [33–36], protein flexibility [37–39], applications to GPCRs [40, 41], and the modelling of cofactors such as metal ions or heme [42, 43]. This is manifested in a large-scale study of FEP applied to active drug discovery projects at Merck KGaA, in which Schindler et al. reported several cases of disappointing outcomes due to various of the above reasons [44].
In addition, new methods and implementation improvements for FE calculations continue to emerge, for instance the efforts on lambda dynamics [45, 46], and non-equilibrium RBFE calculations [25, 47]. Furthermore, there are many other methodologies such as end-point binding FE calculations (for instance MMGBSA, MMPBSA) or pathway based FE calculations that continue to be developed and applied [48]. Therefore, we must balance the increased confidence that simulation-based FE calculations can impact drug discovery, with the need to further understand, test, and overcome limitations of the current methods.
In brief, the issues mentioned above are related to three challenges for FE calculations, (1) an accurate representation of the biological system, (2) an accurate force field, and (3) sufficient sampling. Therefore, despite the importance of FE methods to drug discovery and chemical biology it is surprising that there are no benchmark sets or standard benchmark methodologies that allow calculation approaches to be compared in a manner that will reflect their future performance.
The Drug Design Data Resource [49] (D3R) and Statistical Assessment of the Modeling of Proteins and Ligands [50] (SAMPL) prospective challenges have demonstrated the utility of focusing the community on common benchmark systems and using common methods to analyze performance [51–60]. Mobley and Gilson discussed the need for well-chosen validation datasets and how this will have multiple benefits to understanding and expanding the domain of applicability of FE methods [1]. They focused on validation systems that will confidently converge, and where the underlying issues are well understood. The aim was to describe systems that could be used only to assess method performance in a robust manner. A set of recommendations for comparison of computational chemistry methods has been assembled by Jain and Nicholls [61]. As mentioned above, here we define benchmarking as assessing accuracy relative to experiment and focus on the best practices in the particular field of alchemical protein-ligand free energy calculations. This has implications that will be discussed in more detail throughout this article, for instance, the reliability of the underlying experimental data (structure and bioactivities), the confidence in the system setup such as protein and ligand preparation, the suitability of alchemical perturbations for FE, the statistical power of the dataset, the ability of the datasets to capture challenging real-world applications, and recommendations for analysing results. Essentially, we seek to understand what performance can be achieved when all these variables are handled to the best of our abilities.
Here, our proposed benchmark set augments existing datasets while recommending cleaning up or removing entirely some protein-ligand sets. We highlight key considerations in the construction of a useful set of protein-ligand benchmarks and the preparation of these systems for use as a community-wide benchmark. These recommendations are mirrored in a living benchmark set, which can be used to reliably launch future studies [62]. We seek to improve the initial version of this benchmark set in the future with help of the whole community. We welcome any contribution either to improve the existing set or to expand the set with new protein-ligand sets, if they meet the requirements established in here. We also recommend statistical analyses for assessing and comparing the accuracy of different methods and provide a set of open source tools that implement our recommendations [63]. We hope these materials will become a common standard utilized by the community for assessing performance and comparing methodologies.
3. Prerequisites and Scope
We assume a basic familiarity with molecular dynamics (MD) simulations, as well as alchemical free energy protocols. If you are unfamiliar with both of these concepts we suggest the best practices guides by Braun et al. [64] on molecular simulations and Mey et al. [19] on alchemical free energy calculations as a starting point. Note that the best practices of the latter guide are briefly repeated in Section 5 for completeness. Both guides agree with each other and are complementary. The sections on dataset selection (Sections 4), the analysis of benchmark calculations (Section 6), and the key learnings (Section 7) are unique to the present guide.
4. Dataset selection
Details of our criteria for the construction of good benchmark datasets will follow throughout the rest of the manuscript. Here, we examine the purpose of protein-ligand benchmark datasets, and the rationale for expanding these sets. We propose a core of robust datasets that match our suggested optimal criteria for benchmarking, but emphasize the need to supplement this core with new datasets which explore increasingly difficult challenges in order to continue to expand the domain of applicability of predictive methods. A variety of parameters can guide future datasets.
4.1. Protein Selection
The selection of target proteins in the benchmark set is generally dependent on the availability of experimental data and whether the applied methods are applicable to the specific targets. A good benchmark system (consisting of a protein target and small molecules with available experimental binding data) should ideally be representative of classical drug discovery targets and chemistry; a good benchmark set should also be diverse in terms of targets and chemistry. Expansion of this set to include additional systems should ideally reflect the evolution of drug discovery and the emergence of new target families and chemistries. While binding free energy calculations are agnostic to protein classification, there can be a pragmatic value in expanding benchmark sets to new protein families that may present unexpected inherent difficulties (see Section 4.3).
To merit inclusion in a good benchmark set, the available structural data must meet certain quality thresholds (Section 4.4), and the structure should be adequately prepared for molecular simulation to enable the benchmark to be broadly and readily useful (Section 5.1).
4.2. Ligand Selection
While some methods (such as machine learning and GBSA rescoring) can make rapid predictions of affinity, free energy methods are generally relatively costly in terms of computational effort. In order to make statistically meaningful comparisons among methods, however, a sufficient number of reliable experimental measurements (Section 4.5) will be necessary for a benchmark set. These measurements also need to cover an adequate dynamic range, i.e. the activity range should be sufficiently large. Such a set enables a statistical analysis with sufficient power to distinguish how methods are expected to perform on larger test sets for the same targets (Section 6). In addition, the set of ligands should be both unambiguously specified (with resolved stereochemistry or unambiguous tautomeric or protonation states) and have chemistries that fall within the domain of applicability of the particular free energy method used. In order for standardized benchmark sets to be broadly applicable to a range of methodologies and software packages, we recommend annotating systems in terms of common challenges that may exclude their assessment by certain methods or packages. For relative free energy calculations, these labels should denote transformations that include (1) charge changes, (2) change of the location of a charge, (3) ring breaking, (4) changes in ring size, (5) linker modifications, (6) change in binding mode, and (7) irreversible (covalent) inhibitors. Several of these issues are illustrated in Figure 2. If the ligand sets are sufficiently large, they can then be split into separate subsets (subsets with e.g., different ring sizes or different charges).
Figure 2. Five ligand pairs (A, B) for different targets (with each pair for a single target) having structural differences which can be challenging to simulate.
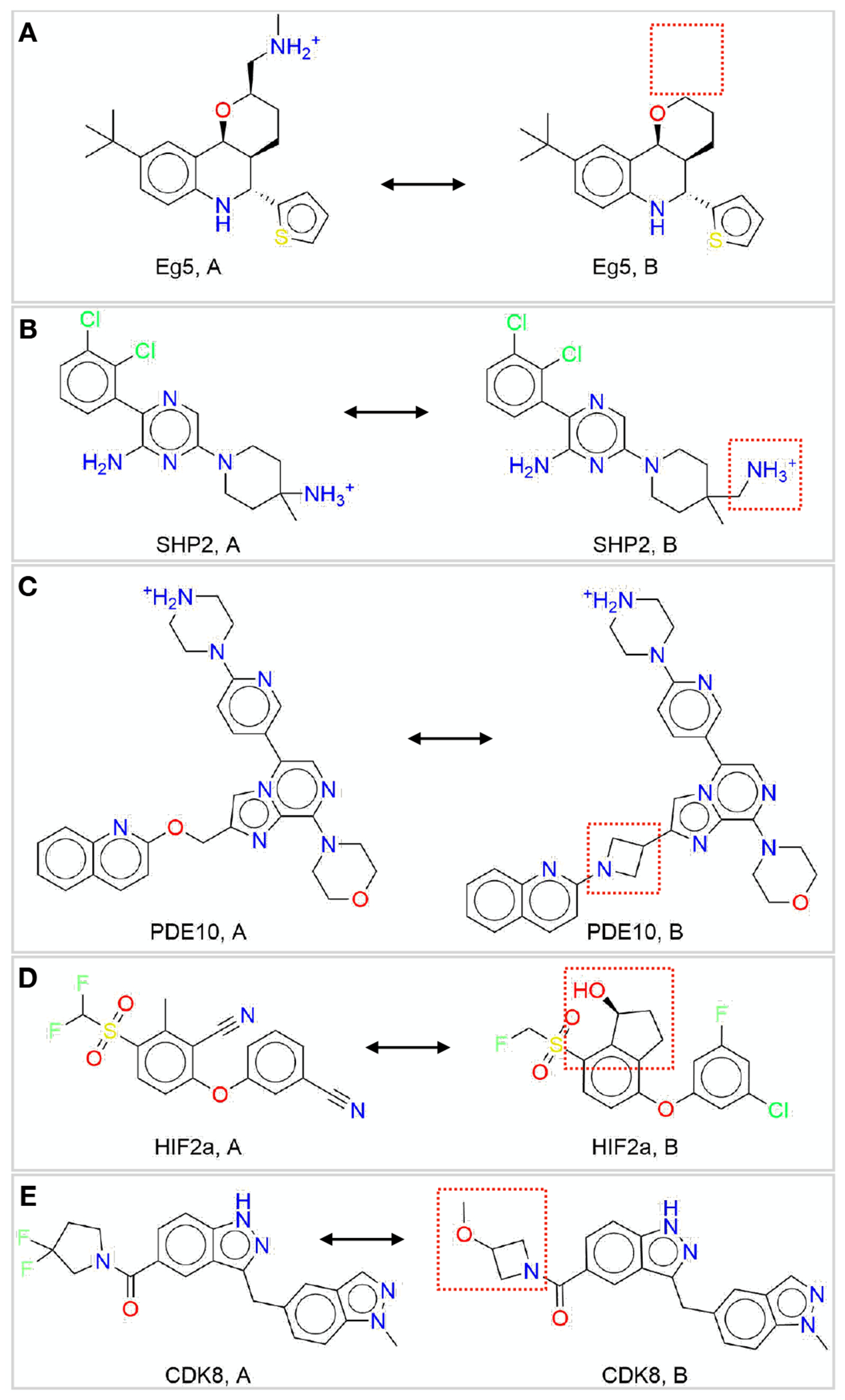
(A) Eg5: charge change, (B) SHP2: charge move, (C) PDE10: linker change, (D) HIF2α: ring creation, (E) CDK8: ring size change.
Adequately sampling ligand conformers can pose a challenge for some methods, especially if the ligands contain many rotatable bonds, invertible stereocenters, or macrocycles. Aromatic rings with asymmetric substitution will usually sample dihedral rotations freely in solvent, but in complex can become trapped in protein pockets during short simulations [65, 66]. Barriers to inversion of pyramidal centers can sometimes be long compared to typical simulation timescales [67]. Macrocycles present more extreme challenges for ligand sampling, and likely require special consideration to ensure their conformation spaces are adequately sampled [68–70].
The chemical diversity of ligands considered for inclusion in a benchmark set also needs to be suitable for the given free energy method. Single RBFEs rely on common structural elements between the molecules being compared, and are hence more appropriate for a congeneric series of ligands. ABFEs are more amenable for comparing sets of small molecules that differ more substantially in scaffold, or where the common structural elements are minimal. In both kinds of calculations, the size of the structural elements that differ between ligands within a congeneric series is also important to consider, since larger changes may also affect the binding mode of the ligand; the quality and availability of crystal structures for representative ligands of this system becomes critical in assessing these assumptions.
4.3. Addressing specific challenges
Besides the challenges mentioned in Sections 4.1 and 4.2, there are specific challenges which can be addressed by a benchmark set. These include water displacement in binding sites, the presence of cofactors in the binding site, slow motions of ligands (e.g. rotatable bonds) and proteins, and activity cliffs. We recommend annotating these challenging cases in the benchmark set.
4.4. Structural Data
A successful free energy calculation requires a well-prepared, experimentally accurate model of the system to be simulated, with structure(s) representative of the equilibrium state of the system. Just as choices made selecting binding data are critical, the choices made when selecting a protein model will impact benchmarking.
Often structural studies use shorter constructs that might be missing several domains compared to the full-length protein. To facilitate crystallization or expression, mutations might have been introduced. In addition, parts of the protein might not be resolved or modelled in available structures. Ideally, such deviations should be kept to a minimum in a benchmark dataset.
Starting structures are typically obtained from experimentally constrained models, most commonly from X-ray diffraction data. Other sources of structures include cryo-EM, NMR, homology models, or machine-learning-based structural models [6, 29, 44, 71]. However, while these sources could be practical for applications, we do not recommended them for input structures of benchmark calculations without additional validation. As free energy calculations are usually run at atomic resolution, the input structure needs to provide the coordinates of all atoms, with those coordinates ideally determined by the experimental model. For X-ray and cryo-EM structures, this requirement is only met by high quality structures. OpenEye Iridium can guide the assessment of X-ray structures [72]. Based on a set of identification criteria, an Iridium score is calculated, which states higher structure quality for lower scores. The Iridium classification categorizes each structure into not trustworthy (NT), mildly trustworthy (MT) and highly trustworthy (HT) categories. It is important to note that the Iridium criteria were designed to assess structures for benchmarking docking and not necessarily for free energy calculations. As such there is one important criterion missing - completeness of the model - which is likely to be far more important for free energy calculations than docking.
Any protein structural assessment should be done using two filters; overall (global) and local. Traditionally, overall quality of the structure (global) had been assessed using X-ray or cryo-EM resolution as it is easily accessible. However, this metric provides a theoretical limit and does not assess the quality of the model. Therefore, it is not a good metric for accuracy, completeness or quality and should only be used alongside other metrics. Iridium, by design, does not set a resolution limit but suggests a resolution threshold of < 3.5 Å [72] because it is difficult to model side chain atoms precisely above that threshold. Stricter thresholds have been suggested (i.e. < 2.0 Å in a recent benchmark [44]).
More meaningful metrics for X-ray structures are R, Rfree and the coordinate error. Currently, equivalent metrics for cryo-EM structures either do not exist or are less well understood. As a result the rest of the discussion will focus on criteria for structures determined using X-ray or neutron diffraction data. It should be noted that cryo-EM maps can still be visualized with the model to get an idea of the agreement between the model and the data. The R-factor is a measure for the difference between the predicted data (by the model) and the measured data. A smaller R-factor indicates an experimentally consistent model. A complication with R-factor is that it is a non-normalized metric. For a given dataset the model with the lowest R-factor is best fit to the data. Unfortunately, for different datasets, even for the same protein, lowest R-factor may not be the highest quality model.
The Rfree-factor is calculated the same way, but uses only a held out randomly selected subset of the measured data. Thus, it can be used to identify overfit models as these result in a larger difference between R-factor and Rfree (typically more than 0.05). Both R-factors are easily accessible for reported crystallographic data, e.g. in the protein data bank (PDB) [99]. The coordinate error, while more difficult to find or calculate, provides the best way to assess the precision and quality of the model:
| (1) |
where is the number of heavy atoms with occupancy of 1, is the volume of the asymmetric unit cell and is the number of non-Rfree reflections used during refinement. A high-quality structure should have a coordinate error < 0.7. Recent PDB entries usually include a coordinate error estimate which can be found by searching for ESU Rfree, Cruick-shank or Blow Density Precision Index (DPI). The coordinate error (as shown in Equation 1) is BlowDPI.
While understanding the global quality of a structure is important, it is the local active site or ligand binding site that will have the largest impact on benchmarking performance. Therefore special care should be taken to assess the ligand and surrounding active site residues. Of highest priority is to identify all unmodeled residues and side chain atoms within 6 to 8 Å of any ligand atom. When multiple structures with similar coordinate error are available, the structure with no missing residues or side chain atoms that meets subsequent criteria should be used. The electron density around the ligand should cover at least 90% of the ligand atom centers, which can be checked visually or by checking for a real space correlation coefficient (RSCC) value > 0.90. Examples for a poor ligand density are shown in Figures 4(A) (in comparison to Figure 4(B) with a good density) and 4(C). Ligand atoms where there are crystal packing atoms within 6 Å should be identified (see Figure 4(D)), as such packing atoms may affect the observed binding mode. All ligand and active site atoms with occupancy < 1.0 should be identified. If there is only partial density for the ligand and the active site residue atoms, these partial-density atoms should be identified (see Figure 4(A)). If alternate conformations for the ligand or active site residues are available, the selected conformation should be determined based on the electron density (see Figure 4(E)). Local metrics such as electron density support for individual atoms (EDIA) [100] or a number of RSCC [101] calculators can indicate if the electron density is sufficient to support the crystallographic placement of a given atom. Covalently bound ligands present as cofactors should be identified and appropriately modelled. Enabling the support of covalent ligand modifications for the free energy calculations has been demonstrated, yet it remains in its early stage of adoption by the community. Hence, we would not recommend including covalent ligands into the standardized benchmark sets [102].
Figure 4. Examples of common challenges encountered when using X-ray crystal structures.
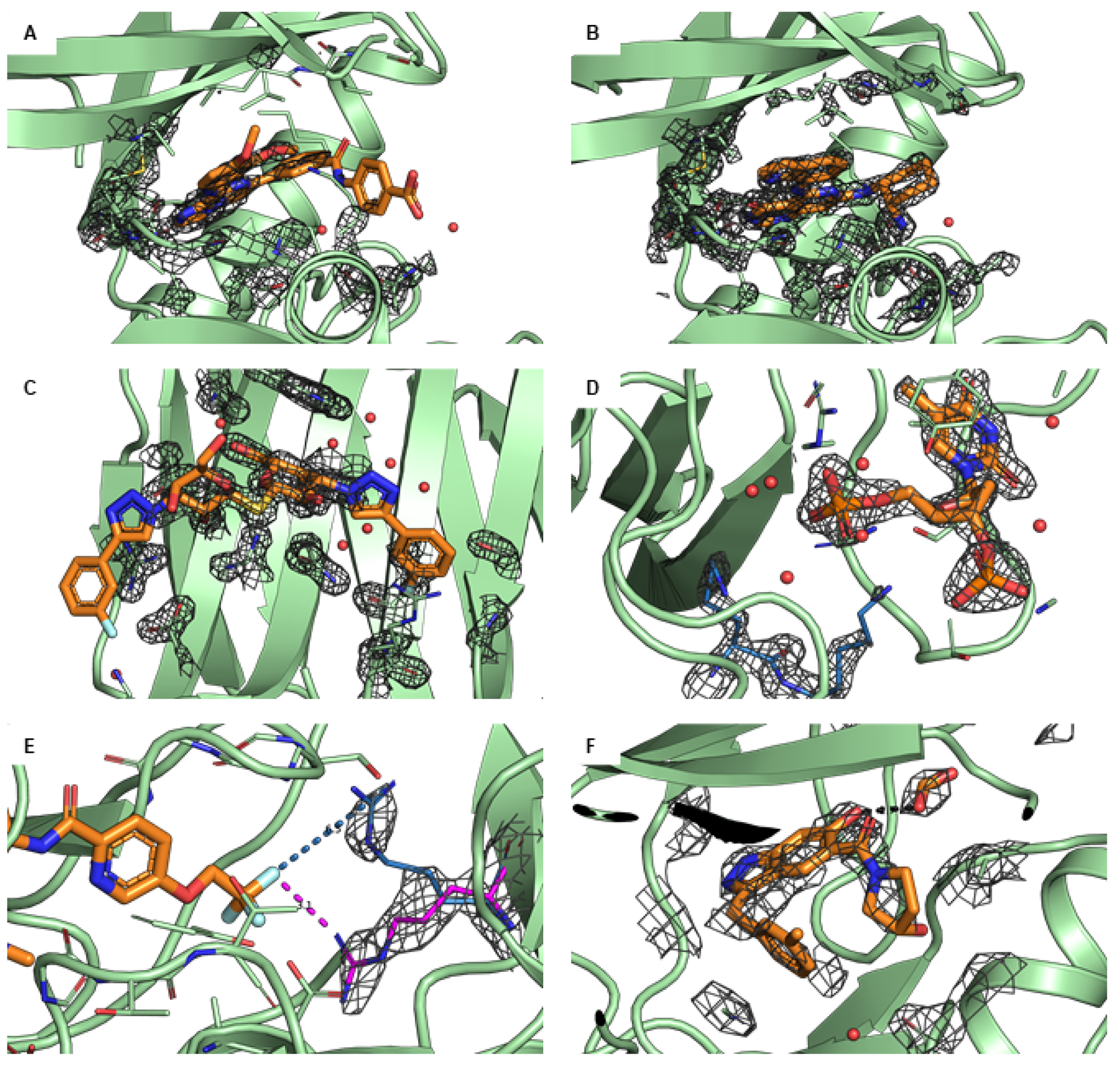
The protein is shown in green and the ligand in orange. If not stated differently, the 2Fo-Fc maps are illustrated as grey isomesh at level. (A) PDB ID 4PV0 shows poor density (at ) for residues in the active site. The beta sheet loop at the top of the active site has residue side chains modeled with no density to support the conformation and the end of the loop has residues that are not modeled. (B) The recommended structure PDB ID 4PX6 for the same protein has complete density (and modeled atoms) for the whole loop (at ). (C) PDB ID 5E89 shows poor ligand density, especially for the m-Cl-phenyl (left) and the hydroxymethyl (center). This means that the ligand conformation, as shown, is not specified by the data, and thus should not be used as input to a computational study unless there is additional data supporting this binding mode. (D) The ligand of PDB ID 1SNC has crystal contacts with the residues K70 and K71 (blue) of the neighboring unit that directly interact with the ligand, potentially affecting the binding mode relative to a solution environment. (E) PDB ID 3ZOV has two alternate side chain conformations. Residue R368 in the B conformation (magenta) has clearly more density () than the A conformation (blue). The B conformation interacts with the ligand (distance 3.2 Å) whereas the A conformation does not interact with the ligand (distance 6.5 Å). If the user does not look at both conformations and chooses A (by default), this would likely be incorrect and miss a potentially important protein-ligand interaction. (F) In PDB ID 5HNB, there is an excipient (formic acid) that interacts directly with the ligand (2.7 Å O-O distance shown in black). The formic acid could be replacing a bridging water. From the data it is not possible to determine how the excipient is affecting the ligand/protein conformation, but for a study of ligand binding in the absence of formic acid, this should be removed.
Additional aspects should be considered beyond the quality of the model and the data (see also structure preparation, Section 5.1). The structure of a complex could be deformed due to crystal contacts or by experimental conditions like additives, pressure or temperature. These conditions might not be representative for the biological environment and therefore biologically active conformation of the complex (see Figure 4(D)). Other factors could play an important role in determining active conformations, such as crystal waters, co-factors or co-binders. These should usually be included to model the natural environment of the protein (see Figure 4(F) and 5(C)). One, however, needs to be cautious when retaining crystallographic waters in the binding site: for the cases where a modelled ligand clashes with the X-ray water, a careful equilibration with position restraints on the ligand atoms may be necessary to ensure further stable simulations. It may be undesired to trap waters near the bound ligand, as overhydration of the binding site may be detrimental to the free energy prediction accuracy due to potentially slow exchange of water between the binding cavity and the bulk [103]. It is also important to remember that for X-ray data, modeling water (versus amino acids or organic compounds) is less precise than for other atoms particularly when the crystal is formed in a high salt environment. The ligand in the experimental structure should be sufficiently close to the ligand to be simulated to have a model of the correct binding mode.
Figure 5. Examples of challenges encountered for ligand modelling using X-ray crystal structures.
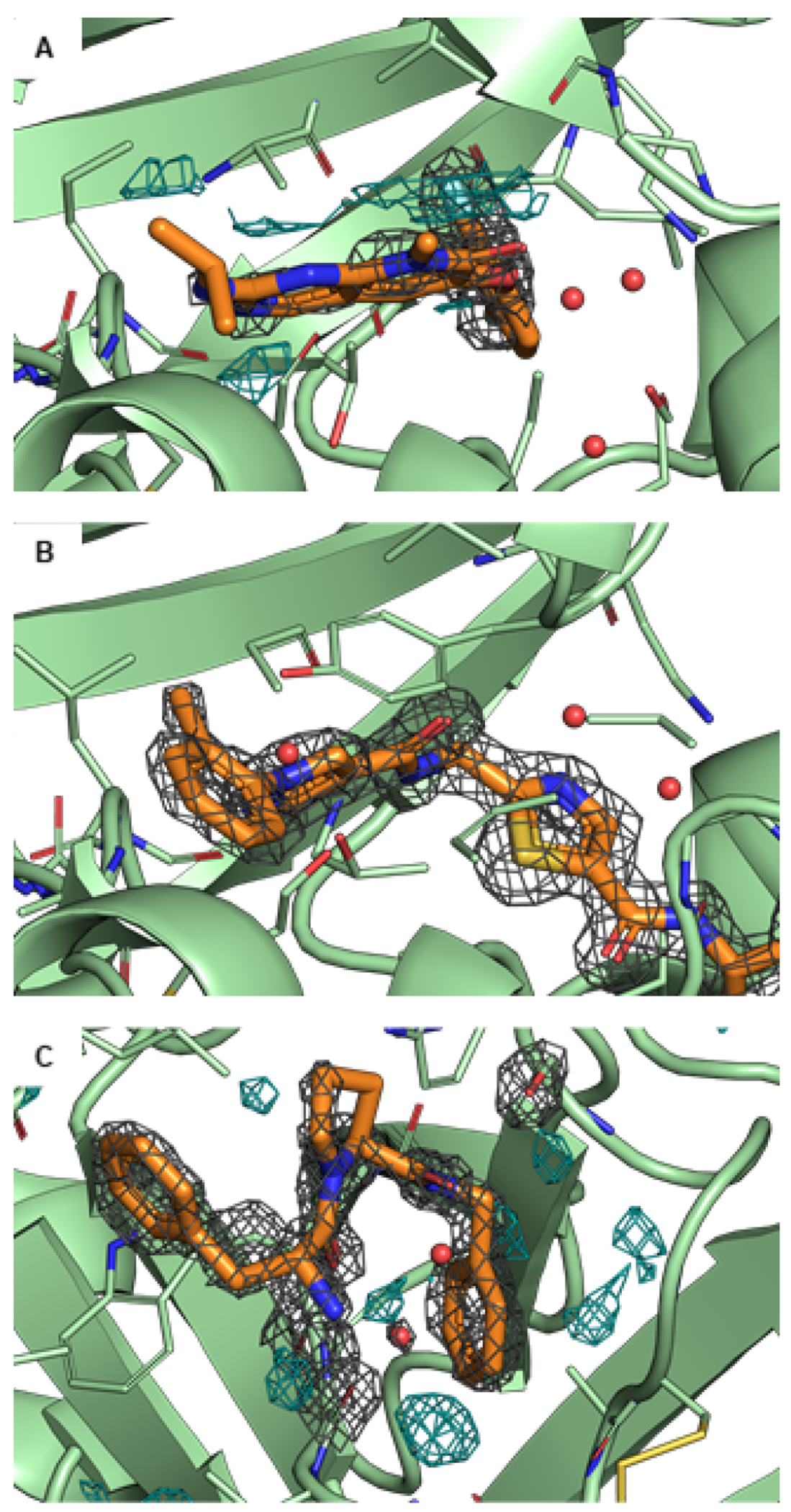
The protein is shown in green and the ligand in orange. If not stated differently, the 2Fo-Fc maps are illustrated as grey isomesh at level. In some panels, the difference density Fo-Fc map is illustrated as cyan isomesh at level. (A) In PDB ID 3FLY, there is significant difference density, likely indicating that the ligand conformation is not modeled correctly. It is suspected that there is a low occupancy alternate conformation that is not modeled. (B) The suggested alternate structure of the same protein, PDB ID 6SFI, has no difference density. (C) PDB ID 2ZFF shows unexplained electron density in the binding pocket (difference map, bottom, center, cyan). This could be either water or a Na+ ion, as Na+ is present and modeled in other sites.
The criteria for selecting high-quality protein-ligand structures are summarized in the checklist “Choose Suitable Protein Structures for Benchmarking”. A use case for these selection criteria to score and select structures from prior benchmarking datasets is found in Table 1.
Table 1. Evaluation of the quality of structural and activity experimental data of the proposed benchmark set.
The structures listed in “Used structure” are those used in the initial version of this dataset, which is drawn in part from previous studies. However, alternate available structures may be superior. In these cases, we provide a PDB ID of a higher quality structure and its quality measures, in the “Alternate structure” field. The alternate structures are sorted according to best structure (lowest Iridium score) first. The footnotes “b” denote structures with similar ligands as the used structure. For each structure, the PDB ID is followed with the Iridium classification and Iridium score in the brackets. The Iridium classification categorizes each structure into not trustworthy (NT), mildly trustworthy (MT) and highly trustworthy (HT) categories. The lower the Iridium score, the better the structure [72]. For the used structures, also the diffraction-component precision indeces (DPI) is listed. We define a high ligand similarity as the OpenEye TanimotoCombo (Shape and Color Tanimoto, range from 0 to 2) being larger than 1.4 (standard cutoff). Regarding activity data (“Ligand Information”), the following metrics are given: The number of ligands N, the dynamic range DR (), and a simulated RMSE. For the calculation of the simulated RMSE, predicted data was drawn from a Gaussian distribution around the experimental value with a standard deviation of , taking also the experimental error into account. The numbers in the brackets are the 95% confidence intervals, obtained by bootstrapping using 1000 bootstrap samples. The quality metrics are color coded to highlight ideal quality (dark green), minimum quality (light green) and low quality (red). The ideal and minimum quality codes correspond to the minimal and ideal requirements of the checklist “Minimal requirements for a dataset”.
| Target | Used structure | Alternate structures | Ligand Information | ||||
|---|---|---|---|---|---|---|---|
| PDB | DPI | N | DR | RMSE | |||
| [kcal mol−1] | |||||||
| BACE[73, 74] | 4DJW (HT, 0.32) | 0.11 | 6UWP (HT, 0.28) | 3INF (HT, 0.33)b | 36 | 4.0 | 0.98 [0.78,1.18] |
| 3TPP (HT, 0.28)a | 3IN3 (HT, 0.36)a,b | ||||||
| 4DJV (HT, 0.31)b | 3LHG (HT, 0.36)b | ||||||
| 3INH (HT, 0.33)b | |||||||
| BACE_HUNT[75–77] | 4JPC (HT, 0.32) | 0.12 | 6UWP (HT, 0.28) | 4JOO (HT, 0.33)b | 32 | 4.9 | 0.97 [0.73, 1.19] |
| 3TPP (HT, 0.28)a | 4RRO (HT, 0.33)b | ||||||
| 4JP9 (HT, 0.31)a,b | 4JPE (HT, 0.35)b | ||||||
| BACE_P2[77, 78] | 3IN4 (HT, 0.59) | 0.28 | 6UWP (HT, 0.28) | 3INF (HT, 0.33)b | 12 | 0.8 | 1.00 [0.59,1.33] |
| 3TPP (HT, 0.28)a | 3IN3 (HT, 0.36)a,b | ||||||
| 4DJV (HT, 0.31)b | 3LHG (HT, 0.36)b | ||||||
| CDK2[74, 79] | 1H1Q (MT, 0.87) | 0.28 | 3DDQ (HT, 0.31)a | 4EOR (HT, 0.39)a,b | 16 | 4.3 | 1.00 [0.67,1.29] |
| CDK8[44, 80] | 5HNB (MT, 0.74) | 0.22 | 5XS2 (HT, 0.33) | 4CRL (HT, 0.42)a | 33 | 5.7 | 0.96 [0.73,1.18] |
| 5IDN (HT, 0.36)c | |||||||
| c-MET[44, 81] | 4R1Y (MT, 0.75)h | 0.17 | 5EOB (HT, 0.28) | 3ZXZ (HT, 0.44)a,c | 24 | 6.2 | 0.99 [0.72,1.26] |
| 3I5N (HT, 0.37)a,c | 4DEG (HT, 0.46)a,c | ||||||
| 3ZC5 (HT, 0.38)a,c | 5EYD (HT, 0.47)a,c | ||||||
| 3CD8 (HT, 0.39)a,c | |||||||
| EG5[44, 82] | 3L9H (MT, 0.88) | 0.18 | 2X7C (HT, 0.32) | 3K3B (HT, 0.41)c | 28 | 3.5 | 0.98 [0.72,1.22] |
| 3K5E (HT, 0.35)a | |||||||
| Galectin[83, 84] | 5E89 (MT, 1.04) | 0.07 | 5NF7 (HT, 0.30) | 4BM8 (MT, 0.38)a, d,b | 8 | 2.7 | 1.04 [0.55,1.42] |
| 1KJR (HT, 0.30)a | 5OAX (HT, 0.54)b | ||||||
| 5ODY (MT, 0.33)b, e, g | |||||||
| HIF2a[44, 85] | 5TBM (HT, 0.35) | 0.17 | 3H82 (HT, 0.30)a | 5UFB (HT, 0.36)b | 42 | 4.6 | 1.03 [0.79,1.27] |
| 6D09 (HT, 0.35)b | |||||||
| Jnk1[74, 86] | 2GMX (NT, -)f | 0.77 | 3ELJ (MT, 0.31)a | 3V3V (MT, 1.5)b, h, e | 21 | 3.4 | 0.98 [0.68,1.26] |
| MCL1[74, 87] | 4HW3 (HT, 0.41) | 0.26 | 6O6F (HT, 0.30) | 4WMU (HT, 0.41)b | 42 | 4.2 | 1.01 [0.80,1.21] |
| 4ZBF (HT, 0.35)b | 4ZBI (HT, 0.45)b | ||||||
| 3WIX (HT, 0.37)a, c | |||||||
| P38(MAPK14) [74, 88] | 3FLY (HT, 0.6) | 0.12 | 6SFI (HT, 0.30) | 3FLN (HT, 0.33) | 34 | 3.8 | 0.99 [0.76,1.22] |
| 3FMK (HT, 0.30 )a, b | 3FMH (HT, 0.43)a, b | ||||||
| PDE2[89, 90] | 6EZF (MT, 0.3) | 0.07 | 6C7E (HT, 0.29) | 6B97 (HT, 0.46)c | 21 | 3.2 | 1.05 [0.75,1.32] |
| 5TYY (HT, 0.30)a | |||||||
| PFKFB3[44, 91] | 6HVI (HT, 0.31) | 0.11 | 6HVH (HT, 0.36)a, b | 40 | 3.8 | 1.04 [0.82,1.25] | |
| PTP1B[74, 92] | 2QBS (MT, 0.33) | 0.15 | 2HB1 (HT, 0.32)a | 2QBR (HT, 0.65)b, a | 23 | 5.2 | 0.95 [0.67,1.21] |
| 2ZMM (MT, 0.33)b, d | |||||||
| SHP2[44, 93] | 5EHR (MT, 0.32) | 0.1 | 5EHP (MT, 0.33)b, g | 6MD7 (HT, 0.35) | 26 | 4.3 | 1.06 [0.76,1.34] |
| 6MDD (HT, 0.35)a | |||||||
| SYK[44, 94] | 4PV0 (MT, 0.69) | 0.19 | 4PX6 (HT, 0.3)a | 4FYO (HT, 0.40)c | 44 | 5.9 | 1.01 [0.81,1.21] |
| Thrombin[74, 95] | 2ZFF (HT, 0.3) | 0.06 | 5JZY (HT, 0.27)b | 3QX5 (HT, 0.28)a, b | 11 | 1.7 | 0.97 [0.63,1.28] |
| TNKS2[96] | 4UI5 (HT, 0.29) | 0.08 | 4PC9 (HT, 0.27)a | 4UVZ (HT, 0.29)b | 27 | 4.4 | 1.04 [0.78,1.28] |
| 4BU9 (HT, 0.29)a, b | |||||||
| TYK2[74, 97, 98] | 4GIH (HT, 0.5) | 0.15 | 3LXP (HT, 0.31)a | 5WAL (MT, 0.48)c, g | 16 | 4.3 | 0.97 [0.60,1.30] |
structure was already available 6 month prior to publication of first benchmark study.
ligand similarity > 1.4
ligand considerably similar > 0.8.
crystal contacts
packing.
alternate conformations.
low ligand density below 0.95.
A choice of the simulation conditions like temperature, ion concentration, other additives like co-factors or membranes require additional considerations. Ideally, these conditions are close to those for the structural experiment, the affinity measurements and physiological conditions. Most likely, a trade-off between all of these has to be found. Where possible select structures where data was collected at room temperature that were crystallized using non-salt precipitants. Be aware that room temperature data will have lower precision and more conformational heterogeneity.
If these requirements are not met, it does not necessarily mean that the data is not usable and the results will not match the experimental measurements. A structure not meeting the requirements may suffice after more manual intervention by the user, ideally an experienced one. Unresolved areas can be modelled with current tools and knowledge about atom interactions, though this can be a cause for concern if these are near the binding site. This concern has been validated, at least anecdotally, in a recent publication where different protein preparation procedures where shown to have a substantial effect on the accuracy of the free energy predictions [104].
Collective intelligence could be a way to mitigate the influence of individuals on the prepared input structures of a benchmark set. On a platform, other scientists could suggest changes to structures and updated versions could be deposited, increasing the quality of the benchmark set. Endorsement and rating of deposited structures could increase the level of trust given to specific structures and the database in general.
4.5. Experimental binding affinity data
Choosing high-quality experimental data is crucial for constructing meaningful benchmarks of methods that predict ligand binding affinities. Evaluating whether experimental data merits inclusion requires an in-depth understanding of the biological system and the particular experimental assay that assesses protein-ligand affinity. While a detailed overview of all experimental affinity measurement techniques is beyond the scope of this best practices guide, this section aims to summarize general aspects that should be considered when evaluating whether an experimental dataset is suitable for benchmarking purposes. We note that, in practice, it is often difficult to identify datasets that meet all the recommendations discussed below.
Overall, it is necessary that the experimental data used in benchmarks intended to measure the accuracy of reproducing experimental data are consistent, reliable, correspond well to the model system that is used in the simulations, allowing robust conclusions on accuracy to be drawn.
4.5.1. Deriving free energies from experimental affinities
Binding of a ligand to a receptor protein can be described as an equilibrium between unbound and bound states with the equilibrium constant of the dissociation Kd as
with [PL] being the concentration of the bound protein-ligand complex and [P] and [L] the concentrations of the unbound protein and unbound ligand respectively. The binding free energy ΔG can be related to the dissociation constant via the following equation
| (2) |
with Boltzmann constant kB, temperature T and standard state reference concentration , which is typically . In many drug discovery projects, potency of compounds is assessed by measuring the half-maximal inhibitory concentration (IC50) of a substance on a biological or biochemical function. This is often converted to pIC50
Typically, the substance is competing in these experiments with either a probe or substrate. For such competition assays, IC50 can be related to the binding affinity of the inhibitor Ki via the Cheng-Prusoff equation
| (3) |
where [S] is the concentration of the substrate and Km the Michaelis constant. Assuming that all binding events result in effective protein inhibition, we can relate . Many assays are conducted using a substrate concentration of [S] = Km. This leads to a conversion factor of 0.5 between IC50 and Ki based on Equation 3 and to a constant offset in ΔG. This offset cancels out for a congeneric ligand series with the same mode-of-action in identical assay conditions. Hence, in this case, ΔpIC50 values are a useful bioactivity that can be compared to relative binding free energy calculations. We can then use the approximation
For absolute calculation comparison to experiment, the offset remains relevant. One suggestion to circumvent the issue could be to transform absolute estimates to , this way cancelling the offset and basing the further benchmarking on the relative free energy differences.
4.5.2. Consistency of datasets
The paucity of experimental affinity measurement data may tempt practitioners to cobble together all available measurements for a given target (say, from a ChEMBL query) to construct a dataset with a sufficiently large number of measurements to provide statistical power in discriminating the performance of different methodologies on a given target. This temptation should generally be resisted, as assay conditions or protocols in different labs might not be comparable. Figure 6 illustrates this by comparing two sets of data obtained by different methods. These differences could, for example, result from the concentration of the substrate (see Equation 3), the protein construct, the incubation time or the composition of the buffer, and might not be sufficiently documented in the reported experimental methodology. However, in comparison to the inherent experimental error (see below), mixing experimental data from different laboratories might add only a moderate amount of noise [105]. To ensure consistency within a dataset such that relative free energy differences are as reliable as possible, we highly recommend the use of data from a single source (e.g., a single publication or a patent).
Figure 6. Experimental uncertainties can be on the order of 0.64 kcal mol−1.
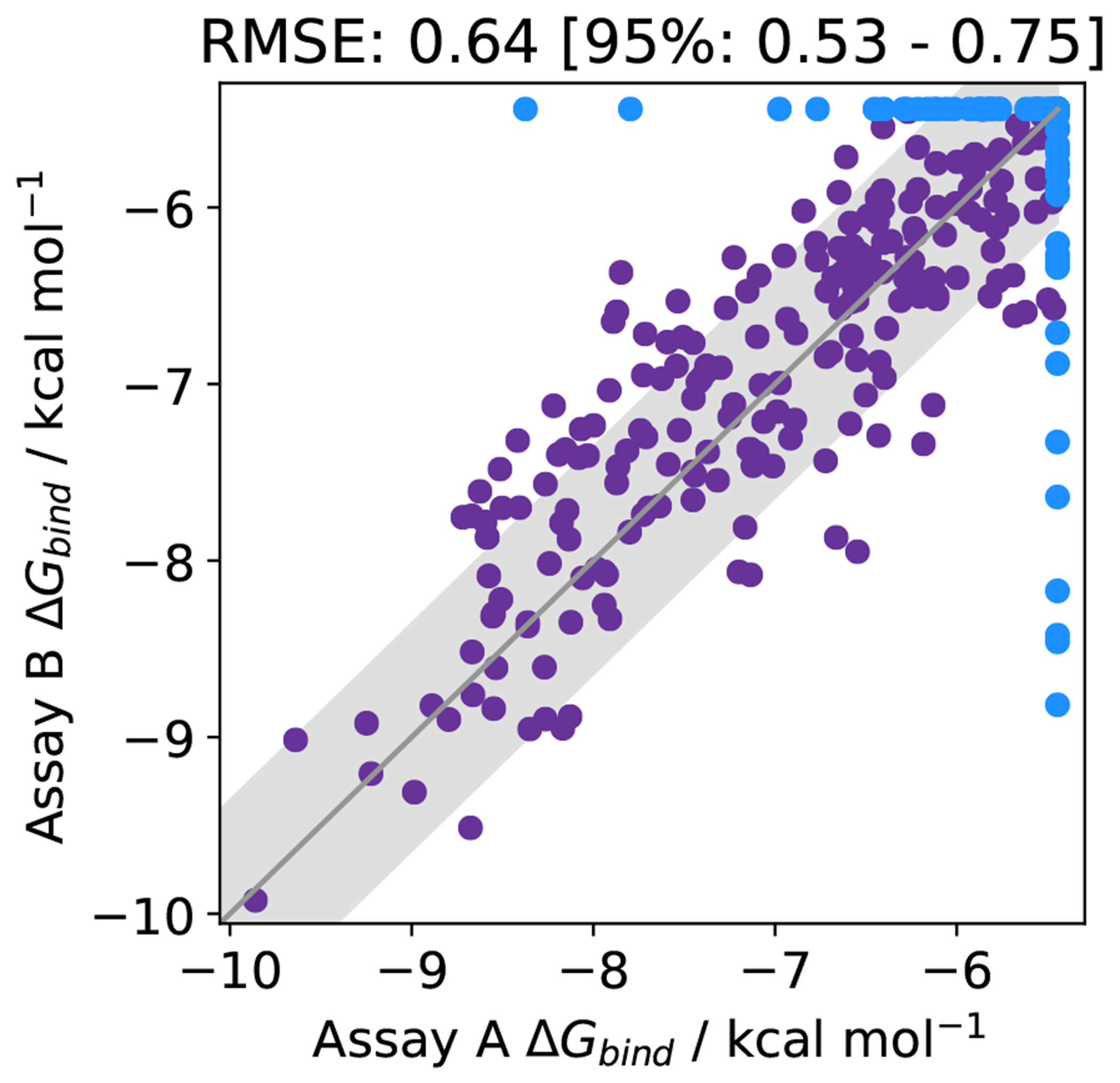
The binding affinity of 365 molecules assayed by two different methods for the open source COVID moonshot project [106]. Molecules that were predicted to bind in one assay, but inactive (i.e., affinity lower than the assay limit) in the other are shown in blue. The RMSE agreement between the methods, for both purple and blue data points is 0.64 kcal mol−1. Data was collected from the PostEra website accessed 22/11/2020 [107]. The grey region indicates an assay variability of 0.64 kcal mol−1.
To avoid rounding or unit conversion errors that often arise from automated or manual data extraction, data should be extracted from the original source.1 Going back to the original publication is also important to identify compounds that are outside of the detection limit of the assay but are still reported with specific numerical values (e.g., reported ). Such ligands should be excluded from benchmark sets to ensure that accuracy measures can be properly evaluated.
4.5.3. Experimental uncertainty
To assess the reliability, ideally, errors are reported for all ligand affinities or at least for a subset. The primary publication of the experimental results is typically the best source of experimental uncertainty as cited affinities may occasionally be subject to rounding differences or unit errors [110]. Errors quoted will likely be an estimate of the repeatability of the assay, rather than true, independent reproducibility. Publications with essential experimental controls reported – such as incubation time and concentration regime to demonstrate equilibrium – can add confidence to the reported affinity, however these may be performed and not reported [111]. Meta-analyses of both repeatability [112] and reproducibility [110] found errors in pKi of 0.3-0.4 log units (0.43-0.58 kcal mol−1) and 0.44 log units (0.64 kcal mol−1) respectively. Another analysis for reproducibility found that variability in pIC50 was even 21-26% higher than for pKi data (0.55 log units) [105]. These values provide a guideline for experimental error, if none is available. Note that for difference measures ΔpIC50, the individual experimental errors propagate as .
4.5.4. Choosing representative experimental assays for FE calculations
There are two main requirements to consider in order to ensure that the experimental data are representative of the physics-based binding free energy that is calculated from the simulations. First, the measured output should reflect or closely correlate with actual protein-ligand binding. Second, the assay conditions and the protein-ligand system used in the simulation should match as closely as possible. The first point relates to choosing the appropriate type of experimental data to compare with. Ideally, these would be biophysical binding data such as KD determined from isothermal titration calorimetry (ITC) or surface plasmon resonance (SPR). However, this type of data is often only available for a small number of compounds in drug discovery projects (and the related literature), typically for a few representatives per series. In addition, ITC data are often only available for a narrow dynamic range [113, 114]. Since having a sufficiently large dataset with a large dynamic range is also very important (see below), it may often be necessary to use data from functional assays (e.g., IC50 from a biochemical assay) instead. For this assay, correlation with a biophysical readout should be checked before using the system as a benchmark dataset [105].
With regards to matching simulation and binding assay, as mentioned above, it is important to have detailed knowledge of the assay conditions available; e.g., salt concentrations and co-factors. This information is needed for setting up a simulation model that closely matches the experimental conditions (see Section 5.1). Generally, salt concentration should match experimental assay conditions to capture screening effects, though sometimes salt identity may be varied because of force field limitations. For a benchmark set, experimental data with assay conditions involving many co-factors or multiple protein partners should be avoided. In addition, one should check which protein construct was used in the structural studies compared to the assay (see Section 4.4). These should match as closely as possible.
4.5.5. Ensuring sufficient statistical power
Finally, a dataset used for benchmarking of free energy calculations needs to be suitable to draw robust conclusions on the success of the methods ideally by both accuracy and correlation statistics. Whether a dataset is suitable depends on the number of data points in the set, the experimental dynamic range and the experimental uncertainty.
Quantifying the experimental uncertainty is necessary for understanding the upper-limit of feasible accuracy for a model [115]. Understanding this is both useful for fair comparison between methods, and for conveying the reliability of a model to medicinal chemists [116]. Building predictive models becomes more difficult with (a) a small experimental dynamic range and (b) large experimental uncertainties. It is useful to understand the upper limit of success a computational method can have for a set of experimental results:
| (4) |
where is the highest achievable R2 for a dataset with a standard deviation of affinities () and an experimental uncertainty of [112]. This relation is illustrated in Figure 7.
Figure 7. The larger the experimental uncertainty, the larger the affinity range required for a given .
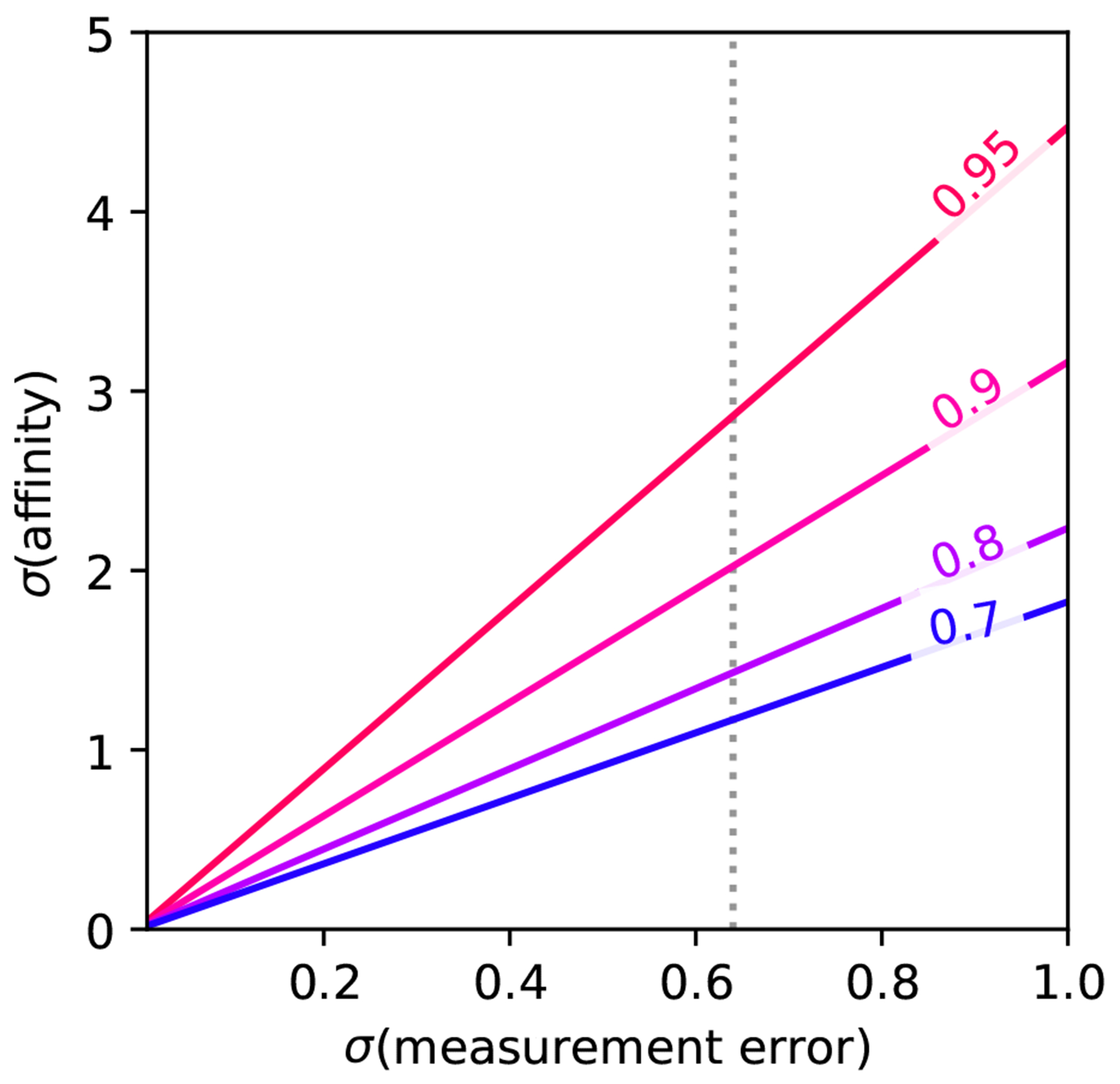
Corresponding to Equation 4, the maximum achievable R2 for a given dataset is limited by the range of affinities and the associated experimental uncertainty. The illustration assumes that (measurement error) and (affinity) are in the same units, with an experimental error of 0.64 kcal mol−1 indicated.
For a typical experimental error of 0.64 kcal mol−1 (see Section 4.5.3) and a desired , a standard deviation of affinities (≈1.5 log units) is required. Assuming a uniform distribution of experimental affinities in the dataset, this corresponds to a required dynamic range of 7.01 kcal mol−1 (e.g., from −12 to −5 kcal mol−1) or ≈ 5 log units (e.g., from 1 nM to ). This dynamic range and the associated standard deviation of affinities also allow to differentiate typical free energy methods from a trivial affinity prediction model where all predicted affinities are equal to the mean experimental affinity . Note that for such a model RMSE is equal to the standard deviation of the affinities , while there is no correlation between predicted and experimental affinities. In practice, experimental datasets with a dynamic range of 7 kcal mol−1 are difficult to obtain. Using the same assumptions as before, a dynamic range of 5 and 3 kcal mol−1 correspond to a standard deviation of affinities of and and hence and respectively. Balancing data availability and achievable , we recommend collecting datasets with a dynamic range of 5 kcal mol−1 (3.7 log units).
In order to robustly evaluate statistics with small confidence intervals, the dataset needs to be sufficiently large. Figure 8(A) and (B) illustrate the dependence of the confidence interval obtained by bootstrapping for correlation statistics and accuracy statistics for simulated toy data. The “experimental” toy data were simulated using a uniform distribution with an affinity range of 7 kcal mol−1. This would be the optimal dynamic range for an experimental error of 0.64 kcal mol−1 (see Section 4.5.3). Predicted toy data were derived from the experimental toy data using a Gaussian distribution with standard deviation of . While the absolute values that can be obtained for the correlation statistics are strongly affected by the dynamic range of the experimental data, the effect on the confidence intervals estimated via bootstrapping is relatively small (very similar results in terms of the size of the confidence intervals can be obtained assuming a dynamic range of 5 kcal mol−1).
Figure 8. The larger the dataset, the smaller the uncertainty in the performance statistics.
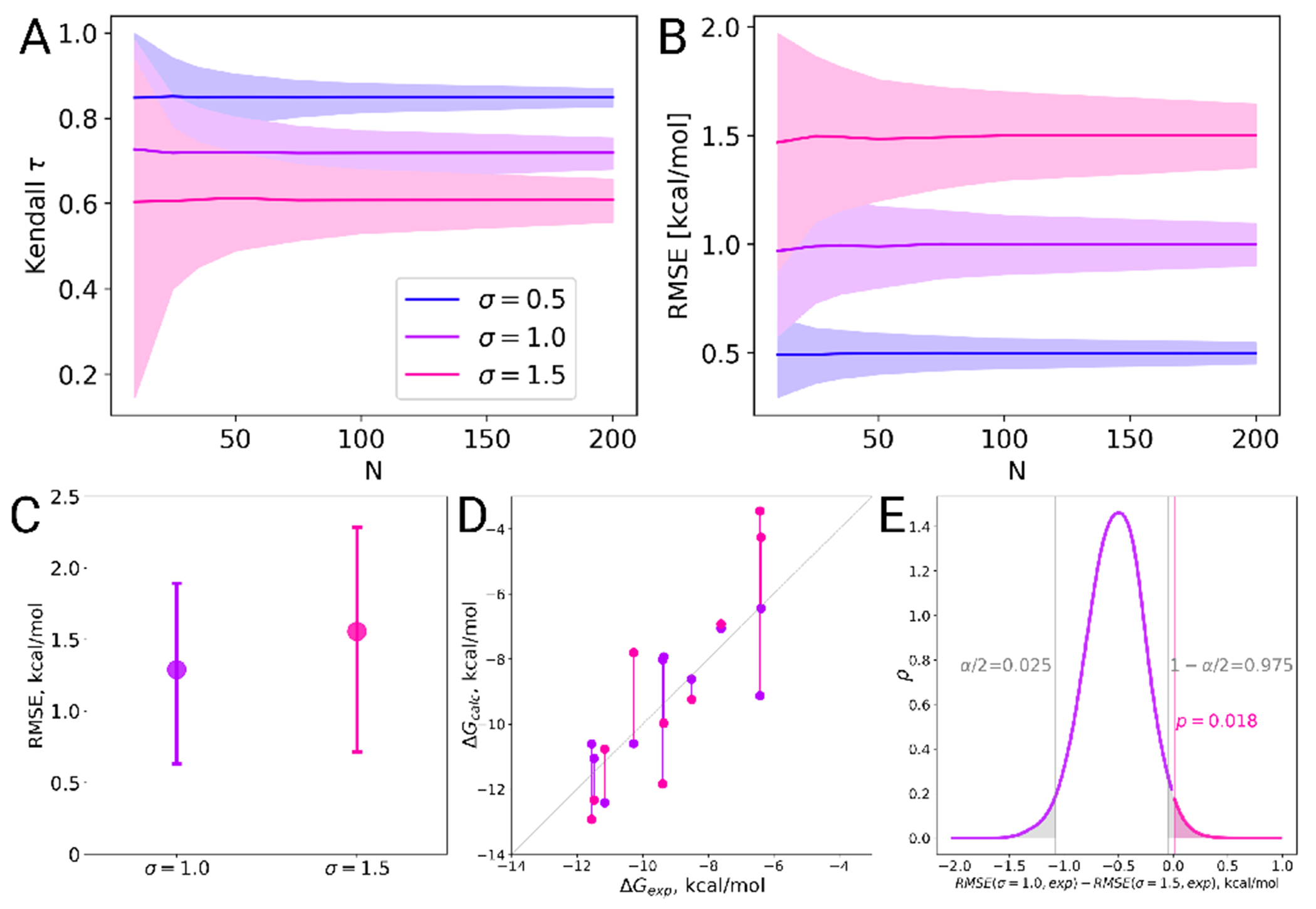
(A) Kendall and (B) RMSE were evaluated for 1,000 toy datasets for a given size of the dataset N. The experimental data were simulated from a uniform distribution over the interval [−12:−5] and the predicted affinities were simulated from the experimental toy data using a Gaussian distribution with different standard deviation . The statistic was evaluated for the whole dataset and 95% confidence intervals were estimated via bootstrapping. These were then averaged over all 1,000 toy datasets. In (C-E) we illustrate a specific case, where two sampled sets of size N =10 were chosen for a closer inspection. (C) Their RMSE values have overlapping confidence intervals. (D) However, when investigating the underlying sets of points in a pair-wise manner, it appears that one case mostly yields values closer to experimental reference than the other. (E) Bootstrap analysis of these dependent samples reveals that the RMSE difference in this case is statistically significant at the confidence level of .
Based on these simulations, we recommend a dataset size of 25 to 50 ligands. For a dataset size of 50, it is possible to distinguish between all three toy methods reliably in terms of RMSE. For an affinity prediction method with Gaussian error this would yield the following estimated statistics: Kendall and . Note that for relative calculations, a smaller number of ligands could be sufficient since multiple edges are typically evaluated for each ligand. On the other hand, for relative calculations, the experimental error for the relative free energies are larger because experimental errors for both ligands add up.
It is important to note that for the case of overlapping error bars, it is not possible to immediately conclude that the compared methods do not differ significantly. This is due to the compared data sets being paired, i.e. the sets are not independent. Analytical rules for deducing whether it is possible to determine if the differences are statistically significant have been nicely summarized by Nicholls [117]. Here, we suggest how to probe for the significance in difference between predictions by means of bootstrap. For the Figure 8 (C), two sets of points were selected from the previous samplings depicted in panels (A) and (B). In this case we used sets of only 10 points each and the resulting RMSE values have overlapping error bars. The sets of points are shown explicitly in the Figure 8D, where it becomes clear that for most of the point pairs the case with has a value closer to the experimental reference than the sampling with . Now to assess the statistical significance of the observed RMSE difference (panel C) we sample with repetition pairs of points in panel D. For every resampling, RMSE values for the two cases are calculated and the difference between the RMSEs is stored. Such a resampling strategy ensures that the dependence between the points is retained. Finally, analyzing the distribution of collected RMSE differences will show whether the difference is statistically significant from zero at a chosen level.
As demonstrated in the example above and Figure 8, uncertainties of the estimated statistics strongly depend on the standard errors of individual free energy predictions. Naturally, this necessitates accurate estimation of uncertainties for the calculated (or ) values. Depending on the free energy protocol and estimator used, an analytical uncertainty estimator might be available. Another possibility is to use bootstrapping, i.e. resample the raw calculation data with repetition to reconstruct the sampling distribution and estimate its standard deviation. However, probably the most reliable, yet computationally demanding, approach to obtaining the standard error is by repeating the whole calculation procedure multiple times [118–120].
As stated before, in practice it is challenging to find datasets that meet these criteria for dynamic range and number of ligands. We therefore currently recommend annotating benchmark datasets according to these criteria to make challenges and limitations visible.
5. How to best set up and run benchmark free energy simulations
5.1. Structure preparation
Starting with an experimental crystal structure, often an X-ray structure for the protein or protein-ligand complex, the most error-prone stage of protein preparation is the translation from this experimental structure into a simulation model: inferring missing atoms and making choices about which X-ray components to include. Having chosen biological unit based on the criteria in the above section, some domains of the structure may be removed if they are large and unlikely to affect the biological activities of interest. The truncation of the system needs to be assessed carefully as it has been shown in some cases, such as the dimeric form of PDE2 and the presence of cyclin with CDK2, as a more authentic representation of the system was beneficial for stability during simulations and improved the free energy calculations. In some cases, though, truncation gains efficiency by decreasing the size of the overall simulation system while maintaining its biological activity, with potentially minimal impact on results. Datasets for benchmarking may be run many times so this efficiency gain can be meaningful.
In addition to the protein itself, the subsystem carried forward from the X-ray structure into simulation may have other components: ligand, cofactors, structural waters, other ligands (if simulating a multimer), post-translational modifications (PTMs), and excipients. The cofactors should be deliberately included or excluded based on their role in the biological activity being modeled, removing a cofactor from its cavity might cause unexpected movements or collapse of the cavity during the simulations. To avoid this, a careful equilibration and solvation of that pocket might be needed. All structural waters close to the protein should be considered for inclusion by carefully verifying that water positions are compatible with the modelled ligands: in principle the MD sampling could allow waters to arrange in equilibrium positions, but experimental and theoretical work has shown that the timescales for this can be impractically long. Also, internal structural waters even very distal from the active site are integral to the protein structure, and omitting them can adversely affect the protein dynamics. Generally, we recommend excluding excipients (often specific to the crystallization media and not present in the assay). PTMs require a judgement call: surface-exposed and distal from the active site they can often be safely excluded, for example glycosylations which could otherwise greatly increase the size of the calculation. This again can save on the overall system size and prevent parameterization difficulties. PTMs proximal to the active site or known to be directly implicated in activity should be retained. Ligands other than that in the active site are again a judgement call: retaining them is only necessary if there is biological cooperativity in the biological assay. As this is in practice often not known, they should be kept if possible.
For the absolute binding free energy calculations, it is also necessary to account for the free energy change in the protein’s transition from its apo to holo state. Therefore, initializing the simulations of the alchemical ligand coupling based on the crystallographically resolved protein’s apo state may facilitate convergence.
5.1.1. Protein preparation
The experimental protein structure frequently has missing coordinates for atoms, residues or groups of residues due to the lack of supporting data (electron density) from the X-ray experiments. These often include N-terminal and C-terminal residues, mobile loops (e.g. the activation loop in kinases), and residue sidechains. Also, there can be extra coordinates available in the structure as “alternate locations” (AltLocs): residue sidechains, or occasionally entire residues or the ligand, for which the experimental density supports more than one distinct orientation in a single X-ray structure solution. For the simulation, the protein must have all the atoms provided for every residue modeled. Missing residue sidechains should always be modeled in, assigning them the most preferred rotamer given the local environment.
If the N- and/or C-terminal residues are missing due to lack of electron density, this may provide a basis for omitting them from the model, but the truncated N- and C-termini should be “capped” by neutral termini, usually an acetate (ACE) cap on the N-terminus and an N-methyl (NME) cap on the C-terminus to mimic the peptide backbone up to the carbon-alpha. Of course, one must be careful not to cap the charged protein termini which are properly resolved in the X-ray: these can be critical for function and structure.
This “capping” tactic can also treat the termini of “gaps”: regions of missing residues over the span of the peptide chain, usually missing loop regions due to lack of experimental density. While capping the ends of a loop instead of modeling the whole loop may be acceptable for MD runs of relatively short duration, over longer simulations there is a risk of having the protein around the capped ends of the missing loop gradually lose its structure. Even if a loop is unstructured (and therefore not resolved in the X-ray structure), its presence still affects the remainder of the structure and can provide stability by restricting movement of the connecting residues, thus raising concerns if these are capped instead. Strategic use of a distance restraints during the simulations can mitigate this liability.
Another possibility for missing loops is to close the ends with a short modeled loop of glycine residues of sufficient size to link the termini without introducing strain, but not necessarily of the full length of the missing loop. There are several reasons why this can be desirable. If the missing loop is particularly large (for instance >15 or 20 amino acids) accurately modeling its conformation could be challenging and introduce more uncertainty and instability to MD simulations. Furthermore, if the missing loop is distal from the binding site and not expected to affect protein-ligand interactions, the replacement only needs to stabilize the termini and avoids the use of restraints.
However, all of these approaches are likely inferior to using a good quality model of the missing loop.
When multiple alternate models of a particular region of the protein are available, the experimental model indicates that this region potentially occupies two (or more) mutually exclusive conformations, but one must be chosen for the model. Again, this selection can be a judgement call depending on where this region occurs relative to the active site: distal from the active site, the choice may be less critical; proximal requires more careful consideration. Higher occupancy for one of the alternate models could provide a reason to choose that particular model for the calculations. For critical or uncertain cases, we recommend repeating test simulations beginning from different models to analyze the sensitivity of the choice.
Once the above issues have been resolved, there remains one more round of decision-making to select sidechain rotamers and protonation states. Protein X-ray experiments usually cannot resolve the positions of hydrogens, making decisions on the protonation states an issue. Another challenge is determining sidechain orientations: sidechain flips are particularly relevant for HIS, ASN, and GLN, because the X-ray crystallography experiments cannot distinguish between different first-row elements O, N, and C. These elements produce similar density and are indistinguishable. This means that even with good electron density the sidechain orientations of ASN and GLN can have either orientation, swapping O and N positions, and thus interchanging H-bond donors and acceptors. The two possible orientations of HIS sidechains effectively interchange N and C positions in the ring. Surface exposed, these different orientations may be of little consequence, but in the interior of the protein, proximal to the active site, or especially interacting with the ligand, this can be very important and can change patterns of hydrogen bond donors and acceptors. In principle these orientations can be sampled over the course of the MD run but only if the trajectory is long enough for the sampling scheme to allow it. Considering that these orientations are experimentally ambiguous, it is a matter of judgement at setup time of whether these sidechains should be reoriented to make a more chemically reasonable model.
Protonation of the protein model is generally straightforward with one key exception: the ionization state of sidechains, especially HIS, ASP and GLU, which may undergo pKa shifts due to changes in the environment. Active site catalytic CYS is another case requiring care, and occasionally LYS can be deprotonated in some circumstances. The two main determining factors are the pH of the biological milieu and the microscopic environment around the ionizable sidechain. In general, the ionization state of each residue is chosen during the setup of the protein and remains constant over the course of the simulation, even if the microenvironment changes. Note that a formal charge on the bound ligand can also affect the ionization state of nearby protein residues; this can be particularly problematic when the ligand charge alchemically changes over the course of a relative free energy calculation. Unlike side-chain rotamers, which may sample other orientations within a simulation, incorrect protonation state assignments cannot correct themselves without the use of constant-pH algorithms, that have not been routinely implemented within free energy calculations yet.
There are a number of tools to automate the steps described in this section, notably the Protein Preparation Wizard [121], the Molecular Operating Environment (MOE) [122], and Spruce [123]. We recommend manual inspections after applying these.
5.1.2. Ligand preparation
In the preparation of the ligand for simulation it is important to verify that the chemical structure is correct. While this is less problematic for structures generated from small-molecule sources, historically it has been a frequent problem for ligands taken from protein-ligand X-ray structures. Since X-ray structures lack protons and do not provide bond orders or other key information, if a PDB structure is used as input, some tool must be applied to supply this information, presenting a frequent source of failure (though, for structures in the RCSB, a ligand SMILES string can provide a more complete representation of the ligand’s identity).
Once the underlying chemical structure, including bond orders and stereochemistry, is correct, the key issues are the tautomer and ionization states. As with the ionizable protein residue discussed above, the main factors are the macroscopic pKa of the ligand (for ionization states), the intrinsic relative stability of different tautomer states, and the perturbing effects of the active site micro-environment of the bound ligand. Compounding the complexity is if the unbound ligand (used as a reference state) would have a different tautomer/ionization state. These need to be carefully examined at setup to make sure there is complementarity between the protein and ligand independently of the alchemical change between ligands, and then to flag and resolve alchemical conversions between inconsistent states of the protein.
5.1.3. Preparation of the complex
Once protein and ligand have been prepared, the complex is assembled and solvated in water with counter-ions at an appropriate ionic strength, or embedded in membrane if the protein belongs to a membrane protein family. Membrane simulations should use an appropriate equilibrated membrane that matches experimental criteria of thickness and area per lipid as well as the appropriate counter ions. Once the system box is constructed the step involves neutralizing the net charge on the protein-ligand complex, but beyond this a higher concentration of salt (usually sodium chloride) is often warranted to mimic the biological milieu being modeled; most assays are run in a significant salt concentration (100 to 150 mM) to emulate biological environments. The salt concentration can strongly affect experimental binding affinities, particularly with highly polar active sites. The ion placement needs to be handled with care, for example by prohibiting insertion of ions within a given distance from the protein-ligand complex. Otherwise, positioning an ion in a close proximity to the bound ligand may destabilize the binding pose, in turn affecting the prediction accuracy [124].
Once the above decisions have been made and the complete simulation system has been set up, it is important to let it relax and equilibrate at simulation temperature and pressure, which should mimic the assay conditions.
5.2. Alchemical free energy calculations pose specific setup challenges
There are an abundance of details that must be considered during the set up of any simulation and in particular for alchemical free energy calculations. These simulations require setting up an alchemical perturbation of the small molecules, but also require making a variety of assumptions with respect to the environment at the two end states. In the following we will address all essential choices that need to be made for the setup. For a very detailed introduction to best practices for alchemical free energy calculations and a much broader discussion on choices for their setup please refer to the relevant best practices guide [19].
5.2.1. Should I run an absolute or relative free energy calculation?
There are two possible ways in which to run alchemical free energy calculations, which both provide free energies of binding, but will require different routes for their setup. Relative free energy calculations provide free energies of binding with respect to a reference ligand, meaning that all compounds that are to be assessed for their binding affinity should share a similar scaffold. In contrast, absolute free energies of binding can be used for a set of ligands that do not share any commonalities, since the reference state for the free energy of binding is the standard state. This is probably the easiest deciding factor in terms of what kind of calculation to run. If the particular benchmark dataset contains ligands that form a congeneric series then a relative calculation is likely a better choice. Of course, congeneric ligand series can also be assessed using absolute free energy calculations, or it may be of interest to compare relative to absolute calculations for a given benchmark dataset.
5.2.2. Alchemical pathway
Choices in topology
The choice of topology may be dictated by the simulation software of choice as not all common MD codes implement all topologies. The topology refers to the way in which a molecule A is changed to molecule B, in case of relative free energy calculations. Selecting either a dual or single topology approach is acceptable, unless performance of different topologies is assessed across the benchmark datasets. For more details on the different topology choices and implementations please refer to Mey et al. [19].
Choices concerning
In order to connect the initial and final state of the alchemical free energy calculation an alchemical pathway must be chosen. This pathway is regulated by a variable , which, in the simplest formulation, at represents molecule A and at molecule B. As free energy is a state function, the computed free energy is in principle independent on the pathway, but different choices in pathway can make the problem computationally more or less tractable. The simplest way to switch between molecule A and B is using a linear switching function for the Hamiltonian of the form:
| (5) |
where is the Hamiltonian, is the set of positions, is the set of momenta and the switching parameter. However, this typical approach fails when atoms are being inserted or deleted, requiring alternate choices, as reviewed elsewhere [19].
For the free energy perturbation (FEP) protocol, considerable care needs to be taken in selecting the switching function and spacing of so-called -windows. Common choices are, how many -windows should be used? What functional form should my switching function take? The concept of difficult and easy transformation is more and more explored, but currently heuristics based on phase space overlap between neighboring -windows is the best way to assess how many windows should be simulated. This can for example be done by looking at the off-diagonals of an overlap matrix [125, 126]. Furthermore, the choice of simulation protocol will influence what switching function and how many -windows should be used.
5.2.3. Choice of simulation protocol
Various simulations protocols for alchemical free energy calculations are available and can be categorized into reference state, independent replica with constant or variable states and ensemble (multiple replica) methods. In reference state methods, one reference state is simulated in a single simulation and free energy differences to other states are extrapolated. Examples for these is one step perturbation [7, 127–130] or enveloping distribution sampling (EDS) [131–135]. In independent replica methods, one or several simulations are performed at different states of the coupling parameter . These parameters may be constant like in discrete thermodynamic integration [9–11] or free energy perturbation [136]. Other methods allow the simulation to adopt discrete states as in self-adjusted mixture sampling [137] or expanded ensemble simulations [138–142]. can also be varied continuously in slow growth thermodynamic integration [143] or dynamics [144–150]. Fast growth or non-equilibrium switching are special cases of independent replica methods where is rapidly changed in non-equilibrium simulations [151–154]. In multiple replica or ensemble methods, two or more replicas of the same system are simulated in parallel and are in equilibrium with each other. In Hamiltonian replica exchange, swaps between replicas at different fixed states are attempted and either accepted or rejected according to the Metropolis-Hastings criterion [155–157]. We provide examples of four of the above protocols, which are summarised in Figure 10. These are: Figure 10(A) independent replicas at constant states, (B) replica exchange, (C) Single replica, self adjusted mixture modelling and (D) non-equilibrium switching. Particularly for (B) and (C) the choice of -spacing will be important, as in (B) it dictates the success of replicas exchanging between and in (C), often tightly spaced replicas allow for a best exploration. Independent replicas are not necessarily recommended, but are still commonly implemented in software packages.
Figure 10. There are four simulations protocols available for for generating samples and evaluating the Hamiltonian at the states.
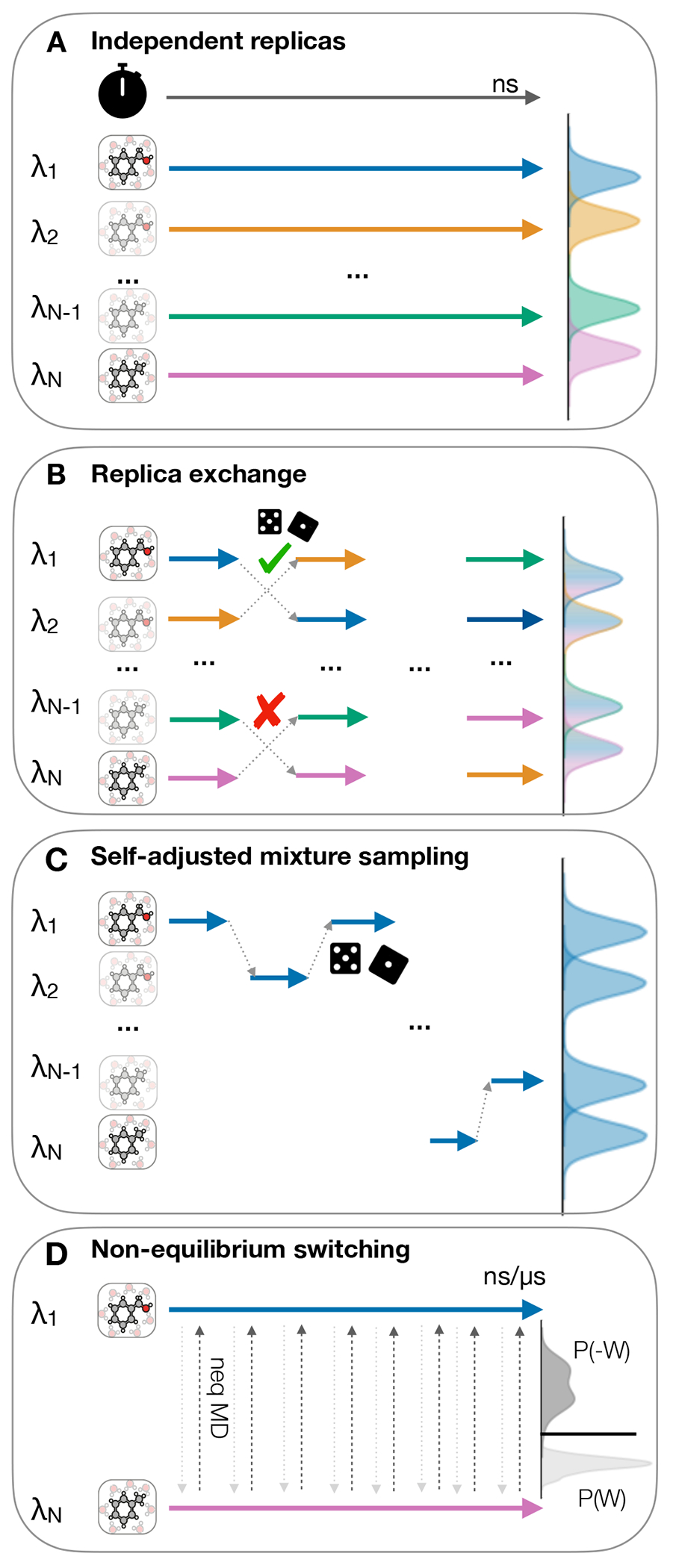
(A) Independent replicas run in parallel at different as indicated by differently colored arrows, (B) Replica exchange attempts after short simulation for each replica (C) Self-adjusted mixture sampling with a single replica exploring all of , (D) Non-equilibrium methods with equilibrium end-state simulation and frequent nonequilibrium switching between end states. The clock icon is indicating the flow of simulation time and the pair of dice indicate a Metropolis Hastings based trial move
5.2.4. End-state environments
When setting up a relative free energy calculation it is important to be aware of the similarity of the ‘end states’, i.e. of the conformational, hydration, and electrostatic environment of ligand A and B. Many of these end-state issues can be addressed with longer sampling, but this may be impractical and should be considered when planning perturbations. Issues can arise, if there are two distinct bound conformations (different binding modes) for ligand A and ligand B, it may be necessary to sample both binding modes, or extend the simulation time to allow for sufficient rearrangements. A similar issue that may be addressed with extended sampling times are scaffold changes that occur between ligand A and B. Different hydration patterns may also cause inaccuracies in computed binding free energies. Probably the most difficult issue to address are changes in charge states that occur either between the two ligands or may even affect the protein depending on the type of ligand binding. Methods to address this issue are double system/single box setups [158] to retain neutral charges, the use of alchemical ions [159], or the post-hoc corrections [160, 161] to values.
For the absolute binding free energy calculations, the situation is further complicated by the need to account for the change in protein’s conformation when transitioning from apo to holo state. Converging larger protein reorganizations may become challenging already in relative free energy calculations [162], thus in estimating absolute binding failure to properly capture this contribution may manifest in a substantial offset of predicted values with respect to experimental measurement [103]. In principle, longer or enhanced sampling could help in improving convergence of large conformational changes [19]. Another option is to explicitly make use of the crystallographic apo state (if it is available) to initialize ligand coupling simulations for the non-equilibrium switching scheme [163] or seed an FEP based simulation [164].
5.2.5. Perturbation maps for relative calculations
In relative free energy calculations a network of perturbations between ligands needs to be constructed. The choice of which relative calculations to carry out is vast and can have a substantial effect on the accuracy of the results. The way in which different ligands are connected by relative alchemical calculations is called a perturbation map. In particular for benchmarking free energy methods, perturbation maps should be held fixed for a given benchmark set, unless the goal is to test different approaches for setting up perturbation maps. In this way each edge of the perturbation map will be maintained across subsequent tests and plots created during the analysis phase later will be comparable.
The simplest way of connecting ligands in a perturbation map is in a star shape, with each connected to a central crystal structure ligand, with the assumption that all ligands of the congeneric series will bind in the same binding mode as the available crystal – which may even be confirmed by other crystals, see Figure 11(A), there are different methods available for creating interconnected perturbation maps using LOMAP [165] or Diffnet [166], as well as some work towards assessing trade off in terms of what network structure will actually provide most reliable estimates with as little computational cost as possible [166, 167]. To date, there are no rigorous guidelines to prioritise perturbations, but we recommend avoiding difficult perturbations such as those mentioned above involving ring breaking, changes in linker length, changes in charge, and where possible attempt to maximise structural similarity in 2D (via the maximum common substructure) and 3D.
Figure 11. Typically either star shaped perturbation maps or multi-connected perturbation maps are used in relative free energy calculations.
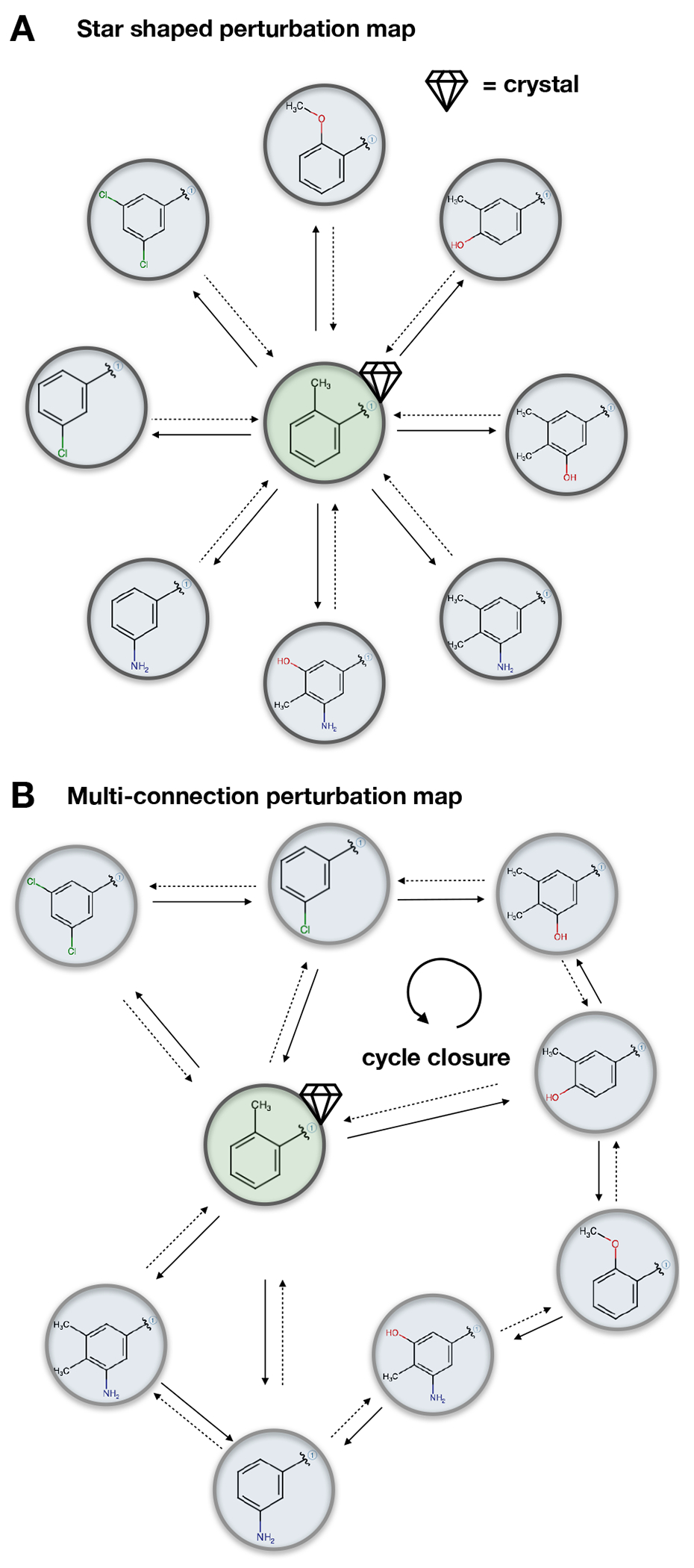
(A) The star map will have a central ligand, of which the crystal structure is known and all other ligands distributed in a star. (B) A multi-connected map introduces redundancies into the network, allows for larger perturbations through multiple connections and allows assessment of robustness of calculations. The diamond and green shading indicates the crystal structure.
When computing absolute binding free energies, one naturally circumvents the need to generate a perturbation map.
6. How to analyse benchmark free energy simulations properly
6.1. Measuring the success of free energy calculations requires careful analysis
Reliable reporting and analysis of the success of calculations is vital for the validation and benchmarking of free energy methods, as well as the dissemination of published results. The reporting and analysis falls into two major categories - visualization of the results, and statistical analysis. Here, we make recommendations for both categories.
6.1.1. Plots of free energy results should adhere to certain common standards
Figures plotting experimental vs. calculated results are a very useful way to gauge the success of a method or a set of calculations. We recommend several key steps to ensure these plots are valuable, communicate accurate information, and are informative and readable. Experimental values (on the x-axis) should be converted into the same units as the free energy results (on the y-axis), and axes should use the same scale. One common issue with plotting free energy results is that different scales are used on the different axes, which can change the appearance of the results, as illustrated in Figure 12, where changes in the axis and ratios can make the data look more correlated.
Figure 12. Changes to the plotting style can change the appearance of the data.
The above three figures illustrate the same toy data. (A) shows the data correctly, with the same units (which are labelled) and scales on both axes. (B) shows the same data, however the limits on the y-axis have been changed such that the scales is not consistent. (C) is also not consistent, but this is due to the scale of the plot, rather than the limits.
Error bars can be very helpful in understanding the uncertainty in the data - both for calculated and experimental values, and thus both experimental and computational error bars should always be included in visualizations of the data. Different sources of error might be used to quantify this, whether an uncertainty directly from a free energy estimator, variance between repeats or a hysteresis-type analysis. If the experimental errors are not reported, the experimental error can be estimated as e.g. 0.64 kcal mol−1 (see Section 4.5.3). How the error bars have been calculated should be reported in the figure caption.
Additionally, experimental values which were not actually measured (e.g. values resulting from a measured KD value which only has experimental bounds, such as ) should not be plotted or should be clearly indicated by different styles and symbols. Such data should not be included in the accuracy or correlation statistics, see discussion in Section 6.1.2. However, confusion matrices and reporting sensitivity, specificity, and precision can be useful for asserting a models’ strength at classifying ligands as binders and non-binders, as demonstrated in [168].
Finally, plots of results across multiple targets should typically be shown as one figure per target when the free energy estimates are obtained from the relative free energy calculations. Differences in the success of free energy methods can vary widely between targets, and combining the data across targets onto a single plot can obscure actual performance on any given target. When considering absolute free energies, the affinity ranges between targets may vary, which may result in analysis picking up the correlation between targets and their affinities, rather than the free energy methods ability to differentiate affinities for a particular target. Therefore, if the aim is to evaluate method accuracy per target, each protein-ligand system needs to be studied separately. On the other hand, for absolute free energy calculations it might be of interest to explore whether the method is able to differentiate binding affinities for different targets. One example of such a scenario where considering all target sets together is necessary is free energy calculations for selectivity analysis of similar proteins, where the targets are not independent parameters [169].
6.1.2. Consistent reporting of statistics, and understanding their limitations is vital for measuring success
Free energy calculations fall into two categories: absolute and relative. Depending on which type of result are being analyzed — absolute or relative — different statistics will be appropriate. Accuracy statistics, such as root mean squared error (RMSE) and mean unsigned errors (MUE) provide information as to how well the computational method recapitulates the experimental results, and allow for a ‘best guess’ as to how far the computation prediction of new ligands’ affinities may be from experiment. Correlation statistics, such as R2, Kendall tau () and Spearman’s rank () indicate how well a method does at ordering the results, at identifying the best and worst ligand in a set, which in an everyday drug design application, where these models may be used to make purchasing decisions or for synthesis planning, may be a more useful metric than accuracy. However, these statistics can have biases when the number of datapoints (i.e. ligands or edges) are low, as discussed in Section 4.5.
One analysis approach that is commonly a mistake, is the use of correlation-type statistics for the benchmarking of relative free energy calculations without defining a clear protocol for the directions of the perturbations. As relative calculations are pairwise comparisons between ligands, the direction, or sign of the calculation is arbitrary. If a ligand A is 2 kcal mol−1 higher affinity than ligand B, this could equally be plotted and reported as ligand B being −2 kcal mol−1 lower affinity than ligand A. The consequence of the possible inversion of data points can shift the correlation statistics, despite the underlying data being consistent. The same set of data points can give a range of statistical results depending on arbitrary sign-flips in the dataset, where there are 2N−1 possible permutations for a set of N relative free energies. While the size of this issue can be affected by the number, range and accuracy of the data points, this can still be problematic, as illustrated in Figure 13. If a clear protocol is used, such as mapping all of the experimental values to either be all positive or all negative, or plotting both A → B and B → A then the statistics quoted will be reproducible, however it is our recommendation to avoid correlation statistics for relative free energy results.
Figure 13. Using correlation statistics with relative free energy results are unreliable.
(A) The original set of N datapoints of relative free energy results yields specific statistics for R2, Kendall and . However, there are 2N−1 possible permutations in the sign for the datapoints, where the changes in sign result in a range of possible statistics from the same underlying data. (B) The distribution of possible values (210–1 = 512) for R2, Kendall and are illustrated in the violin plot. In the following plots ((C)-(H)), the order of permutations are illustrated that result in the lowest (red: (C), (E) and (G)) and highest (green: plots (D), (F) and (H)) correlation statistic. The considered statistics are R2 ((C) and (D)), Kendall ((E) and (F)) and ((G) and (H)). This illustrates how better correlation statistics for the same relative free energy results can be achieved by simply using different definitions of relative ‘directions’ for various edges. For this reason, best practise is to avoid reporting correlation statistics for the reporting of relative free energy calculations, and using accuracy statistics such as RMSE and MUE instead.
Additionally, correlation statistics, which are appropriate for reporting absolute free energy results, can be sensitive to the number of data points, and the range that they cover, as illustrated in Section 4.5, Figure 8. This can be exacerbated by experimental uncertainties, which is covered in Section 4.5. Some statistical measures are available that attempt to capture the inherent experimental range in the analysis, such as GRAM [170] and relative root-mean-squared error (RRMSE). As the number, dynamic range, and experimental uncertainty can all limit the maximum achievable correlation and confidence intervals, it is worth assessing these values a priori when deciding if a particular protein-ligand dataset is appropriate for a benchmark (see Section 4.5).
6.1.3. Bootstrapping is a reliable method for determining confidence intervals for statistics
While statistics are a useful measure of the performance of a method, it is also important to understand how accurate those measures are themselves. Is a MUE of 1.2 kcal mol−1 much better than 1.3 kcal mol−1? Would the performance be likely to change on the addition of new ligands in the series? Is the R2 being heavily leveraged by a handful of outliers? A very detailed summary on comparison and assessment of statistical significance in method performance is provided in a series of publications by Nicholls [117, 171–173]. While for most part these suggestions focus on the analytical estimates, bootstrap analysis also allows for a convenient approach to obtaining confidence intervals for statistics, allowing for a rigorous method comparison. For example, a MUE of 1.2 (0.4) kcal mol−1 is not statistically different than a MUE of 1.3 (0.6) kcal mol−1. Bootstrap analysis provides a measure of accuracy to the statistics through random sampling with replacement. Bootstrapping should be performed on the data used to compute the statistic reported — for relative free energies this illustrate how sensitive the statistics are to the edges chosen, and for absolute free energies: the sensitivity to the ligands in the set. The statistical error for each data point should be incorporated in the bootstrap estimate, where bootstrapping is performed by taking a sample from each data point using its associated variance. It is best practise to report the bootstrapped statistical errors alongside data as 95% confidence intervals to appropriately evaluate the performance of a particular method, and identify if improvements or changes to a model are statistically significant. When comparing multiple methods it is particularly important to carefully consider the exact formulation of the explored question, as the significance level may require adjustment for achieving the same level of confidence in conclusions (see e.g. [117]).
7. Key learnings
7.1. Analysis tools
We developed a python-based analysis package (arsenic) to compute statistics from the results of analyzing binding free energy calculations. If statistics from different approaches and sets of calculations are calculated with this package, users can ensure that they are comparing exactly the same statistics calculated in the same way. Results become invariant to different software and definitions of metrics, especially with respect to error or confidence interval calculations. We also see this as a first step towards a containerized benchmarking of methods as is planned for the SAMPL challenges [50]. There, users will ultimately compare their methods by submissions of containerized methods instead of independently calculated predictions. Thus, all methods will use exactly the same input and their results will be analyzed in the same way.
For the evaluation of X-ray structure quality, we also provide scripts to calculate Iridium scores and classifications. The Iridium score yields an objective evaluation of the structure.
7.2. Benchmark set
We assembled a benchmark set using data from prior benchmark studies of relative binding free energy calculations [44, 74, 174]. During evaluations of the given data (Table 1), we found quality defects which render parts of the data not appropriate for benchmarking according to our established criteria.
We found deficits in the dataset regarding all our established criteria. There are not trustworthy protein structures (e.g. the PDB 2GMX of Jnk1, Section 4.4), too few data points (e.g. only eight ligands of galectin, 4.5), or narrow dynamic ranges (e.g. 0.9 kcal mol−1 in BACE_P2 4.5). We tagged the protein targets as deprecated which did not meet a proposed set of minimal criteria (see our Checklist “Minimal requirements for a dataset”). After improvement by addition of new data (such as binding data for additional ligands or binding data spanning a broader dynamic range, availability/use of higher quality protein structures, etc.), these targets could potentially be added to a benchmark set again.
9. Checklists.
MINIMAL AND IDEAL REQUIREMENTS FOR A DATASET
Summary of the most important points from the checklists above and definition of minimal as well as ideal (boldface) requirements for a benchmark set.
Experimental structure should be Iridium classified as at least MT (ideally HT).
Single source experimental activities (ideally from a biophysical assay).
At least 16 (ideally 25) data points/ligands.
A dynamic range of at least > 3.0 kcal mol−1 or > 2.2 log units (ideally > 5 kcal mol−1 or > 3.7 log units).
Well prepared structures (charge and tautomeric states) checked by at least one other experienced person (ideally by the community).
CHOOSE SUITABLE PROTEIN STRUCTURES FOR BENCHMARKING
Find experimental structural data: Section 4.4
Global criteria
Select the best available structure using DPI or coordinate error (< 0.7)
Ensure experimental data is available, i.e. electron/neutron density or cryo EM map
Ensure the reported Rfree < 0.45 when resolution ≤ 3.5 Å
Ensure that the reported difference between R and Rfree ≤ 0.05
Local criteria
Determine if there are crystal contacts and assess if they affect protein conformation. Select structures with no crystal packing atoms within 6 Å of any ligand atom.
Confirm that the ligand has at least partial density (check visually or real space correlation coefficient (RSCC) > 0.90) and the density is adequate to confirm ligand presence and binding mode
Ensure that all ligand and active site atoms have occupancy >0.80
Identify active site atoms with partial density and confirm these are acceptable and not key contacts
Confirm active site crystallographic waters have density and no difference density
Identify any alternate conformations for ligand and active site atoms. Select the alternate conformation with the highest occupancy and fewest clashes.
Confirm that the ligand is not covalently bound as deposited, and is also not likely to have reacted to become one
Check for any missing loops or residues and side chain atoms in the structure and confirm these are not near the binding site/not key for the study
AFFINITY DATA
Find experimental affinity data: Section 4.5
Select single source data.
Extract binding data from original source and convert carefully.
Remove data points outside detection limits.
Ideally data should be from biophysical assays. With functional assays, more care must be taken.
Assess dataset quality in terms of number of datapoints, experimental affinity range and experimental error to know the maximally achievable precision.
PREPARE THE SYSTEM WITH CARE BECAUSE FAILURES HERE ARE CRUCIAL
Prepare structural data for simulation: Section 5.1
Assess which domains of the X-ray structure are needed and retain domains present in the experimental study, unless it is known that further simplifications can be made without affecting accuracy.
Check other components (cofactors, crystallographic waters, other ligands, PTMs) of the structure and make sure you include everything which is key for the study.
Split the protein and ligand structures to prepare separately.
Protein preparation
Add caps if the structure’s termini are not resolved.
If possible, model missing loops, if loops are too long (> 15 to 20 residues) or too mobile, consider capping the ends and adding restraints, or modeling a short glycine loop that links both ends. These must not be in the binding site.
Inspect for side chain flips of side chains which can fit density similarly when reoriented (HIS, ASN, GLN); confirm that the orientations chosen lead to preferred interactions with the ligand. Evaluate alternate placements if necessary.
Check the protonation states of the ligand and receptor, again checking in the context of the interactions that would be formed with the ligand.
Ligand preparation
Ensure that the chemical structure is correct (bond orders, stereochemistry).
Align the ligand series based on conformations of (X-ray) reference compound(s).
Check tautomer and ionization states. Determine whether multiple possibilities need to be considered.
Check whether alternate rotamers may need to be considered after alignment to reference compound(s).
System preparation
Assemble the protein, ligand and cofactors.
Without removing crystallographic waters and ions, solvate the complex or embed it in a membrane.
Add ions; use an appropriate salt concentration (sodium and chloride ions) to model the assay.
Equilibrate the system.
CAREFULLY SELECT APPROPRIATE SIMULATION DETAILS
Choose simulation setup: Section 5.2
Choose absolute vs. relative calculations.
Choose topology approach and alchemical pathway.
Choose sampling protocol.
Plan a perturbation map if calculations are relative.
PRESENT GRAPHS OF RESULTS IN A CONSISTENT MANNER
Presenting results in an appropriate format: Section 6.1.1
Clearly label the data with titles, legends, and captions.
Plot results with the dependent variable (calculated) on y-axis, and the independent variable (experimental) on the x-axis.
Ensure that the data are reported in the same units on both axes, and labelled. The scale of the axis in real space should be consistent, such that a 1 cm change on the x-axis corresponds to the same change in affinity to 1 cm on the y-axis.
Plot only one target per plot, unless specifically looking at selectivity or considering multiple systems by means of absolute free energy calculations.
USE CAREFUL STATISTICAL ANALYSIS TO QUANTIFY PERFORMANCE
Quantifying the success of a method: Section 6.1.2
Identify which metrics are appropriate for your method. Statistics that measure accuracy, such as RMSE and MUE, are commonplace; correlation statistics are appropriate for absolute free energies, and relative free energies only when perturbation map and direction is consistent among benchmarked methods.
Bootstrap statistics to provide confidence intervals.
Provide confidence intervals for all reported values and avoid overinterpreting results given these intervals.
We acknowledge that the proposed benchmark set does not meet the ideal requirements we established. To date, these requirements are challenging to meet due to scarce high-quality experimental data, especially after applying all the criteria we lay out. Experimental affinity measurements from a single source often do not cover dynamic ranges > 5 kcal mol−1 and much larger dynamic ranges become unrealistic. Large numbers of single source affinity data points are rarely available and additionally impose the practical limitations of large computational resources for benchmarking calculations. As a chain is only as strong as its weakest link, the above points need to be paired with high-quality structural data and a good preparation of the simulation input.
We are continuously improving the benchmark set and we welcome any community contributions and assistance to build a benchmarking dataset that will eventually fulfill the outlined standards.
8. Recommendations
Methods for binding free energy calculations have been continuously developed over the last decades and are increasingly used both in academic research, as well as pharmaceutical industry applications in structure based drug discovery [25, 30, 44], making their validation and benchmarking particularly crucial.
In order to reliably benchmark methods, we provide best practices recommendations for setting up benchmark calculations. This setup begins with the appropriate choice of experimental inputs and data, which includes the choice of target(s) and ligands (Section 4). We require both structural information (Section 4.4) and affinity data (Section 4.5). This input information needs to be adequately prepared to generate simulation inputs (Section 5.1) before the systems are simulated with a specific choice of software, calculation setup, and simulation protocol. Here, we made a variety of recommendations as to how to select and prepare systems for benchmarking.
Benchmarking also requires analysis and comparison with experiment, thus we also recommend standard reporting procedures (Section 6). These provide a mechanism to assess the accuracy of the calculations, present the results and compare to calculations done with other methods. These standard procedures will make it far easier to compare results across studies done by different researchers or using different tools.
Our recommendations are exemplified in publicly available tools for the analysis of calculations (arsenic) and a living protein-ligand benchmark dataset (protein-ligand-benchmark). Note that this is a separate repository from the repository for this LiveCoMS document, which is at (https://github.com/openforcefield/protein-ligand-benchmark-livecoms). This set is living in the sense that we expect it to be subject to ongoing updates, curation, and improvement – both by ourselves and by the community, and we welcome community input via the GitHub issue tracker at protein-ligand-benchmark/issues. Further curation is clearly necessary as our recommendations are in part not fulfilled in the initial version of this benchmark dataset. Partially, this is because we have begun from previously used benchmark sets and are beginning the curation process, but also because it is difficult to find large and accurate experimental datasets meeting all the desired characteristics. Thus, in our initial set, the relevant issues are annotated and we expect the benchmark set to evolve to better meet the recommendations given here.
We hope that our recommended best practices will be adopted and where necessary improved by the community. We believe that these best practices will ultimately help advance the accuracy, applicability, and availability of binding free energy calculations.
Figure 3. The PDB structure validation report percentile score panels for the Jnk1 structures PDB IDs 2GMX and 3ELJ from the RCSB PDB.
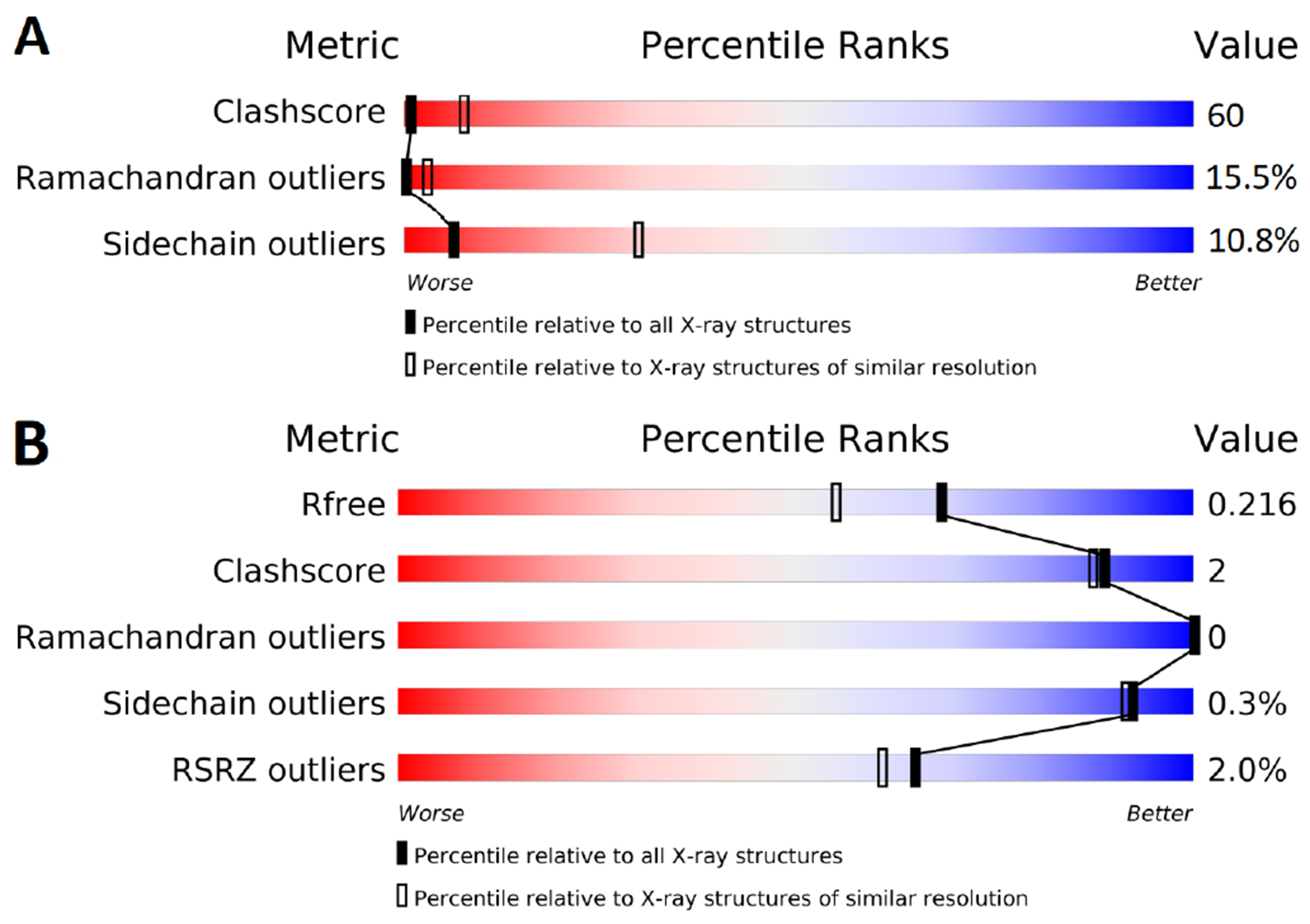
(A) Note that 2GMX is a poorly ranked structure relative to all structures of similar resolution in the PDB. (B) In contrast 3ELJ is as good or better than structures of similar resolution or all structures in the PDB.
Figure 9. Outline of the system preparation steps.
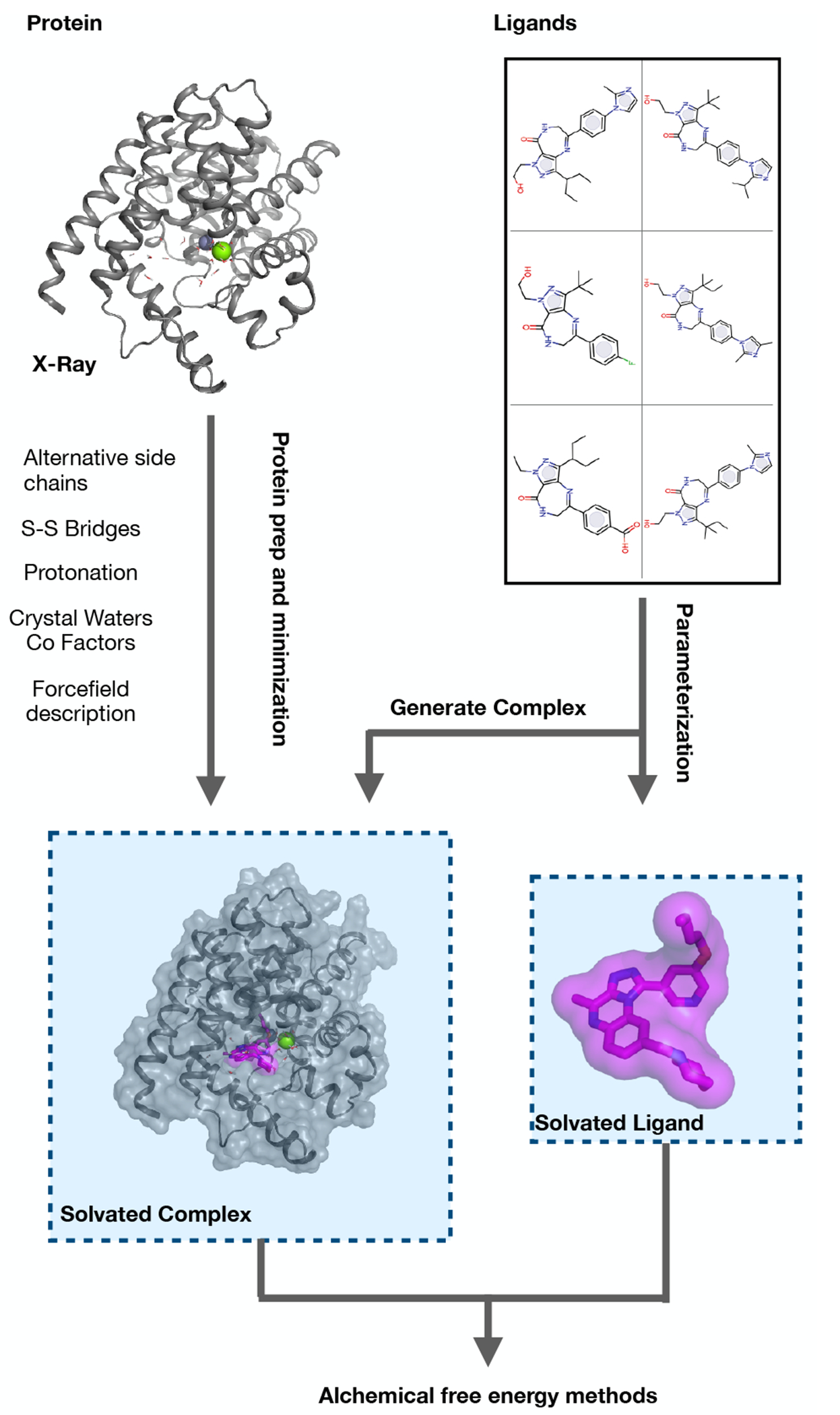
First the protein is prepared (left, Section 5.1.1) by modelling missing atoms, assigning bond orders, protonation and tautomeric states. Similarily, the chemical structure of the ligands is translated into a simulation model (right, Section 5.1.2). The ligands are simulated in two different environments, once complexed with the protein (bottom left) and once in solvent (bottom right). For the solvated complex, the ligand structures need to be docked into the binding site of the protein, typically by using the information of a reference ligand in the X-ray structure.
13. Funding Information
JDC acknowledges support from NIH grant P30 CA008748. We appreciate the financial support of the Open Force Field Consortium (openforcefield.org), and the National Institutes of Health (NIGMS R01GM132386 and R01GM108889). HEBM acknowledges support from a Molecular Sciences Software Institute Investment Fellowship and Relay Therapeutics.
11. Other Contributions
We want to thank the authors of the following publications for establishing the initial protein-ligand benchmark sets: Wang et al.[74], Perez-Benito et al.[175], Gapsys et al.[174] and Schindler et al.[44].
For a more detailed description of contributions from the community and others, see the GitHub issue tracking and changelog at https://github.com/openforcefield/protein-ligand-benchmark-livecoms.
Footnotes
12 Potentially Conflicting Interests
DLM serves on the scientific advisory board for OpenEye Scientific Software and is an Open Science Fellow with Silicon Therapeutics. ASJSM is a consultant for Exscientia. JDC is a current member of the Scientific Advisory Board of OpenEye Scientific Software and a consultant to Foresite Laboratories. HEBM is employed by MSD. DFH, LPB, GT are employed by Janssen.
Excellent examples of significant errors that can be introduced are thoroughly described in this comprehensive United States Geological Survey report on errors in misreporting the solubility and partition coefficient of dichlorodiphenyltrichloroethane (DDT) and its primary metabolite [108], as well as this talk on automatic data extraction errors [109].
This LiveCoMS document is maintained online on GitHub at https://github.com/openforcefield/protein-ligand-benchmark-livecoms; to provide feedback, suggestions, or help improve it, please visit the GitHub repository and participate via the issue tracker.
References
- [1].Mobley DL, Gilson MK. Predicting Binding Free Energies: Frontiers and Benchmarks. Annual Review of Biophysics. 2017; 46(1):531–558. 10.1146/annurev-biophys-070816-033654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].van Gunsteren WF, Daura X, Hansen N, Mark AE, Oostenbrink C, Riniker S, Smith LJ. Validation of Molecular Simulation: An Overview of Issues. Angewandte Chemie International Edition. 2018; 57(4):884–902. 10.1002/anie.201702945. [DOI] [PubMed] [Google Scholar]
- [3].Tsai HC, Tao Y, Lee TS, Merz KM, York DM. Validation of Free Energy Methods in AMBER. Journal of Chemical Information and Modeling. 2020; 60(11):5296–5300. 10.1021/acs.jcim.0c00285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Abel R, Wang L, Mobley DL, Friesner RA. A Critical Review of Validation, Blind Testing, and Real-World Use of Alchemical Protein-Ligand Binding Free Energy Calculations. Current Topics in Medicinal Chemistry. 2017; 17(23):2577–2585. 10.2174/1568026617666170414142131. [DOI] [PubMed] [Google Scholar]
- [5].Abel R, Manas ES, Friesner RA, Farid RS, Wang L. Modeling the Value of Predictive Affinity Scoring in Preclinical Drug Discovery. Current Opinion in Structural Biology. 2018; 52:103–110. 10.1016/j.sbi.2018.09.002. [DOI] [PubMed] [Google Scholar]
- [6].Cournia Z, Allen B, Sherman W. Relative Binding Free Energy Calculations in Drug Discovery: Recent Advances and Practical Considerations. Journal of Chemical Information and Modeling. 2017; 57(12):2911–2937. 10.1021/acs.jcim.7b00564. [DOI] [PubMed] [Google Scholar]
- [7].Zwanzig RW. High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. The Journal of Chemical Physics. 1954; 22(8):1420–1426. 10.1063/1.1740409. [DOI] [Google Scholar]
- [8].Bennett CH. Efficient Estimation of Free Energy Differences from Monte Carlo Data. Journal of Computational Physics. 1976; 22(2):245–268. 10.1016/0021-9991(76)90078-4. [DOI] [Google Scholar]
- [9].Kirkwood JG. Quantum Statistics of Almost Classical Assemblies. Physical Review. 1933; 44(1):31–37. 10.1103/PhysRev.44.31. [DOI] [Google Scholar]
- [10].Kirkwood JG. Quantum Statistics of Almost Classical Assemblies. Physical Review. 1934; 45(2):116–117. 10.1103/PhysRev.45.116. [DOI] [Google Scholar]
- [11].Kirkwood JG. Statistical Mechanics of Fluid Mixtures. The Journal of Chemical Physics. 1935; 3(5):300–313. 10.1063/1.1749657. [DOI] [Google Scholar]
- [12].Jorgensen WL, Ravimohan C. Monte Carlo Simulation of Differences in Free Energies of Hydration. The Journal of Chemical Physics. 1985; 83(6):3050–3054. 10.1063/1.449208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Straatsma TP, Berendsen HJC, Postma JPM. Free Energy of Hydrophobic Hydration: A Molecular Dynamics Study of Noble Gases in Water. The Journal of Chemical Physics. 1986; 85(11):6720–6727. 10.1063/1.451846. [DOI] [Google Scholar]
- [14].Lybrand TP, McCammon JA, Wipff G. Theoretical Calculation of Relative Binding Affinity in Host-Guest Systems. Proceedings of the National Academy of Sciences. 1986; 83(4):833–835. 10.1073/pnas.83.4.833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Merz KM, Kollman PA. Free Energy Perturbation Simulations of the Inhibition of Thermolysin: Prediction of the Free Energy of Binding of a New Inhibitor. Journal of the American Chemical Society. 1989; 111(15):5649–5658. 10.1021/ja00197a022. [DOI] [Google Scholar]
- [16].Pearlman DA, Connelly PR. Determination of the Differential Effects of Hydrogen Bonding and Water Release on the Binding of FK506 to Native and Tyr82→Phe82 FKBP-12 Proteins Using Free Energy Simulations. Journal of Molecular Biology. 1995; 248(3):696–717. 10.1006/jmbi.1995.0252. [DOI] [PubMed] [Google Scholar]
- [17].Chodera JD, Mobley DL, Shirts MR, Dixon RW, Bran son K, Pande VS. Alchemical Free Energy Methods for Drug Discovery: Progress and Challenges. Current Opinion in Structural Biology. 2011; 21(2):150–160. 10.1016/j.sbi.2011.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Mobley DL, Klimovich PV. Perspective: Alchemical Free Energy Calculations for Drug Discovery. The Journal of Chemical Physics. 2012; 137(23):230901. 10.1063/1.4769292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Mey ASJS, Allen BK, Bruce Macdonald HE, Chodera JD, Hahn DF, Kuhn M, Michel J, Mobley DL, Naden LN, Prasad S, Rizzi A, Scheen J, Shirts MR, Tresadern G, Xu H. Best Practices for Alchemical Free Energy Calculations [Article v1.0]. Living Journal of Computational Molecular Science. 2020; 2(1). 10.33011/livecoms.2.1.18378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Wang L, Wu Y, Deng Y, Kim B, Pierce L, Krilov G, Lupyan D, Robinson S, Dahlgren MK, Greenwood J, Romero DL, Masse C, Knight JL, Steinbrecher T, Beuming T, Damm W, Harder E, Sherman W, Brewer M, Wester R, et al. Accurate and Reliable Prediction of Relative Ligand Binding Potency in Prospective Drug Discovery by Way of a Modern Free-Energy Calculation Protocol and Force Field. Journal of the American Chemical Society. 2015; 137(7):2695–2703. 10.1021/ja512751q. [DOI] [PubMed] [Google Scholar]
- [21].Harder E, Damm W, Maple J, Wu C, Reboul M,Xiang JY, Wang L, Lupyan D, Dahlgren MK, Knight JL, Kaus JW, Cerutti DS, Krilov G, Jorgensen WL, Abel R, Friesner RA. OPLS3: A Force Field Providing Broad Coverage of Drug-like Small Molecules and Proteins. Journal of Chemical Theory and Computation. 2016; 12(1):281–296. 10.1021/acs.jctc.5b00864. [DOI] [PubMed] [Google Scholar]
- [22].Roos K, Wu C, Damm W, Reboul M, Stevenson JM, Lu C, Dahlgren MK, Mondal S, Chen W, Wang L, Abel R, Friesner RA, Harder ED. OPLS3e: Extending Force Field Coverage for Drug-Like Small Molecules. Journal of Chemical Theory and Computation. 2019; 15(3):1863–1874. 10.1021/acs.jctc.8b01026. [DOI] [PubMed] [Google Scholar]
- [23].Song LF, Lee TS, Zhu C, York DM, Merz KM. Using AM-BER18 for Relative Free Energy Calculations. Journal of Chemical Information and Modeling. 2019; 59(7):3128–3135. 10.1021/acs.jcim.9b00105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Kuhn M, Firth-Clark S, Tosco P, Mey ASJS, Mackey M, Michel J. Assessment of Binding Affinity via Alchemical Free-Energy Calculations. Journal of Chemical Information and Modeling. 2020; 60(6):3120–3130. 10.1021/acs.jcim.0c00165. [DOI] [PubMed] [Google Scholar]
- [25].Gapsys V, Pérez-Benito L, Aldeghi M, Seeliger D, van Vlijmen H, Tresadern G, de Groot BL. Large Scale Relative Protein Ligand Binding Affinities Using Non-Equilibrium Alchemy. Chemical Science. 2020; 11(4):1140–1152. 10.1039/C9SC03754C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Jiménez J, Škalič M, Martínez-Rosell G, De Fabritiis G. KDEEP : Protein-Ligand Absolute Binding Affinity Prediction via 3D-Convolutional Neural Networks. Journal of Chemical Information and Modeling. 2018; 58(2):287–296. 10.1021/acs.jcim.7b00650. [DOI] [PubMed] [Google Scholar]
- [27].Jiménez-Luna J, Pérez-Benito L, Martínez-Rosell G, Sciabola S, Torella R, Tresadern G, De Fabritiis G. DeltaDelta Neural Networks for Lead Optimization of Small Molecule Potency. Chemical Science. 2019; 10(47):10911–10918. 10.1039/C9SC04606B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Aldeghi M, Ross GA, Bodkin MJ, Essex JW, Knapp S, Biggin PC. Large-Scale Analysis of Water Stability in Bromodomain Binding Pockets with Grand Canonical Monte Carlo. Communications Chemistry. 2018; 1(1):19. 10.1038/s42004-018-0019-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Cournia Z, Allen BK, Beuming T, Pearlman DA, Radak BK, Sheran W. Rigorous Free Energy Simulations in Virtual Screening. Journal of Chemical Information and Modeling. 2020; p. acs.jcim.0c00116. 10.1021/acs.jcim.0c00116. [DOI] [PubMed] [Google Scholar]
- [30].Sherborne B, Shanmugasundaram V, Cheng AC, Christ CD, DesJarlais RL, Duca JS, Lewis RA, Loughney DA, Manas ES, McGaughey GB, Peishoff CE, van Vlijmen H. Collaborating to Improve the Use of Free-Energy and Other Quantitative Methods in Drug Discovery. Journal of Computer-Aided Molecular Design. 2016; 30(12):1139–1141. 10.1007/s10822-016-9996-y. [DOI] [PubMed] [Google Scholar]
- [31].Wang L, Deng Y, Wu Y, Kim B, LeBard DN, Wandschneider D, Beachy M, Friesner RA, Abel R. Accurate Modeling of Scaffold Hopping Transformations in Drug Discovery. Journal of Chemical Theory and Computation. 2017; 13(1):42–54. 10.1021/acs.jctc.6b00991. [DOI] [PubMed] [Google Scholar]
- [32].Liu S, Wang L, Mobley DL. Is Ring Breaking Feasible in Relative Binding Free Energy Calculations? Journal of Chemical Information and Modeling. 2015; 55(4):727–735. 10.1021/acs.jcim.5b00057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Michel J, Tirado-Rives J, Jorgensen WL. Energetics of Displacing Water Molecules from Protein Binding Sites: Consequences for Ligand Optimization. Journal of the American Chemical Society. 2009;131(42):15403–15411. 10.1021/ja906058w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Bruce Macdonald HE, Cave-Ayland C, Ross GA, Essex JW. Ligand Binding Free Energies with Adaptive Water Networks: Two-Dimensional Grand Canonical Alchemical Perturbations. Journal of Chemical Theory and Computation. 2018; 14(12):6586–6597. 10.1021/acs.jctc.8b00614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Ross GA, Russell E, Deng Y, Lu C, Harder ED, Abel R, Wang L. Enhancing Water Sampling in Free Energy Calculations with Grand Canonical Monte Carlo. Journal of Chemical Theory and Computation. 2020; 16(10):6061–6076. 10.1021/acs.jctc.0c00660. [DOI] [PubMed] [Google Scholar]
- [36].Ben-Shalom IY, Lin Z, Radak BK, Lin C, Sherman W, Gilson MK. Accounting for the Central Role of Interfacial Water in Protein–Ligand Binding Free Energy Calculations. Journal of Chemical Theory and Computation. 2020; 16(12):7883–7894. 10.1021/acs.jctc.0c00785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Huang YmM, Chen W, Potter MJ, Chang CeA. Insights from Free-Energy Calculations: Protein Conformational Equilibrium, Driving Forces, and Ligand-Binding Modes. Biophysical Journal. 2012; 103(2):342–351. 10.1016/j.bpj.2012.05.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Fratev F, Sirimulla S. An Improved Free Energy Perturbation FEP+ Sampling Protocol for Flexible Ligand-Binding Domains. Scientific Reports. 2019; 9(1):16829. 10.1038/s41598-019-53133-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Singh N, Li W. Absolute Binding Free Energy Calculations for Highly Flexible Protein MDM2 and Its Inhibitors. International Journal of Molecular Sciences. 2020; 21(13). 10.3390/ijms21134765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Lenselink EB, Louvel J, Forti AF, van Veldhoven JPD, de Vries H, Mulder-Krieger T, McRobb FM, Negri A, Goose J, Abel R, van Vlijmen HWT, Wang L, Harder E, Sherman W, IJzerman AP, Beuming T. Predicting Binding Affinities for GPCR Ligands Using Free-Energy Perturbation. ACS Omega. 2016; 1(2):293–304. 10.1021/acsomega.6b00086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Deflorian F, Perez-Benito L, Lenselink EB, Congreve M, van Vlijmen HWT, Mason JS, Graaf Cd, Tresadern G. Accurate Prediction of GPCR Ligand Binding Affinity with Free Energy Perturbation. Journal of Chemical Information and Modeling. 2020; 60(11):5563–5579. 10.1021/acs.jcim.0c00449. [DOI] [PubMed] [Google Scholar]
- [42].Świderek K, Paneth P. Binding Ligands and Cofactor to L-Lactate Dehydrogenase from Human Skeletal and Heart Muscles. The Journal of Physical Chemistry B. 2011; 115(19):6366–6376. 10.1021/jp201626k. [DOI] [PubMed] [Google Scholar]
- [43].Ono F, Chiba S, Isaka Y, Matsumoto S, Ma B, Katayama R, Araki M, Okuno Y. Improvement in Predicting Drug Sensitivity Changes Associated with Protein Mutations Using a Molecular Dynamics Based Alchemical Mutation Method. Scientific Reports. 2020; 10(1):2161. 10.1038/s41598-020-58877-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Schindler CEM, Baumann H, Blum A, Böse D, Buchstaller HP, Burgdorf L, Cappel D, Chekler E, Czodrowski P, Dorsch D, Eguida MKI, Follows B, Fuchß T, Grädler U, Gunera J, Johnson T, Jorand Lebrun C, Karra S, Klein M, Knehans T, et al. Large-Scale Assessment of Binding Free Energy Calculations in Active Drug Discovery Projects. Journal of Chemical Information and Modeling. 2020; 60(11):5457–5474. 10.1021/acs.jcim.0c00900. [DOI] [PubMed] [Google Scholar]
- [45].Knight JL, Brooks CL. Multisite Dynamics for Simulated Structure–Activity Relationship Studies. Journal of Chemical Theory and Computation. 2011; 7(9):2728–2739. 10.1021/ct200444f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Vilseck JZ, Armacost KA, Hayes RL, Goh GB, Brooks CL. Predicting Binding Free Energies in a Large Combinatorial Chemical Space Using Multisite Dynamics. The Journal of Physical Chemistry Letters. 2018; 9(12):3328–3332. 10.1021/acs.jpclett.8b01284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Rufa DA, Bruce Macdonald HE, Fass J, Wieder M, Grinaway PB, Roitberg AE, Isayev O, Chodera JD. Towards Chemical Accuracy for Alchemical Free Energy Calculations with Hybrid Physics-Based Machine Learning / Molecular Mechanics Potentials. Biophysics; 2020. 10.1101/2020.07.29.227959. [DOI] [Google Scholar]
- [48].Genheden S, Ryde U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opinion on Drug Discovery. 2015; 10(5):449–461. 10.1517/17460441.2015.1032936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Amaro RE, Gilson MK, Drug Design Data Resource; 2021. https://drugdesigndata.org/. [DOI] [PubMed]
- [50].Mobley DL, The SAMPL Challenges; 2021. https://samplchallenges.github.io/.
- [51].Geballe MT, Skillman AG, Nicholls A, Guthrie JP, Taylor PJ. The SAMPL2 Blind Prediction Challenge: Introduction and Overview. Journal of Computer-Aided Molecular Design. 2010; 24(4):259–279. 10.1007/s10822-010-9350-8. [DOI] [PubMed] [Google Scholar]
- [52].Muddana HS, Daniel Varnado C, Bielawski CW, Urbach AR, Isaacs L, Geballe MT, Gilson MK. Blind Prediction of Host-Guest Binding Affinities: A New SAMPL3 Challenge. Journal of Computer-Aided Molecular Design. 2012; 26(5):475–487. 10.1007/s10822-012-9554-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Muddana HS, Gilson MK. Prediction of SAMPL3 Host-Guest Binding Affinities: Evaluating the Accuracy of Generalized Force-Fields. Journal of Computer-Aided Molecular Design. 2012; 26(5):517–525. 10.1007/s10822-012-9544-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Muddana HS, Fenley AT, Mobley DL, Gilson MK. The SAMPL4 Host-Guest Blind Prediction Challenge: An Overview. Journal of Computer-Aided Molecular Design. 2014; 28(4):305–317. 10.1007/s10822-014-9735-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Gathiaka S, Liu S, Chiu M, Yang H, Stuckey JA, Kang YN, Delproposto J, Kubish G, Dunbar JB, Carlson HA, Burley SK, Walters WP, Amaro RE, Feher VA, Gilson MK. D3R Grand Challenge 2015: Evaluation of Protein-Ligand Pose and Affinity Predictions. Journal of Computer-Aided Molecular Design. 2016; 30(9):651–668. 10.1007/s10822-016-9946-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Bannan CC, Burley KH, Chiu M, Shirts MR, Gilson MK, Mobley DL. Blind Prediction of Cyclohexane–Water Distribution Coefficients from the SAMPL5 Challenge. Journal of Computer-Aided Molecular Design. 2016; 30(11):927–944. 10.1007/s10822-016-9954-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Yin J, Henriksen NM, Slochower DR, Shirts MR, Chiu MW, Mobley DL, Gilson MK. Overview of the SAMPL5 Host-Guest Challenge: Are We Doing Better? Journal of Computer-Aided Molecular Design. 2017; 31(1):1–19. 10.1007/s10822-016-9974-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Gaieb Z, Liu S, Gathiaka S, Chiu M, Yang H, Shao C, Feher VA, Walters WP, Kuhn B, Rudolph MG, Burley SK, Gilson MK, Amaro RE. D3R Grand Challenge 2: Blind Prediction of Protein–Ligand Poses, Affinity Rankings, and Relative Binding Free Energies. Journal of Computer-Aided Molecular Design. 2018; 32(1):1–20. 10.1007/s10822-017-0088-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Gaieb Z, Parks CD, Chiu M, Yang H, Shao C, Walters WP, Lambert MH, Nevins N, Bembenek SD, Ameriks MK, Mirzadegan T, Burley SK, Amaro RE, Gilson MK. D3R Grand Challenge 3: Blind Prediction of Protein–Ligand Poses and Affinity Rankings. Journal of Computer-Aided Molecular Design. 2019; 33(1):1–18. 10.1007/s10822-018-0180-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Parks CD, Gaieb Z, Chiu M, Yang H, Shao C, Walters WP, Jansen JM, McGaughey G, Lewis RA, Bembenek SD, Ameriks MK, Mirzadegan T, Burley SK, Amaro RE, Gilson MK. D3R Grand Challenge 4: Blind Prediction of Protein–Ligand Poses, Affinity Rankings, and Relative Binding Free Energies. Journal of Computer-Aided Molecular Design. 2020; 34(2):99–119. 10.1007/s10822-020-00289-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Jain AN, Nicholls A. Recommendations for Evaluation of Computational Methods. Journal of Computer-Aided Molecular Design. 2008; 22(3-4):133–139. 10.1007/s10822-008-9196-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Hahn DF, Wagner J, openforcefield/protein-ligand-benchmark: 0.2.0 Addition of New Targets. Zenodo; 2021. 10.5281/ZENODO.5679599. [DOI] [Google Scholar]
- [63].Macdonald HB, Hahn DF, Henry M, Chodera J, Dotson D, Glass W, Pulido I, openforcefeld/openff-arsenic: v0.2.1. Zenodo; 2022. 10.5281/ZENODO.6210305. [DOI] [Google Scholar]
- [64].Braun E, Gilmer J, Mayes HB, Mobley DL, Monroe JI, Prasad S, Zuckerman DM. Best Practices for Foundations in Molecular Simulations [Article v1.0]. Living Journal of Computational Molecular Science. 2019; 1(1). 10.33011/livecoms.1.1.5957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Kaus JW, Harder E, Lin T, Abel R, McCammon JA, Wang L. How To Deal with Multiple Binding Poses in Alchemical Relative Protein–Ligand Binding Free Energy Calculations. Journal of Chemical Theory and Computation. 2015; 11(6):2670–2679. 10.1021/acs.jctc.5b00214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Sasmal S, Gill SC, Lim NM, Mobley DL. Sampling Conformational Changes of Bound Ligands Using Nonequilibrium Candidate Monte Carlo and Molecular Dynamics. Journal of Chemical Theory and Computation. 2020; 16(3):1854–1865. 10.1021/acs.jctc.9b01066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Koeppl GW, Sagatys DS, Krishnamurthy GS, Miller SI. Inversion Barriers of Pyramidal (XY3) and Related Planar (=XY) Species. Journal of the American Chemical Society. 1967; 89(14):3396–3405. 10.1021/ja00990a004. [DOI] [Google Scholar]
- [68].Wagner V, Jantz L, Briem H, Sommer K, Rarey M, Christ CD. Computational Macrocyclization: From de Novo Macrocycle Generation to Binding Affinity Estimation. ChemMedChem. 2017; 12(22):1866–1872. 10.1002/cmdc.201700478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Yu HS, Deng Y, Wu Y, Sindhikara D, Rask AR, Kimura T, Abel R, Wang L. Accurate and Reliable Prediction of the Binding Affinities of Macrocycles to Their Protein Targets. Journal of Chemical Theory and Computation. 2017; 13(12):6290–6300. 10.1021/acs.jctc.7b00885. [DOI] [PubMed] [Google Scholar]
- [70].Paulsen JL, Yu HS, Sindhikara D, Wang L, Appleby T, Villaseñor AG, Schmitz U, Shivakumar D. Evaluation of Free Energy Calculations for the Prioritization of Macrocycle Synthesis. Journal of Chemical Information and Modeling. 2020; 60(7):3489–3498. 10.1021/acs.jcim.0c00132. [DOI] [PubMed] [Google Scholar]
- [71].Jumper J, Evans R, Pritzel A, Green T, Figurnov M, Ronneberger O, Tunyasuvunakool K, Bates R, Žíidek A, Potapenko A, Bridgland A, Meyer C, Kohl SAA, Ballard AJ, Cowie A, Romera-Paredes B, Nikolov S, Jain R, Adler J, Back T, et al. Highly Accurate Protein Structure Prediction with AlphaFold. Nature. 2021; 596(7873):583–589. 10.1038/s41586-021-03819-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Warren GL, Do TD, Kelley BP, Nicholls A, Warren SD. Essential Considerations for Using Protein–Ligand Structures in Drug Discovery. Drug Discovery Today. 2012; 17(23-24):1270–1281. 10.1016/j.drudis.2012.06.011. [DOI] [PubMed] [Google Scholar]
- [73].Cumming JN, Smith EM, Wang L, Misiaszek J, Durkin J, Pan J, Iserloh U, Wu Y, Zhu Z, Strickland C, Voigt J, Chen X, Kennedy ME, Kuvelkar R, Hyde LA, Cox K, Favreau L, Czarniecki MF, Greenlee WJ, McKittrick BA, et al. Structure Based Design of Iminohydantoin BACE1 Inhibitors: Identification of an Orally Available, Centrally Active BACE1 Inhibitor. Bioorganic & Medicinal Chemistry Letters. 2012; 22(7):2444–2449. 10.1016/j.bmcl.2012.02.013. [DOI] [PubMed] [Google Scholar]
- [74].Wang L, Wu Y, Deng Y, Kim B, Pierce L, Krilov G, Lupyan D, Robinson S, Dahlgren MK, Greenwood J, Romero DL, Masse C, Knight JL, Steinbrecher T, Beuming T,Damm W, Harder E, Sherman W, Brewer M, Wester R, et al. Accurate and Reliable Prediction of Relative Ligand Binding Potency in Prospective Drug Discovery by Way of a Modern Free-Energy Calculation Protocol and Force Field. Journal of the American Chemical Society. 2015; 137(7):2695–2703. 10.1021/ja512751q. [DOI] [PubMed] [Google Scholar]
- [75].Hunt KW, Cook AW, Watts RJ, Clark CT, Vigers G, Smith D, Metcalf AT, Gunawardana IW, Burkard M, Cox AA, Geck Do MK, Dutcher D, Thomas AA, Rana S, Kallan NC, DeLisle RK, Rizzi JP, Regal K, Sammond D, Groneberg R, et al. Spirocyclic β-Site Amyloid Precursor Protein Cleaving Enzyme 1 (BACE1) Inhibitors: From Hit to Lowering of Cerebrospinal Fluid (CSF) Amyloid β in a Higher Species. Journal of Medicinal Chemistry. 2013; 56(8):3379–3403. 10.1021/jm4002154. [DOI] [PubMed] [Google Scholar]
- [76].Ciordia M, Pérez-Benito L, Delgado F, Trabanco AA, Tresadern G. Application of Free Energy Perturbation for the Design of BACE1 Inhibitors. Journal of Chemical Information and Modeling. 2016; 56(9):1856–1871. 10.1021/acs.jcim.6b00220. [DOI] [PubMed] [Google Scholar]
- [77].Keränen H, Pérez-Benito L, Ciordia M, Delgado F, Steinbrecher TB, Oehlrich D, van Vlijmen HWT, Trabanco AA, Tresadern G. Acylguanidine Beta Secretase 1 Inhibitors: A Combined Experimental and Free Energy Perturbation Study. Journal of Chemical Theory and Computation. 2017; 13(3):1439–1453. 10.1021/acs.jctc.6b01141. [DOI] [PubMed] [Google Scholar]
- [78].Malamas MS, Erdei J, Gunawan I, Turner J, Hu Y, Wagner E, Fan K, Chopra R, Olland A, Bard J,Jacobsen S, Magolda RL, Pangalos M, Robichaud AJ. Design and Synthesis of 5,5′-Disubstituted Aminohydantoins as Potent and Selective Human β-Secretase (BACE1) Inhibitors. Journal of Medicinal Chemistry. 2010; 53(3):1146–1158. 10.1021/jm901414e. [DOI] [PubMed] [Google Scholar]
- [79].Hardcastle IR, Arris CE, Bentley J, Boyle FT, Chen Y, Curtin NJ, Endicott JA, Gibson AE, Golding BT, Griffin RJ, Jewsbury P, Menyerol J, Mesguiche V, Newell DR, Noble MEM, Pratt DJ, Wang LZ, Whitfield HJ. N 2 -Substituted O 6 -Cyclohexylmethylguanine Derivatives: Potent Inhibitors of Cyclin-Dependent Kinases 1 and 2. Journal of Medicinal Chemistry. 2004; 47(15):3710–3722. 10.1021/jm0311442. [DOI] [PubMed] [Google Scholar]
- [80].Schiemann K, Mallinger A, Wienke D, Esdar C, Poeschke O, Busch M, Rohdich F, Eccles SA, Schneider R, Raynaud FI, Czodrowski P, Musil D, Schwarz D, Urbahns K, Blagg J. Discovery of Potent and Selective CDK8 Inhibitors from an HSP90 Pharmacophore. Bioorganic & Medicinal Chemistry Letters. 2016; 26(5):1443–1451. 10.1016/j.bmcl.2016.01.062. [DOI] [PubMed] [Google Scholar]
- [81].Dorsch D, Schadt O, Stieber F, Meyring M, Grädler U, Bladt F, Friese-Hamim M, Knühl C, Pehl U, Blaukat A. Identification and Optimization of Pyridazinones as Potent and Selective c-Met Kinase Inhibitors. Bioorganic & Medicinal Chemistry Letters. 2015;25(7):1597–1602. 10.1016/j.bmcl.2015.02.002. [DOI] [PubMed] [Google Scholar]
- [82].Schiemann K, Finsinger D, Zenke F, Amendt C, Knöchel T, Bruge D, Buchstaller HP, Emde U, Stähle W, Anzali S. The Discovery and Optimization of Hexahydro-2H-Pyrano[3,2-c]Quinolines (HHPQs) as Potent and Selective Inhibitors of the Mitotic Kinesin-5. Bioorganic & Medicinal Chemistry Letters. 2010;20(5):1491–1495. 10.1016/j.bmcl.2010.01.110. [DOI] [PubMed] [Google Scholar]
- [83].Delaine T, Collins P, MacKinnon A, Sharma G, Stegmayr J, Rajput VK, Mandal S, Cumpstey I, Larumbe A, Salameh BA, Kahl-Knutsson B, van Hattum H, van Scherpenzeel M, Pieters RJ, Sethi T, Schambye H, Oredsson S, Leffler H, Blanchard H, Nilsson UJ. Galectin-3-Binding Glycomimetics That Strongly Reduce Bleomycin-Induced Lung Fibrosis and Modulate Intracellular Glycan Recognition. ChemBioChem. 2016; 17(18):1759–1770. 10.1002/cbic.201600285. [DOI] [PubMed] [Google Scholar]
- [84].Manzoni F, Ryde U. Assessing the Stability of Free-Energy Perturbation Calculations by Performing Variations in the Method. Journal of Computer-Aided Molecular Design. 2018; 32(4):529–536. 10.1007/s10822-018-0110-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85].Wallace EM, Rizzi JP, Han G, Wehn PM, Cao Z, Du X, Cheng T, Czerwinski RM, Dixon DD, Goggin BS, Grina JA, Halfmann MM, Maddie MA, Olive SR, Schlachter ST, Tan H, Wang B, Wang K, Xie S, Xu R, et al. A Small-Molecule Antagonist of HIF2α Is Efficacious in Preclinical Models of Renal Cell Carcinoma. Cancer Research. 2016; 76(18):5491–5500. 10.1158/0008-5472.CAN-16-0473. [DOI] [PubMed] [Google Scholar]
- [86].Szczepankiewicz BG, Kosogof C, Nelson LTJ, Liu G, Liu B, Zhao H, Serby MD, Xin Z, Liu M, Gum RJ, Haasch DL, Wang S, Clampit JE, Johnson EF, Lubben TH, Stashko MA, Olejniczak ET, Sun C, Dorwin SA, Haskins K, et al. Aminopyridine-Based c-Jun N-Terminal Kinase Inhibitors with Cellular Activity and Minimal Cross-Kinase Activity †. Journal of Medicinal Chemistry. 2006; 49(12):3563–3580. 10.1021/jm060199b. [DOI] [PubMed] [Google Scholar]
- [87].Friberg A, Vigil D, Zhao B, Daniels RN, Burke JP, Garcia-Barrantes PM, Camper D, Chauder BA, Lee T, Olejniczak ET, Fesik SW. Discovery of Potent Myeloid Cell Leukemia 1 (Mcl-1) Inhibitors Using Fragment-Based Methods and Structure-Based Design. Journal of Medicinal Chemistry. 2013; 56(1):15–30. 10.1021/jm301448p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [88].Goldstein DM, Soth M, Gabriel T, Dewdney N, Kuglstatter A, Arzeno H, Chen J, Bingenheimer W, Dalrymple SA, Dunn J, Farrell R, Frauchiger S, La Fargue J, Ghate M, Graves B, Hill RJ, Li F, Litman R, Loe B, McIntosh J, et al. Discovery of 6-(2,4-Difuorophenoxy)-2-[3-Hydroxy-1-(2-Hydroxyethyl)Propylamino]-8-Methyl-8 H -Pyrido[2,3- d]Pyrimidin-7-One (Pamapimod) and 6-(2,4-Difuorophenoxy)-8-Methyl-2-(Tetrahydro-2 H -Pyran-4-Ylamino)Pyrido[2,3- d]Pyrimidin-7(8 H )-One (R1487) as Orally Bioavailable and Highly Selective Inhibitors of P38α Mitogen-Activated Protein Kinase. Journal of Medicinal Chemistry. 2011; 54(7):2255–2265. 10.1021/jm101423y. [DOI] [PubMed] [Google Scholar]
- [89].Buijnsters P, De Angelis M, Langlois X, Rombouts FJR, Sanderson W, Tresadern G, Ritchie A, Trabanco AA, VanHoof G, Roosbroeck YV, Andrés JI. Structure-Based Design of a Potent, Selective, and Brain Penetrating PDE2 Inhibitor with Demonstrated Target Engagement. ACS Medicinal Chemistry Letters. 2014; 5(9):1049–1053. 10.1021/ml500262u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [90].Pérez-Benito L, Keränen H, van Vlijmen H, Tresadern G. Predicting Binding Free Energies of PDE2 Inhibitors. The Difficulties of Protein Conformation. Scientific Reports. 2018; 8(1):4883. 10.1038/s41598-018-23039-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [91].Boutard N, Białas A, Sabiniarz A, Guzik P, Banaszak K, Biela A, Bień M, Buda A, Bugaj B, Cieluch E, Cierpich A, Dudek Ł, Eggenweiler HM, Fogt J, Gaik M, Gondela A,Jakubiec K, Jurzak M, Kitlńska A, Kowalczyk P, et al. Discovery and Structure–Activity Relationships of N -Aryl 6-Aminoquinoxalines as Potent PFKFB3 Kinase Inhibitors. ChemMedChem. 2019; 14(1):169–181. 10.1002/cmdc.201800569. [DOI] [PubMed] [Google Scholar]
- [92].Wilson DP, Wan ZK, Xu WX, Kirincich SJ, Follows BC, Joseph-McCarthy D, Foreman K, Moretto A, Wu J, Zhu M, Binnun E, Zhang YL, Tam M, Erbe DV, Tobin J, Xu X, Leung L, Shilling A, Tam SY, Mansour TS, et al. Structure-Based Optimization of Protein Tyrosine Phosphatase 1B Inhibitors: From the Active Site to the Second Phosphotyrosine Binding Site. Journal of Medicinal Chemistry. 2007; 50(19):4681–4698. 10.1021/jm0702478. [DOI] [PubMed] [Google Scholar]
- [93].Chen YNP, LaMarche MJ, Chan HM, Fekkes P, Garcia-Fortanet J, Acker MG, Antonakos B, Chen CHT, Chen Z, Cooke VG, Dobson JR, Deng Z, Fei F, Firestone B, Fodor M, Fridrich C, Gao H, Grunenfelder D, Hao HX, Jacob J, et al. Allosteric Inhibition of SHP2 Phosphatase Inhibits Cancers Driven by Receptor Tyrosine Kinases. Nature. 2016; 535(7610):148–152. 10.1038/nature18621. [DOI] [PubMed] [Google Scholar]
- [94].Currie KS, Kropf JE, Lee T, Blomgren P, Xu J, Zhao Z, Gallion S, Whitney JA, Maclin D, Lansdon EB, Maciejewski P, Rossi AM, Rong H, Macaluso J, Barbosa J, Di Paolo JA, Mitchell SA. Discovery of GS-9973, a Selective and Orally Efficacious Inhibitor of Spleen Tyrosine Kinase. Journal of Medicinal Chemistry. 2014; 57(9):3856–3873. 10.1021/jm500228a. [DOI] [PubMed] [Google Scholar]
- [95].Baum B, Mohamed M, Zayed M, Gerlach C, Heine A, Hangauer D, Klebe G. More than a Simple Lipophilic Contact: A Detailed Thermodynamic Analysis of Nonbasic Residues in the S1 Pocket of Thrombin. Journal of Molecular Biology. 2009; 390(1):56–69. 10.1016/j.jmb.2009.04.051. [DOI] [PubMed] [Google Scholar]
- [96].Buchstaller HP, Anlauf U, Dorsch D, Kuhn D, Lehmann M, Leuthner B, Musil D, Radtki D, Ritzert C, Rohdich F, Schneider R, Esdar C. Discovery and Optimization of 2-Arylquinazolin-4-Ones into a Potent and Selective Tankyrase Inhibitor Modulating Wnt Pathway Activity. Journal of Medicinal Chemistry. 2019; 62(17):7897–7909. 10.1021/acs.jmedchem.9b00656. [DOI] [PubMed] [Google Scholar]
- [97].Liang J, Tsui V, Van Abbema A, Bao L, Barrett K, Beresini M, Berezhkovskiy L, Blair WS, Chang C, Driscoll J, Eigenbrot C, Ghilardi N, Gibbons P, Halladay J, Johnson A, Kohli PB, Lai Y, Liimatta M, Mantik P, Menghrajani K, et al. Lead Identification of Novel and Selective TYK2 Inhibitors. European Journal of Medicinal Chemistry. 2013; 67:175–187. 10.1016/j.ejmech.2013.03.070. [DOI] [PubMed] [Google Scholar]
- [98].Liang J, van Abbema A, Balazs M, Barrett K, Berezhkovsky L, Blair W, Chang C, Delarosa D, DeVoss J, Driscoll J, Eigenbrot C, Ghilardi N, Gibbons P, Halladay J, Johnson A, Kohli PB, Lai Y, Liu Y, Lyssikatos J, Mantik P, et al. Lead Optimization of a 4-Aminopyridine Benzamide Scaffold To Identify Potent, Selective, and Orally Bioavailable TYK2 Inhibitors. Journal of Medicinal Chemistry. 2013; 56(11):4521–4536. 10.1021/jm400266t. [DOI] [PubMed] [Google Scholar]
- [99].Berman HM. The Protein Data Bank. Nucleic Acids Research. 2000; 28(1):235–242. 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [100].Meyder A, Nittinger E, Lange G, Klein R, Rarey M. Estimating Electron Density Support for Individual Atoms and Molecular Fragments in X-Ray Structures. Journal of Chemical Information and Modeling. 2017; 57(10):2437–2447. 10.1021/acs.jcim.7b00391. [DOI] [PubMed] [Google Scholar]
- [101].Tickle IJ. Statistical Quality Indicators for Electron-Density Maps. Acta Crystallographica Section D: Biological Crystallography. 2012; 68(4):454–467. 10.1107/S0907444911035918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [102].Yu HS, Gao C, Lupyan D, Wu Y, Kimura T, Wu C, Jacobson L, Harder E, Abel R, Wang L. Toward Atomistic Modeling of Irreversible Covalent Inhibitor Binding Kinetics. Journal of Chemical Information and Modeling. 2019; 59(9):3955–3967. 10.1021/acs.jcim.9b00268. [DOI] [PubMed] [Google Scholar]
- [103].Khalak Y, Tresadern G, Aldeghi M, Baumann HM, Mobley DL, de Groot BL, Gapsys V. Alchemical Absolute Protein–Ligand Binding Free Energies for Drug Design. Chemical Science. 2021; 12(41):13958–13971. 10.1039/D1SC03472C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [104].Shih AY, Hack M, Mirzadegan T. Impact of Protein Preparation on Resulting Accuracy of FEP Calculations. Journal of Chemical Information and Modeling. 2020; 60(11):5287–5289. 10.1021/acs.jcim.0c00445. [DOI] [PubMed] [Google Scholar]
- [105].Kalliokoski T, Kramer C, Vulpetti A, Gedeck P. Comparability of Mixed IC50 Data – A Statistical Analysis. PLOS ONE. 2013; 8(4):e61007. 10.1371/journal.pone.0061007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [106].The COVID Moonshot Consortium, Achdout H, Aimon A, Bar-David E, Barr H, Ben-Shmuel A, Bennett J, Bilenko VA, Bilenko VA, Boby ML, Borden B, Bowman GR, Brun J, Bvnbs S, Calmiano M, Carbery A, Carney D, Cattermole E, Chang E, Chernyshenko E, et al. Open Science Discovery of Oral Non-Covalent SARS-CoV-2 Main Protease Inhibitor Therapeutics. Biochemistry; 2020. 10.1101/2020.10.29.339317. [DOI] [Google Scholar]
- [107].The COVID Moonshot Consortium, PostEra Covid Moonshot; 2021. https://covid.postera.ai/covid/activity_data..
- [108].Pontolillo J, Eganhouse RP. The Search for Reliable Aqueous Solubility (Sw) and Octanol-Water Partition Coefficient (Kow) Data for Hydrophobic Organic Compounds: DDT and DDE as a Case Study, vol. 1. US Department of the Interior, US Geological Survey; 2001. https://pubs.usgs.gov/wri/wri014201/pdf/wri01-4201.pdf. [Google Scholar]
- [109].Daga PR, Data Curation: The Forgotten Practice in the Era of AI. Zenodo; 2019. 10.5281/zenodo.3445476. [DOI] [Google Scholar]
- [110].Kramer C, Kalliokoski T, Gedeck P, Vulpetti A. The Experimental Uncertainty of Heterogeneous Public K i Data. Journal of Medicinal Chemistry. 2012; 55(11):5165–5173. 10.1021/jm300131x. [DOI] [PubMed] [Google Scholar]
- [111].Jarmoskaite I, AlSadhan I, Vaidyanathan PP, Herschlag D. How to Measure and Evaluate Binding Affinities. eLife. 2020; 9:e57264. 10.7554/eLife.57264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [112].Sheridan RP, Karnachi P, Tudor M, Xu Y, Liaw A, Shah F, Cheng AC, Joshi E, Glick M, Alvarez J. Experimental Error, Kurtosis, Activity Cliffs, and Methodology: What Limits the Predictivity of Quantitative Structure–Activity Relationship Models? Journal of Chemical Information and Modeling. 2020; 60(4):1969–1982. 10.1021/acs.jcim.9b01067. [DOI] [PubMed] [Google Scholar]
- [113].Wiseman T, Williston S, Brandts JF, Lin LN. Rapid Measurement of Binding Constants and Heats of Binding Using a New Titration Calorimeter. Analytical Biochemistry. 1989; 179(1):131–137. 10.1016/0003-2697(89)90213-3. [DOI] [PubMed] [Google Scholar]
- [114].Chodera JD, Mobley DL. Entropy-Enthalpy Compensation: Role and Ramifications in Biomolecular Ligand Recognition and Design. Annual Review of Biophysics. 2013; 42(1):121–142. 10.1146/annurev-biophys-083012-130318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [115].Brown SP, Muchmore SW, Hajduk PJ. Healthy Skepticism: Assessing Realistic Model Performance. Drug Discovery Today. 2009; 14(7-8):420–427. 10.1016/j.drudis.2009.01.012. [DOI] [PubMed] [Google Scholar]
- [116].Griffen EJ, Dossetter AG, Leach AG. Chemists: AI Is Here; Unite To Get the Benefits. Journal of Medicinal Chemistry. 2020; 63(16):8695–8704. 10.1021/acs.jmedchem.0c00163. [DOI] [PubMed] [Google Scholar]
- [117].Nicholls A. Confidence Limits, Error Bars and Method Comparison in Molecular Modeling. Part 2: Comparing Methods. Journal of Computer-Aided Molecular Design. 2016; 30(2):103–126. 10.1007/s10822-016-9904-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [118].Knapp B, Ospina L, Deane CM. Avoiding False Positive Conclusions in Molecular Simulation: The Importance of Replicas. Journal of Chemical Theory and Computation. 2018; 14(12):6127–6138. 10.1021/acs.jctc.8b00391. [DOI] [PubMed] [Google Scholar]
- [119].Gapsys V, de Groot BL. On the Importance of Statistics in Molecular Simulations for Thermodynamics, Kinetics and Simulation Box Size. eLife. 2020; 9:e57589. 10.7554/eLife.57589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [120].Wan S, Sinclair RC, Coveney PV. Uncertainty Quantification in Classical Molecular Dynamics. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 2021; 379(2197):rsta.2020.0082, 20200082. 10.1098/rsta.2020.0082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [121].Madhavi Sastry G, Adzhigirey M, Day T, Annabhimoju R, Sherman W. Protein and Ligand Preparation: Parameters, Protocols, and Influence on Virtual Screening Enrichments. Journal of Computer-Aided Molecular Design. 2013; 27(3):221–234. 10.1007/s10822-013-9644-8. [DOI] [PubMed] [Google Scholar]
- [122].Molecular Operating Environment (MOE). 1010 Sherbooke St. West, Suite #910, Montreal, QC, Canada, H3A 2R7; 2022. Chemical Computing Group ULC. [Google Scholar]
- [123].Spruce 1.5.0.1. Santa Fe, NM;. http://www.eyesopen.com.OpenEye Scientific Software. [Google Scholar]
- [124].Aldeghi M, Gapsys V, de Groot BL. Accurate Estimation of Ligand Binding Affinity Changes upon Protein Mutation. ACS Central Science. 2018; 4(12):1708–1718. 10.1021/acscentsci.8b00717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [125].Klimovich PV, Shirts MR, Mobley DL. Guidelines for the Analysis of Free Energy Calculations. Journal of Computer-Aided Molecular Design. 2015; 29(5):397–411. 10.1007/s10822-015-9840-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [126].Kuhn M, Firth-Clark S, Tosco P, Mey ASJS, Mackey M, Michel J. Assessment of Binding Affinity via Alchemical Free-Energy Calculations. Journal of Chemical Information and Modeling. 2020; 60(6):3120–3130. 10.1021/acs.jcim.0c00165. [DOI] [PubMed] [Google Scholar]
- [127].Liu H, Mark AE, van Gunsteren WF. Estimating the Relative Free Energy of Different Molecular States with Respect to a Single Reference State. The Journal of Physical Chemistry. 1996; 100(22):9485–9494. 10.1021/jp9605212. [DOI] [Google Scholar]
- [128].Raman EP, Vanommeslaeghe K, MacKerell AD. Site-Specific Fragment Identification Guided by Single-Step Free Energy Perturbation Calculations. Journal of Chemical Theory and Computation. 2012; 8(10):3513–3525. 10.1021/ct300088r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [129].Raman EP, Lakkaraju SK, Denny RA, MacKerell AD. Estimation of Relative Free Energies of Binding Using Pre-Computed Ensembles Based on the Single-Step Free Energy Perturbation and the Site-Identification by Ligand Competitive Saturation Approaches. Journal of Computational Chemistry. 2017; 38(15):1238–1251. 10.1002/jcc.24522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [130].Boresch S, Woodcock HL. Convergence of single-step free energy perturbation. Molecular Physics. 2017; 115(9-12):1200–1213. 10.1080/00268976.2016.1269960. [DOI] [Google Scholar]
- [131].Christ CD, van Gunsteren WF. Enveloping Distribution Sampling: A Method to Calculate Free Energy Differences from a Single Simulation. The Journal of Chemical Physics. 2007; 126(18):184110. 10.1063/1.2730508. [DOI] [PubMed] [Google Scholar]
- [132].Christ CD, van Gunsteren WF. Multiple Free energies from a Single Simulation: Extending Enveloping Distribution Sampling to Nonoverlapping Phase-Space Distributions. The Journal of Chemical Physics. 2008; 128(17):174112. 10.1063/1.2913050. [DOI] [PubMed] [Google Scholar]
- [133].Christ CD, Van Gunsteren WF. Comparison of Three Enveloping Distribution Sampling Hamiltonians for the Estimation of Multiple Free Energy Differences from a Single Simulation. Journal of Computational Chemistry. 2009; 30(11):1664–1679. 10.1002/jcc.21325. [DOI] [PubMed] [Google Scholar]
- [134].Sidler D, Cristòfol-Clough M, Riniker S. Efficient Round-Trip Time Optimization for Replica-Exchange Enveloping Distribution Sampling (RE-EDS). Journal of Chemical Theory and Computation. 2017; 13(6):3020–3030. 10.1021/acs.jctc.7b00286. [DOI] [PubMed] [Google Scholar]
- [135].Perthold JW, Oostenbrink C. Accelerated Enveloping Distribution Sampling: Enabling Sampling of Multiple End States while Preserving Local Energy Minima. The Journal of Physical Chemistry B. 2018; 122(19):5030–5037. 10.1021/acs.jpcb.8b02725. [DOI] [PubMed] [Google Scholar]
- [136].Jorgensen WL, Thomas LL. Perspective on Free-Energy Perturbation Calculations for Chemical Equilibria. Journal of Chemical Theory and Computation. 2008; 4(6):869–876. 10.1021/ct800011m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [137].Tan Z. Optimally Adjusted Mixture Sampling and Locally Weighted Histogram Analysis. Journal of Computational and Graphical Statistics. 2017; 26(1):54–65. 10.1080/10618600.2015.1113975. [DOI] [Google Scholar]
- [138].Lyubartsev AP, Martsinovski AA, Shevkunov SV, Vorontsov-Velyaminov PN. New Approach to Monte Carlo Calculation of the Free Energy: Method of Expanded Ensembles. The Journal of Chemical Physics. 1992; 96(3):1776–1783. 10.1063/1.462133. [DOI] [Google Scholar]
- [139].Lyubartsev AP, Laaksonen A, Vorontsov-Velyaminov PN. Free Energy Calculations for Lennard-Jones Systems and Water Using the Expanded Ensemble Method: A Monte Carlo and Molecular Dynamics Simulation Study. Molecular Physics. 1994; 82(3):455–471. 10.1080/00268979400100344. [DOI] [Google Scholar]
- [140].Lyubartsev AP, Laaksonen A, Vorontsov-Velyaminov PN. Determination of Free Energy from Chemical Potentials: Application of the Expanded Ensemble Method. Molecular Simulation. 1996; 18(1-2):43–58. 10.1080/08927029608022353. [DOI] [Google Scholar]
- [141].Escobedo FA. Optimized Expanded Ensembles for Simulations Involving Molecular Insertions and Deletions. II. Open Systems. The Journal of Chemical Physics. 2007; 127(17):174104. 10.1063/1.2800321. [DOI] [PubMed] [Google Scholar]
- [142].Escobedo FA, Martínez-Veracoechea FJ. Optimized Expanded Ensembles for Simulations Involving Molecular Insertions and Deletions. I. Closed Systems. The Journal of Chemical Physics. 2007; 127(17):174103. 10.1063/1.2800320. [DOI] [PubMed] [Google Scholar]
- [143].Straatsma TP, Berendsen HJC, Postma JPM. Free Energy of Hydrophobic Hydration: A Molecular Dynamics Study of Noble Gases in Water. The Journal of Chemical Physics. 1986; 85(11):6720–6727. 10.1063/1.451846. [DOI] [Google Scholar]
- [144].Kong X, Brooks CL. -Dynamics: A New Approach to Free Energy Calculations. The Journal of Chemical Physics. 1996; 105(6):2414–2423. 10.1063/1.472109. [DOI] [Google Scholar]
- [145].Guo Z, Durkin J, Fischmann T, Ingram R, Prongay A, Zhang R, Madison V. Application of the -Dynamics Method To Evaluate the Relative Binding Free Energies of Inhibitors to HCV Protease. Journal of Medicinal Chemistry. 2003; 46(25):5360–5364. 10.1021/jm030040o. [DOI] [PubMed] [Google Scholar]
- [146].Knight JL, Brooks CL. -Dynamics Free Energy Simulation Methods. Journal of Computational Chemistry. 2009; 30(11):1692–1700. 10.1002/jcc.21295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [147].Knight JL, Brooks CL. Multisite Dynamics for Simulated Structure–Activity Relationship Studies. Journal of Chemical Theory and Computation. 2011; 7(9):2728–2739. 10.1021/ct200444f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [148].Donnini S, Tegeler F, Groenhof G, Grubmüller H. Constant pH Molecular Dynamics in Explicit Solvent with -Dynamics. Journal of Chemical Theory and Computation. 2011; 7(6):1962–1978. 10.1021/ct200061r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [149].Armacost KA, Goh GB, Brooks CL. Biasing Potential Replica Exchange Multisite -Dynamics for Efficient Free Energy Calculations. Journal of Chemical Theory and Computation. 2015; 11(3):1267–1277. 10.1021/ct500894k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [150].Hayes RL, Armacost KA, Vilseck JZ, Brooks CL. Adaptive Landscape Flattening Accelerates Sampling of Alchemical Space in Multisite Dynamics. The Journal of Physical Chemistry B. 2017; 121(15):3626–3635. 10.1021/acs.jpcb.6b09656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [151].Jarzynski C. Nonequilibrium Equality for Free Energy Differences. Physical Review Letters. 1997; 78(14):2690–2693. 10.1103/PhysRevLett.78.2690. [DOI] [Google Scholar]
- [152].Crooks GE. Path-Ensemble Averages in Systems Driven far from Equilibrium. Physical Review E. 2000; 61(3):2361–2366. 10.1103/PhysRevE.61.2361. [DOI] [Google Scholar]
- [153].Hendrix DA, Jarzynski C. A “Fast Growth” Method of Computing Free Energy Differences. The Journal of Chemical Physics. 2001; 114(14):5974–5981. 10.1063/1.1353552. [DOI] [Google Scholar]
- [154].Hummer G. Fast-Growth Thermodynamic Integration: Results for Sodium Ion Hydration. Molecular Simulation. 2002; 28(1-2):81–90. 10.1080/08927020211972. [DOI] [Google Scholar]
- [155].Sugita Y, Okamoto Y. Replica-exchange Molecular Dynamics Method for Protein Folding. Chemical Physics Letters. 1999; 314(1-2):141–151. 10.1016/S0009-2614(99)01123-9. [DOI] [Google Scholar]
- [156].Fukunishi H, Watanabe O, Takada S. On the Hamiltonian Replica Exchange Method for Efficient Sampling of Biomolecular Systems: Application to Protein Structure Prediction. The Journal of Chemical Physics. 2002; 116(20):9058–9067. 10.1063/1.1472510. [DOI] [Google Scholar]
- [157].Zhang BW, Dai W, Gallicchio E, He P, Xia J, Tan Z, Levy RM. Simulating Replica Exchange: Markov State Models, Proposal Schemes, and the Infinite Swapping Limit. The Journal of Physical Chemistry B. 2016; 120(33):8289–8301. 10.1021/acs.jpcb.6b02015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [158].Gapsys V, Michielssens S, Peters JH, de Groot BL, Leonov H. Calculation of Binding Free Energies. In: Kukol A, editor. Molecular Modeling of Proteins, vol. 1215 New York, NY: Springer New York; 2015.p. 173–209. 10.1007/978-1-4939-1465-4_9, series Title: Methods in Molecular Biology. [DOI] [PubMed] [Google Scholar]
- [159].Chen W, Deng Y, Russell E, Wu Y, Abel R, Wang L. Accurate Calculation of Relative Binding Free Energies between Ligands with Different Net Charges. Journal of Chemical Theory and Computation. 2018; 14(12):6346–6358. 10.1021/acs.jctc.8b00825. [DOI] [PubMed] [Google Scholar]
- [160].Rocklin GJ, Mobley DL, Dill KA, Hünenberger PH. Calculating the Binding Free Energies of Charged Species Based on Explicit-Solvent Simulations Employing Lattice-Sum Methods: An Accurate Correction Scheme for Electrostatic Finite-Size Effects. The Journal of Chemical Physics. 2013; 139(18):184103. 10.1063/1.4826261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [161].Reif MM, Oostenbrink C. Net Charge Changes in the Calculation of Relative Ligand-Binding Free Energies via Classical Atomistic Molecular Dynamics Simulation. Journal of Computational Chemistry. 2014; 5(3):227–243. 10.1002/jcc.23490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [162].Lim NM, Wang L, Abel R, Mobley DL. Sensitivity in Binding Free Energies Due to Protein Reorganization. Journal of Chemical Theory and Computation. 2016; 12(9):4620–4631. 10.1021/acs.jctc.6b00532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [163].Gapsys V, Yildirim A, Aldeghi M, Khalak Y, van der Spoel D, de Groot BL. Accurate Absolute Free Energies for Ligand-Protein Binding Based on Non-Equilibrium Approaches. Communications Chemistry. 2021; 4(1):61. 10.1038/s42004-021-00498-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [164].Hahn DF, König G, Hünenberger PH. Overcoming Orthogonal Barriers in Alchemical Free Energy Calculations: On the Relative Merits of -Variations, -Extrapolations, and Biasing. Journal of Chemical Theory and Computation. 2020; 16(3):1630–1645. 10.1021/acs.jctc.9b00853. [DOI] [PubMed] [Google Scholar]
- [165].Liu S, Wu Y, Lin T, Abel R, Redmann JP, Summa CM, Jaber VR, Lim NM, Mobley DL. Lead Optimization Mapper: Automating Free Energy Calculations for Lead Optimization. Journal of Computer-Aided Molecular Design. 2013; 27(9):755–770. 10.1007/s10822-013-9678-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [166].Xu H. Optimal Measurement Network of Pairwise Differences. Journal of Chemical Information and Modeling. 2019; 59(11):4720–4728. 10.1021/acs.jcim.9b00528. [DOI] [PubMed] [Google Scholar]
- [167].Yang Q, Burchett W, Steeno GS, Liu S, Yang M, Mobley DL, Hou X. Optimal Designs for Pairwise Calculation: An Application to Free Energy Perturbation in Minimizing Prediction Variability. Journal of Computational Chemistry. 2020; 41(3):247–257. 10.1002/jcc.26095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [168].Hauser K, Negron C, Albanese SK, Ray S, Steinbrecher T, Abel R, Chodera JD, Wang L. Predicting Resistance of Clinical Abl Mutations to Targeted Kinase Inhibitors Using Alchemical Free-Energy Calculations. Communications Biology. 2018; 1(1):70. 10.1038/s42003-018-0075-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [169].Aldeghi M, Heifetz A, Bodkin MJ, Knapp S, Biggin PC. Predictions of Ligand Selectivity from Absolute Binding Free Energy Calculations. Journal of the American Chemical Society. 2017; 139(2):946–957. 10.1021/jacs.6b11467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [170].Cui G, Graves AP, Manas ES. GRAM: A True Null Model for Relative Binding Affinity Predictions. Journal of Chemical Information and Modeling. 2020; 60(1):11–16. 10.1021/acs.jcim.9b00939. [DOI] [PubMed] [Google Scholar]
- [171].Nicholls A. What Do We Know and When Do We Know It? Journal of Computer-Aided Molecular Design. 2008; 22(3-4):239–255. 10.1007/s10822-008-9170-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [172].Nicholls A What Do We Know?: Simple Statistical Techniques that Help. In: Bajorath J, editor. Chemoinformatics and Computational Chemical Biology, vol. 672 Totowa, NJ: Humana Press; 2011.p. 531–581. 10.1007/978-1-60761-839-3_22, series Title: Methods in Molecular Biology. [DOI] [PubMed] [Google Scholar]
- [173].Nicholls A Confidence Limits, Error Bars and Method Comparison in Molecular Modeling. Part 1: The Calculation of Confidence Intervals. Journal of Computer-Aided Molecular Design. 2014; 28(9):887–918. 10.1007/s10822-014-9753-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [174].Gapsys V, Pérez-Benito L, Aldeghi M, Seeliger D, van Vlijmen H, Tresadern G, de Groot BL. Large Scale Relative Protein Ligand Binding Affinities Using Non-Equilibrium Alchemy. Chemical Science. 2020; 11(4):1140–1152. 10.1039/C9SC03754C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [175].Pérez-Benito L, Casajuana-Martin N, Jiménez-Rosés M, van Vlijmen H, Tresadern G. Predicting Activity Cliffs with Free-Energy Perturbation. Journal of Chemical Theory and Computation. 2019; 15(3):1884–1895. 10.1021/acs.jctc.8b01290. [DOI] [PubMed] [Google Scholar]


