Measurement Error and Misclassification in Orthopedics: when study subjects are categorized in the wrong exposure or outcome groups

Abstract

Datasets available for orthopedic research often contain measurement and misclassification errors due to errors in data collection or missing data. These errors can have different effects on the study results. Measurement error refers to inaccurate measurement of continuous variables (e.g., body mass index) whereas misclassification refers to assigning subjects in the wrong exposure and/or outcome groups (e.g., obesity categories). Misclassification of any type can result in under- or over-estimation of the association between exposures and outcomes. In this paper, we offer practical guidelines to avoid, identify and account for measurement and misclassification errors. We also provide an illustrative example on how to perform a validation study to address misclassification based on real-world orthopedic data. Please visit the following https://youtu.be/9-ekW2NnWrs or videos that explain the highlights of the article in practical terms.

Introduction

The primary purpose of most orthopedic studies is to evaluate the strength of the association between a risk factor (exposure) and surgical outcome(s), such as the association between implant type (exposure) and revision risk (outcome). If the exposure and/or the outcome variables are measured with error, the evaluation of this association with statistical parameters, such as odds ratios, risk ratios, hazard ratios or regression coefficients, becomes inaccurate. The difference between the observed and the true value of exposure and outcome variables is called measurement or misclassification error. Typically, measurement error is the term used for continuous variables_. Examples of data with measurement error on continuous variables include self-reported weight and height values (as compared with actual measurements), or range of motion measurements which may vary depending on the instruments and the individual observers. Measurement error on categorical variables is known as misclassification. An example of misclassification is the classification of patients in the wrong body mass index (BMI) categories. In the presence of measurement error, whether on continuous or categorical variables, there is increased uncertainty of statistical parameters.¹ Correcting or accounting for measurement error is important to obtain unbiased estimates of the association between exposure and outcomes.

Measurement or misclassification errors can be random or systematic. Random errors are unpredictable changes in the data that occur by chance alone. Sometimes referred to as “noise”, random error adds variability to the data and is almost impossible to completely eliminate in observational studies. Systematic error, on the other hand, is an error that systematically alters the exposure or outcome measurements from their true values, consequently limiting the internal validity of a study. This type of systematic error always affects measurements in a similar direction or magnitude, it is predictable, and it can be reduced. For example, a systematic measurement error is the error obtained from the use of a miscalibrated scale that consistently diverts all weight measurements away from the true value. Recall bias with patient-reported outcome measures (PROMs) is also a common source of systematic error in orthopedic studies and can result in underestimation or overestimation of the effectiveness of orthopedic surgeries.²

Bias arising from measurement and misclassification errors is also referred to as information bias. Administrative and registry databases are increasingly available to orthopedic investigators but misclassified data are particularly common in these data sources.³ Although misclassification is frequently acknowledged in orthopedic literature, its potential impact on study findings is rarely examined in-depth or even mentioned.⁴ In this paper, we present potential issues due to misclassification using real-world orthopedic data, and we provide practical recommendations for preventing, detecting, and correcting for bias arising from misclassified exposure and/or outcome variables.

Differential and non-differential misclassification and consequences

Misclassification is the act of assigning someone to the wrong exposure (risk factor) or outcome group. There are two types of misclassification: non-differential and differential (Figure 1). Non-differential misclassification occurs when all subjects in the study are equally likely to be misclassified. This error may lead to an underestimation of the strength of the association between exposure and outcome. On the other hand, differential misclassification occurs when the probability of being misclassified differs between groups being compared. Differential misclassification may result in either over- or underestimation of the association between the exposure and the outcome. It is worth noting that measurement error and misclassification bias can arise in any type of study, irrespective of sample size and can even affect the performance of risk prediction models. ⁵ Both differential and non-differential misclassification can occur on either the exposure or the outcome variables. An example of non-differential misclassification of the outcome is the erroneous ICD-10-coding of surgical complications in hospital discharge data. A common example of differential misclassification of an exposure is the incorrect self-reported medical history by a patient of activities with a perceived negative connotation, such as smoking or alcohol use. These are often under-reported by patients. In the presence of true association, under-classification with respect to an exposure such as smoking or alcohol use causes underestimation of the relative risk and a decrease in the power of the statistical test.

Figure 1.

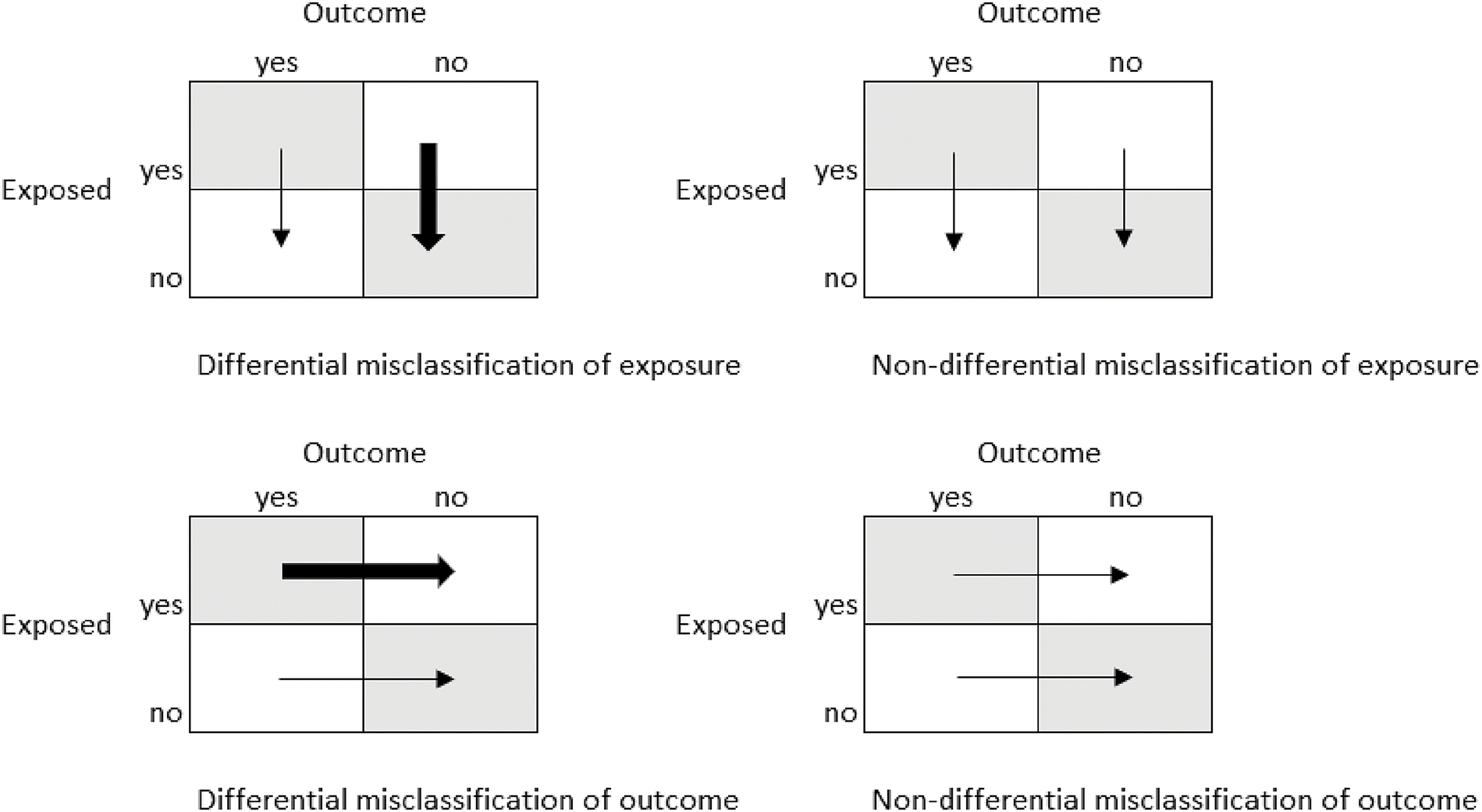
Differential and non-differential misclassification of outcome and exposure

Non-differential misclassification generally biases results towards the null, and the observed risk estimate is closer to the null hypothesis than the true value. This means that the real association between an exposure variable and an outcome may not be identified or may be misinterpreted. Yet there are situations when risk estimates are biased away from the null hypothesis. The bias in the results, such as risk ratio or absolute risk difference, depends upon sensitivity, specificity, and positive and negative predictive values. Sensitivity, or the true positive rate, is the probability of correctly classifying an individual as having the exposure or the outcome, while specificity, or the true negative rate, is the probability of correctly classifying an individual as non-exposure or disease-free. If the misclassification is proportional within exposed and non-exposed individuals for instance, the misclassification of diseased subjects as non-diseased (decrease in sensitivity) where all the non-cases are correctly classified (100% specificity) will alter the risk difference but not the risk ratio. In contrast, if the proportion of misclassified exposed and non-exposed subjects is equal and sensitivity is 100%, a decrease in specificity will underestimate both the risk ratio and the risk difference. Sensitivity, specificity, and positive and negative predictive values are also called bias parameters and can be estimated through internal validation in a subsample of the study population, and if this is not feasible, through literature review or a series of realistic assumptions.

Illustrative Example of Misclassification Bias

Consider the hypothetical example in which we are interested in whether depression (exposure) is a risk factor for periprosthetic joint infections (outcome). We have a cohort of 5000 subjects who underwent primary total knee arthroplasty (TKA). Manual chart review of the electronic health records found 100/5000 subjects developed periprosthetic joint infections (PJI) during the first year of follow-up (Figure 2A), and that 1000/5000 had preexisting depression. Previous results based on the ICD codes recorded during the perioperative period incorrectly classified 30 PJI as non PJI (Figure 2B). This corresponds to 70% sensitivity of ICD codes in identifying PJI. A 30% decrease in sensitivity results in underestimation of the risk difference (from 0.013 to 0.009) but does not influence the risk of PJI associated with depression (RR=1.7). Conversely, a 30% decrease in specificity, meaning 1470 subjects with no PJI are erroneously classified as PJI (Figure 2C), causes both the risk difference and the risk ratio to be underestimated (from 0.013 to 0.009, and from 1.7 to 1 respectively). The underestimation in risk ratio and risk difference occurs whether or not the misclassification of the non-exposed to exposed is proportional across PJI groups. This is also true whether the number of subjects in the PJI group is smaller or larger than the no-PJI group.

Fig. 2.

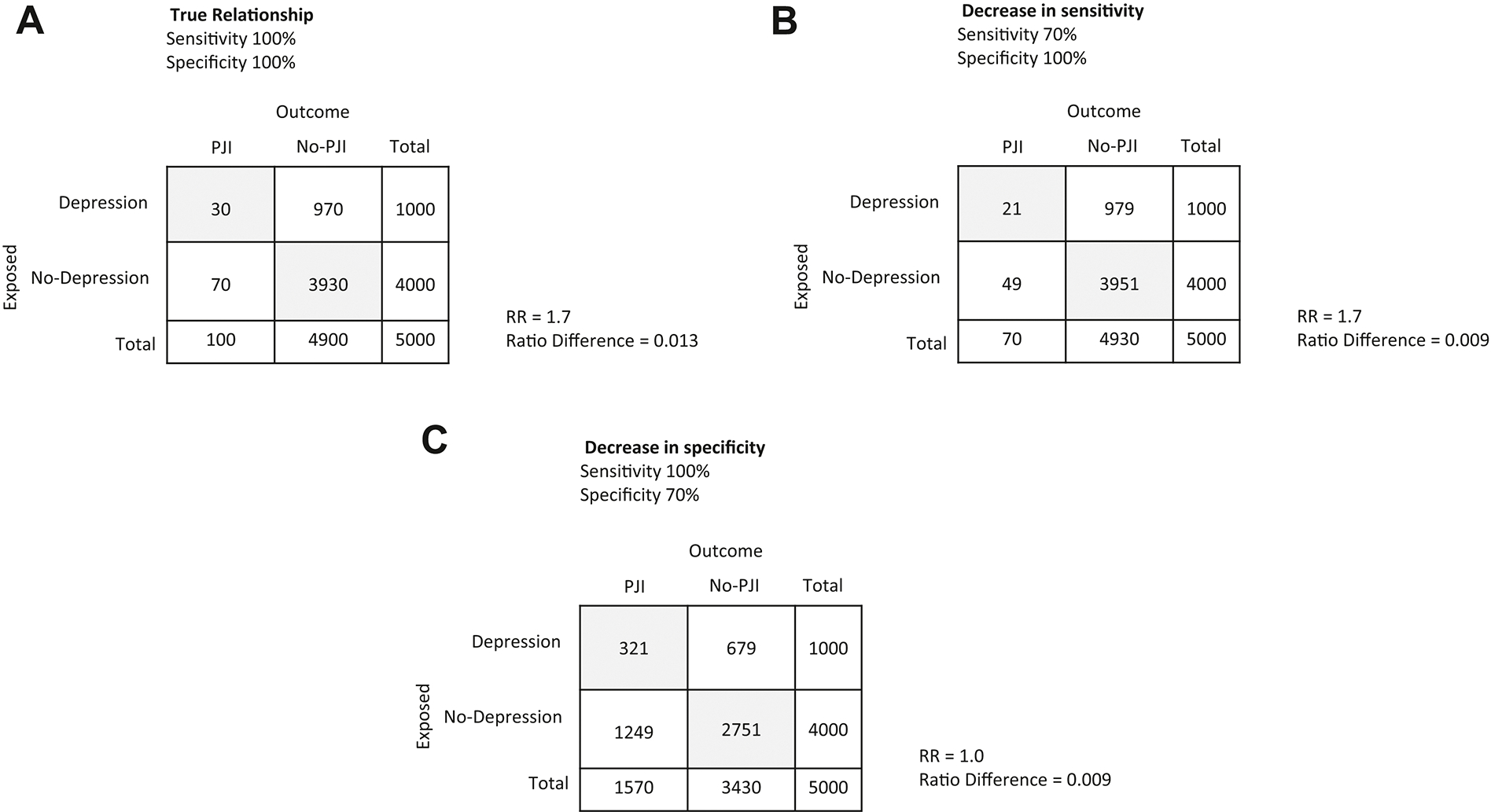
Misclassification bias. (A) true relationship; (B) decrease in sensitivity; (C) decrease in specificity.

Addressing measurement and misclassification bias

The best approach to avoid measurement and misclassification bias is to perform your study using reliable data sources by considering potential sources of systematic error in exposure and outcome variables. At times, measurement and misclassification bias is unavoidable by design or the type of data source. However, formal evaluation is almost always possible. When feasible, the best approach is to verify the validity of the classification of exposures and outcomes through manual chart review. The process of manual chart review should be rigorous as it can also suffer from data entry errors. A common technique to avoid errors in data collection and/or data entry is to have two individuals review the charts and record data in two separate files. Comparison of the two files should identify potential errors and create opportunity for data cleaning for more accurate data.

With large database studies, it is important to recognize that ICD codes can be assigned on a rule-out basis. In the absence of manual chart review, misclassification could be potentially reduced through more stringent definitions, such as the requirement that the diagnosis code be repeated on multiple occasions, or under appropriate clinical circumstances (i.e. listed by a specialist, or evaluated during the hospital stay).

There are several statistical methods to correct for misclassification bias but they all require some information on the extent and direction of misclassification, such as data from an internal or external validation study.⁶ For example, it is not uncommon in the field of orthopedics to classify exposures and outcomes based on diagnosis codes in large database studies. Extensive manual chart review to determine the correct diagnoses is typically not feasible and extremely costly. In these circumstances, validation studies can be performed using a combination of manual review in a subsample of subjects and/or electronic algorithms. A gold standard is established through manual review, followed by an electronic algorithm of codes to correctly classify subjects in each exposure or outcome category. Evaluation of sensitivity and specificity relative to the gold standard can be used as a primary measure of validity.^7–10 If no gold standard exists, and there are sufficient data for a meaningful evaluation, inter-rater variability could be assessed using tests for agreement such as Kappa. This would the magnitude of the discordance and evaluate the potential effect of misclassification on the study results.

How to design a validation study to obtain bias parameters

Validation studies are fundamental in determining how sensitivity and specificity can be used to quantify the bias and consequently correct for misclassification. To adjust the estimates for misclassification, it is possible to apply estimates of sensitivity and specificity found in the literature if the definitions are the same and the prevalence of exposed subjects in the target population is the same as the study population. There are three main approaches to validation and bias parameter estimates.¹¹ To illustrate, we recall the example of PJI patients with depression (exposure) identified using ICD codes where some patients were found to be misclassified when compared to the gold standard manual chart review. The three types of validation approaches, each one with pros and cons:

1. From the population of interest (Figure 3A) select a subsample of patients who were classified as depressed and non-depressed and perform a manual chart review to verify depression diagnoses. As shown in Figure 3B the positive and negative predicted values (PPV, and NPV) are validly estimated but sensitivity and specificity will be biased. This means that the results may not be the same in another study population. If depression is associated with PJI, it is important to stratify within outcome groups (PJI and non-PJI) and estimating predictive values for each individual stratum to avoid implicit assumption of misclassification that might or not be present. In other words, when conducting a validation study, stratifying the validation analysis by other key variables generates estimates of classifications to inform bias-adjusted estimates of the exposure effect. ¹¹ In our example, it is recommended to stratify by depression for PJI misclassification, and by PJI for depression misclassification.

2. Select a subsample within strata of “true” depressed and not depressed. With this approach, the predictive values are not valid, and although the sensitivity and specificity are valid (Figure 3C), the results are more likely to be not transportable to another study population.

3. Select a random subsample for manual chart review. With this validation approach, sensitivity, specificity, PPV and NPV can be validly calculated (Figure 3D). However, since there is no assurance that the distribution of classified and true exposed is representative of the population, the estimated bias parameter could potentially be imprecise.

Fig. 3.

Validation options to handle misclassification bias. (A) full study population; (B) validation on 200 stratified within classified exposed/unexposed; (C) validation on 200 stratified within true exposed/unexposed; (D) validation on 200 random sample.

Although random error, selection bias, and measurement error can all occur in validation studies, it is always the recommended approach to compare the accuracy of a specific measure with a dependable gold standard (such as manual chart review), and therefore quantify and reduce the misclassification bias. Sensitivity analysis should be used more often to account for the uncertainty in the true values of bias parameter. “Bias-level” and “target-adjustment” sensitivity analysis are two of the many techniques available to explore the impact of unmeasured confounders on the estimated association between outcome and exposure.¹² For instance, BMI is an important confounder of the association between surgical approach (exposure) and revision (outcome). If BMI measurement is not available for analysis, sensitivity analysis can be used to determine its impact on the association between exposure and outcome. One way of determining how sensitive is the association between surgical approach and revision is to vary the value of BMI over a range of realistic values. This is called bias-level sensitivity analysis. Target-adjustment sensitivity analysis on the other hand could be helpful in determining the BMI value for which the association between approach and revision reaches a value of interest.

Although always recommended, in some instances it might not be possible to perform a validation study. This is the case with large database studies. Needless to say, it is important to at least understand the potential impact of misclassification on internal/external validity and study inferences. An evaluation of potential implications can help to identify the variable(s) that might require validation. In fact, some misclassification might be manageable in studies where misclassification does not influence the results.

Guidelines for researchers and reviewers

While considering a study involving exposure and outcome, researchers and reviewers should seek answers to the following questions:

1. What are the exposure and outcome variables and how are they measured?

   It is fundamental to correctly identify both the outcome and exposure of interest, or the scales and measures upon which their definitions are based. For instance, since signs and symptoms are unreliable indicators of deep venous thrombosis, the use of Homan’s sign as a study measure for such a variable might not be appropriate, while the use of duplex ultrasound could offer a much more reliable measure.

2. Is misclassification of exposures and outcomes a potential issue for the study?

   • If the study involves the use of administrative or other secondary data to classify the exposure and/or the outcome variables based on ICD-10 diagnoses or CPT procedure codes or other data fields that were not collected specifically for the purpose of the study, misclassification of patients is likely and statistical parameters (e.g. odds ratio, hazard ratio) can be biased.

3. Are there variables derived by dichotomizing continuous measures? It is strongly encouraged not to categorize continuous measures as it can lead to misclassification. Rather than dichotomizing, the association between outcome and exposure can be evaluated without manipulation of either one, and interpreted accordingly¹³.

4. Is potential misclassification bias correctly acknowledged? If so, did the authors make a qualitative or quantitative assessment of its impact on their findings?

   Several techniques can be used to control or account for misclassification bias, including but not limited to:

   • Use direct measurements

   • Ensure data collection is performed using the same methods for outcome and treatment groups

   • Use multiple sources of information to validate each other

   • Adjust estimates using an internal validation study or sensitivity analyses

Finally, if misclassification is likely and it is not corrected for in the statistical analysis, it should at least be addressed as a limitation in the discussion section of any resulting manuscript.