Abstract
Neuronal spike variability is a statistical property associated with the noise environment. Considering a linearised Hodgkin–Huxley model, we investigate how large spike variability can be induced in a typical stellate cell when submitted to constant and noise current amplitudes. For low noise current, we observe only periodic firing (active) or silence activities. For intermediate noise values, in addition to only active or inactive periods, we also identify a single transition from an initial spike-train (active) to silence dynamics over time, where the spike variability is low. However, for high noise current, we find intermittent active and silence periods with different values. The spike intervals during active and silent states follow the exponential distribution, which is similar to the Poisson process. For non-maximal noise current, we observe the highest values of inter-spike variability. Our results suggest sub-threshold oscillations as a possible mechanism for the appearance of high spike variability in a single neuron due to noise currents.
Keywords: White noise, Linearised Hodgkin–Huxley, Spike variability, Spike-trains
Introduction
It is known that neurons are submitted to environment noise from different sources. The origins of such noises range from thermodynamic to quantum effects (Faisal et al. 2008). It is also understood that noise is an integral part of the brain’s functioning and there are evidences suggesting that noise may be beneficial for the neuronal capabilities (Yarom and Hounsgaard 2011). However, high variability of neuronal spikes can be related to elevated levels of noise amplitudes (Protachevicz et al. 2020). An optimal noise is able to generate stochastic resonances in neuronal networks (Vázquez-Rodríguez et al. 2017). Cleanthous (Cleanthous and Christodoulou 2012) suggested that high firing irregularity can optimise the learning process. Li et al. (2018) observed that brain code can arise via silence and active variability.
The cornerstone of mathematical description of a single neuron is the well-known, empirically based, Hodgkin–Huxley (HH) model (Hodgkin and Huxley 1952). The HH model is as effective as computationally complex, being a nonlinear, multiparametered set of coupled differential equations. Some simplified versions of the HH model have been proposed, with the aim of being applied not generally, but rather in specific contexts. Among those, a linearised version of the HH neuron subject to a nonlinear, irreversible reset (associated with the “spike”), oftentimes called “the resonate-and-fire model”, is of particular interest in the description of the dynamics of a single neuron. That linearised neuron model was considered by Erchova et al. (2004) in order to analyse the dynamics of rat entorhinal cortex cells.
The main advantage of using the resonate-and-fire model is the comparatively small set of parameters to be determined for the purpose of fitting experimental data (Engel et al. 2008). For instance, a pronounced characteristic of the stellate cells of rat entorhinal cortex (EC) is the existence of subthreshold membrane oscillations and resonances (Erchova et al. 2004). Cell activities in the entorhinal cortex have been associated to working (Fransén 2005), episodic memory (Umbach et al. 2020), and spatial cognition (Van Cauter et al. 2013). Abnormal alterations in EC have been reported in diseases like epilepsy, Alzheimer, and Schizophrenia (Coutureau and Di Scala 2009).
Stochastic resonance is a phenomenon in which a statistical property can be optimised due to a noise (Gammaitoni et al. 1998). The resonance phenomenon is recurrently obtained due to periodic input signals, however, the regularity on the input is not a necessary condition (Gerstner and Kistler 2002). Guo and Li (2012) demonstrated that the input frequency plays an important role in the stochastic resonance of the HH model when submitted to excitatory and inhibitory currents. Recently, Lu et al. (2020) reported the appearance of inverse stochastic resonance in a single HH model when submitted to Gaussian and non-Gaussian coloured noises. The results of Mino and Durand (2008) suggest that stochastic resonance can induce an oscillatory phenomenon in a recurrent neuronal network where each node is represented by the HH neuron. Zhao et al. reported that the increase of the connection probability between neurons is able to enhance the stochastic resonance, indicating that the network topology affects the signal propagation in feedforward networks composed of coupled FitzHugh-Nagumo neurons (Zhao et al. 2020). Cao et al. showed that noises can enhance more than suppress the coherent resonance in neuronal bursting with spike undershoot (Cao et al. 2020). Some experimental results suggest that noise sources could be non-Gaussian. Following in this direction, Gong et al. (2009) demonstrated that non-Gaussian noises can optimise spiking activities of random complex networks of Hodgkin–Huxley neurons. Nozaki et al. (1999) showed that coloured noise spectrum can modify the signal-to-noise ratio curve and the optimal characteristic depends on the dynamic system. Hänggi et al. (1993) studied the effect of coloured noises in the stochastic resonance of overdamped systems from small to large noise correlations. They reported that coloured noise is able to reduced stochastic resonance.
For some parameters of the linearised HH model, the resonant properties present in the sub-threshold oscillations have a strong influence on the spike events (Verechtchaguina et al. 2007). The simple description of the neuronal model is enough to reproduce activities found in experimental observations. In this way, the basic neuron dynamics can be observed by means of a simple neuron model, while that same dynamics can be difficult to observe in the original HH model (Izhikevich 2001). Furthermore, the resonate-and-fire model permits to derive some analytical results, such as the asymptotic state of a silence neuron when no noise or low noise levels are considered.
In this work, we consider the resonate-and-fire model to study the effects of constant and noise currents in the neuronal dynamics, characterising their firing frequency, pattern, silence or spike predominance, coefficient of variation and local variation of the inter-spike intervals. In our results, we observe continuous neuronal silence and firing for small noise amplitudes. For intermediate amplitude values, these two neuronal activities and a single transition from an initial active to silence states are identified. For large noise amplitudes, an activity of high variability occurs with the appearance of spike-trains permeated by intervals of no spikes. We find values of the noise and constant current amplitudes in which the spike variability is high. By varying the constant and noise currents for a non-maximal noise amplitude, it is possible to identify a higher variability of the inter-spike intervals. In this case, the neuronal dynamics remains greater time intervals in silence periods. In addition, we show that the transition from silence to spike predominance is abrupt for small and intermediate noise amplitudes, and it is smooth for large values of the noise amplitude.
This paper is organised as follows: In Sect. 2, we introduce the neuronal model. Section 3 exhibits the methods to diagnose the neuron dynamics. In Sect. 4, we present our results about firing patterns, mechanism of large variability, and comparison with the LIF neuron. In Sect. 5, we discuss our results about the noise effects, as well as the model limitation. We draw our conclusions in the last section.
Neuronal model
We consider a linearised Hodgkin–Huxley model (Erchova et al. 2004), also known as resonate-and-fire model, given by the following set of two coupled linear differential equations
| 1 |
| 2 |
where V and are the membrane potential and inductance current, respectively. In the first equation, C and R correspond to the capacitance and resistance, respectively, while is a constant current applied in the neuron. In the second equation, L and are related to the inductance and inductive resistance, respectively, and is the resting potential re-scaled as
| 3 |
In Verechtchaguina et al. (2007), they considered a noise ion channel in the deterministic model (Eq. 1 and 2). To do that, they used a white-noise approximation for the external current (Richardson and Gerstner 2005). In such approach, Eqs. (1) and (2) represent the membrane potential of the neuron which satisfies
| 4 |
where the constants , , , and Q are defined as
| 5 |
Equation (4) is readily identified as the equation of motion for a damped harmonic oscillator with external forcing. The parameters , , and are, then, the damping coefficient, the angular frequency, and a constant external force in this analogy, respectively. In addition, Q is related to the noise intensity and represents the Gaussian white noise with unitary standard deviation.
In this model, the neuron generates spikes immediately after the membrane voltage overtakes the threshold potential (). The m-th spike time is identified by . The membrane potential is reset to the value after a time interval ( ms) that the neuron potential overtakes the threshold potential (). Figure 1 shows a representation of the reset rule. As shown in the figure, in the reset rule, potential is restarted to the value of the reset potential (). value can be associated with the period of the neuron in the absolute refractory state. The state of the neuron evolves over time according to the linearized Hodgkin–Huxley model until (and if) such state crosses the threshold potential . If that happens, the neuron continues to evolve linearly until a time interval later, when the reset takes place and the evolution of the states becomes irreversible (U = ). On the other hand, if the state never crosses the threshold, its evolution is always governed by the Eq. (4). The constant forcing, , depends on , and the noise amplitude, Q, depends on both and D, where D is the intensity of the applied white Gaussian noise (Verechtchaguina et al. 2004).
Fig. 1.
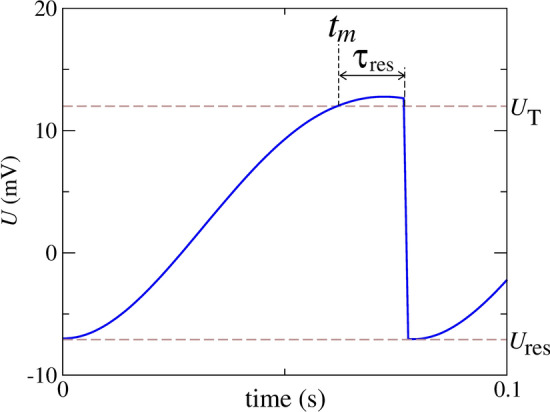
Schematic representation of the reset rule identifying the threshold potential (), m-th spike time (), reset potential (), and time to reset () after the membrane potential overtaking the threshold
The results shown in this work are for initial mV and =0. Although the initial conditions can change the pattern found for small and intermediate noise intensity, they have less influence on the results for high noise. We consider an integration step equal to s. The integration method is the Second-Order Stochastic Runge-Kutta (Honeycutt 1992). The neuron parameters are chosen as for a typical stellate cell according to Table 1 (Verechtchaguina et al. 2007).
Table 1.
Standard parameters (Verechtchaguina et al. 2007)
| Parameter | Description | Value |
|---|---|---|
| C | Neuronal capacitance | F |
| R | Leak resistance | 56.7 M |
| Inductive resistance | 46.1 M | |
| L | Inductance | 1.26 MH |
| D | Noise level | [,] Hz M |
| Constant current | [220,360] pA | |
| Resting potential | -61.5 mV | |
| Threshold potential | 12 mV | |
| Reset potential | -7 mV | |
| Time to reset | 15 ms | |
| Integration step | s | |
| Simulation time | 10 s |
Methods
Coefficient of variation
We consider that the neuron spikes when it crosses the threshold potential . The th inter-spike interval of the neuron is defined as the time difference between two consecutive spikes
| 6 |
where is the time in which the th spike occurs.
In order to monitor the mean coefficient of variation, we calculate the mean value of , , and its standard deviation, . The coefficient of variation (CV) is given by Lengler and Steger (2017)
| 7 |
Local variation
We calculate the local variation (LV) defined as Shinomoto et al. (2009)
| 8 |
where n is the number of inter-spike intervals of the neuron. For regular ISIs, LV is close to 0. This diagnostic detects instantaneous variabilities of ISIs.
Active (A) and the silence (S) durations and their predominance coefficient
We constructed the ISI histogram and identified the value for the active and silence intervals. Figure 2 shows the ISI distribution identifying the active (A) and silence (S) states. This particular histogram turned out to be a bimodal distribution. The active regime is typically characterised by ISI 0.14 s, value identified by a vertical dashed line in the figure. This ISI distribution is also displayed by Verechtchaguina et al. (2007). Based on that information, we consider that when two spikes occur with s, the spikes belong to the same spike-train, whose duration is . On the other hand, when the interval between two adjacent spikes is ISI s, we consider that a silence period occurs.
Fig. 2.
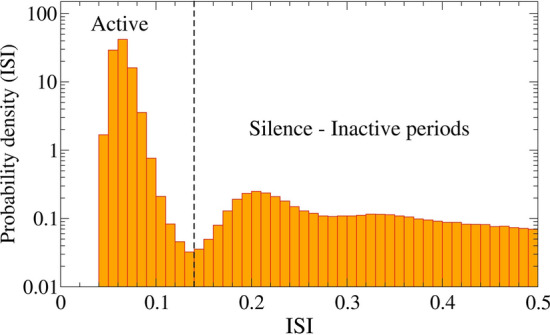
Probability density as function of the ISI values for pA and Hz M
In order to analyse the predominance of the spike-trains or the silence on time, we define the predominant silence-active coefficient N as
| 9 |
where and are the total durations of the active and silent during the stimulation period, respectively. This coefficient ranges from (absolute silence) to (a single, uninterrupted train). indicates an average equal of mix between active and silence durations.
Results
Firing patterns
Figure 3 shows the time series of U for Hz M considering three different values of the constant current applied in the neuron: (a) pA, (b) pA, and (c) pA. In Fig. 3(a), the neuron potential does not overtake the threshold potential and, consequently, there is no firing activity. Figure 3(b) displays an initial spike-train followed by a silence activity. Finally, Fig. 3(c) exhibits a periodic firing activity. These time series of the neuron potentials correspond to intermediate noise levels. For low noise, we observe either only silence or only periodic firing activity, depending on the specific value of . This result is very similar to the case where there is no presence of noise.
Fig. 3.
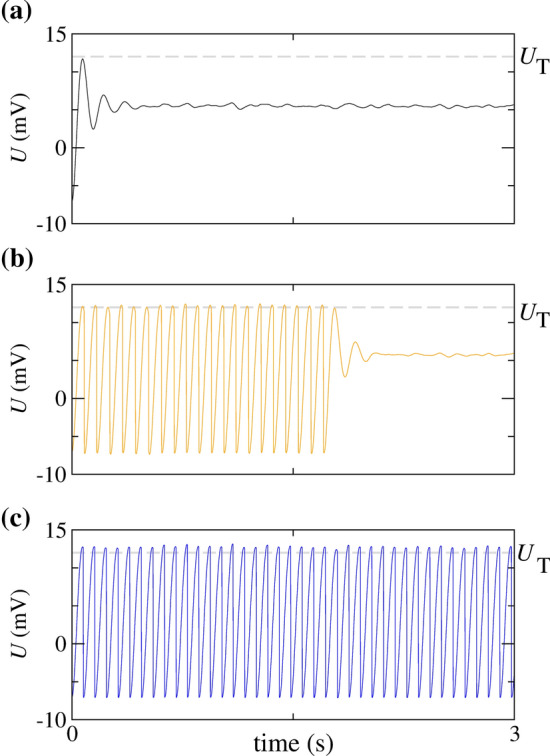
for Hz M, (a) pA, (b) pA, and (c) pA
In Fig. 4, we compute the time evolution of the neuronal potential U for pA and two values of the applied white Gaussian noise intensity, namely, (a) Hz M and (b) Hz M. These values correspond to a large noise amplitude. Figure 4(a) exhibits spike-trains with the active state A and the silence S. By increasing the value of D, we observe a variation in the values of both A and S, as shown in Fig. 4(b).
Fig. 4.
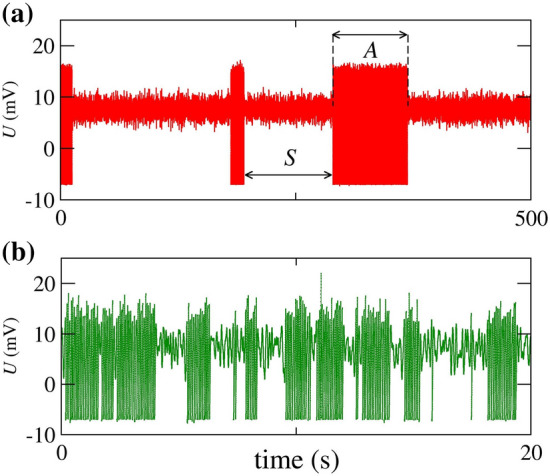
for 320 pA, (a) Hz M, and (b) Hz M
In order to study the neuronal dynamics, we compute the parameter space. Figure 5(a) and (b) show, respectively, the mean firing frequency F—i.e. the average number of spikes in a second—and the pattern related to the firing through colour bars. In Fig. 5(a), we see that F depends on and D, while Fig. 5(b) displays the patterns according to the neuronal activity, where 0 denotes no firing activity, 1 represents the periodic firing, 2 identifies initial spike-train ending in no firing activity, and 3 denotes the oscillatory activity between spike-trains and silence periods. That figure makes it clear that there are regions, in the parameter space, with very distinct qualitative behaviours.
Fig. 5.
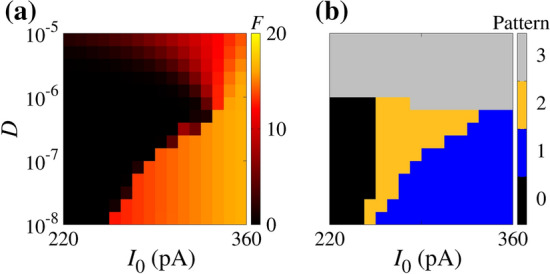
Parameter space for initial condition mV and . In panel (a), the colour bar corresponds to the values of F. The panel (b) displays the regions for the absence of spikes (black), continuous spikes (blue), a single spike train followed by silence activity (orange), and oscillatory activity between active and silence periods (gray). (Color figure online)
Mechanism of large variability
The different patterns of the resonate-and-fire neuron depend on the trajectories in the phase space. Figures 6 and 7 show the five typical trajectories in the phase space. Figure 6(a), (b), and (c) display the silence, initial burst activity, and active dynamics, respectively, which are also shown in Fig. 3, in the same colour representation. In Fig. 6(a), the trajectory does not cross the threshold . This is a linear evolution and the dynamics of the neuron activity is described as a damped harmonic oscillator under the action of constant and white noise external forces. If both forces are removed, the trajectory asymptotes to the null vector of the phase space. The effect of turning the constant force on is a translation in the asymptotic state. Denoting such state by , we find , where and are defined in Eq. (5). Then, by turning the noise force on, we see random deviations from the original trajectory, as seen in Fig. 6(a), while the asymptotic state remains , which we are able to compute analytically. Figure 6(b) shows what happens when a trajectory crosses the threshold potential . It is reset many times after crossing the threshold and, eventually, tends to the same .
Fig. 6.
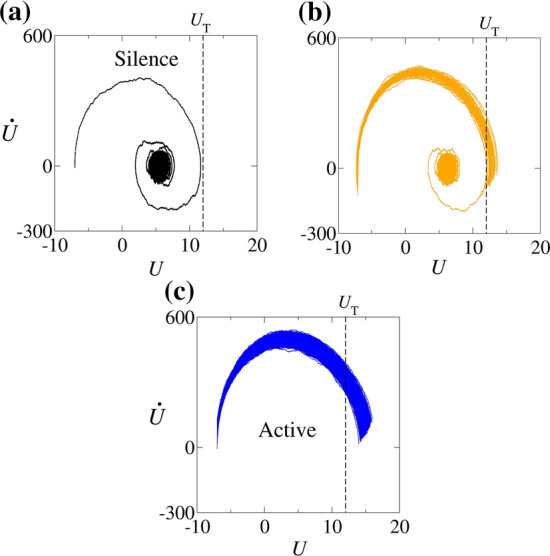
for Hz M, (a) pA (silence), (b) pA (initial burst activity), (c) pA (active). The vertical dashed line represents the threshold potential
Fig. 7.
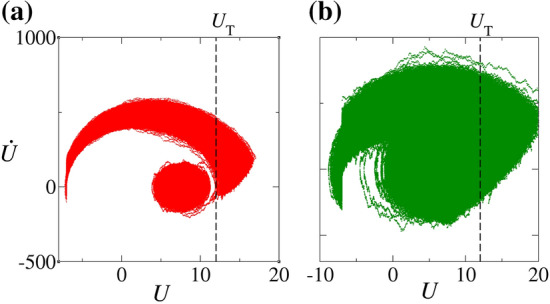
for pA, (a) Hz M and (b) Hz M (green). The dashed line represents the threshold value . (Color figure online)
In Fig. 6(c), the blue line represents the trajectories of the region in the parameter space in which A dominates, as displayed in Fig. 3(c). The trajectory starts on the left side and goes to the right side crossing the threshold potential, , represented by the vertical dashed line. The trajectory is reset to the reset potential () times after crossing the threshold (). This reset operation can be mathematically described by the operation R
| 10 |
where, for any vector lying in the phase space, is the translation operator for , the projection operator for , and represents the function composition. The projection leads the state which crosses the threshold (U, ) to the state (0, ). The projected state is then translated only in the U variable, and it ends up in the state . It can be shown that the reset state does not depend on the U value before the reset, although it depends on the value of . In this way, we may have different states, with the same value of , reset to the same state ( , ). This reset operation R explains the apparent discontinuous vertical line at in Fig. 7.
The trajectory in Fig. 7(a) corresponds to states lying in the region of the parameter space where S dominates. This trajectory corresponds to the U evolution in Fig. 4(a). times after U crosses the threshold , the trajectory is reset according to Eq. 10. The trajectory crosses other times and it is always reset after the time interval . However, before the trajectory crosses , it spends a long time near the region that contains the state of the previous cases. Then, the neuron spends a time orbiting the state before firing and, consequently, the silence prevails. Although trajectories in the upper arch path mostly spike, sometimes they do not. The same is valid for silence trajectories represented in the lower circular path. The trajectory associated with the silence can get out, exceeding the threshold potential. These changes in the trajectory occur due to the presence of noise.
In Fig. 7(b), the trajectory represents the states in the region of the parameter space in which . This trajectory is plotted in Fig. 4(b). Unlike the red trajectory, the green trajectory does not spend much time orbiting and it soon crosses the firing threshold , causing the observed interplay between A and S.
Figure 8(a), (b), and (c) display where the colour bars denote N, CV and LV, respectively. In Fig. 8(a), the white region corresponds to the regimes dominated by the spike-train and the black region by the silence behaviour. We see that the transition from silence to spiking predominance is continuous for large noise amplitudes. Figure 8(b) shows a small region in which the variability in the neuronal activity is large. We consider as initial conditions mV and . If we consider larger values of U as the initial condition, the neuron can not fire for small and intermediate noise amplitudes. Increasing the initial condition of U, the transition from silence to firing under small and intermediate noise amplitudes moves to the right. On the other hand, CV values remain similar to different initial conditions. For large noise intensity, the initial conditions do not have a significant influence on the patterns and CV values. In Fig. 8(c), for regular ISIs, LV is close to 0. This diagnostic tool detects instantaneous variabilities of ISIs. As shown in the figure, large values of CV do not coincide with high LV values. However, the highest values of LV also occur for non-maximal noise and constant current intensities.
Fig. 8.
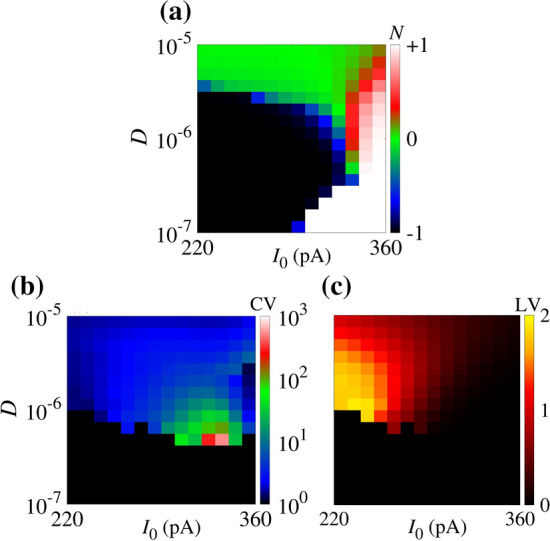
(a) Predominant silence-active coefficient (N), (b) coefficient of variation (CV), and (c) local variation (LV) of inter-spike intervals in the parameter space of . N, CV and LV are calculated considering a time duration equal to s. The initial conditions are mV and . In the resonate model, highest LV values do not coincide with the CV ones
Figure 9 shows (a) N and (b) CV for Hz M as a function of . We observe that a larger variability of spikes occurs for , where and have approximately the same values. Vertical and horizontal brown dashed lines indicate in which .
Fig. 9.
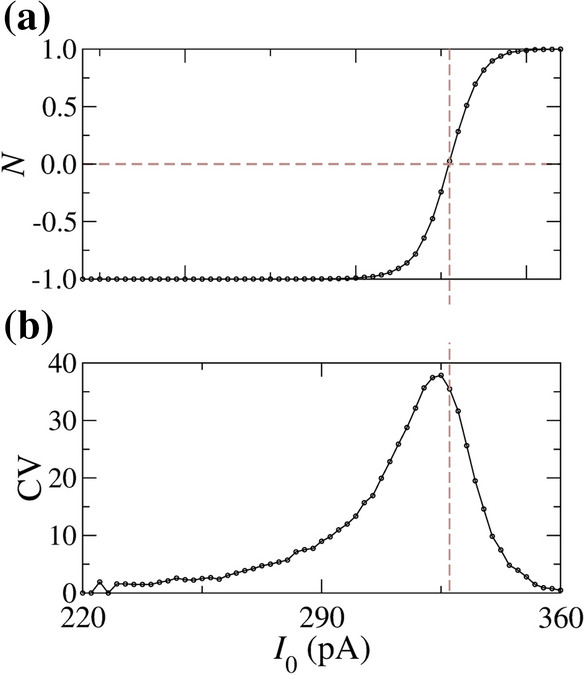
(a) Predominant silence-active coefficient (N) and (b) coefficient of variation of inter-spike intervals for Hz M. The values of N and CV are calculated for a time duration equal to s. The initial conditions are given by mV and
Figure 10(a) and (b) show N and CV for pA as a function of D, respectively. We observe small values of CV for small noise intensities ( Hz M) and higher CV for a certain D value. There is a value of D that maximises CV, taking place between two crossing points, where .
Fig. 10.
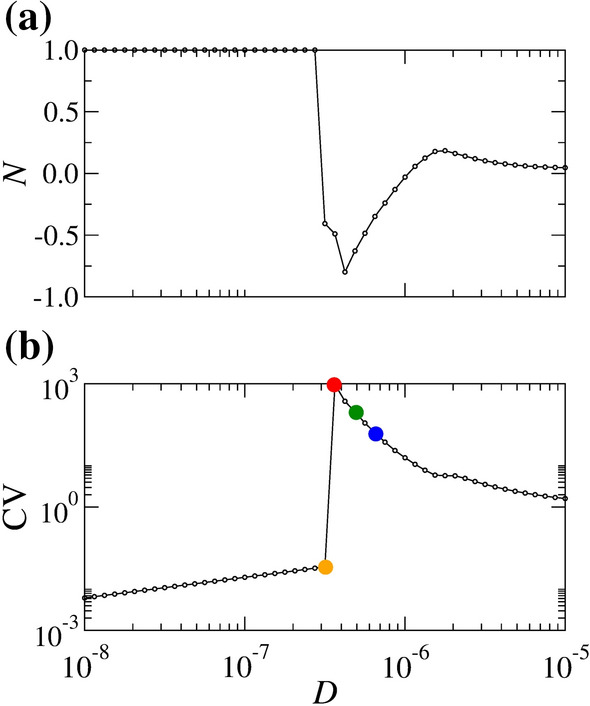
(a) Predominant silence-active coefficient (N) and (b) coefficient of variation of inter-spike intervals (CV) for constant pA. The values of N are calculated considering a time duration equal to s. The initial conditions are given by mV and
Figure 11(a) and (b) display the raster plot for the orange, red, green, and blue circles indicated in Fig. 10(b). We see an initial spike-train activity (orange dots) and long silence periods (red dots) in Fig. 11(a). Smaller spike-trains (green and blue dots) are shown in Fig. 11(b). The increase in D leads to an increase in the number of silence and spike-trains over time, as displayed in Fig. 11(a) and (b).
Fig. 11.
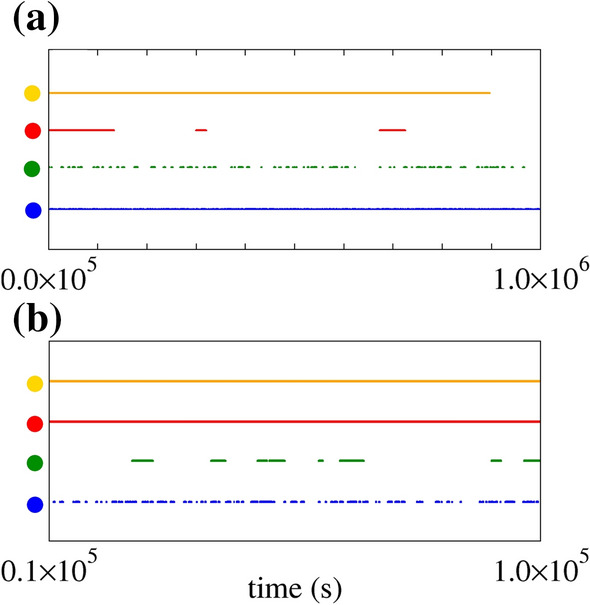
Raster plot for pA, Hz M (orange dots), Hz M (red dots), Hz M (green dots), and Hz M (blue dots). The panel (a) exhibits the entire time interval of spikes, while panel (b) the magnification in interval [0.1,1.0] s. The black dots exhibit a long initial burst activity, while the red, green, and blue dots show the neuronal activities with high variability. CV is larger for red dots than for green and blue dots. (Color figure online)
Figure 12(a) and (b) exhibit the A and S distributions, where the blue points correspond to the blue points shown in Figs. 10(b) and 11(a), (b), respectively. By increasing the noise intensity from the point in which CV is maximum, we observe that the values of A and S converge to an exponential distribution. Exponential distributions suggest an absence of memory, where the events occur in a continuous and independent way (Balakrishnan and Basu 1995). The exponential distributions are related to the Poisson processes that describe the simplest representation of the firings in a stochastic neuron (Gerstner et al. 2014) and are not uncommon in biological processes. For instance, Nobile et al. reported exponential probability density functions for the first-passage-time of an Ornstein-Uhlenbeck process (Nobile et al. 1985).
Fig. 12.
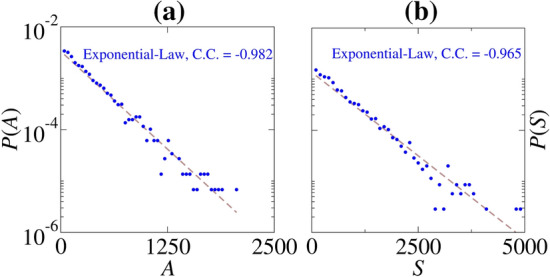
(a) P(A) and (b) P(S) distributions for pA and Hz M (blue points). C.C. is the correlation coefficient of the exponential law. (Color figure online)
Comparison with the LIF neuron
Lánský and Rospars analysed a two-point stochastic neuron model and reported that noise can play a beneficial role in the neuron dynamics (Lánský and Rospars 1995). In the model, they observed that the coefficient of variation of ISIs is high near the silence to spike transition when the mean input is increased. However, as opposed to our results for the resonate-and-fire model, the large variability is not observed in our simulations in the Leak Integrate-and-Fire (LIF).
In order to compare the results of the resonate-and-fire model with the LIF model, we consider constant and Gaussian currents in the LIF model. The LIF model is described by the follow equation
| 11 |
where V and are the membrane potential and membrane time constant, respectively. and are the resting potential and LIF resistance (Gerstner and Kistler 2002). Considering that the current has both constant and white Gaussian noised components, we obtain
| 12 |
where, we consider ms, mV, and , ms (Ostojic 2014). In Fig. 13, we observe that in the LIF model, (a) CV and (b) LV provide similar results, in the sense that the highest values occur in the same D and I parameter values. For the resonate-and-fire model, the highest values of CV and LV do not coincide. In this way, in the integrate-and-fire model, we also observe that there is an optimal noise and constant amplitude which can maximise the coefficient of variation.
Fig. 13.
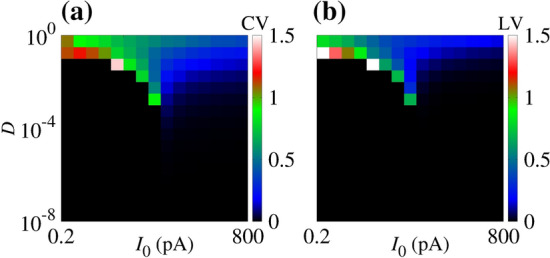
(a) Coefficient of variation (CV) and (b) local variation (LV) of inter-spike intervals on the space parameter of D and for the LIF model
Burkitt reviewed some mechanisms that can cause the firing variability, such as random or balanced excitatory and inhibitory currents, large inhibition, and dendritic nonlinearities (Burkitt 2006). Given the interest in the dynamics of integrator and resonate neurons, we consider the analyses of CV for the LIF model, that is useful to elucidate many questions about neuron dynamics. We also analyse the CV values for the original Hodgkin–Huxley model in the same scenario. As a similar result, we find that the maximal variability is obtained for a certain constant and non-maximal noise amplitude.
Discussion
Many studies focused on the variability of a spike train from a theoretical point of view (Nobile et al. 1985; Lánský and Rospars 1995; Burkitt 2006; Kobayashi 2009) and by performing and analysing experiments (Shinomoto et al. 2009). While most theoretical works focus on a one-dimensional neuron model (e.g., leaky integrate-and-fire model), this research focuses on a two-dimensional model. It is important to mention that other mechanisms, such as threshold variation (Wilbur and Rinzel 1983), random initial condition (Lánský and Smith 1989), and balanced excitation and inhibition (Shadlen and Newsome 1998), can also induce a high variation of the inter-spike intervals. The resonator mechanism can cause large CV values compared to the other mechanisms.
The high variability of inter-spike intervals are observed in vivo and are associated with spike bursts neuron activities (Svirskis and Rinzel 2000). Sometimes, this high variability could not be explained by means of simple models like leak integrate-and-fire (Softky and Kock 1993). Ditlevsen and Lanky highlighted that the classical integrate-and-fire could be not able to reproduce the spiking variability and coefficient of variation of cortex neurons (Ditlevsen and Lansky 2005). The generalisation of the LIF model could enable the description of real data. Wilbur and Rinzel pointed out the basis for the large coefficient of variation related to the bimodal inter-spike distributions (Wilbur and Rinzel 1983). They also associated large variability with clusters of spikes and long silence periods.
In our simulations considering the resonate-and-fire model, we observe that large variability of ISIs is associated with long silence periods and spike-trains. Usually, the silence periods correspond to the subthreshold oscillations of the membrane potential when the neuron variables circulate around the fix point. For low and intermediate noise intensities, the variability is small due to the fact that ISIs assume very close values. In this case, the neuron dynamics do not oscillate more than once between silence and active periods. Close to the maximal noise intensity, the spike variability is not large due to the fact that the silence periods are smaller. The neuron variables are not captured around the fix point for a long time. In the region of the large variability, the main neuron dynamics is below the threshold, however, sometimes noise makes the neuron spikes. In this case, the neuron dynamics stay more time in the silence activity. Wilbur and Rinzel associated the large variability with long silence periods and spike bursts (Wilbur and Rinzel 1983). Besides, we suspect based on the simulations that additive noise can also play an role to increase the variability in a typical resonance curve. The results suggest that the noise can optimize the high variability in a typical resonance curve. In particular, a non-maximal noise amplitude can increase the spike variability.
Furthermore, in the resonate-and-fire model, high CV is due to the change in the firing rate, i.e., the transitions between the silent and the active state. This result is also consistent with Fig. 11. While the red points look regular in the short time window, it exhibits high CV due to the transitions between the silent and the active state. In addition, the LIF model does not generate high CV activity (Fig. 13). These results suggest that the transition between silent and active states is essential for high CV activity.
A limitation of this study is that the resonate-and-fire model is a reduced model of the Hodgkin–Huxley model. There are several approaches to simplify the Hodgkin–Huxley model (Kobayashi and Kitano 2016). Among these models, it is interesting to mention the adaptive threshold model that can accurately predict the spike patterns of cortical neurons (Kobayashi et al. 2009). We plan to consider both this simplified model and the original HH model in future works.
Conclusions
In this work, we consider a linearised Hodgkin–Huxley model, known as resonate-and-fire neuron, to study how a noise current amplitude influences the dynamic behaviour of a single neuron, with a focus on the effect of the inter-spike variability. This model was studied by Verechtchaguina et al. (2007). By means of the parameter space, we identify the firing frequencies and patterns found in the model. We also analyse the mean silence and train durations, as well as the train-silence predominance. Finally, we calculate the coefficient of variation and local variation of the inter-spike intervals.
For small noise current, Hz M, we observe a continuous spike or silence activity depending on the applied constant current. We find an abrupt transition from silence to firing when is increased. For intermediate noise amplitude, Hz M, besides only continuous silence or firing activity, an initial active to silence activity is identified. For large noise, Hz M, silence and spike-trains occur over time. In this way, we classify four different patterns of activity of the membrane potential: sub-threshold oscillations without firing, periodic firing activity, initial spike-train followed by a silence behaviour, and oscillatory activity between spike-train and silence periods.
Considering large noise amplitudes, silence and spike-train activities oscillate over time. In the parameter space, there is a region in which a large variability between the spikes occurs. Regarding the large variability, we observe an interplay between the firings and the asymptotic state. In this case, a continuous transition from silence to active predominance appears when is increased. For the region of large variability, active and silence durations converge to exponential distributions. While large coefficient of variations are due to long silence periods, high local variations are due to the differences in subsequent inter-spike intervals.
For the same initial condition in the parameter space, close to the transition of each neuronal pattern, different activities can occur due to specific noise inputs. Different initial conditions affect mainly the patterns for small and intermediate noise amplitudes. Depending on the initial value of membrane potential, different frequencies and patterns can occur on the parameter space for small noise amplitudes. However, for a large noise amplitude, the results are not affected by the initial condition. For high noise current, we find intermittent active and silence periods. Furthermore, the large variability occurs for a noise intensity that is not the maximum in the considered noise range. Our results suggest sub-threshold oscillations as a possible mechanism for the appearance of high spike variability in a single neuron due to noise currents. In future works, we plan to investigate this phenomenon considering a Markovian process.
Acknowledgements
This work was possible by partial financial support from the following Brazilian government agencies: São Paulo Research Foundation (FAPESP) under Grant Nos. 2020/04624-2 and 2018/03211-6, Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) and Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) under Grant Nos. 407299/2018-1 and 302665/2017-0.
Declarations
Conflict of interest
We wish to confirm that there are no known conflicts of interest associated with this work and there has been no significant financial support for this work that could have influenced its outcome. No conflict of interest exists.
Data availability
The authors confirm that the data supporting the findings of this study are available within the article.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Balakrishnan N, Basu AP. The exponential distribution: theory, methods and applications. London: Routledge; 1995. [Google Scholar]
- Burkitt AN. A review of the integrate-and-fire neuron model: I. Homogeneous synaptic input. Biol Cybern. 2006;95:1–19. doi: 10.1007/s00422-006-0068-6. [DOI] [PubMed] [Google Scholar]
- Cao B, Wang R, Gu H, Li Y. Coherence resonance for neuronal bursting with spike undershoot. Cogn Neurodyn. 2020;15:77–90. doi: 10.1007/s11571-020-09595-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cleanthous A, Christodoulou C. Learning optimisation by high firing irregularity. Brain Res. 2012;1434:115–122. doi: 10.1016/j.brainres.2011.07.025. [DOI] [PubMed] [Google Scholar]
- Coutureau E, Di Scala G. Prog Neuropsychopharmacol Biol Psychiatry. 2009;33(5):753–761. doi: 10.1016/j.pnpbp.2009.03.038. [DOI] [PubMed] [Google Scholar]
- Ditlevsen S, Lansky P. Estimation of the input parameters in the Ornstein–Uhlenbeck neuronal model. Phys Rev E. 2005;71:011907. doi: 10.1103/PhysRevE.71.011907. [DOI] [PubMed] [Google Scholar]
- Engel TA, Schimansky-Geier L, Herz AVM, Schreiber S, Erchova I. Subthreshold membrance-potential resonances shape spike-train patterns in the entorhinal cortex. J Neurophysiol. 2008;100(3):1579–1589. doi: 10.1152/jn.01282.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erchova I, Kreck G, Heinemann U, Herz AVM. Dynamics of rat entorhinal cortex layer II and III cells: characteristics of membrane potential resonance at rest predict oscillation properties near threshold. J Physiol. 2004;560(1):89–110. doi: 10.1113/jphysiol.2004.069930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faisal AA, Selen LPJ, Wolpert DM. Noise in the nervous system. Nat Rev Neurosci. 2008;9(4):292–303. doi: 10.1038/nrn2258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fransén E. Functional role of entorhinal cortex in working memory processing. Neural Netw. 2005;18(9):1141–1149. doi: 10.1016/j.neunet.2005.08.004. [DOI] [PubMed] [Google Scholar]
- Gammaitoni L, Hänggi P, Jung P, Marchesoni F. Stochastic resonance. Rev Mod Phys. 1998;70(1):223–287. [Google Scholar]
- Gerstner W, Kistler WM. Spiking neuron models: single neurons, populations, plasticity. Cambridge: Cambridge University Press; 2002. [Google Scholar]
- Gerstner W, Kistler WM, Naud R, Paninski L. Neuronal dynamics: From single neurons to networks and models of cognition. Cambridge: Cambridge University Press; 2014. [Google Scholar]
- Gong Y, Hao Y, Xie Y, Ma X, Yang C. Non-Gaussian noise optimized spiking activity of Hodgkin–Huxley neurons on random complex networks. Biophys Chem. 2009;144(1–2):88–93. doi: 10.1016/j.bpc.2009.07.001. [DOI] [PubMed] [Google Scholar]
- Guo D, Li C. Stochastic resonance in Hodgkin–Huxley neuron induced by unreliable synaptic transmission. J Theor Biol. 2012;308:105–114. doi: 10.1016/j.jtbi.2012.05.034. [DOI] [PubMed] [Google Scholar]
- Hänggi P, Jung P, Zerbe C, Moss F. Can colored noise improve stochastic resonance? J Stat Phys. 1993;70:25–47. [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117(4):500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honeycutt R. Stochastic Runge–Kutta algorithms. I. White noise. Phys Rev A. 1992;45(2):600–603. doi: 10.1103/physreva.45.600. [DOI] [PubMed] [Google Scholar]
- Izhikevich EM. Resonate-and-fire neurons. Neural Netw. 2001;14:883–894. doi: 10.1016/s0893-6080(01)00078-8. [DOI] [PubMed] [Google Scholar]
- Kobayashi R. The influence of firing mechanisms on gain modulation. J Stat Mech: Theory Exp. 2009;8:P01017. [Google Scholar]
- Kobayashi R, Kitano K. Impact of slow K currents on spike generation can be described by an adaptive threshold model. J Comput Neurosci. 2016;40:347–362. doi: 10.1007/s10827-016-0601-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobayashi R, Tsubo Y, Shinomoto S. Made-to-order spiking neuron model equipped with a multi-timescale adaptive threshold. Front Comput Neurosci. 2009;3:9. doi: 10.3389/neuro.10.009.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lánský P, Rospars JP. Ornstein–Uhlenbeck model neuron revisited. Biol Cybern. 1995;72:397–406. [Google Scholar]
- Lánský P, Smith CE. The effect of a random initial value in neural first-passage-time models. Math Biosci. 1989;93(2):191–215. doi: 10.1016/0025-5564(89)90023-0. [DOI] [PubMed] [Google Scholar]
- Lengler J, Steger A. Note on the coefficient of variation of neuronal spike trains. Biol Cybern. 2017;111(3–4):229–235. doi: 10.1007/s00422-017-0717-y. [DOI] [PubMed] [Google Scholar]
- Li M, Xie K, Kuang H, Liu J, Wang D, Fox GE, Shi Z, Chen L, Zhao F, Mao Y, Tsien JZ. Neural coding of cell assemblies via spike-timing self-information. Cereb Cortex. 2018;28(7):2563–2576. doi: 10.1093/cercor/bhy081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu L, Jia Y, Ge M, Xu Y, Li A. Inverse stochastic resonance in Hodgkin–Huxley neural system driven by Gaussian and non-Gaussian colored noises. Nonlinear Dyn. 2020;100:877–889. [Google Scholar]
- Mino H, Durand DM (2008) Stochastic resonance can induce oscillation in a recurrent Hodgkin–Huxley neuron model with added Gaussian noise. In: 30th conference of proceedings in IEEE engineering medicine and biological society [DOI] [PubMed]
- Nobile AG, Ricciardi LM, Sacerdote L. Exponential trends of Ornstein–Uhlenbeck first-passage-time densities. J Appl Probab. 1985;22(2):360–369. [Google Scholar]
- Nozaki D, Mar DJ, Grigg P, Collins JJ. Effects of colored noise on stochastic resonance in sensory neurons. Phys Rev Lett. 1999;82:2402. [Google Scholar]
- Ostojic S. Two types of asynchronous activity in networks of excitatory and inhibitory spiking neurons. Nat Neurosci. 2014;17(4):594–600. doi: 10.1038/nn.3658. [DOI] [PubMed] [Google Scholar]
- Protachevicz PR, Santos MS, Seifert EG, Gabrick EC, Borges DS, Borges RR, Trobia J, Szezech JD, Jr, Iarosz K, Caldas IL, Antonopoulos CG, Xu Y, Viana RL, Batista AM. Noise induces continuous and noncontinuous transitions in neuronal interspike intervals range. Indian Acad Sci Conf Ser. 2020;3(12):105–109. [Google Scholar]
- Richardson MJE, Gerstner W. Synaptic shot noise and conductance fluctuations affect the membrane voltage with equal significance. Neural Comput. 2005;17:923–947. doi: 10.1162/0899766053429444. [DOI] [PubMed] [Google Scholar]
- Shadlen MN, Newsome WT. The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J Neurosci. 1998;18(10):3870–3896. doi: 10.1523/JNEUROSCI.18-10-03870.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinomoto S, Kim H, Shimokawa T, Matsuno N, Funahashi S, Shima K, Fujita I, Tamura H, Doi T, Kawano K, Inaba N, Fukushima K, Kurkin S, Kurata K, Taira M, Tsutsui K-I, Komatsu H, Ogawa T, Koida K, Tanji J, Toyama K. Relating neuronal firing patterns to functional differentiation of cerebral cortex. PLoS Comput Biol. 2009;5:e1000433. doi: 10.1371/journal.pcbi.1000433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Softky WR, Kock C. The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs. J Neurosci. 1993;13(1):334–350. doi: 10.1523/JNEUROSCI.13-01-00334.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svirskis G, Rinzel J. Influence of temporal correlation of synaptic input on the rate and variability of firing in neurons. Biophys J. 2000;79(2):629–637. doi: 10.1016/S0006-3495(00)76321-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Umbach G, Kantak P, Jacobs J, Kahana M, Pfeiffer BE, Sperling M, Lega B. Time cells in the human hippocampus and entorhinal cortex support episodic memory. Proc Natl Acad Sci USA. 2020;117(45):28463–28474. doi: 10.1073/pnas.2013250117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Cauter T, Camon J, Alvernhe A, Elduayen C, Sargolini F, Save E. Distinct roles of medial and lateral entorhinal cortex in spatial cognition. Cereb Cortex. 2013;23(2):451–459. doi: 10.1093/cercor/bhs033. [DOI] [PubMed] [Google Scholar]
- Vázquez-Rodríguez B, Avena-Koenigsberger A, Sporns O, Griffa A, Hagmann P, Larralde H. Stochastic resonance at criticality in an network model of the human cortex. Sci Rep. 2017;7(13020):1–12. doi: 10.1038/s41598-017-13400-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verechtchaguina T, Schimansky-Geier L, Sokolov IM. Spectra and waiting-time densities in firing resonant and nonresonant neurons. Phys Rev E. 2004;70(031916):1–8. doi: 10.1103/PhysRevE.70.031916. [DOI] [PubMed] [Google Scholar]
- Verechtchaguina T, Sokolov IM, Schimansky-Geier L. Interspike interval densities of resonate and fire neurons. Biosystems. 2007;89(1–3):63–68. doi: 10.1016/j.biosystems.2006.03.014. [DOI] [PubMed] [Google Scholar]
- Wilbur WJ, Rinzel J. A theoretical basis for large coefficient of variation and bimodality in neuronal interspike interval distributions. J Theor Biol. 1983;105(2):345–368. doi: 10.1016/s0022-5193(83)80013-7. [DOI] [PubMed] [Google Scholar]
- Yarom Y, Hounsgaard J. Voltage fluctuations in neurons: signal or noise? Physiol Rev. 2011;91(3):917–929. doi: 10.1152/physrev.00019.2010. [DOI] [PubMed] [Google Scholar]
- Zhao J, Qin Y, Yanqiu Che, Ran H, Li J. Effects of network topologies on stochastic resonance in feedforward neural network. Cogn Neurodyn. 2020;14:399–409. doi: 10.1007/s11571-020-09576-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The authors confirm that the data supporting the findings of this study are available within the article.


