Abstract
Aviation emissions originated from the fuel burn have been hot topics by engineers and policy-makers due to their harmful effects on the environment and thereby human health as well as sustainability. In this study, it is tried that several emission indexes (EIs) involving CO, HC and NOx as well as fuel flow of several commercial aircraft engines (CAEs) are predicted using support vector regression (SVR) and long short-term memory (LSTM) approaches for take-off phase. Moreover, exergo-environmental parameters involving exergy efficiency (ExEFF), wasted exergy ratio (WExR) and environmental effect factor (EEF) pertinent to CAEs are computed employing thermodynamics laws. While establishing the models, rated thrust, by-pass ratio, overall pressure ratio and combustion type of the CAEs are utilized as the model inputs. According to the findings of emission modelling, the coefficient of determination (R2) of EI NOx and EI CO of the CAEs is found as 0.929074 and 0.960277 with SVR, whereas their R2 values are elevated to 0.954878 and 0.989283 with LSTM approach, respectively. However, R2 of EI HC is determined lower with 0.632280 (by SVR) and 0.651749 (by LSTM). On the other hand, exergo-environmental parameters for the CAEs are estimated with high correctness at both models. Namely, R2 of ExEFF and EEF regarding the CAEs are computed as 0.991748 and 0.989067 by SVR; however, these are calculated as 0.994785 and 0.992797 by LSTM method. To model these parameters with low error by using significant design variables as model inputs could help in predicting emission and environmental metrics for new engine designs.
Keywords: Emission modelling, Aircraft emission, Exergy modelling, Support vector regression, Long short-term memory
Introduction
An average growth of air traffic at annual rate has been observed as 5% in recent years (Stettler et al. 2018). When projected to next years, the air traffic system could not meet this significant rise in the aviation sector. Namely, the development of air transportation has led to enlarge civil aviation, thereby spreading market economic worldwide. Even though the novel coronavirus pneumonia undermines this condition, it is predicted that this expansion will be maintained in the next years (Zhu et al. 2021). The reason of growth in the aviation could be attributed that this sector reflects the level of welfare and economic development for the related country. Compared with other transport modes, air transportation has made the travelling more comfortable, safet and reliable (Ekici et al. 2022). For instance, in Europe air traffic has attained to important level for 2 decades by means of no-frills airlines which enable hauling service at cheaper costs (Filippone and Parkes 2021). Moreover, the development of economy leads to quicken air transportation in terms of the rising number of air traffic. The Federal Aviation Administration (FAA) stated that the number of passengers preferring airline transportation will increase with 2.5% at an average annual rate by 2036 (Yang et al. 2018). On the other hand, these intense aircraft activities have led to damage both environment and thereby human health, especially at vicinity of airport since aircraft engines consume a considerable amount of fuel throughout landing and take-off (LTO) phases. Moreover, two stages involving the climb-cruise-descent (CCD) and LTO phases are the main source of aviation emissions. Carbon dioxide, water vapour and several emissions including NOx, CO and HC are emitted to environment due to burning kerosene fuels injected to the combustor of aircraft engine. Also, these emissions commonly lead to global warming, thereby climate change (Xu et al. 2020). Therefore, mitigation of environmental impact depends whether fuel consumption could be decreased at any of these phases. No matter which phases, these emissions have affected environment and human health. Interestingly, the cause of 10,000 premature mortalities per year is attributed to these emissions (Zhu et al. 2021). Since aviation undertakes a significant role for transportation, as expected this sector has caused an increase in the emission intensity of the environment in recent years. Also, effect degree of aviation emission changes location by location (Song and Shon 2012). Furthermore, the concern of air pollution demonstrates different tendency according to the developing and the developed countries. At latter the emissions are prone to decrease, whereas at the former, air pollution has continued to become significant concern owing to the rapid energy demand showing parallelism with population growth (Masiol and Harrison 2014). Moreover, technological development and invention have made energy demand higher worldwide in the last century (Sohret et al. 2015).
In this regard, the scientific communities have focused on poor air quality due to both effects on human health and harmful emissions threatening to environment. For this aim, several methods have been proposed. To mitigate carbon dioxide emissions originated from aircraft, the aviation sector has determined several targets involving carbon neutral growth and annual 1.5% improvement of fuel efficiency up to 2050 (Timmis et al. 2015). Despite the increasing demand for the aviation sector, alleviation of aircraft engine emissions may be possible with the integration of economic, operational and technological measures. Improvement of airframe and engine technology could be ranked as the mitigation strategies that are considered by many engineers. There are several factors such as the age of aircraft fleet and the retirement rate of older aircraft so as to take effect of these technological improvements over time (Dray 2013). However, as it does for other fields, technological advances for low aircraft emission has several challenges such as certification, industry acceptance and the late returning of investment (Filippone and Parkes 2021).
In terms of thermodynamics, to alleviate fuel consumption, thereby environmental damage requires removing irreversibility from the system as much as possible (Dinc et al. 2020). In this context, energy, emission, exergy and economy issues are related with each other employing thermodynamics laws to thermal systems. Thermodynamic, economic and environmental parameters could constitute multi-objective functions of design process of energy-consuming systems (Baklacioglu et al. 2015). Especially, the second law of thermodynamic provides knowing irreversibility occurred in the system. Based on first and second laws, exergy analysis could be performed, quantifying several metrics such as exergy destruction and exergy efficiency that shows how much close to theoretical working boundary. It is thought that exergetic metrics are proper to assess performance of aircraft engine since these tools help in demonstrating environmental sustainability of the engine. Moreover, the causes leading to fuel inefficiency could be understood with exergetic parameters. Therefore, when considering the literature, there are many of studies on thermodynamic and environmental based analyses for aircraft engines (Dinc et al. 2022; Ekici and Sohret 2021; Koruyucu et al. 2021). There are two ways that deal with the environmental effect from aircraft engine. Firstly, the emissions from the landing and take-off phases (LTO cycle) regarding aircraft operations have been addressed. Secondly, the pollutants from climb-cruise-descent phases have been examined focusing their impacts on stratospheric ozone and UV radiation. Therefore, the studies which draw attention to effects of anthropogenic emissions originated from aircraft engine have been the hot topics in this field.
Literature review about emission and exergetic parameters for aircraft engines
When considering the open literature about modelling the exhaust emissions, Yang et al. (2022) tried to predict several parameters such as CO, NOx, HC emissions and the indicated thermal efficiency of gasoline engine employing the artificial neural network (ANN) model including speed, intake pressure and spark timing inputs. According to the authors, all coefficients of determination (R2) were determined larger than 0.97. Moreover, Boomadevi et al. (2021) tried to mitigate CO2 emissions by adding biofuel to jet fuel at different percentages. The authors state that jet fuel with lower biofuel favourably affects performance and emission characteristics compared with the higher mixing rate of biofuel. Moreover, Manigandan et al. (2020) studied effects of various additives to Jet A on emission and performance of the gas turbine engine. R20E (Jet A 70% fuel, 20% rapeseed and 10% ethanol) showed 24% increase in thermal efficiency as well as lower emission due to the influence of ethanol concentration and higher oxygen content. On the other hand, Baklacioglu et al. (2016) dealt with the estimation of energy and exergy efficiencies of turboprop engine used in cargo aircraft by comparing ANN and its improved version with genetic algorithm. The authors state that exergy efficiency of the engine is predicted with R2 of 0.999967 by ANN and R2 of 0.999993 by ANN-GA. Moreover, Aygun and Turan (2022) examined modelling of exergy efficiency of turbofan engine at different flight conditions by comparing least square method and its improved version with genetic algorithm. According to the authors, the latter model provides more accuracy of exergetic parameters with R2 of 0.9999 compared the former model where R2 is 0.9974. Furthermore, Kaba et al. (2022) proposed least square estimation based on genetic algorithm (LSEGA) so as to predict exergy efficiency along with several parameters peculiar to variable cycle turbofan engine. The authors expressed that LSEGA enables the model accuracy to increase up to 0.99995 at third degree function, whereas its R2 is found as 0.9976. Additionally, Kayaalp et al. (2021) scrutinized prediction of exhaust emissions and combustion efficiency for turboprop engine based on LSTM method by using several model inputs involving fuel flow, engine speed and air to fuel ratio (AFR). According to the authors, R2 of these parameters is found more than 0.95 for all output metrics.
When examined the literature in detail, any studies on estimation of emission indexes and exergo-environmental parameters for high by-pass turbofan using support vector regression (SVR) and long short-term memory (LSTM) have not seen to the best of the authors’ knowledge. Therefore, the present study provides the first attempt to calculate and compare emission and exergo-environmental models using SVR and LSTM approaches at take-off phase. Since design variables of turbofan engines are decisive parameters, the modelling of these metrics with different methods make this study original. Main aims and novelties of this research can be highlighted as follows:
To present emission indexes of 171 different turbofan engines at take-off phase
To compute exergetic parameters of 171 different turbofan engines at take-off phase
To model emission indexes and exergetic metrics based on four different engine parameters involving by-pass ratio, overall pressure ratio, combustion type and thrust
To compare the model findings of these parameters obtained by SVR and LSTM approaches
System description
Gas turbine engines have several categories so as to serve different civil and military goals. Of these are turbofan engines, whose name was first mentioned by Rolls-Royce (El-Sayed 2008). The most reliable engine feature has given to turbofan engines ever developed (El-Sayed 2008). Their fundamental features are also that being fuel-efficient and quiet turbine engines. Just as it does the other gas turbine engines, the working mechanism of turbofan engines is that fan and compressors with several stages suck the air and pressurize it so as to enhance cycle efficiency. Most of the air passes from fan case that is a nozzle-shaped chamber. The remaining air is directed to the core section in order to burn with fuel in the combustor. The burnt gases are impinged to turbine blades where turbine power is obtained for turning fan and compressors. Finally, the gases leave from the engine with relatively high velocity and temperature. In this study, one-hundred seventy-one engines were dealt with for analyses. These engines consist of ten different CFM56-5B, thirty-four different LEAP, twenty-four different GE90, fifty-two different GEnx and fifty-one different PW engines. These turbofan engines (not mixed turbofan) are examined for modelling their emission and exergetic parameters based on the International Civil Aviation Organization (ICAO) emission databank. These engines have different by-pass ratio, overall pressure ratio, rated thrust and combustor type excepting their model configuration. Figure 1 presents a typical high by-pass turbofan engine and its main components.
Fig. 1.
Illustration of a typical unmixed high by-pass turbofan engine with its key components
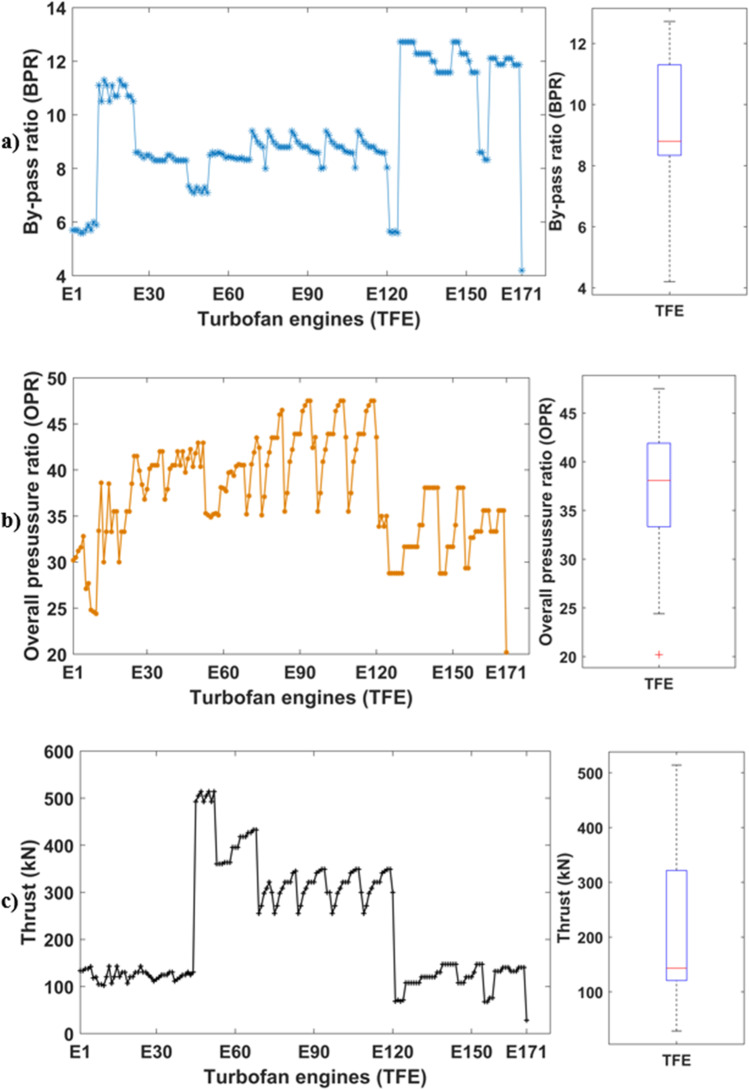
On the other hand, Fig. 2a presents by-pass ratio (BPR) of commercial aircraft engines (CAEs). BPR is defined as the ratio between the mass flow rates of the cold air (fan) and hot air (core) (El-Sayed 2008). As can be recognized, minimum and maximum BPRs are observed as 4.2 and 12.7, respectively. However, the median BPR of these engines is found as 8.8. It means that half of the observations are larger and the remaining half is smaller than 8.8 BPR. As for Fig. 2b, it depicts the overall pressure ratio for turbofan engines considered in the present study. As can be seen in the boxplot, only one outlier exists, which is observed as 20.21. Furthermore, the median OPR is measured as 38.06, whereas the lowest and the highest OPR are observed as 20.21 and 47.5, respectively. Thrust values of turbofan engines are demonstrated in Fig. 2c. According to this figure, the median thrust value is observed as 143.1 kN, whereas the minimum and maximum thrust values are gauged as 28.49 kN and 513.9 kN, respectively.
Fig. 2.
By-pass ratio (a), overall pressure ratio (b) and rated thrust values (c) of different commercial aircraft engines (Databank 2021)
Lastly, fuel flows related to the engines are given in Fig. 3 for take-off phase. As can be realized, there is not any outlier. The highest and the lowest fuel flows are recorded as 0.329 kg/s and 4.69 kg/s, respectively, whereas the median value is gauged as 1.075 kg/s. It should be noted that even though E171 has the lowest fuel flow, it does not mean that it has the minimum environmental effect due to depending on its design parameters. Through this study, this consideration is tried to be partly explained.
Fig. 3.
Fuel flow values of different commercial aircraft engines (Databank 2021)
When considering Figs. 2 and 3, fuel flow is very closely related to the rated thrust, whereas by-pass ratio and overall pressure ratio could not be associated with the rated thrust. Namely, the engine with the highest thrust has the highest fuel flow whereas does not have the highest OPR or BPR. On the other hand, especially, by-pass ratio and overall pressure ratio are two design parameters that the engine designers have tried to improve since 1940 year where early gas turbines were invented. Moreover, since these parameters affect both power and emission production, optimization of thrust and specific fuel consumption have been performed by considering these variables (El-Sayed 2008).
Methodology and thermodynamics background
Exergetic method for turbofan engines
Quantity of energy is of high importance for welfare of people due to its usage in many fields, whereas the rising demand gradually has led to decrease sustainability of energy, whose main pillars are conservation of environment and enhancement of social and human rights. Performance and environmental influences of aircraft engines could be determined using thermodynamic approaches, which consolidate the sustainability concept (Balli et al., 2021a). To comprehend the mechanism regarding the conversion of energy forms to each other necessitates the first law of thermodynamics, whereas whose second law determines how much quality energy forms convert to each other. When implementing both laws of thermodynamics known as exergy analysis, possible improvements about the system or components could be detected, enabling the engineers to increase system efficiency in designing process (Dinc et al. 2020). Since exergetic method considers both quantity and quality of energy, the important knowledge such as exergy destruction and improvement potential rate for thermal systems could be obtained (Balli and Caliskan 2021). Prior to performing exergy analysis, heat transfer, work rate and ambient conditions should be clarified. Thanks to these information, irreversibility level and thereby the produced entropy leading inefficiency could be measured. This computation process helps in understanding improvement capacity of system (Akdeniz and Balli 2022). Equations 1–7 show thermodynamic relations of flow passed components of turbofan engine.
The physical exergy of flow that is obtained by performing energy and entropy analyses is determined in Eq. 1 (Bejan et al. 1995):
| 1 |
where denotes physical exergy of flow, whereas and represent enthalpy and entropy of air or gas, respectively. Also, and identify enthalpy and entropy of ambient air, respectively.
When specific heat of flow is kept as constant, physical exergy of flow could be written in Eq. 2 (Bejan et al. 1995):
| 2 |
For the liquid fuel or the kerosene, chemical exergy per unit mass could be determined in Eq. 3 (Bejan et al. 1995; Dinc and Gharbia 2020):
| 3 |
where and represent specific physical exergy of fuel and fuel exergy grade, respectively, whereas is gauged as 1.067893.
Exergy efficiency
Exergy efficiency could be defined with several ways for different systems. It is ratio of output exergy to input exergy. It is well-known that output exergy has lower value than input exergy due to irreversibility in the system. The general form for exergy efficiency can be expressed in Eq. 4 (Aygun et al. 2021):
| 4 |
where denotes exergy efficiency for the whole engine. Also, and are rated thrust and air inlet velocity at take-off for respective engine, whereas is fuel exergy as MW.
Wasted exergy
This parameter quantifies how much wasted exergy occurs from irreversibility and losses in the system. It can be presented in Eq. 5 (Aygun et al. 2021):
| 5 |
where represents the wasted exergy occurred in the whole system, whereas and denote exergy destruction and exergy loss, respectively.
Wasted exergy ratio
This indicator expresses the ratio of the wasted exergy to fuel exergy. It is written Eq. 6 (Balli et al. 2021b):
| 6 |
where is the wasted exergy ratio for the overall engine, whereas is the fuel exergy.
Environmental effect factor
Thanks to this parameter, environmental impact arisen from aircraft engine could be quantified. It is presented in Eq. 7 (Balli et al. 2021b):
| 7 |
where represents environmental effect factor of the engine. It is non-dimensional metric.
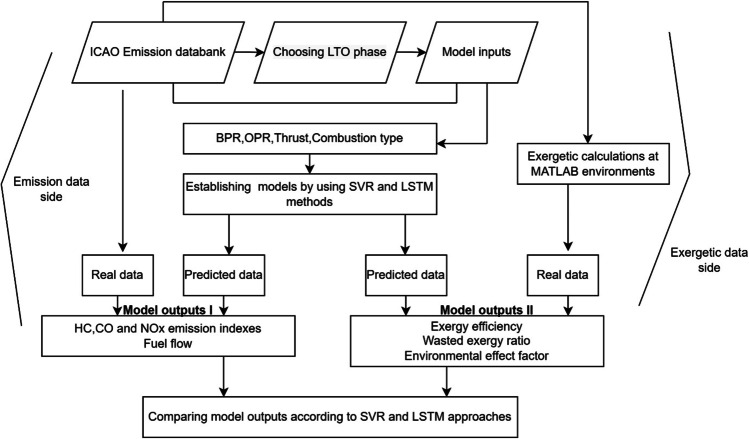
Based on emission indexes obtained from ICAO databank and exergo-environmental metrics computed by MATLAB environment, flowchart is presented in Fig. 4, which shows how procedure is followed while establishing models with SVR and LSTM methods.
Fig. 4.
Flowchart pertinent to modelling emission indexes and exergo-environmental metrics
Dataset and preprocessing
ICAO Emission databank was studied in terms of emission indexes and exergo-environmental metrics. A linear transformation is performed on the original data set with the min–max normalization method. Normalized data is reduced to [0–1] interval. Thus, the model provides better convergence for prediction. The min–max normalization method is shown in Eq. 8 where x' represents the normalized data, x is data itself, xmax is the largest value in the column of the dataset, and xmin is the smallest value in the column of the dataset. In the study, the normalized dataset is divided into two datasets as 80% training and 20% testing. Training and test data are used for prediction in SVR and LSTM models. Mean absolute error (MAE), mean square error (MSE), root mean square error (RMSE) and R2 were used for the performance evaluation of the models.
| 8 |
Support vector regression (SVR)
This method is a classification algorithm developed to find the most suitable hyperplane for separating data with two or more classes. Then, SVR model was developed by Smola and Scholkopf to solve regression tasks (Muthukrishnan 2020). SVR maps data into high-dimensional feature space with a nonlinear mapping method. In this context, it distinguishes itself from other regression-based models and can make successful predictions. Thanks to kernel functions, the data is moved to a high-dimensional feature space where linear separation is possible (Langhammer and Česák 2016).
Suppose the training data is, and y ∈ R. x refers to the input values, and y refers to the output values. The general regression function is defined as in Eq. 9:
| 9 |
Φ indicates the nonlinear mapping of the input to higher-dimensional feature space, and b is bias. The constrained optimization problem is expressed as in Eq. 10. Weight vector w, insensitive loss function ε, penalty factor C to minimize training errors, and and are slack variables (Zhang et al. 2017).
| 10a |
| 10b |
| 10c |
| 10d |
Radial basis function equation is given in Eq. 11.
| 11 |
In this study, radial basis function, polynomial and linear are examined as kernel functions. After introducing the kernel function, the decision function can be expressed as in Eq. 12.
| 12 |
where α is the Lagrange multiplier and xi are the support vectors (Zhang et al. 2017).
Long short-term memory (LSTM)
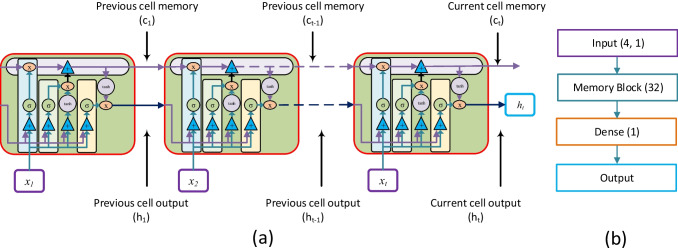
The LSTM model is a type of recurrent neural network (RNN) used for classification/prediction, which has become increasingly popular with the prominence of deep learning. These models have memory that records the information they process. Thanks to this memory, it can benefit from previous knowledge to predict the next output. This is the strength of LSTM in forecasting (Kouchak and Gaffar 2019). The cell structure of the LSTM consists of three gates. These are the forget gate, the input gate, and the output gate. Sigmoid and tangent activation functions are used in the LSTM cell structure. In addition, the current cell state is transferred to the next cell memory ct. The forget gate decides which information is discarded from the cell state. The forget gate consists of previous cell memory ct-1, previous cell output ht-1 and input vectors xt. The formulation of the forget gate is shown in Eq. 13, where σ is the sigmoid activation function, W is the weight vector and bf is the bias in the forget gate. The input gate updates the cell state based on the current input xt and previous cell output ht-1. The input gate is expressed in Eq. 14. bi is the bias at the input gate. The output gate decides the state of the next cell ht, together with the tangent and sigmoid functions, according to the previous cell state. In Eq. 15, the mathematical expression of the output gate is shown. Here bo is the bias at the output gate. Current cell memory ct is shown in Eq. 16 and current cell output ht in Eq. 17 (Song et al. 2020; Yang et al. 2021). The concatenation operation is identified by , and element-wise multiplication is identified by . Figure 5 demonstrates the LSTM model block diagram (Fig. 5a) and the LSTM network model (Fig. 5b).
| 13 |
| 14 |
| 15 |
| 16 |
| 17 |
Fig. 5.
Basic cell structure of LSTM
SVR and LSTM models are developed using the Keras library in Python environment. Manuel search and grid search are mostly used methods for parameter and hyper-parameter optimization. In manual search, the hyper parameter selection is heuristically determined by the expert, while in grid search, all possibilities of hyper-parameters are tried, and these that give the best results are employed. In this study, grid search was used for SVR parameters and LSTM hyper-parameters. Also, the emission outputs (EI HC, EI CO, EI NOx) and fuel flow as well as the exergy outputs (ExEFF, WExR, EEF) separately for four inputs (combustor type, by-pass ratio, overall pressure ratio, rated thrust) in SVR and LSTM models are discussed. When grid search was applied for both models, C = 1, ε = 0.01, gamma = scale and kernel function = rbf were found for the SVR model. For the LSTM model, hyper-parameters were obtained as activation function = ReLU, loss function = MSE, optimizer = Adam, batch size = 4 and learning rate (lr) = 0.001. The LSTM model consists of a single hidden layer dense layer after 32 memory blocks. Each output parameter is calculated separately using four input parameters. Grid search results are shown in Table 1.
Table 1.
Grid search results for SVR parameters and LSTM hyper-parameters
| SVR | C | Cache size | ε | Gamma | Kernel function |
| 1 | 200 | 0.001 | Scale | rbf | |
| LSTM | Activation function | Loss function | Optimizer | Batch size | lr |
| ReLU | MSE | Adam | 4 | 0.001 |
Results and discussion
This section fundamentally could be divided into two sections. First one includes the analyses of HC, CO and NOx emission indexes obtained from the International Civil Aviation Organization (ICAO) databank and exergetic computations encoded at MATLAB environment. As for the second section, it includes modelling of emission and exergetic parameters using SVR and LSTM methods. Although the studies similar to those in first section could be encountered in the literature, comparing of the models of both emission and exergetic metrics for different turbofan engines by using SVR and LSTM is first performed with the present study. This consideration consists of the main motivation of this study. In this framework, Figs. 6 and 7 present emission indexes values for the respective commercial aircraft engines (CAEs), whereas Figs. 8, 9, 10, and 11 indicate the comparative modelling findings for emission and exergo-environmental indexes.
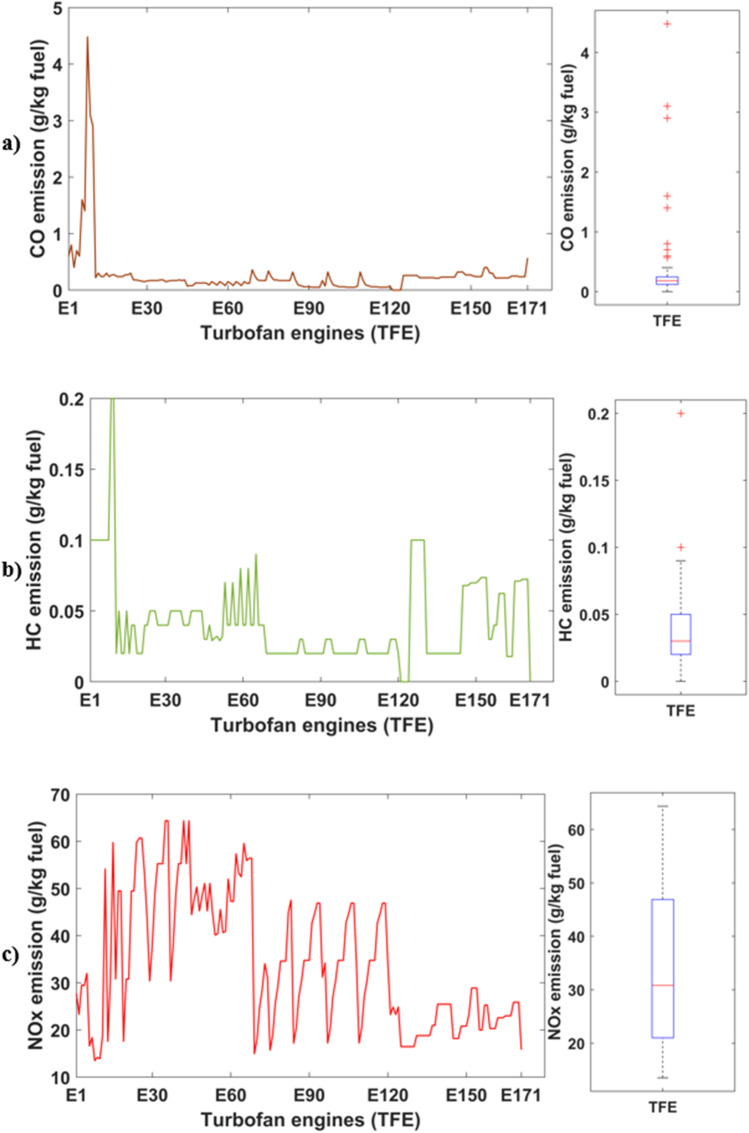
Fig. 6.
HC (a), CO (b) and NOx (c) emission indexes for the CAEs
Fig. 7.
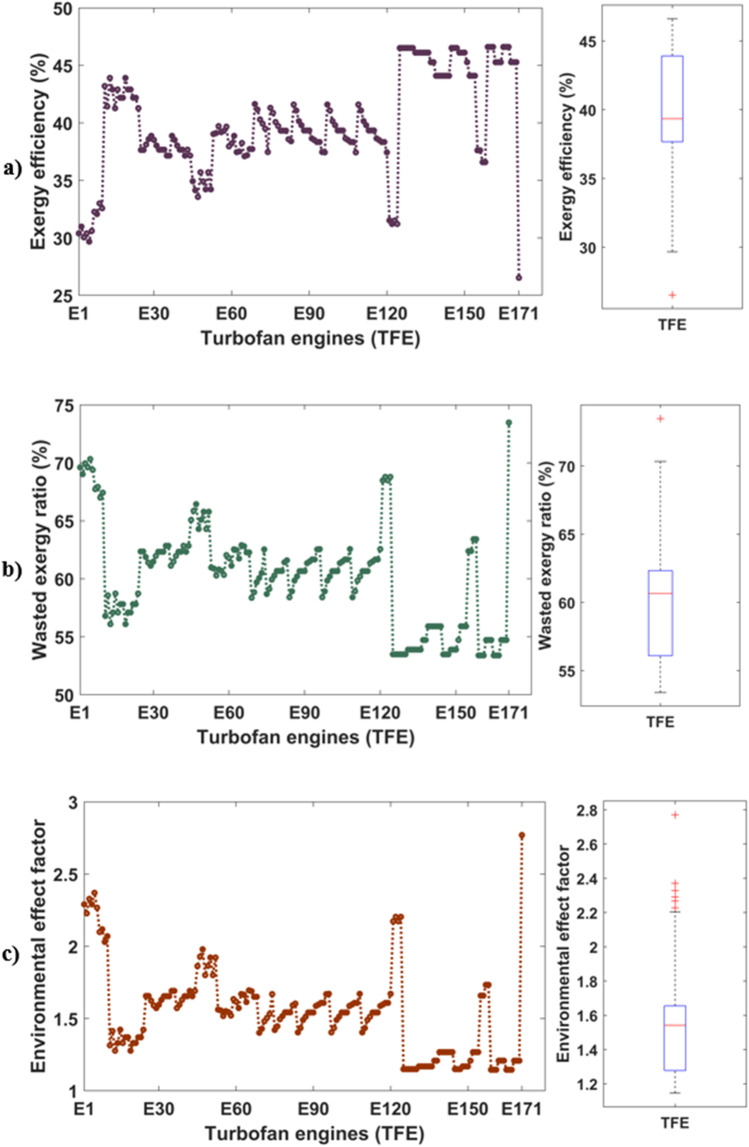
Exergy efficiency (a), wasted exergy ratio (b) and environmental effect factor (c) for the CAEs
Fig. 8.
Comparison of the engine emission indexes prediction results obtained by SVR with actual values
Fig. 9.
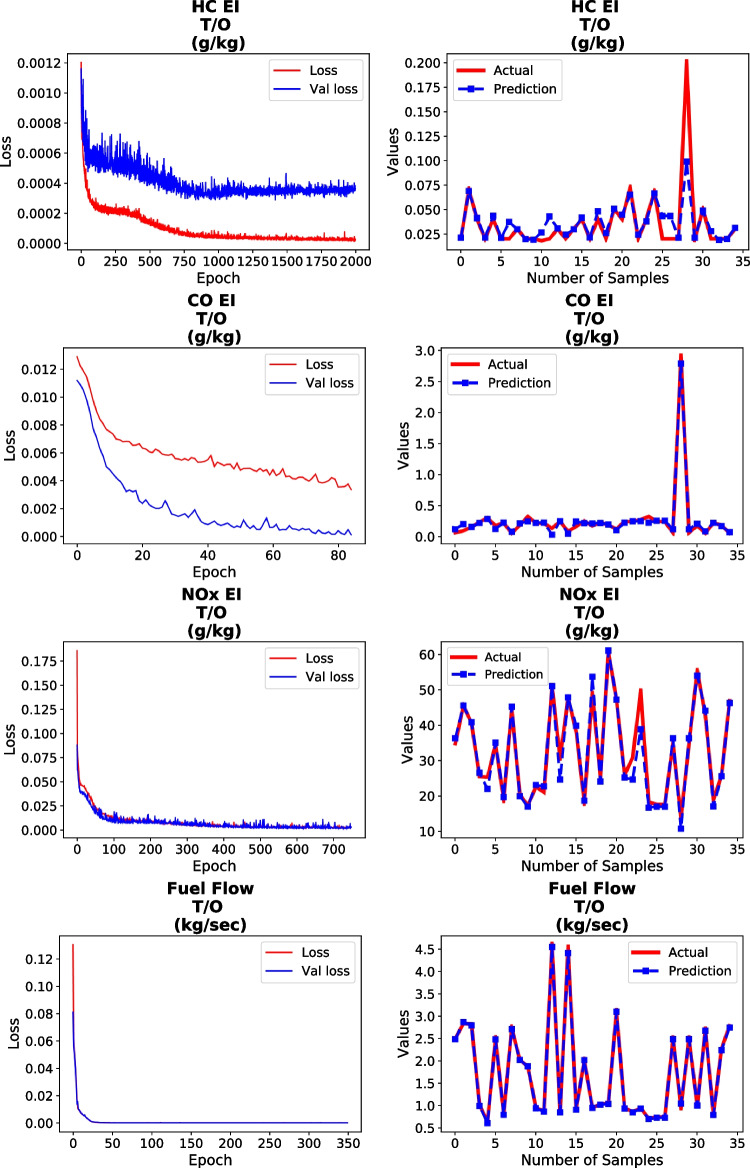
Loss (left) and the engine emission indexes prediction (right) results of the LSTM model
Fig. 10.
Comparison of the exergy prediction results obtained by SVR with actual values
Fig. 11.
Loss (left) and exergy prediction (right) results of the LSTM model
Figure 6a presents variation of HC emission index according to one-hundred seventy-one turbofan engines. The boxplot plotted for this HC emission index (EI) explains minimum, maximum and median HC values as well as their outliers. Namely, the lowest HC belongs to E121-E124 and E171 engines with zero value, while the highest emission is observed at E9 and E10 with 0.2 g/kg fuel. The median value is computed as 0.03 g/kg fuel for all engines. As for Fig. 6b, it shows EI CO values for each turbofan engine considered in this study. Moreover, the boxplot for EI CO of these engines is given at take-off phase. The reason of disparity between emission values could be partially the engine’s design variables and the combustor type. This consideration will be explained in the modelling section with coefficient of determination. In this sense, the median CO emission index of one-hundred seventy-one turbofans is observed as 0.18 g/kg fuel, whereas the minimum and maximum EI of CO are found as 0 and 4.48 g/kg fuel, respectively. Moreover, the number of outliers is computed as ten. These are E1, E2, E4-E10 and E171 engines.
Figure 6c demonstrates EI NOx of turbofan engines given at take-off. As expected, this emission type is observed as the highest at this phase. Several experimental and numeric studies highlight that NOx emission increases as the engine power attains to the highest point, while CO and HC emissions demonstrates adverse behaviour with rising power (Turgut et al., 2015). As can be seen, NOx emissions of turbofan engines differ from each other. The median NOx EI is calculated as 30.8 g/kg fuel, whereas the lowest and the highest values are measured as 13.51 and 64.36 g/kg fuel, respectively. Interestingly, any outlier is not seen for these engines. When considering the engines with the highest EI NOx, even though these engines enjoy relatively high overall pressure ratio, the reason for this could be attributed to the combustion type and relatively low by-pass ratio.
Figure 7a indicates exergy efficiency on engine basis at take-off phase. Exergy efficiency is the measure of thermodynamic performance of the system. The higher exergy efficiency could be obtained with less exergy destruction or less irreversibility. Since the detailed thermodynamic information for each engine is not known, the calculation on the component basis is not able to be performed. Exergy efficiency of turbofan engines is computed by means of data involving fuel flow and thrust. According to this figure, the median exergy efficiency for engines is gauged as 39.34%, while this metric is found as the lowest with 26.52% and determined as the highest with 46.6%. Lastly, the outlier value belongs to E171, being the same with the lowest exergy efficiency. Wasted exergy ratio (WExR) is presented for each turbofan engine in Fig. 7b. It means how much the wasted exergy occurs per unit fuel exergy. Thanks to this metric, turbofan engines with different fuel flow could be compared. The higher WExR means the lower fuel efficiency. As can be observed, the median WExR is detected as 60.65% for all engines whereas its minimum and maximum values are computed as 53.39% and 73.47%, respectively. When examining the lowest WExR for the corresponding engines, their common features are that having relatively higher by-pass ratio. Finally, environmental effect factor (EEF) peculiar to turbofan engines are given in Fig. 7c, this index shows environmental impact for the related engine. Namely, the higher the EEF, the lower the environmental sustainability. Therefore, prediction of this metric could help in achieving environmental goals determined by policy-makers and authorities. It is desired that EEF is close to zero for eco-friendly engine. The median EEF value of the turbofan engines is determined as 1.54, whereas the lowest and the highest EEFs are calculated as 1.14 and 2.72, respectively. As can be seen, a number of the outliers are found as seven.
Evaluation of modelling of emission indexes for the CAEs
SVR and LSTM models were trained using the combustor description, by-pass ratio, overall pressure ratio and rated thrust input values of the engine for take-off phase. An emission output EI HC, EI CO, EI NOx and fuel flow were estimated with SVR and LSTM methods. Combustor description was converted to numeric values. In 20% of 171 data, approximately 35 data were used for testing. In Fig. 8, the emission prediction values of the SVR model are shown graphically. In Fig. 8, actual values are shown with red and predicted values with blue dashed lines. When the EI CO and fuel flow graphs are examined, it is seen that the error rate between the actual and predicted values were less, but this rate was higher for HC EI and NOx EI. On the other hand, LSTM model with 16 memory cells was trained using 80% (136 data) of the dataset. The prediction results performed with the LSTM model are shown graphically in Fig. 9. According to this figure, loss graphs are shown on the left, while prediction results are shown in the right column. Validation loss represents the difference between the actual and the predicted value at the training stage. Loss states the difference between the actual and the predicted value at the test stage. Both values should be converge to zero for a good prediction. The hyper-parameters of the LSTM model are determined by using a grid search algorithm. It should be noted that EI CO, EI HC and EI NOx values were predicted with higher performance in the LSTM model, whereas the estimation of fuel flow is obtained with higher accuracy with SVR method. Similarly, when compared estimation of emission indexes with fuel flow, fuel flow has the higher R2 than those of emission indexes. Additionally, the prediction results of 35 test data obtained from SVR and LSTM models are given in Table 2. The predicted values in Table 2 were obtained by inverse transformation.
Table 2.
Actual and prediction data of engine emission indexes according to SVR and LSTM
| HC EI T/O (g/kg) |
CO EI T/O (g/kg) |
NOX EI T/O (g/kg) |
Fuel Flow T/O (kg/sec) |
|||||
|---|---|---|---|---|---|---|---|---|
| Actual | Prediction | Actual | Prediction | Actual | Prediction | Actual | Prediction | |
| SVR | 0.02 | 0.0210 | 0.06 | 0.0632 | 34.77 | 35.1872 | 2.504 | 2.5082 |
| 0.07 | 0.0709 | 0.09 | 0.0925 | 45.53 | 45.6551 | 2.84 | 2.8117 | |
| 0.04 | 0.0394 | 0.15 | 0.1403 | 40.65 | 39.6458 | 2.832 | 2.8090 | |
| 0.02 | 0.0231 | 0.23 | 0.2263 | 25.46 | 26.6937 | 1.023 | 1.0223 | |
| 0.04 | 0.0330 | 0.3 | 0.3391 | 25.3 | 23.2313 | 0.634 | 0.6578 | |
| 0.02 | 0.0196 | 0.17 | 0.0682 | 34.61 | 34.1023 | 2.505 | 2.5062 | |
| 0.02 | 0.0605 | 0.22 | 0.2260 | 18.82 | 18.5912 | 0.8 | 0.7976 | |
| 0.03 | 0.0288 | 0.05 | 0.0533 | 44.61 | 45.1809 | 2.746 | 2.7488 | |
| 0.02 | 0.0208 | 0.18 | 0.2192 | 20.43 | 20.1096 | 2.023 | 2.0325 | |
| 0.02 | 0.0197 | 0.32 | 0.3151 | 17.22 | 17.2750 | 1.88 | 1.8838 | |
| 0.018 | 0.0305 | 0.217 | 0.2117 | 22.6 | 22.6620 | 0.95 | 0.9505 | |
| 0.02 | 0.0397 | 0.21 | 0.2152 | 20.98 | 21.1822 | 0.88 | 0.8839 | |
| 0.03 | 0.0311 | 0.13 | 0.1257 | 51.07 | 48.8606 | 4.6 | 4.5562 | |
| 0.02 | 0.0213 | 0.24 | 0.2450 | 30.8 | 30.7502 | 0.861 | 0.8571 | |
| 0.03 | 0.0263 | 0.08 | 0.1284 | 47.74 | 47.4060 | 4.53 | 4.3910 | |
| 0.04 | 0.0428 | 0.16 | 0.1559 | 38.19 | 45.6825 | 0.916 | 0.9150 | |
| 0.02 | 0.0200 | 0.25 | 0.2296 | 18.04 | 19.5246 | 2.019 | 2.0313 | |
| 0.04 | 0.0497 | 0.17 | 0.1643 | 48.9 | 55.4343 | 0.96 | 0.9763 | |
| 0.02 | 0.0187 | 0.23 | 0.2456 | 25.46 | 31.9873 | 1.023 | 1.0278 | |
| 0.05 | 0.0524 | 0.18 | 0.2001 | 60.67 | 59.9104 | 1.061 | 1.0566 | |
| 0.04 | 0.0391 | 0.12 | 0.1088 | 47.25 | 47.3078 | 3.115 | 3.1332 | |
| 0.072 | 0.0709 | 0.238 | 0.2385 | 25.9 | 25.6388 | 0.95 | 0.9509 | |
| 0.02 | 0.0213 | 0.24 | 0.2450 | 30.8 | 30.7502 | 0.861 | 0.8571 | |
| 0.04 | 0.0302 | 0.27 | 0.2641 | 49.48 | 36.7847 | 0.946 | 0.9414 | |
| 0.068 | 0.0752 | 0.32 | 0.3154 | 18.2 | 18.2523 | 0.71 | 0.7160 | |
| 0.02 | 0.0287 | 0.24 | 0.2687 | 17.59 | 24.4311 | 0.745 | 0.7404 | |
| 0.02 | 0.0287 | 0.24 | 0.2687 | 17.59 | 24.4311 | 0.745 | 0.7404 | |
| 0.02 | 0.0209 | 0.06 | 0.0632 | 34.77 | 35.1920 | 2.504 | 2.5101 | |
| 0.2 | 0.1005 | 2.9 | 2.3791 | 13.9 | 12.6655 | 0.961 | 0.9861 | |
| 0.02 | 0.0209 | 0.06 | 0.0632 | 34.77 | 35.1920 | 2.504 | 2.5101 | |
| 0.05 | 0.0484 | 0.17 | 0.1634 | 55.26 | 55.2611 | 1.014 | 1.0081 | |
| 0.02 | 0.0266 | 0.05 | 0.0532 | 42.71 | 43.2545 | 2.704 | 2.7106 | |
| 0.02 | 0.0443 | 0.22 | 0.2149 | 18.82 | 19.0153 | 0.8 | 0.7943 | |
| 0.02 | 0.0192 | 0.18 | 0.1192 | 25.74 | 25.9842 | 2.278 | 2.2680 | |
| 0.03 | 0.0309 | 0.05 | 0.0548 | 46.9 | 46.8131 | 2.79 | 2.7828 | |
| LSTM | 0.02 | 0.0211 | 0.06 | 0.1160 | 34.77 | 36.2891 | 2.504 | 2.4857 |
| 0.07 | 0.0685 | 0.09 | 0.1984 | 45.53 | 45.5500 | 2.84 | 2.8754 | |
| 0.04 | 0.0410 | 0.15 | 0.1495 | 40.65 | 40.8070 | 2.832 | 2.7970 | |
| 0.02 | 0.0211 | 0.23 | 0.2185 | 25.46 | 26.5050 | 1.023 | 0.9910 | |
| 0.04 | 0.0433 | 0.3 | 0.2798 | 25.3 | 21.9494 | 0.634 | 0.6108 | |
| 0.02 | 0.0208 | 0.17 | 0.1204 | 34.61 | 35.0258 | 2.505 | 2.4820 | |
| 0.02 | 0.0370 | 0.22 | 0.2227 | 18.82 | 19.6261 | 0.8 | 0.7943 | |
| 0.03 | 0.0296 | 0.05 | 0.0733 | 44.61 | 45.2307 | 2.746 | 2.7171 | |
| 0.02 | 0.0197 | 0.18 | 0.2117 | 20.43 | 19.9023 | 2.023 | 2.0218 | |
| 0.02 | 0.0190 | 0.32 | 0.2427 | 17.22 | 16.9427 | 1.88 | 1.8785 | |
| 0.018 | 0.0265 | 0.217 | 0.2202 | 22.6 | 23.0524 | 0.95 | 0.9409 | |
| 0.02 | 0.0426 | 0.21 | 0.2227 | 20.98 | 22.6765 | 0.88 | 0.8664 | |
| 0.03 | 0.0304 | 0.13 | 0.0271 | 51.07 | 51.1013 | 4.6 | 4.5496 | |
| 0.02 | 0.0241 | 0.24 | 0.2446 | 30.8 | 24.6075 | 0.861 | 0.8479 | |
| 0.03 | 0.0296 | 0.08 | 0.0407 | 47.74 | 47.8316 | 4.53 | 4.4123 | |
| 0.04 | 0.0414 | 0.16 | 0.2390 | 38.19 | 39.8171 | 0.916 | 0.9086 | |
| 0.02 | 0.0213 | 0.25 | 0.2153 | 18.04 | 18.6261 | 2.019 | 2.0186 | |
| 0.04 | 0.0477 | 0.17 | 0.2098 | 48.9 | 53.6669 | 0.96 | 0.9499 | |
| 0.02 | 0.0258 | 0.23 | 0.2176 | 25.46 | 24.0754 | 1.023 | 1.0212 | |
| 0.05 | 0.0504 | 0.18 | 0.1913 | 60.67 | 61.0749 | 1.061 | 1.0412 | |
| 0.04 | 0.0444 | 0.12 | 0.1009 | 47.25 | 47.2464 | 3.115 | 3.1014 | |
| 0.072 | 0.0649 | 0.238 | 0.2226 | 25.9 | 25.1362 | 0.95 | 0.9336 | |
| 0.02 | 0.0241 | 0.24 | 0.2446 | 30.8 | 24.6075 | 0.861 | 0.8479 | |
| 0.04 | 0.0376 | 0.27 | 0.2464 | 49.48 | 38.8237 | 0.946 | 0.9318 | |
| 0.068 | 0.0662 | 0.32 | 0.2227 | 18.2 | 16.6696 | 0.71 | 0.7003 | |
| 0.02 | 0.0431 | 0.24 | 0.2500 | 17.59 | 16.9078 | 0.745 | 0.7300 | |
| 0.02 | 0.0431 | 0.24 | 0.2500 | 17.59 | 16.9078 | 0.745 | 0.7300 | |
| 0.02 | 0.0210 | 0.06 | 0.1160 | 34.77 | 36.2900 | 2.504 | 2.4868 | |
| 0.2 | 0.0987 | 2.9 | 2.7885 | 13.9 | 10.6966 | 0.961 | 1.0483 | |
| 0.02 | 0.0210 | 0.06 | 0.1160 | 34.77 | 36.2900 | 2.504 | 2.4868 | |
| 0.05 | 0.0483 | 0.17 | 0.2054 | 55.26 | 53.9666 | 1.014 | 1.0013 | |
| 0.02 | 0.0278 | 0.05 | 0.0811 | 42.71 | 44.0710 | 2.704 | 2.6773 | |
| 0.02 | 0.0188 | 0.22 | 0.2208 | 18.82 | 16.9837 | 0.8 | 0.7907 | |
| 0.02 | 0.0199 | 0.18 | 0.1645 | 25.74 | 25.5334 | 2.278 | 2.2453 | |
| 0.03 | 0.0310 | 0.05 | 0.0667 | 46.9 | 46.2389 | 2.79 | 2.7494 | |
Table 3 gives error values as well as coefficient of determination obtained by SVR and LSTM. While the R2 value of EI HC was 0.632280 in SVR, it was obtained 0.651749 in LSTM. As seen in Table 3, LSTM predicted the EI CO and EI NOx emission values with a lower error, while SVR predicted the fuel flow with a smaller error. When the prediction results of both models were analysed according to Table 3, it was seen that they made a close prediction to each other.
Table 3.
Prediction outputs of emission indexes of the CAEs according to SVR and LSTM
| Outputs | MSE | RMSE | MAE | R2 | |
|---|---|---|---|---|---|
| SVR | HC EI T/O (g/kg) | 0.000378 | 0.019430 | 0.008109 | 0.632280 |
| CO EI T/O (g/kg) | 0.000419 | 0.020464 | 0.006632 | 0.960277 | |
| NOX EI T/O (g/kg) | 0.004576 | 0.067647 | 0.034913 | 0.929074 | |
| Fuel Flow (kg/sec) | 0.000038 | 0.006149 | 0.002916 | 0.999374 | |
| LSTM | HC EI T/O (g/kg) | 0.000358 | 0.018908 | 0.007490 | 0.651749 |
| CO EI T/O (g/kg) | 0.000113 | 0.010629 | 0.007809 | 0.989283 | |
| NOX EI T/O (g/kg) | 0.002911 | 0.053956 | 0.032637 | 0.954878 | |
| Fuel Flow (kg/sec) | 0.000055 | 0.007392 | 0.005154 | 0.999095 |
Evaluation of modelling of exergo-environmental metrics for the CAEs
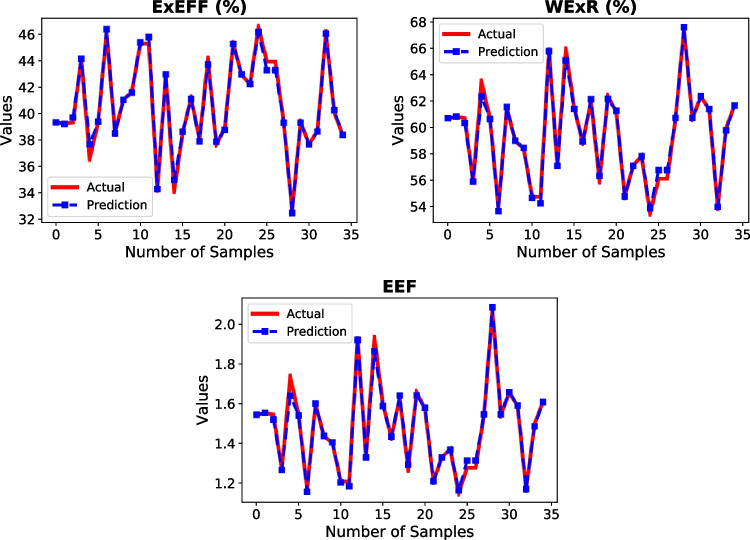
The prediction of ExEFF, WExR and EEF exergy data with SVR is shown in Fig. 10. When the graph of ExEFF is examined, it is seen that the predicted values were very close to the actual values. Predicted values in WExR and EEF graphs were very close to the actual values. Considering the ExEFF, WExR and EEF loss graphs of the LSTM model, it was observed that the loss and validation loss values quickly converge to zero. In addition, when the ExEFF, WExR and EEF estimation graphs of the LSTM model are examined, the prediction values are very close to the actual values (Fig. 11). In Table 4, the real and predicted values of the exergy parameters of the SVR and LSTM models are shown numerically. In the first row of Table 4, the actual value of the ExEFF parameter is 39.34046%. This value was found to be 39.31364% in the estimation made with SVR and 39.18966% with LSTM. The prediction values of both models related to ExEFF, WExR and EEF exergy parameters are given in Table 4 in detail.
Table 4.
Actual and prediction data of exergo-environmental parameters according to SVR and LSTM
| ExEFF (%) | WExR (%) | EEF | ||||
|---|---|---|---|---|---|---|
| Actual | Prediction | Actual | Prediction | Actual | Prediction | |
| SVR | 39.34046 | 39.31364 | 60.65954 | 60.68314 | 1.541912 | 1.54340 |
| 39.19659 | 39.19675 | 60.80341 | 60.80855 | 1.551243 | 1.55291 | |
| 39.30731 | 39.69300 | 60.69269 | 60.31179 | 1.544056 | 1.51918 | |
| 44.09871 | 44.11647 | 55.90129 | 55.87299 | 1.26764 | 1.26538 | |
| 36.58298 | 37.65826 | 63.41702 | 62.32500 | 1.733512 | 1.63925 | |
| 39.32476 | 39.37128 | 60.67524 | 60.62532 | 1.542927 | 1.53946 | |
| 46.11078 | 46.36872 | 53.88922 | 53.62560 | 1.16869 | 1.15592 | |
| 38.50596 | 38.47376 | 61.49404 | 61.53008 | 1.597 | 1.59938 | |
| 41.07822 | 41.03230 | 58.92178 | 58.97227 | 1.43438 | 1.43732 | |
| 41.59592 | 41.57606 | 58.40408 | 58.43171 | 1.404082 | 1.40519 | |
| 45.27871 | 45.36666 | 54.72129 | 54.62608 | 1.208544 | 1.20351 | |
| 45.27783 | 45.77578 | 54.72217 | 54.21756 | 1.208586 | 1.18433 | |
| 34.21988 | 34.25594 | 65.78012 | 65.75272 | 1.922278 | 1.92000 | |
| 42.90441 | 42.93949 | 57.09559 | 57.06131 | 1.330763 | 1.32896 | |
| 34.14011 | 34.95255 | 65.85989 | 65.05442 | 1.929106 | 1.86253 | |
| 38.52253 | 38.61008 | 61.47747 | 61.39065 | 1.595884 | 1.58662 | |
| 41.15961 | 41.08606 | 58.84039 | 58.91888 | 1.429566 | 1.43409 | |
| 38.03319 | 37.87611 | 61.96681 | 62.12710 | 1.629282 | 1.63978 | |
| 44.09871 | 43.68635 | 55.90129 | 56.31141 | 1.26764 | 1.29266 | |
| 37.6461 | 37.85645 | 62.3539 | 62.14638 | 1.656318 | 1.64050 | |
| 38.87107 | 38.75269 | 61.12893 | 61.25183 | 1.572607 | 1.57889 | |
| 45.28148 | 45.25356 | 54.71852 | 54.73597 | 1.208408 | 1.20961 | |
| 42.90441 | 42.93949 | 57.09559 | 57.06131 | 1.330763 | 1.32896 | |
| 42.19015 | 42.20808 | 57.80985 | 57.79413 | 1.370222 | 1.36800 | |
| 46.5175 | 46.14513 | 53.4825 | 53.84715 | 1.149728 | 1.16450 | |
| 43.91094 | 43.25070 | 56.08906 | 56.74866 | 1.277337 | 1.31330 | |
| 43.91094 | 43.25070 | 56.08906 | 56.74866 | 1.277337 | 1.31330 | |
| 39.34046 | 39.29369 | 60.65954 | 60.70305 | 1.541912 | 1.54466 | |
| 32.57506 | 32.44289 | 67.42494 | 67.57367 | 2.069833 | 2.08498 | |
| 39.34046 | 39.29369 | 60.65954 | 60.70305 | 1.541912 | 1.54466 | |
| 37.66919 | 37.64505 | 62.33081 | 62.35867 | 1.65469 | 1.65651 | |
| 38.65094 | 38.62274 | 61.34906 | 61.37908 | 1.587259 | 1.58920 | |
| 46.11078 | 46.03706 | 53.88922 | 53.95838 | 1.16869 | 1.17002 | |
| 40.07009 | 40.23962 | 59.92991 | 59.75925 | 1.495627 | 1.48468 | |
| 38.33785 | 38.36152 | 61.66215 | 61.64433 | 1.608388 | 1.60723 | |
| LSTM | 39.34046 | 39.18966 | 60.65954 | 60.73943 | 1.541912 | 1.55072 |
| 39.19659 | 38.85727 | 60.80341 | 61.07539 | 1.551243 | 1.55184 | |
| 39.30731 | 39.39724 | 60.69269 | 60.65652 | 1.544056 | 1.54151 | |
| 44.09871 | 44.33096 | 55.90129 | 55.95789 | 1.26764 | 1.28154 | |
| 36.58298 | 37.08613 | 63.41702 | 62.98744 | 1.733512 | 1.69056 | |
| 39.32476 | 39.26386 | 60.67524 | 60.67359 | 1.542927 | 1.54445 | |
| 46.11078 | 46.19270 | 53.88922 | 53.69988 | 1.16869 | 1.16263 | |
| 38.50596 | 38.34681 | 61.49404 | 61.48435 | 1.597 | 1.60685 | |
| 41.07822 | 40.94778 | 58.92178 | 59.00543 | 1.43438 | 1.44750 | |
| 41.59592 | 41.6035 | 58.40408 | 58.36387 | 1.404082 | 1.41125 | |
| 45.27871 | 45.23164 | 54.72129 | 54.72406 | 1.208544 | 1.21899 | |
| 45.27783 | 45.65621 | 54.72217 | 54.25777 | 1.208586 | 1.19365 | |
| 34.21988 | 34.00457 | 65.78012 | 65.81808 | 1.922278 | 1.93870 | |
| 42.90441 | 43.24201 | 57.09559 | 56.93317 | 1.330763 | 1.32677 | |
| 34.14011 | 34.66393 | 65.85989 | 65.24701 | 1.929106 | 1.87767 | |
| 38.52253 | 38.36441 | 61.47747 | 61.55020 | 1.595884 | 1.60677 | |
| 41.15961 | 41.01297 | 58.84039 | 58.9443 | 1.429566 | 1.44275 | |
| 38.03319 | 37.79464 | 61.96681 | 62.14258 | 1.629282 | 1.65404 | |
| 44.09871 | 43.90109 | 55.90129 | 56.29051 | 1.26764 | 1.30132 | |
| 37.6461 | 37.97694 | 62.3539 | 62.17177 | 1.656318 | 1.63455 | |
| 38.87107 | 38.43752 | 61.12893 | 61.53153 | 1.572607 | 1.59880 | |
| 45.28148 | 45.35051 | 54.71852 | 54.77947 | 1.208408 | 1.21482 | |
| 42.90441 | 43.24201 | 57.09559 | 56.93317 | 1.330763 | 1.32677 | |
| 42.19015 | 42.35013 | 57.80985 | 57.87802 | 1.370222 | 1.37847 | |
| 46.5175 | 46.891 | 53.4825 | 53.53595 | 1.149728 | 1.15968 | |
| 43.91094 | 43.58782 | 56.08906 | 56.64277 | 1.277337 | 1.31481 | |
| 43.91094 | 43.58782 | 56.08906 | 56.64277 | 1.277337 | 1.31481 | |
| 39.34046 | 39.17654 | 60.65954 | 60.74859 | 1.541912 | 1.55143 | |
| 32.57506 | 32.29752 | 67.42494 | 67.62656 | 2.069833 | 2.06400 | |
| 39.34046 | 39.17654 | 60.65954 | 60.74859 | 1.541912 | 1.55143 | |
| 37.66919 | 37.65133 | 62.33081 | 62.35136 | 1.65469 | 1.66745 | |
| 38.65094 | 38.50682 | 61.34906 | 61.47175 | 1.587259 | 1.59622 | |
| 46.11078 | 45.78215 | 53.88922 | 53.88789 | 1.16869 | 1.17795 | |
| 40.07009 | 40.10662 | 59.92991 | 59.80444 | 1.495627 | 1.49375 | |
| 38.33785 | 38.20965 | 61.66215 | 61.4999 | 1.608388 | 1.61503 | |
The results of the analysis of the exergy parameters are given in Table 5. While the MSE value of the ExEFF parameter was 0.000257 with SVR, this value was found as 0.000163 with the LSTM model. The R2 value of the ExEFF parameter was found as 0.991748 with SVR and 0.994785 with LSTM. The best prediction is achieved when MSE is converged to zero and R2 one. A better prediction was performed with LSTM than SVR for the ExEFF parameter. Considering the other exergy parameters, the LSTM model made a good prediction compared to the SVR.
Table 5.
Prediction outputs of exergo-environmental metrics of the CAEs according to SVR and LSTM
| Outputs | MSE | RMSE | MAE | R2 | |
|---|---|---|---|---|---|
| SVR | ExEFF (%) | 0.000257 | 0.016042 | 0.009610 | 0.991748 |
| WExR (%) | 0.000259 | 0.016106 | 0.009664 | 0.991682 | |
| EEF | 0.000207 | 0.014373 | 0.007886 | 0.989067 | |
| LSTM | ExEFF (%) | 0.000163 | 0.012753 | 0.010826 | 0.994785 |
| WExR (%) | 0.000148 | 0.012172 | 0.008635 | 0.995249 | |
| EEF | 0.000136 | 0.011666 | 0.008833 | 0.992797 |
Conclusions
In this study, emission indexes and environmental parameters of several commercial aircraft engines (CAEs) with different rated thrust, by-pass ratio, different overall pressure ratio or combustor type are first dealt with by incorporating two different prediction models. To estimate fuel flow, CO, HC and NOx emission indexes regarding CAEs, two different methods involving support vector regression and long short-term memory are established by considering 171 individual turbofan engines at take-off phase. On the other hand, exergo-environmental parameters involving exergy efficiency, wasted exergy ratio and environmental effect factor of the CAEs are estimated by using SVR and LSTM methods. The originality of this study is that it couples prediction of both emission and exergetic parameters for turbofan engines. In this framework, the modelling parameters of the CAEs could be divided into two sections as emission and exergo-environmental outputs, whereas the model inputs consist of by-pass ratio, overall pressure ratio, thrust and combustion type of one-hundred seventy-one turbofan engines. Several remarks could be highlighted from analyses performed in the present study as follows:
Amongst CO, HC and NOx emission indexes, EI NOx of the CAEs is observed as the highest value at take-off phase. Namely, it changes between 13.51 and 64.36 g/kg fuel throughout the 171 engines, whereas EI HC is observed as the lowest varying between 0 and 0.2 g/kg fuel at take-off phase.
Variation of EI CO, EI NOx and fuel flow of the CAEs can be greatly explained by by-pass ratio, overall pressure ratio, thrust and combustor type, whereas EI HC depends on these model inputs at relatively lower degree at take-off phase.
R2 of HC emission index of the CAEs is computed as 0.632280 thanks to SVR, whereas its R2 is elevated to 0.651749 with LSTM.
The model accuracy of EI NOx and EI CO regarding the CAEs are increased with LSTM model. Namely, R2 of EI CO increases from 0.960277 to 0.989283, whereas that of EI NOx is enhanced from 0.929074 to 0.954878 compared with SVR method. These findings show that NOx and CO emissions of the engine are very closely related to the considered design parameters for take-off phase.
Fuel flow of the CAEs is predicted with relatively low error for both models. For this metric, minimum square error (MSE) is gauged as 0.000038 with SVR and as 0.000055 with LSTM.
Exergo-environmental indexes of the CAEs are generally estimated with high correctness. Namely, R2 of wasted exergy ratio peculiar to the CAEs is determined as 0.991682 with SVR, whereas it is found as 0.995249 with LSTM.
LSTM method increases R2 value of EEF index of the CAEs from 0.989067 (that is found with SVR) to 0.992797 for take-off phase. The higher R2 means the higher correct prediction for environmental impact from aircraft engine.
According to these results, the engine design parameters such as by-pass ratio, overall pressure ratio and combustion type are important factors on quantifying emission indexes and exergo-environmental metrics at take-off phase. Moreover, these metrics are successfully modelled with both the traditional method SVR and the innovative LSTM model. The prediction values of both models were very close to each other. It is also noteworthy that the difference between both SVR and LSTM methods could be distinctive as the dataset is increased. As a next study, genetic algorithm could be implemented to the findings in this study so as to improve model accuracy of parameters. Also, several modelling techniques could be implemented to the other phases of flight such as climb, approach and idle phases in order to estimate emission indexes. Moreover, different techniques of multi-objective optimization could be applied to aircraft engines so as to find out optimum design parameters giving minimum emission and maximum power throughout LTO cycle.
Nomenclature
- ANN
Artificial neural network
- BPR
By-pass ratio
- CAE
Commercial aircraft engine
- E
Engine
- EI
Emission index
- ExD
Exergy destruction (MW)
- ExEFF
Exergy efficiency
- EEF
Environmental effect factor
- Ex
Exergy
- FAR
Fuel-to air ratio
- ICAO
International Civil Aviation Organization
- LHV
Lower heating value (kJ/kg)
- LSTM
Long short-term memory
- LTO
Landing and take-off
- MAE
Mean absolute error
- MSE
Mean square error
Mass flow rate (kg/s)
- OPR
Overall pressure ratio
- R
Specific gas constant (kJ/kg K)
Coefficient of determination
- RMSE
Root mean square error
- SVR
Support vector regression
- TFE
Turbofan engine
- T/O
Take-off
Thrust (kN)
- V
Velocity (m/s)
Power rate (MW)
- WExR
Wasted exergy ratio
Physical exergy
Specific exergy
Author contribution
Omer Osman Dursun: conceptualization, data curation, formal analysis, investigation, methodology, supervision, validation, visualization, writing—review and editing. Suat Toraman: conceptualization, data curation, formal analysis, investigation, methodology, supervision, validation, visualization, writing—review and editing. Hakan Aygun: conceptualization, data curation, formal analysis, investigation, methodology, supervision, validation, visualization, writing—review and editing
Data availability
Data sharing is not applicable to this article.
Declarations
Ethical approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Omer Osman Dursun, Email: oodursun@firat.edu.tr.
Suat Toraman, Email: storaman@firat.edu.tr.
Hakan Aygun, Email: haygun@firat.edu.tr.
References
- Akdeniz HY, Balli O. Impact of different fuel usages on thermodynamic performances of a high bypass turbofan engine used in commercial aircraft. Energy. 2022;238:121745. doi: 10.1016/j.energy.2021.121745. [DOI] [Google Scholar]
- Aygun H, Turan O. Application of genetic algorithm in exergy and sustainability: a case of aero-gas turbine engine at cruise phase. Energy. 2022;238:121644. doi: 10.1016/j.energy.2021.121644. [DOI] [Google Scholar]
- Aygun H, Cilgin ME, Turan O. Exergo-sustainability indicators of a target drone engine at dynamic loads. Energy. 2021;221:119803. doi: 10.1016/j.energy.2021.119803. [DOI] [Google Scholar]
- Baklacioglu T, Turan O, Aydin H. Dynamic modeling of exergy efficiency of turboprop engine components using hybrid genetic algorithm-artificial neural networks. Energy. 2015;86:709–721. doi: 10.1016/j.energy.2015.04.025. [DOI] [Google Scholar]
- Baklacioglu T, Aydin H, Turan O. Energetic and exergetic efficiency modeling of a cargo aircraft by a topology improving neuro-evolution algorithm. Energy. 2016;103:630–645. doi: 10.1016/j.energy.2016.03.018. [DOI] [Google Scholar]
- Balli O, Caliskan H (2021) Turbofan engine performances from aviation, thermodynamic and environmental perspectives. Energy 232:121031
- Balli O, Ekici S, Karakoc TH. TF33 Turbofan engine in every respect: performance, environmental, and sustainability assessment. Environ Prog Sustain Energy. 2021;40:e13578. doi: 10.1002/ep.13578. [DOI] [Google Scholar]
- Balli O, Ozbek E, Ekici S, Midilli A, Karakoc TH. Thermodynamic comparison of TF33 turbofan engine fueled by hydrogen in benchmark with kerosene. Fuel. 2021;306:121686. doi: 10.1016/j.fuel.2021.121686. [DOI] [Google Scholar]
- Bejan A, Tsatsaronis G, Moran MJ. Thermal design and optimization. New York: Wiley; 1995. [Google Scholar]
- Boomadevi P, Paulson V, Samlal S, Varatharajan M, Sekar M, Alsehli M, Elfasakhany A, Tola S. Impact of microalgae biofuel on microgas turbine aviation engine: a combustion and emission study. Fuel. 2021;302:121155. doi: 10.1016/j.fuel.2021.121155. [DOI] [Google Scholar]
- Databank (2021) Available at: https://www.easa.europa.eu/en/domains/environment/icao-aircraft-engine-emissions-databank. Access 15 Apr 2022
- Dinc A, Gharbia Y. Exergy analysis of a turboprop engine at different flight altitude and speeds using novel consideration. Int J Turbo Jet-Engines. 2020 doi: 10.1515/tjeng-2020-0017. [DOI] [Google Scholar]
- Dinc A, Sohret Y, Ekici S. Exergy analysis of a three-spool turboprop engine during the flight of a cargo aircraft. Aircr Eng Aerosp Technol. 2020;92(10):1495–1503. doi: 10.1108/AEAT-05-2020-0087. [DOI] [Google Scholar]
- Dinc A, Caliskan H, Ekici S, Sohret Y. Thermodynamic-based environmental and enviroeconomic assessments of a turboprop engine used for freight aircrafts under different flight phases. J Therm Anal Calorim. 2022;147:12693–12707. doi: 10.1007/s10973-022-11486-2. [DOI] [Google Scholar]
- Dray L. An analysis of the impact of aircraft lifecycles on aviation emissions mitigation policies. J Air Transp Manag. 2013;28:62–69. doi: 10.1016/j.jairtraman.2012.12.012. [DOI] [Google Scholar]
- Ekici S, Sohret Y. A study on the environmental and economic aspects of aircraft emissions at the Antalya International Airport. Environ Sci Pollut Res. 2021;28:10847–10859. doi: 10.1007/s11356-020-11306-w. [DOI] [PubMed] [Google Scholar]
- Ekici F, Orhan G, Gumus O, Bahce AB. A policy on the externality problem and solution suggestions in air transportation: the environment and sustainability. Energy. 2022;258:124827. doi: 10.1016/j.energy.2022.124827. [DOI] [Google Scholar]
- El-Sayed A F (2008) Aircraft propulsion and gas turbine engines. CRC Press, Boca Raton
- Filippone A, Parkes B. Evaluation of commuter airplane emissions: a European case study. Transp Res Part D: Transp Environ. 2021;98:102979. doi: 10.1016/j.trd.2021.102979. [DOI] [Google Scholar]
- Kaba A, Aygun H, Turan O. Multi-dimensional energetic performance modeling of an aircraft engine with the aid of enhanced least–squares estimation based genetic algorithm method. J Therm Anal Calorim. 2022;147:5913–5935. doi: 10.1007/s10973-021-10922-z. [DOI] [Google Scholar]
- Kayaalp K, Metlek S, Ekici S, Sohret Y. Developing a model for prediction of the combustion performance and emissions of a turboprop engine using the long short-term memory method. Fuel. 2021;302:121202. doi: 10.1016/j.fuel.2021.121202. [DOI] [Google Scholar]
- Koruyucu E, Ekici S, Karakoc TH. Performing thermodynamic analysis by simulating the general characteristics of the two-spool turbojet engine suitable for drone and UAV propulsion. J Therm Anal Calorim. 2021;145:1303–1315. doi: 10.1007/s10973-020-10449-9. [DOI] [Google Scholar]
- Kouchak S M, Gaffar A, (2019) Using bidirectional long short term memory with attention layer to estimate driver behavior, 2019 18th IEEE International Conference On Machine Learning And Applications (ICMLA). IEEE, pp. 315–320
- Langhammer J, Česák J. Applicability of a nu-support vector regression model for the completion of missing data in hydrological time series. Water. 2016;8:560. doi: 10.3390/w8120560. [DOI] [Google Scholar]
- Manigandan S, Atabani A, Ponnusamy VK, Gunasekar P. Impact of additives in Jet-A fuel blends on combustion, emission and exergetic analysis using a micro-gas turbine engine. Fuel. 2020;276:118104. doi: 10.1016/j.fuel.2020.118104. [DOI] [Google Scholar]
- Masiol M, Harrison RM. Aircraft engine exhaust emissions and other airport-related contributions to ambient air pollution: a review. Atmos Environ. 2014;95:409–455. doi: 10.1016/j.atmosenv.2014.05.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muthukrishnan RMJS (2020) Predictive modeling using support vector regression. International Journal of Scientific & Technology Research. Available at: https://www.ijstr.org/final-print/feb2020/Predictive-Modeling-Using-Support-Vector-Regression.pdf. Access 5 Feb 2022
- Song S-K, Shon Z-H. Emissions of greenhouse gases and air pollutants from commercial aircraft at international airports in Korea. Atmos Environ. 2012;61:148–158. doi: 10.1016/j.atmosenv.2012.07.035. [DOI] [Google Scholar]
- Song X, Liu Y, Xue L, Wang J, Zhang J, Wang J, Jiang L, Cheng Z. Time-series well performance prediction based on long short-term memory (LSTM) neural network model. J Petrol Sci Eng. 2020;186:106682. doi: 10.1016/j.petrol.2019.106682. [DOI] [Google Scholar]
- Stettler M, Koudis G, Hu S, Majumdar A, Ochieng W. The impact of single engine taxiing on aircraft fuel consumption and pollutant emissions. Aeronaut J. 2018;122:1967–1984. doi: 10.1017/aer.2018.117. [DOI] [Google Scholar]
- Sohret Y, Dinc A, Karakoc TH. Exergy analysis of a turbofan engine for an unmanned aerial vehicle during a surveillance mission. Energy. 2015;93:716–729. doi: 10.1016/j.energy.2015.09.081. [DOI] [Google Scholar]
- Timmis AJ, Hodzic A, Koh L, Bonner M, Soutis C, Schäfer AW, Dray L. Environmental impact assessment of aviation emission reduction through the implementation of composite materials. Int J Life Cycle Assess. 2015;20:233–243. doi: 10.1007/s11367-014-0824-0. [DOI] [Google Scholar]
- Turgut ET, Cavcar M, Yay OD, Ucarsu M, Yilmaz E, Usanmaz O, Armutlu K, Dogeroglu T, Miake-Lye RC. Analysis of test-cell emission measurements of newly overhauled turbofan engines. J Propul Power. 2015;31:559–572. doi: 10.2514/1.B35328. [DOI] [Google Scholar]
- Xu H, Fu Q, Yu Y, Liu Q, Pan J, Cheng J, Wang Z, Liu L. Quantifying aircraft emissions of Shanghai Pudong International Airport with aircraft ground operational data. Environ Pollut. 2020;261:114115. doi: 10.1016/j.envpol.2020.114115. [DOI] [PubMed] [Google Scholar]
- Yang X, Cheng S, Lang J, Xu R, Lv Z. Characterization of aircraft emissions and air quality impacts of an international airport. J Environ Sci. 2018;72:198–207. doi: 10.1016/j.jes.2018.01.007. [DOI] [PubMed] [Google Scholar]
- Yang X, Xue Q, Yang X, Yin H, Qu Y, Li X, Wu J. A novel prediction model for the inbound passenger flow of urban rail transit. Inf Sci. 2021;566:347–363. doi: 10.1016/j.ins.2021.02.036. [DOI] [Google Scholar]
- Yang R, Yan Y, Sun X, Wang Q, Zhang Y, Fu J, Liu Z. An artificial neural network model to predict efficiency and emissions of a gasoline engine. Processes. 2022;10:204. doi: 10.3390/pr10020204. [DOI] [Google Scholar]
- Zhang S, Wang M, Zheng P, Qiao G, Liu F, Gan L. An easy-to-implement hysteresis model identification method based on support vector regression. IEEE Trans Magn. 2017;53:1–4. [Google Scholar]
- Zhu C, Hu R, Liu B, Zhang J. Uncertainty and its driving factors of airport aircraft pollutant emissions assessment. Transp Res Part D: Transp Environ. 2021;94:102791. doi: 10.1016/j.trd.2021.102791. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data sharing is not applicable to this article.