An extended approach for the generalized powered uniform distribution

Abstract

A new uniform distribution model, generalized powered uniform distribution (GPUD), which is based on incorporating the parameter k into the probability density function (pdf) associated with the power of random variable values and includes a powered mean operator, is introduced in this paper. From this new model, the shape properties of the pdf as well as the higher-order moments, the moment generating function, the model that simulates the GPUD and other important statistics can be derived. This approach allows the generalization of the distribution presented by Jayakumar and Sankaran (2016) through the new ${\mathit{GPUD}}_{(J-S)}$ distribution. Two sets of real data related to COVID-19 and bladder cancer were tested to demonstrate the proposed model’s potential. The maximum likelihood method was used to calculate the parameter estimators by applying the maxLik package in R. The results showed that this new model is more flexible and useful than other comparable models.

Introduction

In recent years, several researchers have proposed different generalizations of new distribution functions of continuous random variables to more broadly model various behaviors related to survival analysis, such as the useful life of a computer. This also allows the study of hazard functions to determine the reliability of devices subject to use and deterioration. Additionally, these extended distributions provide greater flexibility in modeling various real-life problems (Nassar et al. 2018; Sankaran and Jayakumar 2016; Torabi et al. 2018).

This research follows the approach presented in the seminal article of Marshall and Olkin (1997) and other authors, for example, Alshangiti et al. (2014); Jayakumar and Sankaran (2016); and Jose and Krishna (2011), who continued this research and reported different approaches and a new model family under the Marshall–Olkin extended uniform distribution.

The uniform distribution U(0, 1) is closely related to other distributions since it is of fundamental importance to generate random numbers in simulation processes through the inverse transform method, which in turn allows the numerical evaluation of the behavior of statistical models (Law et al. 2000).

Previously reported results, such as those by Rondero-Guerrero et al. (2020), motivated us to consider that statistical distributions are frequently applied to models of real-world phenomena in different areas, such as medical sciences, finance, engineering, and economics, where the analysis of risk and survival functions is included due to their relevance in modeling data from various systems. Therefore, we decided to extend this work and apply it to real-world data to develop a new model that better fits the analyzed data and can be used in many areas, for example, public health policy design.

Our approach is based on the generalization of a new family of functions of the uniform distribution, where an average that we refer to as the powered mean is incorporated. This generalization includes the parameter k, which appears in the power of the values taken by the continuous random variable (Rondero-Guerrero et al. 2020). Furthermore, this proposal generalizes the work of Jayakumar and Sankaran (2016).

This article is structured as follows. In Sect. 2, the general conditions of the new generalized powered uniform distribution (GPUD) family are defined and discussed. In Sect. 3, some interesting properties, such as the hazard function, survival function, moment generating function, moments, and statistics such as quantile, median, asymmetry, and kurtosis, are presented. In Sect. 4, the GPUD approach is used to generalize the work of Jayakumar and Sankaran (2016), allowing us to generate another family of distributions. This family contains the parameter k as the power of the values of the random variable, which provides greater flexibility to this and other models. In Sect. 4, expressions for estimating the parameters of the generalization and a simulation study to determine the performance of maximum likelihood estimators for specific sample sizes are presented. In Sect. 5, the generalization presented by Jayakumar and Sankaran (2016) is applied to two sets of real data, which allows us to adjust the proposed model and empirically demonstrate that the GPUD is more appropriate than other models, such as the Weibull, Weibull exponentiated (Pal et al. 2006), new Marshall–Olkin Weibull (Cui et al. 2020) and Marshall–Olkin exponentiated generalized (García et al. 2020) models. Finally, the conclusions are presented in Sect. 6.

A new family of uniform distribution functions

Based on our research (see Rondero-Guerrero et al. (2020)), a new family of distribution functions, the generalized powered uniform distribution, with a continuous random variable X, was introduced. The respective probability density function is defined as

$$f_{X^k}(x)=\left\{\begin{array}{ccc}\frac{x^k}{(b-a)M_k(a,b)},\hfill & a\le x\le b;& k=0,1,...,n.\\ 0,\hfill & x<a;& x>b\end{array}\right)$$ 1

The term $M_k(a,b)$ is defined as an operator that is herein referred to as the powered mean and is expressed as

$$\begin{array}{c}\hfill M_k(a,b)=\frac{{\sum }_{j=0}^k{a}^{k-j}{b}^k}{k+1}.\end{array}$$ 2

For the case where $k=0$ and $M_0(a,b)=1$, we recover the uniform distribution on (0,1). It is easy to show that Equation (1) is a well-defined pdf, where the mean is $\mu =\frac{a+b}{2}$.

The distribution function (df) corresponding to Eq. (1) is given as

$$\begin{array}{c}\hfill F_{X^k}(x)=P(X<x)=\left\{\begin{array}{ccc}0,& x<a\hfill & \hfill \\ \frac{x^{k+1}-a^{k+1}}{b^{k+1}-a^{k+1}},& a\le x\le b;\hfill & k=0,1,\cdots ,n.\hfill \\ 1,& x\ge b\hfill & \hfill \end{array}\right)\end{array}$$ 3

It should be noted that Eqs. (1) and (3) represent any member of a new family of probability density and distribution functions for different values of the k parameter. These results show that there are many polynomial functions satisfying the pdf and df conditions, that is, $F_{X^k}^{\prime }(x)=f_{X^k}(x)$.

When $a=0$, and $b=1$, the GPUD takes the form

$$\begin{array}{c}\hfill F_{X^k}(x)=x^{k+1},\text{for}k=0,1,2,\cdots ,n.\end{array}$$ 4

It is important to note that the above expression will be used in Sect. 3 when the survival function is defined as

$$\begin{array}{c}\hfill {\overline{F}}_{X^k}(x)=1-F_{X^k}(x)=1-x^{k+1}.\end{array}$$ 5

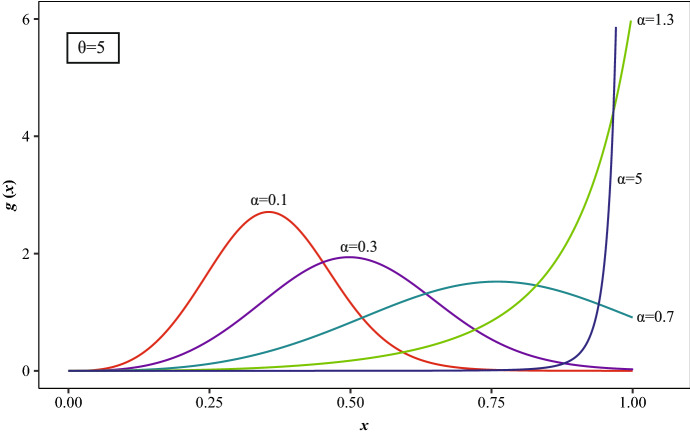
The graphs of $f_{X^k}(x)$ and $F_{X^k}(x)$ are shown in Figs. 1 and 2, respectively, for different values of k. The results in Fig. 1 show that the pdf skews to the right as the value of the parameter k increases. Graphical properties are of great importance because they allow researchers and professional users of statistical methods to determine whether any of these distributions fit the dataset of a specific application.

Fig. 1.

$f_{X^k}\left(x\right)$ for $a=0$, $b=1$, and $k=0,1,2,3,4,5$

Fig. 2.

$F_{X^k}(x)$ for $a=0$, $b=1$, and $k=0,1,2,3,4,5$

General properties of the GPUD

In this section, the general properties of the GPUD are examined to show the flexibility of this new family of distributions that will allow the development of a generalization of the model proposed by Jayakumar and Sankaran (2016), which is studied in Sect. 4.

Hazard function and survival function

From Eqs. (1) and (3) the hazard function and survival function respectively, can be obtained as shown below

$$\begin{array}{c}\hfill h_{X^k(x)}=\frac{f_{X^k}(x)}{{\overline{F}}_{X^k}(x)}=\frac{(k+1)x^k}{1-x^{k+1}},\text{for}a=0,b=1,\text{and}k=0,1,...,n.\end{array}$$ 6

In what follows, we will use the more common notation for the survival function $S_{X^k}(x)={\overline{F}}_{X^k}(x)$, where

$$\begin{array}{c}\hfill S_{X^k}(x)=1-F_{X^k}(x)=1-x^{k+1}\end{array}$$ 7

for $a=0$, $b=1$, and $k=0,1,2,...,n$.

Survival analysis is a topic of great importance for researchers in many disciplines. Both the hazard and survival functions are defined for a nonnegative continuous or discrete random variable X, which is related to data from a lifetime and allows the formulation of statistical models in areas such as medicine, engineering, and biology. For instance, in biomedical research, survival analysis is applied to a random variable related to the time that elapses from the onset of a disease until the patient either recovers or dies.

When working with the hazard function, researchers are interested in the properties of the graphs, as they are useful in identifying whether the distribution can model increasing or decreasing failure rates. Figures 3 and 4 show the shapes of $h_{X^k}(x)$ and $S_{X^k}(x)$, respectively, for different k values.

Fig. 3.

$h_{X^k}(x)$ for $a=0$, $b=1$, and $k=0,1,2,3,4,5$

Fig. 4.

$S_{X^k}(x)$ for $a=0$, $b=1$, and $k=0,1,2,3,4,5$

Moment generating function

A function of great importance in the calculation of higher-order moments is the moment generating function. It is possible to see that a compact expression of it in terms of the powered mean can be obtained.

Theorem 1

The moment generating function of the pdf is given as

$$\begin{array}{c}\hfill {\varphi }_{x^k}(t)=\sum _{l=0}^{\infty }\frac{t^l}{l!}·\frac{M_{k+l}}{M_k}.\end{array}$$ 8

Proof

The moment generating function ${\varphi }_x(t)$ is defined as

$$\begin{array}{c}\hfill {\varphi }_{x^k}(t)=E[e^{\mathit{tx}}]={\int }_{-\infty }^{\infty }{e}^{\mathit{tx}}{f}_{X^k}(x)dx=\frac{1}{(b-a)M_k(a,b)}{\int }_a^b{e}^{\mathit{tx}}{x}^{k}dx,\end{array}$$ 9

By expanding $e^{\mathit{tx}}$ in a Taylor series, one has

$$\begin{array}{c}\hfill {\varphi }_{x^k}(t)=E[e^{\mathit{tx}}]=\frac{1}{(b-a)M_k(a,b)}{\int }_a^b[1+\frac{\mathit{tx}}{1!}+\frac{{(tx)}^2}{2!}+\frac{{(tx)}^3}{3!}+...]x^{k}dx,\end{array}$$ 10

and

$$\begin{array}{c}\hfill {\varphi }_{x^k}(t)=1+\frac{t}{1!}·\frac{M_{k+1}(a,b)}{M_k(a,b)}+\frac{{(t)}^2}{2!}·\frac{M_{k+2}(a,b)}{M_k(a,b)}+\frac{{(t)}^3}{3!}·\frac{M_{k+3}(a,b)}{M_k(a,b)}+\cdots ,\end{array}$$ 11

or in terms of the series, one has

$$\begin{array}{c}\hfill {\varphi }_{x^k}(t)=\sum _{l=0}^{\infty }\frac{t^l}{l!}\frac{M_{k+l}}{M_k}.\end{array}$$ 12

From the above expression, it is possible to obtain all the moments ${\mu }_x^r$.

Moments

Next, the calculation of the higher-order moments for the GPUD are shown, allowing the determination of the mean and variance, among others.

Theorem 2

The $r^{\mathit{th}}$ moment of the pdf is given as

$$\begin{array}{c}\hfill {\mu }_x^r=E_k[x^r]=\frac{M_{k+r}(a,b)}{M_k(a,b)}.\end{array}$$ 13

Proof

The $r^{\mathit{th}}$ moment can be written as

$$\begin{array}{c}\hfill {\mu }_x^r=E_k[x^r]={\int }_{-\infty }^{\infty }{x}^r{f}_{X^k}(x)dx={\int }_a^b{x}^r\left[\frac{x^k}{(b-a)M_k(a,b)}\right]dx,\end{array}$$ 14

from which, one can obtain

$$\begin{array}{c}\hfill {\mu }_x^r=\frac{1}{(b-a)M_k(a,b)}{\int }_a^b{x}^{k+r}dx=\frac{b^{k+r+1}-a^{k+r+1}}{(b-a)M_k(a,b)(k+r+1)},\end{array}$$ 15

Therefore,

$$\begin{array}{c}\hfill {\mu }_x^r=E_k[x^r]=\frac{M_{k+r}(a,b)}{M_k(a,b)}.\end{array}$$ 16

It is worth noting the advantage of the last equation in calculating higher-order moments. For the case where $a=0$ and $b=1$, it is expressed as

$$\begin{array}{c}\hfill {\mu }_x^r(0,1)=\frac{M_{k+r}(0,1)}{M_k(0,1)}=\frac{k+1}{k+r+1}.\end{array}$$ 17

For the U(0, 1) distribution, $k=0$. Thus, for the first moment $r=1$, the mean is $\mu (0,1)=1/2$. From the previous result, we can calculate the corresponding variance

$$\begin{array}{c}\hfill {\sigma }_k^2={\mu }_k^2-{\left[{\mu }_k^1\right]}^2\end{array}$$ 18

for $k=0,1,2,...,n$. This result can be rewritten as

$$\begin{array}{c}\hfill {\sigma }_k^2=\frac{M_{k+2}}{M_k}-{\left[\frac{M_{k+1}}{M_k}\right]}^2.\end{array}$$ 19

We emphasize that the higher-order moments with respect to the mean such that $E_k[{(x-{\mu }_k^1)}^r]$ necessarily involve expressions that are given in terms of the powered mean operator, which shows its relevance and, in addition, an increase in calculations.

For the skewness and kurtosis coefficients, the calculation gives

$$\begin{array}{cc}\hfill {\gamma }_{3_k}& =E\left[{\left(\frac{x-\mu }{\sigma }\right)}^3\right]=\frac{1}{{\sigma }^3}\left[E,(x^3),-,3,\mu ,E,(x^2),+,2,{\mu }^3\right],\hfill \end{array}$$ 20

$$\begin{array}{cc}\hfill {\gamma }_{4_k}& =E\left[{\left(\frac{x-\mu }{\sigma }\right)}^4\right]=\frac{1}{{\sigma }^4}\left[E,(x^4),-,4,\mu ,E,(x^3),+,6,{\mu }^2,E,(x^2),-,3,{\mu }^4\right].\hfill \end{array}$$ 21

To demonstrate the flexibility of the GPUD properties, Table 1 shows the corresponding calculations for ${\mu }_k$, ${\sigma }_k^2$, ${\gamma }_{3_k}$, and ${\gamma }_{4_k}$ for $a=0$, $b=1$, and different values of k. The data in the table indicate that the GPUD has a negative bias for values of $k\ge 1$. Furthermore, the GPUD is a member of the leptokurtic family.

Table 1.

Mean, variance and the coefficients of skewness and kurtosis for the GPUD

(a, b, k)	Mean	Variance	Skewness	Kurtosis
(0, 1, 0)	0.5	0.083	0	−1.2
(0, 1, 1)	0.666	0.055	−0.565	−0.6
(0, 1, 2)	0.75	0.037	−0.860	0.095
(0, 1, 3)	0.8	0.026	−1.049	0.696
(0, 1, 4)	0.833	0.019	−1.183	1.2
(0, 1, 5)	0.857	0.015	−1.283	1.62

Simulation, quantiles and median

Using Eq. (3), the random variable X of GPUD(a, b, k) can be simulated as

$$\begin{array}{c}\hfill x={(a^{k+1}+(b^{k+1}-a^{k+1})u)}^{1/(k+1)},\end{array}$$ 22

where u is the standard uniform distribution. In addition, the $q^{\mathit{th}}$ quantile of GPUD (a, b, k) is given as

$$\begin{array}{c}\hfill x={(a^{k+1}+(b^{k+1}-a^{k+1})q)}^{1/(k+1)}.\end{array}$$ 23

Table 2 shows the median of the GPUD distribution for different values of the parameter k.

Table 2.

Medians of the GPUD distribution

a	b	k	Median
0	1	0	0.5
0	1	1	0.707
0	1	2	0.793
0	1	3	0.840
0	1	4	0.870
0	1	5	0.890

Generalization of Jayakumar and Sankaran’s (2016) distribution using the GPUD approach

After showing the characteristics of the GPUD family, we will see below how this new approach provides greater versatility in modeling specific statistical applications and data analysis, which has allowed us to generalize the results obtained by Jayakumar and Sankaran (2016). These authors introduced what they referred to as the generalized uniform distribution (GUD), where the parameters $(\alpha ,\theta )$ are considered. The survival function reported by the same authors is based on the truncated negative binomial distribution, which allows the Marshall and Olkin (1997) model to be generalized as shown below:

$$\begin{array}{c}\hfill \overline{G}(x;\alpha ,\theta )=\frac{{\alpha }^{\theta }}{1-{\alpha }^{\theta }}[{[F(x)+\alpha \overline{F}(x)]}^{-\theta }-1],\text{for}\theta >0,\alpha >0,\text{and}x\in R.\end{array}$$ 24

The theta parameter allows us to give a greater amplitude and flexibility to the Marshall and Olkin (1997) model, whose survival function is given as

$$\begin{array}{c}\hfill \overline{G}(x;\alpha )=\frac{\alpha \overline{F}(x)}{1-(1-\alpha )\overline{F}(x)},\alpha >0,\text{and}x\in R.\end{array}$$ 25

Note that if $\theta =1$, Eq. (24) is reduced to the model in (25).

Jayakumar and Sankaran (2016) considered the df as $F(x)=x$ and the survival function as $\overline{F}(x)=1-x$, which come from the uniform distribution, and substituting them into Eq. (24) results in

$$\begin{array}{c}\hfill \overline{G}(x;\alpha ,\theta )=\frac{{\alpha }^{\theta }}{1-{\alpha }^{\theta }}{[[x(1-\alpha )+\alpha )]}^{-\theta }-1],\theta >0,0<\alpha <1,\end{array}$$ 26

The corresponding df is

$$\begin{array}{c}\hfill G(x;\alpha ,\theta )=\frac{1-{\alpha }^{\theta }{\left[x,(,1,-,\alpha ,),+,\alpha \right]}^{-\theta }}{1-{\alpha }^{\theta }},\end{array}$$ 27

and the pdf is given as

$$\begin{array}{c}\hfill g(x;\alpha ,\theta )=\frac{(1-\alpha )\theta {\alpha }^{\theta }}{(1-{\alpha }^{\theta }){\left[x,(,1,-,\alpha ,),+,\alpha \right]}^{\theta +1}}.\end{array}$$ 28

GPUD approach

Using the GPUD approach, we now introduce $F_{X^k}(x)=x^{k+1}$ and $S_{X^k}(x)=$ ${\overline{F}}_{X^k}(x)=1-F_{X^k}(x)=1-x^{k+1}$, for $k=0,1,2,...,n$; here, $0<x<1$, and we obtain a new family of distributions with three parameters $(\alpha ,\theta ,k)$, which will be defined as ${\mathit{GPUD}}_{(J-S)}$. The way we develop our generalization is shown below where the survival function is expressed as

$$\begin{array}{c}\hfill {\overline{G}}_{(J-S)}(x;\alpha ,\theta ,k)=\frac{{\alpha }^{\theta }}{1-{\alpha }^{\theta }}\left[{\left[x^{k+1},(1-\alpha ),+,\alpha \right]}^{-\theta },-,1\right]\end{array}$$ 29

for $\theta >0$, $0<\alpha <1$, and $k=0,1,2,3,...,n$.

Therefore, the df of this new ${\mathit{GPUD}}_{(J-S)}$ family is given as

$$\begin{array}{c}\hfill G_{(J-S)}(x;\alpha ,\theta ,k)=\frac{1-{\alpha }^{\theta }{\left[x^{k+1},(1-\alpha ),+,\alpha \right]}^{-\theta }}{1-{\alpha }^{\theta }}.\end{array}$$ 30

The corresponding pdf is given as

$$\begin{array}{c}\hfill g_{(J-S)}(x;\alpha ,\theta ,k)=\frac{{\alpha }^{\theta }}{1-{\alpha }^{\theta }}·\frac{\theta (k+1)(1-\alpha )x^k}{{\left[(1-\alpha ),x^{k+1},+,\alpha \right]}^{\theta +1}}.\end{array}$$ 31

Note: If $k=0$, $\theta >1$ and $\theta \ne 1$, the GUD is obtained as given by Jayakumar and Sankaran (2016). In Figs. 5 and 6, $k=3$, $\theta =5$ and several values of $\alpha$ are considered.

Fig. 5.

$g_{(J-S)}(x)$ for $k=3$, $\theta =5$, and $\alpha =0.1,0.3,0.7,1.3,5$

Fig. 6.

$G_{(J-S)}(x)$ for $k=3$, $\theta =5$, and $\alpha =0.1,0.3,0.7,1.3,5$

Hazard and survival functions of $GPU{D}_{(J-S)}$

The generalization presented herein is relevant because it allows the creation of a wide range of different hazard functions that can be applied to various analyses of survival or reliability studies in diverse areas, such as medicine, engineering, and economics. Generally, we work with a one-dimensional and continuous random variable defined in $[0,\infty )$, which measures the time between events, unless otherwise indicated.

The hazard function given by Jayakumar and Sankaran (2016) is

$$\begin{array}{c}\hfill h(x;\alpha ,\theta )=\frac{g(x;\alpha ,\theta )}{\overline{G}(x;\alpha ,\theta )}=\frac{\theta (1-\alpha )}{[x(1-\alpha )+\alpha ][1-{\left[x,(,1,-,\alpha ,),+,\alpha \right]}^{\theta }]}.\end{array}$$ 32

In our case, using $GPU{D}_{(J-S)}$, where $\overline{F}(x)=1-x^{k+1}$, we obtain a new family of hazard functions given in terms of the parameter k

$$\begin{array}{c}\hfill h_{(J-S)}(x;\alpha ,\theta ,k)=\frac{\theta (1-\alpha )(k+1)x^k}{[\alpha +(1-\alpha )x^{k+1}][1-{\left[\alpha ,+,(1-\alpha ),x^{k+1}\right]}^{\theta }]}.\end{array}$$ 33

In Fig. 7, the behavior of the hazard function $h_{(J-S)}(x;\alpha ,\theta ,k)$ referring to $GPU{D}_{(J-S)}$ for different values of $(\alpha ,\theta ,k)$ is shown. It is important to note that if we substitute the value of $k=1$ in Eq. (33), we obtain the same results reported by the cited authors.

Fig. 7.

$h_{(J-S)}(x)$ for $k=2$, $\theta =7$, and $\alpha =0.1,0.4,0.9,1.6,2.5$

The behavior of the survival function $S_{(J-S)}(x;\alpha ,\theta ,k)$, which refers to $GPU{D}_{(J-S)}$ for different values of $(\alpha ,\theta ,k)$, is shown in Fig. 8.

$$S_{(J-S)}\left(x;\alpha ,\theta ,k\right)=1-\left[\frac{1-{\alpha }^{\theta }{\left[x^{k+1}(1-\alpha )+\alpha \right]}^{-\theta }}{1-{\alpha }^{\theta }}\right].$$ 34

Fig. 8.

$S_{(J-S)}(x)$ for $k=2$, $\theta =7$, and $\alpha =0.1,0.4,0.9,1.6,2.5$

Our model notably provides greater versatility due to the presence of the parameter k, which is an exponent in the random variable’s values, as shown in Figs. 7 and 8.

Parameter estimation of ${\mathit{GPUD}}_{(J-S)}$

There are many methods for estimating unknown parameters from data. In our case, we will consider the maximum likelihood estimation (MLE) (Okasha and Kayid 2016; Torabi et al. 2018). For a sample of the random variable $(x_1,x_2,...,x_n)$, starting from Eq. (31), an additional parameter k is introduced to obtain the generalizations proposed in this article. The log-likelihood function is given as

$$\begin{array}{c}\hfill L(x;\alpha ,\theta ,k)=\prod _{i=1}^n{g}_{(J-S)}(x_i,\alpha ,\theta ,k),\end{array}$$ 35

which from our proposal is expressed as

$$\begin{array}{c}\hfill L(x;\alpha ,\theta ,k)={\left[\frac{{\alpha }^{\theta }\theta (k+1)(1-\alpha )}{1-{\alpha }^{\theta }}\right]}^n·\prod _{i=1}^n{x}_i^k{\left[(1-\alpha ),x_i^{k+1},+,\alpha \right]}^{-(\theta +1)}.\end{array}$$ 36

Note the relevance of the parameter k in the previous expression which comes from the generalization of the work by Jayakumar and Sankaran (2016), where only the parameters $\alpha$ and $\theta$ appear.

The corresponding maximum likelihood function is given as

$$\begin{array}{cc}\hfill lnL(x;\alpha ,\theta ,k)& =n·ln\left[\frac{{\alpha }^{\theta }\theta (k+1)(1-\alpha )}{1-{\alpha }^{\theta }}\right]\hfill \\ \hfill & -(\theta +1)\sum _{i=1}^{n}ln\left[\left(1-\alpha \right)x_i^{k+1}+\alpha \right]+k\sum _{i=1}^{n}ln\left(x_i\right).\hfill \\ \hfill \end{array}$$ 37

To obtain the covariance matrix $I^{-1}(\beta )$ and the corresponding estimators, the partial derivatives of the log-likelihood function are calculated and are given as

$$\begin{array}{cc}\hfill \frac{\partial lnL}{\partial \alpha }=& -\frac{n}{1-\alpha }+\frac{n\theta }{\alpha }+\frac{n{\alpha }^{\theta -1}\theta }{1-{\alpha }^{\theta }}-\left(\theta ,+,1\right)\sum _{i=1}^n\frac{\left(1,-,x_i^{k+1}\right)}{x_i^{k+1}\left(1,-,\alpha \right)+\alpha }\hfill \end{array}$$ 38

$$\begin{array}{cc}\hfill \frac{\partial lnL}{\partial \theta }=& \frac{n}{\theta }+n·ln(\alpha )+\frac{{\alpha }^{\theta }n·ln(\alpha )}{1-{\alpha }^{\theta }}-\sum _{i=1}^{n}ln\left[x_i^{k+1},\left(1,-,\alpha \right),+,\alpha \right]\hfill \end{array}$$ 39

$$\begin{array}{cc}\hfill \frac{\partial lnL}{\partial k}=& \frac{n}{k+1}-\left(\theta ,+,1\right)\sum _{i=1}^n\frac{\left(1,-,\alpha \right)x_i^{k+1}ln\left(x_i\right)}{x_i^{k+1}\left(1,-,\alpha \right)+\alpha }+\sum _{i=1}^{n}ln\left(x_i\right).\hfill \end{array}$$ 40

The maximum likelihood estimators can be obtained numerically by solving the equations, $\frac{\partial lnL}{\partial \alpha }=0$, $\frac{\partial lnL}{\partial \theta }=0$, and $\frac{\partial lnL}{\partial k}=0$.

On the other hand, the second derivatives of the log-likelihood function of $GPU{D}_{(J-S)}$ with respect to $\alpha$, $\theta$, and k are given as

$$\begin{array}{cc}\hfill \frac{{\partial }^{2}lnL}{\partial {\alpha }^2}& =-\frac{n}{{\left(1-\alpha \right)}^2}-\frac{n\theta }{{\alpha }^2}+n\frac{{\alpha }^{\theta }{\theta }^2-{\alpha }^{\theta }\theta +{\alpha }^{2\theta }\theta }{{\alpha }^2{\left(1-{\alpha }^{\theta }\right)}^2}\hfill \\ \hfill & -\left(\theta +1\right)\sum _{i=1}^n-\frac{{\left(1-x_i^{k+1}\right)}^2}{{\left[x_i^{k+1}\left(1-\alpha \right)+\alpha \right]}^2},\hfill \\ \hfill \end{array}$$ 41

$$\begin{array}{cc}& \frac{{\partial }^{2}lnL}{\partial {\theta }^2}=n\left[-,{\theta }^{-2},+,\frac{{\alpha }^{\theta }{\left(ln,\left(\alpha \right)\right)}^2}{1-{\alpha }^{\theta }},+,\frac{{\left({\alpha }^{\theta }\right)}^2{\left(ln,\left(\alpha \right)\right)}^2}{{\left(1,-,{\alpha }^{\theta }\right)}^2}\right],\hfill \end{array}$$ 42

$$\begin{array}{cc}\hfill \frac{{\partial }^{2}lnL}{\partial k^2}& =-n{(k+1)}^{-2}-\left(\theta +1\right)\sum _{i=1}^n\frac{x_i^{k+1}{\left(ln\left(x_i\right)\right)}^2\left(1-\alpha \right)}{x_i^{k+1}\left(1-\alpha \right)+\alpha }\hfill \\ \hfill & +\left(\theta +1\right)\sum _{i=1}^n\frac{{\left(x_i^{k+1}\right)}^2{\left(ln\left(x_i\right)\right)}^2{\left(1-\alpha \right)}^2}{{\left(x_i^{k+1}\left(1-\alpha \right)+\alpha \right)}^2},\hfill \\ \hfill \end{array}$$ 43

$$\begin{array}{cc}& \frac{{\partial }^{2}lnL}{\partial \theta \partial k}=-\sum _{i=1}^n\frac{x_i^{k+1}ln\left(x_i\right)\left(1,-,\alpha \right)}{x_i^{k+1}\left(1,-,\alpha \right)+\alpha },\hfill \end{array}$$ 44

$$\begin{array}{cc}\hfill \frac{{\partial }^{2}lnL}{\partial \alpha \partial k}& =\left(\theta +1\right)\sum _{i=1}^n\frac{x_i^{k+1}ln\left(x_i\right)}{x_i^{k+1}\left(1-\alpha \right)+\alpha }\hfill \\ \hfill & +\left(\theta +1\right)\sum _{i=1}^n\frac{\left(1-x_i^{k+1}\right)x_i^{k+1}ln\left(x_i\right)\left(1-\alpha \right)}{{\left(x_i^{k+1}\left(1-\alpha \right)+\alpha \right)}^2},\hfill \\ \hfill \end{array}$$ 45

$$\begin{array}{cc}\hfill \frac{{\partial }^{2}lnL}{\partial \alpha \partial \theta }& =n\left[{\alpha }^{-1}+\frac{{\alpha }^{\theta }\theta ln\left(\alpha \right)}{\alpha \left(1-{\alpha }^{\theta }\right)}+\frac{{\alpha }^{\theta }}{\alpha \left(1-{\alpha }^{\theta }\right)}+\frac{{\left({\alpha }^{\theta }\right)}^{2}ln\left(\alpha \right)\theta }{{\left(1-{\alpha }^{\theta }\right)}^2\alpha }\right]\hfill \\ \hfill & -\sum _{i=1}^n\frac{-x_i^{k+1}+1}{x_i^{k+1}\left(1-\alpha \right)+\alpha }.\hfill \\ \hfill \end{array}$$ 46

The matrix of the maximum likelihood estimators of $\beta =(\alpha ,\theta ,k)$ for $\widehat{\beta }=(\widehat{\alpha },\widehat{\theta },\widehat{k})$ is given as

$$\begin{array}{c}\hfill I(\beta )=-E\left[\begin{array}{ccc}\frac{{\partial }^{2}lnL}{\partial {\alpha }^2}& \frac{{\partial }^{2}lnL}{\partial \alpha \partial \theta }& \frac{{\partial }^{2}lnL}{\partial \alpha \partial k}\\ \\ \frac{{\partial }^{2}lnL}{\partial \alpha \partial \theta }& \frac{{\partial }^{2}lnL}{\partial {\theta }^2}& \frac{{\partial }^{2}lnL}{\partial \theta \partial k}\\ \\ \frac{{\partial }^{2}lnL}{\partial \alpha \partial k}& \frac{{\partial }^{2}lnL}{\partial \theta \partial k}& \frac{{\partial }^{2}lnL}{\partial k^2}\end{array}\right].\end{array}$$ 47

Therefore, the covariance matrix will be $I^{-1}(\beta )$. The approximate confidence intervals q to the $(1-\delta )100\%$ for the parameters $\alpha$, $\theta$, and k will be $\widehat{\alpha }\pm Z_{\delta /2}\sqrt{V(\widehat{\alpha })}$ , $\widehat{\theta }\pm Z_{\delta /2}\sqrt{V(\widehat{\theta })}$ and $\widehat{k}\pm Z_{\delta /2}\sqrt{V(\widehat{k})}$, respectively, where $V(\widehat{\alpha })$, $V(\widehat{\theta }),$ and $V(\widehat{k})$ are the variances of $\widehat{\alpha }$, $\widehat{\theta }$, and $\widehat{k}$, respectively, which are represented by elements of the principal diagonal of the matrix $I^{-1}(\beta )$ and $Z_{\delta /2}$ is the $\delta /2$ upper percentile of the standard normal distribution.

Simulation, quantiles and the median of ${\mathit{GPUD}}_{(J-S)}$

In this work, we follow the approach proposed by several authors to calculate the inverse function of df, where a known simulation mechanism generates random numbers. To obtain the model that simulates random numbers that have a behavior ${\mathit{GPUD}}_{(J-S)}(x;\alpha ,\theta ,k)$ (Eq. 30), we obtain the inverse function

$$\begin{array}{c}\hfill X=\sqrt[k+1]{\frac{\alpha }{1-\alpha }\left[{\left(1,-,Y,(,1,-,{\alpha }^{\theta },)\right)}^{-1/\theta },-,1\right]}\end{array}$$ 48

where $Y\sim U(0,1)$ and $k=1,2,...,n$.

For the particular case of $k=0$ the result reported by Jayakumar and Sankaran (2016) is obtained

$$\begin{array}{c}\hfill X=\frac{\alpha }{1-\alpha }\left[{\left(1,-,Y,(,1,-,{\alpha }^{\theta },)\right)}^{-1/\theta },-,1\right].\end{array}$$

On the other hand, it is interesting to calculate the $q^{\mathit{th}}$ quartile from the perspective of this research generalization because it gives us information about the usual parameters of the distribution

$$\begin{array}{c}\hfill x_q=\sqrt[k+1]{\frac{\alpha }{1-\alpha }\left[\frac{1}{{\left[1,-,q,(,1,-,{\alpha }^{\theta },)\right]}^{1/\theta }},-,1\right]}.\end{array}$$ 49

In particular, the median is obtained by putting $q=1/2$ in Eq. (49).

In Eq. (49) for $k=0$, the result reported by Jayakumar and Sankaran (2016) is obtained

$$\begin{array}{c}\hfill x_q=\frac{\alpha }{1-\alpha }\left[\frac{1}{{\left[1,-,q,(,1,-,{\alpha }^{\theta },)\right]}^{1/\theta }},-,1\right].\end{array}$$

Table 3 shows the calculation of the medians, to exhibit one of the advantages of our model for different values of the parameters $(\alpha ,\theta ,k)$.

Table 3.

Medians of $GPU{D}_{(J-S)}$ distribution

$\alpha$	$\theta$	k	Median
0.999	1	0	0.500
0.1	5	1	0.017
0.5	2.9	2	0.465
0.2	3.5	3	0.379
0.3	4.5	4	0.516
0.4	6	5	0.605

A simulation study was carried out to verify the MLE’s performance considering different parameter values and sample sizes for $GPU{D}_{(J-S)}$. The different sample sizes considered in the simulation are $n=50,100,500$, and 1000. We used the maxLik package in R to find the parameter estimates. The process was replicated 1000 times for each sample size, and we reported the average parameter estimate and the associated mean square errors. The results are reported in Table 4. As the sample size increases, the mean bias and mean square errors decrease, indicating the consistency property of the MLE.

Table 4.

Simulation results for some different values of the parameters $\alpha ,\theta$, and k

Parameters
$(\alpha ,\theta ,k)$	$\widehat{\alpha }\left(\widehat{S},E,(\widehat{\alpha })\right)$	$\widehat{\theta }\left(\widehat{S},E,(\widehat{\theta })\right)$	$\widehat{k}\left(\widehat{S},E,(\widehat{k})\right)$
$n=50$
0.1, 5.0, 1	0.182 (0.038)	6.560 (1.133)	0.897 (0.026)
0.3, 4.5, 4	0.311 (0.074)	4.553 (1.164)	3.960 (0.142)
0.5, 2.9, 2	0.572 (0.136)	3.535 (1.838)	1.971 (0.083)
0.2, 3.5, 3	0.240 (0.278)	3.970 (1.244)	3.368 (0.135)
0.4, 6.0, 5	0.481 (0.377)	6.427 (1.565)	5.398 (0.360)
$n=100$
0.1, 5.0, 1	0.094 (0.009)	4.955 (0.319)	1.015 (0.013)
0.3, 4.5, 4	0.289 (0.024)	4.318 (0.595)	4.019 (0.060)
0.5, 2.9, 2	0.535 (0.039)	3.287 (0.475)	1.978 (0.035)
0.2, 3.5, 3	0.223 (0.024)	3.821 (0.372)	2.983 (0.046)
0.4, 6.0, 5	0.413 (0.123)	6.318 (0.480)	5.070 (0.064)
$n=500$
0.1, 5.0, 1	0.105 (0.004)	5.274 (0.139)	1.002 (0.008)
0.3, 4.5, 4	0.317 (0.015)	4.538 (0.228)	3.915 (0.038)
0.5, 2.9, 2	0.507 (0.032)	2.966 (0.409)	2.008 (0.028)
0.2, 3.5, 3	0.211 (0.013)	3.681 (0.184)	2.978 (0.044)
0.4, 6.0, 5	0.405 (0.071)	6.118 (0.296)	5.009 (0.046)
$n=1000$
0.1, 5.0, 1	0.105 (0.003)	5.132 (0.118)	0.997 (0.006)
0.3, 4.5, 4	0.305 (0.010)	4.521 (0.162)	3.993 (0.031)
0.5, 2.9, 2	0.503 (0.019)	2.995 (0.137)	2.000 (0.015)
0.2, 3.5, 3	0.208 (0.009)	3.554 (0.093)	2.990 (0.025)
0.4, 6.0, 5	0.399 (0.013)	6.034 (0.025)	5.003 (0.019)

Application to real data

In this section, the practical utility of ${\mathit{GPUD}}_{(J-S)}$ is realized by analyzing two different datasets of real data to show the potential of the new family of distributions. The first set of data is related to the global health problem currently being experienced by the pandemic caused by a new strain of coronavirus (COVID-19), which has infected more than 187 million people around the world and has caused the death of more than 4 million people as of June 31, 2021. Data correspond to people who died from COVID-19 and had diabetes. We analyzed the period from the onset of symptoms to the death of the patient. The data were collected from the Ministry of Health of the Government of Mexico (https://www.gob.mx/salud/documentos/datos-abiertosbases-historicas-direccion-general-de-epidemiologia). All the cases correspond to the period starting on February 27 (when the first person infected with COVID-19 and who also had diabetes appeared in Mexico) and ending on April 20, 2020. A total of 1113 cases were obtained.

We clarify that the information of the referred source is available in days (dates). However, compatible calculation purposes required dividing each data point by the longest lifespan of infected people (76.1 days) to obtain the values of the study variable in the interval $0<x<1$, as this is a requirement of our model. The second set of data refers to the remission time (in months) of a sample of 128 patients with bladder cancer presented by Shakhatreh (2018): 0.08, 0.20, 0.40, 0.50, 0.51, 0.81, 0.90, 1.05, 1.19, 1.26, 1.35, 1.40, 1.46, 1.76, 2.02, 2.02, 2.07, 2.09, 2.23, 2.26, 2.46, 2.54, 2.62, 2.64, 2.69, 2.69, 2.75, 2.83, 2.87, 3.02, 3.25, 3.31, 3.36, 3.36, 3.48, 3.52, 3.57, 3.64, 3.70, 3.82, 3.88, 4.18, 4.23, 4.26, 4.33, 4.34, 4.40, 4.50, 4.51, 4.87, 4.98, 5.06, 5.09, 5.17, 5.32, 5.32, 5.34, 5.41, 5.41, 5.49, 5.62, 5.71, 5.85, 6.25, 6.54, 6.76, 6.93, 6.94, 6.97, 7.09, 7.26, 7.28, 7.32, 7.39, 7.59, 7.62, 7.63, 7.66, 7.87, 7.93, 8.26, 8.37, 8.53, 8.65, 8.66, 9.02, 9.22, 9.47, 9.74, 10.06, 10.34, 10.66, 10.75, 11.25, 11.64, 11.79, 11.98, 12.02, 12.03, 12.07, 12.63, 13.11, 13.29, 13.80, 14.24, 14.76, 14.77, 14.83, 15.96, 16.62, 17.12, 17.14, 17.36, 18.10, 19.13, 20.28, 21.73, 22.69, 23.63, 25.74, 25.82, 26.31, 32.15, 34.26, 36.66, 43.01, 46.12, 79.05.

In this case, a procedure similar to that used for the COVID-19 dataset was implemented. For the second set of data, each data point was divided by 79.051 to obtain values of the study variable in the interval $0<x<1$.

The fit of the ${\mathit{GPUD}}_{(J-S)}$ distribution is compared with the following lifetime distributions for a continuous variable X:

1. Weibull distribution with a pdf

   $$\begin{array}{c}\hfill g(x;\lambda ,\beta )=\frac{\lambda }{{\beta }^{\lambda }}\left(x^{\lambda -1}\right)e^{-{\left(\frac{{}^x}{\beta }\right)}^{\lambda }};\lambda ,\beta >0.\end{array}$$
2. Exponentiated Weibull (EW) distribution (Pal et al. 2006) with a pdf

   $$\begin{array}{c}\hfill g(x;\alpha ,\lambda ,\gamma )=\alpha \gamma {\lambda }^{\gamma }\left(x^{\gamma -1}\right){\left(1,-,{e^{-(\lambda x)}}^{\gamma }\right)}^{\alpha -1}\left({e^{-(\lambda x)}}^{\gamma }\right);\alpha ,\lambda ,\gamma >0.\end{array}$$
3. New Marshall-Olkin Weibull (NMOW) distribution (Cui et al. 2020) with a pdf

   $$\begin{array}{c}\hfill g(x;\theta ,\lambda ,\beta )=\frac{\theta \lambda \beta \left(x^{\beta -1}\right)\left({e^{-(\lambda x)}}^{\beta }\right)}{{\left(\theta ,+,(\theta -1),{e^{-(\lambda x)}}^{\beta }\right)}^2};\theta ,\lambda ,\beta >0.\end{array}$$
4. Kumaraswamy Exponential-Weibull (KwEW) distribution (Cordeiro et al. 2016) with a pdf

   $$\begin{array}{c}\hfill g(x;\alpha ,\gamma ,k,\beta ,\lambda )=\alpha \gamma \left(\lambda ,+,k,\beta ,x^{k-1}\right)e^{-\lambda x-\beta x^k}{\left(1,-,e^{-\lambda x-\beta x^k}\right)}^{-1+\alpha }\\ \hfill ·{\left[1,-,{\left(1,-,e^{-\lambda x-\beta x^k}\right)}^{\alpha }\right]}^{-1+\gamma }{1}_{R_{+}}(x);\alpha ,\gamma ,k,\beta ,\lambda >0.\end{array}$$
5. Alpha power transformed Weibull (APTW) distribution (Dey et al. 2017) with a pdf

   $$\begin{array}{c}\hfill g(x;\alpha ,\beta ,\lambda )=\frac{log\alpha }{\alpha -1}\beta \lambda x^{\lambda -1}{e}^{-\beta x^{\lambda }}{\alpha }^{\left(1,-,e^{-\beta x^{\lambda }}\right)};\beta ,\lambda >0,\text{and}\alpha \ne 0.\end{array}$$
6. Extended Exponentiated Weibull (EEW) distribution (Bidram et al. 2015) with a pdf

   $$\begin{array}{c}\hfill g(x;\lambda ,\alpha ,\beta ,\gamma )=\frac{\gamma \alpha \beta {\lambda }^{\beta }{x}^{\beta -1}{e}^{-{\left(\lambda ,x\right)}^{\beta }}{\left(1,-,{e^{-(\lambda x)}}^{\beta }\right)}^{\alpha -1}}{{\left[1,-,(1-\gamma ),\left(1,-,{\left(1,-,{e^{-(\lambda x)}}^{\beta }\right)}^{\alpha }\right)\right]}^2};\lambda ,\alpha ,\beta ,\gamma >0.\end{array}$$

Table 5 presents the calculations obtained from the seven distributions for the values of the estimators, log-likelihood (–log L), Akaike Information criterion (AIC) and Bayesian information criterion (BIC). According to Jayakumar and Sankaran (2019), $AIC=-2logL+2k$ and $BIC=-2logL+klog(n)$. L is the likelihood function evaluated in the maximum likelihood estimates, k is the number of parameters, and n is the sample (dataset). Additionally, the Crammer–von Mises $(W^{\ast })$, Anderson–Darling $(A^{\ast })$, and Kolmogorov–Smirnov (K-S) statistics and their corresponding $pvalues$ are calculated to test the goodness of fit and have other criteria. Thus, a determination of which of these distributions best fits the dataset can be made. Usually, the smaller the K- S, $W^{\ast }$, and $A^{\ast }$ statistics’ values are, the better the fit to the data.

Table 5.

Parameter estimates and goodness of fit statistics for COVID-19 data

Model	MLEs	−log L	AIC	BIC	$W^{\ast }$	$A^{\ast }$	K-S	$pvalue$
$GPU{D}_{(J-S)}$	$\widehat{\theta }=1.382$	996.80	1987.6	1972.55	0.040	0.286	0.015	0.93
	$\widehat{\alpha }=0.017$
	$\widehat{k}=1.355$
Weibull	$\widehat{\lambda }=1.526$	1049.43	2102.87	2112.90	1.215	7.836	0.063	0.000
	$\widehat{\beta }=0.017$
EW	$\widehat{\alpha }=4.659$	1009.16	2024.32	2039.37	0.109	0.842	0.024	0.539
	$\widehat{\lambda }=15.68$
	$\widehat{\gamma }=0.800$
NMOW	$\widehat{\theta }=23.594$	1012.29	2030.59	2045.63	0.062	0.433	0.017	0.892
	$\widehat{\lambda }=4.784$
	$\widehat{\beta }=2.490$
KwEW	$\widehat{\alpha }=5.135$	1008.85	2027.70	2052.78	0.115	0.883	0.024	0.507
	$\widehat{\gamma }=0.867$
	$\widehat{k}=0.714$
	$\widehat{\beta }=5.990$
	$\widehat{\lambda }=4.440$
APTW	$\widehat{\alpha }=0.008$	998.913	2003.82	2018.87	0.371	2.432	0.031	0.222
	$\widehat{\beta }=5.334$
	$\widehat{\lambda }=1.893$
EEW	$\widehat{\lambda }=5.577$	1010.26	2028.53	2048.58	0.121	0.804	0.020	0.728
	$\widehat{\alpha }=2.691$
	$\widehat{\beta }=1.118$
	$\widehat{\gamma }=0.253$

Note that in Table 5, the K-S statistic of the ${\mathit{GPUD}}_{(J-S)}$ distribution is the smallest compared to the other distributions, and therefore, the value corresponding to the $pvalue$ is the highest, which shows that this new proposal produces the best fit for the COVID-19 dataset.

Figure 9 shows the fit of the different distributions compared with that of ${\mathit{GPUD}}_{(J-S)}$. As seen in this figure, our model presents excellent flexibility, and it is competitive with other widely accepted distributions in use, such as the Weibull distribution or the exponentiated Weibull distribution, among others. On the other hand, Fig. 10 shows the Q-Q plot for COVID-19 data.

Fig. 9.

The fitted pdfs of $GPU{D}_{(J-S)}$, W, EW, NMOW, KwEE, APTW, and EEW for COVID-19 data

Fig. 10.

Q–Q plot for the $GPU{D}_{(J-S)}$ distribution for the COVID-19 dataset

Additionally, referring to Table 6, it is convenient to note that the data correspond to the remission times of bladder cancer. In this case, a similar observation is made for ${\mathit{GPUD}}_{(J-S)}$, where the calculated values of K-S and the value of p show the best fit of the data.

Table 6.

Parameter estimates and goodness of fit statistics for cancer data

Model	MLEs	−log L	AIC	BIC	$W^{\ast }$	$A^{\ast }$	K-S	$pvalue$
$GPU{D}_{(J-S)}$	$\widehat{\theta }=1.592$	150.15	294.30	285.74	0.052	0.409	0.029	0.999
	$\widehat{\alpha }=0.038$
	$\widehat{k}=0.514$
Weibull	$\widehat{\lambda }=1.046$	145.28	294.56	300.27	0.130	0.783	0.070	0.541
	$\widehat{\beta }=0.121$
EW	$\widehat{\alpha }=2.104$	148.42	302.84	311.40	0.052	0.329	0.055	0.820
	$\widehat{\lambda }=16.732$
	$\widehat{\gamma }=0.732$
NMOW	$\widehat{\theta }=11.957$	149.21	304.42	312.98	0.028	0.205	0.031	0.999
	$\widehat{\lambda }=4.567$
	$\widehat{\beta }=1.585$
KwEW	$\widehat{\alpha }=2.947$	148.26	306.52	320.78	0.058	0.368	0.050	0.897
	$\widehat{\gamma }=0.995$
	$\widehat{k}=0.531$
	$\widehat{\beta }=4.538$
	$\widehat{\lambda }=4.390$
APTW	$\widehat{\alpha }=0.050$	148.81	303.62	312.18	0.044	0.273	0.055	0.832
	$\widehat{\beta }=5.540$
	$\widehat{\lambda }=1.241$
EEW	$\widehat{\lambda }=2.636$	149.22	306.44	317.85	0.029	0.211	0.040	0.984
	$\widehat{\alpha }=1.058$
	$\widehat{\beta }=1.501$
	$\widehat{\gamma }=0.080$

Figure 11 also shows the fit of the different distributions compared with ${\mathit{GPUD}}_{(J-S)}$. It can be seen that our model is highly competitive with other distributions. Figure 12 displays the Q-Q plot for bladder cancer data.

Fig. 11.

The fitted pdfs of $GPU{D}_{(J-S)}$, W, EW, NMOW, KwEE, APTW, and EEW for bladder cancer data

Fig. 12.

Q–Q plot for the $GPU{D}_{(J-S)}$ distribution for bladder cancer data

Conclusions

In this article, a new family of uniform distributions on (0,1) with three parameters (a, b, k), which is referred to as the generalized powered uniform distribution (GPUD), was proposed. The method used in this proposal incorporates the parameter k as the power of the values of the continuous random variable, favoring a greater diversity of the probability density and survival and hazard functions. Additionally, some properties were derived from the new distribution. Furthermore, the GPUD results allowed us to generalize the model presented by Jayakumar and Sankaran (2016). As a result, it was possible to generate a new family of distributions called ${\mathit{GPUD}}_{(J-S)}$, which results in excellent flexibility in the cumulative distribution function due to the contribution of the parameter k. Clarifying our GPUD approach has allowed us to generalize other models, such as that presented by Jose and Krishna (2011), which is research in progress. To demonstrate the effectiveness of the model, two sets of real data related to COVID-19 and bladder cancer were adapted, and the maxLik package in R was used to find the estimators of the parameters.

In relation to the second real dataset given in Table 6, the value obtained for the statistic $-log(L)$ based on NMOW was slightly lower (0.94) than that obtained by ${\mathit{GPUD}}_{(J-S)}$.

We highlighted that the Kolmogorov–Smirnov (K-S) goodness of fit statistic of our model was 0.029, which is the lowest value compared to the other distributions. In addition, a value of p = 0.999 for the K-S statistic was achieved using our model, which, along with the value obtained using the NMOW distribution, were the highest values shown in Table 6. Both values provide evidence that our model is highly competitive.

It should be noted that in the first set of real data (see Table 5), the ${\mathit{GPUD}}_{(J-S)}$ distribution, shows the best values of the calculated statistics.

The results obtained show that ${\mathit{GPUD}}_{(J-S)}$ is a valid alternative to other known distributions, such as the Weibull, exponentiated Weibull, and new Marshall–Olkin Weibull distributions, among others, with the added advantage that it provides the versatility of working with the parameter k in the values of the random variable.