PFAS Concentrations in Soil Versus Soil Porewater: Mass Distributions and the Impact of Adsorption at Air-Water Interfaces

Abstract

Determining the risk posed by PFAS leaching from soil to groundwater requires quantification of the magnitude and temporal/spatial variability of PFAS mass discharge from the vadose zone, which is governed in part by the concentrations of PFAS in soil porewater. Porewater concentrations are impacted and mediated by the properties of the PFAS and soil, multiple transport and fate processes, and site conditions. The objective of this research was to delineate the relationship between soil porewater concentrations and soil concentrations, based on a comprehensive model of PFAS mass distribution within a soil sample volume. Measured parameters representing solid-phase sorption and air-water interfacial adsorption are used to illustrate the impact of soil and PFAS properties on the distribution of representative PFAS between soil and soil porewater. Literature data reported for soil and soil porewater concentrations of several PFAS obtained from outdoor lysimeter experiments are used to test the distribution model. Soil-to-porewater concentration ratios predicted with the model compared very well to the measured concentration ratios. The nondimensional distribution coefficient that describes the distribution of PFAS mass amongst all domains within a soil sample was observed to be a function of PFAS molecular size. Numerical simulations conducted for a model fire-training source area were used to illustrate the ranges in magnitude of soil versus porewater concentrations for representative field conditions. The results of the measured and simulated data sets demonstrated the importance of air-water interfacial adsorption for the distribution of the longer-chain PFAS within soil samples. PFAS soil porewater concentrations are anticipated to range from ng/L to mg/L depending upon soil concentrations, which in turn depend upon the nature of the site.

1. Introduction

Per and polyfluoroalkyl substances (PFAS) have been demonstrated to be widespread in soils across the globe (Brusseau et al., 2020). PFAS concentrations are often, but not always, observed to be highest near the surface and to diminish with depth. This is particularly the case for longer-chain PFAS. This distribution has been observed for different types of source sites, including sites impacted by fire-fighting foam applications (Filipovic et al., 2015; Baduel et al., 2017; Dauchy et al., 2019; Brusseau et al., 2020), manufacturing facilities (Davis et al. 2007), and land application of biosolids (Washington et al., 2010; Sepulvado et al. 2011; Pepper et al., 2021; Johnson, 2022). In addition, the concentrations of PFAS in soils are typically significantly higher than those in underlying groundwater, often by orders of magnitude (Anderson et al., 2019; Brusseau et al., 2020). These observations demonstrate that soils are a primary reservoir of PFAS at numerous sites. A critical concern for these sites is the potential for leaching of PFAS from soil, through the vadose zone, to groundwater, as illustrated by field-site investigations (Xiao et al., 2015; Baduel et al., 2017; Weber et al., 2017; Hoisaeter et al., 2019; Dauchy et al., 2019) and mathematical-modeling studies (Guo et al., 2020; Silva et al., 2020; Zeng et al., 2021).

The transport of PFAS in soils and the vadose zone is complex, as it is influenced by several potentially nonlinear, rate-limited interconnected processes. Transport experiments, mathematical-modeling studies, and field investigations have for example illustrated the impacts of solid-phase sorption, adsorption at air-water interfaces, and precursor transformation on PFAS migration (e,g., Gellrich et al., 2012; Vierke et al., 2014; Lyu et al., 2018; Brusseau et al., 2019a, 2019b; Hoisaeter et al., 2019; McLachlan et al., 2019; Guelfo et al., 2020; Guo et al., 2020; Silva et al., 2020; Brusseau et al., 2021; Nickerson et al., 2021). Determining the risk posed by PFAS leaching to groundwater requires quantification of the magnitude and temporal/spatial variability of PFAS mass discharge from the vadose zone. This mass discharge is governed by fluid discharge and the concentrations of PFAS in soil porewater, the latter of which is mediated by operative retention and transformation processes.

PFAS soil porewater concentrations and associated mass discharge can be quantified through the application of mathematical models. Comprehensive models that incorporate mechanistic representations of all relevant processes are important for determining the impact and importance of the various processes influencing transport. However, their application requires significant information for parameter input, which is not always practical. An alternative is the use of screening-level models that have reduced input requirements. For example, a screening model employing analytical solutions for predicting long-term leaching of PFAS has been recently developed (Guo et al., 2022). While the level of input is reduced, there remains the need for characterization efforts to supply required parameters.

Direct measurement of PFAS concentrations in soil porewater is an alternative approach for characterizing mass discharge (Anderson et al., 2021; Quinnan et al., 2021). Porewater sampling can be used in lieu of, or preferably in conjunction with, mathematical modeling for site characterization. Effective use of porewater concentration data requires an understanding of the distribution of PFAS mass within a volume element of soil, and the relationship between soil and porewater concentrations. This relationship is more complex for PFAS compared to most other types of solutes due to the adsorption of PFAS at air-water interfaces, and the dependence of air-water interfacial area on water content and soil properties. This relationship between soil and soil porewater concentrations has not yet been investigated.

The objective of this research is to delineate the relationship between soil porewater concentrations and soil concentrations, based on a comprehensive model of PFAS mass distribution within a soil sample volume. Measured parameters representing solid-phase sorption and air-water interfacial adsorption are used to illustrate the impact of soil and PFAS properties on the distribution of PFAS between soil and soil porewater. Literature data reported for soil and soil porewater concentrations of several PFAS obtained from outdoor lysimeter experiments are used to test the distribution model. Soil-to-porewater concentration ratios predicted with the model are compared to the measured concentration ratios. Numerical simulations conducted for a model fire-training source area are used to illustrate the magnitude of soil versus porewater concentrations for representative field conditions. The importance of air-water interfacial adsorption for mediating the distribution of PFAS within a soil sample is examined using the simulated and measured data sets.

2. Theory

We are interested in the distribution of PFAS among all possible domains within a volume sample of soil in the presence of a variety of phases including air (soil atmosphere), water (porewater), solids, nonaqueous-phase liquid (NAPL), and colloidal and other suspended and dissolved matter. This distribution is described and quantified using the comprehensive retention model of Brusseau (Brusseau, 2018; Brusseau et al., 2019a). The total mass of a select PFAS constituent in a volume of soil is given by:

$$M_t=C_p{V}_p+C_s{M}_s+C_a{V}_a+C_n{V}_n+C_{aw}{A}_{aw}+C_{nw}{A}_{nw}+C_{an}{A}_{an}+C_c{M}_c$$ [1]

where M_t is total mass in the volume of sample (M), C_p is the porewater concentration (M/L³), C_s represents the mass of PFAS sorbed by the soil solids (soil-solids concentration, M/M), C_a is the concentration in the soil atmosphere (M/L³), C_n is the concentration in NAPL present in the sample (M/L³), C_aw represents the mass adsorbed at the air-water interface (air-water interfacial concentration (M/L²), C_nw represents the mass adsorbed at the NAPL-water interface (NAPL-water interfacial concentration (M/L²), C_an represents the mass adsorbed at the air-NAPL interface (air-NAPL interfacial concentration (M/L²), C_c represents the mass associated with colloidal and other suspended and dissolved matter in solution (M/M), A_aw is the total air-water interfacial area (L²), A_nw is the total NAPL-water interfacial area (L²), A_an is the total air-NAPL interfacial area (L²), V_w is the volume of porewater (L³), V_a is the volume of air (L³), V_n is the volume of NAPL (L³), M_s is the mass of soil solids (M), and M_c is the mass of colloidal material (M).

Normalizing the phase volumes, phase masses, and interfacial areas by the total sample volume, V_t, and introducing the equilibrium distribution coefficients results in transformation of equation 1 to:

$$M_t=C_p{\theta }_w{V}_t\left(1+K_{d*}\frac{{\rho }_b}{{\theta }_w}+K_a\frac{{\theta }_a}{{\theta }_w}+K_n\frac{{\theta }_n}{{\theta }_w}+K_{aw*}\frac{a_{aw}}{{\theta }_w}+K_{nw*}\frac{a_{nw}}{{\theta }_w}+K_{an*}\frac{a_{an}}{{\theta }_w}+K_{c*}{X}_c\right)$$ [2]

where K_d* is the nonlinear solid-phase adsorption coefficient (cm³/g), K_n is the NAPL-water partition coefficient (−), K_a is the air-water partition coefficient (Henry’s coefficient, −), K_aw* is the nonlinear air-water interfacial adsorption coefficient (cm³/cm²), K_nw* is the nonlinear NAPL-water interfacial adsorption coefficient (cm³/cm²), K_an* is the nonlinear air-NAPL interfacial adsorption coefficient (cm³/cm²), K_c* is the nonlinear distribution coefficient for sorption by the colloids (cm³/g), a_aw is the specific air-water interfacial area (cm²/cm³), a_nw is the specific NAPL-water interfacial area (cm²/cm³), a_an is the specific air-NAPL interfacial area (cm²/cm³), ρ_b is porous-medium bulk density (g/cm³), θ_a is volumetric air content (cm³/cm³), θ_n is volumetric NAPL content (cm³/cm³), and θ_w is volumetric water content (cm³/cm³). By phase balance, θ_w + θ_a + θ_n = n, where n is porosity. Note that X_c is the concentration of colloidal material in porewater (g/cm³), defined as:

$$X_c=\frac{M_c}{{\theta }_w{V}_t}=\frac{M_c}{V_p}$$ [3]

Both solid-phase sorption and fluid-fluid interfacial adsorption of PFAS may be nonlinear under certain conditions. The nonlinearity of solid-phase sorption is often represented with the Freundlich isotherm. With this approach, the impact of nonlinearity on the magnitude of sorption can be represented by K_d* = K_fC_p0^(N−1), where K_f and N are the Freundlich coefficients and C_p0 is the aqueous concentration of interest. This approach may also be applied to sorption by colloidal matter. When sorption is linear, K_d* = K_d and K_c* = K_c, where the coefficients without asterisks represent constants. A standard approach for representing nonlinear fluid-fluid interfacial adsorption is through use of the Szyszkowski-Langmuir equation, which leads to (using the air-water system as the example): K_aw* = Γ_m/(C_p+a), where Γ_m is the maximum surface excess (=γ₀b/RT), R is the universal gas constant, T is temperature, γ₀ is the surface tension when C_p is zero, and a and b are constants from the Szyszkowski equation that describes surface tension as a function of aqueous concentration. This treatment can also be applied to represent nonlinear NAPL-water and air-NAPL interfacial adsorption processes. Fluid-fluid interfacial adsorption may be treated as linear at lower concentrations (e.g., Brusseau et al., 2021). Under these conditions, K_aw* = K_aw, K_nw* = K_nw, and K_an* = K_an, where the coefficients without asterisks represent constants. The specific concentrations at which fluid-fluid interfacial adsorption may be treated as linear depends upon the particular PFAS and properties of the porewater solution (Brusseau, 2019a). Partitioning between bulk water, NAPL, and air phases is commonly treated as linear.

The terms in parentheses in equation 2 can be defined as the nondimensional distribution coefficient, denoted as R_d:

$$R_d=\left(1+K_{d*}\frac{{\rho }_b}{{\theta }_w}+K_a\frac{{\theta }_a}{{\theta }_w}+K_n\frac{{\theta }_n}{{\theta }_w}+K_{aw*}\frac{a_{aw}}{{\theta }_w}+K_{nw*}\frac{a_{nw}}{{\theta }_w}+K_{an*}\frac{a_{an}}{{\theta }_w}+K_{c*}{X}_c\right)$$ [4]

This term is very similar to the retardation factor developed for aqueous-phase transport of PFAS undergoing retention by all of the relevant processes (Brusseau et al., 2019a). The one difference is the treatment of PFAS mass associated with colloidal matter suspended or dissolved in porewater, which was incorporated into the mobile solution phase for development of the retardation factor for transport. With the introduction of R_d, equation 2 becomes:

$$M_t=C_p{\theta }_w{V}_t{R}_d$$ [5]

The total concentration of the select PFAS, C_t (M/M), is defined as M_t/M_s. Substituting equation 5 gives:

$$C_t=\frac{C_p{\theta }_w{R}_d}{{\rho }_b}$$ [6]

The ratio of total concentration to porewater concentration is therefore:

$$\frac{C_t}{C_p}=\frac{{\theta }_w}{{\rho }_b}{R}_d$$ [7]

Inspection of equation 7 reveals that R_d represents the ratio of total mass present in the soil sample to the mass present as dissolved solute in porewater. The $\frac{{\theta }_w}{{\rho }_b}$ term represents the ratio of porewater volume to soil-solids mass and can be thought of as a unit conversion term. Note that the $\frac{C_t}{C_p}$ term has units of L³/M. A dimensionless ratio can be developed by use of a volume-based total concentration, C_tv (M/L³), defined as M_t/V_t. C_t and C_tv are related by the soil bulk density. C_t is the focus of the present study given that mass-based soil concentrations are the reporting standard.

Equations 2 and 4–7 represent all possible phases in which PFAS can potentially reside within a soil sample. However, several of the phases are unlikely to be relevant for many conditions. For example, many PFAS of concern have low vapor pressures and are thus not measurably present in the vapor phase. In addition, many sites are unlikely to have NAPL present in the vadose zone. Inspection of equation 2 shows that the impact of retention by sorption to colloidal material in porewater will be relatively insignificant for moderate to low concentrations of colloids and for smaller sorption coefficients. Under these preceding conditions, R_d can be simplified to:

$$R_d=\left(1+K_{d*}\frac{{\rho }_b}{{\theta }_w}+K_{aw*}\frac{a_{aw}}{{\theta }_w}\right)$$ [8]

Examining this reduced form will be the focus of the present investigation.

3. Methods

This study comprises four components. For the first component, the ratio of total soil concentration to soil porewater concentration as a function of water saturation will be investigated for representative primary PFAS of concern. This will be accomplished by using measured and estimated parameter values to calculate R_d values using equation 8, and then using these values in equation 7. Three perfluorocarboxylic acids (PFCAs) of different chain length will be used to examine chain-length effects. These three are perfluorobutanoic acid (PFBA), perfluorooctanoic acid (PFOA), and perfluorotridecanoic acid (PFTDA). Perfluorooctane sulfonic acid (PFOS) will also be included in the analysis. A natural sand will be used as the porous medium for these calculations to focus on the impact of air-water interfacial adsorption. Measured values for a_aw are available for this sand from our prior experiments (Brusseau and Guo, 2021), as are K_d and K_aw values for the selected PFAS (Van Glubt et al., 2021). These values are reported in Tables 1 and 2. The calculations are conducted employing constant K_aw values, representing systems with PFAS concentrations in the μg/L range or lower.

Table 1.

PFAS Parameter Values

PFAS	Kaw (cm)	Kd-Sand (cm3/g)	Kd-Eustis (cm3/g)	Kd-Vinton (cm3/g)	Kd-Soila (cm3/g)
PFBA	0.00003	0.07	-	-	0.03
PFHxA	0.0002	-	-	-	0.19
PFOA	0.003	0.15	-	-	1.0
PFNA	0.014	-	-	-	2.5
PFDA	0.07	-	-	-	7.9
PFUnDA	0.128	-	-	-	28
PFTrDA	0.26	2.8	-	-	154
PFBS	0.00017	-	-	-	0.12
PFOS	0.05	0.25	1.9	1.9	5.7
Data Source	Brusseau & Van Glubt, 2021	Van Glubt et al., 2021	Brusseau et al., 2019b	Brusseau et al., 2019b	Brusseau, 2019b

^aMedium for the Felizeter et al. (2021) study

Table 2.

Air-Water Interfacial Area Values

Porous Medium	Range of Sw Valuesb	Range of aaw Valuesc (cm−1)
Sand	0.2–1	0–419
Eustis	0.2–1	0–656
Vinton	0.2–1	0–1026
Soila	0.51–0.68	428–866

^aMedium for the Felizeter et al. (2021) study

^bS_w is water saturation

^cAir-water interfacial area is a function of water saturation

The second component focuses on determining C_t/C_p ratios for PFOS as a function of water saturation for three porous media for which PFOS has different magnitudes of solid-phase sorption and that have different magnitudes of air-water interfacial area. Measured values for a_aw are available for the three media from our prior experiments (Brusseau and Guo, 2021; El Ouni et al., 2021), and are reported in Table 2. Measured K_d values for PFOS for the three media are reported in Table 1. Freundlich N values reported for sorption of PFCAs by soils and sediments are typically in the range of 0.7–1 (see recent compilation reported in Van Glubt et al., 2021), thereby exhibiting relatively moderate nonlinearity. Hence, solid-phase sorption will be treated as linear for the purposes of the first and second components. This treatment has minimal impact on the results.

The third component of the study employs literature data reported for soil and soil porewater concentrations of several PFAS obtained from outdoor lysimeter experiments (Felizeter et al. 2021). These measured data are used to test the distribution model by comparing soil-to-porewater concentration ratios predicted with the model to the measured concentration ratios. Four edible crops (radish, lettuce, pea, and maize) were grown in outdoor lysimeters packed with soil spiked with a mixture of 13 PFAS at 4 concentrations (nominal 0.1, 1, 5, and 10 mg/kg-dw for each PFAS). The PFAS mixture comprised 11 PFCAs, PFOS, and perfluorobutane sulfonic acid (PFBS). The lysimeters were installed in the ground outside, and subject to natural precipitation events as well as additional irrigation. PFAS concentrations were measured in soil, soil porewater, and different plant tissues at harvest. Soil water contents were also reported.

Values for R_d defined in equation 8 were determined using measured and estimated parameter values as follows. The soil employed has an organic-carbon content of 1%. Prior research has indicated that soil organic carbon generally controls sorption of PFCAs and PFOS for soils and sediments with organic-carbon contents in this range and higher (e.g., Higgins and Luthy, 2006; Milinovic et al., 2015; Brusseau et al., 2019b). Therefore, K_d values were estimated from the standard K_d = K_oc f_oc approach, with use of measured K_oc values (Brusseau, 2019). Measured values for K_aw were taken from Brusseau and Van Glubt (2021). Values for a_aw were estimated using measured data reported for several porous media comprising a range of textures (Peng and Brusseau, 2005; Brusseau and Guo, 2021; El Ouni et al., 2021).

The fourth component of the study comprises two sets of numerical simulations for a model fire-training source area. The first set focuses on the long-term distribution of PFAS in the vadose zone and the magnitudes of soil versus porewater concentrations for representative field conditions, while the second set illustrates the impact of a precipitation event on short-term changes in $\frac{C_t}{C_p}$. The mathematical model that was employed to conduct the numerical simulations accounts for transient variably saturated flow, surfactant-induced flow, nonlinear and rate-limited solid-phase sorption, and nonlinear and rate-limited air-water interfacial adsorption (Guo et al., 2020). A 30-year period of operation is used wherein PFAS are released to the vadose zone due to regular fire training activities. This is followed by a post-operation period where the release of PFAS is stopped. The measured properties for a well-characterized soil (Vinton) are used to represent a homogeneous vadose zone.

Three representative PFAS (PFPeA, PFOA, and PFOS) are considered. The PFAS are released to the vadose zone in a 1% diluted AFFF solution at concentrations of 0.23 mg/L, 0.9 mg/L, and 100 mg/L, respectively, for PFPeA, PFOA, and PFOS. Real rainfall and evaporation data at 30-min resolution from a site in New Jersey are used to represent the climatic conditions for a humid region. The details of the model setup and other input parameters are the same as those used in the numerical simulations reported in Guo et al (2022). The analysis in the present study focuses on the post-operation period. In addition to the long-term numerical simulations, a set of short-term (10 day) simulations is conducted to analyze the dynamic changes of porewater concentration and the ratio of total to porewater concentration during and immediately after a relatively large storm. The PFAS concentration at the end of the 30-year contamination period is used as the initial condition for these short-term simulations.

4. Results and Discussion

4.1. The C_t versus C_p relationship as a function of PFAS, soil properties, and water saturation

Inspection of equation 8 reveals that relative distribution of PFAS between the different domains within a soil sample, represented by R_d, is a function of both properties of the PFAS and properties of the soil. It has been demonstrated that both K_d and K_aw are functions of the molecular size of PFAS (e.g., Higgins and Luthy, 2006; Brusseau, 2019a, 2019b). The magnitude of sorption will also be a function of the geochemical properties of the soil, such as the constituent contents and compositions (e.g., organic carbon, clay minerals, metal oxides). The magnitude of air-water interfacial adsorption will be mediated by the amount of air-water interface present, which is a function in part of soil properties (grain size, solid surface area). Finally, it is observed that R_d is a function water content for a given soil and PFAS, both directly through the θ_w terms and indirectly through the dependence of a_aw on water content. It is well established that a_aw increases with decreasing θ_w (e.g., Kim et al., 1997; Anwar et al., 2000; Peng and Brusseau, 2005; Brusseau and Guo, 2021; El Ouni et al., 2021). As a result of these functionalities for R_d, the ratio between C_t and C_p is a function of PFAS molecular size, soil properties, and water content. These dependencies are illustrated in this section.

The C_t/C_p relationship as a function of water saturation is presented in Figure 1 for the four selected PFAS. C_t/C_p is observed to be less than one for PFBA and PFOA over the entire range of water saturation. Inspection of equation 7 reveals that for sufficiently small R_d values, C_t/C_p will be less than one due to the impact of the $\frac{{\theta }_w}{{\rho }_b}$ term (which is always <1). The C_t/C_p decreases with decreasing water saturation for PFBA. This is due to the minimal impact of air-water interfacial adsorption on PFBA distribution within the sample. As a result, the increase in R_d that results from decreasing water saturation is less than the corresponding decrease in the $\frac{{\theta }_w}{{\rho }_b}$ term. Conversely, the C_t/C_p increases with decreasing water saturation for PFOA. This is due to a substantial increase in R_d accruing to the impact of air-water interfacial adsorption and the increase in the magnitude of air-water interfacial area with decreasing water saturation.

Figure 1.

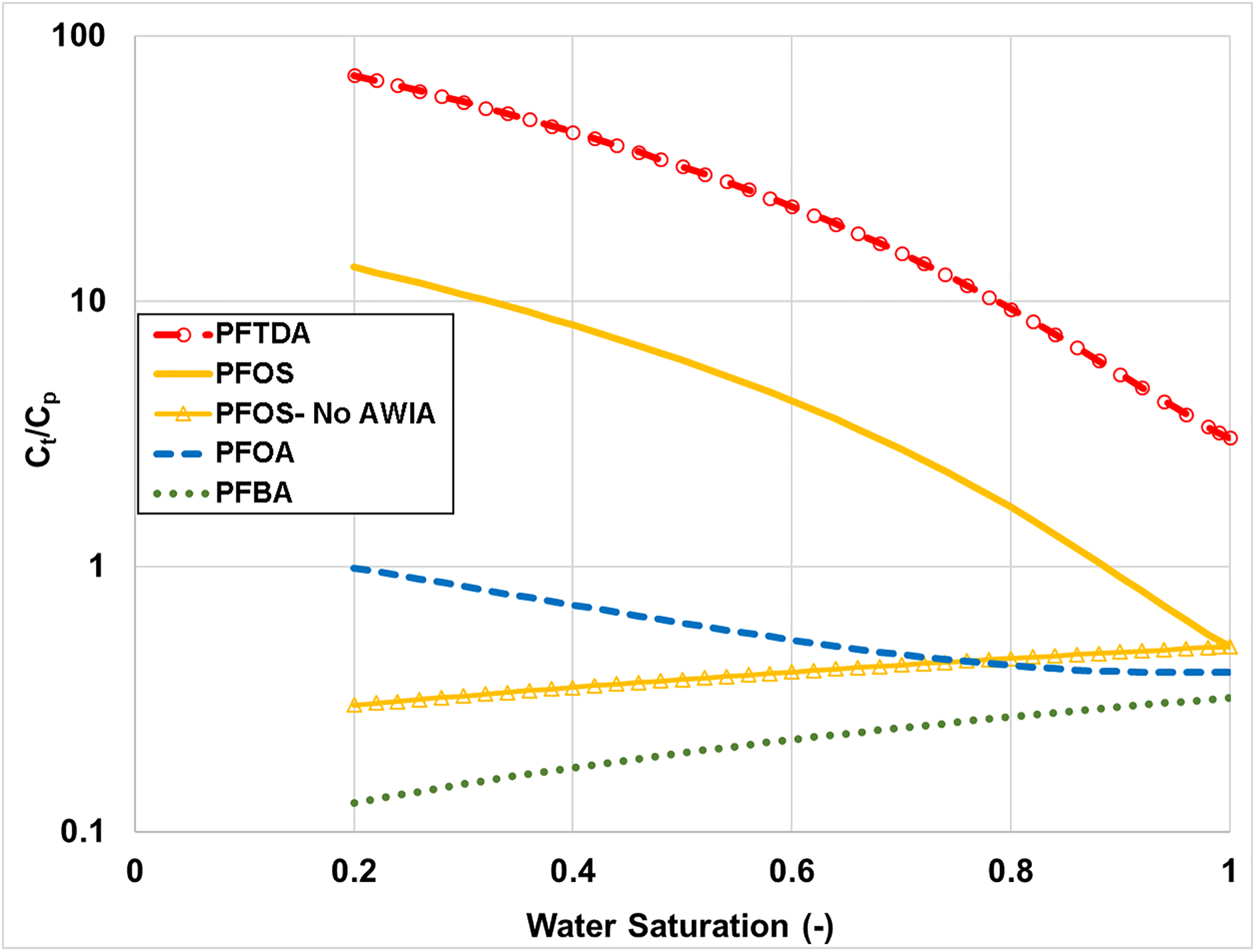
Ratio of total soil concentration (C_t) to porewater concentration (C_p) of an individual PFAS for four representative PFAS. Parameters used are representative of the sand. AWIA represents air-water interfacial adsorption.

In contrast to PFBA and PFOA, the C_t/C_p values for PFTDA and PFOS are >1 for all and almost all water saturations, respectively. This is a result of the larger magnitudes of solid-phase sorption for PFOS and particularly PFTDA (see respective K_d values in Table 1). C_t/C_p increases with decreasing water saturation for PFTDA and PFOS due to the impact of air-water interfacial adsorption as described above for PFOA.

The C_t/C_p relationship for PFOS as a function of water saturation is presented in Figure 2 for three porous media. The C_t/C_p values are largest for the Vinton soil at any given water saturation because this medium has the largest magnitude of air-water interfacial area (Table 2). Conversely, the C_t/C_p values are smallest for the sand due to the smaller K_d and a_aw values.

Figure 2.

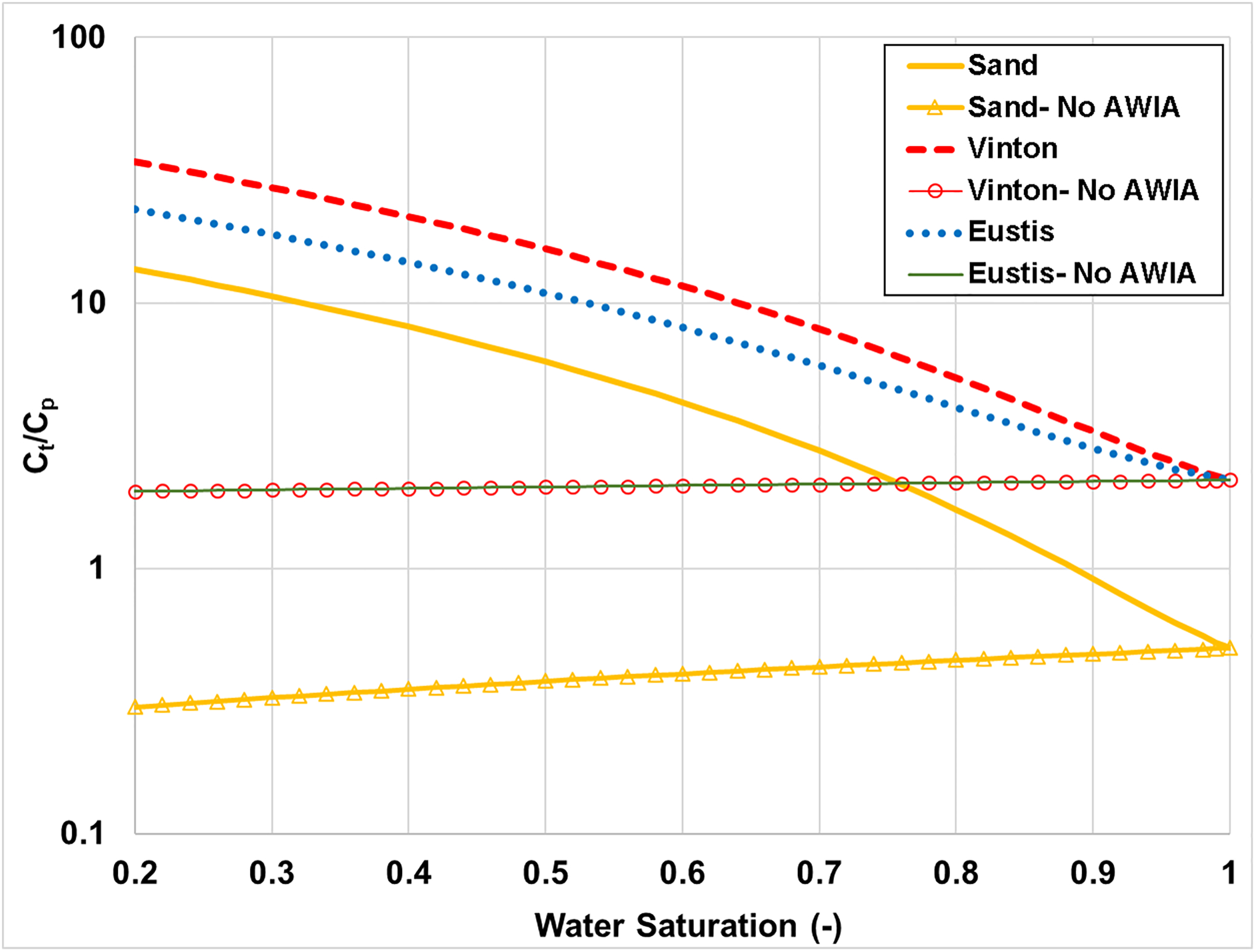
Ratio of total soil concentration (C_t) to porewater concentration (C_p) for PFOS in three porous media. AWIA represents air-water interfacial adsorption.

The specific impact of air-water interfacial adsorption, and the underlying influence of the decrease in water saturation on the relative significance of this process, is illustrated by comparing the PFOS C_t/C_p values for the cases with and without air-water interfacial adsorption in Figures 1 and 2. The divergence between the paired sets of curves progressively increases as water saturation decreases in all cases. Similar results are observed for PFTDA (data not shown). These results highlight the impact of air-water interfacial adsorption on the distribution of longer-chain PFAS within soil samples. This retention process will significantly influence porewater concentrations under certain conditions.

4.2. Prediction of measured soil-to-porewater concentration ratios

The outdoor lysimeter study of Felizeter et al. (2021) represents one of the first to present field-based measurements of PFAS porewater concentrations. The measured porewater concentrations range from 0.1 to ~4000 μg/L depending upon the individual PFAS (Table 3). The measured soil concentrations (C_s) range from ~0.3 to ~8000 μg/kg. The measured soil concentrations are designated as C_s to differentiate them from the theoretical C_t term, as will be discussed in more detail in section 4.5.

Table 3.

Porewater Data from the Felizeter et al. (2021) Study

PFAS	Cp (ug/L)	Rd Measureda
PFBA	36–225	1.0
PFHxA	0.4–127	3.2
PFOA	3–3994	11.6
PFNA	0.2–1777	52.7
PFDA	0.1–293	248
PFUnDA	42–6000	702
PFTDA	5–81	1785
PFBS	3–175	7.4
PFOS	3–548	195

^aCalculated for this study using the raw data reported in Felizeter et al. (2021)

The measured C_s and C_p data reported in the study were used to determine measured C_s/C_p values. Inspection of Table 3 shows that the measured C_s/C_p values are <1 for the shortest-chain PFAS and >1 for the longer-chain PFAS, consistent with the results presented in Figure 1. This again is due to the different magnitudes of retention experienced by the short-chain versus long-chain PFAS under the extant conditions of the experiment. Measured R_d values were calculated with equation 7 using the measured C_s/C_p values, and are presented in Table 3. The measured R_d values range by more than three orders of magnitude, from 1 for PFBA to 1777 for PFTDA. The values are observed to be a function of PFAS size. This is illustrated by Figure 3, wherein log R_d is shown to be a linear function of PFAS molar volume. This is consistent with prior research demonstrating that both log K_d and Log K_aw for PFAS are functions of molar volume (Brusseau, 2019a, 2019b).

Figure 3.

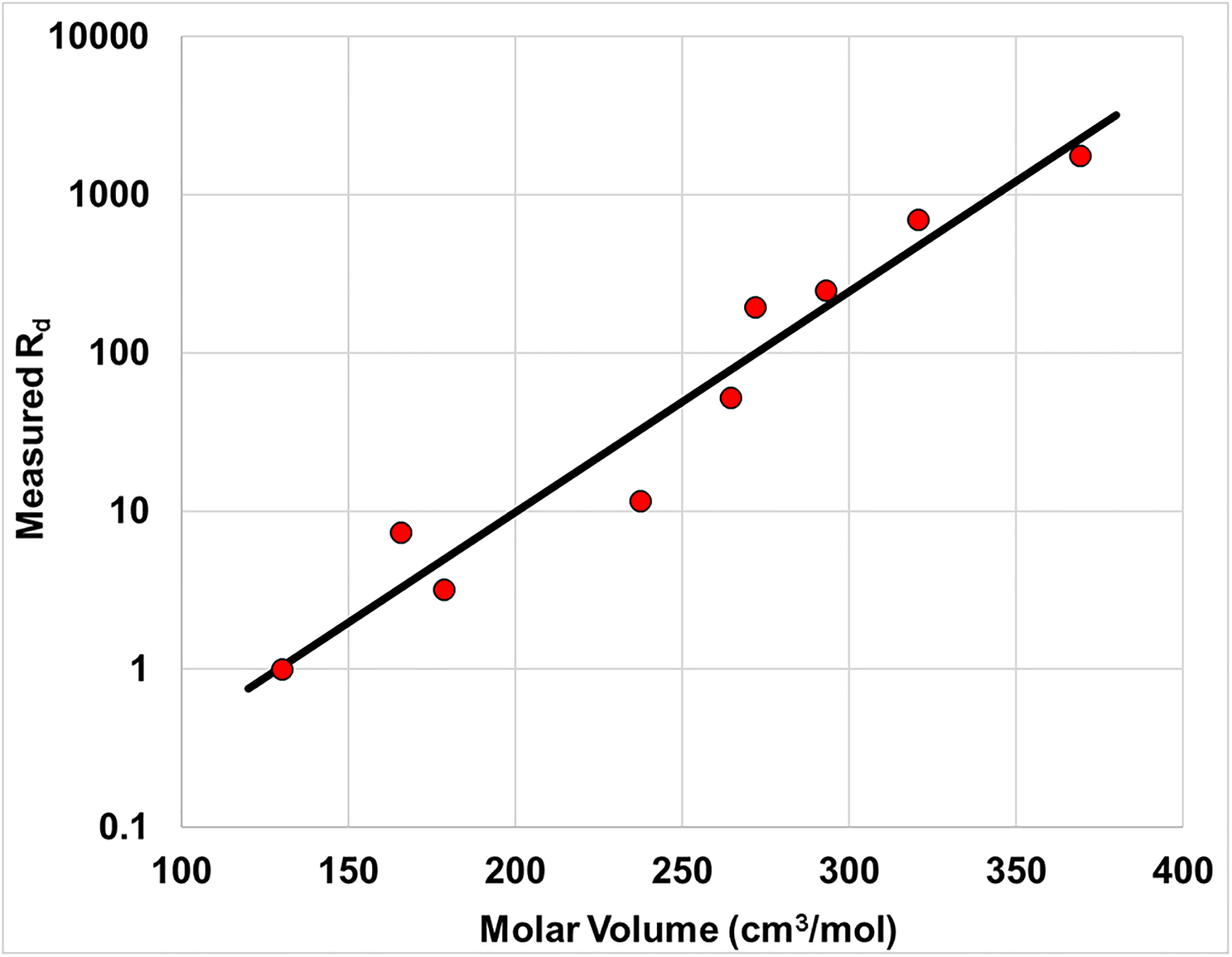
Measured nondimensional distribution coefficients, R_d, as a function of PFAS molar volume. Measured values determined from raw data reported in Felizeter et al., (2021).

Predicted C_t/C_p values were produced with the distribution model using equation 7. This was accomplished with the use of independently-obtained parameters to determine R_d for each PFAS with equation 8. The predicted C_t/C_p values are compared to the measured C_s/C_p values in Figure 4 for two cases, one incorporating air-water interfacial adsorption and one without. The predicted values that incorporate air-water interfacial adsorption match very well to the measured values for all PFAS except PFBS. The excellent predictions of the measured data indicate that the model provides a reasonable representation of PFAS mass distribution within the soil samples. The importance of air-water interfacial adsorption for the longer-chain PFAS is illustrated by the significant differences in the predicted values for the two cases with and without air-water interfacial adsorption.

Figure 4.

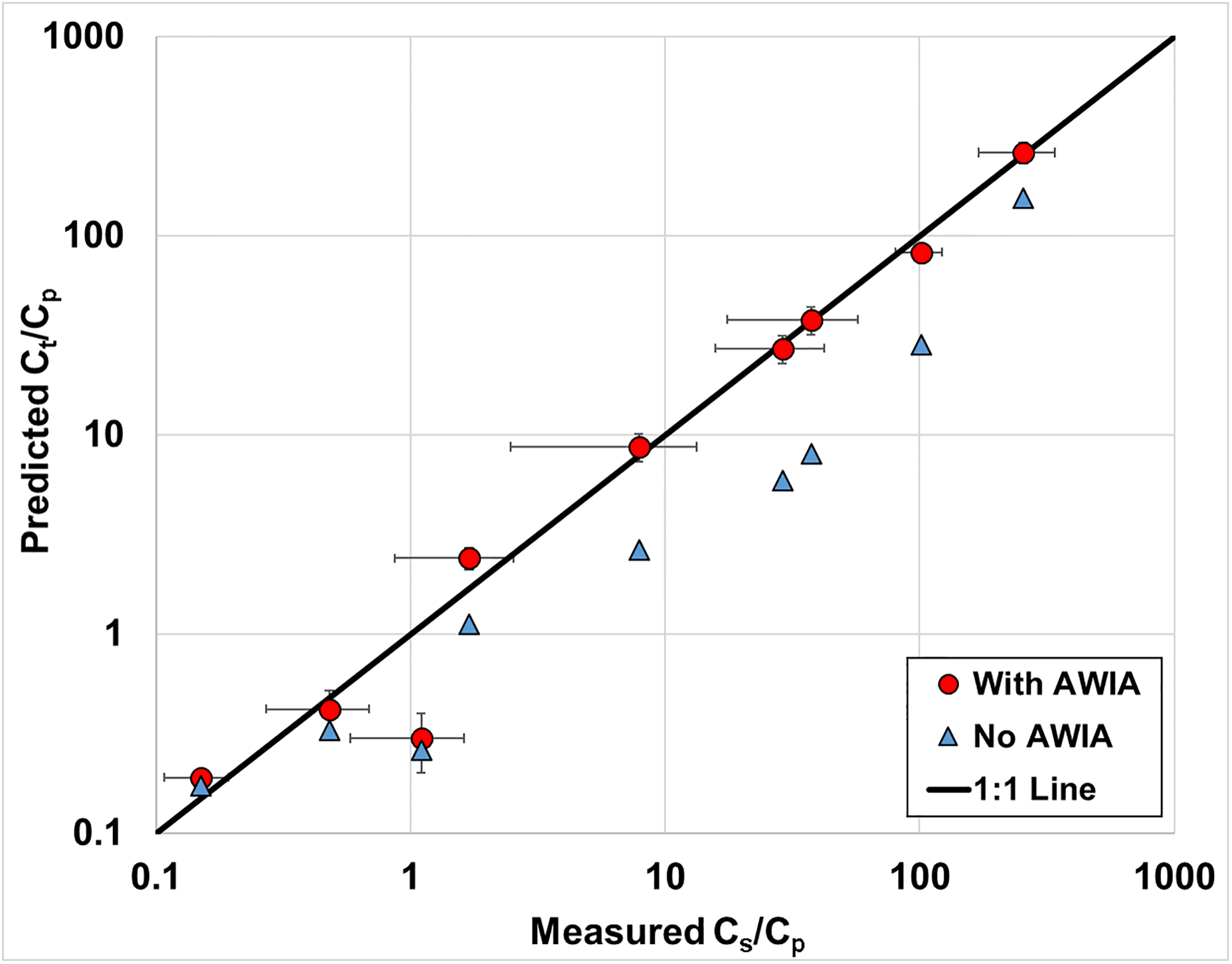
Comparison of predicted and measured porewater concentrations for several PFAS (Table 3). Measured data determined from raw data reported in Felizeter et al., (2021). AWIA represents air-water interfacial adsorption. The error bars represent 95% confidence intervals. The one outlier data point (red circle) is PFBS.

In considering the deviation between predicted and measured values observed for PFBS, it is critical to note that air-water interfacial adsorption is predicted to have minimal impact on PFBS distribution for this soil. Hence, the deviation may be due in part to an inaccurate representation of solid-phase sorption (inaccurate K_d). In addition, the measured values for all PFAS exhibit a degree of variability. This is related in part to variability in the water contents of the individual treatments, which ranged from 0.20 to 0.27, and inherent experimental uncertainty.

4.3. The C_t versus C_p relationship under dynamic short-term and long-term field conditions

The predicted C_t and C_p values, along with the $\frac{C_t}{C_p}$ relationships, simulated for long-term field conditions at a model fire training area site are presented in Figure 5. The total soil concentrations after the 30 years of site operation are observed to range from approximately 1 μg/kg for PFPeA to ~50 μg/kg for PFOA to ~25 mg/kg for PFOS (Figure 5). These concentrations are consistent with PFAS soil-concentration ranges observed at AFFF-impacted sites (Brusseau et al., 2020). The porewater concentrations after the 30 years of operation range from approximately 5 μg/L for PFPeA to 18 μg/L for PFOA to 1300 μg/L for PFOS. These are consistent with porewater concentrations reported at AFFF-impacted sites (Davis et al. 2021; Quinnan et al., 2021). Both PFPeA and PFOA have migrated to the bottom of the simulated vadose zone within the 30 year operation period. Conversely, the PFOS front has migrated to only a 250-cm depth in this timeframe due to its significantly greater retention. The C_t and C_p values for all three PFAS decrease over the post-operation period due to leaching. The downward migration of the contaminant plume is clearly observed for PFOS, with the peaks of both C_t and C_p migrating to successively greater depths over the 50-year post-operation period.

Figure 5.

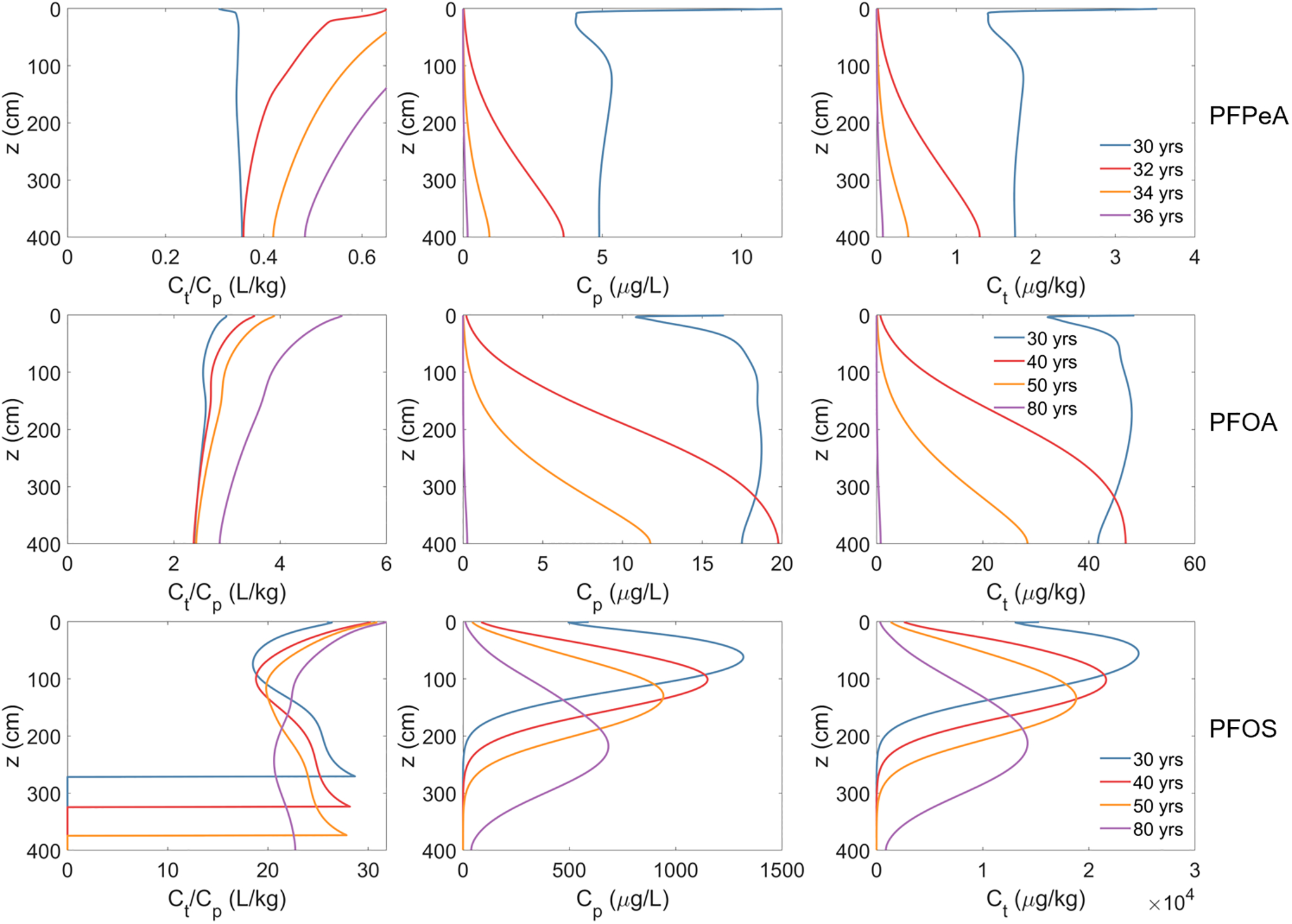
Ratio of total soil concentration (Ct) to porewater concentration (Cp) (left column), Cp (center column), and Ct (right column) from the long-term simulations of PFAS leaching in a model fire training area site during the post contamination period (i.e., after fire training activities stopped). The three rows denote the results for PFPeA, PFOA, and PFOS, respectively.

The C_t/C_p values vary greatly among the three PFAS—the ratio for PFOS is almost 10 and 100 times those for PFOA and PFPeA, respectively (Figure 5). Consistent with Equation 8, the variation is caused primarily by the differences in the relative magnitudes of retention due to solid-phase sorption and air-water interfacial adsorption. Inspection of Figure 5 shows that the C_t/C_p changes in space and time for each PFAS. The changes are driven by spatial and temporal changes in concentration due to the migration of the plume, and accompanying changes in the magnitudes of retention related to nonlinearity of solid-phase sorption and/or air-water interfacial adsorption. The water content changes minimally over time for these long-term simulations (data not shown), and therefore does not measurably impact the observed results.

The C_t/C_p increases with time throughout the depth profile for PFPeA and PFOA, and for the upper ~120 cm for PFOS. This results from the temporal decrease in porewater concentrations and the resultant increase in the magnitude of sorption and/or air-water interfacial adsorption. For PFPeA and PFOA, the porewater concentrations are several orders of magnitude below the concentrations at which air-water interfacial adsorption becomes essentially linear. Thus, the change in C_t/C_p is primarily due to nonlinearity of solid-phase sorption. Conversely, the porewater concentration for PFOS is much higher and the changes in C_t/C_p are caused primarily by nonlinear air-water interfacial adsorption. The PFOS C_t/C_p decreases over time in the deeper interval, reflecting the increase in concentration as the solute front migrates into this interval. The C_t/C_p goes to zero for PFOS in the bottom region of the domain. This occurs where the total and porewater concentrations are zero because the plume has not yet entered that depth interval. This is observed only for PFOS because it has much greater retention than PFOA and PFPeA, and therefore the PFOS front has not yet migrated to the bottom of the interval as noted above.

The short-term simulations (Figure 6) clearly show that different magnitudes of change occur for soil and porewater concentrations for the different PFAS. Significant changes in total soil concentrations are observed for PFPeA during the simulated 10-day storm event. Conversely, there is minimal change in C_t for PFOA and PFOS. This disparity reflects a greater amount of leaching affecting PFPeA due to its significantly lower retention in comparison to PFOA and especially PFOS. In contrast to the relative changes in C_t, the greatest changes in porewater concentrations are observed for PFOS and PFOA whereas minimal changes are observed for PFPeA. As a result, the C_t/C_p varies significantly for the former two, up to 50% for PFOA and up to ~5 times for PFOS, and minimally for PFPeA.

Figure 6.

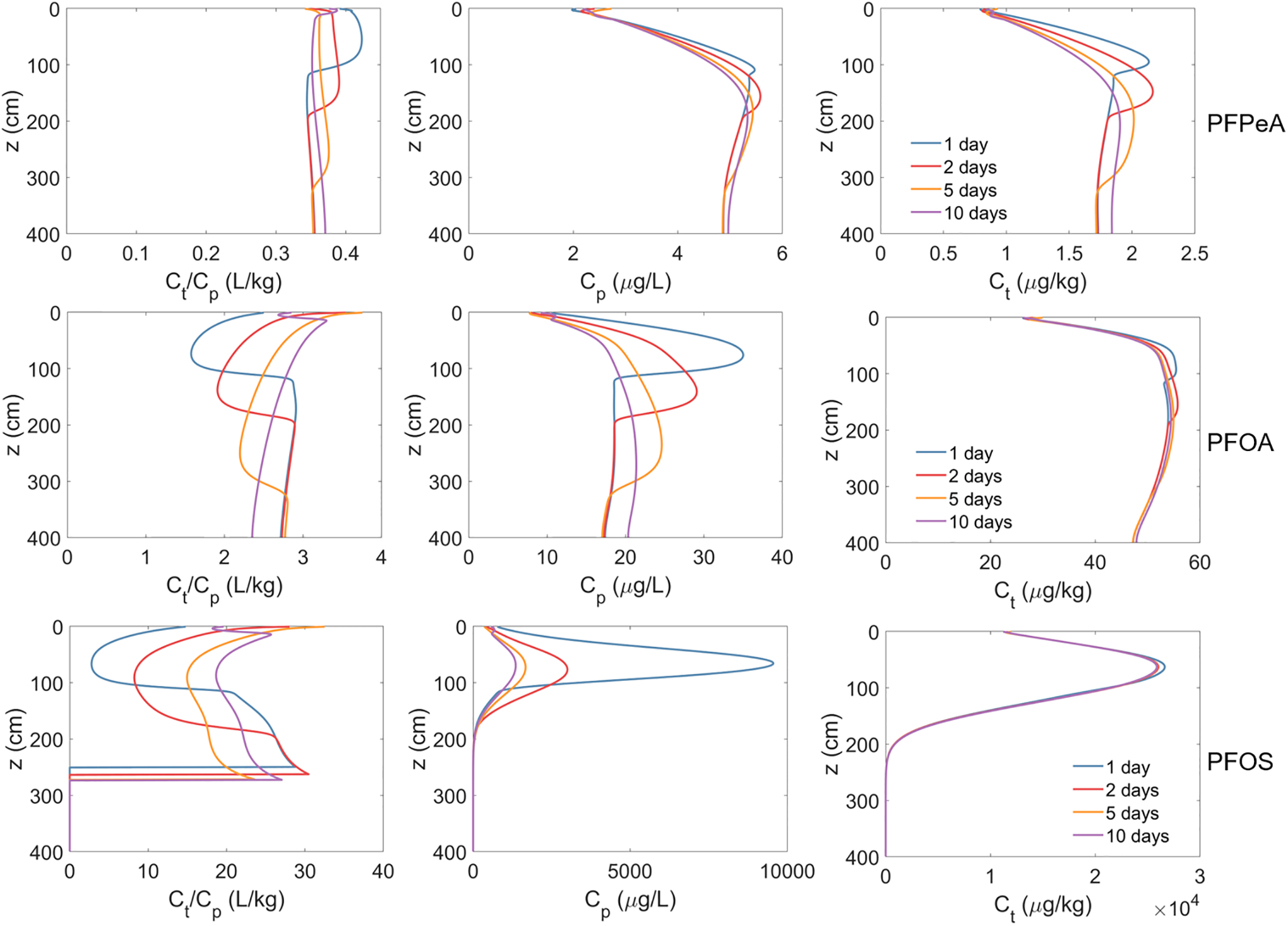
Ratio of total soil concentration (Ct) to porewater concentration (Cp) (left column), Cp (center column), and Ct (right column) from the short-term simulations of PFAS leaching in a model fire training area site. Simulated PFAS concentration in the vadose zone at the end of the contamination period is used as the initial conditions and no PFAS were released to the vadose zone during the simulations. The simulated 60-day period contains one of the largest rainfall events over a period of ten years. The three rows denote the results for PFPeA, PFOA, and PFOS, respectively.

The changes observed for C_p and C_t/C_p are caused by changes in the local water saturation during the infiltration/redistribution event and the subsequent changes in air-water interfacial area caused by these transient water-content conditions (Figure 7). Inspection of Figure 7 shows that the increased water saturation due to the wetting front infiltration destroys air-water interfacial area. As a result, the PFAS adsorbed at the air-water interfaces are subsequently released to the porewater, causing an increase in the porewater concentration. Large changes in C_p and C_t/C_p are observed for PFOA and PFOS because air-water interfacial adsorption provides a significant contribution to total retention. Smaller changes are observed for PFPeA because air-water interfacial adsorption provides a much smaller contribution to total retention. These dynamic changes of porewater concentration due to transient water infiltration are consistent with those reported in our prior work (Guo et al., 2020; Zeng et al., 2021). The transient changes in porewater concentration and the C_t/C_p have important implications for designing and operating porewater sampling lysimeters.

Figure 7.

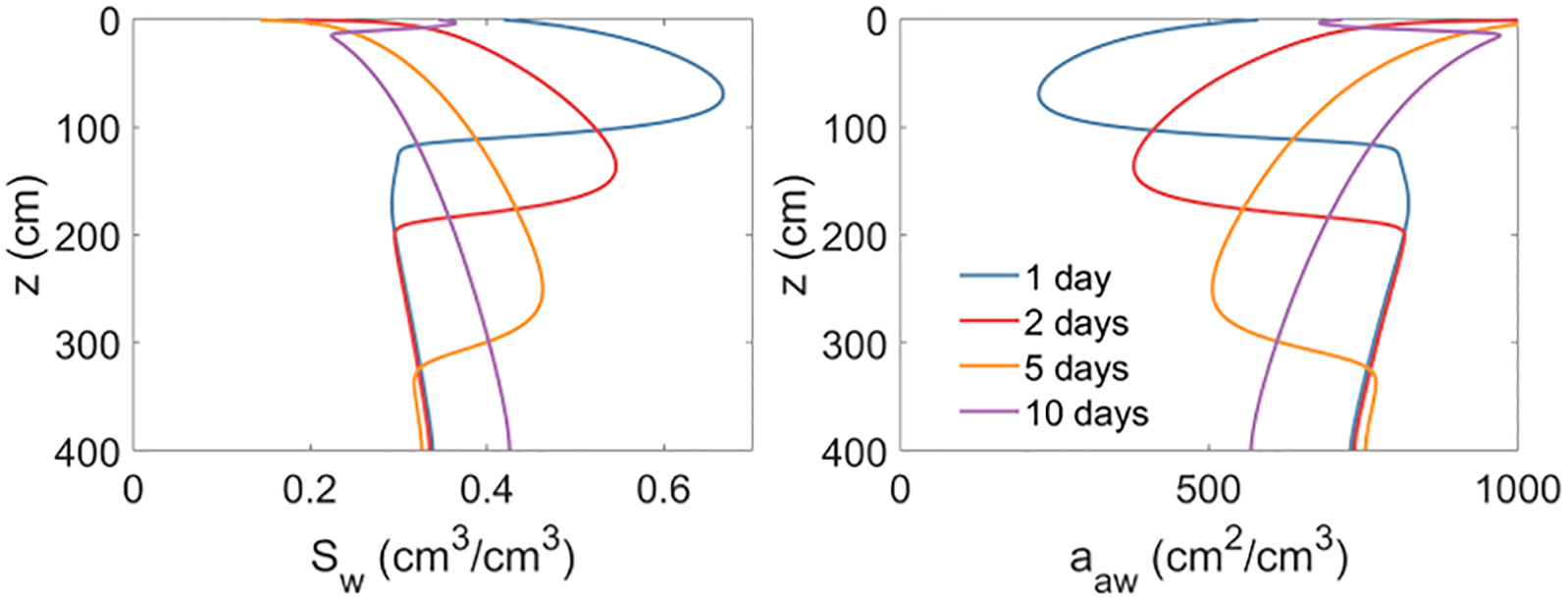
Spatial profiles of water saturation and specific air-water interfacial area during the 10-day period of short-term simulations. The results for the PFPeA simulations are presented here, but the water saturation and air-water interfacial area for the PFOA and PFOS simulations are almost the same as surfactant-induced flow has a relatively minor impact.

4.4. Field measured soil versus porewater concentrations

One of the first full-scale field applications of direct soil porewater sampling for PFAS was reported by Quinnan et al. (2021). This study comprised a test of high-resolution site characterization methods for quantifying PFAS concentrations and mass discharge for an aqueous film-forming foam (AFFF) source area at an Army Airfield facility. Three sampling lysimeters were installed in the vadose zone of the source area. The area was irrigated prior to porewater sample collection to facilitate sample collection. The sections within which each of the lysimeters resided received different magnitudes and rates of irrigation. Soil samples were collected from the intervals in which the lysimeters were installed to provide paired sample sets. The samples were analyzed for 13 PFAS, including PFOS and PFOA. This discussion will focus on the results presented for lysimeter LS-3R and the associated soil samples, which was in the section that received the lowest rate of irrigation.

The highest PFAS soil concentrations were reported for PFOS, which was ~300 μg/kg for the selected section. In comparison, concentrations of 1.8, 1.5, and 1.2 μg/kg were reported for PFNA, PFOA, and PFHxS, respectively, for the same section. The highest PFAS concentrations in soil porewater were also reported for PFOS, 6 μg/L for the selected lysimeter. Concentrations of 0.3, 1, and 1.1 μg/L were reported for PFNA, PFOA, and PFHxS, respectively. Values for C_s/C_p were calculated using the reported concentration pairs. The values range from 51 for PFOS, 6 for PFNA, to values of 1–2 for the shorter-chain PFAS (PFOA, PFHpA, PFHxA, PFPeA, PFHxS, PFHxA). The ratios are observed to be larger for the longer-chain PFAS and smaller for the shorter-chain PFAS, which is consistent with the analyses presented above.

4.5. Practical implications

There are multiple implications to the results of this study. One aspect is the relationship between soil concentrations and total concentrations. If the soil sample is collected in a manner that retains all PFAS mass, then C_s would be equivalent to C_t. Conversely, C_s would be anticipated to be lower than C_t if some fraction of mass is lost during sample collection and processing. Generally, for PFAS with low vapor-pressures, the primary potential source of mass loss may be anticipated to occur via partial drainage of porewater during sample collection and processing. From equations 4 and 8, 1/R_d represents the fraction of PFAS mass present in porewater. For R_d >20, the mass present in porewater represents <5% of the total mass. Hence, it is observed that the loss of some portion of porewater during sample collection and processing will not significantly influence the representativeness of the soil concentrations for samples for which R_d values are relatively large. However, measured C_s values will not be fully representative of C_t when porewater loss occurs for conditions with smaller R_d values. The issue of PFAS recovery during sample processing is a separate issue that can of course affect actual C_s values measured.

The distribution model presented herein can be used to examine the anticipated range of concentrations of PFAS in porewater, based on measured soil concentrations. Brusseau et al. (2020) conducted a meta-analysis of measured PFAS soil concentrations and observed concentrations ranged over many orders of magnitude, depending in part on the type of site. For example, soil concentrations up to 100s of mg/kg have been reported for AFFF-impacted sites. Hence, the associated porewater concentrations for these sites can be anticipated to be in the range of μg/L to mg/L depending upon the specific PFAS and the soil properties and conditions.

Guo et al. (2020) conducted long-term numerical simulations for a model fire-training source area for representative field conditions. Porewater concentrations ranging up to 10’s of mg/L were obtained for PFOS, for a simulated release concentration of 1,000 mg/L. The simulations presented in section 4.3 produced porewater concentrations ranging up to ~1 mg/L for a simulated release concentration of 100 mg/L. As noted in the preceding section, Quinnan et al. (2021) reported porewater concentrations for PFOS ranging up to 6 μg/L for an AFFF-impacted site. Davis et al. (2021) reported a porewater concentration of ~16 mg/L for total PFAS for an AFFF-impacted site. These results are consistent with the concentrations anticipated for sites with relatively high soil concentrations.

In contrast to primary-source sites that typically have relatively high soil concentrations, PFAS porewater concentrations are anticipated to be significantly lower for secondary-source sites such as locations receiving land application of biosolids or treated wastewater. Porewater concentrations are anticipated to be lower still for sites for which no known PFAS sources are nearby. For example, the median of maximum reported PFOS soil concentrations was 2.7 μg/kg for sites with no known nearby PFAS sources (Brusseau et al., 2020). Porewater concentrations are anticipated to be in the ng/L to lower μg/L range for such sites. Discussion of relevant porewater concentrations for transport investigations and risk assessments need to account for these anticipated ranges in concentrations.

5. Conclusion

The objective of this research was to delineate the relationship between soil porewater concentrations and soil concentrations, based on a comprehensive model of PFAS mass distribution within a soil sample volume. The distribution model was used to illustrate the impact of PFAS chain length and soil properties on the ratio of soil concentration to soil porewater concentration. For a given soil, the ratio is greater for longer-chain PFAS. And, for a given PFAS, it is larger for soils with greater sorption capacities and larger air-water interfacial areas. For a given soil and PFAS for which air-water interfacial adsorption is important, the ratio increases with decreasing water content due to the increase in air-water interfacial area.

Measured data reported in the literature for soil and soil porewater concentrations of several PFAS obtained from outdoor lysimeter experiments were used to test the distribution model. Soil-to-porewater concentration ratios predicted with the model compared very well to the measured concentration ratios. The nondimensional distribution coefficient that describes the distribution of PFAS mass among all domains within a soil sample was observed to be a function of PFAS molecular size. Numerical simulations conducted for a model fire-training source area were used to illustrate the magnitudes of soil versus porewater concentrations for representative field conditions. The results of the measured and simulated data sets demonstrated the importance of air-water interfacial adsorption for the distribution of the longer-chain PFAS within soil samples. This work has demonstrated the relationship between porewater concentrations and soil concentrations and the factors that influence the distribution of PFAS within a soil sample. Soil concentrations are what are typically reported for site investigations. However, porewater concentrations represent the mass that is directly subject to migration and mass discharge to groundwater. In addition, porewater concentrations generally comprise what is readily bioavailable to plant roots and soil microorganisms. Thus, the importance of understanding this relationship is evident. PFAS soil porewater concentrations are anticipated to range from ng/L to mg/L depending on soil concentrations, which in turn depend on the nature of the site. These ranges in concentrations need to be accounted for in discussions of relevant porewater concentrations for transport and fate investigations and risk assessments. The distribution model presented herein is anticipated to be useful for developing and enhancing conceptual site models and for conducting site investigations, risk assessments, and remediation-feasibility studies.