Abstract
The peristaltic motion of stomach walls combines with the secretion of digestive enzymes to initiate the process that breaks down food. In this study, the mixing, breakdown, and emptying of a liquid meal containing protein is simulated in a model of a human stomach. In this model, pepsin, the gastric enzyme responsible for protein hydrolysis, is secreted from the proximal region of the stomach walls and allowed to react with the contents of the stomach. The velocities of the retropulsive jet induced by the peristaltic motion, the emptying rate, and the extent of hydrolysis are quantified for a control case as well as for three other cases with reduced motility of the stomach, which may result from conditions such as diabetes mellitus. This study quantifies the effect of stomach motility on the rate of food breakdown and its emptying into the duodenum and we correlate these observations with the mixing in the stomach induced by the wall motion.
I. INTRODUCTION
The human stomach stores, mixes, processes, and grinds ingested food. Understanding these functions is becoming increasingly important as digestion-related disorders and issues related to nutrition are becoming prevalent.1–3 For researchers in the field of medicine, stomach motility plays a key role in gastric disorders such as gastroesophageal reflux disease (GERD), gastroparesis (delayed emptying), and dumping syndrome (rapid emptying) as well as in the pathophysiology of diabetes and functional dyspepsia,4–7 because the rate at which the stomach empties its contents into the duodenum affects the rate at which the nutrients get absorbed in the intestines. Gastric emptying is also important for drug delivery via oral administration as it determines the time it takes for the effects of the drug to manifest themselves.8,9 For researchers in the arena of nutrition and food design, a better understanding of the biomechanical processes involved in gastric mixing and hydrolysis could help answer questions related to the bioavailability of nutrients and the variation in emptying rates and food hydrolysis with food properties.
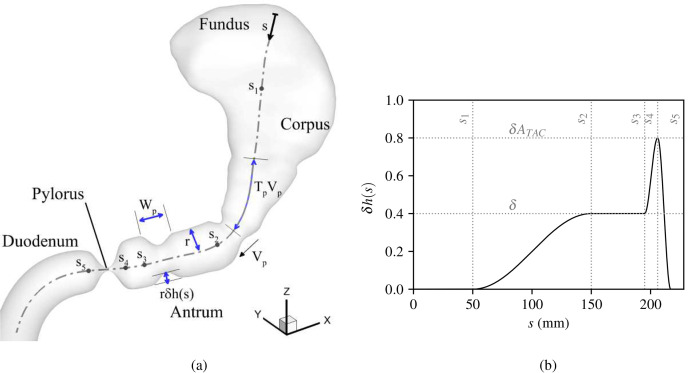
The physical and chemical action of the stomach is highly regional. The stomach has three major regions—the fundus, the corpus, and the antrum (Fig. 1). The fundus and corpus grow or shrink to accommodate the volume of ingested food without affecting the pressure in the lumen. They also contain glands that secrete acid and enzymes to break down food.10 The gastric pacemaker is also present along the greater curvature in the corpus. The pacemaker is responsible for initiating periodic peristaltic waves, known as antral contraction waves (ACWs), which travel toward the pylorus along the stomach walls.11 The amplitude of these waves is small in the region of inception, but it increases gradually till the waves reach the antrum.12,13 At the distal end of the antrum is the pylorus—a small orifice connecting the stomach to the duodenum. The orifice is surrounded by muscular tissues responsible for opening and closing the pylorus. Right before the ACWs terminate at the pylorus, a segmental contraction leads to a high-amplitude collapse of the walls near the pylorus; this event is known as the terminal antral contraction (TAC). TAC propels the trapped gastric contents away from the collapsing orifice thereby generating a retropulsive jet, which facilitates the mixing, grinding, and dissolution of the food. The coordination between the opening/closing of the pylorus and the TAC is crucial to the dynamics of gastric emptying. The terminal antrum and the pylorus close in a sequentially coordinated manner with the pylorus being completely closed before the TAC completely collapses the walls of the terminal antrum.14,15 This coordination regulates emptying and enhances the mixing and grinding of trapped contents.
FIG. 1.
A schematic showing different regions of the stomach.
These muscular activities vary from meal to meal and from person to person. Liquid meals empty faster than solid meals.16 Lower viscosity meals generate deeper indentation ACWs17 than higher viscosity ones. There also exists a feedback loop between the duodenum and the antrum that regulates the rate of caloric availability in the duodenum to about 2–4 kcal/min.18 The meal structure and softness play a role in the emptying rate as well because the pyloric orifice ensures that only particles smaller than 2 mm are emptied while the rest continue to undergo fragmentation and dissolution within the antrum by the action of the retropulsive jet and the ACWs.13 Thus, gastric mixing and emptying are complex processes with intricate neurohormonal control mechanisms that adjust the motility based on multiple food properties.
Studying gastric chemo-fluid dynamics via experiments poses several challenges. In vivo approaches are cost-intensive and ethically constrained. In vitro models, on the other hand, fail to replicate the complex wall motion as well as the chemical response to the food.19 However, the stomach geometry and motility information gleaned from MRI scans and other motility mapping devices20 can be used to construct computational (in silico) models that overcome many of the limitations of these other approaches. This has become possible only in recent decades with the advancement in computational power and algorithms.
There are relatively few examples of studies that have tried to investigate gastric mixing and emptying via computational models. The first work that used computational fluid dynamics (CFD) to investigate flow inside the stomach was based on a 2D stomach model.12,21 Stomach motility was defined from in vivo MRI data to study the rate of gastric emptying. Kozu et al.22,23 studied the mixing of gastric contents in a simplified 2D model of the terminal antrum. An axisymmetric model was also developed by Alokaily et al.24 to study the effect of peristaltic wave parameters and viscosity on the retropulsive jet and recirculation of antral contents. Others have used full 3D stomach geometries as well,25,26 in which a simplified 3D geometric model of the stomach that was symmetric about the central plane was employed. In another study, the effect of posture on the recirculation of gastric contents was investigated using an anatomically realistic geometry.27 Berry et al.28 used flexible printed circuit arrays to map the bioelectrical activity on the stomach walls, which was fed into a CFD model of the stomach to study the recirculation and mixing in the antrum region. Such an approach directly links the computational models with the in vivo observations. Harrison et al.29 used a coupled biomechanical-smoothed particle hydrodynamics (B-SPH) model to see the effect of viscosity and the period between ACWs on the mixing and emptying rate from the stomach. More recently, Ishida et al.15 have investigated the effect of impairment of the coordination between ACW and the opening/closing of pylorus for meals with different viscosities. Hosseini et al.30 have demonstrated a methodology to construct a dynamic model of the stomach from MRI data, which can be used to develop more accurate computational models. Li and Jin31 studied the effect of TAC on the flow field and incorporated acid secretion into their model to understand pH variations inside the lumen. They also studied the stacking of food boluses due to foods of different densities.32 Dufour et al.33 developed an experimental prototype of the antrum and used it to validate their computational model. The numerical simulations mimicked the experiments, providing complementary information, to reveal the effect of different wave parameters and fluid viscosity on the antrum flow field and the mechanical stresses experienced by the contents. A recently described model by Acharya et al.34 has incorporated fluid–structure interaction (FSI) between the fluid contents and the gastric muscle fibers.
Although the interest in this field is growing, computational models of the gastric function lag far behind other disciplines such as cardiovascular and respiratory biomechanics. One key question that has not been addressed by the previous studies is the effect of stomach motility on the hydrolysis of food. Mixing in the stomach facilitates the chemical reaction between the enzymes and the ingested food, which, in turn, determines the composition of the contents (chyme) emptied out of the stomach into the duodenum. The coupling of chemistry and fluid dynamics within the stomach is key to understand the sites of enzymatic activity, the effect of pH gradients, and the outcomes of impairment in stomach motility. Trusov et al.35 carried out multi-species simulations of just the antro-duodenal region to investigate the effect of secretory function disorders, but they did not focus on the effect of stomach motility on food breakdown. Furthermore, since the parietal cells and the chief cells, which secrete gastric enzymes from the walls, are located in the proximal stomach,10 the complete geometry of the stomach is required to accurately capture the transport and activation of enzymes. A full stomach model that incorporates food hydrolysis will facilitate an understanding of the regional differences in enzymatic activity and how these differences evolve over time during gastric digestion.
The effect of stomach motility on gastric digestion can also be studied via computational models since these models allow us to systematically vary key parameters and exclude confounding effects. For example, stomach motility shows a wide variation in response to food properties but may also be affected by disease and dysfunction. Gastroparesis refers to delayed gastric emptying in the absence of any physical obstruction at the gastric outlet. In 2007, the age-adjusted prevalence of gastroparesis in the U.S. per 100 000 people was 24.2, a significant rise from 2.4 in the years 1996–2006.4,36 This could be caused by diabetes, postsurgical, or postinfection complications, but it is also idiopathic in a large subset of patients.4,37 Variations in gastric motility can be caused by other conditions as well. For example, patients with Parkinson's disease have slower gastric emptying and fewer antral contractions of smaller amplitude.10,38 Erythromycin, which is a commonly used antibiotic, has been shown to improve antral contractility thereby increasing the ACW amplitudes.39,40
In this study, we address the following questions: How do the enzymes secreted in the proximal stomach mix with gastric contents and hydrolyze the ingested food? How does the composition of the contents emptied into the duodenum change with time? How do the mixing, hydrolysis, and emptying change with variations in gastric motility? Recently, our model has been used to study the dissolution of orally ingested pills and the delivery of the active pharmaceutical ingredient into the intestines.9,41 Here, we use the same modeling infrastructure to study the hydrolysis of a liquid meal containing protein.
II. METHODOLOGY
A. Stomach model
The geometry of the stomach is obtained from the Virtual Population Library42 and is based on of the body type “Duke” which corresponds to a male adult. The pylorus and the duodenum are added manually using SolidWorks (Dassault Systèmes, Vélizy-Villacoublay, France), because they were not resolved clearly in the available dataset. The duodenum is assumed to be a tubular extension with the same diameter as the antrum. The size of the pyloric opening, which is at the junction between the antrum and the duodenum, is critical for modeling the emptying rate. In the current study, this is modeled as a circular orifice with a maximum opening size of 2 mm based on the literature on the post-prandial state of the stomach.43,44
The amplitude of the ACW at any given axial location is given by , where δ is the nominal strength of the ACWs. The amplitude modulation function h(s) is a factor used to vary the effective strength of the ACWs from zero in the fundus (i.e., no ACW) to δ in the antrum and then to near the pylorus corresponding to the high amplitude collapse of walls due to terminal antral contraction (TAC). This variation, along with the stomach geometry describing the relevant motility parameters, is shown in Fig. 2. A detailed description of the motility model is available in Appendix A.
FIG. 2.
Description of the (a) stomach geometry and wall deformation model, and (b) amplitude modulation function along the centerline [h(s)], which varies the strength of the ACWs along the centerline from 0 in the fundus, to δ in the antrum, and to just before the pylorus.
For this study, the goal was to model a low-calorie liquid meal containing protein, and the caloric density is a key determinant of gastric emptying. So, the velocity, width, and occlusion of the ACWs that we chose for this study (Table I) were measured in response to a liquid meal of low caloric density. These parameters were used by Ferrua and Singh,26 who based it on MRI observations made by Pal and others12,21 after ingestion of a liquid meal with a caloric density of 0.73 kcal/ml. Bornhorst and Singh19 wrote a comprehensive review of the motility measurements made by several researchers. In other studies, while the frequency of the waves was quite consistently observed to be in the range of 2.6–3 waves/min (Refs. 45–49) (i.e., Tp = 20–23 s) and the mean amplitude was found to be between ,49 a larger variation was observed in mean wave speeds, ranging from 1.6 to 2.8 mm/s.45–48,50 Nonetheless, the values chosen for this study are within the range of motility parameters found by most studies conducted on low-calorie liquid meals.
TABLE I.
Motility model parameters based on Ref. 26. Other values of the nominal amplitude of ACWs, δ, were also considered ( 0.20, 0.27, and 0.34) to model the weak motility state of the stomach.
| Parameter | Value |
|---|---|
| Vp | 2.3 mm/s |
| Wp | 20 mm |
| Tp | 20 s |
| δ | 0.4 |
| ATAC | 2.0 |
Gastric disorders have been known to reduce the strength of stomach motility by up to half of that of normal cases.50,51 This can exhibit as a reduction in the amplitude or frequency, but in this study, we focus only on variations in amplitude and choose three reduced motility cases (apart from the healthy/control case with amplitude ): , 0.27, and 0.20, corresponding to 85%, 67.5%, and 50% of the amplitude of the control case.
B. Fluid flow
The stomach lumen is discretized with ∼33 000 triangular elements. This surface mesh is immersed into a Cartesian volume of size 24 × 8 × 16 cm3 in , and directions, respectively, as shown in Fig. 3, with a grid spacing of 0.5 mm in each direction (i.e., a 580 × 160 × 360 grid). Simulations are conducted with a time step size of 0.005 s, and grid and time step refinement studies have been conducted (see Appendix C) to confirm the adequacy of these choices.
FIG. 3.
The triangulated surface mesh is immersed in an outer Cartesian mesh with an open fundus at the top (labeled A) and an open duodenum at the bottom (labeled B).
The gastro-duodenal contents are assumed to have the properties of water (with density ρ = 1000 kg/m3 and dynamic viscosity Pa s), which is a good assumption for liquid meals. The fluid flow is governed by the incompressible Navier–Stokes equations for Newtonian fluid
| (1) |
| (2) |
where m/s2 is acceleration due to gravity. For pressure, a zero gradient boundary condition (BC) ( ) is applied on all boundaries. A no-slip boundary condition is specified on the stomach walls ( ). The lumen model also has two openings—one cutting through the fundus and another through the duodenum (labeled as A and B, respectively, in Fig. 3). The boundary conditions (BC) on these two openings are specified based on the state of the pylorus. When the pylorus is open, the fundic boundary is closed by a zero-velocity BC and the duodenal boundary acts as an outflow with a zero-gradient BC for . When the pylorus is closed, the roles are switched—a no-slip BC is specified at the duodenal boundary and the fundic boundary has a zero-gradient BC. This allows small amounts of inflow or outflow from the corpus as would be expected for an incompressible flow, and this models the accommodative effect of the fundus. Mathematically, with A and B referring to the two openings of the geometry as shown in Fig. 3,
-
•When pylorus is closed,
(3) -
•When pylorus is open,
(4)
The collapsing terminal antrum decreases the stomach volume when the pylorus is open, causing the emptying of gastric contents through the pylorus and outflow via the open duodenum. The pylorus closes immediately before the completion of the collapse of the terminal antrum. Subsequently, the antral relaxation raises the stomach volume back to its original value, which pulls in more food from the fundus region. This flow behavior acts as a model of tonic contractions that forces a net one-way flow through the pylorus. The rate of emptying is determined by the ACW kinematics and the fluid properties.
These equations are solved using ViCar3D, a sharp-interface immersed boundary method (IBM) solver.52 In this solver, the spatial derivatives are discretized using second-order central difference schemes, the equations are advanced in time using a fractional-step method, and the Crank–Nicolson scheme is used to integrate in time. A stabilized bi-conjugate gradient method is used to solve the pressure Poisson equation. More details on the numerical methodology and grid convergence study can be found in earlier works.9,41
C. Gastric digestion model
The chemical kinetics in a postprandial stomach are highly complex with different nutrients undergoing different chemical processing. The breakdown of carbohydrates, for example, begins in our mouth as mastication mixes our salivary amylase with the food bolus. This continues till salivary amylase is exposed to the acidic environment of the stomach where it is deactivated.53 The digestion of carbohydrates, subsequently, resumes in the small intestines. Proteins and lipids, on the other hand, are targeted by enzymes secreted from the gastric walls. The proximal gastric walls contain chief cells that secrete pepsinogen and gastric lipase.10 Pepsinogen is activated in the presence of acid to form pepsin, which hydrolyzes proteins, while gastric lipase helps break down lipids. Each of these enzymes is highly sensitive to pH; pepsin's activity is maximum at a pH of 2 and is completely inactive for pH > 5, and gastric lipase, on the other hand, shows peak activity in the pH range of 5–6.10 The process is further complicated by other factors such as enzyme secretion rates that vary with the composition and physical properties of food as well as time elapsed since meal consumption. Thus, several assumptions need to be made to devise a model for the chemical breakdown of a liquid meal.
For this study, we focus on a single-component liquid meal that contains only protein. Lipids are not considered in this model since they are lighter than water and add the extra complexity of gravity-induced buoyancy effects. We further assume that the stomach has a constant acidic pH at all times throughout the volume, and the enzyme pepsinogen is instantaneously activated into pepsin upon entering the acidic environment of the stomach. This enzyme is secreted from the proximal walls of the stomach as illustrated in Fig. 4.
FIG. 4.
Schematic showing the four different zones for implementing scalar boundary conditions. A and B correspond to the openings where the faces of the computational domain intersect the geometry, C is the portion of the stomach walls that secretes pepsin, and D refers to the walls of the rest of the stomach and the duodenum.
Protein hydrolysis in the current model is assumed to follow first-order catalytic reaction kinetics:
| (5) |
| (6) |
There can be multiple varieties of proteins in a protein meal, and each type of protein exhibits a different reactivity to pepsin. The reaction constants for pepsin's catalysis of each of these proteins are, however, not readily available. Here, we assume that the ingested meal contains only one kind of protein—N-acetyl-L-phenylalanyl-L-phenylalanine ( )—for which the reactivity with pepsin has been studied, and the reaction constants at optimal pH value are available.54
The three species in the model—pepsin, protein, and digesta—are modeled as passive scalars, and an advection-diffusion-reaction equation is used to solve for their concentration
| (7) |
where ci is the concentration of ith species (i = 1, 2, and 3 correspond to pepsin, protein, and digesta, respectively), Di is the diffusion coefficient of that species, and Si is the source term due to the digestion reaction. Given that the mixing in the postprandial stomach is advection dominated, we assume that each species has the same coefficient of diffusion of m2/s.35 Pepsin acts as a catalyst and, therefore, . The source term due to the digestion reaction consumes protein and produces digesta; therefore, , and following Refs. 35 and 54, the value of this consumption/production rate is set to , where c1, c2 represent the concentrations of pepsin and protein, respectively, and kmol/m3.
To discretize the advection–diffusion equation, we use a second-order central-difference scheme for the diffusion terms and a hybrid second-order central and upwind schemes for the advection terms. A fourth-order Runge–Kutta method is used to explicitly integrate the equations in time. At t = 0, the stomach is filled with the homogeneous liquid meal, while the concentration of pepsin and digesta is set to zero throughout the stomach volume. The concentration of protein in the meal is calculated based on the contents of a typical protein shake available in the market—24 g protein in 200 ml water. A zero mass-flux boundary condition is applied on the stomach walls for food and digesta (regions C and D shown in Fig. 4). For pepsin, the flux on the proximal walls of the stomach (region C) is specified using the basal-pepsin-output (BPO) reported by Feldman et al.55 On the rest of the stomach walls (region D), pepsin has zero mass flux. For all the species, a convective boundary condition is implemented at the duodenal outflow boundary, and a zero gradient condition is applied at the fundic boundary. Mathematically,
-
•
Boundary A and D: {pepsin, protein, and digesta},
-
•
Boundary B: {pepsin, protein, and digesta}, where is the average outflow velocity on that boundary.
-
•
Boundary C: pepsin, {protein and digesta}, where is a constant that is defined such that the total amount of pepsin secreted from the walls matches the mass-flux rate of pepsin as reported by Feldman et al.55
D. Simulating over long digestion times
The computational grid consists of ∼25 × 106 points, which were required to resolve the flow through the pylorus and, at the same time, include the duodenum and the entire stomach. Furthermore, simulating a few ACW cycles is not sufficient to capture the trends in meal breakdown. Even though the ACWs are initiated every 20 s, the process of gastric digestion might take anywhere from 30 min to several hours depending on the caloric density and other meal properties.17 Each ACW cycle of 20 s takes ∼6000 h of CPU time to simulate, and we are interested in digestion trends given by O(100) ACWs. This necessitates a computationally efficient approach to modeling gastric digestion. In the current simulations, we made use of the periodicity of the stomach kinematics and the flow inside the stomach model to enable the simulation of digestion over O(100) ACWs at a considerably reduced computational expense.
We assume that the open fundus supplies the food that is emptied in each cycle, and therefore, the volume of the stomach does not change with time. This assumption is valid for the early to mid-stages of the digestion of a meal. The flow inside the stomach is, therefore, driven by the periodic motions of the ACW peristalsis, and consequently, the fluid flow in this stomach achieves a periodic state within a few ACW cycles. The L2-norm of the difference between velocity field of the cycle and the cycle, normalized by the velocity of the ACW, was O( ). In the current procedure, the simulated flow field for the entire third cycle (after two cycles or 40 s of ACW propagation) is recorded/saved to file, and subsequently, only the transport equation for pepsin, protein, and digesta is solved with this recorded velocity field. By eliminating the solving of the momentum and the mass conservation equations, we obtain a speed-up of 8.5 times, and this enables us to simulate digestion for O(1000) s.
III. RESULTS
The development of computational models of the stomach lags far behind that of cardiovascular flows. Only a few studies in the past have computationally investigated gastric fluid dynamics, and in this study, we model the chemo-fluid dynamics of enzymatic hydrolysis of a liquid meal. Our aim is to investigate the effect of reduced motility (due to disease or medication) on fluid flow as well as the rate of breakdown of a liquid meal. The nominal amplitude of the antral contraction waves (ACWs) is varied from 0.4 (the control case) to 0.2 (the weakest motility case). The results are discussed in three parts—fluid flow, protein hydrolysis, and quantification of advective mixing. We conclude with a discussion on the future work and the limitations of our current approach.
A. Flow dynamics
Previous studies have described three key features inside the stomach that plan key roles in gastric mixing and emptying—a retropulsive jet, antral eddies between ACWs, and a pyloric jet. These flow features are reproduced in the current simulations as shown by the streamlines in Fig. 5. The velocity magnitude contours at different time instances and the effect of variations in ACW amplitude are shown in Fig. 6. The retropulsive jet and the eddies between ACWs help transfer gastric contents away from the walls toward the center of the lumen and enhance mixing. The pyloric jet empties the contents into the duodenum and also entrains the pepsin into the jet, while the retropulsive jet returns contents back into the antrum for further grinding and mixing. If the contents included solid food particles, the contents carried away by the retropulsive jet would contain all the solid particles larger than the pyloric orifice (∼2 mm). This repeated grinding of food particles continues till particle size becomes smaller than the pyloric orifice, and the food can pass into the duodenum.
FIG. 5.
Streamtraces colored by velocity magnitudes in the antrum region for control case ( ) showing the three characteristic flow features—pyloric jet, retropulsive jet, and eddies between ACWs.
FIG. 6.
Comparison of velocity magnitude contours shown on a cross section through the antro-duodenal region at three time-instances—(1) t = 0.0: an ACW approaching an about-to-open pylorus, (2) t = 4.75: a fully open pylorus during the event of TAC, and (3) t = 7.75: right after the closing of the pylorus. Notice that the TAC is still under way even after the pylorus has closed, which leads to a very prominent retrograde jet, especially in higher amplitude cases. Here, δ is the fractional amplitude of the ACWs in the antrum, and the duodenum is to the left of the pylorus.
The time sequence in Fig. 6 illustrates the role of the phase between the pyloric sphincter and TAC, i.e., a collapse of the stomach walls right before the ACW terminates at the pylorus. Initially, the ACW approaches a closed pylorus and in this phase, the gastric contents are transferred only to the proximal antrum via the retropulsive jet. As the ACW advances, the pylorus opens and a portion of the chyme trapped between the ACW and the pylorus empties via the pyloric orifice while a larger portion continues to be transported back into the stomach. This is when the TAC begins and increases the velocities of both jets. The pylorus closes before the TAC ends and the trapped chyme is, once again, left with only the retrograde path out of the collapsing segment. The retropulsive jet velocity peaks at this time while the pyloric jet velocity is maximum when the orifice was fully patent and the TAC had set in. The maximum area-averaged jet velocities of both jets are shown in Table II. The pyloric jet velocities are an order of magnitude higher than the retropulsive jet velocities. Both, the retropulsive and pyloric, jet velocities also reduce significantly with weakening motility. The retropulsive jet is, however, affected more adversely, dropping to 13% of the velocity of the control case, as compared to the pyloric jet, which dropped only to 73%. This reveals that weakened motility implies significantly reduced gastric mixing.
TABLE II.
The peak velocity of the two jets is compared for different fractional amplitudes (δ) of ACWs in the antrum. The % in parentheses is calculated by normalizing each case with the corresponding value of the control case ( ).
| δ | Maximum jet velocity (cm/s) | |
|---|---|---|
| Retropulsive jet | Pyloric jet | |
| 0.20 | 0.24 (13%) | 7.30 (73%) |
| 0.27 | 0.43 (23%) | 8.62 (86%) |
| 0.34 | 0.83 (44%) | 9.43 (94%) |
| 0.40 | 1.88 (100%) | 9.99 (100%) |
The volume rate of emptying via the pyloric orifice is a key parameter, because it influences the rate at which nutrients are absorbed in the intestines and it triggers the neurohormonal feedback mechanism56 that controls gastric motility. The emptying rates for different ACW amplitudes are shown in Table III. The emptying rate drops by 35% for the case with the weakest motility.
TABLE III.
Comparison of the volume of fluid emptied through the pylorus per minute for different fractional amplitudes (δ) of ACWs in the antrum. The % in parentheses is calculated by normalizing the emptying rate with that of the control case ( ).
| δ | Emptying rate (ml/min) |
|---|---|
| 0.20 | 2.89 (65%) |
| 0.27 | 3.61 (81%) |
| 0.34 | 4.15 (93%) |
| 0.40 | 4.48 (100%) |
The case with has the same motility parameters used by Pal et al.12 and Ferrua and Singh,26 and these are based on MRI data obtained after ingestion of a 330 ml meal with a caloric density of 0.73 kcal/ml. This case is used to validate the model by comparing the emptying rate of with other studies with a meal of a similar caloric density. As seen in Table IV, the emptying rate obtained from our computational model is reasonably in line with the experimental measurements by other studies of similar viscosity and caloric density meals.
TABLE IV.
The emptying rate of the current model is compared with other experimental works in the literature. The meal properties of the present work correspond to the meal that was used in the imaging study whose motility parameters have been used in our model.12,26
B. Protein hydrolysis
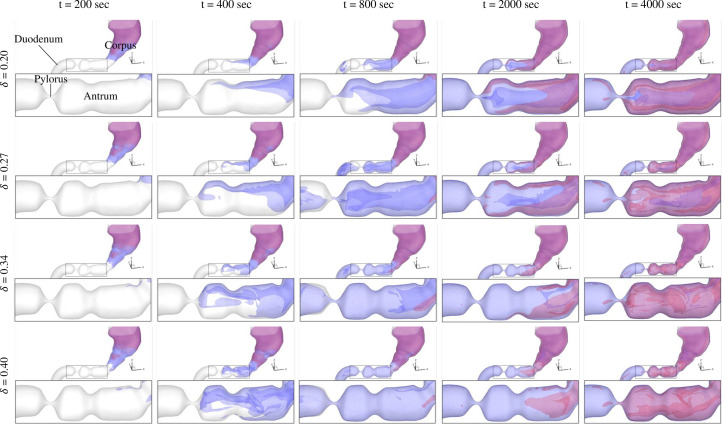
Figure 7 shows the progression of enzymatic hydrolysis of the protein-rich liquid meal for different amplitudes of ACW. The pepsin initiates the hydrolysis of the meal close to the secretion zones in the proximal stomach, where the contents are relatively stagnant. Pepsin is, subsequently, transported away from the proximal walls by diffusion and also by advection in the corpus due to small amplitude ACWs that have originated in the mid-corpus. With these two mechanisms, the pepsin concentration front is slowly transported to the antrum along the stomach walls. The antrum has a much stronger advection due to the larger amplitude ACWs; this results in significantly enhanced mixing as compared to the proximal stomach and leads to faster hydrolysis. The weaker motility cases take longer to transport pepsin from the proximal stomach to the antrum and are also less efficient in mixing it with the protein once pepsin arrives in the antrum. Consequently, the rate of protein hydrolysis suffers as less protein is exposed to the enzyme. A detailed analysis of this mixing is described in Sec. III C.
FIG. 7.
Iso-surfaces of concentration at level 0.01 (normalized with respect to the initial concentration of protein in the stomach) for pepsin (red), and digesta (blue) in the antral region. The meal fills the entire stomach at t = 0, and δ corresponds to the fractional amplitude of the ACWs.
As time progresses, pepsin continues to be secreted from the proximal walls and transported toward the antrum. The increase in the amount of pepsin, combined with the fact that it is not consumed during the chemical reaction, causes the rate of digestion to rise exponentially in time. Eventually, this exponential rise slows down as pepsin starts to empty via the pylorus as well (as seen in Fig. 7) and an asymptote is reached when the amount of pepsin being secreted from the walls is matched by the rate of flux of pepsin through the pylorus. The chyme that empties via the pylorus is a mixture of undigested protein, pepsin, and hydrolyzed protein. Pepsin and undigested protein fluxes are represented in Fig. 8. In the initial stages, almost no pepsin is emptied and most protein empties without being hydrolyzed. At later times, pepsin flux rises almost linearly but the protein flux drops because mixed pepsin starts hydrolyzing at an exponential rate. As we reach h, the exponential rate of hydrolysis starts to slow down and the protein flux starts to stagnate. During digestion, pepsin expelled into the duodenum gets deactivated because of the high pH environment in the duodenum, and from there, pancreatic protease takes over the digestion process.19
FIG. 8.
Amount of (a) unhydrolyzed protein and (b) pepsin emptied per cycle for different cases.
The long duration (5000 s) over which the gastric hydrolysis is simulated allows us to capture the tri-phasic nature of gastric digestion as shown by the digesta emptied per cycle through the pylorus in Fig. 9. It also shows that the poor mixing in the flow translates to the hydrolysis of the meal since weaker motility cases empty lower amounts of digesta per cycle. However, for all cases, initially, there is an exponential rise which changes into a linear growth that eventually asymptotes to a value as . The figure also shows trend lines obtained by fitting the modified Elashoff's model, which has also been used by others to capture the emptying of different gastric components.9,58–60 It is a sigmoid shape function given by
| (8) |
where A(t), in the current study, corresponds to the amount of digesta emptied per cycle (20 s), is the predicted amount of digesta that would empty per cycle at steady state, and α and β are time constants for emptying and initial delay in emptying, respectively. The parameters obtained after curve fitting are shown in Table V. The parameter shows a uniform rise with δ, also shown in Fig. 10, which signifies that stronger motility leads to a faster rate of hydrolysis and emptying of digesta. When the ACW amplitude is halved, the rate of hydrolysis at the steady state dropped to 59% of its original value. The parameter α remains roughly the same for all choices of δ which means that the time constant of these curves is similar. The delay in the emptying rate is due to the time it takes to transport pepsin from secretion zones to the antrum. The rate of secretion of pepsin was the same for all cases but weaker amplitude ACWs are expected to be slower in transporting pepsin and show a longer delay. This delay (given by β) first decreases with rising δ and then remains roughly the same, then decreases again—which translates to weaker motility having a large delay period with a non-linear trend.
FIG. 9.
Amount of digesta (hydrolyzed protein) emptied per cycle for different antral contraction wave (ACW) amplitudes. The symbols denote the total amount of hydrolyzed protein emptied every 20 s from the simulations, and the curves are obtained by fitting the modified Elashoff's model to the simulation data.
TABLE V.
Parameters obtained by fitting the modified Elashoff's model to the digesta emptying rate in Fig. 9 for different amplitudes of ACWs (δ). Here is the predicted amount of digesta that would empty per cycle at the steady state, α is the time constant of emptying, and β is the initial delay in emptying.
| δ | (mmol) | α (s−1) | β |
|---|---|---|---|
| 0.20 | 0.19 (59%) | 0.000 70 | 4.30 |
| 0.27 | 0.24 (75%) | 0.000 68 | 3.84 |
| 0.34 | 0.29 (91%) | 0.000 70 | 3.93 |
| 0.40 | 0.32 (100%) | 0.000 67 | 3.55 |
FIG. 10.
The amount of digesta emptied per cycle at the steady state for different motility cases. This corresponds to the parameter obtained by fitting Elashoff's model to the pyloric emptying rate obtained from simulations.
C. Quantification of advective mixing
The chemical reaction occurs across the interface between the food and the enzyme, i.e., protein and pepsin. ACWs promote this reaction by stretching this interface and increasing the area across which the hydrolysis can occur and many of the observations and trends regarding the hydrolysis can be explained by examining the evolution of the interface between food and enzyme for the various cases. The interface length or area provides a direct measure of the mixing action of the ACWs and we choose to calculate the interface for pepsin, because it is the only component that is not being consumed or produced in the proteolytic process. The procedure to calculate the interface length is mentioned in brief in Appendix B, but a detailed explanation of the calculation can be found in the previous work.61 The procedure results in an interface length field variable ξ, which has values of 0, Δ, or for each grid cell, where Δ is the linear dimension of a grid cell. This interface length field is visualized in Fig. 11 for one plane (s = 16) at t = 1 h. It should be noted, however, that the term interface does not refer to the boundary between two phases as it is generally used in multiphase flows. Here, it only refers to a concentration front of a passive scalar (pepsin) transported across the stomach volume.
FIG. 11.
Calculating the interface at a cross section through the antrum for case at t = 1 h. (a) A plane normal to the centerline in the antrum (s = 16), (b) contours of pepsin concentration on that plane, (c) contours of normalized concentration gradient, and (d) the interface, ξ, formed by the local peaks in this gradient.
Figure 12 compares the interface at x = 12 at t = 1 h for the four motility cases. It is clear that the reaction interface is more widespread in the higher motility cases, which is a consequence of better mixing of pepsin with the contents. The inability to mix pepsin thoroughly results in almost non-existent reaction sites at the center of the stomach lumen. On the other hand, stronger motility exhibits intertwined and layered interfaces which fill the entire lumen.
FIG. 12.
Reaction interfaces for different motility amplitudes at t = 1 h at a plane perpendicular to the centerline in the antrum at s = 16. Subfigure (a) shows the cross section through the antrum lumen with a view normal to the cross section for , and (b), (c), and (d) show this view for 0.20, 0.27, and 0.34, respectively. The enhanced mixing of high-amplitude cases translates to the denser distribution of reaction fronts.
The sum of ξ over the cross-sectional plane normalized by the maximum possible length of the interface at the cross section gives us the interface length (Li), i.e.,
| (9) |
where is an upper bound on the possible interface length at any cross section, N1 and N2 are the grid points inside the lumen in the two orthogonal directions, and Δ is the grid size. Thus, Li denotes the fraction of the lumen that is filled by the interface. The variation in the interface length along the centerline, starting from s = 0 (at the top of the fundus) to s = 20 (right before the pylorus), is shown in Fig. 13. This figure demonstrates that all cases exhibit similar advective mixing in the fundus, but the interface lengths start to become quite different in the antrum region. This is because there is no wall motion in the fundus region, and the pepsin distribution in that region is similar for all cases.
FIG. 13.
The normalized area integral of ξ on the cross-sectional planes gives interface length, Li. (a) Location of a few planes normal to the centerline and (b) a comparison of Li for different motility cases at t = 1 h along the centerline from the fundus to the terminal antrum. The reaction interface is similar for all cases in the proximal stomach, but clear differences arise in the antrum with high motility cases having a higher interface length.
To see how the interface changes in time, we integrate the interface length at each crossection in the antrum region ( ) and normalize it by the length of the centerline to generate a single value at each time step, termed as interface area (Ai). Mathematically,
| (10) |
The variation in the interface area with respect to δ is shown in Fig. 14. This area is a measure of the size of the pepsin's concentration front and quantifies how well it is mixed with the contents of the stomach. There is a transience period after which all cases stabilize to a constant value. It is noted that high ACW amplitude cases not only have a shorter transience time but also a significantly higher overall interface area. Furthermore, to quantify the steady state behavior, the value of the interface area after an hour for each case is also shown, demonstrating a 33% drop when motility decreases from to 0.2.
FIG. 14.
(a) The interface area of pepsin as a function of time and (b) comparison of the interface area at t = 1 h for different ACW amplitudes δ. After initial transience, the interface area stabilizes to a constant value that quantifies how well is pepsin mixed with the gastric contents. The reaction interface area at t = 1 h shows a non-linear trend. Weaker motility cases result in a simpler interface resembling concentric circles without a significant presence at the core of the lumen. In higher motility cases, the interface fills the entire lumen due to stronger advection close to walls as well as near the center, leading to a much higher interface area.
IV. CONCLUSIONS
The computational modeling of gastric digestion is far behind that of other physiological flows, like cardiovascular flows, despite being highly relevant for issues related to the food industry, nutrient bioavailability, drug dissolution, gastric disorders, diabetes, and obesity. The few studies that have developed in silico models have focused on investigating the flow behavior inside the stomach lumen, while a deeper analysis of mixing and chemical hydrolysis, and the role of peristaltic waves in these processes, is missing. Quantifying the consequences of motility on the gastric phase of digestion cannot only help understand the effects of therapeutics, like the use of erythromycin, but also inform the use of surgical procedures like gastric-sleeve surgery or pyloroplasty.62 In this study, we modeled the hydrolysis of a liquid meal containing protein, incorporating enzyme secretion and the consequent catalytic hydrolysis of proteins. The effect of reduced motility on the mixing and the chemical reactions was also studied to highlight the consequences of a gastric disorder on gastric digestion and emptying. The observed linear trends in the variation of the emptying rate, of gastric contents (Table III) as well as the digesta (Fig. 10), with respect to motility, imply that the consequences of simple variations in gastric motility are relatively easy to anticipate. The mixing of contents and the sites of chemical hydrolysis, however, demonstrate a non-linear response toward the same.
The current model provides new data and insight for gastric mixing and food breakdown but has several limitations. First, the stomach volume is held constant over the entire duration of 5000 s simulated here. This assumes that the fundus has sufficient meal content stored so that it can keep supplying small amounts over time to maintain the stomach volume. This assumption made it computationally tractable to capture hydrolysis trends over a long enough digestion period. The model also assumed a uniform pH throughout the stomach volume, and this translates to instant activation of pepsinogen into pepsin. In an actual stomach, the importance of acid secretion and pH microclimates in enzyme activation is expected to be important. We expect the digestion delay phase to last longer if we consider the effect of pH as well. Finally, the stomach shapes vary from subject to subject, but such variations have not been considered in this study. However, the geometry used from the Virtual Population database42 exhibits the overall key features of an adult stomach, including a large volume proximal region that narrows down to the antrum and curvature of the antrum terminating into a narrow pylorus. Future studies will attempt to examine multiple stomach models but that is outside the scope of this study.
Notwithstanding these limitations, the current model allows us to quantify the effects of disorders like gastroparesis on food hydrolysis. We have quantified advective mixing within the stomach and how this mixing is modulated by changes in antral motility. All this information would be extremely challenging to obtain an experimental setting. We were also able to extend the simulations to longer durations and capture trends over a time period that is comparable to the actual digestion timescale. In the future work, we plan to include the effect of meal properties and tonic contractions of the stomach in our models. These features will make this model more complete and viable for a wider range of gastric digestion scenarios.
ACKNOWLEDGMENTS
We acknowledge research funding from the National Science Foundation (NSF) via Award No. CBET 2019405 and the National Institutes of Health (NIH) via Award No. 5R21GM139073-02. This work used the Extreme Science and Engineering Discovery Environment (XSEDE),63 which is supported by the NSF via Grant No. ACI-1548562, through Allocation No. TG-CTS100002.
APPENDIX A: STOMACH MOTILITY
Stomach motility is defined in a manner similar to the model of Ferrua and Singh.26 The peristaltic contractions, known as antral contraction waves (ACWs), deform the walls toward the centerline and propagate distally—from the upper body of the stomach toward the pylorus. The deformation was defined as
| (A1) |
where is the position vector of any point on the wall, is the initial position vector of the point without any deformation, λ is the fractional change in the radius, and is a vector from the point on the wall toward the centerline. essentially specifies the amount of deformation of any point on the stomach walls toward the centerline. The expression for λ is constructed by a summation of equispaced traveling cosine waves, and the expression is multiplied by a factor that varies their amplitude from one region to another. Mathematically, it is given by
| (A2) |
where s is the distance along the centerline, δ corresponds to the nominal deformation due to the wave, h(s) is the amplitude modulation function, which is used to vary the strength of this deformation along the centerline, n is the wave count, is the location of nth wave, is the filter function that restricts the deformation to half-wave-width distance from the center of each wave, and Wp is the width of the wave. The term inside the summation specifies a half-cosine wave centered at , and is zero everywhere else. The factor outside the summation, , denotes the net amplitude of the wave at a location in the centerline, whose variation was shown in Fig. 2.
That amplitude modulation function and filter function are given by
| (A3) |
| (A4) |
| (A5) |
where s1–s5 are locations along the centerline, spyl is the location of the pylorus, ATAC is the factor that controls the strength of collapse of the terminal antrum due to TAC, Vp is the speed of propagation of the ACW, and Tp is the time interval between two subsequent ACWs.
APPENDIX B: CALCULATING INTERFACE
To identify the interface of pepsin, we consider planes passing normal to the stomach centerline. On each plane, we calculate the concentration gradient and then normalize it by the -norm, i.e., . We then find local peaks in this normalized gradient over the plane to identify the interface ξ. If the normalized gradient of a cell is greater than two of its immediate neighbors (north, south, east, and west), then . If the normalized gradient value is greater than all four of its neighbors, then . Each step of this procedure is visualized in Fig. 15 at one plane at t = 1 h. The generated ξ field inside the stomach identifies the concentration front of pepsin. Similar approach has been used in a previous work by Rips and Mittal.61
FIG. 15.
The procedure for calculating the interface, ξ, at a plane perpendicular to the yz-plane at x = 12. (a) The concentration of pepsin on the plane, (b) normalized concentration gradient, (c) local peaks in the gradient over the plane give the interface, and (d) zoomed into the inset with visible grid lines.
APPENDIX C: GRID INDEPENDENCE AND TIME-STEP SIZE
1. Grid independence study
We try three different resolutions of uniform Cartesian grids to choose a grid size for this study: coarse ( , 3 × 106 grid points), medium ( , 24.6 × 106 grid points), and fine ( , 48 × 106 grid points). To compare the results from these grids, we follow a procedure similar to what is carried out in the digestion simulations. We solve the flow field for two ACW cycles (40 s) ensuring that the flow field reaches a periodic state. This is followed by solving the third cycle and saving the flow field from the entire third cycle to a file. From the fourth cycle onward, this saved flow field is used to solve the transport equation of passive scalars in the domain. The time-averaged and the root-mean-squared velocities of the fourth cycle are also calculated for comparing the flow field from the three grids.
Figure 16 shows the comparison of the x-direction velocity component (u) on a horizontal plane z = 4.7 passing through the antrum. The time-averaged (uavg) and the root-mean-squared fluctuating (urms) velocity profiles are compared at different locations on this plane. Figure 17 compares the instantaneous scalar concentration profiles of pepsin after 10 ACW cycles (200 s) at two horizontal planes—one passing through the antrum (z = 4.7) and another through the upper corpus (z = 10). Pepsin was chosen for this comparison because, being a catalyst, its concentration is not affected by protein hydrolysis and is determined purely by advection and diffusion. The two planes were chosen as they correspond to two different regions of the stomach. The scalar transport in the antrum is advection dominated, and the latter has diffusion-dominated scalar transport. We also compared the rate of emptying from each grid, Table VI. Overall, the velocity profiles, concentration profiles, and emptying rates are in close agreement with each other. The coarse grid has discrepancies compared to the medium grid, but the differences between the medium and fine grids are within acceptable limits. Based on this analysis, we chose the medium grid for all simulations presented in this study.
FIG. 16.
Comparison of time-averaged (uavg) and root-mean-squared fluctuating (urms) velocity profiles for coarse ( ), medium ( ), and fine ( ) grid sizes at different locations on a horizontal plane through the antrum. The averaging is done over one ACW cycle (20 s). (a) The chosen plane, z = 4.7, is shown passing through the antrum with lines along which the profiles are compared. (b) Velocity profiles along the corresponding lines on the plane.
FIG. 17.
Comparison of the instantaneous concentration of pepsin after 20 ACW cycles (200 s) at different locations on horizontal planes through the antrum and the upper corpus for coarse ( ), medium ( ), and fine ( ) grid sizes. (a) The chosen planes, z = 4.7 and 10.0, are shown passing through the antrum and corpus, respectively, with lines along which the profiles are compared. (b) Concentration profiles along the corresponding lines on the planes.
TABLE VI.
Fluid emptying rate through the pylorus obtained from coarse ( ), medium ( ), and fine ( ) grid sizes.
| Grid | Emptying rate (ml/min) |
|---|---|
| Coarse | 4.49 |
| Medium | 4.48 |
| Fine | 4.51 |
2. Effect of time-step size
In carrying out the grid convergence study, we had to reduce the time step size for finer grids to meet the Courant–Friedrichs–Lewy (CFL) condition. However, here the focus is on keeping the grid size the same ( ) and varying only the time step size. We employ three different values for —large (0.055 s), medium (0.05 s), and small (0.04 s). Time-step sizes larger than 0.055 could not be chosen otherwise the CFL number became too large and convergence issues arose. Similar to the grid convergence study—we solve for two ACW cycles to reach the periodic state, save the third cycle to a file, and from the fourth cycle onward, we use this saved flow field to solve the scalar transport equations. We also calculate the time-averaged and root-mean-squared velocities of the fourth cycle for comparing the flow fields from different time step sizes.
Figure 18 compares the time-averaged (uavg) and root-mean-squared fluctuating (urms) velocity profiles averaged over one ACW cycle (20 s), and concentration profiles of pepsin after 20 cycles (200 s), at the same locations as in the grid-convergence study. The difference in results between different time step sizes is negligible. The CFL number due to the larger time step was too close to the critical value beyond which convergence issues arose. So, the medium time step size was chosen for all simulations presented in this study.
FIG. 18.
Comparison of the velocity profiles and pepsin concentration for three different time step sizes—small (0.004 s), medium (0.005 s), and large (0.0055 s). The velocity profiles were averaged over one ACW cycle (20 s), and the pepsin concentration is compared after 20 ACW cycles (200 s). (a) Velocity profiles and (b) concentration profiles along different lines in corpus and antrum.
AUTHOR DECLARATIONS
Conflict of Interest
The authors have no conflicts to disclose.
Author Contributions
Sharun Kuhar: Conceptualization (equal); Data curation (equal); Formal analysis (equal); Investigation (equal); Methodology (equal); Software (equal); Visualization (equal); Writing – original draft (equal); Writing – review & editing (equal). Jae Ho Lee: Conceptualization (equal); Methodology (equal); Software (equal). Jung Hee Seo: Conceptualization (equal); Funding acquisition (supporting); Methodology (equal); Software (equal); Supervision (supporting). Pankaj J Pasricha: Conceptualization (equal); Supervision (equal). Rajat Mittal: Conceptualization (equal); Funding acquisition (equal); Methodology (equal); Resources (equal); Supervision (equal); Writing – review & editing (equal).
DATA AVAILABILITY
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
- 1. Barnard N. D., “ Trends in food availability, 1909–2007,” Am. J. Clin. Nutr. 91, 1530S–1536S (2010). 10.3945/ajcn.2010.28701G [DOI] [PubMed] [Google Scholar]
- 2. Casini L., Contini C., Romano C., and Scozzafava G., “ Trends in food consumptions: What is happening to generation X?,” Br. Food J. 117, 705–718 (2015). 10.1108/BFJ-10-2013-0283 [DOI] [Google Scholar]
- 3. Oberlander L., Disdier A.-C., and Etilé F., “ Globalisation and national trends in nutrition and health: A grouped fixed-effects approach to intercountry heterogeneity: Globalisation and the nutrition transition,” Health Econ. 26, 1146–1161 (2017). 10.1002/hec.3521 [DOI] [PubMed] [Google Scholar]
- 4. Grover M., Farrugia G., and Stanghellini V., “ Gastroparesis: A turning point in understanding and treatment,” Gut 68, 2238–2250 (2019). 10.1136/gutjnl-2019-318712 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Koch K. L. and Calles-Escandón J., “ Diabetic gastroparesis,” Gastroenterol. Clin. 44, 39–57 (2015). 10.1016/j.gtc.2014.11.005 [DOI] [PubMed] [Google Scholar]
- 6. Ukleja A., “ Dumping syndrome: Pathophysiology and treatment,” Nutr. Clin. Pract. 20, 517–525 (2005). 10.1177/0115426505020005517 [DOI] [PubMed] [Google Scholar]
- 7. Mizuta Y., Shikuwa S., Isomoto H., Mishima R., Akazawa Y., Masuda J.-i., Omagari K., Takeshima F., and Kohno S., “ Recent insights into digestive motility in functional dyspepsia,” J. Gastroenterol. 41, 1025–1040 (2006). 10.1007/s00535-006-1966-z [DOI] [PubMed] [Google Scholar]
- 8. Hens B., Sinko P. D., Job N., Dean M., Al-Gousous J., Salehi N., Ziff R. M., Tsume Y., Bermejo M., Paixão P., Brasseur J. G., Yu A., Talattof A., Benninghoff G., Langguth P., Lennernäs H., Hasler W. L., Marciani L., Dickens J., Shedden K., Sun D., Amidon G. E., and Amidon G. L., “ Formulation predictive dissolution (fPD) testing to advance oral drug product development: An introduction to the US FDA funded ‘21st Century BA/BE’ project,” Int. J. Pharm. 548, 120–127 (2018). 10.1016/j.ijpharm.2018.06.050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Lee J. H., Kuhar S., Seo J. H., Pasricha P. J., and Mittal R., “ Computational modeling of drug dissolution in human stomach: Effects of posture and gastroparesis on drug bioavailability,” Phys. Fluids 34, 081904 (2022). 10.1063/5.0096877 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Bornhorst G. M., “ Gastric mixing during food digestion: Mechanisms and applications,” Annu. Rev. Food Sci. Technol. 8, 523–542 (2017). 10.1146/annurev-food-030216-025802 [DOI] [PubMed] [Google Scholar]
- 11. O'Grady G., Gharibans A. A., Du P., and Huizinga J. D., “ The gastric conduction system in health and disease: A translational review,” Am. J. Physiol.: Gastrointest. Liver Physiol. 321, G527–G542 (2021). 10.1152/ajpgi.00065.2021 [DOI] [PubMed] [Google Scholar]
- 12. Pal A., Indireshkumar K., Schwizer W., Abrahamsson B., Fried M., and Brasseur J. G., “ Gastric flow and mixing studied using computer simulation,” Proc. R. Soc. London, Ser. B 271, 2587–2594 (2004). 10.1098/rspb.2004.2886 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Schulze K., “ Imaging and modelling of digestion in the stomach and the duodenum,” Neurogastroenterol. Motil. 18, 172–183 (2006). 10.1111/j.1365-2982.2006.00759.x [DOI] [PubMed] [Google Scholar]
- 14. King P. M., Heading R. C., and Pryde A., “ Coordinated motor activity of the human gastroduodenal region,” Dig. Dis. Sci. 30, 219–224 (1985). 10.1007/BF01347887 [DOI] [PubMed] [Google Scholar]
- 15. Ishida S., Miyagawa T., O'Grady G., Cheng L. K., and Imai Y., “ Quantification of gastric emptying caused by impaired coordination of pyloric closure with antral contraction: A simulation study,” J. R. Soc. Interface 16, 20190266 (2019). 10.1098/rsif.2019.0266 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Kelly K. A., “ Gastric emptying of liquids and solids: Roles of proximal and distal stomach,” Am. J. Physiol.: Gastrointest. Liver Physiol. 239, G71–G76 (1980). 10.1152/ajpgi.1980.239.2.G71 [DOI] [PubMed] [Google Scholar]
- 17. Koziolek M., Garbacz G., Neumann M., and Weitschies W., “ Simulating the postprandial stomach: Physiological considerations for dissolution and release testing,” Mol. Pharm. 10, 1610–1622 (2013). 10.1021/mp300604u [DOI] [PubMed] [Google Scholar]
- 18. Brener W., Hendrix T. R., and McHugh P. R., “ Regulation of the gastric emptying of glucose,” Gastroenterology 85, 76–82 (1983). 10.1016/S0016-5085(83)80232-7 [DOI] [PubMed] [Google Scholar]
- 19. Bornhorst G. M. and Singh R. P., “ Gastric digestion in vivo and in vitro: How the structural aspects of food influence the digestion process,” Annu. Rev. Food Sci. Technol. 5, 111–132 (2014). 10.1146/annurev-food-030713-092346 [DOI] [PubMed] [Google Scholar]
- 20. Du P., Liu J. Y. H., Sukasem A., Qian A., Calder S., and Rudd J. A., “ Recent progress in electrophysiology and motility mapping of the gastrointestinal tract using multi-channel devices,” J. R. Soc. N. Z. 50, 316–330 (2020). 10.1080/03036758.2020.1735455 [DOI] [Google Scholar]
- 21. Pal A., Brasseur J. G., and Abrahamsson B., “ A stomach road or ‘Magenstrasse’ for gastric emptying,” J. Biomech. 40, 1202–1210 (2007). 10.1016/j.jbiomech.2006.06.006 [DOI] [PubMed] [Google Scholar]
- 22. Kozu H., Kobayashi I., Nakajima M., Uemura K., Sato S., and Ichikawa S., “ Analysis of flow phenomena in gastric contents induced by human gastric peristalsis using CFD,” Food Biophys. 5, 330–336 (2010). 10.1007/s11483-010-9183-y [DOI] [PubMed] [Google Scholar]
- 23. Kozu H., Kobayashi I., Neves M. A., Nakajima M., Uemura K., Sato S., and Ichikawa S., “ PIV and CFD studies on analyzing intragastric flow phenomena induced by peristalsis using a human gastric flow simulator,” Food Funct. 5, 1839–1847 (2014). 10.1039/C4FO00041B [DOI] [PubMed] [Google Scholar]
- 24. Alokaily S., Feigl K., and Tanner F. X., “ Characterization of peristaltic flow during the mixing process in a model human stomach,” Phys. Fluids 31, 103105 (2019). 10.1063/1.5122665 [DOI] [Google Scholar]
- 25. Singh S. K., “ Fluid flow and disintegration of food in human stomach,” Ph.D. thesis ( University of California, Davis, CA, 2007). [Google Scholar]
- 26. Ferrua M. and Singh R., “ Modeling the fluid dynamics in a human stomach to gain insight of food digestion,” J. Food Sci. 75, R151–R162 (2010). 10.1111/j.1750-3841.2010.01748.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Imai Y., Kobayashi I., Ishida S., Ishikawa T., Buist M., and Yamaguchi T., “ Antral recirculation in the stomach during gastric mixing,” Am. J. Physiol.: Gastrointest. Liver Physiol. 304, G536–G542 (2013). 10.1152/ajpgi.00350.2012 [DOI] [PubMed] [Google Scholar]
- 28. Berry R., Miyagawa T., Paskaranandavadivel N., Du P., Angeli T. R., Trew M. L., Windsor J. A., Imai Y., O'Grady G., and Cheng L. K., “ Functional physiology of the human terminal antrum defined by high-resolution electrical mapping and computational modeling,” Am. J. Physiol.: Gastrointest. Liver Physiol. 311, G895–G902 (2016). 10.1152/ajpgi.00255.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Harrison S. M., Cleary P. W., and Sinnott M. D., “ Investigating mixing and emptying for aqueous liquid content from the stomach using a coupled biomechanical-SPH model,” Food Funct. 9, 3202–3219 (2018). 10.1039/C7FO01226H [DOI] [PubMed] [Google Scholar]
- 30. Hosseini S., Avci R., Paskaranandavadivel N., Palmada N., Suresh V., and Cheng L. K., “ A novel method for time-dependent numerical modeling of gastric motility directly from magnetic resonance imaging,” in 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC) ( IEEE, Montreal, QC, Canada, 2020), pp. 2384–2387. [DOI] [PubMed] [Google Scholar]
- 31. Li C. and Jin Y., “ A CFD model for investigating the dynamics of liquid gastric contents in human-stomach induced by gastric motility,” J. Food Eng. 296, 110461 (2021). 10.1016/j.jfoodeng.2020.110461 [DOI] [Google Scholar]
- 32. Li C., Xiao J., Chen X. D., and Jin Y., “ Mixing and emptying of gastric contents in human-stomach: A numerical study,” J. Biomech. 118, 110293 (2021). 10.1016/j.jbiomech.2021.110293 [DOI] [PubMed] [Google Scholar]
- 33. Dufour D., Tanner F. X., Feigl K. A., and Windhab E. J., “ Investigation of the dispersing characteristics of antral contraction wave flow in a simplified model of the distal stomach,” Phys. Fluids 33, 083101 (2021). 10.1063/5.0053996 [DOI] [Google Scholar]
- 34. Acharya S., Halder S., Kou W., Kahrilas P. J., Pandolfino J. E., and Patankar N. A., “ A fully resolved multiphysics model of gastric peristalsis and bolus emptying in the upper gastrointestinal tract,” Comput. Biol. Med. 143, 104948 (2022). 10.1016/j.compbiomed.2021.104948 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Trusov P. V., Zaitseva N. V., and Kamaltdinov M. R., “ A multiphase flow in the antroduodenal portion of the gastrointestinal tract: A mathematical model,” Comput. Math. Methods Med. 2016, 5164029. 10.1155/2016/5164029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Camilleri M., Bharucha A. E., and Farrugia G., “ Epidemiology, mechanisms, and management of diabetic gastroparesis,” Clin. Gastroenterol. Hepatol. 9, 5–12 (2011). 10.1016/j.cgh.2010.09.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Hereijgers M. J. M., Keszthelyi D., Kruimel J. W., Masclee A. A. M., and Conchillo J. M., “ Antroduodenal motility recording identifies characteristic patterns in gastroparesis related to underlying etiology,” Neurogastroenterol. Motil. 34, e14394 (2022). 10.1111/nmo.14394 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Hardoff R., Sula M., Tamir A., Soil A., Front A., Badarna S., Honigman S., and Giladi N., “ Gastric emptying time and gastric motility in patients with Parkinson's disease,” Mov. Disord. 16, 1041–1047 (2001). 10.1002/mds.1203 [DOI] [PubMed] [Google Scholar]
- 39. Annese V., Janssens J., Vantrappen G., Tack J., Peeters T. L., Willemse P., and Van Cutsem E., “ Erythromycin accelerates gastric emptying by inducing antral contractions and improved gastroduodenal coordination,” Gastroenterology 102, 823–828 (1992). 10.1016/0016-5085(92)90164-T [DOI] [PubMed] [Google Scholar]
- 40. Parkman H. P., Pagano A. P., Vozzelli M. A., and Ryan J. P., “ Gastrokinetic effects of erythromycin: Myogenic and neurogenic mechanisms of action in rabbit stomach,” Am. J. Physiol.: Gastrointest. Liver Physiol. 269, G418–G426 (1995). 10.1152/ajpgi.1995.269.3.G418 [DOI] [PubMed] [Google Scholar]
- 41. Seo J. H. and Mittal R., “ Computational modeling of drug dissolution in the human stomach,” Front. Physiol. 12, 755997 (2022). 10.3389/fphys.2021.755997 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Gosselin M.-C., Neufeld E., Moser H., Huber E., Farcito S., Gerber L., Jedensjö M., Hilber I., Gennaro F. D., Lloyd B., Cherubini E., Szczerba D., Kainz W., and Kuster N., “ Development of a new generation of high-resolution anatomical models for medical device evaluation: The virtual population 3.0,” Phys. Med. Biol. 59, 5287–5303 (2014). 10.1088/0031-9155/59/18/5287 [DOI] [PubMed] [Google Scholar]
- 43. Meyer J., Elashoff J., Porter-Fink V., Dressman J., and Amidon G., “ Human postprandial gastric emptying of 1–3-millimeter spheres,” Gastroenterology 94, 1315–1325 (1988). 10.1016/0016-5085(88)90669-5 [DOI] [PubMed] [Google Scholar]
- 44. Hellström P. M., Grybäck P., and Jacobsson H., “ The physiology of gastric emptying,” Best Pract. Res. Clin. Anaesthesiol. 20, 397–407 (2006). 10.1016/j.bpa.2006.02.002 [DOI] [PubMed] [Google Scholar]
- 45. Marciani L., Young P., Wright J., Moore R., Coleman N., Gowland P. A., and Spiller R. C., “ Antral motility measurements by magnetic resonance imaging,” Neurogastroenterol. Motil. 13, 511–518 (2001). 10.1046/j.1365-2982.2001.00285.x [DOI] [PubMed] [Google Scholar]
- 46. Marciani L., Gowland P. A., Fillery-Travis A., Manoj P., Wright J., Smith A., Young P., Moore R., and Spiller R. C., “ Assessment of antral grinding of a model solid meal with echo-planar imaging,” Am. J. Physiol.: Gastrointest. Liver Physiol. 280, G844–G849 (2001). 10.1152/ajpgi.2001.280.5.G844 [DOI] [PubMed] [Google Scholar]
- 47. Kunz P., Feinle C., Schwizer W., Fried M., and Boesiger P., “ Assessment of gastric motor function during the emptying of solid and liquid meals in humans by MRI,” J. Magn. Reson. Imaging 9, 75–80 (1999). [DOI] [PubMed] [Google Scholar]
- 48. Kwiatek M. A., Menne D., Steingoetter A., Goetze O., Forras-Kaufman Z., Kaufman E., Fruehauf H., Boesiger P., Fried M., Schwizer W., and Fox M. R., “ Effect of meal volume and calorie load on postprandial gastric function and emptying: Studies under physiological conditions by combined fiber-optic pressure measurement and MRI,” Am. J. Physiol.: Gastrointest. Liver Physiol. 297, G894–G901 (2009). 10.1152/ajpgi.00117.2009 [DOI] [PubMed] [Google Scholar]
- 49. Schwizer W., Fraser R., Borovicka J., Asal K., Crelier G., Kunz P., Boesiger P., and Fried M., “ Measurement of proximal and distal gastric motility with magnetic resonance imaging,” Am. J. Physiol.: Gastrointest. Liver Physiol. 271, G217–G222 (1996). 10.1152/ajpgi.1996.271.1.G217 [DOI] [PubMed] [Google Scholar]
- 50. Ajaj W., “ Real time high resolution magnetic resonance imaging for the assessment of gastric motility disorders,” Gut 53, 1256–1261 (2004). 10.1136/gut.2003.038588 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Urbain J. L. C., Vekemans M. C., Bouillon R., Van Cauteren J., Bex M., Mayeur S. M., Van den Maegdenbergh V., Bataille G., Charkes N. D., Malmud L. S., and De Roo M., “ Characterization of gastric antral motility disturbances in diabetes using a scintigraphic technique,” J. Nucl. Med. 34, 576–581 (1993), available at https://jnm.snmjournals.org/content/34/4/576. [PubMed] [Google Scholar]
- 52. Mittal R., Dong H., Bozkurttas M., Najjar F., Vargas A., and von Loebbecke A., “ A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries,” J. Comput. Phys. 227, 4825–4852 (2008). 10.1016/j.jcp.2008.01.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Bornhorst G. M. and Singh R. P., “ Bolus formation and disintegration during digestion of food carbohydrates,” Compr. Rev. Food Sci. Food Saf. 11, 101–118 (2012). 10.1111/j.1541-4337.2011.00172.x [DOI] [Google Scholar]
- 54. Cornish-Bowden A. J., Greenwell P., and Knowles J. R., “ The rate-determining step in pepsin-catalysed reactions, and evidence against an acyl-enzyme intermediate,” Biochem. J. 113, 369–375 (1969). 10.1042/bj1130369 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Feldman M., Cryer B., McArthur K. E., Huet B. A., and Lee E., “ Effects of aging and gastritis on gastric acid and pepsin secretion in humans: A prospective study,” Gastroenterology 110, 1043–1052 (1996). 10.1053/gast.1996.v110.pm8612992 [DOI] [PubMed] [Google Scholar]
- 56. Liu W., Jin Y., Wilde P. J., Hou Y., Wang Y., and Han J., “ Mechanisms, physiology, and recent research progress of gastric emptying,” Crit. Rev. Food Sci. Nutr. 61, 2742–2755 (2021). 10.1080/10408398.2020.1784841 [DOI] [PubMed] [Google Scholar]
- 57. Marciani L., Gowland P. A., Spiller R. C., Manoj P., Moore R. J., Young P., and Fillery-Travis A. J., “ Effect of meal viscosity and nutrients on satiety, intragastric dilution, and emptying assessed by MRI,” Am. J. Physiol.: Gastrointest. Liver Physiol. 280, G1227–G1233 (2001). 10.1152/ajpgi.2001.280.6.G1227 [DOI] [PubMed] [Google Scholar]
- 58. Kong F. and Singh R., “ Disintegration of solid foods in human stomach,” J. Food Sci. 73, R67–R80 (2008). 10.1111/j.1750-3841.2008.00766.x [DOI] [PubMed] [Google Scholar]
- 59. Siegel J. A., Urbain J. L., Adler L. P., Charkes N. D., Maurer A. H., Krevsky B., Knight L. C., Fisher R. S., and Malmud L. S., “ Biphasic nature of gastric emptying,” Gut 29, 85–89 (1988). 10.1136/gut.29.1.85 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Urbain J.-L., Siegel J., Charkes N., Maurer A., Malmud L., and Fisher R., “ The two-component stomach: Effects of meal particle size on fundal and antral emptying,” Eur. J. Nucl. Med. 15, 254 (1989). 10.1007/BF00257543 [DOI] [PubMed] [Google Scholar]
- 61. Rips A. and Mittal R., “ Flutter-enhanced mixing in small-scale mixers,” Phys. Fluids 31, 107107 (2019). 10.1063/1.5115351 [DOI] [Google Scholar]
- 62. Davis J. L. and Ripley R. T., “ Postgastrectomy syndromes and nutritional considerations following gastric surgery,” Surg. Clin. North Am. 97, 277–293 (2017). 10.1016/j.suc.2016.11.005 [DOI] [PubMed] [Google Scholar]
- 63. Towns J., Cockerill T., Dahan M., Foster I., Gaither K., Grimshaw A., Hazlewood V., Lathrop S., Lifka D., Peterson G. D., Roskies R., Scott J. R., and Wilkins-Diehr N., “ XSEDE: Accelerating scientific discovery,” Comput. Sci. Eng. 16, 62–74 (2014). 10.1109/MCSE.2014.80 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.