Data augmentation with Mixup: Enhancing performance of a functional neuroimaging-based prognostic deep learning classifier in recent onset psychosis

Highlights

• •Small sample sizes are a challenge when using deep learning (DL) on fMRI data.
• •We examined effects of a data augmentation procedure called Mixup on fMRI DL.
• •Mixup improved dl-based prediction of clinical outcome in psychosis using fMRI data.

Abstract

Although deep learning holds great promise as a prognostic tool in psychiatry, a limitation of the method is that it requires large training sample sizes to achieve replicable accuracy. This is problematic for fMRI datasets as they are typically small due to the considerable time, cost, and resources necessary to obtain them. A recently developed self-supervised learning method called Mixup may help overcome this challenge. In Mixup, the learner combines pairs of training instances to produce a virtual third instance that is a linear combination of the two instances and their labels. This procedure is also well-suited to the coregistered images typically found in fMRI datasets. Here we compared performance of a task fMRI-based deep learner with Mixup vs without Mixup on predicting response to treatment in recent onset psychosis. Whole brain fMRI time series data were extracted from a cognitive control task in 82 patients with recent onset psychosis and used to predict “Improver” (n = 47) vs “Non-Improver” (n = 35) status, with Improver defined as showing a 20 % reduction in total Brief Psychiatric Rating Scale score after 1 year of treatment. Mixup significantly improved performance (accuracy without Mixup: 76.5 % [95 % CI: 75.9–77.1 %]; accuracy with Mixup: 80.1 % [95 % CI: 79.4–80.8 %]). Ablation showed the improvement was due to improvement in both Improvers and Non-Improvers. These results suggest that using Mixup may significantly improve performance and reduce overfitting of fMRI-based prognostic deep learners and may also help overcome the small sample size challenge inherent to many neuroimaging datasets.

1. Introduction

Response to treatment in early psychosis is highly variable, and reliable prognostic biomarkers are lacking. As a result, trial and error amongst various treatment regimens often remains the basis for care and poor outcomes continue to be common in these individuals. This can be the case even if duration of untreated psychosis is minimized and specialized clinical care is provided. Accordingly, identifying which patients are less likely to have good treatment responses and thus would benefit from alternative and/or supplemental interventions as early as possible is of paramount importance in psychiatry.

To that end, researchers have been increasingly interested developing tools that can predict treatment response in early psychotic illness. Although some evidence suggests that machine learning as applied to brain functional imaging data may be a promising avenue of investigation for this purpose (e.g., Blessing et al., 2020, Cao et al., 2020, Smucny et al., 2021) functional magnetic resonance imaging (fMRI)-based deep learning has not yet garnered mainstream acceptance as a prognostic instrument. One likely reason for this hesitance is that deep learning often requires large sample sizes to perform well within and across datasets. Given the time and expense required to perform neuroimaging studies, such large sample sizes may not be feasible without enlisting large consortia involving multiple research groups.

Overcoming this issue may thus require self-supervised machine learning methods that generate more training data from existing data. Unfortunately, most existing methods are not appropriate for datasets involving coregistered images (such as fMRI datasets) as they involve geometric transformations such as rotation, translation, and mirroring (Tanwar, 2021). One set of data augmentation methods that have been developed for medical imaging are called generative adversarial networks (GANs) (Frid-Adar et al., 2018). GANs, however, have well-known optimization/overfitting issues during the learning phase, including mode collapse (Bau et al., 2019, Google, 2022) and convergence failure (Mescheder et al., 2018), that limit its usage in high dimensional scarce data. A machine learning technique called Mixup, however, was recently developed by Zhang et al. (2017) that may be more applicable for coregistered images. Mixup is a type of self-supervised learning in which the learner self-generates virtually labeled instances into the training sample as a combination of individual data points. In the context of fMRI, this might be activation maps from two individuals (Smucny et al., 2022). Notably, this method differs from another recently developed image instance generation method, Robust-Deep (Sanaat et al., 2022), in that Mixup includes combining instances from different classes (which are assigned soft labels). By adding these virtual instances, the model is given more variations of existing data, smoothing the decision boundaries of the underlying distribution and aiding regularization via vicinal risk minimization (Chapelle et al., 2000). It thus reduces the effect of outliers and, consequently, lessens the likelihood of overfitting (Thulasidasan et al., 2019, Zhang et al., 2020). Indeed, overfitting may be particularly problematic in training fMRI data due to noise (e.g., participant head motion-induced (Power et al., 2012)) making the Mixup method particularly potentially well-suited for fMRI data.

Nonetheless, to our knowledge Mixup has not been utilized for machine learning of fMRI data. In structural MRI (sMRI) studies, however, Panfilov et al. (2019) showed that Mixup improved segmentation accuracy of tibial knee cartilage on an independent dataset by ∼5 %, and Eaton-Rosen et al. (2018) demonstrated the technique helps classify brain gliomas with a Dice score (voxel proportion of true positives) improvement of 5–10 %, depending on the training iteration and Mixup implementation. More recently, Bron et al. (2021) compared performance of a Mixup data-augmented support vector machine (SVM) vs a Mixup data-augmented convolutional neural network (CNN) on classifying patients with Alzheimer's Disease (AD) vs controls. Bron et al. (2021) reported 86 % accuracy using probabilistic gray matter maps for both the SVM and CNN on classifying AD vs controls, although it is unclear how much performance was enhanced from Mixup augmentation.

Based on the performance enhancements demonstrated in sMRI studies, we hypothesized Mixup would also improve accuracy on a binary classification problem based on task fMRI data. Task fMRI datasets pose challenges over static sMRI data, however, because fMRI data have a temporal component. For this experiment, we used fMRI data from a cognitive control task (the AX-Continuous Performance Task (CPT)). Using this task, we have previously reported with logistic regression that cognitive control-associated activation within frontoparietal regions of interest (ROIs) taken on baseline in recent onset schizophrenia (SZ) could predict significant clinical improvement 12 months later (defined as >20 % improvement in total Brief Psychiatric Rating Scale (BPRS) score) with 66 % accuracy (Smucny et al., 2019). We later found using the same sample that deep learning improved predictive accuracy to 73 % (Smucny et al., 2021). Although these early results are promising, the accuracies achieved were still likely too low to be considered clinically useful, particularly for identifying treatment resistant patients (<80 % for both studies). To that end, therefore, in this study we used the AX-CPT data from the same sample to compare deep learning performance without Mixup vs various Mixup implementations. The present study, however, utilizes a fundamentally different data set. Specifically, our previous studies (Smucny et al., 2021, Smucny et al., 2019) used mean activations (across time) within small regions of interest associated with a specific task-associated fMRI contrast, whereas the present study incorporates whole brain voxelwise fMRI time series data into the learner. We used a more data-rich approach for this study to lessen the likelihood of Mixup-induced overfitting.

2. Materials and methods

2.1. Sample

The data sample consisted of 82 individuals with recent onset (<2 years) psychotic disorders (n = 65 people with SZ, n = 17 with Type I bipolar disorder with psychotic features) as described previously (Smucny et al., 2021, Smucny et al., 2019). Neuroimaging AX-CPT data have also been used in previous studies as follows: Lesh et al. (2013) − 18 patients, Lesh et al. (2015) − 20 patients, Niendam et al. (2014) − 11 patients, Smucny et al. (2018) − 43 patients, Smucny et al. (2020) − 29 patients, Yoon et al. (2008) − 6 patients. Individuals were recruited as outpatients from the University of California, Davis (UCD) Early Diagnosis and Preventive Treatment (of Psychosis) (EDAPT) research clinic (https://earlypsychosis.ucdavis.edu). Treatment in the clinic follows a coordinated specialty care (CSC) for early psychosis model delivered by an interdisciplinary treatment team. Treatment includes detailed clinical assessments using gold-standard structured clinical interviews and medical evaluations, targeted pharmacological treatments including low dose atypical antipsychotic treatment, individual and family-based psychosocial education and support, cognitive behavioral therapy for psychosis, and support for education and employment. The Structured Clinical Interview for DSM-IV-TR (SCID) (First et al., 2002) was used for diagnosis of psychopathology. Diagnoses were confirmed by a group of trained clinicians during case-conferences. All patients reported psychosis onset within two years of the date of informed consent. Patients were excluded for a diagnosis of major medical or neurological illness, head trauma, substance abuse in the previous three months (as well as a positive urinalysis on the day of scanning), Weschler Abbreviated Scale of Intelligence-2 score (WASI-2) (Weschler, 1999) score < 70, and magnetic resonance imaging (MRI) exclusion criteria (e.g., claustrophobia, metal in the body). Control participants were excluded for all the above as well as a history of Axis I mental illness or first-degree family history of psychosis. All participants provided written informed consent in accordance with the Declaration of Helsinki and were compensated for participation. The UCD Institutional Review Board approved the study. Medication regimen (type and dose) was assessed by clinical records at baseline and follow-up. Medication compliance was based on self-report. Medicated patients at follow-up all self-reported at least medium compliance with antipsychotic medication during the treatment period (except for two SZ individuals who were missing compliance data at follow-up). Symptoms were assessed using the 24-point Brief Psychiatric Rating Scale (BPRS) (Ventura et al., 1993) rescaled to a lowest score of zero (i.e. score of 24 = score of 0). At baseline, all patients had BPRS scores >= 5 to ensure sufficient resolution to detect a 20 % improvement in score at follow-up.

2.2. Task description

The AX-CPT and associated task parameters have been described in detail elsewhere (Braver et al., 2009, Cohen et al., 1999, Henderson et al., 2012, Lesh et al., 2013, Phillips et al., 2015). Briefly, participants are presented with a series of cues and probes and are instructed to make a target response (pressing a button with the index finger) to the probe letter “X” only if it was preceded by the cue letter “A.” All cues and nontarget probes require nontarget responses (pressing a button with the middle finger). Target sequence trials (i.e., “AX” trials) are frequent (60–70 % occurrence) and set up a prepotent tendency to make a target response when the probe letter X occurs. As a result, a nontarget sequence trial in which any Non-A cue (collectively called “B” cues) is presented and followed by a probe letter X (i.e. “BX” trials) requires proactive cognitive control (e.g. maintenance of the inhibitory rule over the delay time) (Braver et al., 2009). Consistent with prior work (Henderson et al., 2012), individual subject data was only included in analyses if results suggested the subject understood the AX-CPT (specifically, accuracy>44 % on AX trials and 50 % on BY trials at both baseline and follow-up). Participants were combined across two task protocols collected from two MRI scanners over a 14-year period. Parameters for each protocol (AX-CPT I and AX-CPT II) are provided in Supplementary Table 1a. The task was presented using EPrime2 software (Psychology Software Tools, Inc.).

2.3. fMRI scanning parameters and preprocessing

Functional images were acquired with a gradient-echo T2* Blood Oxygenation Level Dependent (BOLD) contrast technique as outlined in Supplementary Table 1b. AX-CPT I was performed in a 1.5 T scanner (GE Healthcare), and AX-CPT II in a 3.0 T scanner (Siemens).

fMRI data were preprocessed using SPM8 (Wellcome Dept. of Imaging Neuroscience, London) as described previously (Smucny et al., 2018, Smucny et al., 2020). Briefly, images were slice-timing corrected, realigned, normalized to the Montreal Neurological Institute (MNI) template using a rigid-body transformation followed by non-linear warping, and smoothed with an 8 mm full-width-half-maximum Gaussian kernel. All individual fMRI runs had<4 mm of translational within-run movement, 3 degrees of rotational within-run movement, and 0.45 mm of average framewise displacement, calculated using the fsl_motion_outliers tool (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FSLMotionOutliers). Mean displacement did not differ between Improvers and Non-Improvers (t = 1.42, p = .16). All participants had at least two fMRI runs surviving these criteria. Preprocessing pipelines were identical for AX-CPT I and II.

2.4. AX-CPT fMRI feature generation

Whole brain, single subject fMRI time series data (75 s high pass filtered, pre-whitened, confound-corrected eigenvariates from SPM8) were extracted from the AX-CPT using an atlas of 5 mm radius ROIs centered at MNI coordinate locations provided by an fMRI meta-analysis by Power et al. (2011). Each frame of the fMRI time series data was mapped to 3D space according to atlas coordinates. Eigenvariates were normalized to values between 0.25 and 1 using an adapted sigmoid function. In this manner, a single subject fMRI time series data was transformed into a series of 3D grayscale images. Frames with>0.5 mm of movement between them were excluded. Counts of included frames for each trial type were AX Trials: Mean = 328, S.D. = 96; AY Trials: Mean = 46, S.D. = 15; BX Trials: Mean = 61, S.D. = 17; BY Trials Mean = 41, S.D. = 9. Scanner field strength (1.5 T or 3 T) was included as a feature. These time series data were then used as features for subsequent deep learning.

2.5. Deep learning procedure: overview

The goal of the deep learner was to use baseline AX-CPT fMRI data to classify patients as either “Improvers” (>20 % improvement in Total BPRS score at 12-month follow-up) or “Non-Improvers” (otherwise). The deep learning architecture created for this task is displayed in Fig. 1. Briefly, for each AX-CPT trial-type (AX, AY, BX, BY), we first created separate models (Shi et al., 2022). Each was a deep CNN model trained from all instances within the same trial type using frames collected before, during, and after the cue/probe. We then used transfer learning to transfer knowledge from the dominant AX trial type model (as AX trials comprised 70 % of AX-CPT I and 60 % of AX-CPT II trials) to other trial-type models to overcome a potential data sparsity issue. Next, we combined knowledge from each trial type model to create an ensemble learner. In this architecture, each trial type model (AX, AY, BX, BY) votes on the prediction and the deep learner learns how to best combine their votes. Finally, we used Mixup to expand the training set by creating additional virtual instances and compared performance to that without using Mixup augmentation. Deep learning was performed using PyTorch (Paszke et al., 2019).

Fig. 1.

Deep learning architecture. Knowledge from the model using the most frequent, “AX” trial type was transferred to models from the other trial types (BX, AY, BY). These models were then combined into an ensemble model to make individual level predictions for learning.

2.6. AX-CPT trial type model creation

For model training, three-dimensional convolutional neural networks were adopted into a spatiotemporal framework as follows. Each fMRI scan was first split into trials, with a “trial” consisting of 4 frames (Cue (A or B) scan, interstimulus scan, Probe (X or Y) scan, interstimulus (rest) scan). Spatiotemporal reorganization was then performed using a method developed by Bengs et al. (2020). Formally, each trial $x\in R^{h\times w\times d\times c\times t}$ was reorganized into $x\in R^{h\times w\times d\times c\bullet t}$, where $h\times w\times d$ is the size of a 3D volume, $c$ is 1 for a grayscale image, and $t$ is the number of consecutive frames. Using this procedure, therefore, multiple frames are concatenated into a single large image. Given the small number of frames, modeling the temporal aspect using a complex deep learning architecture such as transformers (Vaswani et al., 2017) or long-term short memory networks (Yong et al., 2019) was not required. Separate 3D model learners with the same architecture were created for each AX-CPT trial type. Each trial-type model had 3 hidden blocks with a convolutional layer, a batch normalization layer, a max-pooling layer, a ReLU 0/1 activation function layer, and 2 linear feedforward layers before the output layer (Supplementary Table 3).

2.7. Transfer learning

The AX-CPT was imbalanced by trial type prevalence, as far more AX trials were presented relative to other trial types to establish a prepotent response. To improve model performance, we therefore employed a transfer learning approach, in which knowledge (i.e., model weights) were transferred from the most data rich model (the AX trial type model) to the other trial type models as initial weights for these models. We hypothesized this procedure would thus help make up for the shortfall in available training data for the data “poor” models (AY, BX, BY) and reduce overfitting. The weights of the target models were first initialized by the source model. Model weights were then fine-tuned while training on the target domain.

To confirm that our transfer approach improved performance, we compared it to a model in which no information was transferred (see Methods 2.11 for statistical analysis).

3. Creating a network ensemble

Once all four trial-type models were created, we combined them into an overall ensemble learner. We first ensembled the instances using the intermediate output of the first linear layer following each model’s convolutional layers. To learn instance-specific weights, we fixed the embedding vectors, and trained the resulting neural network with 3 linear layers and a Leaky ReLU activation function (to increase training speed). In the training phase, we randomly sampled trials of all four trial-types from a scan. We constructed the input feature vector by concatenation and fed into the shallow ensemble model. This approach enriches the feature space by randomly combining embedding vectors from different trial-types of the same subject. The number of combinations of the trial instances of different types of trials grows polynomially according to the number of trial instances of a single time. In the validation phase, we used the mean pooling multi-instance fusion method (Zeng et al., 2019) to obtain a vector representation out of all instances of a scan from each view. We thus created a single feature vector for each scan by concatenation and hence obtained a unique prediction for a scan.

To confirm that our ensemble approach improved performance, we compared it to a simple (non-ensemble) model that incorporated data from all trial types simultaneously (see Methods 2.11 for statistical analysis).

3.1. Mixup augmentation

In this study, we employed the standard Mixup implementation developed by Zhang et al. (2017). Mixup extends the training distribution by incorporating the prior knowledge that linear interpolations of feature vectors should lead to linear interpolations of the associated targets. It creates new virtual instances by randomly choosing two instances to produce a third that is a linear combination of the two training samples and their labels (see Fig. 2 for example of a Mixup-created virtual instance). Formally:

$$\underset{\_}{\mathit{newdata}}=\lambda \ast data1+\left(1-\lambda \right)data2$$

$$\underset{\_}{\mathit{newlabel}}=\lambda \ast label1+\left(1-\lambda \right)label2$$

Fig. 2.

Sample illustration of a Mixup virtual instance comprised of two different classes. In this example, and fMRI scan of non-improver (left) and a fMRI scan of improver (middle) were linearly interpolated to form a third synthetic scan (right) with a soft label of 50% Improver and 50% Non-Improver.

In these equations, data1 and data2 (and corresponding label1 and label2) are two examples drawn at random from training data. $\lambda \in \left[0,1\right]$ is a fraction taken randomly from a beta distribution, where $\lambda \sim Beta\left(\alpha ,\alpha \right)$, for $\alpha \in \left(0,\infty \right)$. We examined performance with α increasing exponentially starting at 0 (i.e., no Mixup) and going to 0.1, 0.2, 0.5, or 1. Beta distributions for different α values are shown in Fig. 3.

Fig. 3.

Mixup $\lambda$ distributions for α = 0.1, 0.2, 0.5, and 1. Higher values of α create more uniform distributions, with more synthetic instances created in the middle of the feature and outcome spaces.

In the present study, Mixup created virtual instances by combining data between Improvers (intra-Improvers Mixup), Non-Improvers (intra-Non-Improvers Mixup), and between Improvers and Non-Improvers (inter-Improvers-Non-Improvers Mixup). To determine which of these 3 classes of virtual instances most contributed to performance, we also performed an exploratory ablation study in which one class was removed from the Mixup implementation prior to learning. The ablation study was performed using the α value with the highest accuracy.

3.2. Result validation

For each deep learning Mixup implementation (e.g., α = 0.1), 10 replications of 5-fold cross validation were performed. To prevent data leakage from a training set to a validation set, cross validation was performed on the single participant level, with no shared participants, trials or frames between the training set and the evaluation set. Classifier accuracies were calculated by averaging performance across 10 random assortments of 80 % training data and 20 % validation data. 95 % confidence intervals, p values, and t values were calculated based on the results of the 10 assortments.

3.3. Statistical comparison between model implementations

We first determined if our “baseline” (no Mixup) model architecture improved performance vs other baseline alternatives (i.e., without transfer learning, without ensemble learning) by comparing performance metrics (accuracy, accuracy for Improvers, accuracy for Non-Improvers, sensitivity, specificity, receiver operating characteristic area under the curve (ROC AUC), and F1 score) to the primary baseline model using two-tailed t-tests.

To test the hypothesis that Mixup would improve classification performance based on α value, we performed one-way ANOVAs with α as the independent variable and each model performance metric as the dependent variable. Comparison of results from each of the three ablation settings was performed similarly with ablation setting as the independent variable. Significant effects were followed up by post-hoc tests between specific α values/ablation settings to examine the nature of any differences.

Significance for these tests was set to p < .05, with p < .10 considered trend-level.

4. Results

Demographic information has been presented previously (Smucny et al., 2021, Smucny et al., 2019) and is replicated here in Table 1a, Table 1b. Of the total sample of n = 82, 47 people with psychosis were classified as Improvers and 35 as Non-Improvers.

Table 1a.

Demographic information. Numbers in parentheses represent the standard deviation.

N People with Psychosis	82
Age	21.0 (3.2)
Sex (M/F)	59/23
N AX CPT I / N AX CPT II Protocol Participants	52/30
Days to Follow-Up	394.1 (138.5)

Table 1b.

Clinical information at baseline and follow-up. Numbers in parentheses represent the standard deviation.

	Baseline	Follow-Up
Antipsychotics (Med/Unmed)	69/13	60/22
Antipsychotics (CPZ Equivalent Dose, Mg/Day)	227.4 (154.4)	307.3 (305.9)
BPRS Improved/Did Not Improve1	—	47/35 (57.3 % Improved)
Total BPRS Score	42.7 (9.7)	37.3 (9.0)

Abbreviations: BPRS = Brief Psychiatric Rating Scale, CPZ = Chlorpromazine, HC = Healthy Controls.

¹Clinical “improvement” was defined as showing > 20 % decrease (with lowest possible score (24) set to zero) on Total BPRS score at follow-up (vs baseline). Only patients with Total BPRS score >= 29 at baseline were included in the sample.

Classification results comparing the primary baseline (without Mixup) architecture with alternative architectures that either 1) do not include weight transfer from the most common trial type (AX) or 2) train all trial types simultaneously (i.e., no ensemble learning) are presented in Supplementary Table 2. As expected, the primary architecture that includes transfer and ensemble learning significantly outperformed these alternative architectures for almost all performance metrics.

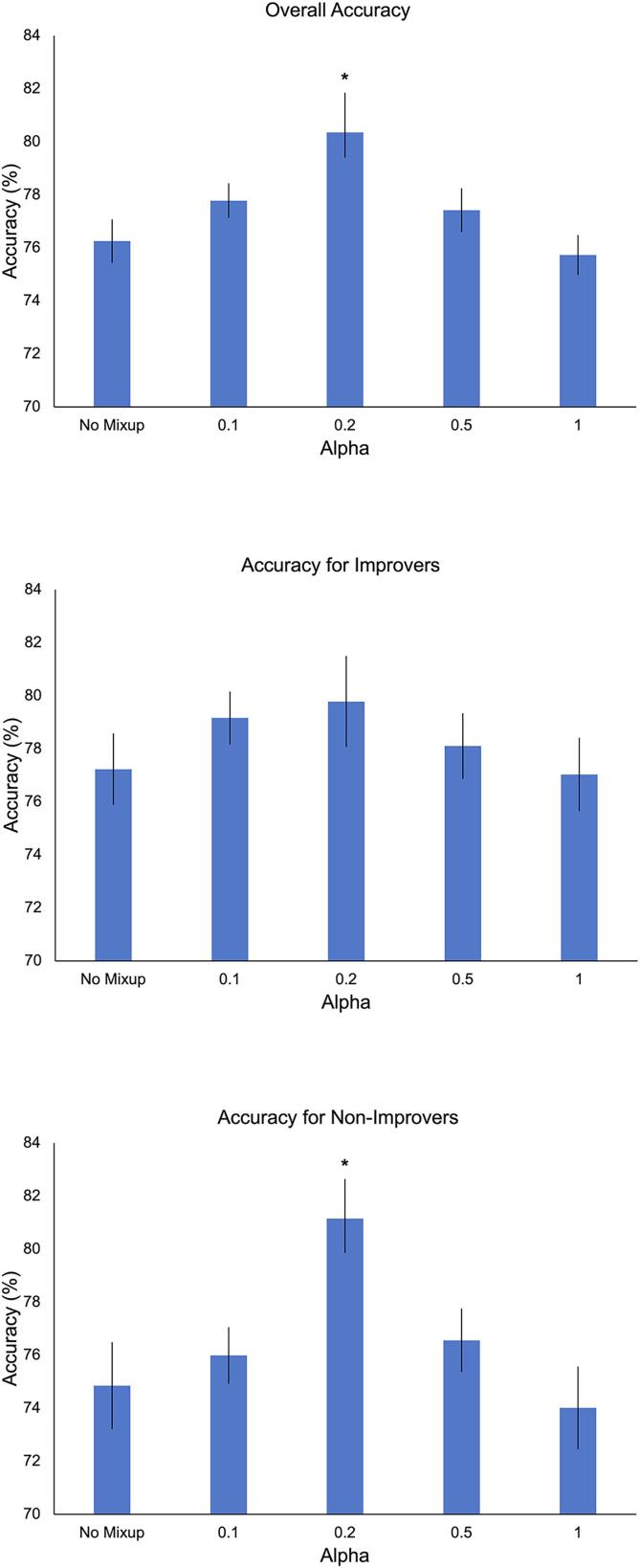
Classification results for various Mixup implementations are presented in Table 2 and Fig. 4. Significant effects of Mixup α value were observed for overall accuracy (F(4,45) = 4.95, p = .002) and accuracy for Non-Improvers (F(4,45) = 4.12, p = .006) but not accuracy for Improvers (F(4,45) = 0.78, p = .54). These effects were driven by greater overall accuracy and accuracy for Non-Improvers at α = 0.2 vs other methods (Fig. 4 legend). The lowest performances were observed at the tail ends of the α distribution, i.e., without Mixup and when α = 1. Overall accuracy and accuracy for non-improvers was 80.4 % and 81.1 %, respectively, when α = 0.2. Significant effects of Mixup α value were also observed for sensitivity (F(4,45) = 5.69, p < .001), ROC AUC (F(4,45) = 5.94, p < .001), and F1 score (F(4,45) = 5.40, p = .001), with a trend-level effect for specificity (F(4,45) = 2.29, p = .074). Mirroring the pattern observed for accuracy, these effects were driven by superior performance at α = 0.2 vs other α values.

Table 2.

Mixup results. Note: Sensitivity = %TP/(%TP+%FN) and specificity = %TN/(%FP+%TN), in which Improvers are the positive class and Non-improvers the negative class. Abbreviations: AUC = Area under the curve, CI = Confidence interval, FN = false negative, ROC = Receiver operating characteristic, FP = false positive, TN = true negative TP = true positive.

Method	%Accuracy (95 % CI)	%Accuracy for Improvers (95 % CI)	%Accuracy for Non-Improvers (95 % CI)	%Sensitivity	%Specificity	%ROC AUC Score	%F1 Score
No Mixup	76.3 (74.4–78.1)	77.2 (74.2–80.3)	74.9 (71.1–78.6)	75.6 (75.9–80.1)	76.8 (76.6–80.6)	75.7 (73.1–78.3)	75.8 (76.6–79.4)
α = 0.1	77.8 (76.3–79.3)	79.2 (76.9–81.4)	76.0 (73.6–78.4)	76.8 (75.2–78.4)	78.5 (76.8–80.2)	77.5 (75.7–79.3)	77.4 (76.0–78.8)
α = 0.2	80.4 (78.2–82.5)	79.8 (75.9–83.7)	81.1 (78.2–84.1)	81.0 (78.8–83.2)	80.0 (77.2–82.8)	79.3 (77.1–81.5)	81.0 (79.0–83.0)
α = 0.5	77.4 (75.6–79.3)	78.1 (75.3–80.9)	76.6 (73.9–79.3)	77.0 (75.1–78.1)	77.8 (75.8–79.8)	77.8 (74.3–81.3)	77.1 (75.3–78.9)
α = 1	75.7 (74.0–77.4)	77.0 (73.9–80.2)	74.0 (70.5–77.5)	74.9 (72.6–77.2)	76.4 (74.4–78.4)	76.5 (73.4–79.6)	75.3 (73.7–76.9)
Ablation Experiments (α = 0.2)
Without Intra-Improvers	78.2 (76.7–79.7)	78.3 (75.9–80.7)	78.0 (74.0–82.0)	78.3 (75.5–81.1)	78.3 (76.7–80.0)	79.0 (76.9–81.1)	77.8 (76.2–79.4)
Without Intra-Non-Improvers	78.3 (76.6–80.0)	79.1 (75.3–82.9)	77.1 (73.5–80.7)	77.8 (75.4–80.2)	79.0 (77.5–80.5)	77.8 (75.2–80.4)	77.9 (76.2–79.5)
Without Inter-Improvers-Non-Improvers	78.3 (76.9–79.7)	78.7 (76.1–81.3)	77.7 (74.8–80.6)	78.1 (75.9–80.1)	78.6 (76.6–80.6)	77.7 (75.4–80.0)	78.0 (76.6–79.4)

Fig. 4.

Mixup results. Error bars represent the standard error. Post-hoc tests for overall accuracy when α = 0.2: *p < .001 vs no Mixup, p = .029 vs α = 0.1, p = .014 vs α = 0.5, p < .001 vs α = 1. Post-hoc tests for accuracy for Non-Improvers when α = 0.2: *p = .002 vs no Mixup, p = .011 vs α = 0.1, p = .022 vs α = 0.5, p < .001 vs α = 1.

Ablation experiments showed no significant effect of ablation setting (Mixup without intra-Improvers, Mixup without Intra-Non-Improvers, Mixup without inter-Improvers-Non-Improvers) in overall accuracy (F(2,27) = 0.01, p = .99), accuracy for Improvers (F(2,27) = 0.09, p = .91), accuracy for Non-Improvers (F(2,27) = 0.07, p = .93), sensitivity (F(2,27) = 0.05, p = .95), specificity (F(2,27) = 0.12, p = .89), ROC AUC (F(2,27) = .00, p = 1.00), or F1 score (F(2,27) = 0.01, p = .99) (Table 2). Thus, no single type of virtual instance was uniquely important for improving Mixup performance.

5. Discussion

In this study, we demonstrate that Mixup can significantly improve performance on an fMRI data-based binary classification task. Specifically, using baseline neuroimaging data from a cognitive control task in people with recent onset psychosis, we found that, with proper hyperparameter tuning, a Mixup algorithm can improve accuracy by ∼ 4 % to above 80 % despite a relatively low sample size (n = 82). Particularly robust results were observed for accuracy for the Non-Improver class, as 81.1 % accuracy was achieved when Mixup α = 0.2. Other performance metrics (sensitivity, specificity, ROC AUC, and F1 score) also peaked when α = 0.2. Ablation experiments suggested that no single type of virtual instance (inter-Improver, inter-Non-Improver, intra-Improver-Non-Improver) was uniquely important for improving Mixup performance. These results suggest that Mixup is a powerful tool for increasing machine learning performance on fMRI data-based classification tasks and may help solve the small data problem inherent in many brain imaging datasets. Furthermore, these findings suggest that baseline fMRI signal during a cognitive control task can effectively predict clinical improvement after one year in recent onset psychosis, particularly for people who do not appreciably improve (defined as > 20 % decrease in total BPRS score in this study). The latter finding also suggests that this method may help provide early identification of people with psychosis who might not benefit from standard treatment options who could then be targeted with alternative forms of treatment (e.g., clozapine, cognitive remediation, or brain stimulation).

To our knowledge, this is the first fMRI study to use Mixup to enhance the performance of a binary classifier. Because of the high costs and long data collection times required to collect fMRI data, fMRI datasets are typically small (n’s < 100 for almost all single-site studies), making machine learning applications impractical for most studies that do not involve large consortia. Here we show that Mixup could be used to achieve > 80 % accuracy in a small (compared to most machine learning studies) sample. Notably, peak performance using the Mixup method was also substantially better than our previous classification attempts using logistic regression (66 % accuracy (Smucny et al., 2019)) and deep learning (70 % accuracy (Smucny et al., 2021)). ∼ 5 % of the improvement was likely due to the differences in features between these studies and the present report, as those previous studies focused on mean frontoparietal activations associated with a cognitive control contrast (B > A cues) whereas the present work used whole-brain, time series data across the entire task. The remaining improvement to above 80 % accuracy, however, was achieved using Mixup. Finally, the fact that > 80 % accuracy was observed in this study suggests that fMRI tasks that functionally assess cognitive control or similar cognitive processes may be particularly powerful as prognostic indicators in psychosis.

Notably, the most accurate Mixup results were achieved with a relatively low alpha value of 0.2. The λ distribution at this value is imbalanced, with most instances at both ends (Fig. 3). This result suggests the relationship between the fMRI data used as features in this task and the clinical outcome variable is largely categorical (as opposed to dimensional), with some “wiggle room” allowed for non-predictive signals (e.g., scanner movement-related noise). Taken one step further, this result suggests an orthogonal perspective, in which Improvers and Non-Improvers may have pharmacologically or neuronally distinct profiles that mechanistically underlie symptomatology. Interestingly, evidence from positron emission tomography studies suggest that individuals with SZ may be treatment-stratified based on levels of striatal presynaptic dopamine, in which people who respond to antipsychotic treatment show higher levels of presynaptic dopamine synthesis capacity compared to those who do not (Demjaha et al., 2012, Potkin et al., 2020). Future studies may examine the effect of incorporating neuromelanin signal as a noninvasive, MRI measurement of dopaminergic tone as an additional predictive feature for machine learning (Carter, 2021, Cassidy et al., 2019, Horga et al., 2021).

6. Conclusions

We have noted in our previous studies that 80 % accuracy is desirable to achieve clinical utility (Smucny et al., 2021, Smucny et al., 2019). Others have argued, however, that the effectiveness of a prognostic indicator should be solely based on their ability to change clinical practice (e.g., Perlis (2011)). Even though we achieved remarkable performance in our study using the Mixup technique, neuroimaging studies often show questionable reproducibility (Elliott et al., 2020). Our results therefore require replication using a larger sample or in independent samples before definitive statements can be made regarding the prognostic clinical utility of the fMRI AX-CPT (Mixup can also be used as part of this procedure, in which virtual instances can be created by combining those from different independent samples). Overall, however, given the dearth of reliable, established methods for predicting outcomes in early psychosis, in combination with our prior work using other machine learning methods we believe that the present study represents an important preliminary step toward developing a predictive algorithm for this purpose.

CRediT authorship contribution statement

Jason Smucny: Conceptualization, Data curation, Supervision. Ge Shi: Investigation, Methodology, Software. Tyler A. Lesh: Supervision. Cameron S. Carter: Funding acquisition, Resources, Supervision. Ian Davidson: Conceptualization, Funding acquisition, Resources, Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article:

Data availability

The authors do not have permission to share data.