Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2022 Nov 3;7(45):41783–41788. doi: 10.1021/acsomega.2c06151

Magnetic and Electronic Structural Properties of the S3 State of Nature’s Water Oxidizing Complex: A Combined Study in ELDOR-Detected Nuclear Magnetic Resonance Spectral Simulation and Broken-Symmetry Density Functional Theory

Ciarán J Rogers 1, Olivia Hardwick 1, Thomas A Corry 1, Felix Rummel 1, David Collison 1, Alice M Bowen 1,*, Patrick J O’Malley 1,*
PMCID: PMC9670293  PMID: 36406523

Abstract

graphic file with name ao2c06151_0006.jpg

ELDOR-detected nuclear magnetic resonance (EDNMR) spectral simulations combined with broken-symmetry density functional theory (BS-DFT) calculations are used to obtain and to assign the 55Mn hyperfine coupling constants (hfcs) for modified forms of the water oxidizing complex in the penultimate S3 state of the water oxidation cycle. The study shows that an open cubane form of the core Mn4CaO6 cluster explains the magnetic properties of the dominant S = 3 species in all cases studied experimentally with no need to invoke a closed cubane intermediate possessing a distorted pentacoordinate Mn4 ion as recently suggested. EDNMR simulations found that both the experimental bandwidth and multinuclear transitions may alter relative EDNMR peak intensities, potentially leading to incorrect assignment of hfcs. The implications of these findings for the water oxidation mechanism are discussed.

Introduction

The oxidation of two water molecules to form one molecule of oxygen has been performed uniquely at ambient conditions by the water oxidizing complex (WOC) of photosystem II (PSII) for around 3 billion years.1,2 Visible light energy is used to sequentially extract four electrons from two water molecules via its core catalytic center, a Mn4O5/6Ca cluster (Figures 1 and 2). The stepwise S state cycle, Figure 1, allows the WOC to produce oxidized Mn centers, and deprotonated substrate water molecules facilitating the ultimate formation of an O–O bond at the S3 or S4 state.3

Figure 1.

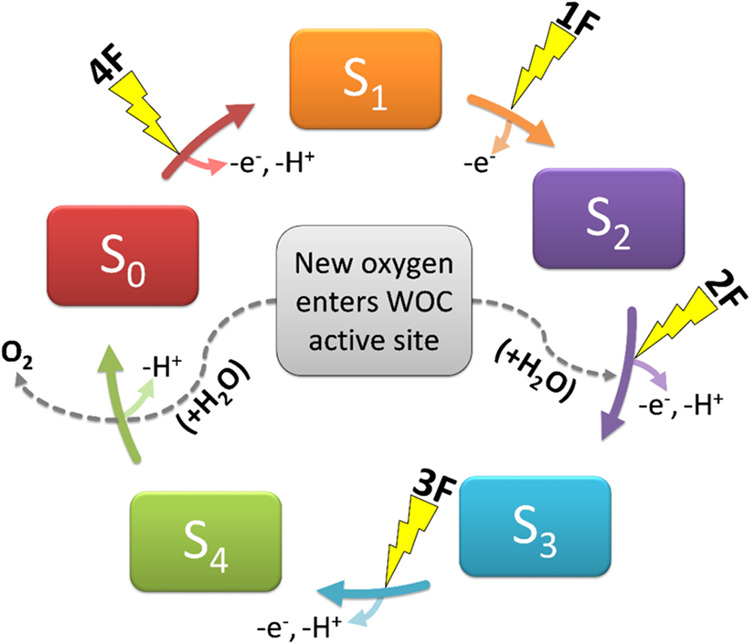
Figure 1

Open in a new tab

Water oxidizing complex (WOC) S state cycle. The four Mn ions of the complex are progressively oxidized with each photon flash (1F, 2F, 3F, 4F).

Figure 2.

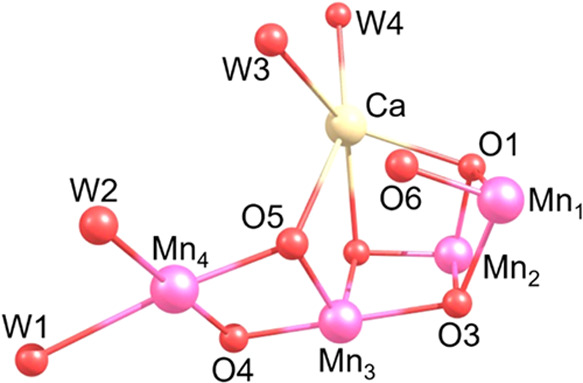
Figure 2

Open in a new tab

Numbering scheme and orientation used throughout for the S3 state core WOC. Color coding: Mn (purple), oxygen (red), and calcium (cream).

Understanding the WOC’s mechanism of low-energy oxidation of water to molecular oxygen has been the subject of a wide number of spectroscopic, crystallographic, and computational studies.4 The penultimate S3 state is a major current focus of contemporary research as it is the last semistable intermediate before oxygen evolution and has been associated with the oxygen–oxygen bond formation step.1,5 The characterization of this state was greatly enhanced by the recent report of an atomic-level X-ray crystal structure of the WOC using X-ray free electron lasers (XFEL), after two light flashes (2F) and poised predominantly in the S3 state.6,7 The core structure obtained from these studies and the main atom numbering is shown in Figure 2.

High-frequency continuous wave electron paramagnetic resonance (EPR) and ELDOR-detected nuclear magnetic resonance (EDNMR) spectroscopy8,9 studies have shown that the S3 state gives rise to an S = 3 EPR spectrum for the cyanobacterium Thermosynechococcus elongatus. The analysis indicated that the four Mn ions are present in the IV oxidation state and octahedrally coordinated. This was supported by broken-symmetry density functional theory (BS-DFT) and Heisenberg–Dirac–van Vleck (HDvV) spin ladder calculations.10−12 XFEL crystallographic studies have shown that an O6 atom is detected in the 2F structure in very close proximity to O5. The presence of an oxo–oxyl bond, [O2]3– or an equilibrium of these forms has been proposed to describe this.13−16 Recently, a five-coordinate precursor S3 state was suggested to explain broadened EPR signals in modified forms of the 2F state relative to the native form.17 This five-coordinate intermediate, remaining an S = 3 system, was proposed to feature a closed cubane (hexacoordinated Mn1 and pentacoordinated Mn4) rather than an open cubane form (both Mn1 and Mn4 hexacoordinated) reported previously for the native system, supporting a pivot or carousel mechanism of water oxidation, where Mn4 is the binding site for a new water or hydroxide in the S2-to-S3 transition.18,19 Similarly broadened EPR signals have been reported by Marchiori et al.20 on glycerol-treated samples, attributing these, by contrast, to an open cubane form. While a closed cubane model has been proposed by many workers for the high-spin S2 state and its role in the transition to the S3 state, other reports based either on DFT-calculated energetics21 or magnetic parameters22 have questioned whether such a conformer exists. In one model proposed by Siegbahn,21 an extra hydroxo ligand is already bound to Mn1 in the S2 state, which was proposed to facilitate the formation of the S3 state and ruled out the participation of a closed cubane form. In another model, protonation of the O4 μ-oxo was proposed22 to give rise to the high-spin form observed by EPR. More recently, it was proposed, based on BS-DFT calculations of hyperfine coupling constants (hfcs) and zero-field splitting (D) values, that an open cubane architecture was preferred for both native and alcohol-modified forms.16

Assignment of spectral bands from EDNMR data to individual hfcs relies on accurate spin Hamiltonian simulations of both the relative intensity and position of spectral peaks in experimental EDNMR spectra. At high frequencies, EDNMR has become the technique of choice for detecting nuclear transitions in the WOC.23−25 This is achieved by employing a long, low-powered high-turning-angle (HTA) microwave pulse to drive polarization transfer between formally forbidden electron transitions (ΔmS = ±1; ΔmI = ±1), which is subsequently detected as a change in the echo intensity of a simple Hahn Echo or Free Induction Decay (FID) detection sequence. EDNMR can be advantageous over analogous hyperfine techniques, namely, electron nuclear double resonance (ENDOR) spectroscopy, as neither radiofrequency (RF) amplifier bandwidth limitations nor microwave pulse selectivity poses a problem in data collection or analysis, as is the case in Davies ENDOR.26 Moreover, EDNMR is robust against fast longitudinal relaxation (T1).27 Previously, EDNMR spectral simulations of the WOC have been performed by approximating the experimental EDNMR spectrum as an ENDOR spectrum using the salt routine in EasySpin,28 although accurate EDNMR spectral simulations on other systems have been reported based on the Liouville equation.29 In this report, we take advantage of the recently reported routine horseradish, implemented in EasySpin30 and described in detail elsewhere,31 but in summary, the horseradish simulation considers all allowed and forbidden transitions for a given spin system and calculates the detection probability and inversion efficiency of each center by identifying connected pump transitions, i.e., those related to the frequency of the HTA pulse, giving a more accurate assignment of the spectrally observed EDNMR bands. Importantly, the central blind spot of the EDNMR experiment, where the HTA pulse saturates the detected EPR transition, centered around υHTA – υObs = 0 MHz, is not modeled explicitly in these calculations.

In this report, we combine this simulation method with broken-symmetry density functional theory (BS-DFT) calculations on large models of the WOC (see the Supporting Information, Figure S1). The models are generated from the 2F structure coordinates to calculate the 55Mn and 14N hfcs to guide our spectral simulations and assignments to specific nuclear peak positions. Our analysis shows that an open cubane structure is appropriate for all modified S3 state forms. As previously demonstrated, proposed alcohol binding sites near the O4 position cause small changes in the exchange coupling constants J (mainly J34),16 which modifies the projection coefficient for Mn3 and Mn4 resulting in small-magnitude, negative and isotropic 55Mn hfcs (Mn3–4). Our EDNMR simulations show that these small-magnitude negative 55Mn hfcs are buried in or near the central blind spot for the W-band EDNMR spectra and their relative intensities will have a strong dependence on the assumptions made to correct for the experimental bandwidth of the resonator.

Results and Discussion

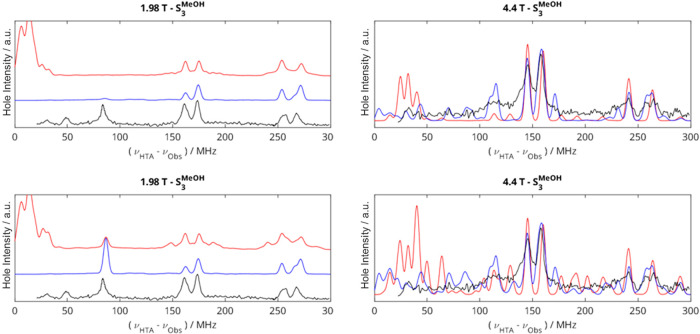
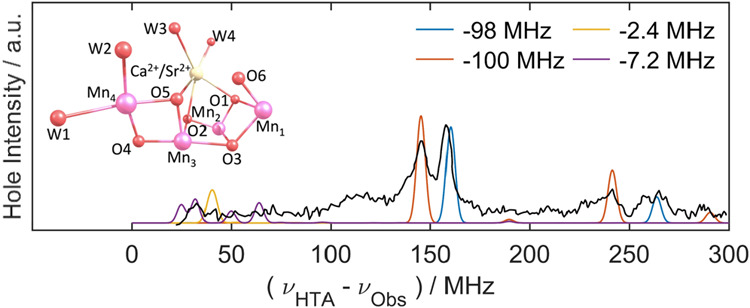
Table 1 shows the calculated isotropic and anisotropic 55Mn and 14N hfcs using BS-DFT calculations on models of methanol and glycerol interactions with the WOC for the S3 state. Small-magnitude negative 55Mn hfcs are calculated for Mn3 and Mn4 and large-magnitude negative values, near 100 MHz, are calculated for the Mn1 and Mn2 positions. The small-magnitude hfcs for the Mn3 and Mn4 positions can be explained by a dimer of dimers model for the S = 3 spin state,9,10 or more exactly by the almost equal contribution of the two lowest-energy broken-symmetry states (notated for Mn1–Mn4) ααβα and αααβ as explained in detail previously.16Table 1 also compares the calculated values with those reported by Marchiori et al.20 and Chrysina et al.,17 who reported open cubane and closed cubane structures, respectively. It is clear that good general agreement is observed between the calculated values and those proposed by Marchiori et al.20 Our DFT calculations suggest that the small-magnitude Mn3 and Mn4 negative hfcs should be interchanged from the Marchiori et al.20 assignments. In addition, Marchiori et al.20 propose an anisotropic hfc for Mn4. This was used to explain the apparently larger zero-field splitting parameter (D value) observed for the glycerol-treated form and suggests a distorted octahedral geometry for Mn4. However, our calculated values in Table 1 indicate that all of the octahedral Mn(IV) ions give rise to an isotropic 55Mn hfc. While it has been assumed that octahedral Mn(IV) ions have low D values ≤ 0.3 cm–1, this has been shown on both experimental and computational grounds to be incorrect, and distortion of one of the Mn ions is not required to increase the D value.16 The BS-DFT calculations shown herein indicate that the hfcs of all Mn ions of the complex exhibit low anisotropy. The hfcs reported by Chrysina et al.17 and Marchiori et al.20 were obtained from simulations of their EDNMR spectra using the salt routine which simulates ENDOR spectra. Implementing the EDNMR-specific horseradish routine, we now use the two hyperfine coupling parameter sets, open cubane and closed cubane, in Table 2, to simulate the exact EDNMR spectra at 94 GHz (Figure 3). The EDNMR spectra are simulated at the low, 1.98 T, and high, 4.4 T, field positions of the W-band EPR spectrum to selectively observe only the single-quantum EPR transition, ms = |−3> → |−2>, of the methanol-treated species as described previously.17 Simulations were performed individually for coupling to each 55Mn nucleus and a single proton and then summed32,33 (Figure 3), following an approach previously used in the analysis of ENDOR data with couplings to multiple nuclei, and also with each pair of 55Mn nuclei and a single proton (Figure 4). In each case, a Lorentzian function with an FWHM of 400 MHz was applied to correct for the inhomogeneities of the B1 field across the bandwidth of the resonator (see the SI; Bandwidth considerations in simulating EDNMR spectra). For the simulations in which there was coupling to two or more 55Mn nuclei, deviations from the summation of the individual simulations were observed at high powers of the HTA microwave pulse, due to multi-quantum transitions involving two or more nuclei. These multi-quantum transitions may be responsible for some of the signals in the experimental EDNMR traces.

Table 1. Calculated Isotropic (Aiso) and Anisotropic (Tnn) 55Mn and 14N hfcs by BS-DFT for the S3 Model Compared with Experimental Values Determined from Simulationsa.

atom labeling from Figure 2 calculated by DFT in this study Marchiori et al.20 Chrysina et al.17
Mn4 Aiso –7.2 –1.7 62.3
T11 0 –1.3 64.7
T22 0 0.7 –30.3
T33 0 0.7 –34.3
Mn3 Aiso –2.4 –7.5 –94.8
T11 0 0 3.5
T22 0 0 –1.7
T33 0 0 –1.7
Mn2 Aiso –100 –96 –98.8
T11 –6 –5 –3.6
T22 2 1 1.8
T33 4 4 1.8
Mn1 Aiso –98 –99 –101.8
T11 –6 –7 –1.2
T22 1 2 –1.2
T33 5 5 –4.3
14N (D1-His332) Aiso –1.3 ND ND
Open in a new tab
a

All values are given in MHz.

Table 2. Hyperfine Couplings (MHz) Used for Horseradish EDNMR Spectral Simulations Presented in Figure 3.

W-band (94 GHz) hyperfine values (MHz) used in simulations
hyperfine matrix Mn1 Mn2 Mn3 Mn4 1H
[A11, A22, A33]—this work (open cubane) [−104, −104, −97.5] [−96.5, −96.5, −91.3] –2.4 –7.2 1
[A11, A22, A33]—Chrysina et al.17 (closed cubane) [−104, −104, −97.5] [−97, −102.5, −97] [−96.5, −96.5, −91.3] [28, 32, 127] 1
Open in a new tab

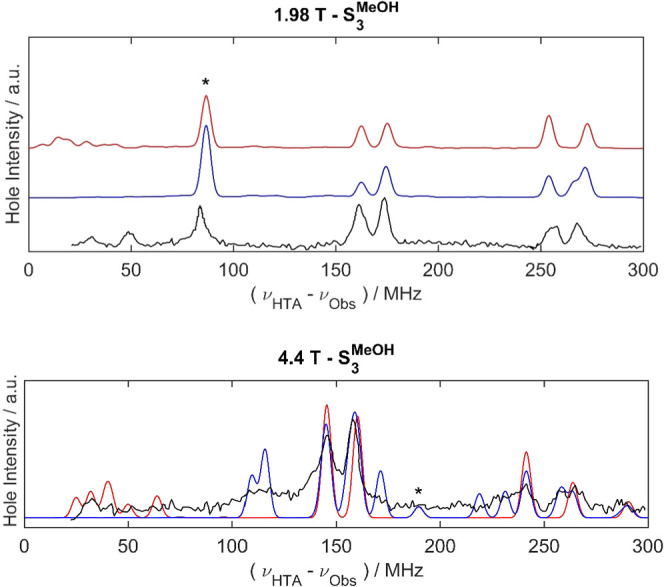
Figure 3.

Figure 3

Open in a new tab

Experimental EDNMR spectra of the methanol-treated PSII reproduced from ref (17) (black); simulated EDNMR spectra summed from simulations with a single 55Mn nucleus using the hfcs from Table 2 for closed cubane (blue) and open cubane (red) structures. 1H resonances are denoted with asterisks and occur around the proton Larmor frequency. The bottom comparison illustrates spectral overlay for 4.4 T simulation to emphasize fit. All simulated data have been multiplied by a Lorentzian function with an FWHM of 400 MHz to mimic the resonator background.

Figure 4.

Figure 4

Open in a new tab

Experimental EDNMR spectra of the methanol-treated PSII reproduced from ref (17) (black); simulated EDNMR spectra summed from simulations with pairs of 55Mn nuclei using the hfcs from Table 2 in the main paper for closed cubane (blue) and open cubane (red) structures, calculated at both low and high field positions with an HTA pulse amplitude of 4.7 × 106 (top) and 4.7 × 107 (bottom) rad s–1. 1H resonances occur around the proton Larmor frequency as shown in Figure 3; 4.4 T simulations are overlaid to emphasize fit. All simulated data have been multiplied by a Lorentzian function with an FWHM of 400 MHz to mimic the resonator background.

It is clear by the inspection of Figure 3 that the simulation of the closed cubane hfcs by Chrysina et al.17 differs from the observed EDNMR spectra, particularly at the high field position of 4.4 T, where sharp signals are calculated at ca. 105, 115, and 170 MHz that are not seen to the same extent in the experimental data. At the low field position of 1.98 T, the closed cubane set provides a reasonable fit to the experimental data; however, the weaker spectral bands at and below 50 MHz—assigned to the anisotropic Mn4 of the closed cubane representation—are not present in the horseradish simulation using these values. The two large-magnitude hfcs (55Mn1 and 55Mn2) are very well reproduced at both low and high field positions and are in agreement with the values of both Chrysina et al.17 and Marchiori et al.20

For the small-magnitude pair of hfcs (55Mn3 and 55Mn4), two prominent single-quantum EDNMR transition frequencies are expected for each coupling, given by υMn55 ± 3|A| and υMn55 ± 2|A|, with + and – corresponding to positive and negative hfc values, respectively.20 The small negative values of the hfcs as calculated by our BS-DFT calculations, Table 1, result in the simulation of spectral peaks of low intensity that lie in a region of the spectrum overlapping and obscured by the central blind spot of the EDNMR experiment. The shape of the central blind spot and experimental background will be greatly affected by B1 inhomogeneities. Consequently, post-processing approximations may distort the experimental data, particularly in the low-frequency region.25 The inhomogeneity of the B1 field at different offset frequencies will further affect the experimental background and relative intensities of the spectral peaks at different frequencies, particularly around the maximum of the B1 field, where changes in B1 are largest with respect to changes in offset frequency. Such uncertainties may explain the non-observance of the EDNMR bands below ∼60 MHz in the W-band (94 GHz) spectra for the methanol-treated samples, as the relative ratio of these peaks to the more well-defined signals at ca. 150 MHz depends on the bandwidth of the resonator.

The simulations presented in Figure 3 do not consider multi-quantum transitions (MQTs) involving more than one 55Mn nucleus. Results from simulations including each pair of 55Mn nuclei show that for the simulation at 4.4 T using the hfcs for the open cubane structure (Table 2) when some MQTs are included, new signals are observed between 100 and 140 MHz, indicating that the broad experimental signal observed at 120 MHz may be due to MQTs. Using the hfcs for both the open and closed cubane cases (Table 2), the inclusion of MQTs arising from two 55Mn nuclei leads to more peaks in the EDNMR spectrum at all frequencies that are not resolved in the experimental data. In particular, both sets of hfcs lead to more MQTs at lower-frequency offsets in the 4.4 T simulation. The number and amplitude of these MQT peaks are reduced in a simulation carried out with an HTA of lower power. This highlights the importance of knowing the bandwidth of the resonator to accurately model EDNMR simulations, particularly in cases where MQTs may be important (further details in the SI, Consideration of multi-quantum effects in EDNMR).

It is important to note that linewidth parameters are added to provide best agreement with the experimental data in all sets of simulations. Experimentally, the observed linewidth depends on the experimental parameters including the pulse lengths used in the detection sequence. Here, the linewidth broadening of simulated peaks is given as a Gaussian with an FWHM of 5 MHz, which reproduces well all major experimental peaks. The linewidth parameter also encodes for the strain of hyperfine values, representing a variation across the molecular configurations present in the sample. It is possible that such variations in the open cubane structure provide larger strains in the hfcs of Mn3 and Mn4, thus reducing the observed amplitude of EDNMR signals from these couplings relative to Mn1 and Mn2. In the simulations of Chrysina et al.,17 using the ENDOR algorithm, a linewidth for the anisotropic Mn4 coupling 3 times larger than that for any other coupling was used.17

Further supporting the open cubane model, the glycerol-treated samples studied by Marchiori et al.20 show a similarly elevated D value to the methanol-treated system, indicating that a similar perturbation occurs, and further, using the horseradish algorithm to re-simulate the experimental data replicates well all experimental peaks (see the SI). In this study, higher-frequency measurements at 130 GHz (D-band), compared to 94 GHz (W-band) by Chrysina et al.,17 further increase the 55Mn Larmor frequency, pushing the EDNMR transitions to higher-frequency values and away from the central blind spot. However, at higher fields, an overlap of small hyperfine values with a 14N spectral peak (υN14 = 17.5 MHz at 5.7 T) begins to occur. Two-dimensional (2D)-EDNMR spectroscopy may help to further aid in signal assignment of the overlapping signals of small-magnitude transitions and 14N transitions at higher fields.29

Conclusions

Broken-symmetry density functional theory (BS-DFT) calculations combined with ELDOR-detected nuclear magnetic resonance (EDNMR) spectral simulations have been used to assign the 55Mn hfcs for modified spectral forms of the water oxidizing complex (WOC) in the penultimate S3 state of the water oxidation cycle. The analysis indicates that an open cubane form of an all-octahedral Mn ion, oxo (O5)–hydroxo (O6), WOC cluster is the dominant S = 3 species observed in all perturbed cases studied experimentally with no need to invoke a closed cubane intermediate possessing a distorted pentacoordinate Mn ion. Currently popular mechanisms for water oxidation, invoking a closed cubane form of the WOC complex as an intermediate state, are not supported by this study.

Methodology and Computational Details

The computational procedure is similar to that described previously in detail.12,22,34 Full details are given in the SI.

Acknowledgments

This research was supported by a grant from the Leverhulme Trust (RPG-2020-003) to P.J.O.M. A.M.B. is grateful to the Royal Society and the EPSRC for their support of a Dorothy Hodgkin fellowship (DH160004) and the University of Manchester for a Dame Kathleen Ollerenshaw Fellowship. A.M.B. and C.J.R. thank the Royal Society for their financial support in the form of an enhancement award (RGF\EA\180287). A.M.B. is also grateful to the Royal Society of Chemistry, the Analytical Chemistry Trust Fund, and the Community for Analytical and Measurement Science for a fellowship (CAMS Fellowship 2020 ACTF ref 600310/09). A.M.B, C.J.R, O.H., and D.C. acknowledge the support of the EPSRC-funded National Research Facility for Electron Paramagnetic Resonance Spectroscopy (EP/V035231/1 and EP/S033181/1). The authors acknowledge use of The University of Manchester Computational Shared Facility (CSF) for this work. The findings supporting this study are provided as the Supporting Information (SI) accompanying this paper, and the data reported in this paper are openly available from the Github repository detailed in the SI file. This study includes a re-analysis of existing data which are openly available at locations cited in the References section of this paper. For the purpose of open access, the author has applied a Creative Commons Attribution (CC BY) license (where permitted by UKRI, “Open Government Licence” or Creative Commons Attribution No-derivatives (CC BY-ND) license may be stated instead) to any Author Accepted Manuscript version arising.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c06151.

  • Full details of computational and simulation methods used; illustrated and XYZ coordinates of models used in BS-DFT calculations; supporting EDNMR simulations; bandwidth considerations in simulating EDNMR spectra; and consideration of multi-quantum effects in EDNMR (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao2c06151_si_001.pdf (770.1KB, pdf)

References

  1. Renger G. Mechanism of light induced water splitting in Photosystem II of oxygen evolving photosynthetic organisms. Biochim. Biophys. Acta, Bioenerg. 2012, 1817, 1164–1176. 10.1016/j.bbabio.2012.02.005. [DOI] [PubMed] [Google Scholar]
  2. Shevela D.; Kern J. F.; Berkeley L.; Whitmarsh J.; Messinger J.; Dennis P. Photosystem II. Biochem. Soc. Trans. 2001, 6, 901–913. [Google Scholar]
  3. Kok B.; Forbush B.; McGloin M. Cooperation of Charges In Photosynthetic O2 Evolution–I. A Linear Four Step Mechanism. Photochem. Photobiol. 1970, 11, 457–475. 10.1111/j.1751-1097.1970.tb06017.x. [DOI] [PubMed] [Google Scholar]
  4. Pantazis D. A. Missing Pieces in the Puzzle of Biological Water Oxidation. ACS Catal. 2018, 8, 9477–9507. 10.1021/acscatal.8b01928. [DOI] [Google Scholar]
  5. Corry T. A.; O’Malley P. J. Electronic-Level View of O-O Bond Formation in Nature’s Water Oxidizing Complex. J. Phys. Chem. Lett. 2020, 11, 4221–4225. 10.1021/acs.jpclett.0c00794. [DOI] [PubMed] [Google Scholar]
  6. Suga M.; Akita F.; Sugahara M.; Kubo M.; Nakajima Y.; Nakane T.; Yamashita K.; Umena Y.; Nakabayashi M.; Yamane T.; Nakano T.; Suzuki M.; Masuda T.; Inoue S.; Kimura T.; Nomura T.; Yonekura S.; Yu L.-J.; Sakamoto T.; Motomura T.; Chen J.-H.; Kato Y.; Noguchi T.; Tono K.; Joti Y.; Kameshima T.; Hatsui T.; Nango E.; Tanaka R.; Naitow H.; Matsuura Y.; Yamashita A.; Yamamoto M.; Nureki O.; Yabashi M.; Ishikawa T.; Iwata S.; Shen J.-R. Light-induced structural changes and the site of O=O bond formation in PSII caught by XFEL. Nature 2017, 543, 131–135. 10.1038/nature21400. [DOI] [PubMed] [Google Scholar]
  7. Young I. D.; Ibrahim M.; Chatterjee R.; Gul S.; Fuller F. D.; Koroidov S.; Brewster A. S.; Tran R.; Alonso-Mori R.; Kroll T.; Michels-Clark T.; Laksmono H.; Sierra R. G.; Stan C. A.; Hussein R.; Zhang M.; Douthit L.; Kubin M.; de Lichtenberg C.; Vo Pham L.; Nilsson H.; Cheah M. H.; Shevela D.; Saracini C.; Bean M. A.; Seuffert I.; Sokaras D.; Weng T.-C.; Pastor E.; Weninger C.; Fransson T.; Lassalle L.; Bräuer P.; Aller P.; Docker P. T.; Andi B.; Orville A. M.; Glownia J. M.; Nelson S.; Sikorski M.; Zhu D.; Hunter M. S.; Lane T. J.; Aquila A.; Koglin J. E.; Robinson J.; Liang M.; Boutet S.; Lyubimov A. Y.; Uervirojnangkoorn M.; Moriarty N. W.; Liebschner D.; Afonine P. V.; Waterman D. G.; Evans G.; Wernet P.; Dobbek H.; Weis W. I.; Brunger A. T.; Zwart P. H.; Adams P. D.; Zouni A.; Messinger J.; Bergmann U.; Sauter N. K.; Kern J.; Yachandra V. K.; Yano J. Structure of photosystem II and substrate binding at room temperature. Nature 2016, 540, 453–457. 10.1038/nature20161. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Boussac A.; Sugiura M.; Rutherford A. W.; Dorlet P. Complete EPR spectrum of the S3-state of the oxygen-evolving photosystem II. J. Am. Chem. Soc. 2009, 131, 5050–5051. 10.1021/ja900680t. [DOI] [PubMed] [Google Scholar]
  9. Cox N.; Retegan M.; Neese F.; Pantazis D. A.; Boussac A.; Lubitz W. Electronic structure of the oxygen-evolving complex in photosystem II prior to O-O bond formation. Science 2014, 345, 804–808. 10.1126/science.1254910. [DOI] [PubMed] [Google Scholar]
  10. Krewald V.; Retegan M.; Cox N.; Messinger J.; Lubitz W.; DeBeer S.; Neese F.; Pantazis D. A. Metal oxidation states in biological water splitting. Chem. Sci. 2015, 6, 1676–1695. 10.1039/C4SC03720K. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Beal N. J.; Corry T. A.; O’Malley P. J. A Comparison of Experimental and Broken Symmetry Density Functional Theory (BS-DFT) Calculated Electron Paramagnetic Resonance (EPR) Parameters for Intermediates Involved in the S2 to S3 State Transition of Nature’s Oxygen Evolving Complex. J. Phys. Chem. B 2018, 122, 1394–1407. 10.1021/acs.jpcb.7b10843. [DOI] [PubMed] [Google Scholar]
  12. Corry T. A.; O’Malley P. J. Evidence of O–O Bond Formation in the Final Metastable S3 State of Nature’s Water Oxidizing Complex Implying a Novel Mechanism of Water Oxidation. J. Phys. Chem. Lett. 2018, 9, 6269–6274. 10.1021/acs.jpclett.8b02793. [DOI] [PubMed] [Google Scholar]
  13. Suga M.; Akita F.; Yamashita K.; Nakajima Y.; Ueno G.; Li H.; Yamane T.; Hirata K.; Umena Y.; Yonekura S.; Yu L.; Murakami H.; Nomura T.; Kimura T.; Kubo M.; Baba S.; Kumasaka T.; Tono K.; Yabashi M.; Isobe H.; Yamaguchi K.; Yamamoto M.; Ago H.; Shen J. An oxyl/oxo mechanism for oxygen-oxygen coupling in PSII revealed by an X-ray free-electron laser. Science 2019, 366, 334–338. 10.1126/science.aax6998. [DOI] [PubMed] [Google Scholar]
  14. Kern J.; Chatterjee R.; Young I. D.; Fuller F. D.; Lassalle L.; Ibrahim M.; Gul S.; Fransson T.; Brewster A. S.; Alonso-Mori R.; Hussein R.; Zhang M.; Douthit L.; de Lichtenberg C.; Cheah M. H.; Shevela D.; Wersig J.; Seuffert I.; Sokaras D.; Pastor E.; Weninger C.; Kroll T.; Sierra R. G.; Aller P.; Butryn A.; Orville A. M.; Liang M.; Batyuk A.; Koglin J. E.; Carbajo S.; Boutet S.; Moriarty N. W.; Holton J. M.; Dobbek H.; Adams P. D.; Bergmann U.; Sauter N. K.; Zouni A.; Messinger J.; Yano J.; Yachandra V. K. Structures of the intermediates of Kok’s photosynthetic water oxidation clock. Nature 2018, 563, 421–425. 10.1038/s41586-018-0681-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Mandal M.; Saito K.; Ishikita H. The Nature of the Short Oxygen–Oxygen Distance in the Mn4CaO6 Complex of Photosystem II Crystals. J. Phys. Chem. Lett. 2020, 11, 10262–10268. 10.1021/acs.jpclett.0c02868. [DOI] [PubMed] [Google Scholar]
  16. Corry T. A.; O’Malley P. J. S3 State Models of Nature’s Water Oxidizing Complex: Analysis of Bonding and Magnetic Exchange Pathways, Assessment of Experimental Electron Paramagnetic Resonance Data, and Implications for the Water Oxidation Mechanism. J. Phys. Chem. B 2021, 125, 10097–10107. 10.1021/acs.jpcb.1c04459. [DOI] [PubMed] [Google Scholar]
  17. Chrysina M.; Heyno E.; Kutin Y.; Reus M.; Nilsson H.; Nowaczyk M. M.; DeBeer S.; Neese F.; Messinger J.; Lubitz W.; Cox N. Five-coordinate MnIV intermediate in the activation of nature’s water splitting cofactor. Proc. Natl. Acad. Sci. U.S.A. 2019, 116, 16841–16846. 10.1073/pnas.1817526116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Askerka M.; Brudvig G. W.; Batista V. S. The O2 -Evolving Complex of Photosystem II: Recent Insights from Quantum Mechanics/Molecular Mechanics (QM/MM), Extended X-ray Absorption Fine Structure (EXAFS), and Femtosecond X-ray Crystallography Data. Acc. Chem. Res. 2017, 50, 41–48. 10.1021/acs.accounts.6b00405. [DOI] [PubMed] [Google Scholar]
  19. Retegan M.; Krewald V.; Mamedov F.; Neese F.; Lubitz W.; Cox N.; Pantazis D. A. A five-coordinate Mn(IV) intermediate in biological water oxidation: spectroscopic signature and a pivot mechanism for water binding. Chem. Sci. 2016, 7, 72–84. 10.1039/C5SC03124A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Marchiori D. A.; Debus R. J.; Britt R. D. Pulse EPR Spectroscopic Characterization of the S3 State of the Oxygen-Evolving Complex of Photosystem II Isolated from Synechocystis. Biochemistry 2020, 59, 4864–4872. 10.1021/acs.biochem.0c00880. [DOI] [PubMed] [Google Scholar]
  21. Siegbahn P. E. M. The S2 to S3 transition for water oxidation in PSII (photosystem II), revisited. Phys. Chem. Chem. Phys. 2018, 20, 22926–22931. 10.1039/C8CP03720E. [DOI] [PubMed] [Google Scholar]
  22. Corry T. A.; O’Malley P. J. Molecular Identification of a High-Spin Deprotonated Intermediate during the S2 to S3 Transition of Nature’s Water-Oxidizing Complex. J. Am. Chem. Soc. 2020, 142, 10240–10243. 10.1021/jacs.0c01351. [DOI] [PubMed] [Google Scholar]
  23. Navarro M. P.; Ames W. M.; Nilsson H.; Lohmiller T.; Pantazis D. A.; Rapatskiy L.; Nowaczyk M. M.; Neese F.; Boussac A.; Messinger J.; Lubitz W.; Cox N. Ammonia binding to the oxygen-evolving complex of photosystem II identifies the solvent-exchangeable oxygen bridge (μ-oxo) of the manganese tetramer. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 15561–15566. 10.1073/pnas.1304334110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Mino H.; Ono T. Applications of pulsed ELDOR-detected NMR measurements to studies of photosystem II: Magnetic characterization of YD tyrosine radical and Mn2+ bound to the high-affinity site. Appl. Magn. Reson. 2003, 23, 571–583. 10.1007/BF03166642. [DOI] [Google Scholar]
  25. Möbius K.; Lubitz W.; Cox N.; Savitsky A. Biomolecular EPR Meets NMR at High Magnetic Fields. Magnetochemistry 2018, 4, 50 10.3390/magnetochemistry4040050. [DOI] [Google Scholar]
  26. Davies E. R. A New Pulse ENDOR Technique. Phys. Lett. A 1974, 47, 1–2. 10.1016/0375-9601(74)90078-4. [DOI] [Google Scholar]
  27. Goldfarb D. Eldor-detected NMR. eMagRes 2017, 6, 101–104. 10.1002/9780470034590.emrstm1516. [DOI] [Google Scholar]
  28. Cox N.; Nalepa A.; Lubitz W.; Savitsky A. ELDOR-detected NMR: A general and robust method for electron-nuclear hyperfine spectroscopy?. J. Magn. Reson. 2017, 280, 63–78. 10.1016/j.jmr.2017.04.006. [DOI] [PubMed] [Google Scholar]
  29. Kaminker I.; Wilson T. D.; Savelieff M. G.; Hovav Y.; Zimmermann H.; Lu Y.; Goldfarb D. Correlating nuclear frequencies by two-dimensional ELDOR-detected NMR spectroscopy. J. Magn. Reson. 2014, 240, 77–89. 10.1016/j.jmr.2013.12.016. [DOI] [PubMed] [Google Scholar]
  30. Stoll S.; Schweiger A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. 10.1016/j.jmr.2005.08.013. [DOI] [PubMed] [Google Scholar]
  31. Wili N.; Richert S.; Limburg B.; Clarke S. J.; Anderson H. L.; Timmel C. R.; Jeschke G. ELDOR-detected NMR beyond hyperfine couplings: A case study with Cu(II)-porphyrin dimers. Phys. Chem. Chem. Phys. 2019, 21, 11676–11688. 10.1039/C9CP01760G. [DOI] [PubMed] [Google Scholar]
  32. Abdalla J. A. B.; Bowen A. M.; Bell S. G.; Wong L. L.; Timmel C. R.; Harmer J. Characterisation of the paramagnetic [2Fe–2S]+ centre in palustrisredoxin-B (PuxB) from Rhodopseudomonas palustris CGA009: g-matrix determination and spin coupling analysis. Phys. Chem. Chem. Phys. 2012, 14, 6526–6537. 10.1039/c2cp24112a. [DOI] [PubMed] [Google Scholar]
  33. Lee H. B.; Marchiori D. A.; Chatterjee R.; Oyala P. H.; Yano J.; Britt R. D.; Agapie T. S = 3 Ground State for a Tetranuclear Mn4IVO4 Complex Mimicking the S3 State of the Oxygen Evolving Complex. J. Am. Chem. Soc. 2020, 142, 3753–3761. 10.1021/jacs.9b10371. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Corry T. A.; O’Malley P. J. Proton Isomers Rationalize the High- and Low-Spin Forms of the S2 State Intermediate in the Water-Oxidizing Reaction of Photosystem II. J. Phys. Chem. Lett. 2019, 10, 5226–5230. 10.1021/acs.jpclett.9b01372. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao2c06151_si_001.pdf (770.1KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES