Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2022 Nov 3;7(45):41189–41200. doi: 10.1021/acsomega.2c04845

Adsorption Behaviors of Different Components of Shale Oil in Quartz Slits Studied by Molecular Simulation

Chunlong Xue 1, Deluo Ji 1, Di Cheng 1, Yutong Wen 1, Huanhuan Luo 1, Ying Li 1,*
PMCID: PMC9670300  PMID: 36406577

Abstract

graphic file with name ao2c04845_0014.jpg

Understanding the adsorption state and molecular behavior of the diverse components of shale oil in shale slits is of critical importance for exploring novel enhanced shale oil recovery techniques, but it is hard to be achieved by experimental measurements. In this paper, molecular dynamics (MD) simulations are performed to quantitatively describe the microbehavior of shale oil mixtures containing different kinds of hydrocarbon components, including asphaltene, in quartz slits. The spatial distributions of all the presenting components are given, the interaction energy between the components and quartz is analyzed, and the diffusion coefficients of all the components are calculated. It was found that asphaltene molecules play a vitally important role in restricting the detachment and diffusion movement of all hydrocarbon components, which is actually a key problem limiting the recovery efficiency of shale oil. The effects of temperature, slit aperture, and the appearance of CO2 on the adsorption behavior of the different shale oil components are examined; the results suggest that the light and medium components are the fractions with the most potential in thermal exploitation, while injection of CO2 is beneficial for the extraction of all the components, especially the medium components. This work gives insights into the effect of asphaltene on shale oil recovery in quartz slits and might provide guidance on the utilization of thermal and CO2-enhanced enhanced oil recovery (EOR) techniques in shale oil production.

1. Introduction

The decline in conventional oil production has triggered the depletion of the world’s resources, and the extraction of shale oil and gas is changing the global energy system.1 In recent years, with advances in fracturing technologies, and lower exploration costs, exploitation of shale oil and gas reservoirs has quickly developed, of which the importance is undeniable.2,3 The very low permeability and abundance of nanopores of shale make the development of shale more complicated than traditional reservoirs, and understanding the microstate and molecular behavior of the shale oil or gas is of great concern for exploring efficient enhanced oil recovery/enhanced gas recovery (EOR/EGR) techniques.4,5 It is widely recognized that shale oil and gas are mainly found in the nano- or micropores of organic and inorganic matrixes, and the storage and mobility of oil and gas in shale reservoirs depend on the type of pores, pore structure, and physical properties of the reservoir. It is important to study the adsorption and diffusion behaviors of the components in shale reservoir pores at the microscopic level, which is not easily characterized, especially for shale oil.

In unconventional shale reservoirs, pore sizes are typically in the nanometer range.6−9 Experimental research has been performed on the adsorption of oil in shale reservoirs;10−14 however, the understanding of the adsorption behavior of shale oil in shale reservoirs is still unclear, mainly because of the composition complexity of shale oils and shale reservoirs. Furthermore, the high pressure conditions of shale oil make it difficult to investigate the effects of the surface chemistry properties of the shale reservoir on the molecular behavior, of which the actual pressure may exceed 30 MPa or above.

Recently, molecular simulation has become a useful tool for studying the behaviors of molecules in nanopores.15−19 For example, molecular dynamics (MD) simulations have been widely used in studying oil and gas reservoir complex systems at the microscopic level, providing a powerful way to characterize the dynamics, structure, and energy properties of the systems at the molecular level.20−22 At the same time, improvements in computational speed and calculation algorithms make it possible to calculate more complex and larger systems and obtain highly accurate results. The adsorption behaviors of hydrocarbon molecules in shale matrices have been described based on simulation studies to help to reveal the adsorption mechanisms.23−28 The molecular structure, diffusion coefficients, and other properties obtained by molecular simulation have been shown to be consistent with the results obtained by experimental means.29 MD simulations have also been used to study the molecular behaviors in flooding processes.30

The adsorption and flow behaviors of multicomponent shale oil in shale reservoirs have been characterized using MD techniques.31−35 It has been found that short chain alkanes have greater diffusion and mobility in shale slits than long chain alkanes, because long chain alkanes preferentially adsorb in shale slits and require more time to undergo conformational changes,31 and heavy components such as long chain alkanes interact more strongly with shale than short chain alkanes.34 However, because the composition of shale oil is complex, understanding about the molecular behaviors of different kinds of shale oil components is still not deep enough, and the key clues to solve the critical problems of shale oil recovery remain to be explored. According to the experimental analysis results,36−39 shale oil contains not only hydrocarbons, such as alkanes and aromatics, but also polar molecules made up of hydrocarbons and heteroatoms, such as asphaltenes. Perez et al.40 measured the adsorption of shale oil mixtures including asphaltene in the kerogen slit and determined that the asphaltene adsorption layer limited the adsorption of other components. Yang et al.41 found that the interactions between kerogen surfaces and asphaltene was the dominant contribution in the adsorption of hydrocarbons. Based on the above discussion, the asphaltenes in shale oil might play a key role in the adsorption behavior of shale oil. But the effect of asphaltenes on the adsorption behavior of each component of shale oil is not clear enough. Based on existing detection results, quartz is one of the typical abundant components of the shale matrix.42,43 Precise study of the microscopic distribution pattern of the complex components of shale oil in quartz slits is meaningful for exploring efficient approaches to enhance recovery.

In this work, a model of a shale slit was constructed by two quartz slabs, and the adsorption behavior of the diverse components of shale oil in a quartz slit was studied using MD methods. The adsorption mechanism and distribution pattern of different shale oil components in the quartz slit were studied. The effect of temperature, slit aperture, and CO2 on the adsorption state and behaviors of the shale oil components in the quartz slit was also investigated. The results of this study give a more in-depth understanding of the molecular states of different kinds of components of shale oil in quartz slits, reveal the key factor of enhancing shale oil recovery, and might provide guidance on the efficient utilization of the thermal and CO2-enhanced EOR technique in shale oil production.

2. Model and Methodology

2.1. Models and Force Field

The (1 0 0) face of α-quartz was used as the slit surface.44,45 The oxygen atoms of Si-O on the surface of the slit are protonated with H atoms to form Si-OH groups. The force field parameters of Si-OH were taken from the work of Warne,46 which has been widely used.26,47,48 The all-atom optimized potentials for liquid simulations (OPLS-AA) force field49 was used for all shale oil molecules. CO2 molecules were modeled by the EPM2 force field.50 The specific force field parameters are shown in Table 1.

Table 1. LJ Parameters and the Charges for Atomic Species of Quartz, CO2.

Atom σ (nm) ε (kJ/mol) q (e)
Si 0.339 2.447 0.310
O (quartz) 0.307 0.711 –0.710
H 0.242 0.125 0.400
C (CO2) 0.276 0.234 0.617
O (CO2) 0.303 0.669 –0.309
Open in a new tab

A flat quartz slit was constructed, the alkanes with different molecular structures and asphaltene, which were chosen as the representative components of shale oil, were put inside randomly, and the construction schematic is shown in Figure 1. A recently reported archipelago type asphaltene structure51,52 was chosen as the representative asphaltene component. The molecular fraction of the shale oil components in the shale oil mixture studied in this work is shown in Table 2, which was set according to the experimental and theoretical analysis results of typical shale oils.41

Figure 1.

Figure 1

Open in a new tab

Simulated hydrocarbons, asphaltene models, quartz slits, and schematic diagram of the construction process of the simulation box. Asphaltene molecules are shown in CPK. Hydrocarbon molecules are represented as lines. Red, yellow, and silver colors represent oxygen, silicon, and hydrogen in quartz, respectively.

Table 2. Molecular Fraction of the Shale Oil Components and Molecular Number of Each Component (Slit Aperture = 8 nm).

  Component Mole fraction % Molecular number
Light component methane 63.5 2100
ethane 7.8 250
propane 4.8 150
n-butane 3.2 110
Medium component n-octane 6.1 210
n-dodecane 6.3 150
toluene 4.8 150
Heavy component asphaltene 4.8 120
Open in a new tab

To facilitate the presentation, the specific components were classified into light (methane, ethane, propane, n-butane), medium (n-octane, n-dodecane, toluene), and heavy (asphaltene) components, respectively, according to molecular weight. Referring to the literature,41 in some parts of the Results and Discussion section, methane was selected as the representative light component, octane was selected as the medium component, and asphaltene was selected as the representative heavy component, in favor of the analysis and clearly exhibiting the results. All the simulation systems are constructed by the Packmol53 package. The simulation system consisted of a slit-shaped quartz slit. For example, for the slit aperture with 8 nm, the simulation box was set by 8 nm apart of two quartz slabs with dimensions of 100.0 Å × 100.0 Å × 98.8 Å.

According to the research objectives, this work is divided into four sections: (1) The adsorption behavior of shale oil components in the quartz slits, which is discussed in section 3.1. The average pressure of the system is close to 21.5 MPa, as shown in Table S1, which is consistent with the pressure region of shale oil reservoirs.54 (2) The effect of slit apertures on the molecular behaviors of shale oil components, which is discussed in section 3.2; temperature is fixed at 358 K. (3) The effect of temperature and pressure on the shale oil distribution in quartz slits, of which the results are discussed in section 3.3; temperature was chosen from 298 to 478 K; the pressures were determined based on bulk density and vary with the corresponding temperature, as shown in the Table S2. (4) The effect of the amount of CO2, which is discussed in section 3.4; the amount of added CO2 molecules55,56 and the system pressure are calculated based on the bulk density and shown in Table S3.

2.2. Simulation Details

First of all, the total energy of the simulation system was minimized using the steepest descent algorithm with a time step of 0.1 fs to remove any contacts and high energy conformations. Then, MD simulations with a canonical ensemble (NVT) were carried out for all simulation systems with periodic boundary conditions applied in the xyz directions. During all the simulations, position restraints are imposed on the quartz plate, in addition to the surface atoms. The predetermined temperature was maintained using the V-rescale thermostat algorithm.57 The bond lengths were constrained by the LINCS algorithm.58 The bulk density (density in the middle of the slit) of the fluid was calculated to identify the bulk phase pressure56,59−63 according to the National Institute of Standards and Technology (NIST) database;55 details are given in the Supporting Information (SI).

The particle mesh Ewald (PME) method64 was used to compute electrostatic interactions. The Lennard-Jones interactions for the nonbonded potential were cut off at 1.2 nm. For all simulation systems, the simulations were performed for 80 ns with a time step of 2 fs. Trajectories of simulation were viewed by VMD 1.9.3.65 The last 10 ns simulation trajectory results were used for further studies. All calculations and analysis, including interaction energy, density distribution, and diffusion properties, were performed using GROMACS (version 2019.6).66,67 The bond interactions, including bond stretching, angle bending, and dihedrals. van der Waals (vdW) and electrostatic (ES) interactions, were calculated for nonbond interactions. vdW interactions were represented by the 12–6 Lennard-Jones function, while ES interactions were represented by Coulomb’s function as follows:

2.2. 1

where qi and qj represent the charges of atom i and atom j, respectively, and rij is the distance between atom i and atom j. LJ parameters (εij and σij) for molecular interactions were calculated based on the Lorentz–Berthelot rule, as follows:

2.2. 2
2.2. 3

3. Results and Discussion

3.1. Microstates and Distribution of the Different Shale Oil Components in the Quartz Slits

The root-mean square displacement (RMSD) of the shale oil components was calculated using eq 4 to confirm the dynamics of shale oil compounds and estimate the required simulation time:

3.1. 4

where N is the number of atoms in selected molecules and ri(0) and ri(t) are the initial position of atom i and the position of atom i at time t, respectively.

Figure 2(a) shows the RMSD of the represented components such as methane, n-octane, and asphaltene in the quartz slit as a function of time. Notably, the RMSD value is higher for both methane and n-octane than that for asphaltene after running for the same time, and the time required for the RMSD value to reach equilibrium is longer for asphaltene than those for methane and n-octane. In general, asphaltene molecules have weak diffusion capability. The variation in the corresponding interaction energy of shale oil molecules’ adsorption process onto the surface in the quartz slit was calculated, as shown in Figure 2(b). The interaction energies for both methane and n-octane reach equilibrium immediately, and there was little change subsequently, while the interaction energy between the quartz surface and asphaltene molecules increases rapidly. The polarity of the aromatic core in asphaltene and the polar groups which can form hydrogen bonds with Si-OH at the quartz surface both provide driving forces for adsorption at the polar surface in quartz slits; the latter one obviously plays a more important role.

Figure 2.

Figure 2

Open in a new tab

(a) RMSD of the shale components, methane, n-octane, and asphaltene, as a function of time. (b) Interaction energy between shale oil components: methane, n-octane, asphaltene, and the quartz slit wall.

The variation in the number of hydrogen bonds between asphaltene and quartz surfaces with time and the schematic diagram of hydrogen bonds are shown in Figure 3. With increasing simulation time, the number of hydrogen bonds between asphaltene and the quartz surface increases rapidly, and it reaches a relatively high stable value after 60 ns. Therefore, both the interaction energy and hydrogen bond interaction between asphaltene and quartz surfaces remain strong, and asphaltene interacts more closely with quartz than methane and n-octane. After running for 60 ns, all the simulation systems reached equilibrium, and the microstates of all the shale oil components can be investigated in detail.

Figure 3.

Figure 3

Open in a new tab

Number of hydrogen bonds between asphaltene and the quartz surface as a function of simulation time.

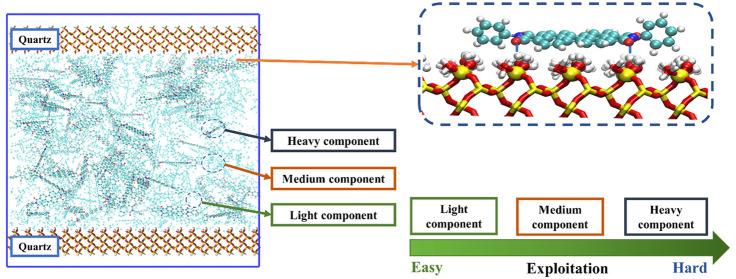
Based on the configuration of shale oil components after equilibrium adsorption, the number density distributions of shale oil components in the quartz slit along the z axis were determined, as shown in Figure 4, which provides basic information about the behaviors of the shale oil molecules in the quartz slit. As shown in Figure 4(a), asphaltene molecules form a tightly adsorbed layer that sticks closely to the quartz surface. To clearly show the distribution of the different components within the quartz slit, including asphaltenes, the number density profiles are shown in Figure 4(b). As expected, the shale oil components’ density distributions are symmetrical to the slit center plane (z = 0), the layered array was found near the two quartz wall surfaces for all the shale oil components, and the density peak of asphaltene located the most closely to the quartz wall, which corresponds well to the differences in interaction energies of the individual components with the quartz slit wall, as shown in Figure 2(b). The light components, such as methane and ethane, tend to distribute in the free volume of the slit away from quartz surfaces, though a part of methane molecules could be distributed near the slit wall. It is worth noting that a large proportion of the medium components, such as n-octane and n-dodecane molecules, accumulate near the quartz surface, though a little farther than the asphaltene molecules, rarely distributed in the middle volume. The aromatic components, such as toluene, distribute pronouncedly at the location near the quartz surface. Such a heterogeneous density distribution displayed the typical microscopic states of the different shale oil components, by which the composition of the produced fluid from the shale could be basically understandable and predictable. The light components in a free volume with fewer constraints could easily diffuse out from the quartz slits and, thus, would be produced easily, while the asphaltene components and medium components are hard to be exploited because of the strong constraints of the quartz slits and the asphaltene molecules might bring out a remarkable influence on the diffusion and output of the medium components.

Figure 4.

Figure 4

Open in a new tab

(a) Schematic representation of the equilibrium adsorption conformation of shale oil in a quartz slit (slit aperture = 8 nm). (b) Number density of each component at 358 K (slit aperture = 8 nm).

The diffusion coefficient is a significant parameter corresponding to the rate of mass transfer. The effect of asphaltene molecules on the adsorption and diffusion behavior of other components of shale oil in the quartz slit was analyzed by calculating the self-diffusion coefficient using Einstein’s relation:

3.1. 5

where N is the number of target molecules in the system, ri(0) is the position of molecule i at the initial time, and ri(t) is the position of molecule i at time t.

The interaction energies between the shale oil components and the quartz in the presence and absence of the asphaltene component were calculated separately and are shown in Figure 5(a). It could be found that, when no asphaltenes are present, the interaction energies between the medium components and the quartz surface are stronger than those of the light components, while the interactions between all the components and the asphaltene molecules are greater than those with the quartz surfaces. As a result, the asphaltene molecules adsorbed on the quartz surfaces play a strong adhesive role to the medium components, and as shown in Figure 5(b), the diffusion coefficient of each component is greater in the absence of asphaltene molecules than that in the presence of asphaltene molecules. These results clearly demonstrated that the asphaltene molecules adsorbed on the surface of the quartz slit wall are the key factor resulting in the stronger constraints of the other shale oil components, especially the medium components, making the extraction of these components more difficult.

Figure 5.

Figure 5

Open in a new tab

(a) Interaction energies of the shale oil components with the pure quartz wall in the presence and absence of asphaltene. (b) Diffusion coefficients of the shale oil components in the slit region in the presence and absence of asphaltene.

To get more insight into the molecular behavior of asphaltene molecules in quartz shale reservoirs more thoroughly, a schematic investigation of the adsorption and aggregation behaviors of asphaltene in quartz slits was explored, and the results are shown in Figure 6. Because of the large number of aromatic rings in the asphaltene molecule, which has a strong π electron effect, the asphaltene molecules could pile one above another and adsorb on the quartz surface in a parallel surface configuration (Figure 6(a)). The distribution of the face-to-face angle between the quartz surface and the polyaromatic planes of the adsorbed asphaltene molecules was calculated as a function of time and is shown in Figure 6(b). The average value of the angle between asphaltene molecules and the quartz surface is found to be 18.69°. Besides, the asphaltene molecules can accumulate in a core-to-core manner, forming a multilayered aggregate structure not only on the surface of the quartz slits, causing slit blockage, but also in the bulk phase, as is shown in Figure 6(c). According to these results, it could be predicted that asphaltene molecules could accumulate in several manners within the quartz slits, causing slit blockage, making the flow and transport of oil and gas molecules in the reservoir more difficult. So, the heavy components with hydrophilic groups in the shale oil, such as asphaltene, play vitally important roles in restricting the detachment and diffusion movement of all the hydrocarbon components, which is actually a key problem limiting the recovery efficiency of shale oil.

Figure 6.

Figure 6

Open in a new tab

(a) Snapshot for asphaltene molecules aggregated at the quartz surface. (b) Angle distribution of the plane of asphaltene molecules on quartz surfaces over time. (c) Snapshot for asphaltene molecules aggregated at the quartz slit; aperture = 2 nm.

3.2. Effect of Slit Aperture on Shale Oil Components’ Distribution in Quartz Slits

In unconventional shale reservoirs, slit apertures are typically in the nanometer range. Characterization of shale pore structures reveals the prevalence of complex multiscale pore networks in shale reservoirs, of which the pores range in size from 1 to 100 nm. The number density distributions of the shale oil components in different quartz slit apertures are calculated (Figure 7). It could be found that the smaller aperture (2.0 nm) is almost occupied by the adsorbed phase due to the interaction overlap between the quartz surfaces and shale oil components, and only a minimal fraction of bulk fluid region exists. With the increase in the slit apertures, some of the shale oil components appear in the slit center region. The percentage of the components in the middle free volume was calculated based on the density distribution, and the results are shown in Figure 8(a). For both light and medium components, as the slit aperture increases, the percentage of shale oil in the intermediate free volume increases. It is concluded that increasing the slit aperture is beneficial for the development of light and medium components. While it is also found that, as the size of the slit aperture increases, the adsorbing state of the asphaltene molecules does not change.

Figure 7.

Figure 7

Open in a new tab

Number densities of the light, medium, and heavy components and shale oil at different quartz slit apertures (358 K): (a) slit aperture = 2 nm; (b) slit aperture = 4 nm; (c) slit aperture = 6 nm; (d) slit aperture = 8 nm; (e) slit aperture = 10 nm; and (f) slit aperture = 16 nm.

Figure 8.

Figure 8

Open in a new tab

(a) Percentage of each component in the free volume at different slit apertures. (b) Diffusion coefficients of the different components in the slit region with various apertures; temperature = 358 K. (c) Interaction energies of methane, n-octane, asphaltene, and the quartz surface with various apertures; temperature = 358 K.

The diffusion behavior of the representative components of shale oil in different slit apertures was investigated. Figure 8(b) illustrates the diffusion coefficients of methane, n-octane, and asphaltene in various quartz slit apertures. The diffusion coefficients of both methane and n-octane molecules increase with increasing slit apertures. Interestingly, the diffusion coefficient of methane molecules increases slowly when the slit aperture reaches 6 nm. As the slit aperture increases, more shale oil molecules are distributed in the free volume, which increases the collision probability between methane molecules, thus affecting the further increase in the diffusion coefficient of methane molecules. For asphaltene, the diffusion coefficients vary little with increasing slit aperture. When the slit aperture reaches 10 nm, the diffusion coefficient is on the order of 10–4 ∼ 10–5 cm2/s. It can be concluded that the asphaltene molecules could not be detached and diffused even in large slit apertures. This is also consistent with the huge interaction energy between the asphaltene molecules and the quartz slit wall, which increases with increasing slit apertures, as shown in Figure 8(c), showing that the restriction strength of the asphaltene molecules on the quartz slit wall increases when the slit aperture increases.

3.3. Effect of Temperature and Pressure on the Shale Oil Components’ Distribution in Quartz Slits

The effect of the variation of temperature and pressure on the shale oil components’ distribution in quartz slits was investigated, to understand and predict the possible efficiency of thermal flooding.41 Since the density distribution of all the shale oil components in the quartz slit is found to be symmetric with the central space, only the results of the density distribution on one side in the quartz slit were shown for the convenience of observation. In this work, the temperature range is chosen from 298 to 478 K; at the same time, pressure varies with the corresponding temperature, from 15.4 to 31.1 MPa. Figure 9(a)–(c) shows the number density distributions of the light, medium, and heavy shale oil components in an 8.0 nm quartz slit from 298 to 478 K. For both light and medium components, there is multilayer adsorption structure near the wall at different temperatures. The peak corresponding to the adsorption layer of the light and medium components decreases with increasing temperature and pressure. The density value of the bulk phase increases with temperature because the interaction between the light, medium component and the quartz slit wall is weakened with temperature increasing. Unlike the light and medium components, the heavy components form two adsorption layers near the quartz slit walls when the temperature is below 378 K and then change to a monolayer as the temperature increases. This is mainly due to the facts that the interaction between the asphaltene molecules and the quartz slit surfaces is still strong enough even at 478 K (Figure 10(b)) and the asphaltene molecules form a uniform adsorbent layer structure with the quartz slit wall.

Figure 9.

Figure 9

Open in a new tab

Number density of light, medium, and heavy components at different temperatures (slit aperture = 8 nm): (a) light components; (b) medium components; (c) heavy components. (d) Percentage of each component in the free volume at different temperatures.

Figure 10.

Figure 10

Open in a new tab

(a) Diffusion coefficients of different components with various temperatures; slit aperture = 8 nm. (b) Interaction energies of methane, n-octane, asphaltene, and quartz surfaces at various temperatures; slit aperture = 8 nm.

To better define the effects of temperature and pressure on the distribution pattern of the shale oil components within the quartz slit, the percentage of the components in the middle free volume was calculated based on the density distribution, which might correspond to the amount of components that could be produced through thermal flooding, and the results are shown in Figure 9(d). As the temperature increases, the percentage of the light and medium components in the middle free volume increased with increasing temperature. The diffusion coefficients and interaction energies with the quartz surface were calculated for methane, octane, and asphaltene, respectively, and the results are shown in Figure 10. Figure 10(a) illustrates that the diffusion coefficients of methane and n-octane increase with temperature increasing and are much larger than the diffusion coefficients of asphaltene molecules, which hardly change with increasing temperature. This phenomenon is consistent with the interaction energy, as shown in Figure 10(b). It could be concluded that increasing temperature has a very limited enhancement effect on the detachment of asphaltene molecules; thereby, the enhancement effects on both the light and medium components were lowered due to the ever-present effect of asphaltene molecules. For example, even if the temperature is increased to 478 K, the lifting efficiency of the medium components can only reach about 36.29%.

3.4. Effect of CO2 on Shale Oil Distribution in Quartz Slits

According to the above discussion, due to the strong interaction between shale oil and asphaltene molecules, and that between the quartz surface and asphaltene molecules, almost all shale oil components are difficult to be extracted. How to overcome this problem is the key to enhancing oil recovery.

In this section, the effect of CO2 on the distribution pattern of shale oil molecules within the quartz slit was investigated. CO2 (20 wt %) of shale oil components was added to the 8 nm quartz slit shale oil model. Figure 11(a) shows a schematic representation of the equilibrium adsorption conformation of shale oil and CO2 in the quartz slit. For the purpose of easy observation, green, orange, and dark blue represent light, medium, and heavy components, respectively. It could be clearly observed that CO2 molecules can not only be adsorbed on the surface of the quartz slit but also distributed within the middle bulk phase volume in the quartz slit, mixed with the light component and the medium component, and a larger part of the medium component diffused into the middle of the bulk phase.

Figure 11.

Figure 11

Open in a new tab

(a) Schematic representation of the equilibrium adsorption conformation of shale oil with CO2, (b) Number density for the shale oil compound in the 8.0 nm quartz slit along with the z axis normal to the slit surface, and schematic representation of the equilibrium adsorption conformation of asphaltene and CO2. (c) Interaction energies of the different components with the quartz wall. (d) Diffusion coefficients of different components in the quartz slit.

To further understand the distribution pattern of all the shale oil components with the presence of CO2 in the quartz slit, the number density distribution of each shale oil component was calculated, and the results are shown in Figure 11(b). The first density peaks of methane, n-octane, and asphaltene molecules appear at −3.53, −3.50, and −3.51 nm, and the first density peak of CO2 appears at −3.64 nm, which indicates that CO2 molecules can enter the inner part of the adsorption layer formed by asphaltenes on the quartz surface (Figure 11(b)), which weakens the interaction between shale oil molecules and the quartz slit wall, as shown in Figure 11(c); thereby, the diffusion coefficient of each component is increased (Figure 11(d)).

By increasing the amount of added CO2 molecules, the pressure of the system was increased in the meanwhile. In this section, the temperature was chosen to be 358 K, above the critical temperature of CO2, and the pressure was adjusted to be above the critical pressure of CO2. The amount of added CO2 was set according to the calculation results of the density of the fluid at the corresponding temperature and pressure. The number density distributions of methane, n-octane, and asphaltene in the quartz slit at different pressures are shown in Figure 12(a)–(c). The distribution of methane molecules within the quartz slit is only slightly affected by the variation of pressure. However, for n-octane molecules, as the pressure continuously increases, more and more n-octane molecules move from the adsorbed layer into the free volume. It was found that with the rising amount of CO2 in the system and as the pressure increases, more CO2 molecules are adsorbed on the surface of the quartz slit, along with more octane molecules desorbing from the quartz surface into the free volume, and the amount of the asphaltene molecules in the closest tight layer on the quartz wall decreases as the amount of CO2 increases. So the presence of CO2 molecules is helpful for the detachment of asphaltene molecules from the quartz walls and also is useful for the diffusion of the light and medium components, which agrees well with the radial distribution function (RDF) profiles in Figure 12(d)–(f). The peaks in the RDF profiles of n-octane are consistently reduced, which means that the average distance between n-octane molecules and the quartz surface increases with the amount of CO2 molecules increasing. The peaks in the RDF profiles of asphaltene reach their lowest value at 58.6 MPa, meaning that more CO2 molecules will cause asphaltene molecules to detach from the quartz wall and move away from it. The results in Figure 12 are consistent with the interaction energy values, which decrease as the pressure increases, and the results are shown in Table 3.

Figure 12.

Figure 12

Open in a new tab

Number density distributions of shale oil components at different CO2 amounts: (a) methane; (b) n-octane; and (c) asphaltene. RDF profiles of the shale oil components and quartz surface at different CO2 amounts: (d) methane; (e) n-octane; and (f) asphaltene.

Table 3. Interaction Energies between Different Components and Quartz (kJ/mol).

  29.8 MPa 34.9 MPa 39.6 MPa 44.7 MPa 49.5 MPa 54.1 MPa 58.6 MPa
van der Waals  
Quartz-methane –277.9 –239.5 –233.7 –210.9 –231.6 –241.1 –260.1
Quartz-n-octane –734.5 –638.6 –493.4 –389.6 –269.7 –211.1 –169.9
Quartz-asphaltene –4616.7 –4960.7 –4935.9 –5062.6 –4776.8 –4610.3 –4310.9
 
Electrostatic  
Quartz-methane –6.9 –4.9 –5.1 –3.7 –4.5 –5.1 –5.4
Quartz-n-octane –33.2 –25.9 –18.8 –11.3 –6.7 –5.3 –3.6
Quartz-asphaltene –3159.6 –3281.5 –3498.6 –3459.1 –3179.5 –3137.1 –2927.9
Open in a new tab

The percentage of each shale oil component presented in the free volume at different pressures was also analyzed, and the results are shown in Figure 13. The percentages of the light and heavy components in the free volume increase slightly, while the percentage of the medium components in the free volume increases remarkably with increasing pressure. When the pressure was 29.8 MPa, the percentage of the medium component in the free volume was 16.71%, and it increases to over 60% when the pressure is increased to 58.6 MPa. Compared with the 36.29% exploitation efficiency achieved by increasing the temperature from 298 to 478 K, as shown in Figure 7(d), inputting CO2 has a more significant enhancement effect on the production of the medium components than the thermal flooding process. So CO2 injection can enhance the recovery of all components of shale oil, especially for the medium and heavy components.

Figure 13.

Figure 13

Open in a new tab

Percentage of each shale oil component in the free volume at different pressures.

4. Conclusions

In this study, the adsorption and diffusion behaviors of diverse shale oil molecules in quartz slits, including light, medium, and heavy components, have been studied by MD simulations. The results show that heavy components such as asphaltenes have significant adsorption capacity on the quartz surface, while the light components, represented by methane, are primarily enriched in the bulk region of quartz slits and the medium components are mainly adsorbed in the intermediate state. In the narrow quartz slit, the asphaltene cluster could reduce the connectivity of the porous shale matrix. The heterogeneous distribution of the shale oil components may correspond to the recovery possibilities in exploitation, and the interactions between the shale oil components and quartz surfaces dominates the adsorption, detachment, and diffusion of all the shale oil components.

The variation in the density distribution of shale oil as the temperature and pressure increase hints at the possibility of thermal flooding oil recovery. The adsorption of light and medium components in the quartz slit decreases, while the adsorption of heavy components strengthens under high temperature, indicating that the light and medium components are the most potential components in thermal exploitation. The injection of CO2 reduces the interaction between the quartz slit wall and asphaltene and all the individual components of the shale oil and is beneficial for enhancing shale oil recovery, especially for medium components, of which the enhancement efficiency can reach as high as more than 60%. This study provides a comprehensive description of the adsorption behavior of shale oil in quartz slits and provides guidance on exploring efficient EOR techniques in shale oil production.

Acknowledgments

This work was financially supported by the National Science Fund of China (No. 21872084, 61575109).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c04845.

  • The method for pressure calculation, the pressure control at different temperature conditions, and the amount of CO2 molecules in systems at different system pressures (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao2c04845_si_001.pdf (155.1KB, pdf)

References

  1. Hughes J. D. Energy: A reality check on the shale revolution. Nature 2013, 494, 307–308. 10.1038/494307a. [DOI] [PubMed] [Google Scholar]
  2. Monteiro P. J. M.; Rycroft C. H.; Barenblatt G. I. A mathematical model of fluid and gas flow in nanoporous media. P. Natl. Acad. Sci. Usa. 2012, 109 (50), 20309–20313. 10.1073/pnas.1219009109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. U.S. Energy Information Administration. Tight oil expected to make up most of U.S. oil production increase through 2040; 2017. [Google Scholar]
  4. Yang Y.; Wang K.; Zhang L.; Sun H.; Zhang K.; Ma J. Pore-scale simulation of shale oil flow based on pore network model. Fuel 2019, 251, 683–692. 10.1016/j.fuel.2019.03.083. [DOI] [Google Scholar]
  5. Kerr R. A. Energy. Natural gas from shale bursts onto the scene. Science 2010, 328 (5986), 1624–6. 10.1126/science.328.5986.1624. [DOI] [PubMed] [Google Scholar]
  6. Perez F.; Devegowda D. Spatial distribution of reservoir fluids in mature kerogen using molecular simulations. Fuel 2019, 235, 448–459. 10.1016/j.fuel.2018.08.024. [DOI] [Google Scholar]
  7. Clarkson C. R.; Solano N.; Bustin R. M.; Bustin A. M. M.; Chalmers G. R. L.; He L.; Melnichenko Y. B.; Radliński A. P.; Blach T. P. Pore structure characterization of North American shale gas reservoirs using USANS/SANS, gas adsorption, and mercury intrusion. Fuel 2013, 103, 606–616. 10.1016/j.fuel.2012.06.119. [DOI] [Google Scholar]
  8. Wang T.; Tian S.; Li G.; Sheng M.; Ren W.; Liu Q.; Tan Y.; Zhang P. Experimental study of water vapor adsorption behaviors on shale. Fuel 2019, 248, 168–177. 10.1016/j.fuel.2019.03.029. [DOI] [Google Scholar]
  9. Wang S.; Javadpour F.; Feng Q. Molecular dynamics simulations of oil transport through inorganic nanopores in shale. Fuel 2016, 171, 74–86. 10.1016/j.fuel.2015.12.071. [DOI] [Google Scholar]
  10. Ojha S. P.; Misra S.; Tinni A.; Sondergeld C.; Rai C. Pore connectivity and pore size distribution estimates for Wolfcamp and Eagle Ford shale samples from oil, gas and condensate windows using adsorption-desorption measurements. J. Petrol. Sci. Eng. 2017, 158, 454–468. 10.1016/j.petrol.2017.08.070. [DOI] [Google Scholar]
  11. Hazra B.; Wood D. A.; Vishal V.; Singh A. K. Pore Characteristics of Distinct Thermally Mature Shales: Influence of Particle Size on Low-Pressure CO2 and N2 Adsorption. Energy Fuel. 2018, 32 (8), 8175–8186. 10.1021/acs.energyfuels.8b01439. [DOI] [Google Scholar]
  12. Awan R. S.; Liu C.; Aadil N.; Yasin Q.; Salaam A.; Hussain A.; Yang S.; Jadoon A. K.; Wu Y.; Gul M. A. Organic geochemical evaluation of Cretaceous Talhar Shale for shale oil and gas potential from Lower Indus Basin, Pakistan. J. Petrol. Sci. Eng. 2021, 200, 108404. 10.1016/j.petrol.2021.108404. [DOI] [Google Scholar]
  13. Ou C.; Li C.; Rui Z.; Ma Q. Lithofacies distribution and gas-controlling characteristics of the Wufeng-Longmaxi black shales in the southeastern region of the Sichuan Basin, China. J. Petrol. Sci. Eng. 2018, 165, 269–283. 10.1016/j.petrol.2018.02.024. [DOI] [Google Scholar]
  14. Lei J.; Pan B.; Guo Y.; Fan Y.; Xue L.; Deng S.; Zhang L.; Ruhan A. A comprehensive analysis of the pyrolysis effects on oil shale pore structures at multiscale using different measurement methods. Energy 2021, 227, 120359. 10.1016/j.energy.2021.120359. [DOI] [Google Scholar]
  15. Cai S.; Li Q.; Liu C.; Liu X. The adsorption of hydrogen sulfide in calcite pores: A molecular simulation study. J. Mol. Liq. 2020, 299, 112253. 10.1016/j.molliq.2019.112253. [DOI] [Google Scholar]
  16. Guo F.; Wang S.; Feng Q.; Yao X.; Xue Q.; Li X. Adsorption and absorption of supercritical methane within shale kerogen slit. J. Mol. Liq. 2020, 320, 114364. 10.1016/j.molliq.2020.114364. [DOI] [Google Scholar]
  17. Zhao J.; Yao G.; Ramisetti S. B.; Hammond R. B.; Wen D. Molecular dynamics investigation of substrate wettability alteration and oil transport in a calcite nanopore. Fuel 2019, 239, 1149–1161. 10.1016/j.fuel.2018.11.089. [DOI] [Google Scholar]
  18. Tian S.; Erastova V.; Lu S.; Greenwell H. C.; Underwood T. R.; Xue H.; Zeng F.; Chen G.; Wu C.; Zhao R. Understanding Model Crude Oil Component Interactions on Kaolinite Silicate and Aluminol Surfaces: Toward Improved Understanding of Shale Oil Recovery. Energy Fuel. 2018, 32 (2), 1155–1165. 10.1021/acs.energyfuels.7b02763. [DOI] [Google Scholar]
  19. Song W.; Yao B.; Yao J.; Li Y.; Sun H.; Yang Y.; Zhang L. Methane surface diffusion capacity in carbon-based capillary with application to organic-rich shale gas reservoir. Chem. Eng. J. 2018, 352, 644–654. 10.1016/j.cej.2018.07.050. [DOI] [Google Scholar]
  20. Sun H.; Zhao H.; Qi N.; Li Y. Molecular Insights into the Enhanced Shale Gas Recovery by Carbon Dioxide in Kerogen Slit Nanopores. J. Phys. Chem. C 2017, 121 (18), 10233–10241. 10.1021/acs.jpcc.7b02618. [DOI] [Google Scholar]
  21. Sun H.; Zhao H.; Qi N.; Zhang K.; Wang Q.; Li Y. Competitive Adsorption of CO2 over N2 in Asphaltene Slit Nanopores Studied by Molecular Simulation. Energy Fuel. 2017, 31 (12), 13979–13984. 10.1021/acs.energyfuels.7b02656. [DOI] [Google Scholar]
  22. Sun H.; Zhao H.; Qi N.; Li Y. Effects of Surface Composition on the Microbehaviors of CH4 and CO2 in Slit-Nanopores: A Simulation Exploration. ACS Omega 2017, 2 (11), 7600–7608. 10.1021/acsomega.7b01185. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Cao Z.; Jiang H.; Zeng J.; Saibi H.; Lu T.; Xie X.; Zhang Y.; Zhou G.; Wu K.; Guo J. Nanoscale liquid hydrocarbon adsorption on clay minerals: A molecular dynamics simulation of shale oils. Chem. Eng. J. 2021, 420, 127578. 10.1016/j.cej.2020.127578. [DOI] [Google Scholar]
  24. Ma Y.; Lu G.; Shao C.; Li X. Molecular dynamics simulation of hydrocarbon molecule adsorption on kaolinite (0 0 1) surface. Fuel 2019, 237, 989–1002. 10.1016/j.fuel.2018.10.063. [DOI] [Google Scholar]
  25. Sedghi M.; Piri M.; Goual L. Atomistic Molecular Dynamics Simulations of Crude Oil/Brine Displacement in Calcite Mesopores. Langmuir 2016, 32 (14), 3375–3384. 10.1021/acs.langmuir.5b04713. [DOI] [PubMed] [Google Scholar]
  26. Yan H.; Yuan S. Molecular Dynamics Simulation of the Oil Detachment Process within Silica Nanopores. J. Phys. Chem. C 2016, 120 (5), 2667–2674. 10.1021/acs.jpcc.5b09841. [DOI] [Google Scholar]
  27. Underwood T.; Erastova V.; Greenwell H. C. Wetting Effects and Molecular Adsorption at Hydrated Kaolinite Clay Mineral Surfaces. J. Phys. Chem. C 2016, 120 (21), 11433–11449. 10.1021/acs.jpcc.6b00187. [DOI] [Google Scholar]
  28. Zhang W.; Feng Q.; Wang S.; Xing X.; Jin Z. CO2-regulated octane flow in calcite nanopores from molecular perspectives. Fuel 2021, 286, 119299. 10.1016/j.fuel.2020.119299. [DOI] [Google Scholar]
  29. Yang Z.; Li Q.; Hua R.; Gray M. R.; Chou K. C. Competitive Adsorption of Toluene and n-Alkanes at Binary Solution/Silica Interfaces. J. Phys. Chem. C 2009, 113 (47), 20355–20359. 10.1021/jp9043122. [DOI] [Google Scholar]
  30. Zhan S.; Su Y.; Jin Z.; Wang W.; Li L. Effect of water film on oil flow in quartz nanopores from molecular perspectives. Fuel 2020, 262, 116560. 10.1016/j.fuel.2019.116560. [DOI] [Google Scholar]
  31. Sang Q.; Zhao X.; Liu H.; Dong M. Analysis of imbibition of n-alkanes in kerogen slits by molecular dynamics simulation for characterization of shale oil rocks. Petrol. Sci. 2022, 19 (3), 1236–1249. 10.1016/j.petsci.2022.01.005. [DOI] [Google Scholar]
  32. Dong X.; Xu W.; Liu R.; Chen Z.; Lu N.; Guo W. Insights into adsorption and diffusion behavior of shale oil in slit nanopores: A molecular dynamics simulation study. J. Mol. Liq. 2022, 359, 119322. 10.1016/j.molliq.2022.119322. [DOI] [Google Scholar]
  33. Zhang M.; Jin Z. Molecular simulation on CO2 adsorption in partially water-saturated kaolinite nanopores in relation to carbon geological sequestration. Chem. Eng. J. 2022, 450, 138002. 10.1016/j.cej.2022.138002. [DOI] [Google Scholar]
  34. Herdes C.; Petit C.; Mejía A.; Müller E. A. Combined Experimental, Theoretical, and Molecular Simulation Approach for the Description of the Fluid-Phase Behavior of Hydrocarbon Mixtures within Shale Rocks. Energy Fuel 2018, 32 (5), 5750–5762. 10.1021/acs.energyfuels.8b00200. [DOI] [Google Scholar]
  35. Zhou J.; Jin Z.; Luo K. H. Insights into recovery of multi-component shale gas by CO2 injection: A molecular perspective. Fuel 2020, 267, 117247. 10.1016/j.fuel.2020.117247. [DOI] [Google Scholar]
  36. Liao L.; Wang Y.; Lu J. Experimental Study on Fractional Compositions of Residual Oil from Shale and Coal of China Using Grain-Based MSSV Pyrolysis. Energy Fuel. 2016, 30 (1), 256–263. 10.1021/acs.energyfuels.5b02486. [DOI] [Google Scholar]
  37. Jarvis J. M.; Billing J. M.; Hallen R. T.; Schmidt A. J.; Schaub T. M. Hydrothermal Liquefaction Biocrude Compositions Compared to Petroleum Crude and Shale Oil. Energy Fuel. 2017, 31 (3), 2896–2906. 10.1021/acs.energyfuels.6b03022. [DOI] [Google Scholar]
  38. Pan L.; Dai F.; Pei S.; Huang J.; Liu S. Influence of particle size and temperature on the yield and composition of products from the pyrolysis of Jimsar (China) oil shale. J. Anal. Appl. Pyrol. 2021, 157, 105211. 10.1016/j.jaap.2021.105211. [DOI] [Google Scholar]
  39. Bunger J. W.; Russell C. P.; Cogswell D. E.. Molecular Composition of Shale Oil. In Oil Shale: A Solution to the Liquid Fuel Dilemma; ACS Symposium Series; Ogunsola, O. I., Hartstein, A. M., Ogunsola, O., Eds.; 2010; American Chemical Society: Washington, DC, Vol. 1032, Chapter 5, pp 103–113 10.1021/bk-2010-1032.ch005 [DOI] [Google Scholar]
  40. Perez F.; Devegowda D. Spatial distribution of reservoir fluids in mature kerogen using molecular simulations. Fuel 2019, 235, 448–459. 10.1016/j.fuel.2018.08.024. [DOI] [Google Scholar]
  41. Yang Y.; Liu J.; Yao J.; Kou J.; Li Z.; Wu T.; Zhang K.; Zhang L.; Sun H. Adsorption behaviors of shale oil in kerogen slit by molecular simulation. Chem. Eng. J. 2020, 387, 124054. 10.1016/j.cej.2020.124054. [DOI] [Google Scholar]
  42. Ross D. J. K.; Marc Bustin R. The importance of shale composition and pore structure upon gas storage potential of shale gas reservoirs. Mar. Petrol. Geol. 2009, 26 (6), 916–927. 10.1016/j.marpetgeo.2008.06.004. [DOI] [Google Scholar]
  43. Liu K.; Ostadhassan M.; Zhou J.; Gentzis T.; Rezaee R. Nanoscale pore structure characterization of the Bakken shale in the USA. Fuel 2017, 209, 567–578. 10.1016/j.fuel.2017.08.034. [DOI] [Google Scholar]
  44. Wright L. B.; Walsh T. R. Facet Selectivity of Binding on Quartz Surfaces: Free Energy Calculations of Amino-Acid Analogue Adsorption. J. Phys. Chem. C 2012, 116 (4), 2933–2945. 10.1021/jp209554g. [DOI] [Google Scholar]
  45. Wang P.; Li X.; Tao Z.; Wang S.; Fan J.; Feng Q.; Xue Q. The miscible behaviors and mechanism of CO2/CH4/C3H8/N2 and crude oil in nanoslits: A molecular dynamics simulation study. Fuel 2021, 304, 121461. 10.1016/j.fuel.2021.121461. [DOI] [Google Scholar]
  46. Warne M. R.; Allan N. L.; Cosgrove T. Computer simulation of water molecules at kaolinite and silica surfaces. Phys. Chem. Chem. Phys. 2000, 2 (16), 3663–3668. 10.1039/b004000m. [DOI] [Google Scholar]
  47. Xiong Y.; Li Z.; Cao T.; Xu S.; Yuan S.; Sjöblom J.; Xu Z. Synergistic Adsorption of Polyaromatic Compounds on Silica Surfaces Studied by Molecular Dynamics Simulation. J. Phys. Chem. C 2018, 122 (8), 4290–4299. 10.1021/acs.jpcc.7b10907. [DOI] [Google Scholar]
  48. Xiong Y.; Cao T.; Chen Q.; Li Z.; Yang Y.; Xu S.; Yuan S.; Sjöblom J.; Xu Z. Adsorption of a Polyaromatic Compound on Silica Surfaces from Organic Solvents Studied by Molecular Dynamics Simulation and AFM Imaging. J. Phys. Chem. C 2017, 121 (9), 5020–5028. 10.1021/acs.jpcc.6b11763. [DOI] [Google Scholar]
  49. Jorgensen W. L.; Maxwell D. S.; Tirado-Rives J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118 (45), 11225–11236. 10.1021/ja9621760. [DOI] [Google Scholar]
  50. Harris J. G.; Yung K. H. Carbon Dioxide’s Liquid-Vapor Coexistence Curve and Critical Properties as Predicted by a Simple Molecular Model. J. Phys. Chem. 1995, 99 (31), 12021–12024. 10.1021/j100031a034. [DOI] [Google Scholar]
  51. Mohammed S.; Gadikota G. The influence of CO2 on the structure of confined asphaltenes in calcite nanopores. Fuel 2019, 236, 769–777. 10.1016/j.fuel.2018.08.124. [DOI] [Google Scholar]
  52. Khalaf M. H.; Mansoori G. A. A new insight into asphaltenes aggregation onset at molecular level in crude oil (an MD simulation study). J. Petrol. Sci. Eng. 2018, 162, 244–250. 10.1016/j.petrol.2017.12.045. [DOI] [Google Scholar]
  53. Martinez L.; Andrade R.; Birgin E. G.; Martinez J. M. PACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations. J. Comput. Chem. 2009, 30 (13), 2157–2164. 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
  54. Wang H.; Chen L.; Qu Z.; Yin Y.; Kang Q.; Yu B.; Tao W. Modeling of multi-scale transport phenomena in shale gas production - A critical review. Appl. Energy 2020, 262, 114575. 10.1016/j.apenergy.2020.114575. [DOI] [Google Scholar]
  55. Lemmon E. W.; McLinden M. O.; Friend D. G.. Thermophysical Properties Of Fluid Systems. NIST Chemistry WebBook; NIST Standard Reference Database 69; 2013. [Google Scholar]
  56. Le T.; Striolo A.; Cole D. R. Propane simulated in silica pores: Adsorption isotherms, molecular structure, and mobility. Chem. Eng. Sci. 2015, 121, 292–299. 10.1016/j.ces.2014.08.022. [DOI] [Google Scholar]
  57. Bussi G.; Donadio D.; Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126 (1), 014101. 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
  58. Hess B. P-LINCS: A Parallel Linear Constraint Solver for Molecular Simulation. J. Chem. Theory Comput. 2008, 4 (1), 116–122. 10.1021/ct700200b. [DOI] [PubMed] [Google Scholar]
  59. Neek-Amal M.; Peeters F. M.; Grigorieva I. V.; Geim A. K. Commensurability Effects in Viscosity of Nanoconfined Water. ACS Nano 2016, 10 (3), 3685–3692. 10.1021/acsnano.6b00187. [DOI] [PubMed] [Google Scholar]
  60. Thomas J. A.; McGaughey A. J. H. Reassessing Fast Water Transport Through Carbon Nanotubes. Nano Lett. 2008, 8 (9), 2788–2793. 10.1021/nl8013617. [DOI] [PubMed] [Google Scholar]
  61. Moh D. Y.; Fang C.; Yin X.; Qiao R. Interfacial CO2-mediated nanoscale oil transport: from impediment to enhancement. Phys. Chem. Chem. Phys. 2020, 22 (40), 23057–23063. 10.1039/D0CP03930F. [DOI] [PubMed] [Google Scholar]
  62. Xu J.; Zhan S.; Wang W.; Su Y.; Wang H. Molecular dynamics simulations of two-phase flow of n-alkanes with water in quartz nanopores. Chem. Eng. J. 2022, 430, 132800. 10.1016/j.cej.2021.132800. [DOI] [Google Scholar]
  63. Zhao Y.; Li W.; Zhan S.; Jin Z. Breakthrough pressure of oil displacement by water through the ultra-narrow kerogen pore throat from the Young–Laplace equation and molecular dynamic simulations. Phys. Chem. Chem. Phys. 2022, 24 (28), 17195–17209. 10.1039/D2CP01643E. [DOI] [PubMed] [Google Scholar]
  64. Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103 (19), 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
  65. Humphrey W.; Dalke A.; Schulten K. VMD: Visual molecular dynamics. J. Mol. Graph 1996, 14 (1), 33–8. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  66. Van Der Spoel D.; Lindahl E.; Hess B.; Groenhof G.; Mark A. E.; Berendsen H. J. GROMACS: fast, flexible, and free. J. Comput. Chem. 2005, 26 (16), 1701–18. 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
  67. Hess B.; Kutzner C.; van der Spoel D.; Lindahl E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4 (3), 435–447. 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao2c04845_si_001.pdf (155.1KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES