Modeling the impact of surveillance activities combined with physical distancing interventions on COVID-19 epidemics at a local level

Abstract

Physical distancing and contact tracing are two key components in controlling the COVID-19 epidemics. Understanding their interaction at local level is important for policymakers. We propose a flexible modeling framework to assess the effect of combining contact tracing with different physical distancing strategies. Using scenario tree analyses, we compute the probability of COVID-19 detection using passive surveillance, with and without contact tracing, in metropolitan Barcelona. The estimates of detection probability and the frequency of daily social contacts are fitted into an age-structured susceptible-exposed-infectious-recovered compartmental model to simulate the epidemics considering different physical distancing scenarios over a period of 26 weeks. With the original Wuhan strain, the probability of detecting an infected individual without implementing physical distancing would have been 0.465, 0.515, 0.617, and 0.665 in designated age groups (0–14, 15–49, 50–64, and >65), respectively. As the physical distancing measures were reinforced and the disease circulation decreased, the interaction between the two interventions resulted in a reduction of the detection probabilities; however, despite this reduction, active contact tracing and isolation remained an effective supplement to physical distancing. If we relied solely on passive surveillance for diagnosing COVID-19, the model required a minimal 50% (95% credible interval, 39–69%) reduction of daily social contacts to keep the infected population under 5%, as compared to the 36% (95% credible interval, 22–56%) reduction with contact tracing systems. The simulation with the B.1.1.7 and B.1.167.2 strains shows similar results. Our simulations showed that a functioning contact tracing program would reduce the need for physical distancing and mitigate the COVID-19 epidemics.

1. Introduction

In 2019, human cases of coronavirus disease 2019 (COVID-19) caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) were first reported in Wuhan, China (Guan et al., 2020; Zhu et al., 2020). SARS-CoV-2 can result in pneumonia and respiratory distress, among other severe clinical signs, especially in elderly patients and those with comorbidities (Guan et al., 2020; Redondo-Bravo et al., 2020; Thakur et al., 2021; Wang et al., 2020; Yang et al., 2020). Following its emergence in China, the virus rapidly spread across all continents, resulting in a pandemic unprecedented in recent history. The rapid surge of COVID-19 cases overwhelmed healthcare systems in many countries and resulted in high excess mortality (Thakur et al., 2021). As the pandemic unfolded, various strategies were proposed and implemented by different authorities to mitigate its impact, first prior to and then later in combination with vaccination campaigns (Anderson, Heesterbeek, Klinkenberg, & Hollingsworth, 2020).

Among these strategies, one of the mainstays has been physical distancing (often known as social distancing), which aims to encourage a minimum physical distance and reduce the frequency of contacts between people (Chu et al., 2020). In order to reduce the frequency of contacts, many authorities have introduced restrictions on social activities, such as suspending public gatherings, closing schools, teleworking, limiting long-distance movements, and so on. Social mixing studies conducted before and after the spread of COVID-19 have demonstrated how the frequency of daily social contacts was reduced by these measures. In Spain, web-based survey research reveals a lower number of daily social contacts when physical distancing measures were imposed during the pandemic compared to pre-COVID estimates of contacts in southern Europe (Mossong et al., 2008; Palmer, Ottow, & Bartumeus, 2021). In the CONNECT study from Québec, Canada, the daily social contacts were reduced by around 50% due to various governmental restrictions when compared to pre-COVID era (Brisson et al., 2021).

Apart from physical distancing, prompt diagnosis and isolation of infectious individuals have also been deemed critical for the control of different infectious diseases, including COVID-19 (Girum, Lentiro, Geremew, Migora, & Shewamare, 2020; Saurabh & Prateek, 2017). Therefore, in addition to passive surveillance, in which diagnostic tests are performed based on clinical suspicion of COVID-19 cases, countries have taken various active approaches to detecting cases. One of the most common approaches is the combination of a disease notification system and contact tracing. After positive cases are reported to public health authorities, depending on the severity of infection and the availability of resources, these cases are isolated in different settings (intensive care units [ICU], hospital wards, quarantine facilities, home isolation, etc.) and authorities track and quarantine their contacts to prevent further transmission (Girum et al., 2020; Kucharski et al., 2020). A well-established notification and contact tracing system can mitigate the transmissibility of infectious diseases. First, reported infectious cases can be isolated to prevent further transmission. Depending on the timeliness of contact tracing, secondary cases can be tracked and quarantined before becoming infectious, avoiding onward transmission to others. Compliance with isolation and quarantine measures directly impacts how the notification and contact tracing system contributes to the mitigation of epidemics. Furthermore, contact tracing should increase the probability of positive cases being diagnosed in the healthcare system since people might be tracked and tested even if they are asymptomatic.

Many researchers have studied and modelled the impact of either contact tracing systems or physical distancing measures on the dynamics of COVID-19 epidemics. However, the influence of the interplay between these two major interventions at a local level is less described in the literature. For example, limiting public gatherings or closing schools may alter the age distribution of an individual's daily social contacts. Since the symptoms and severity of COVID-19 are greatly influenced by the age of the infected, it is reasonable to assume that the efficacy of contact tracing might change alongside different physical distancing measures. Furthermore, if the average number of secondary cases is reduced due to physical distancing measures, the chances of tracing back to the primary cases might also be affected.

In this study, we develop a flexible modeling framework to estimate the effectiveness of a contact tracing system and to represent the interplay between physical distancing and contact tracing measures on COVID-19 dynamics at a local level. To illustrate its applicability, we simulate the epidemic dynamics for different COVID variants on the resident population of the metropolitan area of Barcelona (Spain), considering the implementation of a contact tracing system and testing the influence of various levels of physical distancing.

2. Materials and methods

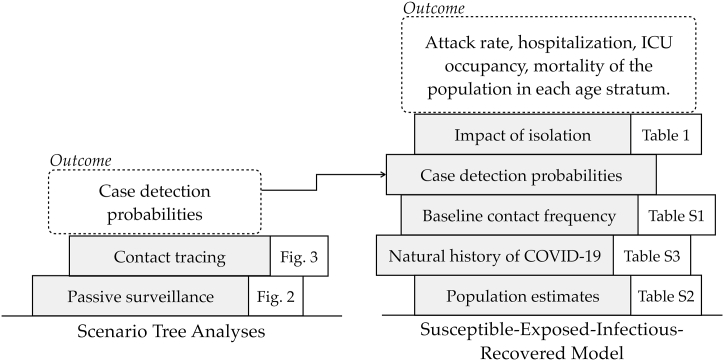
We developed a modeling framework that combined scenario tree (ST) analyses (Food and Agriculture Organization FAO, 2014), which assessed the sensitivity of surveillance actions, with an age-structured susceptible-exposed-infectious-recovered (SEIR) compartmental model to simulate the dynamics of COVID-19 epidemics at the local level, accounting for mitigation measures such as physical distancing.

The ST analysis is frequently employed to demonstrate freedom of disease in animal disease surveillance (Food and Agriculture Organization FAO, 2014). In this work, ST analysis was used to evaluate the probability of detecting an infected person according to his or her age using various potentially overlapping surveillance system components such as passive surveillance and contact tracing. The estimates of the ST analysis combined with other data, including the demographics of the population (age structure, comorbidities), social contact patterns, and natural history of disease, were used as inputs to fit a SEIR model. This SEIR model simulates the epidemic dynamics for the residents of the Barcelona metropolitan area over a period of 26 weeks, comparing three COVID variants with different surveillance strategies and physical distancing interventions. The conceptual and modeling framework are depicted in Fig. 1.

Fig. 1.

Illustration of the modeling framework combining scenario tree analyses and a SEIR epidemiological model.

2.1. Estimating the detection probability of cases of COVID-19

We used ST analysis to estimate the probability of detecting COVID-19 cases according to the age category i combining surveillance components (${p.detect}_i$). Four age strata were designated: (0–14 years of age, 15 to 49, 50 to 64, and above 65). In our study, the ${p.detect}_i$ comprised two components: passive surveillance and contact tracing (either physical or digital). Other components of surveillance, such as population-wide sampling or voluntary screening, were not considered.

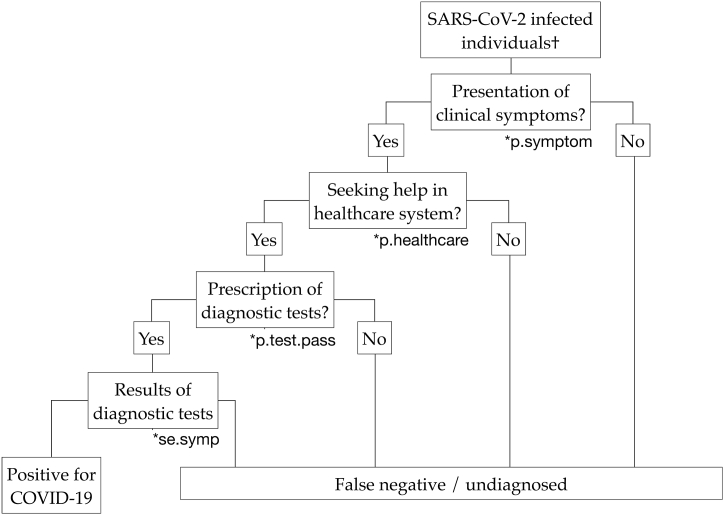
In passive surveillance, the detection probability depends on the probability of presenting clinical symptoms, seeking healthcare, being tested during consultation, and the sensitivity of diagnostic tests (Fig. 2). The detection probability by passive surveillance in each age stratum (${p.detect.pass}_i$) equals the product of the probabilities in each step.

Fig. 2.

Scenario tree diagram representing the probability of detecting cases of COVID-19 by passive surveillance. ^†The detection probability for each age stratum is calculated separately.

In terms of contact tracing, we started by estimating the probability of a COVID-19 case being ‘traceable’ by the contact tracing system (${p.traceable}_i$) and then we accounted for potential losses during the process of contact tracing, such as incompliance, false negativity, etc. (Fig. 3). The parameters used in the ST analysis are listed in Table 1, and more details of the calculation are described in Supplement 1.

Fig. 3.

Scenario tree diagram representing the probability of detecting positive cases by contact tracing. ^†The detection probability for each age stratum is calculated separately. ^‡According to the Spanish guidelines, contacts who were tested negative but developed symptoms of COVID-19 would be managed and re-tested as suspected cases.

Table 1.

Parameters of the scenario tree analyses for the passive surveillance and contact tracing system.

Parameter	Age	Value	Description & Reference
Passive surveillance (seeFig. 3)
${p.symptom}_i$	0–14	0.2	Probability of presenting clinical symptoms after being infected by SARS-CoV-2 in each age stratum.
	15–49	0.4
	50–64	0.5
	≥65	0.6
${p.healthcare}_i$	0–14	0.6	Probabilities of an individual seeking medical attention or consulting a healthcare service after developing clinical symptoms. The default values were assumed based on past experience and may vary significantly depending on the availability of the healthcare system.
	15–49	0.6
	50–64	0.7
	≥65	0.8
${p.test.pass}_i$	0–14	0.7	Probabilities of taking a COVID-19 diagnostic test after the consultation with a healthcare service. The default values were assumed based on past experience and may vary significantly depending on the availability of the healthcare system.
	15–49	0.7
	50–64	0.8
	≥65	0.8
$se.symp$	All	0.95	Sensitivity of the diagnostic test for a symptomatic, SARS-CoV-2 infected patient. In Spain, patients with symptoms for less than 5 days would be tested using antigen-based tests and others by nucleic acid tests (Kortela et al., 2021; Ministerio de Sanidad España, 2020; Woloshin, Patel, & Kesselheim, 2020).
${p.detect.pass}_i$	0–14	0.080	Probabilities of positive cases being detected by passive surveillance (see Fig. 5). Calculated as: ${p.detect.pass}_i={p.symptom}_i\times {p.healthcare}_i\times {p.test.pass}_i\times se.symp$
	15–49	0.160
	50–64	0.266
	≥65	0.365
Active surveillance (seeFig. 4)
${p.cont\_diag}_i$	0–14	variable†	For primary cases in different age strata, this represents the probability of their infected contacts being diagnosed. The numbers were calculated with a baseline (pre-COVID) contact matrix and might change according to different contact matrices used in the calculation. See Supplement 1 for a detailed calculation.
	15–49
	50–64
	≥65
${p.traceable}_i$	0–14	variable†	Probabilities that at least one of the infected contacts was diagnosed, which would make the primary case traceable in the contact tracing system. Calculated as: ${p.traceable}_i=1-{\left(1-{p.cont\_diag}_i\right)}^n$ The numbers were calculated with a baseline (pre-COVID) contact matrix and might change according to different contact matrices used in the calculation. See Supplement 1 for a detailed calculation.
	15–49
	50–64
	≥65
$n$	All	R0‡+1	Average number of directly linked cases. Equals to the effective reproduction number (i.e., secondary cases) plus one (the source of the viruses).
${p.test.act1}_i$	0–14	0.70	Probabilities of a traceable case to be notified and tested for COVID-19. This variable accounted for the errors and incompliance during contact tracing.
	15–49	0.70
	50–64	0.80
	≥65	0.80
$se.contact$	All	0.70	Sensitivity of the diagnostic test for infected close contacts of SARS-CoV-2, regardless of symptoms. In Spain, nucleic acid tests are required to confirm a close contact's being free of SARS-CoV-2 (Ministerio de Sanidad España, 2020).
${p.test.act2}_i$	0–14	0.9	Probabilities of taking a second COVID-19 diagnostic test due to the appearance of clinical symptoms after an initial negative result. This variable accounts for the errors and incompliance of the protocol.
	15–49	0.9
	50–64	0.9
	≥65	0.9
Other parameters regarding the effectiveness of diagnosis and contact tracing
$1/{\gamma }_d$	All	variable	The average time from infection to detection of mild-to-moderate cases (days). Calculated as: $\frac{1}{{\gamma }_d}=-\frac{durationofinfectiousness\left({\gamma }_m\right)}{\ln \left(1-detectionprobability\right)}$
${rr}_i$	All	0.5	Reduction of daily contacts frequency of individuals who were requested to be isolated or quarantined.
${\delta }_e$	All	variable	Probability of ‘exposed’ cases being identified and quarantined before becoming infectious. Calculated as: ${\delta }_e=\left(1-e^{-{\gamma }_d\ast \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\epsilon $}\right.}\right)\times {0.8}^{\S }$

†Calculated with different R0 and contact matrix, see Supplement 1 for detail.

‡See Supplement Table 2 for details.

§Assuming there is a 20% loss or incompliance during contact tracing.

Theoretically, contact tracing can be forward, in which secondary cases are traced due to their contact with a primary case, or backward, when the primary case is traced back after the diagnosis of secondary cases. Since the differentiation might be challenging in reality, in our calculation, forward and backward tracing were considered altogether. Furthermore, the means of contact tracing, either traditionally or digitally, were not differentiated in the model. According to the Spanish guidelines, exposed contacts would be notified by the public health service once the primary case was diagnosed and they would be requested to be quarantined at home for 10 days (Ministerio de Sanidad España, 2020). Furthermore, a diagnostic test would be performed during the 10-day quarantine period. In Spain, nucleic acid tests were required to confirm that an exposed contact was not infected with SARS-CoV-2. Contacts who tested negative and remained asymptomatic would be requested to finish the 10-day quarantine, while those who developed clinical symptoms would be further managed and re-tested as suspected cases (Ministerio de Sanidad España, 2020).

In the ST analysis, we inferred the age distribution of infected contacts to the primary case by estimating the daily social contacts from each age stratum. We used the projected contact matrix generated from the population-based contact diaries of the POLYMOD study (Mossong et al., 2008; Prem, Cook, & Jit, 2017) because there were no social mixing studies focusing on Barcelona or Spanish residents prior to the COVID pandemic. This matrix was then weighted according to the population age structure of the metropolitan area of Barcelona to generate the baseline contact matrix (Table 2).

Table 2.

The baseline social contact matrix generated from the population-based contact diaries in eight European countries of the POLYMOD study.

Age groups	Mean daily contact within each age stratum
	0–14 years	15–49 years	50–64 years	≥65 years
0–14 years	6.28	3.71	0.55	0.24
15–49 years	1.77	11.60	1.60	0.28
50–64 years	1.34	6.52	2.57	0.52
≥65 years	0.89	2.97	1.34	1.55

2.2. Parameterizing the effectiveness of isolation

Other considerations had to be taken into account while estimating the effectiveness of isolation. First, the daily detection rate (${\gamma }_d$) and the time to detection ($1/{\gamma }_d$), which describe the transition of the status of individuals from the ‘Infectious' compartment to the ‘Isolated’ compartment (see Figure S1). We calculated the transition rate by using the probability-rate equation describing the change between two states (Gidwani & Russell, 2020). The equation assumed that the transition rate between the two states (in our case, from ‘Infectious’ to ‘Isolated’) was constant throughout the period of infectiousness. Once an individual was moved into the ‘Isolated’ compartments, we assumed that this individual remained isolated for the rest of the infectious period and the frequency of daily social contacts was reduced by 50%.

As aforementioned, individuals might also be quarantined as infected contacts since the beginning of their infection. The probability of exposed contacts being identified and quarantined before becoming infectious (${\delta }_e$) could be estimated based on the daily detection rate (${\gamma }_d$) and the duration of the ‘exposed’ period ($1/\epsilon$). The calculation of the values for these variables related to the isolation procedure is listed in Table 1.

2.3. Simulating the COVID-19 dynamics using a SEIR compartmental model

The dynamics of COVID-19 epidemics was simulated by a stochastic SEIR compartmental model adapted to the same four-age strata. The model was created based on the structure proposed by Tuite et al. (Figure S1) and tailored to the demographics, social interactions, and epidemiological data of the Barcelona metropolitan area (Tuite, Fisman, & Greer, 2020). The demographics, the social contact matrix and the epidemiological inputs used to fit the model are shown in Table 2, Table S1 and S2. We also took into account the proportion of comorbid conditions related to severe COVID-19 diseases such as cardiovascular diseases, cerebrovascular diseases, obesity, diabetes mellitus, pulmonary diseases, and any active cancers, based on data obtained from the Primary Care Services Information Systems (SISAP), Institut Català de la Salut (ICS), Generalitat de Catalunya (Table S2). To account for the uncertainty in real life, we included a stochastic variable through a simulated realization of the Wiener process during the calculation of the force of infection in the SEIR model (Szabados, 2010).

We hypothesized that all severe cases of COVID-19 would be diagnosed and hospitalized, whereas the probability of detecting mild cases would depend on the probability of detection (${p.detect}_i$). Hospitalized severe patients were assumed to have no contact with the community and the probability of transmission within healthcare institutions was not included. Mild cases would be isolated after their diagnosis. In the scenario of contact tracing, a proportion (calculated according to the detection probability) of exposed contacts were regarded as isolated from the start of their infection. The transmission related to isolated cases or contacts was reduced due to the reduction of social contacts.

The model was run for 26 weeks (182 days), and we assumed that re-infection during this period was not possible after the recovery of COVID-19. The model described the general population in metropolitan Barcelona and the residents of long-term care facilities were not considered. To estimate the maximum possible requirements of ICU beds, we hypothesized that all critically ill patients would be admitted to the ICU before death.

2.4. Scenarios simulated and outputs of the model

Firstly, we assessed how ${p.detect}_i$ would change with the strengthening of physical distancing measures by reducing their daily social contacts from 100% of baseline to 20%. Then, we simulated how overall attack rates, hospitalizations, ICU admissions, and mortalities would change with the same strengthening of physical distancing measures. Furthermore, to demonstrate the effectiveness of contact tracing, we compared the required level of social contacts reduction to keep the overall attack rates under designated thresholds of 5% and 2% within the model period (26 weeks), which corresponded to the World Health Organization epidemiological indicators of COVID-19 community transmission (WHO, 2021).

To represent the epidemic dynamics of the original Wuhan SARS-CoV-2 strain, the B.1.1.7 variant of concern (VOC), and the B.1.167.2 VOC, three different basic reproduction numbers (R0) were used in the simulation (Table S2).

The ST analyses and compartmental model were constructed using the R language programming (version 3.6.3) and RStudio software, version 1.2.5001. The calculation of the differential equations in the model was done by using the deSolve package (Soetaert, Petzoldt, & Setzer, 2010). Overall attack rates, numbers of hospitalizations, ICU admissions, and mortalities were projected in each age stratum. For each simulated scenario, we repeated 200 iterations. The model outputs were presented as the median values and credible intervals of the 200 iterations. We used 95% credible intervals to refer to the range of outcomes from the 2.5th to 97.5th of percentiles. All the data used in our study was publicly available data or anonymized aggregated data, and ethical review was not required.

3. Results

3.1. Estimated probability of detection in different scenarios

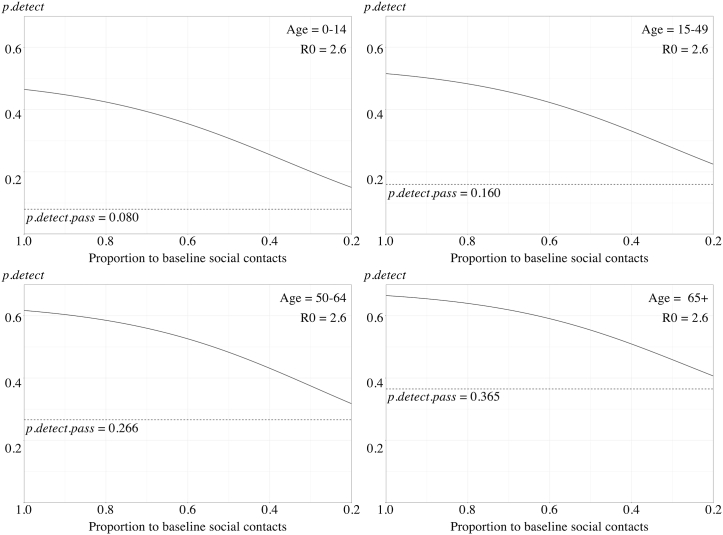
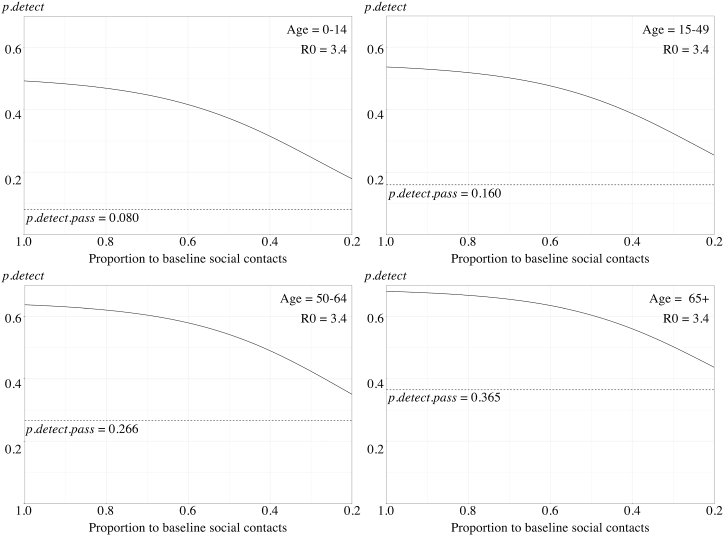
With the scenario tree depicting passive surveillance (Fig. 2) and related variables (Table 1), using passive surveillance, we estimated that the probabilities of detection per age class i (${p.detect.pass}_i$) were 0.080 [0–14 years], 0.160 [15–49 years], 0.266 [50–64 years], and 0.365 [above 65 years]. Since the calculation of passive surveillance depended on the clinical presentation of different age strata, it would not change with the physical distancing measures or R0. When combined with contact tracing, the overall probability of detection (${p.detect}_i$) would vary slightly according to the R0 used in the calculation. With the R0 representing the original Wuhan SARS-CoV-2 strain (R0 = 2.6), the estimated baseline ${p.detect}_i$ (without physical distancing) were 0.465, 0.515, 0.617, and 0.665 in the four age strata, respectively. With the B.1.1.7 VOC (R0 = 3.4), the estimated ${p.detect}_i$ were 0.493, 0.537, 0.637, and 0.680. Finally, with the B.1.167.2 VOC (R0 = 5.1), the estimated ${p.detect}_i$ would further increase slightly to 0.510, 0.551, 0.649, and 0.689, respectively.

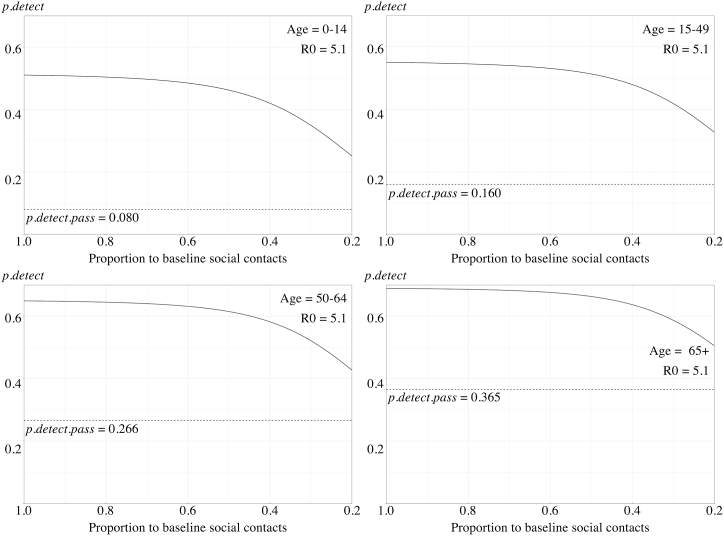
To represent the strengthening of physical distancing, the daily social contacts were reduced gradually from allowing 100% of the baseline (indicating no physical distancing measures in place) to only 20% (indicating an extreme level of physical distancing). With this strengthening of physical distancing, the estimated ${p.detect}_i$ also decreased gradually in the four age strata (Fig. 4). For the original Wuhan strain, the ${p.detect}_i$ with only 20% of baseline daily social contacts allowed were 0.150, 0.225, 0.318 and 0.407; respectively. In our scenario tree model, the decrease of ${p.detect}_i$ was non-linear and was less significant when the R0 was high.

Fig. 4.

A, 4B, 4C. The estimated probability of disease detection reduced with the strengthening of physical distancing measures among different age strata with R0 = 2.6 (A), R0 = 3.4 (B), and R0 = 5.1 (C). The overall detection probabilities (${p.detect}_i$) were represented by solid lines. The detection probability with only passive surveillance (${p.detect.pass}_i$) were represented as dotted horizontal lines.

3.2. How contact tracing impacts the overall attack rates

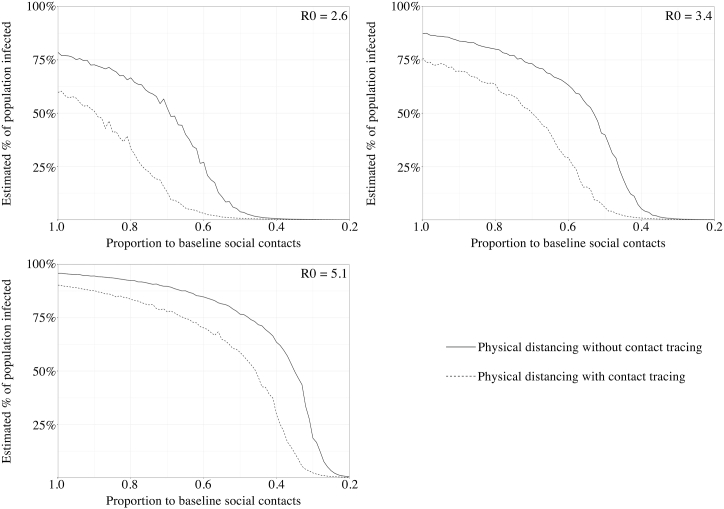
We then projected how the overall attack rates among the residents of the metropolitan area of Barcelona would change at different levels of physical distancing. We began the simulations with daily social contacts equaled to 100% of baseline (i.e., no physical distancing) and gradually reduced them to 20% of baseline. The simulations were performed with or without contact tracing, using three different R0 as aforementioned (Fig. 5).

Fig. 5.

The predicted overall attack rates with different level of physical distancing (represented by a reduced proportion of daily social contacts compared to a baseline) for different basic reproduction number (R0).

With the original Wuhan SARS-CoV-2 strain, if there were no physical distancing measures in place (100% of baseline social contacts) and the diagnosis relied on only passive surveillance (no contact tracing), we predicted that 78.7% of the population in Barcelona would be infected (95% credible interval, 66.0–86.8%). With contact tracing, the proportion of infected decreased to 60.0% of the overall population (95% credible interval, 36.1–77.0%). In both scenarios (with and without contact tracing), with the strengthening of physical distancing, the predicted attack rates would also decrease simultaneously (Fig. 5). When compared to the scenarios without contact tracing, the predicted attack rates were constantly lower in scenarios with contact tracing systems in place. We believed that these results demonstrated the synergistic effect of these two prevention measures, and that contact tracing would remain a valuable adjunctive measure despite the decline in detection probabilities related to physical distancing.

If we aimed to keep the overall attack rate under 5% of the total population during the model simulation, it required a 50% (95% credible interval, 39–69%) reduction of daily social contacts when a contact tracing system was not functioning, as compared to a much lower target of 36% (95% credible interval, 22–50% reduction) when contact tracing is implemented. The thresholds for keeping overall attack rates under 2% of total populations were 56% (95% credible interval, 45–62%) and 43% (95% credible interval, 31–46%) reductions of baseline social contacts, without or with contact tracing, respectively (Table 3).

Table 3.

Estimating the required levels of physical distancing (% of reduction required for baseline daily social contacts) to keep the overall attack rates under designated thresholds in different scenarios.

	Attack rate threshold <5%		Attack rate threshold <2%
Contact tracing system	No	Functioning	No	Functioning
With Original strain	50% (39–69%)†	36% (22–56%)	56% (45–52%)	43% (31–46%)
With VOC B.1.1.7	61% (53–68%)	48% (41–60%)	64% (58–71%)	56% (46–64%)
With VOC B.1.167.2	75% (70–80%)	68% (60–75%)	77% (73–81%)	71% (66–77%)

^†The required reduction of daily social contacts for the given thresholds of attack rates. A higher percentage indicated a more strengthened and strict level of physical distancing.

3.3. Predicted attack rates with different basic reproduction number

We observed similar results with the other two strains in our simulation (Fig. 5). For VOC B.1.1.7, without physical distancing, we predicted that 75.9% (95% credible interval, 62.3–84.2%) and 87.3% of the population (95% credible interval, 80.9–92.6%) would be infected, with and without contact tracing, respectively. As for VOC B.1.167.2, when physical distancing was not implemented, the median predicted infected proportion of the population was 90.3% (95% credible interval, 84.9–93.6%) and 95.8% (95% credible interval, 93.3–97.5%), with and without contact tracing, respectively.

With both variants, the strengthening of physical distancing resulted in a decrease in the estimated population infected in the model (Fig. 5). In the scenarios with both variants, despite the interaction between physical distancing and contact tracing system, implementing contact tracing remained an effective supplement to physical distancing and could further reduced the population infection by COVID-19 in the model. The levels of physical distancing required to control the epidemics are listed in Table 3.

4. Discussion

In this study, we have developed a modeling framework to estimate the detection probability of SARS-CoV-2 infection with different surveillance strategies (passive surveillance with and without active contact tracing). The estimations were then used to simulate the overall attack rates with different levels of physical distancing. We demonstrated how the probability of COVID-19 detection interacts with the physical distancing measures. According to our model, the effectiveness of contact tracing may decrease due to the strengthening of physical distancing measures, but it will remain an effective supplementary approach in controlling epidemics.

Like our study, many researchers have attempted to estimate the effectiveness of contact tracing as part of COVID-19 surveillance and control (Kretzschmar et al., 2020; Quilty et al., 2021; Stuart et al., 2021; Vecino-Ortiz, Congote, Bedoya, & Cucunuba, 2021; Willem et al., 2021). Hypothetic scenarios have been proposed and simulated to assess the potential impacts of active contact tracing deployment. However, some of these scenarios might be difficult to accomplish in real life (e.g., 100% adherence to quarantine, 100% testing of contacts, etc.). In our study, we attempted to quantify the real-life detection probability achieved with the Spanish algorithm of diagnosis and screening (Ministerio de Sanidad España, 2020). Furthermore, most of these models did not consider how physical distancing might impact the performance of contact tracing operational systems (Kretzschmar et al., 2020; Quilty et al., 2021; Vecino-Ortiz et al., 2021). Therefore, we attempted to develop a tool to estimate the interaction between physical distancing measures and contact tracing. Our modeling framework is also quite flexible and can be adapted to fit variables of different healthcare systems or other populations, allowing to compare the effect of similar interventions on different settings.

With the scenario tree analysis, we estimated that the COVID-19 detection probabilities in Catalonia ranged from 8.0% to 36.5% across different age strata if the diagnosis relied solely on passive surveillance. The low detection probability was consistent with the findings of large seroprevalence studies conducted during the first wave of COVID-19 epidemics around the world, when most public health authorities were struggling to trace infected cases (Byambasuren et al., 2021; Grant et al., 2021; Pollán et al., 2020). In Spain, the comparison between reported cases and the seroprevalence in the ENE-COVID study suggested that only 10% of cases were reported by May 2020 (Pollán et al., 2020). The estimates were 12% and 29% in Belgium and Luxembourg, respectively (Grant et al., 2021).

Assuming the contact tracing system to be fully operational, we estimated that the detection probabilities of the original Wuhan strain ranged from 46.7% to 66.5% without physical distancing measures. In our model, the detection probability of COVID-19 would decrease gradually as we strengthened the physical distancing measures and the circulation of viruses was reduced in the population (Fig. 4). This reduction was strongly associated with the reduction in the average numbers of infected contacts. In our estimates, the detection probabilities with extreme physical distancing (with only a 20% baseline of daily social contacts allowed) were 15.8%–43.2%. Despite the reduced detection probability caused by the interaction with physical distancing, contact tracing remained an effective supplementary approach to reducing overall attack rates and epidemics (Fig. 5). Similar results were also demonstrated in the simulation of different strains with higher R0.

In general, prolonged and extreme population-wide lockdowns are often impractical due to their negative socioeconomic impact (Gopinath, 2020). Furthermore, recent studies suggest that prolonged lockdowns might also result in long-term medical problems (López-Bueno et al., 2021; Singh et al., 2020). In our model, we demonstrated that contact tracing could serve as an adjunctive measure to exert similar control of epidemics with a less strict level of physical distancing measures. The requirement of social contacts minimization could be reduced in the presence of contact tracing systems as compared with physical distancing alone (Table 3). Similar to our findings, the synergistic effect of these two control measures was also proposed by other researchers. For example, experience during early epidemics in Taiwan and South Korea demonstrated the combination of case-based (testing and contact tracing) and population-based (social distancing) interventions was important for the early containment of COVID-19 before vaccination was available (Chen & Fang, 2021; Chen, Fang, & Huang, 2021; Ng et al., 2021).

Our study had several limitations and should be interpreted with caution. In the model, we assumed the average compliance to quarantine procedures was 50%. To our knowledge, some countries have implemented various measures to ensure the compliance of quarantine and the impact of contact tracing might increase accordingly with these policies (Ministry of Health and Welfare Taiwan, 2020). Moreover, even in the same healthcare system, compliance could change significantly in different areas or different subpopulations. The capacity of contact tracing by public health authorities might also be heavily impacted by the number of infected cases, which was not considered in our model. Furthermore, estimating the effectiveness of physical distancing is also important when applying our model. Although a drastic reduction of 80% (from 100% to 20%) in the baseline daily contacts was proposed in our study, it might be very difficult to accomplish in real life. In Spain, after the relaxation of nationwide lockdown in May 2020, the number of daily contacts grew rapidly in the area of Barcelona, despite some mobility restrictions being still instated, and the reduction in daily contacts was estimated to be only around 25%.

Furthermore, the time required for establishing a diagnosis was also important for the control of epidemics. Early diagnosis would lead to early isolation of infected individuals and greater reduction of transmission. In our study, the rates of detection were calculated by the probability-rate equation describing the transition between two states (Gidwani & Russell, 2020). In reality, the rate depends largely on the efficiency of the public health service and may vary significantly in different settings. In a study evaluating the contact tracing procedure in the United States, it could take up to more than 10 days to notify the exposed contacts (Lash et al., 2021). Therefore, it is also important for policymakers to monitor the performance of contact tracing system and implement different methodologies to improve its efficiency (Garry, Hope, Zajac, Verrall, & Robertson, 2021). For example, a study in the United Kingdom has demonstrated the correlation between the uptake of the NHS smartphone app and the reduction of local COVID-19 cases (Wymant et al., 2021).

One of the main limitations of our model is that our ST analyses were deterministic. Considering the high complexity of the contact tracing system in real life and its interaction with the contact matrices, it is very likely that a certain amount of randomness should be taken into account during calculation. Therefore, the point estimates of the detection probability obtained in this study should be interpreted with great caution. However, since we included a stochastic factor during the calculation of the force of infection ($\lambda$) in the SEIR model, we believe the final simulations included adequate stochastic variations to represent the possible outcomes in real life.

We made several simplifications during the construction and parameterization of the model. Firstly, in order to reduce the complexity, we only considered the general public in the metropolitan area of Barcelona, and the residents in the long-term care facilities were not included. The model was applied to a closed population and the movement of population was not considered. The coverage of vaccination, healthcare-related infections, and the possibility of re-infection were neither featured in the model. These factors could largely change the magnitude of COVID-19 epidemics. Furthermore, we did not consider the potential false positives of the diagnostic tests since they do not contribute to the transmission of viruses. We also assumed all fatal cases would be admitted to an ICU before death. This assumption is designed to gauge the maximal requirement of ICU beds. Therefore, caution must be taken when comparing our simulations in this study to real-life reports. Due to these simplifications and aforementioned limitations, we were unable to validate our model outputs with real-life observations in the study. The rapid change of our understanding of COVID-19 and local disease containment policies during the epidemics has also increased the difficulty of validation. However, since these factors had little interaction with physical distancing measures and the diagnosis system, we believed that the comparisons between different physical distancing and surveillance strategies in our modeling framework are still informative. Moreover, if necessary, the framework can also be easily modified to accommodate new variables and provide viable simulations of real-life scenarios.

In our study, we assumed that daily social contacts would decrease homogeneously across different age strata. However, it is possible that different policies implemented in real life would affect different populations. Therefore, we also simulated several scenarios with physical distancing policies focusing on different age strata, and the conclusion was similar to current findings (data not shown). Nevertheless, decision-makers should consider how the effects of physical distancing policies might affect different populations (ages, sectors, genders) before applying our results.

In terms of surveillance, several key parameters we used in the calculation required validation when applied in different healthcare systems. These parameters might change significantly with different public health policies and infrastructure. We believe that our calculation provides a possible means to estimate the overall detection probability, but the variables used during the calculation need to be tailored accordingly in different healthcare systems.

In conclusion, we developed a model combining ST analysis and a SEIR compartmental model, which can be used to assess the impact of surveillance strategies and their interactions with physical distancing. In our simulation, the detection probability of COVID-19 with a contact tracing system would decrease gradually as we strengthened physical distancing measures. However, contact tracing would remain a valuable adjunctive measure to mitigate the impact of COVID-19 epidemics.

Funding

F.B. and J.R.B.P. acknowledge funding from the European Commission, under Grants 874735 (VEO), 853271 (H-MIP), and 2020/2094 (NextGenerationEU, through CSIC's Global Health Platform, PTI Salud Global).

Author contributions

G-J. C participated in the conceptualization, software adaptation and design, analysis, and interpretation of the study's data, as well as the writing of the original publication. JP and FB contributed to the analysis and interpretation of data related to contact matrix and social distance, reviewing and editing. AA was in charge of supervision and design of the study; data curation and analysis and interpretation; and reviewing and editing of intellectual content. All authors had full access to all the data in the study and accepted responsibility for submitting it for publication.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Handling Editor: Dr Y. Shao

Appendix A. Supplementary data

The following is/are the supplementary data to this article: