Male pelvic multi-organ segmentation Using Token-based Transformer Vnet

Abstract

Objective:

This work aims to develop an automated segmentation method for the prostate and its surrounding organs-at-risk (OAR) in pelvic computed tomography to facilitate prostate radiation treatment planning.

Approach:

In this work, we propose a novel deep-learning algorithm combining a U-shaped convolutional neural network (CNN) and vision transformer (VIT) for multi-organ (i.e., bladder, prostate, rectum, left and right femoral heads) segmentation in male pelvic CT images. The U-shaped model consists of three components: a CNN-based encoder for local feature extraction, a token-based VIT for capturing global dependencies from the CNN features, and a CNN-based decoder for predicting the segmentation out- come from the VIT’s output. The novelty of our network is a token-based multi-head self-attention (MHSA) mechanism used in the transformer, which encourages long- range dependencies and forwards informative high-resolution feature maps from the encoder to the decoder. In addition, a knowledge distillation strategy is deployed to further enhance the learning capability of the proposed network.

Main results:

We evaluated the network using: 1) a dataset collected from 94 patients with prostate cancer; 2) and a public dataset CT-ORG. A quantitative evaluation of the proposed network’s performance was performed on each organ based on 1) volume similarity between the segmented contours and ground truth using Dice score, segmentation sensitivity, and precision, 2) surface similarity evaluated by Hausdorff distance (HD), mean surface distance (MSD) and residual mean square distance (RMS), 3) and percentage volume difference (PVD). The performance was then compared against other state-of-art methods. Average volume similarity measures obtained by the network over all organs were Dice score = 0.91, sensitivity = 0.90, precision=0.92, average surface similarities were HD = 3.78 mm, MSD = 1.24 mm, RMS = 2.03 mm; average percentage volume difference was PVD = 9.9% on the first dataset. The network also obtained Dice score = 0.93, sensitivity = 0.93, precision=0.93, average surface similarities were HD = 5.82 mm, MSD = 1.16 mm, RMS = 1.24 mm; average percentage volume difference was PVD = 6.6% on the CT-ORG dataset.

Significance:

In summary, we propose a token-based transformer network with knowledge distillation for multi-organ segmentation using CT images. This method provides accurate and reliable segmentation results for each organ using CT imaging, facilitating the prostate radiation clinical workflow.

I. Introduction

During radiation therapy, radiation beams must be guided to the tumor while sparing normal tissue by accurately measuring the contours of the treatment target and organs-at-risk (OARs) using planning CT images. Contour accuracy is crucial for determining the correct conformal prescribed dose distribution for treatment success. However, physicians’ current clinical practice involves manual contour delineation, a labor-intensive and operator-dependent process. For example, in prostate cancer radiation therapy, the prostate must be contoured as a treatment target. The bladder, rectum, and left/right femoral heads are the most common organs contoured as OARs. Physicians would contour these organs based on their understanding of clinical guidelines, which involves inter- and intra-observer variances and takes hours. The contours of these organs are then used during the plan-generating process. Over-contouring on OARs may result in excess radiation on normal tissue, which can cause genitourinary complications. In contrast, under-contour on the prostate may result in an under-dose of cancer cells, leading to cancer recurrence. Therefore, it is desirable to develop a method for accurate automatic segmentation to standardize the radiation treatment workflow by reducing operator-dependent variation and improving efficiency.

Automated multi-organ segmentation can be roughly classified into two categories: model-based and data-based segmentation. Model-based segmentation method pre-defines and utilizes critical image features to locate organs in CT scans, including but not limited to image variance and morphological features for heart segmentation in CT images(Tong et al., 2013); geometric landmarks and pose parameters for lung segmentation(Ecabert et al.); and multi-scale decomposition properties derived from a total variation/L model for lung cancer segmentation(Sun et al.). Despite good quantitative performance and the high interpretability of a model-based algorithm, a pre-determined model cannot fully represent the intricate visual information of organs in CT scans, which could adversely affect model generalization.

By contrast, data-based segmentation can mitigate this issue by automatically learning dataset-specific features as available large-scale public datasets train the models. With a sufficiently large dataset, a data-based segmentation yields excellent generalization and has demonstrated state-of-the-art performance in various tasks of CT-based organ segmentation. Recent data-based medical segmentation algorithms have relied primarily on fully convolutional neural networks (CNN)-based U-net architectures (Isensee et al., 2021; Lu et al., 2019; Ronneberger et al., 2015). U-net consists of an encoder and decoder: the encoder gradually down-samplings the CT scans, which encodes the input into conceptual features across several resolutions. Then, the decoder up-samples the extracted features to assemble an N-organ segmentation. In addition, a skip-connection concatenates the outputs of the encoder and decoder at various image resolutions to preserve information otherwise lost in down-sampling, further improving performance. In pelvic organ segmentation, following the typical U-net architecture, state-of-the-art algorithms utilize additional techniques to assist the network in learning more informative segmentation features. The additional techniques include a localization network to detect the location of each organ before the pixel-level segmentation; a self-attention/transformer mechanism for global feature acquisition, deep supervision for improving generality, and an auxiliary generative adversarial network to transfer CT images to MRI images to obtain better organ-to-tissue contrast (Dong et al.; Lei et al., 2020; Sultana et al., 2020; Balagopal et al.; Pan et al., 2022b). The techniques were proposed to further improve U-net’s performance in CT multi-organ segmentation.

Despite their superior accuracy, CNN-based U-nets inherently have limited ability to model global dependencies due to localized receptive fields(Luo et al., 2016). In medical images, the Vision Transformer (VIT) (Dosovitskiy et al., 2020) has been shown to be an effective method for emphasizing global dependencies and providing better segmentations, especially for those object structures with varying sizes and shapes. Using a transformer between the encoder and decoder of U-net, Chen et al.(Chen et al., 2021) segmented 2D abdominal CT scans by capturing global context from U-net feature maps. Cao et al.(Cao et al., 2021) proposed a U-shaped swim-transformer for 2D CT/MRI segmentation by replacing all the convolutional layers with sliding-window transformer blocks. By replacing the CNN-based encoder with a transformer in the U-net, Hatamizadeh et al.(Hatamizadeh et al., 2022) proposed a multi-organ/multi-tumor segmentation approach in 3D CT scans that achieved state-of-the-art accuracy.

Despite the fact that these models have demonstrated state-of-the-art performance in CT multi-organ segmentation; however, a transformer based on MHSA requires a massive dataset to achieve this performance. Without abundant data, it suffers severe overfitting greatly underperforms extant CNNs (Khan et al., 2021). Therefore, strong technique to reduce overfitting of the transformer is necessary for full realization of the potential for VITs, especially for the pelvic CT segmentation where the data are limited.

In this work, we propose a novel network architecture, Token-based Transformer Vnet (TTVnet), which bridges a 3D U-net (Vnet)(Lu et al., 2019) and VIT to take advantage of both architectures. TTVnet has a similar encoder-decoder structure to Vnet. In addition, we implement a token-based self-attention mechanism(Wu et al., 2020; Pan et al., 2022a), which facilitates us to obtain much stronger performance than VITs with order-of-magnitude less medical data, to enrich the global dependencies in the features from the encoder to the decoder. Motivated by the Data-efficient Vision Transformer(Touvron et al., 2021), a knowledge distillation (KD) strategy is applied to reduce network overfitting and assist the training process. To our best knowledge, we are the first paper utilize a token-based transformer with KD strategy in medical image segmentation. We implemented the network to segment: 1) bladder, prostate, rectum, left femoral head (LFH), and right femoral head (RFH) from 3D a pelvic CT dataset collected from 94 patients in Emory Winship Cancer Institute; 2) liver, bladder, lung, kidney, and bone in CT-ORG dataset. A quantitative evaluation of the network performance is presented.

II. Method

As illustrated in Fig. 1 (a), TTVnet employs a 3D convolutional encoder-decoder architecture with a backbone inherited from Vnet. The encoder (left) consists of four compression stages to learn features from the pelvic data. Then the decoder (right) decompresses the features to assemble an N-class volumetric segmentation. We utilize a token-based self-attention mechanism to forward features between several layers of equal resolution in the encoder to the decoder. Here we introduce the architecture of the network and the mathematical formulation of its components.

Figure 1:

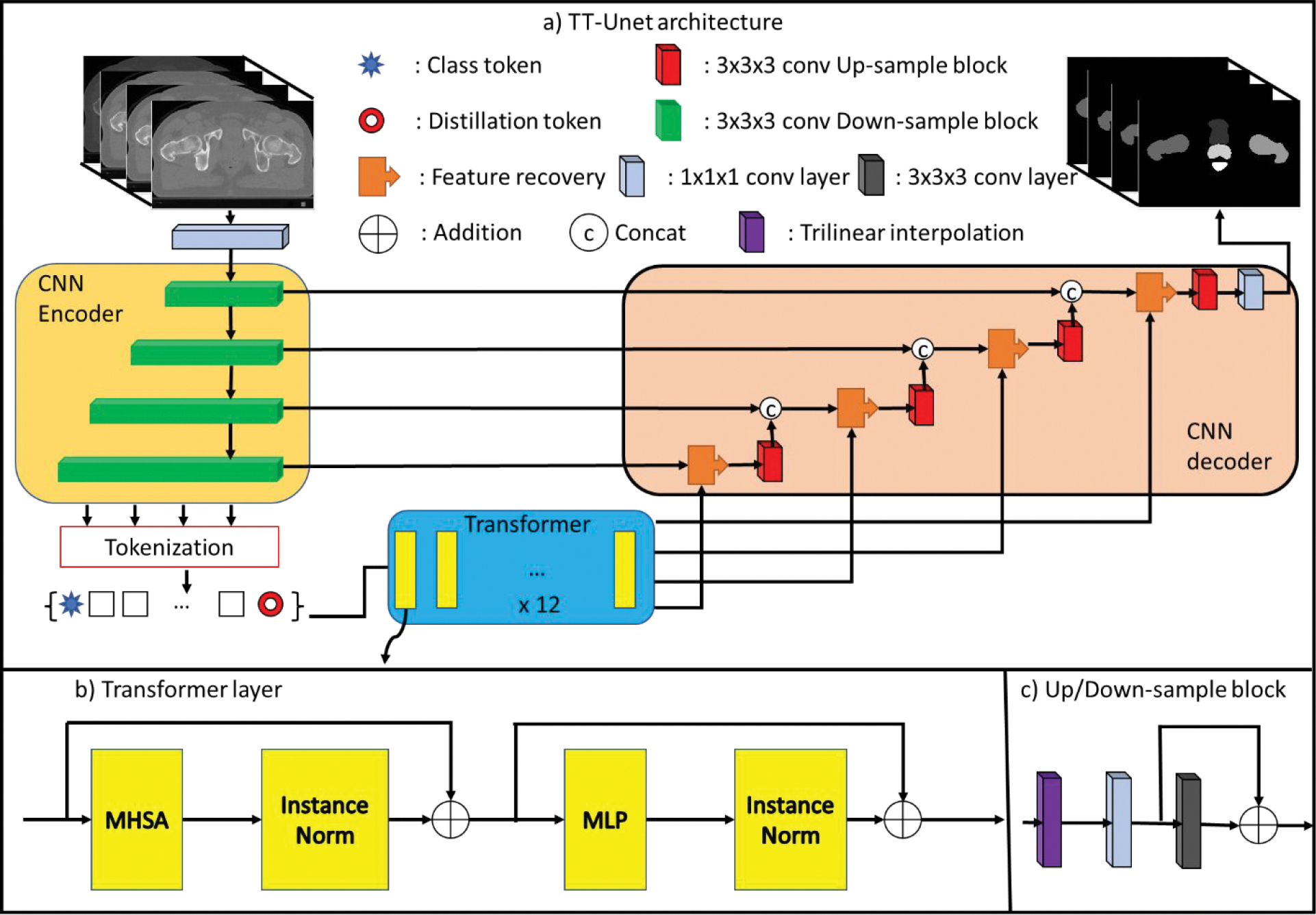
(a) Network structure: transformer (middle) is deployed as a bridge between the Vnet encoder (left) and the decoder (right). The Encoder’s feature maps are first tokenized with class and distillation tokens, then passed to the Transformer block. The output is split into a set of tokens corresponding to each residual block and then passed to the decoder. The number of filters in the first to the fourth layers in the encoder are 128, 256, 512 and 1024, respectively. The numbers of the filters in the decoder mirrors the encoder in an inverse direction. (b) Transformer layer: the transformer layer consists of an MHSA and an MLP. c) Up/Down-sampling block: the block contains a trilinear interpolation followed by two convolutional layers.

II.A. Network architecture

For the encoder’s architecture, we take advantage of the ”shortcut connection” used in ResNet(He et al., 2016), which improves network stability and has been applied in many deep learning applications such as 2D image segmentation. We propose a ResNet-like architecture as the encoder. The input pelvic data is first passed through a convolutional layer with 64 1 × 1 × 1 spatial filter with stride 1, then fed into four down-sampling residual blocks. Each residual block combines one trilinear down-sampling layer with two subsequent 3D-convolutional layers. The first convolutional layer has 1 × 1 × 1 spatial filter with stride 1 in each direction, and the second convolutional layer utilizes 3 × 3 × 3 filters with the same stride. A shortcut connection is applied between the outputs of the first and second convolutional blocks.

The transformer consists of 12 transformer blocks to compute global dependencies inherent in the tokenized feature maps T extracted from the encoder. As shown in Fig. 1 (b), the transformer block combines a Multi-head Self-Attention (MHSA) (Section II.B.2) and a multi-layer linear perceptron (MLP) of two linear layers. The first and second linear layer dimension was set to 3072 and 512, respectively.

The decoder mirrors the encoder’s architecture. First, the transformer’s output features are passed through 4 residual up-sampling blocks with 3 × 3 × 3 convolutional layers with stride 1. Next, the resultant feature maps of the fourth residual block are connected to a 1 × 1 × 1 convolutional layer with the number of channels equal to the number of organ segments desired. Finally, a Softmax activation function is applied, classifying each pixel into one of the segmentation classes corresponding to one of the bladders, prostate, rectum, LFH, and RFHs.

In this network, instance normalization(Ulyanov et al., 2016) followed by the leaky-ReLu activation with a negative slope of 0.2 is applied after every convolutional layer, MHSA module, and linear layer. We utilize the Adam optimizer with an initial learning rate of 0.0001. After that, the learning rate decays to 0.93 of its value every ten epochs. The batch size was 2, and 250 epochs were used.

II.B. Token-based transformer

In general, transformer networks utilize MHSA and MLPs to map a sequence of patch embedding into pixel-level organ segmentation masks. A feature map or image F is split into fixed-size patches. Then feature embedding process condenses the patches into a compact set of information tokens 𝑇, which facilitates the network to focus on important regions instead of the whole input, to reduce overfitting and improve training efficiency. The resultant embedded tokens are then fed to the transformer network. The transformer captures the global information across the patch sequence primarily using the MHSA module. Several sets of weight matrices compute interactions between pixels to capture spatial context across the entire image, including across spatially distant pixels. In this project, we adopt sparse tokenization from the token-based transformer(Wu et al., 2020; Pan et al., 2022a) on the feature maps from each down-sampling block. Rather than encoding all contexts across the entire image, the sparse tokenization models semantic concepts in a few tokens relevant to the organ segmentation. The token-based transformer can then reduce irrelevant features to improve the network’s generalization and accelerate training. Finally, the tokens from convolutional blocks of different scales are concatenation and fed into the transformer to compute the interaction between each pixel across different resolutions. The transformer’s output is then combined with the original patches F to recover the pixel- level details for the final segmentation. In summary, the proposed token-based transformer is formulated in three steps:

1. F is sparsely tokenized as T_in.

2. A transformer network learns spatially-distant concepts from the T_in through the MHSA module.

3. The transformer’s output is finally recovered to the feature maps of the original size of T_out, which is prepared for the decoder.

II.B.1. Sparse tokenization

We first perform tokenization of each input features maps extracted from layers of the encoder. The feature maps F ^1,2,3,4 ∈ R^H×W×L×D from four down-sampling blocks is flattened over the first three dimensions, where H, W,L are sizes of the feature map, D is the channel dimension. Then filter-based tokenizers are adopted to sparsely pool the n’th layer’s feature maps Fⁿ to obtain multi-scale sparse information tokens Tⁿ ∈ R^N×D, where N is the number of tokens. For the feature maps from the first down-sampling block, the 3D filtered-based tokenizer performs the following operation:

$$T^1=softma{x}_{HWL}{(F^1{W}_F)}^T{F}^1$$ (1)

where $W_F\in {ℝ}^{D\times N}$ is a trainable weight matrix forms spatial semantic groups from F¹, and softmax_HWL indicating Softmax operation on the first dimension. In our practice, the multiplication of F¹ and W_F can be represented as L(F¹), where L is a linear layer without bias. The linear layer was further substituted by a convolutional layer conv(F¹) with kernel size of 1 × 1 × 1, which is an efficient approximation of the linear layer(Szegedy et al., 2015).

For the feature maps from the other down-sampling blocks, we perform a recurrent tokenizer which is dependent upon the information token T_prev from the previous down- sampling block. With this guidance, we incrementally refine the tokens as more precise representations. The recurrent tokenizer utilizes two trainable weight matrices, $W_V\in {ℝ}^{D\times N}$ and $W_R\in {ℝ}^{D\times N}$, performs:

$$T^n=softma{x}_{HWL}{\left(F^n{W}_V{T}_{prev}{W}_R\right)}^T{F}^n$$ (2)

where W_V and W_R were replaced by the 1 × 1 × 1 convolutional layer. The number of tokens N was empirically chosen as 128 for all tokenizers; each token’s dimension D was set to 1024. The tokens from all the down-sampling blocks are concatenated in order with an additional class token C_t ∈ R^C×D and a distillation token D_t ∈ R^C×D, where C is the number of classes in the segmentation. We thus arrive at the final information tokens T_final ∈ R^{4×(2×C+N )×D} for the transformer (with four sets of feature maps, each at different resolutions).

II.B.2. Transformer

Each self-attention blocks consists of P transformer layers. As shown in Fig. 1, the trans- former layer combines a Multi-head Self-Attention (MHSA) and a Multi-layer perceptron (MLP). Each MHSA comprises of M parallel self-attention heads, each of which learns global representations by independent Query (Q), Key (K) and Value (V) weight matrices where $Q,K,V\in {ℝ}^{D\times d_k}$. The MHSA performs the following operation:

$$hea{d}_m=softmax(\frac{T_{final}{Q}_i{\left(T_{final}{K}_i\right)}^T}{\sqrt{d_k}})\left(T_{final}{V}_i\right)$$ (3)

$$T_{out}=Concat\left(hea{d}_i,\dots ,hea{d}_M\right)W$$ (4)

where W represents another trainable projection, and T_out ∈ R^{4×(2×C+N )×D} maintains the same shape with the T_final. The number of heads I was empirically set to 16, and the dimension d_k was set to 64.

II.B.3. Feature detail recovery

The transformers’ output T_out are then projected back to the size of their corresponding input feature maps for pixel-level detail recovery (Fig. 1). The output T_out is split, in the order of the concatenation we applied for the sparse information token before the transformer, back into different sets of tokens. The collection of tokens is then fused with the input feature maps to recover the pixel-level details. For the n’th set of tokens, the recovery performs:

$$X_{out}^n=F^n+softma{x}_L(\left(F^n{W}_Q\right){\left(T_{out}^n{W}_k\right)}^T)T_{out}^n$$ (5)

where W_Q and W_K denotes two trainable linear layers (also replaced by 1×1×1 convolutional layer), softma x_L denotes the Softmax operation on the last dimension.

II.C. Knowledge distillation for optimization

The knowledge distillation (KD) strategy initially was implemented in the Data-efficient vision transformer (Touvron et al., 2021), which learns prior information from a state-of-the-art CNN model to prevent the transformer from overfitting with limited data. KD introduces a set of learnable distillation tokens D_t that flow through the transformer along with the information token T and the class tokens C_t, with only D_t and C_t used for predicting the output. The objective of D_t is to match the output produced by the teacher network, while the C_t is to match the ground truth labels. The distillation token, which learned knowledge from a CNN model, can interact with the and T C_t and transfer local inductive biases to the VITs, to improve network performance and efficiency. Motivated by this example, we propose a similar mechanism for prediction combined with the information token T to avoid information loss. As shown in Fig. 2, for the n’th layer’s input tokens, we append a C_n (blue star) and D_n (red circle) to both ends of the information token T_n. The output of the transformer T_out (with the same size of the whole input) are split back into four sets of tokens (since we input tokens from four layers), and each set of the tokens consists of the corresponding C_n, T_n, and D_n. The potions of T_n and C_n are fed into the feature recovery projector (as described in Section. II.B.3.) to be recovered to the feature maps X_ct, which are then passed through the CNN decoder. Similarly, the portion of the T_n and D_n is recovered as X_dt and passed through the identical decoder (as shown in Fig. 3(a)). We aim to optimize the output (Y_c) generated from X_ct with the ground truth segmentations. In parallel, the output (Y_D) generated from X_dt is optimized to the output of the teacher model. In other words, during training the CNN decoder per epoch. Our segmentation thus benefits from the teacher model and the transformer architecture. For training, the optimization can be formulated as:

$$L_{total}=\frac{1}{2}{L}_d\left(Y_C,O_G\right)+\frac{1}{2}{L}_d\left(Y_D,O_T\right)$$ (6)

where L_d refers to the Dice loss(Lu et al., 2019). O_G and O_T refer to the ground truth and the teacher model’s output, respectively. In inference, the prediction is generated by Y_C. In our practice, we applied 3D Deep attention U-net (DVnet) as the teacher model.

Figure 2:

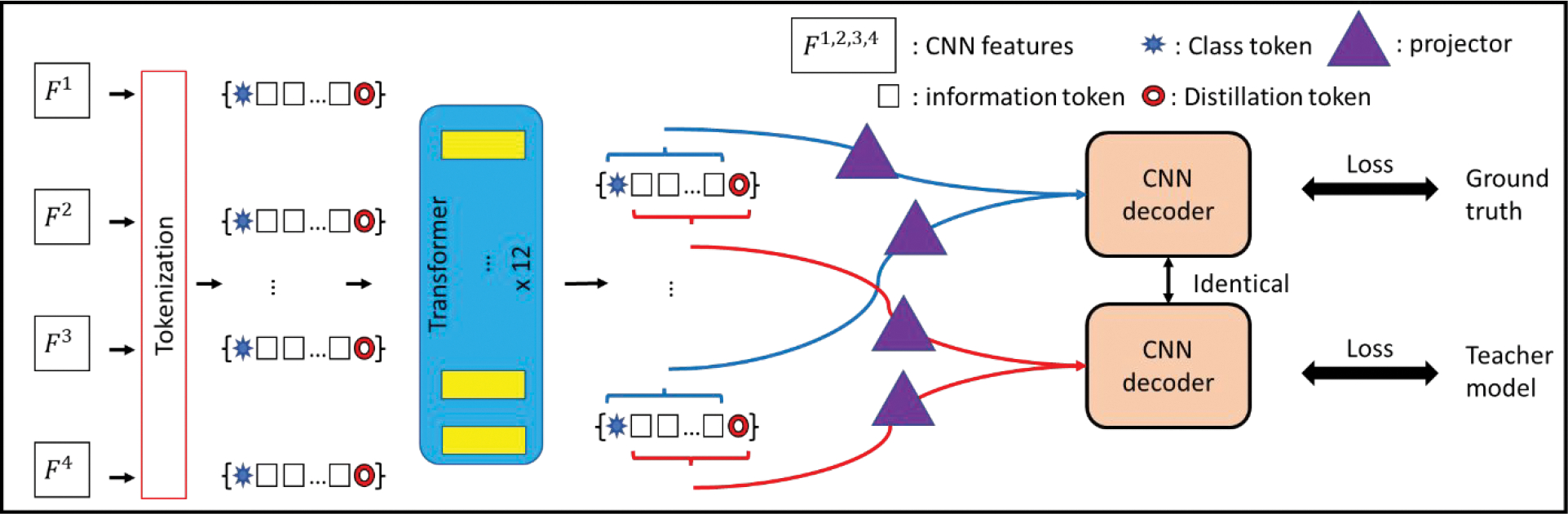
Tokenization with knowledge distillation: The CNN decoder first takes the class token and the information token as input to generate segmentations matching the ground truth. The decoder then takes the distillation token with the information tokens as input for segmentation, aiming to reach the output of the teacher models.

Figure 3:

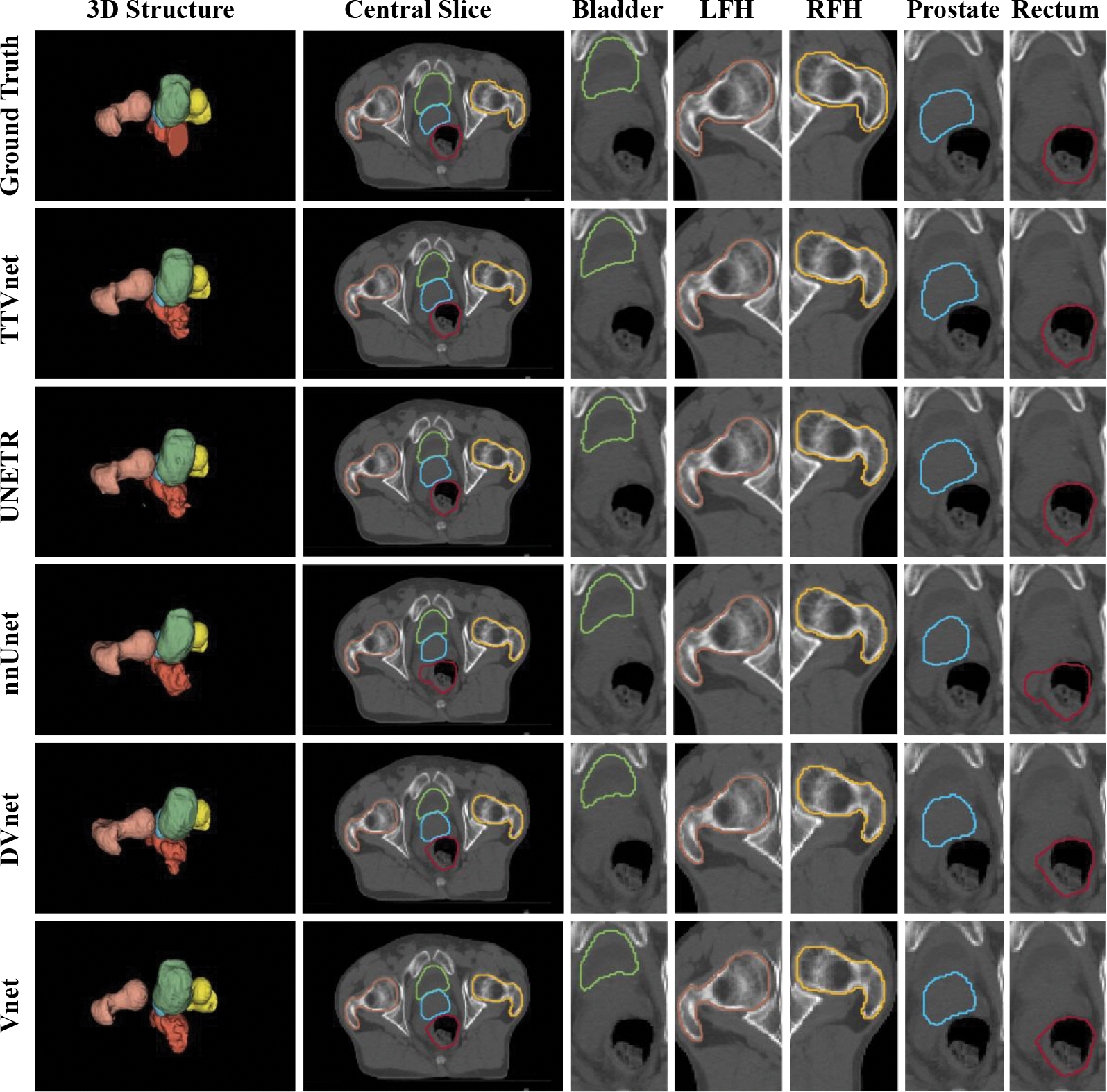
Segmentation result from Private pelvic dataset. The 3D structure, a central slice contains all the organs,and the region-of-interest of each organ from manual contours (row 1), the TTVnet (row 2) and all competing networks (row 3–6): bladder (green), prostate (blue), rectum (red), LFH (yellow) and RFH (brown).

III. Data Acquisition and Preprocessing

All experiments were implemented using the Pytorch framework in Python 3.8.11 on a workstation running Windows 11 and executed on a single Nvidia RTX 6000 GPU with 48GB memory.

III. An Institution dataset: Pelvic organs segmentation dataset

We identified 94 patients with prostate cancer treated with external beam radiation therapy. All patients underwent CT simulation using a Siemens SOMATOM Definition AS CT scanner with a voxel size of 0.977 × 0.977 × 2 mm. Five organs (bladder, prostate, rectum, LFH, and RFHs) were contoured by a radiation oncologist. Another radiologist then modified the segmentations to reach a consensus. The pelvic image volumes and segmentation were resampled to size of 2 × 2 × 1 mm; then centered and cropped in the boundary. The input scans were divided into patches with size of 160 × 160 × 48 for both training and inference. To increase data variation, we applied data augmentation by using elastic deformations (Ronneberger et al., 2015) on the training volumes and segmentation. The deformation field was generated by a normal distribution with a standard deviation of 5 and a spacing of 2 voxels in each direction. In addition, we applied Mixup augmentation (Zhang et al., 2018) with λ = 0.2 on the training data to further improve the stability and generalization. The size for both training and inference, every sample was normalized to −1 to 1. The training time for 250 epochs is about 10.4 hours. More details are shown in the Supplementary material Appendix 2.

III.B. Public dataset: CT organ segmentation dataset (CT-ORG)

A public dataset is also deployed for evaluation. This CT-ORG (Rister et al., 2020) task involves 140 CT scans, with manual contours of the liver, lungs, bladder, kidney, and bones, where the brain is labeled on the minority of scans. We only adopt the 100 scans without the brains for fair comparison and aim to segment the rest of the organs. Each case is resampled with a voxel size of 2 × 2 × 5 mm. The size of input patches is 160 × 128 × 80. The same data augmentation and normalization strategy are utilized as preprocessing. The training time for 250 epochs is about 14.2 hours.

IV. Performance evaluation

Three aspects of segmentation performance were evaluated: volume-based similarity, surface-based distance, and volume difference between automated and ground truth segmentations. The volume-based overlapping was quantified by the Dice similarity coefficient (DSC), sensitivity (the proportion of organ pixels correctly classified), and precision (the ratio of non-organ pixels correctly classified). Greater values indicate greater volume similarity. The surface-based distance was evaluated by Hausdorff distance (HD), mean surface distance (MSD), and residual mean square distance (RMSD). Here, smaller values indicate better surface matching between the automated and manual contours. In addition, we calculate percentage volume difference (PVD) to evaluate the volume size differences, where smaller differences indicate better performance. In assessing the private pelvic dataset, we used five-fold cross-validation to validate the segmentation performance from 94 patients: four sub-groups (75 images) were used for training, and the remainder (19 images) were used for testing. This data splitting for training and inference was repeated until each sub-group was tested. Finally, we report the average evaluation results across all pelvic scans. In evaluating the CT-ORG, we follow the split used in (Rister et al., 2020). The first 19 scans are used for testing, and the rest 81 scans are used to build the training set.

To validate the effectiveness of TTVnet, we run ablation experiments by using the private pelvic dataset. We firstly removed the KD strategy to demonstrate the benefits of knowledge distillation. On the other hand, we replace the token-based mechanism with vanilla VIT (remove the tokenization and feature recovery) and compare the performance between the TTVnet and the TTVnet with vanilla VIT (VITVnet). Then the proposed TTVnet is compared to widely-used segmentation networks, such as 3D U-net (Vnet), 3D Deep attention U-net (DVnet), nnUnet, and UNEt Transformers (UNETR) in both private and public dataset. For fair comparisons, we adopted the same hyper-parameter configuration, except that the input patch size is 160 × 128 × 80 for UNETR, in all networks for comparison. Mann-Whitney U-test was performed for all metrics using a significance threshold (p-value) of 0.05 to evaluate whether the proposed network’s improvement over the compared networks is significant statistical.

V. Result

A visual comparison of the proposed method with all competing techniques is shown in. Fig. 3 and Fig. 4. The quantitative performance for the TTVnet from the ablation study is shown in Table 1. Quantitative analysis results for the TTVnet and other competing 3D networks from the institutional dataset are summarized in Table 2 (more comparisons with competing 2D networks are shown in the (Supplementary material Appendix 1). And the results from the CT-ORG are summarized in Table 3. To efficiently display the performance of the TTVnet, we only show a p-value from Mann-Whitney U-test between the TTVnet with another network. The network is selected based on the following criterion: 1) If the TTVnet shows the best result, then the statistical p-value of TTVnet vs. the second-best model is shown, where p < 0.05 can indicate the TTVnet shows significant improvement. 2) If the TTVnet does not show the best result, the p-value of TTVnet vs. the best model is shown, where p>0.05 can indicate that there is not enough evidence to show the TT-Vnet’s performance is significantly worse than the best model.

Figure 4:

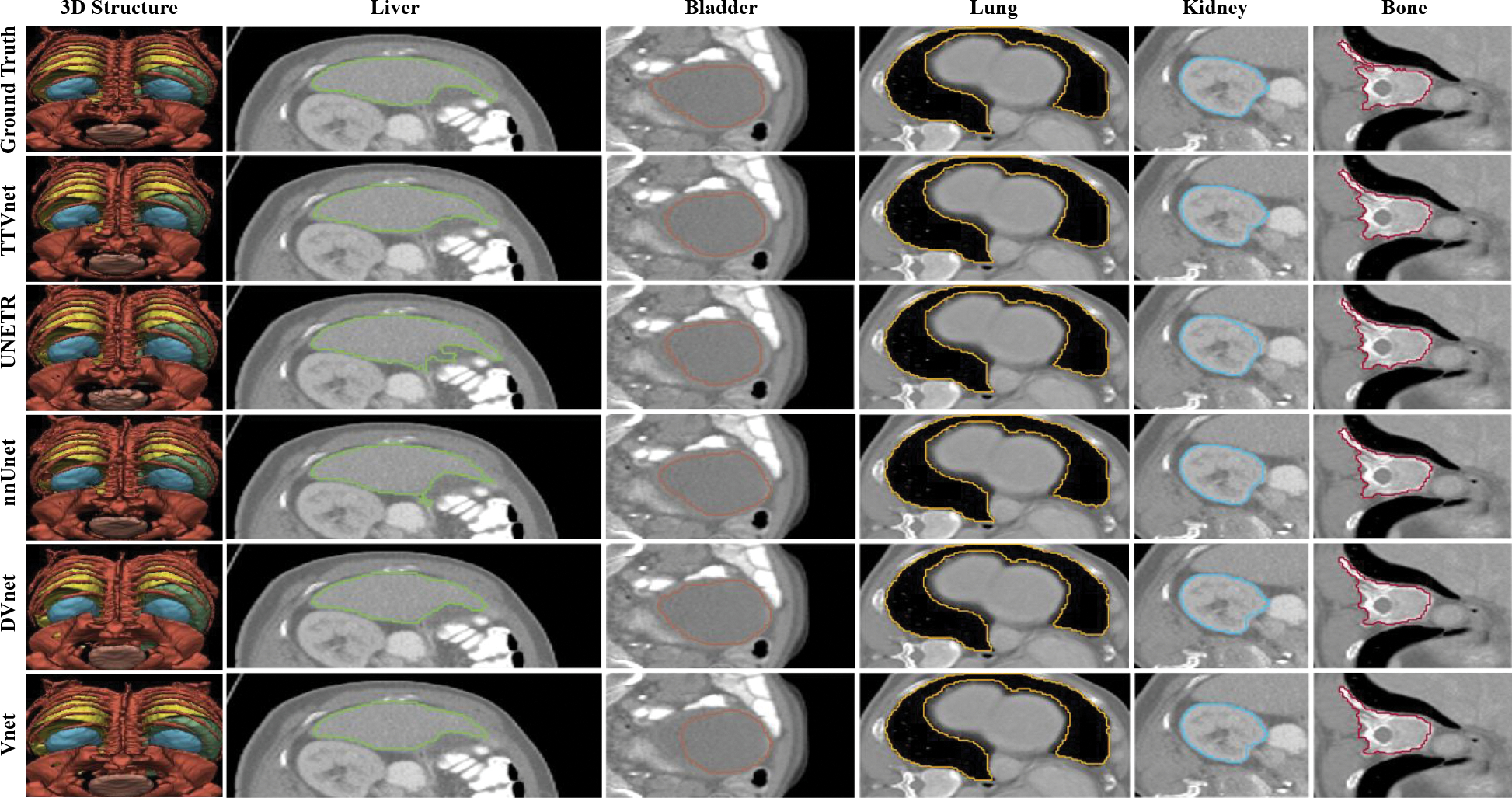
Segmentation result from CT-ORG dataset. The 3D structure, the selected region-of-interest of each organ from manual contours (row 1), the TTVnet (row 2) and all competing networks (row 3–6): liver (green), bladder (blue), lung (yellow), kidney (brown) and bone (red).

Table 1:

Quantitative analysis: Table shows statistics for the volume-based similarity, surface-based similarity, and absolute volume difference for the proposed TTVnet, TTVnet without KD, and VITVnet. “(1)” indicates the TTVnet without KD, “(2)” indicates the VITVnet. The statistical analysis of Mann-Whitney U-Test is presented to compare the TTVnet with the other networks. The best results are bolded.

		Volume-based Similarity			Surface-based Similarity			Volume Difference
Organ	Method	Dice score	Sensitivity	Precision	HD (mm)	MSD (mm)	RMSD (mm)	PVD (%)
Bladder	TTVnet (no DS)	0.93±0.02	0.92±0.042	0.94±0.03	3.53±1.69	1.34±0.321	2.08±0.54	6.8±4.6
	VITVnet	0.91±0.03	0.925±0.04	0.91±0.04	3.64±1.59	1.39±0.398	2.23±0.534	6.5±4.1
	TTVnet	0.94±0.03	0.92±0.045	0.95±0.03	3.16±0.77	1.06±0.425	1.91±0.86	5.8±4.4
Significance: TTVnet vs (1)		<0.001	0.578	<0.001	0.130	<0.001	0.033	0.050
Significance: TTVnet vs (2)		<0.001	0.128	<0.001	<0.001	<0.001	0.002	0.209
LFH	TTVnet (no DS)	0.93±0.03	0.95±0.03	0.92±0.05	2.93±1.25	1.26±0.37	1.80±0.55	9.1±6.3
	VITVnet	0.93±0.03	0.93±0.05	0.92±0.05	3.32±1.16	2.15±1.50	7.86±6.92	9.0±6.3
	TTVnet	0.95±0.03	0.94±0.04	0.95±0.04	2.78±1.06	0.95±0.49	1.42±0.52	7.9±6.0
Significance: TTVnet vs (1)		<0.001	0.071	<0.001	0.271	<0.001	<0.001	0.317
Significance: TTVnet vs (2)		<0.001	0.175	<0.001	0.002	<0.001	<0.001	0.199
RFH	TTVnet (no DS)	0.93±0.03	0.95±0.03	0.92±0.05	3.25±1.02	1.20±0.44	1.91±0.47	10.1±6.6
	VITVnet	0.93±0.02	0.92±0.04	0.93±0.05	2.77±0.60	1.09±0.35	1.78±0.34	8.0±5.6
	TTVnet	0.95±0.02	0.94±0.04	0.95±0.04	2.56±0.77	0.91±0.47	1.50±0.50	7.9±5.5
Significance: TTVnet vs (1)		<0.001	0.092	<0.001	<0.001	<0.001	<0.001	0.008
Significance: TTVnet vs (2)		<0.001	<0.001	<0.001	0.033	0.001	<0.001	0.860
Prostate	TTVnet (no DS)	0.82±0.04	0.84±0.08	0.84±0.09	5.84±1.71	2.14±0.53	3.04±0.80	17.1±10.0
	VITVnet	0.81±0.05	0.86±0.06	0.77±0.13	5.71±2.71	2.26±0.81	3.25±1.13	19.6±13.8
	TTVnet	0.84±0.04	0.87±0.06	0.83±0.08	6.03±1.74	2.03±0.58	2.89±0.64	12.9±9.4
Significance: TTVnet vs (1)		<0.001	0.010	0.103	0.596	0.114	0.115	0.005
Significance: TTVnet vs (2)		<0.001	0.581	0.001	0.135	0.050	0.031	<0.001
Rectum	TTVnet (no DS)	0.86±0.05	0.83±0.09	0.83±0.06	6.59±3.62	1.89±0.81	4.97±2.97	16.8±12.8
	VITVnet (2)	0.83±0.04	0.81±0.08	0.87±0.08	7.28±4.57	2.42±1.04	5.97±3.94	17.1±11.2
	TTVnet	0.89±0.04	0.86±0.08	0.92±0.05	4.28±2.19	1.30±0.52	2.30±0.77	16.9±12.7
Significance: TTVnet vs (1)		<0.001	0.032	<0.001	<0.001	<0.001	<0.001	0.412
Significance: TTVnet vs (2)		<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	0.063

Table 2:

Quantitative analysis for the private pelvic dataset: Table shows statistics for the volume-based similarity, surface-based similarity, and absolute volume difference for the proposed TTVnet, Vnet, DVnet, nnUnet and UNETR. The statistical analysis of Mann-Whitney U-test is also efficiently presented (as described in Section V) to compare the TTVnet with each competing network. The best performance is bolded, and the second-best results are underlined.

		Volume-based Similarity			Surface-based Similarity			Volume Difference
Organ	Method	Dice score	Sensitivity	Precision	HD (mm)	MSD (mm)	RMSD(mm)	PVD (%)
Bladder	V-net	0.92±0.03	0.94±0.03	0.91±0.04	5.34±1.23	3.41±0.38	3.13±0.67	9.0±4.5
	DV-net	0.93±0.02	0.91±0.04	0.96±0.02	5.76±2.37	3.37±0.54	3.09±1.08	10.1±4.6
	nnUnet	0.93±0.02	0.93±0.03	0.93±0.04	4.03±1.46	1.15±0.31	2.05±0.61	6.8±5.0
	UNETR	0.93±0.03	0.91±0.04	0.96±0.03	7.92±5.92	1.66±0.98	3.56±2.38	6.7±5.7
	TTVnet	0.94±0.03	0.92±0.05	0.95±0.03	3.16±0.78	1.06±0.43	1.91±0.86	5.8±4.4
P-values		0.005	0.040	0.412	<0.001	<0.001	<0.001	<0.001
Femoral head (left)	V-net	0.94±0.03	0.93±0.06	0.93±0.04	4.74±0.78	3.13±0.37	2.68±0.43	11.5±6.9
	DV-net	0.93±0.03	0.93±0.05	0.94±0.05	4.71±0.70	3.16±0.38	3.26±1.29	12.1±6.9
	nnUnet	0.94±0.03	0.92±0.05	0.95±0.04	2.75±0.97	1.00±0.53	1.52±0.54	8.1±6.4
	UNETR	0.95±0.03	0.92±0.05	0.95±0.04	2.77±1.09	0.94±0.55	1.48±0.59	8.1±5.8
	TTVnet	0.95±0.03	0.94±0.04	0.95±0.04	2.78±1.06	0.95±0.49	1.42±0.52	7.9±6.0
P-values		0.002	0.250	0.180	0.075	0.055	0.012	0.012
Femoral head (right)	V-net	0.94±0.02	0.94±0.04	0.93±0.05	4.66±0.75	3.15±0.32	2.65±0.40	11.2±6.1
	DV-net	0.93±0.03	0.93±0.04	0.93±0.05	4.99±0.780	3.15±0.36	2.80±0.41	10.3±6.3
	nnUnet	0.95±0.03	0.94±0.04	0.94±0.05	2.67±0.96	0.92±0.50	1.48±0.51	8.3±6.1
	UNETR	0.94±0.03	0.94±0.04	0.94±0.05	2.67±0.82	0.91±0.50	1.44±0.48	7.2±5.3
	TTVnet	0.95±0.02	0.94±0.04	0.95±0.04	2.56±0.77	0.91±0.47	1.50±0.50	7.9±5.5
P-values		0.129	0.203	0.007	0.033	0.680	0.193	0.315
Prostate	V-net	0.83±0.04	0.85±0.07	0.82±0.09	7.15±1.33	4.05±0.39	3.81±0.47	20.1±12.9
	DV-net	0.83±0.04	0.82±0.09	0.83±0.10	7.41±1.12	4.04±0.30	3.82±0.46	23.0±14.9
	nnUnet	0.82±0.05	0.88±0.07	0.78±0.10	7.02±2.17	2.39±0.82	3.16±0.88	16.5±11.5
	UNETR	0.83±0.03	0.84±0.08	0.85±0.08	6.49±1.44	2.26±0.48	3.11±0.44	14.5±9.6
	TTVnet	0.84±0.04	0.87±0.07	0.83±0.08	6.03±1.74	2.03±0.58	2.89±0.64	12.9±9.4
P-values		0.021	<0.001	0.007	0.057	0.083	0.168	0.018
Rectum	V-net	0.86±0.06	0.87±0.10	0.85±0.07	9.04±5.03	4.07±1.13	4.07±1.13	17.8±11.2
	DV-net	0.86±0.04	0.87±0.07	0.89±0.07	8.22±3.87	3.73±0.73	3.73±0.73	17.1±10.8
	nnUnet	0.86±0.05	0.83±0.09	0.90±0.06	7.74±5.04	3.60±1.82	1.94±1.15	22.7±16.8
	UNETR	0.88±0.04	0.89±0.067	0.87±0.08	6.16±3.04	2.89±1.48	1.64±0.68	13.8±10.3
	TTVnet	0.89±0.04	0.85±0.089	0.91±0.05	4.33±2.12	1.27±0.59	1.27±0.59	14.8±11.6
P-values		<0.001	0.538	<0.001	<0.001	<0.001	0.036	0.762

Table 3:

Quantitative analysis for CT-ORG: Table shows statistics for the volume-based similarity, surface-based similarity, and absolute volume difference for the proposed TTVnet, Vnet, DVnet, nnUnet and UNETR. The statistical analysis of Mann-Whitney U-test is also efficiently presented (as described in Section V) to compare the TTVnet with each competing network. The best performance is bolded, and the second-best results are underlined.

		Volume-based similarity			Surface-based similarity			Volume difference
Organ	Method	Dice score	Sensitivity	Precision	HD (mm)	MSD (mm)	RMSD (mm)	PVD (%)
Liver	V-net	0.94±0.02	0.94±0.02	0.94±0.03	6.55±2.14	1.62±0.59	3.38±1.16	3.6±2.4
	DV-net	0.94±0.01	0.94±0.02	0.95±0.03	6.47±2.04	1.56±0.47	3.40±0.97	3.6±2.5
	nnUnet	0.94±0.02	0.95±0.02	0.93±0.02	7.35±3.07	2.26±2.34	7.10±10.37	3.0±2.3
	UNETR	0.94±0.02	0.95±0.02	0.94±0.03	6.75±4.19	2.52±4.72	7.01±16.42	3.3±1.9
	TTVnet	0.96±0.01	0.95±0.02	0.97±0.02	6.12±2.37	1.10±0.40	3.08±1.10	3.6±2.9
P-values		<0.001	0.687	<0.001	0.036	0.002	0.005	0.376
Bladder	V-net	0.83±0.11	0.89±0.10	0.80±0.15	8.23±5.77	2.39±1.36	3.73±2.03	14.7±14.8
	DV-net	0.83±0.12	0.89±0.10	0.79±0.15	8.59±6.82	2.41±1.38	3.91±2.26	14.0±13.0
	nnUnet	0.85±0.12	0.89±0.12	0.84±0.17	10.30±10.00	2.59±2.75	6.32±11.0	19.0±25.2
	UNETR	0.82±0.13	0.89±0.14	0.80±0.16	9.61±5.94	2.77±2.06	5.95±6.48	24.7±32.82
	TTVnet	0.88±0.09	0.90±0.09	0.85±0.13	8.19±7.78	1.84±1.23	3.34±2.34	12.7±10.13
P-values		0.044	0.573	0.872	1.000	0.809	0.872	0.658
Lungs	V-net	0.95±0.04	0.94±0.04	0.97±0.05	17.62±33.31	2.94±4.57	7.90±10.81	4.8±4.3
	DV-net	0.95±0.04	0.94±0.04	0.97±0.06	17.53±34.82	2.77±4.11	7.42±10.43	5.2±4.7
	nnUnet	0.95±0.07	0.93±0.09	0.98±0.04	9.88±4.99	3.54±7.80	8.48±12.6	6.6±9.8
	UNETR	0.90±0.16	0.88±0.20	0.95±0.04	26.42±51.03	10.62±25.01	22.32±41.00	27.6±83.1
	TTVnet	0.97±0.02	0.95±0.03	0.99±0.03	5.45±4.70	1.13±0.82	3.88±2.20	6.4±4.1
P-values		0.002	0.042	<0.001	0.036	0.003	0.018	0.005
Kidney	V-net	0.89±0.08	0.93±0.07	0.92±0.12	4.51±2.60	1.06±0.72	2.21±1.11	11.2±13.7
	DV-net	0.91±0.05	0.91±0.07	0.94±0.06	6.98±12.1	1.38±1.91	3.77±6.14	7.8±9.0
	nnUnet	0.93±0.04	0.94±0.04	0.93±0.06	3.86±2.46	0.75±0.47	2.60±2.50	6.5±6.7
	UNETR	0.90±0.05	0.89±0.06	0.96±0.08	6.99±2.25	1.39±0.47	3.17±0.96	10.0±8.0
	TTVnet	0.94±0.02	0.95±0.04	0.95±0.03	3.70±4.01	0.57±0.50	1.77±1.76	5.2±4.8
P-values		0.295	0.198	0.277	0.008	0.002	0.014	0.227
Bone	V-net	0.86±0.05	0.85±0.07	0.86±0.06	9.83±6.70	2.01±0.97	2.01±0.966	8.8±7.0
	DV-net	0.87±0.04	0.86±0.07	0.88±0.05	8.63±7.34	1.73±0.98	1.73±0.977	8.1±6.8
	nnUnet	0.88±0.05	0.85±0.08	0.91±0.04	7.70±5.34	1.55±0.83	1.55±0.827	9.1±11.1
	UNETR	0.88±0.05	0.86±0.08	0.91±0.05	7.74±6.93	1.70±0.97	1.70±0.967	8.5±10.4
	TTVnet	0.90±0.03	0.90±0.03	0.90±0.04	5.65±1.44	1.15±0.30	1.15±0.301	4.9±4.3
P-values		<0.001	0.001	0.008	0.008	0.049	0.006	0.008

V. An Efficacy of Token-based transformer and knowledge distillation

To demonstrate the contribution of the KD and token-based transformer on segmentation, we compare the results obtained with the proposed TTVnet with the network without KD and VITVnet. The segmentation performance for five-fold cross-validation is shown in Table. 1. The average DSC of the network without KD was 0.93, 0.93, 0.93, 0.82, and 0.86 for bladder, LFH, RFH, prostate, and rectum, respectively. The VITVnet reports average DSC was 0.91, 0.93, 0.930, 0.81 and 0.83. The organs’ DSC were increased to 0.94, 0.95, 0.95, 0.841 and 0.891 when KD is applied. The p-values obtained from the Mann-Whitney U-test show statistically significant improvements by both utilizing the KD strategy and the token-based mechanism. Quantitative and statistical improvements are observed in either sensitivity (more organs pixels were correctly classified) and precision (less non-organ pixels were misclassified) for all organs. Improvements are also observed in surface-based similarities: the KD strategy shows lower quantitative surface distances, in terms of average HD, MSD, and RMSD, for bladder, LFH, RFH, and rectum with corresponding statistically significant improvement. On the other hand, the token-based mechanism shows surface-based improvement for all organs. For volume difference, the KD strategy presents both quantitative and statistical improvement for bladder, RFH and prostate, while the tokenization mechanism improves segmentation accuracy statistically on prostate.

V.B. Contribution of TTVnet

For the private pelvic dataset, in terms of Dice score, the proposed TTVnet yielded non-negligible improvements over prior networks for all organs: performance gains range from 0.006 to 0.017 for bladder, 0.003 to 0.012 for the LFH and RFH, 0.007 to 0.022 for the prostate, and 0.013 to 0.035 for the rectum. Most of the p-values (< 0.05) obtained from the Mann-Whitney U-test indicate that the TTVnet improved Dice score for bladder, LFH, prostate, and rectum at the 5% significance level. Combining the dice score results with the sensitivity and precision, the TTVnet gain quantitatively and statistically improvement mainly on the bladder, prostate, and rectum while showing comparable performance with the corresponding best model in each metric. Similarly, the TTVnet mainly indicates a significant improvement in bladder, prostate, and rectum for the surface-based distance. For these three organs, surface distance improvements range from 0.459 to 4.76 mm for HD, 0.003 to 2.35 for MSD, and 0.138 to 2.80 for RMS. In addition, the TTVnet obtained the smallest volume difference for bladder, LFH, RFH, and prostate in terms of volume-based difference. The statistical analysis shows that the TTVnet can improve segmentation accuracy on bladder, LFH, and prostate while still demonstrating comparable performance with the competing networks on the RFH and rectum. In summary, the higher volume-based similarity, surface-based similarity, and lower volume difference is primarily observed in segmentations of the bladder, prostate, and rectum, indicating the effectiveness of the TTVnet for improving the segmentation accuracy of these organs in pelvic CT images.

For the public CT-ORG dataset, in terms of Dice score, the proposed TTVnet obtains the best performance among all organs: it shows an improvement range quantitatively from 0.016 to 0.018 for liver, 0.025 to 0.042 for bladder, 0.017 to 0.070 for lung, 0.005 to 0.046 for kidney, and 0.017 to 0.042 for bone. The p-values indicate the statistical improvement for liver, bladder, kidney, and bone at the 5% significance level. The TTVnet also improves either sensitivity or precision in the liver, lung, and bone. On the other hand, in terms of surface-based similarity, the TTVnet shows statistically significant improvement in liver, lung, kidney, and bone while still demonstrating quantitively improvement in the bladder. In terms of volume difference, the TTVnet quantitively and statistically improves the segmentation of lung and bone. The TTVnet primarily improves the volume-based similarity and surface-based similarity of liver, lung, and bone. It also improves the Dice score on the bladder and surface-based similarity on the kidney.

VI. Discussion

This work proposes a U-shaped Token-based transformer network (TTVnet) using a knowledge distillation strategy for 3D CT-based pelvic multi-organ segmentation. The TTVnet has three main components: a convolutional encoder for extracting features at different resolutions, a token-based transformer decoder for enriching the global information to the extracted features, and a set of upsampling convolutional blocks for reconstructing the features into an N-class segmentation. One novelty to the TTVnet is that the transformer layers effectively capture global information otherwise lost in pure FCN networks due to their limited receptive field. On the other hand, the novel tokenization and knowledge distillation can effectively assist the transformer, and accordingly improve the network’s generalization, which are evidenced by example training loss and validation dice score in the Supplementary material Appendix 3 Fig. 1 and Fig. 2. TTVnet also incorporates distillation learning with Vnet, which is the process by which our TTVnet (student) learns not only from the ground truth, but also from the output of the Vnet (teacher). Furthermore, distillation learning conveys prior convolutional information from the Vnet to the TTVnet, which provides extra guidance for our network to stabilize the training process and improve network generalization. To our knowledge, this paper presents the first transformer architecture with tokenization and knowledge distillation for multi-organ segmentation in pelvic CT pelvic scans. The proposed network efficiently demonstrates promising segmentation performance compared to current state-of the-art methods, suggesting a feasible approach to automated facilitation of routine prostate radiation treatment planning.

Performance of the TTVnet was investigated in three domains: 1) volume similarity by DSC, sensitivity, and precision; 2) surface similarity by HD, MSD, and RMSD; and 3) volume differences by percentage volume difference. Overall, our proposed TTVnet with distillation demonstrated statistically significant improvement, in terms of different metrics, over the competing networks. Even without distillation, the TTVnet still preserves or surpasses the segmentation performance of all competing networks. Such improvement demonstrates the advantages of transformer architecture in CT-based pelvic multi-organ segmentation and the transformer’s potential to be a reliable backbone for network design in other medical segmentation problems.

However, it is essential to note that the segmentation performance might still be limited. First, compared to CNN-based models with more complex architecture and advanced 3D pelvic CT segmentation techniques, the proposed TTVnet achieved lower accuracy in the prostate and rectum. Dong et al.(Dong et al.), who used an additional Cycle-GAN to perform 3D CT-to- sMRI synthesis and trained the segmentation network in the synthetic sMRI scans to exploit the superior soft-tissue contrast of sMRI, reported DSC was 0.95 ± 0.03 for bladder and 0.87±0.04 for prostate using a dataset of 140-patients pelvic CT images. Similar works utilizing additional networks such as, GAN (Lei et al.) for CT-to-sMRI synthesis and 2D organ localization network before segmentation (Balagopal et al.), reported better segmentation accuracy in terms of DSC than the TTVnet. Second, the teacher model’s segmentation power (e.g., the accuracy) may also affect the TTVnet’s performance. In this work, errors resulting from the teacher model were propagated to the student TTVnet’s and may lead to lower performance. Finally, the model’s performance may be subjected to inter-observer variability inherent in the manually-delineated expert ground truth contours. We hypothesize that the inter-observer variability could impede the teacher model first and, therefore, have a compound effect on the proposed TTVnet through the KD. However, these limitations do not diminish the significance of the proposed TTVnet but call for incorporating more advanced techniques (such as an additional auxiliary network) with this method to improve segmentation performance further. Also, we aim to investigate more powerful teacher models for the distillation process and the inclusion of additional training data to overcome inter-observer variability in the dataset. Moreover, in clinical use, all segmented contours will be finally reviewed by physicians to ensure the contour quality for patient safety.

In the future, the current work will incorporate advanced techniques/networks to support the TTVnet’s segmentation. Future work will also extend the distillation process, such as a more sophisticated teacher model and a more effective method to distillate the knowledge from the teacher model to the student model for segmentation. Furthermore, we will include dosimetric evaluation in the segmentation result in radiation treatment planning. The network’s effect on the planning quality will be investigated. Moreover, the proposed method can also be potentially applied on daily cone-beam CT to provide patient organ contours on treatment day. Physicians can then compare the daily contours with contours from planning CT to decide whether to resume, pause or modify the treatment plan. However, cone-beam CT contains more image artifacts than planning CT. Thus, the feasibility of the proposed method on cone-beam CT needs further evaluation.

VII. Conclusion

This work presents a segmentation network with novel feature forwarding using Token-based self-attention for pelvic CT segmentation. The proposed method yields more accurate contours, in terms of volume-based accuracy and surface-based accuracy, than Vnet and other competing state-of-the-art methods. The network demonstrates potential as an accurate and efficient tool to facilitate prostate radiation treatment planning.