Pricing extreme mortality risk in the wake of the COVID-19 pandemic

Abstract

In pricing extreme mortality risk, it is commonly assumed that interest rate and mortality rate are independent. However, the COVID-19 pandemic calls this assumption into question. In this paper, we employ a bivariate affine jump-diffusion model to describe the joint dynamics of interest rate and excess mortality, allowing for both correlated diffusions and joint jumps. Utilizing the latest U.S. mortality and interest rate data, we find a significant negative correlation between interest rate and excess mortality, and a much higher jump intensity when the pandemic experience is considered. Moreover, we construct a risk-neutral pricing measure that accounts for both diffusion and jump risk premia, and we solve for the market prices of risk based on mortality bond prices. Our results show that the pandemic experience can drastically change investors' perception of the mortality risk market in the post-pandemic era.

1. Introduction

Extreme mortality risk, usually arising from shocks that lead to large-scale losses of life, can put life insurers' profitability and solvency under pressure. Nearly three years into the pandemic, the world has witnessed that the impact of extreme mortality experience can go beyond the insurance industry and even change the landscape of the world economy. In this paper, through pricing mortality catastrophe (CAT) bonds, we aim to enrich our understanding of extreme mortality risk in the wake of the COVID-19 pandemic.

Traditionally, insurance companies mitigate and manage extreme mortality risk by means of reinsurance. In recent decades, insurers have also used insurance-linked securities (ILS) for additional protection against solvency-threatening losses. Originating in the mid-1990s after Hurricane Andrew and the Northridge earthquake, ILS have shown a very strong growth and formed a sizable market.5 The growth is partly attributable to ILS's appealing returns and the general belief that catastrophe risk is uncorrelated with the other risks in the financial market and as such ILS bring diversification benefits.

Various mortality-linked securities (MLS) and in particular mortality CAT bonds have contributed to the early success of the ILS market. In December 2003, Swiss Re issued the first mortality CAT bond of size US$400m via Vita Capital. During the risk period of the bond, if the underlying mortality index exceeded a certain threshold, the bond would be triggered and the principal be reduced or wiped out to compensate for the insurance losses. Since then, numerous MLS have been issued, examples including Swiss Re Vita Capital II of size US$362m, Swiss Re Vita Capital III of size US$705m, Atlas IX Capital of size US$180m, and AXA Benu Capital of size EUR285m.

Pricing MLS requires a thorough understanding of the interaction between extreme mortality risk and the other risks in the market. In academic research, it has been a long-standing assumption that mortality rate and financial market performance are completely independent; see Subsection 1.1 for a brief literature review. However, as Deelstra et al. (2016) point out, dependence between them can exist because natural catastrophes such as earthquakes and severe pandemics can affect human mortality and the financial markets simultaneously, because demographic changes can affect the economy by, e.g., affecting values of financial assets, and because changes in mortality and life expectancy have been linked to accumulation of assets and decline in interest rates. Indeed, the COVID-19 pandemic has triggered concurrent jumps in mortality via health shocks and in interest rate via financial shocks, calling the independence assumption into question. It has already spawned a viewpoint among practitioners that extreme mortality and financial market performance are highly correlated, and has motivated recent empirical research that investigates the relation between extreme mortality and various economic variables; see Subsection 1.1 for more details.

A significant correlation between mortality and financial market performance could distort the market, challenge some traditional views on market behaviors, and carry profound implications for the future mortality risk market. For example, a shift in market sentiment of the low correlation could put MLS's diversification benefits into question and lead to a decline in MLS demand. This motivates us to examine the dependence between interest rate and mortality rate and address the issue in pricing MLS.

In this paper, we choose to work on excess mortality rather than the mortality rate itself as MLS are usually linked to an underlying mortality index.6 We employ a bivariate affine jump-diffusion (AJD) model (2.1) to describe the joint dynamics of interest rate and excess mortality. The AJD setting accounts for both the frequency of jumps and the correlations between the jump components and between diffusions in an integrated way, which makes it an ideal model choice for pricing extreme mortality risk.

The calibration of the proposed continuous-time AJD model requires mortality data of a higher frequency than annual, which have previously been difficult to acquire. Our empirical studies become possible thanks to the U.S. Centers for Disease Control and Prevention (CDC), who, in response to COVID-19, has recently started to collect and compile provisional death counts on a weekly basis. Estimates of weekly excess deaths since January 2017 have also been published by CDC to provide information on the burden of mortality potentially imposed by the pandemic. We are amongst the first to utilize this weekly mortality data to calibrate such a sophisticated model.

Utilizing the most up-to-date U.S. mortality and interest rate data from 2017 to 2022, we calibrate the bivariate AJD model by using the Markov Chain Monte Carlo (MCMC) method, based on an approximation of the transition density function proposed by Pienaar and Varughese (2016). We detect a significant number of joint jumps and find a strong negative correlation between the two jump components, while the two diffusions seem close to independent. Collectively, this comes up with an instantaneous correlation of −0.322 between interest rate and excess mortality.7 For comparison, when only the pre-pandemic data (namely, data from 2017 to 2019) are used for model calibration, we detect much fewer joint jumps, while the estimated correlation coefficients for both jump and diffusion components almost remain unchanged. In this case, the instantaneous correlation between interest rate and excess mortality becomes −0.153.

Next, we follow arbitrage pricing theory to construct a risk-neutral pricing measure that accounts for both diffusion and jump risk premia. The diffusion risk premium is realized via a drift adjustment on the joint dynamics. Note that the jump risk is captured by the compound Poisson processes in our AJD model (2.1). To realize the jump risk premium, we let each jump process remain a compound Poisson process under the pricing measure but with both the intensity and the jump-size distribution adjusted, so that the jump risk premium applies to both the intensity and the size.

To examine the risk premia demanded by the MLS investors, we design in Example 3.1 a hypothetical mortality CAT bond that closely resembles the 2013 Atlas IX Capital Ltd. bond. By assuming that the hypothetical bond would have been traded at the same prices if issued under the then market conditions, we solve for the market prices of risk (MPRs) based on the calibrated AJD model and the price data of the 2013 Atlas bond. To understand the impact of the COVID-19 pandemic experience on the mortality risk market, we derive the investors' MPRs again, but assuming a misalignment between the risk modeling agent's model and the actual model governing the risk processes: the former calibrated with pre-pandemic data only and the latter also with the pandemic data. We find that the investors are earning much lower risk premia than in the previous case. In fact, the investors may end up paying a mortality risk premium in some cases due to severe underestimation of the extreme mortality risk. This demonstrates the imperativeness to employ models that properly account for the pandemic experience.

In addition, based on the estimated prices of the hypothetical bond, we conduct sensitivity analyses against the MPR parameters. As expected, an increase in any of the risk premia, ceteris paribus, will reduce the bond price. We find that the price is much more sensitive to changes in the jump risk premium than to changes in the diffusion risk premium, which reaffirms the necessity of incorporating the jump risk into modeling.

To summarize, our contribution is twofold. First, we employ a bivariate AJD model to describe the joint dynamics of interest rate and excess mortality and we calibrate the model based on a newly compiled U.S. mortality dataset that includes observations during the pandemic. We find that joint jumps occur at a high frequency and lead to a significant negative instantaneous correlation between interest rate and excess mortality. Second, building on the calibrated AJD model, we develop a risk-neutral pricing measure that accounts for both diffusion and jump risk premia. We then solve for the MPRs using secondary market indicative mortality bond prices. Our results shed light on the mortality risk market in the post-pandemic era: The pandemic experience shakes the long-standing belief of independence between mortality risk and financial risk, and is likely to reshape the market. We note that the AJD model equipped with our pricing measure enables us to price other securities such as pandemic bonds. We illustrate the connection of our work with the World Bank's pandemic bonds in Appendix A.1.

The rest of the paper is organized as follows: Section 1 ends with a brief literature review; Section 2 depicts the bivariate AJD model and constructs the risk-neutral pricing measure; Section 3 applies the pricing framework to MLS; Section 4 illustrates our empirical results; Section 5 computes the implied MPRs for various scenarios and conducts sensitivity tests against the MPRs; Section 6 concludes the paper; the Appendix illustrates the connection with the World Bank pandemic bonds and collects long proofs, derivations, and descriptions required for establishing our theory and sampling algorithm.

1.1. A brief literature review

ILS as an innovative solution to insurance risk transfer and mitigation have been extensively studied in the literature. Some recent works include Cummins (2008), Barrieu and Albertini (2009), Braun et al. (2019), Tang and Yuan (2019), Liu et al. (2021), and Beer and Braun (2022). For discussions specifically on MLS, see Lin and Cox (2008), Bauer and Kramer (2016), Li and Tang (2019), and Blake and Cairns (2021).

Studies of ILS in general and MLS in particular are mainly focused on pricing and follow established pricing approaches in incomplete markets. Among the most popular is the actuarial pricing approach, which takes the expectation under the physical measure of the sum of the discounted payoffs to obtain the expected present value and then applies a usually exogenous safety loading coefficient to produce the actuarial price. This approach was prevailing in early times; see Galeotti et al. (2013) and references therein. However, in view of the rapid growth of the ILS market, it is important to incorporate the market price of (extreme) mortality risk to more accurately reflect investors' risk appetite.

In studying ILS, a majority of academic research follows the long-standing assumption that mortality rate and financial market performance are completely independent, despite some sporadic discussions on its deficiency; see, e.g., Biffis (2005), Cairns et al. (2006), Lin and Cox (2008), Bayraktar et al. (2009), Bauer et al. (2010), Chen et al. (2015), and Beer and Braun (2022). Two notable exceptions are Liu et al. (2014) and Deelstra et al. (2016), who price guaranteed annuity options with the correlation between interest and mortality rates accounted for. Specifically, Liu et al. (2014) introduce a bivariate affine model with correlated Brownian motions for interest rate and mortality rate processes, and Deelstra et al. (2016) consider a general affine framework in which interest and mortality rates are driven by systematic and idiosyncratic factors that are affine. Note that, while sharing the same spirit as ours, their main results are largely based on numerical illustrations rather than model calibration using real data as we do.

COVID-19 and the rising pandemic risk are enough to convince some practitioners that the correlation between mortality and interest rates is high. For example, Alloway and Vossos (2020) and Tan (2020), in their analysis of the World Bank's pandemic bonds, cite industry experts' opinion on the high correlations between extreme mortality, the pandemic bond market, and other financial markets. The COVID-19 pandemic has also motivated academic research that aims to uncover relations between extreme mortality and various economic variables. Barro et al. (2020) provide an ex post analysis of the relation between the mortality and economic contraction during the 1918–1920 great influenza pandemic as a reflection on the COVID-19 pandemic. Polyakova et al. (2020) report empirical results on the correlation between the initial economic damage and excess mortality from the COVID-19 pandemic in the U.S. based on the then publicly available data. In a different context, Lin and Zhang (2022) find extreme co-movements between infectious disease events such as Ebola and COVID-19 outbreaks and crude oil futures prices. See also Dacorogna and Cadena (2015) for an early empirical study of the relation between mortality risk and other financial variables. These expert opinions and empirical evidence motivate our research, and we contribute to this strand of literature by providing additional empirical evidence.

There is a large body of literature that models stochastic mortality in discrete time; see Cairns et al. (2011) for a review. In our research, we instead choose a continuous-time model—specifically, a bivariate AJD model for the interest rate and excess mortality. AJD models are rooted in the financial asset pricing literature with pioneering works such as Bates (1996) and Duffie et al. (2000). Since then, affine models have been used frequently in the literature of mortality modeling. We refer the reader to Schrager (2006), Deelstra et al. (2016), and Xu et al. (2020a, 2020b) for works that employ affine models without jumps, and to Biffis (2005), Cox et al. (2006), Lin et al. (2013), and Hainaut and Deelstra (2014) for works that incorporate jumps.

2. The affine jump-diffusion model

Throughout the paper, we use $(\mathrm{\Omega },\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{0\le t\le T},P)$, with ${\mathcal{F}}_T\subset \mathcal{F}$, to denote a filtered probability space that accommodates all sources of randomness, where $0<T<\infty$ denotes the time horizon. Let ${\{r_t\}}_{0\le t\le T}$ be the interest rate process and ${\{{\mu }_t\}}_{0\le t\le T}$ be a mortality-linked reference process. The latter, unless otherwise stated, is specified as an excess mortality process to quantify extreme mortality risk. Denote by ${\left\{{\mathcal{F}}_t^1\right\}}_{0\le t\le T}$ and ${\left\{{\mathcal{F}}_t^2\right\}}_{0\le t\le T}$ the augmented natural filtrations generated by ${\{r_t\}}_{0\le t\le T}$ and ${\{{\mu }_t\}}_{0\le t\le T}$, respectively, and assume without loss of generality that ${\mathcal{F}}_t={\mathcal{F}}_t^1\vee {\mathcal{F}}_t^2$ for $0\le t\le T$.

We will introduce a pricing measure Q. Then $E_t^Q[\cdot ]$ represents the conditional expectation under Q given the information up to time t; that is, $E_t^Q[\cdot ]=E^Q\left[\cdot |{\mathcal{F}}_t\right]$. Nevertheless, when an operation is under the physical probability measure P, we usually omit the superscript P for simplicity. Accordingly, cov, var, and corr denote the covariance, variance, and correlation under P, respectively.

2.1. Dynamics under P

Assume that the bivariate process ${\{{\mathbf{Y}}_t={(r_t,{\mu }_t)}^{⊺}\}}_{0\le t\le T}$ follows an affine jump-diffusion (AJD) process. Precisely, for $0\le t\le T$,

$$d{\mathbf{Y}}_t={\mathbf{K}}_t({\mathit{\theta }}_t-{\mathbf{Y}}_t)dt+{\mathbf{\Sigma }}_t\sqrt{{\mathbf{S}}_t}d{\mathbf{W}}_t+\sum _{i=1}^{m}d{\mathbf{J}}_{i,t},$$ (2.1)

where

• •the elements of ${\mathbf{K}}_t,{\mathbf{\Sigma }}_t\in {\mathbb{R}}^{2\times 2}$, and ${\mathit{\theta }}_t\in {\mathbb{R}}^2$ are all deterministic functions of t;
• •${\mathbf{W}}_t={(W_{1,t},W_{2,t})}^{⊺}$ for $0\le t\le T$ is a standard bivariate Brownian motion;
• •${\mathbf{S}}_t$ is a diagonal matrix with the ith diagonal element given by ${\left[{\mathbf{S}}_t\right]}_{ii}={\alpha }_{i,t}+{\mathit{\beta }}_{i,t}^{⊺}{\mathbf{Y}}_t$ with ${\alpha }_{i,t}\in \mathbb{R}$ and ${\mathit{\beta }}_{i,t}\in {\mathbb{R}}^2$ being deterministic functions of t;
• •for each $i=1,\dots ,m$, ${\mathbf{J}}_{i,t}={\sum }_{k=1}^{N_{i,t}}{\mathbf{X}}_{i,k}$ for $0\le t\le T$ is a bivariate compound Poisson process with intensity ${\lambda }_i>0$ and jump-size distribution $G_i$ defined on ${\mathbb{R}}^2$;
• •the compound Poisson processes ${\{{\mathbf{J}}_{i,t}\}}_{0\le t\le T}$, $i=1,\dots ,m$, are mutually independent.

Note that, automatically, the Brownian motion ${\{{\mathbf{W}}_t\}}_{0\le t\le T}$ and the compound Poisson processes ${\{{\mathbf{J}}_{i,t}\}}_{0\le t\le T}$, $i=1,\dots ,m$, are mutually independent. See Corollary 11.5.3 of Shreve (2004) for this result or see Lemma 13.6 of Kallenberg (1997) for a more general version of it. A feature of this model is that it gives consideration to multiple exogenous events/shocks, realized by the bivariate compound Poisson processes ${\{{\mathbf{J}}_{i,t}\}}_{0\le t\le T}$, $i=1,\dots ,m$, which feed into all dimensions of the joint process ${\{{\mathbf{Y}}_t\}}_{0\le t\le T}$.

In the sequel, we will always assume for simplicity that certain conditions are already imposed on the coefficient functions ${\mathbf{K}}_t$, ${\mathit{\theta }}_t$, ${\mathbf{\Sigma }}_t$, ${\alpha }_{i,t}$, ${\mathit{\beta }}_{i,t}$, and the distributions $G_i$, $i=1,\dots ,m$, to ensure that the SDE (2.1) has a unique strong solution. See Theorem 1.19 of Øksendal and Sulem (2005) for a general result on this; see also Subsection 2.1 of Duffie et al. (2000) and references therein for related discussions.

2.2. The pricing measure Q

In what follows, we introduce our structure of risk premia by following Subsection 3.1 of Duffie et al. (2000). Other closely related works include Dai and Singleton (2000), Duffee (2002), and Lando (2009). Following the terminology of Schönbucher (1998), we are to determine the market price of diffusion risk and the market price of jump risk.

For the diffusion risk captured by ${\{{\mathbf{W}}_t\}}_{0\le t\le T}$, the market price of diffusion risk is assumed to be

$${\mathbf{\Gamma }}_t=\sqrt{{\mathbf{S}}_t}{\mathit{\gamma }}_t,$$ (2.2)

where ${\mathit{\gamma }}_t={({\gamma }_{1,t},{\gamma }_{2,t})}^{⊺}\in {\mathbb{R}}^2$ is a bivariate deterministic function of t. Define

$$Z_{1,t}=\exp \{\underset{0}{\overset{t}{\int }}{\mathbf{\Gamma }}_s^{⊺}d{\mathbf{W}}_s-\frac{1}{2}\underset{0}{\overset{t}{\int }}{\mathbf{\Gamma }}_s^{⊺}{\mathbf{\Gamma }}_{s}ds\},0\le t\le T.$$ (2.3)

We assume that the process ${\{{\mathbf{\Gamma }}_t\}}_{0\le t\le T}$ satisfies a certain integrability condition so that ${\{Z_{1,t}\}}_{0\le t\le T}$ is a martingale under P.

The jump part in (2.1) consists of multiple independent compound Poisson processes under P. When introducing the market price of jump risk, we consider both the jump-frequency risk and the jump-size risk, but restrict our study to structure-preserving equivalent changes of measures, which retain the mathematical tractability of the model. Mimicking Proposition 9.6 of Cont and Tankov (2004), we perform a change of measure such that under the changed measure ${\{{\mathbf{J}}_{i,t}\}}_{0\le t\le T}$, $i=1,\dots ,m$, remain to be independent compound Poisson processes. To be precise, for each i, we change the intensity from ${\lambda }_i$ to ${\lambda }_i^{⁎}>0$, with ${\chi }_i=\frac{{\lambda }_i^{⁎}}{{\lambda }_i}-1$ reflecting the market price of jump-frequency risk. Also, we change the common jump-size distribution from $G_i$ to some distribution $G_i^{⁎}$ which shares the support of $G_i$. Denote by $D_i\subset {\mathbb{R}}^2$ the common support of $G_i$ and $G_i^{⁎}$. By the Radon–Nikodym theorem, there is a positive measurable function $g_i(\mathbf{x})$ such that

$$\frac{d{G}_i^{⁎}}{d{G}_i}(\mathbf{x})=g_i(\mathbf{x}),\mathbf{x}\in D_i,$$ (2.4)

in which the market price of jump-size risk is embedded. Then define

$$Z_{2,t}=\prod _{i=1}^m{e}^{-({\lambda }_i^{⁎}-{\lambda }_i)t}\prod _{k=1}^{N_{i,t}}\left(\frac{{\lambda }_i^{⁎}}{{\lambda }_i}{g}_i\left({\mathbf{X}}_{i,k}\right)\right),0\le t\le T,$$ (2.5)

which is a martingale under P.

Building on (2.3) and (2.5), we define the pricing measure Q by the Radon–Nikodym derivative

$$\frac{dQ}{dP}=Z_{1,T}{Z}_{2,T}.$$ (2.6)

Note that our construction of the equivalent martingale measure Q above is restricted to a finite-time horizon. While this suffices for our study, we would like to point out that the extension to the infinite-time horizon, which is needed when pricing, e.g., perpetuities, is not straightforward.8

Define

$$d{\mathbf{W}}_t^Q=d{\mathbf{W}}_t-{\mathbf{\Gamma }}_{t}dt,0\le t\le T,$$ (2.7)

and then rewrite $d{\mathbf{Y}}_t$ as

$$d{\mathbf{Y}}_t={\mathbf{K}}_t({\mathit{\theta }}_t-{\mathbf{Y}}_t)dt+{\mathbf{\Sigma }}_t\sqrt{{\mathbf{S}}_t}(d{\mathbf{W}}_t^Q+\sqrt{{\mathbf{S}}_t}{\mathit{\gamma }}_{t}dt)+\sum _{i=1}^{m}d{\mathbf{J}}_{i,t}={\mathbf{K}}_t^{⁎}({\mathit{\theta }}_t^{⁎}-{\mathbf{Y}}_t)dt+{\mathbf{\Sigma }}_t\sqrt{{\mathbf{S}}_t}d{\mathbf{W}}_t^Q+\sum _{i=1}^{m}d{\mathbf{J}}_{i,t},$$

where ${\mathbf{K}}_t^{⁎}={\mathbf{K}}_t-{\mathbf{\Sigma }}_t{\mathbf{\Phi }}_t$, ${\mathit{\theta }}_t^{⁎}={({\mathbf{K}}_t^{⁎})}^{-1}({\mathbf{K}}_t{\mathit{\theta }}_t+{\mathbf{\Sigma }}_t{\mathit{\psi }}_t)$, the ith row of ${\mathbf{\Phi }}_t\in {\mathbb{R}}^{2\times 2}$ is given by ${\gamma }_{i,t}{\mathit{\beta }}_{i,t}^{⊺}$, and ${\mathit{\psi }}_t={({\gamma }_{1,t}{\alpha }_{1,t},{\gamma }_{2,t}{\alpha }_{2,t})}^{⊺}\in {\mathbb{R}}^2$. Proposition 2.1 below, the proof of which is provided in Appendix A.2, shows that the AJD structure is preserved under the pricing measure Q:

Proposition 2.1

Under the pricing measure Q,

• • ${\{{\mathbf{W}}_t^Q\}}_{0\le t\le T}$ defined by (2.7) is a standard bivariate Brownian motion;
• • for each $i=1,\dots ,m$ , ${\{{\mathbf{J}}_{i,t}\}}_{0\le t\le T}$ is a bivariate compound Poisson process with intensity ${\lambda }_i^{⁎}$ and common jump-size distribution $G_i^{⁎}$ ;
• • ${\{{\mathbf{W}}_t^Q\}}_{0\le t\le T}$ and ${\{{\mathbf{J}}_{i,t}\}}_{0\le t\le T}$ , $i=1,\dots ,m$ , are mutually independent.

2.3. An important special case

Now consider an important special case that the interest rate process and the excess mortality process evolve according to

$$\{\begin{array}{c}d{r}_t=(m_1-d_1{r}_t)dt+{\sigma }_{1}d{W}_{1,t}+d\sum _{i=1}^{N_t}{X}_{1,i},\hfill \\ d{\mu }_t=(m_2-d_2{\mu }_t)dt+{\sigma }_2({\rho }_{1}d{W}_{1,t}+\sqrt{1-{\rho }_1^2}d{W}_{2,t})+d\sum _{i=1}^{N_t}{X}_{2,i},\hfill \end{array}$$ (2.8)

where, under P,

• •$m_i\in \mathbb{R}$, $d_i\ne 0$, ${\sigma }_i>0$, for $i=1,2$, and ${\rho }_1\in [-1,1]$ are constants;
• •${\{(W_{1,t},W_{2,t})\}}_{0\le t\le T}$ is a standard bivariate Brownian motion;
• •${\{N_t\}}_{0\le t\le T}$ is a Poisson process with intensity $\lambda >0$;
• •${\{{\mathbf{X}}_j={(X_{1,j},X_{2,j})}^{⊺}\}}_{j\in \mathbb{N}}$ is a sequence of independent and identically distributed (i.i.d.) bivariate random vectors such that the generic vector X is normally distributed with marginal means ${\nu }_1$ and ${\nu }_2$, standard deviations ${\varphi }_1$ and ${\varphi }_2$, and correlation coefficient ${\rho }_2$, denoted by $\mathbf{X}\sim N({\nu }_1,{\nu }_2;{\varphi }_1,{\varphi }_2;{\rho }_2)$;
• •${\{N_t\}}_{0\le t\le T}$ and ${\{{\mathbf{X}}_j\}}_{j\in \mathbb{N}}$ are independent.

Note that the model captures the dependence between the interest rate and excess mortality via the diffusion correlation ${\rho }_1$, the concurrent jumps, and the jump correlation ${\rho }_2$.

Conforming to (2.1), the joint dynamics for ${\{{\mathbf{Y}}_t={(r_t,{\mu }_t)}^{⊺}\}}_{0\le t\le T}$ is rewritten as

$$d{\mathbf{Y}}_t={\mathbf{K}}_t({\mathit{\theta }}_t-{\mathbf{Y}}_t)dt+{\mathbf{\Sigma }}_{t}d{\mathbf{W}}_t+d\sum _{i=1}^{N_t}{\mathbf{X}}_i,$$

with

$${\mathbf{K}}_t=\left(\begin{array}{cc}{d}_1\hfill & 0\hfill \\ 0\hfill & d_2\hfill \end{array}\right),{\mathit{\theta }}_t=\left(\begin{array}{c}\frac{m_1}{d_1}\hfill \\ \frac{m_2}{d_2}\hfill \end{array}\right),{\mathbf{\Sigma }}_t=\left(\begin{array}{cc}{\sigma }_1\hfill & 0\hfill \\ {\sigma }_2{\rho }_1\hfill & {\sigma }_2\sqrt{1-{\rho }_1^2}\hfill \end{array}\right).$$

For later use, we calculate the long-term means of $r_t$ and ${\mu }_t$ and their instantaneous correlation as follows. To find the long-term means, we set $E\left[d{r}_t\right]=E\left[d{\mu }_t\right]=0$ and then use equation (2.8) to solve for $E\left[r_t\right]$ and $E\left[{\mu }_t\right]$. Clearly, the long-term means of $r_t$ and ${\mu }_t$ are, respectively,

$$\frac{m_1+\lambda {\nu }_1}{d_1}\text{and}\frac{m_2+\lambda {\nu }_2}{d_2}.$$ (2.9)

To find the instantaneous correlation, first note that

$$\mathrm{cov}(d{r}_t,d{\mu }_t)=E\left[(d{r}_t-E[d{r}_t])(d{\mu }_t-E[d{\mu }_t])\right]=E[{\rho }_1{\sigma }_1{\sigma }_{2}dt+d\sum _{i=1}^{N_t}{X}_{1,i}{X}_{2,i}]={\rho }_1{\sigma }_1{\sigma }_{2}dt+\lambda ({\rho }_2{\varphi }_1{\varphi }_2+{\nu }_1{\nu }_2)dt.$$

Similarly,

$$\mathrm{var}(d{r}_t)={\sigma }_1^{2}dt+\lambda ({\varphi }_1^2+{\nu }_1^2)dt,\mathrm{var}(d{\mu }_t)={\sigma }_2^{2}dt+\lambda ({\varphi }_2^2+{\nu }_2^2)dt.$$

Thus, the instantaneous correlation between $r_t$ and ${\mu }_t$ is

$$\mathrm{corr}(d{r}_t,d{\mu }_t)=\frac{{\rho }_1{\sigma }_1{\sigma }_2+\lambda ({\rho }_2{\varphi }_1{\varphi }_2+{\nu }_1{\nu }_2)}{\sqrt{({\sigma }_1^2+\lambda ({\varphi }_1^2+{\nu }_1^2))({\sigma }_2^2+\lambda ({\varphi }_2^2+{\nu }_2^2))}}.$$ (2.10)

Now we look at the Q version of this special case. We take the simplest choice for the market price of diffusion risk (2.2) that ${\mathbf{\Gamma }}_t={({\gamma }_1,{\gamma }_2)}^{⊺}\in {\mathbb{R}}^2$. Then with $d{W}_{i,t}=d{W}_{i,t}^Q+{\gamma }_{i}dt$ for $i=1,2$, we can rewrite the dynamics as

$$\{\begin{array}{c}d{r}_t=(m_1^{⁎}-d_1{r}_t)dt+{\sigma }_{1}d{W}_{1,t}^Q+d{\sum }_{i=1}^{N_t}{X}_{1,i},\hfill \\ d{\mu }_t=(m_2^{⁎}-d_2{\mu }_t)dt+{\sigma }_2({\rho }_{1}d{W}_{1,t}^Q+\sqrt{1-{\rho }_1^2}d{W}_{2,t}^Q)+d{\sum }_{i=1}^{N_t}{X}_{2,i},\hfill \end{array}$$ (2.11)

with

$$m_1^{⁎}=m_1+{\gamma }_1{\sigma }_1,m_2^{⁎}=m_2+{\gamma }_1{\sigma }_2{\rho }_1+{\gamma }_2{\sigma }_2\sqrt{1-{\rho }_1^2}.$$

We follow Subsection 2.2 to specify the market prices of the jump-frequency risk and jump-size risk. In summary, we have the following, under Q:

• •${\{(W_{1,t}^Q,W_{2,t}^Q)\}}_{0\le t\le T}$ is a standard bivariate Brownian motion;
• •${\{N_t\}}_{0\le t\le T}$ is a Poisson process with intensity ${\lambda }^{⁎}>0$, so that $\chi =\frac{{\lambda }^{⁎}}{\lambda }-1$ reflects the market price of jump-frequency risk;
• •${\{{\mathbf{X}}_j\}}_{j\in \mathbb{N}}$ is a sequence of i.i.d. bivariate random vectors with common distribution function $G^{⁎}$ on ${\mathbb{R}}^2$;
• •${\{N_t\}}_{0\le t\le T}$ and ${\{{\mathbf{X}}_j\}}_{j\in \mathbb{N}}$ are independent.

Example 2.1

Now we employ the normalized multivariate exponential tilting to construct the common distribution $G^{⁎}$ of ${\{{\mathbf{X}}_j\}}_{j\in \mathbb{N}}$ under Q. See Section 5 of Wang (2007) for more details about this distortion approach; see also Cox et al. (2006) and Lin et al. (2013), who apply this approach, in a somewhat simplified situation, to price MLS.

Assume that under P, the generic vector $\mathbf{X}={(X_1,X_2)}^{⊺}$ is bivariate normal with marginal means ${\nu }_1$ and ${\nu }_2$, standard deviations ${\varphi }_1$ and ${\varphi }_2$, and correlation coefficient ${\rho }_2$, as specified before. Let the market prices of jump-size risk be ${\kappa }_1$ and ${\kappa }_2$, respectively. Then the common distribution $G^{⁎}$ is constructed by specifying the measurable function (2.4) to

$$\frac{d{G}^{⁎}}{dG}(\mathbf{x})=g(\mathbf{x})=\phi E[\exp \left\{\sum _{k=1}^2{\eta }_k{V}_k\right\}|\mathbf{X}=\mathbf{x}],\mathbf{x}\in {\mathbb{R}}^2,$$

where

• •the vector $(X_1,X_2,V_1,V_2)$ is jointly normal with $V_1$ and $V_2$, called the reference variables, specified to be standard normal for simplicity;
• •the constants ${\eta }_1$ and ${\eta }_2$ satisfy ${\kappa }_i=-{\sum }_{j=1}^2{\hat{\rho }}_{i,j}{\eta }_j$, $i=1,2$, with each ${\hat{\rho }}_{i,j}$ being the correlation of $X_i$ and $V_j$;
• •φ is a normalizing constant to ensure $E[g(\mathbf{X})]=1$, so that $g(\mathbf{x})$ is a proper Radon–Nikodym derivative over ${\mathbb{R}}^2$.

It is easy to see that under Q the vector X remains bivariate normal with marginal means ${\nu }_1^{⁎}={\nu }_1+{\varphi }_1{\kappa }_1$ and ${\nu }_2^{⁎}={\nu }_2+{\varphi }_2{\kappa }_2$, standard deviations ${\varphi }_1$ and ${\varphi }_2$, and correlation coefficient ${\rho }_2$; that is, only the marginal means are changed.

In this case, the Radon–Nikodym derivative (2.6) is explicated as

$$\frac{dQ}{dP}=\exp \{{\gamma }_1{W}_{1,T}+{\gamma }_2{W}_{2,T}-\frac{1}{2}({\gamma }_1^2+{\gamma }_2^2)T-({\lambda }^{⁎}-\lambda )T\}\prod _{k=1}^{N_T}\left(\frac{{\lambda }^{⁎}}{\lambda }g\left({\mathbf{X}}_k\right)\right)=\exp \{{\gamma }_1{W}_{1,T}+{\gamma }_2{W}_{2,T}-\frac{1}{2}({\gamma }_1^2+{\gamma }_2^2)T-\lambda \chi T\}{(\chi +1)}^{N_T}\prod _{k=1}^{N_T}g\left({\mathbf{X}}_k\right).$$ (2.12)

3. Pricing mortality-linked securities

Consider a general structure of an MLS, which makes payments at time points

$$0<t_1<t_2<\cdots <t_n=T<\infty ,$$

where 0 and T represent the issuance date and the maturity date, respectively. Each payment ${\xi }_{t_k}$ made at time $t_k$ is linked to a certain mortality index. Technically, for each $k=1,\dots ,n$, we assume that ${\xi }_{t_k}$ is measurable with respect to ${\mathcal{F}}_{t_k}^2$. Given the pricing measure Q specified in Section 2, the risk-neutral price of this MLS is

$$P_t=E_t^Q[\sum _{t<t_k\le T}\exp \{-\underset{t}{\overset{t_k}{\int }}{r}_{s}ds\}{\xi }_{t_k}],0\le t<T.$$

Next we introduce a hypothetical bond as our working example, which closely resembles the mortality CAT bond launched in September 2013 by the Atlas IX Capital (hereafter, the Atlas bond). The Atlas bond had a risk period of 1 January 2013 – 31 December 2018. Its principal reduction factor (PRF) was determined by an underlying mortality index which represents the age- and gender-weighted death probability across the U.S. Initially, there were two tranches offered, Class A notes with lower risk and Class B notes with higher risk. In fact, Class A notes were pulled out from the market due to lack of demand. Nevertheless, Class B notes were marketed at US$50m but ended up at US$180m in size, indicating a strong market appetite for the higher-risk layer. The Class B tranche had an attachment probability of 1.16% and an exhaustion probability of 0.74%. The expected loss of the Atlas bond was 0.92% and the coupon rate was 3.25%.9

Example 3.1

Denote by $t_0=0$ the bond issuance date 30 September 2013 and thus the bond maturity date 31 December 2018 is $T=5\frac{1}{4}$. Suppose the bond principal is K and it pays an annual coupon at rate $c=3.25\text{\%}$, payable quarterly. Thus, we have 21 coupon dates, with the first coupon date $t_1=\frac{1}{4}$ corresponding to 31 December 2013, the second coupon date $t_2=\frac{2}{4}$ corresponding to 31 March 2014, and so on, until the last coupon date, also the maturity date, $t_{21}=T=5\frac{1}{4}$, corresponding to 31 December 2018.

Suppose an attachment point a and an exhaustion point b are determined based on a given model, with $0<a<b<\infty$. If the bond is triggered by time T, that is, if ${\mu }^{⁎}={\max }_{0<t_k\le T}{\mu }_{t_k}>a$, then with the PRF defined to be

$$\mathrm{PRF}=\frac{{({\mu }^{⁎}-a)}_{+}-{({\mu }^{⁎}-b)}_{+}}{b-a},$$

the remaining principal at maturity is

$$D=K(1-\frac{{({\mu }^{⁎}-a)}_{+}-{({\mu }^{⁎}-b)}_{+}}{b-a}).$$

Recall the constant coupon rate c assumed at the beginning. Putting together, we have the payoff structure

$$\{\begin{array}{cc}{\xi }_{t_k}=\frac{c}{4}K,\hfill & 0<t_k<T,\hfill \\ {\xi }_T=\frac{c}{4}K+D.\hfill & \hfill \end{array}$$

The full price, with accrued interest included, of the bond at time $0\le t\le T$ is

$$P_t(c)=\frac{c}{4}K\sum _{t<t_k\le T}P(t,t_k)+KP(t,T)-K{E}_t^Q\left[e^{-{\int }_t^T{r}_{s}ds}\frac{{({\mu }^{⁎}-a)}_{+}-{({\mu }^{⁎}-b)}_{+}}{b-a}\right],$$ (3.1)

where $P(t,s)$, for $0\le t\le s<\infty$, is the time t price of a risk-free zero-coupon bond with maturity date s.

4. Empirical studies

4.1. Data description

Our empirical studies focus on the U.S. experience. To calibrate the bivariate AJD model described in Section 2.3, we consider the U.S. weekly mortality and interest rate data for the period of 2017–2022, which are collected from four sources as follows:

CDC COVID-19 Death Data. In response to the COVID-19 pandemic, the CDC is providing weekly updates on national estimates of excess deaths to reflect the burden of mortality potentially associated with the pandemic.10 This excess death dataset is available from January 2017 onwards. We collect national-level weekly observed deaths and the expected deaths for the period January 2017 – April 2022.

CDC WONDER Database. The CDC WONDER online database provides a rich query system for the analysis of public health data and vital statistics. We collect population data for 2017–2019 via the online query “Bridged-Race Population Estimates 1990–2019 Request”.

United States Census Bureau. The United States Census Bureau produces the most up-to-date population data for the U.S. We collect the population estimate for 2020–2022 via its U.S. Population Clock.

Federal Reserve Economic Data (FRED). The weekly interest rate data come from the 3-month treasury bill rates, collected at the same frequency and for the same period as the mortality data.

As we focus on extreme mortality experience, instead of mortality rate, we choose to examine the excess mortality rate defined as

$${\mu }_t=\frac{d_t-E[d_t]}{e_t}\times 100,$$ (4.1)

where $d_t$ is the observed number of deaths during a time period ending at t, and $E[d_t]$ and $e_t$ are, respectively, the expected number of deaths and the population exposure for the same period.11 While excess mortality in the literature is usually defined through death counts per annum, the more granular mortality data allow for a more refined definition based on weekly death counts. Since weekly population exposures are unavailable, for simplicity, we approximate them based on the annual population data assuming equal exposures across weeks in a calendar year.

As one of the most devastating global events since World War II, the COVID-19 pandemic has resulted in substantial excess mortality for most countries. According to the New York Times, there were 574,000 more deaths than usual in the 12-month period from March 2020 to March 2021.12 To combat the COVID-19 pandemic, on 3 March 2020, the Federal Reserve cut the base rate by 50 basis points. As the COVID-19 fear grew, on 15 March 2020, the Federal Reserve further cut the base rate down to near zero. Obviously, the “higher than usual” mortality rate and the “lower than usual” interest rate were not a coincidence, but both resulted from the shock imposed by the COVID-19 pandemic. However, it should be noted that only toward the end of March did the national death tolls start to climb, which then led to a sharp increase in excess mortality in April. Although the jumps in interest rate and excess mortality came from the same source, there was a time lag in the responses of the two processes. In other words, the Federal Reserve proactively adjusted its monetary policy, foreseeing the devastating impacts of COVID-19 on population health and the economy. To address this issue, we argue that from the week ending 6 March 2020, a three-week lag in the interest rate data should be introduced to synchronize the first emergency rate cut by the Federal Reserve and the first observed surge in excess mortality. The adjusted series are shown in Fig. 4.1 .

Fig. 1.

This figure plots weekly interest rate and excess mortality for the U.S. Note that we synchronize the first emergency rate cut by the Federal Reserve and the first observed surge in excess mortality in March 2020.

4.2. Model calibration including the pandemic experience

We first fit the AJD model (2.8) introduced in Section 2.3 to the entire dataset from 2017 to 2022, particularly including the COVID-19 pandemic experience. We adopt the likelihood inference methodology proposed by Pienaar and Varughese (2016), where parameter estimation is performed under the MCMC algorithm implemented via the R package DiffusionRjgqd. Table 4.1 presents the estimated parameter values, as well as their corresponding 95% confidence intervals. The convergence diagnostics for the MCMC sampler, as well as the autocorrelation function (ACF) of MCMC draws, are plotted in Fig. A.1, Fig. A.2 in the Appendix.

Table 1.

Estimated parameters for model (2.8) based on data including the pandemic experience, from 2017 to 2022.

	Estimate	Lower confidence interval	Upper confidence interval
d1	0.297	0.278	0.312
m1	0.006	0.005	0.008
σ1	0.002	0.002	0.002
d2	1.940	0.531	3.230
m2	0.030	−0.085	0.141
σ2	0.126	0.113	0.140
ρ1	−0.039	−0.102	0.010
λ	8.390	5.189	12.004
ν1	0.000	−0.001	0.000
ν2	0.010	−0.003	0.025
ϕ1	0.001	0.001	0.002
ϕ2	0.057	0.047	0.067
ρ2	−0.477	−0.560	−0.396

Fig. A.1.

This figure shows convergence diagnostics for the MCMC sampler. The first 13 panels are trace plots of MCMC draws each corresponding to a single parameter in model (4.2), the final two panels show the evolution of the acceptance rate over the MCMC sampler and jump detection probabilities respectively.

Fig. A.2.

This figure shows the ACF of MCMC draws for each parameter in model (4.2).

The calibrated dynamics of the interest rate process and the excess mortality process are

$$\{\begin{array}{c}d{r}_t=(0.006-0.297r_t)dt+0.002d{W}_{1,t}+d\sum _{i=1}^{N_t}{X}_{1,i},\hfill \\ d{\mu }_t=(0.030-1.940{\mu }_t)dt+0.126(-0.039d{W}_{1,t}+0.99924d{W}_{2,t})+d\sum _{i=1}^{N_t}{X}_{2,i},\hfill \end{array}$$ (4.2)

where, under P,

• •${\{(W_{1,t},W_{2,t})\}}_{0\le t\le T}$ is a standard bivariate Brownian motion;
• •${\{N_t\}}_{0\le t\le T}$ is a Poisson process with intensity 8.390;
• •${\{{\mathbf{X}}_j={(X_{1,j},X_{2,j})}^{⊺}\}}_{j\in \mathbb{N}}$ is a sequence of i.i.d. bivariate random vectors such that the generic vector X is normally distributed with marginal means 0 and 0.01, standard deviations 0.001 and 0.057, and correlation coefficient −0.477, that is, $\mathbf{X}\sim N(0,0.01;0.001,0.057;-0.477)$.

Using the data, we detect joint jumps with an estimated intensity of 8.390 per annum. Moreover, we find a strong negative jump correlation of ${\rho }_2=-0.477$, which means that the excess mortality and interest rate tend to jump in the opposite directions. On the other hand, the two diffusions are nearly independent, with an estimated diffusion correlation of ${\rho }_1=-0.039$. Plugging these calibrated values into (2.10), we obtain the instantaneous correlation

$$\mathrm{corr}(d{r}_t,d{\mu }_t)=-0.322.$$

While the computed instantaneous correlation seems significant, it should be noted that this correlation is largely driven by the observations during 2020–2022. Due to the fact that we only have 5 years and 4 months of data available at the weekly frequency, we may see a smaller correlation if a longer period of data were used. In the proposed AJD model, diffusions represent market fluctuations in their normal range, while jumps are used to capture unusual changes that often result from shocks. Based on the values of ${\rho }_1$ and ${\rho }_2$, as well as the instantaneous correlation calculated above, we find that the significant instantaneous correlation here is mainly caused by the joint jumps. Therefore, under extreme market conditions driven by shocks, the independence assumption can become fundamentally wrong.

4.3. Model calibration excluding the pandemic experience

We now fit model (2.8) to pre-pandemic data only, from 2017 to 2019. The estimated parameters and their 95% confidence intervals are shown in Table 4.2 . The convergence diagnostics for the MCMC sampler and the ACF of MCMC draws are presented in Fig. A.3, Fig. A.4.

Table 2.

Estimated parameters for model (2.8) based on data from 2017 to 2019, which exclude the pandemic experience.

	Estimate	Lower confidence interval	Upper confidence interval
d1	0.727	0.222	1.181
m1	0.016	0.006	0.024
σ1	0.002	0.002	0.003
d2	16.368	9.015	23.134
m2	−0.217	−0.349	−0.094
σ2	0.095	0.086	0.105
ρ1	0.017	−0.049	0.088
λ	1.909	0.497	3.780
ν1	0.000	−0.001	0.001
ν2	0.026	0.001	0.058
ϕ1	0.001	0.000	0.003
ϕ2	0.056	0.041	0.072
ρ2	−0.475	−0.558	−0.384

Fig. A.3.

This figure shows convergence diagnostics for the MCMC sampler. The first 13 panels are trace plots of MCMC draws each corresponding to a single parameter in model (4.3), the final two panels show the evolution of the acceptance rate over the MCMC sampler and jump detection probabilities respectively.

Fig. A.4.

This figure shows the ACF of MCMC draws for each parameter in model (4.3).

The calibrated dynamics of the interest rate process and the excess mortality process are

$$\{\begin{array}{c}d{r}_t=(0.016-0.727r_t)dt+0.002d{W}_{1,t}+d\sum _{i=1}^{N_t}{X}_{1,i},\hfill \\ d{\mu }_t=(-0.217-16.368{\mu }_t)dt+0.095(0.017d{W}_{1,t}+0.99986d{W}_{2,t})+d\sum _{i=1}^{N_t}{X}_{2,i},\hfill \end{array}$$ (4.3)

where, under P,

• •${\{(W_{1,t},W_{2,t})\}}_{0\le t\le T}$ is a standard bivariate Brownian motion;
• •${\{N_t\}}_{0\le t\le T}$ is a Poisson process with intensity 1.909;
• •${\{{\mathbf{X}}_j={(X_{1,j},X_{2,j})}^{⊺}\}}_{j\in \mathbb{N}}$ is a sequence of i.i.d. bivariate random vectors such that the generic vector X is normally distributed with marginal means 0.000 and 0.026, standard deviations 0.001 and 0.056, and correlation coefficient −0.479, that is, $\mathbf{X}\sim N(0.000,0.026;0.001,0.056;-0.475)$.

We again find a strong negative jump correlation of ${\rho }_2=-0.475$ and that the two diffusions can still be seen as independent, with ${\rho }_1=0.017$. However, the estimates of some parameters have changed notably compared to those in Table 4.1. In particular, joint jumps are detected to have a much lower frequency at $\lambda =1.909$ per annum, and the means and variances of the jump sizes tend to be smaller for both the interest rate and excess mortality. Plugging the calibrated values in Table 4.2 into (2.10), we obtain

$$\mathrm{corr}(d{r}_t,d{\mu }_t)=-0.153.$$

That is, due to the less frequent joint jumps, the negative correlation between the interest rate and excess mortality is much weaker—but still significant—in the pre-pandemic world. Moreover, by equation (2.9), the changes result in a substantial increase of the long-term average excess mortality from the pre-pandemic level of −0.010 to the post-pandemic level of 0.059.

5. Implied market prices of risk

Understanding the MPRs is an important step toward understanding the mortality risk market and how it may react to a pandemic. Since precise calibration of the implied MPRs is challenging due to lack of data on relevant market deals, we compute the MPRs based on the hypothetical bond designed in Example 3.1. In doing so, we accept the assumption that the hypothetical bond, if issued on 30 September 2013 under the then market conditions, would have been traded at the same prices as the Atlas bond. This assumption is largely innocuous, since the hypothetical bond closely resembles the Atlas bond in structure, covers the same population, and shares the same attachment and exhaustion probabilities.

The price data used for our calibration are obtained from the Lane Financial L.L.C. annual reviews of the catastrophe insurance market, which include quarter-end indicative secondary market prices of various catastrophe-linked securities. The 2014–2019 reviews, which cover the tenor of the Atlas bond, list the average spreads for the bond indicated by the dealers in the market.

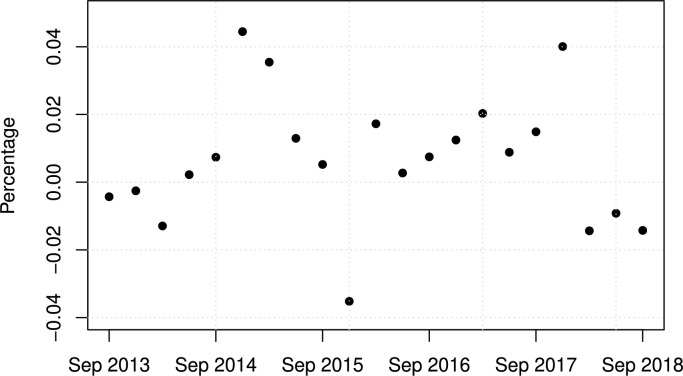
Our secondary market price data contain 21 quarterly observations of market-indicated spreads during the period of September 2013 – September 2018, which we denote by $c_{t_k}^{⁎}$, $t_k=\frac{k}{4}$, $k=0,1,\dots ,20$. We illustrate these spreads in Fig. 5.1 .

Fig. 2.

This figure plots the quarterly market-indicated spreads of the Atlas bond from September 2013 to September 2018 inclusive, published by Lane Financial L.L.C.

Note that the bond price at each time point $t_k$ depends on the level of interest rate and excess mortality at that time. While the interest rate data are available, the excess deaths information from the CDC does not date back to September 2013. Therefore, we project excess deaths based on the information available then using the seasonal ARIMA model proposed by Li and Tang (2022), which incorporates both non-seasonal and seasonal factors in the model. In doing so, we ensure that seasonal patterns are removed from the estimated excess deaths. The estimated quarterly excess mortality is shown in Fig. 5.2 .

Fig. 3.

This figure shows the estimated quarterly excess mortality based on the seasonal ARIMA model.

5.1. Three scenarios

Our pricing measure Q is constructed through the Radon–Nikodym derivative (2.12) with the MPR vector

$$\mathit{\zeta }=({\gamma }_1,{\gamma }_2;{\kappa }_1,{\kappa }_2;\chi ).$$

By (3.1), each spread level $c_{t_k}^{⁎}$, $k=0,1,\dots ,20$, implies a bond price $P_{t_k}^{\mathit{\zeta }}(c_{t_k}^{⁎})$, which should be close to the par value, assumed to be 100 for simplicity. We calibrate the MPRs by searching for the vector ζ that minimizes the sum squared error

$$\sum _{k=0}^{20}{(P_{t_k}^{\mathit{\zeta }}\left(c_{t_k}^{⁎}\right)-100)}^2.$$ (5.1)

Recall model (4.2), estimated with the pandemic data, and model (4.3), estimated without it. We identify the MPRs for three different scenarios:

• S1.The underlying risks follow model (4.2) and the bond trigger levels are designed according to model (4.2);
• S2.The underlying risks follow model (4.3) and the bond trigger levels are designed according to model (4.3);
• S3.The underlying risks follow model (4.2) but the bond trigger levels are designed according to model (4.3).

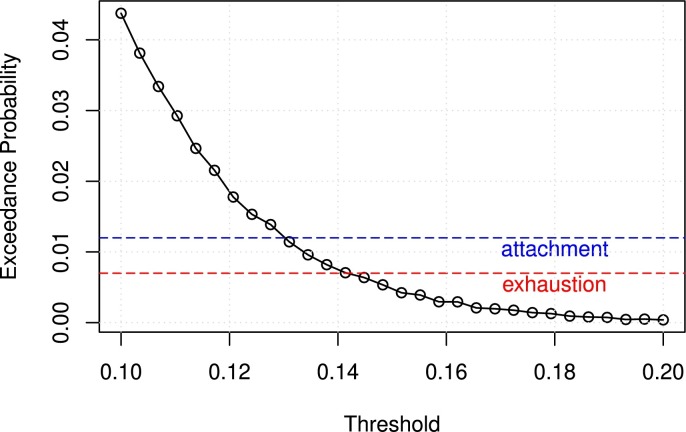
First, we consider scenario S1. To align the bond's attachment and exhaustion probabilities with the Atlas bond's, which are 1.16% and 0.74%, respectively, we simulate 10⁵ paths of the process ${\{{(r_t,{\mu }_t)}^{⊺}\}}_{0\le t\le T}$ under P to estimate the exceedance probabilities for different thresholds. Fig. 5.3 plots the results and suggests that to align with the Atlas bond, the attachment and exhaustion points should be 0.44 and 0.46, respectively.

Fig. 4.

This figure shows the probability that the maximum excess mortality index during the bond tenor, namely, μ^⁎, defined in Example 3.1, exceeds a certain threshold. The probability is estimated using a simulation of 10⁵ paths of the process ${\{{(r_t,{\mu }_t)}^{⊺}\}}_{0\le t\le T}$ under the P measure, where the process follows model (4.2).

Let us now use the indicative prices to derive the MPRs. In our implementation, each price appearing in (5.1) is evaluated using Monte Carlo simulation based on formula (3.1) with 10⁵ paths of ${\{{(r_t,{\mu }_t)}^{⊺}\}}_{0\le t\le T}$. The minimization problem of (5.1) is solved using the new unconstrained optimization with quadratic approximation algorithm (NEWUOA) implemented in the R package minga. The MPR vector is obtained as

$${\mathit{\zeta }}_1=(0.100,0.212;0.178,0.253;0.021).$$ (5.2)

Recall that the set of MPRs maps the measure P to a risk-neutral measure Q, leading to a change of parameters in the process ${\{{(r_t,{\mu }_t)}^{⊺}\}}_{0\le t\le T}$. The comparison between the parameters under the two measures is listed in Table 5.1 . We can see that, investors' perceived parameter values under Q are all greater than or equal to their counterparts under P, and so are the perceived long-term means of the interest rate and excess mortality processes.

Table 3.

This table compares the parameter values (upper panel) and the long-term means of the interest rate process and excess mortality process (lower panel) for each of the three scenarios S1–S3. The parameters without ⁎ are the ones in model (2.8) under P and those with ⁎ are the ones in model (2.11) under Q.

	Scenario S1		Scenario S2		Scenario S3
	Under P	Under Q	Under P	Under Q	Under P	Under Q
Parameter
$m_1\leftrightarrow m_1^{⁎}$	0.006	0.006	0.016	0.016	0.006	0.006
$m_2\leftrightarrow m_2^{⁎}$	0.030	0.056	−0.217	−0.211	0.030	−0.008
${\nu }_1\leftrightarrow {\nu }_1^{⁎}$	0.000	0.000	0.000	0.000	0.000	0.000
${\nu }_2\leftrightarrow {\nu }_2^{⁎}$	0.010	0.024	0.026	0.070	0.010	−0.038
λ↔λ⁎	8.390	8.569	1.909	1.960	8.390	8.416
Long-term mean
${\{r_t\}}_{t\ge 0}$	0.020	0.021	0.0220	0.0221	0.020	0.022
${\{{\mu }_t\}}_{t\ge 0}$	0.059	0.072	−0.0102	−0.0099	0.059	0.039

Next, let us consider scenario S2. This scenario relates to a market where both the issuer/risk modeling agent and investors lack sufficient awareness of the pandemic risk, and thus they design and trade the bond based on model (4.3). Following the procedure for scenario S1, we obtain the exceedance probabilities, as shown in Fig. 5.4 . Note that, to maintain the same trigger probabilities, the attachment and exhaustion points should be lowered to 0.13 and 0.14, respectively. It is worth pointing out that such a bond would be triggered multiple times if traded during the COVID-19 pandemic (see Fig. 5.5 ).

Fig. 5.

This figure shows the probability that the maximum excess mortality index during the bond tenor, namely, μ^⁎ defined in Example 3.1, exceeds a certain threshold. The probability is estimated using a simulation of 10⁵ paths of the process ${\{{(r_t,{\mu }_t)}^{⊺}\}}_{0\le t\le T}$ under the P measure, where the process follows model (4.3).

Fig. 6.

This figure plots the observed excess mortality in 2020.

Using the same optimization algorithm, we obtain the MPR vector

$${\mathit{\zeta }}_2=(0.046,0.062;0.084,0.779;0.027).$$ (5.3)

Again, the set of MPRs leads to a change of measure where the perceived parameter values and long-term means of ${\{{(r_t,{\mu }_t)}^{⊺}\}}_{0\le t\le T}$ under Q are all at least as large as their counterparts under P, as listed in Table 5.1.

Last, we consider scenario S3. This scenario relates to the case where there is significant pandemic risk, with ${\{{(r_t,{\mu }_t)}^{⊺}\}}_{0\le t\le T}$ following model (4.2), but the modeling agent and investors fail to perceive or choose to ignore the risk. They still determine the bond trigger levels according to model (4.3) and still agree on transactions at the prices of the Atlas bond.

Following the same procedure as above to compute the MPRs yields

$${\mathit{\zeta }}_3=(0.221,-0.292;-0.284,-0.842;0.003).$$

We observe from Table 5.1 that, unlike in scenarios S1 and S2, the MPRs in scenario S3 result in some values of the ${\{{(r_t,{\mu }_t)}^{⊺}\}}_{0\le t\le T}$ process under Q lower than under P. This means that the investors, while receiving some positive interest rate risk premium, are receiving negative mortality risk premium. Moreover, note that the negative premium on the mortality jump size is significant enough to flip the sign of the expected jump size. Therefore, a larger jump intensity perceived under Q than under P indicates that the perceived jump risk is actually lower than that under P, further contributing to the negative risk premium.

The message we aim to convey is that turning a blind eye to potential pandemic risk—that is, failing to update the model for bond design to reflect the pandemic risk—could cost investors dearly.13

5.2. On the post-pandemic mortality risk market

In this subsection, we aim to offer a glimpse of how a devastating pandemic experience like the current one could reshape the extreme mortality risk market by, e.g., inducing overreaction, increasing volatility, and prompting industry-wide model recalibration.

We illustrate our results using a three-year hypothetical bond with coupons payable quarterly at 6% per annum, which otherwise shares the same structure as the one in Example 3.1. In this case, our pricing formula (3.1) becomes

$$P_t=100(1.5\text{\%}\sum _{t<t_k\le 3}P(t,t_k)+P(t,3)-E_t^Q\left[e^{-{\int }_t^3{r}_{s}ds}\frac{{({\mu }^{⁎}-a)}_{+}-{({\mu }^{⁎}-b)}_{+}}{b-a}\right]),$$ (5.4)

for $0\le t\le 3$, where $t_k=\frac{k}{4}$, $k=1,\dots ,12$, and ${\mu }^{⁎}={\max }_{0<t_k\le 3}{\mu }_{t_k}$.

Let us first envision a pre-pandemic world, where the modeling agent and investors believe that the underlying risks follow model (4.3), determine the trigger levels accordingly (Fig. 5.4), and price the risk using the MPR vector ${\mathit{\zeta }}_2$ in (5.3). In this case, formula (5.4) leads to a time 0 bond price of 110.0.

Now suppose that the market participants have experienced a pandemic like COVID-19, have opted for model (4.2) to describe the underlying risks, and have updated their MPR vector to ${\mathit{\zeta }}_{\mathbf{1}}$ in (5.2). By formula (5.4), the time 0 bond value is found to be 15.5. While this is an extreme example, it sheds light on a possible overhaul of the pricing mechanism due to the pandemic and the potential disruption it causes to the mortality risk market.

In practice, the sponsor may modify the bond design in response to the pandemic experience by, e.g., raising its trigger levels. In our further analysis, we consider a scenario where the attachment and exhaustion points, respectively, have been raised substantially from 0.13 and 0.14 to, for illustration purpose, 0.3 and 0.32. This leads to attachment and exhaustion probabilities of, respectively, 0.20 and 0.14, which the sponsor is likely unaware of. We now further illustrate our idea by demonstrating how the bond price reacts to the pandemic experience over time.

Recall that the bond price at any time point depends on the interest rate level then and the mortality levels until then. Therefore, to show the bond price evolutions under different scenarios, we generate several paths of ${\{(r_t,{\mu }_t)\}}_{0\le t\le 3}$ and obtain a price curve along each path. The prices on the curves are all computed based on formula (5.4) using simulation with 10⁵ paths.

We present the results for the pre- and post-pandemic markets in Fig. 7, Fig. 8 , respectively. Each figure contains four scenarios generated for the underlying risk process, which lead to either a full return of the principal or a partial reduction to a varying degree.

Fig. 7.

This figure shows the price evolutions for a three-year bond with coupons payable quarterly at 6% per annum and attachment and exhaustion points at 0.13 and 0.14, respectively. Each of (a)–(d) is obtained under a scenario generated for the risk process ${\{{(r_t,{\mu }_t)}^{⊺}\}}_{0\le t\le 3}$. The prices are calculated based on formula (5.4), model (4.3), MPR vector ζ₂ in (5.3), and a simulation with 10⁵ paths.

Fig. 8.

This figure shows the price evolutions for a three-year bond with coupons payable quarterly at 6% per annum and attachment and exhaustion points at 0.3 and 0.31, respectively. Each of (a)–(d) is obtained under a scenario generated for the risk process ${\{{(r_t,{\mu }_t)}^{⊺}\}}_{0\le t\le 3}$. The prices are calculated based on formula (5.4), model (4.2), MPR vector ζ₁ in (5.2), and a simulation with 10⁵ paths.

We observe that, despite the higher trigger points, the bond priced under the updated model of (4.2) should be issued at a much lower price than under model (4.3). Moreover, it is interesting to see that the pandemic experience introduces extra volatility to the post-pandemic mortality risk market, with bond prices that are much more volatile. A comparison of Fig. 7, Fig. 8 shows that while a small change in mortality barely moves the bond price pre-pandemic, it may cause a large swing of the bond price if it occurs post-pandemic. This is not surprising, since in the aftermath of a crisis, even the slightest change in market condition could ripple through the market. Mathematically, any mortality change could get amplified through the model—more so under model (4.2) than under model (4.3)—and cause large fluctuations in bond price. Moreover, the prices obtained under model (4.2) often overreact to mortality surges that trigger the bond, although they also recover faster because the mortality returns to its normal range faster due to the stronger mean reversion under model (4.2) than model (4.3).

To summarize, one may expect a very different post-pandemic mortality risk market from pre-pandemic. The post-pandemic market will likely see MLS prices distressed and more volatile. The distressed price at issuance means a much higher reinsurance premium paid by the MLS sponsor to the bond investors than in the pre-pandemic world. This could change both the supply and demand sides of the MLS market.

5.3. Sensitivity analyses

In this subsection, we conduct sensitivity tests to investigate how the bond issue price would change with respect to some key risk parameters. The bond under consideration is the hypothetical bond defined in Example 3.1, with attachment and exhaustion points set to 0.44 and 0.46, respectively. For the conclusions to hold in the post-pandemic world, in our base model we use (4.2) as the underlying risk process and use ${\mathit{\zeta }}_1$ as the MPR vector.

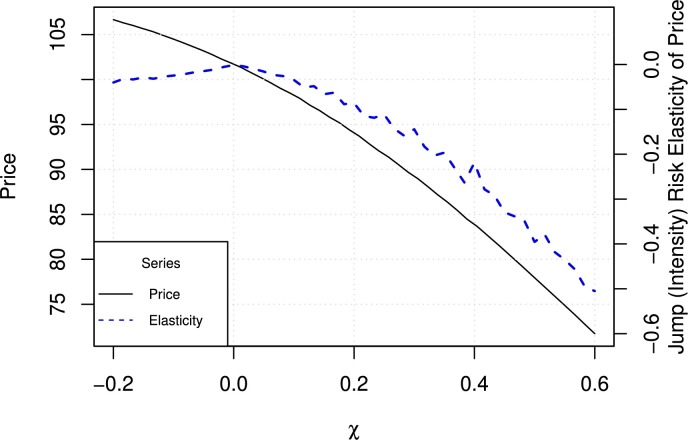
We demonstrate the results in Fig. 9, Fig. 10, Fig. 11 . Specifically, Fig. 9, Fig. 10 show the change of the bond's issue price for varying values of ${\gamma }_1$, ${\gamma }_2$, ${\kappa }_1$, and ${\kappa }_2$, and Fig. 5.10 shows the change of the bond price and jump risk elasticity against the change of χ. Here the jump risk elasticity is defined by

$$\frac{d{P}_0/P_0}{d\chi /|\chi |}$$

and is calculated using forward difference approximation.

Fig. 9.

This figure shows the change of the hypothetical bond price against varying values of γ₁ and γ₂. In our base model, the process ${\{{(r_t,{\mu }_t)}^{⊺}\}}_{0\le t\le T}$ is given by (4.2) and the MPR vector is chosen as ζ₁ in (5.2). The prices are estimated with 10⁵ paths of the risk process.

Fig. 10.

This figure shows the change of the hypothetical bond price against varying values of κ₁ and κ₂. In our base model, the process ${\{{(r_t,{\mu }_t)}^{⊺}\}}_{0\le t\le T}$ is given by (4.2) and the MPR vector is chosen as ζ₁ in (5.2). The prices are estimated with 10⁵ paths of the risk process.

Fig. 11.

This figure shows the changes of the hypothetical bond price and of the jump risk elasticity against varying values of χ. In our base model, the process ${\{{(r_t,{\mu }_t)}^{⊺}\}}_{0\le t\le T}$ is given by (4.2) and the MPR vector is set to ζ₁ in (5.2), except that χ varies from −0.2 to 0.6. The prices are estimated with 10⁶ paths of the risk process.

Not surprisingly, we observe that, ceteris paribus, the bond price decreases in any of the MPR parameters. The bond price is more sensitive to changes in the jump risk premium than to changes in the diffusion risk premium. In particular, the impact of the jump frequency is quite prominent; a moderate increase in the jump-frequency risk premium χ can cause a drastic drop in the bond price. For positive jump-frequency risk premium, the elasticity also decreases in χ, indicating that in the case of a higher jump frequency, the already highly distressed bond price reacts even more strongly to the same percentage change in the jump frequency.

6. Concluding remarks

We employ a bivariate AJD model to describe the joint dynamics of the interest rate and excess mortality and calibrate the model using the most up-to-date U.S. mortality and interest rate data. Our empirical results show that the COVID-19 pandemic experience greatly intensifies the negative instantaneous correlation between the interest rate and excess mortality. We remark that, on the one hand, the strong correlation is no suggestion of causality, but on the other hand, it is not likely coincidental either and indeed calls for a reassessment of the independence assumption widely used in the literature. Then we develop a risk-neutral pricing measure that accounts for both diffusion and jump risk premia, and solve for the market prices of risk with second-market indicative mortality bond prices. We argue that failure to recognize the pandemic risk could cost investors dearly, in the sense that they may receive negative mortality risk premium. In addition, based on some envisioned scenarios we show that the pandemic experience is likely to disconcert the mortality risk market.

During our research, weekly mortality data are available only for five years, which limits us from more in-depth analysis. Consequently, some simplifying assumptions are necessary for model calibration, such as the MPRs and the jump intensity being constant. Another limitation is that some of our conclusions about the post-pandemic market are conjectures that cannot be tested at this stage. Nonetheless, assuming that the mortality risk market continues to grow and timely mortality data of high frequency become more accessible, we expect to improve the calibration and test the conjectures in future research. Lastly, we introduce a three-week lag in the interest rate data to synchronize the first emergency rate cut by the Federal Reserve and the first observed surge in excess mortality at the onset of the COVID-19 pandemic in the U.S. Although in the current research such a synchronization can be done by visually inspecting the data, it is desired to incorporate a lag feature into a bivariate model and then establish a statistical procedure to identify the lag. We will investigate this problem in a future project using a rigorous jump detection algorithm.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests that could have appeared to influence the work reported in this paper.

Appendix A.

A.1. Connection with the World Bank pandemic bonds

It is interesting to notice that the insurance industry's innovation in extreme risk mitigation has recently been applied to disaster relief and post-event recovery by governments and international organizations. In 2017, drawing on lessons from the Ebola outbreak, the World Bank launched first-of-their-kind pandemic bonds to support a US$500 million pandemic emergency financing facility (PEF), which intends to help the world's poorest countries to fight against cross-border, large-scale pandemic outbreaks. At issuance, the bonds were oversubscribed by 200%, indicating a strong demand from investors and great potential for health organizations to transfer pandemic risk to the capital market. The bonds matured in July 2020 and, not surprisingly, were triggered by the COVID-19 outbreak. The PEF has received serious criticisms, mostly on its delayed payouts during the pandemic. Despite the World Bank's decision to scrap plans for a second issue of the pandemic bond, similar financial instruments will likely be developed in the future.

While mortality CAT bonds and pandemic bonds are essentially different financial instruments, we point out that our research on MLS sheds light on future pandemic bond pricing and design. First, the two types of bonds share similarities in triggering mechanisms, potential diversification benefits, and high coupon rates. Second, our results show that the COVID-19 experience can make a huge difference in the prices of mortality CAT bonds. Class A of the World Bank's pandemic bonds offered a fixed annual coupon of 6.5%, and Class B offered 11.1%, both notably higher than other fixed income securities traded in the financial market then. However, the investors' perception and appetite for future pandemic bonds are likely to change after this once-in-a-century pandemic and therefore future pandemic bond issuance should take into account the new information gathered during the COVID-19 pandemic. Third, taking a closer look at their respective stages of development, we anticipate a growth of the pandemic bond market. Issuers of future pandemic bonds may learn from the successful experience of mortality CAT bonds.

A.2. Proof of Proposition 2.1

From Remark 9.3 of Cont and Tankov (2004), we have

$$\frac{d{Z}_{1,t}}{Z_{1,t}}={\mathbf{\Gamma }}_t^{⊺}d{\mathbf{W}}_t,\frac{d{Z}_{2,t}}{Z_{2,t-}}=\sum _{i=1}^{m}d(-({\lambda }_i^{⁎}-{\lambda }_i)t+\sum _{k=1}^{N_{i,t}}(\frac{{\lambda }_i^{⁎}}{{\lambda }_i}{g}_i\left({\mathbf{X}}_{i,k}\right)-1)).$$

It follows that

$$\frac{d\left(Z_{1,t}{Z}_{2,t}\right)}{Z_{1,t-}{Z}_{2,t-}}={\mathbf{\Gamma }}_t^{⊺}d{\mathbf{W}}_t+\sum _{i=1}^{m}d(-({\lambda }_i^{⁎}-{\lambda }_i)t+\sum _{k=1}^{N_{i,t}}(\frac{{\lambda }_i^{⁎}}{{\lambda }_i}{g}_i\left({\mathbf{X}}_{i,k}\right)-1)),$$ (A.1)

which indicates that $Z_{1,t}{Z}_{2,t}$, $0\le t\le T$, is a martingale under P. Furthermore, we show that $Z_{1,t}{Z}_{2,t}{W}_{i,t}^Q$, $0\le t\le T$, is a martingale under P. For this purpose, we expand

$$d\left(Z_{1,t}{Z}_{2,t}{W}_{i,t}^Q\right)=W_{i,t}^{Q}d\left(Z_{1,t}{Z}_{2,t}\right)+Z_{1,t}{Z}_{2,t}d{W}_{i,t}^Q+d\left(Z_{1,t}{Z}_{2,t}\right)d{W}_{i,t}^Q.$$

Then plugging in (2.7) for $d{\mathbf{W}}_t^Q$ and (A.1) for $d\left(Z_{1,t}{Z}_{2,t}\right)$, after some simplification we obtain

$$d\left(Z_{1,t}{Z}_{2,t}{W}_{i,t}^Q\right)=W_{i,t}^{Q}d\left(Z_{1,t}{Z}_{2,t}\right)+Z_{1,t}{Z}_{2,t}d{W}_{i,t}.$$

Thus, $Z_{1,t}{Z}_{2,t}{W}_{i,t}^Q$, $0\le t\le T$, is a martingale under P as claimed.

Now we are ready to verify that ${\{{\mathbf{W}}_t^Q\}}_{0\le t\le T}$ is a standard bivariate Brownian motion under Q. For any $0\le s\le t\le T$,

$$E^Q\left[W_{i,t}^Q|{\mathcal{F}}_s\right]=\frac{1}{Z_{1,s}{Z}_{2,s}}E\left[W_{i,t}^Q{Z}_{1,t}{Z}_{2,t}|{\mathcal{F}}_s\right]=\frac{1}{Z_{1,s}{Z}_{2,s}}{W}_{i,s}^Q{Z}_{1,s}{Z}_{2,s}=W_{i,s}^Q,$$

where the first step applies Lemma 5.2.2 of Shreve (2004) and the second step is due to the martingale property of $Z_{1,t}{Z}_{2,t}{W}_{i,t}^Q$, $0\le t\le T$, under P. Thus, ${\{W_{i,t}^Q\}}_{0\le t\le T}$ is a martingale under Q. Moreover, it has continuous paths, the starting point $W_{i,0}^Q=0$, and the quadratic variation/covariation

$$[W_i^Q,W_j^Q](t)=\{\begin{array}{cc}t,\hfill & \text{if }i=j\text{,}\hfill \\ 0,\hfill & \text{if }i\ne j\text{.}\hfill \end{array}$$

By Lévy's theorem, ${\{{\mathbf{W}}_t^Q\}}_{0\le t\le T}$ is a standard bivariate Brownian motion under Q, as claimed.

Denote by ${\mathcal{H}}_{i,t}$ the sigma field generated by ${\{{\mathbf{J}}_{i,s}\}}_{0\le s\le t}$ for each $i=1,\dots ,m$ and $0\le t\le T$, and let

$$Z_{2,i,t}=e^{-({\lambda }_i^{⁎}-{\lambda }_i)t}\prod _{k=1}^{N_{i,t}}\left(\frac{{\lambda }_i^{⁎}}{{\lambda }_i}{g}_i\left({\mathbf{X}}_{i,k}\right)\right),0\le t\le T.$$

For any ${\mathcal{H}}_{i,T}$ measurable random variable $V_i$ and any bounded measurable function $h_i$, $i=1,\dots ,m$, we have

$$E^Q[\prod _{i=1}^m{h}_i(V_i)]=E[Z_{1,T}{Z}_{2,T}\prod _{i=1}^m{h}_i(V_i)]=E[Z_{2,T}\prod _{i=1}^m{h}_i(V_i)E[Z_{1,T}|{\mathcal{H}}_{1,T}\vee \cdots \vee {\mathcal{H}}_{m,T}]]=E[Z_{2,T}\prod _{i=1}^m{h}_i(V_i)]=\prod _{i=1}^{m}E[Z_{2,i,T}{h}_i(V_i)].$$

This shows that the random variables $V_i$, $i=1,\dots ,m$, are mutually independent under Q, and so are ${\{{\mathbf{J}}_{i,t}\}}_{0\le t\le T}$, $i=1,\dots ,m$, under Q. Moreover, for each $i=1,\dots ,m$, any ${\mathcal{H}}_{i,T}$ measurable random variable follows a probability law under Q that is distorted by the simplified Radon–Nikodym derivative $Z_{2,i,T}$. Following the proof of Proposition 9.6 of Cont and Tankov (2004), we can show that, under Q, each ${\{{\mathbf{J}}_{i,t}\}}_{0\le t\le T}$ is a compound Poisson process with intensity ${\lambda }_i^{⁎}$ and common jump-size distribution $G_i^{⁎}$ for $i=1,\dots ,m$.

The rest of the proof follows directly by Corollary 11.5.3 of Shreve (2004).

A.3. The price of a risk-free zero-coupon bond

Recall the dynamics of the interest rate process given in (2.11) under Q and the distorted distribution function $G^{⁎}$ in Example 2.1. The risk-free zero-coupon bond price is given by

$$P(t,T)=E^Q\left[\exp (-\underset{t}{\overset{T}{\int }}{r}_{s}ds)|{\mathcal{F}}_t^1\right]=e^{\alpha (t)+\beta (t)r_t},$$

where α and β satisfy the ODEs

$$0={\alpha }^{\prime }(t)+m_1^{⁎}\beta (t)+\frac{1}{2}{\sigma }_1^2{\beta }^2(t)+{\lambda }^{⁎}(\underset{\mathbb{R}}{\int }{e}^{\beta (t)z}\frac{1}{\sqrt{2\pi }{\varphi }_1}{e}^{-\frac{{(z-{\nu }_1^{⁎})}^2}{2{\varphi }_1^2}}dz-1),0=-1+{\beta }^{\prime }(t)-d_1\beta (t),$$

with boundary conditions $\alpha (T)=0$ and $\beta (T)=0$. Then

$$\alpha (t)=-\frac{m_1^{⁎}}{d_1}(T-t-\frac{1-e^{-d_1(T-t)}}{d_1})+\frac{{\sigma }_1^2}{2d_1^2}(T-t-\frac{2(1-e^{-d_1(T-t)})}{d_1}+\frac{1-e^{-2d_1(T-t)}}{2d_1})+{\lambda }^{⁎}\underset{t}{\overset{T}{\int }}(e^{{\nu }_1^{⁎}\beta (s)+\frac{1}{2}{\varphi }_1^2{\beta }^2(s)}-1)ds,\beta (t)=-\frac{1-e^{-d_1(T-t)}}{d_1}.$$

The last integral term in $\alpha (t)$ can further be explicitized as

$$\underset{t}{\overset{T}{\int }}(e^{{\nu }_1^{⁎}\beta (s)+\frac{1}{2}{\varphi }_1^2{\beta }^2(s)}-1)ds=\underset{t}{\overset{T}{\int }}\exp \{-{\nu }_1^{⁎}\frac{1-e^{-d_1(T-s)}}{d_1}+\frac{1}{2}\frac{{\varphi }_1^2{(1-e^{-d_1(T-s)})}^2}{d_1^2}\}ds-(T-t)=\underset{0}{\overset{T-t}{\int }}\exp \{-{\nu }_1^{⁎}\frac{1-e^{-d_{1}w}}{d_1}+\frac{1}{2}\frac{{\varphi }_1^2{(1-e^{-d_{1}w})}^2}{d_1^2}\}dw-(T-t).$$

A.4. Preliminaries for univariate (integrated) Ornstein–Uhlenbeck processes with jumps

In view of the pricing formula (3.1), our numerical procedure requires sampling of the excess mortality, the interest rate, and its integration. To prepare for our sampling algorithm, to be detailed in Subsection A.5, we first provide some preliminary results for univariate (integrated) Ornstein–Uhlenbeck (OU) processes with jumps.

Consider a general OU process ${\{x_t\}}_{0\le t\le T}$ with jumps that evolves according to

$$d{x}_t=a(b-x_t)dt+\sigma d{W}_t+d\sum _{i=1}^{N_t}{\xi }_i,$$

where $a\ne 0$, $b\in \mathbb{R}$, and $\sigma >0$ are constants, ${\{W_t\}}_{0\le t\le T}$ is a standard Brownian motion, ${\{N_t\}}_{0\le t\le T}$ is a homogeneous Poisson process, and ${\{{\xi }_i\}}_{j\in \mathbb{N}}$ is a sequence of i.i.d. normal random variables independent of ${\{N_t\}}_{0\le t\le T}$. Its solution is given by

$$x_t=x_0{e}^{-at}+b(1-e^{-at})+\sigma e^{-at}\underset{0}{\overset{t}{\int }}{e}^{as}d{W}_s+e^{-at}\sum _{i=1}^{N_t}{\xi }_i{e}^{a{\tau }_i},$$

where ${\tau }_i$ is the occurrence time of the ith jump. To derive the exact sampling algorithm for the underlying risk processes, we need the conditional distributions of $x_t$ and ${\int }_0^t{x}_{s}ds$ given the filtration generated by ${\left\{N_s\right\}}_{0\le s\le t}$, $0\le t\le T$.

Obviously, at time t, conditional on ${\left\{N_s\right\}}_{0\le s\le t}$, the random variable $x_t$ as the sum of two independent normal random variables is normally distributed. For ${\int }_0^t{x}_{s}ds$, note that it can be written as

$$\sigma \underset{s=0}{\overset{t}{\int }}\underset{u=0}{\overset{s}{\int }}{e}^{-as}{e}^{au}d{W}_{u}ds+\underset{0}{\overset{t}{\int }}{e}^{-as}\sum _{i=1}^{N_s}{\xi }_i{e}^{a{\tau }_i}ds+\underset{0}{\overset{t}{\int }}(x_0{e}^{-as}+b(1-e^{-as}))ds=I_1+I_2+I_3.$$

The term $I_3$ is deterministic. For $I_1$, note that

$$I_1=\sigma \underset{u=0}{\overset{t}{\int }}{e}^{au}\underset{s=u}{\overset{t}{\int }}{e}^{-as}dsd{W}_u=\sigma \underset{u=0}{\overset{t}{\int }}{e}^{au}\frac{(e^{-au}-e^{-at})}{a}d{W}_u=\frac{\sigma }{a}\underset{u=0}{\overset{t}{\int }}(1-e^{-a(t-u)})d{W}_u=\frac{1}{a}(\sigma W_t-\sigma e^{-at}\underset{0}{\overset{t}{\int }}{e}^{as}d{W}_s),$$ (A.2)

where in the first step we applied Theorem IV.64 of Protter (2005). For $I_2$, let $J_{\xi }$ be the jump measure of the compound Poisson process ${\left\{{\sum }_{i=1}^{N_t}{\xi }_i\right\}}_{0\le t\le T}$. We have

$$I_2=\underset{s=0}{\overset{t}{\int }}{e}^{-as}\underset{(u,x)\in (0,s]\times \mathbb{R}}{\int }x{e}^{au}{J}_{\xi }(du,dx)ds=\underset{(u,x)\in [0,t]\times \mathbb{R}}{\int }x{e}^{au}\underset{s=u}{\overset{t}{\int }}{e}^{-as}ds{J}_{\xi }(du,dx)=\frac{1}{a}\underset{(u,x)\in [0,t]\times \mathbb{R}}{\int }x{e}^{au}(e^{-au}-e^{-at})J_{\xi }(du,dx)=\frac{1}{a}\underset{(u,x)\in [0,t]\times \mathbb{R}}{\int }x-x{e}^{-a(t-u)}{J}_{\xi }(du,dx)=\frac{1}{a}(\sum _{i=1}^{N_t}{\xi }_i-e^{-at}\sum _{i=1}^{N_t}{\xi }_i{e}^{a{\tau }_i}),$$ (A.3)

where the second step is due to Fubini's theorem. Thus, given the number of jumps by time t and the times of the jump occurrences, the terms $I_1$ and $I_2$ are independent and normally distributed. This enables us to derive the exact sampling algorithm below.

A.5. Details of the sampling algorithm

To numerically evaluate the pricing formula (3.1), we need to sample ${\left\{(r_t,{\mu }_t,R_t)\right\}}_{0\le t\le T}$ under the Q measure, where $R_t={\int }_0^t{r}_{s}ds$. Recall the dynamics (2.11) and the distorted distribution function $G^{⁎}$ in Example 2.1:

$$d{r}_t=(m_1^{⁎}-d_1{r}_t)dt+{\sigma }_{1}d{W}_{1,t}^Q+d\sum _{i=1}^{N_t}{X}_{1,i},d{\mu }_t=(m_2^{⁎}-d_2{\mu }_t)dt+{\sigma }_2({\rho }_{1}d{W}_{1,t}^Q+\sqrt{1-{\rho }_1^2}d{W}_{2,t}^Q)+d\sum _{i=1}^{N_t}{X}_{2,i}.$$

The two SDEs and equations (A.2) and (A.3) lead to

$$r_t=r_0{e}^{-d_{1}t}+\frac{m_1^{⁎}}{d_1}(1-e^{-d_{1}t})+{\sigma }_1\underset{0}{\overset{t}{\int }}{e}^{-d_1(t-s)}d{\tilde{W}}_{1,s}^Q+\sum _{i=1}^{N_t}{X}_{1,i}{e}^{-d_1(t-{\tau }_i)},$$ (A.4)

$${\mu }_t={\mu }_0{e}^{-d_{2}t}+\frac{m_2^{⁎}}{d_2}(1-e^{-d_{2}t})+{\sigma }_2\underset{0}{\overset{t}{\int }}{e}^{-d_2(t-s)}d{\tilde{W}}_{2,s}^Q+\sum _{i=1}^{N_t}{X}_{2,i}{e}^{-d_2(t-{\tau }_i)},$$ (A.5)

$$R_t=\underset{0}{\overset{t}{\int }}(r_0{e}^{-d_{1}s}+\frac{m_1^{⁎}}{d_1}(1-e^{-d_{1}s}))ds+\frac{{\sigma }_1}{d_1}({\tilde{W}}_{1,t}^Q-\underset{0}{\overset{t}{\int }}{e}^{-d_1(t-s)}d{\tilde{W}}_{1,s}^Q)+\frac{1}{d_1}(\sum _{i=1}^{N_t}{X}_{1,i}-\sum _{i=1}^{N_t}{X}_{1,i}{e}^{-d_1(t-{\tau }_i)}),$$ (A.6)

where

$${\tilde{W}}_{1,t}^Q=W_{1,t}^Q\text{and}{\tilde{W}}_{2,t}^Q={\rho }_1{W}_{1,t}^Q+\sqrt{1-{\rho }_1^2}{W}_{2,t}^Q.$$

Note that, under Q, ${\{{\tilde{W}}_{1,t}^Q\}}_{0\le t\le T}$ and ${\{{\tilde{W}}_{2,t}^Q\}}_{0\le t\le T}$ are two standard Brownian motions satisfying $d{\tilde{W}}_{1,t}^{Q}d{\tilde{W}}_{2,t}^Q={\rho }_{1}dt$, and $(X_{1,i},X_{2,i})$, $i\in \mathbb{N}$, are i.i.d. copies of a generic bivariate normal random vector $(X_1,X_2)\sim N({\nu }_1^{⁎},{\nu }_2^{⁎};{\varphi }_1,{\varphi }_2;{\rho }_2)$.

Suppose that, at time $0\le t<T$, we need to sample in a vectorized way n paths of the processes at, say, m sampling dates $t_1$, …, $t_m$, where $t=t_0<t_1<\cdots <t_m=T$. We obtain the samples in m steps, and in step j, $j=1,\dots ,m$, we use the evolution of the processes over $(t_{j-1},t_j]$ to sample their time $t_j$ values based on their time $t_{j-1}$ values. Specifically, in step j, we first sample the number of jumps and their occurrence times over $(t_{j-1},t_j]$, and then sample from the conditional distribution of $(r_{t_j},{\mu }_{t_j},R_{t_j})$ given the value of $(r_{t_{j-1}},{\mu }_{t_{j-1}},R_{t_{j-1}})$ and the filtration generated by ${\left\{N_s\right\}}_{t_{j-1}<s\le t_j}$.

Consider the jth step and write ${\mathrm{\Delta }}_j=t_j-t_{j-1}$. To sample the diffusion terms in (A.4)–(A.6) over $(t_{j-1},t_j]$, note that

$${\mathrm{var}}^Q\left[{\sigma }_i\underset{t_{j-1}}{\overset{t_j}{\int }}{e}^{-d_i(t_j-s)}d{\tilde{W}}_{i,s}^Q\right]={\sigma }_i^2{e}^{-2d_i{t}_j}\underset{t_{j-1}}{\overset{t_j}{\int }}{e}^{2d_{i}s}ds=\frac{{\sigma }_i^2(1-e^{-2d_i{\mathrm{\Delta }}_j})}{2d_i},i=1,2.$$

Moreover, for $i=1,2$,

$${\mathrm{cov}}^Q[{\sigma }_1({\tilde{W}}_{1,t_j}^Q-{\tilde{W}}_{1,t_{j-1}}^Q),{\sigma }_i\underset{t_{j-1}}{\overset{t_j}{\int }}{e}^{-d_i(t_j-s)}d{\tilde{W}}_{i,s}^Q]={\sigma }_1{\sigma }_i{e}^{-d_i{t}_j}{\mathrm{cov}}^Q[\underset{t_{j-1}}{\overset{t_j}{\int }}d{\tilde{W}}_{1,s}^Q,\underset{t_{j-1}}{\overset{t_j}{\int }}{e}^{d_{i}s}d{\tilde{W}}_{i,s}^Q]={\sigma }_1{\sigma }_i{e}^{-d_i{t}_j}\underset{t_{j-1}}{\overset{t_j}{\int }}{e}^{d_{i}s}dt(1_{(i=1)}+{\rho }_1{1}_{(i=2)})=\frac{{\sigma }_1{\sigma }_i(1-e^{-d_i{\mathrm{\Delta }}_j})}{d_i}(1_{(i=1)}+{\rho }_1{1}_{(i=2)}),$$

and, similarly,

$${\mathrm{cov}}^Q[{\sigma }_1\underset{t_{j-1}}{\overset{t_j}{\int }}{e}^{-d_1(t_j-s)}d{\tilde{W}}_{1,s}^Q,{\sigma }_2\underset{t_{j-1}}{\overset{t_j}{\int }}{e}^{-d_2(t_j-s)}d{\tilde{W}}_{2,s}^Q]=\frac{{\rho }_1{\sigma }_1{\sigma }_2(1-e^{-(d_1+d_2){\mathrm{\Delta }}_j})}{d_1+d_2}.$$

Let ${\left\{({\mathbf{r}}_s,{\mathit{\mu }}_s,{\mathbf{R}}_s)\right\}}_{t\le s\le T}$ denote n paths of the process ${\left\{(r_s,{\mu }_s,R_s)\right\}}_{t\le s\le T}$ and note again that we aim to sample the n paths in a vectorized way. We are now ready to present our sampling algorithm as follows:

• 1.Set $j=1$.
• 2.Sample a vector of n Poisson random variables with mean ${\lambda }^{⁎}{\mathrm{\Delta }}_j$, which we denote by $(K_1,\dots ,K_n)$. Here $K_i$ represents the number of jumps over $(t_{j-1},t_j]$ that occurred on the ith path. Suppose that ${\sum }_{i=1}^n{K}_i=n_J$.
• 3.Sample an $n_J$ dimensional vector of independent uniform random variables taking values in $(0,{\mathrm{\Delta }}_j)$, which we denote by $(U_1,\dots ,U_{n_J})$. The components of $(t_j-U_1,\dots ,t_j-U_{n_J})$ constitute a permutation of the occurrence times of the $n_J$ jumps in step 2.
• 4.Sample $n_J$ i.i.d. copies of the generic pair $(X_1,X_2)$, which we denote by $(X_{1,1},X_{2,1}),\dots$, $(X_{1,n_J},X_{2,n_J})$.
• 5.
  Compute the values of the following three n dimensional vectors:

  $${\mathbf{J}}^r=(\sum _{i=1}^{K_1}{X}_{1,i}{e}^{-d_1{U}_i},\sum _{i=K_1+1}^{K_1+K_2}{X}_{1,i}{e}^{-d_1{U}_i},\dots ,\sum _{i=n_J-K_n+1}^{n_J}{X}_{1,i}{e}^{-d_1{U}_i}),{\mathbf{J}}^R=(\sum _{i=1}^{K_1}{X}_{1,i},\sum _{i=K_1+1}^{K_1+K_2}{X}_{1,i},\dots ,\sum _{i=n_J-K_n+1}^{n_J}{X}_{1,i}),{\mathbf{J}}^{\mu }=(\sum _{i=1}^{K_1}{X}_{2,i}{e}^{-d_2{U}_i},\sum _{i=K_1+1}^{K_1+K_2}{X}_{2,i}{e}^{-d_2{U}_i},\dots ,\sum _{i=n_J-K_n+1}^{n_J}{X}_{2,i}{e}^{-d_2{U}_i}).$$
• 6.
  Draw a sample of size n from a 3 dimensional normal random vector that has a zero mean and a covariance matrix with upper triangular matrix

  $$\left(\begin{array}{ccc}\hfill \frac{{\sigma }_1^2(1-e^{-2d_1{\mathrm{\Delta }}_j})}{2d_1}\hfill & \hfill \frac{{\rho }_1{\sigma }_1{\sigma }_2(1-e^{-(d_1+d_2){\mathrm{\Delta }}_j})}{d_1+d_2}\hfill & \hfill \frac{{\sigma }_1^2(1-e^{-d_1{\mathrm{\Delta }}_j})}{d_1}\hfill \\ \hfill \hfill & \hfill \frac{{\sigma }_2^2(1-e^{-2d_2{\mathrm{\Delta }}_j})}{2d_2}\hfill & \hfill \frac{{\rho }_1{\sigma }_1{\sigma }_2(1-e^{-d_2{\mathrm{\Delta }}_j})}{d_2}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill {\sigma }_1^2{\mathrm{\Delta }}_j\hfill \end{array}\right).$$

  Let ${\mathbf{Z}}^r$, ${\mathbf{Z}}^{\mu }$, and ${\mathbf{Z}}^R$ be the vectors consisting of the components in, respectively, the first, second, and third dimensions of the samples.
• 7.
  Let

  $${\mathbf{r}}_{t_j}={\mathbf{r}}_{t_{j-1}}{e}^{-d_1{\mathrm{\Delta }}_j}+\frac{m_1^{⁎}}{d_1}(1-e^{-d_1{\mathrm{\Delta }}_j})\mathbf{1}+{\mathbf{Z}}^r+{\mathbf{J}}^r,{\mathit{\mu }}_{t_j}={\mathit{\mu }}_{t_{j-1}}{e}^{-d_2{\mathrm{\Delta }}_j}+\frac{m_2^{⁎}}{d_2}(1-e^{-d_2{\mathrm{\Delta }}_j})\mathbf{1}+{\mathbf{Z}}^{\mu }+{\mathbf{J}}^{\mu },{\mathbf{R}}_{t_j}={\mathbf{R}}_{t_{j-1}}+\underset{t_{j-1}}{\overset{t_j}{\int }}(r_0{e}^{-d_{1}s}+\frac{m_1^{⁎}}{d_1}(1-e^{-d_{1}s}))ds\mathbf{1}+\frac{{\mathbf{Z}}^R-{\mathbf{Z}}^r}{d_1}+\frac{{\mathbf{J}}^R-{\mathbf{J}}^r}{d_1},$$

  where 1 denotes an n dimensional vector with all components being 1.
• 8.Repeat steps 2–7 of the procedure for the time intervals $(t_j,t_{j+1}]$, …, $(t_{m-1},T]$.

Data availability

Data will be made available on request.