Predictable Fluctuations in Excitatory Synaptic Strength Due to Natural Variation in Presynaptic Firing Rate

Abstract

Many controlled in vitro studies have demonstrated how postsynaptic responses to presynaptic spikes are not constant but depend on short-term synaptic plasticity (STP) and the detailed timing of presynaptic spikes. However, the effects of short-term plasticity (depression and facilitation) are not limited to short, subsecond timescales. The effects of STP appear on long timescales as changes in presynaptic firing rates lead to changes in steady-state synaptic transmission. Here, we examine the relationship between natural variations in the presynaptic firing rates and spike transmission in vivo. Using large-scale spike recordings in awake male and female mice from the Allen Institute Neuropixels dataset, we first detect putative excitatory synaptic connections based on cross-correlations between the spike trains of millions of pairs of neurons. For the subset of pairs where a transient, excitatory effect was detected, we use a model-based approach to track fluctuations in synaptic efficacy and find that efficacy varies substantially on slow (∼1 min) timescales over the course of these recordings. For many connections, the efficacy fluctuations are correlated with fluctuations in the presynaptic firing rate. To understand the potential mechanisms underlying this relationship, we then model the detailed probability of postsynaptic spiking on a millisecond timescale, including both slow changes in postsynaptic excitability and monosynaptic inputs with short-term plasticity. The detailed model reproduces the slow efficacy fluctuations observed with many putative excitatory connections, suggesting that these fluctuations can be both directly predicted based on the time-varying presynaptic firing rate and, at least partly, explained by the cumulative effects of STP.

SIGNIFICANCE STATEMENT The firing rates of individual neurons naturally vary because of stimuli, movement, and brain state. Models of synaptic transmission predict that these variations in firing rates should be accompanied by slow fluctuations in synaptic strength because of short-term depression and facilitation. Here, we characterize the magnitude and predictability of fluctuations in synaptic strength in vivo using large-scale spike recordings. For putative excitatory connections from a wide range of brain areas, we find that typical synaptic efficacy varies as much as ∼70%, and in many cases the fluctuations are well described by models of short-term synaptic plasticity. These results highlight the dynamic nature of in vivo synaptic transmission and the interplay between synaptic strength and firing rates in awake animals.

Introduction

The firing activity of individual neurons can vary over time because of external stimuli (Hubel and Wiesel, 1959), the behavior of the animal (Churchland et al., 2012; Shenoy et al., 2013), and the internal state of the network (Poulet and Petersen, 2008; McGinley et al., 2015). Although many statistical models assume that coupling between neurons has a fixed strength (Harris et al., 2003; Truccolo et al., 2005; Pillow et al., 2008), firing rate variation can directly affect synaptic strength because of short-term synaptic plasticity (STP). For instance, synapses with short-term depression should be weaker when presynaptic firing rates are higher and stronger when the rates are lower. On the other hand, synapses with short-term facilitation should be stronger when presynaptic firing rates are higher and weaker when the rates are lower. In many studies, STP is induced in vitro by modifying the presynaptic firing rate using external electrical stimulation at different frequencies (Abbott et al., 1997; Tsodyks and Markram, 1997; Fortune and Rose, 2001; Chung et al., 2002; Zucker and Regehr, 2002). These studies illustrate how STP can act to high pass or low pass filter the inputs of neurons and could potentially underlie working memory and decision-making processes (Deng and Klyachko, 2011).

One prediction from these in vitro studies of STP using simple, controlled stimuli is that synaptic strengths should also vary in response to the natural changes in firing rate that occur in vivo. Indeed, slice studies have shown that for neurons receiving naturalistic spike trains as input, synaptic strength varies substantially over time, with patterns matching those predicted by STP (Klyachko and Stevens, 2006; Kandaswamy et al., 2010; Costa et al., 2013). Studies in awake animals have also shown that postsynaptic responses to presynaptic spikes vary depending on the preceding presynaptic interspike intervals (ISIs; Swadlow and Gusev, 2001; Stoelzel et al., 2008, 2009; English et al., 2017) and presynaptic firing rates (Fujisawa et al., 2008; Stoelzel et al., 2015; McKenzie et al., 2021). Together, these findings suggest a general conclusion that the natural variation in presynaptic firing rates in vivo may be accompanied by large fluctuations in synaptic strength and that these changes may be because of the effects of STP on longer timescales.

Quantifying synaptic strength in vivo is a difficult statistical problem. Many studies of synaptic transmission have used intracellular recordings to study the dynamics in individual postsynaptic potentials or currents (Pala and Petersen, 2015, 2018; Sedigh-Sarvestani et al., 2017). Long-term extracellular spike recordings may allow us to track slow fluctuations more easily in vivo. Unlike intracellular signals that contain postsynaptic responses to single presynaptic spikes, extracellular spikes are sparse binary events, and studies of synapses often rely on the cross-correlograms (CCGs) between the presynaptic and postsynaptic spike trains. If two neurons are connected with an excitatory synapse, there is often a fast-onset, short-latency peak in the CCG (Perkel et al., 1967; Fetz et al., 1991), and several techniques have been developed to automatically detect these connected pairs (Barthó et al., 2004; Amarasingham et al., 2012; Kobayashi et al., 2019; Ren et al., 2020).

Synaptic transmission with spikes is often measured by synaptic efficacy using the CCG, which is defined as the excess probability of postsynaptic spiking in the short transmission window following presynaptic spikes (Levick et al., 1972). By focusing on specific presynaptic spike patterns, such as pairs with specific ISIs, previous studies have shown how synaptic efficacy can vary depending on features of presynaptic spike timing (Usrey et al., 2000; Swadlow and Gusev, 2001; English et al., 2017). Modeling individual spike transmission probabilities for the entire spike train can also reveal how presynaptic spike features, as well as different types of plasticity, interact (Ghanbari et al., 2017, 2020; Song et al., 2018; Wei and Stevenson, 2021). Together, descriptive and model-based approaches can track synaptic dynamics in vivo (Swadlow and Gusev, 2001; English et al., 2017; Ghanbari et al., 2017, 2020) and reveal changes associated with learning, behavior, or stimuli (Fujisawa et al., 2008; Ghanbari et al., 2020; McKenzie et al., 2021). Here, we focus on a general description of the ongoing changes in synaptic strength that may be merely because of changes in presynaptic rate. We divide long-term spike recordings into windows to measure the fluctuations in synaptic efficacy on a timescale of minutes and model the changes as a function of presynaptic ISI to build the potential link between these slow changes and STP.

Using in vivo large-scale spike recordings from the Allen Institute Neuropixels dataset (Siegle et al., 2021), we examine natural fluctuations in synaptic efficacy and firing rates and quantify the relationships between them. These recordings from awake, behaving mice contain the spiking of hundreds of neurons from many brain regions while the mice view natural and artificial visual stimuli (Siegle et al., 2021). Because neurons in different brain regions have different firing rates and firing regularity (Mochizuki et al., 2016), we also examine whether putative synapses from different regions show different patterns of efficacy fluctuations. We find that for individual connections the synaptic efficacy often varies substantially over the course of the recording. Interestingly, the efficacy is often correlated with the presynaptic firing rate, with the postsynaptic firing rate, or with both. We then test whether the time-varying efficacy is predictable based on the presynaptic firing. We model the time-varying synaptic effect as a function of presynaptic ISI by fitting a generalized bilinear model (GBLM) to the postsynaptic spike trains. For many connections, the GBLM reproduces the observed efficacy fluctuations, suggesting that these fluctuations can be, at least partly, explained by a cumulative effect of STP. Altogether, these results illustrate how natural fluctuations in firing rate could lead to large, but predictable, changes in synaptic strength in vivo and in many different brain areas.

Materials and Methods

We use the Visual Coding–Neuropixels dataset from the Allen Institute (https://portal.brain-map.org/explore/circuits). During the recordings, head-fixed mice viewed a standardized set of visual stimuli (including Gabor patches, full-field drifting gratings, moving dots, and natural images and movies) while they were free to run on a wheel. We analyze 20 recordings here (electrophysiology sessions 715093703–746083955 and 819186360–847657808), 6 from female mice (125 ± 11.6 d), 14 from male mice (117.8 ± 8.3 d). Nine recordings were from wild-type mice, and the remainder were transgenic Cre lines expressing channelrhodopsin in inhibitory interneuron subtypes (Sst-IRES-Cre; Ai32, Pvalb-IRES-Cre; Ai32 and Vip-IRES-Cre; Ai32). Each recording lasts ∼2.5 h and contains 365–893 well-isolated single units from five or six Neuropixels probes from mouse visual cortex, thalamus, and hippocampus. In 10 recordings, the mice had a resting period that lasted for ∼30 min. This period is referred to as spontaneous activity period for further analysis. Additional information about this dataset can be found in Siegle et al. (2021).

Detection of putative excitatory synaptic connections

We detect putative synaptic connections using the CCGs between pairs of neurons—a source neuron (presynaptic) $i$ and target neuron (postsynaptic) $j$. For the binned spike trains of the two neurons, $n_i$ and $n_j$ (1 when there is a spike and 0 otherwise), the CCG is given by $y_{ij}(m)={\displaystyle {\sum }_t{n}_i(t)n_j(t-m)}$, where $m$ denotes the interval between presynaptic and postsynaptic spikes, and $y_{ij}\left(m\right)$ is the number of the times spikes in $n_i$ and $n_j$ that are separated by an interval $[m-\frac{\Delta t_{bin}}{2},m+\frac{\Delta t_{bin}}{2}]$ for bin size $\Delta t_{bin}$ (1 ms used here).

Given the CCG, we detect putative excitatory synapses in two stages. First, we use a hypothesis test based on the jittered spikes to detect fast changes in the CCG, and then we use a model-based approach to estimate and screen for putative synaptic effects at specific latencies and timescales. Our initial screening of neuron pairs is based on comparing the observed CCG to a null model of the CCG generated using jittered spike times. An exact null distribution can be approximated by directly sampling jittered spike trains. However, here, for computational convenience, we approximate the null distribution using the simplifying assumption that the counts in each bin of the CCG $y_{ij}\left(m\right)$ are independent of each other (Amarasingham et al., 2012). We assume that $y_{ij}\left(m\right)\sim Binomial\left({\mathit{\text{num}}}_{pre},\mu (m)/{\mathit{\text{num}}}_{pre}\right),$ where ${\mathit{\text{num}}}_{pre}$ is the total number of presynaptic spikes and $\mu \left(m\right)=(y_{ij}*f)(m)$, the convolution of the CCG with a jitter function. We use a 10 ms uniform jitter $f\left(t\right)=1$ for $|t|<5ms$, $0$ otherwise. We then compute p values for each bin of the CCG using the cumulative distribution function of the binomial distribution and evaluate statistical significance correcting for multiple comparisons by controlling the false discovery rate using a Benjamini–Hochberg procedure ($\alpha =0.00001$). We then identify pairs of neurons where two criteria are satisfied, (1) there are two neighboring statistically significant bins in the CCG (where m > 0) and (2) the center bin ($m=0$) is not statistically significant. This test yields 0.5% of pairs of neurons that have fast, transient changes in their CCGs.

For each pair of neurons that satisfies the testing criteria we then fit a parametric model that aims to estimate the latency, timescale, and strength of a putative synaptic effect. We fit an extended GLM based on the model used in Ren et al. (2020). Briefly, we describe the CCG using two components, (1) a slow fluctuation because of background fluctuations and (2) a fast, transient effect because of the synaptic effect. The rate of spike counts λ at bin $m$ in a CCG is given by the following:

$$\lambda (m)=\exp \left(s{X}_s\left(m\right)+w\alpha (m,\tau ,\Delta t)\right).$$

Here, $s{X}_s$ describes the slow fluctuation, where $X_s$ represents a set of smooth basis functions learned by applying a low-rank, nonlinear matrix factorization to all the cross-correlograms in the dataset (Ren et al., 2020); and $w\alpha \left(m,\tau ,\Delta t\right)$ represents the fast synaptic effect, where $w$ is the synaptic strength and $\alpha (m,\tau ,\Delta t)$ is an alpha function with a time constant $\tau$ and a latency $\Delta t$ that is then convolved with the autocorrelogram of the presynaptic neuron to account for possible bursting in the neuron. After fitting the parameters $\{s,w,\tau ,\Delta t\}$ using a penalized maximum likelihood method, we select the neuron pairs where the CCG has a strong sharp peak ($w>0.3,\tau <0.8ms$) with a short latency ($\Delta t<10$ ms) and a relatively flat slow fluctuation (the coefficient of variation of the slow fluctuation < 0.15). In the end, we detect 1383 putative excitatory connections (∼0.17% of all pairs of neurons). This screening procedure returns a set of neuron pairs whose CCGs are consistent with the biophysics of excitatory synaptic transmission, which we then characterize in more detail.

Estimating time-varying synaptic efficacy

Synaptic efficacy reflects the (excess) probability of observing a postsynaptic spike following a presynaptic spike. Here, we estimate synaptic efficacy using the model-based approach described in the previous section. Namely, we calculate the efficacy by comparing the model with and without the synaptic effect as follows:

$$\text{eff}={\displaystyle {\sum }_m(\lambda (m)-{\lambda }_{slow}(m))/{\mathit{num}}_{pre}},$$

where ${\lambda }_{slow}$ is $\lambda$ evaluated with $\theta =\{s,w=0\}$ and ${\mathit{num}}_{pre}$ is the number of presynaptic spikes. To estimate changes in observed efficacy over time, we divide the presynaptic and postsynaptic spike trains into 5 min windows with 80% overlap and estimate efficacy for each window. We fit the cross-correlogram for each window using the extended GLM with a fixed alpha function $\alpha (m,\widehat{\tau },\widehat{\Delta t})$, where $\widehat{\tau }$ and $\widehat{\Delta t}$ are the estimated parameters from the overall cross-correlogram of the connection. We calculate the coefficient of variation (CV; the ratio of the SD to the mean) for time-varying efficacy to measure the fluctuation.

For comparison, we also shuffle the postsynaptic spike timings to create surrogate data and then calculate the fluctuations in efficacy that would be expected by chance. With this shuffling, the overall average efficacy is preserved, but any fluctuations in the efficacy over long time periods should be because of chance. To do this shuffling, we find all pairs of presynaptic and postsynaptic spikes with an interval of (0, 25] ms. Then for each presynaptic spike in this subset of spike pairs, we resample the subsequent postsynaptic spikes. Any postsynaptic spikes that do not occur following a presynaptic spike within the interval are not changed. This way the postsynaptic spikes following each presynaptic spike in the CCG are shuffled across time, and any systematic, slow changes in the CCG are removed. For each putative synapse, we do the shuffling 100 times to generate 100 surrogate time-varying efficacies. We can then create a surrogate distribution of the CV for efficacy and calculate a z score for the observed CV to measure how far away it is from the surrogate distribution. In addition, to examine the relationship between the time-varying efficacy and presynaptic firing rate, we calculate Spearman's correlation coefficient, and then similarly calculate a z score for the observed correlation using the surrogate data.

Estimating synaptic efficacy with different presynaptic ISI ranges

To further examine the relationship between efficacy and the presynaptic firing, we also estimate the efficacy for presynaptic spikes with different ISIs. Here, we group the presynaptic spikes by the ISI range their preceding spike fell within and calculate a separate CCG for each subset of presynaptic spikes. We then estimate the efficacy using the extended GLM for each separate ISI range.

Modeling short-term synaptic plasticity with spike train observations

In addition to quantifying the observed efficacy from noisy correlograms, we also aim to assess to what extent changes in efficacy can be explained by STP. Here, we model the time-varying synaptic effect as a function of presynaptic ISI by fitting a GBLM to the postsynaptic spike trains. This model has been previously described (Ghanbari et al., 2017; Wei and Stevenson, 2021) and extends previous models of coupled GLMs (Harris et al., 2003; Truccolo et al., 2005; Pillow et al., 2008; Rebesco et al., 2010) to account for fluctuating excitability and plasticity. Briefly, for each connection, we model the postsynaptic firing rate $\gamma$ at time $t$ as follows:

$$\gamma (t|{\beta }_0(t),{\beta }_s,{\beta }_c,w(t))=\text{exp}({\beta }_0\left(t\right)+{\beta }_s{y}_{slow}(t)+{\beta }_c{y}_{coup}(t)w(t))$$

$$n_{post}\left(t\right)\sim Poisson\left(\gamma \left(t\text{|}{\beta }_0(t),{\beta }_s,{\beta }_c,w(t)\right)\right)$$

$$y_{slow}=n_{pre}*x_{slow}$$

$$y_{coup}=n_{pre}*x_{coup},$$

where $n_{pre}$ and $n_{post}$ are the presynaptic and postsynaptic spike trains, respectively.

Here, ${\beta }_0(t)$ represents a time-varying baseline firing rate, which is estimated using an adaptive filtering algorithm (Wei and Stevenson, 2021). ${\beta }_s{y}_{slow}(t)$ accounts for slow fluctuations that are shared by the presynaptic neuron and postsynaptic neuron, where $y_{slow}$ denotes a set of covariates generated by filtering the presynaptic spike train (cubic B spline functions with four equally spaced knots over 150 ms $x_{slow}$). ${\beta }_c{y}_{coup}(t)w(t)$ represents the contribution from the synaptic effect. Here, ${\beta }_c{y}_{coup}(t)$ describes the stationary coupling effect, where $y_{coup}$ is the presynaptic spike train convolved with the alpha function we learned from the extended GLM $\alpha (m,\tau ,\Delta t)$, and $w(t)$ describes the effects of STP. Namely, we model $w(t)$ as a function of presynaptic ISIs $\Delta t_k$ as follows:

$$w\left(t\right)=1+{\displaystyle {\sum }_k{q}_k(\text{Δ}{t}_k){\displaystyle {\sum }_{l=0}^T\delta (t_k-l)\text{exp}(-\frac{l}{{\tau }_{stp}})}},$$

where $q_k(\text{Δ}{t}_k)$ is a modification function that determines how the synaptic strength increases/decreases following each presynaptic spike at time $t_k$. We model the modifications using a group of raised cosine basis functions $B(\text{Δ}{t}_k)$ and $q_k\left(\text{Δ}{t}_k\right)=\theta B(\text{Δ}{t}_k)$ and assume that the effects of STP decay with ${\tau }_{stp}=200$ ms. We fit the free parameters {${\beta }_0\left(t\right),{\beta }_s,{\beta }_c,\theta$} by maximizing the Poisson log-likelihood as follows:

$$LL{H}_{GBLM}={\displaystyle {\sum }_t(n_{post}\left(t\right)\log \gamma (t)-\gamma (t))}.$$

To estimate the parameters, we use an alternating optimization (coordinate ascent); we fit ${\beta }_0\left(t\right)$ using fixed {${\beta }_s,{\beta }_c,\theta$} and then fit {${\beta }_s,{\beta }_c,\theta$} using fixed ${\beta }_0\left(t\right)$. We repeat this alternating pattern until convergence.

After optimization we then have a model-based estimate of the impact of each individual presynaptic spike and can predict how the efficacy would change over time under a model of short-term plasticity. We calculate GBLM estimated synaptic efficacy in a similar way as we estimate efficacy using CCGs as follows:

$$ef{f}_{GBLM}={\displaystyle {\sum }_t(\gamma (t)-{\gamma }_0(t))/{\mathit{num}}_{pre}},$$

where ${\gamma }_0$ is the postsynaptic rate with the synaptic effect removed ${\beta }_c=0$; $ef{f}_{GBLM}$ then reflects the excess probability of observing a postsynaptic spike because of the occurrence of a presynaptic spike within the model.

For comparison, we also fit a static-synapse model where the synaptic coupling effect is ${\beta }_c{y}_{coup}(t)$ instead of ${\beta }_c{y}_{coup}(t)w(t)$. Under the static-synapse model, the coupling effect stays the same over time and will allow us to assess whether STP, specifically, meaningfully improves the description of spike transmission. To quantify how well a model predicts whether there is a postsynaptic spike after each presynaptic spike, we use receiver operating characteristic (ROC) curves, and the area under the curve (AUC) reflects the performance. For each presynaptic spike, we identify a transmission interval $\left(t_a,t_b\right)$ where the coupling filter (alpha function in GBLM) is >0.5, and then we use the model fit within the transmission interval $1-{\prod }_{t\in \left(t_a,t_b\right)}^{p}p\left(n_{post}=0\text{|}\gamma (t)\right)$ as the score for predicting each individual postsynaptic spike.

Data availability

The MATLAB code for data analysis is available from GitHub at https://github.com/NaixinRen/predictable-fluctuations-in-synaptic-efficacy.

Results

Here, we characterize fluctuations in putative synapses from 20 recordings from the Allen Institute Neuropixels dataset (Siegle et al., 2021). We detect putative excitatory synaptic connections based on the CCGs of pairs of neurons using a two-stage synapse detection method. In stage 1, we use a hypothesis test based on the jittered spikes to detect fast changes in the CCG, and in stage 2, we use a model-based approach to estimate and screen for putative synaptic effects at specific latencies and timescales (see above, Materials and Methods). Figure 1A shows the CCGs of example connections. By using this two-stage screening procedure, our goal is not to detect as many putative synapses as possible but rather to generate a subset of strong putative synapses with CCGs that are consistent with the biophysics of excitatory synaptic transmission, including synaptic latencies (1.29 ± 1.23 SD ms; Fig. 1B) and time constants (0.55 ± 0.13 SD ms; Fig. 1C).

Figure 1.

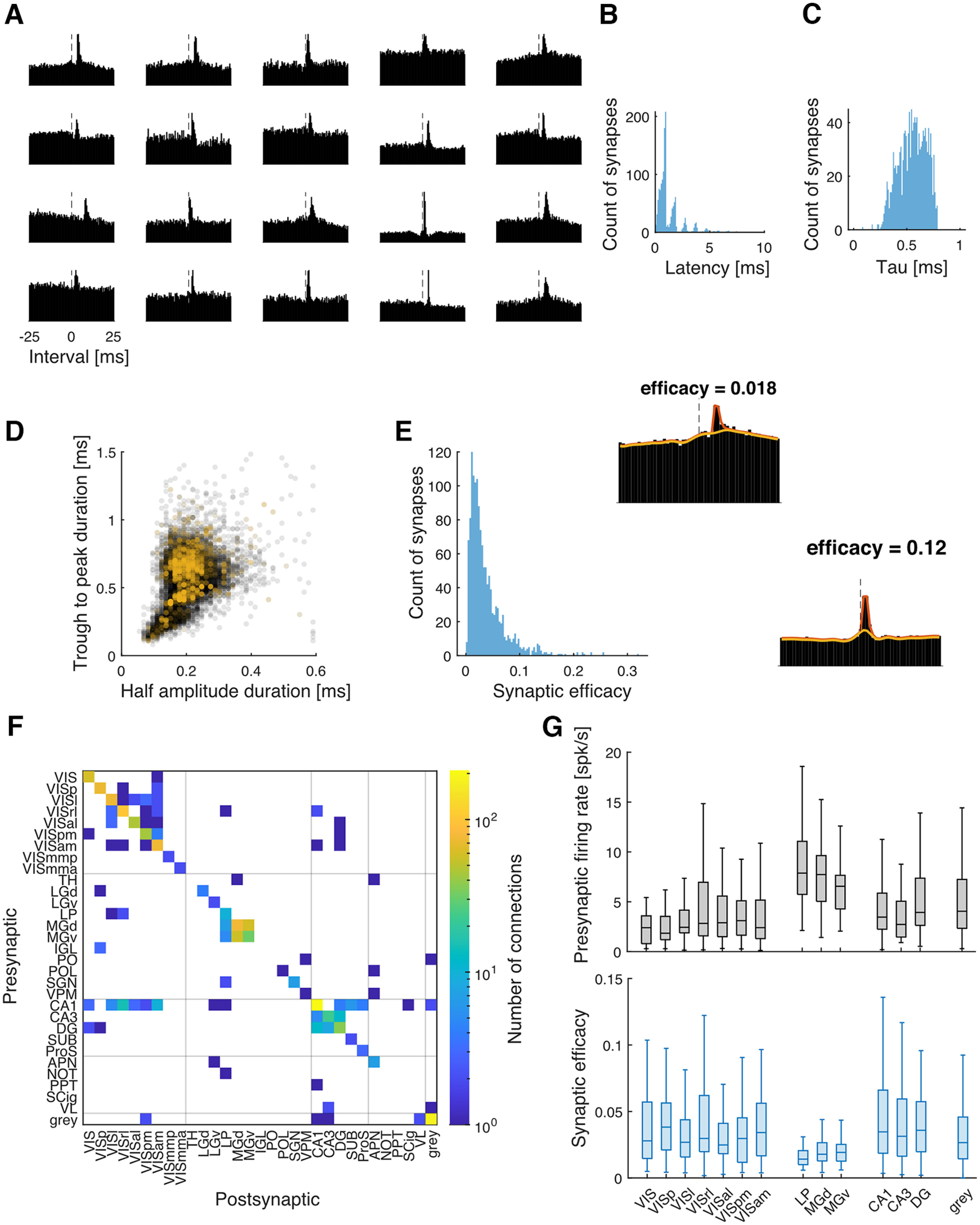
Detection of putative excitatory synaptic connections. A, Examples of CCGs of putative excitatory synaptic connections. The bin size is 0.5 ms here for better visualization. In the analysis, we use 1 ms. B, The histogram of synaptic latency of all the detected synapses. The distribution tends to peak at 1, 2, 3 … [ms] because the bin size of the CCG is 1 ms. C, The histogram of the synaptic time constant of all the detected synapses. D, Two measurements of the duration of waveforms. Each dot represents one neuron. Most putative presynaptic neurons (yellow dots) show broader spike waveforms compared with all the neurons in the dataset (gray dots). E, The histogram of the synaptic efficacy of all the detected synapses. Left, Example CCGs with low or high efficacy and the model fits of the extended GLM (red line, model fits with synaptic effect; yellow line, model fits without synaptic effect). F, Connectivity matrix across different areas (y-axis, presynaptic area; x-axis, postsynaptic area). Color represents the number of connections detected (log transformed). The gridlines separate the brain regions of visual cortex, thalamus, hippocampus, midbrain, and unclassified. Visual cortex (VIS), Primary Visual Area (VISp), Lateral visual area (VISl), Rostrolateral visual area (VISrl), Anteromedial visual area (VISal), Posteromedial visual area (VISpm), Anteromedial visual area (VISam), Mediomedial posterior visual area (VISmmp), Mediomedial anterior visual area (VISmma), thalamus (TH), dorsal/ventral lateral/medial geniculate (LGd/LGv/MGd/MGv), Lateral posterior nucleus (LP), Intergeniculate leaflet of the lateral geniculate complex (IGL), Posterior nucleus (PO), Posterior limiting nucleus (POL), suprageniculate nucleus (SGN), Ventral posteromedial nucleus (VPM), Dentate gyrus (DG), Subiculum (SUB), Prosubiculum (ProS), Anterior pretectal nucleus (APN), Nucleus of the optic tract (NOT), Posterior pretectla nucleus (PPT), Superior colliculus, intermediate grey matter (SCig), lateral ventricle (VL). G, Box plots for the mean firing rate (top) and efficacy (bottom) for brain areas. The areas are grouped by brain regions mentioned above. Only areas with ≥10 efferent synapses are shown here. The line inside each box is the median. The top and bottom edges of the box are the upper and lower quartiles, respectively. The whiskers show the nonoutlier maximum and minimum. The outliers are not shown here.

The presynaptic neurons for the majority of putative synapses that we detect have broad waveforms (Fig. 1D), which previous work has found tend to correspond to excitatory neurons (Connors and Gutnick, 1990; Barthó et al., 2004; Trainito et al., 2019). For each putative synapse, we estimate the overall synaptic efficacy using an extended GLM (see above, Materials and Methods; Fig. 1E). The distribution of synaptic efficacy is approximately log normal (0.037 ± 0.035, mean ± SD; Fig. 1E), consistent in shape with the previous findings on postsynaptic potentials (Buzsáki and Mizuseki, 2014) and efficacy (English et al., 2017). Here, we detect 1383 putative excitatory synapses in total, most of which were between neurons recorded on the same probe (1174 of 1383) and within the same brain area (1090 of 1383; Fig. 1F).

Across the 20 recordings, we identify putative synapses from many labeled brain regions. The regions with >10 efferent synapses included six visual cortical areas (VISp, VISl, VISrl, VISal, VISpm, VISam), three thalamic areas (LP, MGd, MGv), three hippocampal areas (CA1, CA3, DG), and in locations that were not precisely identified (grey or VIS). Synapses from different brain regions have distinct presynaptic firing rates (5.75 ± 9.93 SD spikes/s overall average) and synaptic efficacies (Fig. 1G). Notably, putative synapses from thalamic areas appear to have higher presynaptic rates and lower efficacy on average. Firing rates are expected to fluctuate because of varying stimuli, behavior, and internal state variables. Here, we aim to measure the extent to which the efficacy of putative synapses also fluctuates and to determine whether these fluctuations are predictable.

Presynaptic firing rate and efficacy both fluctuate substantially over time

To examine the natural fluctuations in presynaptic firing rate and synaptic efficacy, we divide the presynaptic and postsynaptic spike trains into 5 min windows with 80% overlap and estimate the presynaptic firing rate and efficacy for each window separately (Fig. 2A,B, example of fluctuations). Here, we calculate the CV (the ratio of the SD to the mean) for both variables for each connection to measure the fluctuation. We find that both presynaptic firing rate and synaptic efficacy fluctuate substantially over time in all areas (Fig. 2C,D; CV for firing rate, 0.55 ± 0.29 SD; CV for efficacy, 0.69 ± 0.46 SD). Although large fluctuations in firing rate are expected, large fluctuations in synaptic efficacy of this scale are somewhat unexpected during ongoing behavior. When firing rates are low, efficacy estimates are noisy, and some variation in efficacy is expected purely by chance. However, the observed fluctuations are not simply explainable by measurement error. Here, we compare the observed fluctuations in efficacy to surrogate data where postsynaptic spike trains are shuffled to remove any systematic fluctuations over long timescales but preserve the overall efficacy (see above, Materials and Methods, Estimating time-varying synaptic efficacy). For each putative synapse, we shuffle 100 times to create a null distribution for CV of efficacy and calculate a z score for the observed CV using the mean and SD of the null distribution. The average z score across all putative synapses is 3.26, suggesting that the observed efficacy fluctuations are substantially higher in most cases than would be expected by chance. In addition, we find that the CV for firing rate is correlated with CV for efficacy for individual synapses ($r=0.24,p<0.001$). Averaging within brain regions, we also find that the CV of firing rate and the CV of efficacy are positively correlated across regions ($r=0.77,p<0.01$; n = 14 regions with ≥10 putative synapses). Regions with greater fluctuations in the presynaptic firing rates tend to have higher fluctuations in the efficacies of their putative synapses.

Figure 2.

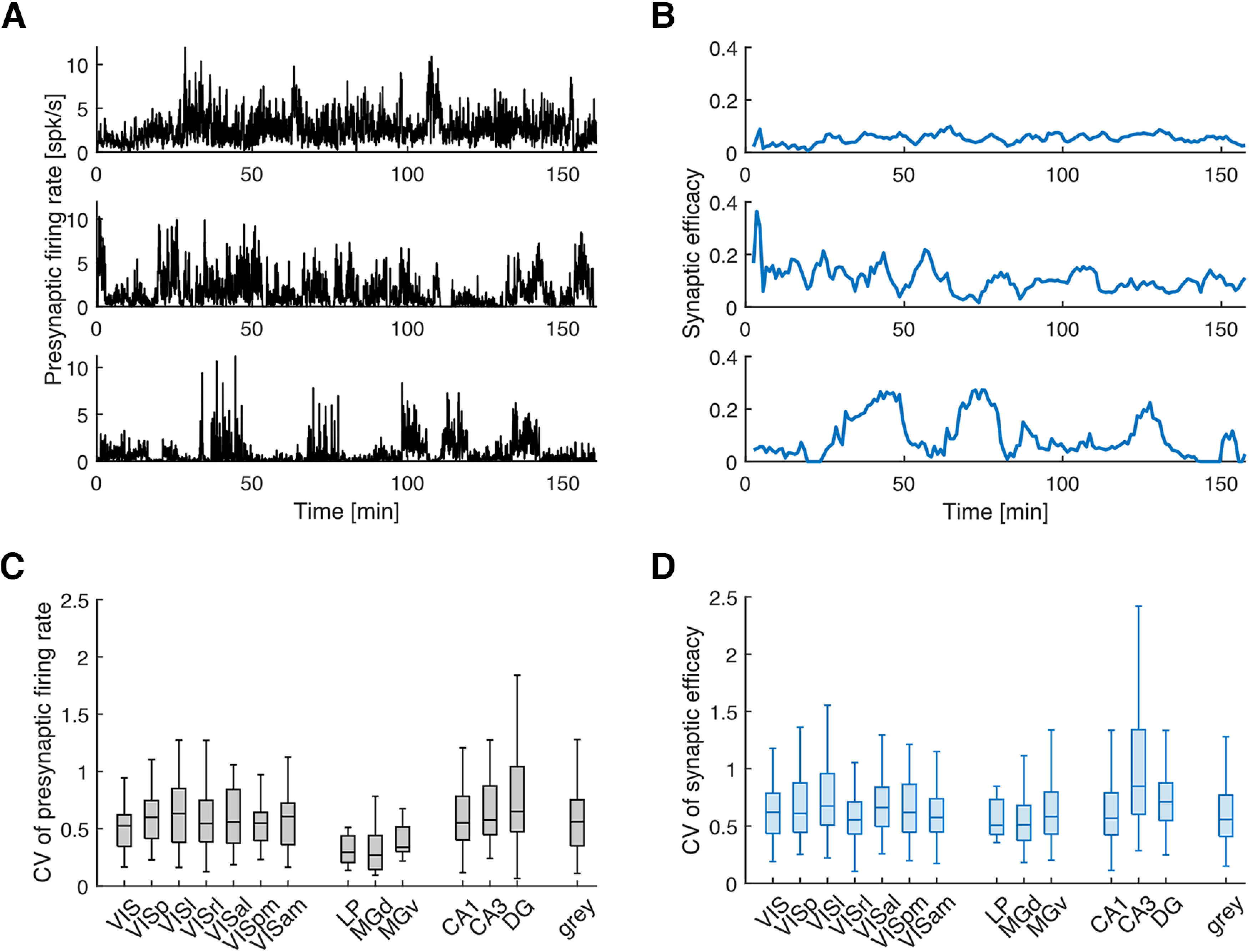
Fluctuations in presynaptic firing rate and synaptic efficacy. A, B, Three examples for fluctuations in presynaptic firing rate (A) and synaptic efficacy (B), respectively. Top, Low CV. Middle, Moderate CV. Bottom, High CV. The firing rates in A are estimated using optimal time bins that are generated based on Shimazaki and Shinomoto (2010) for better visualization on finer timescales. The efficacy in B is estimated based on the 5 min window described in Materials and Methods. C, D, The box plots for CVs of presynaptic firing rate (C) and synaptic efficacy (D) for each area. Only areas with ≥10 efferent synapses are shown here. The notations are the same as in Figure 1.

Efficacy fluctuations mirror fluctuations in the presynaptic firing rate for individual neuron pairs

The efficacies of putative synapses appear to fluctuate substantially in vivo across multiple brain regions. To examine these fluctuations in more detail, we calculate correlations between the time-varying presynaptic firing rate and time-varying synaptic efficacy for individual connections. The average absolute Spearman's correlation is 0.32 ± 0.22 SD (983 of 1383 connections are statistically significant; p < 0.05; Fig. 3A,B). As with the CV of efficacy fluctuations, these correlations do not appear to be simply because of chance. By shuffling the postsynaptic spike times as described above we can also measure to what extent the observed Spearman's correlation for each synapse differs from that expected by chance (see above, Materials and Methods, Estimating time-varying synaptic efficacy). Here, the average z score of the synapses with positive correlation coefficient is 2.34, and the average z score of the synapses with negative correlation coefficient is −1.83 (Fig. 4A–C, third column). This suggests that efficacy fluctuations may be predicted based on the presynaptic firing rate, with positive or negative correlations larger than expected by chance, depending on the neuron pair. For comparison, we also examine the correlation between the fluctuations in the postsynaptic firing rate and synaptic efficacy; the average absolute Spearman's correlation in this case is 0.38 ± 0.23 SD (1095 of 1383 connections are significant; p < 0.05; Fig. 3C,D). Positive correlations between the fluctuations in postsynaptic firing rate and synaptic efficacy are somewhat expected as the excitability of the postsynaptic neuron may affect both and increased synaptic efficacy might causally affect the firing rate of the postsynaptic neuron (>75% of the synapses show a positive correlation in Fig. 3C). However, the correlation between the fluctuations in the presynaptic firing rate and efficacy is less predictable and worth exploration. To further determine the influence of the presynaptic firing rate on synaptic efficacy, for each putative synapse, we run a linear regression predicting the time-varying efficacy from the log-transformed time-varying postsynaptic firing rate and the log-transformed time-varying presynaptic firing rate. The Wald test shows that for 67.1% of the putative synapses, the presynaptic firing rate makes a statistically significant contribution to the prediction (928 of 1383, p < 0.05). For many synapses, the fluctuations in the synaptic efficacy mirror the natural fluctuations in presynaptic firing rate.

Figure 3.

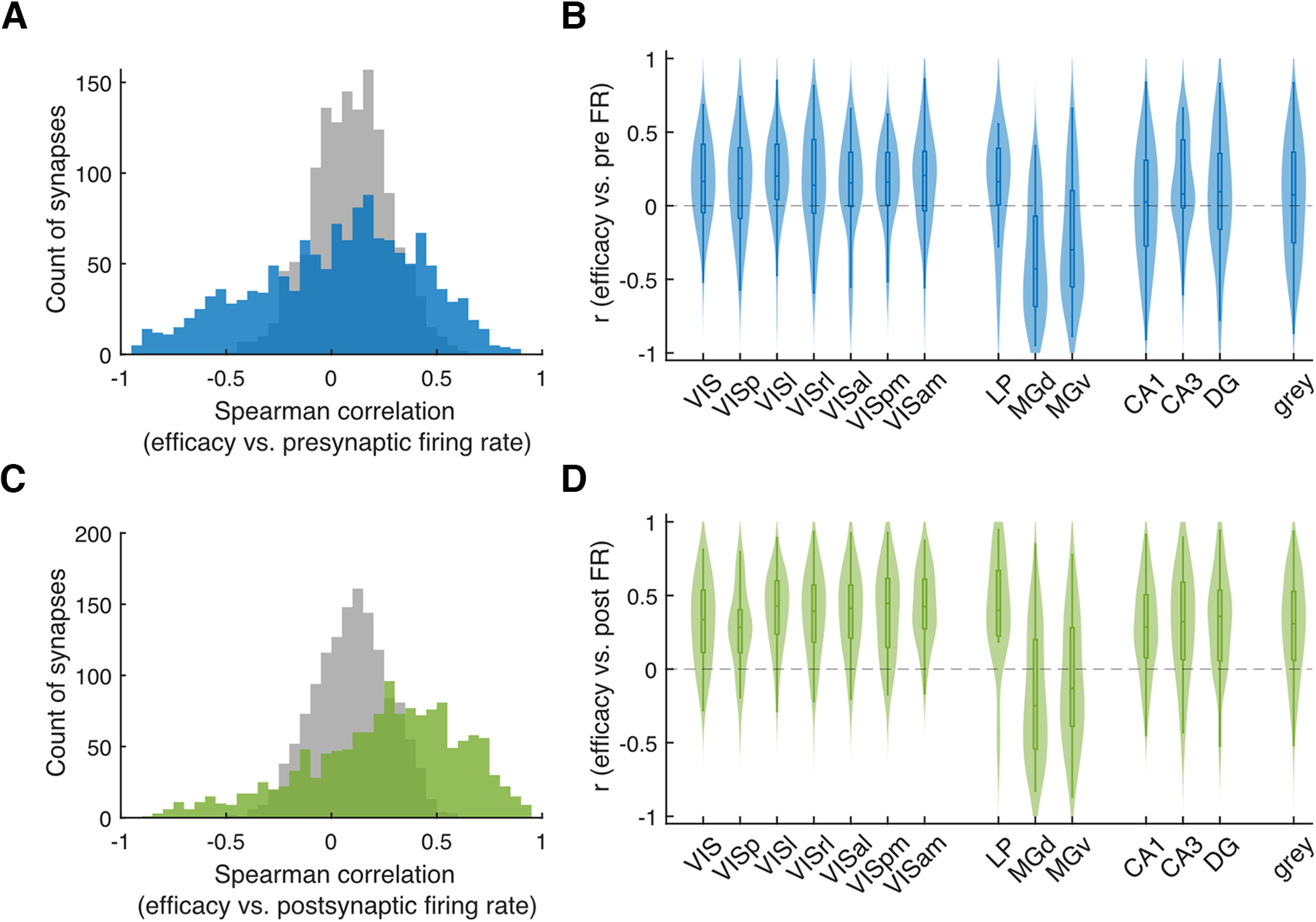
Correlation between the fluctuation in synaptic efficacy and that in the presynaptic and postsynaptic firing rate. A, C, Histogram of the Spearman's correlation between the fluctuations in synaptic efficacy and the natural fluctuations in the presynaptic firing rate (A, blue) or the postsynaptic firing rate (C, green) and the corresponding distributions generated using postsynaptic spikes jittered on a uniform interval of [−1,1] s (gray). B, D, Violin plot of the Spearman's correlation for presynaptic firing rate (B) or postsynaptic firing rate (D) for each area. Only areas with ≥10 efferent synapses are shown.

Figure 4.

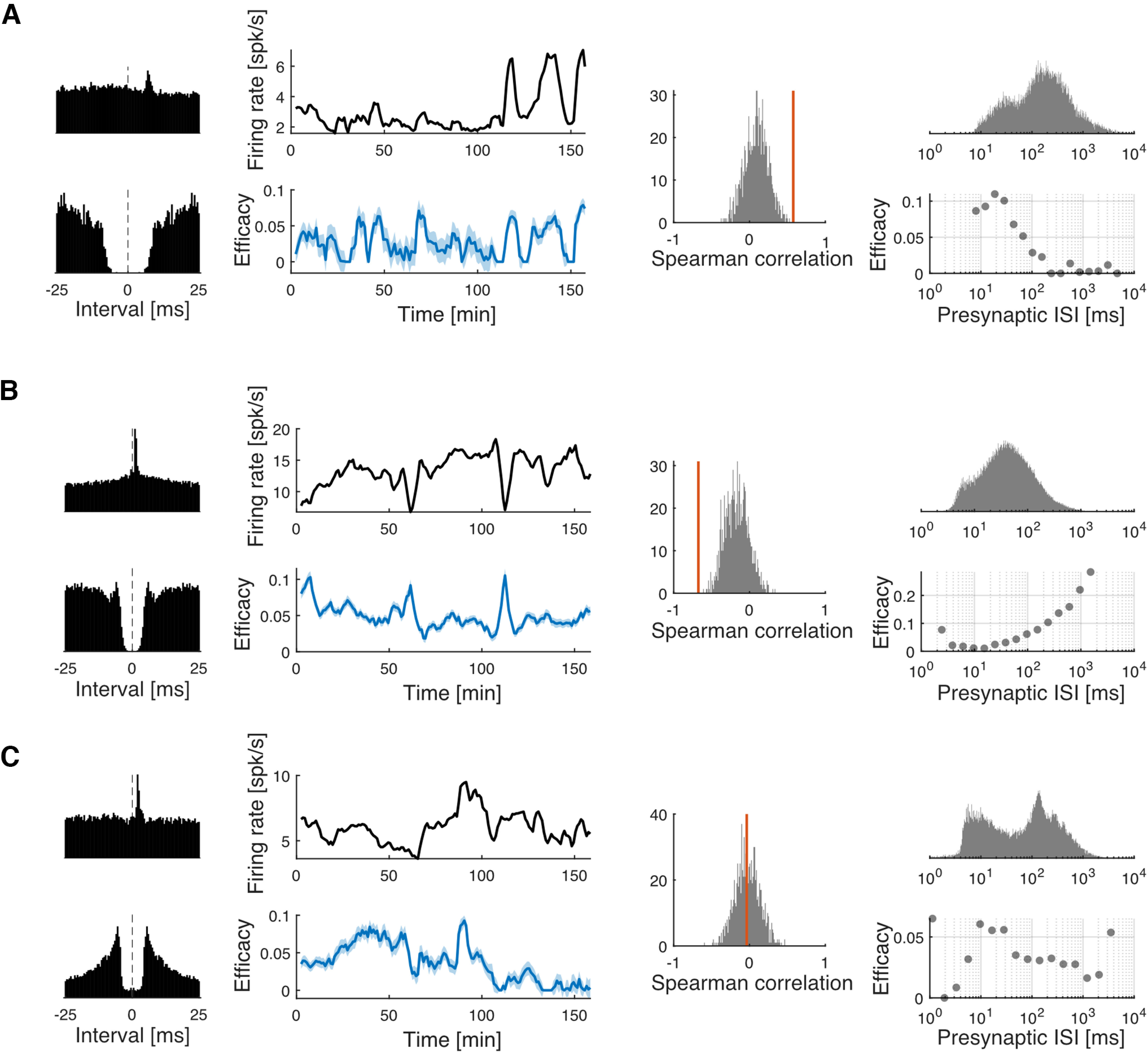
Three kinds of relationships between the fluctuations in synaptic efficacy and presynaptic firing rate. A, An example putative synapse (DG–CA3), where there is a positive correlation between the synaptic efficacy and the presynaptic firing rate. B, An example putative synapse (APN–APN), where there is a negative correlation between the synaptic efficacy and the presynaptic firing rate. C, An example putative synapse (CA1–VIAam), where the relationship between the synaptic efficacy and the presynaptic firing rate is not clear. First column (A–C), CCG (top) and autocorrelogram (ACG, bottom). Second column (A–C), The fluctuations in the presynaptic firing rate (top) and the synaptic efficacy (bottom). The shaded area represents 1 SD. Third column (A–C), The distribution of Spearman's correlation from surrogate, shuffled data (gray, 1000 samples shown for visualization). The red bar shows the observed correlation from the original data. Note that in C the observed correlation is close to zero. This does not mean the fluctuation in synaptic efficacy is random, it just indicates that the fluctuation in synaptic efficacy is not correlated with presynaptic firing rate. Fourth column, The distribution of the presynaptic ISI (top) and the efficacy estimated for presynaptic spikes with different ISIs using the extended GLM.

One concern with this analysis may be that some of the putative synapses are false positives. To address this concern, we consider jittered data where the fast changes in the CCGs are removed. We calculate efficacy using the same neuron pairs where the postsynaptic spikes are jittered on a uniform interval of [−1, 1] s. We find that the Spearman's correlation between firing rate and efficacy in this case is substantially smaller compared with the original spikes (Fig. 3A,C, gray).

One potential explanation for the correlation between presynaptic rate and efficacy is short-term STP. If a synapse exhibits short-term synaptic depression, higher presynaptic firing rates lead to a depletion of resources and lower efficacy, leading to a negative correlation. On the other hand, if a synapse exhibits short-term synaptic facilitation, higher presynaptic rates lead to an increase in release probability and higher efficacy, leading to a positive correlation. In other cases, facilitation and depression may coexist, leading to nonmonotonic relationships between presynaptic rate and efficacy. Here, we find a range of relationships (Fig. 4A,B) as well as cases where there are clear fluctuations but no clear relationship between presynaptic rate and efficacy (Fig. 4C). Previous studies have found short-term changes in synaptic efficacy in vivo by showing how synaptic efficacy varies depending on the preceding presynaptic ISIs (Swadlow and Gusev, 2001; Stoelzel et al., 2008, 2009; English et al., 2017; Ghanbari et al., 2020). As previous studies have done, here, we estimate efficacies at different presynaptic ISI ranges (see above, Materials and Methods, Estimating synaptic efficacy with different presynaptic ISI ranges). We find that the relationships between efficacy and presynaptic ISI (Fig. 4A–C, fourth column) are often consistent with the correlation between efficacy and presynaptic firing rates we find on a minute timescale. For example, the putative synapse in Figure 4A exhibits short-term facilitation, and there is a consistent efficacy–ISI relationship where short presynaptic ISI leads to high efficacy. Overall, this suggests that fluctuations in synaptic efficacy can potentially be predicted in detail by modeling STP as a function of presynaptic ISI.

A model of short-term plasticity reproduces efficacy fluctuations

Because many synapses show a facilitating or depressing relationship between the presynaptic firing rate and synaptic efficacy, we examine explanatory models based on STP. Here, we build a GBLM that aims to describe the detailed (1 ms bins) postsynaptic spiking by modeling STP, slow fluctuations in postsynaptic excitability, and slow common input to both the presynaptic and postsynaptic neurons (see above, Materials and Methods). Here, we estimate a modification function that describes how the synaptic strength changes following the occurrence of presynaptic spikes at a given ISI, and we use adaptive smoothing to track slower fluctuations in the postsynaptic rate. Altogether, this model captures the probability of postsynaptic spiking following every single presynaptic spike and allows us to track how the time-varying synaptic strength increases (facilitation) or decreases (depression) following presynaptic spikes with specific intervals.

To quantify how well the models predict the postsynaptic spiking after a presynaptic spike, we use ROC curves, where the AUC reflects performance (see above, Materials and Methods). We find that the GBLM predicts postsynaptic spikes better than the chance level (AUC, 0.68 ± 0.05 SD). In the 10 recordings where there is a 30 min period of spontaneous activity, we find that the GBLM predicts postsynaptic spikes better than the chance level even when only examining this spontaneous period where we calculate the AUC using only the spikes during the spontaneous activity (AUC, 0.67 ± 0.06 SD). Although many putative synapses involve neurons in nonvisual regions, this comparison illustrates how fluctuations in efficacy are predictable even in the absence of specific visual stimuli and are not merely an artifact of fast stimulus correlations.

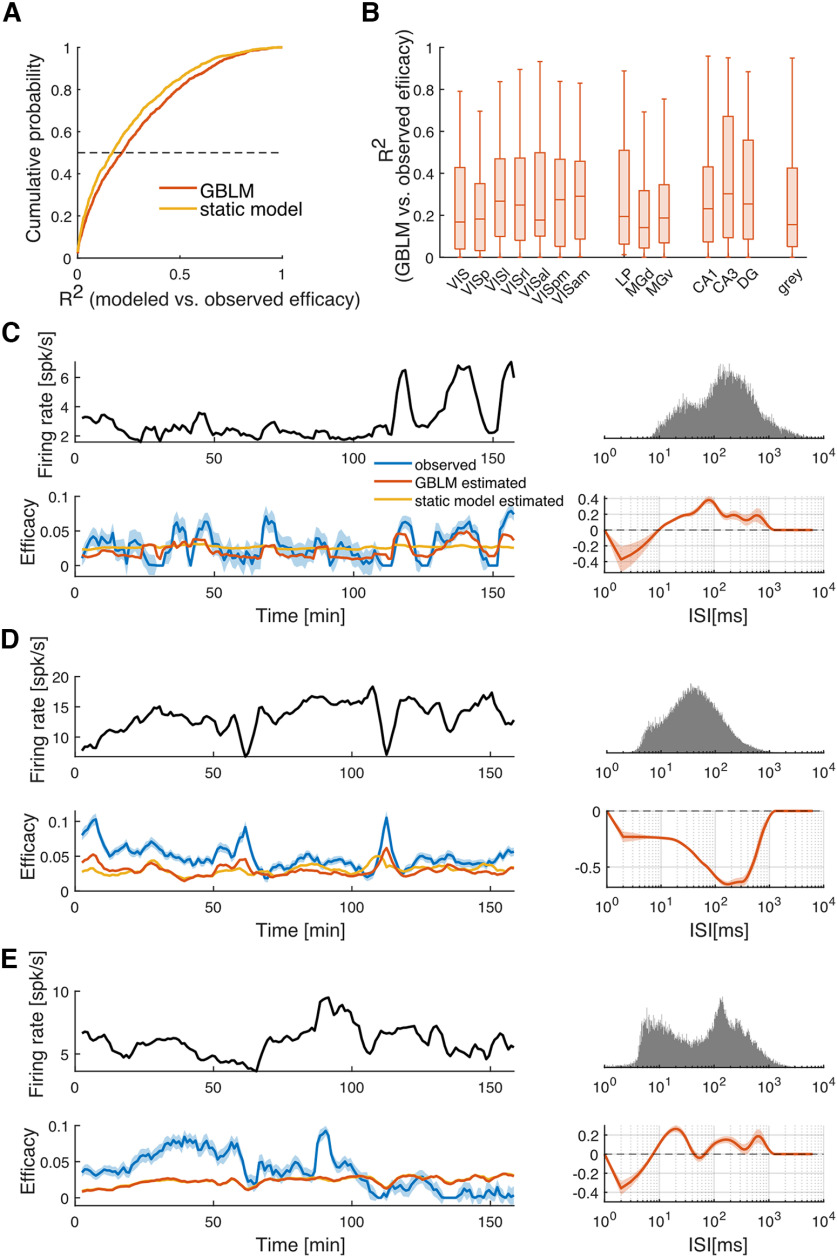
The GBLM provides a model of the time-varying impact of each individual presynaptic spike. However, to illustrate how slow fluctuations in efficacy might be explainable by STP more directly, we evaluate the predictions of the GBLM across 5 min windows as before. We find that the median coefficient of determination ($R^2$) between the GBLM estimated efficacy and the observed efficacy is 0.22 [0.07–0.43 interquartile range (IQR); Fig. 5A; 86.6% statistically significant, $p<0.05$], and the results do not vary substantially across different brain regions (Fig. 5B). Moreover, the modification function of presynaptic ISI from the GBLM tends to be consistent with the relationship between presynaptic firing rate and observed synaptic efficacy (Fig. 5C–E). As a comparison, we also build a static-synapse model without STP, where the synaptic coupling stays the same over time (see above, Materials and Methods). In this case, the median coefficient of determination between the static model estimated efficacy and the observed efficacy 0.17 (0.05–0.37 IQR; Fig. 5A; 83.3% of them show $p<0.05$). The static model can reproduce some fluctuations in the synaptic efficacy, indicating that some of the fluctuations can be attributed to non-STP components, such as the excitability of the postsynaptic neuron (Gal et al., 2010) or slow common inputs shared by the presynaptic and postsynaptic neurons. However, there is 30% improvement in the median $R^2$ when comparing the GBLM to the static model, which suggests that STP plays a role in the efficacy fluctuations as well. For many connections, the GBLM can reproduce fluctuations in the synaptic efficacy with high fidelity, suggesting that STP can, at least partially, explain the relationship between fluctuations in the presynaptic firing rate and synaptic efficacy.

Figure 5.

GBLM of STP reproduces the fluctuation in synaptic efficacy. A, The cumulative probability of $R^2$ between the model estimated efficacy and the observed efficacy. The dotted line shows the median (50% cumulative probability). B, Box plot of $R^2$ for different areas. Only areas with ≥10 efferent synapses are shown. The notations are the same as in Figures 1–4. C–E, The synapses are the same as those shown in Figure 4. Left, The fluctuations in the presynaptic firing rate (top) and the synaptic efficacy (bottom). The blue line is the observed efficacy. The orange line is the GBLM estimated efficacy. The yellow line is the static model estimated efficacy. Right, The distribution of the presynaptic ISI (top) and the modification function estimated from the GBLM. The shaded orange area represents 1 SE.

To characterize the diversity of STP patterns in the putative excitatory connections examined here, we further analyze the modification functions estimated from the GBLM. The modification function gives a simple description of how the synaptic effect varies as a function of the presynaptic ISI. When the modification is positive, synaptic strength is facilitated, and when it is negative it is depressed. However, the influence of the modification function, overall, depends on the ISI distribution. Although the modification function may be negative (for ISI < 10 ms in Fig. 5C, e.g.), this will only influence the synaptic strength when spikes occur with those particular ISIs. Here, we align the modification function by ISI distributions. We sample the modification function at the 5th–95th percentiles of the ISI distribution (with 5% increments) and normalize by dividing the ISI-scaled function by the absolute value of its average. To see if there is any structure in the modification functions for all the putative synapses, we use hierarchical clustering on the ISI-scaled modification function (Euclidean distance with unweighted average linkage). We find the functions are broadly split into two clusters with some putative synapses mostly facilitating and others mostly depressing. However, the specific ISI range where facilitation or depression occurs varies widely across putative synapses (Fig. 6A). Summarizing the ISI-scaled modification functions with their average, we find that the overall level of facilitation or depression appears to vary across brain regions (Fig. 6B) in a similar trend as the relationship between the minute-level fluctuations in presynaptic firing rate and efficacy (Fig. 3B). These results suggest that differences in the association between efficacy and presynaptic rate that we observe on ∼1 min timescales may be related to differences in STP on subsecond timescales.

Figure 6.

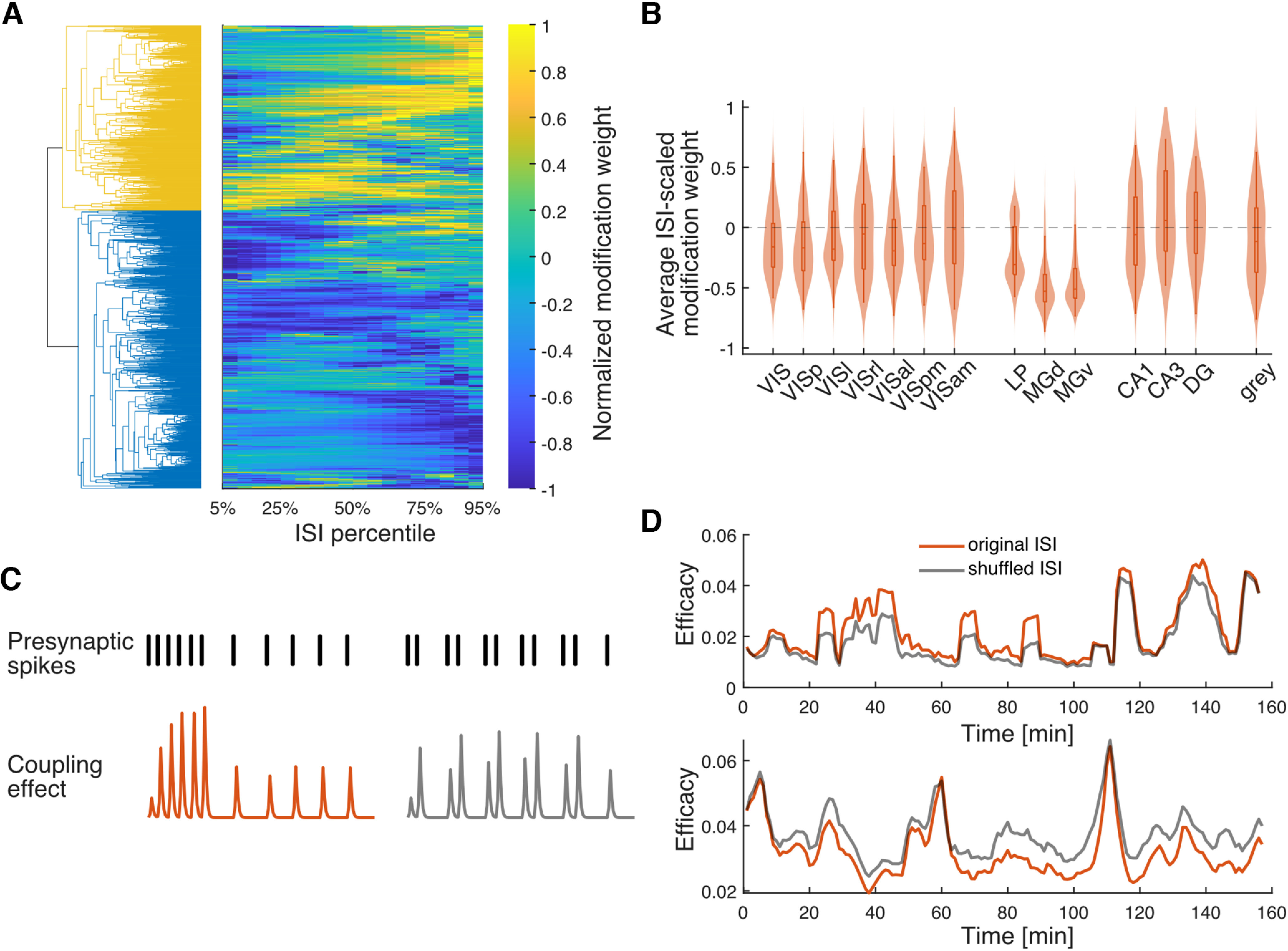
Hierarchical clustering for modification functions. A, Right, The modification functions of all putative synapses sorted based on the clustering results; each row represents one modification function. Left, The dendrogram of the hierarchical clustering. Colors represent the top two clusters. B, The violin plot of the mean of the modification function for each brain area. Only areas with ≥10 efferent synapses are shown. C, Schematic illustrating how the same modification rule and presynaptic ISI distribution can result in different efficacy fluctuations. Top, Two example presynaptic spike trains with the same number of spikes and the same ISI distribution but different ISI sequences. Bottom, The resulting coupling effects for both spike trains simulated using one facilitation modification function. Note that the presynaptic spike train on the left results in a synaptic strength that is stronger on average than the train on the right. D, The GBLM estimated efficacy from the original data (the orange lines in Fig. 6D are the same as the orange lines in Fig. 5C,D (bottom), and from the postsynaptic activity reconstructed using shuffled presynaptic spikes (gray).

Although the sign of the modification functions estimated with the GBLM typically reflects the positive or negative correlation between the minute-level fluctuations in the presynaptic firing rate and synaptic efficacy, it is also important to note that this relationship is not one to one. The modification function summarizes how the putative synaptic weight changes based on the single preceding ISI, whereas the overall efficacy in a time window is a result of not only the preceding ISI but also the sequence of presynaptic ISIs within the window. The same ISI distribution can give rise to different efficacy fluctuations depending on the specific order of the presynaptic spikes (Fig. 6C). To illustrate the influence of specific presynaptic spike patterns on the observed efficacy fluctuations, we compared postsynaptic responses to the original spikes with responses to shuffled presynaptic ISIs with the same modification function. For each example synapse (same as those in Fig. 5C,D), we shuffle the presynaptic ISI within a 1 min window, so the ISI distribution and minute-level fluctuation in the presynaptic firing rate are preserved but the ISI sequence is randomized. We then reconstruct the postsynaptic activities using the GBLM parameters estimated from the original data where the coupling effect changes as a function of the shuffled presynaptic spike train. For both synapses, the predicted efficacy fluctuations with shuffled presynaptic ISIs (Fig. 6D, gray lines) are weaker compared with the predicted fluctuations from the original presynaptic spikes (Fig. 6D, orange lines) even under the same modification functions. These differences demonstrate how, in addition to the modification function and the overall presynaptic rate, the detailed sequence of presynaptic spikes plays a role in determining the correlation between presynaptic firing rate and synaptic efficacy.

Discussion

In this study we examine associations between fluctuations in firing rates and efficacies of putative excitatory synapses using large-scale extracellular spike recordings from awake, behaving mice. Using both descriptive and model-based analysis we identify three main findings. First, we found that for many putative synapses there are substantial fluctuations in the synaptic efficacy that occur on a slow timescale of minutes alongside the expected variations in presynaptic and postsynaptic firing rates. Second, we found that these slow fluctuations in synaptic efficacy are often correlated (either positively or negatively) with fluctuations in presynaptic rate. And third, by fitting a detailed 1 ms resolution model of postsynaptic spiking probability where synaptic effects have short-term plasticity, we show that these slow fluctuations in synaptic efficacy are consistent with the cumulative effects of STP in many cases.

Although previous studies have shown that synaptic efficacy varies in vivo with learning, behavior, and stimuli (Fedulov et al., 2007; Fujisawa et al., 2008; Ghanbari et al., 2020; McKenzie et al., 2021), differences in efficacy across conditions may partially reflect differences in presynaptic firing rates and spike patterns across conditions. Firing rates depend both on external variables, such as stimuli and movement (Ben-Yishai et al., 1995; Kang et al., 2004; Vogels et al., 2005), as well as internal variables, such as arousal, attention, adaption, and excitability (Gilbert and Sigman, 2007; Gal et al., 2010; Goris et al., 2014). Firing rate fluctuations can occur spontaneously (Teich et al., 1990; Yaksi and Friedrich, 2006; Faisal et al., 2008) and are influenced by brain state and the population activity of the surrounding neurons (Tsodyks et al., 1999; Poulet and Petersen, 2008; McGinley et al., 2015). These many sources of firing rate variability occur simultaneously in vivo and may have complex effects on synaptic efficacy because of diversity in both cell types and synaptic dynamics. Understanding how synaptic efficacy is affected by presynaptic firing rates first may allow us to better understand the influence of specific external or internal variables.

Here, we find that the brain regions with larger fluctuations in the presynaptic firing rate (measured by CV) also show larger fluctuations in efficacy of putative excitatory synapses. It is important to note that this observation is just based on the putative excitatory synapses we detected. Synapse detection from spikes is biased toward strong synapses between neurons with high firing rates. Moreover, most synapses analyzed here are between neurons within the same brain area and detected on the same probe. These findings thus represent only a partial picture of the overall synaptic dynamics in these regions. However, the correlations we observe are consistent with our core hypothesis that firing rate variation leads directly to fluctuations in synaptic efficacy because of STP. Here, we find such patterns not just across brain areas, but for many individual synapses, fluctuations in synaptic efficacy mirror fluctuations in the presynaptic firing rate. Synaptic efficacy can be affected by the postsynaptic activity as well (Abbott and Nelson, 2000; Ibata et al., 2008; Sjöström et al., 2008), but here we find that the presynaptic firing rate is still predictive, even after accounting for the postsynaptic firing rate. Previous in vitro experiments have shown that natural spike patterns lead to changes in synaptic strength consistent with STP on short timescales (Klyachko and Stevens, 2006; Kandaswamy et al., 2010). Here, we find evidence that synaptic efficacy fluctuates with presynaptic firing rate in vivo, during behavior, with large fluctuations on timescales of minutes.

Using a model-based approach to predict postsynaptic spiking on 1 ms timescales (GBLM), we also examined to what extent the slow fluctuations in synaptic efficacy can be explained by STP. Here, we modeled the time-varying synaptic effect using a modification function where the synaptic effect changes as a function of presynaptic ISI. We find the GBLM can predict when individual postsynaptic spikes will occur after a presynaptic spike better than chance level, as well as accurately describe the slow fluctuations in efficacy on timescales of minutes. The modification functions estimated by the model show a range of ISI–efficacy relationships, both depressing and facilitating, and the distribution of this relationship varies in different brain areas. Previous intracellular studies have shown that short-term synaptic dynamics often depend on the presynaptic and postsynaptic neuron type and brain area (Thomson and Lamy, 2007; Blackman et al., 2013; Lee et al., 2019; Campagnola et al., 2022), and the presynaptic spike statistics that drive STP also vary with cell type and brain area (Mochizuki et al., 2016). A more detailed comparison of in vivo results with previous in vitro results (Seeman et al., 2018) may help determine to what extent in vitro results generalize to naturalistic settings. Similarly, comparisons to previous in vivo studies, such as those finding depression in thalamocortical synapses, (Chung et al., 2002; Swadlow and Gusev, 2002; Bruno and Sakmann, 2006), can help determine to what extent these results generalize across species and experimental settings.

It should be noted that by using the GBLM we are only able to partially reproduce the fluctuations in the synaptic efficacy using the presynaptic firing activity, and many other factors could contribute to variation in synaptic efficacy. First, our model does not account for the long-term changes in the synaptic efficacy. Previous work has found that long-term plasticity can be induced in the visual cortex after repeated visual stimulation (Heynen and Bear, 2001; Frenkel et al., 2006; Cooke and Bear, 2010; Sale et al., 2011), as well as in hippocampus after behavioral training (Gruart et al., 2006; Whitlock et al., 2006; Fedulov et al., 2007). A model that accounts for the long-term plasticity may give a better prediction for the fluctuations in synaptic efficacy (Stevenson and Kording, 2011; Linderman et al., 2014; Song et al., 2018; Wei and Stevenson, 2021). Second, in our model, the STP rules themselves are assumed to be fixed for the whole recording. However, experiments have shown that the induction of long-term potentiation and long-term depression tend to shift STP itself to be more depressing or more facilitating, respectively (Markram and Tsodyks, 1996; Hardingham et al., 2007; Costa et al., 2015, 2017), which may allow for more flexibility in signal transmission (Carvalho and Buonomano, 2011). Third, although we have a term in our model to describe the slow fluctuation in network shared by the presynaptic and postsynaptic neurons, it does not account for the fast synaptic effect of other potential presynaptic neurons (Harris et al., 2003). A postsynaptic neuron can receive thousands of synaptic inputs, and correlated presynaptic inputs can affect the synaptic responses (Salinas and Sejnowski, 2000; Reinartz et al., 2014; Lee et al., 2016). Finally, we model STP as a function of presynaptic ISI to directly examine the influence of presynaptic firing, but there are also many alternative models for short-term synaptic dynamics (Hennig, 2013). Our results find that ∼20% of the variance in efficacy explained by the GBLM, but better models may be able to improve on this result and more accurately predict fluctuations in synaptic efficacy in vivo.

Using extracellular spike recordings from behaving mice, we find that the substantial fluctuations in the efficacy of putative excitatory synapses can be partially predicted by modeling short-term synaptic plasticity. Large-scale spike recordings have the advantage of allowing us to study putative connections between many brain areas for long periods of time (>2 h). Data from a wide range of synapses across the entire brain, may drive richer theoretical and normative models of synaptic transmission (Pfister et al., 2010; Hennig, 2013). However, studying synapses from spikes has the disadvantage that it requires sufficient numbers of presynaptic spikes to accurately estimate efficacy. Advances in stimulation and recording techniques may make it possible to study fluctuations on faster timescales (Kwan and Dan, 2012; English et al., 2017; Walker et al., 2021; Hage et al., 2022), and systematic fluctuations in efficacy for inhibitory synapses may also occur (Reyes et al., 1998; Beierlein et al., 2003; Ma et al., 2012). Although disentangling the complex relationships between synaptic efficacy and external or internal variables in vivo is an ongoing challenge in systems neuroscience, our results here highlight the potentially important role of STP in driving slow fluctuations in synaptic efficacy. In putative excitatory synapses from a wide range of brain areas, we find that short-term synaptic dynamics may lead to large, predictable fluctuations on longer timescales.