Abstract
COVID-19 has had a major negative impact on the travel industry, especially on the aviation sector. Along with travel restrictions to contain the spread of the virus, a drastic drop in demand—mainly caused by the decrease in the willingness to travel—has also been registered. This study explores the impact of COVID-19 on airline pricing curves, in terms of the price level, price dispersion, and the extent to which intertemporal price discrimination is applied. By analyzing all major European flights departing from and arriving in Italy, the results reveal a 31% overall decrease in airline price per kilometer. Additionally, price dispersion dropped, and price discrimination intensity was found to have decreased as a result of COVID-19. These outcomes can be explained in light of two major impacts of the pandemic on air travel demand, namely the variation in the passenger mix and travelers’ higher price sensitivity. Further analyses indicate that—along with other market and flight characteristics—market concentration, introduced interventions to prevent and control COVID-19, and airline- and destination-types play an important role in determining prices, price dispersion, and the price discrimination intensity.
Keywords: Passenger mix, Price dispersion, Price discrimination, Revenues, Pricing strategies
1. Introduction
The COVID-19 pandemic has had a disrupting impact on almost all industries. The travel sector, involving the movements of goods and people across country boundaries, is one of the most affected. At first, the COVID-19 pandemic resulted in the implementation of numerous travel restrictions, thus reducing the possibility of travel. Later, additional side effects of COVID-19, such as higher travel-associated anxiety and lower perceived safety, contributed to an overall decrease in travel demand (e.g., Lamb et al., 2020).
One of the most affected travel sectors is aviation, which recorded a drastic decrease in air travel demand and sees an overall perception of uncertainty about its future (Garrow and Lurkin 2021; Kim and Sohn 2022). In response to this, several scholars began to investigate the impact of COVID-19 on different facets of the aviation industry (Sun et al., 2021) related to finance (Maneenop and Kotcharin 2020; Vinod 2020), operations (Budd et al., 2020), and management (Bauer et al., 2020; Qiu, 2021) aspects.
Our study explores and estimates the impact of the COVID-19 pandemic on airline pricing curves, in terms of not only airfares but also price dispersion and the extent to which intertemporal price discrimination is applied. We base our analyses on an extensive dataset comprising more than 400,000 European flights departing from or arriving in Italy and, by means of a panel fixed effect regression, contribute to the literature by quantifying how the acknowledged determinants of pricing curves differently affect the variables of our interest before and during COVID-19. The outcomes demonstrate an overall decrease in prices of more than −30%, varying according to market destination and operating carrier.
The remainder of this paper is structured as follows. Section 2 overviews the main factors affecting prices, price dispersion, and the intertemporal price discrimination usually applied by carriers. Section 3 introduces the potential expected impact of COVID-19 on airline revenues due to variations in price sensitivity and passengers mix. Section 4 describes the methodology applied in the study. Descriptive statistics and preliminary results are shown in Section 5. Section 6 provides the outcomes of our analysis and the related discussion. Finally, Section 7 concludes our work.
2. Literature review
The pricing strategies of air carriers have been comprehensively studied in the literature. Scholars provide evidence of several factors affecting airfares. This section briefly recaps the studies on airline pricing, focusing on the factors recognized to impact prices, price dispersion, and the related intertemporal price discrimination strategies usually applied by air carriers.
Air transport prices are generally affected by two different sets of factors, namely market and flight characteristics. The former includes all those attributes related to origin and destination airports and local areas. These features comprise distance, market size, territories' population and richness, and market competition (Brueckner et al., 2013; Cattaneo et al., 2018; Malighetti et al., 2009; Obermeyer et al., 2013; Wan et al., 2009). Distance and market size—measured in terms of origin and destination market population, the number of offered seats on the market, or the flight frequency—are found to be positively correlated with prices (e.g., Malighetti et al., 2009; Wan et al., 2009). Similarly, territories’ richness, proxied with the average annual household income of the cities on a route or the gross domestic product (GDP) per capita of the connected areas, are determinants positively affecting airfares (e.g., Malighetti et al., 2009; Wan et al., 2009). Market competition plays a crucial role in determining the flight prices offered, although its effect is not straightforward. Most studies indicate that high competition leads to lower prices (Borenstein 1989; Brueckner et al., 2013). Evidence on the effect of competition on price discrimination largely demonstrates that higher competition, leading to higher pressure on prices, induces a greater ability for price discrimination (Cattaneo et al., 2016; Giaume and Guillou 2004; Malighetti et al., 2009). On the contrary, there is no common evidence regarding the effect of competition on price dispersion. While Borenstein and Rose (1994) and Stavins (2001) demonstrate that lower market concentration is associated with higher price dispersion, more recent studies find that competition has a negative effect on price dispersion (Dai et al., 2014; Gaggero and Piga 2011; Gerardi and Shapiro 2009; Howell and Grifell-Tatjé 2022).
Flight characteristics comprise attributes that are specific to the offered flight, varying between departing (such as day and hour) and reservation (such as advance booking days and number of available seats) features (Alderighi et al., 2015; Cattaneo et al., 2016; Escobari 2012; Mumbower et al., 2014). Because flight tickets are a revenue-managed good (Talluri and Van Ryzin 2004) having a limited capacity (i.e., number of available seats) and a pre-determined expiration (i.e., departure) date, the number of available seats and the days to departure are two key determinants of prices, jointly affecting airlines strategies (Alderighi et al., 2015; Escobari 2012). Other factors significantly affecting prices are the time of departure and the departing day of the week (DOW) (e.g., Cattaneo et al., 2016; Mantin and Koo 2010). A few studies also investigate the impact of day of the week purchase on prices and price dispersion (Mantin and Koo 2010; Morlotti et al., 2017; Puller and Taylor 2012). Ultimately, other factors are taken into consideration less frequently, such as the impact of delays (Forbes 2008); case-specific events, such as the de-hubbing by a legacy or low-cost carrier (Tan and Samuel 2016); or airline alliances (Wan et al., 2009).
Price discrimination and price dispersion may be correlated. Indeed, most of the variations in prices are associated with price discrimination strategies. In this paper, we analyze price dispersion and price discrimination separately. Grounding on previous studies on airline prices (Borenstein and Rose 1994; Cui et al., 2019; Gaggero and Piga 2011; Gerardi and Shapiro 2009; Howell and Grifell-Tatjé 2022), the Gini coefficient of inequality is used as a measure of price dispersion.1 The Gini coefficient of inequality ranges between 0 and 1 and values closer to one indicate greater inequality, that is higher price dispersion.
The most studied and recognized price discrimination strategy in airline pricing is the so-called intertemporal price discrimination, accounting for changes in airfares as departure day approaches. Indeed, airlines are acknowledged to apply such a strategy in order to maximize their revenues by relying on the different price elasticities of demand characterizing market segments. Market segmentation in the air transport industry commonly distinguishes between business (low-elastic) and leisure (high-elastic) passengers (e.g., Koenigsberg et al., 2008; Puller and Taylor 2012). This is largely corroborated in price elasticity studies (Morlotti et al., 2017; Mumbower et al., 2014), providing multiple insights on how price elasticity varies according to different departure and booking features, recognized to be the typical features that distinguish business from leisure travelers.
The acknowledged increasing price trend as departure day approaches has been demonstrated and modelled in several papers (e.g., Malighetti et al., 2009; Mantin and Rubin 2018). The simplest and most effective way to model price as departure day approaches is defined as in Malighetti et al. (2009):
| (1) |
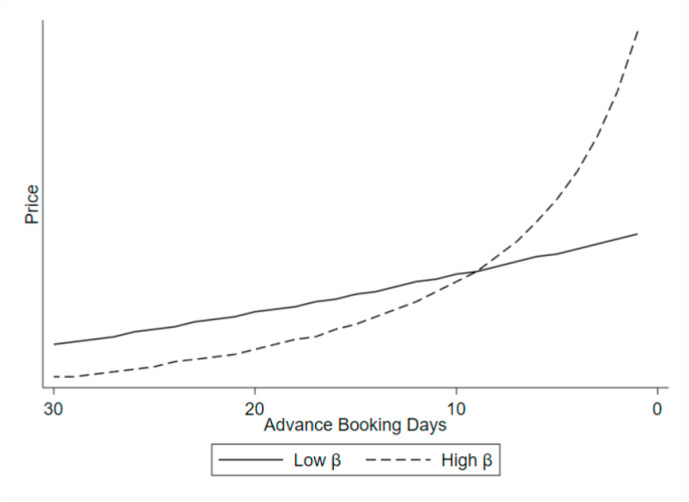
where is the fixed charge applied when the flight is fully booked, is the highest price level reached during the last day before departure (the lower the , the higher is the offered fare), and is the relationship between days to departure and prices. is the key parameter that identifies the extent to which airlines practice intertemporal price discrimination: a low implies a steady price trend, while a high positive reflects significantly discounted fares on advance purchases (see Fig. 1 ). In other words, considering a time span of a month, a higher (lower) indicates that the price offered 30 days in advance is (not) significantly lower than the price offered the day before departure.2 In this study, we rely on Equation 1 to estimate the price discrimination intensity of flights in our sample and to test the effect of COVID-19.
Fig. 1.
Variation of prices as departure day approaches in relation to different values at the same average price.
3. Airline revenues and the impact of COVID-19
As in other industries, airline revenues () are expressed as the product between prices and quantity, representing airfares ( and the number of seats sold (:
| (2) |
Demand can be expressed as a function of price, following a negative exponential form (Anjos et al., 2005; Malighetti et al., 2009). At each time , demand () is:
| (3) |
where depends on price at time , , and two parameters: and . represents the market size, that is, the market saturation quantity when price is set to 0, while is the price at which demand becomes elastic; it is defined as a function of time.3 Substituting Equation 3 in Equation 2, we obtain airline revenues as a function of prices, as well as and :
| (4) |
Revenue maximization arises when the derivative of the revenue function with respect to price is 0 (First Order Condition—FOC). Applying the FOC to Equation 4, for each time , we can compute the point at which revenue maximization occurs:
| (5) |
Solving Equation 5, we obtain that equals 0 when .
By representing revenues as a function of price as in Equation 4, Fig. 2 depicts its maximization occurring at (solid line). The COVID-19 pandemic has strongly impacted on the economy of all sectors, especially transportation. Accordingly, it has affected the airline revenues curve in multiple ways. First, we expect a vertical compression of the curve (dashed line in Fig. 2: ), due to changes in the parameter representing a decreasing proportion of individuals who are willing to travel, thereby decreasing the market saturation demand when the price is set to 0. Second, a change in the mix of passengers and in their related price sensitivity is registered.4 As a result of the COVID-19 pandemic, business interactions are adapted to online meetings, thus reducing the necessity of business passengers to travel (Hansmann and Binder 2021; Suau-Sanchez et al., 2020). Equally, we believe that price sensitivity has changed in relation to COVID-19. Specifically, linked to the decreasing overall willingness to travel, we expect passengers, especially those travelling for leisure purposes, to be more price elastic than usual, by travelling only if prices greatly drop. These variations lead to changes in the parameter of equation 3, with it being a combination of the passenger mix and the related price elasticity of demand (see footnote 3). The reduction in the number of business passengers travelling and the increasing price sensitivity would imply a horizontal compression in the revenue curve (dotted line in Fig. 2: .
Fig. 2.
Revenue curves at different levels of A and B.
Variations in and parameters lead to changes in the revenue curve, decreasing the maximum level () and affecting the optimal price level that can be offered ( variation). Interestingly, under the assumptions of a revenue-maximization objective and of a demand function as in Equation 3, the optimal price level does not depend on the demand shock due to COVID-19 (i.e., on the market size at price equal to 0). A lower would greatly affect the airline's overall profits, but not the optimal pricing to maximize profits (or minimize losses, which seems more likely in this case). Rather, the optimal pricing depends on the price sensitivity of passengers at each time . Considering the abovementioned expected consequences of COVID-19, in this paper, we analyze the impact of COVID-19 on the airfares offered by airlines, indirectly reflecting the effect of the pandemic on revenue price curves. We expect a consistent drop in the average prices offered by airlines during the COVID-19 pandemic, mirroring its dual impact on the change in the passenger mix in favor of more price-sensitive passengers (normally travelling for leisure purposes) and on the overall increase of price sensitivity, where low prices act to stimulate demand.
4. Methods
4.1. Empirical analysis
To assess the impact of COVID-19 on airfares, price dispersion, and airlines' intertemporal price discrimination, we rely on a fixed effect panel regression model with robust standard errors, with each observation corresponding to a flight. The time variable is equal to 2, as we observe each flight price's behavior before and after COVID-19.5 The estimating equation is as follows:
| (6) |
where refers to the dependent variable, is a vector of independent variables, is the unknown intercept for each flight, , is the error term, and is the time binary variable, controlling for the effect of the COVID-19 pandemic on the dependent variable. includes the following time varying characteristics:
-
—
weekly market concentration, computed as the Herfindahl–Hirschman Index (HHI) on the number of offered airline seats in a specific origin-destination market ();
-
—
market size, computed by the product of the population of the origin and destination countries ();
-
—
market richness, computed by the product of the GDP per capita of the origin and destination countries ();
-
—
A dummy equal to 1 whether the flight occurs during holidays or the day before holidays.
To account for time invariant variables (), we include interaction terms of the vector with the time binary factor, allowing us to capture differences in the partial effects of time invariant variables relative to COVID-19. comprises the flight destination () and the carrier type (. is equal to one when the offered flight departs and arrives in the same country, zero otherwise. is equal to one when the operating airline is a low-cost carrier, zero otherwise. Equation 6 becomes:
| (7) |
takes three different values, namely the average flight price per kilometer (), price dispersion (), and , computed per flight as in Equation 1.6 Additionally, recognizing the potential causality issue between our dependent variables and market concentration, represented by HHI, we implement a two-stage instrumental variable panel regression with fixed effect. Starting from Equation 7, our model is divided into two stages:
1st stage:
| (8) |
2nd stage:
| (9) |
In the first stage, represents the weekly market concentration observed on the route where flight is offered at time and is the selected instrumental variable. In the second stage, is the predicted weekly market concentration from the first stage. and are the unknown flight-specific intercepts of the first and second stages, respectively, while and are the error terms. In both stages, is the product of the time binary variable with a vector of time invariant factors, while is the vector of time varying explanatory variables as in Equation 6, without .
The reliability of a two-stage instrumental variable approach depends on the chosen , which needs to be correlated with the instrumented variable while, simultaneously, not affecting the dependent one. Similar to former studies (Cattaneo et al., 2018, 2022; Mumbower et al., 2014), for each market of flight , we employ as an instrument variable the weekly HHI in other markets with similar lengths of haul (i.e., origin-destination markets with a distance of ±10% compared to market m). Our test reveals that the selected instrumental variable is appropriate and not weak (Kleibergen–Paap Wald statistic: 75.135—p-value<0.01).
4.4. Data and sources
We rely on a dataset including the airfares of the major European routes departing from (and arriving in) Italy in 2019 and 2020 (see Fig. 3 for an overview of the routes included in the analysis). The data was downloaded from an online fare aggregator platform providing information on all possible air travel alternatives for a specific origin and destination market. The gathered data consists of the daily economy fares of all flights operated on 92 airport pairs, offered from one month to one day to departure. Overall, we recorded information on more than 400,000 flights, 82% of which were offered before COVID-19. For the analysis, we take into consideration only flights offered both before and after COVID-19, on the same market and by the same carrier, thus departing during the same week of the year and in the same DOW, at the same hour of the day, and with more than 15 observed prices (i.e., with a fare history of more than two weeks). This results in an overall data sample of 68,282 flights (Table 1 ).
Fig. 3.
Considered markets.
Table 1.
Sample size.
| No. of observations | Before COVID-19 | After COVID-19 | Total |
|---|---|---|---|
| Overall | 327,606 | 73,243 | 400,849 |
| Matched according to departing month, DOW, and time interval* | 117,408 | 59,823 | 177,231 |
| Matched according to departing week, DOW, and time interval* | 71,004 | 52,002 | 123,006 |
| Matched according to departing week, DOW, and hour | 34,141 | 34,141 | 68,282 |
*Time interval refers to morning, lunch, evening, and night hours.
The weekly market concentration () and the classification of low-cost airlines were retrieved from the OAG database, while the population and the GDP per capita of each departing and arriving country were obtained from Eurostat. Ultimately, was derived by means of a nonlinear regression model fitting Equation 1.7
5. Descriptive statistics and preliminary results
Table 2 shows the descriptive statistics of the main variables included in our model, before and after COVID-19. Overall, a 34% fall in average airline prices, from €158 to €104, was recorded. Similarly, the average price per kilometer also dropped, from 0.242€/km to 0.167€/km (−31%). After COVID-19, and also displayed a drop in their average value. Indeed, in 2020, a drop in not only the population but also the GDP per capita of the considered countries was recorded. In terms of population, the highest drop was registered for Italy: from 60.4 million people in 2019 to 59.6 million (−1.2%). United Kingdom and Spain present the highest drop in GDP per capita (−11%), followed by Italy (−9%) and France (−8%). Given the reduction of alternative flights offered after COVID-19, the average market concentration increased (from 68.4% to 71.5%), as carriers mainly tended to abandon secondary and thinner routes.
Table 2.
Descriptive statistics of variables before and after COVID-19.
| Variable | Before COVID-19 |
After COVID-19 |
T-test P-value | ||
|---|---|---|---|---|---|
| Mean | St. Dev. | Mean | St. Dev. | ||
| (€) | 158.445 | 98.969 | 103.824 | 73.540 | <0.01 |
| (€/km) | 0.242 | 0.162 | 0.167 | 0.131 | <0.01 |
| – price dispersion | 0.151 | 0.098 | 0.131 | 0.104 | <0.01 |
| – price discrimination | 0.077 | 0.109 | 0.055 | 0.103 | <0.01 |
| (billion)* | 2,966,396 | 1,653,980 | 2,944,188 | 1,636,463 | 0.973 |
| (million)* | 1009.028 | 99.534 | 880.118 | 87.210 | 0.340 |
| + | 0.684 | 0.311 | 0.715 | 0.313 | <0.01 |
* T-test at country-market level. + T-test at weekly -market combination level.
An interesting outcome emerges from the difference in the average values of the Gini index and of , estimated as in Equation 1. The average value of price dispersion () decreased from 0.151 to 0.131 (−13%). Consistently, average values dropped from 0.08 to 0.06 (−29%), suggesting a lower intertemporal price discrimination strategy applied by carriers after COVID-19. Fig. 4 illustrates how price per kilometer varies over time. Both left and right panels, representing price per kilometer before and after COVID-19, respectively, depict an increasing trend as the departure day approaches, thus implying that the well-known intertemporal price discrimination is applied both before and after COVID-19. However, interesting differences emerge. Before COVID-19, on average, the price per kilometer at 30 days to departure is 0.179€, which is more than double that of the day before departure—0.407€. After COVID-19, the ratio between the price per kilometer the day before and at 30 days to departure is equal to 1.8, suggesting a steadier price over time ( equal to 0.134€ and 0.246€ at 30 days and one day to departure, respectively).
Fig. 4.
Price per kilometer by day of advance.
To test the significance of differences before and after COVID-19, we perform a paired t-test, determining whether the mean difference between variables in the two studied periods for matching flights is 0. The t-test p-values lower than 0.01 displayed in Table 2 suggest that the difference in the mean values of , , , and are different from 0. Therefore, COVID-19 significantly impacts these factors. On the contrary, no significant differences are found in the estimates of and .
Table 3 presents the descriptive statistics before and after COVID-19 of , and at varying flight characteristics, namely the operating carrier and market destination. Around 33% of the flights included in our sample are offered by low-cost carriers and 60% of flights are domestic (i.e., departing from and arriving in Italy). On average, is lower in domestic markets than in international ones (by around −0.03€ per kilometer). In both domestic and international markets, decreases by around 0.08€. Price dispersion does not seem to significantly vary due to COVID-19 in international markets. On the contrary, a significant decrease is registered in domestic markets’ price dispersion (−30%). Differences emerge when evaluating . Price discrimination was found to be lower in international markets both before and after COVID-19 and to decrease with COVID-19. However, the estimates on the domestic markets reflect a large change before and after COVID-19, varying from 0.091 to 0.056, respectively, corresponding to a variation of −38%, compared to −5% for international flights. This difference suggests that while airlines normally apply important price discrimination in domestic markets, with COVID-19, their pricing curves more closely resemble those of international markets (see Fig. 5 a).
Table 3.
Average price per kilometer and by flight destination, type of carrier, and carrier before and after COVID-19.
| No. of Flights |
– Average Price per Kilometer |
– Price Dispersion |
– Price Discrimination |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Before COVID-19 |
After COVID-19 |
T-test P-value | Before COVID-19 |
After COVID-19 |
T-test P-value | Before COVID-19 |
After COVID-19 |
T-test P-value | ||||||||
| Mean | St. Dev. | Mean | St. Dev. | Mean | St. Dev. | Mean | St. Dev. | Mean | St. Dev. | Mean | St. Dev. | |||||
| Flight destination | ||||||||||||||||
| Domestic | 20,458 | 0.252 | 0.152 | 0.177 | 0.125 | <0.01 | 0.158 | 0.108 | 0.126 | 0.110 | <0.01 | 0.091 | 0.121 | 0.056 | 0.106 | <0.01 |
| International | 13,683 | 0.227 | 0.174 | 0.151 | 0.137 | <0.01 | 0.140 | 0.082 | 0.139 | 0.094 | 0.231 | 0.056 | 0.084 | 0.053 | 0.098 | 0.010 |
| Carrier type | ||||||||||||||||
| Low-cost | 11,296 | 0.133 | 0.072 | 0.075 | 0.068 | <0.01 | 0.174 | 0.102 | 0.171 | 0.111 | 0.027 | 0.091 | 0.130 | 0.061 | 0.118 | <0.01 |
| Full-service | 22,845 | 0.296 | 0.167 | 0.212 | 0.131 | <0.01 | 0.139 | 0.095 | 0.111 | 0.094 | <0.01 | 0.070 | 0.096 | 0.052 | 0.094 | <0.01 |
| Carrier | ||||||||||||||||
| AZ | 16,362 | 0.298 | 0.148 | 0.216 | 0.114 | <0.01 | 0.140 | 0.101 | 0.097 | 0.090 | <0.01 | 0.079 | 0.103 | 0.049 | 0.092 | <0.01 |
| FR | 5783 | 0.119 | 0.069 | 0.052 | 0.049 | <0.01 | 0.227 | 0.100 | 0.220 | 0.122 | <0.01 | 0.136 | 0.158 | 0.089 | 0.150 | <0.01 |
| U2 | 4431 | 0.152 | 0.072 | 0.099 | 0.076 | <0.01 | 0.124 | 0.068 | 0.122 | 0.067 | 0.109 | 0.047 | 0.066 | 0.033 | 0.057 | <0.01 |
| KL | 1667 | 0.245 | 0.086 | 0.179 | 0.059 | <0.01 | 0.116 | 0.053 | 0.122 | 0.071 | <0.01 | 0.036 | 0.043 | 0.048 | 0.072 | <0.01 |
| AF | 1257 | 0.323 | 0.174 | 0.226 | 0.131 | <0.01 | 0.141 | 0.073 | 0.163 | 0.103 | <0.01 | 0.046 | 0.067 | 0.073 | 0.117 | <0.01 |
| BA | 1233 | 0.280 | 0.147 | 0.138 | 0.093 | <0.01 | 0.180 | 0.094 | 0.214 | 0.102 | <0.01 | 0.075 | 0.100 | 0.102 | 0.127 | <0.01 |
| VY | 1048 | 0.124 | 0.056 | 0.094 | 0.055 | <0.01 | 0.095 | 0.060 | 0.112 | 0.072 | <0.01 | 0.033 | 0.053 | 0.030 | 0.060 | 0.222 |
| LH | 918 | 0.434 | 0.178 | 0.372 | 0.173 | <0.01 | 0.130 | 0.058 | 0.111 | 0.074 | <0.01 | 0.047 | 0.040 | 0.044 | 0.084 | 0.453 |
| IB | 599 | 0.147 | 0.069 | 0.086 | 0.038 | <0.01 | 0.140 | 0.089 | 0.124 | 0.068 | <0.01 | 0.060 | 0.119 | 0.022 | 0.053 | <0.01 |
| UX | 524 | 0.128 | 0.066 | 0.059 | 0.029 | <0.01 | 0.104 | 0.061 | 0.115 | 0.081 | <0.01 | 0.028 | 0.043 | 0.026 | 0.063 | 0.429 |
Fig. 5.
Price per kilometer by time period (before or after COVID-19) and market destination (panel a) or carrier type (panel b).
Distinctions emerge between low-cost and full-service carriers. Consistently, low-cost carriers offer lower prices with respect to traditional ones. However, the difference in the offered prices shrinks with COVID-19. While the average price per kilometer decreases by around −0.06€ (−44%) for low-cost carriers, this value reaches −0.08€ for full-service carriers (−28%). Also the price dispersion and the discrimination measures record a drop with COVID-19 for both traditional and low-cost airlines. For what concerns price dispersion, the Gini coefficient is higher in case the operating carrier is a low-cost, both before and after COVID-19. Normally, low-cost airlines are found to engage in more price discrimination than traditional ones. This continues to happen after COVID-19, despite the difference being reduced (see Fig. 5b).
The last part of Table 3 illustrates the statistics for the top 10 carriers in terms of offered flights in our sample. The majority of flights are offered by Alitalia (AZ–48% of observations), followed by Ryanair (FR–17%), and easyJet (U2–13%). All carriers’ airfares are found to be lower after COVID-19. The highest discounts are offered by British Airways (−0.14€/km), Air France (−0.10€/km), and Alitalia (−0.08€/km). Ryanair is the carrier that presents the highest decrease in fares (−56%), with the lowest average price drops being registered for Vueling (−0.03€/km) and easyJet (−0.05€/km). Vueling (VY), Lufthansa (LH), and Air Europa (UX) are the only airlines that do not present a significant variation in their price discrimination strategy (), while easyJet (U2) is the only carrier whose price dispersion does not change significantly with COVID-19. Most of the airlines show a reduction in both price dispersion and the value, in line with the estimates of low-cost and full-service carriers.8 Fig. 6 reveals the average price per kilometer as departure day approaches for Alitalia (AZ) and Vueling (VY), reflecting very different patterns. Both pricing patterns record average lower values after COVID-19; however, after COVID-19, the curves greatly flatten out for AZ (panel a), while maintaining a similar trajectory for VY (panel b).
Fig. 6.
Price per kilometer by day of advance and carrier.
6. Results and discussion
The results of the panel regression with fixed effect are depicted in Table 4 . Columns 1 to 3 display the outcomes of the simplest model, as in Equation 6. COVID-19 has a significant negative impact on the average price per kilometer, price dispersion, and price discrimination, reducing by −0.07€ and and by −0.05. Consistent with previous literature (e.g., Borenstein 1989; Brueckner et al., 2013; Morlotti et al., 2017), a higher market concentration was found to lead to higher average prices per kilometer. When carriers operate as monopolists, the average price per kilometer is 0.03€ higher. Interestingly, the coefficient is positive and significant also for and , indicating that higher competition leads to a steadier price trend, also in relation to the days to departure. This is in line with results from previous studies (Dai et al., 2014; Gaggero and Piga 2011; Gerardi and Shapiro 2009; Howell and Grifell-Tatjé 2022), who demonstrated that competition induces lower price dispersion, although it opposes the belief that higher pressure on prices by competitors leads to a greater ability for price discrimination (Cattaneo et al., 2016; Giaume and Guillou 2004; Malighetti et al., 2009). Reasonably, the average price per kilometer increases for flights departing during holidays and the price dispersion and price discrimination intensity decrease. Ultimately, market size () and market richness () coefficients significantly impact both and .
Table 4.
Panel regression with fixed effects.
| Variables | (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
||
|---|---|---|---|---|---|---|---|---|
| −0.0715*** (0.0030) | −0.5305*** (0.0582) | −0.0497*** (0.0025) | ||||||
| Y | N | N | −0.0604*** (0.0050) | −0.4507*** (0.0636) | −0.0304*** (0.0039) | |||
| Y | N | Y | −0.0741*** (0.0032) | −0.5979*** (0.0579) | −0.0470*** (0.0026) | |||
| Y | Y | N | −0.0211*** (0.0056) | −0.4942*** (0.0644) | −0.0552*** (0.0044) | |||
| Y | Y | Y | −0.0545*** (0.0030) | −0.3619*** (0.0516) | −0.0494*** (0.0031) | |||
| 0.0305*** (0.0027) | 0.2779*** (0.0381) | 0.0382*** (0.0031) | 0.0341*** (0.0027) | 0.2603*** (0.0384) | 0.0339*** (0.0031) | |||
| 0.0131*** (0.0028) | −0.2338*** (0.0552) | −0.0138*** (0.0026) | 0.0154*** (0.0028) | −0.2212*** (0.0552) | −0.0146*** (0.0026) | |||
| −0.0001*** (0.0000) | 0.0003 (0.0003) | 0.0003*** (0.0000) | −0.0003*** (0.0000) | −0.0002 (0.0006) | 0.0002*** (0.0000) | |||
| 0.0001*** (0.0000) | −0.0026*** (0.0004) | −0.0004*** (0.0000) | 0.0003*** (0.0000) | −0.0021*** (0.0005) | −0.0003*** (0.0000) | |||
| Constant |
0.4331*** (0.0564) |
−1.2699 (1.1604) |
−0.7861*** (0.0540) |
0.9662*** (0.1133) |
0.1256 (2.0229) |
−0.5702*** (0.0801) |
||
| Observations | 68,282 | 68,282 | 68,282 | 68,282 | 68,282 | 68,282 | ||
| R-squared | 0.2825 | 0.0123 | 0.0451 | 0.2927 | 0.0139 | 0.0483 | ||
| Number of flights | 34,141 | 34,141 | 34,141 | 34,141 | 34,141 | 34,141 | ||
Robust standard errors in parentheses; ***p < 0.01, **p < 0.05, *p < 0.1.
Columns 4 to 6 add to the initial model the time invariant variables and , as in Equation 7. Generally, the results corroborate the outcomes previously discussed. COVID-19 has a negative impact on the average price per kilometer, on price dispersion, and on . During COVID-19, the average price per kilometer decreases more for domestic than for international routes and more for traditional carriers' than for low-cost carriers’ flights. Combined effects demonstrate that the decrease in is equal to −0.06€ (−0.07€) for full-service carriers operating international (domestic) flights. For low-cost carriers, the decrease in the average price per kilometer is −0.02€ (−0.05€) for international (domestic) markets. Even if the decrease in is greater in domestic markets for both low-cost and full-service carriers, the airfares of flights operated by low-cost carriers in international markets decrease by a smaller amount compared to traditional carriers, for which the effect on domestic and international markets slightly differs. Differences emerge for price dispersion and . While the general results suggest a larger negative price dispersion variation associated with full-service carrier flights and in domestic markets, the highest decrease in the price discrimination coefficient () after COVID-19 is registered for international flights operated by low-cost carriers.
Several possible factors contribute to these results. First, because the drop in business passengers’ demand mainly affects traditional carriers, price sensitivity increases more than for low-cost carriers, thus leading to a larger price range. Second, as offered fares are generally higher for traditional carriers in the pre COVID-19 setting, they have more room for price-drop related demand stimulation. Additionally, even when air tourism partially restarted in summer 2020, there were several restrictions that remained in place for most international flights. This was not the case for domestic markets which experienced partial recoveries during the summer and fall seasons, as tourists preferred unrestrained domestic destinations (before the COVID-19 pandemic regained strength in October 2020). Thus, airlines adapt more to a market comprising a higher portion of price-sensitive tourists by decreasing prices on domestic routes, where there was a higher possibility to stimulate demand. Ultimately, given the drop in business passengers, airlines faced a more homogenous demand, thereby reducing the need for intertemporal price discrimination for both traditional and low-cost carriers. However, the decrease was more significant for low-cost carriers, which tend to rely more on intertemporal price discrimination to better capture the portion of less price-elastic passengers who usually purchase their seats a few days before departure.
Table 5 shows the results of the two-stage panel regression with fixed effect of the full model (Columns 4 to 6 of Table 4). Column 1 displays the first stage as in Equation 8. The selected instrumental variable (), representing the average weekly market concentration in similar markets, positively and significantly impacts . With COVID-19, the market concentration increases due to the large number of flights that are no longer operating (margins equal to +2.70%). Eventually, market concentration is found to be lower in larger markets and during holidays.
Table 5.
Two-stage panel regression with fixed effect of the full model.
| Variables | (1) |
(2) |
(3) |
(4) |
||
|---|---|---|---|---|---|---|
|
|
|
|
|
|||
| 1st stage | 2nd stage | 2nd stage | 2nd stage | |||
| 0.9127*** (0.0275) | ||||||
| Y | N | N | 0.0470*** (0.0085) | −0.0878*** (0.0054) | −1.1372*** (0.0873) | −0.0457*** (0.0046) |
| Y | N | Y | −0.0740*** (0.0057) | −0.0829*** (0.0032) | −0.8176*** (0.0623) | −0.0519*** (0.0027) |
| Y | Y | N | −0.0252*** (0.0087) | −0.0336*** (0.0056) | −0.8087*** (0.0761) | −0.0622*** (0.0046) |
| Y | Y | Y | −0.0375*** (0.0057) | −0.0652*** (0.0031) | −0.6307*** (0.0576) | −0.0554*** (0.0032) |
| 0.1900*** (0.0167) | 4.1642*** (0.2932) | 0.1210*** (0.0136) | ||||
| −0.0204*** (0.0047) | 0.0177*** (0.0030) | −0.1633*** (0.0587) | −0.0133*** (0.0027) | |||
| −0.0007*** (0.0000) | −0.0002*** (0.0000) | 0.0018** (0.0007) | 0.0003*** (0.0000) | |||
| 0.0003*** (0.0001) | 0.0001*** (0.0000) | −0.0049*** (0.0006) | −0.0003*** (0.0000) | |||
| Constant |
2.2718*** (0.1292) |
0.6829*** (0.1128) |
−6.9692*** (2.1634) |
−0.7285*** (0.0856) |
||
| Observations | 68,282 | 68,282 | 68,282 | 68,282 | ||
| R-squared | 0.0797 | |||||
| Number of flights | 34,141 | 34,141 | 34,141 | 34,141 | ||
Robust standard errors in parentheses; ***p < 0.01, **p < 0.05, *p < 0.1.
Estimations from the first stage are included as regressors in the second stage, for , and . Although with slightly different magnitudes, the outcomes of the two-stage regression, accounting for the potential reverse causality existing between price, price dispersion, or price discrimination and market concentration, are similar to those reported in Table 4.
The variable in Equations 6 and 7 represents a cut-off point dividing our sample in two periods, before and after COVID-19. However, after the COVID-19 outbreak, European and national authorities proposed different interventions to prevent and control the spread of the disease. For what concerns the travel and tourism industry, one of the most impacting interventions is the mandatory quarantine for international travelers. Accordingly, in the following paragraph, we show how the mandatory quarantine affects prices and price curves.
A new factor () is included as interaction with the dummy variables considered in the full model. is a dummy variable equal to one if the departing or arriving airport is located in a country where mandatory quarantine for international travelers is required, zero otherwise. Details on the countries and the periods when mandatory quarantine for international travelers was applied are collected from the dataset on country response measures to COVID-19 of the European Centre for Disease Prevention and Control (ECDPC). Being the measure applied only to international travelers, our sample is limited to international flights.
Results are available in Table 6 . Consistently with previous results, COVID-19 negatively affects , price dispersion and intertemporal price discrimination and no interesting differences emerge when considering the control variables. negatively affects all the explored dependent variables.9 Specifically, after COVID-19, more than doubled the decrease in the average price per kilometer (from −0.0693 to −0.1393 and from −0.0378 to −0.0796 for traditional and low-cost carriers, respectively). Similarly, price dispersion and price discrimination are 1.6 times lower. Interestingly, the decrease in the average price per kilometer and in price dispersion due to the quarantine is greater for traditional carriers than for low-cost carriers.
Table 6.
Panel regression with fixed effects, controlling for the impact of mandatory quarantine for international travelers.
| Variables | (1) | ||||
|---|---|---|---|---|---|
| Y | N | N | −0.0693*** | −0.8585*** | −0.0491*** |
| (0.0054) | (0.0758) | (0.0054) | |||
| Y | Y | N | −0.0378*** | −1.0660*** | −0.0944*** |
| (0.0057) | (0.0765) | (0.0060) | |||
| Y | N | Y | −0.0699*** | −0.5467*** | −0.0308*** |
| (0.0049) | (0.0723) | (0.0046) | |||
| Y | Y | Y | −0.0418*** | −0.5221*** | −0.0452*** |
| (0.0054) | (0.0722) | (0.0052) | |||
| 0.0306*** | 0.3202*** | 0.0430*** | |||
| (0.0056) | (0.0499) | (0.0053) | |||
| 0.0155*** | −0.0782 | −0.0056 | |||
| (0.0044) | (0.0633) | (0.0042) | |||
| −0.0001 | 0.0023** | 0.0001 | |||
| (0.0001) | (0.0010) | (0.0001) | |||
| 0.0001** | −0.0040*** | −0.0003*** | |||
| (0.0000) | (0.0005) | (0.0000) | |||
| Constant | 0.5813** | −5.5939* | 0.0616 | ||
| (0.2798) | (3.0964) | (0.2058) | |||
| Observationsa | 23,232 | 23,232 | 23,232 | ||
| R-squared | 0.2786 | 0.0365 | 0.0428 | ||
| Number of flights | 11,616 | 11,616 | 11,616 | ||
Robust standard errors in parentheses; ***p < 0.01, **p < 0.05, *p < 0.1.
The dataset is limited to international flights. Due to data unavailability, the dataset does not include flights from or to Switzerland and Great Britain.
7. Conclusion
Our study explores the impact of COVID-19 on airline price curves. We rely on a unique dataset of all major European flights departing from and arriving in Italy during 2019 and 2020. By considering only the flights operated both before and after COVID-19, we assess the existing differences in terms of average price per kilometer and price discrimination intensity. The results reveal an overall average decrease of 31%, with interesting differences in terms of the operating carrier. In relative terms, the average price per kilometer registers the highest drop for low-cost carriers (−44%), especially for Ryanair, for which the average price per kilometer more than halves after COVID-19. Intriguing results are also found for price dispersion and , the estimated parameter that takes into account the price discrimination level emerging from price curves. After COVID-19, the price dispersion and the price discrimination level decrease on average by −13% and −29%, respectively. Normally, price discrimination is more intense in flights operated by low-cost carriers and on international routes. After COVID-19, the difference by carrier type and especially by market destination shrinks, revealing more similar curves. Indeed, values decrease by −38% in domestic markets and only by −5% in international ones.
Further analyses demonstrate the importance of accounting for multiple factors when studying the impact of COVID-19 on price curves (in terms of average price per kilometer, price dispersion, and ). We base our analysis on a two-stage panel regression with fixed effect to test the impact of market and flight characteristics on the variables of interest, correcting for the potential causality issue occurring between our dependent variables and competition, expressed as the weekly market concentration, by means of an instrumental variable approach. The results indicate that both market and flight characteristics play a significant role. The decrease in the average price per kilometer slightly differs among full-service carriers operating on international and domestic routes (−0.06€ and −0.07€, respectively), while for low-cost carriers, the decrease in the average price per kilometer of domestic flights (−0.05€) is almost three times that of international flights (−0.02€). Differences emerge also for price dispersion and , for which the largest decrease after COVID-19 is registered for domestic flights operated by traditional carriers and international flights operated by low-cost carriers, respectively. Ultimately, we explore the impact of mandatory quarantine of international travelers on price curves. Outcomes reveals a further drop in prices, , and associated with that intervention.
Our study contributes to the current literature on airline pricing by estimating the impact of COVID-19 on prices, price dispersion, and price discrimination. The outcomes of our study can be interpreted in light of the expected impact of COVID-19 on the passenger mix as well as on their price sensitivity. COVID-19 has led to a decrease in the proportion of business passengers flying, because of the increase in remote meetings and smart working hours. Additionally, passengers’ willingness to travel has also decreased, due to all the potential risks associated with taking a flight during the pandemic (e.g., Lamb et al., 2020), as higher anxiety, and lower perceived safety. To this end, lower prices can be used as an instrument to stimulate individuals to travel.
This study opens up avenues for future research. First, it would be interesting to enlarge the sample size, considering additional geographical settings apart from the Italian-European one. Intriguing differences could emerge considering the different acknowledged propensities for flying and intensity of travelling in other contexts, such as the in the United States. Second, taking into account the revenue management applied by airlines, it would be interesting to test how the capacity and the price level of different fare buckets have varied with COVID-19, exploring if and how different airlines have adapted their strategy in relation to the pandemic. Third, when the COVID-19 pandemic is finally considered as ended or fully under control, an appropriate panel analysis on a larger time span should be conducted to better understand the impact of COVID-19 in the short, medium, and long terms, providing more evidence on the needed time for the air travel sector to recover (Gudmundsson et al., 2021). Indeed, most of COVID-19 effects on fares are likely to be transitory. Average prices are expected to increase again due to the potential positive future effect of the reduction in COVID-19 cases on people's willingness to travel (Kim and Sohn 2022). However, effects on price discrimination are not easily predictable and could be lasting longer. This is particularly true in view of the prospective decreased necessity of business passengers to travel, leading to variations in the passenger mix with respect to the pre-COVID-19 period. This would constitute bad news for both airlines' profits and price sensitive (leisure) passengers, as a decrease in price discrimination intensity implies that lower discounts would be offered for early bookings.
Credit author statement
Chiara Morlotti: Conceptualization, Methodology, Data Curation, Formal analysis, Writing - Original Draft, Writing - Review & Editing.
Renato Redondi: Conceptualization, Methodology, Writing - Original Draft, Writing - Review & Editing, Supervision.
Declarations of competing interest
None.
Footnotes
Different measures of price dispersion may be used to account for price variation in airfares. The Gini index of inequality is the most used measure in the air transport industry, as it is based on the entire flight price history and it is scale invariant, allowing to make comparisons among different markets (Gaggero and Piga 2011). Other popular indices of price dispersion include the interquartile range (IQR) and the coefficient of variation (CV) (e.g., Cui et al., 2019). IQR is computed as the difference between the 75th and 25th percentiles of the airfare distribution, while CV is the ratio of the flight price history standard deviation to its average (Cui et al., 2019). For the sake of comparability, analysis with these two measures of price dispersion is included in the Appendix. Qualitatively, results corroborate the outcomes derived by using the Gini coefficient of inequality as index of price dispersion.
Given the airline tendency to increase prices as departure day approaches, price dispersion and intertemporal price discrimination are generally correlated. However, they are not measuring the same phenomenon. A high price dispersion may be due to price increases or drops occurring at any time during the booking time span. A high positive indicates an increasing trend of prices along the booking time span. Please note that, the estimated derived from Equation 1 could be both positive and negative. A negative would suggest the presence of significant discounts closer to departure day. In this study, coherently with the intertemporal price discrimination applied by airlines, no evidence of negative values is registered.
Price elasticity of demand (η) represents the change in demand in relation to a change in price and is thus computed as . From Equation 2, it is possible to compute as In the presence of more than one segment, is the quantity weighted averaged price elasticity of demand in different segments , i.e., .
Former literature highlights a difference in the impact of COVID-19 on business and leisure trips, expecting a faster recovery of leisure demand (Suau-Sanchez et al., 2020). This theory is supported by a change in the passenger mix in European traffic, in favor of a greater portion of leisure passengers in 2020. In Italy, the Italian Institute of Statistics (ISTAT 2022), reported a 4-percentage point drop in the share of business trips, from 11% in 2019 to around 7% in 2020, and remained stable in 2021.
Since all flights depart or arrive in Italy, we select March 8, 2020, as the day that defines the time interval before or after COVID-19. This corresponds to the date of the Italian Prime Ministerial Decree (DPCM 8 Marzo, 2020) aimed at defining the measures to contain and manage the epidemiological emergency caused by the COVID-19 pandemic.
The dependent variable representing price dispersion is the log-odds ratio of the Gini index, computed as , providing an unbounded value (Cui et al., 2019; Gaggero and Piga 2011; Gerardi and Shapiro 2009; Howell and Grifell-Tatjé 2022).
Average R-squared = 0.965 with a 95% confidence interval from 0.964 to 0.965.
In the cases of KLM (KM), Air France (AF) and British Airways (BA), both price dispersion and β values increase after COVID-19. In our sample, these carriers operate in markets normally used to connect Italian major airports to their respective hubs (Fig. 3). In 2020, during COVID-19, major European hubs were among the few to remain open to some intercontinental traffic and important variations in carriers' networks and market competition were verified. Average market concentration increased, especially for traditional airlines (77% vs 71%—t-test p-value <0.01), as some carriers tended to greatly limit the offered services in (or even abandon) some routes. As shown below in Table 5, the higher the HHI, the higher the price discrimination and dispersion. This can explain the higher values for some of the traditional carriers in our sample, other things being equal. Statistics reported in Table 3 are the result of different factors affecting airlines' pricing curves, thus interpretation is not straightforward. We test the impact of multiple flight-, airline-, and market-features on the variables of interest in Section 6.
Two-stage panel regression results, controlling for the effect of mandatory quarantine, are available in the Appendix. No relevant differences emerge.
Appendix.
Table 7.
Panel regression with fixed effects with, as dependent variables, two alternative measures of price discrimination, namely the interquartile range (IQR), and the coefficient of variation (CV)
| Variables$ | (5) |
(6) |
(7) |
(8) |
||
|---|---|---|---|---|---|---|
|
|
|
|||||
| 2nd stage | 2nd stage | |||||
| Y | N | N | −0.0198*** | −0.0731*** | −0.0640*** | −0.1939*** |
| (0.0044) | (0.0077) | (0.0053) | (0.0111) | |||
| Y | N | Y | −0.0450*** | −0.1443*** | −0.0591*** | −0.1829*** |
| (0.0024) | (0.0049) | (0.0027) | (0.0060) | |||
| Y | Y | N | −0.0056 | −0.0866*** | −0.0259*** | −0.1419*** |
| (0.0048) | (0.0086) | (0.0053) | (0.0108) | |||
| Y | Y | Y | −0.0185*** | −0.0378*** | −0.0358*** | −0.0851*** |
| (0.0023) | (0.0057) | (0.0027) | (0.0069) | |||
| 0.0378*** | 0.0768*** | 0.2890*** | 0.7638*** | |||
| (0.0026) | (0.0054) | (0.0163) | (0.0334) | |||
| 0.0010 | −0.0346*** | 0.0048* | −0.0244*** | |||
| (0.0021) | (0.0047) | (0.0024) | (0.0059) | |||
| 0.0000 | 0.0002*** | 0.0002*** | 0.0006*** | |||
| (0.0000) | (0.0001) | (0.0000) | (0.0001) | |||
| 0.0000 | −0.0006*** | −0.0001*** | −0.0011*** | |||
| (0.0000) | (0.0001) | (0.0000) | (0.0001) | |||
| Constant | 0.0378*** | 0.0768*** | 0.2890*** | 0.7638*** | ||
| (0.0026) | (0.0054) | (0.0163) | (0.0334) | |||
| Observations | 68,282 | 68,282 | 68,282 | 68,282 | ||
| R-squared | 0.1088 | 0.0645 | ||||
| Number of flights | 34,141 | 34,141 | 34,141 | 34,141 | ||
Robust standard errors in parentheses; ***p < 0.01, **p < 0.05, *p < 0.1.
IQR is computed as the difference between the 75th and 25th percentiles of the airfare distribution (Cui et al., 2019).
CV is the ratio of the flight price history standard deviation to its average.
Table 8.
Two-stage panel regression with fixed effects, controlling for the impact of mandatory quarantine for international travelers
| Variables | (1) |
(2) |
(3) |
||
|---|---|---|---|---|---|
| Y | N | N | −0.1408*** | −1.5448*** | −0.0852*** |
| (0.0082) | (0.1014) | (0.0066) | |||
| Y | Y | Y | −0.0755*** | −1.4277*** | −0.1135*** |
| (0.0082) | (0.0974) | (0.0068) | |||
| Y | N | N | −0.1608*** | −1.4185*** | −0.0767*** |
| (0.0087) | (0.1043) | (0.0068) | |||
| Y | Y | Y | −0.0838*** | −0.9245*** | −0.0663*** |
| (0.0071) | (0.0879) | (0.0059) | |||
| 0.4748*** | 4.5834*** | 0.2676*** | |||
| (0.0331) | (0.3257) | (0.0240) | |||
| 0.0185*** | −0.0493 | −0.0041 | |||
| (0.0062) | (0.0728) | (0.0047) | |||
| −0.0012*** | −0.0076*** | −0.0004*** | |||
| (0.0001) | (0.0014) | (0.0001) | |||
| −0.0001 | −0.0055*** | −0.0004*** | |||
| (0.0001) | (0.0006) | (0.0000) | |||
| Constant | 3.7404*** | 24.7217*** | 1.6581*** | ||
| (0.4119) | (4.1673) | (0.2747) | |||
| Observationsa | 23,232 | 23,232 | 23,232 | ||
| Number of flights | 11,616 | 11,616 | 11,616 | ||
Robust standard errors in parentheses; ***p < 0.01, **p < 0.05, *p < 0.1.
The dataset is limited to international flights. Due to data unavailability, the dataset does not include flights from or to Switzerland and Great Britain.
References
- Alderighi M., Nicolini M., Piga C.A. Combined effects of capacity and time on fares: insights from the yield management of a low-cost airline. Rev. Econ. Stat. 2015;97(4):900–915. [Google Scholar]
- Anjos M.F., Cheng R.C.H., Currie C.S.M. Optimal pricing policies for perishable products. Eur. J. Oper. Res. 2005;166(1):246–254. [Google Scholar]
- Bauer L.B., Bloch D., Merkert R. Ultra Long-Haul: an emerging business model accelerated by COVID-19. J. Air Transport. Manag. 2020;89 doi: 10.1016/j.jairtraman.2020.101901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borenstein S. Hubs and high fares: dominance and market power in the U.S. Airline industry. Rand J. Econ. 1989;20(3):344. [Google Scholar]
- Borenstein S., Rose N.L. Competition and price dispersion in the U.S. Airline industry. J. Polit. Econ. 1994;102(4):653–683. [Google Scholar]
- Brueckner J.K., Lee D., Singer E.S. Airline competition and domestic US airfares: a comprehensive reappraisal. Econ. Transport. 2013;2(1):1–17. [Google Scholar]
- Budd L., Ison S., Adrienne N. European airline response to the COVID-19 pandemic – contraction, consolidation and future considerations for airline business and management. Res. Transport. Bus. Manag. 2020;37 doi: 10.1016/j.rtbm.2020.100578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cattaneo M., Malighetti P., Morlotti C., Redondi R. Quantity price discrimination in the air transport industry: the easyJet case. J. Air Transport. Manag. 2016;54:1–8. [Google Scholar]
- Cattaneo M., Malighetti P., Redondi R., Salanti A. Changes in frequencies and price variations on point-to-point routes: the case of easyJet. Transport. Res. Pol. Pract. 2018;112:60–70. [Google Scholar]
- Cattaneo M., Morlotti C., Malighetti P., Redondi R. Airports and population density: where benefits outweigh costs. Reg. Stud. 2022:1–14. [Google Scholar]
- Cui Y., Orhun A.Y., Duenyas I. How price dispersion changes when upgrades are introduced: theory and empirical evidence from the airline industry. Manag. Sci. 2019;65(8):3835–3852. [Google Scholar]
- Dai M., Liu Q., Serfes K. Is the effect of competition on price dispersion nonmonotonic? Evidence from the U.S. Airline industry. Rev. Econ. Stat. 2014;96(1):161–170. [Google Scholar]
- DPCM 8 Marzo . Gazzetta Ufficiale; 2020. DECRETO DEL PRESIDENTE DEL CONSIGLIO DEI MINISTRI 8 Marzo 2020. Decreto del Presidente del Consiglio dei Ministri:3. [Google Scholar]
- Escobari D. Dynamic pricing, advance sales and aggregate demand learning in airlines. J. Ind. Econ. 2012;60(4):697–724. [Google Scholar]
- Forbes S.J. The effect of air traffic delays on airline prices. Int. J. Ind. Organ. 2008;26(5):1218–1232. [Google Scholar]
- Gaggero A.A., Piga C.A. Airline market power and intertemporal price dispersion. J. Ind. Econ. 2011;59(4):552–577. [Google Scholar]
- Garrow L., Lurkin V. How COVID-19 is impacting and reshaping the airline industry. J. Revenue Pricing Manag. 2021;1 20(1):3–9. 2021 20. [Google Scholar]
- Gerardi K.S., Shapiro A.H. Does competition reduce price dispersion? New evidence from the airline industry. J. Polit. Econ. 2009;117(1):1–37. [Google Scholar]
- Giaume S., Guillou S. Price discrimination and concentration in European airline markets. J. Air Transport. Manag. 2004;10(5):305–310. [Google Scholar]
- Gudmundsson S.V., Cattaneo M., Redondi R. Forecasting temporal world recovery in air transport markets in the presence of large economic shocks: the case of COVID-19. J. Air Transport. Manag. 2021;91 doi: 10.1016/j.jairtraman.2020.102007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansmann R., Binder C.R. Reducing personal air-travel: restrictions, options and the role of justifications. Transport. Res. Transport Environ. 2021;96 [Google Scholar]
- Howell C., Grifell-Tatjé E. Market heterogeneity and the relationship between competition and price dispersion: evidence from the U.S. airline market. Transport Pol. 2022;125:218–230. [Google Scholar]
- ISTAT Number of trips by purpose. 2022. https://www.istat.it/it/files//2022/04 Retrieved.
- Kim M., Sohn J. Passenger, airline, and policy responses to the COVID-19 crisis: the case of South Korea. J. Air Transport. Manag. 2022;98 doi: 10.1016/j.jairtraman.2021.102144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koenigsberg O., Muller E., Vilcassim N.J. EasyJet® pricing strategy: should low-fare airlines offer last-minute deals? Quant. Market. Econ. 2008;6(3):279–297. [Google Scholar]
- Lamb T.L., Winter S.R., Rice S., Ruskin K.J., Vaughn A. Factors that predict passengers willingness to fly during and after the COVID-19 pandemic. J. Air Transport. Manag. 2020;89 doi: 10.1016/j.jairtraman.2020.101897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malighetti P., Paleari S., Redondi R. Pricing strategies of low-cost airlines: the Ryanair case study. J. Air Transport. Manag. 2009;15(4):195–203. [Google Scholar]
- Maneenop S., Kotcharin S. The impacts of COVID-19 on the global airline industry: an event study approach. J. Air Transport. Manag. 2020;89 doi: 10.1016/j.jairtraman.2020.101920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mantin B., Koo B. Weekend effect in airfare pricing. J. Air Transport. Manag. 2010;16(1):48–50. [Google Scholar]
- Mantin B., Rubin E. Price volatility and market performance measures: the case of revenue managed goods. Transport. Res. E Logist. Transport. Rev. 2018;120:35–50. [Google Scholar]
- Morlotti C., Cattaneo M., Malighetti P., Redondi R. Multi-dimensional price elasticity for leisure and business destinations in the low-cost air transport market: evidence from easyJet. Tourism Manag. 2017;61 [Google Scholar]
- Mumbower S., Garrow L.A., Higgins M.J. Estimating flight-level price elasticities using online airline data: a first step toward integrating pricing, demand, and revenue optimization. Transport. Res. Pol. Pract. 2014;66(1):196–212. [Google Scholar]
- Obermeyer A., Evangelinos C., Püschel R. Price dispersion and competition in European airline markets. J. Air Transport. Manag. 2013;26:31–34. [Google Scholar]
- Puller S.L., Taylor L.M. Price discrimination by day-of-week of purchase: evidence from the U.S. airline industry. J. Econ. Behav. Organ. 2012;84(3):801–812. [Google Scholar]
- Qiu L. Zero displacement cost model: a simplified RM model for post-COVID-19 O&D management. J. Revenue Pricing Manag. 2021;20(1):21–32. [Google Scholar]
- Stavins J. Price discrimination in the airline market: the effect of market concentration. Rev. Econ. Stat. 2001;83(1):200–202. [Google Scholar]
- Suau-Sanchez P., Voltes-Dorta A., Cugueró-Escofet N. An early assessment of the impact of COVID-19 on air transport: just another crisis or the end of aviation as we know it? J. Transport Geogr. 2020;86 doi: 10.1016/j.jtrangeo.2020.102749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun X., Wandelt S., Zheng C., Zhang A. COVID-19 pandemic and air transportation: successfully navigating the paper hurricane. J. Air Transport. Manag. 2021;94 doi: 10.1016/j.jairtraman.2021.102062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talluri K., Van Ryzin G. Springer US; Boston, MA): 2004. The Theory and Practice of Revenue Management. [Google Scholar]
- Tan K.M., Samuel A. The effect of de-hubbing on airfares. J. Air Transport. Manag. 2016;50:45–52. [Google Scholar]
- Vinod B. The COVID-19 pandemic and airline cash flow. J. Revenue Pricing Manag. 2020;4 19(4):228–229. 2020 19. [Google Scholar]
- Wan X., Zou L., Dresner M. Assessing the price effects of airline alliances on parallel routes. Transport. Res. E Logist. Transport. Rev. 2009;45(4):627–641. [Google Scholar]