Summary
Models are widely used tools in aquatic science to understand the mechanism of phytoplankton growth and anticipate the occurrence of harmful algal blooms (HABs). However, model parameterization remains challenging and issues that may introduce prediction uncertainty exist. Many models use the Monod equation to predict cyanobacteria growth rate based on ambient nutrient concentrations. The half-saturation concentrations in the Monod equation varies greatly among different studies and depends on environmental conditions. In this study we estimated the growth rate due to nutrient limitations for two cyanobacteria species (Microcystis aeruginosa and Dolichospermum flos-aquae) using a modified Monod model which allows the half-saturation concentration to vary according to initial nitrogen (N) conditions. The model is calibrated against observations from laboratory experiment where cyanobacteria growth and ambient nutrient concentrations were measured simultaneously, which is rarely done in the literature. Our results show this modified model produce better predictions on growth rate and biomass, indicating many commonly used mechanistic models may need improvement regarding phytoplankton growth representation. Furthermore, our study quantifies the flexibility in cyanobacteria growth parameter across a wide range of environmental N in eutrophic lakes thus provides important information for large-scale modelling applications.
Keywords: Cyanobacteria growth rate, Nitrogen, Phosphorus, Physiological trait, Monod equation
1. Introduction
Cyanobacteria-dominated harmful algal blooms (HABs) are increasingly causing global environmental concerns because of their disturbance to aquatic ecosystems (Paerl et al. 2016a, 2016b), economic impacts (Dodds et al. 2009), and detriments to human health (Harke et al. 2016). Efforts to control HABs have focused on the two essential elements that limit primary production (Elser et al. 2007); nitrogen (N) and phosphorus (P). Nutrient control has a demonstrated success at decreasing biomass and toxicity of cyanobacteria blooms (Gobler et al. 2016). Microcystis aeruginosa and Dolichospermum flos-aquae (species formerly assigned to genus Anabaena) are two taxa that cause HABs (Harke et al. 2016; Li et al. 2016). Consequently, they have been the subjects of numerous studies designed to quantify their growth kinetics in response to nutrient availabilities. Such information is important to precisely predict the timing and magnitudes of HABs and to support decision-making in environment management.
In natural ecosystems where resource availabilities fluctuate and are rarely at equilibrium (Beversdorf et al. 2015), cyanobacteria growth and nutrient metabolism are highly dynamic and vary greatly with environmental cues (Harke and Gobler 2015). Modeling has been widely used to simulate ecosystem dynamics and models have been developed to predict phytoplankton growth and to identify their environmental controls (James and Boriah 2010; Rousso et al. 2020). Despite the enormous diversity of different modeling approaches, they share a common objective; to mathematically represent biological processes, which requires parametrization of cyanobacteria physiological traits. Specifically, there are two commonly used approaches to describe nutrient limitation of phytoplankton growth. First, the Monod equation, hypothesizes that growth rate is a function of the ambient concentration of the limiting nutrient, and requires model users to assign a value for the half-saturation concentration of the limiting nutrient (Monod 1949):
| 1) |
where is the theoretical maximum growth rate achieved at non-limiting nutrient concentration, S is ambient nutrient concentration, and is half-saturation concentration. In the second approach, cellular nutrient content (q) is a variable, and growth rate is modeled as a function of q using the Droop equation based on the assumption that nutrients are stored in the cell before being utilized (Droop 1974):
| 2) |
where is the theoretical maximum growth rate, q is the amount of nutrient per cell, is defined as the minimal cellular nutrient content below which phytoplankton will not grow. It has been suggested that the Monod equation has limitations for failing to consider nutrient luxury uptake and storage (Sommer 1991). However, it is still being widely used in current modeling practice (Table 1), since measuring external nutrient concentrations has more feasibility than measuring intracellular nutrient content.
Table 1.
List of aquatic ecosystem models and their governing equations for phytoplankton nutrient limitation
| Model | Equation to describe nutrient limitation | Reference | Application example |
|---|---|---|---|
| CE-QUAL-W2 | Monod equation | (Cole and Wells 2000) | (Kim et al. 2019) |
| EFDC | Monod equation | (Hamrick, 1996) | (Jiang et al. 2018) |
| CAEDYM | Monod and Droop equations | (Hipsey et al. 2006) | (Robson and Hamilton 2004) |
| PCLake | Droop equation | (Janse and van Liere 1995) | (Bucak et al. 2018) |
| PROTECH | Monod and Droop equations | (Reynolds et al. 2001) | (Gray et al. 2019) |
| BLOOM/GEM | Monod and other | (Hydraulics, 2011) | (Li et al. 2015) |
When applying models that employ the Monod equation, users must specify value for and , which are typically derived from reported values in the scientific literature (Robson et al. 2018). The issues associated with such approach are: 1) Reported values from the literature are obtained from experiments under different conditions thus parameters vary broadly both within and among species, and 2) Treating the half-saturation concentration as one static value may not account for the ability of a phytoplankton species to adjust growth kinetics in response to changing environmental conditions (Song and Ward 2007). From a physiological perspective, changes in nutrient uptake activities may explain the variation in the half-saturation concentrations because studies have found changes in the transcription of nutrient (N and P) acquisition and transport genes at varied ambient nutrient conditions in cyanobacteria (Harke and Gobler 2015, Wang et al. 2018). Further, M. aeruginosa’s maximum growth rate from Ghaffar et al. (2017) is less than half of the value reported by Amano et al. (2012), and reported half-saturation concentrations for phosphate from different studies differ by two orders of magnitude (Table 2). On the other hand, reported D. flos-aquae physiological traits are relatively rare in the literature, but studies on other filamentous N2-fixing cyanobacteria (e.g. Cylindrospermopsis raciborskii) have found high variability in maximum growth rate (Xiao et al. 2020), and half-saturation concentrations for phosphate (Table 2). Simply applying published physiological traits on modeling practice may introduce significant uncertainty in model predictions. Furthermore, different laboratory culture studies were conducted under different experimental conditions (e.g., temperature, light intensity; Table 2), which are known to alter cyanobacteria physiological traits. In fact, there are studies showing that cyanobacteria half-saturation concentration for nutrient uptake varies depending on ambient nutrient concentrations (Chen and Liu. 2015). However, most models do not represent such flexibility.
Table 2.
Summary of published maximum growth rate and half-saturation concentration of nutrients (N and P) for two cyanobacteria. Maximum growth rates are transformed using models to account the effects of temperature and photoperiod (Xiao et al. 2020).
| Species | Physiological traits | Value | Reference | Experimental conditions (temperature, light intensity, and photoperiod) |
|---|---|---|---|---|
| M. aeruginosa | Maximum growth rate | 0.32 /d | (Ghaffar et al. 2017) | 28 °C; 30 µmol/ m2 /s; 12h |
| 0.77 /d | (Amano et al. 2012) | 20 °C; 27 µmol/ m2 /s; 14h | ||
| 0.87 /d | (Baldia et al. 2007) | 23 °C; 9 µmol/ m2 /s; 12h | ||
| 0.85 /d | (Orr and Jones 1998) | 20 °C; 38 µmol/ m2 /s; 14h | ||
| Half-saturation concentration for nitrate | 0.07 µM | (Mikawa et al. 2016) | 20 °C; 27 µmol/ m2 /s; 14h | |
| 0.6 µM | (Sugimoto et al. 2016) | 20 °C; 27 µmol/ m2 /s; 14h | ||
| 37 µM | (Baldia et al. 2007) | 23 °C; 9 µmol/ m2 /s; 12h | ||
| Half-saturation concentration for phosphate | 0.05 µM | (Amano et al. 2010) | 20 °C; 27 µmol/ m2 /s; 14h | |
| 0.34 µM | (Ghaffar et al. 2017) | 28 °C; 30 µmol/ m2 /s; 12h | ||
| 0.64 µM | (Baldia et al. 2007) | 23 °C; 9 µmol/ m2 /s; 12h | ||
| 23 µM | (Tan et al. 2019) | 25 °C; 45 µmol/ m2 /s; 12h | ||
| C. raciborskii | Maximum growth rate | 0.29 /d | (Amaral et al. 2014) | 25 °C; 80 µmol/ m2 /s; 16h |
| 1.30 /d | (Isvánovics et al. 2000) | 21 °C; 140 µmol/ m2 /s; 12h | ||
| 1.45 /d | (Kenesi et al. 2009) | 26 °C; 100 µmol/ m2 /s; 12h | ||
| Half-saturation concentration for phosphate | 0.02 µM | (Willis et al. 2017) | 28°C; 80 µmol/ m2 /s; 12h | |
| 0.03 µM | (Isvánovics et al. 2000) | 21 °C; 140 µmol/ m2 /s; 12h | ||
| 0.67 µM | (De Nobel et al. 1997) | 20 °C; 150 µmol/ m2 /s; 12h |
The objective of this study is to establish parameter values for cyanobacteria growth models using the Monod nutrient-limitation function with a specific emphasis on the non-diazotrophic strain, M. aeruginosa, and the diazotrophic strain, D. flos-aquae. Maximum growth rates and nutrient half-saturation concentrations were estimated based on laboratory measurements where nutrient concentrations were carefully controlled to yield the varied nutrient conditions that cyanobacteria could experience in natural habitats. More importantly, we hypothesized that a modified Monod model (i.e., the variable K model) that allows variable half-saturation concentration based on initial N concentration will yield more accurate predictions in cyanobacteria growth than using a static half-saturation concentration across 3 different initial N concentrations (i.e., the constant K model).
2. Results
2.1. Model predictive performance comparison
Overall, we observed a decreasing trend in M. aeruginosa growth rate as dissolved nutrient decreased through time. For cultures with 23 μM initial N concentration, M. aeruginosa growth rate decreased from ~ 0.35 day−1 on day 1 to less than 0.1 day−1 on day 6 then stayed at low rate for the rest of the experiment. Two models were both able to predict this pattern and using the variable Κ model did not show much advantage over the constant Κ model (Fig. 1 A, B). For cultures with 184 μM initial N concentration, M. aeruginosa growth rate predictions by constant Κ model were higher than observations from day 1 to day 7, and predictions were lower than observations from day 8 to day 14 (Fig. 1 C). On the other hand, the variable K model had better prediction in growth rate (Fig. 1 D). In cultures with 1152 μM initial N concentration, M. aeruginosa growth rate declined gradually from ~ 0.5 day−1 on day 1 to 0.3 day−1 on day 11. Growth rate predictions by the constant Κ model were lower than the observations (Fig. 1 E) and the difference between predictions and observations was more distinct from day 7 to day 14 (Fig. 1 E). In contrast, predictions by the variable K model fit the observation variations better (Fig. 1 F).
Figure 1.
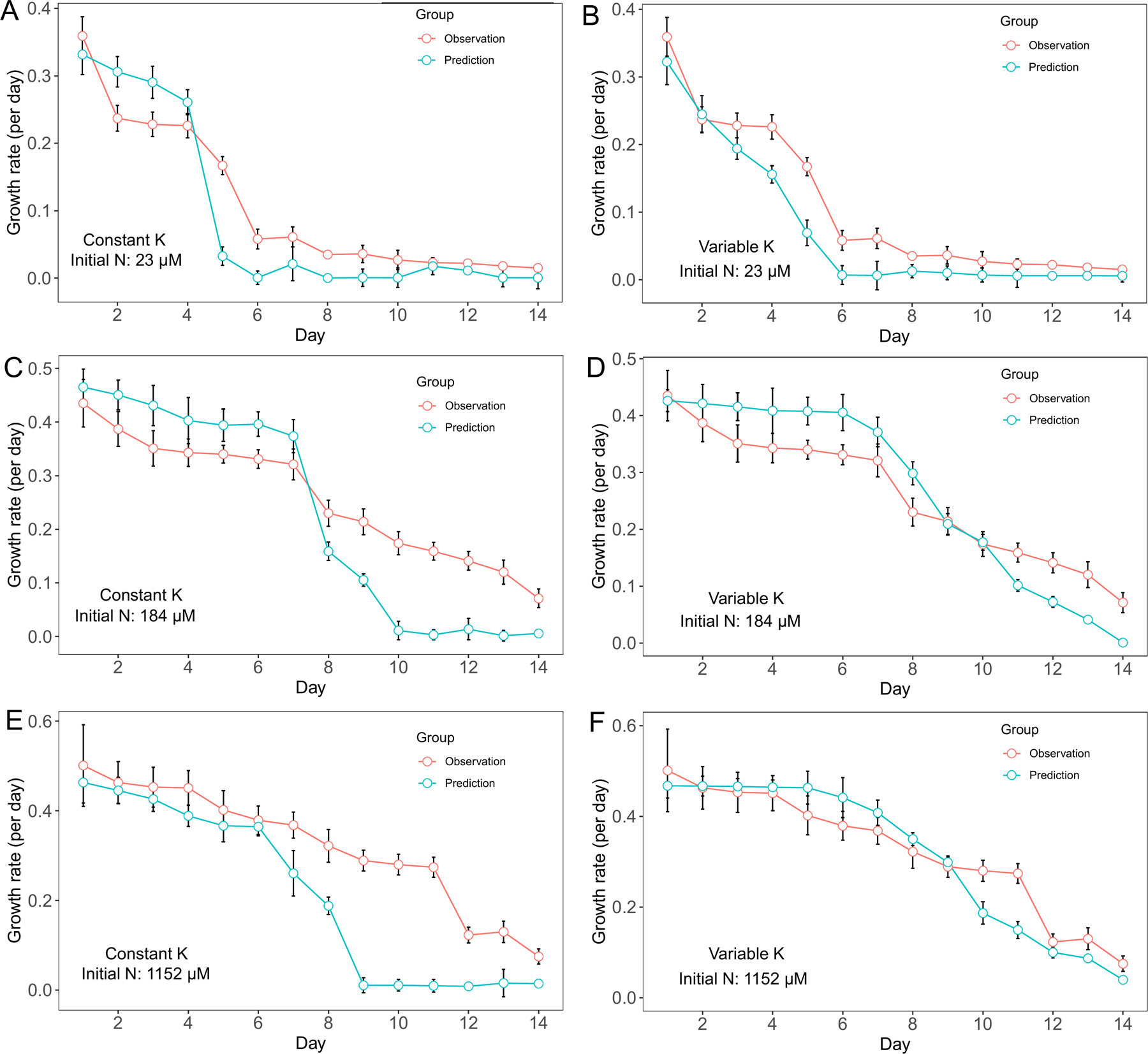
Model performance comparison for M. aeruginosa growth rate prediction between constant half saturation concentration model and variable half saturation concentration model under different initial N concentrations.
Similarly, D. flos-aquae growth rate decreased with decreasing nutrient concentrations. In cultures with 23 μM initial N concentration, the variable K model had better growth rate predictions than the constant K model from day 10 to day 14 (Fig. 2 A, B). In cultures with 184 μM initial N conditions, the constant K model was able to capture growth rate variation from day 1 to day 7 while the variable K model had more accurate predictions from day 7 to day 14 (Fig. 2 C, D). In cultures with 1152 μM initial N conditions, growth rates predicted by the variable K model were more accurate from day 7 to day 14 although the predictions were higher than the observations from day 1 to day 7 (Fig. 2 E, F).
Figure 2.
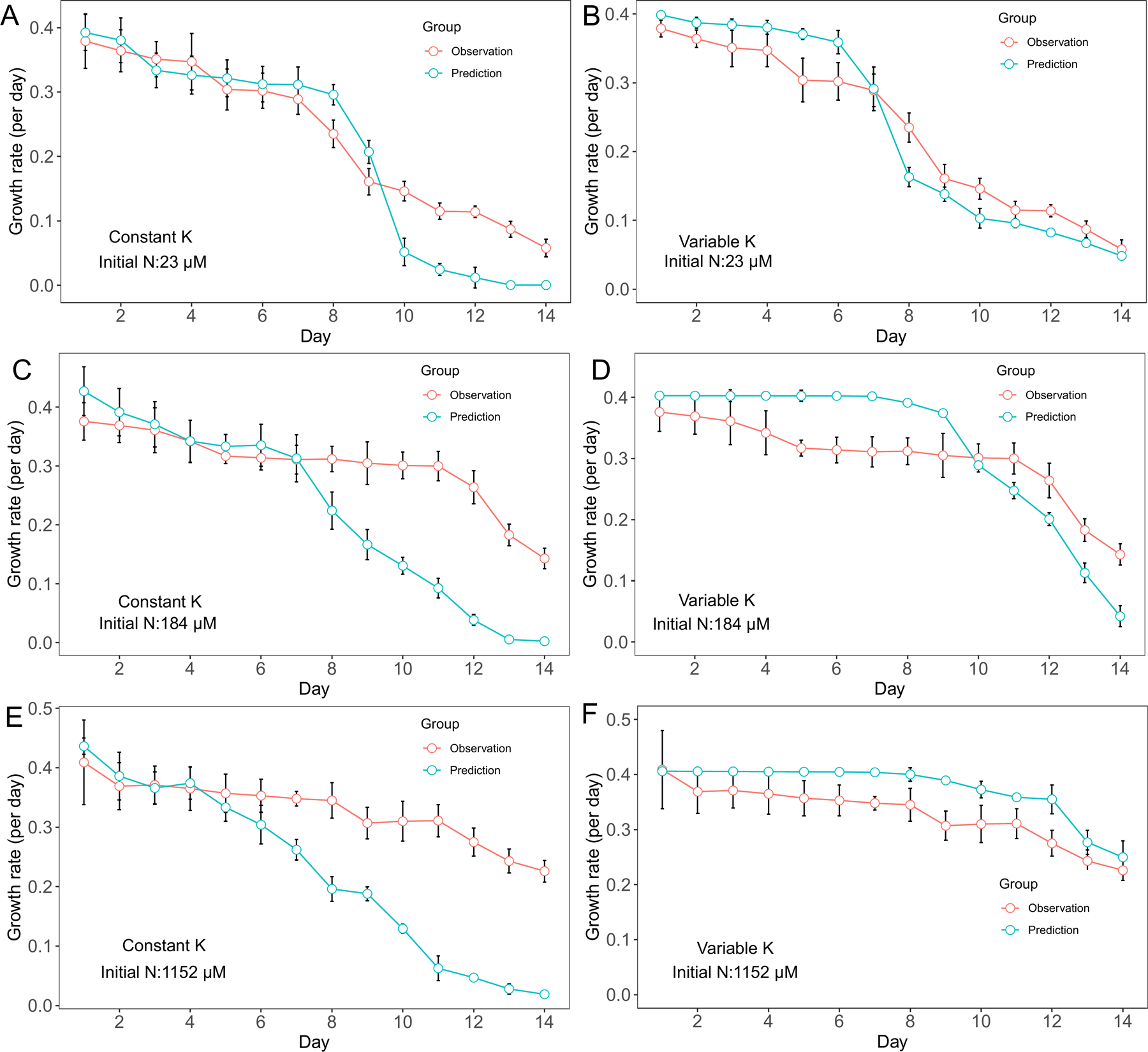
Model performance comparison for D. flos-aquae growth rate prediction between constant half saturation concentration model and variable half saturation concentration model under different initial N concentrations.
For M. aeruginosa, we observed biomass increased after nitrate N concentration depleted in cultures with 23 μM and 184 μM initial N conditions. Since cyanobacteria biomass is calculated based on growth rate, we observed similar patterns in biomass predictions. Overall, the variable K model had better predictions in biomass for M. aeruginosa (Fig. 3), although the performance difference between two models was not obvious in cultures with 23 μM initial N conditions (Fig. 3A, B). On the other hand, the variable K model exhibited advantage over the constant K model in D. flos-aquae biomass predictions for all 3 initial N conditions (Fig. 4). Overall, we found that the variable K model had better performance since the RMSE was significantly lower than using the constant K model (Welch two sample t-test, t = 79.07, df = 5.16, p < 0.001 for M. aeruginosa. t = 13.99, df = 5.20, p < 0.001 for D. flos-aquae). Using the variable K model, the maximum growth rate was estimated as 0.48 /d and 0.41 /d for M. aeruginosa and D. flos-aquae, respectively.
Figure 3.
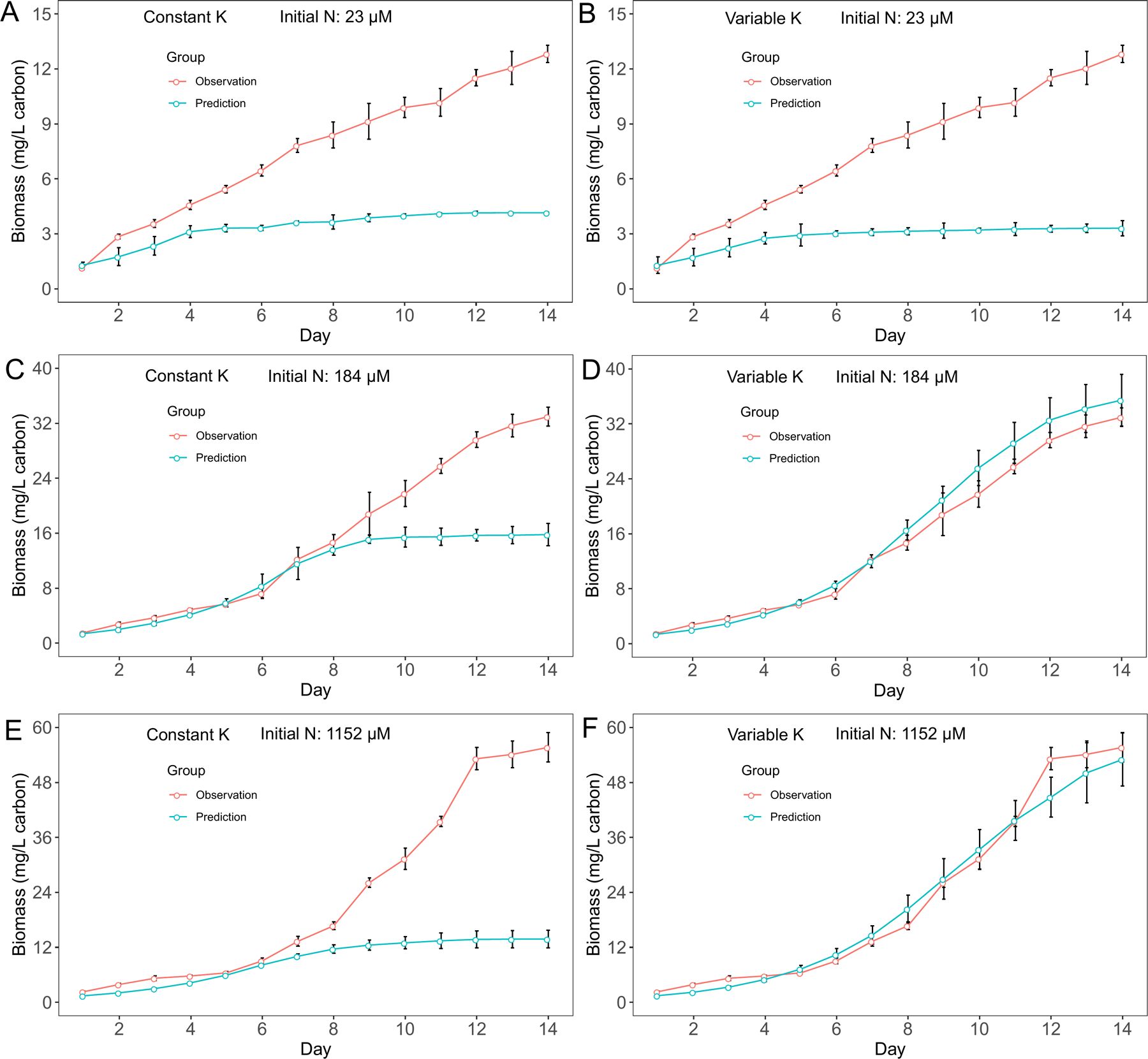
Model performance comparison for M. aeruginosa biomass prediction between constant half saturation concentration model and variable half saturation concentration model under different initial N concentrations.
Figure 4.
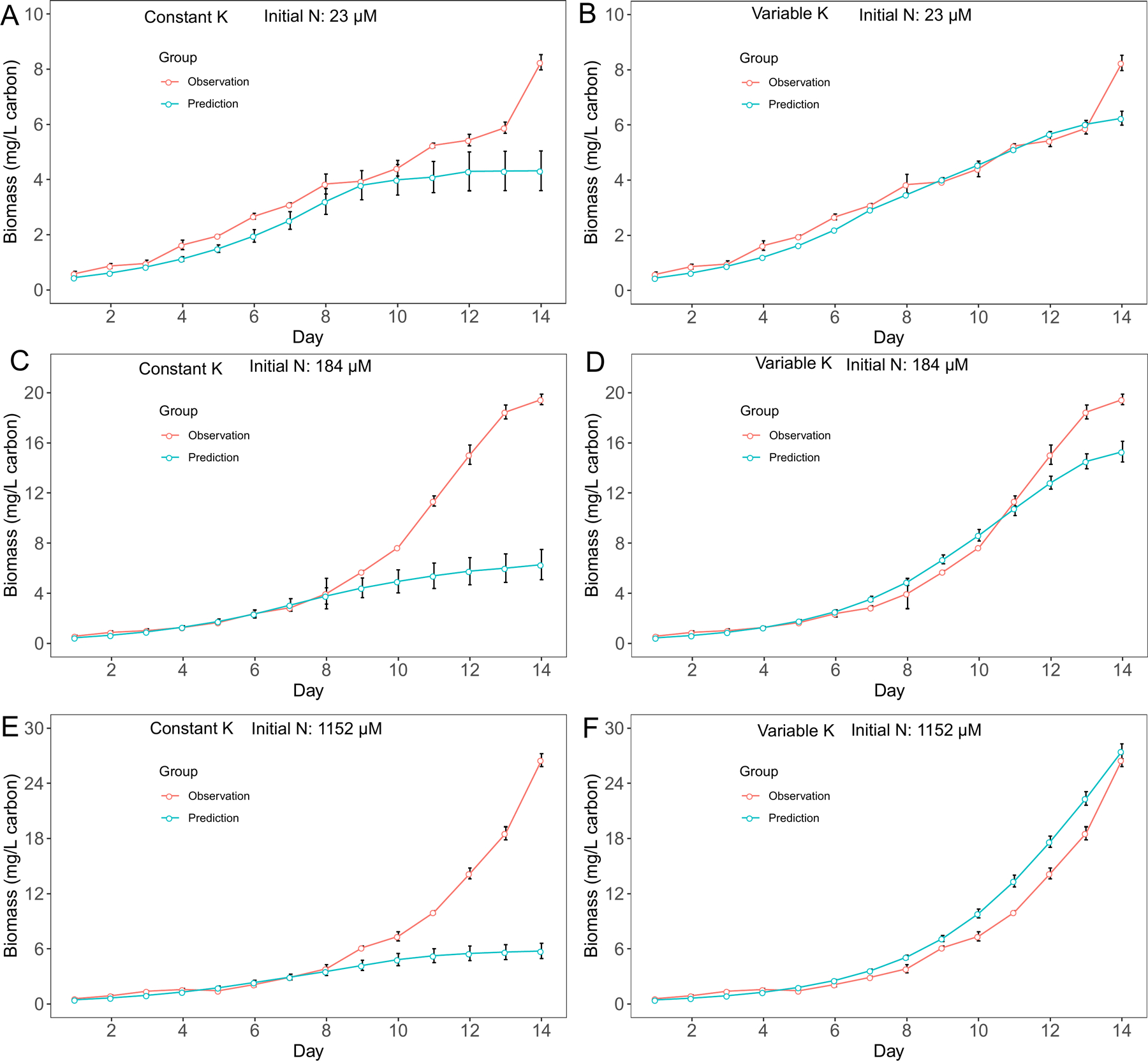
Model performance comparison for D. flos-aquae biomass prediction between constant half saturation concentration model and variable half saturation concentration model under different initial N concentrations.
2.2. Half-saturation concentration of nitrate
Using the variable K model, we found different due to different initial N concentrations (two-way ANOVA, df = 2, F = 113.1, p < 0.001), species (df = 1, F = 54.98, p < 0.001) and the interaction of species and initial N concentrations (df = 2, F = 24.43, p < 0.001). For M. aeruginosa, was estimated as 0.12 μM in cultures with 23 μM initial N conditions (Fig. 5A) and higher initial N concentrations (184 μM) resulted in a greater of 0.90 μM. However, the in cultures with 1152 μM initial N conditions was not statically different from 184 μM initial N conditions (p = 0.75). On the other hand, D. flos-aquae exhibited greater value than M. aeruginosa in cultures with 23 μM and 1152 μM initial N concentrations (Fig. 5A). Additionally, we found that two species had similar with 184 μM initial N conditions (p = 0.99).
Figure 5.
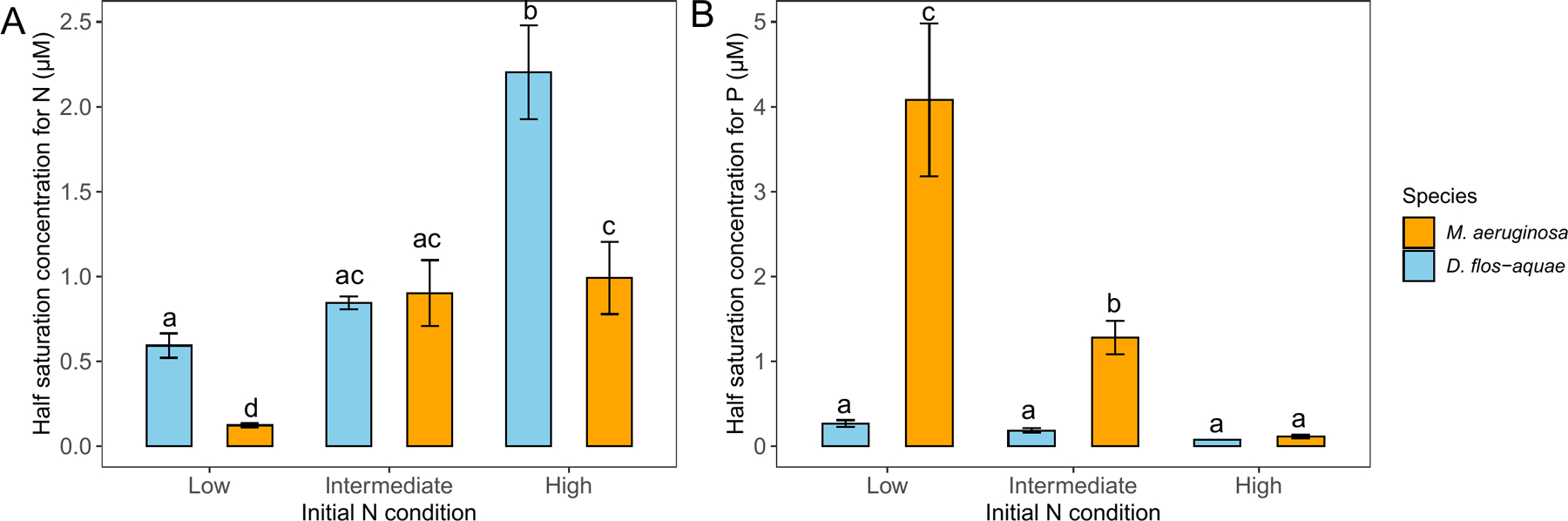
Half saturation concentration of nitrate-N (A) and phosphate-P (B) for M. aeruginosa and D. flos-aquae under different initial N conditions. Letters indicate significant difference by Tukey’s post hoc comparison
2.3. Half-saturation concentration of phosphate
Similarly, we found different values due to different initial N concentrations (two-way ANOVA, df = 2, F = 48.07, p < 0.001), species (df = 1, F = 86.26, p < 0.001), and the interaction of N concentration and species (df = 2, F = 40.22, p < 0.001). For M. aeruginosa, the was estimated as 4.1 μM in cultures with 23 μM initial N conditions (Fig. 5B), 1.30 μM with 184 μM initial N conditions, and 0.11 μM in cultures with 1152 μM initial N conditions. In contrast, D. flos-aquae exhibited lower than M. aeruginosa across 3 initial N concentrations and we found no significant difference in for D. flos-aquae regardless of initial N concentrations.
3. Discussion
While the flexibility in phytoplankton nutrient kinetics has been recognized (Bonachela et al. 2011), many models still use the Monod equation with static parameter values for nutrient half-saturation concentration (Table 1). In this study, we simulated nutrient-limited cyanobacteria growth rates using a modified Monod model that allows dynamic half-saturation concentrations of N and P according to the initial nutrient conditions. Our results indicated that nutrient half-saturation concentration is a dynamic trait both within and among cyanobacterial species and dependent on the initial nutrient concentration. Thus, many commonly used mechanistic models may need improvement regarding phytoplankton growth representation to yield more accurate predictions, and more rigorous assessments are required when applying parameter values obtained from literature culture studies.
3.1. Cyanobacteria N limitation
It is conventionally assumed that N-fixing cyanobacteria have a competitive advantage over other phytoplankton because they can overcome N limitation by fixing N2 (Smith 1983). However, studies have found contradictory evidence showing no increase of N-fixing cyanobacterial biovolume when ambient N concentration decreased (Kolzau et al. 2018) and indicating strict growth tradeoff caused by increased energy demand during diazotrophy (Osburn et al. 2021). It’s typically assumed that N-fixing cyanobacteria have a lower half-saturation concentration for dissolved inorganic N than other phytoplankton (Shimoda and Arhonditsis, 2016). Our model demonstrated decrease in growth rate due to the depletion of ambient N in D. flos-aquae with low-N scenario (Fig. 2) and more importantly, indicated the for diazotrophic growing cyanobacteria is not different from the non-dizotrophic cyanobacteria (Fig. 5). Although our study did not directly test the competition between two cyanobacteria species, our results suggest that M. aeruginosa may outcompete D. flos-aquae when environmental N is scarce because they may achieve the maximum growth rate at a lower nitrate-N concentration than D. flos-aquae (Fig. 5). Our results support the field observations that M. aeruginosa can dominate in N-limited lakes (Liu et al. 2011; Jankowiak et al. 2019). The ability to fix atmospheric N2 may contribute to the more constrained N stoichiometry in diazotrophic cyanobacteria species than other phytoplankton taxa, as observed in field studies and culture experiments (Dickman et al. 2006; Osburn et al. 2021). Additionally, our model revealed a lower for M. aeruginosa than D. flos-aquae under N-rich conditions (1152 μM initial N concentration, Fig. 5A), indicating a species-specific N metabolic trait. Our model is capable of making credible predictions for non-diazotrophic growing D. flos-aquae; however, simulating diazotroph growth rate without combined N source may require more sophisticated models that consider photosynthesis, intracellular carbon and nitrogen reserve (for example Rabouille et al. 2006 and Grover et al. 2020).
3.2. Cyanobacteria P limitation
We found that D. flos-aquae had lower half-saturation concentrations for P than M. aeruginosa in cultures with low N and intermediate N conditions (Fig. 5). It has been demonstrated that P has structural and functional roles for diazotrophically growing cyanobacteria, which may increase their P requirement (Mills et al. 2004; Scott and McCarthy 2010). In fact, we found that D. flos-aquae started N2 fixation on day 5 with low N conditions (Fig. S6A) and day 11 with intermediate N conditions (Fig. S6B), therefore D. flos-aquae acquired P more rapidly than M. aeruginosa. Previous studies on D. flos-aquae monocultures have reported similar results (Yema et al. 2016) and further demonstrated that D. flos-aquae upregulated the genes involved in P uptake in response to N limitation (Wang et al. 2018). In contrast, M. aeruginosa growth rate was mainly limited by N rather than P in cultures with 23 μM initial nitrate (Fig. S4), resulting in a much greater half-saturation concentrations for P (Fig. 5B). Our nutrient treatment created a wide range of N: P initial ratio from 2 to 100 (by mole), representing P-sufficient and P-limited systems that cyanobacteria blooms may occur (Scott et al. 2019). Microcystis is known to uptake P in excess relative to immediate metabolic demand (Jacobson and Halman 1982). Our results suggest that such high-affinity uptake for P was facilitated by an N-rich environment because we found the lowest in the cultures with 1152 μM initial nitrate. Further, some cyanobacteria may accumulate polyphosphate intracellularly and consume those stored P to support growth in P-limited environments, which can partly explain the plasticity in their C: P stoichiometry (Willis et al. 2017). Additionally, both M. aeruginosa and D. flos-aquae can migrate in water column by manipulating their gas vesicles, thereby gaining access to benthic P (Gobler et al. 2016; Li et al. 2016). This trait may contribute their ability to form blooms in deep oligotrophic lakes (Reinl et al. 2021).
3.3. Intraspecific variation in cyanobacterial growth parameters
Parameterization is arguably one of the most important tasks in model applications (Robson et al. 2018). However different studies reported drastically different parameter values, even within species (Table 2). For example, the maximum growth rate of a particular cyanobacteria strain depends on the experimental conditions, and there are models that represent effects of temperature and photoperiod by which model users can convert published values to specific conditions (Grimaud et al. 2017, Xiao et al. 2020). While there is growing evidence showing that cyanobacteria actively adjust nutrient (N, P) acquisition in response to changing environmental nutrient availabilities (Harke et al. 2012; Wang et al. 2018), half-saturation concentrations of N and P are still treated as constant in some commonly applied models that use the Monod equations to describe nutrient limited phytoplankton growth (see references in Table 1). Our study demonstrates that the Monod model with flexible half saturation concentration makes more accurate predictions on cyanobacteria growth rate and biomass. Furthermore, we quantified the Monod model parameters that can be used to predict cyanobacteria blooms across a wide range of nitrate concentrations in eutrophic lakes.
3.4. Monod vs. Droop model
The Monod model is generally considered to be less physiologically accurate for representing phytoplankton growth than the Droop model (Sommer 1991), which computes population averaged growth rate based on population averaged nutrient cell quotas. However, for biogeochemical process prediction, the Droop model may introduce an error due to the intra-population variations in nutrient cell quotas (Lomnicki, 1999). In this study, we found that cyanobacteria N and P cell quotas varied as initial nitrate concentration increased (Fig. S7). Further, we found that Dolichospermum P quota increased when population initiated N fixation (Fig. S8B), likely due to the increased P requirement to support diazotrophic growth. On the other hand, we found that N-limited Microcystis populations have a greater P cell quota than P-limited populations (Fig. S8B). Overall, our results weakly support the utility of the Droop model for simulating batch culture cyanobacteria populations (Fig. S9, Fig. S10). However, it has been recognized early that the Droop model fits better for steady-state single-nutrient simulations (Burmaster, 1979). Incorporating additional physiological features such as cell size and cell age may improve the predictive accuracy for Droop type models (Hellweger and Kianirad, 2007).
3.5. Conclusions and Implications
Anticipating cyanobacterial HABs occurrence and predicting population dynamics by mathematical models has been widely used as a tool to assist water resources management. Although it is acknowledged that cyanobacterial blooms are triggered by the interaction of a variety of factors, nutrients have been demonstrated to be a critical predictor of cyanobacterial HAB models (Rousso et al. 2020). Therefore, nutrient limitation parameters may pose major controls on model predictions. In this study, we estimated cyanobacteria growth due to nutrient limitations (N and P) based on the Monod model, and further demonstrated the flexibility in cyanobacteria growth parameters that reflect their physiological and ecological traits for two HAB-forming species. Our work improves current understanding about cyanobacteria bloom ecology, provides insights for a wide variety of large-scale aquatic modelling applications.
4. Experimental procedures
4.1. Cultures, culture maintenance, and experimental conditions
The unicellular non-diazotrophic cyanobacterium Microcystis aeruginosa strain 2385 and the filamentous diazotrophic cyanobacterium Dolichospermum flos-aquae strain 1444 were obtained from the culture collection of algae at the University of Texas at Austin (UTEX). Cultures were maintained on batch cultures with sterile 0.5x BG-11 medium (Sigma C3601), with 8800 µM NaNO3 and 115 µM K2HPO4 as initial nutrient concentrations. Batch cultures were grown in Erlenmeyer flasks at 26 °C on a 14h-10h light-dark cycle and irradiance of ~ 100 μmol /m2 /s measured by a quantum meter (Spectrum Technologies, 3415FQF). Cultures were maintained by transferring 1% cell culture into freshly prepared medium monthly.
4.2. Effects of dissolved N and P on cyanobacteria growth rates
To examine the effects of dissolved N and P on non-diazotrophic and diazotrophic cyanobacteria growth, quadruplicate experimental units were made by diluting N-free BG-11 to 5% and supplementing with vitamin B12 (concentration of 1.35 µg/L). Three N-availability treatments were created by varying initial N concentrations in the media (23, 184, 1152 µM as nitrate-N for N treatment 1, 2, and 3, respectively), whereas initial P concentrations in the media were the same (11.5 µM) for all treatments. We expected to see N-limited cyanobacteria population in the cultures with 23 µM initial nitrate and P-limited population in the cultures with 1152 µM initial nitrate concentrations due to the N: P stoichiometries. These nutrient concentrations are comparable to field observations in eutrophic lakes (Scott et al. 2019). In this study, nitrate was chosen over ammonium as the N source because of reported prohibitive effects of ammonium on M. aeruginosa at high concentrations (Chen et al. 2019), and nitrate is the stable form of inorganic N in well-mixed oxic lake ecosystems. The initial cell densities to start the experimental blooms were ~ 9.0 ×108, 1.0×109 cells/L for M. aeruginosa and D. flos-aquae, respectively. Cells were grown in 2000-mL Erlenmeyer flasks (culture volume of 1200 mL) for 14 days on a light: dark cycle of 14h: 10h at a constant temperature of 26°C and light intensity of ~ 100 μ mol/m2/s measured by a quantum meter (Spectrum Technologies, 3415FQF). The flasks were shaken each day during the experiment to homogenize culture and prevent settling. Growth was monitored by measuring in vivo chlorophyll a fluorescence (Relative fluorescence unit, RFU; Turner Designs Trilogy) during the experiment. Additionally, 2 mL sub-samples were preserved with Lugol’s iodine daily for cell enumeration. On days 5, 7, 9, 11, 12, and 14 of the experiment, cells were collected by filtering through 0.7µm pre-combusted glass fiber filters (GF/F) for POC measurements.
For M. aeruginosa, cell concentrations were determined using a flow cytometer (BD Diagnostic Systems, FACS55 Verse, San Jose, CA, USA), using the forward-scatter side-scatter method as previously described by Wagner et al. (2019). Quality control was performed using standardized beads to check for instrument functionality. For D. flos-aquae, cell count was performed using a light microscopy at 400X magnification (Nikon Eclipse 80i) on a subset of samples and cell counts were related to in vivo chlorophyll a fluorescence (R2= 0.94, p < 0.001, degrees of freedom = 26, Supplementary Information, Fig. S1). The obtained linear equation was applied to in vivo chlorophyll a data for samples without direct cell count to predict cell concentration.
To quantify biomass (POC), filters were first dried at 60°C in an oven and POC was measured using an elemental analyzer (Thermo-Fisher Flashsmart NC soil, CE Elantech, USA). The concentration of POC was determined by comparing the peak area obtained from the unknown sample to the known weight of standard (aspartic acid). We found that POC concentrations were correlated to cell concentration and a significant linear relationship was found for M. aeruginosa (R2 = 0.91, p < 0.001, degrees of freedom = 81, Supplementary Information, Fig. S2). The correlation equation was applied to cell concentrations to infer biomass when POC measurement was unavailable (day 2–4, 6, 8, 10, and 13). For D. flos-aquae, POC was correlated to RFU and a significant (R2= 0.92, p < 0.001, degrees of
freedom = 76, Supplementary Information, Fig. S3) linear relationship was established. The correlation equation was applied to D. flos-aquae RFU to infer biomass for samples without direct POC measurement (day 2–4, 6, 8, 10 and 13).
We used cell concentrations to calculate the specific growth rate (μ) from the following equation:
| 3) |
where C1 and C2 are the cell concentrations for M. aeruginosa or/and D. flos-aquae on day t1 and day t2.
Dissolved inorganic N and P (DIN, DIP) concentrations were analyzed according to spectrophotometric standard methods (APHA, 1998) using a Lachat QuikChem autoanalyzer (Lachat Instrument, USA). When DIN/DIP measurements were not available (day 2–4, 6, 8, 10 and 13), we fit models to measured data based on the Akaike Information Criterion (AIC), thus DIN/DIP concentrations were predicted from regressions. Additionally, we assigned less weight on observations without direct measurement. The temporal variations of DIN and DIP concentrations for M. aeruginosa and D. flos-aquae are in the Supplementary Material (Fig. S4, Fig. S5).
4.3. Model theory and configuration
The Monod model (Monod 1949) is widely used to describe phytoplankton-specific growth rates in response to resource concentrations/availabilities. Overall, cyanobacteria growth rate was formulated as the product of the maximum growth rate and appropriate limitation functions as:
| 4) |
where and are the Monod equations for N and P limitation, respectively. And is light limitation equation. Any number of additional limitation functions could be included, such as limitations due to micronutrients or constraints due to temperature or salinity. The Monod limitation functions for N and P are,
| 5) |
| 6) |
where [NO3] is the concentration of nitrate in the media (µM), is the half-saturation concentration of nitrate (µM) for each species, [PO4] is the concentration of phosphate in the media (µM), is the half-saturation concentration of phosphate (µM) for each species. Additionally, the maximum growth rate was estimated for each species. Cyanobacteria biomass was calculated based on the initial carbon concentration and cumulative additions to biomass from variable modeled growth rate.
The experiments were designed to examine the effects of DIN and DIP concentrations on cyanobacteria growth rates. The light intensity was set sufficiently high to avoid light-limiting conditions. Initially, cyanobacteria growth should not be limited by light intensity, however, as biomass accumulates, light penetration through the medium decreases, therefore light extinction due to chlorophyll-a was considered and incorporated into the model. Steele’s equation (Steele 1962) was used to describe light limitation:
| 7) |
where I is the light intensity (μmol/m2/s) and Iopt is the optimal light intensity (μmol/m2/s).
The light extinction coefficient was calculated as a function of chlorophyll-a concentration using Riley’s empirical equation (Riley 1956):
| 8) |
where K is the extinction coefficient, and [Chl] is the chlorophyll-a concentration (μg/L). Because chlorophyll-a was not measured in this study, the concentration was estimated from cyanobacteria biomass (POC) using the C:Chl ratio, which was also considered as an adjustable model parameter (Table 3).
Table 3.
Parameter definitions, unit and ranges for M. aeruginosa growth model
| Parameter | Definition | Units | Range | Reference |
|---|---|---|---|---|
| Optimal light intensity | µmol/ m2 /s | 20–200 | (Hesse et al. 2001; McCausland et al. 2005) | |
| Half-saturation concentration of nitrate N | µM | 0.1–37.8 | (Donald et al. 2013; Baldia et al. 2007) | |
| Half-saturation concentration of phosphate P | µM | 0.05–23.2 | (Amano et al. 2010; Tan et al. 2019) | |
| Carbon to chlorophyll-a mass ratio | n/a | 30–500 | (Sathyendranath et al. 2009) | |
| Maximum growth rate | /d | 0.1–1.0 | (Fujimoto et al. 1997; Isvánovics et al. 2000) |
Light intensity in water was calculated according to the Beer–Lambert Law (Weiskerger et al. 2018):
| 9) |
where I the light intensity (μmol /m2 /s) in the incubator, the constant 0.06 /m is the light extinction coefficient of pure water, and K (/m) is the extinction coefficient calculated from (8), d is the water depth, which was 0.1 meter in this study. The cyanobacteria growth model was written in FORTRAN with parameter definitions, units, ranges and references listed in Table 3, 4.
Table 4.
Parameter definitions, unit and ranges for D. flos-aquae growth model
| Parameter | Definition | Unit | Range | Reference |
|---|---|---|---|---|
| Optimal light intensity | µmol/ m2 /s | 20–200 | (Hesse et al. 2001; McCausland et al. 2005) | |
| Half-saturation concentration of nitrate N | µM | 0.1–37.8 | (Donald et al. 2013; Baldia et al. 2007) | |
| Half-saturation concentration of phosphate P | µM | 0.02–0.67 | (Willis et al. 2017; De Nobel et al. 1997) | |
| Carbon to chlorophyll-a mass ratio | n/a | 30–500 | (Sathyendranath et al. 2009) | |
| Maximum growth rate | /d | 0.1–1.0 | (Fujimoto et al. 1997; Isvánovics et al. 2000) |
Our initial model calibration indicated that light limitation was negligible even in the cultures with the greatest biomass (cell concentration), therefore we focused on discussing nutrient limitations and nutrient-related parameters. Firstly, we ran and calibrated the model against observations using one half-saturation concentration of nitrate, one half-saturation concentration of phosphate across three initial N conditions (i.e., the constant K model). Secondly, we ran and calibrated the model using three different half-saturation concentrations of nitrate and phosphate depending on initial N concentrations (i.e., the variable K model). We used one maximum growth rate for each species in two modelling approaches. Then we compared the performance of two modeling approaches by calculating the root mean square error (RMSE):
| 10) |
where is the number of samples and is the error.
4.4. Model calibration
The cyanobacteria growth model was calibrated with the model-independent parameter estimation software, PEST (Doherty 2004), which was developed to facilitate data interpretation, model calibration, and predictive analyses. It assesses parameters and searches for optima through an objective function, which is a weighted sum-of-squared residuals (differences between the model predictions and corresponding observations). Best-fit parameters are those that minimize the objective function:
| 11) |
where ωi is the weight associated with the ith residual, ri, and m is the number of observations.
In this study, growth rates and biomass were measured from four replicates (identical experimental units), therefore, these observations were assigned weights inversely proportional to the standard deviations of the four replicates. Measured growth rates from (3) and biomass for M. aeruginosa and D. flos-aquae are in the Supplementary Materials (Table S1).
4.5. Statistical analysis
Because the experiments were conducted in quadruplicate, we obtained 4 sets of observations (growth rate and biomass) for each species at each initial N concentrations. Therefore, we calibrated the model 4 times yielding 4 values for each parameter. We used a two-way analysis of variance (ANOVA) to test for differences among initial N concentrations, species, and their interaction for and . Significant main effects and interactions were compared using a Tukey’s post hoc multiple comparison test (R Core Team 2017).
Supplementary Material
Originality-Significance Statement.
The Monod equation is commonly used to describe the growth of bacteria and phytoplankton according to ambient nutrient concentrations. Although a growing number of studies has shown the flexibility in cyanobacteria nutrient metabolism, the half-saturation concentration in Monod equation is still considered as a static constant in many aquatic environment modelling applications. In this study, we demonstrated that a modified Monod model with variable half-saturation concentrations for nitrogen and phosphorus produced better prediction on cyanobacteria growth across a wide range of ambient nitrogen concentrations that may promote harmful algal blooms in eutrophic lakes. Our work quantified the physiological traits for two ubiquitous cyanobacteria and advances the understanding about harmful algal bloom ecology.
Acknowledgements
We dedicate this work to the memory of our coauthor, colleague, and friend, Dr. Scott C. James (SCJ), who passed away unexpectedly as we made the final preparations on the manuscript. Research reported in this publication was supported by the National Institute of Environmental Health Sciences of the National Institutes of Health under award number 1P01ES028942 to JTS and SCJ. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- American Public Health Association (APHA). 1999. Standard methods for the examination of water and wastewater 18th ed. American Water Works Association, Washington, D.C. [Google Scholar]
- Amano Y, Sakai Y, Sekiya T, Takeya K, Taki K, and Machida M 2010. Effect of phosphorus fluctuation caused by river water dilution in eutrophic lake on competition between blue-green alga Microcystis aeruginosa and diatom Cyclotella sp. J. Environ. Sci 22: 1666–1673. doi: 10.1016/S1001-0742(09)60304-1 [DOI] [PubMed] [Google Scholar]
- Amano Y, Takahashi K, and Machida M 2012. Competition between the cyanobacterium Microcystis aeruginosa and the diatom Cyclotella sp. under nitrogen-limited condition caused by dilution in eutrophic lake. J Appl Phycol 24: 965–971. doi: 10.1007/s10811-011-9718-8 [DOI] [Google Scholar]
- Amaral V, Bonilla S, and Aubriot L 2014. Growth optimization of the invasive cyanobacterium Cylindrospermopsis raciborskii in response to phosphate fluctuations. Eur. J. Phycol 49: 134–141. doi: 10.1080/09670262.2014.897760 [DOI] [Google Scholar]
- Baldia SF, Evangelista AD, Aralar EV, and Santiago AE 2007. Nitrogen and phosphorus utilization in the cyanobacterium Microcystis aeruginosa isolated from Laguna de Bay, Philippines. J. Appl. Phycol 19: 607–613. doi: 10.1007/s10811-007-9209-0 [DOI] [Google Scholar]
- Beversdorf LJ, Miller TR, and McMahon KD 2015. Long-term monitoring reveals carbon–nitrogen metabolism key to microcystin production in eutrophic lakes. Front. Microbiol 6. doi: 10.3389/fmicb.2015.00456 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonachela JA, Raghib M, and Levin SA 2011. Dynamic model of flexible phytoplankton nutrient uptake. PNAS 108: 20633–20638. doi: 10.1073/pnas.1118012108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brownlow JW, James SC, and Yelderman JC 2018. Uncertainty analysis: influence of hydraulic fracturing on overlying aquifers in the presence of leaky abandoned wells. Environ. Earth Sci 77: 477. doi: 10.1007/s12665-018-7586-0 [DOI] [PubMed] [Google Scholar]
- Bucak T, Trolle D, Tavşanoğlu ÜN, Çakıroğlu Aİ, Özen A, Jeppesen E, and Beklioğlu M 2018. Modeling the effects of climatic and land use changes on phytoplankton and water quality of the largest Turkish freshwater lake: Lake Beyşehir. Sci. Total Environ 621: 802–816. doi: 10.1016/j.scitotenv.2017.11.258 [DOI] [PubMed] [Google Scholar]
- Burmaster DE 1979. The unsteady continuous culture of phosphate-limited Monochrysis lutheri droop: Experimental and theoretical analysis. Journal of Experimental Marine Biology and Ecology 39: 167–186. doi: 10.1016/0022-0981(79)90012-1 [DOI] [Google Scholar]
- Chen W, & Liu H 2015. Intracellular nitrite accumulation: the cause of growth inhibition of Microcystis aeruginosa exposure to high nitrite level, Phycol. Res 63: 197–201. [Google Scholar]
- Chen Q, Wang M, Zhang J, Shi W, Mynett AE, Yan H, and Hu L 2019. Physiological effects of nitrate, ammonium, and urea on the growth and microcystins contamination of Microcystis aeruginosa: Implication for nitrogen mitigation. Water Res 163: 114890. doi: 10.1016/j.watres.2019.114890 [DOI] [PubMed] [Google Scholar]
- Cole TM, & Wells S 2000. CE-QUAL-W2: A two-dimensional, laterally averaged, Hydrodynamic and Water Quality Model, Version 3.0. Instruction Report EL-2000
- De Nobel WT, Jef Huisman, Jacky L. Snoep, Luuc R. Mur, 1997. Competition for phosphorus between the nitrogen-fixing cyanobacteria Anabaena and Aphanizomenon, FEMS Microbiology Ecology, 24, 259–267. doi: 10.1111/j.1574-6941.1997.tb00443.x [DOI] [Google Scholar]
- Dodds WK, Bouska WW, Eitzmann JL, Pilger TJ, Pitts KL, Riley AJ, Schloesser JT, and Thornbrugh DJ 2009. Eutrophication of U.S. freshwaters: Analysis of potential economic damages. Environ. Sci. Technol 43: 12–19. doi: 10.1021/es801217q [DOI] [PubMed] [Google Scholar]
- Doherty J 2004. PEST model-independent parameter estimation user manual. Watermark Numerical Computing, Brisbane, Australia 3338: 3349. [Google Scholar]
- Donald DB, Bogard MJ, Finlay K, Bunting L, Leavitt PR (2013) Phytoplankton-specific response to enrichment of phosphorus-rich surface waters with ammonium, nitrate, and urea. PLoS ONE 8(1): e53277. doi: 10.1371/journal.pone.0053277 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Droop M (1974). The nutrient status of algal cells in continuous culture. Journal of the Marine Biological Association of the United Kingdom, 54(4), 825–855. doi: 10.1017/S002531540005760X [DOI] [Google Scholar]
- Elser JJ, Bracken MES, Cleland EE, and others. 2007. Global analysis of nitrogen and phosphorus limitation of primary producers in freshwater, marine and terrestrial ecosystems. Ecol. Lett 10: 1135–1142. doi: 10.1111/j.1461-0248.2007.01113.x [DOI] [PubMed] [Google Scholar]
- Fujimoto N, Sudo R, Sugiura N, Inamori Y 1997. Nutrient-limited growth of Microcystis aeruginosa and Phormidium tenue and competition under various N:P supply ratios and temperature. Limnol. Oceanogr, 42, 250–256 [Google Scholar]
- Ghaffar S, Stevenson RJ, and Khan Z 2017. Effect of phosphorus stress on Microcystis aeruginosa growth and phosphorus uptake. PLoS One 12: e0174349. doi: 10.1371/journal.pone.0174349 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gobler CJ, Burkholder JM, Davis TW, Harke MJ, Johengen T, Stow CA, and Van de Waal DB 2016. The dual role of nitrogen supply in controlling the growth and toxicity of cyanobacterial blooms. Harmful Algae 54: 87–97. doi: 10.1016/j.hal.2016.01.010 [DOI] [PubMed] [Google Scholar]
- Gray E, Elliott JA, Mackay EB, Folkard AM, Keenan PO, and Jones ID 2019. Modelling lake cyanobacterial blooms: Disentangling the climate-driven impacts of changing mixed depth and water temperature. Freshwater Biol 64: 2141–2155. doi: 10.1111/fwb.13402 [DOI] [Google Scholar]
- Grimaud GM, Mairet F, Sciandra A, and Bernard O 2017. Modeling the temperature effect on the specific growth rate of phytoplankton: A review. Rev. Environ. Sci. Biotechnol 16: 625–645. doi: 10.1007/s11157-017-9443-0 [DOI] [Google Scholar]
- Grover JP, Scott JT, Roelke DL, and Brooks BW 2019. Dynamics of nitrogen-fixing cyanobacteria with heterocysts: a stoichiometric model. Mar. Freshwater Res 71: 644–658. doi: 10.1071/MF18361 [DOI] [Google Scholar]
- Hamrick JM, 1996. User’s manual for the environmental fluid dynamics computer code. Aquat. Ecosyst. Health Manage
- Harke MJ, Berry DL, Ammerman JW, and Gobler CJ 2012. Molecular response of the bloom-forming cyanobacterium, Microcystis aeruginosa, to phosphorus limitation. Microb. Ecol 63: 188–198. doi: 10.1007/s00248-011-9894-8 [DOI] [PubMed] [Google Scholar]
- Harke MJ, and Gobler CJ 2015. Daily transcriptome changes reveal the role of nitrogen in controlling microcystin synthesis and nutrient transport in the toxic cyanobacterium, Microcystis aeruginosa. BMC Genomics 16: 1068. doi: 10.1186/s12864-015-2275-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harke MJ, Steffen MM, Gobler CJ, Otten TG, Wilhelm SW, Wood SA, and Paerl HW 2016. A review of the global ecology, genomics, and biogeography of the toxic cyanobacterium, Microcystis spp. Harmful Algae 54: 4–20. doi: 10.1016/j.hal.2015.12.007 [DOI] [PubMed] [Google Scholar]
- Hellweger FL, and Kianirad E 2007. Individual-based modeling of phytoplankton: Evaluating approaches for applying the cell quota model. Journal of Theoretical Biology 249: 554–565. doi: 10.1016/j.jtbi.2007.08.020 [DOI] [PubMed] [Google Scholar]
- Hesse K, Dittmann E, and Börner T 2001. Consequences of impaired microcystin production for light-dependent growth and pigmentation of Microcystis aeruginosa PCC 7806. FEMS Microbiol. Ecol 37: 39–43. doi: 10.1111/j.1574-6941.2001.tb00851.x [DOI] [Google Scholar]
- Hipsey MR, Romero JR, Antenucci JP, Hamilton D, 2006. Computational Aquatic Ecosystem Dynamics Model. v. 2.3 Science Manual. Centre for Water Research, the University of Western Australia (online)
- Hydraulics., Delft3D-WAQ Detailed Description of Processes Technical Reference Manual
- WL| Delft Hydraulics (Deltares), Delft.
- Isvánovics V, Shafik HM, Présing M, and Juhos S 2000. Growth and phosphate uptake kinetics of the cyanobacterium, Cylindrospermopsis raciborskii (Cyanophyceae) in throughflow cultures. Freshwater Biol 43: 257–275. doi: 10.1046/j.1365-2427.2000.00549.x [DOI] [Google Scholar]
- James SC, and Boriah V 2010. Modeling algae growth in an open-channel raceway. J. Comput. Biol 17: 895–906. doi: 10.1089/cmb.2009.0078 [DOI] [PubMed] [Google Scholar]
- Jankowiak J, Hattenrath-Lehmann T, Kramer BJ, Ladds M, and Gobler CJ 2019. Deciphering the effects of nitrogen, phosphorus, and temperature on cyanobacterial bloom intensification, diversity, and toxicity in western Lake Erie. Limnol. Oceanogr 64: 1347–1370. doi: 10.1002/lno.11120 [DOI] [Google Scholar]
- Janse JH, and van Liere L 1995. PCLake: A modelling tool for the evaluation of lake restoration scenarios. Water Sci. Technol 31: 371–374. doi: 10.1016/0273-1223(95)00392-Z [DOI] [Google Scholar]
- Jiang L, Li Y, Zhao X, and others. 2018. Parameter uncertainty and sensitivity analysis of water quality model in Lake Taihu, China. Ecol. Modell 375: 1–12. doi: 10.1016/j.ecolmodel.2018.02.014 [DOI] [Google Scholar]
- Kenesi G, Shafik HM, Kovács AW, Herodek S, and Présing M 2009. Effect of nitrogen forms on growth, cell composition and N2 fixation of Cylindrospermopsis raciborskii in phosphorus-limited chemostat cultures. Hydrobiologia 623: 191–202. doi: 10.1007/s10750-008-9657-9 [DOI] [Google Scholar]
- Kim D, Kim Y, and Kim B 2019. Simulation of eutrophication in a reservoir by CE-QUAL-W2 for the evaluation of the importance of point sources and summer monsoon. Lake Reservoir Manage 35: 64–76. doi: 10.1080/10402381.2018.1530318 [DOI] [Google Scholar]
- Kolzau S, Dolman AM, Voss M, and Wiedner C 2018. The response of nitrogen fixing cyanobacteria to a reduction in nitrogen loading. Int. Rev. Hydrobiol 103: 5–14. doi: 10.1002/iroh.201601882 [DOI] [Google Scholar]
- Li X, Dreher TW, and Li R 2016. An overview of diversity, occurrence, genetics and toxin production of bloom-forming Dolichospermum (Anabaena) species. Harmful Algae 54: 54–68. doi: 10.1016/j.hal.2015.10.015 [DOI] [PubMed] [Google Scholar]
- Li Z, Chen Q, and Xu Q 2015. Modeling algae dynamics in Meiliang Bay of Taihu Lake and parameter sensitivity analysis. Journal of Hydro-environment Research 9: 216–225. doi: 10.1016/j.jher.2014.10.001 [DOI] [Google Scholar]
- Liu X, Lu X, and Chen Y 2011. The effects of temperature and nutrient ratios on Microcystis blooms in Lake Taihu, China: An 11-year investigation. Harmful Algae 10: 337–343. doi: 10.1016/j.hal.2010.12.002 [DOI] [Google Scholar]
- Lomnicki A, 1999. Individual-based models and the individual-based approach to population ecology. Ecol. Modell 115, 191–198. [Google Scholar]
- McCausland MA, Thompson PA, and Blackburn SI 2005. Ecophysiological influence of light and mixing on Anabaena circinalis (Nostocales, Cyanobacteria). Eur. J. Phycol 40: 9–20. doi: 10.1080/09670260400019758 [DOI] [Google Scholar]
- Mikawa M, Sugimoto K, Amano Y, Machida M, and Imazeki F 2016. Competitive growth characteristics between Microcystis aeruginosa and Cyclotella sp. accompanying changes in river water inflow and their simulation model. Phycol. Res 64: 123–132. doi: 10.1111/pre.12129 [DOI] [Google Scholar]
- Mills MM, Ridame C, Davey M, La Roche J, and Geider RJ 2004. Iron and phosphorus co-limit nitrogen fixation in the eastern tropical North Atlantic. Nature 429: 292–294. doi: 10.1038/nature02550 [DOI] [PubMed] [Google Scholar]
- Monod J 1949. The growth of bacterial cultures. Annu. Rev. Microbiol 3: 371–394. [Google Scholar]
- Orr PT, and Jones GJ 1998. Relationship between microcystin production and cell division rates in nitrogen-limited Microcystis aeruginosa cultures. Limnol. Oceanogr 43: 1604–1614. doi: 10.4319/lo.1998.43.7.1604 [DOI] [Google Scholar]
- Osburn FS, Wagner ND, and Scott JT 2021. Biological stoichiometry and growth dynamics of a diazotrophic cyanobacteria in nitrogen sufficient and deficient conditions. Harmful Algae 103: 102011. doi: 10.1016/j.hal.2021.102011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paerl HW, Otten TG, and Joyner AR 2016a. Moving towards adaptive management of cyanotoxin-impaired water bodies. Microb. Biotechnol 9: 641–651. doi: 10.1111/1751-7915.12383 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paerl HW, Scott JT, McCarthy MJ, and others. 2016b. It takes two to tango: When and where dual nutrient (N & P) reductions are needed to protect lakes and downstream ecosystems. Environ. Sci. Technol 50: 10805–10813. doi: 10.1021/acs.est.6b02575 [DOI] [PubMed] [Google Scholar]
- R Core Team (2017). R: A language and environment for statistical computing R Foundation for Statistical Computing, Vienna, Austria. [Google Scholar]
- Rabouille S, Staal M, Stal LJ, and Soetaert K 2006. Modeling the dynamic regulation of nitrogen fixation in the cyanobacterium Trichodesmium sp. Appl. Environ. Microbiol 72: 3217–3227. doi: 10.1128/AEM.72.5.3217-3227.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reinl KL, Brookes JD, Carey CC, and others. 2021. Cyanobacterial blooms in oligotrophic lakes: Shifting the high-nutrient paradigm. Freshwater Biol n/a: 1–14. doi: 10.1111/fwb.13791 [DOI]
- Reynolds CS, Irish AE, and Elliott JA 2001. The ecological basis for simulating phytoplankton responses to environmental change (PROTECH). Ecol. Modell 140: 271–291. doi: 10.1016/S0304-3800(01)00330–1 [DOI] [Google Scholar]
- Riley GA 1956. Oceanography of Long Island Sound, 1952–1954, II. Phys. Oceanogr. Bull. Bing. Ocean. Coll 15: 15–46. [Google Scholar]
- Robson BJ, Arhonditsis GB, Baird ME, and others. 2018. Towards evidence-based parameter values and priors for aquatic ecosystem modelling. Environmental Modelling & Software 100: 74–81. doi: 10.1016/j.envsoft.2017.11.018 [DOI] [Google Scholar]
- Robson BJ, and Hamilton DP 2004. Three-dimensional modelling of a Microcystis bloom event in the Swan River estuary, Western Australia. Ecol. Modell 174: 203–222. doi: 10.1016/j.ecolmodel.2004.01.006 [DOI] [Google Scholar]
- Rousso BZ, Bertone E, Stewart R, and Hamilton DP 2020. A systematic literature review of forecasting and predictive models for cyanobacteria blooms in freshwater lakes. Water Res 182: 115959. doi: 10.1016/j.watres.2020.115959 [DOI] [PubMed] [Google Scholar]
- Sathyendranath S, Stuart V, Nair A, and others. 2009. Carbon-to-chlorophyll ratio and growth rate of phytoplankton in the sea. Mar. Ecol.: Prog. Ser 383: 73–84. doi: 10.3354/meps07998 [DOI] [Google Scholar]
- Schoffelen NJ, Mohr W, Ferdelman TG, Littmann S, Duerschlag J, Zubkov MV, Ploug H, and Kuypers MMM 2018. Single-cell imaging of phosphorus uptake shows that key harmful algae rely on different phosphorus sources for growth. Sci. Rep 8: 17182. doi: 10.1038/s41598-018-35310-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott JT, and McCarthy MJ 2010. Nitrogen fixation may not balance the nitrogen pool in lakes over timescales relevant to eutrophication management. Limnol. Oceanogr 55: 1265–1270. doi: 10.4319/lo.2010.55.3.1265 [DOI] [Google Scholar]
- Scott JT, McCarthy MJ, and Paerl HW 2019. Nitrogen transformations differentially affect nutrient-limited primary production in lakes of varying trophic state. Limnol. Oceanogr. Lett 4: 96–104. doi: 10.1002/lol2.10109 [DOI] [Google Scholar]
- Shimoda Y, and Arhonditsis GB 2016. Phytoplankton functional type modelling: Running before we can walk? A critical evaluation of the current state of knowledge. Ecological Modelling 320: 29–43. doi: 10.1016/j.ecolmodel.2015.08.029 [DOI] [Google Scholar]
- Smith VH 1983. Low nitrogen to phosphorus ratios favor dominance by blue-green algae in lake phytoplankton. Science 221: 669–671. doi: 10.1126/science.221.4611.669 [DOI] [PubMed] [Google Scholar]
- Sommer U 1991. A Comparison of the Droop and the Monod models of nutrient limited growth applied to natural populations of phytoplankton. Funct. Ecol 5: 535–544. doi: 10.2307/2389636 [DOI] [Google Scholar]
- Song B, and Ward BB 2007. Molecular cloning and characterization of high-affinity nitrate transporters in marine phytoplankton. J. Phycol 43: 542–552. doi: 10.1111/j.1529-8817.2007.00352.x [DOI] [Google Scholar]
- Steele JH 1962. Environmental Control of Photosynthesis in the Sea. Limnol. Oceanogr 7: 137–150. doi: 10.4319/lo.1962.7.2.0137 [DOI] [Google Scholar]
- Sugimoto K, Negishi Y, Amano Y, Machida M, and Imazeki F 2016. Roles of dilution rate and nitrogen concentration in competition between the cyanobacterium Microcystis aeruginosa and the diatom Cyclotella sp. in eutrophic lakes. J. Appl. Phycol 28: 2255–2263. doi: 10.1007/s10811-015-0754-7 [DOI] [Google Scholar]
- Tan X, Gu H, Zhang X et al. Effects of phosphorus on interspecific competition between two cell-size Cyanobacteria: Synechococcus sp. and Microcystis aeruginosa. Bull Environ Contam Toxicol 102, 231–238 (2019). 10.1007/s00128-018-2527-x [DOI] [PubMed] [Google Scholar]
- Tonkin M, and Doherty J 2009. Calibration-constrained Monte Carlo analysis of highly parameterized models using subspace techniques. Water Resour. Res 45. doi: 10.1029/2007WR006678 [DOI] [Google Scholar]
- Wagner ND, Osburn FS, Wang J, Taylor RB, Boedecker AR, Chambliss CK, … & Scott, J. T. (2019). Biological stoichiometry regulates toxin production in Microcystis aeruginosa (UTEX 2385). Toxins, 11(10), 601. doi: 10.3390/toxins11100601 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S, Xiao J, Wan L, Zhou Z, Wang Z, Song C, Zhou Y, and Cao X 2018. Mutual dependence of nitrogen and phosphorus as key nutrient Elements: one facilitates Dolichospermum flos-aquae to overcome the limitations of the other. Environ. Sci. Technol 52: 5653–5661. doi: 10.1021/acs.est.7b04992 [DOI] [PubMed] [Google Scholar]
- Weiskerger CJ, Rowe MD, Stow CA, Stuart D, and Johengen T 2018. Application of the Beer–Lambert model to attenuation of photosynthetically active radiation in a shallow, eutrophic lake. Water Resour. Res 54: 8952–8962. doi: 10.1029/2018WR023024 [DOI] [Google Scholar]
- Willis A, Posselt AJ, and Burford MA 2017. Variations in carbon-to-phosphorus ratios of two Australian strains of Cylindrospermopsis raciborskii. Eur. J. Phycol 52: 303–310. doi: 10.1080/09670262.2017.1286524 [DOI] [Google Scholar]
- Xiao M, Hamilton DP, O’Brien KR, Adams MP, Willis A, and Burford MA 2020. Are laboratory growth rate experiments relevant to explaining bloom-forming cyanobacteria distributions at global scale? Harmful Algae 92: 101732. doi: 10.1016/j.hal.2019.101732 [DOI] [PubMed] [Google Scholar]
- Yema L, Litchman E, and de Tezanos Pinto P 2016. The role of heterocytes in the physiology and ecology of bloom-forming harmful cyanobacteria. Harmful Algae 60: 131–138. doi: 10.1016/j.hal.2016.11.007 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


