Simulation of energy-resolved mass spectrometry distributions from surface-induced dissociation

Abstract

Understanding the relationship between protein structure and experimental data is crucial for utilizing experiments to solve biochemical problems and optimizing the use of sparse experimental data for structural interpretation. Tandem mass spectrometry (MS/MS) can be used with a variety of methods to collect structural data for proteins. One example is surface-induced dissociation (SID), which is used to break apart protein complexes (via a surface collision) into intact subcomplexes and can be performed at multiple laboratory frame SID collision energies. These energy-resolved tandem MS/MS experiments have shown that the profile of the breakages depends on the acceleration energy of the collision. It is possible to extract an appearance energy (AE) from energy-resolved mass spectrometry (ERMS) data, which shows the relative intensity of each type of subcomplex as a function of SID acceleration energy. We previously determined that these AE values for specific interfaces correlated with structural features related to interface strength. In this study, we further examined the structural relationships by developing a method to predict the full ERMS plot from structure, rather than extracting a single value. First, we noted that for proteins with multiple interface types, we could reproduce the correct shapes of breakdown curves, further confirming previous structural hypotheses. Next, we demonstrated that interface size and energy density (measured using Rosetta) correlated with data derived from the ERMS plot (R² = 0.71). Furthermore, based on this trend, we used native crystal structures to predict ERMS. The majority of predictions resulted in good agreement, and the average root-mean-square error (RMSE) was 0.20 for the 20 complexes in our dataset. We also show that if additional information on cleavage as a function of collision energy could be obtained, the accuracy of predictions improved further. Finally, we demonstrated that ERMS prediction results were better for the native than for inaccurate models in 17/20 cases. An application to run this simulation has been developed in Rosetta, which is freely available for use.

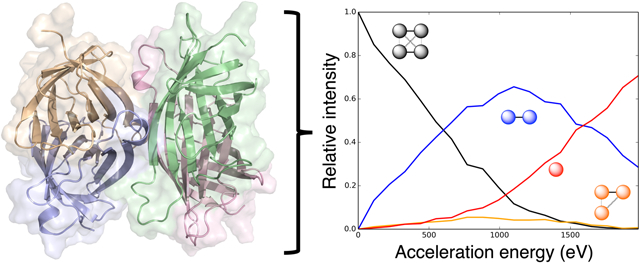
Graphical Abstract

Introduction

Data from tandem mass spectrometry (MS/MS) experiments increasingly provides valuable structural information for proteins and protein complexes. An assortment of different techniques can be used to measure various types of structural information.^1-5 For example, ion mobility (IM) can provide information on size and shape,^6-8 chemical cross-linking (XL) can provide information on residue distances and contacts,^9-11 and covalent labeling can provide information on solvent accessibility and flexibility of residues.^12-16 The resulting structural information can then be used to better understand the roles of the specific proteins in biological processes. These sparse data have also been combined with computational modeling methods^{17, 18} to improve the accuracy of structural predictions.^19-29

Surface-induced dissociation (SID) is an ion activation method that provides information on the native structure of protein complexes, in the form of mass-to-charge (m/z) measurements of subcomplexes.^30-34 After soft ionization (using nanoelectrospray ionization, which allows the protein to largely retain a native-like structure despite gas phase conditions^35-37), complexes are intentionally collided with a surface at hyperthermal energies. When this process occurs, the majority of the collision energy is converted to internal energy, cleaving the non-covalent protein-protein interfaces and breaking the complex into various subcomplexes. The relative intensities of these resulting subcomplex types are measured using MS/MS. The experiment is then repeated at multiple acceleration energies to measure a profile of interface cleavage. The results of these experiments, energy-resolved mass spectrometry (ERMS) data are often plotted as ERMS plots, which show the relative intensity of each resulting subcomplex type as a function of the acceleration energy towards the surface. From these data, complex stoichiometry and connectivity can be pieced together as interfaces break.³³ We have also demonstrated previously that these data can measure the relative strengths of specific protein-protein interfaces.³⁸ We hypothesized that weaker interfaces would break at lower acceleration energies, while stronger interfaces would require more energy to break. Previously, we quantified this for a subset of the interfaces in each protein complex. This metric was the appearance energy (AE), which was defined as the acceleration energy when the resulting subcomplexes (after the breakage of the interface) reached 10% of the relative intensity. Using this metric, we showed that (i) structural features measuring interface strength correlated with the AE values, (ii) the AE could be reliably predicted from the structure of a specific interface, and (iii) that this information was beneficial in scoring output structures from protein-protein docking experiments, which would then be used to accurately predict the structure of a complex.^{39, 40} Though this work showed promising results, one downside was the extraction of only one AE value for a given interface, disregarding much of the information contained in the ERMS data.

In this work, we extend our modelling efforts to utilize the entire information contained within the SID ERMS data. We developed a method to predict full ERMS data from complex structure. The application to run this simulation in Rosetta is freely available for use (see Supporting Information for more information). We first noted that for proteins with multiple different interfaces, we could reproduce the correct shapes of ERMS plots, providing further corroboration that interface strength indeed determines the shape of these curves. We then demonstrated that interface size and energy density (measured using Rosetta) strongly correlated with interface strengths derived from the ERMS data. We subsequently used this correlation to model the breakages and predict the distributions. Of the 20 complexes tested, the majority produced accurate results using the native structures as input. Finally, we showed, by performing a simple docking study, that our method was sensitive to structural accuracy, where non-nativelike models had predicted ERMS that were poorer fits to experimental curves than those of native structures.

Methods

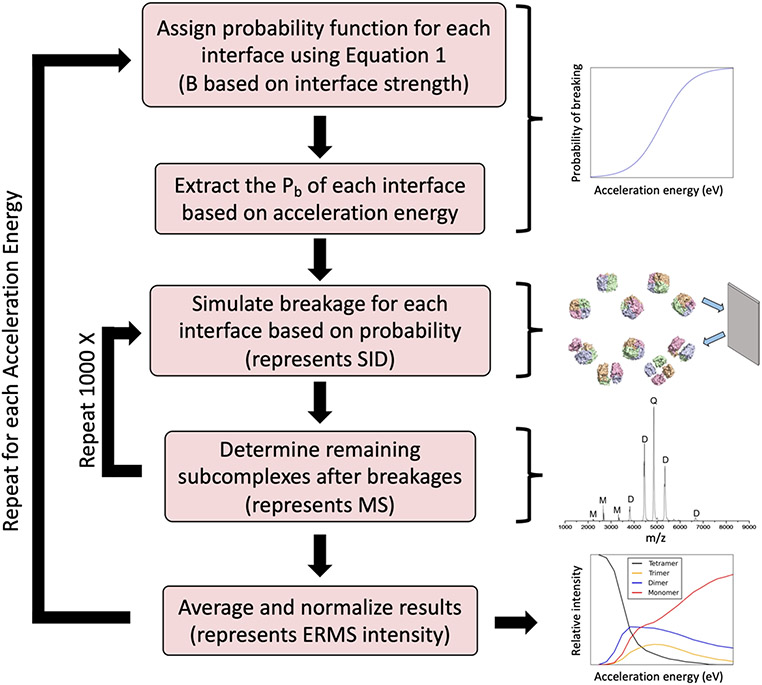
The method described in this section was developed to simulate interface breakage that occurs during SID and predict energy-resolved mass spectrometry (ERMS) data. Notably, we do not simulate the dynamics of SID at the molecular level, but rather simply predict abundances of products after the collision, as will be discussed further. ERMS plots show the relative intensity of each type of subcomplex (and precursor) as a function of the SID acceleration energy. The method is based on simulating breakages for each interface using a probability function that depends on the interface strength (structural features) and the acceleration energy. The simulation method uses the probability function for each type of interface within a complex and the ERMS plot is predicted using the method described below.

Probability function

The probability function used for each interface is shown in Equation 1. This function defines the probability that an interface breaks (P_b) based on the interface strength (B, midpoint of the curve) and acceleration energy (X). At the midpoint, there is a 50% probability for the interface to break. We chose a fade function where the probability increases as acceleration energy increases based on the observed shapes of the SID ERMS plots. Examples of this function (A = 0.0025 eV⁻¹, B = 2000 eV and A = 0.0150 eV⁻¹, B = 2000 eV) are shown in Figure S1. The midpoint of the function (B) can shift in either direction to accommodate for differences in interface strengths. For example, a higher B would indicate a stronger interface, that requires more energy to break, and thus the probability curve is shifted to the right. The function also has a steepness parameter that has been set to slightly different values depending on the conditions (A, described in detail later in the methods). This steepness determines the sharpness or softness of the breakage threshold. Methodology for obtaining the parameters A and B for each simulation will be described in the following sections.

$$P_b=1-\frac{1}{1+e^{A(X-B)}}$$ (1)

Simulation process

After probability functions are assigned for each interface in the complex (defined based on the complex oligomeric state and symmetry), the following simulation process is performed for each acceleration energy on the ERMS plot x-axis as shown in Figure 1 and described here. At each acceleration energy, the breakage probability is extracted from the function (Equation 1). Next, the breakage (or lack thereof) of each interface is simulated based on these probabilities (using a random number generator). Based on the remaining connectivity, the resulting subcomplexes are enumerated. This process of simulating the breakage is repeated 1000 times and the frequencies of observed subcomplexes are averaged and the values of each subcomplex type are normalized, such that they sum to 1. The process is repeated for each acceleration energy. Breakage is allowed to occur only when the acceleration energy exceeds zero, i.e., at x = 0, the precursor is set to intensity of one and the remaining subcomplexes set to zero. The results of this process provide the data needed to construct the predicted ERMS plot (relative intensity of each subcomplex type as a function of acceleration energy).

Figure 1:

Flowchart describing the ERMS plot simulation process.

While simulations can be performed from structure directly, additional information may be provided to improve the predictions, if available. If SID experiments were performed to determine the acceleration energy where breakage of the precursor begins to occur, predictions can be improved further. Rather than starting breakage after zero, the breakage is then started after the breakage cutoff (defined as highest acceleration energy with less than 95% precursor).

Benchmark set

The benchmark set used in this study primarily contains proteins with ERMS data published previously.³⁸ These proteins include triose phosphate isomerase (8TIM), streptavidin (1SWB), neutravidin (1AVE), pyruvate kinase (1AQF), concanavalin A (1JBC), transthyretin (5HJG), D-sialic acid aldolase (6ALD), hemoglobin (1GZX), tryptophan synthetase (1WBJ), cholera toxin B (1FGB), C-reactive protein (1GNH), serum amyloid P (1SAC), beta-lactoglobulin (6QI6), lysozyme (4R0F), and enolase (1E9I). A few additional proteins were also included in the dataset:^{41, 42} IspD (1VGT), Can (1T75), DeoC (1KTN), Upp (2EHJ), and HFq (1HK9). In all cases experiments were performed on a Waters Synapt G2 or G2s mass spectrometer, operated in mobility mode. Protein complexes were prepared for spray under charge-reducing conditions.⁴³ In total, the dataset contained 6 homodimers (C2 symmetry), 8 homotetramers (D2 symmetry), 2 heterotetramers (one with D2 symmetry, one with C2 symmetry), 3 homopentamers (C5 symmetry), and 1 homohexamer (C6 symmetry). The complex types and connectivities are shown for each complex in Table S1. The PDB structures were first relaxed in Rosetta using the REF2015 scoring function.⁴⁴ Next, interface properties were calculated using Rosetta InterfaceAnalyzer⁴⁵ for each type of interface in each complex (in some complexes, multiple interfaces are symmetric and thus equivalent). From this calculation, interface surface area (dSASA_int) and energy per interface residue (per_residue_energy_int) were extracted for use in determining breakage probabilities as described in the following section.

For each of the experimental ERMS data individually, optimal values of B (midpoint of probability curve) were determined to maximize agreement between predicted and experimental data. These values were then used to observe a correlation between experimental data (optimal B from ERMS) and structure (interface features). The metric used to quantify agreement between predicted and experimental ERMS data was root-mean-square error (RMSE), which was calculated based on the relative intensity difference at each value of acceleration energy over each subcomplex type.

Determination of probability midpoint (B)

As mentioned previously, the inputs to the ERMS simulation algorithm are probability curves for each interface. These probability curves are modulated based on interface strength using the midpoint of the fade function (B, stronger interface corresponds to higher B). The B values were determined based on the observed correlation between the following interface features: interface surface area (SA [dSASA_int], positive correlation) and energy per interface residue (PRE [per_residue_energy_int], negative correlation). The function to determine B from interface structure is provided in Equation 2. The values of the weights for both options (without and with knowledge of breakage cutoff) are provided in Table S2. To determine the optimal weights, we used the Python simplex algorithm (minimizing χ²) and linear regression.⁴⁶

$$B=w_{SA}\ast SA+w_{PRE}PRE+w_{int}$$ (2)

Determination of probability steepness (A)

For the majority of systems, the steepness (A) of the probability curve was set to the following values: A = 0.0025 eV⁻¹ without breakage cutoff, A = 0.0020 eV⁻¹ with breakage cutoff. However, for dimers with particularly rigid subunits, the steepness was set to a higher value to account for the sharper observed slopes of the ERMS plots. The higher steepness (A = 0.0150 eV⁻¹ with and without breakage cutoff) was used for all dimers that had intrasubunit disulfide bonds.

Results and Discussion

Here, we describe a method to simulate energy-resolved mass spectrometry (ERMS) data from SID-MS/MS experiments for protein complexes with a variety of oligomeric states (predict the data, not to physically simulate at the molecular level). ERMS plots show the relative intensity of each subcomplex type after SID as a function of the acceleration energy. We observed correlations between experimental data and interface structure. Based on the strength of each interface (as measured by size and Rosetta energy), a probability curve was constructed using a fade function to define the probability of breaking each interface as a function of acceleration energy (see Figure S1 for examples). Using this probability curve for each interface, breakages were simulated for 1000 complexes at each acceleration energy. The resulting averaged, normalized data were then used to construct the predicted ERMS plot and compared to experimental results for a dataset containing dimers, tetramers, pentamers, and hexamers (see Table S1). All systems are referred to by the PDB ID in Table S1 and given in the methods.

SID dissociation competition pathways for tetramers match predictions from structure

Based on the design of our simulation algorithm, proteins that exhibited one unique type of interface between exactly two subunits (C2 dimers, C5 pentamers, and C6 hexamers) produced ERMS plots with similar shapes, but varying strengths (shifts in acceleration energies). However, for the tetramers, there were multiple different types of interfaces (three types each for nine D2 tetramers and two types for 1WBJ, a linear C2 tetramer). For this reason, multiple shapes for the ERMS plots were observable, depending on the relative probability curve midpoint (B) values of the respective interfaces. We previously discussed the experimental tetramer SID breakage patterns and their qualitative relationship to structure for the D2 tetramers,³⁸ but we will revisit the discussion in the context of predicting ERMS data here.

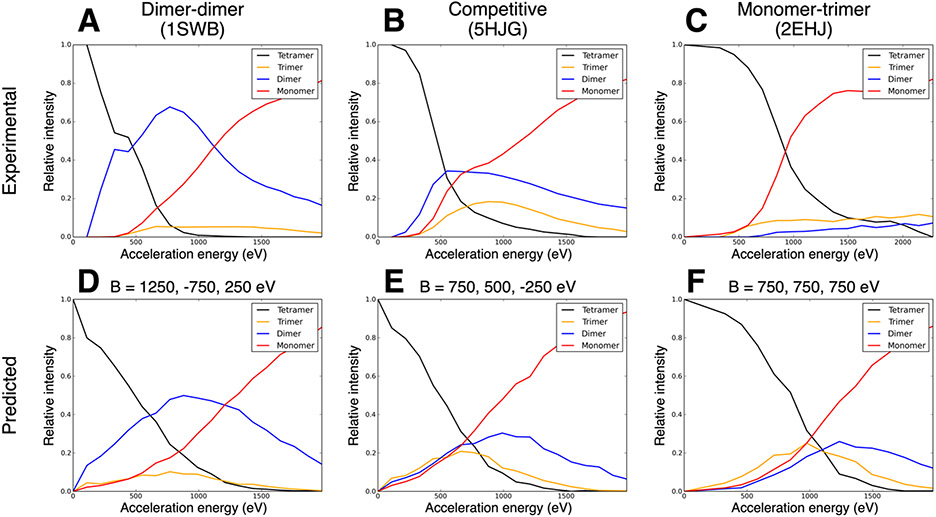
As tetramers break into subcomplexes, there is the possibility of competition between the pathway that forms two dimers and the pathway that forms one monomer and one trimer. Thus, the experimental ERMS plots can be roughly classified as dimer-dimer, competitive (i.e., both pathways occur significantly at the same energies), or monomer-trimer, as shown in Figure 2A, 2B, and 2C, respectively. In previous work,³⁸ we noted that dimer-dimer ERMS plots were likely to result from tetramers with a single dominant interface (in terms of size, i.e., a dimer of dimers) and that monomer-trimer ERMS plots were likely to come from tetramers with relatively even interface sizes. Table S3 (first three columns) shows the structural prediction (based on the relative interface strengths as outlined above) and the actual ERMS shape. Except for one (6ALD), all cases either agree or almost agree (a competitive pathway is involved, at least at higher energies). Based on this previous observation, we sought to test whether the relationship between relative interface strength and ERMS breakdown pathway could be reproduced using the simulation method described here. To test this, we predicted ERMS data under the following conditions: one strong interface (dimer-dimer expected), relatively even interfaces (monomer-trimer expected), and somewhere in between (competitive expected). As predicted, setting B values to match these conditions (B=1200, −750, 250 eV; B=750, 500, −250 eV; B=750, 750, 750 eV, respectively) produced ERMS plots with these three relative shapes, as shown in Figure 2D, 2E, and 2F. While the hypothesized ratios of interface strengths could reproduce the observed shapes relatively well, the monomer-trimer shape of the prediction exhibited a pathway that appeared to be shaped more similar to dimer-dimer than experimentally observed for many complexes (Figure 2F). However, based on the methodology, this can be understood. If all interfaces were even, then monomer-trimer was more likely than dimer-dimer (3 interfaces breaking compared to 4, all with equal probability, ex: A_B, A_C, and A_D versus A_D, A_C, B_C, and B_D), however dimer-dimer is still likely to occur for a fraction of complexes in the simulation. Despite these understood discrepancies, using relatively even interfaces was best able to reproduce the monomer-trimer shape.

Figure 2:

(A-C) Examples of experimental ERMS plots for tetramers of the three possible pathways: dimer-dimer (1SWB), competitive (5HJG), and monomer-trimer (2EHJ), respectively. (D-F) Examples of predicted ERMS plots with the corresponding hypothesized relative interface strengths for the three pathways.

While the previous discussion relates to the D2 tetramers, we also tested a linear, C2 tetramer (1WBJ, see Table S1 for connectivity diagram). In this case, if the outer interface is weaker, then monomer-trimer is expected and if the inner interface is weaker, dimer-dimer is expected. The experimental ERMS plot showed a slight preference for monomer-trimer (within the pathway competition). Based on this, the prediction would be that the outer interface was slightly weaker than the inner, but on the same order of strength. This expected observation matched the calculated interface areas remarkably well: 2961 Å and 3615 Å, respectively. Similar to the D2 tetramers, the shapes of the different observed pathways could be constructed based on the hypothesized relative interface strengths (outer interface stronger: dimer-dimer, inner interface stronger: monomer-trimer, relatively even strength: competitive) using the simulation method (data not shown).

Structural features relating to interface strength correlate with experimental data

To (i) examine correlations between structure and experimental data and (ii) develop an approach to predict ERMS from structure, we first determined the optimal values of the probability curve midpoint (the optimal B value) that would most closely reproduce the experimental ERMS data (without yet taking structure into account). For the majority of proteins in the dataset, a constant value of the probability steepness (A) was used. However, to account for the observed steeper slopes in the ERMS plots for dimers with particularly rigid subunits, a higher value of A was used in these cases (defined as dimers with at least one intrasubunit disulfide bond). For dimers with more rigid subunits, less energy is redistributed into unfolding the subunits after the SID collision. For this reason, the dissociation (from dimer to monomers) occurs closer to an “all or nothing” pathway once the acceleration energy reaches a certain threshold, i.e., either breaks close to completely or little at all. On the other hand, less rigid dimers undergo a more gradual dissociation (with respect to the increasing acceleration energy). In the dataset, two proteins met this criterion for a larger A value (4R0F and 6QI6). An example comparison of the effect of these different steepnesses on the probability curve is shown in Figure S1. The curve with larger steepness has a smaller range of acceleration energies that produces a probability of breaking in the ~0.2-0.8 range. This same phenomenon was not observed for complexes larger than dimers. We hypothesize that this was due to the larger number of degrees of freedom for the larger complexes. Because they have more possible avenues to redistribute energy, the rigidity might play less of a role in breakage slope.

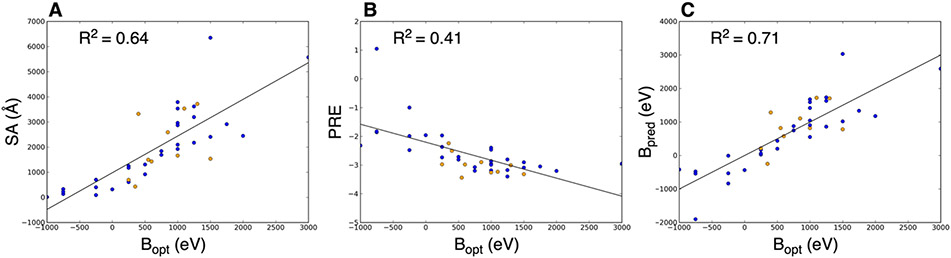
We hypothesized that interfaces with higher optimal B values (a value extracted from experimental data) would have stronger structural features, i.e., larger interface area, more favorable energy, etc. To test this, we calculated interface features using the relaxed crystal structures for the complexes in our dataset. As noted in the previous section and in previous work,³⁸ relative interface size between different interfaces correlated with the shapes of the tetramer ERMS plots (see first 3 columns of Table S3: structure class, experimental class, and prediction class). Here, we examined the correlations between optimal B (experimental) and interface features, as shown in Figure 3. Panels A and B of Figure 3 show correlations between interface surface area (SA) and per residue energy of interface (PRE), respectively, with the optimal B. The observed correlations matched the expected trends. Larger interfaces tended to have higher optimal B values (R² = 0.64), i.e., dissociate at higher acceleration energies. Stronger interfaces (lower PRE) tended to also have higher optimal B values (R² = 0.41). These data demonstrate that (i) the entire ERMS data correlate with structural features of protein-protein interfaces (rather than just “onset” appearance energy) and (ii) that the previously qualitatively observed phenomenon regarding interface sizes and tetramer shape can be generalized quantitatively.

Figure 3:

Correlations between structural features and experimental data for all interfaces. (A) and (B) show correlation between surface area (SA) and Rosetta per-residue interface energy (PRE), respectively, with the optimal B values from the experimental data (B_opt). (C) shows the predicted B value (B_pred) used in the simulations calculated using Equation 2. Blue points are tetramer interfaces and orange points are non-tetramer interfaces (dimer, pentamer, or hexamer).

ERMS data can be reliably predicted from structure

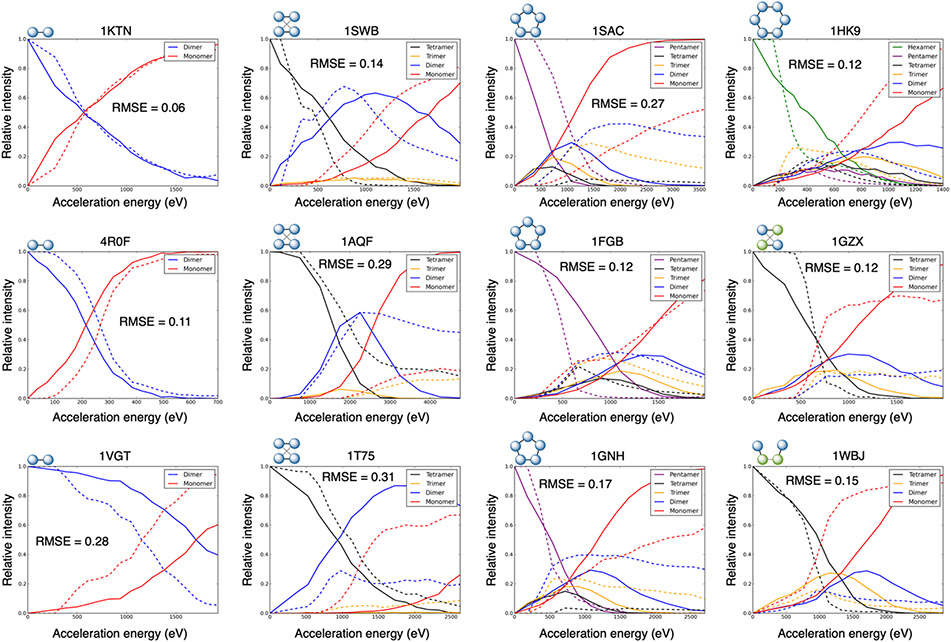
To use these correlations in the prediction method (i.e., to predict ERMS data from structure), we used a combination of the SA and PRE to determine the B input for the simulation. The correlation between predicted B and optimal B value is shown in Figure 3C (corresponding to Equation 2) and had an R² value of 0.71. The resulting ERMS plot predictions are shown in Figure 4 and S2. Overall, the average RMSE was 0.20 (median of 0.18) with only three cases of root-mean-square error (RMSE) greater than 0.30, indicating good agreement with the experimental data for most of the 20 benchmark cases. The breakdown of average RMSE of the different complex types is the following for dimers, tetramers, pentamers, and hexamer, respectively: 0.26, 0.18, 0.19, and 0.12.

Figure 4:

Predicted ERMS plots for select complexes (remaining shown in Figure S2). The following complexes shown here by PDB ID: 1KTN, 4R0F, 1VGT, 1SWB, 1AQF, 1T75, 1SAC, 1FGB, 1GNH, 1HK9, 1GZX, and 1WBJ. Solid line: prediction, dotted line: experimental ERMS.

The dimer results varied the most. The best RMSE of 0.06 was observed for PDB ID 1KTN, while the two worst predictions were for 8TIM and 6QI6, with RMSE values of 0.36 and 0.53 respectively. Of the six dimers in the dataset, two had RMSE less than 0.2, two had RMSE greater than 0.2 and less than 0.3, and two had RMSE greater than 0.3. This variability for dimers can be explained by the need to predict the single B value very accurately to match the experimental ERMS plot, while the other complex types were more forgiving. The pentamers and hexamers were all at least moderately accurate (RMSE < 0.30 for all). For the tetramers, we additionally examined the shapes of the predicted ERMS plots, as discussed previously. Though the RMSE was poor for a couple cases (1AQF: RMSE = 0.29 and 1T75: RMSE = 0.31), in every case, the RMSE was low and/or the shape matched the experimental shape (dimer-dimer vs. monomer-trimer vs. competitive), as shown in Table S3. There were three cases where a competitive ERMS was predicted for a dimer-dimer or monomer-trimer (1GZX: RMSE = 0.12, 2EHJ: RMSE = 0.20, and 6ALD: RMSE = 0.19), however, the RMSEs were still low (indicating the general breakage occurring at acceleration energies near the actual).

Furthermore, when comparing the accuracy of each subcomplex type over all the predictions, the monomer curves were typically the most inaccurate. This is likely due the monomers having the most variability in the experimental curves, where they can vary from 0 up to almost 1 in many cases. This is likely due to the fact that monomers can be produced from secondary cleavage in addition to primary. This phenomenon is further emphasized when comparing the monomer experimental curves to trimers (which are typically low intensity and stable regardless of acceleration energy and predictions are very accurate). The average RMSE values for the monomers, dimers, trimers, tetramers, pentamers, and hexamers were 0.26, 0.20, 0.08, 0.11, 0.14, and 0.15, respectively.

Improved accuracy for ERMS data prediction with additional information

While we demonstrated in the previous section that SID ERMS data can be predicted directly from structure, additional information can also be included in the predictions to improve the results further. In the previously described method, simulated breakage occurs immediately at acceleration energies greater than 0 eV. However, for some cases, the experimental ERMS plots reveal that the complexes do not start to break until they reach slightly larger energies. For example, in the predicted ERMS plot for 1SAC in Figure 4 (solid line), breakage occurs immediately after 0 eV. However, in the experimental ERMS plot (dotted line), breakage is only observed for acceleration energies higher than 360 eV. If that specific energy where breakage begins is known (via an experiment), then the simulations can be adjusted to begin breakage at that point. The breakage cutoff was defined as the maximum observed acceleration energy with at least 95% precursor (ex: breakage cutoff = 360 eV for 1SAC). Including this additional information improved the predictions, as will be described further. However, we also sought to explore the origin of these breakage cutoffs and whether they correlated with structure. The extracted breakage cutoffs did weakly correlate with structural features of the protein complexes such as total number of residues, number of residues per chain, SA of largest interface, and Rosetta ∆G of the strongest interface, as shown in Figure S3. This generally indicates that larger complexes and complexes with larger or stronger interfaces tend to only begin breaking at higher SID acceleration energies, which are correlated with ion activation energies. This is consistent with RRKM (Rice–Ramsperger–Kassel–Marcus) theory (kinetic theory of fragmentation by mass spectrometry), which shows that fragmentation will only occur once the pathway-dependent activation energy for a given fragmentation reaction has been exceeded to allow fragmentation at a particular rate, which is determined by the instrument time frame. The excess energy that is required to drive a fragmentation reaction with an instrument-dependent rate is called the kinetic shift. Thus, overall, the reaction rate depends on the activation energy and the kinetic shift. Fragmentation kinetics are determined by the activation free energy (ΔG^#), i.e., barrier height and not the equilibrium thermodynamic value of ΔG. We did not calculate the microstates above the barrier (transition state, TS) to determine (or, at least, estimate) the kinetic shift. As Beynon and Gilbert noted,⁴⁹ at high (internal) energies and for large molecules this procedure becomes increasingly impracticable (see, page 43 in ⁴⁹). Our approach is somewhat related to Cooks’ kinetic method in that dissociation trends are used to determine thermodynamic parameters.⁵⁰ Generally speaking, the larger the size of the protein complex the larger and stronger the interface area, which drives the correlation between the experimentally observed fragmentation efficiency and laboratory SID energy (see curves in Figure 4). Lastly, we note that the Prell group recently showed that the conversion of lab frame SID collision energy likely increases in efficiency with ion size.⁵¹ We do not have direct evidence for T–V transfer as a function of protein complex size and, especially, about the kinetic shift. Furthermore, we previously showed that interface features (similar to the features used in this work) correlated much better than overall size with SID dissociation.³⁸ Thus, Prell’s results (albeit important for unfolding protein ions) have no direct influence on our interpretation.

When including the breakage cutoff, the ERMS predictions improved notably overall, as shown in Figure S4. Note that different parameters were used for these simulations based on the observed correlations (the R² value between predicted and optimal B also improved slightly to 0.72). The average RMSE of these predictions was 0.17 (median of 0.15) with only two cases of RMSE greater than 0.30, indicating good agreement with the experimental data for all but a few cases. The breakdown of average RMSE of the different complex types was the following for dimers, tetramers, pentamers, and hexamer, respectively: 0.20, 0.17, 0.16, and 0.13. Overall, 16/20 cases improved with the additional information and different weights, though the average RMSE difference between the original and new values for the other 4/20 was only 0.01. The average improvement in RMSE for the remaining 16 was 0.04. While the data suggest that the additional information can be beneficial, the prediction method from structure alone was nearly as accurate.

ERMS predictions using native protein models were more accurate than for those from non-native structures

As the ERMS prediction method was developed to accurately predict ERMS data for relaxed native structures, we hypothesized that prediction results would be inferior for inaccurate structures (which have high RMSD to the native structure). To test this hypothesis, we performed simple docking simulations (see Supporting Information for details) that allowed for the generation of high RMSD protein complex models. A set of 25 models with RMSD in the range of 15-30 Å were chosen. To curate this set, we specifically chose structures that also had favorable Rosetta interface scores (independent of structural accuracy). These structures were then used to predict ERMS data using the method developed in this work (without including breakage cutoff information). In this experiment, we found that the average RMSE of the incorrect structures (comparing ERMS prediction to experimental ERMS) was worse than that of the native for 17/20 cases, the same for 1/20 cases, and better for only 2/20 cases (which were both already inaccurate for the native structures, RMSE > 0.35), as shown in Table S4. These results indicated that inaccurate models with favorable interface scores (meaning that they could possibly be in competition with low RMSD models when ranking in a blind test) matched the experimental data significantly worse than natives when using our ERMS prediction method.

Conclusions

We have developed a method to predict ERMS distributions for SID experiments from the structures of protein complexes. Based on the interface strengths in a complex, the computational method simulates breakages based on a probability curve that was able to reproduce the shape of the experimental curves. Using this method, ERMS data were reliably predicted (average RMSE of 0.20), and for cases with multiple competing dissociation pathways, the correct pathway was typically predicted. We also demonstrated that there is a correlation between structural features of all protein-protein interfaces in a complex and the entire ERMS plot. Next, we showed that the prediction results can be improved further if the acceleration energies where the complex begins to break apart are known, though the method was accurate for most cases without this additional information. Finally, based on a simple docking study, it was observed that incorrect structures with favorable scores predicted worse ERMS data than native structures using the same method.

This novel algorithm for predicting full SID ERMS data from structure represents a significant improvement from previous modeling efforts. This method allows us to model entire ERMS data, rather than a single appearance energy, as was the focus of previous work. The prediction method has been developed as a Rosetta application, which is freely available for use. The application can handle any structure with arbitrary connectivity, but has been benchmarked against some relatively simple complex stoichiometries here. A tutorial can be found in the Supporting Information. The ERMS prediction results obtained with high RMSD models showed that inaccurate structures which Rosetta flags as favorable can be identified to be unfavorable based on SID ERMS prediction. This preliminary study demonstrated the potential of our method in SID-guided protein complex prediction in future work to assist in scoring. Future work will focus on incorporating the ERMS prediction algorithm to guide complex modeling methods. This method could be applicable to any complex where multiple potential structures can be generated computationally (e.g. by symmetric docking or other), benefitting model selection. Furthermore, because SID provides information on interface strength, integrative modeling could be performed with additional types of MS data providing different structural information, such as overall size/shape from ion mobility²¹ and buried/exposed residues from covalent labeling.⁵²