Influence of aging on mechanical properties of the femoral neck using an inverse method

Abstract

Today, we are facing rapid aging of the world population, which increases the incidence of hip fractures. The gold standard of bone strength assessment in the laboratory is micro-computed finite element analysis (μFEA) based on micro-computed tomography (μCT) images. In clinics, the standard method to assess bone fracture risk is based on areal bone mineral density (aBMD), measured by dual-energy X-ray absorptiometry (DXA). In addition, homogenized finite element analysis (hFEA) constructed from quantitative computed tomography reconstructions (QCT) predicts clinical bone strength more accurately than DXA. Despite considerable evidence of degradation of bone material properties with age, in the past fifty years of finite element analysis to predict bone strength, bone material parameters remained independent of age. This study aims to assess the influence of age on apparent modulus, yield stress, and strength predictions of the human femoral neck made by laboratory-available bone volume fraction (BV/TV) and μFEA; and by clinically available DXA and hFEA. Using an inverse method, we test the hypothesis that FEA material parameters are independent of age. Eighty-six human femora were scanned with DXA (aBMD) and with QCT. The femoral necks were extracted and scanned at 16 μm resolution with μCT. The grayscale images were downscaled to 32 μm and 65 μm for linear and non-linear analyses, respectively, and segmented. The μFE solver ParOSolNL (non-linear) and a standard hFEA method were applied to the neck sections with the same material properties for all samples to compute apparent modulus, yield stress, and strength. Laboratory-available BV/TV was a good predictor of apparent modulus (R² = 0.76), almost as good as μFEA (R² = 0.79). However, yield stress and strength were better predicted by μFEA (R² = 0.92, R² = 0.86, resp.) than BV/TV (R² = 0.76, R² = 0.76, resp.). For clinically available variables, prediction of apparent modulus was better with hFEA than aBMD (R² = 0.67, R² = 0.58, resp.). hFEA outperformed aBMD for predictions of yield stress (R² = 0.63 vs R² = 0.34 for female and R² = 0.55 for male) and strength (R² = 0.48 vs R² = 0.33 for female and R² = 0.15 for male). The inclusion of age did not improve the multiple linear models for apparent modulus, yield stress, and strength. The resolution of the μFE meshes seems to account for most morphological changes induced by aging. The errors between the simulation and the experiment for apparent modulus, yield stress, and strength were age-independent, suggesting no rationale for correcting tissue material parameters in the current FE analysis of the aging femoral neck.

Highlights

• •Eighty-six human femoral necks DXA and μCT scanned and tested in compression
• •μFEA described 79 % of apparent modulus, 92 % of yield stress, and 86 % of bone strength
• •DXA predicts well the apparent modulus but poorly the yield stress and bone strength; hFEA outperformed DXA predictions
• •No indications of age-dependencies for apparent modulus, yield stress, and bone strength calculated with FEA were found
• •FEA material parameters are independent of age and can be kept constant

1. Introduction

Hip fracture is a significant burden for the patient and a high economic cost for society (Williamson et al., 2017). The fracture risk is correlated with the aging of the population (Wu et al., 2021) with the increased fall risk (Winner et al., 1989) and the decrease in bone mass, especially for women after menopause (Cummings and Melton, 2002). Health loss to hip fractures will double by 2040, and the cost will increase by 65 % (Hagen et al., 2020). Today, people over 60 years in Europe represent 23 % of the total population and will increase to 32 % in 2050 (Percentage of total population aged 60 years or over, platform.who.int, n.d.).

To assess the fracture risk, the primary indicator of bone strength (Ebbesen et al., 1999) used in the clinic is the dual-energy X-ray absorptiometry (DXA) (Bouxsein et al., 2020), which measures the areal bone density (aBMD) at the hip. Furthermore, bone strength can be predicted with finite element analysis (FEA) of the bone based on quantitative computed tomography (QCT), which was FDA-approved in 2019 (Keaveny et al., 2020).

In research, ex vivo samples, like the femoral necks of this study, can be scanned at high resolutions with micro-computed tomography (μCT), and the images are transformed into a mesh for micro finite element analysis (μFEA).

The effects of aging on bone are multiple. Changes in tissue mineral density (TMD) with age have different observations in the literature. Laval-Jeantet et al. (1983) found a decrease in the density, Mirzaali et al. (2016) and McCalden et al. (1993) did not report any change, and Currey et al. (1996) described an increase in the tissue mineral density. The organic part composed mainly of collagen type I increases in amount with age (Boskey and Coleman, 2010) and the collagen cross-linking, especially the advanced glycation end products (AGEs) (Boskey and Coleman, 2010; Saito and Marumo, 2010). The bone porosity (Boskey and Coleman, 2010; McCalden et al., 1993) and the linear micro-cracks density rise with age (Schaffler et al., 1995; Courtney et al., 1996) while the water content is reduced (Timmins and Wall, 1977).

The X-ray-based imaging techniques account for porosity and micro-cracks densities but are not sensitive to collagen or water changes. Several experiments were performed on the bone to assess the mechanical properties and changes with aging.

At a microscopic scale, no significant relationship was observed between the plane strain modulus measured with micro-indentation and age (Mirzaali et al., 2016).

At a macroscopic scale, the elastic modulus, yield stress, and strength decrease with the porosity of the bone tissue (Mirzaali et al., 2016; McCalden et al., 1993). As porosity increases with age, the elastic modulus in compression and tension declines (Burstein et al., 1976; Mirzaali et al., 2016; Zioupos and Currey, 1998) but was also reported as stable with age for the cortical femur in tension (McCalden et al., 1993). The yield stress decreases only in compression with age (Mirzaali et al., 2016). The ultimate stress decreases with age (Burstein et al., 1976; McCalden et al., 1993; Zioupos and Currey, 1998) or is age-independent (Mirzaali et al., 2016).

Since the 70s, when FEA has been applied to the bone (Brekelmans et al., 1972), age-independent material parameters have been used despite age's previously described influence on human bone material properties. Therefore, this study aims to evaluate the influence of aging on femoral neck material properties and the need to incorporate age-dependent material parameters into FEA.

We will set up an experiment to test human femoral necks in compression, measure the displacement and reaction force and compare the elastic modulus, the yield stress, and strength with the laboratory predictions of the bone volume fraction (BV/TV) and μFEA and the clinical predictions of DXA and hFE. The influence of age will be assessed with an inverse method.

2. Materials and methods

2.1. Sample preparation

Eighty-six fresh-frozen human femora (Fig. 1, a) were obtained with the informed consent of the donors from the Center for Anatomy and Cell Biology of the Medical University of Vienna and stored at −20 °C. The median age of the donors was 80 (56 to 96), forty-height were female donors, thirty-four were male donors, and four were unknown. The femora were cut perpendicularly (Fig. 1, b) to the neck axis (Exakt 300, EXAKT, Germany) into 10 mm parallel sections (Fig. 1, c). In addition to the informed consent given by the last will of all body donors, this study was approved by the ethical committee of the Medical University of Vienna. This thickness was chosen after performing a homogenized finite analysis (hFEA) to examine the strain distribution along the neck's axis. It was calculated that a thickness of 20 mm induced high strain concentrations at the boundaries. In contrast, the strain distribution was more homogeneous for a 10 mm section, ideal for reproducing a transcervical fracture, as it is one of the most frequent hip fracture types (Karagas et al., 1996).

Fig. 1.

a) Proximal femur b) cut of the neck section c) 10 mm thick parallel cut d) lapping e) template for positioning f) template placement g) sample ready for testing h) global compression setup.

Both cut surfaces were manually lapped (PM5, Logitech, United Kingdom) to obtain plane surfaces (Fig. 1, d). The sections were then dried at room temperature for a minimum of two days before testing to prevent water seeping during strain measurement.

2.2. Imaging

Dual-energy X-ray absorptiometry (DXA) scans of the proximal femoral necks (Lunar iDXA, GE Healthcare, USA) were performed using two water bags of approximately 10 cm thickness to mimic the soft tissues. Each femur was scanned with a quantitative computed tomography device (Somaton Definition AS, Siemens Medical Systems, Germany) with a resolution of 0.48 × 0.48 × 0.6 mm, while a phantom (BDC700, QRM, Germany) allowed a post-calibration of the images in Hounsfield units. The neck sections were scanned with micro-computed tomography (μCT) (μCT 100, Scanco Medical, Switzerland) at 16 μm spatial resolution. The grayscale images were converted into bone mineral densities (BMD) with a calibration equation obtained with a calibration phantom of the manufacturer. Each scan was pre-segmented with its otsu threshold (Otsu, 1979), and then all the grayscale images were segmented with the average of the individual threshold. The bone masks were obtained with morphological operations (Buie et al., 2007). The tissue bone mineral density, calculated by averaging the BMD of the segmented volume and prone to partial volume effect, was corrected to be independent of the ratio of the bone surface over bone volume. BV/TV was calculated as the ratio of the segmented bone volume over the total neck volume.

2.3. Mechanical testing

The experimental setup consisted of a sand-blasted plate screwed to a ball joint mounted on top of a load cell (662-04D, MTS Systems Co., USA). An hFE analysis was performed to align the femoral neck samples with the center of the ball joint to minimize the post-yield reaction torques. A template allowed an accurate positioning of the sample (Fig. 1, e, f). A servo-hydraulic testing machine (Mini Bionix 858, MTS Systems Co., USA) applied a compressive strain to the top plate of 0.35 % strain to the samples for five cycles at 0.5 mm/min (Fig. 1, g, h). Two spots on the surface of the bone samples were marked with a dark pen, and reflective particles were painted (Albedo100 Permanent, Albedo100, Sweden) for optimal displacement tracking (laserXtens 1-15HP, Zwick-Roell, Germany). The stiffness was calculated with a linear regression of the 1/3 upper force-displacement curve, i.e. between 0.35 and 0.23 % strain during the last unloading cycle. The yield point was determined with a 0.1 % strain offset criterion, and the samples were loaded until failure, where the maximal force reached was defined as the ultimate force. Intensive variables' apparent elastic modulus was calculated as the stiffness multiplied by the sample's height and divided by the mean cross-section area along the neck axis, yield stress was calculated as the yield force divided by the mean cross-section, and strength as the ultimate force divided by the mean cross-section area.

2.4. Simulations

Homogenized finite element (hFE) models with isotropic 1.5 mm resolution were set-up from the QCT reconstructions and executed with Abaqus (Abaqus 2021, Simulia Dassault Systèmes, France). A custom plasticity with damage material model (UMAT) (Schwiedrzik and Zysset, 2013) equipped with an isotropic quadric yield surface (Schwiedrzik et al., 2013) was used to reproduce the elastic and post-yield behavior of bone. The material constants were assigned based on the mean BMD value in a sphere with a radius r = 1 mm centered in each finite element (Dall’Ara et al., 2012). The hFE models were compressed axially with 0.4 mm at the top plane with constrained in-plane elements and free rotations. In contrast, the finite elements of the bottom plane were fully constrained, mimicking the experimental boundary conditions.

The segmented images were then pre-processed with MedTool 4.5 (Dr. Pahr Ingenieurs e.U., Pfaffstätten, Austria) to generate micro finite element (μFE) input files for the ParOSolNL solver (Stipsitz et al., 2020). The same elastic modulus of 16.1 GPa was assigned to all samples, and tensile yield stress σ⁺ = 0.109 GPa, compressive yield stress σ⁻ = 0.143 GPa, hardening modulus E_H = 0.05 GPa, and critical damage D_C = 0.915 for the non-linear simulations. The bottom elements were fixed, and the top elements were assigned with −0.02 mm and −0.28 mm displacement for linear and non-linear simulations. The linear simulation used a mesh resolution of 32 μm, and the non-linear simulations were run with a mesh resolution of 64 μm to shorten the computational time. The linear simulations included up to 99 million elements, and the non-linear to 12 million elements. The apparent elastic modulus (stiffness multiplied by the height divided by the cross-section area), yield stress (0.1 % offset), and strength (maximum stress) were calculated similarly to the experiment.

2.5. Statistics

Data analysis was performed with Python 3.8 (Van Rossum and Drake, 2009) with NumPy (Harris et al., 2020), Pandas (McKinney, 2010), and Matplotlib (Hunter, 2007) libraries, and statistics with the libraries Statsmodels OLS (Seabold and Perktold, 2010) for linear and multiple linear regressions, Scipy (Virtanen et al., 2020) for normality and difference in location between distributions, and Seaborn regplot (Waskom, 2021) for the confidence interval.

A Shapiro-Wilk test revealed that age, DXA, and yield stress were not normally distributed. Therefore, a Mann-Whitney test was used to evaluate the difference in location between male and female distributions.

The multiple linear regressions were defined as follows:

$$\mathrm{y}={\mathrm{\beta }}_0+{\mathrm{\beta }}_1{\mathrm{x}}_1+{\mathrm{\beta }}_2{\mathrm{x}}_2+{\mathrm{\beta }}_3{\mathrm{x}}_3+\mathrm{ϵ}$$

where y is the dependent variable (experimental apparent elastic modulus, yield stress or strength), β₀ the intercept, x₁ the μFEA elastic modulus, yield stress or strength and β₁ its associated slope, x₂ the age of donors and its slope β₂, x₃ the sex of donors and its slope β₃, and finally ϵ the residuals.

The root mean square error (RMSE) was calculated with the eval_meas library of Statsmodels as:

$$\text{RMSE}=\sqrt{\frac{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{ŷ}}_{\mathrm{i}}-{\mathrm{y}}_{\mathrm{i}}\right)}^2}{\mathrm{n}}}$$

The Akaike information criterion (AIC) was used to assess the relative quality of the multiple linear regression model with the μFE prediction, age, and sex and the μFE prediction alone. AIC was computed with the eval_meas library of Statsmodels as:

$$\mathrm{AIC}=-2\mathrm{k}+2\mathrm{llf}$$

Where k is the number of parameters and llf the value of the log-likelihood.

A p value p ≤ 0.01 was considered statistically significant.

3. Results

During the compression experiment, the load cell's maximum load range/capability was reached for forty samples, leading to forty-four measurements of strength and fifty-eight of yield stress. Moreover, two samples were lost during testing because of a failure of displacement tracking. The DXA aBMD, yield stress, and strength were significantly different between male and female donors (Table 1).

Table 1.

Descriptive table of age, DXA, BV/TV, apparent modulus experiment and μFE simulation, yield stress experiment and simulation, and strength experiment and simulation. MW is the abbreviation for the Mann-Whitney U test between female and male groups, with a star * indicating a significant difference.

Variables	Units	Global		Female		Male		MW p value
		n	min, median, max	n	min, median, max	n	min, median, max
Age	yrs	82	56, 80, 96	48	56, 80, 96	34	57, 80, 92	0.682
aBMD	g / cm2	86	0.36, 0.65, 1.19	48	0.41, 0.61, 0.95	34	0.36, 0.73, 1.19	0.003*
BV/TV	–	86	0.12, 0.26, 0.39	48	0.17, 0.26, 0.39	34	0.12, 0.25, 0.37	0.668
Eexp	GPa	84	0.38, 2.74, 6.28	48	0.96, 2.69, 5.50	33	0.38, 2.91, 6.28	0.829
EμFE	GPa	85	0.45, 2.37, 4.07	48	1.16, 2.43, 4.01	34	0.49, 2.26, 4.07	0.349
yield stressexp	MPa	58	4.26, 14.75, 33.17	40	8.58, 15.37, 33.17	14	4.26, 11.36, 17.61	0.001*
yield stressμFE	MPa	86	3.30, 16.55, 31.34	48	8.05, 17.21, 30.19	34	3.30, 16.99, 31.34	0.621
strengthexp	MPa	43	4.77, 16.27, 23.36	31	10.95, 17.47, 23.36	10	4.77, 12.42, 15.94	0.001*
strengthμFE	MPa	86	4.75, 21.34, 38.03	48	11.35, 22.00, 38.03	34	4.75, 20.83, 37.71	0.261

Please note that four samples have unknown sex, thus the difference of numbers between global and the sum of female + male.

3.1. Influence of age

The areal bone density (aBMD) decreased with age (Fig. 2, a). Similarly, the bone volume fraction (BV/TV) decreased marginally with age (R² = 0.09) (Fig. 2, b). In contrast, tissue mineral density increased moderately with age (R² = 0.06) (Fig. 2, c).

Fig. 2.

Age dependence of the a) areal bone mineral density (aBMD) b) bone volume fraction (BV/TV), c) tissue mineral density (TMD) d) experimental apparent elastic modulus e) experimental yield stress and f) experimental ultimate strength g) μFEA apparent elastic modulus h) μFEA yield stress i) μFEA strength.

The experimental apparent elastic modulus, yield stress, and strength decreased slightly with age but not significantly (Fig. 2, d, e, f). The μFEA apparent elastic modulus, yield stress, and strength, which include the non-failure samples, decreased significantly with age (Fig. 2, g, h, i).

3.2. Prediction of mechanical properties

The bone volume fraction BV/TV was a good predictor of apparent modulus (R² = 0.76) and the yield stress (R² = 0.76) and a medium predictor of the strength (R² = 0.65) (Fig. 3, a, b, c). The correlations between the μFEA and the elastic modulus, the yield stress, and the strength were high (R² = 0.79, R² = 0.92, R² = 0.86, resp.) (Fig. 3, d, e, f). The aBMD was analyzed separately between female and male groups, as the descriptive analysis indicates a significant difference between males and females. The clinically available aBMD was decent for predicting apparent modulus (female R² = 0.53 and male R² = 0.77) but bad for predicting the yield stress (female R² = 0.34 and male R² = 0.55) and the strength, where only the female prediction was significant (female R² = 0.33, male R² = 0.15). Homogenized finite element analysis based on QCT images was better than aBMD for the apparent modulus, yield stress, and strength (R² = 0.67, R² = 0.63, R² = 0.49, resp.) (Fig. 3).

Fig. 3.

Left column: apparent elastic prediction, middle column: yield stress prediction, right column: strength prediction, top row: bone volume fraction predictors, middle-high row: micro finite element predictors, middle-low row: DXA aBMD predictors, bottom row: homogenized finite element predictors. F is for female, M for male, and N/A for not available.

Multiple linear regression models of the elastic modulus (Table 2) show that age is not significantly different from zero. Conversely, the sex is statistically different from zero for aBMD model. The reduced models, without age and sex, were very close to the extended models, except for the aBMD reduced model that shows a reduction of R²_adj = 0.66 to R²_adj = 0.56.

Table 2.

Multiple linear regression models of the apparent elastic modulus.

Indep. variables	coef	[0.025	0.975]	P > |t|	No. Obs	R2	R2adj	AIC
Intercept	−1.73	−3.106	−0.344	0.02*	81	0.76	0.75	132
BV/TV	16.45	14.256	18.649	<0.001*
Age	0.00	−0.010	0.017	0.59
Sex (male)	0.17	−0.0.75	0.408	0.17
Intercept	−1.29	−1.845	−0.737	<0.001*	81	0.75	0.75	131
BV/TV	16.15	14.085	18.216	<0.001*
Intercept	−0.50	−1.664	0.668	0.40	81	0.80	0.79	119
E μFE	1.32	1.159	1.476	<0.001*
Age	0.00	−0.010	0.014	0.70
Sex (male)	0.25	0.028	0.476	0.03
Intercept	−0.14	−0.519	0.241	0.47	81	0.78	0.78	121
E μFE	1.29	1.137	1.441	<0.001*
Intercept	−0.85	−2.970	1.275	0.43	62	0.67	0.66	128
DXA aBMD	5.60	4.492	6.712	<0.001*
Age	0.00	−0.017	0.024	0.73
Sex (male)	−0.78	−1.141	−0.419	<0.001*
Intercept	−0.30	−1.071	0.466	0.43	62	0.57	0.56	141
DXA aBMD	4.71	3.812	5.611	<0.001*
Intercept	1.51	−0.321	3.334	0.10	62	0.68	0.66	127
E hFE	1.54	1.242	1.844	<0.001*
Age	−0.01	−0.031	0.008	0.24
Sex (male)	−0.01	−0.353	0.330	0.95
Intercept	0.49	0.006	0.970	0.05	62	0.67	0.67	124
E hFE	1.59	1.302	1.877	<0.001*

Abbreviation: DXA aBMD: dual-energy X-ray absorptiometry areal bone density, BV/TV: bone apparent density, hFEA: homogenized finite element analysis, μFEA: micro finite element analysis, E: elastic modulus. * p ≤ 0.01.

Yield stress predicted with multiple linear regression models (Table 3) shows that age is not significantly different from zero. Conversely, the sex is statistically different from zero for aBMD. The reduced models, without age and sex, were very close to the extended models, except for aBMD with a reduction of R²_adj = 0.54 to R²_adj = 0.21.

Table 3.

Multiple linear regression model of the yield stress.

Indep. variables	coef	[0.025	0.975]	P > |t|	No. Obs	R2	R2adj	AIC
Intercept	−3.89	−11.515	3.732	0.31	54	0.79	0.77	255
BV/TV	83.06	68.754	97.371	<0.001*
Age	−0.01	−0.078	0.67	0.88
Sex (male)	−1.95	−3.575	−0.322	0.02*
Intercept	−6.21	−9.654	−2.773	<0.001*	54	0.76	0.76	257
BV/TV	88.60	74.841	102.358	<0.001*
Intercept	0.35	−4.138	4.847	0.87	40	0.92	0.92	137
yield strength μFE	0.98	0.862	1.092	<0.001*
Age	−0.00	−0.048	0.044	0.92
Sex (male)	−0.71	−1.854	0.426	0.21
Intercept	−0.52	−1.995	0.963	0.48	40	0.92	0.92	134
yield strength μFE	1.01	0.914	1.111	<0.001*
Intercept	−5.33	−22.559	11.895	0.53	41	0.54	0.50	230
DXA aBMD	31.20	17.941	44.458	<0.001*
Age	0.04	−0.109	0.192	0.58
Sex (male)	−6.39	−9.121	−3.659	<0.001*
Intercept	2.17	−4.877	9.215	0.54	41	0.26	0.24	245
DXA aBMD	21.96	10.525	33.402	<0.001*
Intercept	9.24	−1.007	19.488	0.08	41	0.71	0.68	211
yield strength hFE	0.70	0.509	0.882	<0.001*
Age	−0.04	−0.153	0.073	0.48
Sex (male)	−2.79	−5.091	−0.491	0.02
Intercept	3.87	0.961	6.785	0.01*	41	0.65	0.64	214
yield strength hFE	0.78	0.596	0.964	<0.001*

Abbreviation: DXA aBMD: dual-energy X-ray absorptiometry areal bone density, BV/TV: bone apparent density, hFEA: homogenized finite element analysis, μFEA: micro finite element analysis, yield stress with 0.1 % offset. * p ≤ 0.01.

Strength predicted with BV/TV, μFEA, aBMD, and hFE multiple linear regressions (Table 4) show no significant difference from zero for age. The sex was different from zero for aBMD but also BV/TV and hFE.The highest degradation due to age and sex removal was for the aBMD linear regression (from R²_adj = 0.43 to R²_adj = 0.05).

Table 4.

Multiple linear regression model of the strength.

Indep. variables	coef	[0.025	0.975]	P > |t|	No. Obs	R2	R2adj	AIC
Intercept	−0.63	−9.438	8.185	0.89	41	0.72	0.70	184
BV/TV	77.97	56.783	99.164	<0.001*
Age	−0.00	−0.082	0.073	0.91
Sex (male)	−2.64	−4.404	−0.884	0.01*
Intercept	−4.35	−9.188	0.492	0.08	41	0.65	0.65	189
BV/TV	89.97	68.779	111.160	<0.001*
Intercept	2.66	−2.665	7.985	0.32	41	0.87	0.86	152
strength μFE	0.79	0.661	0.911	<0.001*
Age	−0.01	−0.063	0.042	0.68
Sex (male)	−1.03	−2.318	0.252	0.11
Intercept	0.57	−1.473	2.608	2.608	41	0.86	0.86	151
strength μFE	0.84	0.729	0.945	<0.001*
Intercept	4.67	−15.114	24.462	0.63	34	0.48	0.43	179
DXA aBMD	20.72	4.495	36.937	0.01*
Age	0.01	−0.150	0.177	0.87
Sex (male)	−5.98	−8.523	−3.428	<0.001*
Intercept	7.18	−3.752	18.109	0.19	34	0.08	0.05	194
DXA aBMD	15.58	−3.300	34.458	0.10
Intercept	12.39	−0.298	25.078	0.06	34	0.60	0.56	170
strength hFE	0.64	0.324	0.950	<0.001*
Age	−0.05	−0.179	0.086	0.48
Sex (male)	−3.54	−6.031	−1.052	0.01*
Intercept	4.86	0.540	9.172	0.03	34	0.48	0.47	174
strength hFE	0.83	0.523	0.140	<0.001*

Abbreviation: DXA aBMD: dual-energy X-ray absorptiometry areal bone density, BV/TV: bone apparent density, hFEA: homogenized finite element analysis, μFEA: micro finite element analysis. * p ≤ 0.01.

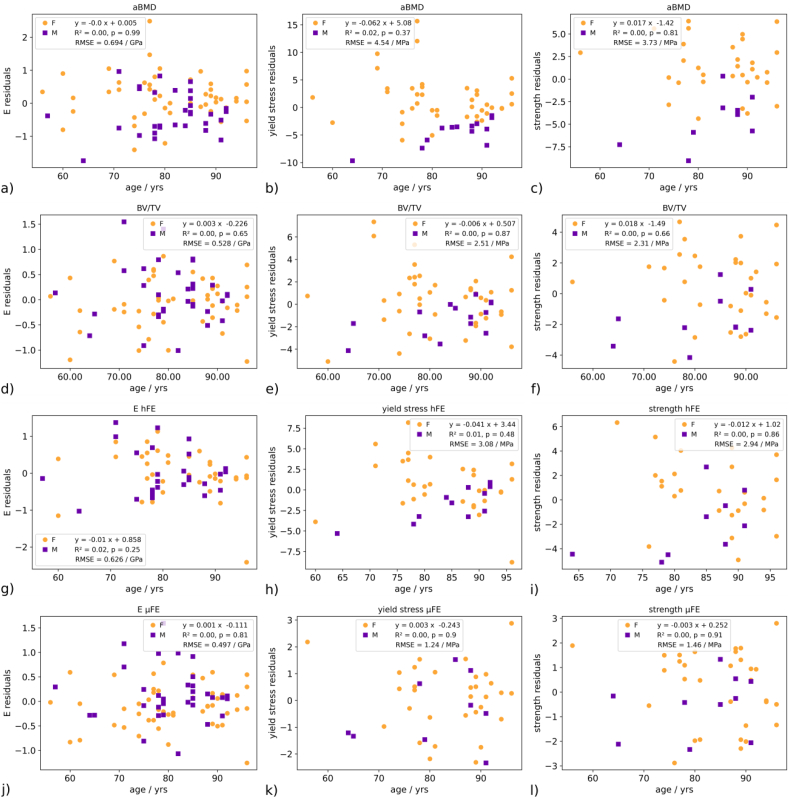
The residual plots of age are available in the appendices.

4. Discussion

We evaluated the influence of age in a controlled ex vivo experiment with an inverse μFE method to assess the need for fixed or age-dependent FE material parameters. Moreover, we compared laboratory-available BV/TV and μFEA with clinically available aBMD and QCT-based hFEA predictions of apparent elastic modulus, yield stress, and strength.

We found that ex vivo μFEA is a better predictor of femoral neck mechanical properties than bone volume fraction. Moreover, clinically available DXA was outperformed by hFEA prediction of femoral bone apparent modulus, yield stress, and strength. Age did not improve the multi-linear models, meaning that the predictions of FEA are not enhanced by making bone material parameters dependent on age.

4.1. Experiment

The femoral neck aBMD decreases with age, which is extensively reported in the literature (Keaveny et al., 2010; Havill et al., 2007). Similarly, the bone volume fraction of the femoral neck acquired by μCT declines with age, which is also reported by Chen et al. (2010). TMD measurements with μCT depend on the segmented volume and, therefore, on the resolution and the calibration of the gray images. Accordingly, we corrected TMD to account for these confounding effects. The slight increase in corrected TMD with age was not significant, reflecting the trend reported in the literature (McCalden et al., 1993; Roschger et al., 2003; Mirzaali et al., 2016). In fact, the uncorrected TMD showed a similar increase in mineralization with aging.

The apparent elastic modulus in compression declines slightly with age without being significant, explained by an inverse relation with porosity, which rises with age (Burstein et al., 1976; Mirzaali et al., 2016). Similarly, yield stress and strength are slightly decreasing with age but not significant, which may be attributed to a reduced set of samples with a narrower age range.

Although not included in the results, work to failure, reported to decrease with age (Wang et al., 2002; Zioupos and Currey, 1998; Currey et al., 1996), follows the same trend as the apparent elastic modulus, yield stress, and strength with the same lack of significance.

The experiment has several limitations. First, the femoral bone sections were tested dry. Dehydration increases the elastic modulus by 10–40 % (Rho and Pharr, 1999; Wolfram et al., 2010; Guidoni et al., 2010) and increases strength by a similar amount but reduces ductility in the post-yield behavior of bone. Nevertheless, as Wolfram et al. (2010) suggested, the relative tissue properties between the samples are dominated by composition and lamellar organization and seem to be maintained by the drying process.

Second, the samples were tested quasi-statically at 0.5 mm/min, far from a physiological deformation rate due to a fall. A 3 to 4 times more brittle behavior was reported by Pithioux et al. (2004) between dynamic and quasi-static tests of bovine bone. Again, according to Varga et al. (2016), the relative mechanical properties between the samples appear to be preserved by changing the loading rate.

However, we cannot exclude that dry conditions or low strain rates may mask specific aging effects on human bone tissue.

Third, the deformation is measured on the bone's surface instead of between the ball joint's center of rotation and the top plate. Only the variables requiring the deformation, such as the stiffness and elastic modulus, are sensitive to rotation errors, which have limited amplitudes during the elastic phase (Varga et al., 2011). An additional measurement system was fixed on the top and bottom plates to track the displacement and rotations to assess the on-surface measurement error. The comparison with the on-sample and inter-plates deformations showed a minor error after yielding occurred. Moreover, the tracking points are not situated on the very top and bottom of the sample but 0.25 mm below. The tracking is 5 % shorter than the entire sample's height, so the experiment elastic modulus is expected to be 5 % higher.

Fourth, axial compression of the neck along its axis is physiological but not perfectly representative of the loading from a fall on the greater trochanter. Fractures in the neck are a mix of compression, tension, and shear and depend on the impact angle. Our goal was to reproduce a trans-cervical femoral fracture in a well-controlled testing environment. Indeed, most samples have fractured in the middle, reproducing one of the most occurring hip fractures (Karagas et al., 1996; Wu et al., 2021).

Finally, the donor's medical history, such as medications and bone-related diseases, is unknown.

4.2. Laboratory variables

BV/TV is almost as good as μFEA at predicting the apparent elastic modulus because the stiffness of the neck, a cylindrical-like geometry, is well described by a global averaging of the bone volume fraction. Apparent modulus is calculated with the total displacement during the elastic phase of the experiment, which is prone to measurement errors with displacements smaller than 30 μm and geometrical errors like planarity. Yield and ultimate stress require local modeling of bone damage, which μFEA can achieve at the used resolution but not the BV/TV with its phenomenological approach. The μFEA is based on segmented images of bone. The segmentation method has a high impact on the results, and using the average threshold of the individual Otsu thresholds is a choice that can be applied to all samples. The elastic modulus prediction with μFEA is based on μCT images downscaled to 32 μm, which can capture Haversian canals with a diameter of about 100 μm for the femur (Frost, 1961) and part of the porosity but not the micro-cracks with a thickness below ten μm (O'Brien et al., 2000).

Moreover, the micro-cracks density in the femoral neck (Rabelo et al., 2018) is lower than in the diaphysis (Norman et al., 2008; Wasserman et al., 2005), suggesting that micro-cracks may have less influence on the mechanical bone properties of the neck than other anatomical regions. Nevertheless, the femoral neck remains a region where fracture occurrence is high for older people (Wu et al., 2021).

The simulated yield stress and strength were based on 64 μm meshes where porosity is partially captured. We evaluated the bone volume fraction difference between 32 μm and 64 μm images, which was negligible (R² = 1.00, slope = 1.01) and confirmed by the prediction of apparent elastic modulus at 32 and 64 μm that showed a similar slope of 0.97 and R² of 99 %. Accordingly, the volume fraction and architecture of the femoral necks could be correctly described, and the deviations in the experiments are dominated by fluctuations in material properties related to composition (e.g. AGEs), sub-micron porosity, lamellar orientation, or micro-cracks.

4.3. Clinical variables

The hFEA outperformed DXA prediction of apparent modulus but is more pronounced for yield stress and ultimate stress. The prediction superiority of hFE over aBMD for post-yield variables was extensively reported in the literature (Cody et al., 1999; Fleps et al., 2022; Rezaei et al., 2017; Zysset et al., 2013).

4.4. Special cases

Blastic tumors were found in two samples, and the errors of apparent modulus between the experiment and μFEA of those samples were lower than the mean absolute error. The ultimate force of blastic tumors in vertebral bodies was reported to be reasonably well predicted with hFEA (Stadelmann et al., 2020). Additionally, an apparent sample modulus from a donor with a fractured neck that healed in a poorly organized structure has been predicted with a lower error than the average error, indicating the robustness of both μFEA and hFEA computations of non-standard bone geometries and compositions.

4.5. Influence of age

The multiple linear models (Table 1) showed that age does not significantly contribute to BV/TV, uFEA, aBMD, and hFE models of apparent elastic modulus, yield stress, and strength.

Removing age and sex from the models does not highly deteriorate the adjusted coefficient of determination and AIC. On the contrary, a study with QCT-based FEA (Rezaei et al., 2017) showed a significant difference for age but not sex with the prediction of proximal femur stiffness and ultimate force.

The objectives were not to assess the influence of age on the femoral bone mechanical properties but to answer the question: does FEA require age-dependent material parameters? With the multiple linear models, we saw that age is not significantly different from zero, i.e. not improving the FEA models. The morphological changes with aging, such as the reduction of bone volume fraction and porosity, mainly influence the bone mechanical properties, overshadowing collagen's aging and the expected increase of micro-cracks. In fact, the magnitude of the expected bone tissue degradation beyond porosity may be smaller than the errors of the experiments validating our FEA models. Therefore, in the limit of our narrow age range and experimental testing conditions, we accept the hypothesis that FEA material parameters are independent of age and can be kept constant with current knowledge and technology. The significant difference in age with the QCT/FEA stiffness and ultimate force prediction found by Rezaei et al. (2017) may be explained by several factors. First, the entire proximal femur was tested, which involves larger experimental errors as a single section of the femoral neck. Then, the tests were performed in wet conditions at a higher strain rate. More importantly, the age range is lower in the present study. Despite the significant influence of age reported by Rezaei et al. (2017), the improvement in the prediction of stiffness and ultimate force remains very limited (1 and 4 percentage points of R², resp.).

4.6. Influence of sex

On the contrary, the sex is different from zero for the DXA model of apparent elastic modulus, yield stress, and strength, which is confirmed by an improvement of both the adjusted coefficient of determination and AIC. The sex dependence of DXA was also reported by Rezaei et al. (2017). The sex dependence of DXA is due to its not fully intensive nature occasioned by the projection in a direction that is size dependent. A close look at the average neck volume between female and male samples reveals a significant difference in the means (p < 0.001).

The sex is significantly different from zero also for the BV/TV model of the yield stress and the BV/TV and hFE models of strength. In general, DXA is sensitive to sex, whereas FEA is not. Indeed, the adjusted coefficient of determination of all variables is not drastically improved by the sex parameter, confirmed by a limited reduction of the AIC value, except for DXA.

5. Conclusion

The study's objective was to answer the question: does FEA require age-dependent material parameters? With the multiple linear models, we saw that age is not significantly different from zero, i.e. not improving the FEA models. The morphological changes with aging, such as the reduction of bone volume fraction and porosity, mainly influence the bone's mechanical properties, overshadowing collagen's aging and the expected increase of micro-cracks. In fact, the magnitude of the expected bone tissue degradation beyond porosity may be smaller than the errors of the experiments validating our FEA models. Therefore, in the limit of our narrow age range and experimental testing conditions, we accept the hypothesis that FEA material parameters are independent of age and can be kept constant with current knowledge and technology.

CRediT authorship contribution statement

Benjamin Voumard: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Resources, Data curation, Writing – original draft, Visualization, Project administration. Pia Stefanek: Software, Resources, Writing – review & editing. Michael Pretterklieber: Resources, Writing – review & editing. Dieter Pahr: Software, Resources, Writing – review & editing. Philippe Zysset: Conceptualization, Methodology, Resources, Writing – review & editing, Supervision, Project administration, Funding acquisition.

Declaration of competing interest

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: Dieter Pahr reports a relationship with Dr. Pahr Ingenieurs e.U. that includes: CEO and owner.

Appendix A

Fig. 4.

Residuals. Left column: elastic modulus prediction, middle column: yield stress prediction, right column: strength prediction. Rows a), b), and c): DXA aBMD predictor; d), e), f): BV/TV predictor; g), h) i): hFE predictor; j), k), l): μFE predictor. None of the residuals is age-dependent.

Data availability

Data will be made available on request.