Dynamically Personalized Detection of Hemorrhage

Abstract

Rapid detection of hemorrhage is of major interest to the critical care community, enabling clinicians to take swift actions to mitigate adverse outcomes. In this paper, we describe a model that allows rapid detection of the onset of hemorrhage by monitoring the Central Venous Pressure (CVP). As opposed to prior work in the domain, our model does not rely on prior availability of a stable physiology of a patient as a baseline of reference, and it makes generative assumptions on the monitored vital sign. This allows for rapid on-the-fly personalization to a previously unseen patient’s physiology. This property makes the proposed approach particularly relevant to e.g. trauma care and other scenarios where reference hemodynamic data may not be readily available for any new patient. We compare our model against strong discriminative alternatives and demonstrate its potential utility through empirical evaluation.

1. Introduction

Hemorrhage, a critical condition associated with substantial blood loss, can lead to hemodynamic instability, multi-organ dysfunction, and death (Gutierrez et al., 2004). Early detection of hemorrhage is of significance to critical care medicine, as it can help prevent the loss of significant amounts of blood and subsequent hypovolemic shock, allowing timely application of treatment within the critical ‘golden hours’, and enabling favorable patient outcomes (Rivers et al., 2001). However, standard practice relies on monitoring macro-level indicators of hypovolemia, such as increased heart rate and decreased blood pressure, and yields noticeable indications only after a large amount of blood loss has already taken place (Bárdossy et al., 2011). In this study, we develop models aimed at reducing the time to detection of hemorrhage, hoping that they can guide clinicians in taking proactive steps to mitigate its adverse consequences in patients.

Technical Significance

Prior approaches to the problem of hemorrhage detection in vital sign time series have predominantly relied upon supervised methods. They have been facing challenges stemming from a wide diversity of vital sign presentation between individual patients, typically addressed by normalizing currently monitored data to baselines of reference collected from the specific individuals when they were in stable condition (Wertz et al., 2019). Those approaches may work well in e.g. scheduled surgery scenarios, but do not scale well to e.g. trauma patients who are rushed to treatment without the luxury of having stable reference data available. We therefore propose an alternative autoregressive system for hemorrhage detection that does not depend on an individual’s stable physiological characteristics and instead relies on the instantaneous waveform data for inference. At the test time, our model allows rapid personalization to data of a previously unseen patient in order to discern between bleeding and non-bleeding phases of the vital sign trajectory.

Clinical Relevance

Hemorrhage is a common experience of patients in trauma or certain types of surgeries. If not timely discovered and treated, it leads to a substantial risk of mortality and long-term morbidity in survivors (Kauvar and Wade, 2005; Hu, 2004; Mastracci et al., 2012). However, due to the limitations of the sensitivities of physiological vital signs used in current medical practice and their bed-side interpretation, the diagnosis of hemorrhage and resuscitation are often delayed (Bárdossy et al., 2011). We aim to facilitate early discovery of hemorrhage during the initial stage of bleeding using the hemodynamic vital signs collected in bed-side monitoring units. Our results will support more timely treatment of bleeding patients, guide allocation of relevant clinical resources, and result in improved patient outcomes.

2. Prior Work

Both the clinical and machine learning communities are gaining interest in the automatic detection of hemorrhage and subsequent hypovolemic shock. For instance, Falck et al. (2018) applied deep neural networks with Gated Recurrent Units (Cho et al., 2014) and dilated causal convolution (van den Oord et al., 2016) to the high-frequency waveform data of multiple vital signs after normalization with subject-specific baseline characteristics collected during stable state, and achieved Area under Receiver Operating Characteristic Curve (AUC) greater than 0.9 for 30 minutes into bleeding. In intensive care scenarios, this reliance on personal baseline normalization may be overly optimistic as we do not have the luxury of observing the stable physiological characteristics if a patient is already bleeding.

Romero Zambrano et al. (2015) trained Random Forest model with patterns that characterized the sequential changes in the shape of Arterial Blood Pressure (ABP) waveform, which achieved AUC 0.75 and 0.85 at 1 minute and 5 minute post bleeding onset respectively. Lei et al. (2017) classified the respiration cycles during non-bleeding and bleeding phases by learning representative clusters of the correlation structures between central venous blood pressure waveforms observed at the top of the inspiration and bottom of the expiration phases of each respiration cycle, separately for non-bleeding and bleeding phases. Their work achieved AUC 0.862 for 30 minutes into bleeding. Guillame-Bert et al. (2014) used random forest classifiers and regressors for early bleed detection and estimation of the amount of blood lost from a comprehensive set of multiple high-frequency vitals. They have demonstrated the ability to reliably detect hemorrhage within a couple of minutes from its onset. Of further relevance to our work, they found central venous pressure waveform to be the most impactful vital sign for the task, and emphasized the importance of measuring timeliness of detection as an operationally important performance metric, besides accuracy of the classification algorithms that can be quantified with e.g. AUC. In clinical practice, rapid detection with high recall rates allows bleeding to be identified and treated timely, while highly specific discrimination attainable at a later time may be less beneficial for effective clinical intervention. Based on that, we argue that generative or single-class models may be more naturally tailored to the task of fast detection of hemorrhage than more common supervised methods, unless the latter are optimized for minimum latency of detection and maximum recall, instead of just AUC or accuracy of prediction. We further elaborate on the importance of rapid detection in Section 6.

Unsupervised methods have been studied and utilized by researchers in bed-side monitoring applications. For instance, Fiterau et al. (2011) proposed a probabilistic model to predict heart failure alarms by leveraging multiple vital signs in an unsupervised fashion, thus the model was able to adapt to a patient’s real-time status. Our method is motivated by a similar idea: by utilizing only the instantaneous physiological state of a patient, the model should be able to adapt and capture the change to make rapid predictions immediately without requiring any baseline data from a stable state.

3. Data and Featurization

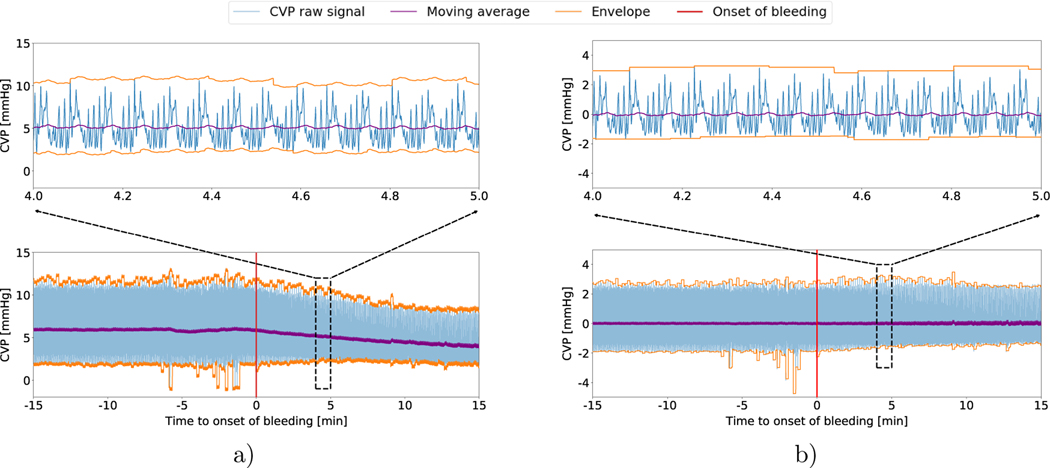
We utilize a real-world laboratory animal dataset. 21 healthy Yorkshire Pigs were sedated and surgically retrofitted to measure the Central Venous Pressure (CVP) and other vital signs. Following the surgery, the pigs were stabilized for a period of 30 minutes (referred to as the ‘stable’ phase in the paper). Following this, each individual pig was bled at a constant rate of 20mL/min until mean arterial pressure (MAP) dropped to 30 mmHg (referred to as the ‘bleeding’ phase). During both the stable phase and the bleeding phase, The CVP raw waveform data was collected at a frequency of 250Hz which we downsampled to 50Hz (uniform subsampling with a 20% duty cycle) for all subsequent experiments described in the paper. Fig 1 demonstrates the Central Venous Pressure Waveform for a single subject during both the stable and bleeding phase.

Fig. 1:

a) The raw CVP signal of a single subject from 15 minutes preceding bleeding onset to 15 minutes post bleeding onset, with its moving average and envelope. Notice how the moving average and the envelope changes post the onset of bleeding. We zoom into the waveform data during a 1-minute time window. b) The CVP signal in a) after normalization with the moving average and envelope of buffer window.

3.1. Featurization

Buffer Window (${𝓧}_t$) :

At each time step, we use the observations over the past 10 second window of the raw signal to aggregate statistics required for computing the features for the model. These statistics include the signal moving average, m_t (mean of the raw signal over the entire Buffer Window) and the signal envelope, e_t (the maximum and minimum value of the signal over the buffer period.)

Regressive Feature Window (X_t):

At each instance, we normalize the signal by subtracting the statistics computed from the current Buffer Window. This involves subtracting the moving average from the raw signal and dividing the result by the signal envelope to obtain the standardized signal, ${\overline{x}}_t$. This standardized signal accumulated over a period of 1 second is used as the multivariate feature representation (${\overline{X}}_t$) for the proposed model and the High Frequency (HF) baselines.

Note that since the standardization is conducted on-the-fly and uses only the data from the current Buffer Window, our approach does not need to rely on the baseline physiology from the stable non-bleeding phase. This deliberate design choice enables our model to be deployed at test time even if no information about an individual’s baseline physiology is available as is the case in trauma care scenarios.

4. The Proposed Model for Rapid Detection Of Hemorrhage (RaDeOH)

4.1. Emission Model

For each patient in our Training Set, we construct two separate models corresponding to the the Stable and Bleeding Phase respectively. We call them emission models and train them in an autoregressive fashion to estimate $P\left(x_{t+1}\mid {\tilde{X}}_t,z_{t+1},\text{Θ}\right)$. Here, ${\tilde{X}}_t$ are the observations in the immediately preceding step and $X_{t+1}$ is the predicted value of the signal at time step $t+1$. $z_{t+1}$ is a binary variable corresponding to whether the model was fit on the bleeding or the non-bleeding phase and Θ corresponds to the learned model parameters.

Readers familiar with time series modelling would naturally consider the class of Auto-regressive Moving Average (ARMA) family as an appropriate choice for the emission models. However, we would like to point out that the assumptions of ARMA may make the model somewhat sensitive to artifacts. In particular, these models assume $P\left(x_{t+1}\mid X_t,\text{Θ}\right)\approx \text{N}\left(f\left({\text{Θ}}^{\top }{X}_t\right),{\sigma }^2\right)$ with $f(.)$ typically being linear. Since the Normal distribution has unbounded support, for maximum a posteriori inference the output is unbounded. We restrict our model such that the output in expectation is bounded with respect to the immediate signal history and thus somewhat well behaved, while allowing for non-linear interactions within the co-variates with the use of multilayer perceptrons.

A question arises on the choice of parameterization for the emission models corresponding to each unique patient. Unified parameterizations (or architectures) for all the individuals may be too restrictive, and so at the training time we fit multiple alternative models and choose the parameterization which leads to empirically the best discriminative performance on a held out set of observations made for the same training individual.

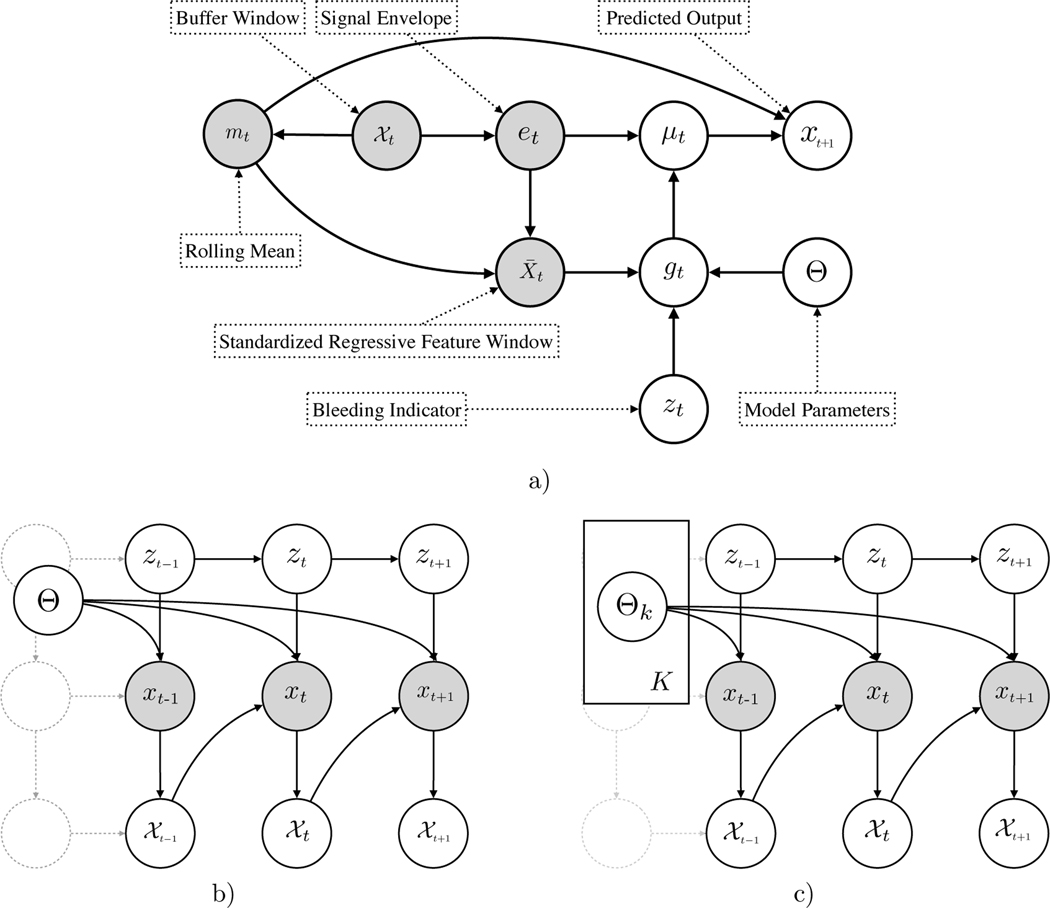
From the directed acyclic assumptions in Fig. 2 and the generative process as in Table 1 we can write the Conditional Probability under the model as

$$\mathrm{Pr}\left(x_{t+1}\mid {\tilde{X}}_t,m_t,z_{t+1},\text{Θ}\right)=\sum _{g_t}\mathrm{Pr}\left(g_t\mid {\tilde{X}}_t,z_{t+1},\text{Θ}\right)\mathrm{Pr}\left(x_{t+1}+m_t\mid {\mu }_t,{\sigma }^2\right)$$ (1)

Fig. 2:

a) The emission model for an individual subject. The observed variables include the raw signal over the buffer window, ${𝓧}_t$, the derived statistics, m_t, e_t, and the standardized signal ${\overline{X}}_t$. g_t is a Bernoulli output of the model with the parameters Θ. b) The model with latent temporal dependencies (emission specifics have been abstracted out.) c) The model with personalization through the ‘Emission Mixture Model’, at test time.

Table 1:

The Generative Model

1.	Transition to the latent state, zt+1, conditioned on the previous state, zt
	$z_{t+1}\mid z_t=T\left(z_{t+1},z_t\right)$
2.	Compute the envelope (et) and rolling mean (mt) using previous ${𝓧}_t$
3.	Compute the standardized signal ${\overline{X}}_t$ using $X_t,e_t,m_t$
4.	Draw a Bernoulli gt given ${\overline{X}}_t$ and Θ
	$g_t\mid {\overline{X}}_t,\text{Θ}\sim \text{Bernoulli}\left(f\left({\overline{X}}_t,\text{Θ}\right)\right)$
5.	Select μt from gt
	${\mu }_t=e_t^{\uparrow }$, if gt = 1, ${\mu }_t=e_t^{\downarrow }$, if gt = 0
6.	Draw xt, given μt as,
	$x_t\mid ,{\mu }_t,\sigma \sim \text{Normal}\left({\mu }_t,{\sigma }^2\right)$

4.2. Personalization - An Emission Mixture Model

In the previous section we described a unique Emission Model for each of the K individuals in our training dataset. At test time however, we observe emissions from a previously unseen test patient. It is natural to assume that different patients have different underlying physiologies responsible for heterogeneous cardiovascular function and diverse appearance in the lens of vital signs. Thus a single individual emission model may not be generalizable enough to describe the trajectory of a previously unseen patient. We instead hypothesize that the new patient can be described as a mixture of the previously learnt subject-specific Emission Models, drawing from the database of historical patients.

$$\mathrm{Pr}\left(x_{t+1}\mid {\tilde{X}}_t,m_t,z_{t+1}=\mathbf{0},\mathbf{\Theta }\right)=\sum _k{\alpha }_k{\mathrm{Pr}}^{(k)}\left(x_{t+1}\mid {\tilde{X}}_t,m_t,z_{t+1}=\mathbf{0},{\text{Θ}}^k\right)$$ (2)

$$\widehat{\alpha }=\arg {\max }_{\alpha }\left[\prod _{x_{t+1}\in {𝓧}_t}\mathrm{Pr}\left(x_{t+1}\mid {\tilde{X}}_t,m_t,z_{t+1}=0,\Theta \right)\right]\text{s.t.}\sum _k\alpha =1$$ (3)

In order to obtain the counterfactual emission model, or the model corresponding to the bleeding phase, we can simply fix the mixture parameters and replace the Emission Models with their respective counterfactuals corresponding to the bleeding phase.

$$\mathrm{Pr}\left(x_{t+1}\mid {\tilde{X}}_t,m_t,z_t=\mathbf{1},\mathbf{\Theta }\right)=\sum _k{\widehat{\alpha }}_k{\mathrm{Pr}}^{(k)}\left(x_{t+1}\mid {\tilde{X}}_t,m_t,z_t=\mathbf{1},{\text{Θ}}^k\right)$$ (4)

Greedy Selection.

To compare how personalization impacts performance of the model, we compare it to a greedy selection strategy where, instead of a weighted average of the individual emission models we instead select one model from the K trained models that best describes the held-out unseen subject at test time. Results corresponding to this strategy are hereafter referred to as RaDeOH-G.

4.3. Learning

Note there are two learning phases in our framework. The first involves learning the emission model parameters for each individual in the dataset. The second phase involves on-the-fly learning of the mixing components at test time.

Emission Model Parameters, Θ.

We train a separate autoregressive models, $\mathrm{Pr}\left(x_{t+1}\mid {\tilde{X}}_t,m_t,z_t,\mathbf{\Theta }\right)$ for each individual subject in the training dataset. Notice from Eq. 1 that the loss corresponding to the modeling assumption may be written as:

$$\ell \ell \left(\text{Θ};x_{t+1}\right)=\log \sum _{g_t\in \{0,1\}}\mathrm{Pr}\left(g_t\mid {\tilde{X}}_t,z_t\right)\mathrm{Pr}\left(x_{t+1}\mid {\mu }_t+e_t,{\sigma }^2,g_t\right)$$ (5)

For pragmatic reasons, we use the following form of the loss for a single observation:

$$\mathbf{\text{NLL}}\left(\text{Θ};x_{t+1}\right)=-\log \sum _{g_t\in \{0,1\}}\exp \left({\text{log-Sigmoid}}_{\left(g_t\right)}\left({\overline{X}}_t,\text{Θ},\mathit{f}\right)-\frac{{\Vert x_{t+1}-\left(m_t+e_t^{(k)}\right)\Vert }_{\mathbf{2}}}{{\sigma }^2}\right),{\sigma }^2=1$$ (6)

Here f is a potentially nonlinear function that operates on the input, ${\widehat{X}}_t$ with the parameter set Θ. The summation outside is made numerically stable using the log-sum-exp trick. For the purposes of this paper, for f we experiment with both linear functions and 1- and 2-hidden-layer Multilayer Perceptrons with ReLU activations. We train these models via backpropagation using the popular first order optimizer, Adam (Kingma and Ba, 2014) over the entire dataset as $\mathbf{NLL}(\text{Θ};𝓓)=\sum _{x\in 𝓓}\mathbf{NLL}(\text{Θ};x)$.

We fit separate models for the stable and bleeding phases, and choose the set which gives the best discriminative performance in terms of Area under Receiver Ooperating Characteristic Curve for a held out set of observations randomly sampled from each individual in the training set.

Mixing Parameters, α.

The second set of parameters to be learnt are the mixture weights in order to personalize the model to the unseen subject at test time. As mentioned previously, this personalization is carried out only on the first 10 seconds of observations corresponding to the buffer window ${𝓧}_t$. The mixing parameters are a simplex that sum to one, a constraint we incorporate by using a softmax over the mixing weights. Thus the optimization objective for Eq. 3 can be written as:

$$\mathbf{P}-\mathbf{Loss}\left(\mathit{\alpha };x_{t+1}\right)=-\log \sum _k\exp \left({\text{log-Softmax}}_k(\mathit{\alpha })-\mathbf{NLL}\left(\mathbf{\text{Θ}};x_{t+1}\right)\right)$$ (7)

Here, k represents an indiviudal subject in the dataset. We minimize this objective over the buffer window at test time, $\mathbf{P-Loss}(\mathit{\alpha };𝓓)=\sum _{x\in {𝓧}_t}\mathbf{P-Loss}(\mathit{\alpha };x)$. Similar to other parameters, we train these weights using Adam over a fixed number of epochs.

4.4. Inference

At test time, we are interested in inferring z_t given the past history of observations $\left\{x_1,x_2,\dots ,x_t\right\}$ and the learnt model parameters, Θ. In this section, we demonstrate that even with the conditionals on the observation on the previous timesteps, inference is similar to the filtering process in standard Hidden Markov Models or more commonly, the forwards algorithm.

For notational simplicity we denote the observed sequence as x_1:t. We emphasize that we are primarily interested in the conditional distribution $P\left(z_t\mid x_{1:t}\right)$.

The joint $P\left(z_1,X_1\mid \text{Θ}\right)$ is $P\left(X_1\mid z_1,\text{Θ}\right)P\left(z_1\mid \text{Θ}\right)$, but from the directed acyclic assumptions encoded in the model, $z_1⫫\text{Θ}$, this simplifies to $\alpha \left(z_1\right)=P\left(X_1\mid z_1,\text{Θ}\right)P\left(z_1\right)$. Now from Bayes Theorem, the posterior probability is given by,

$$\mathrm{Pr}\left(z_1\mid x_1,\text{Θ}\right)=\frac{\mathrm{Pr}\left(x_1\mid z_1,\text{Θ}\right)\mathrm{Pr}\left(z_1\right)}{{\int }_{z_1}\mathrm{Pr}\left(x_1\mid z_1,\text{Θ}\right)\mathrm{Pr}\left(z_1\right)}.$$ (8)

Note that $\mathrm{Pr}\left(z_1\right)$ is a prior, and in the simplest case it can be assumed uninformative, i.e. uniform. $\mathrm{Pr}\left(X_1\mid z_1,\text{Θ}\right)$ can be computed using the fitted models, $\mathrm{Pr}\left(x_1\mid z_1=\mathbf{1},\text{Θ}\right)$ and $\mathrm{Pr}\left(x_1\mid z_1=\mathbf{0},\text{Θ}\right)$.

Let us now consider the case, where we want to infer z₂ given {x₁, x₂}. Note that the joint distribution is:

$$\gamma \left(z_2\right)=\mathrm{Pr}\left(z_2,x_1,x_2\mid \text{Θ}\right)=\mathrm{Pr}\left(x_2\mid z_2,x_1,\text{Θ}\right)\mathrm{Pr}\left(z_2,x_1\mid \text{Θ}\right).$$ (9)

We can rewrite $\mathrm{Pr}\left(z_2,x_1\mid \text{Θ}\right)$ as, $\underset{z_1}{\int }\mathrm{Pr}\left(z_2,x_1\mid z_1,\text{Θ}\right)\mathrm{Pr}\left(z_1\mid \text{Θ}\right)$ Note that $z_2⫫x_1,\mid z_1,\text{Θ}$, thus, Eq. 9 can be rewritten as:

$$\gamma \left(z_2\right)=\mathrm{Pr}\left(z_2,x_1,x_2\mid \text{Θ}\right)=\mathrm{Pr}\left(x_2\mid z_2,x_1,\text{Θ}\right)\underset{z_1}{\int }\mathrm{Pr}\left(z_2\mid z_1\right)\mathrm{Pr}\left(x_1\mid z_1,\text{Θ}\right)d{z}_1.$$ (10)

Here, $P\left(z_2\mid z_1\right)$ are the transition probabilities. Note that from this we can derive the familiar recurrence relations corresponding to the forwards algorithm for HMMs as:

$$\gamma \left(z_t\right)=\mathrm{Pr}\left(z_t,x_{1:t}\mid \text{Θ}\right)=\mathrm{Pr}\left(x_t\mid z_t,x_{t-1},\text{Θ}\right)\underset{z_{t-1}}{\int }\mathrm{Pr}\left(z_t\mid z_{t-1}\right)\gamma \left(z_{t-1}\right)d{z}_{t-1}.$$ (11)

Now, proceeding as in Eq. 8, we can get $\mathrm{Pr}\left(z_t\mid x_{1:t},\text{Θ}\right)$ using a definition of the conditional:

$$\mathrm{Pr}\left(z_t\mid x_{1:t},\text{Θ}\right)=\frac{\mathrm{Pr}\left(x_{1:t},z_t\mid \text{Θ}\right)}{{\int }_{z_t}\mathrm{Pr}\left(x_{1:t},z_t\mid \text{Θ}\right)d{z}_t}.$$ (12)

The transition matrix $\mathrm{Pr}\left(z_t\mid z_{t-1}\right)$ that governs the probability of transition from one state to another is a 2 × 2 matrix. For practical implementation, we do not learn the transition matrix, but instead fix it to be symmetric, with the probability of transition from stable to bleeding being a hyperparameter, τ, and the probability of the reverse transition being (1 − τ) ensuring the row marginals of the transition matrix sum to one. τ is tuned during cross validation.

5. Baselines

We compare RaDeOH against two types of discriminative models that we describe as High Frequency and Low Frequency based on the temporal features used to train these baselines.

5.1. High Frequency Reference Models

The High Frequency (HF) models rely on the same set of autoregressive features as RaDeOH. Similar to RaDeOH, these models are trained on CVP data downsampled to 50Hz and standardized using the buffer window. We train a separate model for each of the subjects in our training data and tune hyper-parameters for each individual model on a held-out set of observations from the same subject. At the test time, we ensemble the outputs from each individual model to obtain predictions for the held-out subjects. We choose Logistic Regression (LR), Random Forest (RF), and Multilayer Perceptron (MLP) as the HF classifiers. The hyperparameters tuned for each of these model types are shown in the Appendix.

5.2. Low Frequency Reference Models

As mentioned in Section 1, the visible physiological indicators often used by clinicians to diagnose or monitor hemorrhage in current practice, such as decreased blood pressure, gradually emerge as the bleeding proceeds. Compared to the autoregressive features that can reflect the instantaneous changes in the waveforms used in HF models, these gradual trends change at much lower rates. We represent these low frequency (LF) trends of CVP with the moving linear slopes of the signal moving average and envelope, derived by fitting the least-squares linear regressions to the trailing time windows of 60 and 120 seconds at each time step. These are the features used to train Logistic Regression models, referred to as ‘LF-60’ and ‘LF-120’ in later sections, to mimic the performance attainable by human clinicians in current practice. For the LF models, we concatenate linear slopes of all subjects in the training set to train a single model, and use it to predict the held-out subject at the test time.

6. Results

We evaluate the models in a Leave-One-Subject-Out-Cross-Validation (LOSOCV) protocol. For RaDeOH and the HF baselines, we test the model on an individual held-out subject and average these predictions over all the models, and for LF baselines, we train a single model in each iteration in LOSOCV and obtain predictions for the held-out subject. We report the averaged Activity Monitoring Operator Characteristic (AMOC) (Fawcett et al., 1999; Jiang et al., 2009) that report the False Positive Rate (FPR) as a fucntion of the Time to First True Detection (T2FD), to demonstrate the tradeoffs between latency of detection and predictive error rates. We define the first ‘True Detection’, as the amount of time from the onset of hemorrhage that the model triggers alarms at the minimum frequency of 5Hz (10% duty cycle of the sampling frequency) sustained over a duration of at least 2 seconds (Fig. 3).

Fig. 3:

The Activity Monitoring Operating Characteristic for RaDeOH compared to the baselines. RaDeOH considerably outperforms the baselines within the first 5 minutes from the onset of bleeding. False positive rates decrease with the amount of time allowed to make the determination, and for RaDeOH, they are below 1% within the first two minutes and drop to 0.1% within about another minute from the onset of bleeding.

For each of the individual Activity Monitoring Operating Characteristic (AMOC) curves, we may sometimes run into a scenario that below a certain threshold of classifier sensitivity, the false positive rate (FPR) does not fall for higher times to detection, making averaging over these thresholds difficult. Since we perform filtering during inference, RaDeOH is more prone to this condition arising out of numerical challenges as opposed to the baselines. In order to mitigate these effects, for all such lower thresholds the FPR is extrapolated to the FPR at the next higher threshold at which the FPR is well defined. This strategy is pessimistic and we would like to point out that it favors the baseline models more than our proposed approach, ensuring a conservative comparison.

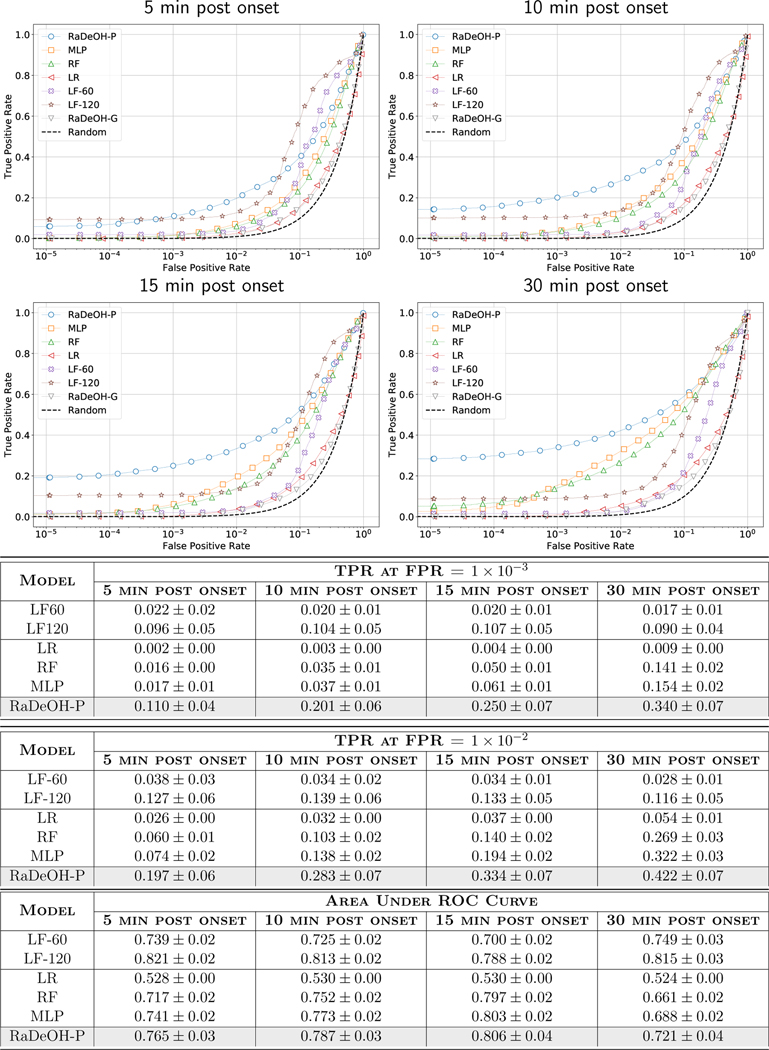
For completeness, we also report the True Positive Rates (TPR) at those thresholds and the Receiver Operating Characteristic (ROC) diagrams in Fig. 4 at different horizons of 5, 10, 15 and 30 minutes into bleeding. However, we maintain that the model selection for the applications where timeliness of detection is the key driving factor, the AMOC provides a more immediately relevant assessment than ROC. While the LF-60, LF-120 seem to have higher recall rates as compared to RaDeOH, high FPRs for these models reduce their practical utility.

Fig. 4:

ROC curves comparing the performance of RaDeOH versus the HF and LF Baselines at different horizons of the onset of bleeding.

7. Conclusion

We proposed a novel approach for rapid detection of hemorrhage using Central Venous Pressure waveform data that leverages only the instantaneous physiological characteristics of patients. Compared to previous work in hemorrhage detection, our method does not require normalization with the patients’ stable status data as personal reference, or require a period long enough for the commonly used physiological indicators of hemorrhage to become humanly noticeable for assessment. With only short time window of CVP observation, our method outperforms popular discriminative classifiers including Logistic Regression, Random Forest and Multilayer Perceptron trained on the same set of autoregressive features, in terms of time to detection (as shown in AMOC data) and overall discriminative power (as shown in ROC data) during early stages of bleeding, i.e. the initial few minutes from the onset of hemorrhage. By alleviating the need for stable reference data of each subject, our method is particularly applicable to monitoring emergency and trauma patients or patients undergoing unscheduled surgeries for whom such reference data may not be immediately available. These characteristics of RaDeOH could improve clinical practice by timely and reliably informing medical personnel of emerging health crises that can be discerned from routinely collected high frequency bedside monitoring data, in all monitored patients.

Our current work has several limitations that can be overcome with additional research. Currently, we only utilize the Central Venous Pressure (CVP) waveform data. One obvious next step is to incorporate other vital signs available in clinical or field care settings, including both non-invasively collected data such as Plethysmography, and the invasive measurements such as Arterial Blood Pressure. Our prior research into parsimony of hemodynamic data indicated potential benefits from including such additional data whenever available (Wertz et al., 2019). For practical applicability, it would be desirable to devise models that could pragmatically use whatever data that is being instantaneously available, even a small subset of generally measurable vital signs, e.g. due to limited access to some means of hemodynamic monitoring in the field, or due to limitations of the patient’s health status. The proposed graphical model formulation could allow incorporating incomplete data with minor extensions, making the method applicable in a wider range of health care settings. We also consider extending the model to identify other physiological states of clinical importance such as the emergence of sepsis or hemorrhagic shock (in our data, some subjects developed hemorrhagic shock in the course of bleeding and required aggressive resuscitation). Another direction of possible future development is to enable simultaneous prediction of multiple types of conditions. Such multi-tasking approach would be particularly useful for rapid disambiguation among conditions that may initially present with similar symptoms but require different therapies, such as e.g. hypotension due to hypovolemia vs. endotoxic shock.

Appendix A

The hyperparameters tuned for each of the High Frequency (HF) baseline models are listed in the table below.

Table 2:

Each classifier is tuned with all combinations of hyperparameters, and the set of hyperparameters that achieves the best AUC on the held-out set of each subject is chosen to fit the best model.

Model	parameters	values
LR	Penalty C (inverse of regularization strength)	11, 12 10−3, 10−2, 10−1, 1, 10, 102
RF	Number of trees Maximum depth of the trees	10, 20, 50 3, 5, 10
MLP	Number of hidden layers Number of nodes in hidden layer 1 Number of nodes in hidden layer 2	1, 2 30 20