Computational Investigation of Substituent Effects on the Fluorescence Wavelengths of Oxyluciferin Analogs

Abstract

Oxyluciferin, which is the light emitter for firefly bioluminescence, has been subjected to extensive chemical modifications to tune its emission wavelength and quantum yield. However, the exact mechanisms for various electron-donating and withdrawing groups to perturb the photophysical properties of oxyluciferin analogs are still not fully understood. To elucidate the substituent effects on the fluorescence wavelength of oxyluciferin analogs, we applied the absolutely localized molecular orbitals (ALMO)-based frontier orbital analysis to assess various types of interactions (i.e. permanent electrostatics/exchange repulsion, polarization, occupied-occupied orbital mixing, virtual-virtual orbital mixing, and charge-transfer) between the oxyluciferin and substituent orbitals. We suggested two distinct mechanisms that can lead to red-shifted oxyluciferin emission wavelength, a design objective that can help increase the tissue penetration of bioluminescence emission. Within the first mechanism, an electron-donating group (such as an amino or dimethylamino group) can contribute its highest occupied molecular orbital (HOMO) to an out-of-phase combination with oxyluciferin’s HOMO, thus raising the HOMO energy of the substituted analog and narrowing its HOMO-LUMO gap. Alternatively, an electron-withdrawing group (such as a nitro or cyano group) can participate in an in-phase virtual-virtual orbital mixing of fragment LUMOs, thus lowering the LUMO energy of the substituted analog. Such an ALMO-based frontier orbital analysis is expected to lead to intuitive principles for designing analogs of not only the oxyluciferin molecule, but also many other functional dyes.

1. Introduction

Firefly bioluminescence has fascinated the humankind for thousands of years, but it was not until the late 1950s[1] when the light-emitting process was found to arise from the luciferase enzyme and its natural substrate, which is now commonly called firefly luciferin. The substrate was first purified by Bitler and McElory[1] and then identified by White, McCapra, and Field[2, 3] to be D(−)-2-(6-hydroxy-2-benzothiazolyl)-Δ²-thiazoline-4-carboxylic acid (LUC, Fig. 1a). These efforts allowed them to propose a now widely-accepted bioluminescence mechanism that, in the belly of firefly beetles, the luciferase enzyme catalyzes a reaction of firefly oxyluciferin with ATP and O₂ molecules to produce an electronically excited oxyluciferin anion (Fig. 1b), whose relaxation yields the characteristic green-yellow light emission.

Figure 1:

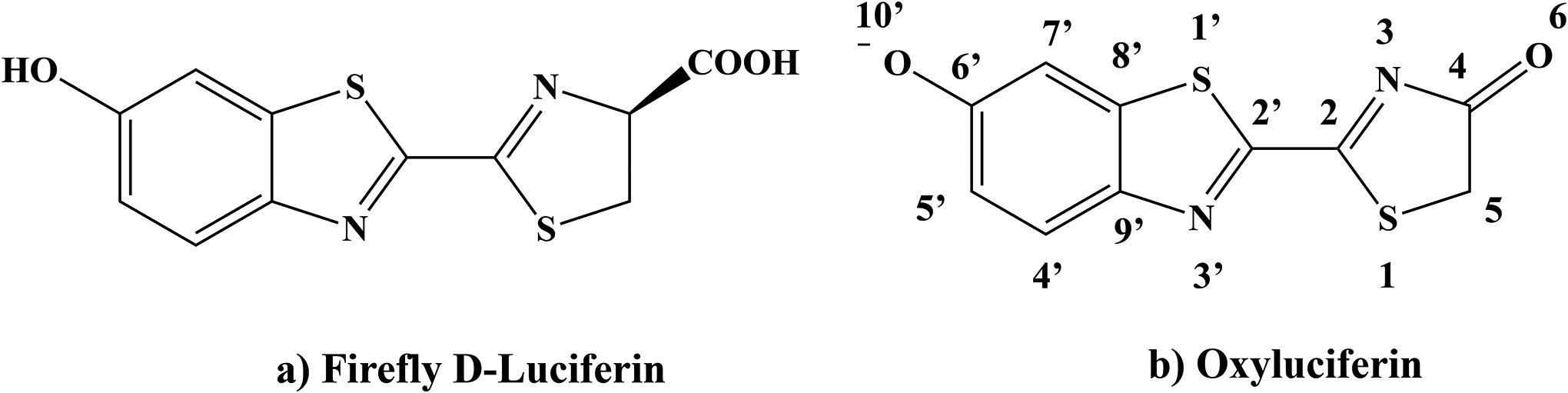
The chemical structures of firefly luciferin (LUC) and oxyluciferin (OLU).

While there were earlier suggestions that either the keto or enol tautomer of oxyluciferin might play a key role in the light emission, the scientific debate persists.[4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15] In this work, we will focus on the keto-form of the oxyluciferin (OLU, Fig. 1b).

With firefly bioluminescence (fBL) assays routinely employed in biochemistry research, there is a constant push to shift the emission color from the common green-yellow to the red and near-infrared regions. Luminescence with a longer wavelength is less harmful and can penetrate much deeper into human/animal tissues due to reduced absorption from hemoglobin and other molecules in the tissue. There are two general approaches to modulate the fBL emission wavelengths: chemical modifications to the oxyluciferin fluorophore and environmental changes such as amino acid mutations of the luciferase enzyme.

The oxyluciferin emitter can be modified in at least four ways to achieve a substantial red shift in the bioluminescence wavelength. Firstly, the C4’, C5’, and C7’ sites of the benzothiazole ring (see Fig. 1b) can be functionalized with one or more substituents, leading to analogs such as 7’-F-5’-allyl-oxyluciferin,[16] 5’-alkynyl-oxyluciferin,[17] 5’- and 7’-Br-oxyluciferin,[18, 16] 7’-Cl-oxyluciferin,[16] and 7’-allyl-oxyluciferin.[19] Secondly, a conjugated bridge (such as one or multiple double bonds or a conjugate ring) can be inserted between the benzothiazole and 4(5H)-thiazolone moieties to increase the conjugation length, leading to infra-oxyluciferin,[20] PhOH-Luc,[21] etc. Thirdly, the benzothiazole ring can be modified, with examples such as D-quinolyl-oxyluciferin.[22] Lastly, following the design of 6’-amino-oxyluciferin,[23] many other researchers have replaced the 6’-hydroxyl group with other linear or cyclic amino groups, leading to AkaLumine,[24, 25, 26] CycLuc10,[27, 28] Cyb-oxyluciferin,[28] NH₂-Np-oxyluciferin,[29] and DmaV-oxyluciferin.[30]

An alternative approach to tune the bioluminescence emission wavelength is to genetically modify the luciferase enzyme.[31, 32, 33, 34, 35] This was inspired by the natural variation of bioluminescence emission colors:[36, 37, 38, 39] north American firefly Photinus pyralis (λ_em = 560 nm),[40] click beetle Pyrophorus plagiophthalamus (λ_em = 590 nm),[41] and railroad worm (λ_em = 630 nm),[42, 35, 43] all with the same oxyluciferin substrate. In the early 2000s, Branchini and coworkers developed a red-emitting (614 nm) mutant of Photinus pyralis luciferase.[33] Later, Kato and coworkers reported a mutant of Luciola cruciata luciferase, which emits in both yellow-green (560 nm) and red region (613 nm) using oxyluciferin as substrate.[31] Prescher and coworkers genetically engineered luciferases to facilitate the bioluminescence emission of the oxyluciferin analogs with C4’ and C7’ substituents. [44, 18, 45] More recently, Miyawaki and coworkers performed laboratory-directed evolution to develop mutated Akaluc luciferases that are most compatible with the AkaLumine luciferin substrate (shown in Fig. 2).[26] Naumov and coworkers provided a comprehensive review of the structural, biochemical, and photophysical properties of beetle bioluminescence in Phrixothrix hirtus.[35, 43]

Figure 2:

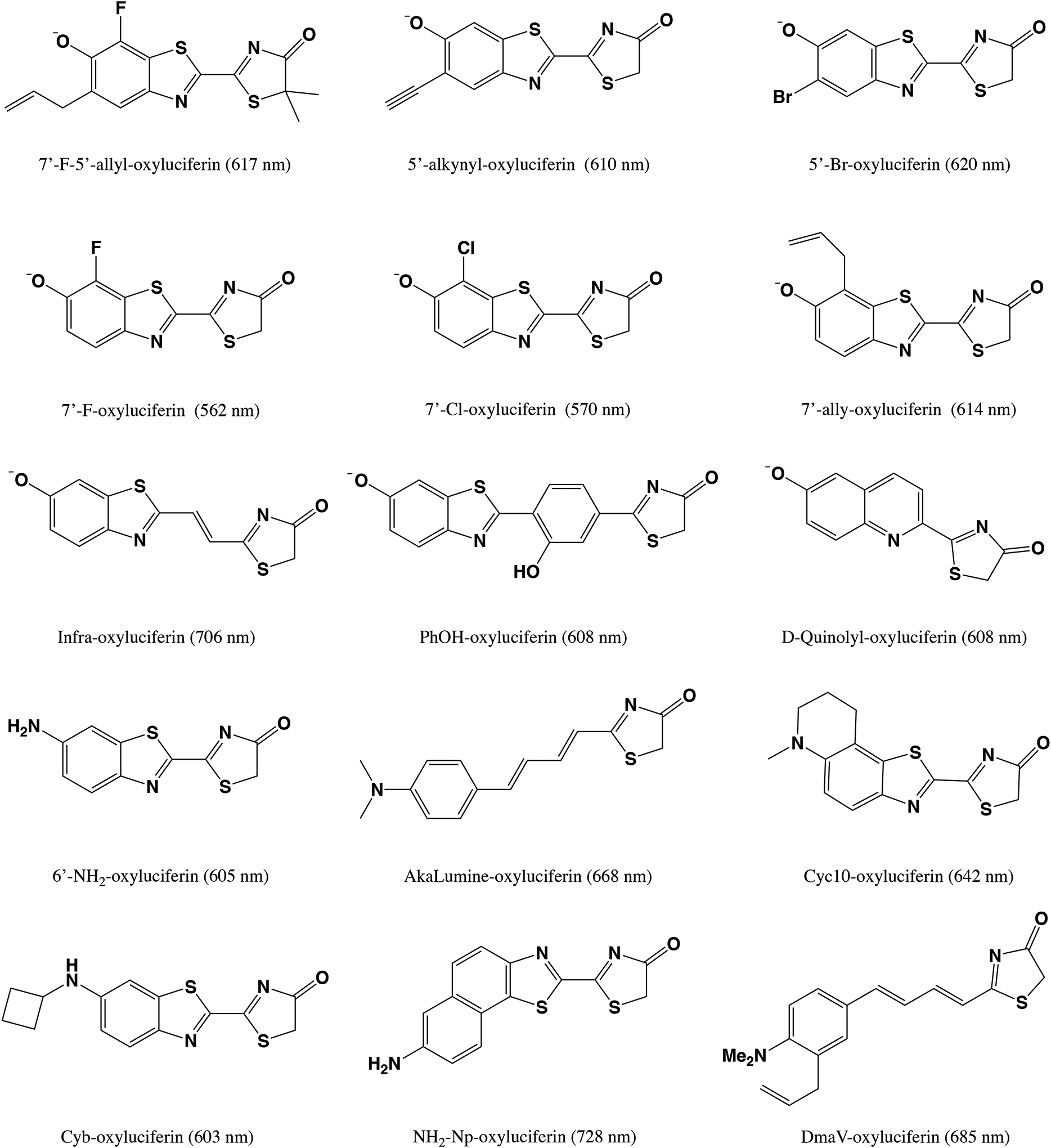
Selected oxyluciferin analogs and their bioluminescence wavelengths (in nm).[16, 17, 18, 16, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 28, 29, 30] For PhOH-oxyluciferin, its bioluminescence wavelength was measured with the G2 mutant of luciferase.[21] The bioluminescence wavelength of NH₂-Np-oxyluciferin was reported with the CBR2opt luciferase mutant.[29]

In this work, we will focus primarily on the modulation of the emission wavelength via chemical modifications to the oxyluciferin fluorophore. Specifically, we will perform computational modeling of the effect of substituent groups on the fluorophore. We note that computational studies have been performed by several research groups to elucidate bioluminescence mechanism[6, 12, 46, 47, 48, 49, 7, 50] as well as to design novel oxyluciferin analogs.[51, 52, 53, 54]

In 2014, Liu and coworkers reported TDDFT absorption and fluorescence wavelengths of oxyluciferin analogs where the 6’-hydroxyl group of the benzothiazole was replaced with electron-donating substituents.[51] In particular, OMe and N(CH₃)₂ caused a red-shift in the emission wavelength due to the hyperconjugation effect of the methyl groups, whereas N(CH₃)CH=CH₂ and N(C₆H₅)₂ groups red-shifted the emission owing to the electron-donating conjugation effect. Later, Liu and coworkers carried out an even more comprehensive computational study of oxyluciferin analogs.[52] They reviewed eight classes of analogs and performed an elaborate screening based on their fluorescence wavelengths obtained from gas-phase TDDFT calculations. The most red-shifted oxyluciferin analog, which was called “star”, was then further analyzed in conjunction with wild-type luciferase and its mutants using QM/MM calculations. Most recently, Navizet and coworkers investigated Benzothiophene-Oxy (nitrogen atom replaced by a methine), Dihydropyrrolone-Oxy (sulfur atom replaced by methylene), and Allylbenzothiazole-Oxy (introduction of an allyl group to the C7’ site) analogs and probed the effects of these substitutions within the protein environment.[53] They reported a good agreement between experimental bioluminescence wavelengths of oxyluciferin analogs and the corresponding computed emission wavelengths based on QM/MM calculations. It has also been suggested by computational studies that some oxyluciferin analogs can serve as effective light-emitting materials in OLED applications. For instance, Min and coworkers replaced the benzothiazolyl ring of oxyluciferin with phenyl, anthryl, or pyrenyl rings and computed the excited-state properties of those analogs, [54] based on which they predicted that oxyluciferin analogs could emit with a variety of colors, such as blue, green, orange, and red.

Inspired by all these experimental and computational research on oxyluciferin analogs, we carried out this work to further elucidate the substituent effects on the oxyluciferin molecule. Specifically, we modified the OLU structure at three different sites, C7’, C5’, and C4’ in Fig. 1b, with 14 functional groups. These included several electron-donating groups with varying Hammett σ_p constant:[55] CHCH₂(−0.04) > OH (−0.37) > NH₂(−0.66) > NHCH₃ (−0.70) > N(CH₃)₂ (−0.83). Also included were multiple electron-withdrawing groups: NO₂(0.78) > CN(0.66) > CF₃(0.54) > COCH₃(0.50) > Br(0.23) ~ Cl(0.23) ~ CCH(0.23) > I(0.18) > F(0.06). Out of these compounds to be analyzed in this work, several have already been studied in the past. Urano and coworkers synthesized 7’-fluoro-oxyluciferin and 7’-chloro-oxyluciferin analogs.[16] The oxyluciferin analog with an alkynyl substituent at C5’ were developed and tested by Prescher and coworkers.[17] The same research group later also reported brominated oxyluciferin analogs using C4’, C5’, and C7’ sites.[18] In the aforementioned computational study by Liu and coworkers,[52] the effects of fluorine and hydroxyl groups at C4’ and C7’ positions of oxyluciferin structure were analyzed (See SI Table S11).[52] We also note that the nitro group by itself tends to quench fluorescence, but a nitro-functionalized OLU can serve as a useful precursor for imaging cellular locations and interactions.[56]

In our computational modeling, we assessed the effects of electron-donating and electron-withdrawing substituents on the excited-state properties of oxyluciferin analogs. In particular, the absolutely localized molecular orbitals (ALMO)-based analysis was carried out on selected mono-substituted oxyluciferin analogs to obtain a detailed picture of the interactions between substrate and substituent orbitals.[57] With the aid of such a fragment molecular orbital-based tool, we sought to unravel basic principles for the engineering of frontier orbitals of oxyluciferin analogs, which can potentially facilitate the design of a more effective bio-imaging toolkit.

2. Computational Methods and Details

2.1. Ground State and Excited State Calculations

All electronic ground-state calculations were performed using the density functional theory (DFT) method,[58, 59, 60] whereas excited-state calculations were carried out using the time-dependent density functional theory (TDDFT) method.[61, 62, 63] The calculations were performed with the qchem 5.0 software package.[64]

Functionals.

In the main text of this article, computational results (absorption/emission wavelengths and ALMO-based frontier orbital analysis) using the ωB97X-D functional [65] are presented. Three other density functionals (B3LYP,[66, 67, 68] M06–2X,[69] and CAM-B3LYP[70]) were also employed for TDDFT absorption wavelength calculations (See SI Tables S1–S4), among which CAM-B3LYP was also used for emission wavelength calculations (See SI Table S5).

Basis sets and integration grids.

Most of the DFT and TDDFT absorption/emission results were obtained using the 6–311++G** basis set [71] and the SG-1 numerical integration grid,[72] where the latter is a pruned (50, 194) grid [73] (50 radial shells with 194 Lebedev points in each). Additionally, several other basis sets, such as 6–311+G* and aug-cc-pVTZ,[74, 75] were used to compute TDDFT absorption wavelengths of oxyluciferin. As shown in the SI Table S6, relative to the 6–311++G** values, the absorption wavelength of oxyluciferin computed using the aug-cc-pVTZ basis set changed by no more than 2.0 nm. The effect of using a larger integration grid is also marginal, with the computed absorption wavelengths changing by no more than 0.1 nm between SG-1 [72] and a finer (99,590) grid [76] (Table S7). In ALMO-based frontier orbital analysis calculations, the 6–31G(d) basis set[77, 78] was employed.

Implicit solvent models.

In order to account for solvent effect on oxyluciferin anion, we used the polarizable continuum model (PCM) [79, 80] for water molecules, specifically the C-PCM [81, 82, 83] model as implemented in qchem using a smoothly-discretized solvent cavity (with Bondi radii and a scaling factor of 1.2).[84] For absorption energy calculations, ground-state geometry optimizations were carried out using C-PCM, and vertical excitation energies were then computed using TDDFT and the non-equilibrium linear-response C-PCM model.[85, 86, 87] As indicated by the results tabulated in the SI Table S8, the TDDFT absorption wavelengths obtained using C-PCM and IEF-PCM [88, 89] solvent models differed by only 2.3 nm, indicating the marginal difference between these two types of PCM models in capturing the solvation effect on TDDFT excitation energies. To obtain fluorescence emission wavelengths, we also optimized excited-state structures using TDDFT with equilibrium PCM. The solvatochromic effect of various implicit solvents on the absorption and emission wavelengths was also reported in SI Table S9. For example, the emission wavelength of OLU was computed to be 579.1 nm in water (ϵ_static: 78.3; ϵ_optical: 1.78), which is a polar solvent. In contrast, a non-polar solvent such as benzene (ϵ_static: 2.27; ϵ_optical: 2.25) yielded a blue shift in the emission wavelength (532 nm) of OLU. The effect of explicit water models on the absorption and emission spectra of the oxyluciferin molecule will be discussed in future publications.

Geometry optimization

The convergence criteria for ground state and excited state geometry optimizations were set to 3 × 10⁻⁴ a.u. for maximum force, 1.2 × 10⁻³ a.u. for maximum displacement, and 1.0 × 10⁻⁶ a.u. for energy change. The vibrational analyses were performed at the optimized ground-state geometries, which confirmed that these geometries are true minima on the corresponding potential energy surfaces. Different OH- and NHCH₃-substituted OLU rotamers were considered and listed in the SI Fig. S1.

2.2. Absolutely-localized Frontier Orbital Analysis

The ALMO-based energy decomposition analysis procedure[90, 91, 92, 93] was previously extended to handle covalently bonded molecular fragments, giving rise to an analysis scheme for substituent effects on the energy and composition of frontier molecular orbitals.[57] Most recently, some of us have employed this analysis tool to elucidate the underlying physics of frontier molecular orbital engineering involved in the design of thermally activated delayed fluorescence (TADF) emitters. [94] Below, we will briefly summarize the procedure of this analysis (see Fig. 3 for a schematic illustration) as implemented within a development version of qchem 5.0.[64]

Figure 3:

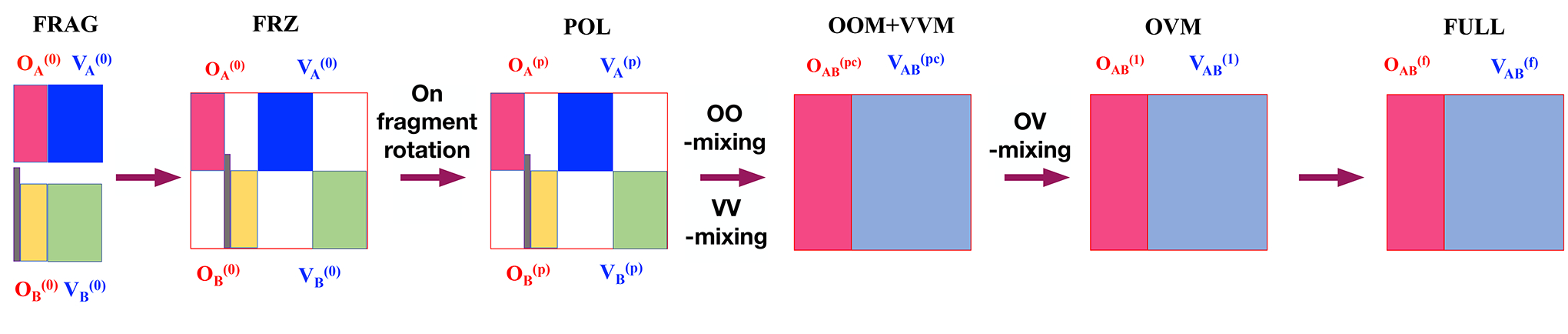
ALMO-based scheme for analyzing substituent effects on fluorophore frontier orbitals. “A” and “B” denote the OLU and substituent fragments, respectively. The vertical bar in gray corresponds to the link C–X orbital between two fragments i.e., the single bond connecting the OLU core and the substituent. O_A, O_B correspond to the occupied orbitals of the fragments A and B respectively, whereas V_A, V_B correspond to the virtual orbitals of the fragments A and B respectively. OOM, VVM, and OVM correspond to the occupied-occupied mixing, the virtual-virtual mixing, and the occupied-virtual mixing respectively.

Fragment (FRAG) State:

Firstly, we divided a substituted oxyluciferin analog (OLU–Sub) into two fragments — the oxyluciferin core (OLU) and a substituent group (Sub) — to construct the “isolated” fragment orbitals. In order to have both fragments retain a closed-shell electronic structure, the main fragment, in this case, oxyluciferin, was saturated with a hydrogen link atom (Fragment A: OLU–H). Meanwhile, the substituent group was terminated with a phenyl ring (Fragment B: Sub–Ar). The molecular orbitals of each of these fragments were only allowed to be expanded in the atomic orbital basis functions located on the same fragment. After performing self-consistent field (SCF) calculations on each fragment, orbital localization was carried out to identify the localized C–Sub bond orbital (connecting the aryl group and the substituent group (in fragment B) as well as the localized OLU–H bond orbital (from fragment A). These two localized bond orbitals were then tailored and kept frozen during the subsequent SCF calculations on fragments A and B to obtain the other absolutely-localized fragment orbitals on OLU and Sub. For further details, we refer the reader to the Supplementary Information of Ref. 57.

Frozen (FRZ) State:

In order to account for the effects of permanent electrostatics and exchange-repulsion on frontier orbitals, two sets of fragment orbitals (with the OLU–H bond orbital removed) were combined together to obtain an idempotent one-particle density matrix. It is possible to further separate the permanent electrostatics and exchange-repulsion terms,[91] but this is not pursued in this work because our focus lies with the frontier orbitals.

Polarized (POL) State:

In this state, two sets of frozen fragment orbitals are allowed to polarize each other while restricted to stay absolutely-localized on their respective fragments. The orbital relaxations in this step thus include only occupied-virtual mixings within each fragment while leaving the C–Sub bond frozen.

OOM+VVM State:

Diagonalizing the non-vanishing occupied-occupied block of the Fock matrix within the basis of supersystem polarized orbitals, one can obtain the pseudocanonical occupied orbitals and their energies (see Eqs. 9 and 10 in Ref. 57). The occupied-occupied mixing can lead to an increase in the HOMO energy if a substantial out-of-phase combination of fragment occupied orbitals occurs. In order to rigorously capture the virtual-virtual orbital mixing effect, we diagonalize the corresponding block of the Fock matrix within the basis of projected virtual orbitals to obtain pseudocanonical virtual orbitals and their corresponding energies (see Eqs. 11–13 in Ref. 57). A substantial in-phase combination of fragment frontier virtual orbitals can result in a noticeable lowering in the LUMO energy.

OVM State:

After oo- and vv-mixing, a single diagonalization of the Fock matrix is performed to obtain mixing of occupied-virtual orbitals. This step causes a rearrangement of the electron density across the OLU and Sub fragments and potentially produces a net charge transfer. Unlike oo- and vv-mixing, the ov-mixing step can lower the HOMO energy and elevate the LUMO energy.

Full State:

In the final step after the OVM stage, the orbitals will be further relaxed to converge the energy to the absolute minimum obtained from standard DFT calculations. Fully converged orbitals can then be correlated to polarized occupied and virtual orbitals using Eqs. 14–15 in Ref. 57 to obtain orbital-interaction diagrams.

3. Results and Discussions

3.1. Computed Emission Wavelengths

For oxyluciferin analogs with a single substituent group attached at the C7’, C5’, or C4’ site, our computed emission wavelengths and oscillator strengths are summarized in Table 1.

Table 1:

Computed emission wavelengths (λ_em, in nm) and oscillator strengths (f) of oxyluciferin and its analogs in aqueous solution at TD-ωB97X-D/6–311++G**/C-PCM level of theory. Substituent groups are ordered according to the wavelengths of the C7’-OLU analogs. Δλ_em is the difference between the computed emission wavelengths of the unsubstituted oxyluciferin and a substituted OLU analog.

Group	site C7’			site C5’			site C4’
	λ em	Δλem	f	λ em	Δλem	f	λ em	Δλem	f
NO2	490.5	−88.6	1.232	583.7	4.6	1.009	654.0	74.9	0.635
CN	517.7	−61.4	1.279	564.6	−14.5	1.204	587.4	8.3	1.164
COCH3	519.5	−59.6	1.288	589.7	10.6	1.165	598.2	19.1	1.158
CF3	528.3	−50.8	1.304	560.7	−18.4	1.186	575.0	−4.1	1.218
I	559.0	−20.1	1.269	571.7	−7.4	1.342	581.9	2.8	1.186
CCH	561.0	−18.1	1.236	580.6	1.5	1.337	589.5	10.4	1.181
Br	561.1	−18.0	1.267	569.6	−9.5	1.325	579.0	−0.1	1.191
Cl	563.7	−15.4	1.266	568.0	−11.1	1.303	577.9	−1.2	1.192
H	579.1	0.0	1.270	579.1	0.0	1.270	579.1	0.0	1.270
F	584.2	5.1	1.230	563.2	−15.9	1.297	571.2	−7.9	1.200
CHCH2	592.1	13.0	1.232	597.5	18.4	1.349	599.8	20.7	1.107
OH-2	662.7	83.6	1.089	586.0	6.9	1.388	584.2	5.1	1.164
OH	665.8	86.7	1.007	574.1	−5.0	1.383	579.7	0.6	1.174
NH2	825.8	246.7	0.793	640.9	61.8	1.402	605.7	26.6	1.031
N(CH3)2	882.0	302.9	0.719	645.3	66.2	1.428	608.4	29.3	1.048
NCH3H	888.5	309.4	0.741	651.6	72.5	1.384	596.4	17.3	0.993
NHCH3	925.8	346.7	0.658	689.5	110.4	1.367	614.6	35.5	1.031

First, let us compare these wavelengths against available experimental values. Earlier, Urano and coworkers reported the fluorescence wavelength of 7’-F-oxyluciferin to be 540.0 nm, which is 10 nm longer than that of 7’-Cl-oxyluciferin (530 nm) in a basic medium (pH: 10.0).[16] Our TD-ωB97X-D calculations predicted slightly longer emission wavelengths of both analogs: 7’-F-oxyluciferin (584.2 nm) and 7’-Cl-oxyluciferin (563.7 nm), but with a correct trend regarding the spectral shift between the two analogs. In a separate work, Prescher and coworkers found the fluorescence wavelengths of C7’-, C5’-, and C4’-bromine substituted oxyluciferin to be comparable to that of D-luciferin.[18] From our TDDFT calculations, we also observed marginally blue-shifted bromo-oxyluciferin analogs: compared with the emission wavelength of unsubstituted oxyluciferin, the blue shift is 18.0 nm with bromination at C7’, 9.5 nm at C5’, and 0.1 nm at the C4’ site.

As a separate validation of TDDFT calculations on oxyluciferin analogs, we also computed the fluorescence wavelengths of seven C6’ oxyluciferin analogs in the PBS buffer and compared them to the experimental results reported by Miller and coworkers [95] (see SI Table S10). SI Fig. S2B shows a good correlation (R² = 0.973; y = 0.992x − 0.258) between our computed TDDFT emission wavelengths and the experimental values.

Together, these comparisons confirmed that TDDFT is able to reliably predict spectral shifts of substituted oxyluciferin analogs.

3.1.1. Site C7’

Upon their attachment to the C7’ site, most substituent groups were predicted to cause a substantial shift in the emission wavelength of the chromophore (Table 1 and Fig. 4). Moreover, the spectral shift was strongly correlated with the electron-donating or withdrawing capability of each substituent group, as measured by the Hammett σ_p constants.

Figure 4:

Computed emission wavelengths (λ_em) of C7’-functionalized oxyluciferin analogs versus the Hammett σ_p constants of the corresponding substituent groups. Emission wavelengths were obtained from TD-ωB97X-D/6–311++G**/C-PCM calculations.

Among the electron-donating groups, the 7’-NH₂ group was predicted to yield an emission wavelength of 825.8 nm, which amounted to a substantial red-shift of 246.7 nm from that of OLU. Even longer wavelengths were obtained for 7’-NCH₃H-oxyluciferin (888.5 nm), its 7’-NHCH₃-oxyluciferin conformer (925.8 nm, with the methyl group pointing away from the 6’-oxygen atom), and 7’-N(CH₃)₂-oxyluciferin (882.0 nm). In these molecules, the methyl group(s) affected the electronic structure mainly through hyperconjugation (see Fig. S10), namely the methyl group(s) of NHCH₃ and N(CH₃)₂ directly contributed p-like orbitals to the HOMO of the modified chromophores. Specifically, due to the out-of-phase combinations between these p-like orbitals and the HOMO of 7’-amino-OLU, the HOMO energy of the full system got further raised from −6.1715 eV (the 7’-NH₂ analog) to −6.0137 eV (the 7’-NHCH₃ or NCH₃H analog) or −6.0027 eV (the 7’-N(CH₃)₂ analog), thus narrowing the HOMO-LUMO gap and causing a red shift in the emission wavelength (See SI Fig. S10). Unlike these nitrogen-based electron-donating groups, a smaller red shift was obtained for the 7’-hydroxyl analog (662.7 nm and 665.8 nm), which has two conformers (OH and OH–2) with the H atom pointing away from the 6’–oxygen atom in the latter conformation, as well as the 7’-vinyl analog (592.1 nm). This trend in the emission wavelength can be traced to the relatively lower HOMO energies of these two oxyluciferin analogs, −6.5797 eV and −6.6096 eV, respectively.

In contrast, the attachment of electron-withdrawing groups (except for the fluorine substituent) resulted in blue-shifted emission peaks. The 7’-NO₂-oxyluciferin analog was found to have the shortest emission wavelength of 490.5 nm. The CN and COCH₃ groups at the C7’ site of oxyluciferin yielded emission wavelengths of 517.7 nm and 519.5 nm, respectively, and a slightly longer emission wavelength (528.3 nm) was predicted for the 7’-CF₃-oxyluciferin analog. The effect of all four halogens was predicted to be marginal: the I-analog (559.0 nm), Br-analog (561.1 nm), and Cl-analog (563.7 nm) displayed a blue shift of 20.1 nm, 18.0 nm, and 15.4 nm in the oxyluciferin emission spectra, respectively, while the analog with C7’-fluorine substitution (584.2 nm) was predicted to have an emission peak slightly red-shifted by 5.1 nm compared to that of unsubstituted oxyluciferin.

To interpret the emission wavelength shifts caused by these groups, one might consider the charge-transfer (CT) character of the S₁ state of the unsubstituted oxyluciferin anion.[10, 96] As shown in Fig. 5, upon the S₀ → S₁ excitation of the oxyluciferin anion, the net electrostatic potential fitted (ESP) charge transfer (from the benzothiazole ring to the 4(5H)-thiazolone ring) was predicted to be 0.236 e⁻ with TD-ωB97X-D calculations. Intuitively, one would have expected an electron-donating/withdrawing group on the benzothiazole ring to facilitate/hinder the charge transfer to the 4(5H)-thiazolone ring during the S₀ → S₁ transition, thus reducing/increasing the excitation energy. However, this is not supported by Table S12, where the computed net changes in the Mulliken and ESP charges of the 4(5H)-thiazolone ring of oxyluciferin analogs upon the S₀ → S₁ transition are shown to be uncorrelated with the electron-donating or withdrawing capabilities of various groups.

Figure 5:

ESP charges for the S₁ (top panel) and S₀ (bottom panel) states obtained from TD-ωB97X-D/6–311++G**/C-PCM calculations. The relaxed electron density matrix was employed to calculate the ESP charges for the S₁ state.

3.1.2. Site C5’

In contrast to the C7’ site, most of the electron-donating and withdrawing groups had a much smaller impact on the emission wavelengths of OLU when attached to the C5’ site. Furthermore, as shown in Fig. 6, there is no apparent correlation between the computed emission wavelengths and the Hammett σ_p constants of the substituents. Out of all substituent groups, only the amino-based electron-donating groups have a noticeable effect on the emission wavelength of C5’–analogs. For instance, The 5’-NHCH₃-oxyluciferin analog was found to have the longest emission wavelength of 689.5 nm. Its 5’-NCH₃H conformer yielded a shorter emission wavelength of 651.6 nm. Similarly, functionalization with the N(CH₃)₂ and NH₂ groups resulted in red-shifted oxyluciferin analogs emitting at 645.3 nm and 640.9 nm, respectively. The substitution effect of all other electron-donating substituents at the C5’ site of oxyluciferin was marginal. For instance, the 5’-(OH)-oxyluciferin analog (574.1 nm) caused a slight blue shift of 5.0 nm compared to oxyluciferin, whereas its another conformer 5’-(OH-2)-oxyluciferin resulted in a red-shift of 6.9 nm. The emission wavelength of the 5’-vinyl-oxyluciferin analog was predicted to be 597.5 nm, which is 18.4 nm longer than that of the OLU anion.

Figure 6:

Computed emission wavelengths (λ_em) of C5’-functionalized oxyluciferin analogs versus the Hammett σ_p constants of the corresponding substituent groups. Emission wavelengths were obtained from TD-ωB97X-D/6–311++G**/C-PCM calculations.

Similarly, unlike the effects of having electron-withdrawing groups at C7’, substitution by these groups at the C5’ site did not cause a significant blue shift in the emission spectra. The substitution of CN and CF₃ groups at the C5’ site resulted in marginally blue-shifted oxyluciferin analogs emitting at 564.6 nm and 560.7 nm, respectively. The substitution of all halogens (F, Cl, Br, and I) at the C5’ site also resulted in slightly blue-shifted analogs. On the other hand, the C5’-substituted analogs such as 5’-CH₃CO-oxyluciferin (589.7 nm), 5’-NO₂-oxyluciferin (583.7 nm), and 5’-ethynyl-oxyluciferin (580.6 nm) actually led to a small red shift (10.6 nm, 4.6 nm, and 1.5 nm, respectively) in the emission wavelengths.

Clearly, these predicted variations in emission wavelengths, which are somewhat irregular, also cannot be explained based on how the charge transfer associated with the S₀ →S₁ transition of the oxyluciferin anion is facilitated or hindered by these substituents.

3.1.3. Site C4’

Similar to the case of site C5’, there also lacks a clear correlation between the emission wavelengths and Hammett σ_p constants for C4’-analogs (see Fig. 7). The addition of electron-donating groups, such as NHCH₃, N(CH₃)₂, and NH₂ to the C4’ site of oxyluciferin resulted in computed emission wavelengths in the red to orange region at 614.6/596.4 nm, 608.4 nm, and 605.7 nm, respectively. The 4’-OH-oxyluciferin (584.2 nm) and 4’-(OH-2)-oxyluciferin (579.7 nm) analogs displayed even smaller red shifts (5.1 and 0.6 nm) relative to the oxyluciferin anion. The oxyluciferin analog with a C4’-vinyl group was predicted to emit at 599.8 nm, which is 20.7 nm longer than the emission wavelength of OLU.

Figure 7:

Computed emission wavelengths (λ_em) of C4’-functionalized oxyluciferin analogs versus the Hammett σ_p constants of the corresponding substituent groups. Emission wavelengths were obtained from TD-ωB97X-D/6–311++G**/C-PCM calculations.

Very surprisingly, the 4’-nitro-oxyluciferin analog was also shown to produce a noticeably red-shifted emission wavelength of 654.0 nm. This is counterintuitive because, as shown in Table S12, an electron-withdrawing NO₂ group on the C4’-site of benzothiazole ring hinders the net partial charge transfer from the benzothiazole ring to the 4(5H)-thiazolone ring (0.0682e ⁻ for 4-nitro-OLU versus 0.236 e⁻ for OLU) during the S₀ → S₁ transition, which is presumably causing a blue shift.

Oxyluciferin analogs with a few other electron-withdrawing groups, such as 4’-CH₃CO-oxyluciferin (598.2 nm), 4’-CN-oxyluciferin (587.4 nm), 4’-CCH-oxyluciferin (589.5 nm), and 4’-I-oxyluciferin (581.9 nm) also emit at slightly longer wavelengths than oxyluciferin. Meanwhile, other oxyluciferin analogs with electron-withdrawing groups, such as 4’-CF₃-oxyluciferin (575.0 nm), 4’-F-oxyluciferin (571.2 nm), and 4’-Cl-oxyluciferin (577.9 nm), were found to be marginally blue-shifted.

Putting together the observations at the three sites, it is clear that the Hammett σ_p constants can be employed to explain the substituent effects on the spectroscopic properties of a few selected oxyluciferin analogs (mostly C7’-analogs) but become less effective for C5’ and C4’ analogs. This observation also holds for absorption wavelengths computed using various functionals (Figs. S1–S4) and emission wavelengths with the CAM-B3LYP functional (Fig. S5). Most intriguingly, the red shift caused by the electron-withdrawing NO₂ group in C4’-nitro-oxyluciferin cannot be rationalized based on the empirical Hammett constants. To shed light on this, below we will pursue an analysis of the frontier orbitals of oxyluciferin analogs.

3.2. Frontier Orbital Analysis

3.2.1. Correlation Between HOMO–LUMO Gap and Emission Wavelength

For oxyluciferin and its analogs, the HOMO–LUMO transition dominates the TDDFT S₁ → S₀ emission. Specifically, the amplitude for HOMO→LUMO excitation was computed to be 0.985 for the unsubstituted oxyluciferin anion. Among the analogs, the smallest HOMO→LUMO amplitudes of 0.981 were obtained for C7’-CCH−, C7’-CHCH₂−, C7’-CN−, and C7’-CH₃CO-oxyluciferin analogs, whereas the largest amplitudes of 0.989 were found for the C4’-NO₂−, C7’-NHCH₃−, and C7’-NHCH₃ oxyluciferin analogs (See SI Tables S13–S15).

Given such dominance by the HOMO→LUMO excitation, we plotted the computed HOMO-LUMO gaps (converted to nm) of oxyluciferin analogs and their emission wavelengths in Fig. 8A. A significant correlation (R² = 0.962) between the HOMO–LUMO gaps and emission wavelengths was observed when the ωB97X-D functional was used. Similarly, the computed HOMO-LUMO gaps using the CAM-B3LYP functional also exhibited a remarkable correlation (R² = 0.967) with the emission wavelengths (SI Figs. S8–S9). This suggests that, in order to interpret the shifts in the emission wavelengths among various oxyluciferin analogs, it would be beneficial to understand the variation in their HOMO-LUMO gaps.

Figure 8:

(A) HOMO-LUMO gaps (converted to nm) vs. TDDFT emission wavelengths (in nm) of oxyluciferin analogs. (B) HOMO and LUMO orbital contours for oxyluciferin and selected analogs. All results were collected from ωB97X-D/6–311++G**/C-PCM(water) calculations.

Below we shall focus on the effects of NH₂ and NO₂ groups, both as representative substituents, at the C7’/C5’/C4’ sites of oxyluciferin. As shown in Fig. 8B, the incorporation of the NH₂ group at the C7’ site of oxyluciferin reduced the HOMO-LUMO gap from 5.521 to 4.757 eV. Moreover, such a narrowing of 0.764 eV of the gap was caused mostly by the elevation of the HOMO energy by 0.710 eV (from −6.882 to −6.172 eV), while the LUMO energy was lowered marginally by 0.054 eV (from −1.361 to −1.415 eV). In contrast, the attachment of the NO₂ group to the C7’-site increased the HOMO-LUMO gap from 5.521 eV to 6.014 eV. The nitro group caused a widening of the HOMO-LUMO gap by 0.493 eV by lowering the HOMO energy by 0.612 eV and the LUMO energy by only 0.119 eV. Surprisingly, when NO₂ group was placed at the C4’ site, the HOMO-LUMO gap got reduced by 0.291 eV. For that analog, both HOMO and LUMO were lowered in their energy, but it was the latter (LUMO) that was subjected to a larger shift of −0.503 eV.

This brings up some intriguing questions:(a) how do the amino group orbitals interact with the fluorophore to raise the HOMO energy? (b) why do the nitro group have the opposite effect, namely lowering LUMO energy? and (c) what is causing the aforementioned dramatically different effects upon the attachment of the nitro group at C4’ and C7’ sites? This calls for a qualitative analysis of the underlying interactions between fluorophore and substituent orbitals, which will be provided in the next two subsections within the framework of ALMO analysis as described in Section 2.2 and illustrated in Fig. 3.

3.2.2. Effect of amino group on three sites of OLU

Within the ALMO analysis, the FRZ, POL, and OVM intermediate states all provide a variational upper bound to the FULL SCF energy. The total polarization energy (i.e., the difference between the FRZ and POL states) varied from −2.4 kcal/mol for C4’-, −2.9 kcal/mol for C5’-, to −3.3 kcal/mol for C7’-amino substitution. This suggests that the amino group does not significantly stabilize the analogs through the polarization effect at the three sites. As shown in Fig. 9, the difference between the HOMO energies in the FRAG state and FRZ state is marginal for all three amino-substituted analogs, indicating that the effect of permanent electrostatic/Pauli repulsion is not significant between the amino group and oxyluciferin. Shape-wise, HOMOs and LUMOs of these three analogs remained essentially the same in the FRAG, FRZ, and POL states.

Figure 9:

Effect of the amino group on the HOMO and LUMO of oxyluciferin when attached to the C7’ (panel A), C5’ (panel B), and C4’ (panel C) sites. All results were collected from ALMO-based analysis using the ωB97X-D functional and 6–31G(d) basis set. The orbital energy values were reported in eV. The energies of the intermediate states relative to the full SCF energy of each analog were shown in the parentheses.

As shown in Fig. 9, the extension of both orbitals to the amino group occurred, if at all, through oo-mixing. Specifically, in the case of C7’- and C5’-amino substitutions, the HOMO energy was increased when moving from the POL state to the OOM+VVM state by 0.752 eV (−2.478 vs −3.230 eV) and 0.437 eV (−2.816 vs −3.253 eV), respectively. After such a large increase in the HOMO energy due to oo-mixing, the HOMO energy converges further to the FULL state through ov-mixing. In contrast to the significant changes in HOMO energies associated with the C7’- and C5’-amino analogs, the HOMO energy of the C4’-amino-oxyluciferin only changed minimally (< 0.05 eV) from the POL state to the OOM+VVM state.

On the other hand, the LUMOs and their energies did not change dramatically across the entire ALMO analysis procedure for all three amino-substituted oxyluciferin fluorophores. In the case of C5’- and C4’-amino substitutions, the LUMO energy increased by roughly 0.158 and 0.154 eV, respectively, due to vv-mixing. Meanwhile, the LUMO energy only increased by 0.043 eV for C7’-amino substitution.

To further understand the effect of amino groups on the oxyluciferin substrate, we projected the frontier orbitals of the fully-converged frontier orbitals of C7’-amino-oxyluciferin onto the absolutely-localized polarized fragment orbitals. In Fig. 10, the interactions between polarized amino and oxyluciferin fragment orbitals that give rise to the full-system HOMO and LUMO were shown along with the corresponding projection coefficients. Clearly, the amino group HOMO undergoes an out-of-phase mixing with the oxyluciferin occupied orbitals (HOMO and HOMO-2), which led to an overall increase in the full-system HOMO energy. As such, a destructive (i.e. antibonding-like) interaction of the HOMO of a fluorophore with the highest occupied orbital of an electron-donating group is the key to the elevation of the HOMO energy.

Figure 10:

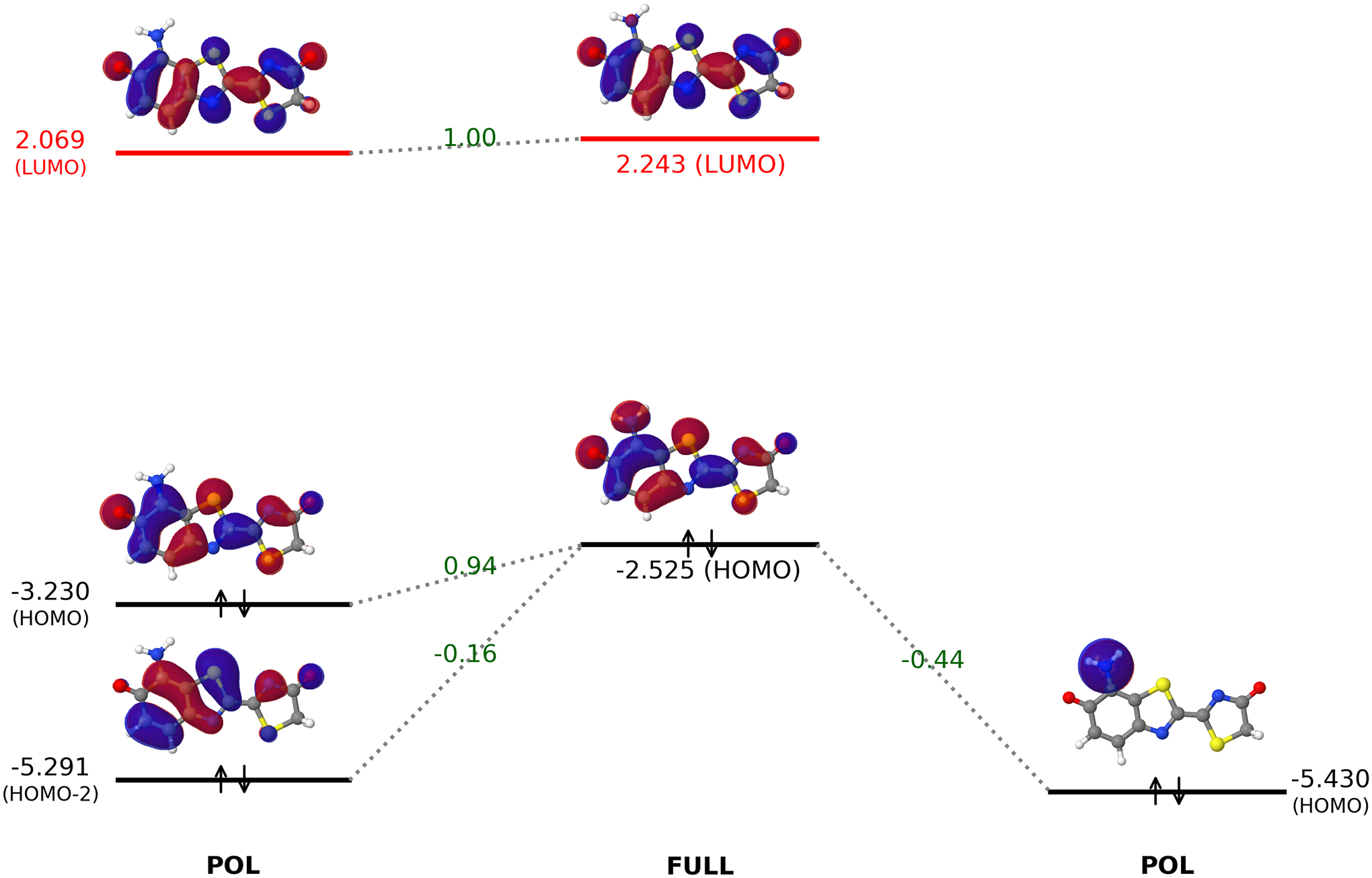
Interactions between the polarized oxyluciferin and amino group orbitals to yield the fully converged MOs of 7’-amino-oxyluciferin. The calculations for orbital interaction analysis were performed in the gas–phase using the ωB97X-D/6–31G(d) level of theory. All orbital energies are in eV.

The impact of occupied-occupied orbital mixing on the HOMO-LUMO gap of amino-substituted OLU analogs is more compactly shown in the first column of Fig. 11. Clearly, the strength of the net impact follows the order C7’ > C5’ > C4’, which coincides with the weight of their respective carbon atomic orbitals within the OLU HOMO. Namely, the OLU HOMO, as shown in Figs. 9 and 10, receives the largest contribution from C7’-carbon, followed by C5’-carbon, while C4’-carbon has the smallest contribution. Accordingly, the HOMO energy is raised the most with the C7’-amino group and the least with the C4’-amino group.

Figure 11:

Decomposition of the effects of the amino, methylamino, acetyl, cyano, and nitro groups on the HOMO and LUMO of the oxyluciferin analogs obtained from the ALMO-based analysis. All energy values (in eV) were acquired at the ωB97X-D/6–31G(d) level of theory.

To design new fluorophores featuring smaller HOMO-LUMO gaps, therefore, one should attach strong electron-donating groups to atoms where the HOMO has large weights.

3.2.3. Effect of nitro group on three sites of OLU

Unlike the amino group, the nitro group shifted the HOMO and LUMO energies substantially from the FRAG to the FRZ state. Specifically, the HOMO energy was lowered by 0.913, 0.658, and 0.564 eV, respectively, for C7’-, C5’-, and C4’-nitro-oxyluciferin, as shown in Fig. 12. Meanwhile, the LUMO energy was reduced by 0.413, 0.576, and 0.541 eV, respectively. Such a significant contribution from permanent electrostatics/Pauli repulsion was expected for the nitro substituent, which has a larger dipole moment due to the presence of two electronegative oxygen atoms.

Figure 12:

Effect of the nitro group on the HOMO and LUMO of oxyluciferin when attached to the C7’ (panel A), C5’ (panel B), and C4’ (Panel C) sites. All results were collected from gas–phase ALMO-based calculations using the ωB97X-D functional and 6–31G(d) basis set. The orbital energy values were reported in eV. The energies of the intermediate states relative to the full SCF energy of each analog were shown in the parentheses.

For C7’-nitro substitution, the HOMO energy was raised from −4.102 eV (FRZ) to −3.787 eV (POL) due to the polarization interaction. From this point onward, the HOMO energy gradually shifted back to the full-SCF value of −3.996 eV. Even smaller polarization effect on the HOMO energy was observed for C4’ and C5’-nitro-substituted analogs (−3.804 →−3.698 eV and −3.610 → −3.509 eV, respectively).

As far as the LUMO is concerned, the largest virtual-virtual mixing occurred on the C4’-nitro-oxyluciferin analog, where the LUMO energy was reduced by 0.341 eV (1.914 → 1.573 eV). This is the primary cause for the narrowing of the HOMO-LUMO gap of this analog. In contrast, nitro groups at the C7’ and C5’ sites reduced the LUMO energy by only 0.023 and 0.112 eV, respectively, through vv-mixing. The LUMOs then remained more or less constant after the oo- and vv-mixing stage.

The orbital interaction analysis shown in Fig. 13 revealed that the LUMO+1 orbital of the nitro group was combined with OLU’s LUMO and LUMO+2. The resultant virtual orbital has a lower energy due to the constructive (i.e. bonding-like) combination. Among the three sites, the C4’-carbon is shown in Figs. 12 and 13 to have the most substantial contribution to the isolated (and polarized) fluorophore LUMO and thus lowered the LUMO energy the most. The corresponding vv-mixing then caused the most significant reduction to the HOMO-LUMO gap, as shown in the last column of Fig. 11 and in Fig. 12. Therefore, in order to lower the LUMO energy in frontier molecular orbital engineering, one can attach strong electron-withdrawing groups with unoccupied π* orbitals to sites where the LUMO has large weights.

Figure 13:

Interaction between the polarized oxyluciferin and nitro group orbitals to produce fully converged MOs of 4’-nitro-oxyluciferin. The calculations for orbital interaction analysis were performed at the ωB97X-D/6–31G(d) level of theory. All orbital energies are in eV.

In Fig. 11, in addition to NH₂ and NO₂ groups, the substituent effects of another electron-donating group, NHCH₃, and two other electron-withdrawing groups, COCH₃ and CN are shown. Consistent with the predicted emission wavelength results (with a larger basis set and C-PCM solvation model) in Sec. 3.1, the NHCH₃ group at the C7’ site substantially narrowed the HOMO-LUMO gap, while smaller changes were observed for the HOMO-LUMO gaps in other cases. The corresponding orbital evolution and interaction analysis diagrams for 7’-NHCH₃-OLU and 4’-COCH₃-OLU can be found in SI Figs. S11–S12 and S13–S14 respectively.

4. Conclusions

Through a systematic computational study of oxyluciferin analogs with substituent groups at C7’, C5’, and C4’-sites, we found that

• Substitution of EDGs (such as NH₂, NHCH₃, OH groups) at the C7’ position of OLU caused a red shift in the computed emission wavelength, while EWGs (such as NO₂ and CN groups) blue-shifted the emission wavelength. There was a strong correlation between the Hammett parameters σ_p and computed λ_em for the C7’-OLU analogs.

• There was no correlation between σ_p and computed λ_em for the C4’- and C5’-OLU analogs. Most surprisingly, the OLU analog with the NO₂ group at the C4’ position was predicted to emit at a significantly longer wavelength (by 74.9 nm) compared to that of OLU.

• The oo-mixing between the HOMO of the OLU core and the high-lying occupied orbitals of EDGs (such as an amino group) raised the HOMO level and significantly reduced the HOMO-LUMO gap. On the other hand, the vv-mixing between OLU’s LUMO and the lowest-lying virtual orbitals of EWGs (such as a nitro group) lowered the LUMO level and also caused a red-shifted emission.

To summarize, the overall design strategies for fluorophores with red-shifted emission wavelengths are: strong electron-donating groups (such as amino and dimethylamino groups) can be attached to sp² carbon atoms with a substantial contribution to the fluorophore HOMO, whereas strong electron-withdrawing groups (such nitro and cyano groups) to carbon atoms with a considerable LUMO contribution.