Theory of tip structure–dependent microtubule catastrophes and damage-induced microtubule rescues

Significance

Microtubule dynamics are important for numerous cellular processes. However, a complete understanding of the behavior of these polymers is still lacking. Here we combine several kinds of data into a comprehensive model. It suggests that the energy barrier for protofilament straightening may be a destabilizing factor, explaining dependences of catastrophe on microtubule age and tubulin concentration. Modeling indicates that the mechanism of rescue is different from a simple reversal of catastrophe; rescues are very rare in the defect-free microtubule lattice. Experimentally, we find that the rescue frequency and the rate of tubulin incorporation into microtubule lattice are dramatically reduced when microtubules are isolated from the coverslip, suggesting that lattice damage and repair is the dominant mechanism of rescue.

Abstract

Microtubules are essential cytoskeletal polymers that exhibit stochastic switches between tubulin assembly and disassembly. Here, we examine possible mechanisms for these switches, called catastrophes and rescues. We formulate a four-state Monte Carlo model, explicitly considering two biochemical and two conformational states of tubulin, based on a recently conceived view of microtubule assembly with flared ends. The model predicts that high activation energy barriers for lateral tubulin interactions can cause lagging of curled protofilaments, leading to a ragged appearance of the growing tip. Changes in the extent of tip raggedness explain some important but poorly understood features of microtubule catastrophe: weak dependence on tubulin concentration and an increase in its probability over time, known as aging. The model predicts a vanishingly rare frequency of spontaneous rescue unless patches of guanosine triphosphate tubulin are artificially embedded into microtubule lattice. To test our model, we used in vitro reconstitution, designed to minimize artifacts induced by microtubule interaction with nearby surfaces. Microtubules were assembled from seeds overhanging from microfabricated pedestals and thus well separated from the coverslip. This geometry reduced the rescue frequency and the incorporation of tubulins into the microtubule shaft compared with the conventional assay, producing data consistent with the model. Moreover, the rescue positions of microtubules nucleated from coverslip-immobilized seeds displayed a nonexponential distribution, confirming that coverslips can affect microtubule dynamics. Overall, our study establishes a unified theory accounting for microtubule assembly with flared ends, a tip structure–dependent catastrophe frequency, and a microtubule rescue frequency dependent on lattice damage and repair.

Microtubules are hollow cylindrical polymers of tubulin. In most cells, they are composed of 13 laterally connected strands of αβ-tubulin dimers, called protofilaments. Microtubules elongate and shorten intermittently, gaining and losing microns of length (1). This dynamic behavior helps to reorganize the cytoskeleton, changing and maintaining cell shape; it contributes to membrane remodeling, repositioning of organelles, and segregation of duplicated chromosomes during mitosis [reviewed in (2)]. Stochastic switches from microtubule assembly to disassembly are called catastrophes; the reverse switches are called rescues. Changes in catastrophe and rescue frequencies alter the distribution of microtubule lengths in the cell and the localizations of their dynamic tips, which function as force generators and hubs for signaling and adaptor proteins (3). The frequencies of those switches are tightly regulated in the cell to control microtubule dynamics throughout the cell cycle. For example, the rescue frequency is reduced about four- to sevenfold, and the catastrophe frequency is increased about two- to threefold when mammalian somatic cells enter mitosis (4). This change in microtubule dynamics is thought to be critical for chromosome search and capture (5, 6). The rates of catastrophes and rescues are also known to be subject to spatial regulation in cells through protein effectors, which can be differentially recruited to subpopulations of microtubules, for example, by posttranslational tubulin modifications (7, 8).

A classic guanosine triphosphate (GTP) cap model, explaining catastrophes and rescues, posits that microtubules assemble with a stabilizing cap composed of several layers of GTP-bound tubulins; a loss of the stabilizing cap due to GTP hydrolysis or stochastic detachment of the GTP-tubulins from the microtubule tip triggers microtubule catastrophe; rescue occurs as a result of stochastic regain of the GTP cap (9). The existence of the GTP cap and its key role for dynamic instability are supported by extensive evidence from various sources (10–12); the importance of the GTP hydrolysis is also confirmed by numerous experimental observations (13–16). However, after the formulation of the GTP cap model, a body of evidence has been accumulated to suggest that additional factors may also contribute to the mechanisms of microtubule catastrophe and rescue.

There are at least two well-documented experimental observations about microtubule catastrophe that are currently poorly understood: a relatively weak dependence of microtubule catastrophe time on soluble tubulin concentration (17, 18) and the increasing probability of catastrophe over microtubule growth time, known as microtubule aging (19, 20). The weak dependence of catastrophe frequency on tubulin concentration has been hard to explain, as most existing models predict a significant increase in microtubule stability when the polymers acquire longer GTP caps at higher tubulin concentrations [reviewed in (21)]. A dedicated study has emphasized the difficulty of the problem and put forward a long-range through-lattice coupling of tubulins as a possible but rather complex solution (22). The nature of microtubule aging has been also in focus of several studies, which have proposed a set of hypotheses about the process, including the accumulation of irreversible defects of unclear nature, propagating with the growing microtubule end (20, 21), the accumulation of multiple reversible destabilizing features at the growing end (23), or a slow tapering of the microtubule tip (24). Intriguingly, it has been reported that multistep catastrophes could be induced by lattice defects introduced by tubulin-targeting drugs (25). However, the mechanism of this long-range effect and whether the lattice defects can mediate aging in the absence of drugs is not yet clear. None of the existing models for microtubule aging have taken into account recent structural information, indicating that microtubules grow by association of bent GTP-bound tubulin dimers to curved protofilaments at the tip. This concept of microtubule growth is distinct from previously discussed models of microtubule assembly with blunt (26) or sheet-like tips (27, 28), so the analysis of its implications with respect to microtubule transitions between assembly to disassembly may bring novel insights.

The mechanism of microtubule rescue also remains elusive. It is unclear how the GTP cap is regained to stop microtubule disassembly and whether a stochastic acquisition of the GTP cap is the major mechanism of rescue. Important insights into the origin of rescues have come from recent studies of the dynamics of microtubule shafts. It has become increasingly clear that a microtubule wall is not a perfect static lattice, but rather it may have multiple defects and may also incorporate GTP-tubulins from solution, suggesting that the rescue may be caused by external factors rather than a simple reversal of the catastrophe (29–34). Several modeling studies have investigated the effects of GTP islands in the microtubule wall, all suggesting that the latter should serve as an important driver of rescues (34–37). However, it remains unclear whether GTP islands play the major role in the mechanism of rescue or whether this transition can occur without incorporation of tubulin into the microtubule shaft.

Here, we have developed a Monte Carlo model of microtubule dynamics, which is computationally simple and yet detailed enough to account for major structural features of the protofilaments at the dynamic microtubule tips. We show that when our model is parameterized to represent lateral bonds with high activation barriers, accumulation of lagging curved protofilaments at the growing microtubule tips can destabilize these polymers, explaining the age-dependent catastrophes and weak dependence of catastrophe frequency on free tubulin concentration. Rescues are predicted to be very rare unless patches of GTP-tubulin are embedded into the microtubule shaft. Using a modified in vitro assay, in which growing microtubules are isolated from any contact with the surface of the coverslip, we demonstrate that spontaneous rescues are indeed very rare. The rate of incorporation of fluorescently labeled tubulin into the shaft of isolated microtubules is also significantly reduced compared to the conventional microtubule assay, in which microtubule contacts with the surface of the coverslip are possible. These results suggest that microtubule damage and repair is the predominant mechanism of the rescues that have been observed in conventional coverslip-based assays in vitro. We speculate that this mechanism should also play a key role in the crowded environment of living cells.

Four-State Monte Carlo Model of Microtubule Dynamics.

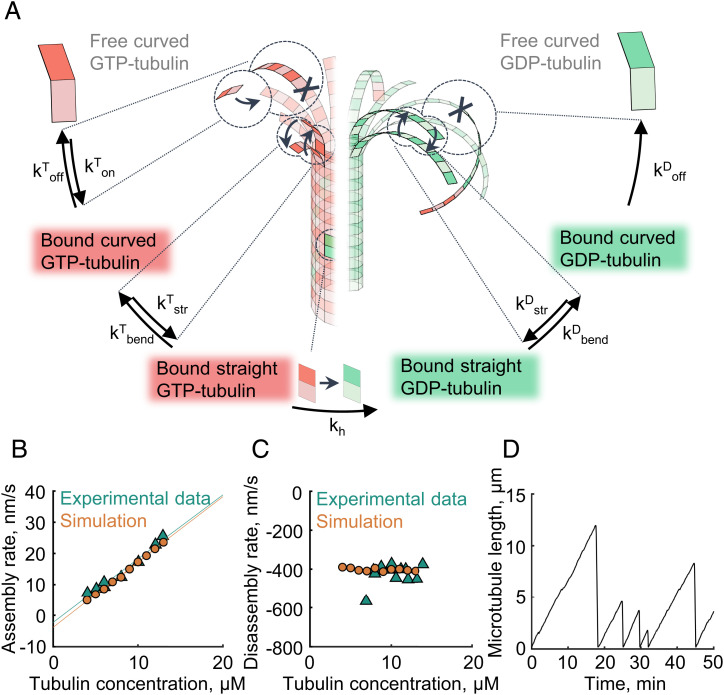
To understand the mechanisms underlying microtubule catastrophes and rescues, in light of the structural findings about the bent shapes of GTP-tubulin dimers in solution (38–40) and the flared appearance of the growing microtubule tip (41–46), we have formulated a four-state Monte Carlo model (Fig. 1A). We introduce two conformational states of the tubulin dimer: 'curved' and ‘straight'. These states are considered in addition to the two nucleotide states (GTP or guanosine diphosphate bound), which were commonly considered in previous two-state models. Overall five possible types of events are permitted in the simulation: longitudinal attachment of a tubulin dimer to the tip of the protofilament; longitudinal breakage of a curved protofilament; tubulin dimer straightening, implying formation of lateral bonds with any adjacent tubulin in the straight state; tubulin dimer bending, implying breakage of all of its lateral bonds with the neighbors, if any; and GTP hydrolysis, which can occur if the tubulin dimer is longitudinally capped by another GTP dimer in the straight state (47, 48). Based on structural data (38, 44, 49) and in contrast to the assumptions of most previous models, we postulate that GTP hydrolysis does not affect the equilibrium curvature of the tubulin protofilament. Rather, it weakens the tubulin dimer’s bonds with adjacent tubulins or increases the bending energy of the interdimer interface. All types of events can occur stochastically, governed by their respective kinetic rate constants (see SI Appendix, Table S1 for complete list of model parameters). We assume thermodynamic equilibria for longitudinal bond formation and breakage and protofilament straightening and bending processes. Therefore, kinetic rate constants, describing those processes, are linked to the free energies of the lateral and longitudinal tubulin–tubulin bonds and the bending energy of tubulin dimers (more details provided in the SI Appendix, Methods).

Fig. 1.

Four-state model of microtubule dynamics. (A) Schematic of the four-state Monte Carlo model. Arrows depict kinetic transitions between the states. Red corresponds to the GTP-bound tubulin states, and green corresponds to the GDP-bound tubulin states. (B) Dependence of microtubule assembly rate on tubulin concentration in the model and published experiments (18). (C) Dependence of the microtubule disassembly rate on tubulin concentration in the model and published experiments (17). (D) Microtubule length versus time in a simulation.

To constrain model parameters, we calibrated the model to reproduce a set of established experimental facts, such as dependences of microtubule growth and shortening rates on soluble tubulin concentration and the average length of curved protofilaments at the tip (Fig. 1 B and C and SI Appendix, Fig. S1). With that parameterization, microtubules elongate in the simulation while their protofilaments rapidly fluctuate between the curved and straight states, due simply to thermal energy. They repeatedly form and break lateral bonds between any consecutive events of longitudinal bond breakage or formation. This assembly mechanism is in agreement with our previous description, using a more detailed Brownian dynamics model, which we used to examine the mechanics and force generation by microtubule tips (50). However, in contrast with the Brownian dynamics simulations, the current four-state Monte Carlo model is computationally simpler and therefore allows the simulation of microtubule dynamics on the time scale of hours, which is necessary to examine relatively rare transitions between growth and shortening phases. Indeed, assuming a plausible rate of GTP hydrolysis (k_hydr ∼ 0.1/s), microtubule catastrophes are readily observed in the simulation with a frequency of one or two events every 10 min, in agreement with experimental data (Fig. 1D).

Results

Kinetically Disfavored Straightening of Lagging Curved Protofilaments May Induce Progressive Raggedness of the Microtubule Tip.

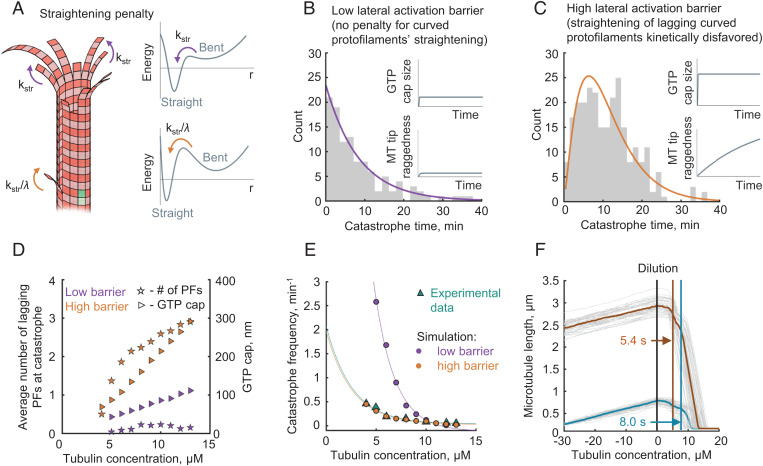
We asked whether the four-state model could provide insights into the age dependence of microtubule catastrophes and their relatively weak sensitivity to soluble tubulin concentration. Following the general idea proposed by Coombes et al. (24), we hypothesized that an evolving configuration of the growing microtubule tip might serve as the second factor, besides GTP-hydrolysis, to foster microtubule destabilization. In the previous models, kinetic penalties for tubulin incorporation were based on the idea of sterically disfavored “bucket” and “corner” positions; these were essential to obtain sufficiently ragged microtubule ends (20, 24, 51). Our model is based on the well-documented presence of flaring protofilaments at the microtubule end, with geometry distinct from that previously considered. Therefore, we reasoned that the raggedness of the tip might instead arise from impeded straightening of curved protofilaments in presence of adjacent protofilaments (Fig. 2A). Such an impediment could originate from the activation energy barriers of the lateral tubulin–tubulin interactions. In other words, curved protofilaments must overcome some repulsion from their adjacent neighbors before a lateral bond can form. This effect might be caused by such factors as electrostatic repulsions between negatively charged tubulins or the energy needed to remove water molecules from the solvated tubulin surfaces before they can form a lateral bond (50). Moreover, a recent molecular dynamics study has suggested that an activation energy barrier in the tubulin–tubulin interaction profile may arise simply as a sum of the protofilament twist–bend deformation energy and the lateral attractive energy potential (52).

Fig. 2.

Possible role of heterogeneous protofilament straightening kinetics for microtubule catastrophe and aging. (A) Schematic showing a lagging curved protofilament and its slower rate of straightening (orange arrows). Straightening of protofilaments in the absence of lateral neighbors occurs without an activation barrier (purple arrows). (B) Distribution of the microtubule growth times until catastrophe in the case of the low activation barrier, λ = 1. Purple solid line represents an exponential fit. The inset schematically shows the dependences of the GTP cap size and the microtubule tip raggedness on the microtubule assembly time. (C) Distribution of the microtubule growth times until catastrophe in the case of the high activation barrier, λ = 105. Orange solid line represents a fit with Gamma-distribution probability density function. The inset schematically shows the dependences of the GTP cap size and microtubule tip raggedness on the microtubule assembly time. (D) Average number of lagging protofilaments at catastrophe (stars, left y axis) and average size of GTP cap size (triangles, right y axis) as functions of tubulin concentration for two model parametrizations: with a high (orange) and a low (purple) lateral activation barrier. The size of the GTP cap was calculated as the average number of GTP-tubulin dimers per protofilament, multiplied by 8 nm. (E) Dependence of the catastrophe frequency on tubulin concentration in simulations with a low barrier (purple) and high barrier (orange) and in the experiment (green) (18). (F) Simulation of tubulin dilution experiment. In the first stage of the simulation (time less than 0), microtubules grow with tubulin concentration 10 µM. At time = 0 s, tubulin concentration is changed to 0. It takes the microtubules a few seconds (delay time) to start a rapid depolymerization. The delay time is 5.4 s for older microtubules (orange average curve), which have been elongating for 160 s from the onset of the simulation. The delay time is 8.0 s for younger microtubules (blue average curve), which have been elongating for 35 s from the onset of the simulation. Gray curves show results of n = 50 individual simulations for each case.

We tested two alternative model parameterizations, with or without kinetic penalties for protofilament straightening, in order to see whether such penalties have any significant impact on microtubule catastrophe in the simulations. The first parameterization represented the low lateral activation barrier case. Here we did not impose any penalty for protofilament straightening in the presence of adjacent protofilaments. We started our analysis by considering the simplest case in which microtubules assemble with GTP hydrolysis switched off (SI Appendix, Fig. S2). These simulations have shown that both the lateral and the longitudinal bonds affect tip raggedness (quantified as the SD of the ends of straight segments of protofilaments). The lateral bonds determined the extent of the tip raggedness at saturation (SI Appendix, Fig. S2A). The longitudinal bonds were the dominant factor determining the kinetics of tip raggedness increase over time (SI Appendix, Fig. S2B). However, switching GTP hydrolysis on with other parameters unchanged almost completely eliminated the raggedness of the tip, making it rather blunt (SI Appendix, Fig. S2 C and D). This happened because small groups of laterally connected protofilaments could no longer efficiently elongate independently, due to the weakening of tubulin–tubulin bonds caused by GTP hydrolysis (Video S1). The lack of evolution of the microtubule tip configuration resulted in a constant probability of catastrophe over time, which was entirely determined by the chance of stochastic rupture of the GTP cap. As a result, the predicted dependence of microtubule lifetimes before catastrophe was exponential, suggesting a single-step catastrophe without aging in this case (Fig. 2B).

Our second model parameterization represented the case of high lateral activation barrier. We varied the kinetic penalty for straightening a curved protofilament in the presence of two longer adjacent protofilaments, λ, and assessed the extent of raggedness of the tip in each case (SI Appendix, Fig. S2E). The simulations revealed that sufficiently high λ values could drive formation of lagging curved protofilaments and make the microtubule tips progressively more ragged over time, even in the presence of GTP hydrolysis (SI Appendix, Fig. S2F). The appearance of the growing tips in these simulations was reminiscent of some microtubule tip structures previously visualized at higher tubulin concentrations via cryoelectron tomography (44, 50).

High Activation Barriers for Lateral Tubulin Interactions Explain Age Dependence of Microtubule Catastrophes and Their Weak Sensitivity to Soluble Tubulin Concentration.

In the simulations with high λ values, lower GTP hydrolysis rates were needed to match the experimentally observed catastrophe rates (SI Appendix, Fig. S3). This happened because the higher raggedness of the growing tip additionally destabilized the GTP cap. The stability of the growing tip depended on both the number of the lagging protofilaments and the extent of their lagging behind others. In the beginning of the microtubule growth cycle, the microtubule tip had a small number of lagging protofilaments, and they were not lagging too far behind, having a higher chance to catch up with the leading protofilaments. This made the younger microtubules more stable than the older ones (SI Appendix, Fig. S4 A and B and Video S2).

We looked for λ values to match experimentally observed microtubule stability and kinetics of the microtubule aging. A kinetic penalty for straightening, λ ∼ 100, was sufficient to reproduce the experimentally observed Gamma-distribution of microtubule lifetimes, a hallmark of microtubule aging (19, 20) (Fig. 2C and SI Appendix, Fig. S4 C and D). As estimated from the Kramers formula for the mean first passage time (53), such a kinetic penalty is equivalent to an activation barrier of about 5 kT (see SI Appendix, Fig. S5 and SI Appendix for more detail). This value does not exceed the previous activation barrier estimates from the analysis of temperature dependence of microtubule dynamics and force development (50, 54).

Importantly, both the number of lagging protofilaments and the GTP cap size increased with tubulin concentration in our simulations (Video S3 and Fig. 2D). As these two factors oppositely contribute to microtubule stability, they buffered the frequency of microtubule catastrophe, explaining the weak dependence of this parameter on tubulin concentration (Fig. 2E). Likewise, with this parameterization, the model quite accurately described the delay times before microtubule catastrophes induced by rapid tubulin dilution (Video S4) (55, 12). It also accounts for the age dependence of that process, explaining why younger microtubules should depolymerize later upon rapid tubulin dilution, compared to older microtubules, polymerized at the same tubulin concentration (56) (Fig. 2F).

Four-State Model Predicts that Spontaneous Rescues Are Rare.

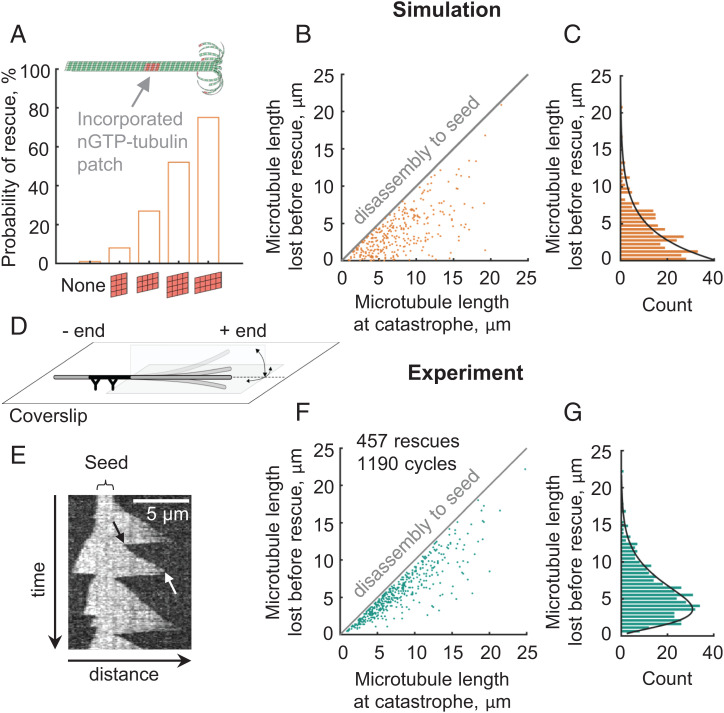
Interestingly, the fully calibrated four-state model predicted a low frequency of spontaneous rescues, ranging from 0 to 0.2/min at tubulin concentrations from 4 to 13 μM. It is important to note, though, that in the simulations we assumed a perfect, defect-free microtubule lattice. However, it had been previously shown that GTP-tubulins can incorporate into a microtubule shaft if the shaft was assembled with some structural defects or it was perturbed by mechanical stress, severing enzymes or motor proteins (29–34, 57, 58). The sites of the lattice repair with GTP-tubulins contribute to microtubule rescue both in cells and in vitro (29, 31, 33, 59). To examine how efficiently the lattice repair sites would promote rescues in our model, we mimicked them with patches of tubulin dimers, containing nonhydrolyzable GTP (nGTP), artificially embedded into microtubule lattice in the simulation. Consistent with some previous modeling studies (35, 36), such nGTP-tubulin patches significantly boosted the rescue probability (Fig. 3A and Video S5). A single patch as small as 4 × 4 nGTP-tubulin dimers could increase the chance of microtubule rescue to about 50% at 10 μM tubulin concentration (Fig. 3A). The simulations also suggest that not only the size but also the geometry of nGTP tubulin patches is important: laterally oriented nGTP-tubulin patches are more efficient in promoting rescues than longitudinally oriented patches of the same size (Fig. 3A).

Fig. 3.

Frequency and positions of microtubule rescues in the four-state model and in a conventional in vitro assay. (A) Probability of microtubule rescue in the simulations, depending on the size and orientation of the nGTP-tubulin patch incorporated into the microtubule shaft, based on n = 100 simulations for each case. (B) Dependence of the rescue positions in the simulations with randomly positioned GTP-islands (5 protofilaments wide × 3 dimers long) on the microtubule length at catastrophe. Microtubules were disassembling from the lengths, distributed as in experimental data (see panel F). (C) Distribution of the microtubule length lost before rescue in the simulations with randomly positioned 5 × 3 dimer nGTP-tubulin patches. Black solid line represents an exponential fit. (D) Schematic of the conventional in vitro assay for observations of microtubule dynamics. (E) Representative kymograph of microtubule dynamics in the conventional assay, visualized with DIC microscopy. The black arrow points to a rescue. The white arrow points to a catastrophe. (F) Dependence of the rescue positions in the conventional in vitro assay on the microtubule length at catastrophe. (G) Distribution of the microtubule length lost before rescue in the conventional in vitro assay. Black solid line represents a fit with Gamma-distribution probability density function.

Conventional In Vitro Assay Reveals that Microtubule Rescues Are Localized Nonrandomly Along the Microtubule Lattice.

When the nGTP-tubulin patches, mimicking the sites of repaired lattice, are randomly positioned along the microtubule shaft, the model predicts an exponential distribution of microtubule length lost between the times of catastrophe and rescue (Fig. 3 B and C). To test this simple prediction, we performed a conventional in vitro assay to visualize and quantify the dynamics of the microtubules, which were assembled from purified bovine brain tubulin (Video S6). Microtubule seeds, stabilized with the GTP analog GMPCPP, were immobilized on a silanized coverslip via antibodies, and the rest of the surface was blocked with a polymer, pluronic F127 (Fig. 3D). Label-free, dynamic extensions of microtubules were imaged with differential interference contrast (DIC) microscopy to analyze the frequency and positions of rescues (Fig. 3E). We gave special care to select for analysis only the microtubules that did not intersect with other microtubules or with any visible debris in the field of view; we also did not process microtubules that exhibited even transient nonspecific sticking to the passivated coverslip, as judged by the change of the extent of their thermal fluctuations. Overall, we observed 457 rescues on 384 microtubules that passed the above criteria. The average rescue frequency was 1.7/min, which is within the wide range of previously reported values (17, 27, 33, 37, 60, 61). However, this value is higher than 0–0.2/min predicted by the four-state model in the absence of nGTP-tubulin patches. Interestingly, we noticed that rescues in the conventional in vitro assay most often occurred closer to the microtubule seed than expected for a random event (Fig. 3F). Thus, the distribution of the microtubule lengths lost after catastrophe and before rescue was nonexponential, strongly suggesting that the positions of these experimental rescues were not random (Fig. 3G). A similar distribution of rescue positions has been also reported recently but not further investigated (37).

Microtubules Isolated From Any Contact With a Coverslip Have a Significantly Lower Frequency of Rescue.

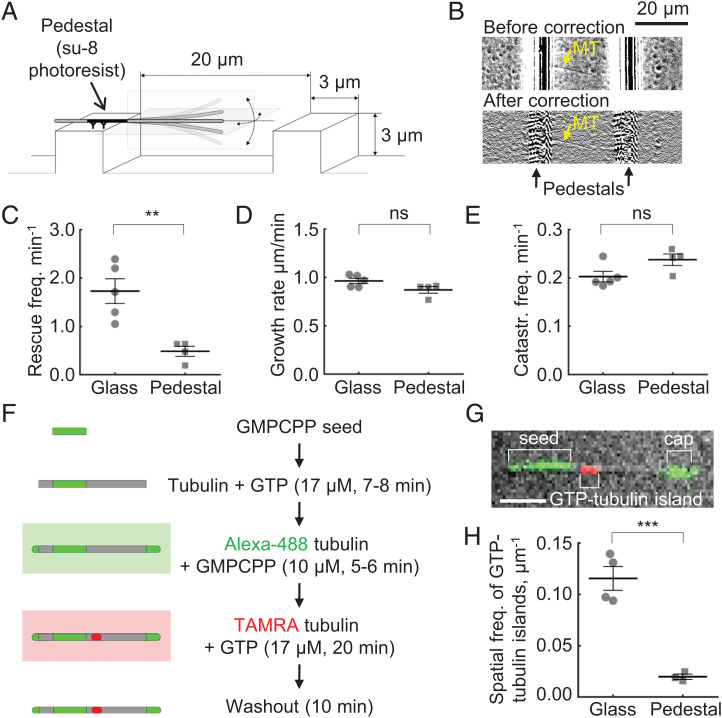
We hypothesized that the peak in the distribution of rescue positions and its shift toward the seed, nucleating the microtubule, could be explained by nonspecific microtubule contacts with the coverslip. It is conceivable that such transient contacts, which might occur despite our efforts to prevent them, could promote microtubule damage and its repair by GTP-tubulins, incorporating into microtubule shaft from solution, or microtubules could stick transiently to the coverslip, and this adhesion might inhibit depolymerization. To eliminate these possibilities, we designed a modified in vitro assay to isolate microtubules from any interaction with the coverslip. For that, periodic 3 × 3 μm pedestals were microfabricated from SU-8 photoresist on the coverslip, via photolithography (Fig. 4A). The micropedestals were separated from each other by 20 μm gaps, so the dynamic extensions of microtubules, growing from the pedestal-attached GMPCPP seeds, were well separated from a surface of the coverslip. We visualized microtubule dynamics with DIC microscopy, applying a custom-developed algorithm to process the collected stacks of images and to construct kymographs along the microtubules overhanging from the micropedestals (Fig. 4B and SI Appendix, Figs. S6 and S7 and Video S7). Comparison of microtubule dynamics in this modified assay and the conventional coverslip-based assay revealed no differences in the microtubule growth rates or catastrophe frequencies. However, the rescue frequency of microtubules isolated from the coverslip was dramatically lower than that of the conventional assay (Fig. 4 C–E and SI Appendix, Fig. S8 A and B). In the rare instances when two microtubules occasionally crossed each other, we observed rescues at their intersections (Video S8), suggesting that the imaging quality in our modified assay was sufficient to detect the rescues in the cases when they were expected. There were not many events of this kind (and they were excluded from analysis), as we deliberately tried to design the experiments in the way that would avoid microtubule crossings. In order to further verify that the markedly reduced rescue frequency was not due to imaging limitations in the vicinity of the pedestal edge, we carried out observations of microtubule dynamics in presence of the end-binding protein, EB1, and a microtubule stabilizing drug, paclitaxel. These conditions were selected to boost microtubule rescue frequency and thereby shift the rescue positions away from the pedestal edge for better visualization of the microtubule tip dynamics. As expected from published work (62), the combination of EB1 and paclitaxel elevated catastrophe and rescue frequencies in the conventional assay on the surface of the coverslip (SI Appendix, Figs. S8C and S9 A–C and Video S9). The distribution of the microtubule length lost between the times of catastrophe and rescue shifted away from the microtubule seeds and became close to exponential, suggesting that the rescue sites in presence of EB1 and paclitaxel were positioned randomly (SI Appendix, Fig. S9D). However, in the pedestal assay we still observed very few rescues (SI Appendix, Fig. S9 D and C and Video S10). Most microtubules clearly depolymerized to the seed (SI Appendix, Figs. S8D and S9 C and D). The absence of rescues in the presence of EB1 and paclitaxel in the pedestal assay was surprising to us, but this observation is consistent with the proposition that although paclitaxel converts lattice damage into rescue sites when the microtubules are assembled on the coverslip (59), it cannot efficiently induce rescue sites in the isolated microtubules, whose lattice is probably more intact.

Fig. 4.

Quantification of microtubule dynamics and GTP incorporation in the pedestal assay. (A) Schematic of the modified assay, in which microtubules are nucleated from the seeds, overhanging from microfabricated pedestals. (B) Dynamic microtubule (marked with a yellow arrow) in the pedestal assay, imaged with DIC. The same field of view is shown before and after a flare correction algorithm was applied. (C) Average rescue frequency in the conventional (coverslip) and modified (pedestal) assays. Each point corresponds to an independent experiment. (D) Average microtubule growth rate in the conventional (coverslip) and modified (pedestal) assays. Each point corresponds to an independent experiment. (E) Average catastrophe frequency in the conventional (coverslip) and modified (pedestal) assays. Each point corresponds to an independent experiment. (F) Schematic of the experiments for quantification of GTP-tubulin incorporation into the microtubule shaft. (G) Representative image of a microtubule, nucleated from Alexa-488-labeled GMPCPP seed (green), stabilized with an Alexa-488-labeled GMPCPP cap (green) and an incorporated TAMRA-5-labeled tubulin island (red). The image represents on overlay of DIC and two fluorescent channels. Scale bar is 3 μm. (H) Quantification of the probability to observe an incorporated island per microtubule length unit in the conventional (coverslip) assay versus the modified (pedestal) assay. Microtubule dynamics in the conventional and pedestal assays were compared with a two-sided unpaired t test; ns, difference not significant; *P < 0.05; ***P < 0.001.

Overall, we conclude that the rescue frequency of the microtubules, isolated from the contacts with the surface of the coverslip, is low and close to the values predicted by the four-state Monte Carlo model.

Proximity of Microtubules to the Coverslip Promotes Incorporation of Soluble Tubulin Into the Microtubule Shaft.

To examine how the proximity of the coverslip affects microtubule damage and repair with GTP-tubulin incorporating into microtubule shaft, we nucleated microtubules from Alexa-488-labeled GMPCPP-tubulin seeds, which were immobilized either on a conventional flat coverslip or on SU-8 pedestals. Microtubules were first polymerized from the seeds in the presence of unlabeled GTP-tubulin and then capped by the addition of Alexa-488 GMPCPP tubulin (Fig. 4F). Next, the capped microtubules were washed with a buffer containing tetramethylrhodamine (TAMRA)-labeled GTP tubulin and incubated for 18–20 min to allow its incorporation into microtubule lattice. The flow chamber was then washed with a buffer containing no tubulin, and the microtubules were imaged with DIC and two epifluorescence channels to visualize the microtubule seed, the shaft, the cap and any incorporated patches of TAMRA-tubulin (Fig. 4G). Consistent with our expectation, the TAMRA-tubulin indeed incorporated into microtubule shaft with a significantly higher rate in the conventional assay compared to the pedestal assay (Fig. 4H and SI Appendix, Fig. S10 A and B). By visualizing TAMRA-labeled GMPCPP caps, we checked in control experiments that this difference could not be explained by a slightly different sensitivity of the fluorescence detection in the two assays (SI Appendix, Fig. S10 C–E).

Discussion

The four-state Monte Carlo model formulated here provides a computationally simple framework to analyze microtubule dynamics on the time scale relevant for analysis of relatively rare events, such as catastrophes and rescues. In contrast to the previous dimer-scale Monte Carlo models (22, 63–65), the additional curvature dimension of the four-state model enables explicit description of the protofilament straightening and bending behavior at the microtubule tip. Using the Brownian dynamics approach, we previously argued that the thermally driven transitions of tubulin dimers from the bent to the straight configuration are important for microtubule assembly (50). For isolated protofilaments such transitions are very fast, on the order of megahertz. However, the presence of lateral interactions between adjacent protofilaments in a microtubule is expected to slow them down. Here we show with the four-state Monte Carlo model that kinetically disfavored straightening of curved protofilaments in the presence of straight adjacent neighbors promotes microtubule tip raggedness, thereby destabilizing microtubule growth. This finding explains several enigmatic observations about microtubule catastrophes: the aging phenomenon (19, 20), the weak dependence of catastrophe frequency on tubulin concentration (17, 61), and the age dependence of the delays before microtubule depolymerization after a rapid decrease in soluble tubulin concentration (12, 55). Thus, lagging protofilaments emerge in our model as the second major factor besides the GTP hydrolysis determining microtubule catastrophes. A possible role of the evolving tip configuration in microtubule stability was initially proposed based on the models of microtubule assembly with straight protofilaments at the tip (20, 24, 23). However, we suggest a different scenario of the tip evolution here, taking into account the flared morphology of the growing microtubule end seen in some recent structural studies. Some fairly dramatic instances of microtubule tip raggedness have been also documented via electron cryotomography (50). However, the missing wedge problem in electron tomography has precluded an exhaustive characterization of the lagging curved protofilaments as a function of tubulin concentration to date. It is possible that in real microtubules, lagging curved protofilaments promote a switch in the number of protofilaments of the microtubule either via a collapse in the region with missing protofilaments, leading to a lattice with fewer protofilaments, or as a result of insertion of more than one protofilament into the gap, leading to a lattice with more protofilaments. Both cases are likely to lead to some accumulated stress, promoting microtubule destabilization (25).

Our model emphasizes the importance of the lateral activation barrier for tubulin–tubulin interactions as the origin of microtubule tip raggedness. The existence of substantial lateral activation barriers is supported by a significant temperature sensitivity of microtubule assembly and disassembly (54, 66, 67). Moreover, the lateral activation energy barriers are essential for the ability of microtubules to develop high pulling forces during depolymerization (50). Our results highlight a possibility that the lateral activation barrier may be modulated by microtubule-associated proteins (MAPs) to control microtubule catastrophes. For example, TOG (tumor overexpressed gene) domain-containing polymerases, which bind to tubulins in their curved conformation (39), and end-binding proteins, which associate between two adjacent protofilaments (68), are well positioned to affect the activation barrier for the lateral bond formation, thereby increasing catastrophe frequency (69, 70).

Some interesting predictions of the four-state model include an increased raggedness of the microtubule tip (Fig. 2D) and a saturated microtubule growth rate that should be observed at high tubulin concentrations (SI Appendix, Fig. S11A). The first of these predictions is in line with the evidence from electron cryomicroscopy, which had revealed a correlation between the microtubule tip taper and tubulin concentration (27). The second prediction is supported by the previously documented signs of saturation of microtubule assembly rate at high tubulin on-rates, in the presence of MAPs and crowding agents (71). This is consistent with our conclusion that the growth rate could become limited by the rate of lateral bond formation rather than the rate of longitudinal tubulin association to the tips of curved protofilaments from solution (SI Appendix, Fig. S11B). Analogous measurements with pure MAP-free tubulin in the future would provide a clearer test for the model. To date, however, it has been challenging to achieve sufficient microtubule assembly rates in the absence of MAPs, because microtubules nucleate spontaneously at high tubulin concentrations. Interestingly, we have also found that the fully calibrated four-state model recapitulates the effect of the GTP hydrolysis rate on the variance of microtubule growth, a phenomenon recently documented in vitro by comparing microtubules polymerized in presence of GTP and its nonhydrolyzable analog, GMPCPP (72). For example, when microtubules are simulated to elongate at a 10 nm/s assembly rate, they exhibit an approximately threefold difference in the extent of the growth fluctuations depending on the GTP hydrolysis rate (38.8 ± 0.7 nm²/s with k_hydr = 0.09/s; 13.4 ± 0.4 nm²/s with k_hydr = 0/s, data are mean ± SEM), in decent agreement with the published data (72).

Rescues have been the “dark side” of microtubule dynamics, because of the technical difficulties of observing these transitions; they occur with a relatively low frequency, and there is a poorly understood lack of reproducibility of results between different studies, leading to at least an order of magnitude of scatter in the rescue frequency measurements (17, 27, 33, 37, 60, 61). A number of studies have established that microtubule lattice repair sites, containing GTP tubulins, will form when the lattice is deformed, is in contact with intersecting objects, or is damaged by laser irradiation or severing enzymes; these structures potently drive rescues both in vitro and in cells (30–34). It has been tricky, however, to visualize the incorporation of GTP-tubulins into the lattice without artificially inducing it or affecting microtubule dynamics. The best available GTP-tubulin-binding probes, such as end-binding proteins (12, 73) and antibodies against GTP-tubulin (29), suffer from relatively slow binding–unbinding kinetics and may themselves affect GTP hydrolysis or alter microtubule dynamics. Therefore, computational modeling remains among the few valuable tools to interrogate the relationship between lattice damage, its repair and microtubule dynamics. In our current four-state Monte Carlo model, for the sake of simplicity, we neither permitted dissociation of tubulin subunits from the microtubule shaft nor considered their incorporation into the shaft from solution. The model in its current form also does not allow an explicit description of any kind of structural defects in the microtubule lattice, such as changes of the number of protofilaments or the helical pitch. We envision that lifting these limitations in the future will be important for elucidating the origin of the lattice damage and repair sites. However, even in the current formulation, our model points to a major role of the lattice-incorporated GTP-tubulins in the mechanism of microtubule rescue, suggesting that defect-free microtubule shafts should experience barely any rescues. This prediction seems at odds with the fact that microtubule rescues can be observed in vitro. However, we have resolved this contradiction experimentally by finding that the rescue frequency and incorporation of GTP tubulins into microtubule lattice from solution are dramatically reduced when microtubules are assembled from the seeds overhanging from microfabricated pedestals, being well separated from the coverslip, in contrast to a conventional in vitro assay. This implies that in the conventional in vitro assay, measurements of the rescue frequency depend on the coverslip surface preparation, at least partially explaining a large variance in existing experimental estimates of the rescue frequencies. We find that rescues are rare for the isolated microtubules, at the lower end of the range of published reports (8, 33, 37). We speculate that promoting lattice defects and their repair through incorporation of GTP-tubulins into the microtubule shaft may be the dominant mechanism for rescues in the crowded environment of the cell, where microtubules intersect with other cytoskeletal elements and organelles (29, 31, 74) and the lattice defects may be modulated by severing enzymes (33) or even motor proteins (57, 75).

Materials and Methods

Computational Modeling.

Detailed description of the model and its calibration is provided in the SI Appendix, Methods section. A full list of model parameters is given in SI Appendix, Table S1. The simulations were carried out in MATLAB 2017b. Program code is available at https://github.com/ngudimchuk/Four_State_MT_model.

Experimental Procedures.

Tubulin was isolated from bovine brain through thermal cycling (76) and labeled with Alexa-488-SE (Invitrogen), TAMRA-5-SE (Lumiprobe), and digoxigenin-SE (Invitrogen) as described in (77). EB1-eGFP-6His protein was expressed in Escherichia coli, purified via affinity chromatography, and filtered through a 200 kDa column before snap-freezing to remove possible aggregates (Advantec). Stable microtubule seeds were polymerized in the presence of GMPCPP (Jenna Biosciences). For conventional in vitro assay, a flow chamber was assembled from a silanized coverslip, incubated with anti-digoxigenin antibodies (Roche), and blocked with Pluronic F127. In the modified in vitro assays, instead of the silanized coverslips we used coverslips with microfabricated pedestals (3 µm high, 3 µm wide, and 20 µm apart). The pedestals were manufactured from SU-8 photoresist, via photolithography as described in SI Appendix, Methods. The flow chamber was perfused with a solution of GMPCPP seeds to immobilize them on the pedestals in the orientation parallel to the flow (150 µL/min). To image microtubule dynamics, a solution of 17 μM tubulin was introduced into the flow chamber. In experiments, described in SI Appendix, Figs. S8 C and D and S9, the solution was additionally supplemented with 100 nM EB1-eGFP-6His and 9 nM paclitaxel to boost the rescue frequency. Nine to 15 fields of view were imaged at 0.07–0.1 fps with DIC microscopy using a Nikon Ti microscope, equipped with an Andor iXon3 camera. To quantify the incorporation of GTP tubulin into microtubule shaft, microtubules, polymerized in the conventional or pedestal assay for 7–8 min, were capped in presence of 10 μM Alexa488-tubulin and 2 mM GMPCPP for 5–6 min. Next, a solution with 17 μM TAMRA-5-SE tubulin was introduced into the flow chamber for 18–20 min. Microtubules were imaged in the green and red fluorescent channels and DIC. Collected data were analyzed in ImageJ. Custom scripts were developed to correct for flare near the pedestals for quantification microtubule dynamics and tubulin incorporation into the microtubule shaft (see SI Appendix, Methods). All experiments were done at 32 °C in the buffer, containing 80 mM K-Pipes pH 6.8, supplemented with 1 mM MgCl₂, 1 mM ethylene glycol-bis(β-aminoethyl ether)-N,N,N′,N′-tetraacetic acid, 5 mg/mL bovine serum albumin, 0.08 mg/mL catalase, 0.1 mg/mL glucose oxidase, 12 mg/mL glucose, 1 mM DTT, 0.5% β-mercaptoethanol, and 2 mM Mg-GTP (except for the cases when Mg-GTP was substituted for GMPCPP). Additional details on experimental procedures and analysis are provided in the SI Appendix, Methods section.

Data, Materials, and Software Availability

All study data are included in the article and/or supporting information.